- Department of Evolutionary Studies of Biosystems, School of Advanced Sciences, SOKENDAI (The Graduate University for Advanced Studies), Hayama, Japan
In social evolution theory, unconditional cooperation has been seen as an evolutionarily unsuccessful strategy unless there is a mechanism that promotes positive assortment between like individuals. One such example is kin selection, where individuals sharing common ancestry and therefore having the same strategy are more likely to interact with each other. Conditional cooperation, on the other hand, can be successful if interactions with the same partners last long. In many previous models, it has been assumed that individuals act conditionally on the past behavior of others. Here I propose a new model of conditional cooperation, namely the model of coordinated cooperation. Coordinated cooperation means that there is a negotiation before an actual game is played, and that each individual can flexibly change their decision, either to cooperation or to defection, according to the number of those who show the intention of cooperation/defection. A notable feature of my model is that individuals play an actual game only once but can still use conditional strategies. Since such a negotiation is cognitively demanding, the target of my model here is exclusively human behavior. I have analyzed cultural evolutionary dynamics of conditional strategies in this framework. Results for an infinitely large population show that conditional cooperation not only works as a catalyst for the evolution of cooperation, but sustains a polymorphic attractor with unconditional cooperators, unconditional defectors, and conditional cooperators being present. A finite population analysis is also performed. Overall, my results provide one explanation of why people tend to take into account others' decisions even when doing so gives them no payoff consequences at all.
1. Introduction
Prevalence of altruistic traits in nature has been an evolutionary paradox since Darwin (1859). It is because defectors, also called cheaters or free-riders, avoid the cost of cooperation but enjoy its benefit, and hence act detrimentally against evolution of cooperation. Now there is a consensus among evolutionary biologists that positive assortment is a key to its evolution (Lehmann and Keller, 2006; Nowak, 2006b; West et al., 2007; Fletcher and Doebeli, 2009). Positive assortment means cooperators are more likely to meet and interact with other cooperators than by chance, and so are defectors.
A viscous population (Hamilton, 1964; Taylor, 1992; Wilson et al., 1992) provides an excellent occasion for such positive assortment to occur. Limited dispersal creates an environment where those who share the common ancestry tend to cluster in a spatially structured population. In such a situation, whether kin recognition is present or not, cooperation with neighbors tends to result in cooperation with another cooperator. This process is known as kin selection.
In contrast, conditional cooperation is another mechanism to achieve positive assortment (Fletcher and Doebeli, 2009). The success of the famous Tit-for-Tat strategy (Axelrod and Hamilton, 1981; Nowak and Sigmund, 1992) and other variants (Nowak and Sigmund, 1993) suggests that helping only those who have helped in the past (Trivers, 1971; Axelrod, 1984; Alexander, 1987; Nowak and Sigmund, 2005) is a strong driving force for the evolution of cooperation. In these cases, positive assortment does not necessarily mean genetic assortment but means behavioral assortment; whatever different genetic architecture is behind cooperation, those who behave cooperatively at a phenotypic level come together and interact with each other.
A vast majority of previous models of evolution of conditional cooperation has assumed repeated interactions, where the same group of individuals interact repeatedly, or, in the case of indirect reciprocity, one repeatedly interacts with different others, but their past history of actions is available as reputation. In either case, it is a well established fact that a long repetition is a key to success (Nowak, 2006b).
However, an experiment suggests that people behave conditionally on others' choices even in a one shot interaction (Fischbacher et al., 2001). In their four-player public goods game experiment, Fischbacher et al. (2001) asked each of the four players to submit a contribution table, which describes how much one would like to contribute to a public good for all 21 possible average contributions by the other three players. If one assumes that everyone should behave rationally, two predictions follow. Firstly, the best choice is to contribute nothing irrespective of others' decisions. Secondly, and more interestingly, there should be no incentives at all to base one's contribution on others', because the game used in that experiment was a linear public goods game. To understand the second point more, here is the payoff function used in their experiment;
where πi is the payoff of i-th player, and 0 ≤ gj ≤ 20 is j-th player's contribution to a public good. This functional form clearly suggests that for each additional unit amount of contribution, i-th player loses 0.6 units irrespective of others' decisions and hence that taking others into account makes no sense. Despite these predictions, Fischbacher et al. (2001) found that a significant fraction of participants made a positive contribution in this experiment, and that 50% of participants were “conditional cooperators” who monotonically increased their contribution with increased average contribution by the others. Interestingly, they also found the existence of “unconditional defectors” who persistently contributed nothing.
The experiment by Fischbacher et al. (2001) suggests that people have strong preference to coordinate their behavior with others, if possible, even in a one-shot interaction. One may think that a one-shot interaction in the real world is truly “one-shot” in the sense that no communication outside the game is allowed, but it is not necessarily true. There is sometimes a stage of negotiation or discussion by the participants before the actual game is played, where they talk with each other and can coordinate their behavior. One good example is international negotiation about the global climate change, where many hours of discussion are performed before participants finally decide whether or not to cooperate (Smead et al., 2014).
The aim of this paper is to explicitly model the process of negotiation that occurs prior to the game to understand its potential role in the evolution of cooperation. In that sense, my model is specific to human behavior because it is hard to imagine that non-human animals are engaged in negotiation before social interactions. I am in particular interested in whether it explains the emergence and maintenance of conditional cooperators in a linear public goods game. As a result of my analysis, I find that conditional cooperators and unconditional ones are sustained in the population through frequency dependent selection for a wide range of parameters. I will also discuss my model limitations in Discussion.
2. Model
2.1. Public Goods Game
I study a linear public goods game played by n(≥ 2) players. Each player ultimately chooses one action, either cooperation (hereafter abbreviated as C) or defection (abbreviated as D). Each cooperator pays the cost c for a public good, but defectors do not. The total payment is aggregated, multiplied by the factor r, and equally redistributed to the participants of the game irrespective of their contribution to the public good. Therefore, when there are k cooperators and n − k defectors in the game, their payoffs are given respectively as
When one pays the cost c, it yields the net benefit of rc to the group. Equivalently, for each additional contribution c, each individual obtains the benefit of rc/n. Hereafter I assume 1 < r < n such that contribution to the public good is beneficial to a group (i.e., rc > c) but not to an individual (i.e., rc/n < c).
2.2. Strategies
In order to consider coordinated actions by players, here I assume that players in the game possess a conditional strategy. More specifically, a player refers to the actions of the other n − 1 players and conditions its own action (C or D) on the number of cooperators among those n − 1 players. Because the number of cooperators excluding self can be either 0, 1, …, or n − 1 (= n possibilities), a conceivable strategy takes the form of an n-digit sequence of letters of C or D, the k-th letter (1 ≤ k ≤ n) of which corresponds to the action prescribed by that strategy when the number of cooperators excluding self is exactly equal to k − 1. For example, CCC…CC is the strategy that always prescribes cooperation irrespective of others' actions, which is so called ALLC strategy. The strategy DDD…DD always defects, so it is called ALLD strategy. Of course more complicated strategies are possible; for example, the strategy CDCDCD… prescribes cooperation when the number of cooperators excluding self is even, and defection when odd. There are 2n possible strategies in total.
Out of all conceivable strategies, I especially pay attention to simple ones; those which have a minimum threshold level for cooperation. In other words, I consider strategies in the form of
The strategy represented by Equation (3) cooperates when the number of cooperators excluding self is at least k, otherwise defects. Let us call this strategy Ck. Obviously C0 is the ALLC strategy and Cn is the ALLD strategy. In between are strategies that cooperate only if some others cooperate. In other words, the index number k represents the degree of resistance against cooperation. In the following I will consider only those (n + 1) strategies, from C0 to Cn.
2.3. How Negotiation Proceeds
Since players condition their actions on other players' actions, which in turn are dependent on other players' actions, it is not straightforward to predict the final consequence of the game interaction. Therefore I model the negotiation stage prior to the actual game in the following way. First, to each of the n players, his/her initial thought, either C or D, is assigned by some specific rule. Here, thought means one's temporal but not final decision, which is observable to everyone, but does not affect one's payoff at all. It is instructive to imagine, for example, n human agents at a negotiation table. Those agents simultaneously announce their initial thoughts, and therefore I can assume that perceiving others' thoughts is easy and costless. A combination of all players' thought, that is usually expressed by an n-tuple of C or D, is called a state. Given an initial state in the negotiation stage, a player is randomly chosen, and is given an opportunity to change his/her thought, from C to D, or from D to C, if his/her conditional strategy prescribes so. For example, if a C3 strategist, currently having thought C, finds only two other C's in the group, he/she changes his/her thought to D, because he/she needs at least three other C players to keep his/her current thought to play C. This change of his/her thought is announced to everyone. In the next step, a player is randomly chosen again for an update, and this procedure is repeated until no one wants to change his/her thought. I call such a final state stationary state. In Section A in the Supplementary Material I prove that there always exists at least one stationary state, so this negotiation surely ends. However, multiple stationary states are possible, and which stationary state is reached depends on players' initial thought and the order of updates. Once a stationary state is reached, all players transform their thought to an actual action in the public goods game, they obtain payoffs, and the game ends. Here I exclude the possibility of lying (that is, one takes the opposite action to his/her thought at the stationary state in the negotiation), and this point will be discussed more in Discussion.
2.4. Example
To facilitate a better understanding of the model, consider an example of the three-person game played by individuals X, Y, and Z. Suppose that X and Y adopt strategy C1 while Z adopts strategy C2. Below I will represent the temporal thought of those three players by a triplet, such as (X, Y, Z) = (D, C, C).
Suppose that the initial state is (D, C, C). If players chosen randomly in the first four update steps are Y, Z, X, and Z in this order, the following state transition occurs;
In the first step Y is chosen. Y finds there is one cooperator, Z, and that satisfies his threshold. Therefore Y does not change his thought. In the second step Z is chosen. Z finds there is one cooperator, Y, but that does not satisfy his threshold. Therefore Z changes from C to D. In the third step, X is chosen. X finds that there is one cooperator, Y, and that satisfies his threshold. Therefore X changes from D to C. In the fourth step, Z is chosen. In contrast to the second step, Z finds two cooperators, X and Y, which satisfies his threshold. Therefore Z changes from D to C. It is easy to see that (C, C, C) is a stationary state for them. Thus they play an actual public goods game, all of them pay the cost of cooperation, and enjoy the benefit from the public good.
It is notable that in the transition shown in Equation (4), individual Z made two changes, from D to C and from C to D. Such a transition is possible depending on the order of updates. In addition, it is not difficult to see that (D, D, D) is another stationary state. For example, if players randomly chosen in the first two steps are Z and Y in this order, the following transition occurs, leading to no cooperation.
2.5. Initial State
As I have seen above, initial states have a great impact on the consequence of negotiation. Players may have predisposition either toward C or D, but here I assume that each player independently has initial thought C with probability p, and initial thought D with probability 1 − p. When p = 0, it means that the default action is D. This is true when cooperation takes the form of active contribution; cooperation means doing something and defection means doing nothing. For example, monetary investment to a public good often takes this form. In contrast, p = 1 means that the default action is C. This is true when defection takes the form of active exploitation; defection means doing something and cooperation means doing nothing. Forest conservation can be a good example of this. Cutting trees and selling timber is exploitative defection, whereas not cutting trees is passive cooperation. Therefore I cannot necessarily set the value of p a priori. Instead, I treat p as my model parameter.
Another rationale behind the parameter p, especially when it is between 0 and 1, is that it reflects some uncertainty in the game. It could be the case that players do not perfectly know the payoff structure of the game at the beginning, in which case they may temporarily choose either one of the actions.
Although the value of p can possibly be chosen independently and strategically by different strategies, here I assume for simplicity that p is common among all the strategies. Therefore p is not an evolutionary trait but a model constant in this paper.
2.6. Population Game and Evolutionary Dynamics
So far I have explained the public goods game played by n players, but I will also consider a population of players. Suppose that there is a population of players of size M (either infinitely large or finite). For each public goods game n players are randomly chosen from the population, they play a one-shot public goods game with a negotiation stage described above, and return to the population. Such n-person games are played many times, and each individual obtains an average payoff per game, which I will denote by w.
Time change of frequencies of strategies can be studied by evolutionary dynamics, which are based on a simple criterion that successful strategies increase in frequency. Note that equations of evolutionary dynamics can describe both genetic evolution, in which information is transmitted through genetic materials, and cultural evolution, in which information such as ideas or norms can be transmitted culturally, in a quite similar form (Traulsen et al., 2009, 2010); here it is natural to consider cultural evolution. For an infinitely large population, M = ∞, the evolutionary dynamics of (n + 1) strategies, from C0 to Cn are described by the replicator equation (Taylor and Jonker, 1978; Hofbauer and Sigmund, 1998; Nowak, 2006a);
where xk and wk are the frequency and the average payoff of strategy Ck, respectively. The average payoff in the population, , is calculated as . The dynamics is defined in the n-dimensional simplex, Sn+1, where xk's are non-negative and they sum up to unity.
For a finite population, M < ∞, a frequency-dependent Moran process (Nowak et al., 2004) and pairwise comparison processes (Traulsen et al., 2005, 2007) are standard models to describe its evolutionary dynamics. Similarly to the infinite population case, players are engaged in many n-person games and obtain average payoffs. In each elementary step of updating, two players are randomly chosen from the population (with replacement). The first player compares his payoff with that of the second player. Let Δ be the payoff of the second player minus that of the first. Then the first player copies the strategy of the second player with probability
otherwise he stays with the current strategy. Here, the parameter s > 0 is called intensity of selection (or inverse temperature). The functional form of Equation (7) comes from the Fermi distribution function in physics (Traulsen et al., 2006, 2007), so this process is sometimes referred to as Fermi process (Traulsen and Hauert, 2009). Equation (7) suggests that the first player is more likely to copy the strategy of the second player if the payoff difference, Δ, is larger.
Because of a finite population size, once all players adopt the same strategy, no other strategies can invade the population. Such a phenomenon is called fixation. In order to avoid fixation of strategies, I consider mutation in strategies. With a positive probability, μ > 0, the first player who is chosen in an elementary step of updating changes his strategy to another random strategy, irrespective of the payoff difference, Δ. Under the limit of μ → 0, a newly arising mutant in a resident population either goes to extinct or takes over the whole population before a next mutant arises. Such limit is sometimes referred to as adiabatic limit (Sigmund et al., 2010, 2011). In the adiabatic limit only possible transitions are those from one monomorphic population to another, so fixation probabilities between two strategies characterize the process (see Section B in the Supplementary Material).
3. Two-Person Game
3.1. Payoffs
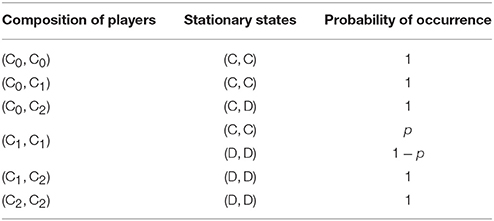
First I study the n = 2 person game. Let ak,ℓ be the payoff of a Ck player matched with a Cℓ player. There are six different types of encounters, (C0, C0), (C0, C1), (C0, C2), (C1, C1), (C1, C2), and (C2, C2). It is easy to confirm that the stationary state of each encounter except (C1, C1) is unique. According to Table 1, payoffs are
On the other hand, the encounter (C1, C1) needs consideration. There are two stationary states, (C, C) and (D, D). If the initial state is (C, C) (which occurs with probability p2) or (D, D) (which occurs with probability (1 − p)2), it is already a stationary state. If the initial state is (C, D) or (D, C) (which occurs with probability 2p(1 − p)), however, who updates first matters. If the one with thought C is chosen for an update, he changes to D and mutual defection results. If the one with thought D is chosen for an update, he changes to C and mutual cooperation results. These chances are even. Therefore, for the encounter (C1, C1), the probability that they arrive at mutual cooperation is , and that of mutual defection is . As a result, I obtain
To summarize, I have obtained the following payoff matrix of the game;
3.2. Infinite Population
Evolutionary game dynamics based on the payoff matrix, Equation (9), are shown in Figure 1 for the three separate cases, (a) p = 0, (b) 0 < p < 1, and (c) p = 1.
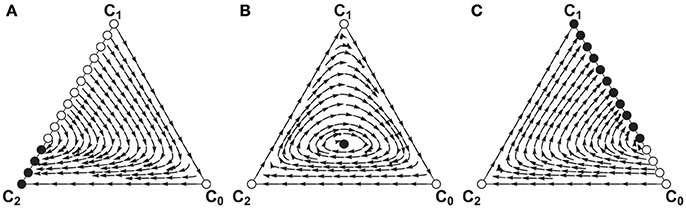
Figure 1. Replicator dynamics of the two-person game played in an infinitely large population. (A) When p = 0, (B) when 0 < p < 1, and (C) when p = 1. Filled circles represent Lyapunov stable equilibria, whereas open circles represent unstable ones. Parameter: r = 1.6.
Firstly I look at the two extreme cases. When p = 0 (see Figure 1A), everyone initially chooses defection. Therefore no cooperation arises unless there is at least one C0 player. Obviously C1 is invaded by C0, which in turn is invaded by C2. In the absence of C0 strategy, C1 and C2 are neutral. There is a continuum of fixed points on the C1-C2 edge, a part of the segment including the C1 corner consists of unstable fixed points; introduction of C0 players drives the population away from these fixed points. The other segment including the C2 corner consists of stable fixed points. Its mirror image is obtained when one considers the case of p = 1 (Figure 1C), where C2 invades C0 but it is invaded by C1. The C0-C1 edge consists of unstable and stable segments.
Dynamics are in between these extreme cases when 0 < p < 1 (see Figure 1B). There is an internal fixed point and myriads of closed orbits surround it. Strategy C1 invades the population of C2, which is invaded by C0, which is invaded by C2. The edges of the simplex constitute a heteroclinic cycle. The frequencies of strategies at the internal fixed point is given as
It is worthwhile to mention that the two-player game dynamics are equivalent to the dynamics of ALLC, ALLD, and Tit-For-Tat (TFT) strategies in a repeated Prisoner's Dilemma game (Brandt and Sigmund, 2006; Sigmund, 2010). To see this, consider a two-person Prisoner's Dilemma game with the following payoff matrix;
where C is the cost and B is the benefit of cooperation, and consider a repeated game of this Prisoner's Dilemma with a discounting factor, δ. ALLC players always cooperate. ALLD players always defect. TFT players cooperate in the first round, and then imitate whatever the opponent did in the previous round. I also consider errors; I assume that an erroneous defection occurs with probability (1 − k)ϵ when one intends cooperation, and that an erroneous cooperation occurs with probability kϵ when one intends defection. Let A′ be the payoff matrix of this repeated game, each pivot representing a payoff per round. In the double limit of δ → 1 and then ϵ → 0, it turns to be
which is formally equivalent to Equation (9) with the transformation of B ≡ rc/2, C ≡ c − (rc/2) and k ≡ p (see Figure 3 of Brandt and Sigmund, 2006). This correspondence makes sense, because the negotiation stage in my model can be interpreted as hypothetical rounds of the repeated game where payoffs are not counted. The limit δ → 1 means that I count only payoffs in future rounds after a stationary state is reached.
I also find differences between the two models. In my model, players' thought is updated asynchronously such that at most one player can change his thought (C to D, or D to C) in one updating event. In contrast, players in the repeated game change their actions (C to D, or D to C) in a synchronous fashion; each player takes into account the previous action by the partner. Another difference is that, while errors are not assumed in my model, the model of the repeated game does consider erroneous defection and cooperation. It is interesting that my parameter p, that is the probability that initial intension is C, correspond exactly to the parameter k in the repeated game model, which represents the fraction of erroneous cooperation among all erroneous moves.
3.3. Finite Population
To simplify the analysis, I consider the adiabatic limit, μ → 0, and strong selection, s → ∞. More precisely speaking, I first take the limit μ → 0 and then take the limit s → ∞.
Under the adiabatic limit, the population is almost always monomorphic in strategies. Therefore I can consider the stationary distribution over the three strategies; namely how much proportion of time the stochastic game dynamics spends at each monomorphic state. Let qk (k = 0, 1, 2) represent the fraction of time that the stochastic process spends at the monomorphic population of strategy Ck. Calculations in Section C in the Supplementary Material show that for M ≥ 3, the following result holds;
Computer simulations confirm the validity of this result (Figure 2). To understand the significance of the result, it is instructive to consider a traditional framework of social dilemma, where only C0 and C2 strategies are possible. In this case, irrespective of the value of p, the stationary distribution of the Fermi process under the adiabatic limit and strong selection is
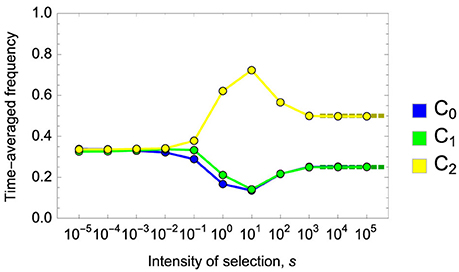
Figure 2. Time-averaged frequencies of strategies in the Fermi process for the two-person game for various intensity of selection, s. Dark-colored dotted lines in the right show the stationary distribution of strategies, , predicted by Equation (13) for the adiabatic limit. Note that there is a considerable overlap between blue (strategy C0) and green (strategy C1) dots and lines. When s is close to zero, each strategy has approximately the frequency of one third. Parameters: M = 36, p = 0.5, r = 1.5 and c = 1.0. Mutation rate was set to μ = 10−4 per elementary updating step. M elementary steps constitute one generation. Time average was taken over 108 generations.
Equation (13) thus suggests that the existence of coordinated cooperators, C1, has a great impact on evolutionary dynamics. For 0 < p < 1, unconditional cooperation (C0) is attained a quarter of the time during evolution. This is because a C1 mutant in the population of C2 players has 50% chance of fixation; once a C1 player replicates to two by chance, those two C1 players have a positive (=p) chance of establishing mutual cooperation and thus they can outcompete C2 players. However, C1 players are invaded by C0 players, because a dyad of C1 players sometimes fail to establish mutual cooperation, which is disadvantageous compared with C0. Obviously C0 is invaded by C2, and such an evolutionary cycle repeats. In other words, coordinated cooperators C1 work as a catalyst of cooperation. If they exist, sociality is promoted and rationality is hindered.
Such an effect is much more dramatic when p = 1. In this case strategies C0 and C1 are completely neutral to each other, and the only difference between them is whether or not they can establish mutual cooperation in the population of C2 without being cheated. In fact, strategy C0 is easily exploited by C2 but C1 is not. Therefore, for a large M, the population is dominated by C1 most of the time.
4. Three-Person Game
4.1. Payoffs
Next I consider the n = 3 person game. Let ak,ℓ1ℓ2 be the payoff of a Ck player matched with a Cℓ1 player and a Cℓ2 player. Obviously ak,ℓ1ℓ2 = ak,ℓ2ℓ1 holds. In the three-person game with four different strategies from C0 to C3 there are 20 possible encounters, which are listed up in Table 2. For each case, the probability with which negotiation reaches each possible stationary state is calculated (see Section D in the Supplementary Material). As a result I arrive at the following payoff matrix;
Because I assume random matching of players, the average payoff of a Ck player is calculated as
where xℓ represents the frequency of Cℓ players in the population.
4.2. Infinite Population
As before I consider the replicator equation, Equation (6). Since the payoff is already quadratic in x, as in Equation (16), the resulting replicator dynamics are highly non-linear. As a result, I have to largely rely on numerical simulations to study the whole dynamics. However, the evolutionary dynamics restricted on either of the six edges of the simplex S4 are rather easy to study, because they are essentially reduced to a one-dimensional system.
I will hereafter consider when 0 < p < 1. The analysis in Section E in the Supplementary Material shows that behavior on four of the six edges is straightforward; C2 increases on the C3-C2 edge, C1 increases on the C2-C1 edge, C0 increases on the C1-C0 edge, and C3 increases on the C0-C3 edge. Therefore, there always exists a heteroclinic cycle connecting the four vertices of the simplex: C3 → C2 → C1 → C0 → C3. As for the C0-C2 edge, if
holds there exists one unstable equilibrium (which I hereafter call P02) and the system shows bistability. If r is smaller than 3/2, strategy C2 dominates C0. If r is greater than (3 + 3p)/(1 + 2p), strategy C0 dominates C2.
On the C1-C3 edge, in contrast, if
holds there exists one stable equilibrium (which I hereafter call Q13) and the system allows the coexistence of the two strategies. If r is smaller than 3/2, strategy C3 dominates C1. If r is greater than (6 − 3p)/(3 − 2p), strategy C1 dominates C3.
Numerical simulations suggests that when r < 3/2 the dynamics either converge to a trimorphic equilibrium or an evolutionary cycle with strategies C1, C2 and C3 present but C0 absent (see Figure 3). When r > 3/2, the outcome of evolutionary dynamics seems to rely on the stability of the dimorphic rest point, Q13. It is possible to show that Q13 is always stable against the invasion of C2. However, it is stable against the invasion of C0 only when r is below some threshold, rc = rc(p). When 3/2 < r < rc the system converges to the dimorphic equilibrium, Q13, with strategies C1 and C3 present. When r > rc, the system converges to a trimorphic equilibrium with strategies C0, C1 and C3 present but C2 absent. Figure 3 shows the phase diagram in the (p, r)-space according to this classification as well as long term consequences of evolutionary dynamics. It is easy to see there that the instability/stability of Q13 accurately predicts whether strategy C0 is present or absent after a long run.
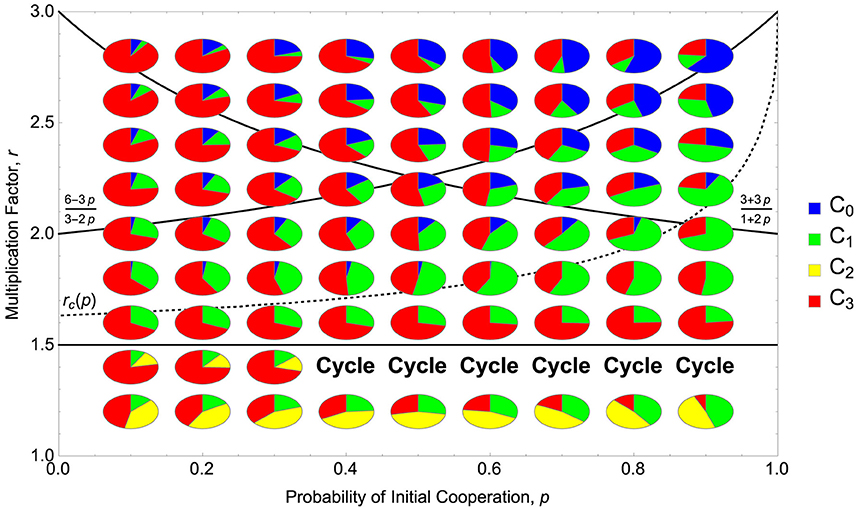
Figure 3. Long-term consequences of replicator dynamics of the three-person game in an infinitely large population. Numerical calculations were performed from the initial condition in which all the four strategies were equally abundant (frequency = 1/4). If dynamics converge to a fixed point, its composition of strategies is shown by a small pie chart. “Cycle" means that the dynamics do not converge but show stable oscillation among three strategies, C1, C2, and C3. The three solid lines represent r = 3/2, (6 − 3p)/(3 − 2p) and (3 + 3p)/(1 + 2p), respectively. The dotted line represents r = rc(p), above which the unstable equilibrium Q13 is not robust against the invasion of C0. Parameters studied: p ∈ {0.1, 0.2, …, 0.8, 0.9} and r ∈ {1.2, 1.4, …, 2.6, 2.8}.
4.3. Finite Population
As before I consider the adiabatic limit and strong selection. The analysis for an infinite population above showed that a coexisting equilibrium (Q13) can exist on the C1-C3 edge. In this case a C1 mutant appearing in the finite population of C3 or vice versa is highly likely to lead the population to a stable mixture of C1 and C3, and the population will be trapped for a considerably long time there. Nevertheless stochasticity eventually causes either one of the strategies to fixate in the population, and the assumption of the adiabatic limit guarantees that no second mutation occurs before the first mutant either disappears or fixates in the population.
Section F in the Supplementary Material shows the full analysis of the Fermi process. For 0 < p < 1, I find that the stationary distribution differs between the four parameter regions shown in Figure 4. Similarly to section 3.3, let qk (k = 0, 1, 2, 3) be the fraction of time that the Fermi process spends at the monomorphic population of strategy Ck in the stationary distribution. For a large M, the following result holds;
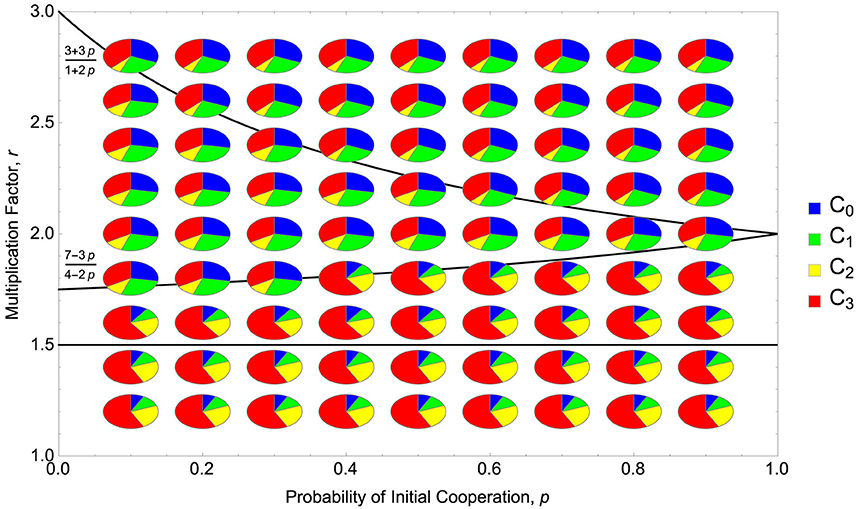
Figure 4. A stationary distribution of the Fermi process of the three-person game in a finite population of size M(≫1). Each small pie chart represents how much fraction of time the Fermi process stays at each monomorphic state. The three solid lines represent r = 3/2, (7 − 3p)/(4 − 2p) and (3 + 3p)/(1 + 2p), respectively. Parameters studied: p ∈ {0.1, 0.2, …, 0.8, 0.9} and r ∈ {1.2, 1.4, …, 2.6, 2.8}.
Compare this result with the result of a conventional model that allows only C0 and C3, which is
Obviously the existence of strategies C1 and C2 dramatically increases the possibility of cooperation. For example, Equation (19) states that evolution favors strategies other than full defection (C3) 62.5% of the time when r is large. Remember that without C1 and C2 full defection (C3) prevails over full cooperation (C0) because the former exploits the benefit yielded by the latter. However, as I saw in section 4.2, strategies C1 and C2 always create an invasion path of C3 → C2 → C1 → C0. Additionally, when r is large there are other invasion paths, such as C3 → C2 → C0 and C3 → C1 → C0. These paths contribute to the evolutionary success of more cooperative strategies. I have confirmed the validity of the analytical results [Equation (19)] by computer simulations for parameters that do not allow the existence of stable equilibrium Q13 in the corresponding infinite population model (Figures 5, 6). Note that when Q13 exists and when the population size M is large, it takes enormous time to numerically confirm Equation (19) due to the reason described in the beginning of this subsection. Analyses for the cases of p = 0 and p = 1 are found in Section F in the Supplementary Material.
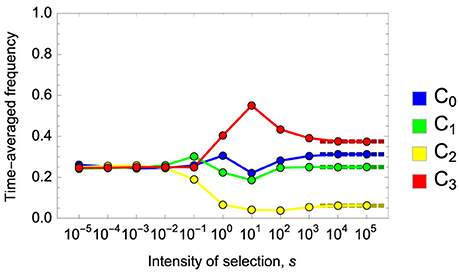
Figure 5. Time-averaged frequencies of strategies in the Fermi process for the three-person game for various intensity of selection, s. Dark-colored dotted lines in the right show the stationary distribution of strategies, , predicted by Equation (19) for the adiabatic limit. When s is close to zero, each strategy has approximately the frequency of one fourth. Parameters: M = 36, p = 0.5, r = 2.5 and c = 1.0. Mutation rate was set to μ = 10−4 per elementary updating step. M elementary steps constitute one generation. Time average was taken over 108 generations.
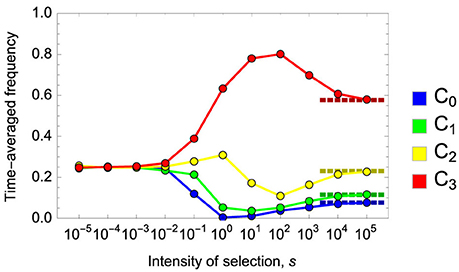
Figure 6. Time-averaged frequencies of strategies in the Fermi process for the three-person game for various intensity of selection, s. Multiplication factor is set to r = 1.25. The other parameters are the same as in Figure 5. The predicted stationary distribution under the adiabatic limit is in this case.
5. Discussion
This paper explicitly models the process of negotiation among players, including conditional cooperators, to study its evolutionary consequences. There is much similarity between my model here and previous models of repeated games. In particular, my strategy Ck, which changes his/her own thought to cooperation if and only if k or more than k others show the thought of cooperation, corresponds to strategy Ta proposed by Boyd and Richerson (1988), which cooperates in the next round of the repeated Prisoner's Dilemma game if and only if a or more than a others play cooperation in the current round. A very similar formulation is also found in Segbroeck et al. (2012), where their RM strategy cooperates if M or more than M individuals (including self) cooperated in the previous round. Two major differences between the current model and those previous models are; that (i) only the final state of negotiation affects one's payoff in my model whereas each round of the repeated game yields a payoff to players in the models of Boyd and Richerson (1988) and Segbroeck et al. (2012), and that (ii) players update their thought asynchronously in the negotiation stage in my model whereas all players update their actions synchronously in Boyd and Richerson (1988) and Segbroeck et al. (2012). Conditional cooperators in my model can detect unconditional defectors during negotiation at no cost and avoid being exploited by them, while conditional cooperators in Boyd and Richerson (1988) and Segbroeck et al. (2012) can detect unconditional defectors only after being exploited by them in the first round of the repeated game and hence detection of unconditional defectors is costly there (compare Figures 2, 3 of Brandt and Sigmund, 2006 to understand how the payoff in the first round qualitatively changes evolutionary dynamics). Similar phenomena, though the modeling framework is quite different from the current one, were found in the continuous-time, two-player “coaction” model by van Doorn et al. (2014), where the authors found that (i) real time coaction in response to partner's behavior (analogous to my negotiation stage) generally favors cooperation but that (ii) once delay in information about the behavior of one's partner is introduced, as is often the case with discrete-round repeated Prisoner's Dilemma games, achieving cooperation becomes more difficult. Therefore, the introduction of a negotiation stage, if the possibility of lying is suppressed by some mechanism such as punishment (Sigmund et al., 2010; Quiñones et al., 2016) or ostracism (Nakamaru and Yokoyama, 2014), contributes to enhancing the efficiency of conditional cooperation.
It is notable that my model explains the presence of conditional cooperation not as an evolutionarily stable strategy (ESS). For example, a classical ESS analysis of the Tit-For-Tat strategy (Axelrod and Hamilton, 1981) predicts that everyone should adopt conditional cooperation at an evolutionary equilibrium. However, recent experiments strongly suggest that there is wide variation in behavior among people (Fischbacher et al., 2001; Martinsson et al., 2013). My analysis here, in contrast, predicts evolutionary coexistence of many types of players. In fact, I have found, for both two-player and three-player games and in both infinite and finite population analyses, that the existence of conditional cooperators creates a cycle of invasion, in which unconditional defectors are invaded by conditional cooperators, which are invaded by unconditional cooperators, which are then invaded by unconditional defectors. As a result, cooperation is sustained to some degree in the population. Note that, although my model predicts such cyclical invasion over time, it should be best interpreted as the possibility of polymorphism, because the evolutionary model here inevitably simplifies other factors of human decision making. A similar evolutionary cycle has been found in Segbroeck et al. (2012). Conditional cooperators work as an evolutionary catalyst; they create an evolutionary advantage of being a cooperator, and self-sustain their presence in the population. This is quite in contrast to a population with unconditional defectors and unconditional cooperators only, where defection is a dominating strategy.
As mentioned in the Model section, my negotiation model makes a very strong assumption; that players can never change the action (i.e., never tell a lie) once the negotiation reaches a stationary state. It can be understood such that players make a commitment before the game is actually played. Recently, a series of papers analyzed the effect of such pre-commitments on evolution of cooperation (Han et al., 2013, 2015a,b, 2017a,b; Sasaki et al., 2015; Han and Lenaerts, 2016) and found that pre-commitments were effective in enhancing cooperation. Those works typically assume that players can choose whether they make a costly commitment before the game. If one breaks the commitment he or she has to pay a fine. It has been shown that a large fine enhances the success of commitment strategies (Han et al., 2013, 2015a, 2017a). Another possible way to suppress those who make a fake commitment would be to exclude them from other games in the future. I have not modeled these “outside-game” possibilities in this paper but have concentrated on describing the one-shot negotiation game.
Among those papers on pre-commitments, Han et al. (2017a) has notable similarity to my current model, because both study public goods games and consider conditional cooperators who are keen to the behavior of others in the group. Through a finite population game dynamics analysis, Han et al. (2017a) essentially found a similar evolutionary cycle, from unconditional defectors to conditional cooperators, then to unconditional cooperators, and then to unconditional defectors again. In contrast, there is a remarkable difference between these two models. In my model players make “commitments” to cooperate or to defect depending on the number of other cooperators and defectors during a process of dynamic negotiation. In the model of Han et al. (2017a), however, all players except pure defectors first do make commitments to cooperate, and then count the number of committers to see if this number exceeds their threshold to actually play the public goods game.
My model does not rely on the mechanism of direct reciprocity in the sense that the same individuals do not have to interact repeatedly. This feature is shared by models of generalized reciprocity (Hamilton and Taborsky, 2005; Pfeiffer et al., 2005; Chiong and Kirley, 2015), where individuals make decisions based on the previous encounter with other group members. A driving force of evolution of generalized reciprocity is assortment of cooperative strategies (Rankin and Taborsky, 2009) based on contingent movement of individuals between groups (Hamilton and Taborsky, 2005), a small group size (Pfeiffer et al., 2005) (but see Barta et al. (2011), where random drift helps generalized reciprocity to overcome initial disadvantage in a large group), or network structure (van Doorn and Taborsky, 2012). Generalized reciprocity has been proposed as a mechanism that does not require high cognitive ability, and hence is applicable to cooperation by non-human animals (Rutte and Taborsky, 2007; Schneeberger et al., 2012; Leimgruber et al., 2014; Gfrerer and Taborsky, 2017) as well as empathy-based cooperation by humans (Bartlett and DeSteno, 2006; Stanca, 2009). In contrast, a driving force of cooperation in my model is coordination of behavior based on negotiation and pre-commitments. Therefore, its scope of application is rather cognition-based cooperation (and defection), which characterizes another aspect of human sociality (Knoch et al., 2006; Baumgartner et al., 2011; Ruff et al., 2013; Yamagishi et al., 2016).
A technical advantage of employing the finite population analysis is that, in contrast to replicator dynamics analysis for an infinitely large population where outcomes can be dependent on initial conditions and many complexities can arise due to high dimensionality, it can predict a stationary probability distribution that is independent of initial conditions. There is limitation in my analysis based on the adiabatic limit and strong selection, though, because mutation rate must be unrealistically low for the Fermi process to reach either end of the C1-C3 edge (i.e., fixation of one strategy) despite the tendency of evolutionary coexistence of those two strategies due to negative frequency-dependent selection. Nevertheless, I believe that this methodology can give us some insights that would not have been derived by replicator dynamics analyses.
There is a growing interest in studying negotiation processes to see how flexibility in behavior shapes an evolutionary outcome (McNamara et al., 1999; McNamara, 2013; Quiñones et al., 2016; Ito et al., 2017). My negotiation model here is such an attempt to reveal the origin of conditional cooperators and to explain why we observe both cooperation and defection in the real world.
Author Contributions
The author confirms being the sole contributor of this work and approved it for publication.
Funding
This work was supported by JSPS KAKENHI (JP25118001, JP25118006, JP16H06324) to HO.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2018.00062/full#supplementary-material
References
Axelrod, R., and Hamilton, W. (1981). The evolution of cooperation. Science 211, 1390–1396. doi: 10.1126/science.7466396
Barta, Z., McNamara, J. M., Huszár, D. B., and Taborsky, M. (2011). Cooperation among non-relatives evolves by state-dependent generalized reciprocity. Proc. R. Soc. B 278, 843–848. doi: 10.1098/rspb.2010.1634
Bartlett, M. Y., and DeSteno, D. (2006). Gratitude and prosocial behavior: helping when it costs you. Psychol. Sci. 17, 319–325. doi: 10.1111/j.1467-9280.2006.01705.x
Baumgartner, T., Knoch, D., Hotz, P., Eisenegger, C., and Fehr, E. (2011). Dorsolateral and ventromedial prefrontal cortex orchestrate normative choice. Nat. Neurosci. 14, 1468–1474. doi: 10.1038/nn.2933
Boyd, R., and Richerson, P. J. (1988). The evolution of reciprocity in sizable groups. J. Theor. Biol. 132, 337–356. doi: 10.1016/S0022-5193(88)80219-4
Brandt, H., and Sigmund, K. (2006). The good, the bad and the discriminator – errors in direct and indirect reciprocity. J. Theor. Biol. 239, 183–194. doi: 10.1016/j.jtbi.2005.08.045
Chiong, R., and Kirley, M. (2015). Promotion of cooperation in social dilemma games via generalised indirect reciprocity. Connect. Sci. 27, 417–433. doi: 10.1080/09540091.2015.1080226
Fischbacher, U., Gächter, S., and Fehr, E. (2001). Are people conditionally cooperative? Evidence from a public goods experiment. Econ. Lett. 71, 397–404. doi: 10.1016/S0165-1765(01)00394-9
Fletcher, J. A., and Doebeli, M. (2009). A simple and general explanation for the evolution of altruism. Proc. R. Soc. B 276, 13–19. doi: 10.1098/rspb.2008.0829
Gfrerer, N., and Taborsky, M. (2017). Working dogs cooperate among one another by generalised reciprocity. Sci. Rep. 7:43867. doi: 10.1038/srep43867
Hamilton, I. M., and Taborsky, M. (2005). Contingent movement and cooperation evolve under generalized reciprocity. Proc. R. Soc. B 272, 2259–2267. doi: 10.1098/rspb.2005.3248
Hamilton, W. (1964). The genetical evolution of social behaviour, I & II. J. Theor. Biol. 7, 1–52. doi: 10.1016/0022-5193(64)90038-4
Han, T. A., and Lenaerts, T. (2016). A synergy of costly punishment and commitment in cooperation dilemmas. Adapt. Behav. 24, 237–248. doi: 10.1177/1059712316653451
Han, T. A., Pereira, L. M., and Lenaerts, T. (2015a). Avoiding or restricting defectors in public goods games? J. R. Soc. Interface 12:20141203. doi: 10.1098/rsif.2014.1203
Han, T. A., Pereira, L. M., and Lenaerts, T. (2017a). Evolution of commitment and level of participation in public goods games. Auton. Agent. Multi Agent Syst. 31, 561–583. doi: 10.1007/s10458-016-9338-4
Han, T. A., Pereira, L. M., Martinez-Vaquero, L. A., and Lenaerts, T. (2017b). Centralized versus personalized commitments and their influence on cooperation in group interactions, in Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence (AAAI-17) (San Francisco, CA: The AAAI Press), 2999–3005.
Han, T. A., Pereira, L. M., Santos, F. C., and Lenaerts, T. (2013). Good agreements make good friends. Sci. Rep. 3:2695. doi: 10.1038/srep02695
Han, T. A., Santos, F. C., Lenaerts, T., and Pereira, L. M. (2015b). Synergy between intention recognition and commitments in cooperation dilemmas. Sci. Rep. 5:9312. doi: 10.1038/srep09312
Hofbauer, J., and Sigmund, K. (1998). Evolutionary Games and Population Dynamics. Cambridge: Cambridge University Press.
Ito, K., McNamara, J., Yamauchi, A., and Higginson, A. (2017). The evolution of cooperation by negotiation in a noisy world. J. Evol. Biol. 30, 603–615. doi: 10.1111/jeb.13030
Knoch, D., Pascual-Leone, A., Meyer, K., Treyer, V., and Fehr, E. (2006). Diminishing reciprocal fairness by disrupting the right prefrontal cortex. Science 314, 829–832. doi: 10.1126/science.1129156
Lehmann, L., and Keller, L. (2006). The evolution of cooperation and altruism. A general framework and classification of models. J. Evol. Biol. 19, 1365–1378. doi: 10.1111/j.1420-9101.2006.01119.x
Leimgruber, K. L., Ward, A. F., Widness, J., Norton, M. I., Olson, K. R., Gray, K., et al. (2014). Give what you get: capuchin monkeys (cebus apella) and 4-year-old children pay forward positive and negative outcomes to conspecifics. PLoS ONE 9:e87035. doi: 10.1371/journal.pone.0087035
Martinsson, P., Pham-Khanh, N., and Villegas-Palacio, C. (2013). Conditional cooperation and disclosure in developing countries. J. Econ. Psychol. 34, 148–155. doi: 10.1016/j.joep.2012.09.005
McNamara, J. M. (2013). Towards a richer evolutionary game theory. J. R. Soc. Interface 10:20130544. doi: 10.1098/rsif.2013.0544
McNamara, J. M., Gasson, C. E., and Houston, A. I. (1999). Incorporating rules for responding into evolutionary games. Nature 401, 368–371. doi: 10.1038/43869
Nakamaru, M., and Yokoyama, A. (2014). The effect of ostracism and optional participation on the evolution of cooperation in the voluntary public goods game. PLoS ONE 9:e108423. doi: 10.1371/journal.pone.0108423
Nowak, M., and Sigmund, K. (2005). Evolution of indirect reciprocity. Nature 437, 1291–1298. doi: 10.1038/nature04131
Nowak, M. A. (2006a). Evolutionary Dynamics. Cambridge, MA: Belknap Press, Harvard University Press.
Nowak, M. A. (2006b). Five rules for the evolution of cooperation. Science 314, 1560–1563. doi: 10.1126/science.1133755
Nowak, M. A., Sasaki, A., Taylor, C., and Fudenberg, D. (2004). Emergence of cooperation and evolutionary stability in finite populations. Nature 428, 646–650. doi: 10.1038/nature02414
Nowak, M. A., and Sigmund, K. (1992). Tit for tat in heterogeneous populations. Nature 355, 250–253. doi: 10.1038/355250a0
Nowak, M. A., and Sigmund, K. (1993). A strategy of win-stay, lose-shift that outperforms tit for tat in prisoner's dilemma. Nature 364, 56–58. doi: 10.1038/364056a0
Pfeiffer, T., Rutte, C., Killingback, T., Taborsky, M., and Bonhoeffer, S. (2005). Evolution of cooperation by generalized reciprocity. Proc. R. Soc. B 272, 1115–1120. doi: 10.1098/rspb.2004.2988
Quiñones, A. E., van Doorn, G. S., Pen, I., Weissing, F. J., and Taborsky, M. (2016). Negotiation and appeasement can be more effective drivers of sociality than kin selection. Philos. Trans. R. Soc. B 371:20150089. doi: 10.1098/rstb.2015.0089
Rankin, D. J., and Taborsky, M. (2009). Assortment and the evolution of generalized reciprocity. Evolution 63, 1913–1922. doi: 10.1111/j.1558-5646.2009.00656.x
Ruff, C. C., Ugazio, G., and Fehr, E. (2013). Changing social norm compliance with noninvasive brain stimulation. Science 342, 482–484. doi: 10.1126/science.1241399
Rutte, C., and Taborsky, M. (2007). Generalized reciprocity in rats. PLoS Biol. 5:e196. doi: 10.1371/journal.pbio.0050196
Sasaki, T., Okada, I., Uchida, S., and Chen, X. (2015). Commitment to cooperation and peer punishment: its evolution. Games 6, 574–587. doi: 10.3390/g6040574
Schneeberger, K., Dietz, M., and Taborsky, M. (2012). Reciprocal cooperation between unrelated rats depends on cost to donor and benefit to recipient. BMC Evol. Biol. 12:41. doi: 10.1186/1471-2148-12-41
Segbroeck, S. V., Pacheco, J. M., Lenaerts, T., and Santos, F. C. (2012). Emergence of fairness in repeated group interactions. Phys. Rev. Lett. 108:158104. doi: 10.1103/PhysRevLett.108.158104
Sigmund, K., De Silva, H., Traulsen, A., and Hauert, C. (2010). Social learning promotes institutions for governing the commons. Nature 466, 861–863. doi: 10.1038/nature09203
Sigmund, K., Hauert, C., Traulsen, A., and De Silva, H. (2011). Social control and the social contract: the emergence of sanctioning systems for collective action. Dyn. Games Appl. 1, 149–171. doi: 10.1007/s13235-010-0001-4
Smead, R., Sandler, R. L., Forber, P., and Basl, J. (2014). A bargaining game analysis of international climate negotiations. Nat. Clim. Change 4, 442–445. doi: 10.1038/nclimate2229
Stanca, L. (2009). Measuring indirect reciprocity: whose back do we scratch? J. Econ. Psychol. 30, 190–202. doi: 10.1016/j.joep.2008.07.010
Taylor, P. (1992). Altruism in viscous populations – an inclusive fitness model. Evol. Ecol. 6, 352–356. doi: 10.1007/BF02270971
Taylor, P., and Jonker, L. (1978). Evolutionary stable strategies and game dynamics. Math. Biosci. 40, 145–156. doi: 10.1016/0025-5564(78)90077-9
Traulsen, A., Claussen, J. C., and Hauert, C. (2005). Coevolutionary dynamics: from finite to infinite populations. Phys. Rev. Lett. 95:238701. doi: 10.1103/PhysRevLett.95.238701
Traulsen, A., and Hauert, C. (2009). Stochastic evolutionary game dynamics, in Reviews of Nonlinear Dynamics and Complexity, Vol. 2, ed H. G. Schuster (Weinheim: Wiley-VCH Verlag GmbH & Co. KGaA), 25–62.
Traulsen, A., Hauert, C., De Silva, H., Nowak, M. A., and Sigmund, K. (2009). Exploration dynamics in evolutionary games. Proc. Natl. Acad. Sci. U.S.A. 106, 709–712. doi: 10.1073/pnas.0808450106
Traulsen, A., Nowak, M. A., and Pacheco, J. M. (2006). Stochastic dynamics of invasion and fixation. Phys. Rev. E 74:011909. doi: 10.1103/PhysRevE.74.011909
Traulsen, A., Pacheco, J. M., and Nowak, M. A. (2007). Pairwise comparison and selection temperature in evolutionary game dynamics. J. Theor. Biol. 246, 522–529. doi: 10.1016/j.jtbi.2007.01.002
Traulsen, A., Semmann, D., Sommerfeld, R. D., Krambeck, H.-J., and Milinski, M. (2010). Human strategy updating in evolutionary games. Proc. Natl. Acad. Sci. U.S.A. 107, 2962–2966. doi: 10.1073/pnas.0912515107
Trivers, R. (1971). The evolution of reciprocal altruism. Q. Rev. Biol. 46, 35–57. doi: 10.1086/406755
van Doorn, G. S., Riebli, T., and Taborsky, M. (2014). Coaction versus reciprocity in continuous-time models of cooperation. J. Theor. Biol. 356, 1–10.
van Doorn, G. S., and Taborsky, M. (2012). The evolution of generalized reciprocity on social interaction networks. Evolution 66, 651–664. doi: 10.1111/j.1558-5646.2011.01479.x
West, S., Griffin, A., and Gardner, A. (2007). Evolutionary explanations for cooperation. Curr. Biol. 17, R661–R672. doi: 10.1016/j.cub.2007.06.004
Wilson, D., Pollock, G., and Dugatkin, L. (1992). Can altruism evolve in purely viscous populations? Evol. Ecol. 6, 331–341. doi: 10.1007/BF02270969
Keywords: conditional cooperation, evolutionary game theory, negotiation, replicator dynamics, finite population
Citation: Ohtsuki H (2018) Evolutionary Dynamics of Coordinated Cooperation. Front. Ecol. Evol. 6:62. doi: 10.3389/fevo.2018.00062
Received: 28 September 2017; Accepted: 30 April 2018;
Published: 23 May 2018.
Edited by:
Tatsuya Sasaki, F-Power Inc., JapanReviewed by:
The Anh Han, Teesside University, United KingdomMichael Taborsky, Universität Bern, Switzerland
Xiaojie Chen, University of Electronic Science and Technology of China, China
Copyright © 2018 Ohtsuki. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hisashi Ohtsuki, b2h0c3VraV9oaXNhc2hpQHNva2VuLmFjLmpw
 Hisashi Ohtsuki
Hisashi Ohtsuki