- Terrestrial Ecology Unit (TEREC), Department of Biology, Ghent University, Ghent, Belgium
Decision-making under uncertain conditions favors bet-hedging (avoidance of fitness variance), whereas predictable environments favor phenotypic plasticity. However, entirely predictable or entirely unpredictable conditions are rarely found in nature. Intermediate strategies are required when the time lag between information sensing and phenotype induction is large (e.g., transgenerational plasticity) and when cues are only partially predictive of future conditions. Nevertheless, current theory regards plasticity and bet-hedging as distinct entities. We here develop a unifying framework: based on traits with binary outcomes like seed germination or diapause incidence we clarify that diversified bet-hedging (risk-spreading among one’s offspring) and transgenerational plasticity are mutually exclusive strategies, arising from opposing changes in reaction norms (allocating phenotypic variance among or within environments). We further explain the relationship of this continuum with arithmetic mean maximization vs. conservative bet-hedging (a risk-avoidance strategy), and canalization vs. phenotypic variance in a three-dimensional continuum of reaction norm evolution. We discuss under which scenarios costs and limits may constrain the evolution of reaction norm shapes.
Introduction
Changing conditions can promote evolutionary change in various ways (Botero et al., 2015; Tufto, 2015). One commonly envisioned mode of evolution is the continuous change of trait means as result of changing mean conditions (Darwin, 1859). Yet, although trait changes in response to novel conditions are widely observed (e.g., due to climate change, Piao et al., 2019), they frequently result from phenotypic plasticity (Boutin and Lane, 2014), i.e., changes of the phenotype in response to an environmental cue. Phenotypic plasticity may provide a short-term relief from changing conditions (Charmantier et al., 2008; Chevin et al., 2010), but also shield a genotype from selection and thereby prevent evolution (Oostra et al., 2018), or it may facilitate evolution via genetic accommodation (Kelly, 2019). In any case, phenotypic plasticity is a pervasive evolutionary strategy, and considered a major factor in a rapidly changing climate (Fox et al., 2019).
The time scale of phenotypic change depends on the time scale of environmental fluctuation (Rando and Verstrepen, 2007; Stomp et al., 2008). Fluctuations over very rapid timescales can be addressed by reversible plasticity, which includes, for example, the induction of plant defense when herbivores are present (Green and Ryan, 1972). Gradual long-term changes, on the other hand, are addressed by genetic adaptation. Between those extremes lie environmental fluctuations that are roughly on the scale of one life span. When environments change over the course of an organism’s development, they can be tackled by irreversible developmental plasticity, i.e., plastic adjustment of developmental pathways that lead to alternative phenotypes (Botero et al., 2015). For example, some Daphnia can produce protective phenotypes when chemical cues from predators are sensed during development (Krueger and Dodson, 1981). When environments are constant throughout an organism’s life time but change from one generation to the next, phenotypic change can be induced in the offspring generation. These are referred to as anticipatory parental effects (Burgess and Marshall, 2014) or intergenerational inheritance (Perez and Lehner, 2019). For example, aphids that live under crowded conditions may produce winged offspring that can leave the colony and avoid high predation pressure or plant deterioration (Braendle et al., 2006). Lastly, when environmental fluctuations last for several generations, epigenetic modifications may be integrated into the germ line and affect multiple succeeding generations. This is referred to as transgenerational plasticity or non-genetic inheritance (Perez and Lehner, 2019; Adrian-Kalchhauser et al., 2020). For the remainder of the article we will refer to all these irreversible changes simply as phenotypic plasticity, ignoring the potential physiological constrains that may limit their evolution. They all have in common that there is a long delay between information sensing and phenotype induction.
Although often assumed, phenotypic plasticity does not need to be adaptive (Ghalambor et al., 2007; Arnold et al., 2019). Plasticity requires some environmental cue on which the induction of phenotypic change is based, and uncertainty around the future environmental state may turn plasticity maladaptive (Burgess and Marshall, 2014; Donelson et al., 2018). Such unpredictable conditions instead favor bet-hedging, which refers to the reduction of fitness variance (Cohen, 1966; Seger and Brockmann, 1987; Starrfelt and Kokko, 2012). Bet-hedging can be achieved by avoiding risky investments (conservative bet-hedging), or by spreading the risk among one’s offspring (diversified bet-hedging), i.e., producing offspring with varying phenotypes (Seger and Brockmann, 1987; Starrfelt and Kokko, 2012). Although empirical evidence is difficult to obtain (Simons, 2011), bet-hedging is a likely explanation for high trait variance or unexpected trait means in many systems, such as the seed dormancy of desert annuals (Cohen, 1966), diapausing strategies of insects (Hopper, 1999) and annual killifish (Furness et al., 2015), wing dimorphisms (Grantham et al., 2016), facultative sexual reproduction (Gerber and Kokko, 2018), dispersal and partial migration (Goossens et al., 2020).
At fluctuations of intermediate time scales where there is a delay between information sensing and phenotype induction, both phenotypic plasticity (e.g., Baker et al., 2019) and bet-hedging (e.g., Venable, 2007) may be expected to evolve. Various theoretical studies have clarified the conditions that may lead to one or the other (Botero et al., 2015; Tufto, 2015), but although occurring potentially simultaneously, bet-hedging and plasticity are nevertheless often treated independently (Donelson et al., 2018). Moreover, when diversified bet-hedging and plasticity are considered jointly, there is no clear consensus about their exact relationship. Adaptive offspring variance that is needed for diversified bet-hedging might be either established by developmental instability (Simons and Johnston, 1997; Kærn et al., 2005; Veening et al., 2008; Woods, 2014; Dueck et al., 2016; Perrin, 2016) or by overly relying on cues with little predictive power (“microplasticity,” Simons and Johnston, 2006; “hyperplasticity,” Scheiner and Holt, 2012). With this article we aim to clarify the relationship between bet-hedging and plasticity, with special attention to readers that are familiar with plasticity but less familiar with bet-hedging theory. We will first use one simple numerical example (insect diapause) to explain the relationship of diversified bet-hedging, conservative bet-hedging and arithmetic mean maximization in detail. We will then extend the consideration to a range of environments whose state is partially predictable, thereby adding the potential for phenotypic plasticity. Lastly, we generalize from our example and describe a method to quantify phenotypic plasticity and bet-hedging based on reaction norm shapes.
An Example
Common examples of bet-hedging are transgenerational biphenisms, i.e., the parent decides among two possible physiological states of the offspring in the face of uncertainty (e.g., Cohen, 1966; Grantham et al., 2016; Maxwell and Magwene, 2017; see Simons, 2011 for further examples). One of these examples is the timing of insect diapause (Halkett et al., 2004; Pélisson et al., 2013), which we will use to illustrate the theory throughout this article.
Multivoltine insects benefit from exponential population growth throughout the growing season, but need to produce an overwintering (diapausing) generation before the onset of cold weather (Kivelä et al., 2016). Aphids, for example, reproduce by parthenogenesis during summer, which enables particularly quick population growth; in autumn they invest in sexual offspring that produce diapausing eggs, as frost kills the soft-bodied insects and only eggs survive (Simon et al., 2002). The struggle to keep the growing season long on one hand and to avoid death on the other hand puts diapause timing under intense selection pressure. If the onset of frost would be invariant, day length could be used as reliable cue of impeding winter, so plasticity in response to day length is expected to evolve. However, if just one generation faces early frosts, all offspring may simultaneously die and the genotype is driven to extinction, regardless of their otherwise high growth rates. Under unpredictable or only partially predictable conditions, bet-hedging strategies may therefore be expected to evolve (Halkett et al., 2004).
For the remainder of this article we will use examples that are loosely based on aphid overwintering. We will assume that parthenogenetic offspring (P1) may produce four offspring when environmental conditions are mild, but face a 90% mortality rate when conditions change. In contrast, diapausing offspring (P2) only replace themselves with 1 offspring in either environment. Hence we assign phenotype P1 a fitness value of 4 in E1 (summer), but only 0.1 in E2 (winter), whereas phenotype P2 achieves 1 fitness in either environment. We assume that the evolution of these growth rates is constrained, so only the proportion of each phenotype may evolve.
Arithmetic Mean Maximization, Diversified Bet-Hedging and Conservative Bet-Hedging
We wish to explain the bet-hedging concept in detail with a few numerical examples. We first consider an entirely unpredictable environment, in which an aphid mother cannot collect any information about the potential environment of their offspring, i.e., there is a 50% chance that the offspring will face beneficial summer conditions (E1), but also a 50% chance for harsh winter conditions (E2). A genotype that invests exclusively in parthenogenesis (P1) achieves on average 2.05 fitness (Table 1), while increasing the proportion of diapausing offspring (P2) lowers arithmetic mean fitness. Nevertheless, a genotype that invests exclusively in diapause (P2) is more successful on the long term, because the parthenogenetic genotype nearly dies out every two years. For example, a parthenogenetic population would decline to 16% of its original size over four years (4 ∗ 0.1 ∗ 4 ∗ 0.1), while the population size of the diapausing genotype would remain constant. The arithmetic mean obviously fails here as predictor of long-term population growth.
If there are multiple decisions to make and the outcome is multiplicative, the geometric mean is a much better predictor for long-term growth, because it is sensitive to variance among years (Cohen, 1966; Seger and Brockmann, 1987; Starrfelt and Kokko, 2012). In the above example of population growth over multiple years, the lower arithmetic mean fitness was more than compensated by the reduction in fitness variance, therefore the risk-averse strategy achieved higher geometric mean fitness than the arithmetic mean maximization (AMM) strategy. This risk-aversive strategy of investing in lower fitness fluctuation at the cost of arithmetic mean fitness is called conservative bet-hedging (CBH), akin to investing in gold when stock markets fluctuate. The risky strategy of maximizing arithmetic mean fitness (AMM), on the other hand, is superior when fluctuations are low, and an analogy in economics would be the investment in a highly profitable product that is not insured against loss (“unhedged”).
Now let us consider a genotype with high developmental instability, i.e., whose offspring phenotype is randomly determined (Table 1). This means that the arithmetic mean fitness is not reduced as strongly as that of the risk-aversive phenotype (100% P2), but the fitness fluctuation between E1 and E2 is also not as great as that of the arithmetic mean maximizer (100% P1). This genotype will increase in population size over four years by the factor 1.89 (2.5 ∗ 0.55 ∗ 2.5 ∗ 0.55), so in this example it is clearly superior to both CBH and AMM. Investing equally in both phenotypes (P1 and P2) breaks down the fitness correlation among the offspring, as half of the offspring takes a risk, while the other half plays it safe (Starrfelt and Kokko, 2012). This strategy is similar to investing in a portfolio of stocks rather than a single stock and is called diversified bet-hedging (DBH).
The geometric mean can be calculated for any phenotype proportion p (proportion of P2) between 0 and 100% (Figure 1A, solid blue line), showing that actually neither of the three strategies (AMM, CBH, DBH) is optimal. Instead, p = 0.61, i.e., a mix of CBH and DBH, yields the highest geometric mean fitness (Table 1). Starrfelt and Kokko (2012) explored the relationship among AMM, CBH and DBH in great detail, and explained fitness optimization as a three-way trade-off between maximizing the arithmetic mean, reducing fitness variance, and reducing fitness correlation among the offspring. However, as outlined in our example, this three-way relationship breaks down to a simple linear gradient when there are exactly two phenotypes to choose from.
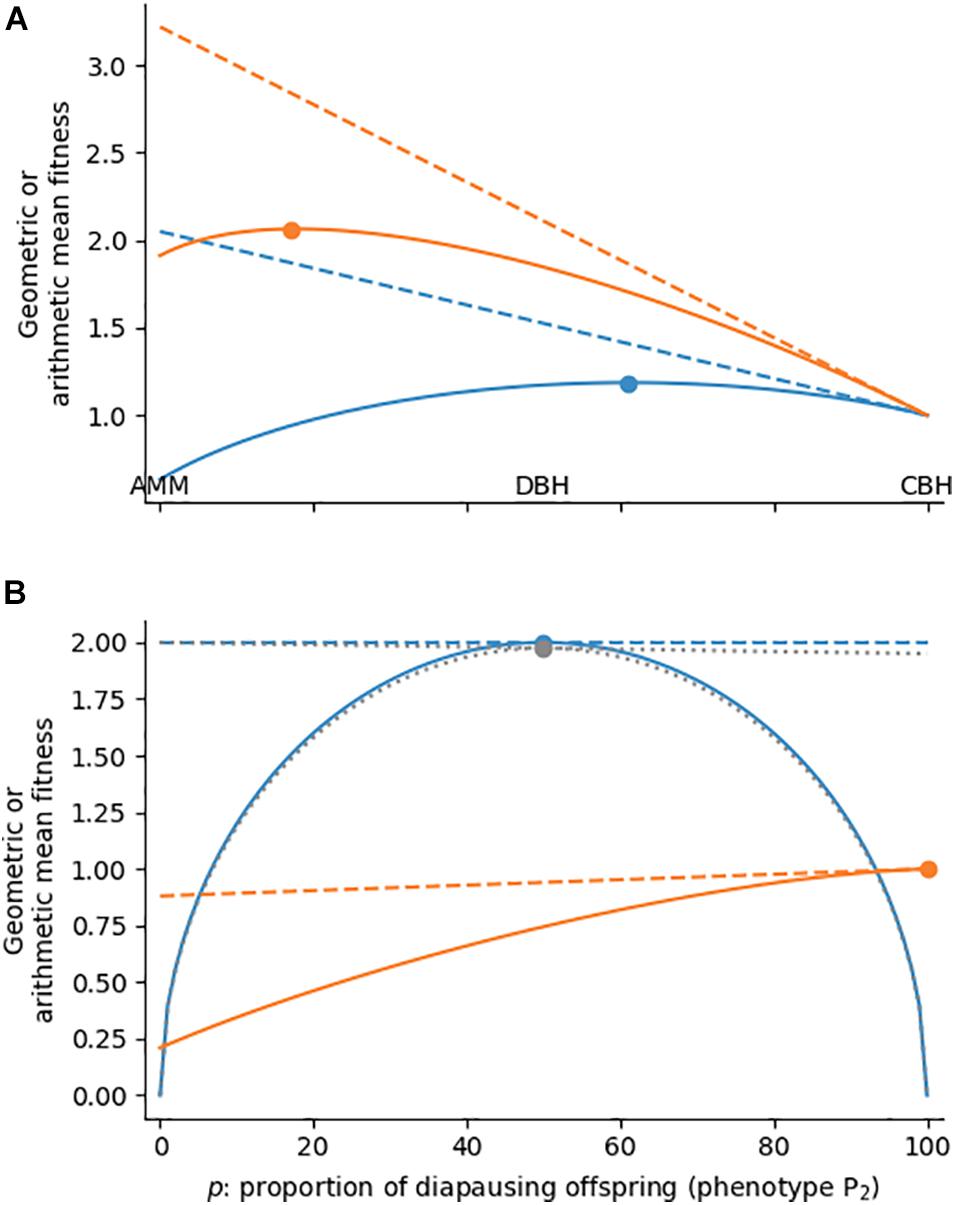
Figure 1. Geometric (solid lines) and arithmetic mean fitness (dashed lines) when a genotype can express two discrete phenotypes in a two-state environment. (A) Conflict between geometric and arithmetic mean maximization. Environment E2 (e.g., winter) occurs with frequencies of 0.5 (blue) or 0.2 (orange). Phenotype P2 represents a risk-averse phenotype (e.g., diapausing offspring) with 1 fitness in either environment, the alternative phenotype is a phenotype with higher arithmetic mean fitness (4 fitness in E1, 0.1 in E2). (B) No or little conflict between arithmetic and geometric mean maximization. Blue line: E2 occurs with frequency 0.5 and P1 and P2 are specialists for E1 and E2, respectively (4 fitness if matched, 0 fitness if mismatched); gray: same as blue line, but P2 has 3.9 fitness in E2; orange: fitness is the same as in panel (A), but E2 occurs with frequency 0.8. Colored dots represent the maxima of the respective functions.
The same principles also apply when the two environments do not occur with equal frequency, e.g., when the probability of E2 (winter) is reduced to 20%. In this case the arithmetic mean fitness of P1 and P2 needs to be weighted by the frequencies of E1 and E2. Nevertheless, arithmetic mean fitness is still a linear function of the phenotype proportion p (Figure 1A, dashed orange line), and increasing the proportion of P2 constitutes a change from AMM towards DBH or CBH. In this example with only occasionally adverse conditions, the optimum lies at p = 0.17 (solid orange line), i.e., much closer to an AMM strategy. If the frequency of E2 is raised to 70%, on the other hand, the optimal strategy moves with p = 0.90 close to pure CBH (not shown). The optimal strategy thus strongly depends on the environmental frequency.
We wish to complete this description of fitness maximization in a single environment with two last special cases. First, we consider the production of two specialist phenotypes, in which P1 achieves a fitness of 4 in E1, but none in E2, while P2 achieves 0 fitness in E1 but 4 fitness in E2 (thus deviating from the aphid example). With these parameters geometric mean fitness peaks at p = 0.5 (Figure 1B, blue solid line), so a strategy that maximizes developmental instability is optimal. Yet, the mixed production of offspring does not constitute DBH, because the diversification does not come at the cost of arithmetic mean fitness (i.e., the dashed blue line is flat). If, however, the growth rates of the two phenotypes are slightly uneven, e.g., reduced to 3.9 for P2 in E2, the same investment in P2 would lower arithmetic mean fitness (dotted gray lines), and hence technically classify as a diversified bet-hedging strategy. This borderline example shows that the classification of bet-hedging strategies is not only a question of whether arithmetic mean fitness is reduced, but rather by how much. The second special case concerns very high probabilities of adverse conditions. When the frequency of E2 is raised to 0.9, it carries so much weight that the arithmetic mean fitness does not decrease, but increase with the proportion of P2 (Figure 1B, dashed orange line). The strategy that avoids variance is hence also the one which maximizes arithmetic mean fitness, so increasing geometric mean fitness (solid orange line) does not come at the cost of arithmetic mean fitness and CBH becomes impossible. In general, the linear gradient from AMM over DBH to CBH (and, in fact, the occurrence of bet-hedging) breaks down, when there is no conflict between arithmetic mean maximization and reduction of fitness variance. We will avoid these special situations in the remainder of the article.
Calculating Optimal Reaction Norm Shapes
We so far discussed the optimal phenotype proportion in a single, isolated environment. However, the benefit of diapause lies in adapting to a continually changing environment. Like in many other insects, aphid diapause is mainly governed by night length. Aphids exclusively reproduce by parthenogenesis under long-day (short night) conditions, but transition to the production of sexual forms under long-night conditions (Marcovitch, 1923). The diapause decision can hence be visualized as a biphenic reaction norm, in which the x-axis represents a continuous night length and the y-axis represents a probability (or, from the mother’s perspective, a proportion) of diapause induction between 0 and 100%. This reaction norm to night length generally follows a logit-curve that ranges from a probability of zero under short nights to a probability of 1 under long nights, and the inflection point at which half of the offspring are diapausing forms is called critical day length (Danilevskii, 1965). The night length response is additionally modulated by temperature (warm temperatures delay diapause), but we ignore the additional plasticity in response to temperature in our considerations.
We will now use the diapause example to illustrate how to calculate optimal reaction norm shapes. Imagine an environment in which winter onsets over many years always occur at 14 h night length. Obviously night length would be a reliable cue and plasticity in response to night length can be expected to evolve. Conversely, night length is useless as cue for a plastic response if winter onset fluctuates randomly. Between those extremes lies an only partially reliable cue, i.e., there is between-years variation in the relationship of night length and winter onset. For example, winter onset may in some years coincide with a night length of 14 h, but fall in other years on an earlier (13.8 h) or later (14.5 h) date, which can be described by a normal distribution with a mean of 14 h and some standard deviation. We now use three different scenarios of how environmental conditions (winter onset) may vary: 1) Winter onset fluctuates according to a normal distribution N1(14, 1) with a mean cue value of 14 h and standard deviation 1; 2) Winter onset follows a normal distribution N2(14, 4) with a mean cue value of 14 h and standard deviation 4, thus simulating lower predictability by night length; 3) Winter onset fluctuates according to a normal distribution N3(14, 2) with standard deviation 2, but half of the winters are mild enough that offspring of type P1 (e.g., parthenogenetic offspring) can survive.
The cumulative distribution function of N describes the probability that winter will occur at a night length of c or lower (Figure 2A). If, for example, an aphid lives in an environment of exactly 14 hours night length, it can expect that the offspring will experience winter conditions with a 50% probability (the optimal phenotype proportion is then 0.61, see Table 1). At 13 h night length winter onset is less probable (18%) for environment N1 (blue line) than for N2 (41%, orange line), because winter onset variability is lower. In N3 the probability distribution must be multiplied by 0.5, i.e., with the chance that winter is mild (green line). This reduces the probability of winter onset at c = 13 h to 16%. Given these environmental frequencies and the fitness values introduced earlier (parthenogenesis: 4/0.1; diapause: 1/1; in summer/winter conditions, respectively), one can now calculate the optimal proportion p as described in section “Arithmetic Mean Maximization, Diversified Bet-Hedging and Conservative Bet-Hedging.” This proportion is 0.47 (nearly pure DBH) in scenario 1, as there is considerable risk of unfavorable conditions, but in scenarios 2 and 3 the ratios drop to 0.12 and 0.11, respectively. Thus, DBH is favored over pure AMM with increasing probability of winter conditions. The same calculations can be performed along the whole range of c, so the complete optimal reaction norm can be calculated if mean and standard deviation of the environment-cue relationship are known (Figures 2B,C).
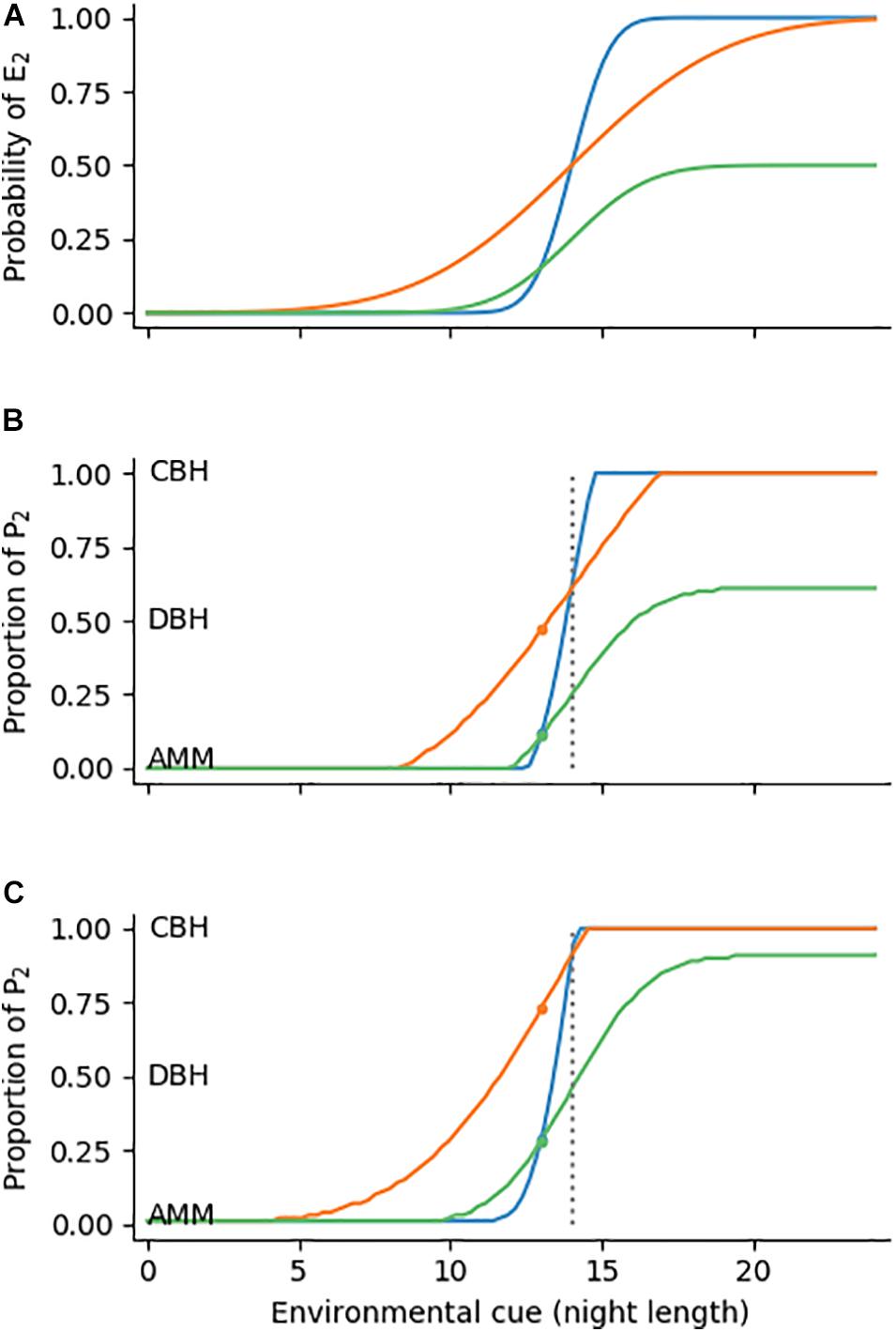
Figure 2. Panel (A) Probability of encountering environment E2 (winter conditions) for different values of an environmental cue c (e.g., night length). E2 fluctuates around c according to three normal distributions N1(14,1), N2(14,4), and 0.5 * N3(14,2) (blue, orange, green). Shown are cumulative probability functions of the three distributions. (B) Optimal reaction norm shapes (e.g., proportion p of diapausing offspring for different night lengths) under the three scenarios of environmental uncertainty introduced in panel (A). As in the main text, fitness of P1 (parthenogenesis) is 4 in E1 and 0.1 in E2, whereas fitness of P2 is always 1. (C) optimal reaction norm shapes when fitness of P1 is 4/0 and fitness of P2 is 1.8/1.8 in E1/E2, respectively. Dotted lines represent c = 14 h, small colored dots refer to the examples given in the main text.
With these considerations we explained the reaction norm shape as a series of binary decisions. In each of these decisions, phenotype proportions may range from AMM to CBH, with DBH in between. The overall degree of bet-hedging is hence defined by the reaction norm shape, and in our specific examples mostly correlates with the reaction norm slope (Figure 2B, orange and blue lines) and range (green line). However, as indicated by the skew in the orange line towards the lower range of c (AMM is discouraged even under low risk) in Figure 2C, more complex shapes are also possible and the relative contribution of each strategy is difficult to quantify. Furthermore, our examples are based on cumulative densities of normal distributions, but depending on the environmental cue, other shapes (e.g., bimodal, sinusoid) are possible. We hence require summary statistics that adequately describe the reaction norm shape.
Classification of Reaction Norm Shapes
In this section we will describe some typical reaction norm shapes and discuss useful summary statistics to describe the overall degree of plasticity, arithmetic mean maximization, conservative bet-hedging and diversified bet-hedging. First, let us assume a “plastic” reaction norm (Figure 3A, dark blue line). A step function describes a sudden switch from one phenotype (AMM) to the other (CBH), and the number of environments in which a mix of phenotypes is produced is minimized. This function maximizes the standard deviation of phenotype proportions p across environments. We refer to the variance of p as . The opposite of a step function is one in which the mother’s decision is entirely independent of the environmental cue, i.e., left to developmental instability, and both phenotypes are produced in equal measure (DBH; Figure 3A, light blue line). While is zero, there is variance in phenotypes within each environment (). The trait choice is a Bernoulli draw and the variance of each p is calculated as p ∗ (1 – p), so we define across environments as the mean Bernoulli variance. The two variance components (among and within environments) complement each other, and we define their sum as the phenotypic variance of the genotype. It is not possible to maximize both (steep slope, high range) and (minimal departure from 50%) at once, but intermediate reaction norms with mixed contributions of and are possible (solid and dashed medium blue lines). The trade-off between and can be described by the ratio r = . r thus describes the degree of developmental (in)stability across environments.
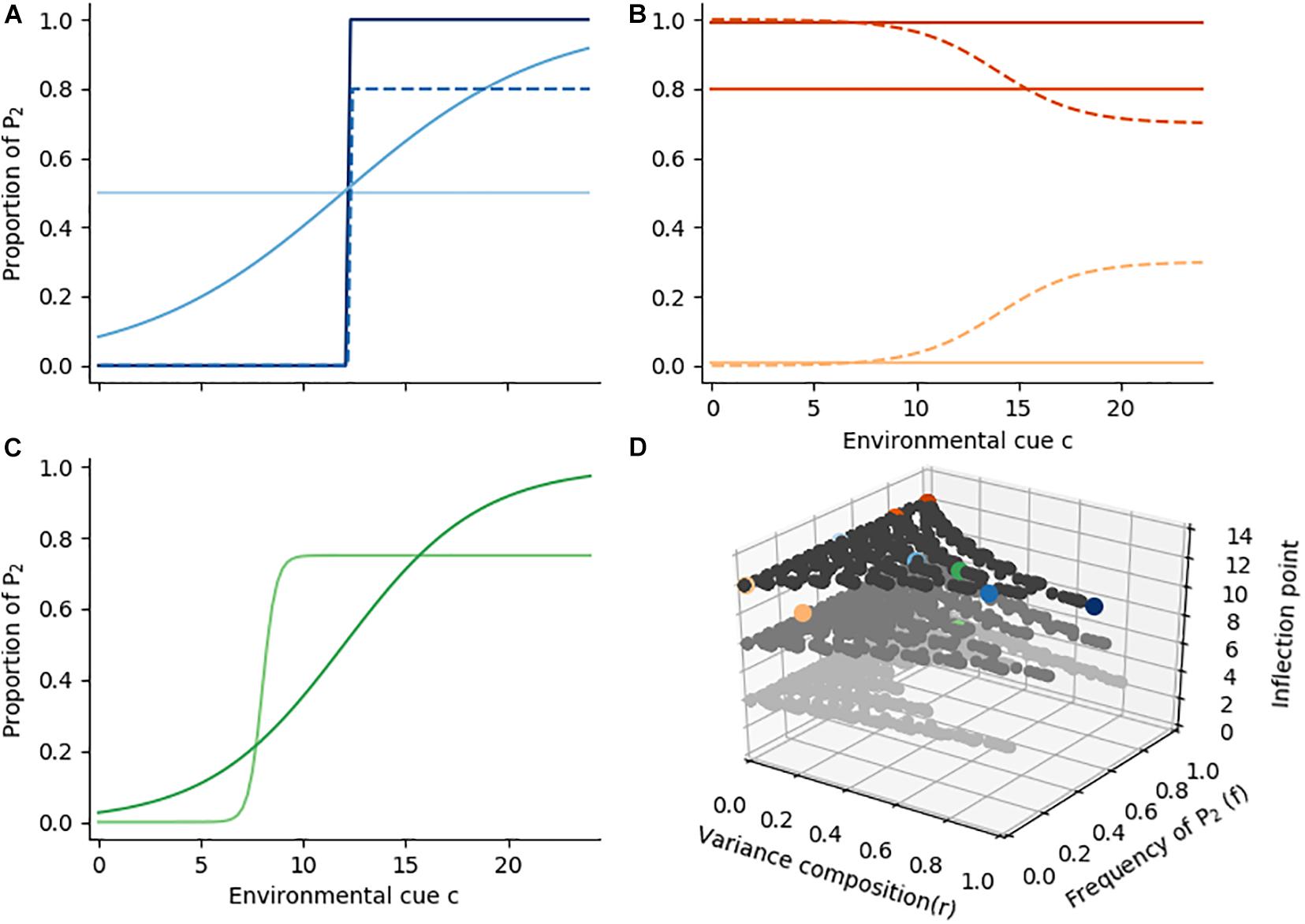
Figure 3. Example reaction norm shapes. (A) Four reaction norm shapes that exhibit high phenotypic variance. Variance may occur exclusively among environments (dark blue), exclusively within each environment (light blue), or as a mix of both variance components (medium blue, solid and dashed). We refer to the ratio of the variance components (among : within) as r. (B) Three different reaction norms with r = 0 (solid lines), and two different reaction norms with r = 0.14 (dashed). The reaction norms differ in the mean frequency f of phenotype P2, which also affects the phenotypic variance s (i.e., the sum of variance among and within environments). Reaction norms with f = 0 (light orange) and f = 1 (dark orange) are canalized (s = 0), and phenotypic variance is maximized at f = 0.5 (see panel A). (C) Two logistic reaction norms with the same f and r, but different inflection points. (D) possible parameter space of r, f, and inflection points. Gray dots depict sample reaction norms across the range of possible parameters (darkness scales with z-axis), colored dots indicated samples from panels (A–C) in their respective color.
The variance composition is not the only parameter in which reaction norms may vary. Reaction norms may, for example, be flat (r = 0), but the proportion of P2 (p) might be zero (Figure 3B, light orange line), 0.8 (dark orange) or 1 (darkest line) in all environments. These reaction norms differ in the mean frequency of phenotype P2 across environments, which we denote as f. A frequency of zero indicates a pure AMM strategy, while f = 1 is a pure CBH strategy. A mean frequency of 0.5 indicates a reaction norm with maximal phenotypic variance (s), enabling the aforementioned gradient from phenotypic plasticity to DBH (Figure 3A, solid lines). As with Figure 3A, intermediate reaction norm shapes are also possible: a reaction norm may, for example, range from p = 0 to p = 0.3 or from p = 0.7 to p = 1 (Figure 3B, dashed lines). Reaction norms can thus vary from complete canalization to high phenotypic variance, and we express their shape by mean frequency of phenotype P2 and by the variance composition. A canalized reaction norm may be only expressing risk-aversive phenotypes, or only expressing arithmetic mean optimizers, whereas high phenotypic variance may indicate steep plastic reaction norms or DBH.
The two shape parameters f and r reflect the reaction norm shape to a reasonable extent, but as summarizing statistics they cannot sufficiently describe all its features. For example, the reaction norms in Figure 3C both share the same mean frequency (0.5) and variance composition (0.47), but the strategies under environments that correspond to a low cue c differ considerably. In our aphid example these two strategies differ in the mean timing of diapause induction, which is an important consideration when the onset of seasons is under directional change (IPCC, 2014). This mean timing can be assessed by calculating the inflection point (called critical day length for diapause reaction norms), but for non-logistic reaction norms or more complicated reaction norm shapes a different approach, e.g., based on autocorrelation patterns, is required.
In summary we discussed three important parameters that describe a reaction norm shape: The frequency f, the variance composition r (among:within environments), and (for logistic reaction norms) the inflection points. These three parameters are partially interdependent of one another, and can be drawn as three perpendicular axes (Figure 3D; see also Supplementary Figure S1 for an alternative representation). The resulting parameter space has three distinct ends which conform to maximum plasticity (i.e., a step-function, dark blue dot), CBH (dark orange), and AMM (light orange). Parameters outside these bounds are not possible, e.g., DBH and plasticity cannot occur in canalized reaction norms, and on the other hand mean frequencies of 0.5 necessarily imply phenotypic variance by DBH or plasticity.
Reaction Norm Evolution
So far we described optimal strategies in a single environment (Section “Arithmetic Mean Maximization, Diversified Bet-Hedging and Conservative Bet-Hedging”), calculated optimal reaction norm shapes (Section “Calculating Optimal Reaction Norm Shapes”), and explored which reaction norm shapes are generally possible (Section “Classification of Reaction Norm Shapes”). We now return to our aphid diapause example to illustrate how optimal reaction norms change when environmental conditions and fitness functions are altered. We will cover cases with more frost-resistant parthenogenetic forms (i.e., higher fitness of P1 in E2), harsher summer environments (lower fitness of P1 in E1), and three forms of change in the environment that are directly relevant for aphid biology: first, mean winter onset may vary with latitude, with earlier winter onset at high latitudes (Danilevskii, 1965). Secondly, winter onset dates may vary among years, which is the condition that should lead to bet-hedging in diapause timing (Halkett et al., 2004). Lastly, aphid populations in warmer climates frequently lost the ability to produce sexual forms and reproduce by parthenogenesis throughout the year (anholocyclic life cycles, Simon et al., 2002). The preparation for winter makes only sense if there is sufficient change in environmental conditions, so this kind of canalization (obligate development) is expected at southern latitudes.
We start with environments that vary in among-years predictability. Using night length (in hours) as a cue c, we consider scenarios where winter onset is normally distributed with a mean cue c of 14 and standard deviations ranging from 0 to 10. In our standard example with growth rates of 4/0.1 (parthenogenetic) and 1/1 (diapausing), the optimal mean frequency f of risk-aversive (diapausing) phenotypes increases with environmental variance (Figure 4A, blue solid line), while the variance ratio r (among : within environments) decreases (Figure 4C, blue solid line). Thus, a greater tendency towards DBH and CBH is expected to evolve across environments in unpredictable conditions (see also Figure 4B, blue lines). With decreasing growth rate of P1 in E1(parthenogenesis in summer) the optimal ratio decreases less sharply and the frequency of P2 (diapause) increases more strongly (solid orange and green lines in Figure 4A, green lines in Figure 4B). Here the riskier strategy pays off less, and the balance is shifted towards CBH. When the growth rate of P1 in E2 (winter) is raised to 0.33 (frost tolerance) both r and f change less steeply with environmental unpredictability (dashed lines), i.e., the optimal reaction norms tend towards AMM. Increasing the growth rate in E2 further to 0.66 (dash-dotted lines) leads to a strategy that ignores environmental risk, except when the chance of mild (summer) conditions is very low. The range of environments that feature a sufficiently low chance of P1 decreases with increasing environmental variance, causing a drop of both f and r as a sign of canalization to AMM (Figure 4D). Overall, both CBH and DBH can be expected under unpredictable conditions, but their relative benefits vary depending on the arithmetic mean fitness of risk-aversive and risk-prone phenotypes.
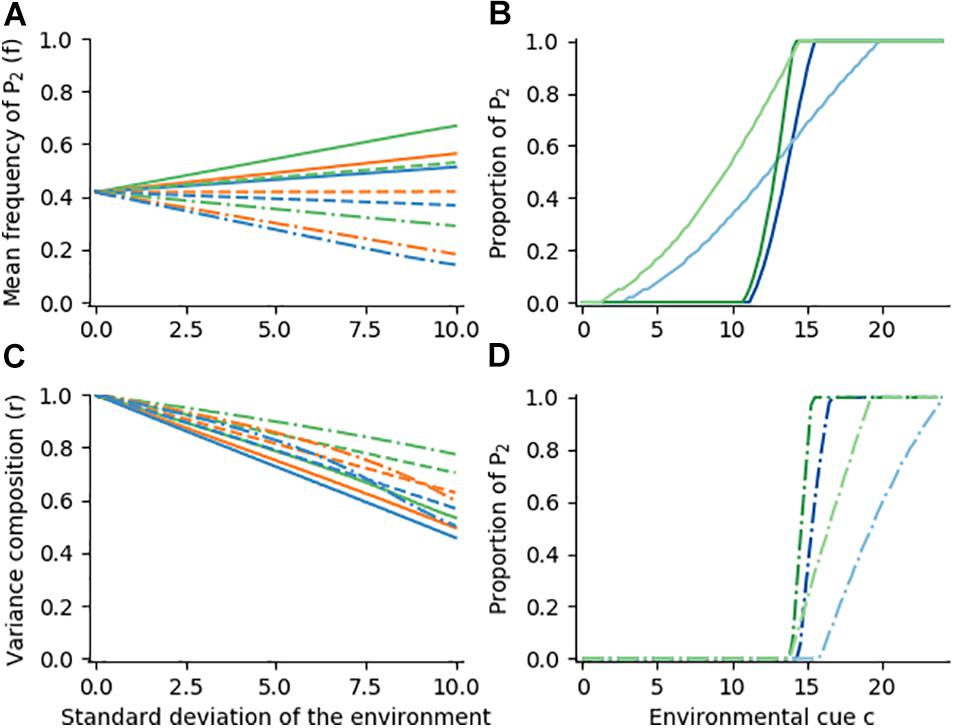
Figure 4. Optimal reaction norm shapes for various growth rate functions and different levels of environmental predictability. Environments are normally distributed around a cue c with a mean of 14. Mean frequency f of phenotype P2 (Panel A) and variance composition r (Panel C) are plotted against standard deviation of the environment. Growth rates of P2 (diapause) are always 1 for both environments (summer and winter); growth rates of P1 (parthenogenesis) in E1/E2 are 4/0.1 (blue, solid), 3/0.1 (orange, solid), 2/0.1 (green, solid); 4/0.33, 3/0.33, 2/0.33 (dashed blue, orange and green lines); and 4/0.66, 3/0.66, 2/0.66 (dash-dotted blue, orange and green lines). Panels (B–D) show optimal reaction norms for environments with standard deviations of 2 (darker shade) and 8 (lighter shade) in the according line styles and colors.
We now simulate global changes in the probability of events, for instance increased or decreased probabilities of severe winters. For the latter, we multiply the normal distribution by 0.5, overall halving the probability of being in the harsh environment E2 (see also Figure 2A). This discourages risk-aversion and, for example, having all offspring diapausing is no longer beneficial (Figure 5). When the growth rate of P1 is either 4 (summer) or 0.1 (winter), the frequency f stagnates at 0.2 to 0.25, while the ratio r decreases from 0.47 to 0.17 (Figures 5A,C, solid blue line). This is because the reaction norm range is constrained (Figure 5B). A lower growth rate of P1 in E1 restores phenotypic variance (Figures 5A,C, orange and green lines), as it reduces its arithmetic mean fitness and makes the alternative phenotype again more profitable (Figure 5B, green lines). Lowering the environmental risk further increases the benefit of arithmetic mean maximization (dashed lines) and eventually leads to AMM under all environmental conditions (dash-dotted lines). Overall, Figure 5 shows that a global reduction of the probability for E2 may discourage CBH, and instead favor AMM. For example, a lower risk of freezing in winter may explain the existence of anholocyclic lines.
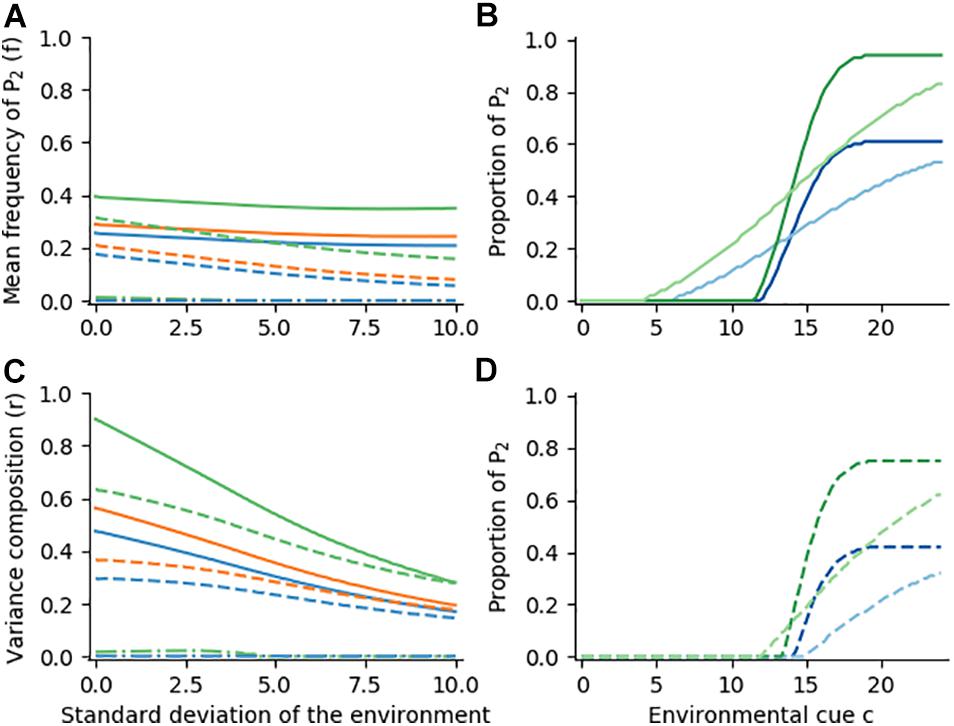
Figure 5. Optimal reaction norm shapes for various growth rate functions and different levels of environmental predictability. Environments are normally distributed around a cue c with a mean of 14, but multiplied by 0.5. Panels, growth rates, coloring and line styles are the same as Figure 4.
A third axis of environmental variation concerns changes in mean environments. Moving the distribution of environments to a mean c of 9 h simulates the change of winter onset with latitude, as well as the effects of a changing climate. Although highly relevant for the optimization of fitness, the changes in optimal reaction norm shapes are trivial to describe. We refer to Supplementary Material S2 for further exploration.
In general, we find that r and f evolve with changes in environmental predictability (Figure 4, solid lines), leading to CBH and DBH in unpredictable environments. Changes in the fitness function (growth rates in our example) may, however, affect the balance of AMM and CBH, and very low rewards for CBH instead lead to the evolution of risky strategies that seek to maximize the arithmetic mean (Figure 4, dash-dotted lines). When the probability of adverse conditions is globally lowered across the range of environments (e.g., mild winters), the reaction norm range can become constricted, which further affects the balance of the fitness maximization strategies. Lastly, f additionally depends strongly on the mean environment (e.g., winter onset, Supp. S2), but within reasonable limits the general shape of the reaction norms is not affected.
Discussion
Phenotypic plasticity can help organisms adapt to changing conditions (Fox et al., 2019), but this requires a predictable cue (Bonamour et al., 2019). Especially for transgenerational plasticity cues are not entirely predictable (Burgess and Marshall, 2014; Donelson et al., 2018), which, at least under some conditions, favors bet-hedging instead (Botero et al., 2015; Tufto, 2015). Nevertheless, the value of bet-hedging strategies as alternatives to plasticity is frequently overlooked.
Starrfelt and Kokko (2012) have explained bet-hedging, including its mathematical foundation, in great detail. The main finding was that arithmetic mean fitness maximization, diversified bet-hedging and conservative bet-hedging form a three-way trade-off of conflicting strategies. However, it was difficult to see how these strategies play out in practice (Haaland et al., 2020). We provided a simple, detailed calculation of fitness based on insect diapause as example. Based on this system with only two possible phenotypes (biphenisms) we described how a conflict between arithmetic and geometric mean optimization can result in bet-hedging (Figures 1A,B). We explained that the three strategies form a gradient, in which arithmetic mean maximization (AMM) and conservative bet-hedging (CBH) are represented by distinct phenotypes, and diversified bet-hedging (DBH) by a mixture of the two extremes. We also extended the concept by adding a cue the organisms can respond to, thereby incorporating reaction norms and the potential for phenotypic plasticity. We identified the mean phenotype frequency f and the variance composition r as two summary statistics of reaction norms that allow distinguishing between AMM, CBH, DBH and plasticity, and the sum s of the variance components as a measure of phenotypic variance. Moreover, for logistic reaction norm shapes we discuss the inflection point as a third useful summary statistic.
Arithmetic Mean Maximization vs. Conservative Bet-Hedging
In section “Arithmetic Mean Maximization, Diversified Bet-hedging and Conservative Bet-hedging” we described AMM, DBH and CBH as a linear gradient of strategies to cope with a single environment. When extended to multiple environments, a flat reaction norm at p = 0 (Figure 3B, light orange line) maximizes arithmetic mean fitness (see also Figure 1A), and any adaptive deviation from this line incorporates some bet-hedging (in the cases we consider; see Figure 1B for exceptions). Thus, the mean phenotype frequency f is a direct measure of the degree of CBH in a reaction norm shape. We illustrated that f correlates with the frequency of the harsh environment E2 (compare Figure 4A and Supplementary Figure S1, panel A), but f also changes with the degree of environmental variance: higher environmental risk shifts optimal reaction norms towards DBH and CBH (Figure 4A, solid lines; Figure 4B, dark blue vs. light blue lines), in line with expectations from other studies (Simons, 2011; Tufto, 2015). This shift is particularly noticeable when the potential fitness gain from a risk-prone strategy is low (Figure 4B green lines; Figure 2C, orange lines). If, on the other hand, the risk is reduced and the potential pay-off high (Figure 4A, dashed and dot-dashed lines; Figure 5), the optimal reaction norm shapes are shifted towards risk-prone (AMM) strategies (Halkett et al., 2004). Thus our framework made clear that arithmetic mean maximization and variance avoidance form exact opposites on a gradient of strategies that is reflected by f (Figure 3D, y-axis).
We have illustrated that frequencies or means of reaction norms that mismatch with environmental means might serve a function. Recent climate change imposes novel environmental conditions, and species or populations whose trait means do not evolve in concert with environmental means are often considered as under risk (e.g., Charmantier and Gienapp, 2014), ignoring that this phenotype-environment mismatch may in fact be due to an adaptive CBH strategy. This is not to say that CBH can be invoked whenever environmental variance is observed (Simons, 2011), but any combination of mean maximization and variance avoidance (f) has the potential to be adaptive depending on life history and environmental variance.
Phenotypic Plasticity vs Diversified Bet-Hedging
Reaction norms that are not entirely canalized exhibit some degree of phenotypic plasticity and/or diversified bet-hedging (Figures 3A,B,C), and we expressed their relative contribution with the variance ratio r. When environmental cues convey reliable information, a high r is adaptive, i.e., phenotypes change with the environmental cues, but vary only little for any given cue (solid dark blue lines in Figures 2B, 3A, 4B; Botero et al., 2015; Tufto, 2015). This reaction norm pattern is commonly referred to as phenotypic plasticity, or, when the offspring phenotype is dictated by the (grand-) parental environment, as inter- or transgenerational plasticity (Perez and Lehner, 2019). A low r, on the other hand, corresponds to DBH across the range of possible environments (orange line in Figure 2B, solid light blue lines in Figures 3A,B), and occurs predominantly when cues convey little information about the optimal phenotype (Cohen, 1966). Our simple models based on aphid diapause illustrate such a negative relationship between r and cue variance for all but the most extreme growth rate functions (Figures 4C, 5C). We therefore see phenotypic plasticity and diversified bet-hedging as a continuum of evolutionary strategies that is based on the reaction norm shape (Figure 3D, x-axis).
This definition extends classical concepts of bet-hedging and transgenerational plasticity. Plasticity has a long history of being related to reaction norm shapes (Woltereck, 1913; Bradshaw, 1965), but diversified bet-hedging is not as easily visualized, nor is the relationship with plasticity entirely clear. On the one hand, developmental instability has been seen as a cause of diversified bet-hedging (Simons and Johnston, 1997; Kærn et al., 2005; Woods, 2014; Dueck et al., 2016; Perrin, 2016). Low copy numbers e.g., of transcriptional regulators (Volfson et al., 2006) cause sampling errors that ultimately lead to expression of alternative phenotypes. On the other hand, DBH might be produced by a reaction norm to noise (“microplasticity,” Simons and Johnston, 2006; “hyperplasticity,” Scheiner and Holt, 2012). For example, Maxwell and Magwene (2017) engineered a yeast model that evolved a response to estradiol, a compound that was entirely unrelated to fitness but ensured phenotypic variance in a fluctuating environment. Accordingly, the relationship between diversified bet-hedging and plasticity might be perceived as nested or as one of two competing strategies. We instead distinguish them as the two extremes on a continuum of strategies, that correspond to a continuum of reaction norm shapes.
Fixed vs. Flexible Development
The phenotype frequency f and the variance composition r are not entirely independent (Figure 3D), because phenotypic variance s, i.e., the sum of variance among and within environments, is a quadratic function of f: when f is zero (pure AMM or CBH, Figure 3B) there is no phenotypic variance and hence no potential for DBH or phenotypic plasticity. When f is 0.5, on the other hand, DBH, phenotypic plasticity, or a mix of the two strategies is necessarily required (Figures 3A,D).
In section “Reaction Norm Evolution” we altered the amplitude between summer and winter conditions, both by changing the fitness of the phenotypes (Figure 4, green and orange lines) and by affecting the global probability of E2 (Figure 5). Reductions in the difference between summer and winter led to a reduction of phenotypic variance, i.e., to a decrease in f towards canalization (Figures 4A, Figures 5B,D), illustrating that phenotypic variance is not beneficial when environments are stable. The relationship between the variance composition r and environmental variance was, however, maintained (Figure 5C, dark vs. light lines in Figure 5B). The benefits of plasticity and DBH under predictable and unpredictable conditions, respectively, were thus also apparent under partially canalizing conditions.
Our examples clarified that phenotypic variance is a function of f in binomial reaction norms, and as such it is equally related to both phenotypic plasticity and diversified bet-hedging. The opposite of phenotypic variance (i.e., of plasticity and DBH) in our models is environmental canalization, a term which so far has been used ambiguously (Debat and David, 2001), as it was considered either the opposite of plasticity (Waddington, 1942; Van Buskirk and Steiner, 2009) or of developmental noise (Gibson and Wagner, 2000; Zhang and Hill, 2005) alone. Phenotypic plasticity is regarded an essential component of climate change adaptation (Fox et al., 2019), precisely because of the variance it entails; moreover, de-canalization by phenotypic plasticity may accelerate evolution through genetic accommodation (Kelly, 2019). We argue that the same mechanisms may apply for all modes of phenotypic variance, including diversified bet-hedging.
The Importance of Mean Timing
We introduced the inflection point as additional important reaction norm shape parameter (Figure 3C, z-axis in Figure 3D; Supplementary Figure S1). In our example the inflection point determined the mean timing of phenotypic change (i.e., the phenology), and clearly depended on the mean timing of environmental change (Supplementary Figure S2). The inflection point (called critical day length in diapause reaction norms) is known to change with latitude (Danilevskii, 1965; Bradshaw, 1976), and questions regarding its evolution are highly important under climate change (Saikkonen et al., 2012; Zohner et al., 2016). While limited to logistic reaction norms, we think the inflection point as reaction norm shape parameter deserves special attention, because many phenological traits are of binary nature (e.g., bird arrival, migration onset, plant germination and flowering) and hence modeled as logistic reaction norms.
Outlook
The world is simultaneously changing in climate means, variability and predictability (IPCC, 2014; Lenton et al., 2017; Bathiany et al., 2018), and there are many phenomenological studies on responses to climate change (Parmesan and Yohe, 2003; Badeck et al., 2004; Cohen et al., 2018). However, only few detailed case-studies on the mechanisms of adaptation (Nussey et al., 2005; Gienapp et al., 2013; Lane et al., 2018) exist, and one cannot assume that a matching mean timing or a high level of plasticity is always adaptive (Boutin and Lane, 2014), just like one cannot assume CBH or DBH to be an optimal solution (Simons, 2011) – but one can analyze reaction norm shapes with the proposed shape parameters to decide whether it has the potential for adaptive tracking, arithmetic mean maximization, plasticity, bet-hedging or canalization (Joschinski and Bonte, 2020).
There is ample room to extend our framework. First of all, we focussed only on the optimal reaction norm shape. This ignores that CBH and DBH are often nearly equally suited strategies to cope with environmental uncertainty (Starrfelt and Kokko, 2012), i.e., the shape and curvature of the geometric mean fitness curve (Figure 1A) requires further consideration. Secondly, we have restricted our arguments to binary trans-generationally inherited traits, as these are commonly treated both empirically (Venable, 2007; Maxwell and Magwene, 2017; Scholl et al., 2020) and theoretically (Cohen, 1966; Halkett et al., 2004; Starrfelt and Kokko, 2012; Kivelä et al., 2016; Gerber and Kokko, 2018). For continuous traits, e.g., offspring size (Marshall et al., 2008), our calculations may not apply, because AMM, DBH and CBH need not lie on a linear gradient (i.e., intermediate trait values need not incur highest trait variance). Nevertheless, theory regarding Gaussian functions arrives at a similar conclusion: that offspring variance evolves to the amount of environmental mismatch that is not already covered by phenotypic plasticity (Tufto, 2015). This is equivalent to our finding that only the variance composition (r) changes with environmental variability, whereas the degree of phenotypic variance remains relatively constant (e.g., Figure 5B). Other possible extensions would include plastic responses that take place within an individual’s life time. The opportunity for both within- and transgenerational plasticity may not only make one strategy obsolete (Luquet and Tariel, 2016), but also lead to complex interactions among the two (Fuxjäger et al., 2019). Similarly, fitness may include multiplicative instances within an individual’s lifetime (e.g., iteroparity), shifting the balance from DBH towards CBH strategies, or conversely sum across generations (“fine-grained” environments), moving the balance towards AMM strategies (Haaland et al., 2020). Lastly, there are also potential bet-hedging strategies that appear entirely unrelated to transgenerational plasticity. These include, for example, an iteroparous life history (Garcia-Gonzalez et al., 2015), hotspots for genetic mutations (“contingency loci”, Rando and Verstrepen, 2007), and sexual reproduction in general (Li et al., 2017). A unification with these alternative strategies might lead to a better understanding of adaptation to rapid climate change.
Conclusion
In this review we rephrased reaction norm evolution as a complex trade-off among four strategies. It is increasingly recognized that changes in climate extremes and in predictability are as important as changes in means (IPCC, 2014; Donelson et al., 2018) – focusing only on strategies to match the mean is hence not fruitful. For example, failure to shift mean phenology with climate change (Gienapp et al., 2013) is not problematic per se – it could be mitigated by concurrent changes in phenotypic variance. Similarly, the lack of both phenotypic plasticity and mean change may not have severe fitness consequences, if the lack of plasticity is mitigated by diversified bet-hedging. It is the combination along all three axes that defines fitness in a given environment.
Data Availability Statement
All code necessary to produce the figures is included in the Supplementary Material S3.
Author Contributions
JJ and DB developed the theory and contributed to the final version of the manuscript. JJ wrote the first draft. DB supervised the work. Both authors contributed to the article and approved the submitted version.
Funding
JJ was financially supported by a DFG research fellowship (398170603). DB is funded by FWO project G018017N.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2020.517183/full#supplementary-material
Supplementary Figure 1 | Possible parameter space of r and f for different inflection points. Grey dots depict sample reaction norms across the range of possible parameters (darkness scales with inflection point).
Supplementary Figure 2 | Optimal reaction norm shapes for various growth rate functions and different levels of environmental predictability. Environments are normally distributed around a cue c with a mean of 9 h, all other parameters, coloring and line styles are the same as Figure 4.
Supplementary Table 1 | Python code that was used to generate the figures in the manuscript.
References
Adrian-Kalchhauser, I., Sultan, S. E., Shama, L. N. S., Spence-Jones, H., Tiso, S., Valsecchi, C. I. K., et al. (2020). Understanding “non-genetic” inheritance: insights from molecular-evolutionary crosstalk. Trends Ecol. Evol. (in press). doi: 10.1016/j.tree.2020.08.011
Arnold, P. A., Nicotra, A. B., and Kruuk, L. E. B. (2019). Sparse evidence for selection on phenotypic plasticity in response to temperature. Philos. Trans. R. Soc. B 374:20180185. doi: 10.1098/rstb.2018.0185
Badeck, F. W., Bondeau, A., Bottcher, K., Doktor, D., Lucht, W., Schaber, J., et al. (2004). Responses of spring phenology to climate change. New Phytol. 162, 295–309. doi: 10.1111/j.1469-8137.2004.01059.x
Baker, B. H., Sultan, S. E., Lopez-Ichikawa, M., and Waterman, R. (2019). Transgenerational effects of parental light environment on progeny competitive performance and lifetime fitness. Philos. Trans. R. Soc. B 374:20180182. doi: 10.1098/rstb.2018.0182
Bathiany, S., Dakos, V., Scheffer, M., and Lenton, T. M. (2018). Climate models predict increasing temperature variability in poor countries. Sci. Adv. 4:eaar5809. doi: 10.1126/sciadv.aar5809
Bonamour, S., Chevin, L.-M., Charmantier, A., and Teplitsky, C. (2019). Phenotypic plasticity in response to climate change: the importance of cue variation. Philos. Trans. R. Soc. B 374:20180178. doi: 10.1098/rstb.2018.0178
Botero, C. A., Weissing, F. J., Wright, J., and Rubenstein, D. R. (2015). Evolutionary tipping points in the capacity to adapt to environmental change. PNAS 112, 184–189. doi: 10.1073/pnas.1408589111
Boutin, S., and Lane, J. E. (2014). Climate change and mammals: evolutionary versus plastic responses. Evol. Appl. 7, 29–41. doi: 10.1111/eva.12121
Bradshaw, A. D. (1965). Evolutionary significance of phenotypic plasticity in plants. Adv. Gen. 13, 115–155. doi: 10.1016/S0065-2660(08)60048-6
Bradshaw, W. E. (1976). Geography of photoperiodic response in diapausing mosquito. Nature 262, 384–386. doi: 10.1038/262384b0
Braendle, C., Davis, G. K., Brisson, J. A., and Stern, D. L. (2006). Wing dimorphism in aphids. Heredity 97, 192–199. doi: 10.1038/sj.hdy.6800863
Burgess, S. C., and Marshall, D. J. (2014). Adaptive parental effects: the importance of estimating environmental predictability and offspring fitness appropriately. Oikos 123, 769–776. doi: 10.1111/oik.01235
Charmantier, A., and Gienapp, P. (2014). Climate change and timing of avian breeding and migration: evolutionary versus plastic changes. Evol. Appl. 7, 15–28. doi: 10.1111/eva.12126
Charmantier, A., McCleery, R. H., Cole, L. R., Perrins, C., Kruuk, L. E. B., and Sheldon, B. C. (2008). Adaptive phenotypic plasticity in response to climate change in a wild bird population. Science 320, 800–803. doi: 10.1126/science.1157174
Chevin, L.-M., Lande, R., and Mace, G. M. (2010). Adaptation, plasticity, and extinction in a changing environment: towards a predictive theory. PLoS Biol. 8:e1000357. doi: 10.1371/journal.pbio.1000357
Cohen, D. (1966). Optimizing reproduction in a randomly varying environment. J. Theor. Biol. 12, 119–129. doi: 10.1016/0022-5193(66)90188-3
Cohen, J. M., Lajeunesse, M. J., and Rohr, J. R. (2018). A global synthesis of animal phenological responses to climate change. Nat. Clim. Change 8, 224–228. doi: 10.1038/s41558-018-0067-3
Danilevskii, A. S. (1965). Photoperiodism and Seasonal Development of Insects, 1st Edn. Edinburgh: Oliver & Boyd.
Darwin, C. (1859). On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life. London: J. Murray.
Debat, V., and David, P. (2001). Mapping phenotypes: canalization, plasticity and developmental stability. Trends Ecol. Evol. 16, 555–561. doi: 10.1016/S0169-5347(01)02266-2
Donelson, J. M., Salinas, S., Munday, P. L., and Shama, L. N. S. (2018). Transgenerational plasticity and climate change experiments: where do we go from here? Glob. Change Biol. 24, 13–34. doi: 10.1111/gcb.13903
Dueck, H., Eberwine, J., and Kim, J. (2016). Variation is function: are single cell differences functionally important? BioEssays 38, 172–180. doi: 10.1002/bies.201500124
Fox, R. J., Donelson, J. M., Schunter, C., Ravasi, T. C., and Gaitán-Espitia, J. D. (2019). Beyond buying time: the role of plasticity in phenotypic adaptation to rapid environmental change. Philos. Trans. R. Soc. B 374:20180174. doi: 10.1098/rstb.2018.0174
Furness, A. I., Lee, K., and Reznick, D. N. (2015). Adaptation in a variable environment: phenotypic plasticity and bet-hedging during egg diapause and hatching in an annual killifish. Evolution 69, 1461–1475. doi: 10.1111/evo.12669
Fuxjäger, L., Wanzenböck, S., Ringler, E., Wegner, K. M., Ahnelt, H., and Shama, L. N. S. (2019). Within-generation and transgenerational plasticity of mate choice in oceanic stickleback under climate change. Philos. Trans. R. Soc. B 374:20180183. doi: 10.1098/rstb.2018.0183
Garcia-Gonzalez, F., Yasui, Y., and Evans, J. P. (2015). Mating portfolios: bet-hedging, sexual selection and female multiple mating. Proc. R. Soc. B 282:20141525. doi: 10.1098/rspb.2014.1525
Gerber, N., and Kokko, H. (2018). Abandoning the ship using sex, dispersal or dormancy: multiple escape routes from challenging conditions. Philos. Trans. R. Soc. B 373:20170424. doi: 10.1098/rstb.2017.0424
Ghalambor, C. K., McKay, J. K., Carroll, S. P., and Reznick, D. N. (2007). Adaptive versus non-adaptive phenotypic plasticity and the potential for contemporary adaptation in new environments. Funct. Ecol. 21, 394–407. doi: 10.1111/j.1365-2435.2007.01283.x
Gibson, G., and Wagner, G. (2000). Canalization in evolutionary genetics: a stabilizing theory? BioEssays 22, 372–380.
Gienapp, P., Lof, M., Reed, T. E., McNamara, J., Verhulst, S., and Visser, M. E. (2013). Predicting demographically sustainable rates of adaptation: can great tit breeding time keep pace with climate change? Philos. Trans. R. Soc. B 368:20120289. doi: 10.1098/rstb.2012.0289
Goossens, S., Wybouw, N., Van Leeuwen, T., and Bonte, D. (2020). The physiology of movement. Mov. Ecol. 8:5. doi: 10.1186/s40462-020-0192-2
Grantham, M. E., Antonio, C. J., O’Neil, B. R., Zhan, Y. X., and Brisson, J. A. (2016). A case for a joint strategy of diversified bet hedging and plasticity in the pea aphid wing polyphenism. Biol. Lett. 12:20160654. doi: 10.1098/rsbl.2016.0654
Green, T. R., and Ryan, C. A. (1972). Wound-induced proteinase inhibitor in plant leaves: a possible defense mechanism against insects. Science 175, 776–777. doi: 10.1126/science.175.4023.776
Haaland, T. R., Wright, J., and Ratikainen, I. I. (2020). Generalists versus specialists in fluctuating environments: a bet-hedging perspective. Oikos 129, 879–890. doi: 10.1111/oik.07109
Halkett, F., Harrington, R., Hullé, M., Kindlmann, P., Menu, F., Rispe, C., et al. (2004). Dynamics of production of sexual forms in aphids: theoretical and experimental evidence for adaptive “coin-flipping” plasticity. Am. Nat. 163, E112–E125. doi: 10.1086/383618
Hopper, K. R. (1999). Risk-spreading and bet-hedging in insect population biology. Annu. Rev. Entomol. 44, 535–560. doi: 10.1146/annurev.ento.44.1.535
IPCC (2014). Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to The Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Geneva: IPCC.
Joschinski, J., and Bonte, D. (2020). Diapause is not selected as a bet-hedging strategy in insects: a meta-analysis of reaction norm shapes. bioRxiv [Preprint]. doi: 10.1101/752881
Kelly, M. (2019). Adaptation to climate change through genetic accommodation and assimilation of plastic phenotypes. Philos. Trans. R. Soc. B 374:20180176. doi: 10.1098/rstb.2018.0176
Kivelä, S. M., Välimäki, P., and Gotthard, K. (2016). Evolution of alternative insect life histories in stochastic seasonal environments. Ecol. Evol. 6, 5596–5613. doi: 10.1002/ece3.2310
Krueger, D. A., and Dodson, S. I. (1981). Embryological induction and predation ecology in Daphnia pulex. Limnol. Oceanogr. 26, 219–223. doi: 10.4319/lo.1981.26.2.0219
Kærn, M., Elston, T. C., Blake, W. J., and Collins, J. J. (2005). Stochasticity in gene expression: from theories to phenotypes. Nat. Rev. Genet. 6, 451–464. doi: 10.1038/nrg1615
Lane, J. E., McAdam, A. G., McFarlane, S. E., Williams, C. T., Humphries, M. M., Coltman, D. W., et al. (2018). Phenological shifts in North American red squirrels: disentangling the roles of phenotypic plasticity and microevolution. J. Evol. Biol. 31, 810–821. doi: 10.1111/jeb.13263
Lenton, T. M., Dakos, V., Bathiany, S., and Scheffer, M. (2017). Observed trends in the magnitude and persistence of monthly temperature variability. Sci. Rep. 7:5940. doi: 10.1038/s41598-017-06382-x
Li, X.-Y., Lehtonen, J., and Kokko, H. (2017). Sexual reproduction as bet-hedging [preprint]. bioRxiv. doi: 10.1101/103390
Luquet, E., and Tariel, J. (2016). Offspring reaction norms shaped by parental environment: interaction between within- and trans-generational plasticity of inducible defenses. BMC Evol. Biol. 16:209. doi: 10.1186/s12862-016-0795-9
Marcovitch, S. (1923). Plant lice and light exposure. Science 58, 537–538. doi: 10.1126/science.58.1513.537-a
Marshall, D. J., Bonduriansky, R., and Bussière, L. F. (2008). Offspring size variation within broods as a bet-hedging strategy in unpredictable environments. Ecology 89, 2506–2517. doi: 10.1890/07-0267.1
Maxwell, C. S., and Magwene, P. M. (2017). When sensing is gambling: an experimental system reveals how plasticity can generate tunable bet-hedging strategies. Evolution 71, 859–871. doi: 10.1111/evo.13199
Nussey, D. H., Postma, E., Gienapp, P., and Visser, M. E. (2005). Selection on heritable phenotypic plasticity in a wild bird population. Science 310, 304–306. doi: 10.1126/science.1117004
Oostra, V., Saastamoinen, M., Zwaan, B. J., and Wheat, C. W. (2018). Strong phenotypic plasticity limits potential for evolutionary responses to climate change. Nat. Commun. 9:1005. doi: 10.1038/s41467-018-03384-9
Parmesan, C., and Yohe, G. (2003). A globally coherent fingerprint of climate change impacts across natural systems. Nature 421:37. doi: 10.1038/nature01286
Pélisson, P.-F., Bernstein, C., François, D., Menu, F., and Venner, S. (2013). Dispersal and dormancy strategies among insect species competing for a pulsed resource. Ecol. Entomol. 38, 470–477. doi: 10.1111/een.12038
Perez, M. F., and Lehner, B. (2019). Intergenerational and transgenerational epigenetic inheritance in animals. Nat. Cell Biol. 21, 143–151. doi: 10.1038/s41556-018-0242-9
Perrin, N. (2016). Random sex determination: when developmental noise tips the sex balance. BioEssays 38, 1218–1226. doi: 10.1002/bies.201600093
Piao, S., Liu, Q., Chen, A., Janssens, I. A., Fu, Y., Dai, J., et al. (2019). Plant phenology and global climate change: current progresses and challenges. Glob. Change Biol. 25, 1922–1940. doi: 10.1111/gcb.14619
Rando, O. J., and Verstrepen, K. J. (2007). Timescales of genetic and epigenetic inheritance. Cell 128, 655–668. doi: 10.1016/j.cell.2007.01.023
Saikkonen, K., Taulavuori, K., Hyvönen, T., Gundel, P. E., Hamilton, C. E., Vänninen, I., et al. (2012). Climate change-driven species’ range shifts filtered by photoperiodism. Nat. Clim. Change 2, 239–242. doi: 10.1038/nclimate1430
Scheiner, S. M., and Holt, R. D. (2012). The genetics of phenotypic plasticity. X. Variation versus uncertainty. Ecol. Evol. 2, 751–767. doi: 10.1002/ece3.217
Scholl, J. P., Calle, L., Miller, N., and Venable, D. L. (2020). Offspring polymorphism and bet hedging: a large-scale, phylogenetic analysis. Ecol. Lett. 23, 1223–1231. doi: 10.1111/ele.13522
Seger, J., and Brockmann, H. J. (1987). “What is bet-hedging?,” in Oxford Surveys in Evolutionary Biology, eds D. J. Futuyma and J. Antonovics (Oxford, UK: Oxford University Press), 182–211.
Simon, J.-C., Rispe, C., and Sunnucks, P. (2002). Ecology and evolution of sex in aphids. Trends Ecol. Evol. 17, 34–39. doi: 10.1016/S0169-5347(01)02331-X
Simons, A. M. (2011). Modes of response to environmental change and the elusive empirical evidence for bet hedging. Proc. R. Soc. B 278, 1601–1609. doi: 10.1098/rspb.2011.0176
Simons, A. M., and Johnston, M. O. (1997). Developmental instability as a bet-hedging strategy. Oikos 80, 401–406. doi: 10.2307/3546608
Simons, A. M., and Johnston, M. O. (2006). Environmental and genetic sources of diversification in the timing of seed germination: implications for the evolution of bet hedging. Evolution 60, 2280–2292. doi: 10.1111/j.0014-3820.2006.tb01865.x
Starrfelt, J., and Kokko, H. (2012). Bet-hedging–a triple trade-off between means, variances and correlations. Biol. Rev. 87, 742–755. doi: 10.1111/j.1469-185X.2012.00225.x
Stomp, M., van Dijk, M. A., van Overzee, H. M. J., Wortel, M. T., Sigon, C. A. M., Egas, M., et al. (2008). The timescale of phenotypic plasticity and its impact on competition in fluctuating environments. Am. Nat. 172, E169–E185. doi: 10.1086/591680
Tufto, J. (2015). Genetic evolution, plasticity, and bet-hedging as adaptive responses to temporally autocorrelated fluctuating selection: a quantitative genetic model. Evolution 69, 2034–2049. doi: 10.1111/evo.12716
Van Buskirk, J., and Steiner, U. K. (2009). The fitness costs of developmental canalization and plasticity. J. Evol. Biol. 22, 852–860. doi: 10.1111/j.1420-9101.2009.01685.x
Veening, J.-W., Smits, W. K., and Kuipers, O. P. (2008). Bistability, epigenetics, and bet-hedging in bacteria. Annu. Rev. Microbiol. 62, 193–210. doi: 10.1146/annurev.micro.62.081307.163002
Venable, D. L. (2007). Bet hedging in a guild of desert annuals. Ecology 88, 1086–1090. doi: 10.1890/06-1495
Volfson, D., Marciniak, J., Blake, W. J., Ostroff, N., Tsimring, L. S., and Hasty, J. (2006). Origins of extrinsic variability in eukaryotic gene expression. Nature 439, 861–864. doi: 10.1038/nature04281
Waddington, C. H. (1942). Canalization of development and the inheritance of acquired characters. Nature 150, 563–565. doi: 10.1038/150563a0
Woltereck, R. (1913). Weitere experimentelle untersuchungen über Artänderung, speziell über das Wesen quantitativer Artunterschiede bei Daphniden. Mol. Gen. Genet. 9, 146–146. doi: 10.1007/BF01876686
Woods, H. A. (2014). Mosaic physiology from developmental noise: within-organism physiological diversity as an alternative to phenotypic plasticity and phenotypic flexibility. J. Exp. Biol. 217, 35–45. doi: 10.1242/jeb.089698
Zhang, X.-S., and Hill, W. G. (2005). Evolution of the environmental component of the phenotypic variance: stabilizing selection in changing environments and the cost of homogeneity. Evolution 59, 1237–1244. doi: 10.1111/j.0014-3820.2005.tb01774.x
Keywords: phenotypic plasticity, trans-generational plasticity, bet-hedging, coin-flipping, gene-by-environment interaction, canalization, adaptation, climate change
Citation: Joschinski J and Bonte D (2020) Transgenerational Plasticity and Bet-Hedging: A Framework for Reaction Norm Evolution. Front. Ecol. Evol. 8:517183. doi: 10.3389/fevo.2020.517183
Received: 03 December 2019; Accepted: 05 November 2020;
Published: 26 November 2020.
Edited by:
Dalial Freitak, University of Graz, AustriaReviewed by:
Thomas Haaland, University of Zurich, SwitzerlandHeikki Helanterä, University of Oulu, Finland
Copyright © 2020 Joschinski and Bonte. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jens Joschinski, SmVucy5Kb3NjaGluc2tpQHVnZW50LmJl
 Jens Joschinski
Jens Joschinski Dries Bonte
Dries Bonte