Recovering the Metabolic, Self-Thinning, and Constant Final Yield Rules in Mono-Specific Stands

1. Introduction

Power-law relations in ecology remain a subject of fascination and research interest given their simultaneous ubiquity and practical significance (Thompson, 1942; Vogel, 1988; Niklas, 1994; Brown and West, 2000; Farrior et al., 2016; West, 2017). That a complex phenomenon such as competition among plants may be succinctly summarized by a power-law expression between measures of plant size (e.g., biomass) and crowding (e.g., density) is arguably one of the most important examples prominently featured in ecological textbooks and research articles alike (Perry et al., 2008). In terrestrial ecology, two power-law relations have emerged between biomass and density, both developed for dense mono-specific stands (Shinozaki and Kira, 1956; Yoda, 1963): the self-thinning or Yoda's rule and the constant final yield rule. The usage of the term “rule” reflects the extensive experimental evidence supporting the universal character of the exponents of the size-density relations. The significance of these power-law relations to crop production, forestry and ecosystem management is rarely in dispute and has been reviewed elsewhere (Willey and Heath, 1969; Drew and Flewelling, 1977, 1979; White, 1981; Westoby, 1984; Peet and Christensen, 1987; Friedman, 2016). However, the ecological mechanisms responsible for their apparent universal character remains a subject of inquiry and debate since their inception in 1864 (Spencer, 1864). This debate frames the scope of this review.

1.1. The Self-Thinning Rule

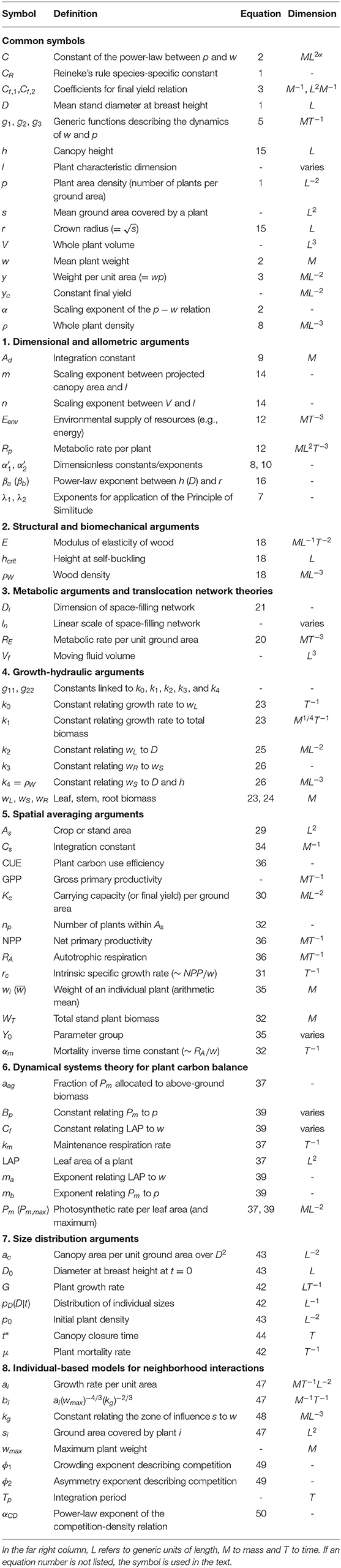
Self-thinning, depicted in Figure 1A, describes a natural process in a single stand whereby the number of plants per unit area (p) decreases as average plant (or mean individual) above-ground weight (w) increases as time t progresses. That is, the relation between w(t) and p(t) is associated with transient dynamics initiated when p(t) begins to decline from its initial value with increasing time due to overcrowding. Self-thinning is, by definition, a process arising from space-filling where vegetation has covered the whole area under consideration. Self-thinning is presumed to be a process intrinsic to many managed and unmanaged terrestrial plant communities, whose composition and structure are influenced by competition for resources available proportionally to space—whether above-ground (e.g., photosynthetically active radiation) or below-ground (e.g., water and nutrients) (Zhang et al., 2011; Hecht et al., 2016). Therefore, w-p temporal trajectories of self-thinning have considerable implications for forest management practices (Ge et al., 2017; Zhang et al., 2019). It is to be noted, however, that p(t) reductions due to ice storms, hurricanes, fires, diseases, or other disturbances are not considered in the w − p relations described by self-thinning.

FIGURE 1

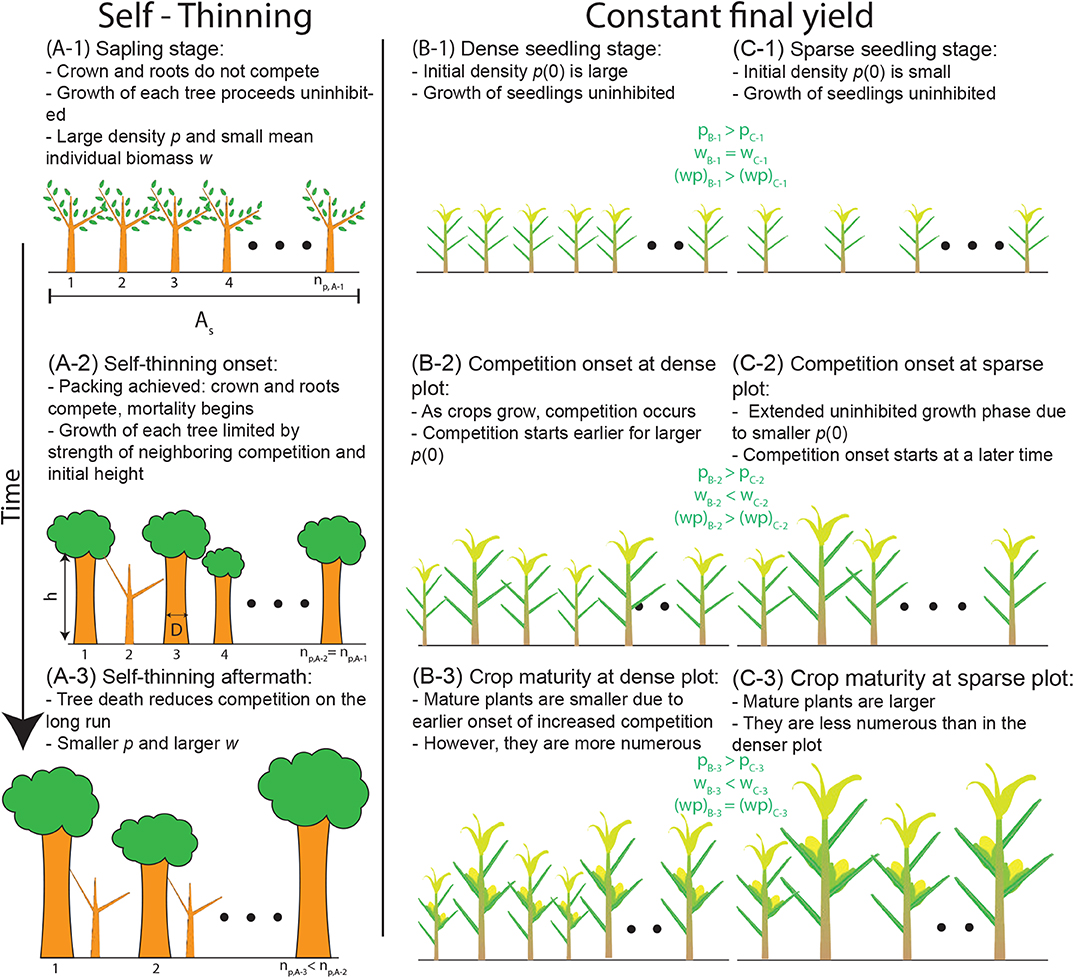
Figure 1. Conceptual representations of (A) self-thinning and (B,C) the constant final yield rule. (A) Self-thinning is initiated after crowding occurs, resulting in decreasing plant density p(t) with time t. (B) A high initial planting density p₀ is compensated for by poor growth conditions for each individual resulting in a small individual biomass w at harvest after an initial growth time period (B-3). (C) Conversely, a small p₀ allows for improved growth conditions leading to higher w at harvest after the same growth time period (C-3). The choice of a woody species in column (A) and a herbaceous species in columns (B,C) is to highlight the wide applicability of the self-thinning and constant final yield rules. Symbols: n_p refers to the number of plants in a plot, A_s is the plot ground area, D is the stem diameter, h is the plant height, p = n_p/A_s is the plant density, w is the mean individual biomass, and the product wp is the total biomass per unit ground area at time t. Subscripts refer to the different scenarios shown.

As shown in Figure 1A, self-thinning does not describe the entire temporal trajectory of w − p and only “kicks in” when the w(t) is large enough for a given initial density to initiate intense resource competition (i.e., space-filling). At the early stage of stand establishment, w(t) may increase rapidly while the density remains at its maximum p(t) = p₀, where p₀ = p(0) is the initial (or planting) density, until the space-filling requirement is reached.

Quantitative studies on a possible occurrence of universal w − p scaling emerged from data in the early 1930s in forestry (Reineke, 1933). Using measurements collected in many overstocked forests in California (USA), presumed to be experiencing self-thinning, p was empirically linked to the mean diameter at breast height D using

$\begin{array}{ll}log(p)=C_R-1.605log(D),& (1)\end{array}$

where C_R is a species specific constant. This equation states that plant density decreases as size increases across forest stands. Equation (1) is commonly referred to as Reineke's rule or Reineke's stand density index in forestry. Contrary to initial expectations by Reineke, the coefficient −1.605 appeared invariant across many species (12 out of 14 studied), age and environmental conditions. Thus, Reineke concluded that determining density of stocking in even-aged stands using Equation (1) has the advantages of freedom from correlation with age and site quality, and thus offers simplicity and general applicability.

Reineke's rule can be recast as a power-law of the form $p=e^{C_R}{D}^{-1.605}$. It is evident that when linking w to D using a power-law expression derived from allometry, Reineke's rule can also be formulated as a relation between plant biomass and crowding instead of plant size and crowding. Yoda (1963) and others later popularized similar power-law expressions extending the range downward from mature forest stands to seedlings of herbaceous plants,

$\begin{array}{ll}w(t)=Cp{(t)}^{-\alpha },& (2)\end{array}$

where both w(t) and p(t) are time-dependent (Figure 2). Equation 2 is hereafter referred to as Yoda's self-thinning rule when setting the exponent α = 3/2.

FIGURE 2

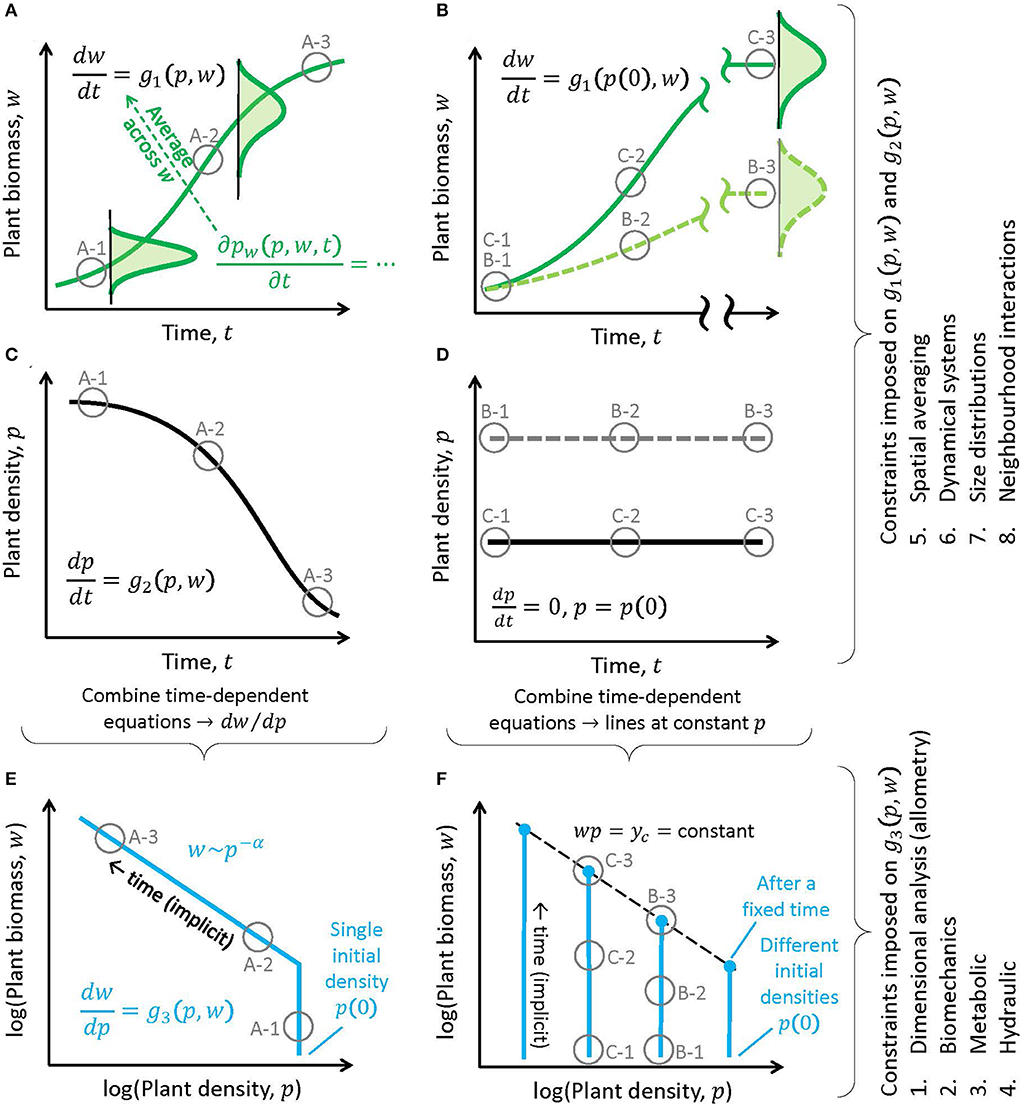
Figure 2. Linkages between dynamic equations for individual plant biomass (w) and density (p; Equation 5) for the self-thinning rule (w = Cp^−α; left panels) and the constant final yield rule (y_c = wp; right panels). (A,B) Illustration of the time evolution of w (green curves: mean biomass; green curves with shaded area: probability densities of individual biomass in size-structured models). (C,D) Illustration of the time evolution of p. Combining the dynamic equations in subplots (A–C) and (B–D), respectively, leads to a single equation describing trajectories in the w − p phase space (Equation 6): (E) when starting from a single initial density, different experiments and arguments show that α could vary from 1 to 3/2, or (F) multiple stands starting from different sowing densities achieve the same biomass per unit area y at a fixed point in time after sowing. Brackets right of the subplots: how constraints are imposed on the functions g_1(.), g_2(.), and g_3(.) of Equations (5) and (6); constraint numbering refers to the model categories discussed in the text (see also Figure 3). Gray circles and labels correspond to the scenarios depicted in Figure 1.

The generality of this expression and the limited variability of the exponent α imply that annual and perennial crops, herbaceous plants, and trees are expected to respond to crowding in a surprisingly similar manner (White and Harper, 1970; Gorham, 1979; Antonovics and Levin, 1980). Moreover, density manipulation experiments seem to yield α = 3/2, yet C varies (Dean and Long, 1985). An α ≈ 3/2 was reported even in mixtures of Sinapis alba and Lepidium sativum, sown together at high densities, after having undergone collective self-thinning as described elsewhere (Bazzaz and Harper, 1976) (see Table S1). Nevertheless, some variability in α has been found (typically between 1 to 3/2), based on both theoretical arguments (reviewed in section 2) and empirical evidence, motivating this review.

1.2. The Constant Final Yield Rule

Equation (2) relates trends of w(t) and p(t) with time t in a single stand, but these two quantities can also be multiplied to calculate the biomass per unit area y(t) = w(t)p(t). The constant final yield rule applies when stands sown at different initial densities p₀ all achieve the same biomass per unit area or yield y_c at a fixed time after sowing (i.e., y_c ≠ f(p₀); Figures 1B,C, 2). To illustrate how this rule can be obtained, relations between initial planting density and stand-level yield of the following form are considered (Shinozaki and Kira, 1956; Holliday, 1960; Willey and Heath, 1969; Watkinson, 1980)

$\begin{array}{ll}\frac{1}{y(p_0|t)}=\frac{C_{f,1}(t)}{p_0}+C_{f,2}(t),& (3)\end{array}$

where y is a function of p₀ across stands at a fixed time t after sowing. In Equation (3), C_f,1 and C_f,2 are species-specific parameters that change with time (Kikuzawa, 1999). When intense resource competition has had long enough time to appreciably affect stand structure (t >> 0 where t = 0 is sowing time), the constant final yield rule dictates that $C_{f,1}{p}_0^{-1}$ becomes small compared to C_f,2 and $y(p_0|t)=y_c(t)=C_{f,2}^{-1}(t)$ (Figure 1).

When density-driven mortality or self-thinning is absent (i.e., p(t) = p₀), this rule leads to an exponent −1 between w(p₀|t) and p₀, as it can be shown by multiplying both sides of Equation (3) by p₀, and recalling that y(t) = w(t)p(t). This gives a relation between mean individual plant mass at steady-state and initial density,

$\begin{array}{ll}\frac{1}{w(p_0|t)}=C_{f,1}(t)+C_{f,2}(t)p_0,& (4)\end{array}$

or $w(p_0|t)=C_{f,2}(t)p_0^{-1}$ when C_f,1 is negligible compared to C_f,2 p₀ as noted earlier. Equation (4) describes how w varies with p₀ at a fixed time after sowing (comparing different stands) whereas Equation (2) describes temporal changes in w on the same stand.

In contrast to Equation (4), Equation (3) also applies with the presence of mortality. In other words, the constant final yield rule and density-driven mortality, or self-thinning, are not mutually exclusive. Constant final yield has received experimental support in crops (Shinozaki and Kira, 1956; Holliday, 1960) and in a number of tree species in forest stands (Pacala and Weiner, 1991; Xue and Hagihara, 1998; Kikuzawa, 1999) (Table S1).

1.3. Interpreting Self-Thinning Exponents

A range of α values can be derived from contrasting theoretical arguments suggesting that α = 3/2 (for the self-thinning rule) and α = 1 (for constant, time-independent yield y ≠ f(t)) are not universal values, but rather that α may be context-dependent. On the one hand, if indeed different constraints lead to specific exponents, it might be possible to infer which processes shape forest development from observed α values. For example, different types of plant-plant interactions lead to contrasting exponents in individual-based models (as shown later in section 2.8). In turn, knowledge of the constraints at play would allow predicting how α shifts in response to changing conditions (e.g., climate and land use). On the other hand, as shown in the following, several arguments lead to similar α values, making it difficult to establish which one is dominant (Table 1).

TABLE 1

Table 1. Summary of the studied mechanisms leading to a different exponent α (Equation 2) along with the most pertinent equations and assumptions used.

An obvious question to pursue is how the exponent α reflects constraints or mechanisms controlling competition among mono-specific plants. The multiple mechanisms covered in this review are summarized in Table 1 and relations between them are featured in Figure 3. That multiple mechanisms can result in the same α is not new (Pickard, 1983). What is original here is the establishment of a link between the constraint(s) on competition, the transient dynamics leading to power-law relations between w and p, and the numerical value of α. Extensions proposed here are distinguished from published arguments in subsections labeled “Extended Analysis” (some of which are expanded in the Supplementary Material). This effort is motivated both by the lack of a synthesis of the mathematical foundations of the self-thinning and constant final yield rules, and by the need to quantify how the scaling exponents may vary under future conditions, with implications for agricultural and forest management.

FIGURE 3

Figure 3. The various mechanisms leading to the power-law relation w(t) = C[p(t)]^−α reviewed here. The mechanisms are grouped based on how growth and mortality are treated and whether time, age class, and resource competition among individuals are explicitly considered. Note: in all temporally dynamic mechanisms, mortality is explicit. However, an explicit account of growth does not preclude an implicit account of mortality.

2. Theory

Additional definitions are now introduced: l is a characteristic dimension of the plant, the one most sensitive to growth, V is the whole plant volume (product of projected crown area and height), ρ is the whole plant density, i.e., the individual plant mass over the entire individual plant volume, and s is the mean ground area covered by an individual plant or tree. From these definitions, w = ρV and crown radius is defined as $r=\sqrt{s}$. The symbols and definitions are listed in Table 2.

TABLE 2

Table 2. List of symbols with definitions, equation where they are first used, and dimensions.

Mechanistic studies, the subject of this review, typically begin with the carbon balance of the individual plant, where the carbon gains and costs as well as their constraints must be considered. Mortality and its associated effects on stand density must also be parameterized. Hence, these studies lead to a dynamical system coupling the individual scale (e.g., the single plant weight) with the plot or ecosystem scale (e.g., the density). This two-scale system may be represented by the general expression

$\begin{array}{l}\frac{dw}{dt}=g_1(p,w);\\ \frac{dp}{dt}=g_2(p,w),& (5)\end{array}$

where g₁(.) and g₂(.) are functions that do not explicitly vary in time (i.e., the system of equations is autonomous) and must be determined from structural, hydraulic, energetic, and physiological constraints on competition. In this two-equation system, t can be eliminated to yield

$\begin{array}{ll}\frac{dw}{dp}=\frac{g_1(p,w)}{g_2(p,w)}=g_3(p,w).& (6)\end{array}$

Depending on the choices made for g₁(.) and g₂(.) [and thus for g₃(.)] or their constraints, a solution of the form w = Cp^−α can be recovered under certain conditions. The focus here is on the connection between the exponent α and the constraints imposed on g₁(.), g₂(.), or g₃(.). The tactics explored to solve Equation (6) for the various constraints include (Figure 3) (1) allometric constraints and dimensional analysis (Shinozaki and Kira, 1956; White and Harper, 1970; Miyanishi et al., 1979; Kikuzawa, 1999), (2) structural constraints and other biomechanical arguments (McMahon, 1973; Givnish, 1986), (3) energetic constraints, metabolic arguments, and network transport theories (West et al., 1997; Enquist et al., 1998), (4) hydraulic constraints (Niklas and Spatz, 2004), (5) spatial averaging arguments at extended lifespans (Roderick and Barnes, 2004), (6) dynamical systems theory (von Bertalanffy, 1957) where g₁(.) and g₂(.) are specified (Hozumi, 1977; Hara, 1984; Perry, 1984; Pahor, 1985; Dewar, 1993), and (7-8) models with local interactions for resources among individuals of different sizes, or where p is linked to the dynamics of w via neighborhood interactions shaping the competition for resources (Aikman and Watkinson, 1980; Adler, 1996; Li et al., 2000; Chu et al., 2010; Coomes et al., 2011; Deng et al., 2012; Lin et al., 2013). In short, these approaches differ based on how growth and mortality are treated, and whether time, size class, and resource competition among individuals are explicit in the model. The essential elements of these approaches are briefly reviewed and connections between them highlighted.

2.1. Mechanism 1: Dimensional Analysis and Allometric Constraints

The “Principle of Similitude” is a statement about the dimensional consistency of any mathematical expression relating physical quantities to each other, such as mass, length, and time as described in Equation (5) (Spencer, 1864). It states, simply, that terms on both sides of an equation describing a physical state need to have the same dimension. Although evident, its consequences, first pointed out by Fourier (in 1822), allow for significant results to be derived (Lemons, 2018). The “Principle of Similitude” is now invoked in the context of w-p power-law relations.

2.1.1. Extended Analysis: Applying the Principle of Similitude

The dimensions needed to describe dw/dp are mass ([M]) and length ([L]), where [M] and [L] signify units of mass and length. An expression for g₃(.) is sought by inspecting a list of variables it might depend on such as w, p, ρ, s, r, and then combining these variables in groups that preserve the dimensions of dw/dp. The analysis is focused only on the period where self-thinning occurs, i.e., p(t) < p₀, not the entire trajectory linking w to p at all times. Self-thinning only commences when the length scales associated with plant position in a stand (but not necessarily plant height) are related to p. This means that p must be retained to carry [L] into the equation for g₃(.). If g₃(.) is assumed to be independent of w, then the only mass unit available in this list of variables is ρ. Dimensional considerations of w and p alone (having dimensions of mass [M] and the inverse of surface area [L]⁻², respectively) result in

$\begin{array}{ll}\frac{dw}{dp}=\frac{\left[M\right]}{{\left[L\right]}^{-2}}\propto p^{{\lambda }_1}{\rho }^{{\lambda }_2}\propto {\left(\frac{1}{{\left[L\right]}^2}\right)}^{{\lambda }_1}{\left(\frac{\left[M\right]}{{\left[L\right]}^3}\right)}^{{\lambda }_2}.& (7)\end{array}$

Matching the units on the most left-hand side to the most right-hand side requires λ₂ = 1, and 2λ₁ + 3λ₂ = −2, or λ₁ = −5/2. Hence, $g_3(\rho ,p)\propto \rho p^{-5/2}$ (a power-law as expected from such dimensional analysis). Replacing the proportionality symbol with a dimensionless constant ${\alpha }_1^{\prime }$ results in

$\begin{array}{ll}\frac{dw}{dp}={\alpha }_1^{\prime }\rho p^{-5/2}.& (8)\end{array}$

Provided ρ is not impacted by p, although it can vary in time, the ordinary differential Equation (8) can be solved to yield

$\begin{array}{ll}w=A_d-(2/3){\alpha }_1^{\prime }{p}^{-3/2},& (9)\end{array}$

where A_d is an integration constant that must be determined from other considerations. This argument apparently recovers Yoda's rule without any explicit considerations to p declining with increasing t as necessary for self-thinning. However, assuming that the length scales are all related to p implicitly means that crowding has occurred.

Likewise, if w replaces ρ, then dimensional considerations alone result in

$\begin{array}{ll}\frac{dw}{dp}={\alpha }_2^{\prime }\frac{w}{p},& (10)\end{array}$

where ${\alpha }_2^{\prime }$ is a dimensionless constant. Solving this equation leads to $w=A_d{p}^{{\alpha }_2^{\prime }}$, which again is a power-law. In this case, dimensional analysis fails to determine the numerical value of the exponent ${\alpha }_2^{\prime }$, but it still predicts a power-law relation between w and p. Clearly, the choice of variables impacting g₃(.) or the constraints imposed on it affects the value of the exponent α. For example, if the constraint is a constant total mass in time (i.e., dy/dt = 0), then it directly follows that

$\begin{array}{ll}\frac{d(wp)}{dt}=w\frac{dp}{dt}+p\frac{dw}{dt}=0\Rightarrow \frac{dw}{dp}=-1\frac{w}{p}.& (11)\end{array}$

That is, the constant total mass in time acts as a new constraint, allowing the determination of ${\alpha }_2^{\prime }=-1$ and the achievement of a constant yield y_c.

The main constraint on the outcome of competition may be a constant energy (or limiting resource) per unit area supplied by the environment R_env. When this constant (in time) supply satisfies the ecosystem metabolic demands per unit area, R_env = pR_p, where R_p is basal metabolic rate per individual plant, then

$\begin{array}{ll}\frac{d{R}_{env}}{dt}=0=\frac{d(p{R}_p)}{dt}\Rightarrow \frac{dp}{p}=-1\frac{d{R}_p}{R_p}.& (12)\end{array}$

This system yields $p~R_p^{-1}$. In metabolic theory, R_p is uniquely determined by w and the temperature of the environment (Brown et al., 2004). Employing Kleiber's law (Kleiber, 1932)

$\begin{array}{ll}{R}_p~w^{3/4}& (13)\end{array}$

and inserting this result into $p~R_p^{-1}$, directly recovers the exponent α = 4/3 (i.e., the metabolic argument).

2.1.2. Allometry and Growth Habits as Constraints

Self-thinning is initiated when packing is achieved: the ground area is entirely covered by the plants or trees as discussed elsewhere (Miyanishi et al., 1979). It is emphasized that the probability that some local densities will achieve packing before the majority does is neglected, because p is a property that pertains to the whole ground area. If plant growth is three-dimensional (i.e., height and crown diameter are increasing proportionally with increasing individual biomass) and ρ is constant, then V ~ l³, w ~ ρl³, s ~ l². Self-thinning occurs when s ~ p⁻¹. When this point is reached, l ~ s^1/2 ~ p^−1/2. Thus, all length scales are now linked to p as foreshadowed earlier. Yoda's rule is directly recovered by noting that w ~ ρl³ ~ ρp^−3/2, which is the key result in Equation (9). This argument assumes that the increment of plant size is isometric and proportional in all three dimensions (Miyanishi et al., 1979). Linking w to l, and all length scales to p, is akin to setting g₃(.) of Equation (6) to uniquely depend on the density (p) over the course of self-thinning.

Other growth habits may now be analyzed, and two limiting cases are illustrated: prostrate ground cover plants (i.e., 2-D growth) to etiolated seedlings (i.e., 1-D growth). To place these growth habits in a framework that employs allometric scaling, it is assumed that V ~ l^m and s ~ lⁿ. Hence, w ~ ρl^m and at the incipient point of self-thinning, the condition s ~ p⁻¹ must be maintained. These assumptions lead to

$\begin{array}{ll}w=C{p}^{-m/n},& (14)\end{array}$

where m = 3 (i.e., 3-D growth) and n = 2 recovers Yoda's rule, and C is a proportionality constant. For prostrate ground cover plants, m = 2 and n = 2 resulting in w ~ p⁻¹. For etiolated seedlings, the cross-sectional area is assumed constant and growth only occurs in the vertical (a race to harvest light). Hence, m = 1 and, with mean ground area covered by a plant being constant, requires s to be constant and thus n = 0. Hence, w ~ p^−1/0 yields infinite exponent, or stated differently, no self-thinning is to be expected (Miyanishi et al., 1979).

2.1.3. Extended Analysis: Reineke's vs. Yoda's Rules

Having covered the growth habits, it is now instructive to distinguish between a vertical dimension (canopy height h) and a horizontal dimension (canopy radius r), which allow recasting Equation (14) as

$\begin{array}{ll}log(p)=\frac{n}{m}log(C)-\frac{n}{m}log\left[\rho (r^{2}h)\right],& (15)\end{array}$

where w = ρ(r²h). When Equation (15) is combined with an allometric expression linking h to r of the form $h~r^{{\beta }_a}$, and when relating r to stem diameter D of the form $r~D^{{\beta }_b}$ (Enquist et al., 2009), the outcome is

$\begin{array}{ll}log(p)=\frac{n}{m}log\left(\frac{C}{\rho }\right)-{\beta }_b(2+{\beta }_a)\frac{n}{m}log(D).& (16)\end{array}$

Comparing Equation (16) with Reineke's Equation (1) suggests that the exponents of the height-to-canopy radius (β_a) and canopy radius-to-stem diameter (β_b) allometries must be constrained by

$\begin{array}{ll}1.605\frac{m}{n}={\beta }_b(2+{\beta }_a).& (17)\end{array}$

For m = 3 and n = 2 (i.e., Yoda's rule), β_b(2 + β_a) ≈ 2.4. The immediate consequence of this combination is that V ~ (r²h) ~ D^2.4. Conversion of D to a characteristic scale l ~ r, results in $V~l^{\frac{2.4}{{\beta }_b}}$ and not V ~ l³. Notably, scaling relations discussed elsewhere (Enquist et al., 2009) provide β_a = 1.14 and β_b = 0.684 so that β_b(2 + β_a) ≈ 2.2, lower than the 2.4 value obtained above. Therefore, only for particular choices of the coefficient in Reineke's Equation (1) and of the scaling exponents β_a and β_b, can the relation V ~ l³ be recovered. In fact, this corroborates the point made by the incisive analysis of Weller (1987) that Yoda's exponent $\alpha =\frac{3}{2}$ may be the exception rather than the rule.

As the stand becomes crowded, more individuals are suppressed. Acclimation allows suppressed individuals to survive longer by decreasing the carbon investment in diameter relative to height and maintaining smaller crowns closer to the top of the canopy. These adjustments decrease β_b of the entire stand. A reduction in β_b is expected to reduce the slope of the p − w scaling (e.g., m/n in Equation 17). The reduction in crown size of suppressed individuals reduces the wind-induced drag force, allowing these trees to maintain structural integrity despite the lower taper.

2.2. Mechanism 2: Structural and Biomechanical Constraints

Relations between height and diameter can be derived to further constrain allometric scaling based on self-buckling or structural considerations. The key observation regarding self-buckling for trees is that the critical height for buckling (h_crit) plotted against tree base diameter (D) follows a power-law of the form $h_{crit}~D^{2/3}$ for nearly every American tree species (McMahon, 1973) (Table S1). This h − D scaling was consistent with the incipient point of buckling of tall columns (due to their own weight) given by the elastic buckling criterion (or Euler-Greenhill formula)

$\begin{array}{ll}{h}_{crit}\propto \frac{E}{{\rho }_W}{D}^{2/3},& (18)\end{array}$

where E is the modulus of elasticity, ρ_W is the density of wood. If Equation (18) describes an allometric scaling law, then for 3-D growth, l ~ D, $V~D^2{h}_{crit}~D^{8/3}$, and s ~ D². Employing once more the allometric scaling framework presented previously, w ~ (ρ)l^{m = 8/3}, and s ~ l^{n = 2}. Inserting these estimates of m and n in Equation (14) result in (McMahon, 1973)

$\begin{array}{ll}w~p^{-4/3}.& (19)\end{array}$

This scaling is intermediate between a steady state biomass per individual (α = 1) and Yoda's rule (α = 3/2). Connections between the aforementioned scaling law in Equation (19) and metabolic arguments (i.e., Kleiber's law) have already been noted (McMahon, 1973). However, the scaling law in Equation (19) can also be derived without resorting to self-buckling, using a variant of the growth-hydraulic constraint (Niklas and Spatz, 2004), as well as metabolic constraints, as described later on. Additional implications of self-buckling are explored in the Supplementary Material.

2.3. Mechanism 3: Metabolic Limitations

Metabolic arguments and their connection to the exponent α have been popularized by the work of West, Enquist, and Brown (West et al., 1997; Enquist et al., 1998; Brown et al., 2004). To sustain a total biomass per unit ground area wp requires a rate of energy (or other limiting resource) supply from the environment per unit area of at least R_E = pR_p, where R_p is the metabolic rate per plant (energy or resource use per time per plant). In living organisms, the basal metabolic rate R_p varies with size and is given by Kleiber's law (Equation 13) (Kleiber, 1932; Banavar et al., 1999). Hence, $R_E=p{R}_p~p{w}^{3/4}$.

2.3.1. A Steady State Resource Balance

The case of a limiting essential resource is first considered. When the external environmental supply of this resource (= E_env) is balanced, or fully exploited, by the stand (or ecosystem) metabolic demand R_E, then

$\begin{array}{ll}{E}_{env}=R_E~p{w}^{3/4},& (20)\end{array}$

resulting in w ~ p^−4/3 when E_env is set to a constant (e.g., a given annual shortwave radiation or precipitation rate). For all practical purposes, Equation (20) is an equilibrium argument (constant resource supply) with a constraint shaping g₁(.) in Equation (5) at a given supply E_env. It is also interesting to note that Equation (20) suggests a link between the constant C in Equation (2) and environmental conditions, as $C~E_{env}^{4/3}$. The debate on the difference between the 4/3 and the 3/2 exponents are highlighted as they offer a new perspective on links between the scaling exponent α and the constraints. The α = 4/3 exponent has experimental support when average “mature” plant weight is plotted against p₀ for different species spanning nine orders of magnitude by weight (Enquist et al., 1998) and appears consistent with a number of spatially explicit simulation studies discussed elsewhere (Deng et al., 2012) (Table S1). Such an inter-species comparison, however, fundamentally differs from plotting w(t) against p(t) for a single stand across time (Yoda, 1963).

2.3.2. Extended Analysis: Constraints on the Trans-location Network Distribution

It has been argued that distributed trans-location networks evolved from a need for effective connectivity with increased size (i.e., analogous to the economy of scale in microeconomics). Distributed trans-location networks occur in biological systems (including respiratory networks) and in inanimate systems alike (e.g., river networks). The flow rate in an arbitrary trans-location network can be derived as a function of the local connectivity as discussed elsewhere (Banavar et al., 1999). For the problem at hand, this trans-location network may represent the phloem, where metabolic products derived from photosynthesis (mainly carbohydrates) are being translocated from leaves, or the xylem, where water is transported to the leaves. In this network derivation, a moving fluid volume filling the network is assumed to be V_f. The V_f scales with the product of the number of links in the network and the distance between nodes. In a D_i-dimensional space-filling network (i.e., a network that can deliver fluid to all the domain), the number of links is proportional to $l_n^{D_i}$, where l_n is a linear scale of the network. The distance among links is also proportional to l_n. Hence, $V_f~l_n^{D_i}\times l_n=l_n^{D_i+1}$, or $l_n~V_f^{1/(D_i+1)}$. For a constant fluid density, w ~ V_f and $R_p~l_n^{D_i}$. It directly follows that the metabolic rate for an individual is given by

$\begin{array}{ll}{R}_p~w^{D_i/(1+D_i)}.& (21)\end{array}$

For R_E = pR_p = E_env = constant, it follows that $R_p~p^{-1}$ as before. As a result, Equation (21) is used to obtain

$\begin{array}{ll}w~p^{-(1+1/D_i)}.& (22)\end{array}$

For D_i = 3, the 3/4 metabolic scaling exponent is recovered from Equation (21), and α = 4/3 is now recovered from Equation (22) in a manner that is compatible with Kleiber's law without resorting to critical height and self-buckling. Interestingly, the analysis here also suggests that Yoda's 3/2 scaling exponent is recovered for D_i = 2 (i.e., $R_p~w^{2/3}$). A 2-D translocation network may be incompatible with Yoda's original assumption of proportional growth in all three dimensions. This incompatibility is one of the salient features of the aforementioned controversy surrounding the 4/3 vs. the 3/2 self-thinning scaling exponent.

2.4. Mechanism 4: Hydraulic Constraints on Growth

In addition to structural and energy supply constraints discussed as mechanisms 2 and 3, a hydraulic constraint can be formulated by imposing a steady-state transpiration rate from the roots to the leaves. This constraint may be viewed as a “network-on-network” supply constraint. There are three networks that must be coordinated: a root network that must harvest water and nutrients from the soil, a xylem network that must deliver water to leaves, and distributed end-nodes for water loss through leaves. It is assumed that these three networks are sufficiently coordinated so that no severe “bottleneck” in one network routinely impairs the function of the other two networks (Thompson and Katul, 2012; Huang et al., 2018). Based on this view, a simplified version of a growth-hydraulic constraint (Niklas and Spatz, 2004) is now reviewed. In this mechanism, it is assumed that the annual increment of dry matter per plant scales (i) linearly with standing leaf biomass w_L that provides metabolic products and (ii) with w^3/4 as in Kleiber's law. Hence, equating these two assumptions results in

$\begin{array}{ll}{k}_0{w}_L=k_1{w}^{3/4},& (23)\end{array}$

where k₀ and k₁ denote allometric constants. With w defined by the sum of leaf, stem, and root mass (i.e., w = w_L + w_S + w_R) results in

$\begin{array}{ll}{k}_0{w}_L=k_1{(w_L+w_S+w_R)}^{3/4}.& (24)\end{array}$

The hydraulic component of this argument is framed as follows (Niklas and Spatz, 2004): the amount of water absorbed by roots per unit time must pass through stems, experience a phase transition and then exit through the stomata distributed on leaf surfaces. Because this amount of water loss is conserved throughout the plant (i.e., no storage or capacitive effects on time scales commensurate with stand development), w_L must scale with the hydraulically functional cross-sectional area of stems and roots (sapwood area). The key assumption is that the sapwood area is proportional to the square of the stem diameter (i.e., D²). The assumption need not imply that the diameter of the water transporting vessels is proportional to D, but that D reflects the total number of vessels of fixed diameter. Viewed from this perspective, this assumption may also be interpreted as another expression of the so-called da Vinci rule, or the pipe flow model of Shinozaki (Shinozaki et al., 1964; Horn, 2000), and leads to $w_L=k_2{D}^2$. Substituting w_L in Equation 24 and rearranging the terms lead to

$\begin{array}{ll}{\left(\frac{k_0}{k_1}{k}_2{D}^2\right)}^{4/3}-k_2{D}^2=w_S+w_R.& (25)\end{array}$

Two additional assumptions are required (Niklas and Spatz, 2004): an allometric relation between root and stem biomass (w_R = k₃w_S) and a relation between stem biomass and stem volume (i.e., $w_S=k_4(D^{2}h))$, where k₄ = ρ_W, but the notation of Niklas and Spatz (2004) is maintained in the following. Hence, Equation (25) can be formulated as

$\begin{array}{ll}{\left(\frac{k_0}{k_1}{k}_2{D}^2\right)}^{4/3}-k_2{D}^2=(1+k_3)k_4(D^{2}h),& (26)\end{array}$

from which it follows that h ∝ D^2/3 and $w_S\propto D^{8/3}$. Upon comparison with the Euler-Greenhill formula (Equation 18), the same h ∝ D^2/3 scaling has been recovered from metabolic and hydraulic constraints acting in concert (i.e., in coordination), not from mechanical limits on tree height, nor from energy supply by the environment. Combining these outcomes with w ∝ (D²h) = D^8/3, s ~ D², and s ~ p⁻¹ (or D ∝ p^−1/2) at the point where self-thinning commences, recovers the metabolic formulation w ~ p^−4/3. Here, geometric packing (i.e., s ~ p⁻¹) leading to self-thinning is necessary to arrive at α = 4/3, which was not the case in the metabolic arguments.

2.4.1. Extended Analysis: An Alternative Hydraulic Link to Stem Diameter

The aforementioned arguments may be generalized to include other linkages between sapwood area and stem diameter. One such linkage is the so-called Hess-Murray law that predicts the optimal blood vessel tapering in cardiovascular systems. This linkage leads to $w_L\propto D^3$ (Murray, 1926; McCulloh et al., 2003) instead of D². Starting again from Equation (24), the aforementioned argument leads to

$\begin{array}{ll}\frac{{\left(\frac{k_0}{k_1}{k}_2{D}^2\right)}^{4/3}-k_2{D}^3}{D^2(1+k_3)k_4}=h,& (27)\end{array}$

or h ~ D^2/3 for small D only, not for any D as it was the case for the Da Vinci rule. For intermediate or large D, $h~g_{11}{D}^{2/3}-g_{22}D$ (g₁₁ and g₂₂ are constants linked to k₀, k₁, k₂, k₃, k₄), which does not exhibit a unique exponent provided $D<{(g_{11}/g_{22})}^3$. The connection between the da Vinci rule (along with the pipe flow model) and water transport has been the subject of debate outside the scope of the present work (Bohrer et al., 2005), with some arguing that the da Vinci rule is compatible with structural, rather than water transport theories (Eloy, 2011).

2.5. Mechanism 5: Spatial Averaging Arguments

This approach explicitly considers that stands generally comprise individuals of different sizes, even in even-aged mono-cultures, owing to small genetic variability as well as variations in site micro-environmental factors, impacting growth potential and access to resources. It is thus necessary to consider the effect of spatial averaging over individuals within the crop or stand area A_s. By definition, p = n_p/A_s where n_p is the number of individual plants within area A_s. Also, the arithmetic mean weight of all individuals within A_s is defined as

$\begin{array}{ll}\overline{w}=\frac{1}{n_p}{\displaystyle \sum _{i=1}^{i=n_p}}{w}_i,& (28)\end{array}$

where w_i is the weight of each individual plant. Equation (28) can be rearranged to yield (Roderick and Barnes, 2004)

$\begin{array}{ll}\overline{w}=\left(\frac{A_s}{n_p}\right)\frac{1}{A_s}{\displaystyle \sum _{i=1}^{i=n_p}}{w}_i=(p^{-1})\frac{1}{A_s}{\displaystyle \sum _{i=1}^{i=n_p}}{w}_i.& (29)\end{array}$

It was suggested that over an extended life span, the total stand biomass dynamics eventually reaches a steady-state such as in the experiments of Shinozaki and Kira (1956) on soybean, a herbaceous species, where mortality was absent (Table S1). If such steady-state conditions are attained within a single stand, then

$\begin{array}{ll}\frac{1}{A_s}{\displaystyle \sum _{i=1}^{i=n_p}}{w}_i=K_c,& (30)\end{array}$

where K_c is a constant carrying capacity determined by the available resources supporting maximum biomass per unit area. Equation (30) implies that α = 1 because $w=K_c{p}^{-1}$ as long as K_c is constant. The derivation of Equation (30) makes no assumption about p₀, p(t) or w(t), or that y(t) follows logistic growth as in the competition-density effect (Shinozaki and Kira, 1956; Xue and Hagihara, 1998). Equation (30) was also shown to apply for a pine stand (Xue and Hagihara, 1998).

For prostrate ground cover plant growth, the emergent scaling law was already shown to be w(t) ~ p(t)⁻¹ using an entirely different set of assumptions. Evidently, the α = 1 scaling exponent can be recovered from multiple mechanisms. It is demonstrated next that (i) w(t) ~ p(t)⁻¹ may still reflect a correct minimum exponent under weak self-thinning style competition and (ii) novel links can be established between the newly derived exponent here and other “conservative” ratios describing stand carbon dynamics.

2.5.1. Extended Analysis: Recovering the α = −1 Exponent From a Dynamical System

The previous argument can be extended by relaxing the assumption of steady state, showing that the same result is obtained in a more general case. As a point of departure from prior work (Roderick and Barnes, 2004), the α = 1 exponent is now analyzed using the framework of Equation (5). To facilitate this analysis, the total stand weight $W_T=n_p\overline{w}$ is assumed to vary logistically in time using (Verhulst, 1838)

$\begin{array}{ll}\frac{d{W}_T}{dt}=r_c{W}_T\left(1-\frac{W_T}{A_s{K}_c}\right),& (31)\end{array}$

where r_c is the intrinsic growth rate. This assumption has been used in the original work of Shinozaki and Kira (1956) at the individual level and generalized by others at the stand level (e.g., Xue and Hagihara, 1998). Such assumption is equivalent to prescribing g₁(.) and g₂(.) of Equation (5). Instead of analyzing the dynamics at an equilibrium point W_T/A_s = K_c being constant, it is instructive to explore the transient dynamics where n_p = pA_s begins to decline in time. This type of competition is intended to resemble some but not all aspects of self-thinning (i.e., being a transient and operating when dn_p/dt < 0) while maintaining a density-dependent logistic form for total biomass (instead of constant K_c) used by Shinozaki and Kira (1956). In particular, we ask under what conditions such a “stylized competition” remains compatible with scaling laws associated with a steady state yield or the self-thinning rule (or intermediates). A minimal model describing the n_p decline is

$\begin{array}{ll}\frac{d{n}_p}{dt}=A_s\frac{dp}{dt}=A_s{g}_2(p)=-{\alpha }_m{n}_p,& (32)\end{array}$

where α_m is a mortality inverse time constant. Equation (32) specifies the reduction in the number of plants through mortality as proportional to the number of plants n_p thus making n_p an exponential function of time. Again, viewed from the perspective of Equations (5), these approximations are equivalent to specifying g₂(p) and g₁(w, p) via Equation (31) when recalling that W_T = n_pw. By eliminating time t in Equations (31) and (32) (as before, to obtain Equation 6), an ordinary differential equation describing the variations of w with n_p can be explicitly derived,

$\begin{array}{ll}\frac{dw}{d{n}_p}+\frac{w}{n_p}\left[1+\frac{r_c}{{\alpha }_m}\left(1-\frac{n_{p}w}{K_c{A}_s}\right)\right]=0.& (33)\end{array}$

The general solution of Equation (33) is given by

$\begin{array}{ll}w(t)=\frac{A_s}{n_p(t)}{K}_c\left[\frac{1}{1+C_s{K}_c{A}_s{n}_p{(t)}^{(r_c/{\alpha }_m)}}\right],& (34)\end{array}$

where C_s is an integration constant. Noting again that $p^{-1}=A_s/n_p$, Equation (34) can be expressed as

$\begin{array}{ll}w(t)=K_{c}p{(t)}^{-1}\left[\frac{1}{1+Y_{0}p{(t)}^{(r_c/{\alpha }_m)}}\right],& (35)\end{array}$

where $Y_0=C_s{K}_c{A}_s^{(r_c/{\alpha }_m+1)}$. Equation (35) recovers $w(t)=K_{c}p{(t)}^{-1}$ when $Y_0{p}^{(r_c/{\alpha }_m)}<<1$. When $Y_0{p}^{(r_c/{\alpha }_m)}>>1$, Equation (35) predicts a $w~p^{-\left[1+(r_c/{\alpha }_m)\right]}$. For $Y_0{p}^{(r_c/{\alpha }_m)}$ of the order of unity, no unique scaling exponent exists, although any power-law approximation to this solution must yield exponents exceeding unity in magnitude, which is the sought result. This finding offers an explanation as to why the exponent α varies between 1 and 2 across many data sets a priori conditioned on dn_p/dt < 0 (i.e., when mortality begins to play a role).

2.5.2. Extended Analysis: the Effects of Invariant Carbon-Use Efficiency on Self-Thinning

The quantity r_c/α_m reflects the ratio of two time scales: one associated with net carbon gain of an individual plant (1/r_c) and another associated with its mortality (1/α_m). The time scale for carbon gain may be associated with the net primary productivity (NPP) of an individual plant, so that r_c ~ NPP/w (Thurner et al., 2016). In self-thinning stands where carbon loss in respiration is not compensated by photosynthesis in highly suppressed individuals (under light competition), it may be (simplistically) assumed that carbon starvation is the causal mechanism of mortality. Thus, the mortality time scale is associated with autotrophic respiration R_A, so that α_m ~ R_A/w and

$\begin{array}{ll}\frac{r_c}{{\alpha }_m}=\frac{\text{NPP}}{R_A}=\frac{\text{CUE}}{1-\text{CUE}},& (36)\end{array}$

where NPP=CUE×GPP, GPP is the gross primary productivity, R_A=GPP-NPP=(1-CUE) GPP, and CUE is the plant carbon use efficiency (0 < CUE < 1). Therefore, this link between r_c/α_m and CUE offers a new perspective about α and carbon use efficiency; i.e., $\alpha =1+(r_c/{\alpha }_m)={(1-\mathrm{\text{CUE}})}^{-1}$. This estimate of α is expected to be an upper limit, because α_m is likely to be underestimated when mortality time scale is estimated from R_A.

The value of plant CUE typically ranges between 0.4 and 0.8 depending on species, plant age, and growing conditions, with values even lower than 0.4 in mature trees and generally higher values in rapidly growing crop species (Manzoni et al., 2018). For an intermediate CUE=0.47 (typical in forests; Waring et al., 1998), large scaling exponents are obtained, w ~ p^−1.88 as already foreshadowed. For relatively inefficient plants with CUE=1/3, w ~ p^−3/2, recovering Yoda's rule. The metabolic argument w ~ p^−4/3 can only be recovered for CUE=1/4. This argument is prone to large uncertainties due to both the qualitative link between parameters r_c and α_m, and CUE, and the uncertainties in CUE estimates. Nevertheless, plants that are more effective in converting resources to biomass are expected to exhibit steeper w − p scaling relations, a conjecture to be explored in future studies.

Up to this point, it was assumed that at the individual plant scale, the entire biomass captured in w is alive and contributes to respiration. However, for a preset total biomass, lower initial density may lead to greater live crown ratio at the incipient point of self-thinning. Hanging onto large branches at the bottom of long crowns contributes little to annual photosynthesis (Oren et al., 1986), but requires investment in maintaining active sapwood, cambium, and phloem. Thus, the initial planting density can play a role in determining the fraction of live to total biomass at the start of self-thinning. At that point, despite similarities in stand density, mean total individual tree biomass (Peet and Christensen, 1987), and leaf area (Dean and Long, 1985), stands characterized by individuals with a higher fraction of live to total biomass may exhibit higher whole-tree respiration rates per unit of leaf area and, therefore, reduced CUE and α.

2.6. Mechanism 6: Dynamical Systems Theories for Plant Carbon Balance

A number of approaches have been proposed that recover the self-thinning rule from a mechanistic representation of the plant carbon balance (Hozumi, 1977; Pickard, 1983; Hara, 1984; Perry, 1984; Pahor, 1985; Voit, 1988). Common to all these approaches is the so-called von Bertalanffy equation (von Bertalanffy, 1957; Perry, 1984) or a variant of it that applies to individual plants as discussed in Figure 3. Using the framework of Equation (5), this equation represents g₁(w, p) as

$\begin{array}{ll}\frac{dw}{dt}=g_1(w,p)=a_{ag}{P}_m(p)\text{LAP}(w)-k_{m}w,& (37)\end{array}$

where a_ag is the fraction of photosynthesis allocated to biomass, LAP is the leaf area of an individual plant, assumed to vary with w, P_m is the photosynthetic rate per unit leaf area, varying with p (e.g.,due to light competition), and k_m is the rate of maintenance respiration (whereas mortality is described by Equation 32). The overarching assumption of von Bertalanffy equation is that resource acquisition must traverse a limiting surface area (here LAP; scales as ~ l²) whereas respiratory and maintenance costs vary with plant size (or mass, w; scales as ~ l³). Variants to Equation (37) include complex expressions for photosynthetic gains, respiratory losses, connections between P_m and p (such connections are the subject of spatially explicit models discussed later), and the partitioning of w into metabolically active and inactive parts.

The goal of this section is not to review all of them but to offer links between the von Bertalanffy equation and the general framework set in Equation (5). Equation (37) is coupled to Equation (32) after eliminating time t and substituting n_p = A_sp to yield

$\begin{array}{ll}\frac{dw}{dp}-\frac{k_m}{{\alpha }_m}\frac{w}{p}=-\frac{1}{p}\frac{a_{ag}{P}_m\text{LAP}}{{\alpha }_m}.& (38)\end{array}$

Mechanistic models link LAP to w using allometric rules and P_m to p assuming that increases in p reduces the main resource driving photosynthesis such as photosynthetically active radiation (Perry, 1984). For example, LAP and P_m may be expressed as

$\begin{array}{l}\text{ LAP}=C_f{w}^{m_a};\\ \frac{P_m}{P_{m,max}}=1-exp\left[-B_p{p}^{m_b}\right].& (39)\end{array}$

Here, m_a ≈ 0.81 and C_f ≈ 0.011 when LAP is treated as all sided (in m²) and w is expressed in grams (determined for a wide range of species), whereas B_p = 4.61 and m_b was varied as a control parameter (plausible values for most species in Perry, 1984). The representation in Equation (39) preserves the autonomous nature of Equation (38) thereby linking the phase-space of the p − w trajectories directly to model parameters. It also provides a complete description of g₃(w, p) in Equation (6). However, a unique power-law solution of the form w = Cp^−α is not apparent even though model calculations suggest an approximate power-law with exponent α = 1.0 − 1.8 for plausible parameter combinations. We now seek to clarify the connection between the von Bertalanffy equation and the exponent α for certain approximations revising the mathematical form of g₃(.).

2.6.1. Extended Analysis: Power-Laws From the von Bertalanffy Equation

To extract power-law features from the von Bertalanffy equation and place them in the framework of Equation (5), it is assumed again that individual GPP = a_agP_mLAP = R_A/(1 − CUE) and R_A ≈ k_mw, resulting in an estimate of a_agP_mLAP = k_mw/(1 − CUE). Hence, Equation (38) reduces to

$\begin{array}{ll}\frac{dw}{dp}-\frac{w}{p}\frac{k_m}{{\alpha }_m}\frac{\text{CUE}}{\text{CUE}-1}=0.& (40)\end{array}$

The solution to Equation (40) is now a power-law of the form

$\begin{array}{ll}w~p^{-\frac{k_m}{{\alpha }_m}\frac{\text{CUE}}{\text{1– CUE}}}.& (41)\end{array}$

Yoda's rule is recovered when $(k_m/{\alpha }_m)=(3/2)({\mathrm{\text{CUE}}}^{-1}-1)$ whereas the metabolic exponent is recovered when $k_m/{\alpha }_m=(4/3)({\mathrm{\text{CUE}}}^{-1}-1)$. Because CUE ≈ 0.5 (Waring et al., 1998; Manzoni et al., 2018), this analysis leads to a unique relation between respiratory and mortality time scales, and the exponent α given by k_m/α_m ≈ 3/2, 4/3, or 1. That is, the exponent α may be related to the ratio of the two aforementioned time scales.

2.6.2. Phase Space Trajectories Constraints on α

Dynamical systems theory has been used to explore self-thinning empirically by modeling the w − p time-course in crowded plant populations (Hara, 1984). The dynamical system can be expressed in terms of relative quantities, namely (relative) mortality rate (i.e., $p^{-1}\frac{dp}{dt}$) and relative growth rate (i.e., $w^{-1}\frac{dw}{dt}$). Among the choices of the functions linking p and w to relative mortality and growth rate, generalized Gompertz functions are empirically well-supported (Hara, 1984; Tsoularis and Wallace, 2002). With such choices, the dynamical systems theory can establish explicit dependencies of the empirical coefficients and the exponent α and plausibility constraints. Such a plausibility constraint is the imposition that equilibrium points are stable fixed points (as expected in self-thinning). A key result is that several combinations of the empirical parameters of the Gompertz function lead to exponents commensurate with the “rule of constant yield” or Yoda's thinning rule, while other exponents are possible with other empirical parameter combinations. The details are illustrated in the Supplementary Material.

2.7. Mechanism 7: Size Distribution Arguments

The self-thinning rule can also be obtained by following the temporal evolution of a population of individuals characterized by a certain size, which is interpreted as a stochastic variable. Without loss of generality, stem diameter D can be considered as the relevant size and can be linked to plant height and mass using allometric relations. For size-structured populations, it can be shown that the distribution of individuals of size D conditioned at time t, p_D(D|t), is determined by the von Foerster equation (von Foerster, 1959; Hara, 1988; Kohyama, 1992; Strigul et al., 2008)

$\begin{array}{ll}\frac{\partial p_D(D|t)}{\partial t}=\frac{\partial \left[G(D,t)p_D(D|t)\right]}{\partial D}-\mu (D,t)p_D(D|t),& (42)\end{array}$

where G is the growth rate (i.e., G = dD/dt) and μ is a mortality rate applied to plant density. In addition, a boundary condition p_D(D₀|t = 0) (i.e., where D₀ is the diameter at birth) must be specified. In principle, the self-thinning and constant yield laws could be obtained from the solution p_D(D|t) of Equation (42) for specific choices of the functions G and μ, and the allometric relations between D and w. Here, a simplified approach is followed using the perfect crown plasticity rationale by Strigul et al. (2008) though by no means is this approach unique (Kohyama, 1992). As before, the focus is on a mono-specific, even-aged stand with negligible mortality until canopy closure, a constant growth rate (so that D(t) = D₀ + Gt), small but finite initial stem diameter and diameter variance (D₀ ≪ Gt), and constant allometric coefficient linking canopy area per unit ground area to stem diameter (here a_c =canopy area per unit ground area over D²). With these conditions and assumptions, integrating the distribution p_D(D|t) over all initial sizes, the total canopy area per unit ground area is calculated as,

$\begin{array}{ll}{\displaystyle {\int }_0^{\infty }}{p}_D(D_0|t=0)a_c{(D_0+Gt)}^2\text{d}{D}_0\approx a_c{p}_0{G}^2{t}^2,& (43)\end{array}$

where ${(D_0+Gt)}^2\approx {(Gt)}^2$ is the canopy area per unit area and p₀ is, as before, the initial plant density. When canopy closure occurs, the canopy area per unit ground area reaches 1. Hence, the canopy closure time t^* can be calculated as

$\begin{array}{ll}1=a_c{p}_0{G}^2{t}^2\Rightarrow t^{*}={\left(G\sqrt{a_c{p}_0}\right)}^{-1}.& (44)\end{array}$

Upon canopy closure (t > t^*), plant growth must adjust to maintain a closed canopy as time progresses, which requires lowering plant density through the death of suppressed, shaded plants according to,

$\begin{array}{ll}Gt={\left(a_c{p}_0\right)}^{-\frac{1}{2}}.& (45)\end{array}$

These constraints allow finding the scaling relation between plant biomass and density in the two regimes - before (t < t^*) and after (t > t^*) canopy closure. For t < t^*, plant biomass w ~ D²h, where h is the plant height as before. However, neither D nor h depend on plant density because they only depend on time before canopy closure. As a consequence, plant biomass w ~ p⁰ when t < t^*. In contrast, for t > t^*, plant biomass depends on plant density because after canopy closure Equation (45) yields,

$\begin{array}{ll}w~D^{2}h=G^2{t}^{2}h=h{\left(a_{c}p\right)}^{-1}~{\left(a_{c}p\right)}^{-\frac{3}{2}},& (46)\end{array}$

where isometric scaling of height and diameter (i.e., h ~ D) was assumed to recover Yoda's rule (last term).

2.8. Mechanism 8: Neighborhood Interaction Arguments

As a bridge to the general framework in Equation (5), the equations specifying g₁(w_i) for an individual i must now include interaction terms with adjacent individuals to explicitly account for competition. Upon specifying mortality and solving w_i for each individual, the solution yields the mean biomass w and g₂(p) by aggregating over all surviving individuals (i.e., the stand-scale). Hence, w(t) − p(t) trajectories are constructed thereby allowing the determination of α. The previously discussed carbon balance approaches only accounted for competition indirectly by varying the average individual's photosynthetic rate with p. Also, size-structured population approaches accounted for interactions among individuals implicitly. Individual-based models (Aikman and Watkinson, 1980; Westoby, 1982; Hara, 1988; Thomas and Weiner, 1989; Adler, 1996; Li et al., 2000; Stoll et al., 2002; Strigul et al., 2008; Chu et al., 2010; Coomes et al., 2011; Deng et al., 2012; Rivoire and Le Moguedec, 2012; Rüger and Condit, 2012; Lin et al., 2013) are often characterized as either spatially explicit, where plant spatial coordinates are specified, or spatially implicit, where only the zone of influence of each plant is tracked assuming equal spacing among individuals. Such models recover the 3/2 or 4/3 exponents for a wide range of mortality conditions or metabolic thresholds, while others exhibit greater sensitivity to competition between adjacent plants. These models follow a continuum of competition modes bounded by two limiting cases: size asymmetric competition where the largest plants acquire all the resources in overlapping areas to size symmetric competition where resources in overlapping areas are divided equally among interacting individuals regardless of their size (Weiner, 1990; DeMalach et al., 2016). Obviously, the degree of competition among individuals increases in all such models when the plot area A_s available for growth is diminished. These models can recover increased variability, skewness, or bi-modality in the histograms of individual plant biomass w_i as self-thinning is initiated at the stand level. A parsimonious, spatially implicit model is now considered to explore how different competition modes, initial densities, and experimental durations result in different α values. While some spatially explicit, more complex models are more realistic, the spatially implicit model explored here strikes a balance between simplicity and the ability to grasp all the proposed power-law exponents.

2.8.1. Competition and Mortality in Spatially Implicit Models

In this model, the growth rate of an individual plant i is assumed to be (Aikman and Watkinson, 1980)

$\begin{array}{ll}\frac{d{w}_i}{dt}=a_i{s}_{i}f(s_i)-b_i{w}_i^2,& (47)\end{array}$

where a_i and b_i are constants for a given stand, reflecting growth rate per unit area and the need for more resources as individual plant biomass increases, b_i depends on the maximum individual biomass w_max, and s_i measures the space occupied by plant i, which is linked to its size by a prescribed allometric relation

$\begin{array}{ll}{s}_i={\left(\frac{w_i}{k_g}\right)}^{2/3},& (48)\end{array}$

where k_g is a constant relating the area or zone of influence s to plant weight w. The 2/3 exponent is derived from dimensional considerations for isometric growth as discussed in section 2.1. The function f(s_i) encodes all of the spatial competition on the growth rate of plant i. To represent the space limitation and the two end-members of symmetric vs. asymmetric size-based competition, f(s_i) was represented as (Aikman and Watkinson, 1980)

$\begin{array}{ll}f(s_i)={\left[1+{\left(\frac{{\displaystyle {\sum }_j}{s}_j}{A_s}\right)}^{{\varphi }_1}{\left(\frac{\overline{s}}{s_i}\right)}^{{\varphi }_2}\right]}^{-1},& (49)\end{array}$

where the term $\frac{\sum _j{s}_j}{A_s}$ describes the space availability for resource acquisition (i.e., a measure of crowding) and $\frac{\overline{s}}{s_i}$ measures the relative size of plant i compared to the mean size $\overline{s}$. The two exponents ϕ₁ and ϕ₂ describe the importance of each mode of competition, representing respectively the roles of crowding and size asymmetry. The plot size A_s sets the spatial domain for competition. The initial number of uniformly distributed plants within A_s defines p₀. By varying ϕ₁ and ϕ₂, various modes of competition can be explored and their effect on α tracked. Mortality of plant i occurs when its carbon balance first becomes negative (i.e., dw_i/dt < 0). Needless to say, mortality need not occur when dw_i/dt < 0 (at least not on short time scales) though a negative carbon balance at the individual level implies a progressive competitive disadvantage and an increasing likelihood of mortality. Two related issues are addressed: The effect of f(s_i) on (i) the value of the self-thinning exponent α and (ii) the emergence of constant final yield when varying p₀ across multiple stands, waiting for a fixed duration, and observing w and p at each stand separately as shown in Figure 1 (Weiner and Freckleton, 2010).

Because growth and mortality in Equations (47) and (48) are proportional to powers of biomass (w_i) without distinguishing live and dead parts, this model is more appropriate for herbaceous species rather than forests. The individual tree biomass in high density forests may consist of a considerable proportion of dead biomass, reducing respiration costs. To avert this complexity, large initial densities and growth rates are used as is the case in crops. In fact, the range of parameter values used here (Table S3) are within the range used in Aikman and Watkinson (1980) and which were shown to agree with stand structure observations in even-aged monoculture competition experiments (Ford, 1975).

2.8.2. Effects of Competition Type on α and the Emergence of Constant Final Yield

For the first set of model runs, the power-law relation between individual biomass w(p₀|T_p) at a fixed time after sowing T_p and initial density p₀ is examined, where T_p is the integration period of the simulation (Figure 4). A constant integration period of T_p = 50 days is maintained for these runs during which no mortality occurs as is the case in the seminal work of Shinozaki and Kira (1956). Here,

$\begin{array}{ll}w(p_0|T_p)~p_0^{-{\alpha }_{CD}},& (50)\end{array}$

where the subscript CD stands for competition-density. The model runs here compare different plots at different p₀ and at a fixed period after sowing. Clearly, α_CD = 1 corresponds to the constant final yield rule as in Equation (3). In Figure 4A, for small p₀, normalized biomass per individual at the end of the simulation w(p₀|T_p)/w_max appears to be insensitive to p₀. As p₀ increases, variations in α_CD occur depending on choices made about ϕ₁ and ϕ₂. Figure 4B shows that at relatively low crowding exponent (ϕ₁ = 5) and relatively large size asymmetry exponent (ϕ₂ = 5), α_CD = 1, corresponding to invariant biomass per ground area y(p₀|T_p) = y_c regardless of the initial sowing density. This is therefore a manifestation of the constant final yield rule but not of self-thinning since mortality is absent. As the crowding exponent becomes large (ϕ₁ → 10), α_CD becomes bounded between 4/3 and 3/2, and insensitive to variations in the size asymmetry exponent ϕ₂. These cases are compatible with neither the constant final yield rule nor the self-thinning rule.

FIGURE 4

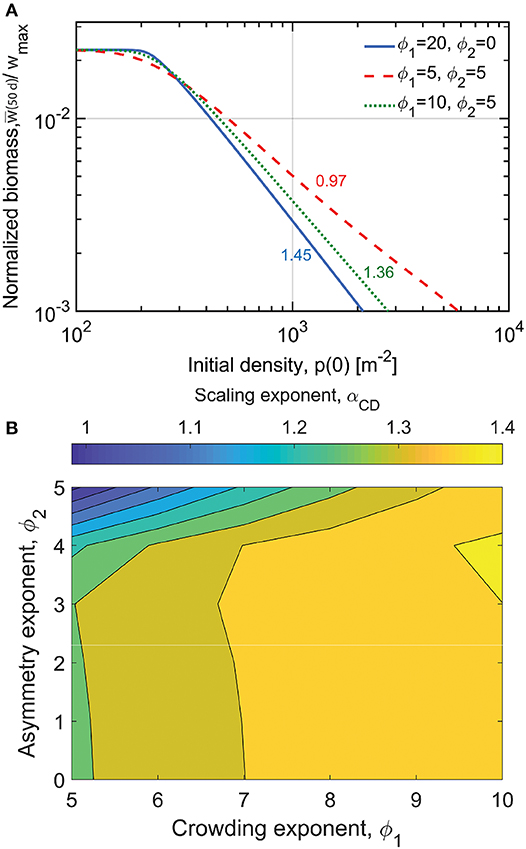
Figure 4. (A) Each line represents modeled normalized biomass per individual for multiple simulations of different initial density p₀ after a fixed integration period of 50 days. The lines correspond to the three competition scenarios indicated in the legend. The corresponding scaling exponent α_CD is displayed next to each plotted line. (B) Variation in α_CD driven by different competition scenarios for crops (as determined by high initial plant densities and growth rates). Model parameters are found in Table S3.

The temporal patterns of y(t) = w(t)p(t) associated with various choices of p₀ and ϕ₂ are shown in Figure 5 for different plant properties and a longer integration period of T_p = 150 days to assess the robustness of the results (see Table S2). The longer period allows for the presence of mortality whose onset in time is depicted using circles in Figure 5 (p(t) < p₀). Here, an intermediate crowding exponent ϕ₁ = 10 is kept as a constant. Biomass per ground area reaches an equilibrium that is sensitive to p₀ for low ϕ₂ values of 3 and 5 (Figures 5A,B). This does not conform to the constant final yield rule. For the highly size asymmetric mode of competition set by ϕ₂ = 7, the steady state biomass becomes independent of p₀ (Figure 5C), consistent with the constant final yield rule as presented by Xue and Hagihara (1998) when density-driven mortality occurs. The fact that a constant biomass is achieved for large ϕ₂ underscores that the phenomenon of the constant final yield only applies to certain types of plants competing for certain limited resources.

FIGURE 5

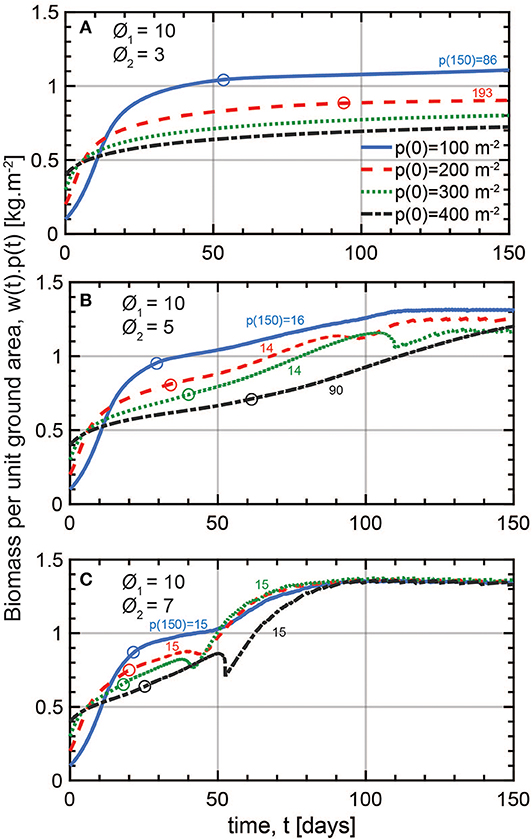
Figure 5. Modeled temporal variations of biomass per unit ground area with time for three competition types with less and more prominent size asymmetry effect (respectively smaller and larger ϕ₂). (A) At low ϕ₂, model runs with different initial densities p₀ (m⁻²) result in divergent final yields. Mortality only occurs in the low density plots as indicated by the circles. The final densities [p(150) in m⁻²] as indicated by the color-coded numbers on their corresponding curves are not very different from p₀. (B) At medium size asymmetry, final yields are closer than in (A), but differences still occur after 150 days. Mortality is present in all four plots. (C) At high size asymmetry, final yields are the same regardless of p₀ 90 days into the simulation which corresponds to the constant final yield rule. All plots reach the same low final density of 15 m⁻². Model parameters are found in Table S3. Circles designate the onset of mortality in time and color-coded numbers are the final densities at the end of the 150 days corresponding to each simulation.

Self-thinning is shown in Figure 6 and Figure S1. The differences between experiments conducted at a single stand experiencing self-thinning sampled through time (Equation 2), and multiple stands with varying p₀ at a fixed period after sowing (Equations 4 and 50) is seen by comparing Figure 6B and Figure 4B. The discrepancy in the contour plots underscores the fact that the meaning of the scaling exponent α and α_CD is not equivalent. As earlier noted, one of the highly cited critiques on the universality of the self-thinning exponent was an empirical analysis by Weller (1987). Weller noted that when analyzing multiple stands with different p₀, exponents differing from those tracking self-thinning in a single stand were obtained. The differences between these two experimental setups have been discussed elsewhere (Weiner and Freckleton, 2010), but are quantified here using the same spatially implicit model (as well as a range of ϕ₁ and ϕ₂).

FIGURE 6

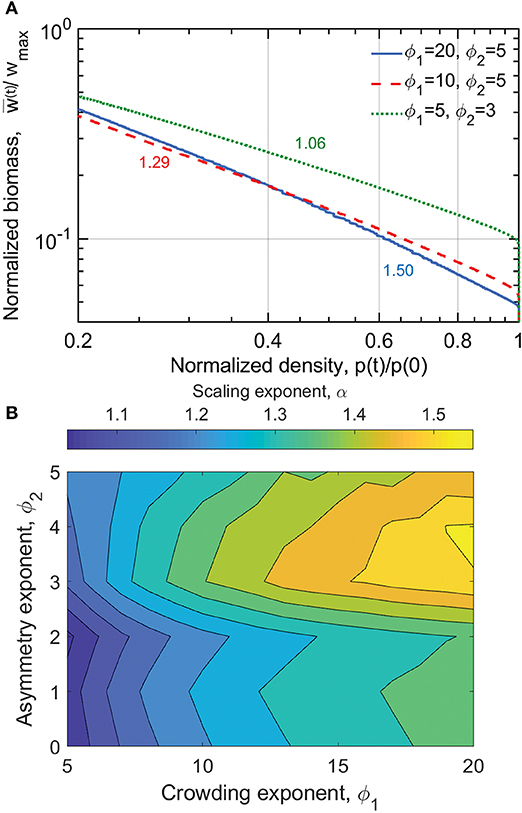
Figure 6. (A) Modeled normalized biomass per individual as a function of normalized plant density for the three competition scenarios indicated in the legend; time progresses from right to left as plants grow and density decreases. The corresponding scaling exponents α are written next to the plotted lines. (B) Variation in α driven by different competition scenarios. Model parameters are found in Table S3.

In Figure 6, it is seen that the stronger the influence of space availability on competition (ϕ₁), the steeper the power-law relation between w(t) and p(t). The effect of size asymmetry on the α is more nuanced (Figure 6B). It is therefore seen that Yoda's definition of self-thinning, where α = 3/2 is achieved only when competition for space is high (ϕ₁ > 15) and size asymmetry is moderate to high (ϕ₂ > 3; Figure 6B). The green dashed line of Figure 6A where α = 1.06 is equivalent to the scenario in Figure 5C where the biomass per ground area is invariant with respect to p₀. Figure 6B shows that all 3 aforementioned exponents (α ≈ 1, 4/3, 3/2) can be recovered from the same zonal model, depending on choices of ϕ₁ and ϕ₂.

3. Impacts On Forest Management, Future Outlook, and Conclusions

Competition for resources among same-species individuals sharing the same resource niche can be as complex as interactions among individuals of different species (Perry et al., 2008). That such competition among individuals of the same species results in power-law relations between the mean weight of an individual w and plant density p remains scientifically challenging to explain. Yet, such power-law relations are appealing to agricultural and forestry practitioners and have routinely been used in crop and forest management. In this context, mortality is only due to resource competition between individual plants, neglecting mortality due to external factors such as ice storms, hurricanes, forest fires, extended droughts, insect outbreaks, and human thinning of forests for management. As such, they set an “upper bound” on mean individual size for a given stocking (or planting) density (Luyssaert et al., 2011). In the case of crop management, initial planting density emerges as a key determinant of individual biomass and elapsed time when the steady state yield is reached; whereas in the case of forest management the w − p trajectories serve as a guide to when, and how much and often stands must be thinned to either maximize profitability or to mitigate hazards such as forest fires, insect outbreaks, or drought-induced mortality.

As already alluded to by Reineke (1933), forest density management utilizes size-density indices because they are presumably independent of site quality and stand age and the self-thinning line has taken center stage in determining management regimes (Begin et al., 2001). Such a presumably time-invariant power-law relation between w and p enables forest managers to also compare levels of growing stock regardless of differences in site quality or stand age. A particular set of management objectives resulting in an ideal p value can be projected forward or backward in time to a different development stage using the aforementioned w − p trajectories if the power-law exponent is known (e.g., α = 3/2). The self-thinning rule is a particularly powerful tool in combination (or as a part of) growth models to inform managers when the stands reach a particular management regime (Landsberg and Waring, 1997).

This review has focused on the many hypothetical mechanisms generating power-law relations between w and p due to the constraints imposed on resource competition in monospecific plots. Depending on the resource constraints (e.g., structural, allometric, hydraulic, supply of energy) and the type of competition imposed, multiple arguments suggest that the exponent of the power-law solution to dw/dp = g₃(w, p) converges toward one of the three α values: 1, 4/3, 3/2 (Table 1). The different α values reflect the numerous environmental influences and physiological factors and the degree of asymmetry of the competitive interaction (e.g., light interception is dominated by the tallest trees; Craine and Dybzinski, 2013). Therefore, for foresters aiming to optimize productivity, they should manage tree density based on the specific resource constraints shaping inter-plant competition. Often, the cultivation strategy maximizing plant density also minimizes resource availability such as soil water, i.e., the tragedy of the commons (Hardin, 1968). However, forest managers may be able to avoid this risky strategy by balancing resource use and plant density. This may be increasingly relevant in a changing climate where frequent and extended droughts are becoming a reality in many parts of the world. If storm intensities and inter-arrival times change in relatively short time-scales, then rooting profiles that successfully harnessed soil water in the past might become less effective (Farooq et al., 2009).

The theoretical results presented can be used to generate hypotheses on what controls α, to be tested in specific experiments or simulation studies. For example, species characterized by contrasting growth patterns or hydraulic traits could be grown under the same conditions to test predicted patterns of α. Similarly, trends in α could be assessed along climatic and edaphic gradients to test predicted deviations from the 3/2 or 4/3 values. The focus was purposely restricted to monospecific stands, but self-thinning also occurs in diverse communities, though niche complementarity and facilitation effects can become important drivers of the plant mass-density relations (Loreau and Hector, 2001). It is possible that denser communities containing a greater number of small individuals (belonging to more than one species) emerge when these effects are at play compared to monospecific stands. To tackle this problem, models describing a multitude of species (or functional traits), or capturing differences across individuals, should be used, which we expect will require a broader range of scaling exponents as the communities become more diverse.

The finding that the self-thinning exponent is not invariant has several consequences for forest managers designing their thinning regimes based on an invariant self-thinning rule (Drew and Flewelling, 1977). Time variance has been attributed to stand aging, canopy closure and environmental change, including increasing aridity in many parts of the world. Several amendments to the size-density indices presented in this text have been proposed elsewhere to take these effects into account (Zeide, 2001; Ge et al., 2017; Aguirre et al., 2018; Bravo-Oviedo et al., 2018; Zhang et al., 2019). Forest managers may expect a given self-thinning slope based on data from space-for-time substitution and, thus, set their thinning or harvest operations based on this expectation (Drew and Flewelling, 1979). For example, the self-thinning rule can be used to characterize “reference” conditions and, based on that, define indicators of the degree of land use intensity (Luyssaert et al., 2011). Such indicators quantify how far a given stand is from either a pristine forest or a stand following the self-thinning rule. However, as shown here, the shape of the self-thinning rule may vary depending on growth conditions and therefore indicators based on this curve may be sensitive to the chosen exponent and intercept.

A line of inquiry of increasing relevance to crops and plantation forestry alike is the effect of environmental change (e.g., elevated atmospheric CO₂, or air temperature) on C or α. Do the w − p trajectories remain the same or are they altered with these changes? Does elevated atmospheric CO₂ simply speed up the trajectories in the w − p phase plane? Does α remain constant but C likely to vary due to changes in leaf area index or other ecosystem properties? These are but a few of the questions that could motivate future work (Brunet-Navarro et al., 2016; Jump et al., 2017; Bravo-Oviedo et al., 2018). The implications of these answers to forest management cannot be overstated. If C or α vary under future conditions, management tactics will need to be adjusted accordingly. Even if the parameters of the self-thinning rule do not change, higher CO₂ and air temperature may promote growth (in absence of other limitations), resulting in faster movements along the w − p trajectory. This alone would require adjusting the thinning schedule. Modeling studies suggest that maintaining under-stocked stands (below the self-thinning curve) by more frequent or intense thinning could compensate negative impacts of future environmental conditions on the tree C balance (Collalti et al., 2018). However, for new thinning approaches to be effective, they will need to be based on a self-thinning rule that accounts for future growth conditions. For example, Equation (41) suggests that lower values of α can be expected if autotrophic respiration increases more than GPP in a warmer world, or if stands become nutrient-limited or age faster, resulting in lower CUE (Collalti et al., 2018). The use of such power-law expressions in forest management map onto the famous quote by the great Russian physicist Lev Landau:

Money is in the exponent. And exponent needs to be calculated precisely.

Power law relations between measures of biomass and density have been the subject of over a century of experimentation and theoretical analysis. They not only describe biomass development as a function of density for a single stand but also steady-state biomass as a function of maximum density for species ranging nine orders of magnitude by weight. The ubiquity and relative invariance of these power law relations makes them a research breeding ground to uncover the underlying mechanisms of inter-plant competition and develop effective management strategies for forests and croplands increasingly suffering from aridity in a changing climate.

Data Availability Statement

All sources of data used in this study are included in the article/Supplementary Material.

Author Contributions

GK, RO, and SM conceived the initial ideas and design of the manuscript. AM and SM designed all the figures and illustrations and were responsible for ideas in the extended analysis. ML and GV contributed to the literature review and checked derivations and dimensional consistencies. AM and GK developed and conducted all model simulations. All authors contributed to the writing of the manuscript and provided their consent to publish this work.

Funding

GK and AM acknowledge support from the National Science Foundation (NSF-DGE-1068871, NSF-EAR-1344703, NSF-AGS-1644382, and NSF-IOS-1754893). SM and ML were partly supported by the Swedish Research Council Formas (2016-00998). GV acknowledges support from the Swedish Research Council Formas (2018-01820) and Trees and Crops for the Future (TC4F)—a co-operative project between established research environments at the Swedish University of Agriculture (SLU), Umeå University and Skogforsk. RO acknowledges support from the Erkko Visiting Professor Programme of the Jane and Aatos Erkko 375th Anniversary Fund through University of Helsinki, Finland.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank N. Christensen, the editor CT, and the two reviewers for their helpful comments and suggestions.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2020.00062/full#supplementary-material

References

Adler, F. R. (1996). A model of self-thinning through local competition. Proceedings of the National Academy of Sciences 93, 9980–9984. doi: 10.1073/pnas.93.18.9980

PubMed Abstract | CrossRef Full Text | Google Scholar

Aguirre, A., del Río, M., and Condés, S. (2018). Intra-and inter-specific variation of the maximum size-density relationship along an aridity gradient in Iberian pinewoods. Forest Ecol. Manage. 411, 90–100. doi: 10.1016/j.foreco.2018.01.017

CrossRef Full Text | Google Scholar

Aikman, D., and Watkinson, A. (1980). A model for growth and self-thinning in even-aged monocultures of plants. Ann. Bot. 45, 419–427. doi: 10.1093/oxfordjournals.aob.a085840

CrossRef Full Text | Google Scholar

Antonovics, J., and Levin, D. A. (1980). The ecological and genetic consequences of density-dependent regulation in plants. Annu. Rev. Ecol. Syst. 11, 411–452. doi: 10.1146/annurev.es.11.110180.002211

CrossRef Full Text | Google Scholar

Banavar, J. R., Maritan, A., and Rinaldo, A. (1999). Size and form in efficient transportation networks. Nature 399:130. doi: 10.1038/20144

PubMed Abstract | CrossRef Full Text | Google Scholar

Bazzaz, F., and Harper, J. (1976). Relationship between plant weight and numbers in mixed populations of Sinapsis alba (L.) rabenh., and Lepidium sativum L. J. Appl. Ecol. 13, 211–216. doi: 10.2307/2401940

CrossRef Full Text | Google Scholar

Begin, E., Begin, J., Belanger, L., Rivest, L.-P., and Tremblay, S. (2001). Balsam fir self-thinning relationship and its constancy among different ecological regions. Can. J. Forest Res. 31, 950–959. doi: 10.1139/x01-026

CrossRef Full Text | Google Scholar

Bohrer, G., Mourad, H., Laursen, T. A., Drewry, D., Avissar, R., Poggi, D., et al. (2005). Finite element tree crown hydrodynamics model (Fetch) using porous media flow within branching elements: a new representation of tree hydrodynamics. Water Resour. Res. 41:W11404. doi: 10.1029/2005WR004181

CrossRef Full Text | Google Scholar

Bravo-Oviedo, A., Condés, S., del Río, M., Pretzsch, H., and Ducey, M. J. (2018). Maximum stand density strongly depends on species-specific wood stability, shade and drought tolerance. Forest. Int. J. Forest Res. 91, 459–469. doi: 10.1093/forestry/cpy006

CrossRef Full Text | Google Scholar

Brown, J. H., Gillooly, J. F., Allen, A. P., Savage, V. M., and West, G. B. (2004). Toward a metabolic theory of ecology. Ecology 85, 1771–1789. doi: 10.1890/03-9000

CrossRef Full Text | Google Scholar

Brown, J. H., and West, G. B. (2000). Scaling in Biology. Oxford University Press.

Google Scholar

Brunet-Navarro, P., Sterck, F. J., Vayreda, J., Martinez-Vilalta, J., and Mohren, G. M. (2016). Self-thinning in four pine species: an evaluation of potential climate impacts. Ann. Forest Sci. 73, 1025–1034. doi: 10.1007/s13595-016-0585-y

CrossRef Full Text | Google Scholar

Chu, C.-J., Weiner, J., Maestre, F. T., Wang, Y.-S., Morris, C., Xiao, S., et al. (2010). Effects of positive interactions, size symmetry of competition and abiotic stress on self-thinning in simulated plant populations. Ann. Bot. 106, 647–652. doi: 10.1093/aob/mcq145

PubMed Abstract | CrossRef Full Text | Google Scholar

Collalti, A., Trotta, C., Keenan, T. F., Ibrom, A., Bond-Lamberty, B., Grote, R., et al. (2018). Thinning can reduce losses in carbon use efficiency and carbon stocks in managed forests under warmer climate. J. Adv. Model. Earth Syst. 10, 2427–2452. doi: 10.1029/2018MS001275

PubMed Abstract | CrossRef Full Text | Google Scholar

Coomes, D. A., Lines, E. R., and Allen, R. B. (2011). Moving on from metabolic scaling theory: hierarchical models of tree growth and asymmetric competition for light. J. Ecol. 99, 748–756. doi: 10.1111/j.1365-2745.2011.01811.x

CrossRef Full Text | Google Scholar

Craine, J. M., and Dybzinski, R. (2013). Mechanisms of plant competition for nutrients, water and light. Functional Ecology 27, 833–840. doi: 10.1111/1365-2435.12081

CrossRef Full Text | Google Scholar

Dean, T., and Long, J. N. (1985). Response of self-thinning to artificially reduced levels of leaf area in monocultures of Trifolium pratense. Ann. Bot. 55, 361–366. doi: 10.1093/oxfordjournals.aob.a086913

CrossRef Full Text | Google Scholar

DeMalach, N., Zaady, E., Weiner, J., and Kadmon, R. (2016). Size asymmetry of resource competition and the structure of plant communities. J. Ecol. 104, 899–910. doi: 10.1111/1365-2745.12557

CrossRef Full Text | Google Scholar

Deng, J., Ran, J., Wang, Z., Fan, Z., Wang, G., Ji, M., et al. (2012). Models and tests of optimal density and maximal yield for crop plants. Proc. Natl. Acad. Sci. U.S.A. 109, 15823–15828. doi: 10.1073/pnas.1210955109

PubMed Abstract | CrossRef Full Text | Google Scholar

Dewar, R. C. (1993). A mechanistic analysis of self-thinning in terms of the carbon balance of trees. Ann. Bot. 71, 147–159. doi: 10.1006/anbo.1993.1019

CrossRef Full Text | Google Scholar

Drew, T. J., and Flewelling, J. W. (1977). Some recent Japanese theories of yield-density relationships and their application to monterey pine plantations. Forest Sci. 23, 517–534.

Google Scholar

Drew, T. J., and Flewelling, J. W. (1979). Stand density management: an alternative approach and its application to Douglas-fir plantations. Forest Sci. 25, 518–532.

Google Scholar

Eloy, C. (2011). Leonardo's rule, self-similarity, and wind-induced stresses in trees. Phys. Rev. Lett. 107:258101. doi: 10.1103/PhysRevLett.107.258101

PubMed Abstract | CrossRef Full Text | Google Scholar

Enquist, B. J., Brown, J. H., and West, G. B. (1998). Allometric scaling of plant energetics and population density. Nature 395:163. doi: 10.1038/25977

CrossRef Full Text | Google Scholar

Enquist, B. J., West, G. B., and Brown, J. H. (2009). Extensions and evaluations of a general quantitative theory of forest structure and dynamics. Proc. Natl. Acad. Sci. U.S.A. 106, 7046–7051. doi: 10.1073/pnas.0812303106

PubMed Abstract | CrossRef Full Text | Google Scholar

Farooq, M., Wahid, A., Kobayashi, N., Fujita, D., and Basra, S. M. A. (2009). Plant drought stress: effects, mechanisms and management. Agron. Sustain. Dev. 29, 185–212. doi: 10.1051/agro:2008021

CrossRef Full Text

Farrior, C., Bohlman, S., Hubbell, S., and Pacala, S. W. (2016). Dominance of the suppressed: power-law size structure in tropical forests. Science 351, 155–157. doi: 10.1126/science.aad0592

PubMed Abstract | CrossRef Full Text | Google Scholar

Ford, E. (1975). Competition and stand structure in some even-aged plant monocultures. J. Ecol. 63, 311–333. doi: 10.2307/2258857

CrossRef Full Text | Google Scholar

Friedman, S. P. (2016). Evaluating the role of water availability in determining the yield-plant population density relationship. Soil Sci. Soc. Am. J. 80, 563–578. doi: 10.2136/sssaj2015.11.0395

CrossRef Full Text | Google Scholar

Ge, F., Zeng, W., Ma, W., and Meng, J. (2017). Does the slope of the self-thinning line remain a constant value across different site qualities?–An implication for plantation density management. Forests 8:355. doi: 10.3390/f8100355

CrossRef Full Text | Google Scholar

Givnish, T. J. (1986). Biomechanical constraints on self-thinning in plant populations. J. Theor. Biol. 119, 139–146. doi: 10.1016/S0022-5193(86)80069-8

CrossRef Full Text | Google Scholar

Gorham, E. (1979). Shoot height, weight and standing crop in relation to density of monospecific plant stands. Nature 279:148. doi: 10.1038/279148a0

CrossRef Full Text | Google Scholar

Hara, T. (1984). Modelling the time course of self-thinning in crowded plant populations. Ann. Bot. 53, 181–188. doi: 10.1093/oxfordjournals.aob.a086679

CrossRef Full Text | Google Scholar

Hara, T. (1988). Dynamics of size structure in plant populations. Trends Ecol. Evol. 3, 129–133. doi: 10.1016/0169-5347(88)90175-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Hardin, G. (1968). The tragedy of the commons. Science 162, 1243–1248. doi: 10.1126/science.162.3859.1243

PubMed Abstract | CrossRef Full Text | Google Scholar

Hecht, V. L., Temperton, V. M., Nagel, K. A., Rascher, U., and Postma, J. A. (2016). Sowing density: a neglected factor fundamentally affecting root distribution and biomass allocation of field grown spring barley (Hordeum vulgare L.). Front. Plant Sci. 7:944. doi: 10.3389/fpls.2016.00944

PubMed Abstract | CrossRef Full Text | Google Scholar

Holliday, R. (1960). Plant population and crop yield. Nature 186, 22–24. doi: 10.1038/186022b0

CrossRef Full Text | Google Scholar

Horn, H. S. (2000). “Twigs, trees, and the dynamics of carbon in the landscape,” in Scaling in Biology, 199–220. Santa Fe Institute Studies on the Sciences of Complexity. Oxford: Oxford University Press.

Google Scholar

Hozumi, K. (1977). Ecological and mathematical considerations on self-thinning in even-aged pure stands. Bot. Mag. 90, 165–179. doi: 10.1007/BF02488355

CrossRef Full Text | Google Scholar

Huang, C.-W., Domec, J.-C., Palmroth, S., Pockman, W. T., Litvak, M. E., and Katul, G. G. (2018). Transport in a coordinated soil-root-xylem-phloem leaf system. Adv. Water Resour. 119, 1–16. doi: 10.1016/j.advwatres.2018.06.002

CrossRef Full Text | Google Scholar

Jump, A. S., Ruiz-Benito, P., Greenwood, S., Allen, C. D., Kitzberger, T., Fensham, R., et al. (2017). Structural overshoot of tree growth with climate variability and the global spectrum of drought-induced forest dieback. Glob. Change Biol. 23, 3742–3757. doi: 10.1111/gcb.13636

PubMed Abstract | CrossRef Full Text | Google Scholar

Kikuzawa, K. (1999). Theoretical relationships between mean plant size, size distribution and self thinning under one-sided competition. Ann. Bot. 83, 11–18. doi: 10.1006/anbo.1998.0782

CrossRef Full Text | Google Scholar

Kleiber, M. (1932). Body size and metabolism. Hilgardia 6, 315–353. doi: 10.3733/hilg.v06n11p315

CrossRef Full Text | Google Scholar

Kohyama, T. (1992). Density-size dynamics of trees simulated by a one-sided competition multi-species model of rain forest stands. Ann. Bot. 70, 451–460. doi: 10.1093/oxfordjournals.aob.a088502

CrossRef Full Text | Google Scholar

Landsberg, J., and Waring, R. (1997). A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. Forest Ecol. Manage. 95, 209–228. doi: 10.1016/S0378-1127(97)00026-1

CrossRef Full Text | Google Scholar

Lemons, D. S. (2018). Dimensional Analysis for Curious Undergraduates: A Student's Guide to Dimensional Analysis. Cambridge, MA: Cambridge University Press.

Li, B.-L., Wu, H.-I., and Zou, G. (2000). Self-thinning rule: a causal interpretation from ecological field theory. Ecol. Modell. 132, 167–173. doi: 10.1016/S0304-3800(00)00313-6

CrossRef Full Text | Google Scholar

Lin, Y., Berger, U., Grimm, V., Huth, F., and Weiner, J. (2013). Plant interactions alter the predictions of metabolic scaling theory. PLoS ONE 8:e57612. doi: 10.1371/journal.pone.0057612

PubMed Abstract | CrossRef Full Text | Google Scholar

Loreau, M., and Hector, A. (2001). Partitioning selection and complementarity in biodiversity experiments. Nature 412, 72–76. doi: 10.1038/35083573

PubMed Abstract | CrossRef Full Text | Google Scholar

Luyssaert, S., Hessenmöller, D., Von Lüpke, N., Kaiser, S., and Schulze, E. (2011). Quantifying land use and disturbance intensity in forestry, based on the self-thinning relationship. Ecol. Appl. 21, 3272–3284. doi: 10.1890/10-2395.1

CrossRef Full Text | Google Scholar

Manzoni, S., Čapek, P., Porada, P., Thurner, M., Winterdahl, M., Beer, C., et al. (2018). Reviews and syntheses: carbon use efficiency from organisms to ecosystems-definitions, theories, and empirical evidence. Biogeosciences 15, 5929–5949. doi: 10.5194/bg-15-5929-2018

CrossRef Full Text | Google Scholar

McCulloh, K. A., Sperry, J. S., and Adler, F. R. (2003). Water transport in plants obeys Murray's law. Nature 421, 939–942. doi: 10.1038/nature01444

PubMed Abstract | CrossRef Full Text | Google Scholar

McMahon, T. (1973). Size and shape in biology: elastic criteria impose limits on biological proportions, and consequently on metabolic rates. Science 179, 1201–1204. doi: 10.1126/science.179.4079.1201

PubMed Abstract | CrossRef Full Text | Google Scholar

Miyanishi, K., Hoy, A., and Cavers, P. (1979). A generalized law of self-thinning in plant populations (self-thinning in plant populations). J. Theor. Biol. 78, 439–442. doi: 10.1016/0022-5193(79)90342-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Murray, C. D. (1926). The physiological principle of minimum work: I. the vascular system and the cost of blood volume. Proc. Natl. Acad. Sci. U.S.A. 12:207. doi: 10.1073/pnas.12.3.207

PubMed Abstract | CrossRef Full Text | Google Scholar

Niklas, K. J. (1994). Plant Allometry: The Scaling of Form and Process. Chicago, IL: University of Chicago Press.

Google Scholar

Niklas, K. J., and Spatz, H.-C. (2004). Growth and hydraulic (not mechanical) constraints govern the scaling of tree height and mass. Proc. Natl. Acad. Sci. U.S.A. 101, 15661–15663. doi: 10.1073/pnas.0405857101

PubMed Abstract | CrossRef Full Text | Google Scholar

Oren, R., Schulze, E.-D., Matyssek, R., and Zimmermann, R. (1986). Estimating photosynthetic rate and annual carbon gain in conifers from specific leaf weight and leaf biomass. Oecologia 70, 187–193. doi: 10.1007/BF00379238

PubMed Abstract | CrossRef Full Text | Google Scholar

Pacala, S., and Weiner, J. (1991). Effects of competitive asymmetry on a local density model of plant interference. J. Theor. Biol. 149, 165–179. doi: 10.1016/S0022-5193(05)80275-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Pahor, S. (1985). On the -3/2 power thinning law in plant ecology. J. Theor. Biol. 112, 535–537. doi: 10.1016/S0022-5193(85)80020-5

CrossRef Full Text | Google Scholar

Peet, R. K., and Christensen, N. L. (1987). Competition and tree death. Bioscience 37, 586–595. doi: 10.2307/1310669

CrossRef Full Text | Google Scholar

Perry, D. A. (1984). A model of physiological and allometric factors in the self-thinning curve. J. Theor. Biol. 106, 383–401. doi: 10.1016/0022-5193(84)90037-7

CrossRef Full Text | Google Scholar

Perry, D. A., Oren, R., and Hart, S. C. (2008). Forest Ecosystems. Baltimore, MD: JHU Press.

Google Scholar

Pickard, W. (1983). Three interpretations of the self-thinning rule. Ann. Bot. 51, 749–757. doi: 10.1093/oxfordjournals.aob.a086526

CrossRef Full Text | Google Scholar

Reineke, L. H. (1933). Perfecting a stand-density index for even-aged forests. J. Agric. Res. 46, 627–630.

Google Scholar

Rivoire, M., and Le Moguedec, G. (2012). A generalized self-thinning relationship for multi-species and mixed-size forests. Ann. Forest Sci. 69, 207–219. doi: 10.1007/s13595-011-0158-z

CrossRef Full Text | Google Scholar

Roderick, M., and Barnes, B. (2004). Self-thinning of plant populations from a dynamic viewpoint. Func. Ecol. 18, 197–203. doi: 10.1111/j.0269-8463.2004.00832.x

CrossRef Full Text | Google Scholar

Rüger, N., and Condit, R. (2012). Testing metabolic theory with models of tree growth that include light competition. Func. Ecol. 26, 759–765. doi: 10.1111/j.1365-2435.2012.01981.x

CrossRef Full Text | Google Scholar

Shinozaki, K., and Kira, T. (1956). Intraspecific competition among higher plants. VII. Logistic theory of the CD effect. J. Inst. Polytech. Osaka City Univ. Ser. 7, 35–72.

Google Scholar

Shinozaki, K., Yoda, K., Hozumi, K., and Kira, T. (1964). A quantitative analysis of plant form-the pipe model theory: I. Basic analyses. Jpn. J. Ecol. 14, 97–105.

PubMed Abstract | Google Scholar

Spencer, H. (1864). The Principles of Biology. London, UK: Williams and Norgate.

Stoll, P., Weiner, J., Muller-Landau, H., Müller, E., and Hara, T. (2002). Size symmetry of competition alters biomass-density relationships. Proc. R. Soc. Lond. B Biol. Sci. 269, 2191–2195. doi: 10.1098/rspb.2002.2137

PubMed Abstract | CrossRef Full Text | Google Scholar

Strigul, N., Pristinski, D., Purves, D., Dushoff, J., and Pacala, S. (2008). Scaling from trees to forests: tractable macroscopic equations for forest dynamics. Ecol. Monogr. 78, 523–545. doi: 10.1890/08-0082.1

CrossRef Full Text | Google Scholar

Thomas, S. C., and Weiner, J. (1989). Including competitive asymmetry in measures of local interference in plant populations. Oecologia 80, 349–355. doi: 10.1007/BF00379036

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, D. W. (1942). On Growth and Form. Cambridge, UK: Cambridge University Press.

Google Scholar

Thompson, S. E., and Katul, G. G. (2012). Hydraulic determinism as a constraint on the evolution of organisms and ecosystems. J. Hydraul. Res. 50, 547–557. doi: 10.1080/00221686.2012.732969

CrossRef Full Text | Google Scholar

Thurner, M., Beer, C., Carvalhais, N., Forkel, M., Santoro, M., Tum, M., et al. (2016). Large-scale variation in boreal and temperate forest carbon turnover rate related to climate. Geophys. Res. Lett. 43, 4576–4585. doi: 10.1002/2016GL068794

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsoularis, A., and Wallace, J. (2002). Analysis of logistic growth models. Math. Biosci. 179, 21–55. doi: 10.1016/S0025-5564(02)00096-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Verhulst, P.-F. (1838). Notice sur la loi que la population suit dans son accroissement. Correspondance mathématique et physique publiée par a. Quetelet 10, 113–121.

Google Scholar

Vogel, S. (1988). Life's Devices: The Physical World of Animals and Plants. Princeton, NJ: Princeton University Press.

Voit, E. (1988). Dynamics of self-thinning plant stands. Ann. Bot. 62, 67–78. doi: 10.1093/oxfordjournals.aob.a087637

CrossRef Full Text | Google Scholar

von Bertalanffy, L. (1957). Quantitative laws in metabolism and growth. Q. Rev. Biol. 32, 217–231. doi: 10.1086/401873

PubMed Abstract | CrossRef Full Text | Google Scholar

von Foerster, H. (1959). “Some remarks on changing populations,” in The Kinetics of Cellular Proliferation, ed J. F. Stohlman (New York, NY: Grune and Stratton), 382–407.

Google Scholar

Waring, R., Landsberg, J., and Williams, M. (1998). Net primary production of forests: a constant fraction of gross primary production? Tree Physiol. 18, 129–134. doi: 10.1093/treephys/18.2.129

PubMed Abstract | CrossRef Full Text | Google Scholar

Watkinson, A. (1980). Density-dependence in single-species populations of plants. J. Theor. Biol. 83, 345–357. doi: 10.1016/0022-5193(80)90297-0

CrossRef Full Text | Google Scholar

Weiner, J. (1990). Asymmetric competition in plant populations. Trends Ecol. Evol. 5, 360–364. doi: 10.1016/0169-5347(90)90095-U

PubMed Abstract | CrossRef Full Text | Google Scholar

Weiner, J., and Freckleton, R. P. (2010). Constant final yield. Annu. Rev. Ecol. Evol. Syst. 41, 173–192. doi: 10.1146/annurev-ecolsys-102209-144642

CrossRef Full Text | Google Scholar

Weller, D. E. (1987). A reevaluation of the -3/2 power rule of plant self-thinning. Ecol. Monogr. 57, 23–43. doi: 10.2307/1942637

CrossRef Full Text | Google Scholar

West, G. (2017). Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies. New York, NY: Penguin.

West, G. B., Brown, J. H., and Enquist, B. J. (1997). A general model for the origin of allometric scaling laws in biology. Science 276, 122–126. doi: 10.1126/science.276.5309.122

PubMed Abstract | CrossRef Full Text | Google Scholar

Westoby, M. (1982). Frequency distributions of plant size during competitive growth of stands: the operation of distribution-modifying functions. Ann. Bot. 50, 733–735. doi: 10.1093/oxfordjournals.aob.a086416

CrossRef Full Text | Google Scholar

Westoby, M. (1984). The self-thinning rule. Adv. Ecol. Res. 14, 167–225. doi: 10.1016/S0065-2504(08)60171-3

CrossRef Full Text | Google Scholar

White, J. (1981). The allometric interpretation of the self-thinning rule. J. Theor. Biol. 89, 475–500. doi: 10.1016/0022-5193(81)90363-5

CrossRef Full Text | Google Scholar

White, J., and Harper, J. (1970). Correlated changes in plant size and number in plant populations. J. Ecol. 58, 467–485. doi: 10.2307/2258284

CrossRef Full Text | Google Scholar

Willey, R. W., and Heath, S. B. (1969). The quantitative relationships between plant population and crop yield. Adv. Agron. 21, 281–321. doi: 10.1016/S0065-2113(08)60100-5

CrossRef Full Text | Google Scholar

Xue, L., and Hagihara, A. (1998). Growth analysis of the self-thinning stands of Pinus densiflora Sieb. et Zucc. Ecol. Res. 13, 183–191. doi: 10.1046/j.1440-1703.1998.00256.x

CrossRef Full Text | Google Scholar

Yoda, K. (1963). Self-thinning in overcrowded pure stands under cultivated and natural conditions (intraspecific competition among higher plants. J. Biol. Osaka City Univers. 14, 107–129.

Google Scholar

Zeide, B. (2001). Natural thinning and environmental change: an ecological process model. Forest Ecol. Manage. 154, 165–177. doi: 10.1016/S0378-1127(00)00621-6

CrossRef Full Text | Google Scholar

Zhang, W.-P., Jia, X., Bai, Y.-Y., and Wang, G.-X. (2011). The difference between above- and below-ground self-thinning lines in forest communities. Ecol. Res. 26, 819–825. doi: 10.1007/s11284-011-0843-2

CrossRef Full Text | Google Scholar

Zhang, X., Cao, Q. V., Lu, L., Wang, H., Duan, A., and Zhang, J. (2019). Use of modified Reineke's stand density index in predicting growth and survival of Chinese fir plantations. Forest Sci. 65, 1–8. doi: 10.1093/forsci/fxz033

CrossRef Full Text | Google Scholar