- 1Department of Environmental Control, Northwest German Forest Research Institute (NW-FVA), Göttingen, Germany
- 2Thünen Institute of Forest Ecosystems, Eberswalde, Germany
- 3State Agency for Nature, Environment and Consumer Protection of North Rhine-Westphalia, Recklinghausen, Germany
- 4Department of Silviculture and Forest Ecology of the Temperate Zones, University of Göttingen, Göttingen, Germany
- 5Institute of Geography, University of Hamburg, Hamburg, Germany
- 6German Environment Agency, Dessau-Roßlau, Germany
- 7Public Enterprise Sachsenforst, Pirna, Germany
A reliable quantification of total inorganic nitrogen (TIN) deposition to forests is required for the evaluation of ecological effects of TIN inputs to forests and to monitor the success of clean-air policy. As direct measurements are scarce, different modeling approaches have been developed to estimate TIN deposition to forests. Three common methods are the (i) “canopy budget model,” (ii) “inferential method,” and (iii) “emission based estimates” using a chemical transport model. Previous studies have reported considerable and site-specific differences between these methods, complicating the interpretation of results. We use data from more than 100 German intensive forest monitoring sites over a period of 16 years for a cross-comparison of these approaches. Non-linear mixed-effect models were applied to evaluate how factors like meteorology, terrain and stand characteristics affect discrepancies between the model approaches. Taking into account the uncertainties in deposition estimates, there is a good agreement between the canopy budget and the inferential method when using semi-empirical correction factors for deposition velocity. Wet deposition estimates of the emission based approach were in good agreement with wet-only corrected bulk open field deposition measurements used by the other two approaches. High precipitation amounts partly explained remaining differences in wet deposition. Larger discrepancies were observed when dry deposition estimates are compared between the emissions based approach and the other two approaches, which appear to be related to a combination of meteorological conditions and tree species effects.
Introduction
During the last 70 years emissions of nitrogen (N) species to the atmosphere from traffic, industrial processes, and agriculture have drastically increased over pre-industrial levels and a significant decrease in the next decades in Europe is not expected (Simpson et al., 2014). The resulting atmospheric deposition of inorganic N to forests is an important determinant of tree growth (Etzold et al., 2020), rendering nitrogen deposition an essential input variable in decision support systems for forestry under environmental change (Panferov et al., 2011; Thiele et al., 2017) and carbon uptake (Du and De Vries, 2018). Accurate quantification of N deposition is also necessary for the estimation of nitrate leaching from forest ecosystems (MacDonald et al., 2002; Johnson et al., 2018; Vuorenmaa et al., 2018) and the calculation of N budget changes in forest soils (Fleck et al., 2019). On a political and administrative level, N deposition estimates are required to assess the success of clean air policy (Hettelingh et al., 2017), the exceedance of critical loads for eutrophication and acidification (De Vries et al., 2015) and in the context of licensing procedures for nitrogen emitting facilities.
The total deposition (TD) of N into forest ecosystems occurs via three pathways (Unsworth and Fowler, 1987): Wet deposition (WD) comprises deposition via rain, snow and hail; dry deposition (DD) consists of gases and particles deposited on surfaces or directly taken up by vegetation; and occult deposition (OD) refers to the deposition of fog. DD and OD to forests is typically larger compared to other land cover types, due to the large surface area of the canopy and their high aerodynamic roughness. The sum of DD and OD is also referred to as interception deposition (ID, Ulrich, 1994). Unlike WD, which is fairly easy to assess (Staelens et al., 2008; Dämmgen et al., 2013), the quantification of ID is much more challenging. As OD is often of orographic origin, it usually only contributes significantly to TD in mountainous regions (Kirchner et al., 2014; Hunová et al., 2016).
The accurate quantification of DD fluxes to forests is still challenging due to a large variety of N species, their chemical reactivity, a high uncertainty in the estimation of deposition velocities (Saylor et al., 2019) and different deposition pathways including bi-directional fluxes (Wichink Kruit et al., 2012). Currently, micrometeorological methods (e.g., eddy covariance and gradient techniques) are regarded as the most accurate approaches to quantify DD and OD (Marques et al., 2001; Mohr et al., 2005; Schmitt et al., 2005; Brümmer et al., 2020). However, micrometeorological methods require a considerable measurement effort and observational data are therefore typically only available for short observation periods at a limited number of locations.
Three other methods are frequently used where information on deposition of total inorganic nitrogen (TIN) is required. Firstly, the canopy budget model (CBM) approach developed by Ulrich (1994) and modified many times (e.g., Draaijers and Erisman, 1995; De Vries et al., 2001; Staelens et al., 2008) is applicable where assessments of open field and throughfall precipitation and element concentrations are available, e.g., for intensive forest monitoring sites (De Vries et al., 2003; Meesenburg et al., 2004, 2016; Talkner et al., 2010). The application of the Ulrich (1994) CBM is straightforward and requires no empirical parameters. However, estimates of TIN deposition with CBM are questionable due to debatable assumptions, limited understanding of canopy ion exchange processes and propagation of measurement errors in calculations (Staelens et al., 2008; Adriaenssens et al., 2013).
Secondly, for monitoring sites with observations of ambient air concentrations of major gaseous N species (e.g., NH3 and NO2), DD can be estimated using the inferential method (IFM), i.e., by multiplying the concentrations with deposition velocities (Zimmermann et al., 2006). A variety of approaches is used to inform deposition velocities, ranging from dynamic models based on stomatal conductance and atmospheric conditions to land-use specific empirical long-term averaged deposition velocities (e.g., Schrader and Brümmer, 2014). At an intermediate level of complexity, published deposition velocities are adapted for site specific conditions based on semi-empirical correction factors (Schmitt et al., 2005; Kirchner et al., 2014). The IFM approach suffers from considerable variances in deposition velocities as shown by different review studies (e.g., Staelens et al., 2012; Schrader and Brümmer, 2014). In addition, the observation of NO2 and NH3 ambient air concentrations yield an extra uncertainty of ±30% (Schaub et al., 2016). At the end, DD calculated with the IFM needs to be combined with measurements of WD to yield TIN TD.
The third method to estimate TIN deposition is a combination of emission inventories and a chemical transport model using meteorological data for the simulation of the regional circulation (referred to as emission based method, EBM, in the following). A range of modeling systems exist (Vivanco et al., 2018). For Germany, the German Environmental Agency has funded the development of an emission-based approach that yields features with a higher spatial resolution compared to some European scale models (Schaap et al., 2018). Approaches with higher spatial resolution have been used in Germany for many years (Gauger et al., 2008; Builtjes et al., 2011; Schaap et al., 2015, 2017, 2018) and its results have been included in numerous impact studies (Hauck et al., 2012; Fleck et al., 2017, 2019; Thiele et al., 2017). In Germany, the EBM approach integrates emission inventories and a large number of local measurements of wet or bulk deposition to TIN deposition estimates with complete spatial coverage. Major challenges lie in the accuracy and spatio-temporal resolution of emission data and the parametrization of receptor-specific deposition processes with respect to DD and OD (Saylor et al., 2019).
Previous studies comparing TIN deposition derived with different methods occasionally reported considerable site-specific discrepancies. This is true for micrometeorological methods and CBM (Marques et al., 2001; Mohr et al., 2005), IFM and CBM (Schmitt et al., 2005; Kirchner et al., 2014) as well as EBM and CBM (Schaap et al., 2018) or multi-approach intercomparisons (Brümmer et al., 2020). Contrarily, Zimmermann et al. (2006) found a good agreement between CBM and IFM, while in the study of Thimonier et al. (2019) a throughfall based method (although not a CBM), IFM and EBM generally yielded similar rates of TIN deposition with notable exceptions at some sites. These findings suggest that comparisons of deposition estimates are most informative when carried out across a large number of sites and long observation periods.
Model intercomparisons can support the interpretation of results from single methods and indicate conditions where specific approaches are more or less reliable. The aim of this study is to contribute a systematic comparison of three common approaches to estimate TIN deposition to forests for an extended geographic and temporal coverage. Based on data from around 100 intensive forest monitoring sites (42 sites for IFM) in Germany over a period of 16 years, we derive TIN deposition estimates with (i) the “canopy budget model” (CBM), (ii) the “inferential method” (IFM), and (iii) “emission based estimates” (EBM). We evaluate the discrepancies between the different approaches using mixed effect models in order to analyze if they are determined by spatial, temporal, meteorological, and site specific factors. Where applicable, model discrepancies were analyzed separately for wet deposition (WD), dry deposition (DD), and total deposition (TD). In this study, we hypothesize that the difference between the methods can be partly explained by meteorology, terrain characteristics, site specific factors and levels of ambient air concentrations.
Materials and Methods
In the following subchapters a description of the assessments and models is provided. The overall study design is summarized in Table 1.
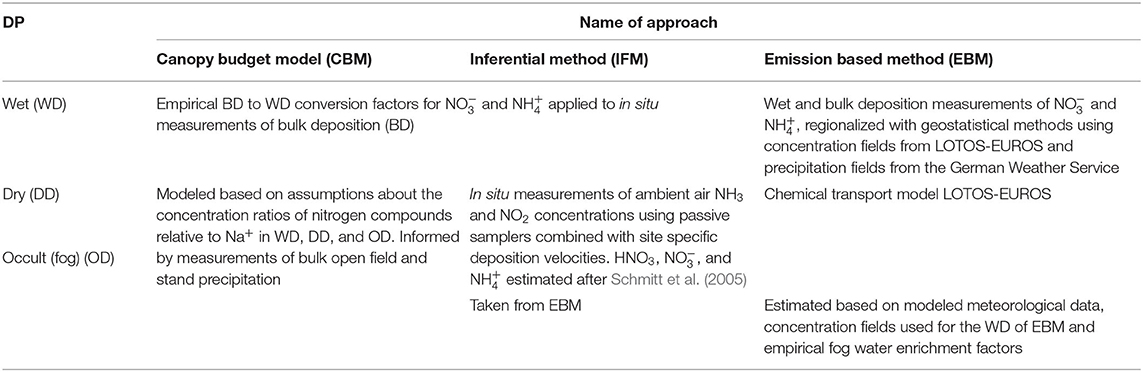
Table 1. Calculation approaches of total inorganic nitrogen fluxes for the different deposition pathways (DP) and methods.
Study Sites and Data Coverage
In Germany, data collection under the International Co-operative Programme on Assessment and Monitoring of Air Pollutions Effects on Forests (ICP Forests) is conducted since more than two decades (Ferretti and Schaub, 2014). As part of this program, atmospheric deposition is assessed at intensive monitoring plots (“Level II”) by means of precipitation sampling in the forest stands and at nearby open field sites (De Vries et al., 2003). Hundred and four sites with varying temporal coverage and a variety of forest stand types were examined for this study (Figure 1). The most frequent tree species is Norway spruce [34] (Picea abies (L.) H. Karst), followed by European beech [30] (Fagus sylvatica L.), Scots pine [17] (Pinus sylvestris L.), oak [8], (Quercus robur L. and Qu. petraea (Matt.) Liebl.), Douglas fir [1] [Pseudotsuga menziesii (Mirbel) Franco], European larch [1] (Larix decidua Mill.) and stands with more than one dominant tree species [13].
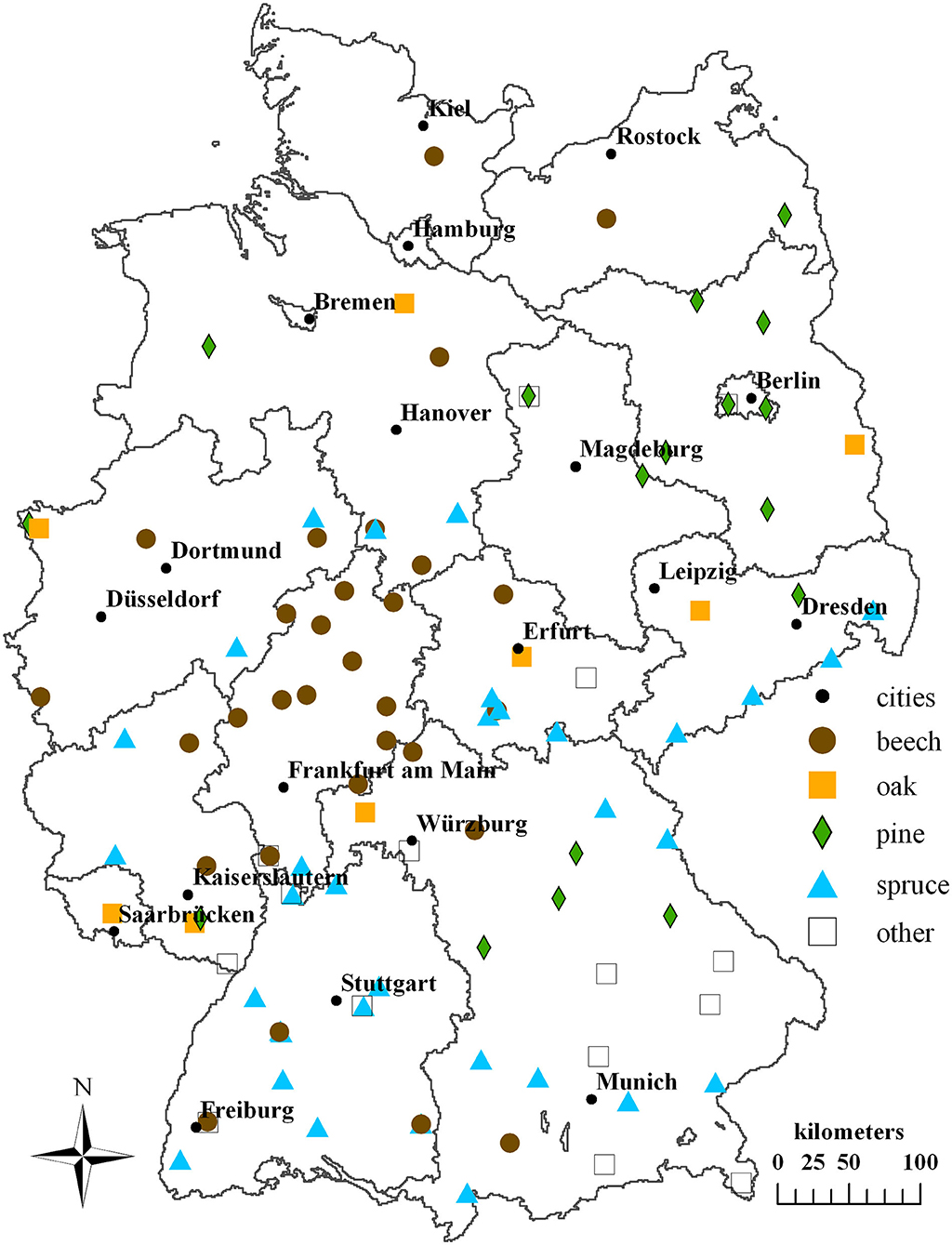
Figure 1. Location of 104 German intensive monitoring plots considered in the study. Symbols representing beech, oak, spruce and pine dominated forest sites and sites with other trees (Douglas fir, larch, mixed forest).
The plots are located at altitudes between 10 and 1,522 m a.s.l. Mean air temperature and mean annual precipitation (1981–2010) ranged from 2.6 to 10.9°C and from 558 to 2,444 mm, respectively. While data according to EBM approach are available for all plots and years in the period 2000–2015, application of the CBM and the IFM approach is limited by the availability, completeness and quality of observations. The CBM and IFM were calculated for 1,237 and 194 site-years, respectively. Further information on the sites and data availability is provided in the supplementary material (Supplementary Table 1).
Sampling Procedures, Chemical Analysis and Data Quality
Deposition assessments for the CBM approach were conducted according to the ICP Forests Manual on sampling and analysis of deposition (Clarke et al., 2016). In short, open field deposition was collected by 3–6 continuously open bulk samplers at sites in the vicinity of the forest stands. Between 9 and 27 collectors are placed under the forest canopy in varying spatial arrangements in order to cover the spatial variation in throughfall deposition. At plots with European beech, stemflow is assessed at a subset of the trees (Clarke et al., 2016). Usually, samples from multiple samplers are pooled in order to reduce the analytical effort.
Samples are collected at least fortnightly, filtered, and then stored in the dark at about 4°C or below before chemical analyses are performed. For some plots samples are mixed to monthly samples. Deposition samples were analyzed for Na+, , and , and a range of other parameters by different laboratories. Due to the standardized methods (Clarke et al., 2016), data are comparable and laboratory results are checked with currently recommended methods (Mosello et al., 2005): (1) the ion balance, (2) a comparison between measured and calculated conductivity, (3) a comparison between the sum of the inorganic forms of nitrogen and total nitrogen, and (4) the Na/Cl ratio. If analytical results are suspicious, analyses are repeated. The QA/QC procedures further included the use of control charts for internal reference material to check long-term comparability within national laboratories (König et al., 2013) as well as participation in periodic ring tests to check comparability between laboratories (Marchetto et al., 2006).
The three deposition fluxes (bulk open field, throughfall, stemflow) are then calculated by multiplication of the precipitation amount with the corresponding ion concentration in the analyzed precipitation samples and summed up to annual rates. Only annual open field and throughfall deposition fluxes, which were based on at least 292 days of collection (80% of the year) have been included. In case of data gaps (between 0 and 20% of the year), the corresponding deposition rate has been extrapolated to full temporal coverage based on the assumption that daily deposition fluxes in the unobserved time periods equal the average daily deposition fluxes in the observed period for the respective plot, sampler and year (Fischer et al., 2007). For stemflow (on average amounting to approximately 10–16% of the Na+, and throughfall deposition flux), longer data gaps frequently occurred. They were filled based on plot- and substance-specific average ratios between stemflow and throughfall deposition rates for those measurement periods where throughfall was available. Finally, the stand precipitation (ST) deposition flux was calculated as the sum of throughfall and stemflow for beech plots and equaled the throughfall flux for all other plots.
Ambient air concentrations of NO2, and NH3 were assessed at 43 sites by passive samplers in different years (Supplementary Table 1). Measurements were made using IVL passive samplers usually at 2 m above ground, installed in the open field where bulk open field precipitation was assessed (Schaub et al., 2016). The samples were mostly processed and analyzed by the Swedish Environment Research Institute (IVL). More details on the samplers are given in Swaans et al. (2007). All years with a data completeness of <80% for a specific air pollutant were excluded for the respective measurement site (Schaub et al., 2016).
Approaches to Estimate Total Inorganic Nitrogen Deposition
N deposition to forests consists of several N components. We refer to TIN as the substances and (ions in precipitation and aerosols) as well as NH3, NO2, and HNO3 (gases). The three approaches compared in this study cover these components to a slightly different extent. The EBM reports deposition rates for oxidized N (NOy) which also includes compounds like HNO2 and NO. The canopy budget model also accounts for these substances as they mostly react to N forms captured by the measurements used for the method (Thimonier et al., 2019). The canopy budget model, however, only partly covers the deposition of gases in general (see below). The inferential method explicitly models the deposition fluxes of the five TIN compounds. These differences must be taken into account for the interpretation of results. The deposition of organic N is not the specific subject of this study. In the following, the three methods are briefly described.
Canopy Budget Model
A number of CBM versions exist and differences between models were evaluated in other studies (Staelens et al., 2008; Adriaenssens et al., 2013). We selected the approach of Ulrich (1994) as a relatively robust and conservative version [the approach probably underestimates TIN TD for several reasons (Meesenburg et al., 2009), see Discussion)]. Based on the assessment of and in bulk open field precipitation and ST, dry deposition of gaseous and particulate N species is estimated. Therefore, the sum of the calculated and TD is referred to as TIN TD. In detail, the CBM of Ulrich (1994) calculates the TD of the nitrogen components (NC) and as the sum of WD and interception deposition (ID):
Wet deposition was estimated from bulk open field precipitation based on correction factors from Gauger et al. (2002). Due to the high temporal and spatial variability of the factors, this can only be considered as a rough approximation. More details on the limitations are given in section Uncertainties in Methods and Measurements. The ID is conceptually split into (1) particulate ID (IDpart, NC), consisting of particulate DD and OD, and (2) gaseous deposition (IDgas, NC).
The model assumes that concentration ratios of substances (Na+:NC) in IDpart are similar to concentration ratios of substances in WD. Furthermore, it is assumed that IDpart of sodium can be estimated as the difference of ST and WD (zero net canopy exchange of Na+). Based on these assumptions, IDpart of each of the two nitrogen compounds can be estimated as:
The ID of gaseous N species is estimated as the share of ST that is not explained by WD or IDpart of and , respectively.
If the sum of WD and IDpart exceeds ST, no gaseous deposition can be calculated (treated as zero). Finally TIN TD is calculated as the sum of TD of and . For more details, the underlying assumptions and limitations see Ulrich (1994) or Meesenburg et al. (2009). Note that the CBM yields an estimate of ID but does not allow to differentiate between DD and OD. Therefore, the OD and DD fluxes of the other two methods (IFM and EBM, see below) are also aggregated to yield the respective ID fluxes. As the OD share among the ID is usually relatively small, and in order to reduce the complexity of the figures and tables, we present the results for OD and DD together as “dry” deposition (Table 1).
Inferential Method (IFM)
Calculation procedure
The inferential method (IFM, also referred to as “concentration method”, e.g., Peters and Eiden, 1992), calculates the dry deposition flux (DD; g m−2 s−1) as the product of the concentration (c; μg m−3) in the ambient air at a defined reference height (z) and a proportionality constant, the deposition velocity (vd; cm s−1) according to the following basic equation (Wesely and Hicks, 2000):
Following Thimonier et al. (2019) we focused on NH3, NO2, HNO3 (gases), and and (aerosols). As in-situ measurements were only available for NH3 and NO2, the calculation of DD based on vd and ambient air concentration was only applied for these substances, which usually account for a large part of TIN DD (Flechard et al., 2011). The contribution of HNO3, , and to DD was estimated following Schmitt et al. (2005). In detail, we proceeded as follows: (1) we obtained WD of and in the same way as for the CBM approach (Table 1). (2) We then calculated the DD of , , and HNO3, gas based on an empirical relationship (Schmitt et al., 2005) from open field deposition, separately for broadleaved and coniferous forest. OD is not included here (Schmitt et al., 2005). (3) Gaseous DD of NH3 and NO2 was calculated by multiplying annual average ambient air concentrations with deposition velocities (see below). (4) As independent data to inform OD estimates was not available, we used the OD from the EBM approach (see below) also in the IFM approach (Table 1). The contribution of this deposition pathway is usually very small. (5) The TIN TD estimate of the IFM is then calculated as the sum of the deposition fluxes from steps 1–4. (6) In order to allow a separate comparison of the deposition fluxes, we subtracted WD (from step 1) from the TD (step 5). Although this flux contains small parts of OD, we refer to it as dry deposition (DD) in subsequent steps of analyses (same for the other two methods).
Estimation of deposition velocities for NO2 and NH3
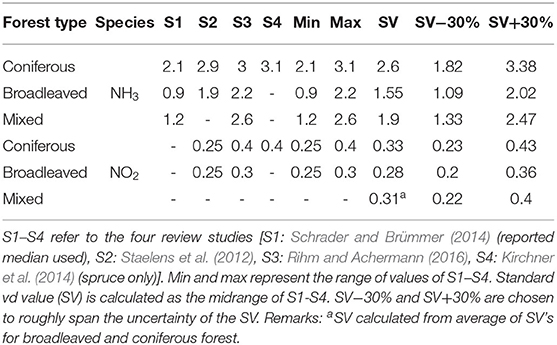
Previous reviews of deposition velocities for different forest types and substances reported a large variability of vd values, which appeared to be sensitive to several parameters such as receptor surface properties, meteorological conditions as well as seasonal, and diurnal variations (Hunová et al., 2016). To account for this variability, we derived two sets of deposition velocities. In the standard case, we used forest type specific vd values for each substance across Germany and the complete observation period. In a second case, we used semi-empirical site and season specific correction factors following Kirchner et al. (2014), to roughly account for the major spatial and temporal variations in vd.
In order to establish the fixed “forest type specific values” of the deposition velocity, we rely on four review studies, each covering several publications. We extracted the vd values for NH3 and NO2 reported to be best suited (median of vd's in one case) for the respective forest type by each of the four studies. We then aggregated these four values into one value per forest type and N species by using the midrange (average of the lowest and highest value). In order to roughly account for the range of uncertainty, we also calculate “standard value+30%” and “standard value-30%” (Table 2).
The second set of deposition velocities was based on these “forest type specific values” but adjusted by five types of site specific correction factors, proposed for spruce stands in the Bavarian Alps (Kirchner et al., 2014) and an additional correction factor to account for the relevance of other tree species elsewhere in Germany.
with: vdcor: corrected deposition velocity; vdlit: “forest type specific” deposition velocity based on literature references (cf. Table 2) and the correction factors: ksea: season; kincl: slope inclination; kwind: wind speed; kinv: inversion weather condition; kup: slope upwind and ktree: tree species.
Dry deposition strongly depends on the season (Marner and Harrison, 2004; Mohan, 2016). Kirchner et al. (2014) therefore proposes the following seasonally dependent factors (ksea): Spring (1.1); summer (1.2), autumn (1.0), and winter (0.8). A consideration of the different lengths of winter periods as proposed by Schmitt et al. (2005) has been omitted. The correction factor (kincl) for the slope inclination (incl; %, see below for data source) is obtained according to Kirchner et al. (2014): kincl = 0.01 × incl+0.6. Parameterization of kwind is based on regionalized wind speed from 109 wind stations using a Leeward index according to Dietrich et al. (2019). Wind speed is known to have a strong effect on deposition fluxes (Lin et al., 1994; Gallagher et al., 1997; Erisman and Draaijers, 2003; Mohan, 2016). Based on the average wind speed in Germany at 10 m height of ~3.4 m s−1, the following classes with the corresponding correction factors were developed, assuming DD increases with wind speed due to a higher turbulence and transport into the forest: <1 m s−1: 0.7; 1.0–1.9 m s−1: 0.8; 2.0–2.9 m s−1: 0.9; 3.0–3.9 m s−1: 1.0; 4.0–4.9 m s−1: 1.1; 5.0–5.9 m s−1: 1.2; ≥6 m s−1: 1.3. For meteorological inversions, Kirchner et al. (2014) proposed the following correction factors (kinv) related to frequency of their occurrence: “rare”: 1.0; frequent: 0.9; very frequent: 0.8. As no corresponding information is usually available for the investigated sites, we calculated the terrain exposure index (TEI) as predictor. The TEI is a terrain parameter, which indicates the degree to which a particular location is sheltered against advective flows and is thus particularly suitable to accumulation of cold air (Dietrich et al., 2019). The index values and correction factors are classified as follows: ≥1.2: 1.4; <1.2–≥1.1: 1.2; <1.1–≥1: 1.0; <1–≥0.9: 0.9 and <0.9: 0.8. Kirchner et al. (2014) have integrated upslope winds into their approach because they can periodically transport emissions from source regions (Benedict et al., 2013). However, the occurrence of slope upwinds and its influence on vd values (kup) is difficult to parameterize. Due to the high surface roughness of forests, this effect was only considered for slopes >5°. According to Kirchner et al. (2014), north-exposed slopes are less affected than south exposed ones. Accordingly, a kup factor of 1.1 was assigned for the celestial directions NW, N, NE, and E, for W and SE exposed slopes a factor of 1.2 and for SW and S exposed slopes a factor of 1.3. Vd values obtained from reviews are often stratified according to forest type (coniferous vs. deciduous). The approach by Kirchner et al. (2014) has been developed for spruce stands but only 34 of the 104 plots included in this study were pure spruce stands. The leaf area index (LAI) in spruce stands is often higher than in pine stands (Panferov et al., 2009; Goude et al., 2019). Zhang et al. (2003) found generally higher vd values for stands with higher LAI values. Corresponding, vd values for pine were assumed to be lower by a factor of 0.7 und for spruce to be 1.3 times higher compared to the “forest type specific values” for coniferous forest. For the same reasons (Bequet et al., 2011) we set a ktree of 0.9 for oak and 1.1 for beech trees. For all other trees ktree was set to 1.0.
Emission Based Deposition Model (EBM)
The approach for quantifying TIN deposition with the EBM is described in detail in Schaap et al. (2018). The deposition fluxes estimated by the EBM were provided by the German Environment Agency. In short, four major calculation steps are conducted in this model: (1) the chemical transport model LOTOS-EUROS (Schaap et al., 2008; Manders et al., 2017) is used to calculate DD as a product of modeled ambient air concentration fields of N species and modeled deposition velocities. Critical input data are meteorological data in high temporal resolution, spatial information of N emissions and receptor properties for dry deposition (e.g., land cover). (2) In the next step, modeled rain water concentrations from the LOTOS-EUROS model are used in combination with a few 100 stations of precipitation chemistry monitoring in Germany. These data serve to adjust the modeled rain water concentration distribution from the LOTOS-EUROS model using residual kriging. The generated concentration field is multiplied with high resolution precipitation data (1 × 1 km), to yield WD estimates (Table 1). (3) OD is calculated from fog water concentrations [estimated from previously determined rainwater concentration field and so called enrichment factors–Schaap et al. (2018)] in combination with cloud water deposition rates, which were calculated following the approach by Katata et al. (2008, 2011). In Katata et al. (2008) a simple linear regression for the fog deposition velocity has been derived from numerical experiments with a detailed multilayer land surface model (4) Finally WD, DD, and OD were combined in a spatial resolution of 1 × 1 km for the years 2000–2015. For each grid cell, land cover type specific deposition rates are available, including coniferous forest, deciduous forest, and mixed forest. Thus, deposition rates at the ICP Forests monitoring sites were extracted from the EBM results based on site coordinates and tree species / stand type (see Figure 1). In line with the CBM and the IFM approach, we refer to the sum of DD and OD estimates as “dry deposition.”
Derivation of Large Scale Ambient Air Concentrations, Meteorological and Terrain Data
Differences in deposition estimates between the three approaches might be affected by a range of factors including meteorological and terrain characteristics as well as the level of ambient air concentrations. Daily data of temperature (T), solar radiation (RA), relative humidity (RH), wind speed (W), and precipitation (P) were obtained for the period from 1981 to 2015 using the observational data of the German Meteorological Service (Deutscher Wetterdienst, DWD). The regionalization of the daily meteorological data from the climate and precipitation stations of the DWD to the intensive monitoring plots was performed using the methods described in Dietrich et al. (2019). Terrain parameters [altitude, slope, aspect, terrain exposure index (TEI)] were also derived following Dietrich et al. (2019). The slope orientation of the plots was transformed into a continuous variable (aspect index) between 0 and 1 following Roberts and Cooper (1989).
Discrepancies between model estimates might also be affected by the degree of air pollution at the sites. To account for this aspect, we included the annual average NH3 and NOX concentrations as predictors in the statistical models. Because in-situ measurements were only available at the much smaller subset of plots for which the IFM approach could be calculated, we relied on modeled ambient air concentrations to provide data for all plots over the entire observation period. In order to ensure independence from the chemical transport model used in the EBM approach (LOTOS-EUROS), we utilized data from the EMEP MSC-W model (Simpson et al., 2012). Annual average air concentrations based on emissions and meteorology for the years 2000–2015 according to the 2019 reporting status were obtained from EMEP MSC West (MET Norway; https://emep.int/mscw/mscw_moddata.html). Data was extracted for the grid cells in which the ICP Forests monitoring sites are located.
Statistical Analysis of Spatial and Temporal Differences Between the Methods
We compared the three model types with summary statistics. For the IFM, we used the version with site specific correction factors vdcor. We also tested a version with site specific correction factors but excluding the tree species-specific correction (ktree) and another version with the forest type specific vd only. To quantify the statistical association between the estimated deposition rates from the different methods, the root mean square error (RMSE), as well as the mean bias error (MBE), the mean absolute error (MAE), the coefficient of determination (R2) and Legates and McCabe's efficiency (E1) were used (Table 3). The E1 (Legates and McCabe, 2013) provides additional information with E1 = 1 indicating a perfect fit while E1 = 0.0 indicates a model that is no better than the baseline comparison (the observed mean value—Null model). Substantially flawed results are indicated by negative E1 values (Legates and McCabe, 2013).
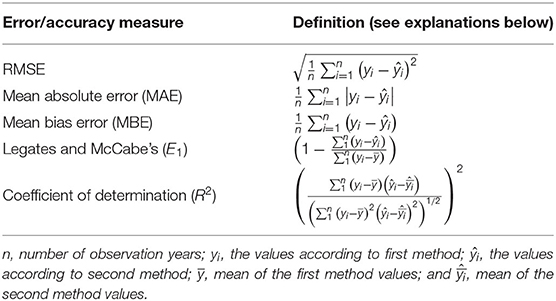
Table 3. Definitions of comparison indicators [after Li (2017), adapted].
We used a mixed effect model to relate the differences between deposition estimates (ΔTINy, p) from the three approaches to potential explanatory factors taking into account the “pseudo-replicated” structure of the data (same plots in different years) (Zuur et al., 2009). The model structure is as follows:
were ΔTINy,p is the difference in TIN deposition in year y at plot p; b0: the intercept term; f1, f2,.fn: unspecified (potentially) non-linear spline smoothing functions; x1,yp, x2,yp,.,xn,yp: 1. n predictor variables in year y at plot p; Zp: a row in a model matrix including dummy variables for coding random effects for plots p, where p = 1,.,104; bp: a vector of random effects; ε: an independent and identically normally distributed error term with standard deviation eyp. Standard software to parameterize this type of model is available from the R (R Development Core Team, 2018) library mgvc (Wood, 2006), with additional calls to the libraries MASS (Venables and Ripley, 2003) and nlme (Pinheiro et al., 2018). The distribution of the response variable was checked with the function “fitdist” of the package “fitdistrplus v1.0-14” (Delignette-Muller and Dutang, 2015). In case of data deviating from normal distribution, logarithmic or square root transformations were performed with constants added where necessary to avoid negative values.
All explanatory variables are summarized in Table 4. It should be noted that some of these variables (e.g., wind speed) are already included in the semi-empirical factors for IFM. Therefore, significant effects of these parameters could also indicate deficient parameterization of the IFM. We used high-resolution regionalized climate data instead of precipitation observations at the intensive monitoring plots as explanatory variables for the statistical models. This allows us to keep explanatory variables independent from input data of the three methods we aim to compare. To identify the factors that influenced the differences in deposition estimates between the three approaches, we used a boosting framework called component-wise gradient boosting (Mayr et al., 2017), implemented in the R-package mboost (Hothorn et al., 2020). The preselection of potentially appropriate model variables takes into account parametric, non-parametric, spatial, and random effects (Bühlmann and Yu, 2003; Bühlmann and Hothorn, 2007). In mboost, the major tuning parameter of boosting is the number of iterations “mstop.” To prevent overfitting, we used the implemented k-fold cross validation function to choose an appropriate number of boosting iterations. For the final model selection, we fitted the generalized additive mixed models (GAMM) with the preselected variables from the mboost procedure. Finally, all variables with a very low accumulated in-bag risk reduction (these values can be used to reflect variable importance) and non-significant (p < 0.05) effects were then stepwise removed from the model.
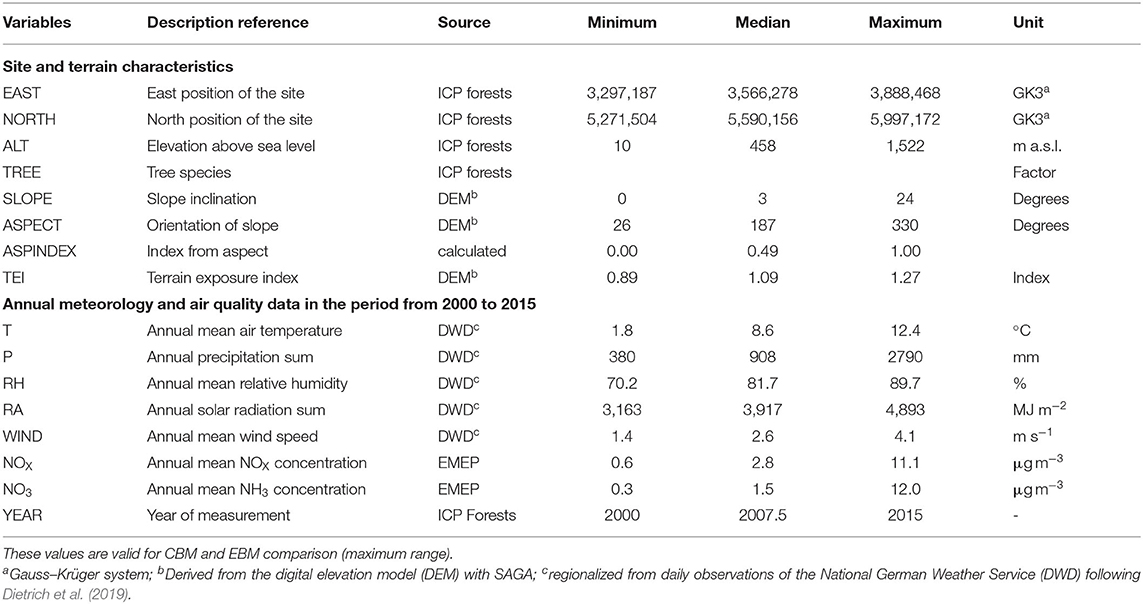
Table 4. Summary of data sources for explanatory variables in the statistical models to analyze the differences in TIN deposition between the three approaches.
Results
Magnitude and Variability of Total Inorganic Nitrogen Deposition
For the 1,237 annual observations considered in our study, the TIN TD averaged over time per plot ranges between 6.1 and 47.1 kg ha−1 a−1 and between 8.8 and 36.8 kg ha−1 a−1 with a mean of 20 and 18 kg ha−1 a−1 and a coefficient of variation of 36 and 26% for CBM and EBM, respectively (Table 5). There was considerable variation in estimated DD for the CBM approach. The coefficient of variation calculated across all stands and years was 50%. As expected the data of the EBM approach shows a clearly lower variability (29%).
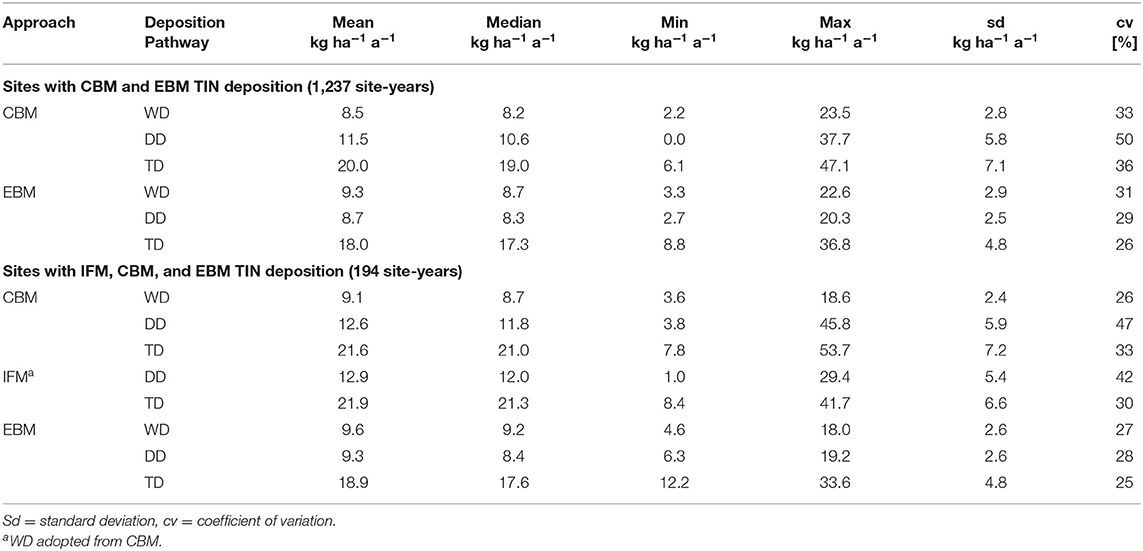
Table 5. Descriptive statistical values of the three approaches for estimation of total inorganic nitrogen (TIN) deposition (canopy budget–CBM; inferential method–IFM; emission based–EBM) for the different deposition pathways [wet deposition (WD), dry deposition (DD), and total deposition (TD)].
Comparison of the Canopy Budget and the Inferential Method
Since both methods use identical observations of WD, the comparison focuses on dry and total deposition. For both dry and total deposition, the use of forest type specific vd values without further corrections shows a large dispersion and discrepancy (E1, RMSE, MAE) between the two methods and the bias is relative high (Figure 2, Table 6). When site specific correction factors are taken into account, the agreement between the two methods considerably improves. The R2 is relatively high, the E1 rises substantially above zero, the RMSE and MAE are about halved, and also the MBE is low (−0.3 kg ha−1 a−1) for TD estimates (Table 6).
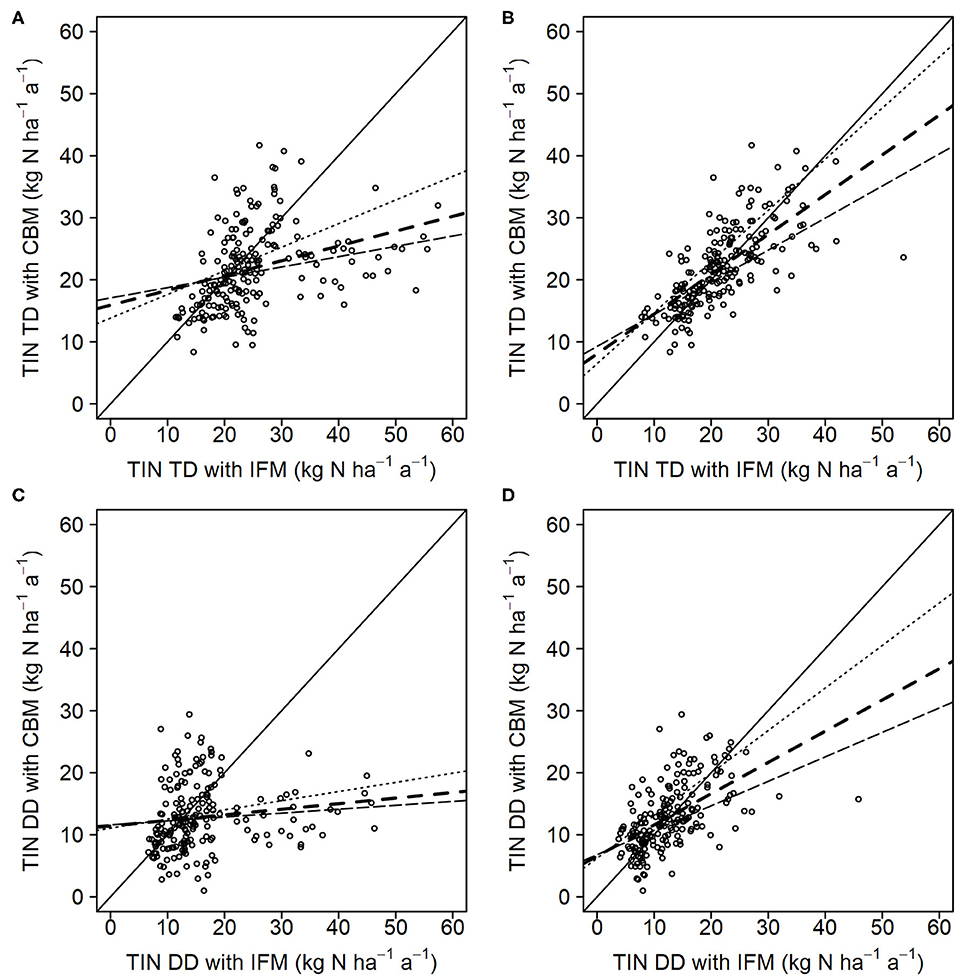
Figure 2. Comparison of total deposition (TD) (A,B) and dry deposition (DD) (C,D) of total inorganic nitrogen (TIN) between canopy budget (CBM) and inferential method (IFM) (n = 194 site-years from 42 sites). (A,C) calculated with forest type specific deposition velocities; (B,D) calculated with site specific deposition velocities. The solid black line represents the 1:1 line and the dashed lines represents the linear regressions lines for vdmean (- - - -), vdmin (····), and vdmax (——–) (see also Table 2). For vdmin and vdmax only the regression lines were displayed and not the individual points. All statistical parameters are given in Table 6.
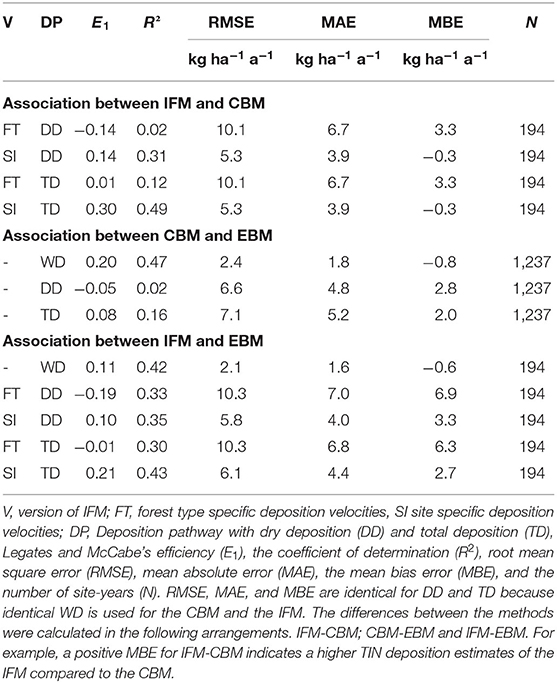
Table 6. Indicators for the association between canopy budget (CBM), inferential (IFM) and emission based method (EBM).
Comparison of the Canopy Budget and the Emission Based Method
Estimates for the comparison of the CBM and EBM approaches are available for a large set of plots and years (Table 6, Figure 3). There is an overall good agreement (R2 = 0.47) between CBM and EBM estimates for WD (Figure 3A). On average, the wet-only corrected TIN bulk deposition (CBM) is 0.8 kg ha−1 a−1 lower than WD from EBM (Table 6). For DD, large discrepancies between CBM and EBM appeared (R2 = 0.02; E1 = −0.05, Figure 3B). However, the bias of 2.8 kg N ha−1 a−1 is lower than for the EBM-IFM comparison (bias of 3.3 kg N ha−1 a−1). Due to the weak agreement of the DD estimates, the association between the TD with R2 = 0.16 is also very weak (Figure 3C). The TIN TD calculated with EBM is lower on average by 2 kg N ha−1 a−1 compared with CBM. To compensate for interannual variability, also plot-specific mean values were compared (Figure 3D). Using this aggregated values, the regression line approaches more closely the 1:1 line.
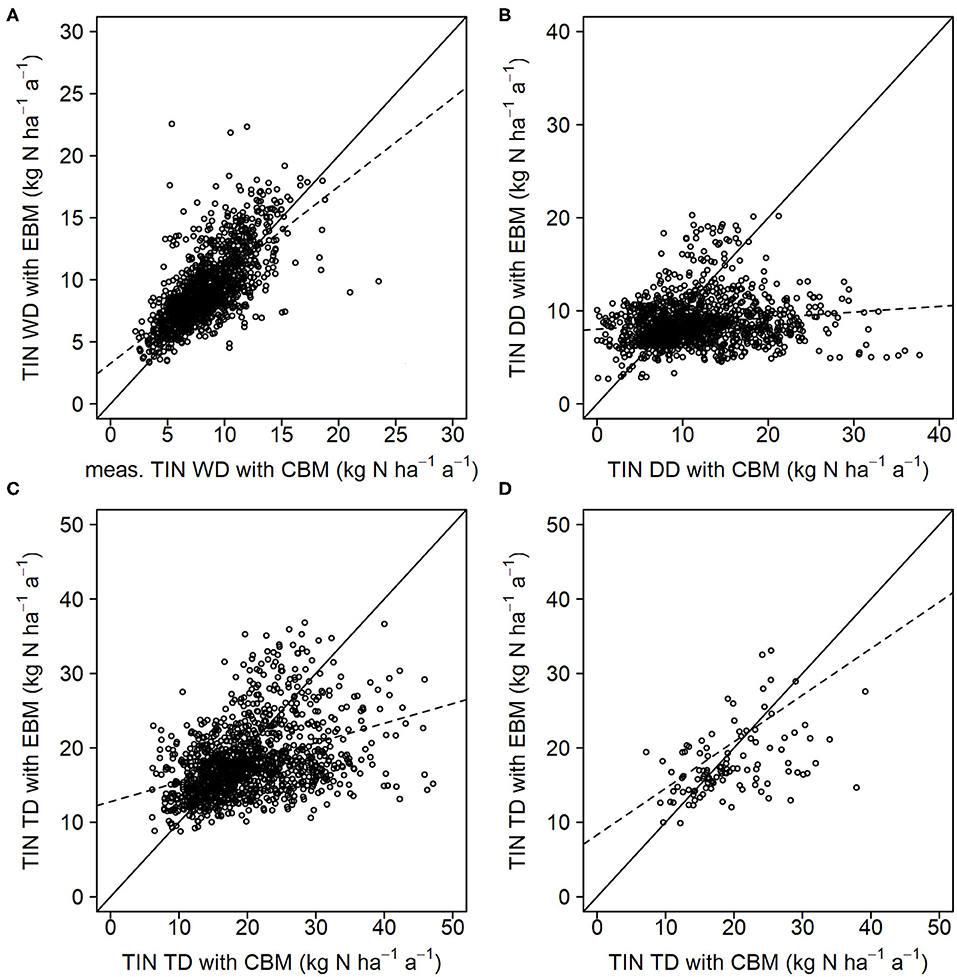
Figure 3. Comparison of yearly wet deposition (WD) (A), dry deposition (DD) (B), and total deposition (TD) (C) of total inorganic nitrogen (TIN) between emission based (EBM) and canopy budget method (CBM) (n = 1,237 site-years from 104 sites). (D) TD with site-specific mean values. The solid black line represents the 1:1 line and the dashed line represents the linear regressions line. All statistical parameters are given in Table 6.
Comparison of the Inferential and the Emission Based Method
When comparing the wet-only corrected bulk open field deposition of the reduced dataset (i.e., only for those plots where IFM estimates are available) to WD of the EBM approach, the mean bias error (MBE) is slightly lower (−0.6 kg N ha−1 a−1) compared to the complete dataset (Figure 4E and Table 6). In contrast, the DD from the IFM clearly shows higher values if calculated with site specific correction factors, compared to EBM (3.3 kg ha−1 a−1, Figure 4B). As MBE of WD and DD compensate each other partly, the overall difference between the TIN TD estimates amounts to 2.7 kg N ha−1 a−1. If IFM is calculated only with forest type specific deposition velocities, the association with the EBM approach is significantly deteriorated (Figure 4 and E1 values in Table 6). For this version, the MBE increases to 6.9 and 6.3 kg N ha−1 a−1 for DD and TD, respectively.
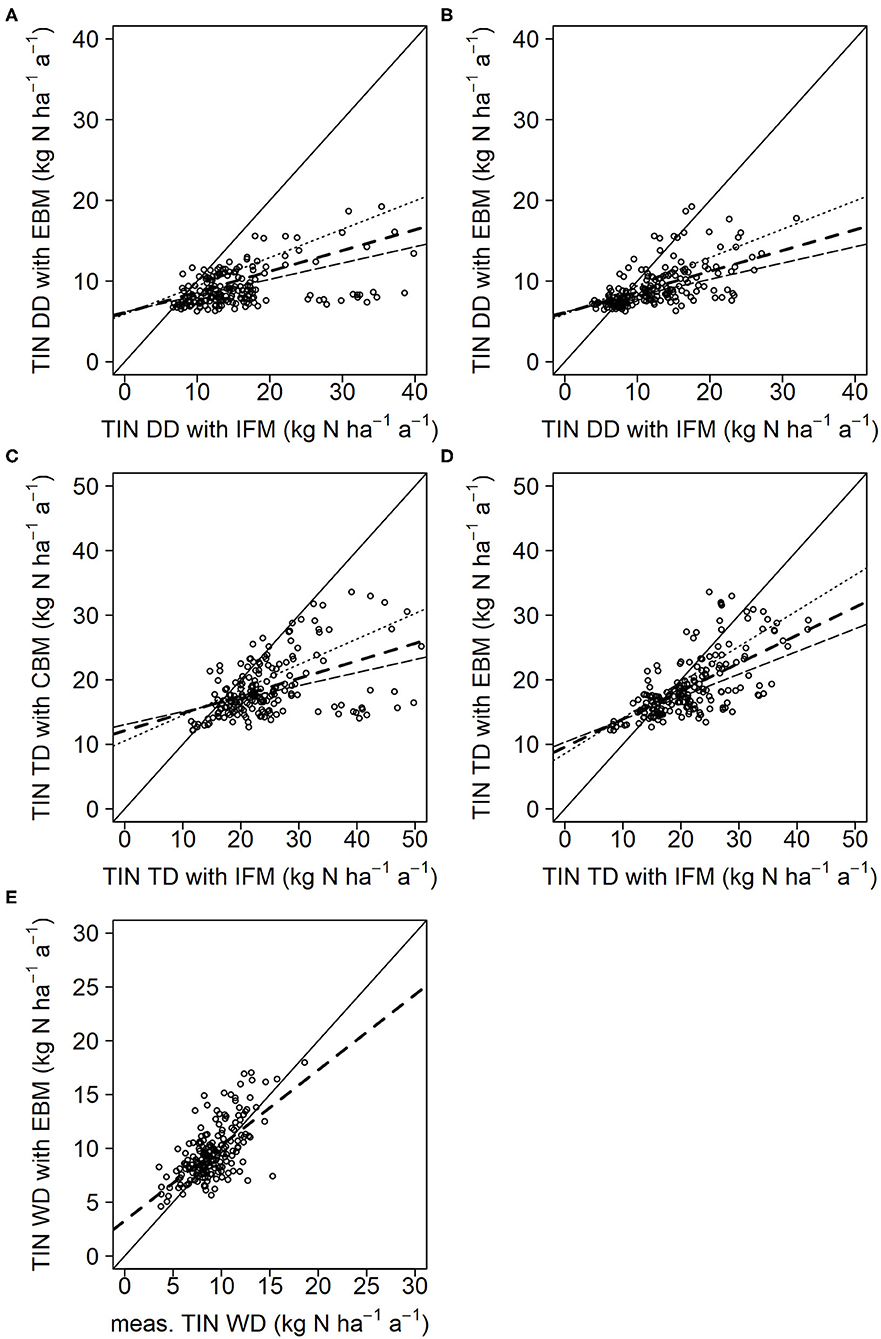
Figure 4. Comparison of dry deposition (DD) (A,B), total deposition (TD) (C,D) and wet deposition (WD) (E) of total inorganic nitrogen (TIN) between emission based (EBM) and inferential method (IFM) (n = 194 site-years from 42 sites). (A,C) calculated with forest type specific deposition velocities; (B,D) calculated with site specific deposition velocities. The solid black line represents the 1:1 line and the dashed lines represents the linear regressions lines for vdmean (- - - -), vdmin (····), and vdmax (——–) (see also Table 2). For vdmin and vdmax only the regression lines were displayed and not the individual points. All statistical parameters are given in Table 6.
Factors Influencing the Difference Between N Estimation Methods
The differences between the annual TIN fluxes calculated with the three methods were examined for possible influences of spatial, temporal, meteorological and relief factors. For each combination of models (CBM, IFM, EBM) and deposition pathway (WD, DD, TD) the best model as identified by the boosting procedure for variable selection is indicated in Table 7. The cross-comparison of the approaches is hindered by the unequal number of replicates. While 1,237 data points (deposition rates for specific plots-years) are available for the CBM-EBM comparison, only 194 are available for the IFM-EBM and IFM-CBM comparison, respectively. This is due to the limited number of available in-situ ambient air concentration measurements, which are required for the IFM approach. This means that differences in effects found for the CBM-EBM and the IFM-EBM comparisons, respectively, could be either caused by the difference in the amount and identity of input data or by the difference in methods (CBM, IFM). In order to evaluate this aspect, we repeated the analyses (GAMMs) for the CBM-EBM comparison, including only those observations, which are available for the IFM/EBM comparison (n = 194) (Table 7). When comparing the results, the different spatial coverage must be taken into account. For example, there are no measurements of ambient NO2 and NH3 concentrations available from Bavaria. With the exception of slope inclination, orographic parameters do not actually appear in any of the models.

Table 7. Significance and direction of the effects explaining differences between TIN deposition estimates for different deposition pathways (DP) and pairs of models.
There are several significant effects on ΔTIN in the different models with varying effect strength. In the following, mainly effects with a high effect strength will be addressed, since they contribute most to the explained variance of the differences between the models. For example, in the CBM-EBM comparison the effect strength for precipitation is between 2 and −6 kg ha−1 a−1 (Figure 5A) whereas for the year of measurement this range is only about 1.5 kg ha−1 a−1 (Figure 5E, note the logarithmic scale). The ΔTIN values for WD between CBM and EBM can only be explained to a small extent by the variables included in our analyses (R2 = 0.36). The variables with the largest explanatory power are precipitation (Figure 5A) and the location of the plots (Figure 6). The greater the amount of precipitation, either the EBM approach seems to systematically overestimate WD or the measurements of open field deposition used in the CBM and IFM are too low.
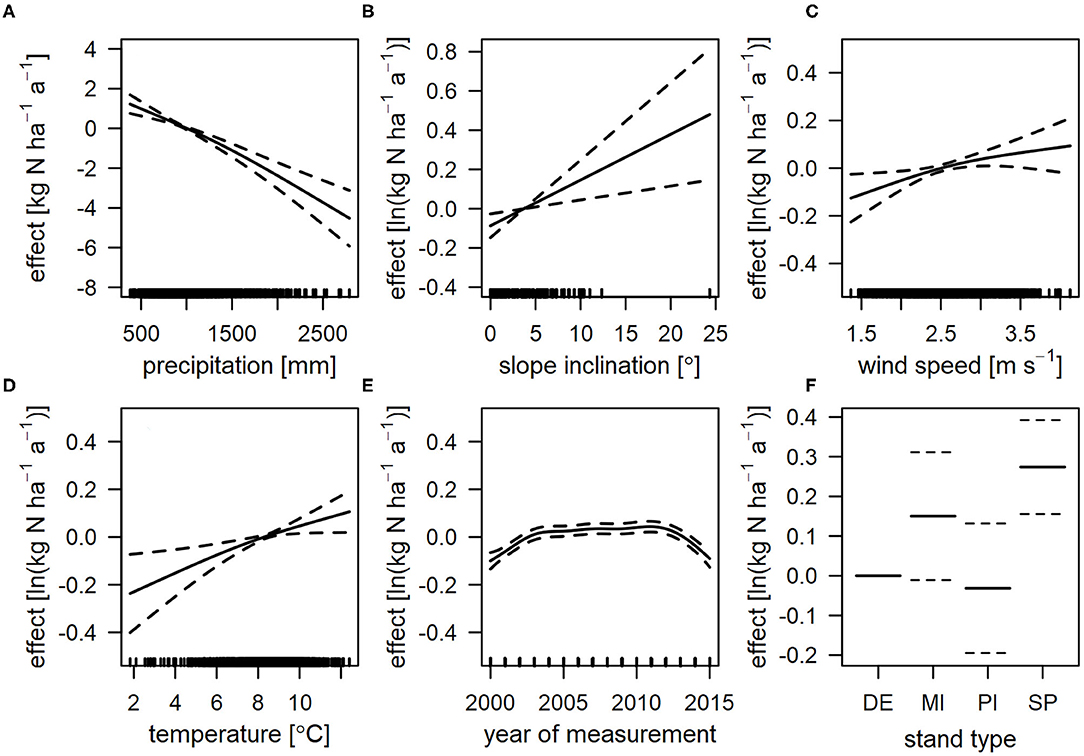
Figure 5. Partial effect of precipitation (A), slope inclination (B), wind speed at 2 m height (C), temperature (D), year of measurement (E), and stand type (F) on ΔTIN between the canopy budget (CBM) and emission based method (EBM) for wet deposition (A) and dry deposition (B–F). Positive effects indicate a tendency for higher TIN deposition estimates of the CBM compared to the EBM. Note the log-transformed data for dry deposition. Dashed lines indicate 95% pointwise prognosis intervals. The covariate is displayed as marks along the x-axis. (DE, deciduous forest; MI, mixed forest; PI, pine forest; SP, spruce forest).
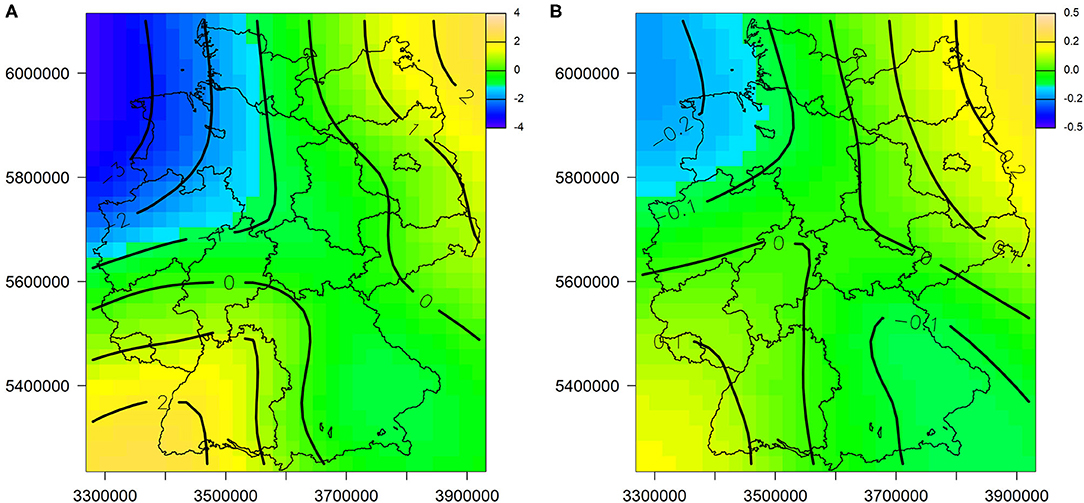
Figure 6. Partial effect of geographic location on ΔTIN between the canopy budget and emission based method for wet deposition (A) and dry deposition (B). Positive effects indicate a tendency for higher TIN deposition estimates of the CBM compared to the EBM. The values along the isolines indicate the impact on ΔTIN in kg ha−1 a−1 on the left and on ΔTIN in ln(kg ha−1 a−1) on the right side. The axes represent Gauss-Krüger coordinates.
In addition, higher TIN WD rates by the EBM approach can also be observed in northwest Germany (Figure 6A). In contrast, somewhat lower WD rates are estimated by the EBM compared to open field measurements in northeast and southwest Germany (Figure 6A). Note that positive effects indicate a tendency for higher TIN deposition estimates of the CBM as compared to the EBM (Figures 5, 6).
For the comparison of CBM and EBM with respect to dry deposition estimates a larger number of influential variables were identified than for WD. With increasing temperature, wind speed and slope inclination, the difference of DD estimates between EBM and CBM tends to increase (Figure 5). A relatively high sensitivity on ΔTIN is indicated for the partial effect of tree species (Figure 5F). While the differences are insignificant for all other tree species, they are significant for spruce forests (Table 7). In contrast to WD, the spatial trends for DD are only weak (Figure 6B). Similarly, the temporal effect is only poor. However, especially since 2012, there has been a slight downward trend, i.e., a tendency for higher values of the EBM compared to the CBM (Figure 5E).
For the comparison of the TIN total deposition between the IFM and the CBM (possible for 194 plot-years), the variable selection algorithm suggested the location of plots and tree species as the sole potentially relevant explanatory variables. However, these effects turned out to be insignificant in the GAMM, with a corresponding low explanatory power (R2 = 0.12).
As for the CBM-IFM comparison, the IFM-EBM comparison was also limited to the 194 plot-years with observed ambient air quality (Figure 7). For WD, the statistical model identified year of measurement and a spatial effect as explanatory variables. In contrast to the comparison of CBM and EBM a significant effect of precipitation rates was not found. It should be noted that there are only very few stations with very high annual precipitation rates in the IFM subset of plots, e.g., the Bavarian Alps are missing. Although a precipitation effect on differences in WD was invisible, the statistical model identified a tendency for higher TD estimates of the EBM compared to IFM for plot-years with high regionalized precipitation rates. Another effect identified for the IFM-EBM comparison is a systematically lower TIN DD estimate of EBM compared to the IFM for spruce sites (Figure 7E). This effect of tree species is in agreement with the results of the larger set of plots used for the EBM-CBM comparison (see above). The IFM-EBM comparison also indicates an effect of solar radiation, NOx and NH3 air concentrations (based on data from the EMEP model) for dry deposition. However, the prognosis intervals show a high uncertainty. The comparison of the IFM and EBM methods does not reveal any spatial pattern for TD, which is likely due to the limited sample size.
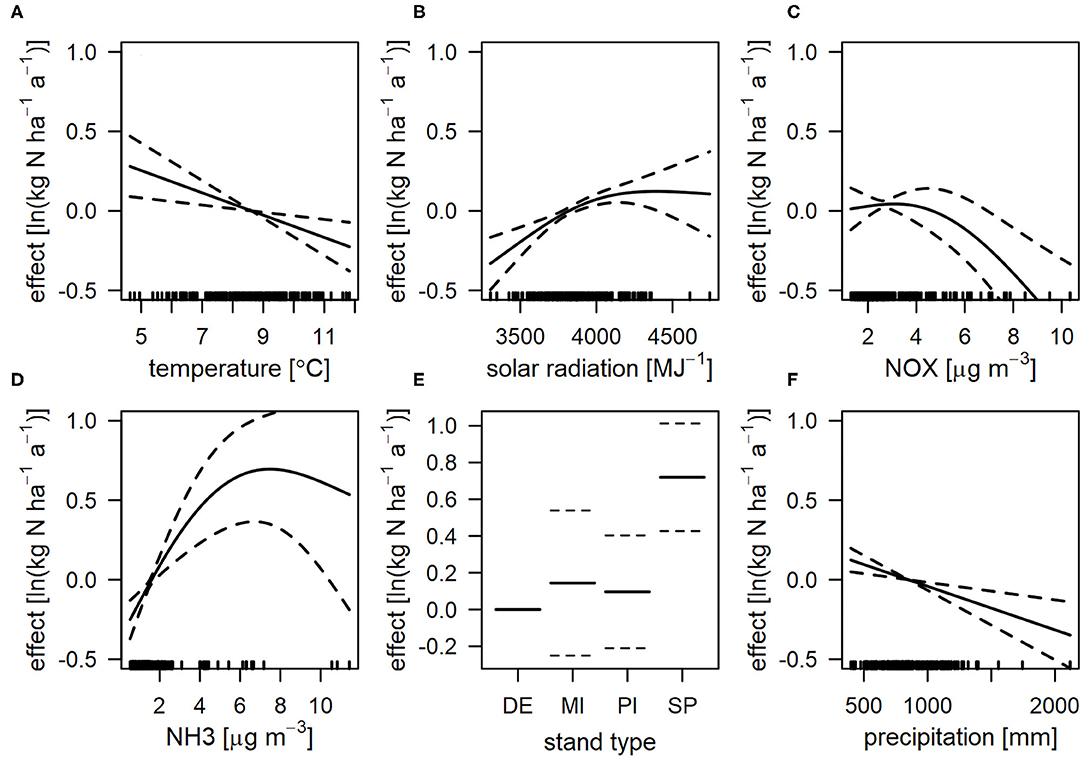
Figure 7. Partial effect of temperature (A), solar radiation (B), NOX concentration (C), NH3 concentration (D), stand type (E), and precipitation (F) on ΔTIN between the inferential (IFM) and emission based method (EBM) for dry deposition (A–E), and total deposition (F). Positive effects indicate a tendency for higher TIN deposition estimates of the IFM compared to the EBM. Note the log-transformed data. Dashed lines indicate 95% pointwise prognosis intervals. The covariate is displayed as marks along the x-axis. (DE, deciduous forest; MI, mixed forest; PI, pine forest; SP, spruce forest).
In summary, main findings are:
- Similar effects found for DD estimates in the CBM-EBM (n = 1,237) and the IFM-EBM (n = 194) comparison for spruce plots. Here, the EBM tends to lower TIN DD estimates. Both CBM and IFM show this tendency, either with or without tree species specific correction (see IFM variant VT), when compared to the EBM.
- The effects of the different meteorological and air concentration variables differ between model comparisons of the respective variants (Table 7). For example solar radiation is significant for IFM-EBM but not for the other variants. However, this can also be an effect of the limited sample size. It can be seen for TD, that when comparing CBM and EBM (n = 1,237), all variables listed in the table are significant, with the exception of solar radiation.
- Spatial and temporal effects are mainly shown for the comparison between CBM and EBM. This is likely also the result of the much larger sample size. Spatial effects with a large effect strength are mainly apparent for WD.
- With the exception of slope inclination, orographic parameters do not actually appear in any of the models.
Discussion
We compared three commonly used models for the estimation of TIN deposition to forests: a canopy budget model (CBM, Ulrich, 1994), the inferential method (IFM) based on observations of ambient air concentrations and an emission-based-approach (EBM) using a chemical transport model (LOTOS-EUROS). The relatively large number of plot-years included in this study allowed us to identify general patterns of differences between the three approaches. At the same time, the amount of data made it impossible to analyze each plot-year in detail. Therefore, although several important explanatory variables were included in the statistical models, some patterns occurring at specific subsets of the data might not be well-represented in the results. The discussion comprises two main sections: (1) uncertainties in methods and measurements; (2) comparison of TIN deposition estimates between the three methods.
Uncertainties in Methods and Measurements
The three methods to estimate TIN deposition compared in this study (CBM, IFM, and EBM) are frequently applied because they can be used with relatively low effort compared to methodologically advanced micrometeorological methods. This also implies, however, that each method suffers from substantial limitations. Ellermann et al. (2018) estimated the uncertainty on nitrogen deposition for Danish land areas to be 27–43%. They interpret the high uncertainty as a result of partial uncertainties of the various N species that contribute to TIN TD. In this study, the uncertainty of the different methods can only be quantified very roughly, as the results are obtained from a combination of measurements and models with different input data and many assumptions. The following aspects of uncertainty for the three models should be considered when interpreting the results.
For WD measurements alone, uncertainties of 10–40% can be assumed due to errors in sampling and analysis (Zimmermann et al., 2006). The higher small-scale variability in forest stands is taken into account by a higher number of collectors, therefore the uncertainty in throughfall deposition is expected to be of comparable, but potentially somewhat larger, magnitude. A further uncertainty results from the application of uniform conversion factors to convert from bulk to wet deposition. These factors do not only affect wet deposition, but also the results of the CBM method and the estimation of particulate deposition from observed wet deposition for the IFM method. The national average values we used (0.95 for , 0.9 for ) have a standard deviation of 0.25 and 0.22 for and , respectively. They are based on 79 () and 86 () plot-years of parallel wet and bulk sampling across Germany (Gauger et al., 2008). Bulk to wet conversion factors can vary greatly between regions and are particularly uncertain for ammonium, where losses from bulk collectors have been reported (Stedman et al., 1990; Fürst, 2016). The canopy budget model is also affected by the wet-only conversion for sodium (tracer substance in the CBM). We used the national average of 0.81 for Na+, but the spatio-temporal variability for this value across Germany is very high (standard deviation = 0.2; Gauger et al., 2008). Further studies are required to identify variables that could explain the spatio-temporal variability and could accordingly allow for a regionalization of the conversion factors.
The CBM approach according to Ulrich (1994) relies on the robust measurements of six flux rates (Na+, , for both open field and stand precipitation). While other canopy budget models (Draaijers and Erisman, 1995; De Vries et al., 2001) require even more parameters and assumptions, the accurate monitoring of these fluxes is still challenging. Contamination with biological material can alter the composition especially of throughfall and stemflow, which is sometime challenging to detect despite the rigorous QA/QC rules applied (Mosello et al., 2005). Furthermore, the CBM approach relies on the assumption of similar concentration ratios (:Na+ and :Na+) in interception deposition and wet deposition. It has primarily been formulated for areas where cloud water droplets dominantly contribute to interception deposition and where substantial amounts of the airborne tracer substance (Na+) are present (Ulrich, 1994). Deviations from these conditions are expected for the majority of the German intensive monitoring plots. The resulting uncertainties in deposition estimates remain to be investigated. Comparisons between micrometeorological methods and CBM have reported high deviations (Gallagher et al., 1997; Mohr et al., 2005). Another weakness of the CBM approach according to Ulrich (1994) is that it conceptually underestimates TIN DD as net uptake of TIN in the canopy compensates DD fluxes. Uptake of TIN in the canopy may occur via stomatal uptake of gaseous N species by the trees or via ion exchange. The conversion of inorganic to organic N species by microorganisms in the canopy additionally contributes to the underestimation of TIN DD. Canopy budget models with explicit parameterization of canopy uptake (Draaijers and Erisman, 1995; De Vries et al., 2001) estimate on average higher TIN deposition rates (Mohr et al., 2005).
Flechard et al. (2011) demonstrated that discrepancies between N deposition estimates from different IFM models at one site can be several times larger than between sites. One possible reason for this is that the IFM approach usually is a combination of observations and modeling with numerous assumptions. This also applies to the IFM approach used in our study. The gaseous components NO2 and NH3 were assessed at the intensive monitoring sites. The accuracy level of these measurements is stated to be about ±30% (Schaub et al., 2016). Other aspects, such as the low sampling frequency of passive samplers may cause biased results (Schrader et al., 2018).
A probably larger uncertainty is harbored in the parametrization of deposition velocity vd. Several mechanistic models for vd exist, which e.g., utilize detailed information on meteorology and soil water availability to model stomatal opening. This allows for the parametrization of stomatal exchange if ambient air concentrations compared to foliar concentrations are known (Wichink Kruit et al., 2012). While the complexity of these comprehensive models offers the opportunity for an accurate quantification of dry deposition fluxes, additional uncertainty arises from assumptions about input parameters. We chose a different approach, starting from typical deposition velocities from the literature (“forest type specific values”). These forest type specific values were adjusted using the most important determinants for vd in order to derive “semi-empirical correction factors.” The results show a much better agreement with the two other methods (CBM, EBM) than the uncorrected version. In order to account for other tree species at a majority of the intensive forest monitoring sites in Germany, we extended the IFM approach established by Kirchner et al. (2014) at 9 spruce sites in the Bavarian Alps by the tree species specific correction term. This extension and the use of the terrain exposure index (TEI) as a proxy for the frequency of inversion weather conditions were the only modifications made. Applying these semi-empirical correction factors reduced the bias between the IFM and both the EBM and the CBM approach substantially (Table 6). Additionally, in order to illustrate the uncertainty caused by the forest type specific deposition velocity values, the results for 30% higher and lower vd, which roughly corresponds to the variability of vd from the literature, were integrated as regression lines (Figures 2, 4).
Since the deposition of gaseous HNO3 and particulate and often only accounts for a small proportion of dry deposition (Thimonier et al., 2019) and no observations are available, we used an empirical relationship (Schmitt et al., 2005) which can be parameterized by forest type and bulk deposition of TIN. The equations were obtained from 77 monthly measured deposition values of the different N species and the coefficient of determination was 0.92. We performed a limited test whether the approach can be transferred to other deposition and meteorological regimes based on the deposition data reported by Thimonier et al. (2019), which resulted in an underestimation of about 1 kg N ha−1 a−1. However, the test is only valid to a limited extent. Data used for model parameterization and evaluation come from different years but partly from the same sites. Furthermore, only bulk deposition was measured at these sites, so the average conversion factors for Germany to estimate WD (Gauger et al., 2008) had to be used. Therefore, we can only assume that a rough estimate of gaseous HNO3 and particular and deposition is possible with this approach.
The EBM approach contains uncertainties at very different methodological and spatial levels. Comparison of spatial data in a 1*1 km grid resolution as for the EBM with point data as for the CBM and IFM should be done very carefully, especially in areas with complex orography or in regions with a fine-grained land cover pattern (edge effects) and with a high variability of N emissions. Actual deposition rates at a specific location may differ from the average of the corresponding EBM grid cell, although EBM output is reported on a land cover specific level (conifer, broadleaved and mixed forest). Similar to the other two approaches, EBM is affected by the uncertainties in wet deposition assessments. More importantly, as precipitation is highly variable in space and time, further uncertainty originates from the regionalization of precipitation, depending on regionalization strategy, orographic conditions and scale. Considering these challenges to correctly estimate TIN WD, the average deviation of −0.8 kg N ha−1 a−1 compared to wet-only-corrected bulk deposition measurements for 1,237 plot-years in Germany is remarkably low. For dry deposition estimation Saylor et al. (2019) pointed out that the algorithms used in atmospheric chemistry models to predict particle deposition velocity are highly uncertain. In particular, estimates for forests show a weak agreement with available measurements (Saylor et al., 2019). Furthermore, the performance of EBM depends on the spatial resolution and quality of their input data, in particular the emission inventory. Meteorological data are available in a high temporal, but low spatial resolution of 7 × 14 km (Schaap et al., 2018). Accordingly, Simpson et al. (2011) estimated an error of TIN deposition estimates of 30% for the different regional models and approaches in Europe. A conceptual problem faced by all types of models is that relations established at specific locations are extrapolated to other areas (e.g., assumption of the CBM, dry deposition velocities, scavenging ratios, fog water enrichment factors) and proper parametrization of the transfer of these relations to other locations is challenging.
Comparison of TIN Deposition Estimates Between the Three Methods
We found on average a difference of −0.3 kg ha−1 a−1 and +3.3 kg ha−1 a−1 between the CBM and IFM approaches, with and without applying the extended semi-empirical deposition velocity correction factors given by Kirchner et al. (2014), respectively. The correction improves the fit between CBM and IFM across Germany (lowlands and mountain ranges), although it has been developed for the Bavarian Alps. Schmitt et al. (2005) found slightly higher estimates of the IFM (median difference +2.4 kg N ha−1 a−1) when compared to a different CBM (De Vries et al., 2001), which, however, usually yields higher estimates of TIN deposition, compared to the Ulrich (1994) model used in our study (Mohr et al., 2005). Zimmermann et al. (2006) found a good agreement between the two methods, while Kirchner et al. (2014) stated that the two methods deviated at all sites. A slightly lower TIN deposition estimated by the CBM compared to the IFM may be expected due to the conceptual underestimation of TIN deposition by the specific type of CBM we used (Ulrich, 1994). However, the regression functions from Schmitt et al. (2005) used in the IFM approach for estimating HNO3, , and deposition may also lead to additional uncertainty of the deposition rates.
The statistical analysis of the differences in estimated TIN deposition between the IFM and CBM approaches found no significant effects of tree species, measurement year, coordinates, altitude, slope, aspect, aspect index, terrain exposure index (TEI), wind speed, air concentrations or precipitation. A large effect of the random factor “site” in the mixed model might indicate that further site-specific properties exists which contribute to the observed differences between model estimates in addition to random errors. Stand height, canopy closure, frontal area index (total area of roughness elements projected in the wind direction per unit ground area), crown density, and/or stand volume could be some of these site specific factors affecting local deposition processes (Erisman and Draaijers, 2003; Vesala et al., 2005; De Schrijver et al., 2007; Nakai et al., 2008).
A few studies exist where CBM and/or IFM have been compared to micro-meteorological measurements of higher accuracy. Recently, Brümmer et al. (2020) have tested an eddy covariance approach for total reactive nitrogen in a forested area of the Bavarian forest with low levels of N deposition. For the period 2016–2018 they report a measured TIN DD rate of around 4.4 kg ha−1 a−1 compared to estimates of 5.2 and 6.9 kg ha−1 a−1 from the same EBM as used in our study (based on an uncorrected and an improved classification of land use types, respectively). In parallel, a CBM approach is conducted at the site since several years (Beudert and Breit, 2014). However, the CBM results are not comparable with our study, because the variants of the CBMs they use clearly differ from the Ulrich (1994) model used in our study. Mohr et al. (2005) found clearly lower N fluxes (−27 kg N ha−1 a−1) with the CBM compared to a micrometeorological method at a site exposed to high ambient air levels of NH3.
The comparison of WD using the EBM approach with the CBM shows a fairly good agreement. However, there seems to be a systematic deviation for estimates with increasing precipitation rates (Figure 5A). This effect mainly originates from two mountainous stations. At these stations, the simulated precipitation amount clearly exceeds the open field precipitation observations. If the corresponding stations are excluded from the statistical analysis, the effect is still significant, but the effect strength is somewhat smaller (results not shown). The deviation in the precipitation data might be caused by a systematic underestimation of precipitation amount for observations with a large proportion of snow or strong rain events (sampler overflow) and/or low performance of regionalization models for precipitation in orographic complex landscapes as used for WD estimation (1*1 km). The elevated deviance between EBM and CBM estimates in some regions might be attributable to the uniform application of bulk to wet conversion factors (Figure 6A).
The EBM approach estimates on average lower DD compared to CBM and IFM approaches (Table 6). This pattern is more distinct for spruce plots (Figure 5F, Figure 7E) and does not diminish if the tree-species correction factor of the IFM approach is deactivated (Table 7, model “IFMVT-EBM”). As the CBM and the IFM rely on independent approaches to estimate the dry deposition, this might indicate that the EBM deposition estimates are less reliable for spruce plots. When interpreting the partial effects, however, the relationship between individual variables must always be taken into account. Accordingly, the change in nitrogen deposition should not be deduced directly from the tree species spruce, for example, but rather the respective precipitation conditions (and other variables) at the site must also be considered. Several meteorological parameters significantly affect the differences between DD estimates, which are also known to have an effect on deposition rates [e.g., via stomatal resistance, particle deposition velocity; Han et al. (2011), Mohan (2016)]. On the other hand, the different terrain parameters hardly contribute to an explanation. This may be due to incorporation of terrain information into the regionalization of the climatic variables that were used as predictors (Dietrich et al., 2019).
In a previous comparison between the EBM used in our study and the CBM according to De Vries et al. (2001), TIN TD estimates were reported to roughly agree (Schaap et al., 2018). At some locations, however, differences of up to 40% were found (Schaap et al., 2018). Our analysis is, however, not directly comparable to the Schaap et al. (2018) study, as (1) a different type of CBM was used; (2) a larger number of plots with an extended regional coverage of Germany and longer observation periods are included; (3) a bulk-to-wet correction of , , and Na+ fluxes has been applied prior to CBM calculations as recommended by Adriaenssens et al. (2013) in order to harmonize the WD calculation between the three approaches. This correction increases the estimated TIN TD of the CBM by ~1.2 kg ha−1 a−1 on average.
Conclusions and Outlook
The demand for N deposition estimates with high accuracy as well as large spatial and temporal resolution is growing. Forests pose a special challenge in this regard, due to the high importance of dry deposition, which is more difficult to quantify. In the framework of long-term monitoring at ICP Forests sites in Germany, we compared three methods for the estimation of total inorganic nitrogen deposition to forests (CBM, IFM, EBM). If all approaches would yield accurate results, we would have expected similar TIN deposition estimates from the IFM and the EBM and lower values from the CBM, as it includes a conceptual underestimation. Contrarily, we found the EBM provided on average lowest estimates. The deviation between the EBM and both of the other methods was especially pronounced for the dry deposition at spruce plots. Differences of dry deposition estimates between all methods were found to be affected by meteorological conditions, which are known to regulate deposition velocity. The average discrepancy in TIN deposition according to the method yielding on average highest deposition rates (IFM) and the method suggesting on average lowest deposition rates (EBM) was 6.3 kg N ha−1 a−1 (uncorrected IFM) or 2.7 kg N ha−1 a−1 (IFM with site specific corrections). We hypothesize that a combination of different factors contribute to the discrepancies between the three approaches. They include the comparison of observations at the plot scale (CBM, IFM) with gridded information (EBM, based on a 1 × 1 km resolution and coarser for some calculation steps), conceptual limitations of the utilized CBM version, and varying accuracy of the EBM for different forest types.
As all methods are subject to considerable uncertainty, we cannot conclude whether any of the methods provides more or less accurate estimates. Instead, the results can only indicate aspects worthwhile to consider for future methodological improvements. Recent developments contributing to a more accurate quantification of TIN deposition to forests include for example (i) continuous improvements of EBM and the underlying emission inventories (Schaap et al., 2015, 2017, 2018), (ii) networks of low-cost monitoring stations for ambient air concentrations and meteorological conditions improving data availability (e.g., Karagulian et al., 2019; Weissert et al., 2020), and (iii) ongoing research in CBM and similar approaches, like surface-wash and surrogate surface sampling (Aguillaume et al., 2017; Karlsson et al., 2019). In addition, more high-accuracy validation datasets (e.g., Brümmer et al., 2020) are required to quantify the performance of the different modeling approaches.
Data Availability Statement
The datasets generated for this study are available on request from the institutions holding the data: Climate and terrain data by Institute of Geography, University of Hamburg, Germany. Emission based deposition data by UBA, Dessau, Germany. Measured deposition and air concentrations by Thünen Institute of Forest Ecosystems, Eberswalde, Germany. Deposition calculated by inferential methods by Northwest German Forest Research Institute (NW-FVA). Requests to access these datasets should be directed to Jan Wehberg,amFuLndlaGJlcmdAdW5pLWhhbWJ1cmcuZGU=; Markus Geupel,bWFya3VzLmdldXBlbEB1YmEuZGU=; Anne-Kartin Prescher,YW5uZS5wcmVzY2hlckB0aHVlbmVuLmRl; Bernd Ahrends,YmVybmQuYWhyZW5kc0Budy1mdmEuZGU=.
Author Contributions
BA and AS: designed the study, developing of methods, preparation of deposition data, and data analysis. JW: regionalization of climate data and realization of terrain analysis. A-KP: preprocessing and aggregation of air concentration data. MG: emission based deposition data. HA and HM: supervising the work. All authors contributed to writing.
Funding
The evaluation was based on data that was collected by partners of the official UNECE ICP Forests Network (http://icp-forests.net/contributors). Part of the data was co-financed by the European Commission. Partial funding of data collection was provided by the European Union under Council Regulation (EEC) 3528/86 on the Protection of Forests against Atmospheric Pollution, the Regulation (EC) 2152/2003 concerning monitoring of forests and environmental interactions in the community (Forest Focus) and by the project LIFE 07 ENV/D/000218 Further Development and Implementation of an EU-level Forest monitoring Systeme (FutMon).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the numerous staff involved in operating the intensive forest monitoring in Germany in the last decades. We thank the German Environmental Agency for providing the data from EBM approach. However, it should be noted that this paper does not necessarily reflect the opinion or the policies of the German Federal Environment Agency.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/ffgc.2020.00103/full#supplementary-material
References
Adriaenssens, S., Staelens, J., Baeten, L., Verstraeten, A., Boeckx, P., Samson, R., et al. (2013). Influence of canopy budget model approaches on atmospheric deposition estimates to forests. Biogeochemistry 116, 215–229. doi: 10.1007/s10533-013-9846-0
Aguillaume, L., Izquieta-Rojano, S., García-Gómez, H., Elustondo, D., Santamaría, J., Alonso, R., et al. (2017). Dry deposition and canopy uptake in mediterranean holm-oak forests estimated with a canopy budget model: a focus on N estimations. Atmos. Environ. 152, 191–200. doi: 10.1016/j.atmosenv.2016.12.038
Benedict, K. B., Day, D., Schwandner, F. M., Kreidenweis, S. M., Schichtel, B., Malm, W. C., et al. (2013). Observations of atmospheric reactive nitrogen species in rocky mountain national park and across northern Colorado. Atmos. Environ. 64, 66–76. doi: 10.1016/j.atmosenv.2012.08.066
Bequet, R., Campioli, M., Kint, V., Vansteenkiste, D., Muys, B., and Ceulemans, R. (2011). Leaf area index development in temperate oak and beech forests is driven by stand characteristics and weather conditions. Trees 25, 935–946. doi: 10.1007/s00468-011-0568-4
Beudert, B., and Breit, W. (2014). Kronenraumbilanzen zur Abschätzung der Stickstoffgesamtdeposition in Waldökosysteme des Nationalparks Bayerischer Wald. 2014. Project: 24314. Available online at: https://wwwumweltbundesamt.de/sites/default/files/medien/370/dokumente/kronenraumb ilanzen_stickstoffgesamtdeposition_nationalpark_bayerisches_wald_-_bericht sjahr_2013_im_forellenbach.pdf (accessed August 30, 2020).
Brümmer, C., Schrader, F., Wintjen, P., Zöll, U., and Schaap, M. (2020). FORESTFLUX–Standörtliche Validierung der Hintergrunddeposition reaktiver Stickstoffverbindungen. Dessau-Roßlau: Federal Environment Agency.
Bühlmann, P., and Hothorn, T. (2007). Boosting algorithms: regularization, prediction and model fitting. Stat. Sci. 22, 477–505. doi: 10.1214/07-STS242
Bühlmann, P., and Yu, B. (2003). Boosting with the L2 loss: regression and classification. J. Am. Stat. Assoc. 98, 324–339. doi: 10.1198/016214503000125
Builtjes, P., Hendriks, E., Koenen, M., Schaap, M., Banzhaf, S., Kerschbaumer, A., et al. (2011). Erfassung, Prognose und Bewertung von Stoffeinträgen und ihren Wirkungen in Deutschland (Modelling of Air Pollutants and Ecosystem Impact - MAPESI). Dessau-Rosslau: Texte Umweltbundesamt.
Clarke, N., Zlindra, D., Ulrich, E., Mosello, R., Derome, J., Derome, K., et al. (2016). “Part XIV: sampling and analysis of deposition,” in Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests, ed UNECE ICP Forests Programme Coordinating Centre (Eberswalde: Thünen Institute of Forest Ecosystems). Available online at: http://icp-forests.net/page/icp-forests-manual (accessed August 30, 2020).
Dämmgen, U., Matschullat, J., Zimmermann, F., Strogies, M., Grünhage, L., Scheler, B., et al. (2013). Emission reduction effects on bulk and wet-only deposition in Germany - evidence from long-term observations. Part 1: general introduction. Gefahrstoffe Reinhalt. Luft 72, 49–54.
De Schrijver, A., Geudens, G., Augusto, L., Staelens, J., Mertens, J., Wuyts, K., et al. (2007). The effect of forest type on throughfall deposition and seepage flux: a review. Oecologia 153, 663–674. doi: 10.1007/s00442-007-0776-1
De Vries, W., Hettelingh, J.-P., and Posch, M, . (eds). (2015). “Critical loads and dynamic risk assessments,” in Environmental Pollution, Vol. 25, (Dordrecht; Heidelberg; New York, NY; London: Springer), 644. doi: 10.1007/978-94-017-9508-1
De Vries, W., Reinds, G. J., van der Salm, C., Draaijers, G. P. J., Bleeker, A., Erisman, J. W., et al. (2001). Intensive Monitoring of Forest Ecosystems in Europe. Technical Report 2001, Brussels; Geneva: EC, UNECE, Forest Intensive Monitoring Coordinating Institute (FIMCI). Available online at: https://www.icp-forests.org/pdf/TRLII2001.pdf (accessed August 30, 2020).
De Vries, W., Reinds, G. J., and Vel, E. (2003). Intensive monitoring of forest ecosystems in Europe 2: atmospheric deposition and its impacts on soil solution chemistry. For. Ecol. Manag. 174, 97–115. doi: 10.1016/S0378-1127(02)00030-0
Delignette-Muller, M. L., and Dutang, C. (2015). fitdistrplus: an R package for fitting distributions. J. Stat. Softw. 64, 1–34. doi: 10.18637/jss.v064.i04
Dietrich, H., Wolf, T., Kawohl, T., Wehberg, J., Kändler, G., Mette, T., et al. (2019). Temporal and spatial high-resolution climate data from 1961 to 2100 for the German national forest inventory (NFI). Ann. For. Sci. 76, 1–14. doi: 10.1007/s13595-018-0788-5
Draaijers, G. P. J., and Erisman, J. W. (1995). A canopy budget model to assess atmospheric deposition from throughfall measurements. Water Air Soil Pollut. 85, 2253–2258. doi: 10.1007/BF01186169
Du, E., and De Vries, W. (2018). Nitrogen-induced new net primary production and carbon sequestration in global forests. Environ. Pollut. 242(Pt B), 1476–1487. doi: 10.1016/j.envpol.2018.08.041
Ellermann, T., Nygaard, J. R., Christensen, J. H., Løfstrøm, P., Geels, C., Nielsen, I. E., et al. (2018). Nitrogen deposition on danish nature. Atmosphere 9:447. doi: 10.3390/atmos9110447
Erisman, J. W., and Draaijers, G. P. J. (2003). Deposition to forests in Europe: most important factors influencing dry deposition and models used for generalisation. Environ. Pollut. 124, 379–388. doi: 10.1016/S0269-7491(03)00049-6
Etzold, S., Ferretti, M., Reinds, G. J., Solberg, S., Gessler, A., Waldner, P., et al. (2020). Nitrogen deposition is the most important environment driver of growth of pure, even-aged and managed European forests. For. Ecol. Manag. 458:117762. doi: 10.1016/j.foreco.2019.117762
Ferretti, M., and Schaub, M. (2014). Monitoring European forests-detecting and understanding changes. For. Ecol. Manag. 311, 1–2. doi: 10.1016/j.foreco.2013.08.027
Fischer, R., Mues, V., Ulrich, E., Becher, G., and Lorenz, M. (2007). Monitoring of atmospheric deposition in European forests and an overview on its implication on forest condition. Appl. Geochem. 22, 1129–1139. doi: 10.1016/j.apgeochem.2007.03.004
Flechard, C. R., Nemitz, E., Smith, R. I., Fowler, D., Vermeulen, A. T., Bleeker, A., et al. (2011). Dry deposition of reactive nitrogen in European ecosystems: a comparison of inferential models across the NitroEurope network. Atmos. Chem. Phys. 11, 2703–2728. doi: 10.5194/acp-11-2703-2011
Fleck, S., Ahrends, B., Sutmöller, J., Albert, M., Evers, J., and Meesenburg, H. (2017). Is biomass accumulation in forests an option to prevent climate change induced increases in nitrate concentrations in the North German Lowland? Forests 8, 1–28. doi: 10.3390/f8060219
Fleck, S., Eickenscheidt, N., Ahrends, B., Evers, J., Grüneberg, E., Ziche, D., et al. (2019). “Nitrogen status and dynamics in German forest soils,” in Ecological Studies (Analysis and Synthesis), Vol. 237, eds N. Wellbrock, and A. Bolte (Berlin: Springer Verlag), 123–166. doi: 10.1007/978-3-030-15734-0_5
Fürst, A. (2016). Influence of the sampling interval on the measured deposition results and on the calculated impacts. Forstschutz Aktuell 62, 1–4.
Gallagher, M. W., Beswick, K. M., Duyzer, J., Westrate, H., Choularton, T. W., and Hummelshoj, P. (1997). Measurements of aerosol fluxes to speulder forest using a micrometeorological technique. Atmos. Environ. 31, 359–373. doi: 10.1016/S1352-2310(96)00057-X
Gauger, T., Anshelm, F., Schuster, H., Draaijers, G. P. J., Bleeker, B., Erisman, J. W., et al. (2002). Kartierung Ökosystembezogener Langzeittrends Atmosphärischer Stoffeinträge und Luftschadstoffkonzentrationen in Deutschland und Deren Vergleich mit Critical Loads und Critical Levels. Forschungsvorhaben im Auftrag des BMU/UBA, FE-Nr. 299 42 210. Stuttgart: Institut für Navigation, Univ. Stuttgart.
Gauger, T., Haenel, H.-D., Rösemann, C., Dämmgen, U., Bleeker, A., Erisman, J. W., et al. (2008). National Implementation of the UNECE Convention on Long-Range Transboundary Air Pollution (Effects)/Nationale Umsetzung UNECE-Luftreinhaltekonvention (Wirkungen): Part 1: Deposition Loads: Methods, Modelling and Mapping Results, Trends. Dessau-Roßlau: Federal Environment Agency.
Goude, M., Nilsson, U., and Holmström, E. (2019). Comparing direct and indirect leaf area measurements for Scots pine and Norway spruce plantations in Sweden. Eur. J. For. Res. 138, 1033–1047. doi: 10.1007/s10342-019-01221-2
Han, Y., Hu, Y., and Qian, F. (2011). Effects of air temperature and humidity on particle deposition. Chem. Eng. Res. Des. 89, 2063–2069. doi: 10.1016/j.cherd.2011.02.001
Hauck, M., Zimmermann, J., Mascha, J., Dulamsuren, C., Bade, C., Ahrends, B., et al. (2012). Rapid recovery of stem growth at reduced SO2 levels suggests a major contribution of foliar damage in the pollutant-caused dieback of Norway spruce during the late 20th century. Environ. Pollut. 164, 132–141. doi: 10.1016/j.envpol.2012.01.026
Hettelingh, J. P., Posch, M., and Slootweg, J. (2017). European Critical Loads: Database, Biodiversity and Ecosystems at Risk. CCE Final Report 2017, Bilthoven: National Institute for Public Health and the Environment.
Hothorn, T., Buehlmann, P., Kneib, T., Schmid, M., and Hofner, B. (2020). mboost: Model-Based Boosting. R Package Version 2.9-2. Available online at: https://CRAN.R-project.org/package=mboost (accessed August 30, 2020).
Hunová, I., Kurfürst, P., Vlcek, O., Stráník, P., Schovánkova, J., and Srbova, D. (2016). Towards a better spatial quantification of nitrogen deposition: a case study for Czech forests. Environ. Pollut. 213, 1028–1041. doi: 10.1016/j.envpol.2016.01.061
Johnson, J., Graf Pannatier, E., Carnicelli, S., Cecchini, G., Clarke, N., Cools, N., et al. (2018). The response of soil solution chemistry in European forests to decreasing acid deposition. Glob. Change Biol. 24, 3603–3619. doi: 10.1111/gcb.14156
Karagulian, F., Barbiere, M., Kotsev, A., Spinelle, L., Gerboles, M., Lagler, F., et al. (2019). Review of the performance of low-cost sensors for air quality monitoring. Atmosphere 10:506. doi: 10.3390/atmos10090506
Karlsson, P. E., Pihl-Karlsson, G., Hellsten, S., Akselsson, C., Ferm, M., and Hultberg, H. (2019). Total deposition of inorganic nitrogen to Norway spruce forests–applying a surrogate surface method across a deposition gradient in Sweden. Atmos. Environ. 2019:116964. doi: 10.1016/j.atmosenv.2019.116964
Katata, G., Kajino, M., Hiraki, T., Aikawa, M., Kobayashi, T., and Nagai, H. (2011). A method for simple and accurate estimation of fog deposition in a mountain forest using a meteorological model. J. Geophys. Res. Atmos. 116:D20102. doi: 10.1029/2010JD015552
Katata, G., Nagai, H., Wrzesinsky, T., Klemm, O., Eugster, W., and Burkard, R. (2008). Development of a land surface model including cloud water deposition on vegetation. J. Appl. Meteorol. Climatol. 47, 2129–2146. doi: 10.1175/2008JAMC1758.1
Kirchner, M., Fegg, W., Römmelt, H., Leuchner, M., Ries, L., Zimmermann, R., et al. (2014). Nitrogen deposition along differently exposed slopes in the bavarian alps. Sci. Total Environ. 470–471, 895–906. doi: 10.1016/j.scitotenv.2013.10.036
König, N., Cools, N., Derome, K., Kowalska, A., De Vos, B., Fürst, A., et al. (2013). “Data quality in laboratories: methods and results for soil, foliar, water, and chemical analyses,” in Forest Monitoring: Methods for Terrestrial Investigations in Europe With an Overview of North America and Asia, eds M. Ferretti, and R. Fischer (Oxford: Elsevier), 19–32.
Legates, D. R., and McCabe, G. J. (2013). A refined index of model performance: a rejoinder. Int. J. Climatol. 33, 1053–1056. doi: 10.1002/joc.3487
Li, J. (2017). Assessing the accuracy of predictive models. PLoS ONE 12:e0183250. doi: 10.1371/journal.pone.0183250
Lin, J. J., Noll, K. E., and Holsen, T. M. (1994). Dry deposition velocities as a function of particle size in the ambient atmosphere. Aerosol Sci. Technol. 20, 239–252. doi: 10.1080/02786829408959680
MacDonald, J. A., Dise, N. B., Matzner, E., Armbruster, M., and Gundersen, P. (2002). Nitrogen input together with ecosystem nitrogen enrichment predict nitrate leaching from European forests. Glob. Change Biol. 8, 1028–1033. doi: 10.1046/j.1365-2486.2002.00532.x
Manders, A. M. M., Builtjes, P. J. H., Curier, L., Denier Van Der Gon, H. A. C., Hendriks, C., Jonkers, S., et al. (2017). Curriculum vitae of the LOTOS–EUROS (v2.0) chemistry transport model. Geosci. Model Dev. 10, 4145–4173. doi: 10.5194/gmd-10-4145-2017
Marchetto, A., Mosello, R., Tartari, G., Derome, J., Derome, K., Sorsa, P., et al. (2006). Atmospheric Deposition and Soil Solution Working Ring Test 2005-Laboratory Ring Test for Deposition and Soil Solution Sample Analyses Between the Countries Participating in the ICP Forests Level II Monitoring Programme. Pallanza: Office National des Forêts, Département Recherche.
Marner, B., and Harrison, R. M. (2004). A spatial refined monitoring based study of atmospheric nitrogen deposition. Atmos. Environ. 38, 5045–5056. doi: 10.1016/j.atmosenv.2004.06.016
Marques, M. C., Gravenhorst, G., and Ibrom, A. (2001). Input of atmospheric particles into forest stands by dry deposition. Water Air Soil Pollut. 130, 571–576. doi: 10.1023/A:1013899032454
Mayr, A., Hofner, B., Waldmann, E., Hepp, T., Meyer, S., and Gefeller, O. (2017). An update on statistical boosting in biomedicine. Comput. Math. Methods Med. 2017, 1–12. doi: 10.1155/2017/6083072
Meesenburg, H., Ahrends, B., Fleck, S., Wagner, M., Fortmann, H., Scheler, B., et al. (2016). Long-term changes of ecosystem services at Solling, Germany: recovery from acidification, but increasing nitrogen saturation? Ecol. Indic. 65, 103–112. doi: 10.1016/j.ecolind.2015.12.013
Meesenburg, H., Eichhorn, J., and Meiwes, K. J. (2009). “Atmospheric deposition and canopy interactions,” in Functioning and Management of European Beech Ecosystems. Ecological Studies, Vol. 208, eds R. Brumme, and P. K. Khanna (Berlin: Springer-Verlag), 265–302. doi: 10.1007/b82392_16
Meesenburg, H., Merino, A., Meiwes, K. J., and Beese, F. (2004). Effects of long-term application of ammonium sulphate on nitrogen fluxes in a beech ecosystem at Solling, Germany. Water Air Soil Pollut. Focus 4, 415–426. doi: 10.1023/B:WAFO.0000028368.77125.2b
Mohan, S. M. (2016). An overview of particulate dry deposition: measuring methods, deposition velocity and controlling factors. Int. J. Environ. Sci. Technol. 13, 387–402. doi: 10.1007/s13762-015-0898-7
Mohr, K., Meesenburg, H., Horvath, B., Meiwes, K. J., Schaaf, S., and Dämmgen, U. (2005). Bestimmung von Ammoniak-Einträgen aus der Luft und Deren Wirkungen auf Waldökosysteme (ANSWER-Projekt). Landbauforschung Völkenrode Sonderheft, 279. Braunschweig: Bundesforschungsanstalt für Landwirtschaft (FAL).
Mosello, R., Amoriello, M., Amoriello, T., Arisci, S., Carcano, A., Clarke, N., et al. (2005). Validation of chemical analyses of atmospheric deposition in forested European sites. Int. J. Limnol. 64, 93–102. doi: 10.4081/jlimnol.2005.93
Nakai, T., Sumida, A., Daikoku, K., Matsumoto, K., Van Der Molen, M. K., Kodama, Y., et al. (2008). Parameterisation of aerodynamic roughness over boreal, cool- and worm-temperate forests. Agric. For. Meteorol. 148, 1916–1925. doi: 10.1016/j.agrformet.2008.03.009
Panferov, O., Ahrends, B., Nuske, R. S., Thiele, J. C., and Jansen, M. (2011). “Challenges in climate-driven decision support systems in forestry,” in Efficient Decision Support Systems–Practice and Challenges in Multidisciplinary Domains, ed C. Jao (InTechOpen), 459–478. doi: 10.5772/19217
Panferov, O., Doering, C., Rauch, E., Sogachev, A., and Ahrends, B. (2009). Feedbacks of windthrow for Norway spruce and Scots pine stands under changing climate. Environ. Res. Lett. 4:045019. doi: 10.1088/1748-9326/4/4/045019
Peters, K., and Eiden, R. (1992). Modelling the dry deposition velocity of aerosol particles to a spruce forest. Atmos. Environ. 26, 2555–2564. doi: 10.1016/0960-1686(92)90108-W
Pinheiro, J. D., Bates, S., Debroy, D., Sarkar, and R. C. Team (2018). nlme: Linear and Nonlinear Mixed Effects Models. R package version 3.1-137. Available online at: https://CRAN.R-project.org/package=nlme (accessed August 30, 2020).
R Development Core Team (2018). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. Available online at: http://www.R-project.org (accessed August 30, 2020).
Rihm, B., and Achermann, B. (2016). Critical Loads of Nitrogen and Their Exceedances. Swiss Contribution to the Effects-Oriented Work Under the Convention on Long-Range Transboundary Air Pollution (UNECE). Bern: Federal Office for the Environment.
Roberts, D. W., and Cooper, S. V. (1989). “Concepts and techniques of vegetation mapping,” in: Land Classifications Based on Vegetation: Applications for Resource Management, eds D. Ferguson, P. Morgan, and F. D. Johnson (Ogden: USDA Forest Service General Technical Report INT-257), 90–96.
Saylor, R. D., Baker, B. D., Lee, P., Tong, D., Pan, L., and Hicks, B. B. (2019). The particle dry deposition component of total deposition from air quality models: right, wrong or uncertain? Tellus. B Chem. Phys. Meteorol. 71:1550324. doi: 10.1080/16000889.2018.1550324
Schaap, M., Hendriks, C., Kranenburg, R., Kuenen, J., Segers, A., Schlutow, A., et al. (2018). PINETI-3: Modellierung Atmosphärischer Stoffeinträge von 2000 bis 2015 zur Bewertung der Ökosystem-Spezifischen Gefährdung von Biodiversität durch Luftschadstoffe in Deutschland. Dessau-Roßlau: Texte Umweltbundesamt.
Schaap, M., Timmermans, R. M. A., Roemer, M., Boersen, G. A. C., and Builtjes, P. J. H. (2008). The LOTOS–EUROS model: description, validation and latest developments. Int. J. Environ. Pollut. 32, 270–290. doi: 10.1504/IJEP.2008.017106
Schaap, M., Wichink Kruit, R., Hendriks, C., Kranenburg, R., Segers, A., and Builtjes, P. (2017). Modelling and Assessment of Acidifying and Eutrophying Atmospheric Deposition to Terrestrial Ecosystems (PINETI-2); Part I: Atmospheric Deposition to German Natural and Semi-Natural Ecosystems During 2009, 2010 and 2011. Dessau-Roßlau: Umweltbundesamt. Available online at: https://www.umweltbundesamt.de/publika-tionen/modelling-assessment-of-acidifying-eutrophying (accessed August 30, 2020).
Schaap, M., Wichink Kruit, R. J., Hendriks, C., Kranenburg, R., Segers, A., Builtjes, P., et al. (2015). Atmospheric Deposition to German Natural and Semi-Natural Ecosystems During 2009. Project No. (FKZ) 3712 63 240-1. Dessau-Roßlau: Umweltbundesamt.
Schaub, M., Calatayud, V., Ferretti, M., Brunialti, G., Lövblad, G., Krause, G., et al. (2016). “Part XV: monitoring of air quality,” in Manual on Methods and Criteria for Harmonized Sampling, Assessment, Monitoring and Analysis of the Effects of Air Pollution on Forests, ed UNECE ICP Forests Programme Co-ordinating Centre (Eberswalde: Thünen Institute of Forest Ecosystems), 11. Available online at: http://www.icp-forests.org/manual.htm (accessed August 30, 2020).
Schmitt, M., Thöni, L., Waldner, P., and Thimonier, A. (2005). Total deposition of nitrogen on Swiss long-term forest ecosystem research (LWF) plots: comparison of the throughfall and the inferential method. Atmos. Environ. 39, 1079–1091. doi: 10.1016/j.atmosenv.2004.09.075
Schrader, F., and Brümmer, C. (2014). Land use specific ammonia deposition velocities: a review of recent studies (2004-2013). Water Air Soil Pollut. 225:2114. doi: 10.1007/s11270-014-2114-7
Schrader, F., Schaap, M., Zöll, U., Kranenburg, R., and Brümmer, C. (2018). The hidden cost of using low-resolution concentration data in the estimation of NH3 dry deposition fluxes. Sci. Rep. 8:969. doi: 10.1038/s41598-017-18021-6
Simpson, D., Andersson, C., Christensen, J. H., Engardt, M., Geels, C., Nyiri, A., et al. (2014). Impacts of climate and emission changes on nitrogen deposition in Europe: a multi-model study. Atmos. Chem. Phys. 14, 6995–7017. doi: 10.5194/acp-14-6995-2014
Simpson, D., Asas, W., Bartnicki, J., Berge, H., Bleeker, A., Kees, C., et al. (2011). “Atmospheric transport and deposition of reactive nitrogen in Europe,” in European Nitrogen Assessment (ENA), eds M. A. Suttion, C. M. Howard, J. W. Erisman, G. Billen, A. Bleeker, P. Greenfellt, H. van Grinsven and B. Grizzetti (New York, NY: Cambridge University Press), 664.
Simpson, D., Benedictow, A., Berge, H., Bergström, R., Emberson, L. D., Fagerli, H., et al. (2012). The EMEP MSC-W chemical transport model andndash; technical description. Atmos. Chem. Phys. 12, 7825–7865. doi: 10.5194/acp-12-7825-2012
Staelens, J., Houle, D., De Schrijver, A., Neirynck, J., and Verheyen, K. (2008). Calculating dry deposition and canopy exchange with the canopy budget model: review of assumptions and application to two deciduous forests. Water Air Soil Pollut. 191, 149–169. doi: 10.1007/s11270-008-9614-2
Staelens, J., Wuyts, K., Adriaenssens, S., Avermaet Van, P., Buysse, H., Bril Van Den, B., et al. (2012). Trends in atmospheric nitrogen and sulphur deposition in northern Belgium. Atmos. Environ. 49, 186–196. doi: 10.1016/j.atmosenv.2011.11.065
Stedman, J. R., Heyes, C., and Irwin, J. G. (1990). A comparison of bulk and wet-only precipitation collectors at rural sites in the United Kingdom. Water Air Soil Pollut. 52, 377–395. doi: 10.1007/BF00229445
Swaans, W., Goalen, E., De Fré, R., Damen, E., Van Avermaet, P., Roekens, E., et al. (2007). Laboratory and field validation of a combined NO2-SO2 radiello passive sampler. J. Environ. Monit. 9, 1231–1240. doi: 10.1039/b708925b
Talkner, U., Krämer, I., Hölscher, D., and Beese, F. O. (2010). Deposition and canopy exchange processes in central-German beech forest differing in tree species diversity. Plant Soil 336, 405–420. doi: 10.1007/s11104-010-0491-2
Thiele, J. C., Nuske, R., Ahrends, B., Panferov, O., Albert, M., Staupendahl, K., et al. (2017). Climate change impact assessment—a simulation experiment with Norway spruce for a forest district in Central Europe. Ecol. Model. 346, 30–47. doi: 10.1016/j.ecolmodel.2016.11.013
Thimonier, A., Kosonen, Z., Braun, S., Rihm, B., Schleppi, P., Schmitt, M., et al. (2019). Total deposition of nitrogen in Swiss forests: comparison of assessment methods and evaluation of changes over two decades. Atmos. Environ. 198, 335–350. doi: 10.1016/j.atmosenv.2018.10.051
Ulrich, B. (1994). “Nutrient and acid-base budget of central european forest ecosystems,” in Effects of Acid Rain on Forest Processes, eds D. Godbold, and A. Hüttermann (New York, NY: Wiley-Liss), 1–50.
Unsworth, M. H., and Fowler, D. (1987). “Deposition of pollutants on plants and soils; principles and pathways,” in Air Pollution and Ecosystems, ed P. Mathy (Dordrecht: Springer Netherlands), 68–84. doi: 10.1007/978-94-009-4003-1_10
Venables, W. N., and Ripley, B. D. (2003). Modern Applied Statistics With S. New York, NY: Springer.
Vesala, T., Suni, T., Rannik, Ü., Keronen, P., Markkanen, T., Sevanto, S., et al. (2005). Effect of thinning on surface fluxes in a boreal forest. Glob. Biogeochem. Cycles 19, 1–11. doi: 10.1029/2004GB002316
Vivanco, M. G., Theobald, M. R., García-Gómez, H., Garrido, J. L., Prank, M., Aas, W., et al. (2018). Modeled deposition of nitrogen and sulfur in Europe estimated by 14 air quality model systems: evaluation, effects of changes in emissions and implications for habitat protection. Atmos. Chem. Phys. 18, 10199–10218. doi: 10.5194/acp-18-10199-2018
Vuorenmaa, J., Augustaitis, A., Beudert, B., Bochenek, W., Clarke, N., De Wit, H. A., et al. (2018). Long-term changes (1990–2015) in the atmospheric deposition and runoff water chemistry of sulphate, inorganic nitrogen and acidity for forested catchments in Europe in relation to changes in emissions and hydrometeorological conditions. Sci. Total Environ. 625, 1129–1145. doi: 10.1016/j.scitotenv.2017.12.245
Weissert, L., Alberti, K., Miles, E., Miskell, G., Feenstra, B., Henshaw, G. S., et al. (2020). Low-cost sensor networks and land-use regression: interpolating nitrogen dioxide concentration at high temporal and spatial resolution in Southern California. Atmos. Environ. 223:117287. doi: 10.1016/j.atmosenv.2020.117287
Wesely, M. L., and Hicks, B. (2000). A review of the current status of knowledge on dry deposition. Atmos. Environ. 34, 2261–2282. doi: 10.1016/S1352-2310(99)00467-7
Wichink Kruit, R. J., Schaap, M., Sauter, F. J., Van Zanten, M. C., and Van Pul, W. A. J. (2012). Modeling the distribution of ammonia across Europe including bi-directional surface-atmosphere exchange. Biogeosciences 9, 5261–5277. doi: 10.5194/bg-9-5261-2012
Wood, S. N. (2006). Generalized Additive Models: An Introduction With R. Boca Raton: Texts in Statistical Science, Chapman and Hall. doi: 10.1201/9781420010404
Zhang, L., Brook, J. R., and Vet, R. (2003). A revised parameterization for gaseous dry deposition in air quality models. Atmos. Chem. Phys. 3, 2067–2082. doi: 10.5194/acp-3-2067-2003
Zimmermann, F., Plessow, K., Queck, R., Bernhofer, C., and Matschullat, J. (2006). Atmospheric N- and S-fluxes to a spruce forest-comparison of inferential modelling and the throughfall method. Atmos. Environ. 40, 4782–4796. doi: 10.1016/j.atmosenv.2006.03.056
Keywords: nitrogen, canopy budget model, inferential method, forest, deposition, Germany
Citation: Ahrends B, Schmitz A, Prescher A-K, Wehberg J, Geupel M, Andreae H and Meesenburg H (2020) Comparison of Methods for the Estimation of Total Inorganic Nitrogen Deposition to Forests in Germany. Front. For. Glob. Change 3:103. doi: 10.3389/ffgc.2020.00103
Received: 24 June 2020; Accepted: 07 August 2020;
Published: 16 September 2020.
Edited by:
Iva Hůnová, Czech Hydrometeorological Institute, CzechiaReviewed by:
Anna Avila, Ecological and Forestry Applications Research Center (CREAF), SpainJeroen Staelens, Flanders Environment Agency, Belgium
Copyright © 2020 Ahrends, Schmitz, Prescher, Wehberg, Geupel, Andreae and Meesenburg. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bernd Ahrends, YmVybmQuYWhyZW5kc0Budy1mdmEuZGU=
 Bernd Ahrends
Bernd Ahrends Andreas Schmitz
Andreas Schmitz Anne-Katrin Prescher
Anne-Katrin Prescher Jan Wehberg5
Jan Wehberg5 Markus Geupel
Markus Geupel Henning Meesenburg
Henning Meesenburg