Vaccination strategies in the disease–behavior evolution model

1 Introduction

The outbreak of infectious diseases seriously endangers human health and social development [1, 2]. Intense research effort has been devoted to developing epidemic spreading models [3, 4]. In addition, previous studies [5–8] have also shown that the spread of infectious diseases interacts with individual behavior. Many studies focus on vaccination, which is considered one of the most successful and cost-effective health interventions [9, 10]. Individuals continuously adjust their attitude toward vaccination during the spread of infectious diseases. In-depth research on the dynamic evolution of individual vaccination behavior and its impact on the epidemic is of great significance for formulating more effective public health policies. Many studies have primarily constructed disease–behavior-coupled models from the perspective of information dissemination or economic costs [11–13]. The dissemination of disease-related information inhibits the spread of infectious diseases and contributes to the recovery of infected individuals [14]. [15] found that vaccination coverage increases as people become sensitive to disease-related information, which increases the likelihood of herd immunity. Researchers have explored the dynamics of epidemic spreading in situations where vaccines are not fully effective. [16] studied both the case of a fixed immunity loss rate and an asymptotic total loss scenario based on the assumption of limited knowledge and temporary immunity. [17] pointed out that curbing the spread of negative information and improving vaccine effectiveness are effective means to prevent and control epidemics. Information-driven vaccination behavior significantly reduces the social cost of infection and facilitates the process of disease eradication [18] but ignores individual considerations of vaccine costs and vaccine spillover effects. The reason is that unvaccinated, self-interested individuals are dedicated to obtaining protection from other vaccinated individuals [19, 20]. For instance, [21] combined classical game theory with an epidemic model, revealing the “free-rider” behavior of self-interested individuals. [22, 23] found that the Nash equilibrium of vaccination game based on the vaccination cost could not form herd immunization due to conflict between herd and individual interests.

Psychological and behavioral experiments indicate that individual behavior tends to deviate from the rational criterion under the expected utility theory, exhibiting bounded rationality [24, 25]. For vaccination, even if a rational decision model predicts that vaccines will be accepted by individuals, in reality, low-cost and highly effective vaccines may still be rejected [26]. [10] proposed a two-stage vaccination game model that includes the disease spreading stage and the vaccination strategy update stage and illustrates the vaccine dilemma due to evolving psychological perceptions based on vaccine costs. Therefore, studying the impact of bounded rationality on individual vaccination decisions is crucial for disease control [27–29]. Prospect theory (PT) [30], which explains the decision-making process of individuals in the case of risk and uncertainty, not only captures the subjective perception of risk but also reveals the key role of bounded rationality in decision-making. PT contains two core concepts, namely, the weighting effect (WE), which describes an individual’s subjective perception probability [31, 32], and the framing effect (FE), which indicates an individual’s subjective evaluation of payoffs [33, 34]. In relevant studies, [35] developed an imperfect vaccination evolutionary game model, accounting for subjective perception and individual social differences. The results revealed that the epidemic threshold is significantly influenced by social differences in the epidemic spreading layer. [36] proposed an evolutionary vaccination game model in multiplex networks, incorporating an information-epidemic spreading process into vaccination dynamics. They found that the effect of information dissemination on vaccination decisions depends on vaccination costs, network topology, and the evolutionary stage of the system.

However, two-stage vaccination game models fail to capture the interactive dynamics between individual vaccination behavior and epidemic spreading. Moreover, traditional vaccination game models focus only on vaccination costs and payoffs, neglecting individual psychological cognition, i.e., perceptions of infection risk and vaccination behaviors of neighbors. In this work, we propose a disease–behavior-coupled model where individuals are exposed to the risk of infection and make vaccination decisions at each time step. In the context of free vaccines, we mainly focus on psychological perceptions of influence risk. Here, an individual will have a vaccination behavior if their vaccination opinion is higher than a critical value. Given the general preference of individuals for reliable information sources, we assume that individuals make vaccination decisions based on local disease-related information. Each individual updates his/her vaccination opinion based on the weighted aggregation of the vaccination behaviors of neighbors and then adjusts his or her vaccination behavior at each time step. Specifically, the opinion weights depict the perceptions of infection risk, which are related to individual states. In addition, we study the dynamics of the coupled model and analyze the vaccination coverage of the proposed model in network models and real-world social networks.

The main contributions of our work are as follows: 1) we propose a coupled disease–behavior model to study the dynamic interactions between the spread of infectious diseases and the vaccination behaviors of individuals. Vaccination behavior is dominated by individuals’ bounded rationality about infection risk, which is characterized by opinion weights. 2) The vaccination opinion in the co-evolution model could exhibit limited rationality. A relatively small infection fraction makes individuals underestimate the infection risks, while a large infection fraction leads individuals to “lie down” and be unwilling to defend themselves against infectious diseases. The phenomenon is verified with simulation results. 3) We find that vaccination coverage will reach convergence, which is strongly related to individual vaccination strategies. The opinion critical θ for an individual to get vaccinated has a decisive effect on the vaccination evolution game, leading to a clear phase transition in vaccination coverage versus the opinion critical. The link density of a network might influence vaccination coverage. Moreover, we analyze the performance of three vaccination strategies by administrators on the coupled model and find the advantage of the random-first vaccination strategy in promoting group vaccination. Compared with the random selection strategy, the high-degree individual priority vaccination strategy and the low-degree individual priority vaccination strategy exhibit low efficiency and high social costs. The findings in this work provide some clues for understanding the co-evolution of vaccination behavior and epidemic spread.

The remainder of this paper is arranged as follows: Section 2 illustrates the disease–behavior-coupled model in detail, which includes the dynamics of infectious disease spread and the evolution of vaccination behavior. The vaccination coverage of vaccination strategies by individuals and administrators is studied in network models and real-world networks in Section 3. Section 4 provides the conclusion.

2 Disease–behavior coupled model

2.1 Notations and preliminaries

We use nodes to represent the individuals in society and edges to indicate the interactions between members. A social interaction network could be characterized by an adjacency matrix $\mathbf{A}={\left[a_{ij}\right]}_{N\times N}$. a_ij = 1 if there is a link between nodes i and j; otherwise, a_ij = 0. In this work, we focus on finite-size, undirected, and unweighted networks [37]. The disease–behavior coupled model is composed of two parts: the susceptible–infected–vaccinated (SIV) spread model [38] and the evolution rules of vaccination behavior.

2.2 Spread of infectious diseases

We first introduce the SIV model, where individuals have three possible states: susceptible (S), infected (I), and vaccinated (V). The diagram of the state transition is depicted in Figure 1. A susceptible individual i would like to be vaccinated at time t with a probability $f_i^V(t)$. Without the loss of generality, we here assume that the vaccine is fully immune and long-term effective; in other words, vaccinated individuals will not be infected. An infected individual infects susceptible neighbors with an infection probability β and cures with a recovery probability γ [39]. Let the symbols $p_i^S(t)$, $p_i^I(t)$, and $p_i^V(t)$ denote the probabilities of being susceptible, infected, and vaccinated for individual i at time t, respectively. Then, there is the equation $p_i^S(t)+p_i^I(t)+p_i^V(t)=1$. The transition probability $q_i^S(t)$ of susceptible individual i not being infected by neighbors is defined as follows:

$q_i^S\left(t\right)={\displaystyle \prod _{j=1}^N}\left(1-a_{ij}\cdot p_j^I\left(t\right)\cdot \beta \right).(1)$

Figure 1

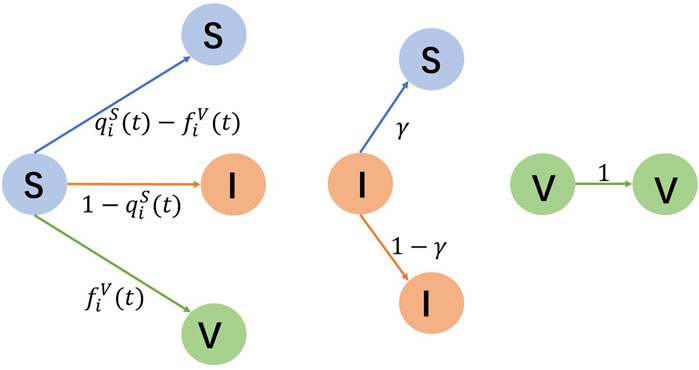
Figure 1. Transition of susceptible (S), infected (I), and vaccinated (V) states. S-individuals either remain susceptible or shift to be infected and vaccinated. I-individuals have a probability γ of reverting to be susceptible. V-individuals stay vaccinated.

The continuous-time Markov approach can accurately characterize the dynamics of infectious diseases [40]. However, the state transition matrix is hardly available, especially for large-scale networks [41]. Therefore, we use the microscopic Markov chain approach [42, 43] to describe the probability of individual i being susceptible, infected, and vaccinated at each moment as

$\left\{\begin{array}{c}{p}_i^S\left(t+1\right)=p_i^I\left(t\right)\cdot \gamma +p_i^S\left(t\right)\cdot \left(q_i^S\left(t\right)-f_i^V\left(t\right)\right),\hfill \\ p_i^I\left(t+1\right)=p_i^I\left(t\right)\cdot \left(1-\gamma \right)+p_i^S\left(t\right)\cdot \left(1-q_i^S\left(t\right)\right),\hfill \\ p_i^V\left(t+1\right)=p_i^S\left(t\right)\cdot f_i^V\left(t\right)+p_i^V\left(t\right).\hfill \end{array}\right.(2)$

Notably, the dynamics will reach a steady state at the end of the spread process. Then, the probabilities of individual i being susceptible, infected, and vaccinated no longer vary with time, namely, $p_i^S(t+1)=p_i^S(t)=p_i^S$, $p_i^I(t+1)=p_i^I(t)=p_i^I$, and $p_i^V(t+1)=p_i^V(t)=p_i^V$, respectively. Naturally, the proportions of susceptible, infected, and vaccinated individuals in the population remain constant. We obtain $q_i^S(t+1)=q_i^S(t)=q_i^S$ according to Eq. 1. Since the infection and recovery probabilities of infected individual are also constant, the transition probability of susceptible individual i to be vaccinated is constant, that is, $f_i^V(t+1)=f_i^V(t)=f_i^V$. Then, we rewrite Eq. 2 as

$\left\{\begin{array}{c}{p}_i^S=p_i^I\cdot \gamma +p_i^S\cdot \left(q_i^S-f_i^V\right),\hfill \\ p_i^I=p_i^I\cdot \left(1-\gamma \right)+p_i^S\cdot \left(1-q_i^S\right),\hfill \\ p_i^V=p_i^S\cdot f_i^V+p_i^V.\hfill \end{array}\right.(3)$

Based on the expression $p_i^S+p_i^I+p_i^V=1$, we get Eq. 4 from Eq. 3

$\left\{\begin{array}{c}{p}_i^S=\frac{\gamma \cdot \left(1-p_i^V\right)}{1+\gamma -q_i^S},\hfill \\ p_i^I=\frac{\left(1-q_i^S\right)\cdot \left(1-p_i^V\right)}{1+\gamma -q_i^S}.\hfill \end{array}\right.(4)$

Furthermore, there is $p_i^V=p_i^S\cdot f_i^V+p_i^V$ from Eq. 3. Therefore, the necessary condition for the steady state of the coupled model is $p_i^S\cdot f_i^V=0$. When $p_i^S=0$, we get $p_i^I=0$ according to Equation 3. Therefore, there are only vaccinated individuals in the population, that is, $p_i^V=1$. When $f_i^V=0$ and $p_i^S\ne 0$, individuals exist in three states.

Let the symbols R_S, R_I, and R_V denote the proportions of susceptible, infected, and vaccinated individuals, respectively. Naturally, the three proportions satisfy R_S + R_I + R_V = 1 and are calculated using the Eq. 5:

$\left\{\begin{array}{c}{R}_S=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{p}_i^S,\hfill \\ R_I=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{p}_i^I,\hfill \\ R_V=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{p}_i^V.\hfill \end{array}\right.(5)$

2.3 Evolution of vaccination behavior

The evolution process of vaccination behavior is the other important component of the coupled model. Let the notations y_i(t) and Y_i(t) denote the vaccination opinion and vaccination behavior of individual i ∈ {1, 2, … , N} at time t, respectively. The relationship between y_i(t) and Y_i(t) is defined as Eq. 6 that

$Y_i\left(t\right)=Sgn\left(y_i\left(t\right)-\theta \right)=\left\{\begin{array}{cc}\hfill 1,\hfill & \hfill y_i\left(t\right)\ge \theta ,\hfill \\ \hfill -1,\hfill & \hfill \text{\hspace{0.17em}else\hspace{0.17em}},\hfill \end{array}\right.(6)$

where the symbol θ indicates the opinion critical value for an individual to get vaccinated and Sgn(.) is the sign function. When Y_i(t) = 1, individual i gets vaccinated at time t. Otherwise, i is out of vaccination. Notably, the increase in y_i(t) indicates the enhancement of willingness for individual i to get vaccinated. The transition probability $f_i^V(t)$ of being vaccinated for susceptible individual i at time t equals to y_i(t), when y_i(t) ≥θ at time t.

We use behavior vector $\mathbf{Y}(t)={\left[Y_1(t),Y_2(t),\dots ,Y_N(t)\right]}^T$ to represent behaviors of all individuals in the social network of size N at time t. Correspondingly, there is an opinion vector $\mathbf{y}(t)={\left[y_1(t),y_2(t),\dots ,y_N(t)\right]}^T$. The proportion of vaccinated individuals R_V(t) at time t, named vaccination coverage, is computed as Eq. 7 that:

$R_V\left(t\right)=\frac{{\sum }_{i=1}^N{Y}_i\left(t\right)+{\sum }_{i=1}^N\left|Y_i\left(t\right)\right|}{2N}.(7)$

A diagonal matrix Λ(t) = diag(λ₁₁(t), λ₂₂(t), …, λ_NN(t)) is used to ensure that vaccinees cannot revert to being unvaccinated during the evolution process. If individual i is vaccinated, the element λ_ii(t) = 0; otherwise, λ_ii(t) = 1. In the disease–behavior-coupled model, individuals obtain vaccination opinions based on local information, namely, the perceptions of infection risk and vaccination behaviors of their neighbors. Here, when the number of infected neighbors increases, individuals perceive more disease risk and mitigate their willingness to receive vaccines. Meanwhile, when the number of infected nodes reaches a rather large number, individuals may have group psychology and give up vaccination. When the number of susceptible neighbors increases, individuals lessen their fear of disease and their inclination to receive vaccines. Individual vaccination behavior can be influenced by herd mentality [44], which is the tendency for people in a group to conform to the behavior of others in the group rather than acting as individuals. When the number of vaccinated neighbors increases, individuals are more likely to get vaccinated due to the influence of herd mentality. To simplify the complexity, we assume that individuals do not take into account their own opinion of the previous moment. We designed an opinion weight matrix $\mathbf{W}(t)={\left[w_{ij}(t)\right]}_{N\times N}$ to characterize the perceptions of infection risk. The symbol w_ij(t) indicates the influence weight of individual j on i at time t. The mathematical expression of opinion weight is shown as follows:

$w_{ij}\left(t+1\right)=\left\{\begin{array}{cc}\frac{1}{|N_i^I\left(t\right)|},\hfill & j\in N_i^S\left(t\right)\text{\hspace{0.17em}or\hspace{0.17em}}j\in N_i^V\left(t\right),\hfill \\ \frac{1}{|N_i^S\left(t\right)|+|N_i^V\left(t\right)|},\hfill & j\in N_i^I\left(t\right),\hfill \\ 0,\hfill & \text{others},\hfill \end{array}\right.(8)$

where the symbols $N_i^S(t)$, $N_i^V(t)$, and $N_i^I(t)$ denote the set of susceptible, vaccinated, and infected neighbors of individual i at time t, respectively; and |.| represents the cardinality of a set. Let the symbol N_i be the neighbors of individual i, thus $|N_i|=|N_i^S(t)|+|N_i^V(t)|+|N_i^S(t)|$. Particularly, for the extreme cases that all neighbors of individual i are infected or not infected, Eq. 8 is no longer applicable, and let the weight w_ij(t) = 1 if individuals i and j are neighbors.

Hence, we get the expression of individual vaccination opinion evolution equation as Eq. 9

$y_i\left(t+1\right)={\lambda }_{ii}\left(t\right)\cdot {\displaystyle \sum _{j=1}^n}{w}_{ij}\left(t\right)\cdot Y_j\left(t\right)+\left(1-{\lambda }_{ii}\left(t\right)\right)\cdot Y_i\left(t\right),(9)$

and the corresponding matrix form is

$\begin{array}{cc}\hfill \mathbf{y}\left(t+1\right)& =\mathrm{\Lambda }\left(t\right)\cdot \mathbf{W}\left(t\right)\cdot \mathbf{Y}\left(t\right)+\left(\mathbf{E}-\mathrm{\Lambda }\left(t\right)\right)\cdot \mathbf{Y}\left(t\right)\hfill \\ \hfill & =\left[\mathrm{\Lambda }\left(t\right)\cdot \mathbf{W}\left(t\right)+\left(\mathbf{E}-\mathrm{\Lambda }\left(t\right)\right)\right]\cdot \mathbf{Y}\left(t\right)\hfill \end{array}.(10)$

If the individual i is vaccinated at time t, we get y_i(t + 1) = Y_i(t), which indicates that a vaccinated individual will maintain their current state. Otherwise, there is $y_i(t+1)={\sum }_{j=1}^n{w}_{ij}(t)\cdot Y_j(t)$. The vaccination opinion y_i(t + 1) will be influenced by the vaccination behaviors of neighbors of individual i at time t. Moreover, the maximum number of possible neighbors for each node is N − 1 in the connected network with N nodes. If the neighbor number of node i is N − 1 and all neighbors are infected at time t, the minimum value of y_i(t) is obtained from Eq. 10, and y_i(t) = −N + 1. If the neighbor number of node i is N − 1 and all neighbors are vaccinated at time t, the maximum value of y_i(t) is N − 1. Hence, the bounds of y_i(t), i ∈ {1, 2, … , N} in the coupled model are between −N + 1 and N − 1.

From Eq. 10, the opinion vector y(t) is related to Λ(0), W(t), and Y(0). The opinion weight matrix W(t) depends on the degrees of nodes in the network and the infection status of neighbors. The values of Y(0) and Λ(0) depend on the initial vaccinees. Naturally, y(t) is determined by the network structure, initial vaccinees, and infection status of neighbors. Hence, changes in the value of θ reveal the role of network structure, initial vaccinees, and size of infected neighbors on vaccination behavior.

3 Evolutionary vaccination game in network models and real-world networks

We here study the vaccination coverage of the disease–behavior-coupled model in network models and real-world networks. Two types of vaccination strategies, namely, strategies by individuals and strategies by administrators, are studied. The individual vaccination strategy is based on the perceptions of infection risk and vaccination behaviors of neighbors, as introduced in Section 2. The vaccination strategies by administrators are used to select initial vaccinees. In this work, three vaccination strategies by administrators, namely, largest-first strategy (LFS), smallest-first strategy (SFS), and random-first strategy (RFS), were used. The LFS is used to select the initially vaccinated nodes based on the nodal degrees from large to small, and the SFS is the opposite. Naturally, RFS is used to randomly adopt the initial vaccinees. Notably, the network models are scale-free (SF) networks [45] and Erdos–Ranyi (ER) networks [46] with N = 1,000 and the average degrees $<k>=4$, $<k>=8$, and $<k>=16$, respectively. The real social networks are email network [47], Facebook friendship network [48], and LastFM users’ network [49]. The email network, generated using email data from a large European research institution, comprises 1,005 nodes and 25,571 edges. In the email network, users are represented as nodes and communication between them is represented as connected edges. The Facebook friendship network has been collected from survey participants using the Facebook application and consists of 4,039 nodes and 88,234 edges. The Facebook network is composed of users as nodes and friend relationships between them as edges. The LastFM users’ network, consisting of 7,624 nodes and 27,806 edges, was collected from the public API in March 2020. Nodes are LastFM users from Asian countries, and edges are mutual follower relationships between them. In addition, each simulation result is the average of 50 times under the same parameters to avoid the accidentality of a single simulation.

3.1 Convergence of vaccination coverage of the coupled model

We first verify the convergence of the disease–behavior-coupled model in network models and the real-world social networks through Monte Carlo simulations. We attempt different combinations of all parameters, where the effective spreading rate β/γ ranges from 0.01 to 100, the opinion critical θ ranges from −N + 1 to N − 1, the number of initially infected nodes N^I(0) ranges from 1 to N, and the number of initially vaccinated nodes N^V(0) ranges from 1 to N. Without the loss of generality, the initially infected nodes are randomly selected since, in practice, infected individuals appear by chance.

We find that the proportion of vaccinated individuals R_V will converge to a constant, regardless of the effective spreading rate, opinion critical, and initially infected nodes. Hence, we give an illustration with the effective spreading rate β/γ = 0.4, the number of initially infected nodes N^I(0) = 50, and opinion critical θ = 0. The convergence of the model with three strategies, i.e., LFS, SFS, and RFS, are shown in Figure 2.

Figure 2

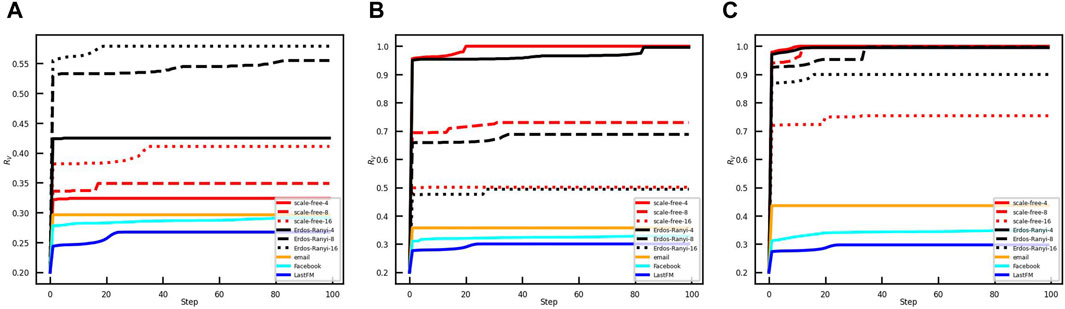
Figure 2. Convergence of vaccination coverage of the coupled model in the different networks. The ratio of initial vaccinees in the networks is 0.2. The red, black, yellow, azure, and blue lines show vaccination coverage in scale-free networks, ER random networks, email network, Facebook network, and LastFM network, respectively. The initial vaccinees are selected with (A) LFS, (B) SFS, and (C) RFS.

Vaccination coverage is influenced by the strategies by the administrator, network topology, and link density of the network. For the LFS, the vaccination coverage is the largest in the ER random networks compared to that in the SF networks and real-world networks. If the network topology and network size are given, the vaccination coverage is larger when the link density of the network is larger. However, the result is the opposite for SFS and RFS. Moreover, Figure 2 shows that vaccination coverage for LFS will converge to a smaller value than that for SFS and RFS.

3.2 Influence of opinion critical on vaccination coverage

The vaccination opinion critical θ in the coupled model represents the psychological threshold for vaccine acceptance. A higher opinion critical indicates that individuals are less inclined to prefer vaccines. We here study the role of opinion critical on vaccination coverage under the conditions of the effective spreading rate β/γ = 0.4, the number of initially infected nodes N^I(0) = 50, and the initial vaccinee ratio R_V(0) = 0.2. Figure 3 illustrates the variation of opinion critical θ from −1 to 1 in different networks. Under the different network structures and initial vaccination strategies, vaccination coverage decreases as the opinion critical increases from negative to positive values. Figures 3A–C show that in the Erdos–Ranyi networks, the SFS and LFS are both affected by the link density. The link density is higher; the psychological threshold for full vaccination coverage is lower with the SFS. However, with the LFS, θ for full vaccination coverage increases with the link density. Moreover, Figures 3D–F demonstrate that in the scale-free networks with the SFS, the psychological threshold for full vaccination coverage decreases with the increase in the link density. In contrast, the LFS exhibits a higher psychological threshold for full vaccination coverage as the link density of the network increases. The finding verifies the opposing results presented in Figures 2A,B.

Figure 3

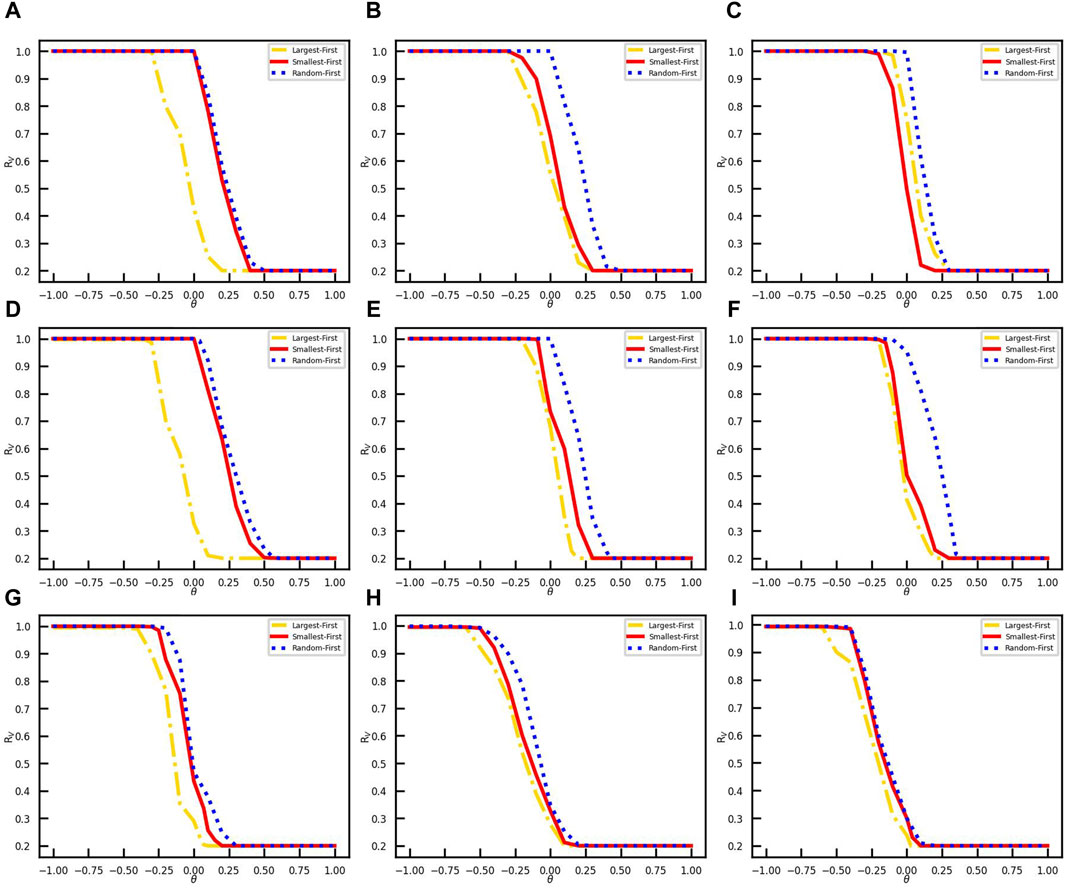
Figure 3. Influence of opinion critical on vaccination coverage in different networks. The vaccination coverages R_V are obtained with three vaccination strategies, i. e., LFS, SFS, and RFS in yellow dot-line, red line, and blue dots. (A) Erdos–Ranyi-4 network. (B) Erdos–Ranyi-8 network. (C) Erdos–Ranyi-16 network. (D) Scale-free-4 network. (E) Scale-free-8 network. (F) Scale-free-16 network. (G) Email network. (H) Facebook network. (I) LastFM network.

3.3 Comparison of the three vaccination strategies

We further study the performances of the three vaccination strategies on the social cost in different networks. In complex network models such as Price’s model and BA model, the node degree is used as an important indicator of the node’s attractiveness to new nodes and ability to develop new links [50]. In this work, the social influence or status of a node is related to the degree $d_i={\sum }_{j=1}^N{a}_{ij}$ of an individual i in the social networks. We assume that persuading a more influential person to get vaccinated will cost more socially. Hence, the social cost of initially vaccinated individuals is given as Eq. 11,

$E_{sc}=\frac{{\sum }_{i\in N^V\left(0\right)}{d}_i}{{\displaystyle \sum _{j=1}^N}{d}_j},(11)$

where N^V(0) is the set of initially vaccinated nodes and E_sc is the social cost of strategy. It should be noted that the vaccine is free for individuals, but there is a social cost to the government in promoting vaccination. We study the effect of the social cost of each strategy on vaccination coverage. We conduct experiments under the same initial conditions with the effective spreading rate β/γ = 0.4, the number of initially infected nodes N^I(0) = 50, and opinion critical θ = 0. The vaccination coverage corresponding to each strategy at one social cost is the average of the results of 50 simulation experiments with the same parameters. We conducted the simulation experiment by setting the social cost E_sc values in 0.1, 0.02, 0.005, and 0.001 step sizes in turn. The approximate range of the minimum social cost is first determined in large steps, and then the step size of the experimental parameters is gradually reduced to determine an accurate minimum social cost. The relationship between social cost E_sc and vaccination coverage R_V is shown in Figure 4. We find that vaccination coverage will be reached when the social cost is greater than a threshold, which is listed in Table 1.

Figure 4

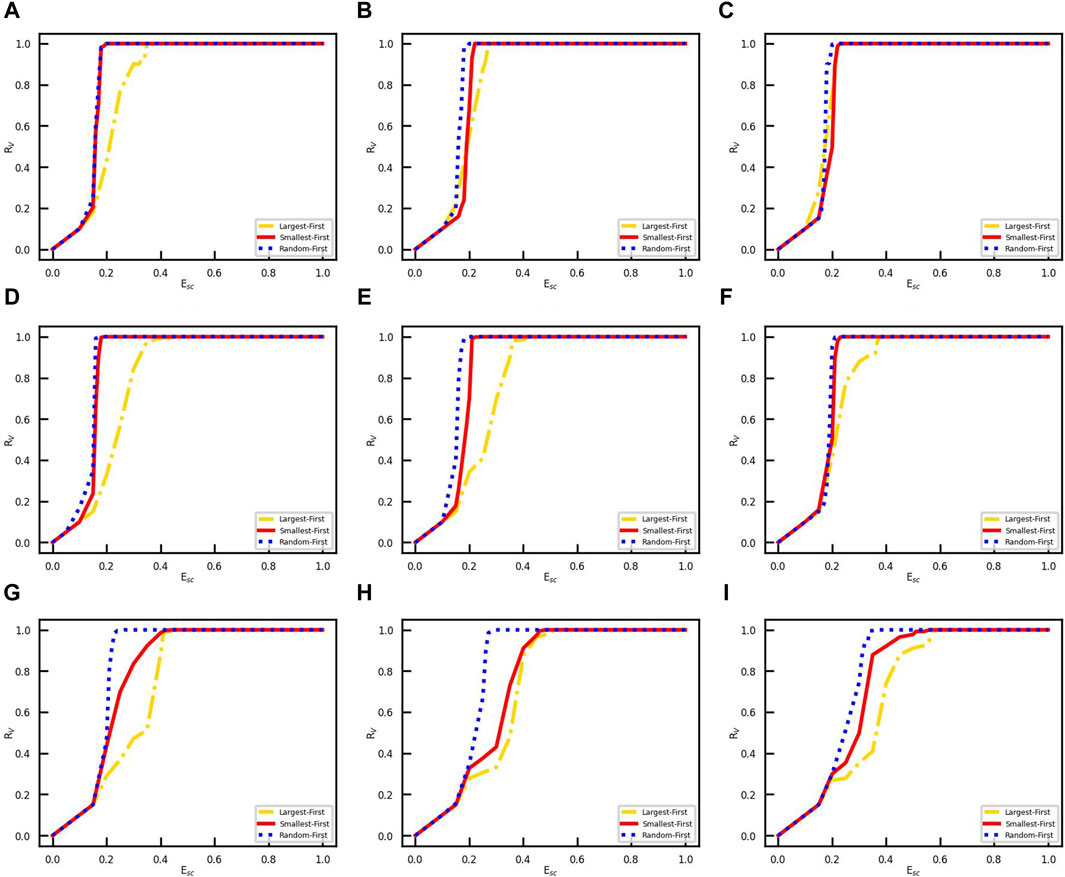
Figure 4. Vaccination coverage for different E_sc values. The vertical coordinate R_V denotes the rate of finally vaccinated nodes in the network, and the horizontal coordinate indicates the initially vaccinated degree. (A) Erdos–Ranyi-4 network. (B) Erdos–Ranyi-8 network. (C) Erdos–Ranyi-16 network. (D) Scale-free-4 network. (E) Scale-free-8 network. (F) Scale-free-16 network. (G) Email network. (H) Facebook network. (I) LastFM network.

Table 1

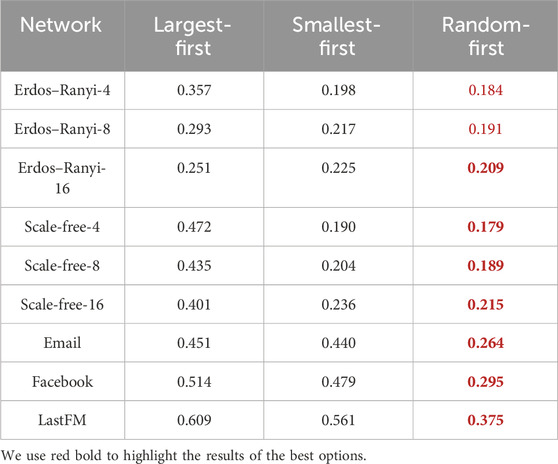
Table 1. Minimum social cost for the three strategies to reach vaccination coverage in networks with various typologies.

The results show that with the LFS, the minimum social cost E_sc for vaccination coverage decreases as the link density increases in the same network topology. However, the social cost threshold for the SFS and RFS gradually increases as the link density increases in the same network topology. In addition, we compare the performance of three strategies on the same network; surprisingly, RFS always needs the minimum social cost for vaccination coverage, both in network models and real-world networks. Then, the performance of the SFS is superior to that of the LFS.

3.4 Role of the effective spreading rate

We then explore the effect of the effective spreading rate β/γ on vaccination coverage under three vaccination strategies, i.e., LFS, SFS, and RFS. Figure 5 demonstrates that the effective spreading rate β/γ has a double-edged role in the diffusion of vaccination behavior when the social cost E_sc is less than the minimum social cost of the three strategies, as shown in Table 1.

Figure 5

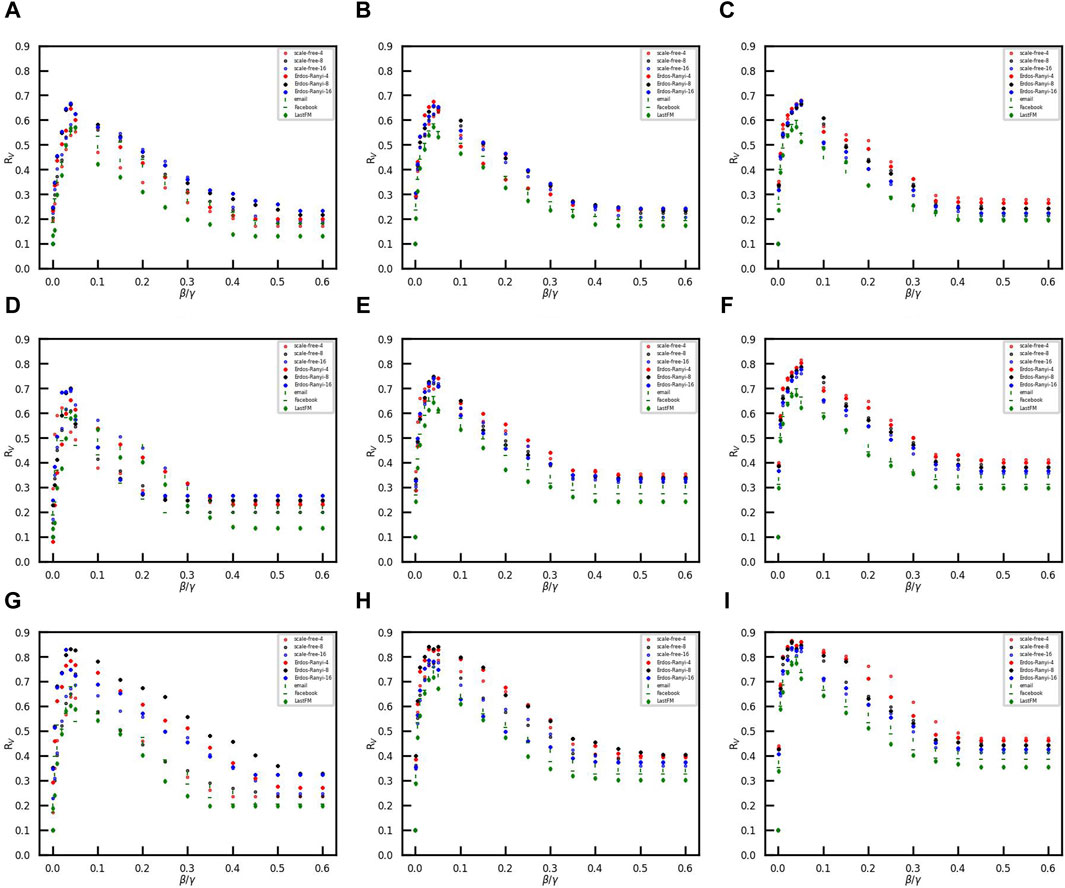
Figure 5. Vaccination coverage versus the effective spreading rate in the different networks. The ratio of initial vaccinees is 0.1, and the number of initial infected nodes is 50. (A–C) Opinion critical is 0.1..(D–F) Opinion critical is 0. (G–I) Opinion critical is −0.1. The initial vaccinees are selected with the largest-first strategy in (A, D, and G), with the smallest-first strategy in (B, E, and H), and with random-first strategy in (C, F, and I).

When the effective spreading rate increases from small to large, vaccination coverage R_V first increases and then decreases. The phenomenon might be explained by the limited rationality of vaccination opinions. When the effective spreading rate is small, the number of infected individuals is also small. Therefore, susceptible individuals tend to ignore the risk of disease and refuse vaccination. However, when the effective spreading rate is large, the number of infected individuals is large. A large number of infected individuals leads to a tendency for susceptible individuals to coexist with the virus rather than resist disease transmission. The confidence of individuals in vaccines crumbles, and many individuals shift toward abandoning self-loathing due to the panic caused by rapid outbreaks of disease. Only if the effective spreading rate is moderate, individuals are not only aware of the risk of disease, but also inclined to accept the vaccine. As a result, the proportion of vaccinees is higher than that in the other two scenarios. Emphasizing the dangers of infectious diseases and reducing panic are both essential to increasing vaccination coverage in epidemic control. It is a primary concern for government policymakers to promote herd immunization when faced with the outbreak of infectious diseases.

4 Conclusion

In this work, we propose a coupled disease–behavior evolution model, providing a new perspective on the interactions between vaccination behavior and the spread of infectious diseases. We portray the mental choices of individuals facing disease risk and vaccination by the variable opinion weights, which capture the vaccination behaviors of neighbors. The vaccination strategy by individuals is based on their mental choices and exhibits limited rationality about infection risk. A large infection fraction may lead individuals to adopt negative strategies to resist infectious diseases, while a relatively small infection fraction makes individuals adopt positive strategies. A clear phase transition appears in the vaccination coverage compared to the opinion critical θ of an individual to be vaccinated. Meanwhile, the performance of three vaccination strategies, namely, LFS, SFS, and RFS, by the administrator is compared in this work. We find that with the three initial vaccination strategies, vaccination coverage, which is influenced by the link density of the network and network topology, always converges to a constant. The vaccination coverage of RFS and SFS is consistently higher than that of LFS. Persuading individuals with high influence to get vaccinated at the initial time is not optimal for promoting the diffusion of vaccination behavior. RFS has the best performance on both network models and real-world networks among the three strategies when studying the effect of the opinion critical and the social cost. In addition, the role of the effective spreading rate is not one-sided since the vaccination opinion exhibits limited rationality. Vaccination coverage R_V first increases and then decreases as the effective spreading rate increases from small to large. Controlling for outbreak information to make individuals perceive a “false and appropriate effective spreading rate” is an efficacious way to motivate individuals to be vaccinated.

The phenomena revealed by this work could provide a new perspective for guiding group vaccination opinions and improving vaccination coverage. The model introduced here also has some limitations and challenges. We did not account for the variability of opinion critical of different groups that belong to the same social network. Individuals between different groups have a greater difference in their opinion critical than individuals within a group. As an individual acquires information, his or her opinion critical may change. In addition, we focus on the neighbors’ influence, but the influence of non-neighboring individuals or global information also merits further investigation.

Data availability statement

Publicly available datasets were analyzed in this study. These data can be found at: email network: https://snap.stanford.edu/data/email-Eu-core.html; Facebook network: https://snap.stanford.edu/data/ego-Facebook.html; and LastFM: https://snap.stanford.edu/data/feather-lastfm-social.html.

Author contributions

LZ: data curation, formal analysis, methodology, software, writing–original draft, and writing–original draft. JD: writing–review and editing. BQ: formal analysis, methodology, writing–review and editing, and writing–review and editing. CL: conceptualization, funding acquisition, methodology, writing–review and editing, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (grant nos. U23A20331, 62173095, and 62002184) and the Natural Science Foundation of Shanghai (grant no. 21ZR1404700).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Zino L, Rizzo A, Porfiri M. On assessing control actions for epidemic models on temporal networks. IEEE Control Syst Lett (2020) 4:1–802. doi:10.1109/LCSYS.2020.2993104

CrossRef Full Text | Google Scholar

2. Baker RE, Mahmud AS, Miller IF, Rajeev M, Rasambainarivo F, Rice BL, et al. Infectious disease in an era of global change. Nat Rev Microbiol (2022) 20:193–205. doi:10.1038/s41579-021-00639-z

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Funk S, Salathe M, Jansen VAA. Modelling the influence of human behaviour on the spread of infectious diseases: a review. J R Soc Interf (2010) 7:1247–56. doi:10.1098/rsif.2010.0142

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Shang YL. Analytical solution for an in-host viral infection model with time-inhomogeneous rates. Acta Physica Pol B (2015) 46:1567. doi:10.5506/APhysPolB.46.1567

CrossRef Full Text | Google Scholar

5. Glass RJ, Glass LM, Beyeler WE, Min HJ. Targeted social distancing designs for pandemic influenza. Emerging Infect Dis (2006) 12:1671–81. doi:10.3201/eid1211.060255

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Mao L, Yang Y. Coupling infectious diseases, human preventive behavior, and networks–a conceptual framework for epidemic modeling. Soc Sci Med (2012) 74:167–75. doi:10.1016/j.socscimed.2011.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Calabro GE, Carini E, Tognetto A, Giacchetta I, Bonanno E, Mariani M, et al. The value(s) of vaccination: building the scientific evidence according to a value-based healthcare approach. Front Public Health (2022) 10:786662. doi:10.3389/fpubh.2022.786662

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Kuga K, Tanimoto J. Which is more effective for suppressing an infectious disease: imperfect vaccination or defense against contagion? J Stat Mech Theor Exp (2018) 2018:023407. doi:10.1088/1742-5468/aaac3c

CrossRef Full Text | Google Scholar

9. Andre FE, Booy R, Bock HL, Clemens J, Datta SK, John TJ, et al. Vaccination greatly reduces disease, disability, death and inequity worldwide. Bull World Health Organ (2008) 86:140–6. doi:10.2471/blt.07.040089

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Feng X, Wu B, Wang L. Voluntary vaccination dilemma with evolving psychological perceptions. J Theor Biol (2018) 439:65–75. doi:10.1016/j.jtbi.2017.11.011

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Wang Z, Andrews MA, Wu ZX, Wang L, Bauch CT. Coupled disease–behavior dynamics on complex networks: a review. Phys Life Rev (2015) 15:1–29. doi:10.1016/j.plrev.2015.07.006

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Wang W, Liu QH, Liang JH, Hu YQ, Zhou T. Coevolution spreading in complex networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Shaham A, Chodick G, Shalev V, Yamin D. Personal and social patterns predict influenza vaccination decision. BMC Public Health (2020) 20:222–12. doi:10.1186/s12889-020-8327-3

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Kabir KA, Kuga K, Tanimoto J. Analysis of sir epidemic model with information spreading of awareness. Chaos, Solitons and Fractals (2019) 119:118–25. doi:10.1016/j.chaos.2018.12.017

CrossRef Full Text | Google Scholar

15. Xia S, Liu JM. A belief-based model for characterizing the spread of awareness and its impacts on individuals’ vaccination decisions. J R Soc Interf (2014) 11:20140013. doi:10.1098/rsif.2014.0013

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Shang YL. Immunization of networks with limited knowledge and temporary immunity. Chaos: Interdiscip J Nonlinear Sci (2021) 31:053117. doi:10.1063/5.0045445

CrossRef Full Text | Google Scholar

17. Yin Q, Wang Z, Xia C, Bauch CT. Impact of co-evolution of negative vaccine-related information, vaccination behavior and epidemic spreading in multilayer networks. Commun Nonlinear Sci Numer Simulation (2022) 109:106312. doi:10.1016/j.cnsns.2022.106312

CrossRef Full Text | Google Scholar

18. Buonomo B. Effects of information-dependent vaccination behavior on coronavirus outbreak: insights from a siri model. Ricerche di Matematica (2020) 69:483–99. doi:10.1007/s11587-020-00506-8

CrossRef Full Text | Google Scholar

19. Xin Y, Gerberry D, Just W. Open-minded imitation can achieve near-optimal vaccination coverage. J Math Biol (2019) 79:1491–514. doi:10.1007/s00285-019-01401-z

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Wang XY, Jia DY, Gao SP, Xia CY, Li XL, Wang Z. Vaccination behavior by coupling the epidemic spreading with the human decision under the game theory. Appl Math Comput (2020) 380:125232. doi:10.1016/j.amc.2020.125232

CrossRef Full Text | Google Scholar

21. Bauch CT, Galvani AP, Earn DJD. Group interest versus self-interest in smallpox vaccination policy. Proc Natl Acad Sci (2003) 100:10564–7. doi:10.1073/pnas.1731324100

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Li XJ, Li C, Li X. Vaccinating sis epidemics in networks with zero-determinant strategy. In: 2017 IEEE International Symposium on Circuits and Systems (ISCAS) (IEEE); May 28-31, 2017; Baltimore, MD, USA (2017). p. 2275–8.

CrossRef Full Text | Google Scholar

23. Li XJ, Li C, Li X. Minimizing social cost of vaccinating network sis epidemics. IEEE Trans Netw Sci Eng (2017) 5:326–35. doi:10.1109/TNSE.2017.2766665

CrossRef Full Text | Google Scholar

24. Simon HA. A behavioral model of rational choice. Q J Econ (1955) 69:99–118. doi:10.2307/1884852

CrossRef Full Text | Google Scholar

25. Hota AR, Sundaram S. Game-theoretic vaccination against networked sis epidemics and impacts of human decision-making. IEEE Trans Control Netw Syst (2019) 6:1461–72. doi:10.1109/TCNS.2019.2897904

CrossRef Full Text | Google Scholar

26. Oraby T, Bauch CT. Bounded rationality alters the dynamics of paediatric immunization acceptance. Scientific Rep (2015) 5:10724–12. doi:10.1038/srep10724

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ibuka Y, Chapman GB, Meyers LA, Li M, Galvani AP. The dynamics of risk perceptions and precautionary behavior in response to 2009 (h1n1) pandemic influenza. BMC Infect Dis (2010) 10:296–11. doi:10.1186/1471-2334-10-296

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Dr?kowski D, Trepanowski R. Reactance and perceived disease severity as determinants of covid-19 vaccination intention: an application of the theory of planned behavior. Psychol Health Med (2021) 27:2171–8. doi:10.1080/13548506.2021.2014060

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Wolff K. Covid-19 vaccination intentions: the theory of planned behavior, optimistic bias, and anticipated regret. Front Psychol (2021) 12:648289. doi:10.3389/fpsyg.2021.648289

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kahneman D, Tversky A. Prospect theory: an analysis of decision under risk. Econometrica (1979) 47:263–91. doi:10.2307/1914185

CrossRef Full Text | Google Scholar

31. Yang YX, Park LT, Mandayam NB, Seskar I, Glass A, Sinha N. Prospect pricing in cognitive radio networks. IEEE Trans Cogn Commun Networking (2015) 1:56–70. doi:10.1109/TCCN.2015.2488636

CrossRef Full Text | Google Scholar

32. Jhala K, Natarajan B, Pahwa A. Prospect theory-based active consumer behavior under variable electricity pricing. IEEE Trans Smart Grid (2019) 10:2809–19. doi:10.1109/TSG.2018.2810819

CrossRef Full Text | Google Scholar

33. Wang YP, Saad W, Sarwat AI, Hong CS. Reactive power compensation game under prospect-theoretic framing effects. IEEE Trans Smart Grid (2018) 9:4181–93. doi:10.1109/TSG.2017.2652846

CrossRef Full Text | Google Scholar

34. Rahi GE, Etesami SR, Saad W, Mandayam NB, Poor HV. Managing price uncertainty in prosumer-centric energy trading: a prospect-theoretic stackelberg game approach. IEEE Trans Smart Grid (2019) 10:702–13. doi:10.1109/TSG.2017.2750706

CrossRef Full Text | Google Scholar

35. Li C, Dai JY, Li X. A new species of Entedon Dalman (Hymenoptera, Eulophidae) and three newly recorded species from China. IEEE Trans Comput Soc Syst (2023) 1172:1–14. doi:10.3897/zookeys.1172.104676

CrossRef Full Text | Google Scholar

36. Li XJ, Li C, Li X. The impact of information dissemination on vaccination in multiplex networks. Sci China Inf Sci (2022) 65:172202. doi:10.1007/s11432-020-3076-1

CrossRef Full Text | Google Scholar

37. Proskurnikov AV, Tempo R. A tutorial on modeling and analysis of dynamic social networks. part i. Annu Rev Control (2017) 43:65–79. doi:10.1016/j.arcontrol.2017.03.002

CrossRef Full Text | Google Scholar

38. Liu Q, Jiang DQ, Shi NZ, Hayat T, Alsaedi A. Nontrivial periodic solution of a stochastic non-autonomous sisv epidemic model. Physica A: Stat Mech its Appl (2016) 462:837–45. doi:10.1016/j.physa.2016.06.041

CrossRef Full Text | Google Scholar

39. Mei WJ, Mohagheghi S, Zampieri S, Bullo F. On the dynamics of deterministic epidemic propagation over networks. Annu Rev Control (2017) 44:116–28. doi:10.1016/j.arcontrol.2017.09.002

CrossRef Full Text | Google Scholar

40. Mieghem PV, Omic J, Kooij R. Virus spread in networks. IEEE/ACM Trans Networking (2009) 17:1–14. doi:10.1109/TNET.2008.925623

CrossRef Full Text | Google Scholar

41. Wang W, Tang M, Stanley HE, Braunstein LA. Unification of theoretical approaches for epidemic spreading on complex networks. Rep Prog Phys (2017) 80:036603. doi:10.1088/1361-6633/aa5398

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Granell C, Gómez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys Rev Lett (2013) 111:128701. doi:10.1103/PhysRevLett.111.128701

PubMed Abstract | CrossRef Full Text | Google Scholar

43. de Arruda GF, Rodrigues FA, Moreno Y. Fundamentals of spreading processes in single and multilayer complex networks. Phys Rep (2018) 756:1–59. doi:10.1016/j.physrep.2018.06.007

CrossRef Full Text | Google Scholar

44. Valle SYD, Hethcote HW, Hyman JM, Castillo-Chavez C. Effects of behavioral changes in a smallpox attack model. Math Biosciences (2005) 195:228–51. doi:10.1016/j.mbs.2005.03.006

CrossRef Full Text | Google Scholar

45. Barabási AL, Albert R. Emergence of scaling in random networks. Science (1999) 286:509–12. doi:10.1126/science.286.5439.509

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Erdös P, Rényi A. On random graphs i. Publicationes Mathematicae Debrecen (1959) 6:290–7. doi:10.5486/pmd.1959.6.3-4.12

CrossRef Full Text | Google Scholar

47. Yin H, Benson AR, Leskovec J, Gleich DF. Local higher-order graph clustering. In: Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (ACM); August 13-17, 2017; Halifax, NS (2017). p. 555–64.

PubMed Abstract | CrossRef Full Text | Google Scholar

48. McAuley J, Leskovec J. Learning to discover social circles in ego networks. In: Proceedings of the 25th International Conference on Neural Information Processing Systems (NIPS); December 3-8, 2012; Lake Tahoe (2012). p. 539–47.

Google Scholar

49. Rozemberczki B, Sarkar R. Characteristic functions on graphs: birds of a feather, from statistical descriptors to parametric models. In: Proceedings of the 29th ACM International Conference on Information and Knowledge Management (ACM); October 19-23, 2020; Virtual Event, Ireland (2020). p. 1325–34.

CrossRef Full Text | Google Scholar

50. Newman EJM. The structure and function of complex networks. SIAM Rev (2003) 45:167–256. doi:10.1137/S003614450342480

CrossRef Full Text | Google Scholar