Many factors point to the underlying instability of preferences in choice behavior. In particular, discounting reveals some effects not consistent with stable preferences. In discounting, the subjective value of a reward reduces as the uncertainty of or delay to obtaining it increases. The function relating subjective value to delay or probability must be exponential with a constant discount rate to respect transitivity over time, i.e., if A > B and B > C, then A > C (“ > ” = is preferred to). If the discount rate varies with value or time, then it is possible for transitivity to be violated, i.e., for preferences to be unstable. And people do show unstable, preference reversals over time in intertemporal choice more consistent with a hyperbolic discounting function (e.g., Myerson and Green, 1995). Thus, while someone may prefer £100 for certain now rather than £110 tomorrow, they will prefer £110 in a year and a day over £100 in a year’s time. People discount rate is very high initially, more rapid than the exponential, but over time it decreases leading to a flatter function than the exponential. Consequently, the £10 difference is almost totally discounted in the short term, but in a year’s time the extra day barely reduces the subjective value we attach to gaining an extra £10.
Further effects are inconsistent with the reasonable assumption that delay works by increasing uncertainty. For example, the magnitude of a reward seems to have opposite effects for uncertainty and delay. Amount has opposite effects on the discounting of delayed and probabilistic rewards (Green et al., 1999). So, in temporal discounting people seem to discount small amounts more than large amounts, e.g., they prefer £10 now to £20 in a year but prefer £200 in a year to £100 now. However, in probabilistic discounting people seem to discount large amounts more than small amounts, e.g., they prefer £20 with a 50% chance to £10 for certain but prefer £100 for certain rather than £200 with a 50% chance. This picture is further complicated by the fact that for discounting losses, there seems to be no effect of amount for temporal discounting and inconsistent effects for probabilistic discounting (e.g., Mitchell and Wilson, 2010). These effects of amount not only violate the axioms of expected utility theory but are also not consistent with descriptive decision theories such as prospect theory.
Jones and Oaksford (2011) observed that most of these results were obtained using gambles, whereas most people rarely receive a gain or incur a loss outside the context of a transaction, e.g., a choice of paying £10 now to own a commodity now or of paying £20 in 6 months time to own the commodity now. Kusev et al. (2009) showed that precautionary decision content, as in insurance situations, altered people’s choice behavior consistent with an increase in the probability weighting function for low probability events in prospect theory. Similarly, Jones and Oaksford (2011) argued that using transactional problem content rather than gambles may alter people’s decision-making. In particular, they suggested that this content may reveal more consistent effects of amount across temporal and probabilistic discounting.
Transactions – but not gambles – will bring to mind previous instances of purchasing different commodities for different amounts. In particular, people would also be expected to have access to a commodity’s rate of depreciation or appreciation and they would know that the more expensive a commodity, the lower its depreciation is expected to be. Indeed, for some of their most costly purchases, people have the reasonable expectation of long-run appreciation. This information implies that in a transaction, people may discount small costs more than larger costs. So they will prefer to pay £100 now for the weekly shop rather than £200 in a week because its subjective value in a week’s time will be far less than £100 if not zero. In contrast, they may well be happy to pay £200K for a new flat in 10 years rather than £100K now. The flat is likely to be worth more than £100K in 10 years, and so, over time, its subjective value is not likely to decrease much. Jones and Oaksford (2011) also made the same prediction, more discounting for small costs than larger costs, for probabilistic discounting with transactional content.
They report four experiments testing the predicted effects of transactional content on cost discounting. All these experiments used the standard adaptive staircase method to zero in on people’s certainty equivalent values for three amounts given different delays and probabilities. Temporal and probabilistic discounting curves were generated by plotting the certainty equivalent value normalized by cost amount against delay or odds against loss respectively for each amount. The area under the discounting curves (AUC) was used as the dependent variable indicating the degree of discounting: the lower the area under the curve the higher the rate of discounting. Figure 1, Panel A shows the mean AUC values using transactional content for both delay and probabilistic discounting in Jones and Oaksford’s (2011) Experiment 3, which was a replication of their Experiment 1. Both experiments showed the same pattern of discounting small costs more than large costs, i.e., lower mean AUC values for lower amounts. The trends were significant in all cases and in the same direction for both temporal (delay) and probabilistic discounting. Figure 1, Panel B shows the mean AUC values for their Experiment 4, which used gambles rather than transactions. For delay discounting, this experiment replicated previous findings of no effect for discounting losses. For probabilistic discounting of losses, a similar effect of more discounting for smaller amounts was observed. Moreover, for both the temporal and probabilistic case, people discounted more (lower AUC values) for transactions than for gambles.
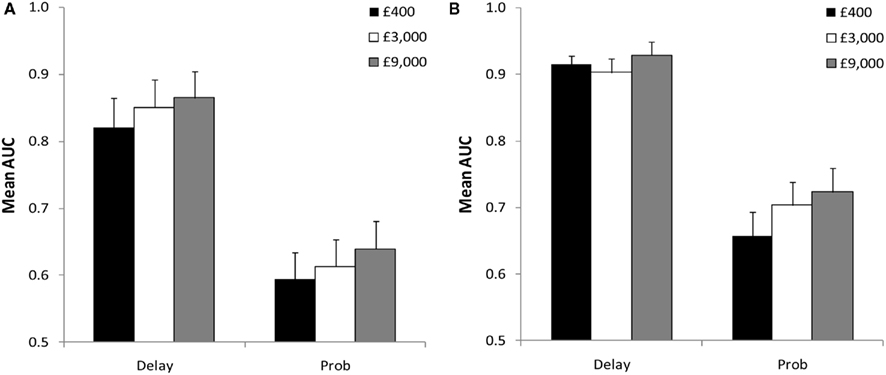
Figure 1. Mean AUC values at different levels of cost amount using transactions (A) and gambles (B) taken from Jones and Oaksford’s (2011) Experiments 3 and 4 respectively. Error bars represent SE. AUC, area under the curve; Prob, probability.
Like precautionary decisions (Kusev et al., 2009), transactions cannot be treated like pure gambles. A cost is not a pure loss because in a transaction there is always a linked gain associated with the purchased commodity. For delay discounting these differences result in a magnitude effect for transactions (Panel A) not observed for gambles (Panel B). Moreover, for transactions this effect is paralleled for probabilistic discounting of costs (Panel A). This is the first time that such parallel effects of amount have been observed for probabilistic and delay discounting. However, for probabilistic discounting, this effect was also observed for gambles (Panel B). A possible explanation is that gambles are described by prospects, which, like transactions, emphasize an implicit linked gain.
There are some outstanding problems. For example, for probabilistic discounting with gambles, why are smaller losses discounted more than larger losses but larger gains discounted more than smaller gains? Jones and Oaksford (2011) proposed the following possible explanation. Green et al. (1999) and Prelec and Loewenstein (1991) argued that in probabilistic discounting, gains implicitly involve corresponding losses (i.e., the possibility of wining nothing). They argued that the negative value attached to the possible loss increases faster than the positive value associated with the gain as the gain amount increases. By parity of reasoning, one could argue that losses implicitly involve corresponding gains (i.e., the possibility of losing nothing). This line of reasoning suggests that the positive value attached to the possible gain increases faster than the negative value associated with the loss as the loss amount increases. In both cases, the implicit gain or loss associated with the possibility of no change in one’s financial position increases in subjective value, positive or negative, faster with amount than the subjective values attached to the possibility corresponding to an actual loss or gain. Such an account could explain the peanuts effect for probabilistic gains (overall subjective value will decrease with amount) and a magnitude effect for probabilistic losses (overall subjective value will increase with amount).
Such an account is not consistent with prospect theory, in which losses loom larger than gains. So, such an explanation works for probabilistic gains, but explaining the reverse effect for losses would seem to require gains to loom larger than losses. Of course, how implicit losses and gains behave when the focus of attention is on the corresponding gains and losses has not been explored. Consequently, much further work needs to be done before a complete account of the effects of amount on intertemporal choice, using transactions or gambles is forthcoming. How consistent such an account is with current descriptive decision theory or with standard discounted utility models remains uncertain.
Nonetheless, Jones and Oaksford’s (2011) results show that transactions make transparent a factor, the differential depreciation of high and low value items, that reveals a more stable pattern of preferences in people’s discounting behavior at least with respect to variation in cost amount. Consistent with standard discounted utility models, these results are consistent with the view that time or delay affects decision-making by increasing uncertainty. Moreover, it is arguable that people’s behavior with transactional problem content is the general case and consequently how they behave with this kind of content more indicative of the rationality, or not, of their behavior in the real world. A similar trend to seeing more of people’s decision-making behavior as rational or least conforming to the dictates of standard expected utility theory emerges in Regenwetter et al. (2011). They point out that it is actually quite difficult to establish inconsistency of variable choice behavior with deterministic axioms like transitivity in expected utility theory. They use the example of a student observing their supervisor’s behavior when choosing between three on campus locations to meet. Choice proportions seem to reveal underlying intransitivity of choice until Regenwetter et al. (2011) reveal that the supervisor’s choice of location to meet is based on how close it is to where she is teaching that day. That is, there is an underlying consistent basis for the choice although the revealed preferences seem intransitive. That is, the revealed preferences seem unstable although the latent preferences are stable.
In sum, there is emerging evidence that people’s choice behavior may be less irrational or inconsistent with expected utility theory and discounted utility models than first thought. People’s preferences are more stable for transactions than for gambles. Our research on transactions in cost discounting makes a small contribution to this literature that suggests exploring more fully the effects of transactions on discounting behavior when participants are asked to act as sellers as well as buyers, and when, as in real world transactions, payment and receipt of goods can vary more widely.
References
Green, L., Myerson, J., and Ostaszewski, P. (1999). Amount of reward has opposite effects on the discounting of delayed and probabilistic outcomes. J. Exp. Psychol. Learn. Mem. Cogn. 25, 418–427.
Jones, S., and Oaksford, M. (2011). Transactional problem content in cost discounting: parallel effects for probability and delay. J. Exp. Psychol. Learn. Mem. Cogn. 37, 739–747.
Kusev, P., van Schaik, P., Ayton, P., Dent, J., and Chater, N. (2009). Exaggerated risk: prospect theory and probability weighting in risky choice. J. Exp. Psychol. Learn. Mem. Cogn. 35, 1487–1505.
Mitchell, S. H., and Wilson, V. B. (2010). The subjective value of delayed and probabilistic outcomes: outcome size matters for gains but not for losses. Behav. Process. 83, 36–40.
Myerson, J., and Green, L. (1995). Discounting of delayed rewards: models of individual choice. J. Exp. Anal. Behav. 64, 263–276.
Prelec, D., and Loewenstein, G. (1991). Decision making over time and under uncertainty: a common approach. Manage. Sci. 37, 770–786.
Citation: Jones S and Oaksford M (2011) Preferences show greater stability for transactions than for gambles in cost discounting. Front. Psychology 2:293. doi: 10.3389/fpsyg.2011.00293
Received: 30 June 2011;
Accepted: 11 October 2011;
Published online: 15 November 2011.
Copyright: © 2011 Jones and Oaksford. This is an open-access article subject to a non-exclusive license between the authors and Frontiers Media SA, which permits use, distribution and reproduction in other forums, provided the original authors and source are credited and other Frontiers conditions are complied with.
*Correspondence:bWlrZS5vYWtzZm9yZEBiYmsuYWMudWs=

