Phase transitions in complex functional liquid crystals—The entropy effect

1 Introduction

Liquid Crystals combine molecular mobility along with the self-assembly of functional building blocks in either anisotropic materials (lamellar and columnar phases) or in ordered isotropic (cubic micellar or cubic bi- or tricontinuous) mesophases. Lamellar, columnar and cubic network phases provide continuous transport, conducting or guiding pathways for light, quasiparticles such as excitons or polarons and for ionic species (Sergeyev et al., 2007; Lee et al., 2016; Kato et al., 2018; Hecht et al., 2019). Owing to the advancement of synthesis and purification procedures, the design of increasingly complex systems is possible, in which various functions are combined, for example donor-acceptor dyads (Lee et al., 2016; Hecht et al., 2019; Lehmann and Hügel, 2015), or even donor-acceptor combined with light harvesting systems (Lehmann et al., 2019a; Dechant et al., 2021). Such materials can segregate their individual building blocks in different nanospaces. Regarding only the functional building blocks of the liquid crystal, this is called double or triple nanosegregation. Many rather large complex molecular systems further reveal either glassy phases at low temperature or slowly transform to more ordered soft crystals or crystals (Paraschiv et al., 2006; Xiao et al., 2016; Maier et al., 2017). The latter may even improve their performance as quasiparticle transport systems, since in a soft crystal templated by a liquid crystal phase, the overall morphology can be retained but the interaction of functional building blocks are optimized (Ivanov et al., 2006). Thus, in the ideal case, in which two electrodes of a device have to be contacted, a liquid crystal should flow into the contact gap and a monodomain should bridge the contacts where slow cooling provides optimized device performance by a templated transformation to a defect-free soft crystalline material with a number of tailored functions. This is an idealized vision for the complete self-assembly control and possible optimization of devices like organic transistors, organic light emitting diodes, electrochromic or organic photovoltaic cells. The actual functional layer is not necessarily liquid crystalline, but for the generation process, the liquid crystal state is of crucial importance (Sun et al., 2015). The growth of monodomains and the correct alignment of the anisotropic mesophases, however, require either low viscosity and application of external fields or the suitable surface interactions and the cooling from the isotropic state of matter (Grelet and Bock, 2006; Brunet et al., 2011). The latter is crucial for tailor-made complex molecules, which often consist of large aromatic building blocks contributing to inherent high viscosities and high clearing temperatures in the mesophases. Thus annealing alone, demonstrated to align some mesogens by surface interaction, will not deliver generally the expected results in the bulk material (Dechant et al., 2021). Temperatures at which lower viscosities are achieved are often above 250°C, at which undesired slow decomposition of the organic material sets in. Generally, it is known that monodomains and surface aligned materials can be obtained from the isotropic liquid by slow cooling (Grelet and Bock, 2006). Consequently, when complex mesogens are designed, clearing temperatures below 200°C will be favorable for the device engineering. This perspective article will discuss some design strategies for selected examples in order to obtain lower clearing temperatures for complex soft matter based on thermodynamic considerations.

2 Discussion

2.1 Nanosegregation, cohesive energy density difference, nanosegregation and phase transition temperatures

In order to take the challenge of phase engineering, it is important to understand the concepts behind the formation and the stability of columnar, lamellar and cubic network liquid crystals. The basis of their self-assembly is the nanosegregation (Tschierske, 1998; Tschierske et al., 2014). In a simple case, an aromatic building block is decorated with flexible aliphatic chains. These two building blocks segregate in so-called nanophases in higher ordered liquid crystal self-assemblies – these are no phases in the sense of thermodynamics, but rather nanospaces, in which one of the building blocks is located. It is now extremely important to note that it is not the cohesive energy density effective in one nanophase, i.e., the strong and favorable interaction between identical building blocks (enthalpy), that keeps the nanosegregated structure together in a certain temperature range. Instead, it is the cohesive energy density difference (CED) between the different building blocks, which determines the temperature at which the building blocks mix to generate either nematic or isotropic liquid phases. The larger the CED or its corresponding measure, i.e., the difference of the solubility parameters Δδ = δ_core - δ_chain, the more difficult it is to mix the nanophases, which is necessary to generate more disordered phases. Thus, nanosegregated liquid crystalline phases generated by mesogens corresponding to larger Δδ values reveal higher stabilities and higher transition temperatures. In principle, both nanophases may be highly fluid low viscous liquids at high temperature, thus the thermal energy overcomes already the individual cohesive energies between the identical nanosegregated building blocks, but the cohesive energy density difference (CED) does not permit the mixing of both components, which are still nanosegregated in either lamellae, columns or cubic networks. Consequently, one method to tailor the transition temperatures of a system with a predefined functional building block is the exchange of the flexible peripheral chains. Tschierske presented some show cases in the Handbook of Liquid Crystals based on a pentaerythritol core with a defined cohesive energy density δ_core, which he calculated according to D.D. Lawson (Barton, 1991; Tschierske et al., 2014). This δ_core value is always higher than that of peripheral flexible chains δ_chain. By exchanging the original eight decyl chains by semiperfluorinated chains (C₄H₈C₆F₁₃), the much smaller cohesive energy density of the perfluorinated units significantly increases the CED between chains and the core and thus the clearing temperature increases by more than 80°C. According to calculated values, the cohesive energy density increases from RF < RSi < RH < RO [RF = perfluorinated carbon chains; RSi = oligo (siloxanes) with methyl substituents, RH = alkyl chains, RO = oligo (ethyleneoxy) chains] (see Supplementary Information). It is expected that RF and RSi increase CED and thus the nanosegregation tendency increases relative to mesogens with alkyl chains, while oligo (ethyleneoxy) chains, decrease this tendency and should therefore lower the transition temperatures relative to alkyl derivatives. This concept works well with smaller π-systems like triphenylene (Figure 1) (Boden et al., 1986; Terasawa et al., 2003; Terasawa et al., 2007; Zelcer et al., 2007). While the oligo (ethyleneoxy) derivatives 1a, b melt at low temperature or even produce only an isotropic oil (Boden et al., 1986), alkyl derivatives 2a, b form stable liquid crystal phases, which are even more stabilized when semiperfluorinated chains are attached (compounds 4a, b) (Terasawa et al., 2003; Terasawa et al., 2007). This clearly highlights the power of the CED concept for molecular designing and phase engineering. In contrast, siloxane derivatives should produce more stable mesophases than alkyl chain derivatives. The unexpected low transition temperature for compound 3b originates from an entropy effect which is discussed in Sections 2.3, 2.4 (Zelcer et al., 2007).

FIGURE 1

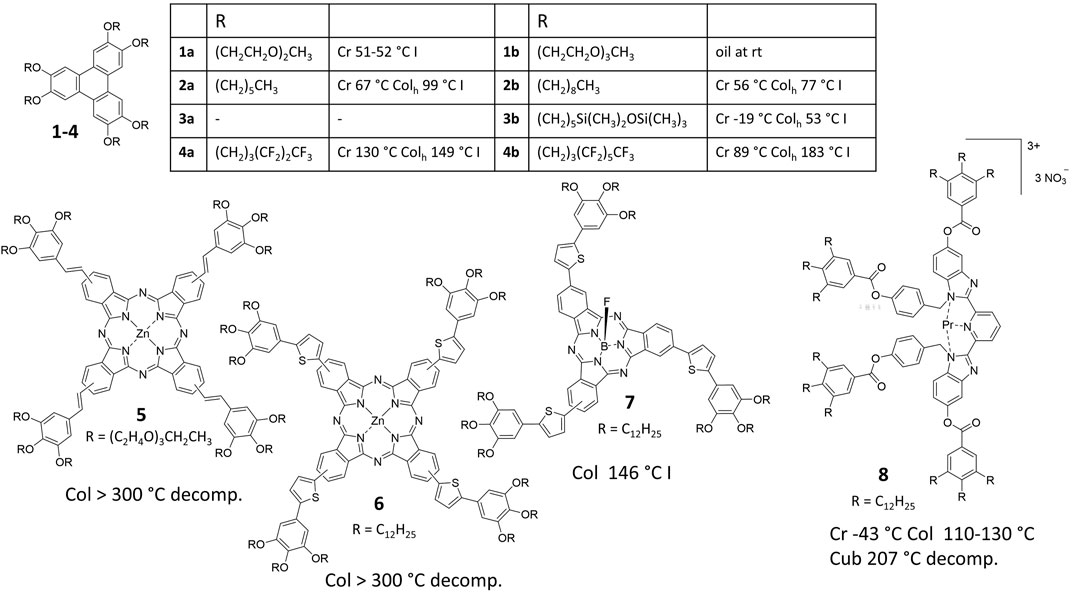
FIGURE 1. Transition temperature control by cohesive energy density difference (CED) and the number of peripheral chains.

For larger and stronger segregating zinc phthalocyanine star mesogens 5 this concept does apparently no longer work because even for oligo(ethyleneoxy) chain derivatives no clearing is observed before the decomposition of the molecules (Lehmann et al., 2019a). From structural investigations it is evident, that the flat core aggregates strongly with π–π-distances of only 3.4 Å. A strong decrease in the clearing temperature was observed when the molecular topology was changed from flat zinc phthalocyanines 6 to a cone-shaped boron subphthalocyanines 7, from over 350°C–146°C, although the magnitude of CED is almost identical [Δδ (6) = 21.0 MPa^1/2 versus Δδ (7) = 20.2 MPa^1/2] (Lehmann et al., 2021) (see Supplementary Information). One important parameter for this enormous decrease in clearing temperature might be the different molecular size, which impact on the Flory-Huggins interaction parameter (Tschierske et al., 2014) showing a 30% lower value for the boron subphthalocyanine 7. Indeed, at constant CED the increase of molecular size impacts significantly on the nanosegregation tendency as emphasized by Tschierske (Tschierske, 1998; Tschierske et al., 2014)—the larger the size of the molecule, the smaller can be the CED between different building blocks in order to find nanosegregated LC materials. In this special example, however, the cone-shape and the fluorine tip prevents a strong regular stacking in close π-stacks, evidenced by X-ray scattering (Lehmann et al., 2021). Although these cone-shaped mesogens possess extremely large dipole moments of approximately 14 D, which should increase dipole-dipole intermolecular interactions, the van der Waals interactions are tremendously reduced. The latter are the sum of interactions over the complete π -surface and scale with intermolecular distance d⁻⁶. The increase in distance and simultaneous reduction of the π -surface in the boron subphthalocyanine example outranges the interaction of large dipole moments and consequently results in reduced clearing temperatures by more than 200°C.

2.2 Flexible chains – a reservoir of entropy

Sorai and Saito emphasized that “The alkyl chain can acquire a large amount of entropy [ca. 10JK^-1 (mol of CH₂)⁻¹] upon disordering, which modulates the relative thermodynamic stability of aggregated states.” (Sorai and Saito, 2003) In liquid crystals these chains are highly mobile and serve as a kind of solvent. Further, they detailed that the degree of order of aliphatic chains depends on the type of phase. For example, in lamellar phases the chains tend to be more ordered than in cubic bicontinuous phases, while the mesogen cores are more disordered in the lamellar phase and more ordered in the cubic phase. Thus in the case, in which cubic bicontinuous phases transform to a lamellar phase, entropy from the chain reservoir can be transferred to the core.

In general the large entropy change derived when more ordered chains sequentially increase entropy until they achieve their complete degree of freedom in the isotropic phase may be used to engineer phase transition temperatures. For example, this was shown by a mesogenic ligand tailored to form room temperature lanthanide-containing mesogens such as compound 8 (Figure 1). (Escande et al., 2007) The large entropy changes at the crystal-liquid crystal transitions of these types of mesogens guaranteed low melting temperatures as low as −43°C. For most of the complexes the clearing temperatures were still above 200°C, at which the materials decomposed. There are other examples of phthalocyanines for which the increase in the number of chains decrease also the temperature of the clearing transition (Ishikawa et al., 2018). However, this strategy is limited, when certain phase structures are needed. In the general phase diagram lamellar phases exist for molecules, in which the volume of flexible chains and functional conjugate building blocks possess a ratio of approximately 1 : 1. The increase in the volume fraction of the flexible chains either by temperature increase or by design (chain lengths or chain number) affords a change in the structure at defined volume fractions from smectic to cubic bicontinuous, columnar and eventually cubic micellar mesophases (Tschierske, 1998; Tschierske et al., 2014). Moreover, the addition of chains increases the molecular size, which impacts on the nanosegregation and, thus, on the stability of the liquid crystal. Consequently, such a strategy is only of limited suitability for the phase transition engineering of large complex systems.

2.3 Entropy as unique parameter for phase transition temperatures – The concept

As outlined in Section 2.2, entropy is an important parameter, which has to be considered for the engineering of phase transition temperatures. Therefore, it is necessary to focus more on the thermodynamic aspects to develop other strategies to bring melting and clearing temperatures to an accessible range for complex mesogens. Phase transitions are generally order-disorder transitions for which ΔH = TΔS, since ΔG = 0. It follows that the experimental transition enthalpies measured by differential scanning calorimetry also provide the transition entropies. These are obviously generated by the attenuation of interaction energy. Consequently, in an ideal case, in which in a complex system the phase structure and the intermolecular interaction can be kept constant, i.e., ΔH = const., but the transition entropy ΔS can be increased, the transition temperature T must decrease. For example, if a phase transition for material A₁ occurs at 100°C (373 K), then a 10% increase in the transition entropy of the related material A₂ with an identical phase structure and interaction energy, will lower the transition temperature by 34 K. Accordingly, if the original transition of material A₁ is at 200°C (473 K) then the decrease in transition temperature for material A₂ will be 43 K. Eventually, we can conclude that if a strategy for molecular design can be envisioned which increases the transition entropy at a roughly constant interaction energy then the phase transition temperatures can be tailored to fit the required temperature range for a defined application. Indeed, there is a strategy, which is widely used to connect two incompatible building blocks to each other – the flexible spacers (Janietz, 1996; Lee et al., 2016). The flexible spacers are usually adjusted to the length of the peripheral chains in order to be commensurate with the aliphatic nanophase, but to the best of the authors knowledge, it has never been considered as a main factor to control phase transition temperatures, although there are numerous examples showing the effectiveness of this concept, which is highlighted with some examples in Section 2.4.

2.4 Selected examples of complex systems

When the star-shaped, shape-persistent donor–acceptor mesogen 9a was designed, the strongly nanosegregating fullerene unit had to be attached via an aliphatic spacer in order to prevent macroscopic separation of the system (Figure 2). (Lehmann and Hügel, 2015) The design originates from the idea to fill the intrinsic free space between the conjugated arm scaffold with fullerene guests (Lehmann et al., 2019b). The short spacer keeps the fullerene clearly close to the center of the mesogen and as predicted, a columnar mesophase with an isolated fullerene triple helix could be confirmed by X-ray scattering and modelling. Here the spacer is only a connector, folded in the cavity of the star mesogen. The special double nanosegregation of fullerenes side-by-side with oligo (phenyleneethenylenes) additionally increases the transition temperature by more than 75°C, compared to the parent system without spacer and fullerene. This clearly showed the increasing intermolecular interaction energy within this donor-acceptor structure. In order to investigate the change in structure by elongating the spacer, the molecules with C8 and C14 spacers (9b, 9c) were prepared. (Lehmann et al., 2019c). Interestingly, it has been found that the structure remains similar—i) the columnar diameters are demonstrated to be almost identical in the series of compounds 9 and are controlled by the identical size of the shape-persistent conjugated scaffold and ii) the fullerenes still form triple helices. The unique difference is the spacers, which cannot nanosegregate together with the aliphatic nanophase and result in variations of helical pitches and diameters of the triple helices as a function of spacer lengths. With increasing spacer lengths the clearing temperatures for the transition from columnar phases to the isotropic liquid decreases considerably from 281°C to 240°C–205°C. Taking into account the original data of compound 9a and the idealized calculation assuming a constant transition enthalpy, the experimental transition temperatures of 9b, 9c are obtained, assuming a 8% and 16% increase of transition entropy. Thus, in this model, the elongation of the spacer by six CH₂ groups each equally contributes to the transition entropy (see Supplementary Information) and consequently, as expected, to the decrease of the transition temperatures. These results can be only understood if the position of the fullerene is rather defined relatively to the molecule’s center in the columnar liquid crystal phase. Consequently, the spacers are partially frozen in specific conformations. After the transition to the isotropic phase the spacer gains its complete conformational freedom and thus, longer spacers generate larger transition entropies than shorter ones. This can be rationalized considering a single C-C bond of an aliphatic chain frozen in one of the three possible staggered conformations. If the single bond can rotate, it populates all three staggered conformations equally. Thus, the transition from maximum conformational freedom to the completely frozen state leads to an entropy loss of Rln3 = 9.13 JK⁻¹mol⁻¹ per single bond and 54.8 JK⁻¹mol⁻¹ for six bonds (R being the gas constant). This value is much larger than the transition entropy for compound 9a (5.2 JK⁻¹mol⁻¹) (see Supplementary Information) and hence, the aliphatic spacers lose only a fraction of their mobility. However, this is only a qualitative calculation with the transition at 281°C transition as a reference point. Although the real system seems to behave almost ideal, it deviates for example from the perfect picture in the different energy values of the transition enthalpy of compounds 9b, 9c. They should not change in that model. The diverging enthalpies from a constant value can be rationalized by interactions of fullerenes of different columns, since the spacer lengths are sufficiently large to allow for such contacts forming helical fullerene networks. As a result, the interaction energy between the mesogens and the transition enthalpy is slightly modified by additional fullerene aggregation.

FIGURE 2

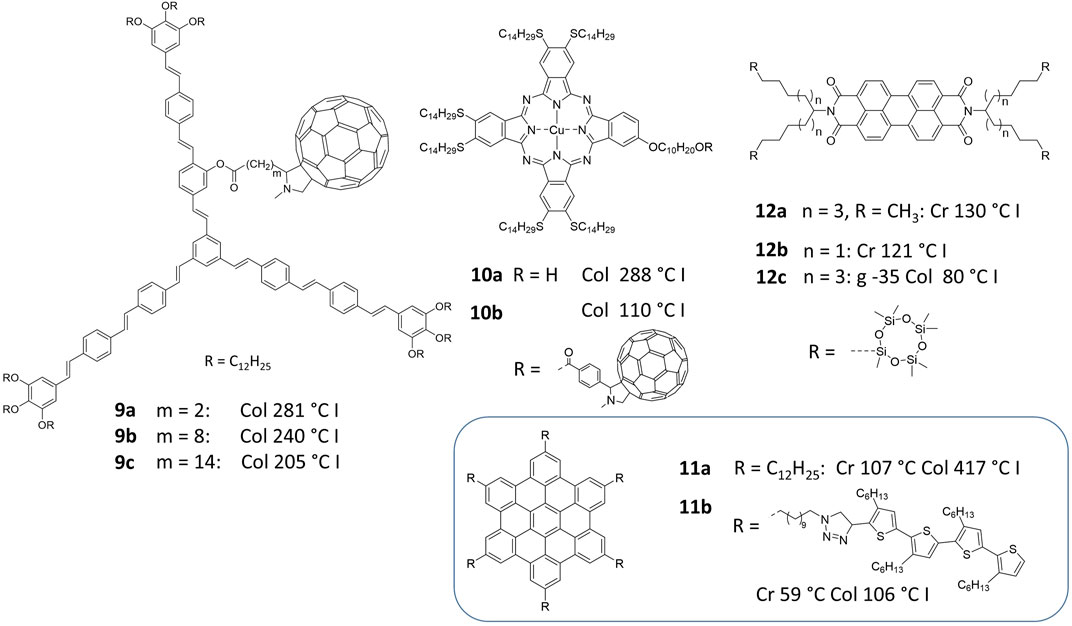
FIGURE 2. The transition entropy strategy–double nanosegregated structures linked by flexible spacers.

There are many phthalocyanine mesogens similar to structure 10b, in which the fullerenes are attached via spacers to the core (Felder-Flesch et al., 2014; Ishikawa et al., 2014). In contrast to the star mesogens, the spacers in 10a, 10b are part of the aliphatic nanophase, nevertheless, the clearing temperature decrease for the fullerene derivative 10b by more than 150°C compared with 10a. This reveals that the entropy effect becomes effective when the fullerene is nanosegregated from the column and consequently the spacer conformations are restricted in the LC phase. Originally such phases are described to possess similar helical fullerene structures than the star mesogens (Ishikawa et al., 2014). Recent reinvestigations of these systems, however, suggest instead that the phase is a lamellar columnar phase, in which fullerenes nanosegregate in layers (Lehmann et al., 2019d).

The most impressive example has been published by Hu et al. with a hexabenzocoronene (HBC) 11b. (Hu et al., 2014). The parent mesogens such as 11a typically clear at temperatures above 400°C. However, the hybrid structure 11b with six oligo (thiophenes) attached via spacers to the HBC core reveals an incredible low clearing temperature at 106°C. This can only be explained by the entropy effect based on the double nanosegregation of the HBC in the center and the oligo (thiophenes) in the periphery (double cables), while the spacers are restricted to certain conformations in the LC phase. Interestingly, this huge effect was not further discussed in that report.

Eventually, siloxane decorated mesogens are an interesting class of compounds. Siloxanes are prepared by hydrosilylation of olefin terminated aliphatic chains. Although the CED predicts that compounds should be even more strongly nanosegregated the triphenylene example (compound 3b, Figure 1) reveals an opposite effect (Zelcer et al., 2007). Thus, it can be regarded as a double nanosegegated system in which triphenylenes and siloxane units are nanosegregated and are held together by conformationally restricted aliphatic spacers. Thus, the entropy-gain upon clearing decreases considerably the clearing temperature. One of the most impressive examples are the perylenebisimide systems of Funahashi et al. with cyclic siloxanes 12b, c attached to a swallow-tailed spacer (Funahashi et al., 2013). Here the longer spacer leads to a clearing temperature as low as 80°C, which is a 50 K decrease compared with the parent system 12a (Sergeyev et al., 2007). Perylenebisimides are often found to possess high clearing temperatures owing to the strong π-stacking interactions. The decoration with cyclic siloxanes attached by spacers is therefore a smart strategy to control transition temperatures.

Finally, it should be noted that this strategy has been discussed from a qualitative point of view. Although the total entropy changes of a material transforming from the solid to the isotropic liquid can be computed with acceptable accuracy (Acree and Chickos, 2006), for liquid crystals, these values are usually overestimated. The reason for this is, that in complex systems, often, not all phase transitions, changes in heat capacity and the possible aggregations in the isotropic liquid are known. Moreover, since the structure of a spacer is not accessible before and after a transition, its quantitative contribution to the transition entropy will remain unclear. It is certainly not the maximum possible entropy, since the spacer would then needed to be completely frozen in a fluid phase.

3 Conclusion

Functional thermotropic liquid-crystals with high complexity, such as donor–acceptor systems, frequently possess a high cohesive energy density. A high cohesive energy density difference (CED) results when these building blocks are combined with flexible chains of low cohesive energy density. The substantial CED together with a large size of the system lead to high clearing temperatures at which decomposition of the material is likely to occur. The first strategy to lower the clearing temperature will be the tuning of an enthalpy factor by increasing the cohesive energy of the flexible periphery of the mesogens by the choice of the nature of chains. Chains with a higher cohesive energy density lower the clearing temperatures, because of the decreasing CED. An entropy factor which mainly effects the transition from a crystalline state to the liquid crystal is the number of the flexible chains attached to the system. But this strategy expands the molecular volume and thus, the nanosegregation tendency and the clearing temperature increase, too. Eventually, it may shift the volume fraction of incompatible building blocks towards values for which unwanted LC morphologies are anticipated. A highly effective strategy to lower the clearing temperature is demonstrated to be a variable spacer linkage with long aliphatic chains between two incompatible building blocks. The spacer possesses a limited degree of freedom in the liquid crystal phase when the building blocks are located at defined positions (double or triple nanosegregation). The mixing of the incompatible units at the clearing temperature produces an additional entropy gain which consequently lowers the transition temperature. Since the spacer typically contributes minimally to the transition enthalpy this strategy is highly promising when the clearing temperature has to be adjusted with unchanged phase morphology.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

ML has developed the concept and has written the manuscript.

Funding

ML is grateful for the funding of the DFG (LE1571/8-1 and LE1571/11-1). The results of these projects have stimulated the concept of the present perspective.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/frsfm.2023.1089726/full#supplementary-material

References

Acree, W. E., and Chickos, J. S. (2006). Phase change enthalpies and entropies of liquid crystals, J. Phys. Chem. Ref. Data 35, 1051–1330.

CrossRef Full Text | Google Scholar

Barton, A. F. M. (1991). ORC Handbook of Solubility Parameters and Other Cohesion Parameters. 2. Boca Raton, FL, USA: CRC Press.

Google Scholar

Boden, N., Bushby, R. J., Ferris, L., Hardy, C., and Sixl, F. (1986). Designing new lyotropic amphiphilic mesogens to optimize the stability of nematic phases. Liq. Cryst. 1, 109–125. doi:10.1080/02678298608086498

CrossRef Full Text | Google Scholar

Brunet, T., Thiebaut, O., Charlet, E., Bock, H., Kelber, J., and Grelet, E. (2011). Anchoring transition in confined discotic columnar liquid crystal films. Europhys. Lett. 93, 16004. doi:10.1209/0295-5075/93/16004

CrossRef Full Text | Google Scholar

Dechant, M., Lehmann, M., Uzurano, G., Fujii, A., and Ozaki, M. (2021). The liquid crystal Click procedure for oligothiophene-tethered phthalocyanines – self-assembly, alignment and photocurrent. J. Mater. Chem. C 9, 5689–5698. doi:10.1039/d1tc00710f

CrossRef Full Text | Google Scholar

Escande, A., Guénée, L., Nozary, H., Bernardinelli, G., Gumy, F., Aebischer, A., et al. (2007). Rational tuning of melting entropies for designing luminescent lanthanide-containing thermotropic liquid crystals at room temperature. Chem. Eur. J. 13, 8696–8713. doi:10.1002/chem.200700560

PubMed Abstract | CrossRef Full Text | Google Scholar

Felder-Flesch, D., Guillon, D., and Donnio, B. (2014). “Fullerene-containing liquid crystals,” in Handbook of Liquid Crystals. Editors J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. Gleeson, and P. Raynes (Weinheim, Germany: Wiley), Vol. 5, 317–361.

CrossRef Full Text | Google Scholar

Funahashi, M., Yamaoka, M., Takenami, K., and Sonoda, A. (2013). Liquid-crystalline perylene tetracarboxylic bisimide derivatives bearing cyclotetrasiloxane moieties. J. Mater. Chem. C 1, 7872–7878. doi:10.1039/c3tc31567c

CrossRef Full Text | Google Scholar

Grelet, E., and Bock, H. (2006). Control of the orientation of thin open supported columnar liquid crystal films by the kinetics of growth. Europhys. Lett. 73, 712–718. doi:10.1209/epl/i2005-10459-5

CrossRef Full Text | Google Scholar

Hecht, M., Schlossarek, T., Stolte, M., Lehmann, M., and Würthner, F. (2019). Photoconductive core–shell liquid-crystals of a perylene bisimide J-aggregate donor–acceptor dyad. Angew. Chem. Int. Ed. Engl. 58, 12979–12983. doi:10.1002/anie.201904789

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, N., Shao, R., Shen, Y., Chen, D., Clark, N. A., and Walba, D. M. (2014). An electric-field-responsive discotic liquid-crystalline hexa-peri-hexabenzocoronene/oligothiophene hybrid. Adv. Mater. 26, 2066–2071. doi:10.1002/adma.201304371

PubMed Abstract | CrossRef Full Text | Google Scholar

Ishikawa, A., Ono, K., Ohta, K., Yasutake, M., Ichikawa, M., and Itoh, E. (2014). Discotic liquid crystals of transition metal complexes 50: Spiranthes-like supramolecular structure of phthalocyanine-fullerene dyads. J. Porphyr. Phthalocyanines 18, 366–379. doi:10.1142/s1088424614500072

CrossRef Full Text | Google Scholar

Ishikawa, A., Watarai, A., Yasutake, M., and Ohta, K. (2018). Discotic liquid crystals of transition metal complexes 56: Synthesis of mesogenic phthalocyanine-fullerene dyads and influence of the substitution position of alkoxy chains and the kind of terminal groups on appearance of the helical supramolecular structure. J. Porphyr. Phthalocyanines 22, 693–715. doi:10.1142/s108842461850092x

CrossRef Full Text | Google Scholar

Ivanov, D. A., Gearba, R. I., Anokhin, D., Magonov, S., and Lehmann, M. (2006). Two-stage self-assembly of star-shaped mesogens in double helices. Programme Making and Special Events Preparation 94, 655–656.

Google Scholar

Janietz, D. (1996). Covalently linked donor-acceptor mesogens based on disc-shaped penta-alkynes. Chem. Commun., 713–714. doi:10.1039/cc9960000713

CrossRef Full Text | Google Scholar

Kato, T., Uchida, J., Ichikawa, T., and Sakamoto, T. (2018). Functional liquid crystals towards the next generation of materials. Angew. Chem. Int. Ed. Engl. 57, 4355–4371. doi:10.1002/anie.201711163

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, K. J., Woo, J. H., Xiao, Y., Kim, E., Mazur, L. M., Kreher, D., et al. (2016). Structure–charge transfer property relationship in self-assembled discotic liquid-crystalline donor– acceptor dyad and triad thin films. RSC Adv. 6, 57811–57819. doi:10.1039/c6ra08039a

CrossRef Full Text | Google Scholar

Lehmann, M., Baumann, M., Lambov, M., and Eremin, A. (2021). Parallel polar dimers in the columnar self-assembly of umbrella-shaped subphthalocyanine mesogens. Adv. Funct. Mater. 2021, 2104217. doi:10.1002/adfm.202104217

CrossRef Full Text | Google Scholar

Lehmann, M., Dechant, M., Holzapfel, M., Schmiedel, A., and Lambert, C. (2019). Fullerene-filled liquid-crystal stars: A supramolecular click mechanism for the generation of tailored donor–acceptor assemblies. Angew. Chem. Int. Ed. Engl. 58, 3610–3615. doi:10.1002/anie.201812465

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, M., Dechant, M., Hügel, M., Scheuring, N., and Ghosh, T. (2019). Fullerene-filled stilbene stars: The balance between isolated C60 helices and 3D networks in liquid-crystal self-assemblies. Chem. Eur. J. 58, 3352–3361. doi:10.1002/chem.201805606

CrossRef Full Text | Google Scholar

Lehmann, M., Dechant, M., Lambov, M., and Gosh, T. (2019a). Free space in liquid crystals - molecular design, generation, and usage. Acc. Chem. Res. 52, 1653–1664. doi:10.1021/acs.accounts.9b00078

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, M., Dechant, M., Lambov, M., and Gosh, T. (2019b). Free space in liquid crystals - molecular design, generation, and usage. Acc. Chem. Res. 52, 1653–1664. doi:10.1021/acs.accounts.9b00078

PubMed Abstract | CrossRef Full Text | Google Scholar

Lehmann, M., and Hügel, M. (2015). A perfect match: Fullerene guests in star-shaped oligophenylenevinylene mesogens. Angew. Chem. Int. Ed. Engl. 54, 4110–4114. doi:10.1002/anie.201410662

PubMed Abstract | CrossRef Full Text | Google Scholar

Maier, P., Grüne, M., and Lehmann, M. (2017). A star-shaped oligo(phenylenevinylene) liquid crystal host with an anthracene guest - a double nanosegregating supermesogen. Chem. Eur. J. 23, 1018–1022. doi:10.1002/chem.201604505

PubMed Abstract | CrossRef Full Text | Google Scholar

Paraschiv, I., Giesbers, M., van Lagen, B., Grozema, F. C., Abellon, R. D., Siebbeles, L. D. A., et al. (2006). H-bond-stabilized triphenylene based columnar discotic liquid crystals. Chem. Mater. 18, 968–974.

CrossRef Full Text | Google Scholar

Sergeyev, S., Pisula, W., and Geerts, Y. H. (2007). Discotic liquid crystals: A new generation of organic semiconductors. Chem. Soc. Rev. 36, 1902–1929. doi:10.1039/b417320c

PubMed Abstract | CrossRef Full Text | Google Scholar

Sorai, M., and Saito, K. (2003). Alkyl chains acting as entropy reservoir in liquid crystalline materials. Chem. Rec. 3, 29–39. doi:10.1002/tcr.10046

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, K., Xiao, Z., Lu, S., Zajaczkowski, W., Pisula, W., Hanssen, E., et al. (2015). A molecular nematic liquid crystalline material for high-performance organic photovoltaics. Nat. Commun. 6, 6013. doi:10.1038/ncomms7013

PubMed Abstract | CrossRef Full Text | Google Scholar

Terasawa, N., Monobe, H., and Kiyohara, K. (2007). Mesomorphic properties of symmetrical and asymmetrical triphenylene homologues possessing fluoroalkylated side chains. Liq. Cryst. 34, 311–324.

CrossRef Full Text | Google Scholar

Terasawa, N., Monobe, H., Kiyohara, K., and Shimizu, Y. (2003). Fluorination effect of the peripheral chains on the mesomorphic properties in discotic liquid crystals of hexasubstituted triphenylene. Chem. Lett. 32, 214–215. doi:10.1246/cl.2003.214

CrossRef Full Text | Google Scholar

Tschierske, C. (2014). “Microsegregation in liquid crystalline systems: Basic concepts,” in Handbook of Liquid Crystals. Editors J. W. Goodby, P. J. Collings, T. Kato, C. Tschierske, H. Gleeson, and P. Raynes 2 (Weinheim, Germany: Wiley VCH), 5, 1–43. Chapter 1.

CrossRef Full Text | Google Scholar

Tschierske, C. (1998). Non-conventional liquid crystals—The importance of micro-segregation for self-organisation. J. Mater. Chem. 8, 1485–1508. doi:10.1039/a800946e

CrossRef Full Text | Google Scholar

Xiao, Y., Su, X., Sosa-Vargas, L., Lacaze, E., Heinrich, B., Donnio, B., et al. (2016). Chemical engineering of donor–acceptor liquid crystalline dyads and triads for the controlled nanostructuration of organic semiconductors. CrystEngComm 18, 4787–4798. doi:10.1111/j.1469-7580.2011.01469.x

CrossRef Full Text | Google Scholar

Zelcer, A., Donnio, B., Bourgogne, C., Cukiernik, F. D., and Guillon, D. (2007). Mesomorphism of hybrid siloxane-triphenylene star-shaped oligomers. Chem. Mater. 19, 1992–2006. doi:10.1021/cm062949b

CrossRef Full Text | Google Scholar