Abstract
Runoff has recently become the main source of mass loss from the Greenland Ice Sheet and is an important contributor to global sea level rise. Linking runoff to surface meltwater production is complex, as meltwater can be retained within the firn by refreezing or perennial liquid water storage. To constrain these uncertainties, the outputs of two offline snow/firn models of different complexity (IMAU-FDM and SNOWPACK) are compared to assess the sensitivity of meltwater retention to the model formulation (e.g., densification, irreducible water content, vertical resolution). Results indicate that model differences are largest in areas where firn aquifers form, i.e., particularly along the south-eastern margin of the ice sheet. The IMAU-FDM simulates higher densification rates for such climatic conditions and prescribes a lower irreducible water content than SNOWPACK. As a result, the model predicts substantially lower amounts of refreezing and liquid water storage. SNOWPACK performs better for this area, confirmed both by density profiles from firn cores and radar-inferred observations. Refreezing integrated over the entire ice sheet and averaged for the period 1960–2014 amounts to 216 Gt a−1 (IMAU-FDM) and 242 Gt a−1 (SNOWPACK), which is 41 and 46% of the total liquid water input (snowmelt and rainfall). The mean areal extents of perennial firn aquifers for 2010–2014 simulated by the models are 55,700 km2 (IMAU-FDM) and 90,200 km2 (SNOWPACK). Discrepancies between modeled firn profiles and observations emphasize the importance of processes currently not accounted for in most snow/firn models, such as vertical heterogeneous percolation, ponding of water on impermeable layers, lateral (sub-)surface water flow, and the issue of ill-constrained refreezing conditions at the base of firn aquifers.
1. Introduction
The Greenland Ice Sheet (GrIS) is the largest freshwater reservoir in the Northern Hemisphere and its complete deglaciation would cause a sea level rise of 7.4 m (Bamber et al., 2013). Studying the GrIS mass balance is important, since surface melt along the margins is rapidly increasing, and its current mass loss is more than double that of the Antarctic Ice Sheet (van den Broeke et al., 2016). Between 2000 and 2008, ice discharge and runoff contributed equally to the total mass loss of the GrIS (van den Broeke et al., 2009). In recent years (2009–2012), the relative contribution of meltwater runoff to total mass loss increased to 68% (Enderlin et al., 2014). It is likely that this trend will continue in the future, especially as progressively more outlet glaciers of the GrIS will lose contact with the ocean when the ice sheet retreats further inland (Goelzer et al., 2012).
Runoff is related to the amount of surface melt, which increased significantly in recent years (van Angelen et al., 2014). Primary causes of enhanced melting are atmospheric warming, which is further enhanced by polar amplification (Bekryaev et al., 2010), and the darkening of the ice sheet (van As et al., 2013). The darkening is caused by dust, glacial cyanobacteria, and algae (Wientjes et al., 2011; Yallop et al., 2012) and by snow grain growth (Tedesco et al., 2016). Expansion of the melt area is additionally amplified by the hypsometry of the ice sheet, with the surface slope decreasing toward higher elevations (Mikkelsen et al., 2016). However, the effect of increased surface meltwater on runoff is not straightforward, as meltwater can be retained within the firn due to refreezing and liquid water storage, or in supra- and subglacial hydrological systems (Livingstone et al., 2013). Understanding the short- and long-term effects of meltwater buffering is hence crucial for projecting future contributions of the GrIS to global sea level rise.
The surface of the GrIS can be divided into an ablation and accumulation area, separated at the equilibrium line altitude (ELA). Refreezing in the ablation area happens mainly at the beginning of the melt season, when meltwater percolates into the cold snowpack accumulated during the previous winter. This storage is however only temporary due to the negative annual surface mass balance (SMB). Still, refreezing delays the exposure of bare ice in the ablation zone (Reijmer et al., 2012) and hence reduces melt by maintaining a higher surface albedo. As soon as all available pore space in the snow is saturated, meltwater may laterally run off through an efficient drainage system (Smith et al., 2015) and accumulate in supraglacial lakes or drain into crevasses or moulins. The accumulation zone can be further divided into the dry snow and the percolation zone. The former is not affected by surface melt and/or rainfall and is hence irrelevant for liquid water retention. On the GrIS, this zone is vanishing, as e.g., in mid-July 2012, almost the entire ice sheet experienced surface melt (Nghiem et al., 2012; Bennartz et al., 2013). The percolation zone is demarcated by the dry snow line at its upper boundary and the ELA at its lower limit and it is divided in two parts by the runoff line. In the upper part, all melt is retained locally whereas a certain fraction of meltwater drains laterally into the lower part. These areas are of particular interest for studying refreezing processes as they may have the potential to buffer a considerable amount of meltwater (Harper et al., 2012).
Vertical meltwater percolation happens through a homogeneous wetting front (Colbeck, 1972) and/or through heterogeneous piping, where water (and latent energy) is efficiently transported to greater depth. Piping events seem to be linked to layer transitions (in terms of density or grain size) with ponding water conditions (Humphrey et al., 2012). A further important effect of refreezing is the formation of ice layers. Thick ice layers, with a vertical extent of up to several meters, may prevent meltwater from reaching greater depths and hence induce lateral runoff before all pore space is filled (Machguth et al., 2016). At the end of the melt season, low surface temperatures induce conductive heat loss in the firn and thereby refreeze liquid water that is held by capillary forces (irreducible water). At some locations however, refreezing is suppressed by high annual snowfall rates that isolate the liquid water from the cold winter atmosphere (Kuipers Munneke et al., 2014). These perennial water bodies are called firn aquifers and their abundance is particularly high along the south-eastern margin of the GrIS (Forster et al., 2014).
Many unknown factors, including current and future rates of rainfall (Doyle et al., 2015), remain in quantifying past, current and future refreezing on the GrIS. A study by Reijmer et al. (2012), where refreezing is compared between two regional climate models (RCMs) that explicitly simulate refreezing and different refreezing parameterizations, indicates that the RCMs agree reasonably well with respect to the amount of refreezing, whereas the parameterizations differ substantially. Currently, most models that simulate refreezing explicitly do not account for processes such as impermeable layers, vertical heterogeneous percolation (Hirashima et al., 2014; Avanzi et al., 2016) or lateral water movement within the firn (Cox et al., 2015). Uncertainty about the total amount of pore space in the firn for refreezing is also rather large: Harper et al. (2012) assume that all pore space is available for refreezing and that lateral runoff only occurs if the underlying firn is totally saturated. Machguth et al. (2016) however suggest that thick ice layers, which seem to form on large horizontal scales and after substantial surface melt, could render the underlying pore space unavailable for surface melt water, enhancing runoff. Furthermore, our lack of knowledge about sub- and englacial water storage introduces additional uncertainties in the amount of runoff predicted by climate models (Rennermalm et al., 2013; Smith et al., 2015). A study by Vernon et al. (2013) also highlights the importance of accurately modeling refreezing and indicates that the relatively good model agreement in terms of GrIS integrated SMB may be the result of regionally compensating errors.
In this study, we compare the results of two one-dimensional numerical snow/firn models of different complexity, with a special focus on refreezing and liquid water retention on the GrIS. Both models are forced with the most recent outputs of the regional atmospheric climate model RACMO2.3 (Noël et al., 2015). The primary goal is to assess the sensitivity of refreezing and liquid water storage to the model formulation. A more comprehensive understanding of these processes is highly relevant in estimating current and particularly future GrIS runoff amounts, which contribute substantially to the rise in global sea level. The following section provides an overview of the snow/firn models used, a description of the forcing and spin-up procedure, and a brief description of the observational data. Subsequently, the model's performance is assessed with density profiles from firn cores. Finally, the spatial and temporal patterns of refreezing, liquid water storage, and near-surface ice layers in the models are analyzed and discussed.
2. Models, methods, and data
The snow/firn models considered in this study are the IMAU-FDM (Ligtenberg et al., 2011) and SNOWPACK (Bartelt and Lehning, 2002; Lehning et al., 2002a,b). Both models are one-dimensional, i.e., there is no lateral exchange of mass and energy between neighboring grid cells, and they are formulated in a Lagrangian framework, in which the coordinate system moves vertically with the ice matrix. The largest difference between the models concerns the densification scheme, the amount of irreducible water content, the vertical resolution and the general complexity.
2.1. IMAU-FDM
The IMAU-FDM was developed for interactive coupling to an RCM to simulate firn on polar ice sheets (Ligtenberg et al., 2011). It contains a semi-empirical scheme to compute dry firn densification (Arthern et al., 2010):
Equation (1) contains a calibration factor (Mo), which is specifically derived for the GrIS and depends on annual mean accumulation (Kuipers Munneke et al., 2015). Here, ρ is the firn density and ρi the density of ice, t is time, ḃ is the mean annual accumulation over a reference period, g is the gravitational acceleration, C is a coefficient depending on density, T is the instantaneous local firn temperature and Tav the mean annual temperature at the surface, Ec and Eg are the activation energies for self-diffusion of water molecules through the ice lattice and for grain growth, and R is the ideal gas constant. The model time step depends on the occurrence of melt and is reduced from 3600 s (dry snow) to 300 s (wet snow) to capture vertical water percolation more accurately. Heat conduction (k) through the snow/firn is computed as (Anderson, 1976):
The specific heat capacity of ice is computed as a function of temperature. The vertical water percolation is simulated with a bucket scheme where melt water runs through all layers within one model time step and water is retained as ice or liquid water based on the availability of pore space and cold content. The irreducible water content is set to a relatively low value of 2% of the pore volume to mimic processes that allow an effective vertical water transport to lower layers, such as piping (Greuell and Konzelmann, 1994; Reijmer et al., 2012). Layer merging and splitting is constrained to the upmost layer of the model. If the upper layer thickness exceeds 0.2 m due to a positive SMB (snowfall, sublimation, snow drift), the layer is split into two equal parts. If the layer thickness is reduced to below 0.1 m due to a negative SMB (sublimation, snowdrift, melt), the layer is merged with the one below.
2.2. Snowpack
SNOWPACK, a state-of-the-art snow model, was originally designed to model seasonal snow cover in alpine areas and as a tool to study avalanche formation and snow hydrology. Recently, it has also been successfully applied to polar regions (Dadic et al., 2008; Groot Zwaaftink et al., 2013; Van Tricht et al., 2016). SNOWPACK simulates microstructural snow properties such as grain size, bond size, dendricity, and sphericity and links these quantities to thermal and mechanical snow properties. Densification of snow is calculated by combining the constitutive relation for snow (Lehning et al., 2002b): with the definition of strain rate (): to yield:
L is thereby the thickness of a snow layer, σs the overburden pressure and ηs the viscosity of snow. The viscosity is a function of microstructural snow properties, temperature, overburden pressure, and liquid water content (the presence of liquid water decreases viscosity) and can be computed for temperatures ranging from -80° to 0°C (Groot Zwaaftink et al., 2013). Close to the surface, SNOWPACK considers the influence of wind speed on snow compaction. A formulation simulating an enhanced impact of wind speed on near-surface snow compaction, which was implemented for Antarctic experiments (Groot Zwaaftink et al., 2013), is not used, as the fresh snow density scheme (Equation 6) is already calibrated to yield snow densities valid for the topmost couple of centimeters on the GrIS. Thermal conductivity is computed as a function of (I) conduction through ice, pore space, and liquid water and (II) latent heat transport, which is induced by a water vapor gradient. Additionally, the effect of wind pumping is considered by linking the thermal conductivity near the surface to the vertical wind velocity gradient in the snow. Above a volumetric ice content of 0.55, a simpler formulation is used where the effective conduction is the sum of conduction through ice, water, and air. In the version we use, vertical water transport can be simulated by the bucket scheme or by the Richards equation. In contrast to the bucket scheme, Richards equation solves explicitly for the balance between capillary suction and gravity (Wever et al., 2014). Recently, a scheme for simulating preferential flow was implemented (Wever et al., 2016), but this version has not yet been applied to Greenland. For this study, the bucket scheme is chosen to enable a direct comparison with the IMAU-FDM and because this scheme is computationally less demanding. The irreducible water content is computed as a function of snow density (Coléou and Lesaffre, 1998; Wever et al., 2014) and is limited to a maximum volumetric value of 8%. This value is based on an expert judgment on maximal water retention by capillary suction.
Layer merging and splitting criteria are checked for every layer in SNOWPACK. Splitting ensures a sufficient near-surface resolution to capture small-scale temperature and moisture gradients. Merging depends on a threshold for thickness, which is a linear function of depth, and the similarity of layer properties (volumetric contents and microstructural properties). The reduction of layers by merging is necessary to limit the computational demand of the model. SNOWPACK runs, in contrast to the default value of 900 s, with a time step of 1800 s to increase computational efficiency. Sensitivity experiments with the larger time step confirmed the numerical stability and revealed no significant deviation in the output compared to a run with the default time step. The intermittent use of a smaller time step (300 s) for the IMAU-FDM is possible due to the model's lower computational demand. Minor modifications are introduced to the model to use it for the GrIS and to allow a direct comparison with the IMAU-FDM:
A SMB forcing mode is implemented to drive the model with SMB-components instead of meteorological observations (see subsection Model Forcing and Spin-up). The internal energy balance scheme of SNOWPACK is hence switched off. This ensures equal SMB fluxes (including melt amounts) for both models.
The density of the uppermost element is kept constant during sublimation, snowdrift and melt.
The layer merging thresholds for sphericity, grain size, and volumetric ice content are no longer constants but functions of depth. The thresholds for sphericity and grain size start to linearly increase from a depth of 10 m and the threshold for volumetric ice content from a depth of 50 m. The resulting decrease in vertical resolution at greater depth is necessary to keep the number of layers in a computationally reasonable range.
The IMAU-FDM approach of dealing with layers that are depleted of pore space but contain both ice and liquid water is adapted. For such layers, additional compaction leads to a decrease in the liquid water content of the layer until the density of ice is reached. The excess water is moved to the subjacent layer.
To improve the agreement with observations, the tunable factors in the snow viscosity scheme (Groot Zwaaftink et al., 2013) for the activation energy of snow Qs and the critical exponent β are set to 16,080 J mol−1 and 0.3, respectively.
2.3. Model forcing and spin-up
Both models are forced at the upper boundary with output from the regional atmospheric climate model RACMO2.3. This model is specifically adapted to simulate climate conditions over ice sheets and contains a multilayer snow model, physically identical to the IMAU-FDM but with fewer vertical layers, an albedo scheme based on prognostic snow grain size (Kuipers Munneke et al., 2011) and a drifting snow routine (Lenaerts et al., 2012). RACMO2.3 was run for the period 1958–2015 on an 11 km horizontal resolution grid and a domain including Greenland, Iceland, Svalbard, and part of arctic Canada. Evaluations of RACMO2.3 indicate that the model is capable of realistically simulating present-day surface characteristics on the GrIS and that it improves upon previous RACMO versions (Noël et al., 2015).
Three-hourly time series of RACMO2.3 cumulative snowfall, rainfall, evaporation/sublimation, snowdrift erosion/deposition, surface melt, and instantaneous skin temperature are used to force both models. Applying the same boundary conditions to both models allows an objective comparison of the internal processes. A minor difference in the forcing concerns sublimation and evaporation. In the IMAU-FDM, the sum of these mass fluxes is exclusively treated as sublimation. In SNOWPACK, deposition depends on the skin temperature, where ice is added at skin temperatures below 0°C and water under melting conditions. When mass is removed, all liquid water is removed before sublimating the ice matrix. The forcing data are linearly interpolated to the model time step. By using three-hourly data, the diurnal temperature cycle is reasonably well captured—a relevant process for near-surface refreezing. The heat equation is solved with a Dirichlet boundary condition at the top (skin temperature) and a Neumann condition at the bottom (zero heat flux) in both models. A further required boundary condition is the fresh snow density. For this study, a simple parameterization is used where fresh snow density (ρ0) is related to the mean annual surface temperature (Tav) (Kuipers Munneke et al., 2015):
Both models are run on the RACMO2.3 spatial grid and ice mask (Figure 1). However, to decrease computational time, the models are run on a checkerboard grid in the interior of the ice sheet, i.e., only every second RACMO2.3 cell is simulated. Within approximately 40 km of the ice sheet margins, all grid cells are run to resolve the greater climate gradients.
Figure 1

Map of Greenland with ratio of liquid to solid surface mass input (Rliq/sol) averaged over 1960–2014 for the RACMO2.3 ice mask. Additionally, the 8 drainage basins, the location of the firn cores (gray) and the transect (red) used in this study are shown. Firn cores that are discussed in detail are labeled.
A spin-up for both snow/firn models is conducted to initialize the models with reasonable firn profiles in 1960. In accordance with Kuipers Munneke et al. (2015), we assume that a 20-year reference period (1 January 1960–31 December 1979) is representative for the pre-1960 climate. The spin-up for an individual location is performed by iterating over the reference period for an appropriate number of times (niter) to refresh the entire firn layer. Due to the individual densification schemes of the models (Equations 1, 5), niter is determined differently for the IMAU-FDM and SNOWPACK:
IMAU-FDM: A steady-state solution of Equation (1) can be computed (Ligtenberg et al., 2011) and applied to the reference period. This yields an approximation of the firn thickness for each location and allows the calculation of niter together with the surface mass flux over the reference period. For locations with a negative SMB, niter is set to 2 to initialize a reasonable winter snow cover over bare ice.
SNOWPACK: Equation (5) does not allow the derivation of a steady-state solution and hence another spin-up strategy is adopted. It is assumed that the firn layer at each location is entirely refreshed after accumulating 70 m water equivalent of solid input. Combining this assumption with the surface solid mass flux over the reference period yields niter for each location. To decrease computational time, niter is limited to 2 for locations with a liquid (snowmelt, rainfall) to solid (snowfall, sublimation, snowdrift) surface mass input ratio (Rliq/sol) higher than 2.5. These locations are situated in the ablation zone where only seasonal snow but no firn is present. An analysis of the density profiles obtained by the spin-up confirmed that all niter-values were selected sufficiently large to refresh the firn layer at each location.
The spin-up in both models is initialized with firn density profiles computed with the steady-state solution of Equation (1) and with vertically constant temperatures that are equal to the average surface temperature over the reference period. These temperatures are additionally corrected for latent heat release by refreezing according to Reeh (2008).
2.4. Observational data
All firn cores, except the one for location FA13 (Figure 1), are taken from the data set compiled by Kuipers Munneke et al. (2015). Density values of these profiles are usually calculated over a vertical distance of 0.5–2 m, hence the data of these cores do not capture thin layer variations such as ice lenses. The core used for location FA13 is described in Koenig et al. (2014). Evaluation of the models with firn cores is performed by selecting the closest grid cell and available time step of the models. The locations of all firn cores are shown in Figure 1. We also use data from airborne radar, which was on board the NASA Operation IceBridge (OIB) aircraft spring campaigns between 2010 and 2014 before the onset of surface-melt (Miège et al., 2016). The data are used to evaluate the horizontal extent of firn aquifers and ice layers simulated by the two numerical models. The Accumulation Radar was built and is operated by the Center for Remote Sensing of Ice Sheets (CReSIS) at the University of Kansas to image near-surface (up to approximately 400 m depth) internal structure of the ice sheet with a 65 cm vertical resolution (Rodriguez-Morales et al., 2014). The Accumulation Radar is well suited to image the presence of a water table in the firn characterized by a bright reflector in the radar images (Forster et al., 2014; Miège et al., 2016).
2.5. Model output processing
Both models provide time series and vertically resolved data for each grid cell. The vertically resolved data are first mass-conservatively resampled to a common grid. Subsequently, these data and the time series are bilinearly interpolated from the checkerboard grid to the full ice mask. Temporal resampling is either done mass-conservatively for flux quantities or with linear interpolation for the remaining data.
3. Results and discussion
3.1. Evaluation of models with vertical density profiles
A summary of the model performances in simulating average firn density in the topmost 30 m is shown in Figure 2, with the colors indicating the ratio of liquid to solid mass input at the surface (Rliq/sol). Generally, the skills are comparable, with both models overestimating density in regions with relatively high amounts of liquid water input. It is important to note that the firn core samples shown in Figure 2 do not capture all occurring surface conditions on the GrIS, with some regions being rather over- or underrepresented. Despite the similar patterns shown in Figure 2, there are some notable differences, which are subsequently addressed by means of selected firn cores in Figure 3. First of all, the IMAU-FDM shows a better agreement with observed profiles for locations with low Rliq/sol-values where SNOWPACK exhibits a larger scattering with mean densities being typically slightly underestimated. The lower scattering in the IMAU-FDM can be explained by the tuning of the model's densification scheme with these cores. Density biases in SNOWPACK, particularly at greater depth, are likely related to the fact that its densification scheme was developed for alpine snow cover (Lehning et al., 2002b). Seasonal snow has a relatively short lifetime and hence overburden pressures that occur on an ice sheet are never reached. Relevant processes for the later densification stages are therefore likely not fully incorporated in the densification scheme. SNOWPACK overestimates near-surface densities for the firn cores with the lowest mean annual surface temperatures (<−28°C), which are located in the north-eastern part of the GrIS. For locations with temperatures between −26° and −28°C, near-surface density is generally in line with observations (Figure 3A), whereas for higher temperatures, SNOWPACK tends to underestimate near-surface densities (Figure 3B).
Figure 2
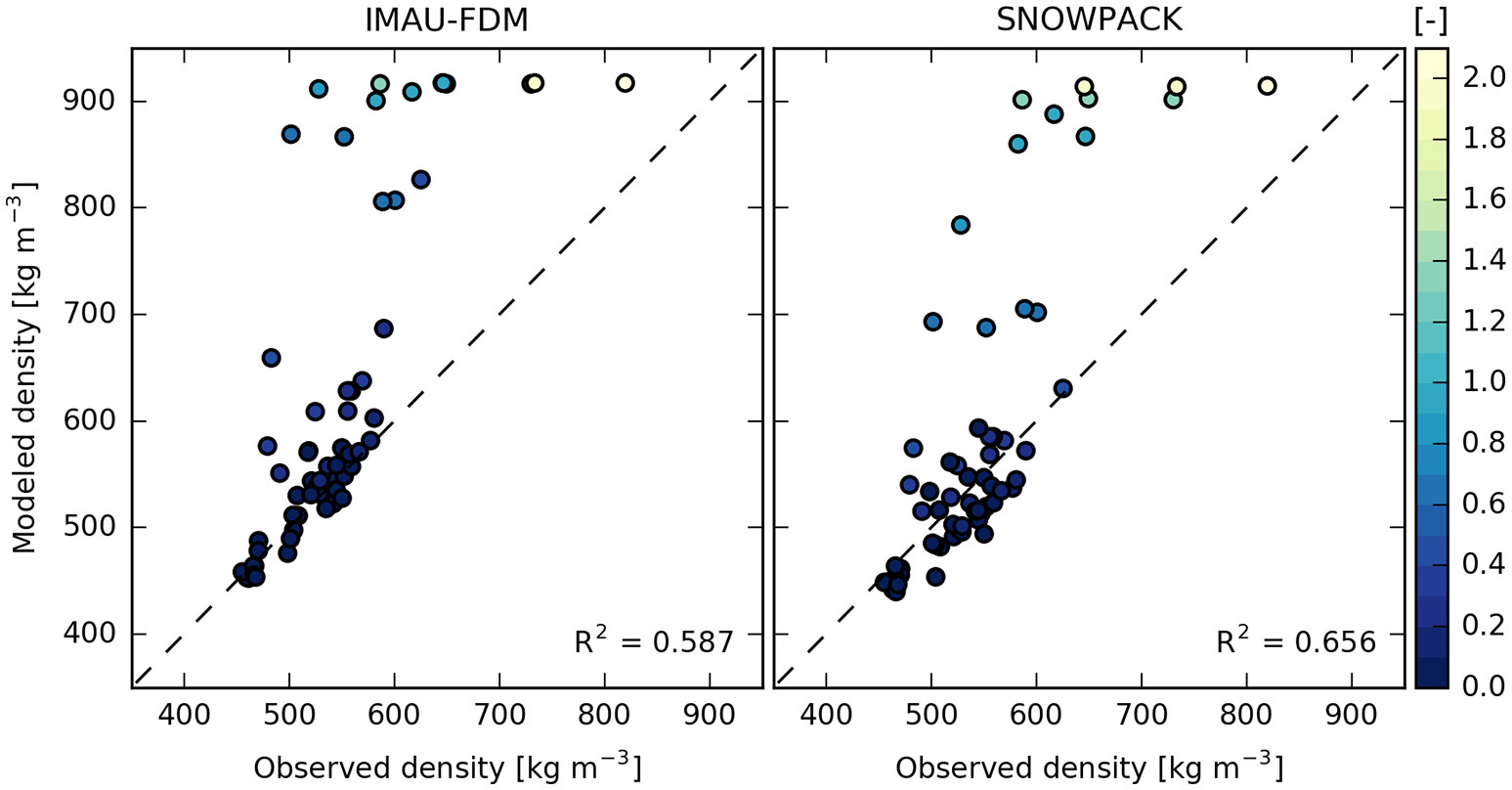
Modeled vs. observed average firn density of the topmost 30 m. Colors indicate the ratio of liquid to solid surface mass input (Rliq/sol). Note that some shallow firn cores do not extend down to 30 m and hence only the available part is considered.
Figure 3
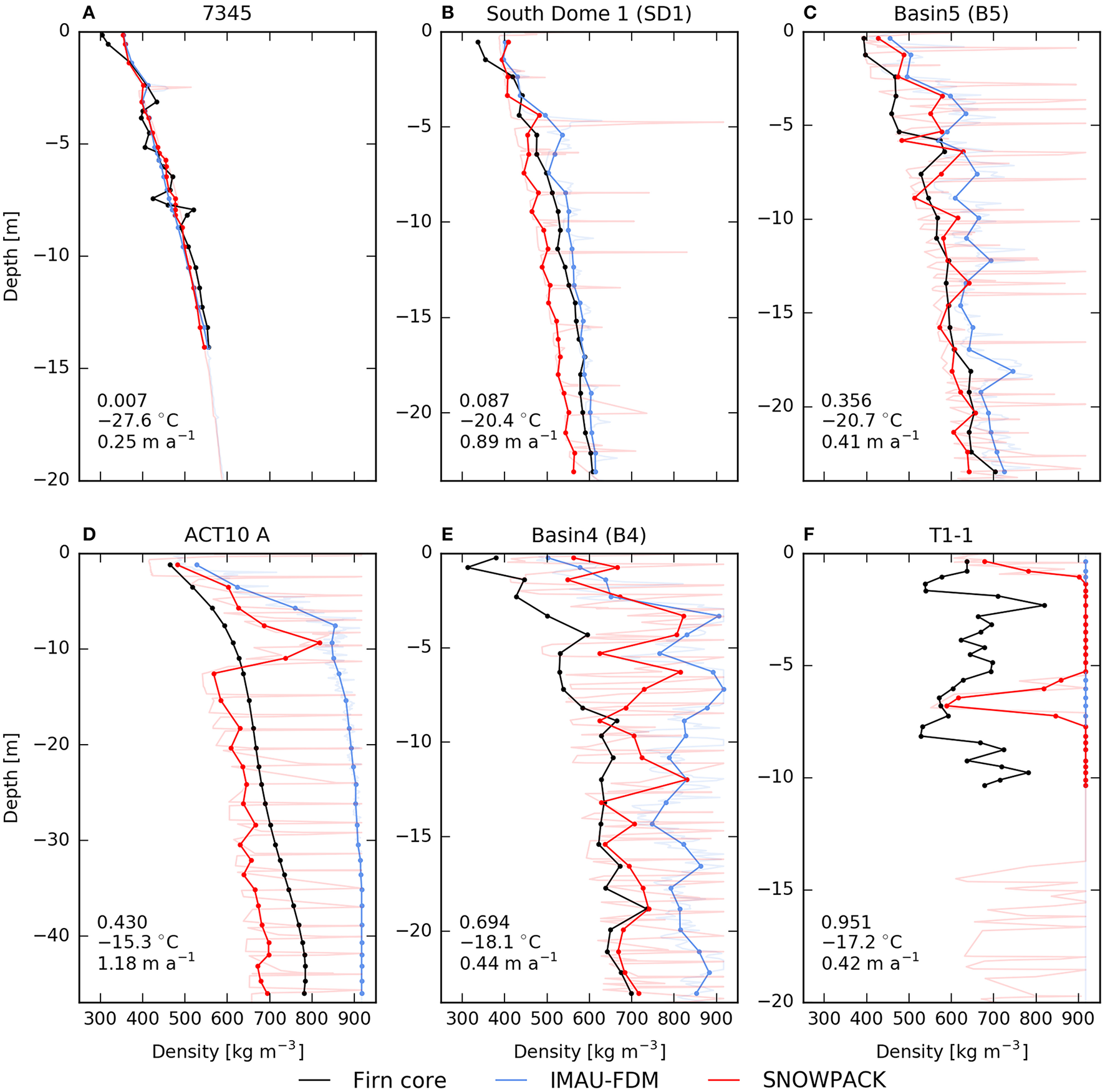
Observed (black) and modeled (IMAU-FDM: blue, SNOWPACK: red) firn density profiles for 6 locations from different surface climate zones (A–F). The numbers in the lower left corner state the ratio of liquid to solid surface mass input (Rliq/sol), the mean annual surface temperature and the mean annual solid accumulation. The shaded profiles are model outputs at native vertical resolution whereas the thick lines represent profiles resampled to the vertical resolution of the firn cores.
For locations with Rliq/sol-values larger than approximately 0.2, the IMAU-FDM reveals a positive bias in mean density where SNOWPACK indicates a better agreement (Figure 3C and following Figures). The simulation of surface melt-freeze crusts and ice layers in SNOWPACK, which occurs at locations with considerable amounts of surface melt is addressed in subsection Formation of Ice Layers. Location ACT10 A (Figure 3D) has a relatively high mean annual surface temperature and accumulation rate and is located relatively close to observed firn aquifers. At this site, the IMAU-FDM reveals a particularly pronounced density overestimation whereas SNOWPACK is in better agreement with the observed density. The high-density spike around 10 m depth in the SNOWPACK profile is caused by a recent (around 2005) increase in liquid surface input and subsequent refreezing. Its absence in the observed density profile suggests an underestimation of vertical water transport in SNOWPACK, which does not account for vertical heterogeneous percolation in the used version. The relevance of the mismatch between the models under these climate conditions will be further discussed in subsection Perennial Firn Aquifers.
For locations with even higher Rliq/sol-values (>0.6), both models consistently overestimate mean density (Figures 3E,F), but SNOWPACK exhibits a lower bias. For relatively high Rliq/sol-values (close to 1 and above), the IMAU-FDM generally simulates bare ice profiles. As discussed in Kuipers Munneke et al. (2015), the overestimated density at high-melt locations could be caused by inaccurate atmospheric forcing, i.e., too much refreezing caused by an overestimation of surface melt or too little pore space caused by an underestimation of accumulation. Alternatively, errors in the snow/firn models could be responsible for this density bias due to an overestimation of refreezing caused by underestimating vertical water flow or ignoring lateral runoff due to impermeable ice layers. However, it seems likely that the IMAU-FDM overestimates densification rates for such locations as SNOWPACK still simulates available pore space for locations with an Rliq/sol-value close to 1 (Figure 3F). The pore space in the upper part of this density profile was recently filled with refreezing meltwater, where the low density spike at around 7 m depth was caused by an intermediate period with a lower Rliq/sol-value. This mismatch between the modeled and observed density may suggest again an underestimation of vertical water transport in SNOWPACK or points to the inability of the model to allow for lateral runoff at the surface.
Finally, a bias in fresh snow density could also contribute to density overestimations. This is supported by the fact that the uppermost measured firn densities are lower than values simulated by both models for the majority of the locations (not shown). Compared to other parameterizations [e.g., Groot Zwaaftink et al. (2013)], the fresh snow density formulation used in this study indeed predicts rather high values (between 320 and 480 kg m−3). However, it is challenging to formulate an accurate and robust parameterization due to the numerous influencing factors (temperature, wind speed, humidity) and the sparse availability of observational data for the GrIS when it comes to real surface density, instead of the average over the first tens of centimeters.
3.2. Refreezing and runoff
The mean spatial refreezing patterns of both models are similar (Figure 4), although the absolute magnitude differs significantly in some regions. In the northern and north-eastern part of the GrIS (basins 1 and 2), basin-integrated amounts of refreezing are slightly higher in the IMAU-FDM. This can be explained by lower refreezing amounts in SNOWPACK in the ablation zone and for some regions close to the ELA (Figures 5A,B). The model difference in the ablation zone is caused by two factors: (I) in SNOWPACK, part of the surface melt evaporates whereas in the IMAU-FDM, a latent-heat flux is always linked to a mass change of the ice matrix and (II) a combined effect of model differences in vertical resolution and merging of summer snowfall into subjacent ice layers. In contrast to SNOWPACK, merging in the IMAU-FDM is performed regardless of differences in layer properties. Hence, snowfall is merged into subjacent ice layers, which results in comparably thick surface layers (approximately 0.1 m) with pore space available for liquid water retention and refreezing. During subsequent surface melt, this void space remains available longer than in SNOWPACK. The difference close to the ELA is caused by SNOWPACK simulating higher mean densities in the upmost 20 m. This leads to less available pore space for refreezing during the melt season. SNOWPACK therefore also predicts higher runoff amounts for these two basins (Figures 6D–F).
Figure 4
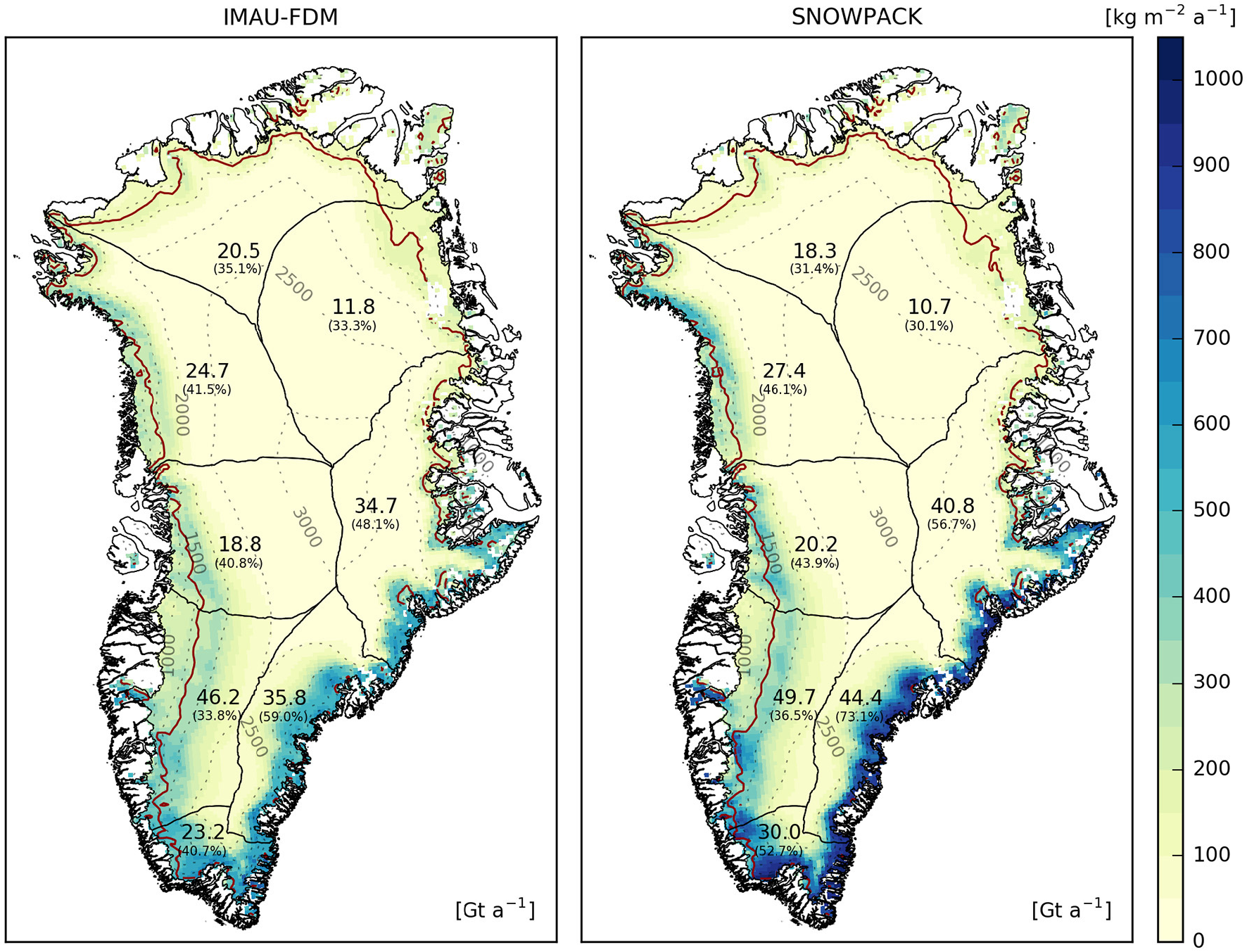
Refreezing amounts averaged over the years 1960–2014 for both models. The red line marks the ELA derived with SMB components from RACMO2.3 but runoff is taken from the respective snow/firn model. Numbers provided in the drainage basins represent basin-integrated values of refreezing. The values in brackets express refreezing as a fraction of liquid surface mass input (melt and rainfall).
Figure 5

Difference (SNOWPACK–IMAU-FDM) in monthly refreezing amounts for June (A), July (B), and August (C) averaged over the years 1960–2014. The blue (IMAU-FDM) and red (SNOWPACK) lines mark the ELA derived with SMB components from RACMO2.3 but with runoff taken from the respective snow/firn model.
Figure 6

Mean (1960–2014) seasonal cycle of refreezing (A–C) and runoff (D–F) for the 8 GrIS drainage basins and the two models. The right column represents the difference of these two variables between the models.
Refreezing in the three basins on the eastern, south-eastern, and southern GrIS (basins 3–5) is substantially larger (approximately 18–29%) in SNOWPACK. In early June, the discrepancy is small because both models provide mostly enough pore space and cold content to refreeze percolating meltwater. In July, when surface snowmelt amounts peak, SNOWPACK simulates considerably higher refreezing values (Figure 5B). In both models, near-surface firn in the vicinity of the ice sheet margins is temperate at this time, hence the difference is mainly caused by the higher irreducible water content and vertical resolution in SNOWPACK, which leads to more near-surface refreezing due to diurnal temperature variations (Figures 6A,B). For all three basins, the difference in refreezing peaks in late July or early August with a decay toward autumn (Figure 6C). This decaying difference is caused by the higher amounts of irreducible water in SNOWPACK, which refreeze in autumn when firn temperatures steadily decrease. Runoff generation is thus persistently smaller for basins 3–5 compared to the IMAU-FDM (Figures 6D–F).
For basins 6–8, SNOWPACK simulates slightly higher mean area-integrated refreezing values. These higher values are primarily restricted to the accumulation zone. There, deeper firn temperatures are well below 0°C in both models, and SNOWPACK simulates layers with porous firn, in contrast to the IMAU-FDM. This void space is subsequently filled with percolating meltwater that refreezes, particularly during the last decade of the simulation period when liquid mass input at the surface increases significantly. In the ablation area, refreezing is generally lower in SNOWPACK; especially in August (Figure 5C). Hence runoff in SNOWPACK is lower for these basins at the beginning of the melt season but this pattern reverses in August when the refreezing difference in the ablation zone starts to dominate. The reason behind the generally lower amounts of refreezing in SNOWPACK in the ablation zone is the same as for basins 1 and 2. Mean annual GrIS integrated values of refreezing are 216 Gt a−1 (123 mm w.e. a−1) for the IMAU-FDM and 242 Gt a−1 (138 mm w.e. a−1) for SNOWPACK, respectively. Reijmer et al. (2012) found refreezing values for the GrIS in the range of 54–151 mm w.e. a−1 averaged over the period 1958–2008; depending on the RCM, refreezing parameterization, and ice mask used. The values obtained in this study are comparable but in the higher part of the range; particularly the one simulated by SNOWPACK.
3.3. Perennial firn aquifers
In this study, perennial firn aquifers are defined as liquid water bodies in the firn that persist throughout the winter. Observed firn aquifers on the GrIS normally reveal saturated conditions, i.e., the entire pore space is filled with liquid water (Forster et al., 2014; Koenig et al., 2014). The models applied in this study are however not capable of simulating such conditions in the used configuration, because ponding of liquid water within the firn is not allowed. To compare observed and modeled firn aquifer locations, we therefore apply the term perennial firn aquifer to both saturated and unsaturated conditions.
Both models simulate firn aquifers, but there are significant differences in the horizontal extent and the stored liquid water mass (Figure 7). Apart from the south-eastern GrIS, SNOWPACK produces extensive firn aquifers on the southern tip of the GrIS, along the north-western edge, and on Sukkertoppen ice cap. The IMAU-FDM fails to predict significant firn aquifers in the northwest and the general amount of liquid water stored is small compared to SNOWPACK. Comparing the spatial occurrence of firn aquifers in the models with radar-derived locations (Miège et al., 2016) indicates a good agreement; particularly for SNOWPACK (Table 1). Compared to this version of the IMAU-FDM, the previous better agreement of RACMO2.1 data with firn aquifer observations (Forster et al., 2014) can be attributed to a different densification scheme, as described by Reijmer et al. (2012). By comparing radar-inferred with modeled data, it is important to remember that observations indicate detections of water tables (saturated conditions) whereas the models show the occurrence of perennial liquid water without pore space saturation. The models' (particularly SNOWPACK's) apparent overestimation of the firn aquifer's horizontal extent downstream of the mapped locations may be explained by: (I) crevasses that evacuate stored liquid water and prevent the realization of a water table, (II) complex bedrock topography, which is not captured by the model's horizontal resolution and hinders the formation of firn aquifers, and (III) flight tracks not covering the entire area near the ice margin. The IMAU-FDM also indicates some areal overestimation upstream of the mapped locations, especially along the south-eastern margin (inset panel Figure 7A). This is caused by near-surface temperate firn conditions. In SNOWPACK, densification rates are lower, implying stronger downward advection of cold winter snowfall and hence cold conditions where all percolating meltwater refreezes. SNOWPACK indicates some areal overestimation on the western GrIS. Generally, these amounts of stored liquid water are rather small (<200 kg m−2) and hence likely below the detection limit of the radar (Miège et al., 2016). Some isolated locations of radar-inferred firn aquifers are not captured by both models. This might be due to errors in RACMO2.3 forcing or the horizontal resolution of the models being too coarse to resolve small-scale climatic conditions required for firn aquifer formation.
Figure 7

Vertically integrated liquid water content averaged over April (2010–2014) before the onset of the melt season for IMAU-FDM (A) and SNOWPACK (B). Numbers provided in the drainage basins represent basin-integrated values of liquid water mass. Black dots mark the position of radar-derived firn aquifers from Operation IceBridge Accumulation Radar flights 2010–2014 (Miège et al., 2016). The sub-panels in the lower right corner show a zoom-in of the south-eastern margin of the GrIS. Note the different color scales for both panels.
Table 1
| IMAU-FDM | SNOWPACK | |||
|---|---|---|---|---|
| Area | Extent | km2 | 55,700 | 90,200 |
| (liquid water >200 kg m–2) | (0) | (60,900) | ||
| Coverage of observed | – | 48.2% | 67.7% | |
| firn aquifers by models | ||||
| Liquid mass | Irreducible water | Gt | 0.8 | 75.8 |
| Pore space saturation | Gt | 44.5 | 299.7 | |
| Observational constrained | Gt | 22.7 | 158.2 | |
| pore space saturation |
Modeled firn aquifer characteristics averaged over April (2010–2014) before the onset of the melt season.
Storage amounts assuming pore space saturation are derived by adding model runoff to void pore space of wet layers until full saturation is established. The observational constrained values are derived by limiting the areal extent of firn aquifers by radar-derived observations.
To account for the models' inability to allow for saturation of pore volume by liquid water, estimates of water storage considering saturation are provided, which form an upper boundary for the stored mass (Table 1). However, these estimates are likely too high, because no water tables were detected for large areas in the vicinity of the ice sheet margin where both models simulate firn aquifers (inset panels Figure 7). As mentioned, this is most likely related to the presence of crevasses and/or complex bedrock topography. To address this issue, observation-constrained storage volumes are derived where water saturation is only computed for grid boxes where firn aquifers have been observed. The corrected storage amounts are 22.7 Gt for the IMAU-FDM and 158.2 Gt for SNOWPACK, respectively. The value simulated by SNOWPACK is in the same range as an earlier derived estimate of 140 ± 20 Gt for 2013 (Koenig et al., 2014).
The large difference in the amount of liquid water stored in both models can be attributed to two factors: (I) densification rates in areas with substantial amounts of refreezing are considerably higher in the IMAU-FDM (Figure 3D) and (II) the irreducible water content, which is larger in SNOWPACK. The first factor is related to applying Equation (1) to areas where refreezing causes a considerable amount of latent heat release within the firn. This equation is derived by approximating the local temperature with the mean annual surface temperature (Arthern et al., 2010) and hence likely overestimates densification rates for locations where the vertically averaged firn temperature significantly exceeds the mean annual surface temperature. This was confirmed by experiments where the steady-state solutions of Equation (1) was applied to firn aquifer areas with varying Tav. The comparably high densification rates in the IMAU-FDM result in a shallow firn layer whose vertical extent is often too small to insulate liquid water from the cold winter surface temperatures. If the vertical extent is large enough, the storage capacity is still lower compared to SNOWPACK due to the smaller irreducible water content. The issue of firn aquifers forming in the IMAU-FDM at too shallow depths was also discussed by Kuipers Munneke et al. (2014) and the deficiency of modeling vertical preferential flow was mentioned as a possible explanation. It seems however that the overestimation of densification rates in the IMAU-FDM in these areas also largely contributes to this bias. Additionally, firn aquifer formation in SNOWPACK is favored by the near-surface thermal conductivity. In winter, mean snow densities over the topmost couple of meters are lower than in the IMAU-FDM, implying lower values of heat conduction and hence less heat loss to the atmosphere. During the melt season, thermal conductivity in SNOWPACK is larger than in the IMAU-FDM because it is a function of the liquid water content, which is additionally higher in SNOWPACK.
A more in-depth validation of the models based on in-situ data is possible for location FA13, where a firn core was extracted in April 2013 (Koenig et al., 2014). As mentioned above, the high densification rate in the IMAU-FDM results in a density profile reaching bare ice already at a depth of approximately 5 m (Figure 8D). In this model, the formation of a perennial firn aquifer is thus not possible, as the overlaying snow/firn is not thick enough to insulate the seasonally occurring liquid water from refreezing in winter. As a result, a relatively constant amount of surface melt is refrozen in the IMAU-FDM and the excess water is running off (Figure 8C). SNOWPACK on the other hand simulates the formation of a perennial firn aquifer. At the start of the simulation period, the firn column is cold (not shown) and provides enough pore space to refreeze all surface melt (Figures 8A,C). In other words, the Rliq/sol-value is not high enough for a firn aquifer to form. Towards the end of the simulation period, this value increases until a firn aquifer appears in the warm summer of 2010 (Figure 8B). Comparing this modeled aquifer with the in-situ observation of April 2013 yields a reasonable agreement in terms of vertical liquid water extent; especially the depth of the water table is accurately simulated (within approximately 2 m; Figure 8D). Evaluating the density profile of SNOWPACK indicates two major discrepancies: First of all, the model reveals a positive density bias in the uppermost 12 m. The temporal evolution of volumetric ice content (Figure 8A) shows that density recently increased due to enhanced refreezing caused by an increase in the surface liquid input (Figure 8C). This positive density bias might suggest that near-surface refreezing is overestimated in SNOWPACK. In nature, part of the liquid water that refreezes in the model may percolate into the subjacent firn aquifer, a process that would also explain the mismatch in the vertical extent of the modeled and observed aquifer. Position FA13 therefore appears to be an interesting location to test a heterogeneous water percolation scheme. Secondly, SNOWPACK seems to underestimate density in the deeper part of the core. This could be linked to the densification scheme underestimating compaction rates at high overburden pressure and/or the underestimation of the influence of liquid water on snow viscosity.
Figure 8

Firn evolution between 1960 and 2014 for the modeled grid cell where firn core FA13 (39.04° W, 66.18° N, 1563 m a.s.l.) was extracted. The panels on the left show the temporal evolution of the volumetric ice (A) and water content (B) and the mass fluxes (C). The panel on the right (D) shows the density profiles of the models at the time when the firn core was retrieved. The shaded area indicates the range of dry (only ice matrix) and wet (ice matrix with liquid water) firn density.
Modeling firn aquifers with the current, one-dimensional column models and model settings remains challenging for several reasons: First of all, both models only allow for irreducible amounts of water in the firn without considering full saturation due to water ponding on impermeable layers. However, implementing this feature without allowance for subsurface lateral water flow would likely lead to complete saturation of all available pore space at some locations, with the water table raising above the firn surface. Secondly, the implemented approach of compacting layers that are depleted of pore space and contain both ice and liquid water needs more detailed consideration. In our simulations, mean firn temperatures below aquifers are mostly at the melting point as a result of the initial firn temperature and the lower boundary condition for the heat equation (zero heat flux). Hence, the implemented approach prevents the continuous accumulation of liquid water at greater depth in temperate firn. In reality, it is likely that part of this liquid water refreezes as superimposed ice due to sub-zero temperatures either caused by cold initial firn/ice or a downward-directed heat flux at the bottom of the model domain. However, these thermodynamic conditions, which co-determine the lower boundary of firn aquifers, are poorly known. Thirdly, there are indications that the bucket scheme, at least when used in combination with the irreducible water formulation by Coléou and Lesaffre (1998), is not able to transport water efficiently enough to greater depths; hence an improved model should also allow for preferential water flow.
3.4. Formation of ice layers
Figures 3B–F show that, when surface melt rates are sufficiently high, SNOWPACK simulates thin annual melt-freeze crusts or ice lenses at the surface that are subsequently buried under winter accumulation. These high-density layers are not simulated by the IMAU-FDM due to its coarser vertical resolution and less discriminating layer merging scheme. Modeling such sharp layer transitions is important because their occurrence has been linked to meltwater ponding and subsequent piping events (Marsh and Woo, 1984; Humphrey et al., 2012). However, SNOWPACK likely overestimates the density of such layers with the SMB forcing mode, which was implemented to force both models with the same mass fluxes at the upper boundary. In alpine conditions, SNOWPACK only generates melt-freeze crusts but not actual ice layers at the surface during the melt season. Tests with running SNOWPACK in the default mode generally reduce the formation of these high density layers because the subsurface temperature profile is allowed to exceed the melting point after solving the heat equation, which induces melt in several layers. In the implemented SMB forcing mode however, melt is applied by subsequently and completely melting layers from the top downwards (equal to the IMAU-FDM). This mode enhances the formation of surface ice layers at locations that experience periodic amounts of melt, for instance the day-night-cycle, and could hence be considered a model artifact. On the other hand, there are physical interpretations that support the formation of surface ice lenses in polar conditions as (I) the snowpack is generally cooler than the seasonal snowpack (higher refreezing capacity), (II) the surface energy loss due to longwave radiative cooling at elevated surfaces is larger, and (III) the daily melt cycles are more regular and persistent. Thin ice layers are also found in firn cores (Machguth et al., 2016), however there are indications that such layers also form below the surface due to meltwater percolation (Humphrey et al., 2012). In the current SNOWPACK configuration, the model is relatively insensitive to thin, high-density layers as the vertical water transport is simulated by the bucket scheme. Using more complex schemes such as the recently implemented preferential flow scheme (Wever et al., 2016), which allows downward water percolation in sub-freezing snow and is sensitive to marked layer transitions, would require a more detailed study of this feature. A GrIS-wide evaluation of this phenomenon is currently difficult due to the limited availability of firn cores with high vertical resolution.
Thicker ice layers, with a vertical extent of several meters, are simulated by both models, especially after the extreme melt events in 2012. A cross-section of simulated firn density along a transect in west Greenland for April 2014 is shown in Figure 9. The IMAU-FDM, simulating higher densification rates in regions with considerable amounts of refreezing, predicts continuous ice in the topmost 20 m until an elevation of approximately 2000 m a.s.l. Higher up, an area where porous firn is covered by a thick near-surface ice layer is simulated. SNOWPACK models this transition at a somewhat lower elevation of approximately 1850 m a.s.l., in spite of the higher irreducible water content. The radar-inferred observation indicates a better agreement with SNOWPACK but suggest that this transition is located at an even lower elevation. Additionally, both models overestimate the thickness of near-surface ice layers. This is probably related to the neglecting of lateral runoff at the surface and the application of the bucket scheme, which fills available pore space in a sequential top-down-mode.
Figure 9

Firn cross-section along the transect (66.97° N/−47.50° E – 66.97° N/−45.21° E) for April 2014. The upper two panels (A,B) show firn densities simulated by the models and the lower panel (C) the relative power return measured by the OIB Accumulation Radar. This cross-section partially overlaps with the radar transect described in Machguth et al. (2016) and its geographical extent is shown in Figure 1.
4. Conclusions
Two numerical models, the IMAU-FDM, developed for coupling to an RCM, and SNOWPACK, developed as a stand-alone model, have been used offline to simulate firn evolution on the GrIS for the period 1960–2014. Forcing was provided by 3-h output of mass fluxes and skin temperature from RACMO2.3. Model evaluation using observed density profiles indicates that the IMAU-FDM slightly outperforms SNOWPACK for relatively cold and dry locations. For locations with intermediate ratios of liquid to solid mass inputs at the surface (Rliq/sol), SNOWPACK performs better than the IMAU-FDM. This is also true for locations where perennial firn aquifers form. For locations with high Rliq/sol-values (>0.6), both models overestimate near-surface density. This is either related to the snow/firn models deficiency to account for inhomogeneous vertical percolation and/or lateral surface runoff or to inaccurate meteorological forcing.
Our evaluation suggests that areas where firn aquifers form exhibit the highest sensitivity to the model's parameterization of liquid water retention (refreezing and perennial liquid water storage). Three factors are thereby of major relevance: (I) The snow/firn densification rate determines the amount of available pore space for refreezing or liquid water storage. These rates are apparently overestimated in the IMAU-FDM and more accurately simulated by SNOWPACK. It seems however that at least for location FA13, SNOWPACK underestimates densification rates at greater depths. Beside densification, the prescribed values of irreducible water content (II) co-determine the amounts of retained meltwater. The values prescribed in SNOWPACK are considerably higher than in the IMAU-FDM and are in better agreement with observed values (Coléou and Lesaffre, 1998; Schneider and Jansson, 2004). However, it seems that SNOWPACK overestimates near-surface refreezing with these comparably high amounts of prescribed irreducible water content–at least in combination with the bucket scheme. Finally, refreezing at the base of firn aquifers (and hence the formation of superimposed ice) is determined by the thermodynamic conditions (III) at the base of the aquifers. These conditions are largely unknown and it is probable that the models underestimate refreezing at the bottom of firn aquifers as temperatures below are predominantly at the melting point in both simulations.
This study also indicates that SNOWPACK is a suitable tool to perform offline firn simulations for the GrIS. Due to the dynamical layer merging, which was used in a more aggressive setting in this study, it is feasible to perform multi-century long spin-up runs while maintaining thin heterogeneous layers, which are crucial factors for preferential water flow. With the aggressive layer merging switched on, the computational time is comparable to that required by the IMAU-FDM. Furthermore, SNOWPACK also models microstructural snow properties and includes a recently implemented preferential flow algorithm (Wever et al., 2016).
Considering the findings of this study, there are several processes that should be improved or included in future large-scale numerical snow/firn models: First of all, the densification schemes of both models should be further improved. Both schemes reveal inaccuracies under certain conditions; therefore it would be advantageous to have one formulation that is accurate for all climatic conditions and overburden pressures on the GrIS. Further research should also focus on the influence of liquid water on snow viscosity, as there is currently no direct empirical evidence to support this link. However, the validation of a densification scheme for locations with considerable amounts of surface melt remains challenging, as density profiles evolve as a combination of compaction and mass gain due to refreezing. Secondly, tests with impermeable layers could be conducted which are both relevant for saturated conditions within firn aquifers and lateral surface runoff. However, the relationship between vertical water permeability and ice layer thickness is, especially on the horizontal scale of a current regional climate model, rather uncertain. The feature of ponding water conditions is already integrated in SNOWPACK and was tested for superimposed ice formation on the Kongsvegen glacier in Svalbard (Obleitner and Lehning, 2004). Furthermore, alternative (heterogeneous) vertical water percolation schemes should be tested as our results indicate that SNOWPACK, and likely other models that compute the irreducible water content according to Coléou and Lesaffre (1998), tend to overestimate near-surface liquid water retention and subsequent refreezing. Finally, the fresh snow density parameterization, which has a strong effect on the availability of near-surface pore space for refreezing, should be further refined.
Funding
CS received financial support from the Netherlands Polar Programme (NPP) of the Netherlands Organization for Scientific Research (NWO). MV is supported by the Netherlands Earth System Science Center (NESSC).
Conflict of interest statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The handling Editor declared a shared affiliation, though no other collaboration, with one of the authors LK and states that the process nevertheless met the standards of a fair and objective review.
Statements
Author contributions
CS carried out the SNOWPACK experiments, model comparison and wrote the manuscript. CR and MV supervised this study, NW provided SNOWPACK support, RF provided the Operation IceBridge Accumulation Radar data, LK provided the firn core data for location FA13, PK carried out the IMAU-FDM run and provided the firn core dataset, ML co-developed SNOWPACK, SL provided experience and support in applying SNOWPACK to the GrIS, SRML co-developed the IMAU-FDM, CM processed and provided the Operation IceBridge Accumulation Radar data, and BN provided the RACMO2.3 forcing data. All authors revised the manuscript.
Acknowledgments
ECMWF at Reading (UK) is acknowledged for use of the supercomputing system. Charles Fierz (WSL Institute for Snow and Avalanche Research SLF) is acknowledged for additional SNOWPACK support and advice. Graphics were made using Python Matplotlib (version 1.5.1).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. The handling Editor declared a shared affiliation, though no other collaboration, with one of the authors LK and states that the process nevertheless met the standards of a fair and objective review.
References
1
AndersonE. A. (1976). A Point Energy and Mass Balance Model of a Snow Cover. Technical Report NWS19, NOAA.
2
ArthernR. J.VaughanD. G.RankinA. M.MulvaneyR.ThomasE. R. (2010). In situ measurements of Antarctic snow compaction compared with predictions of models. J. Geophys. Res. Earth Surf.115:F03011. 10.1029/2009JF001306
3
AvanziF.HirashimaH.YamaguchiS.KatsushimaT.De MicheleC. (2016). Observations of capillary barriers and preferential flow in layered snow during cold laboratory experiments. Cryosphere10, 2013–2026. 10.5194/tc-10-2013-2016
4
BamberJ. L.GriggsJ. A.HurkmansR. T. W. L.DowdeswellJ. A.GogineniS. P.HowatI.et al. (2013). A new bed elevation dataset for Greenland. Cryosphere7, 499–510. 10.5194/tc-7-499-2013
5
BarteltP.LehningM. (2002). A physical SNOWPACK model for the Swiss avalanche warning: Part I: numerical model. Cold Regions Sci. Technol.35, 123–145. 10.1016/S0165-232X(02)00074-5
6
BekryaevR. V.PolyakovI. V.AlexeevV. A. (2010). Role of polar amplification in long-term surface air temperature variations and Modern Arctic Warming. J. Clim.23, 3888–3906. 10.1175/2010JCLI3297.1
7
BennartzR.ShupeM. D.TurnerD. D.WaldenV. P.SteffenK.CoxC. J.et al. (2013). July 2012 Greenland melt extent enhanced by low-level liquid clouds. Nature496, 83–86. 10.1038/nature12002
8
ColbeckS. C. (1972). A Theory of water percolation in snow. J. Glaciol.11, 369–385.
9
ColéouC.LesaffreB. (1998). Irreducible water saturation in snow: experimental results in a cold laboratory. Ann. Glaciol.26, 64–68.
10
CoxC.HumphreyN.HarperJ. (2015). Quantifying meltwater refreezing along a transect of sites on the Greenland ice sheet. Cryosphere9, 691–701. 10.5194/tc-9-691-2015
11
DadicR.SchneebeliM.LehningM.HutterliM. A.OhmuraA. (2008). Impact of the microstructure of snow on its temperature: a model validation with measurements from Summit, Greenland. J. Geophys. Res. Atmospheres113:D14303. 10.1029/2007JD009562
12
DoyleS. H.HubbardA.van de WalR. S. W.BoxJ. E.van AsD.ScharrerK.et al. (2015). Amplified melt and flow of the Greenland ice sheet driven by late-summer cyclonic rainfall. Nat. Geosci.8, 647–653. 10.1038/ngeo2482
13
EnderlinE. M.HowatI. M.JeongS.NohM.-J.van AngelenJ. H.van den BroekeM. R. (2014). An improved mass budget for the Greenland ice sheet. Geophys. Res. Lett.41, 866–872. 10.1002/2013GL059010
14
ForsterR. R.BoxJ. E.van den BroekeM. R.MiègeC.BurgessE. W.van AngelenJ. H.et al. (2014). Extensive liquid meltwater storage in firn within the Greenland ice sheet. Nat. Geosci.7, 95–98. 10.1038/ngeo2043
15
GoelzerH.HuybrechtsP.RaperS. C. B.LoutreM.-F.GoosseH.FichefetT. (2012). Millennial total sea-level commitments projected with the Earth system model of intermediate complexity LOVECLIM. Environ. Res. Lett.7:045401. 10.1088/1748-9326/7/4/045401
16
GreuellW.KonzelmannT. (1994). Numerical modelling of the energy balance and the englacial temperature of the Greenland Ice Sheet. Calculations for the ETH-Camp location (West Greenland, 1155 m a.s.1.). Global Planet. Change9, 91–114. 10.1016/0921-8181(94)90010-8
17
Groot ZwaaftinkC. D.CagnatiA.CrepazA.FierzC.MacelloniG.ValtM.LehningM. (2013). Event-driven deposition of snow on the Antarctic Plateau: analyzing field measurements with SNOWPACK. Cryosphere7, 333–347. 10.5194/tc-7-333-2013
18
HarperJ.HumphreyN.PfefferW. T.BrownJ.FettweisX. (2012). Greenland ice-sheet contribution to sea-level rise buffered by meltwater storage in firn. Nature491, 240–243. 10.1038/nature11566
19
HirashimaH.YamaguchiS.KatsushimaT. (2014). A multi-dimensional water transport model to reproduce preferential flow in the snowpack. Cold Reg. Sci. Technol.108, 80–90. 10.1016/j.coldregions.2014.09.004
20
HumphreyN. F.HarperJ. T.PfefferW. T. (2012). Thermal tracking of meltwater retention in Greenland's accumulation area. J. Geophys. Res. Earth Surf.117:F01010. 10.1029/2011JF002083
21
KoenigL. S.MiègeC.ForsterR. R.BruckerL. (2014). Initial in situ measurements of perennial meltwater storage in the Greenland firn aquifer. Geophys. Res. Lett.41, 81–85. 10.1002/2013GL058083
22
Kuipers MunnekeP.LigtenbergS. R.van den BroekeM. R.van AngelenJ. H.ForsterR. R. (2014). Explaining the presence of perennial liquid water bodies in the firn of the Greenland Ice Sheet. Geophys. Res. Lett.41, 476–483. 10.1002/2013GL058389
23
Kuipers MunnekeP.LigtenbergS. R. M.NoëlB. P. Y.HowatI. M.BoxJ. E.Mosley-ThompsonE.et al. (2015). Elevation change of the Greenland Ice Sheet due to surface mass balance and firn processes, 1960–2014. Cryosphere9, 2009–2025. 10.5194/tc-9-2009-2015
24
Kuipers MunnekeP.van den BroekeM. R.LenaertsJ. T. M.FlannerM. G.GardnerA. S.van de BergW. J. (2011). A new albedo parameterization for use in climate models over the Antarctic ice sheet. J. Geophys. Res. Atmospheres116:D05114. 10.1029/2010JD015113
25
LehningM.BarteltP.BrownB.FierzC. (2002a). A physical SNOWPACK model for the Swiss avalanche warning: Part III: meteorological forcing, thin layer formation and evaluation. Cold Reg. Sci. Technol.35, 169–184. 10.1016/S0165-232X(02)00072-1
26
LehningM.BarteltP.BrownB.FierzC.SatyawaliP. (2002b). A physical SNOWPACK model for the Swiss avalanche warning: Part II. Snow microstructure. Cold Reg. Sci. Technol.35, 147–167. 10.1016/S0165-232X(02)00073-3
27
LenaertsJ. T. M.van den BroekeM. R.van AngelenJ. H.van MeijgaardE.DéryS. J. (2012). Drifting snow climate of the Greenland ice sheet: a study with a regional climate model. Cryosphere6, 891–899. 10.5194/tc-6-891-2012
28
LigtenbergS. R. M.HelsenM. M.van den BroekeM. R. (2011). An improved semi-empirical model for the densification of Antarctic firn. Cryosphere5, 809–819. 10.5194/tc-5-809-2011
29
LivingstoneS. J.ClarkC. D.WoodwardJ.KingslakeJ. (2013). Potential subglacial lake locations and meltwater drainage pathways beneath the Antarctic and Greenland ice sheets. Cryosphere7, 1721–1740. 10.5194/tc-7-1721-2013
30
MachguthH.MacFerrinM.van AsD.BoxJ. E.CharalampidisC.ColganW.et al. (2016). Greenland meltwater storage in firn limited by near-surface ice formation. Nat. Clim. Change6, 390–393. 10.1038/nclimate2899
31
MarshP.WooM. (1984). Wetting front advance and freezing of meltwater within a snow cover 1. Observations in the Canadian Arctic. Water Resour. Res.20, 1853–1864. 10.1029/WR020i012p01853
32
MiègeC.ForsterR. R.BruckerL.KoenigL. S.SolomonD. K.PadenJ. D.et al. (2016). Spatial extent and temporal variability of Greenland firn aquifers detected by ground and airborne radars. J. Geophys. Res. Earth Surf.121, 2381–2398. 10.1002/2016JF003869
33
MikkelsenA. B.HubbardA.MacFerrinM.BoxJ. E.DoyleS. H.FitzpatrickA.HasholtB.BaileyH. L.LindbäckK.PetterssonR. (2016). Extraordinary runoff from the Greenland ice sheet in 2012 amplified by hypsometry and depleted firn retention. Cryosphere10, 1147–1159. 10.5194/tc-10-1147-2016
34
NghiemS. V.HallD. K.MoteT. L.TedescoM.AlbertM. R.KeeganK.ShumanC. A.DiGirolamoN. E.NeumannG. (2012). The extreme melt across the Greenland ice sheet in 2012. Geophys. Res. Lett.39:L20502. 10.1029/2012GL053611
35
NoëlB.van de BergW. J.van MeijgaardE.Kuipers MunnekeP.van de WalR. S. W.van den BroekeM. R. (2015). Evaluation of the updated regional climate model RACMO2.3: summer snowfall impact on the Greenland Ice Sheet. Cryosphere9, 1831–1844. 10.5194/tc-9-1831-2015
36
ObleitnerF.LehningM. (2004). Measurement and simulation of snow and superimposed ice at the Kongsvegen glacier, Svalbard (Spitzbergen). J. Geophys. Res. Atmospheres109:D04106. 10.1029/2003JD003945
37
ReehN. (2008). A nonsteady-state firn-densification model for the percolation zone of a glacier. J. Geophys. Res. Earth Surf.113:F03023. 10.1029/2007JF000746
38
ReijmerC. H.van den BroekeM. R.FettweisX.EttemaJ.StapL. B. (2012). Refreezing on the Greenland ice sheet: a comparison of parameterizations. Cryosphere6, 743–762. 10.5194/tc-6-743-2012
39
RennermalmA. K.MoustafaS. E.MioduszewskiJ.ChuV. W.ForsterR. R.HagedornB.et al. (2013). Understanding Greenland ice sheet hydrology using an integrated multi-scale approach. Environ. Res. Lett.8:015017. 10.1088/1748-9326/8/1/015017
40
Rodriguez-MoralesF.GogineniS.LeuschenC. J.PadenJ. D.LiJ.LewisC. C.et al. (2014). Advanced Multifrequency Radar Instrumentation for Polar Research. IEEE Trans. Geosci. Remote Sens.52, 2824–2842. 10.1109/TGRS.2013.2266415
41
SchneiderT.JanssonP. (2004). Internal accumulation in firn and its significance for the mass balance of Storglaciaren, Sweden. J. Glaciol.50, 25–34. 10.3189/172756504781830277
42
SmithL. C.ChuV. W.YangK.GleasonC. J.PitcherL. H.RennermalmA. K.et al. (2015). Efficient meltwater drainage through supraglacial streams and rivers on the southwest Greenland ice sheet. Proc. Natl. Acad. Sci. U.S.A.112, 1001–1006. 10.1073/pnas.1413024112
43
TedescoM.DohertyS.FettweisX.AlexanderP.JeyaratnamJ.StroeveJ. (2016). The darkening of the greenland ice sheet: trends, drivers, and projections (1981–2100). Cryosphere10, 477–496. 10.5194/tc-10-477-2016
44
van AngelenJ. H.van den BroekeM. R.WoutersB.LenaertsJ. T. M. (2014). Contemporary (1960–2012) evolution of the climate and surface mass balance of the greenland ice sheet. Surv. Geophys.35, 1155–1174. 10.1007/s10712-013-9261-z
45
van AsD.FaustoR. S.WilliamT. C.BoxJ. E. (2013). Darkening of the Greenland ice sheet due to the meltalbedo feedback observed at PROMICE weather stations. Geol. Surv. Denmark Greenl. Bull.28, 69–72. 10.5167/uzh-131201
46
van den BroekeM.BamberJ.EttemaJ.RignotE.SchramaE.van de BergW. J.et al. (2009). Partitioning Recent Greenland Mass Loss. Science326, 984–986. 10.1126/science.1178176
47
van den BroekeM. R.EnderlinE. M.HowatI. M.Kuipers MunnekeP.NoëlB. P. Y.van de BergW. J.et al. (2016). On the recent contribution of the Greenland ice sheet to sea level change. Cryosphere10, 1933–1946. 10.5194/tc-10-1933-2016
48
Van TrichtK.LhermitteS.LenaertsJ. T. M.GorodetskayaI. V.L'EcuyerT. S.NoëlB.et al. (2016). Clouds enhance Greenland ice sheet meltwater runoff. Nat. Commun.7:10266. 10.1038/ncomms10266
49
VernonC. L.BamberJ. L.BoxJ. E.van den BroekeM. R.FettweisX.HannaE.HuybrechtsP. (2013). Surface mass balance model intercomparison for the Greenland ice sheet. Cryosphere7, 599–614. 10.5194/tc-7-599-2013
50
WeverN.FierzC.MittererC.HirashimaH.LehningM. (2014). Solving Richards Equation for snow improves snowpack meltwater runoff estimations in detailed multi-layer snowpack model. Cryosphere8, 257–274. 10.5194/tc-8-257-2014
51
WeverN.WürzerS.FierzC.LehningM. (2016). Simulating ice layer formation under the presence of preferential flow in layered snowpacks. Cryosphere10, 2731–2744. 10.5194/tc-10-2731-2016
52
WientjesI. G. M.Van de WalR. S. W.ReichartG. J.SluijsA.OerlemansJ. (2011). Dust from the dark region in the western ablation zone of the greenland ice sheet. Cryosphere5, 589–601. 10.5194/tc-5-589-2011
53
YallopM. L.AnesioA. M.PerkinsR. G.CookJ.TellingJ.FaganD.et al. (2012). Photophysiology and albedo-changing potential of the ice algal community on the surface of the greenland ice sheet. Int. Soc. Microb. Ecol.6, 2302–2313. 10.1038/ismej.2012.107
Summary
Keywords
firn modeling, refreezing on Greenland, meltwater retention, firn aquifer, ice layer
Citation
Steger CR, Reijmer CH, van den Broeke MR, Wever N, Forster RR, Koenig LS, Kuipers Munneke P, Lehning M, Lhermitte S, Ligtenberg SRM, Miège C and Noël BPY (2017) Firn Meltwater Retention on the Greenland Ice Sheet: A Model Comparison. Front. Earth Sci. 5:3. doi: 10.3389/feart.2017.00003
Received
20 September 2016
Accepted
11 January 2017
Published
27 January 2017
Volume
5 - 2017
Edited by
William Tad Pfeffer, University of Colorado Boulder, USA
Reviewed by
Evgeny Andreevich Podolskiy, Hokkaido University, Japan; Leigh A. Stearns, University of Kansas, USA
Updates
Copyright
© 2017 Steger, Reijmer, van den Broeke, Wever, Forster, Koenig, Kuipers Munneke, Lehning, Lhermitte, Ligtenberg, Miège and Noël.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christian R. Steger c.r.steger@uu.nl
This article was submitted to Cryospheric Sciences, a section of the journal Frontiers in Earth Science
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.