The prediction of karst-collapse susceptibility levels based on the ISSA-ELM integrated model

Karst collapse, a sudden geological hazard with complex mechanisms and low predictability, presents significant threats to urban safety and sustainable development by jeopardizing human lives and infrastructure. To address the limitations of conventional prediction methods, in this study, we introduce an enhanced predictive model, the improved sparrow search algorithm-optimized extreme learning machine (ISSA-ELM), for accurate karst-collapse susceptibility assessment. The methodology incorporates two key innovations: first, it applies a Singer chaotic mapping technique to enhance the sparrow search algorithm (SSA), effectively mitigating local optima entrapment by increasing population diversity and enhancing global search capabilities. Second, the optimized ISSA automatically adjusts the initial weights and thresholds of the ELM, whereas a five-fold cross-validation is used to determine the optimal hidden layer configuration, forming an adaptive and intelligent prediction framework. When validated against 20 datasets from a representative karst region, the proposed model achieved exceptional performance, with a mean absolute error (MAE) of 0.0544 and a coefficient of determination (R²) of 0.9914, significantly surpassing the prediction accuracy of conventional ELM and SSA-ELM models. The results underscore the ISSA-ELM’s superior nonlinear fitting capability, enhanced generalization performance, and outstanding stability in practical engineering applications. This research offers a solid scientific foundation for risk classification and hazard mitigation strategies while introducing a novel methodological framework through the integration of innovative algorithms. The proposed technical pathway provides significant theoretical advancements and practical engineering values for geological disaster prediction systems.

1 Introduction

Karst collapse, a prominent geological hazard, arises from the interaction between karst formation processes and groundwater dynamics. It often results in sudden surface subsidence or structural failure which occurs due to the progressive development of subsurface voids and fractures (Bouzerda et al., 2024; Wang et al., 2024; Xiaozhen et al., 2024). With its concealed nature, intricate triggering mechanisms, and significant destructive potential, karst collapse poses substantial challenges to urban development and infrastructure security in vulnerable regions. Conducting an accurate susceptibility assessment is crucial for enhancing disaster prevention frameworks and guiding sustainable land-use planning.

The development of karst collapse prediction methodologies has progressed through distinct phases, evolving from qualitative evaluations (Gao et al., 2009; Luo and Shen, 2018) to more sophisticated quantitative analyses. Early research primarily established qualitative models based on genetic mechanism analysis. Subsequent interdisciplinary advancements introduced semi-quantitative approaches, including Fisher discriminant analysis (Huang et al., 2011; Jiang and Jiang, 2012) and the Analytic Hierarchy Process (AHP) (Jiyuan et al., 2021; YanHua et al., 2022). Additionally, quantitative frameworks such as fuzzy logic systems (Zhang et al., 2021; Zhuang, 2022) and grey system theory (Qiu, 2004; Meng et al., 2009; Gao et al., 2018; Ding et al., 2019) were developed. More recently, machine learning techniques have significantly enhanced prediction accuracy by modeling complex nonlinear relationships. Techniques such as backpropagation neural networks (BPNNs) (Bao and Hu, 2002; Chen et al., 2005; Yang et al., 2023; Journal of Chemistry, 2023), entropy-weighted cloud models (Chen et al., 2019; Wei et al., 2021), support vector machines (SVMs) (Lai and Qiao, 2008; En et al., 2011; Zhou et al., 2020), random forests (RFs) (Wang et al., 2022; Ren et al., 2023), and extreme learning machines (ELMs) (Xie et al., 2021) have been widely applied. Despite these advancements, current methodologies face several limitations. First, conventional statistical methods (e.g., AHP and fuzzy analysis) rely heavily on expert judgment, leading to subjective biases and challenges in determining objective weights. Second, data-driven models (e.g., BPNN and RF) often experience optimization challenges, including convergence to local minima and sensitivity to parameter selection. Additionally, traditional ELM implementations suffer from instability due to random weight initialization, compromising their reliability in engineering applications.

To address these constraints, in this study, we propose an optimized prediction framework (ISSA-ELM) that integrates an improved sparrow search algorithm (ISSA) with the extreme learning machine architecture. The method uses a three-fold optimization strategy: First, principal component analysis (PCA) reduces the dimensionality of collapse-influencing factors, minimizing multicollinearity while retaining essential diagnostic information. Second, Singer chaotic mapping enhances the standard sparrow search algorithm (SSA) by improving population diversity, expanding the search space, and preventing premature convergence. Third, an adaptive optimization framework combines the refined ISSA with K-fold cross-validation to optimize ELM hyperparameters, ensuring robust model generalization. Empirical validation through case studies in representative karst regions demonstrates that the ISSA-ELM outperforms conventional methods in predictive accuracy, particularly for susceptibility zonation. This methodological advancement offers a novel paradigm for regional-scale geological risk management, providing both theoretical insights and practical values for geological disaster prevention and land-use planning.

2 Theory of the ISSA-ELM integrated model

2.1 Principal component analysis

PCA, initially proposed by Pearson (1901), is a widely adopted dimensionality reduction technique. It converts multiple indicators into a smaller set of comprehensive variables (Zhou et al., 2020; Cao et al., 2015). This approach not only reduces data complexity but also preserves key relationships among variables. The main steps of PCA are as follows.

2.1.1 Data standardization

Given n samples and p influencing factors, the original data matrix is represented as shown in Equation 1:

$Z={\left(z_{ij}\right)}_{n\times p},\left(i=1,2,3,\cdots ,n;j=1,2,3,\cdots ,p\right).(1)$

Standardization is applied using the formula as shown in Equation 2:

$Z^{*}={\left({z_{ij}}^{*}\right)}_{n\times p},\left(i=1,2,3,\cdots ,n;j=1,2,3,\cdots ,p\right),(2)$

where

$z^{*}=\frac{z_{ij}-\frac{1}{n}{\sum }_{i=1}^n{z}_{ij}}{\sqrt{\frac{1}{n-1}{\sum }_{i=1}^n{\left(z_{ij}-\overline{z_j}\right)}^2}},\left(i=1,2,3,\cdots ,n;j=1,2,3,\cdots ,p\right).(3)$

In Equation 3, z_ij is the observed value of the jth variable of the ith sample, and $\overline{{\mathrm{z}}_{\mathrm{j}}}$ is the sample mean of the jth variable.

2.1.2 Correlation coefficient matrix calculation

The correlation coefficient matrix R can be calculated using Equation 4:

$\mathrm{R}=\frac{1}{n-1}{{\mathit{Z}}^{*}}^T{\mathit{Z}}^{*},(4)$

where ${\mathrm{Z}}^{*}$ represents the standardized data matrix.

2.1.3 Eigenvalue and eigenvector computation

The eigenvalues ${\mathrm{\lambda }}_1\ge {\mathrm{\lambda }}_2\ge {\mathrm{\lambda }}_3\ge \dots \ge {\mathrm{\lambda }}_{\mathrm{p}}$ of the correlation coefficient matrix R are calculated, and their corresponding orthogonal eigenvectors are as follows:

$a_i={\left(a_{i1},a_{i2},a_{i3},\mathsf{\dots }\mathsf{,}{a}_{ip}\right)}^T,\left(i=1,2,3,\mathsf{\dots }\mathsf{,}p\right).$

2.1.4 Variance contribution rate and cumulative Variance contribution rate

The variance contribution rate ${\beta }_i$ and the cumulative variance contribution rate $\beta \left(i\right)$ can be calculated using Equations 5, 6:

${\beta }_i=\frac{{\lambda }_i}{{\sum }_{i=1}^p{\lambda }_i},\left(i=1,2,3,\cdots ,p\right),(5)$

$\beta \left(i\right)={\displaystyle \sum _{i=1}^p}{\beta }_i,\left(i=1,2,3,\cdots ,p\right).(6)$

2.1.5 Principal component selection

Principal components are selected when the cumulative variance contribution rate reaches 85% or higher, ensuring most of the original data information is retained (Zhou et al., 2020).

2.2 Sparrow search algorithm

The SSA is a swarm intelligence optimization algorithm introduced by Xue and Shen (2020). It simulates the foraging and anti-predation behaviors of sparrow flocks to find optimal solutions. The sparrow population consists of discoverers, followers, and sentinels, represented by an $\mathrm{n}\times \mathrm{d}$ matrix (as shown in Equation 7), where $\mathrm{n}$ is the number of sparrows, $\mathrm{d}$ denotes the dimension, and ${\mathrm{x}}_{\text{nd}}$ represents the jth dimension of the ith sparrow. The fitness value for each sparrow is represented as ${\mathrm{F}}_{\mathrm{x}}$ (as shown in Equation 8).

$\mathit{X}=\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1d}\\ x_{21}& x_{22}& \cdots & x_{2d}\\ ⋮& ⋮& \ddots & ⋮\\ x_{n1}& x_{n2}& \cdots & x_{nd}\end{array}\right],(7)$

${\mathit{F}}_x=\left[\begin{array}{c}f\left(\left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1d}\end{array}\right]\right)\\ f\left(\left[\begin{array}{cccc}{x}_{21}& x_{22}& \cdots & x_{2d}\end{array}\right]\right)\\ ⋮\\ f\left(\left[\begin{array}{cccc}{x}_{n1}& x_{n2}& \cdots & x_{nd}\end{array}\right]\right)\end{array}\right].(8)$

2.2.1 Discoverer update

Discoverers locate new food sources using Equation 9:

$X_{i,j}^{t+1}=\left\{\begin{array}{l}{X}_{i,j}^t·\mathit{exp}\left(\frac{-i}{\alpha ·{iter}_{\mathit{max}}}\right),R_2<ST\\ X_{i,j}^t+Q·\mathit{L},R_2\ge ST\end{array}\right.,(9)$

where ${iter}_{\mathit{max}}$ denotes the maximum number of iterations; $X_{i,j}^t$ is the position of the ith sparrow in the jth dimension at the t-th iteration; $\mathrm{\alpha }\in \left(0,1\right]$, $\mathrm{Q}\in \left[0,1\right]$, and ${\mathrm{R}}_2\in \left[0,1\right]$ are random numbers, representing the warning values, respectively; L is a matrix of ones; and $\text{ST}$ takes values between [0.5,1], representing the safety value.

When ${\mathrm{R}}_2\ge \text{ST}$, it indicates that the foraging area is not safe, and all sparrows need to fly to other safe foraging locations.

2.2.1.1 Follower update

Followers adjust their positions by tracking discoverers to accelerate convergence using Equation 10:

$X_{i,j}^{t+1}=\left\{\begin{array}{l}Q·\mathit{exp}\left(\frac{X_{worst}^t-X_{i,j}^t}{i^2}\right),i>\frac{n}{2}\\ X_p^{t+1}+\left|X_{i,j}^t-X_p^{t+1}\right|{\mathit{A}}^{+}·\mathit{L},i\le \frac{n}{2}\end{array}\right.,(10)$

where $X_p^{t+1}$ is the best position where the discoverers are located, ${\mathrm{X}}_{\text{worst}}^{\mathrm{t}}$ is the current globally worst position, and ${\mathrm{A}}^{+}={\mathrm{A}}^{\mathrm{T}}·{\left(\mathrm{A}·{\mathrm{A}}^{\mathrm{T}}\right)}^{-1}$ is a matrix, with each element being 1 or −1.

When $i>\frac{\mathrm{n}}{2}$, it indicates that the ith follower has not obtained food and needs to move to other places to forage.

2.2.1.2 Sentinel update

Sentinels monitor threats and adjust their positions using Equation 11:

$X_{i,j}^{t+1}=\left\{\begin{array}{l}{X}_{best}^t+\theta \left|X_{i,j}^t-X_{best}^t\right|,f_i>f_g\\ X_{i,j}^t+K\left|\frac{X_{i,j}^t-X_{worst}^t}{\left(f_i-f_w\right)+\epsilon }\right|,f_i=f_g\end{array}\right.,(11)$

where ${\mathrm{X}}_{\text{best}}^{\mathrm{t}}$ is the global optimal position in the sparrow population at the t-th generation, $\mathrm{\epsilon }$ is a constant, $\mathrm{\theta }$ is the step–size control coefficient, $\mathrm{K}\in \left[-1,1\right]$ is a random number, ${\mathrm{f}}_{\mathrm{i}}$ is the fitness value of the ith sparrow currently, ${\mathrm{f}}_{\mathrm{g}}$ is the current global best fitness value, and ${\mathrm{f}}_{\mathrm{w}}$ is the current global worst fitness value.

When ${\mathrm{f}}_{\mathrm{i}}>{\mathrm{f}}_{\mathrm{g}}$, it indicates that the sparrow is currently at the edge of the population and is vulnerable to predator attacks; when ${\mathrm{f}}_{\mathrm{i}}={\mathrm{f}}_{\mathrm{g}}$, it indicates that the sparrows in the middle of the population are aware of the danger of being preyed upon and need to move closer to other sparrows.

2.3 Improved sparrow search algorithm

The conventional SSA often experiences issues related to local convergence and reduced population diversity in later iterations (Lv et al., 2021; Liu et al., 2022). To mitigate these challenges, the Singer chaotic mapping is introduced to enhance population initialization. The formula for Singer chaotic mapping is shown in Equation 12:

$X_{k+1}=u\left(7.86x_k-23.32x_k^2+28.75x_k^3-\mathrm{13.3.2875}{x}_k^4\right),(12)$

where $u\in \left(0.9,1.08\right)$ is a control parameter and $x_k\in \left[0,1\right]$ is a random number.

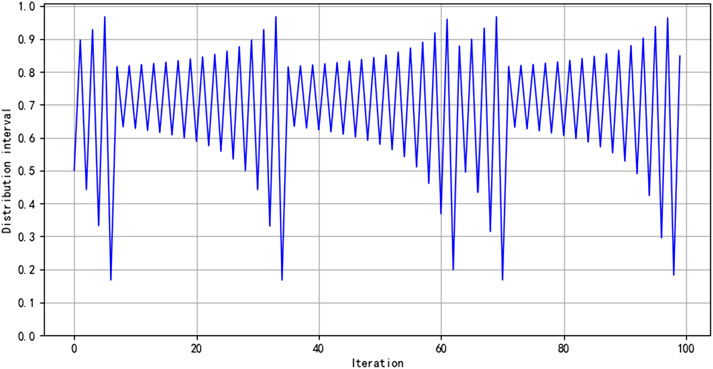
As shown in Figure 1, the value range of the Singer mapping lies within the interval [0, 1]. By replacing the random initialization method with its chaotic characteristics, the search space can be made more uniform, enhancing the uniformity and diversity of the sparrow population, and thereby improving the global search ability.

Figure 1

Figure 1. Distribution of the Singer map after 100 iterations.

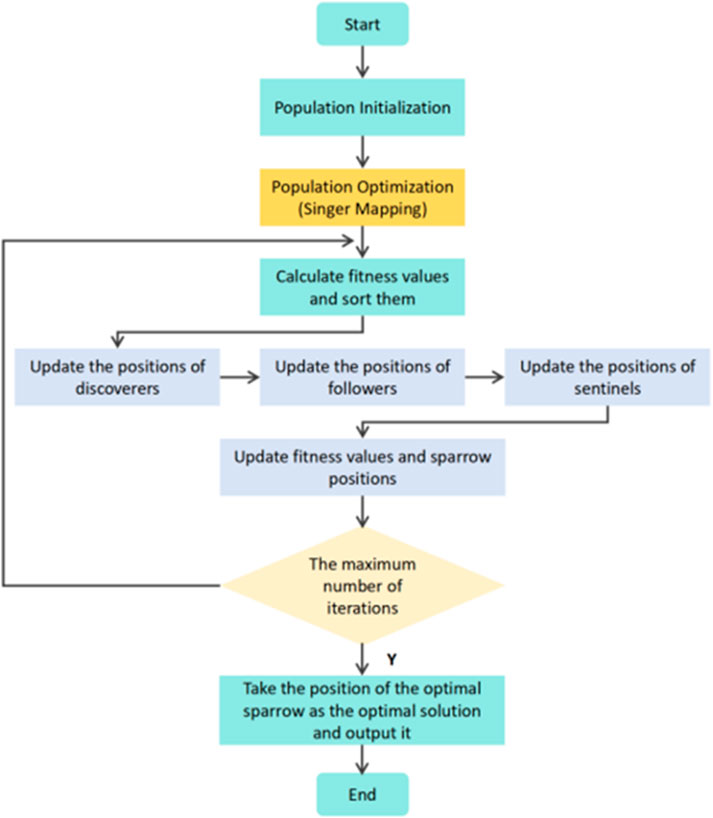
The steps of the improved SSA are outlined as follows:

(1) Use the chaotic mapping to initialize the population, the number of iterations, and the proportions of discoverers and followers.

(2) Compute the fitness values, and arrange them in order.

(3) Update the positions of discoverers.

(4) Update the positions of followers.

(5) Update the positions of sentinels.

(6) Recalculate the fitness values, and update the positions of the sparrows.

(7) Repeat until the maximum number of iterations is reached.

The flowchart of the improved SSA is presented in Figure 2.

Figure 2

Figure 2. Flowchart of the ISSA.

2.4 Extreme learning machine

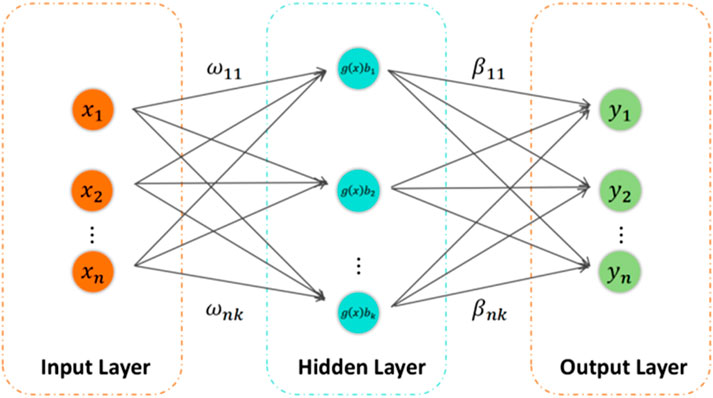
The ELM is a computationally efficient algorithm designed for training single-hidden-layer feedforward neural networks (SLFNs). First introduced by Huang et al. (2006), ELM offers significant improvements in training speed and generalization capability. Its applications are widespread across various domains, including classification, regression, and prediction tasks.

The ELM algorithm follows a simple structure, as illustrated in Figure 3, comprising an input layer, a hidden layer, and an output layer. Unlike traditional neural networks, ELM assigns random values to the input-layer weights and hidden-layer threshold. The output-layer weights are then calculated using a generalized matrix, enabling efficient and accurate chaotic recognition outcomes.

Figure 3

Figure 3. ELM structure.

The mathematical representation of the output model for a single-hidden-layer neural network with L hidden-layer nodes and an activation function $\mathrm{g}\left(x\right)$ is given in Equation 13:

$y_j={\displaystyle \sum _{i=1}^L}{\beta }_i\mathrm{g}\left({\mathrm{\omega }}_{\mathrm{i}}·x_j+b_i\right),\left(j=1,2,3,\cdots ,n\right),(13)$

where ${\mathrm{x}}_{\mathrm{j}}$ denotes the input value, ${\mathrm{y}}_{\mathrm{j}}$ represents the actual output value, ${\mathrm{\omega }}_{\mathrm{i}}$ is the input weight matrix, ${\mathrm{b}}_{\mathrm{i}}$ denotes the hidden-layer threshold, ${\beta }_i$ is the output weight matrix, and g(x) is typically a sigmoid function (Jiang and Shi, 2023)

The primary objective of the ELM algorithm is to minimize the output error, which can be expressed in Equation 14:

$‖\mathit{H}\mathit{\beta }-\mathit{T}‖=\mathit{min},(14)$

where there exist ${\beta }_i$, ${\omega }_i$, and $b_i$ such that

$\mathit{H}\mathit{\beta }=\mathit{T}.(15)$

This relationship shown in Equation 15 consists of N equations that can be represented in a matrix form as shown in Equation 16:

$\mathit{H}=\left[\begin{array}{ccc}\mathrm{g}\left({\mathrm{\omega }}_1·x_1+b_1\right)& \cdots & \mathrm{g}\left({\mathrm{\omega }}_{\mathrm{L}}·x_1+b_L\right)\\ \mathrm{g}\left({\mathrm{\omega }}_1·x_2+b_1\right)& \cdots & \mathrm{g}\left({\mathrm{\omega }}_1·x_2+b_1\right)\\ ⋮& \ddots & ⋮\\ \mathrm{g}\left({\mathrm{\omega }}_1·x_N+b_1\right)& \cdots & \mathrm{g}\left({\mathrm{\omega }}_{\mathrm{L}}·x_1+b_L\right)\end{array}\right],(16)$

where H is the hidden-layer output matrix, β is the weight matrix connecting the hidden and output layers, and T represents the desired output.

The least-squares solution for the output-layer weights can be efficiently obtained using the Moore–Penrose generalized inverse matrix ${\mathit{H}}^{+}$, as shown in Equation 17:

$\mathit{\beta }={\mathit{H}}^{+}\mathit{T}.(17)$

A notable limitation of ELM is its sensitivity to the random initialization of input-layer weights and hidden-layer threshold, leading to potential instability. To mitigate this issue, the ISSA is applied for parameter optimization. By enhancing the search process and avoiding local optima, the ISSA improves both the accuracy and robustness of the ELM model.

2.5 Hyperparameter optimization of the prediction model

The ELM algorithm randomly assigns input-layer weights and hidden-layer threshold. Without appropriate adjustment, this randomness may reduce the functionality of certain hidden-layer nodes, leading to algorithmic instability. Furthermore, although a larger number of hidden-layer nodes can enhance performance, an excessive number of nodes may result in overfitting, whereas too few nodes can cause underfitting, thereby reducing the prediction accuracy (Xie et al., 2021).

To mitigate these issues, in this study, we employ a combined approach using the ISSA and K-fold cross-validation to optimize the hyperparameters of the ELM prediction model. The optimized parameters include input-layer weights, hidden-layer thresholds, and the number of hidden nodes (N). The hyperparameter optimization process consists of the following steps:

(1) Initialization: set the sparrow population size, maximum number of iterations, proportions of initial discoverers and followers, and the number of hidden nodes.

(2) Fitness function calculation: define the mean squared error (MSE) between the predicted and actual values as the model’s fitness function, represented in Equation 18:

$\text{Fitness}=\frac{1}{n}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{n}}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{{\mathrm{y}}_{\mathrm{i}}}\right)}^2,(18)$

where ${\mathrm{y}}_{\mathrm{i}}$ represents the actual grade of karst-collapse susceptibility of the ith sample, $\overline{{\mathrm{y}}_{\mathrm{i}}}$ denotes the predicted value for the i-th sample, and $n$ is the number of samples.

(3) Ranking and selection: compute the fitness values and rank individuals. Those with higher fitness values are designated as discoverers in the sparrow population.

(4) Position update: update the positions of discoverers, followers, and vigilant individuals using Formulas 9–11, and then, recalculate fitness values.

(5) Iteration check: assess whether the maximum number of iterations is reached. If so, terminate training and output the global optimal parameters (optimal weights, hidden-layer biases, and N). Otherwise, repeat steps (2–4).

(6) K-fold cross-validation: perform five-fold cross-validation to determine the optimal number of hidden nodes. The data are split into five subsets, with each subset used once as a validation set, whereas the remaining subsets form the training set. The optimal number of hidden nodes is determined by minimizing the average error across the five models, as shown in Equation 19:

$\text{MAE}=\frac{1}{5}{\displaystyle \sum _{i=1}^n}\left(y_i-\overline{y_i}\right).(19)$

(7) Output: provide the final optimal parameter combination, including input-layer weights, hidden-layer threshold, and the number of hidden nodes.

2.6 Prediction process of karst collapse susceptibility using the ISSA-ELM model

The ISSA-ELM-based karst-collapse susceptibility prediction model is illustrated in Figure 4, with its overall flowchart depicted in Figure 5. The prediction process consists of the following steps:

(1) Data collection and preprocessing: Real-world data are collected from key karst collapse exploration areas. Data preprocessing is performed by removing outliers and imputing missing values using the mode. PCA is then applied for dimensionality reduction.

(2) Data division: The dataset is split into a training set and a test set. The training set is used to train the ISSA-ELM model, whereas the test set is used for prediction and model evaluation.

(3) Hyperparameter optimization: The ELM model’s hyperparameters, including the sparrow population size, maximum iterations, proportions of discoverers and followers, and the number of hidden nodes, are initialized. The initial model is trained and evaluated using MSE and MAE. The optimal hyperparameters are determined when the error reaches its minimum.

(4) Prediction: The ISSA-ELM model, with the optimized hyperparameters, is used to predict karst-collapse susceptibility. The final model parameters are applied for prediction tasks.

Figure 4

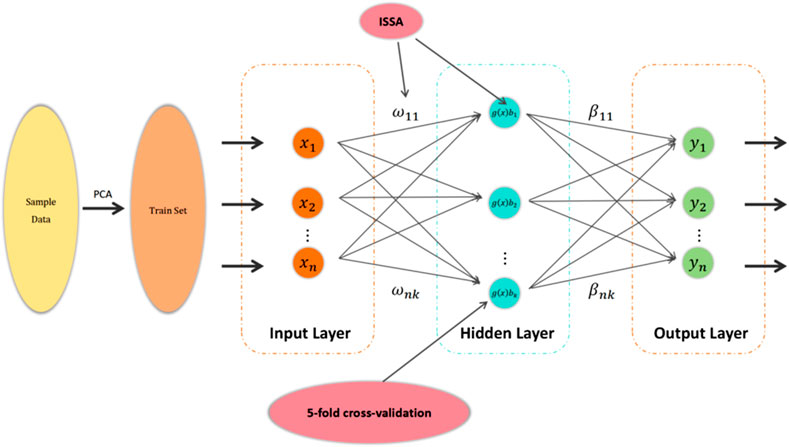
Figure 4. Framework of the karst-collapse susceptibility prediction model based on the ISSA-ELM model.

Figure 5

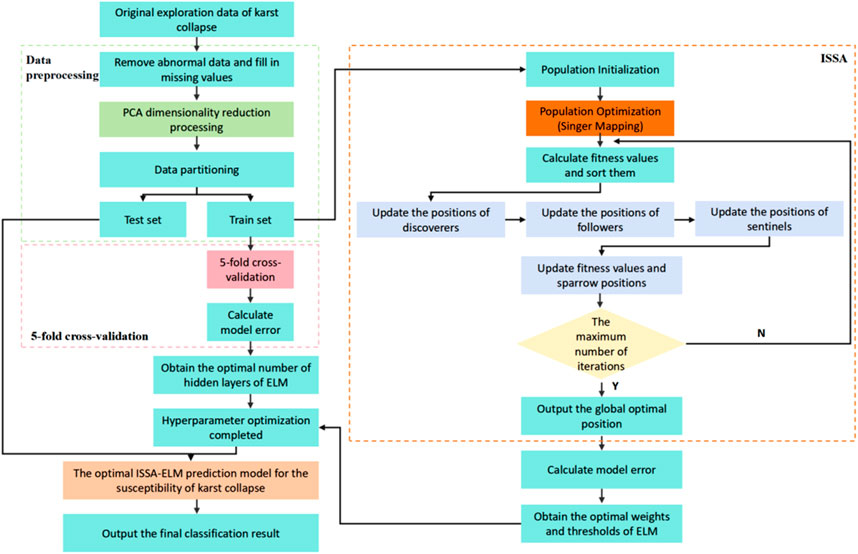
Figure 5. Overall flowchart of the karst-collapse susceptibility prediction model based on the ISSA-ELM model.

2.7 Evaluation methods

To comprehensively evaluate the predictive performance of various karst-collapse susceptibility models, the following indicators are applied.

2.7.1 Coefficient of determination (R²)

${\mathrm{R}}^2=1-\frac{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right)}^2}{{\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\overline{\mathrm{y}}\right)}^2}.(20)$

In Equation 20, ${\mathrm{y}}_{\mathrm{i}}$ is the actual value of the ith sample, $\widehat{{\mathrm{y}}_{\mathrm{i}}}$ is the predicted value of the ith sample, $\overline{\mathrm{y}}$ is the mean of the actual values, and n is the total number of samples. A coefficient value closer to 1 indicates a better model fit.

2.7.2 Mean squared error

$\text{MSE}=\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}}{\left({\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right)}^2.(21)$

2.7.3 Mean absolute error

$\text{MAE}=\frac{1}{\mathrm{n}}\sum _{\mathrm{i}=1}^{\mathrm{n}}\left|{\mathrm{y}}_{\mathrm{i}}-\widehat{{\mathrm{y}}_{\mathrm{i}}}\right|.(22)$

Smaller MSE (Equation 21) and MAE (Equation 22) values indicate a more accurate model, with the predicted values closely matching the actual values.

3 General situation of the project

3.1 Overview of the geological environment

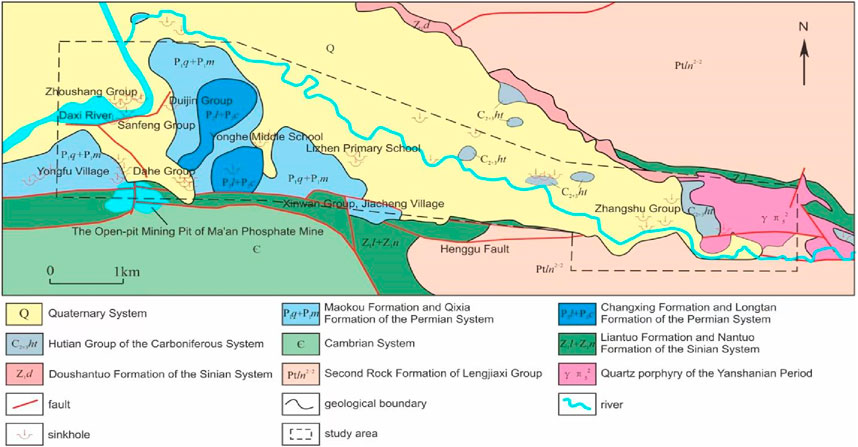
The study area is located in Yonghe Town, in the northeastern part of Liuyang City, Hunan Province. The terrain generally slopes from higher elevations in the south and northeast to lower elevations in the central and western regions. The primary geological and environmental conditions are as follows:

(1) Physical geography: the region is characterized by denudation–erosion hilly landforms and dissolution–erosion valley landforms. The hills are primarily located in the southern part and the Qibaoshan area to the east. These positive landforms are composed mainly of sandstones, slates, and dolomites from the Upper Sinian System (Zb), Cambrian System (∈), Longtan Formation (P₂l), and Changxing Formation (P₂c) of the Upper Permian System. In contrast, negative landforms composed of dolomites, marls, and limestones interbedded with shales are prevalent in the northern and western parts. These belong to the Hutian Group (C₂₊₃ht) of the Middle and Upper Carboniferous Systems and the Qixia Formation (P₁q) of the Lower Permian System.

Dissolution–erosion valley landforms are dominant in the northern and western regions, characterized by broad valleys and alluvial plains formed through erosional and depositional processes. These areas are covered by upper silty clay and sandy gravel layers from the Holocene Series (Q_h^al) of the Quaternary System. The underlying bedrock mainly comprises marls, limestones interbedded with shales, and dolomites. The area experiences an average annual rainfall of 1574.7 mm, with maximum and minimum recorded rainfalls of 2096.1 mm and 1079.1 mm, respectively. Rainfall is most concentrated in June, contributing over 16% of the annual total. The Daxi River, the second largest tributary of the Liuyang River, flows from north to west across the study area (Figure 7).

(2) Stratigraphic lithology: the stratigraphic sequence in the study area, from the oldest to the youngest, includes the second segment of the second lithologic unit of the Lengjiaxi Group (Ptln^2-2), the Liantuo Formation (Z₁l) and Nantuo Formation (Z₁n) of the Lower Sinian System, the Doushantuo Formation (Z₂d) of the Upper Sinian System, the Cambrian System (∈), the Hutian Group (C₂₊₃ht) of the Middle and Upper Carboniferous Systems, the Qixia Formation (P₁q) and Maokou Formation (P₁m) of the Lower Permian System, the Longtan Formation (P₂l) and Changxing Formation (P₂c) of the Upper Permian System, and the Quaternary System (Q) (Figure 6).

Soluble rock strata are predominantly found in the Changxing Formation, the Qixia Formation, and the Hutian Group. The Hutian Group and the first (P₁q¹) and second (P₁q²) segments of the Qixia Formation consist of interbedded limestones, shales, argillaceous limestones, and dolomites, displaying well-developed karst features.

(3) Geological structure: the Yonghe Syncline is a minor fold structure oriented in a north-northwest direction. The syncline core consists of the Changxing Formation, with the wings comprising the Longtan Formation, the Maokou Formation, and the Qixia Formation. The strata dip gently, with angles ranging from 10° to 20°.

Several faults are present, including two strike-slip faults, two reverse faults, one transverse thrust fault, and two unidentified faults. The most prominent is the transverse thrust fault, which traverses the northern edge of the Ma’anling Phosphate Mine (Figure 6).

(4) Hydrogeological conditions: the groundwater in the area consists of karst water, bedrock weathering fissure water, and pore water within loose rock formations.

Figure 6

Figure 6. Relationship diagram among karst development, strata, and faults in the study area.

3.2 Overview of karst collapses

A total of 38 karst collapses were documented within the 14-km² exploration area (Figure 7), resulting in a collapse density of 2.71 occurrences per km². These collapses are primarily concentrated in regions with well-developed soluble rocks, significant fault activity, and strong surface water–groundwater interactions. The most affected areas include the Yueshan-Ou’s-Dahe area of Yongfu Village; the Juxiang Community, Yonghe Old Street, Huayuan Village of Yanxi Town; and the Nanshan-Jiacheng Village, Li Zhen Primary School (Old), Xinwan-Xinping regions.

Figure 7

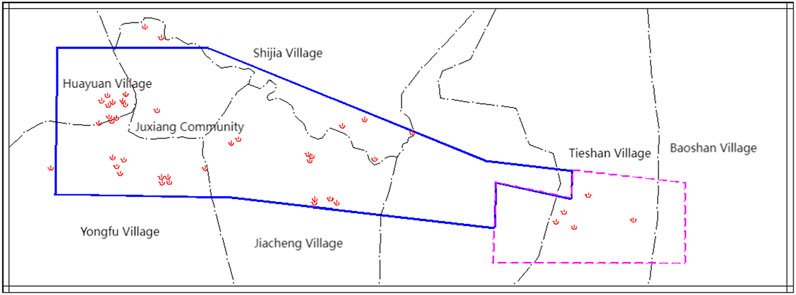
Figure 7. Distribution map of karst-collapse points in the exploration area (the blue solid line represents the scope of the exploration area, and the dotted line represents the scope of the prediction area).

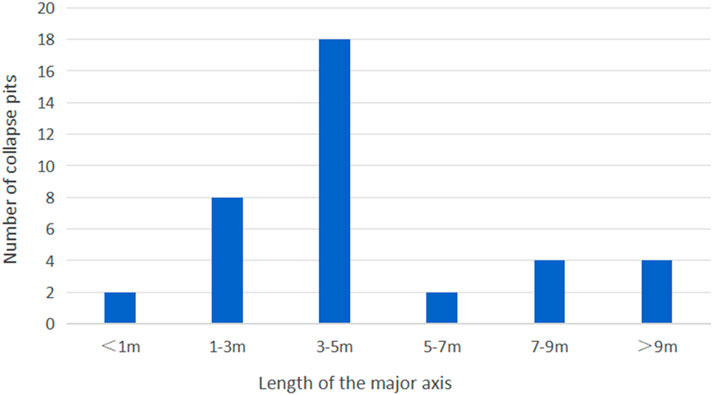
Most collapses are small-scale, with long-axis lengths ranging from 1 to 7 m, accounting for 73% of incidents (Figure 8).

Figure 8

Figure 8. Scale situation of the long axis of the collapse pits.

Xinwu Group, Jiacheng Village collapse (Figure 9a): this circular collapse pit has a long-axis length of approximately 3.5 m, a short-axis length of 2.5 m, and a depth of 1.2 m. The pit contains water, with the water level approximately 0.2 m below the surface. Bedrock is not visible, and the surrounding area consists of alluvial gravel-bearing silty clay, negatively impacting agricultural activities.

Figure 9

Figure 9. Examples of planar morphological characteristics of karst-collapse pits. (a) Karst collapse in the Xinwu Group of Jiacheng Village (T23). (b) Karst collapse in the Xinwan Group of Jiacheng Village (T27). (c) Karst collapse in the Xinping Group of Jiacheng Village (T30). (d) Karst collapse in the Shixing Group of Shijia Village (T32).

Xinwan Group, Jiacheng Village collapse (Figure 9b): this collapse is nearly circular, with a long-axis length of 2.3 m, a short-axis length of 2.2 m, and a depth of 10 m. The water level inside the pit is approximately 5 m. The primary triggering factors were groundwater extraction and heavy rainfall. Situated on a river terrace, the surrounding soil consists of silty clay with pebbles, forming a single-layer structure approximately 1 m thick. The underlying bedrock is limestone. Due to its instability, this collapse presents a continuous risk to local production and daily life.

3.3 Formation mechanism of karst collapses

The occurrence of karst collapses results from the complex interplay and cumulative effects of multiple formation mechanisms (Hu et al., 2001; Chen and Cao, 2023; Feng, 2025). Based on comprehensive investigations, in-depth research, and detailed exploration within the study area, the primary formation conditions include karst development characteristics, overburden properties, and hydrodynamic features.

(1) Impact of the karst development degree on karst collapses: karst development serves as the essential foundation and prerequisite for the occurrence of karst collapses. Statistical analysis indicates that most collapse pits in the study area are located within or near intense karst development zones. Notably, collapses are most prevalent in strata with well-developed karst, particularly within the second segment of the Qixia Formation (P₁q²) of the Lower Permian System and the Hutian Group (C₂₊₃ht) of the Middle and Upper Carboniferous Systems. This strong correlation underscores the critical influence of karst development on the formation of collapses.

(2) Influence of overburden characteristics on karst collapses: the overburden comprises Quaternary loose soil layers that cover the bedrock surface. Collapse pits are primarily concentrated in covered karst regions, where the thickness of the Quaternary loose layer generally does not exceed 20 m. Areas with alluvial and diluvial deposits that lack a clay layer at the base are particularly vulnerable to collapse formation. From a geotechnical perspective, these soil layers exhibit low shear strength and limited resistance to seepage-induced deformation, making them susceptible to piping processes and subsequent collapses.

For instance, in the collapse-affected section spanning the Zhoushang Group of Huayuan Village, Juxiang Community, Yonghe Old Street, Mingshan Group of Yongfu Village, Yueshan, Ou’s Group, and Dahe Group, the soil structure consists predominantly of gravel-bearing silty clay formed through alluvial and diluvial processes, along with residual slope-derived crushed stone soil. The total thickness of the soil layer ranges from 5.5 to 13.5 m. In these areas, the upper silty clay layer is relatively thin, and the absence of a water-retaining clay layer at the base facilitates the infiltration of atmospheric precipitation, surface water seepage, and the upward movement of water and sand during the increase in the karst water level. Consequently, the thickness and physical properties of the overburden significantly regulate the collapse process.

(3) Effect of hydrodynamic characteristics on karst collapses: the study area contains two distinct groundwater layers: the upper-layer Quaternary pore water and the lower-layer karst water. The upper-layer pore water is primarily stored in silty clay, pebble-bearing soil, and residual crushed stone soil from Quaternary alluvial and diluvial facies. Recharge sources include atmospheric precipitation and seepage from nearby surface water bodies such as the Daxi River. During recharge, seepage forces can trigger piping within the soil layer, leading to cavity formation, which may expand and eventually result in collapse.

The lower-layer karst water mainly originates from the limestone aquifer of P₁q and the limestone karst–cave aquifer of C₂₃ht, both exhibiting significant karst development and high water-bearing capacity. Groundwater extraction often lowers the karst water level, prompting the continuous recharge of upper-layer pore water into the karst aquifer. Fine-grained soil particles are transported by the flowing water, further accelerating the collapse process. In conclusion, the coexistence of the two-layer groundwater system, the presence of a significant hydraulic gradient, and the infiltration of surface water bodies jointly alter the hydrodynamic characteristics of the region, playing a pivotal role in the formation of karst collapses.

3.4 Determination of influencing factors for the susceptibility of karst collapses

The development of karst collapses is influenced by the combined effects of multiple factors. Nonlinear relationships exist not only among these factors but also between each factor and the occurrence of karst collapses (Chen and Cao, 2023). Through extensive on-site investigations and comprehensive analyses of the formation mechanisms of numerous karst collapses, this study identified the key factors for predicting karst-collapse susceptibility.

3.4.1 Karst development degree

Soluble rocks provide the material basis for karstification, with their solubility directly impacting the extent of karst development. In the region extending from the Zhoushang Group of Huayuan Village to Juxiang Community, Yonghe Old Street, Yueshan Group, Ou’s Group, and Dahe Group, 29 karst collapses have occurred. Borehole data from 15 boreholes revealed karst caves in five of them, yielding a karst–cave encounter rate of 33.3%. Among the six identified caves, five developed within the second member of the Lower Permian Qixia Formation (P₁q²), characterized by thick-bedded dark gray limestone with a faint flesh-red tinge, interbedded with thin layers of marl and dolomite. Geophysical interpretation indicated that 76.98% of the 505 detected anomalies were karst related, predominantly in the Qixia Formation.

3.4.2 Distance from intra-area faults

Fault structures provide conduits for groundwater flow and play a decisive role in karst development. On-site investigations revealed that karst collapses are concentrated along concealed and unidentified faults on both sides of the NW-trending secondary faults within the northern plate of the Henggu Fault. Notably, four collapses in Yongfu Village, Yonghe Town, occurred approximately 200 m west of a concealed fault. This positive correlation highlights the influence of fault zones on collapse occurrence.

3.4.3 Thickness of the overlying soil layer

The development and distribution of karst collapses are closely linked to the thickness of the Quaternary layer. Survey results indicated that the Quaternary layer in the Dahe Group, Yueshan Group, Ou’s Group, and Mingshan Group of Yongfu Village, as well as in the Zhoushang Group, Juxiang Community, and Yonghe Old Street in Huayuan Village, ranged from 5.50 to 13.5 m. Additionally, the thickness of the upper silty clay layer was generally ≤3 m. The presence of a thin silty clay layer facilitates water infiltration and groundwater-level fluctuations, increasing the likelihood of collapses.

3.4.4 Groundwater fluctuation range

Karst water fluctuates between confined and unconfined states near the bedrock surface, contributing to collapse occurrence. Survey data from the Yueshan Group and Ou’s Group regions indicated that groundwater levels ranged from 9.27 to 25.90 m during the wet season, with the bedrock surface buried at depths of 15.00–30.70 m. During the dry season, groundwater levels decrease by 5–10 m, maintaining their position near the bedrock surface. This fluctuation promotes the “bellows effect,” characterized by piping and suction erosion of the overlying soil, which increases the risk of collapse.

3.4.5 Distance from the center of the artificial pumping funnel

Before October 2016, mining at the Ma’an Phosphate Mine reached an elevation of approximately ±0 m, affecting an area within a 2-km radius, primarily around Huayuan Village, Juxiang Community, Yongfu Village, and Yonghe Middle School. Investigations documented 89 instances of house and ground cracking, accounting for 44.9% of all cases, alongside 22 collapse pits (57.9%). Since the cessation of mining activities, a significant decrease in collapses and cracking incidents has been observed, underscoring the impact of groundwater extraction on collapse susceptibility.

3.4.6 Development density of existing ground collapses

A total of 38 ground collapses were identified within the study area, distributed as follows: 16 collapses in the Mingshan Group, Yueshan Group, Ou’s Group, and Dahe Group of Yongfu Village; 12 in the Zhoushang Group, Juxiang Community, and Yonghe Old Street in Huayuan Village; three in the Yonghe Middle School and Nanshan Group area of Jiacheng Village; seven in the Li Zhen Primary School (Old), Xinwan Group, and Xinping Group area; and four in the Tieshan Village and Qibaoshan Village area. The density of existing collapses was considered a key predictive indicator.

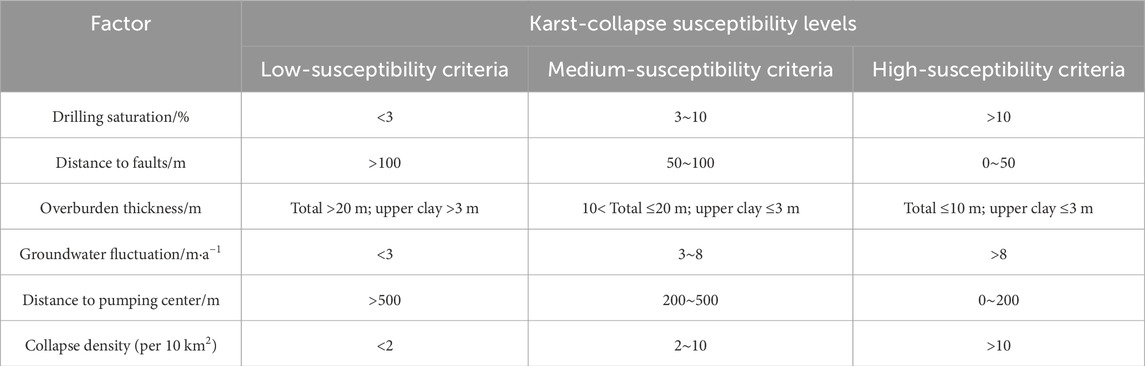
Following the relevant guidelines (Ministry of Natural Resources of the People’s Republic of China, 2023) and building on previous studies (Huang et al., 2011; YanHua et al., 2022), in this study, we integrated field survey results, geophysical exploration data, and borehole data to identify six key factors influencing karst-collapse susceptibility (Table 1). Through a comprehensive analysis of the field survey data, the susceptibility levels of karst collapse were assessed. To effectively represent the likelihood of collapse occurrences, the susceptibility levels were classified into three categories: low susceptibility, medium susceptibility, and high susceptibility, corresponding to category labels 1, 2, and 3, respectively (Table 2).

Table 1

Table 1. Classification of influencing factors for karst-collapse susceptibility.

Table 2

Table 2. Class labels for the grading of expected output parameters.

4 Case analysis

4.1 Data collection and preprocessing

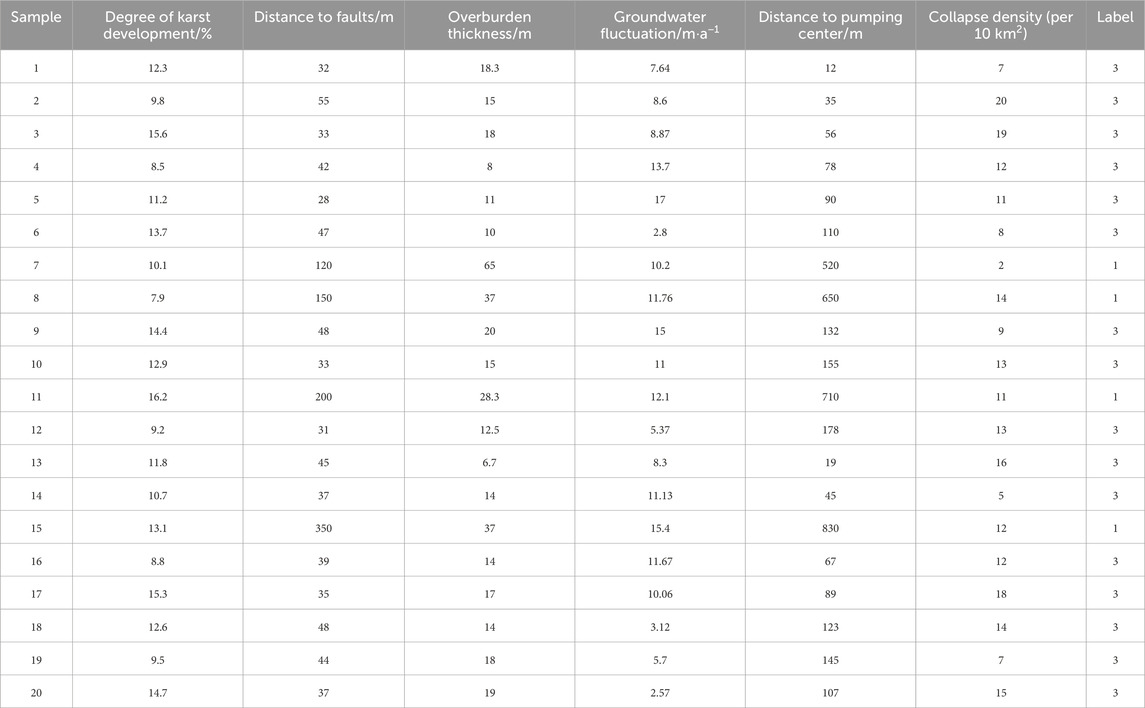
The karst-collapse-affected area in Yonghe Town, Liuyang City, Hunan Province, was selected as the research subject. A total of 20 sets of sample data were collected within the exploration zone, comprising 16 samples from collapsed pits and four samples from non-collapsed pits representing locations with no recent collapses within 1 km of the sampling points and also considered similar geological settings (like lithology and stratigraphy) and hydrogeological conditions (groundwater levels, flow, and quality) (Table 3). This dataset was used to evaluate the feasibility of the ISSA-ELM model for predicting the karst-collapse susceptibility.

Table 3

Table 3. Sample dataset.

Given the complex interrelationships among various influencing factors of karst collapses, using all factors as inputs could introduce information redundancy. To mitigate this, PCA was applied to reduce the dimensionality and remove correlations among six key factors: the degree of karst development, the distance from faults, the thickness of the overlying soil layer, the groundwater fluctuation range, the distance from the center of the artificial pumping funnel, and the development density of preexisting ground collapses. This approach retained the essential information while minimizing redundancy.

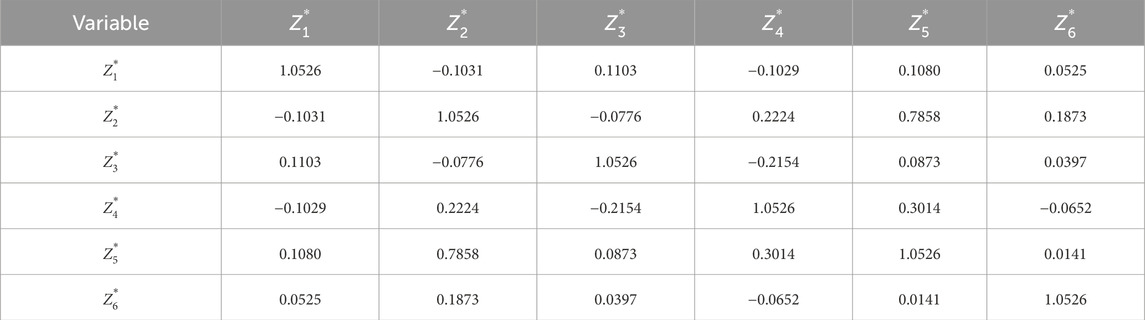
The original data were standardized to eliminate the impact of differing units and magnitudes. A standardized covariance matrix was then calculated (Table 4), followed by an in-depth correlation analysis to explore the relationships among the influencing factors. Eigenvalues and contribution rates were derived from the covariance matrix, and principal components were selected based on a cumulative contribution rate exceeding the widely accepted threshold of 85% (Table 5).

Table 4

Table 4. Covariance matrix of six variables.

Table 5

Table 5. Eigenvalues of the covariance matrix for each variable.

As shown in Table 5, the cumulative contribution rate of the first five principal components was 96.87%, surpassing the 85% threshold. Therefore, these five principal components were chosen to represent the original six variables.

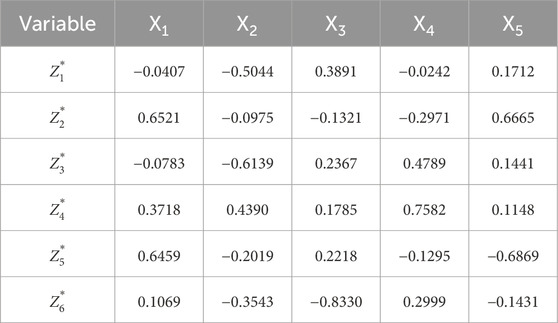
Based on the eigenvector matrix (Table 6), the principal components were expressed as follows:

Table 6

Table 6. Eigenvectors corresponding to the eigenvalues of the covariance matrix of six variables.

The karst-collapse-affected area in Yonghe Town, Liuyang City, Hunan Province, was selected as the research subject. A total of 20 sets of sample data were collected within the exploration zone, comprising 16 samples from collapsed pits and four samples from non-collapsed pits representing locations with no recent collapses within 1 km of the sampling points (Table 3). This dataset was used to evaluate the feasibility of the ISSA-ELM (improved sparrow search algorithm-extreme learning machine) model for predicting karst-collapse susceptibility.

Given the complex interrelationships among various influencing factors of karst collapses, using all factors as inputs could introduce information redundancy. To mitigate this, PCA was applied to reduce dimensionality and remove correlations among six key factors: the degree of karst development, the distance from faults, the thickness of the overlying soil layer, the groundwater fluctuation range, the distance from the center of the artificial pumping funnel, and the development density of preexisting ground collapses. This approach retained essential information while minimizing redundancy.

The original data were standardized to eliminate the impact of differing units and magnitudes. A standardized covariance matrix was then calculated (Table 4), followed by an in-depth correlation analysis to explore the relationships among the influencing factors. Eigenvalues and contribution rates were derived from the covariance matrix, and principal components were selected based on a cumulative contribution rate exceeding the widely accepted threshold of 85% (Table 5).

As shown in Table 5, the cumulative contribution rate of the first five principal components was 96.87%, surpassing the 85% threshold. Therefore, these five principal components were chosen to represent the original six variables.

Based on the eigenvector matrix, the principal components were expressed as follows:

${\mathrm{X}}_1=-0.0407{\mathrm{Z}}_1^{*}+0.6521{\mathrm{Z}}_2^{*}-0.0783{\mathrm{Z}}_3^{*}+0.3718{\mathrm{Z}}_4^{*}+0.6459{\mathrm{Z}}_5^{*}+0.1069{\mathrm{Z}}_{6,}^{*}$

${\mathrm{X}}_2=-0.5044{\mathrm{Z}}_1^{*}-0.0975{\mathrm{Z}}_2^{*}-0.6139{\mathrm{Z}}_3^{*}+0.4390{\mathrm{Z}}_4^{*}-0.2019{\mathrm{Z}}_5^{*}-0.3543{\mathrm{Z}}_{6,}^{*}$

${\mathrm{X}}_3=0.3891{\mathrm{Z}}_1^{*}-0.1321+0.2367{\mathrm{Z}}_3^{*}+0.1785{\mathrm{Z}}_4^{*}+0.2218{\mathrm{Z}}_5^{*}-0.8330{\mathrm{Z}}_{6,}^{*}$

${\mathrm{X}}_4=-0.0242{\mathrm{Z}}_1^{*}-0.2971{\mathrm{Z}}_2^{*}+0.4789{\mathrm{Z}}_3^{*}+0.7582{\mathrm{Z}}_4^{*}-0.1295{\mathrm{Z}}_5^{*}+0.2999{\mathrm{Z}}_{6,}^{*}$

${\mathrm{X}}_5=0.1712{\mathrm{Z}}_1^{*}+0.6665{\mathrm{Z}}_2^{*}+0.1441{\mathrm{Z}}_3^{*}+0.1148{\mathrm{Z}}_4^{*}-0.6869{\mathrm{Z}}_5^{*}-0.1431{\mathrm{Z}}_{6,}^{*}$

where ${\mathrm{Z}}_1*$, ${\mathrm{Z}}_2*$, ${\mathrm{Z}}_3*$, ${\mathrm{Z}}_4*$, ${\mathrm{Z}}_4*$, ${\mathrm{Z}}_5*$, and ${\mathrm{Z}}_6*$ represent the standardized values of the degree of karst development, the distance from faults, the thickness of the overlying soil layer, the groundwater fluctuation range, the distance from the pumping funnel center, and the development density of existing ground collapses, respectively.

The principal components were subsequently calculated using these expressions (Table 7) and used for training the ISSA-ELM model.

Table 7

Table 7. Sample principal components of 20 sets of original data.

4.2 Optimization of model parameters

From the PCA-processed dataset, 14 samples were designated as the training set, whereas the remaining six samples were used as the test set. This 7:3 split ensured a balanced approach, maintaining sufficient data for training while reserving a representative subset for evaluating the model’s generalization performance.

The ISSA-ELM model parameters were configured as follows: population size N = 20, maximum iterations = 100, warning threshold ST = 0.6, proportion of discoverers PD = 0.7, and proportion of scouts SD = 0.2.

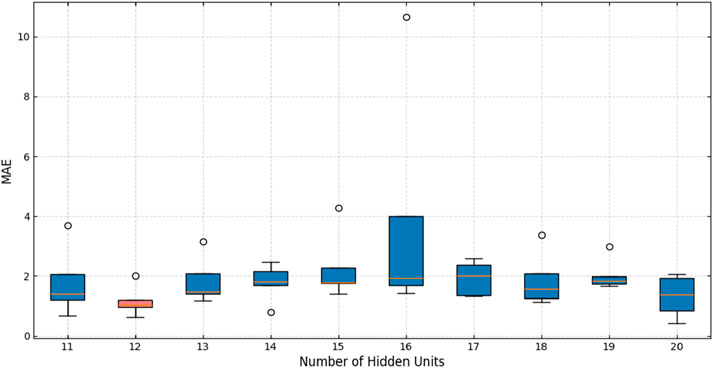
The number of hidden-layer nodes significantly affects model performance. In the ELM model, the number of input-layer nodes was set to 5, corresponding to the number of principal components. The sigmoid function was applied as the activation function. The number of hidden-layer nodes was selected within the range [2n+1, N] (where n is the number of nodes in the input layer n = 5, and N denotes the total number of input samples N = 20), resulting in a range of [11, 20] (Jiang and Shi, 2023). A five-fold cross-validation approach was used to determine the optimal number of hidden-layer nodes, balancing computational efficiency and robust evaluation. The MAE index results (Figure 10) indicated that the optimal number of hidden layers was 12 as it produced a concentrated MAE distribution without significant outliers.

Figure 10

Figure 10. Error graph of five-fold cross-validation.

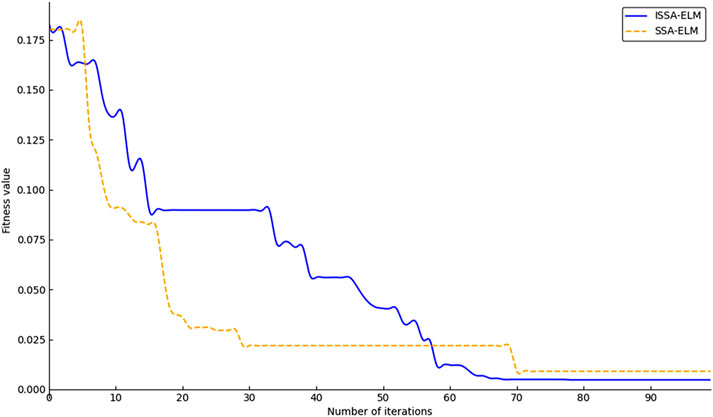
The PCA-processed data were input into the ISSA-ELM and SSA-ELM models for iterative comparisons. The resulting optimization curves (Figure 11) showed that the ISSA-ELM model achieved rapid convergence. After 63 iterations, its fitness value stabilized at approximately 0.0047. In contrast, the SSA-ELM model exhibited a slower convergence rate, requiring 70 iterations to reach a fitness value of approximately 0.009. These findings demonstrate that the ISSA-ELM model is closer to the global optimal solution and outperforms the SSA-ELM model in terms of both optimization capabilities and search speed.

Figure 11

Figure 11. Adaptation graph.

4.3 Prediction of karst-collapse susceptibility

The optimal parameter combination was identified using the ISSA in conjunction with a five-fold cross-validation technique. These optimized parameters were then applied to the ELM model, resulting in the ISSA-ELM model. To comprehensively evaluate the effectiveness of PCA for data preprocessing and to assess the predictive capability of the ISSA-ELM model in karst-collapse susceptibility prediction, validation experiments were conducted using two independent datasets. One dataset consisted of 20 sets of raw field-measured data from the exploration area, whereas the other contained PCA-processed data to reduce dimensionality and mitigate redundancy.

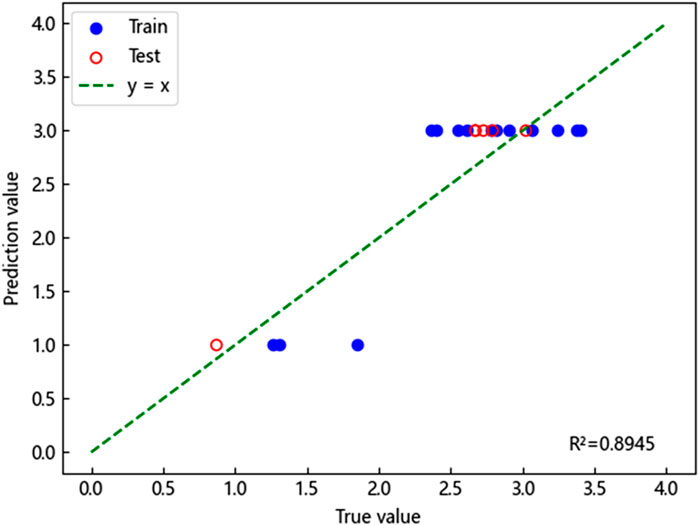
The training datasets were used to develop the ISSA-ELM model, which was subsequently applied to the test datasets to generate predictions. The predicted values were then compared to the actual values to assess the model’s predictive accuracy (refer to Figures 12–14). A comparative analysis was also performed to evaluate the relative performance of the ISSA-ELM model, the SSA-ELM model, and the conventional ELM model.

Figure 12

Figure 12. Prediction results of the ISSA-ELM model (without PCA processing).

Figure 13

Figure 13. Prediction results of the ISSA-ELM model (with PCA processing).

Figure 14

Figure 14. Prediction results of the SSA-ELM model.

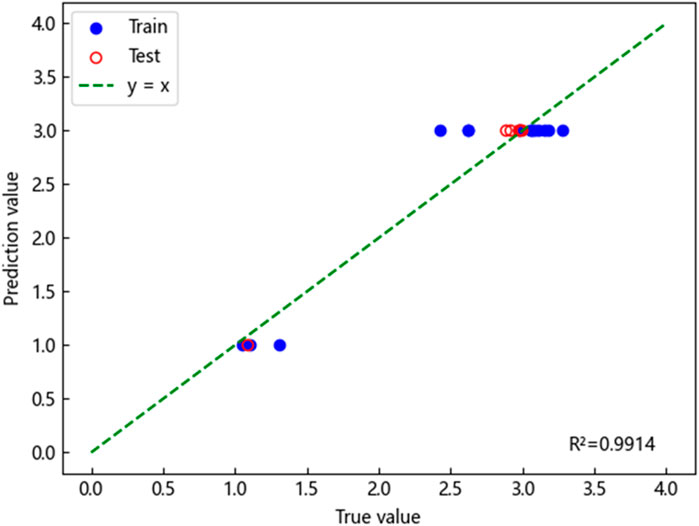
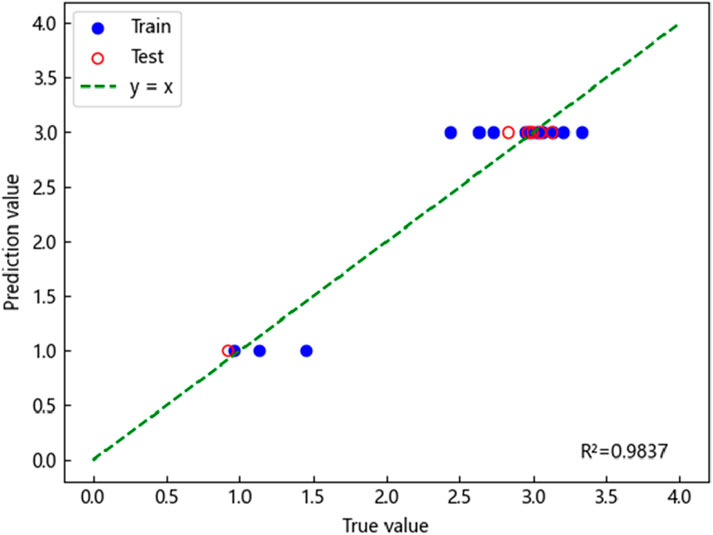
The fitting results demonstrated that the predicted and actual values for all three models exhibited a generally linear relationship, indicating a reasonable degree of accuracy. However, the coefficient of determination (${\mathrm{R}}^2=0.9914$) for the PCA-processed ISSA-ELM model was significantly higher than that for both the non-PCA-processed ISSA-ELM model (${\mathrm{R}}^2=0.8945$) and the SSA-ELM model (${\mathrm{R}}^2=0.9837$). This finding suggests that applying PCA preprocessing effectively enhances the predictive accuracy by reducing noise and eliminating redundant information.

Furthermore, the ISSA-ELM model’s predicted values displayed a superior alignment with actual values, reflecting the model’s ability to capture complex nonlinear relationships among the influencing factors of karst collapse. This improvement in predictive capability highlights the robustness and reliability of the ISSA-ELM model as an effective tool for karst-collapse susceptibility assessment. Its strong performance offers valuable insights for practical applications in geological hazard management and regional risk assessment.

4.4 Analysis of error metrics

To further evaluate the performance of the ISSA-ELM model, three quantitative metrics were applied: ${\mathrm{R}}^2$, MSE, and MAE, as described in Section 2.7. A comprehensive comparative analysis was conducted to assess the predictive accuracy and generalization capability of the ISSA-ELM model against the SSA-ELM model and the conventional ELM model (Figure 15)

Figure 15

Figure 15. Comparison of error metrics among various models.

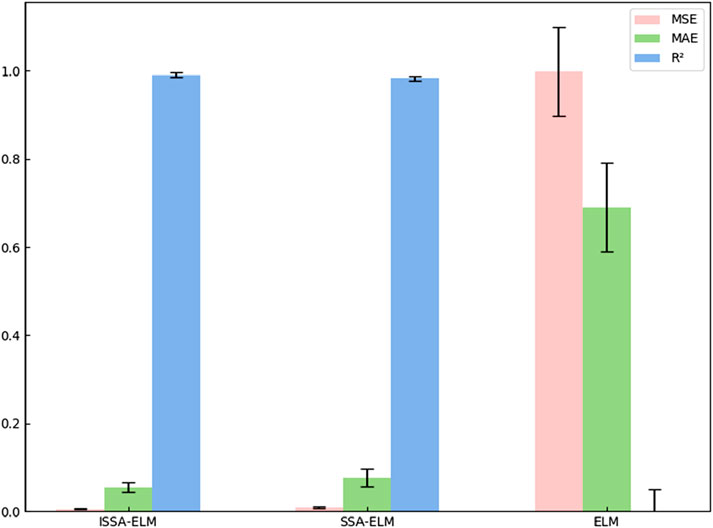
The results presented in Figure 15 indicate that the ISSA-ELM model achieved the lowest MSE (0.0047) and MAE (0.0544) among all models. In comparison, the SSA-ELM model reported an MSE of 0.0091 and an MAE of 0.0766, whereas the ELM model exhibited a significantly higher MSE of 0.9988 and an MAE of 0.6903. These results clearly demonstrate the superior predictive accuracy and robustness of the ISSA-ELM model. The enhanced convergence of the ISSA, facilitated by the integration of the Singer chaotic map, effectively mitigated the limitations of traditional sparrow search algorithms, preventing premature convergence and ensuring optimal parameter selection.

Furthermore, the goodness-of-fit coefficient (${\mathrm{R}}^2$) of the ISSA-ELM model was markedly higher than those of the SSA-ELM and ELM models. This result reflects the ISSA-ELM model’s excellent generalization performance, indicating its ability to make accurate predictions across diverse datasets. The reduced error values and consistent prediction accuracy further validate the model’s reliability and stability.

In summary, the ISSA-ELM model exhibits substantial advantages in karst-collapse susceptibility prediction. Its remarkable accuracy, minimized prediction errors, and robust generalization capacity make it an effective and reliable tool for geohazard risk assessment. Consequently, the model can serve as a valuable decision-support system for policymakers, urban planners, and geotechnical engineers engaged in geological disaster prevention and management.

4.5 Model validation

To comprehensively evaluate the effectiveness and accuracy of the ISSA-ELM model in predicting the karst-collapse susceptibility, the evaluation area shown in Figure 7 was designated as the primary study region. Subsequently, the prediction scope was expanded to cover the entire Yonghe Town. A karst-collapse susceptibility zoning map was generated using MAPGIS software, as illustrated in Figure 16.

Figure 16

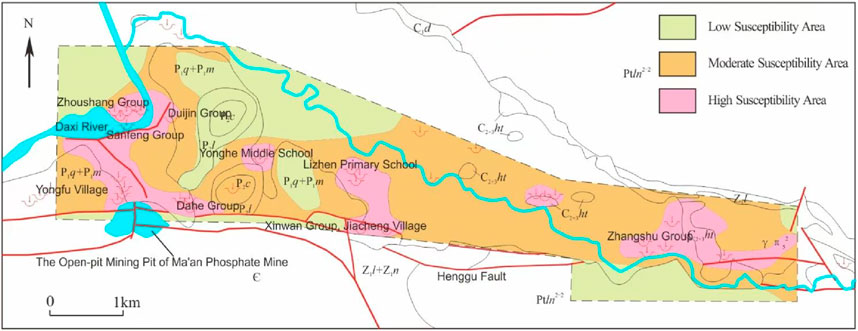
Figure 16. Zoning map of karst-collapse susceptibility grades in Yonghe Town, Liuyang City, Hunan Province conclusions.

The results reveal that Yonghe Middle School, Lizhen Primary School—Xinwan Group of Jiacheng Village, Sanfeng Group—Dahe Group, and Zhangshu Group are classified as high-susceptibility zones. Conversely, Duijin Group and Zhoushang Group are identified as low-susceptibility areas, with other regions falling under medium-susceptibility zones.

Notably, numerous collapse pits were identified in Jingquan Village, Tieshan Village, and Qibaoshan Village, all located in proximity to the Qibaoshan mining area. Although most pits have been backfilled, a substantial secondary collapse occurred in the Zhangshu Group of Tieshan Village. This incident further substantiates the predictive reliability of the ISSA-ELM model, which accurately identified high-susceptibility regions. The model’s capacity to predict secondary collapses post-backfilling highlights its practical applicability in real-world scenarios.

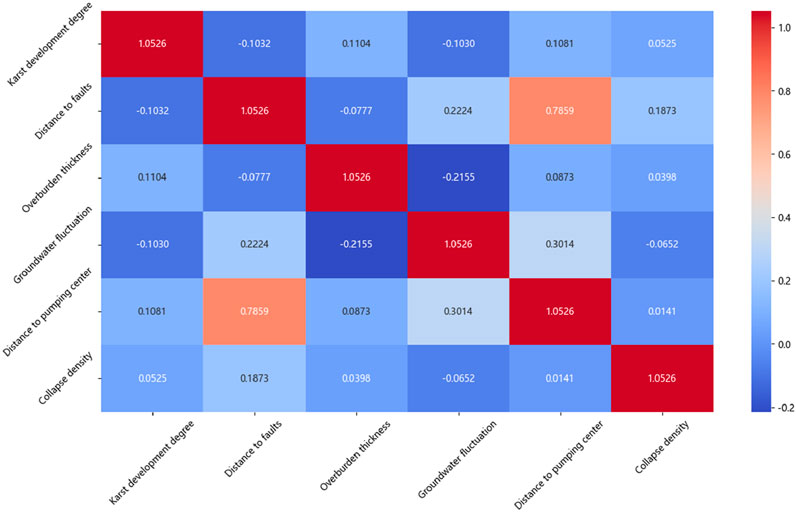
The correlation analysis of influencing factors, presented in Section 4.1 (Figure 17), further corroborates these findings. Proximity to intra-area faults and the distance from the pumping funnel center were identified as primary determinants of karst-collapse susceptibility. These insights provide a strong basis for the implementation of targeted disaster prevention and mitigation measures.

Figure 17

Figure 17. Correlation diagram of influencing factors of karst collapses.

To mitigate the risk of karst collapses effectively, comprehensive monitoring and preventive measures are essential in high-susceptibility regions. Advanced remote sensing, geophysical exploration techniques, and real-time monitoring systems can provide early warnings and facilitate rapid response efforts. Additionally, evidence-based management strategies, including regulated groundwater extraction and optimized land-use planning, should be prioritized to minimize collapse incidents.

Furthermore, this research provides valuable theoretical support for urban planning, particularly in the determination of disaster-avoidance distances. Policymakers and urban planners can utilize the susceptibility zoning map to make informed decisions, ensuring that critical infrastructure and densely populated areas are located outside high-susceptibility zones.

5 Conclusion

(1) In this study, we used PCA for dimensionality reduction in karst-collapse susceptibility factors. Comparative analysis confirmed that the application of PCA significantly enhanced the predictive accuracy of the ISSA-ELM model, resulting in a 10.83% increase in R². This demonstrates the effectiveness of PCA in reducing data redundancy and extracting critical features.

(2) To overcome the limitations of the traditional SSA, including local optima convergence and slow convergence speed, the Singer chaotic map was introduced for population initialization. This enhancement resulted in the development of the ISSA, which was integrated with the ELM model. The ISSA-ELM model exhibited superior predictive performance across 20 measured datasets, achieving an MAE of 0.0544, an MSE of 0.0047, and an R² of 0.9914. These results highlight the model’s exceptional accuracy and robust generalization capability compared to conventional ELM and SSA-ELM models.

(3) The optimal number of hidden-layer nodes in the ELM model was determined through a rigorous five-fold cross-validation approach. This method effectively mitigated the risks of underfitting and overfitting while maximizing the use of limited data. The selected optimal number of nodes (N = 12) further demonstrated the effectiveness of this approach in fine-tuning model hyperparameters.

(4) The ISSA-ELM model was applied for the first time to predict karst-collapse susceptibility. The generated susceptibility zoning map showed a significant spatial correlation between high-susceptibility zones and densely populated areas, including schools and villages. Through correlation analysis, the primary influencing factors were identified, offering a solid theoretical foundation for determining disaster-avoidance distances in urban planning. The findings provide essential guidance for policymakers in developing evidence-based disaster prevention and mitigation strategies.

(5) Despite its promising results, this study has certain limitations:

① Limited dataset: the dataset used for model training and validation was relatively small, which may affect the model’s generalizability.

② Activation function selection: only the sigmoid activation function was applied, with no comparative analysis involving other functions. Future studies could explore Tanh or ReLU activation functions to assess their impact on model performance.

③ Data imbalance: the dataset contained limited non-disaster-point data, potentially resulting in an incomplete representation of non-disaster areas. Techniques such as the synthetic minority over-sampling technique (SMOTE) could be applied to address this imbalance.

④ Normalization methods: the study did not investigate the effects of different normalization methods, leaving the potential impact of alternative approaches unexplored.

(6) To further refine and validate the ISSA-ELM model, future research should focus on the following aspects:

① Dataset expansion: incorporating additional data from various karst regions will improve model training and validation.

② Activation function evaluation: comparative studies of different activation functions, including Tanh and ReLU, can optimize model performance.

③ Algorithmic enhancements: developing hybrid optimization strategies could further mitigate the risk of local optima in the sparrow algorithm.

④ Data balancing: applying algorithms like SMOTE will balance the sample distribution and enhance model robustness.

⑤ Normalization analysis: evaluating the impact of different normalization methods will provide insights into their influence on prediction accuracy.

⑥ Generalizability assessment: applying the ISSA-ELM model to other karst regions with diverse geological and hydrological conditions will assess its broader applicability.

By addressing these aspects, future research can further enhance the predictive accuracy, stability, and practical applicability of the ISSA-ELM model. Ultimately, this will contribute to more effective karst-collapse prevention and improved risk management strategies.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

JW: conceptualization, data curation, and writing – original draft. YY: methodology, supervision, and writing – review and editing. XY: data curation, supervision, validation, and writing – original draft. YuL: data curation, investigation, and writing – review and editing. YaL: data curation, investigation, and writing – review and editing. DH: software, validation, and writing – review and editing. YH: software and writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

The authors are grateful to the Hunan Institute of Territorial Spatial Survey and Monitoring, providing access to field data and technical support.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1581090/full#supplementary-material.

References

Bao, H. M., and Hu, C. S. (2002). Neural network prediction of karst ground collapse. J. Eng. Geol. 10 (3), 299–304. doi:10.3969/j.issn.1004-9665.2002.03.014

CrossRef Full Text | Google Scholar

Bouzerda, M., Mehdi, K., Boualla, O., Fadili, A., Najib, S., and Saied, M. (2024). Inventory and geomorphological analysis of karstic collapse dolines in Sahel-Doukkala (Morocco). Carbonates Evaporites 39 (4), 93. doi:10.1007/s13146-024-01007-7

CrossRef Full Text | Google Scholar

Cao, B., Bai, G., and Li, H. (2015). Prediction and analysis of gas content based on PCA-GA-BP neural network. J. Saf. Sci. Technol. (5), 84–90. doi:10.11731/j.issn.1673-193x.2015.05.013

CrossRef Full Text | Google Scholar

Chen, D., and Cao, Y. (2023). Numerical simulation of karst collapse in qingling Town, wuhan. J. Phys. Conf. Ser. 2565 (1), 012034. doi:10.1088/1742-6596/2565/1/012034

CrossRef Full Text | Google Scholar

Chen, X. J., Chen, L. J., Song, Y., and Pengyan, B. (2019). Prediction and analysis of karst collapse with entropy - normal cloud model. J. Eng. Geol. 27 (6), 1389–1394. doi:10.13544/j.cnki.jeg.2018-347

CrossRef Full Text | Google Scholar

Chen, H. F., Zhu, M. Q., Xia, R. Y., Tang, J. S., and Liang, B. (2005). Analysis on epikarst spring with BP ANN in Luota, Hunan Province. Carsologica Sin. (4), 300–304 doi:10.3969/j.issn.1001-4810.2005.04.008

CrossRef Full Text | Google Scholar

Ding, H., Wu, Q., Zhao, D., Mu, W., and Yu, S. (2019). Risk assessment of karst collapse using an integrated fuzzy analytic hierarchy process and grey relational analysis model. Geomechanics Eng. 18 (5), 515–525. doi:10.12989/gae.2019.18.5.515

CrossRef Full Text | Google Scholar

En, W., Long-Cang, S., Li-Hong, L., and Bi-Juan, H. (2011). Prediction model for water level of sinkholes in karst region based on improved SVM. J. Hohai Univ. Nat. Sci. 39 (1), 20–23. doi:10.1007/s12182-011-0118-0

CrossRef Full Text | Google Scholar

Feng, T. (2025). Mechanism and stability analysis of karst collapse in jingquan water source area of tengzhou city. Singapore: Springer. doi:10.1007/978-981-97-7251-3_20

CrossRef Full Text | Google Scholar

Gao, C., Li, S., Wang, J., Li, L., and Lin, P. (2018). The risk assessment of tunnels based on grey correlation and entropy weight method. Geotech. Geol. Eng. 36, 1621–1631. doi:10.1007/s10706-017-0415-5

CrossRef Full Text | Google Scholar

Gao, Z. J., Ma, H. H., Wang, M., and Cheng, S. C. (2009). Preliminary exploration of the prediction model for karst ground collapse. Chin. J. Geol. Hazard Control. 20 (4), 66–71. doi:10.3969/j.issn.1003-8035.2009.04.014

CrossRef Full Text | Google Scholar

Hu, R., Yeung, M., Lee, C., S., W., and J., X. (2001). Regional risk assessment of karst collapse in Tangshan, China. Environ. Geol. 40 (11), 1377–1389. doi:10.1007/s002540100319

CrossRef Full Text | Google Scholar

Huang, G. B., Zhu, Q. Y., and Siew, C. K. (2006). Extreme learning machine: theory and applications. Neurocomputing 70 (1/3), 489–501. doi:10.1016/j.neucom.2005.12.126

CrossRef Full Text | Google Scholar

Huang, R. D., Han, M., Zhang, X. J., Zhang, H., Jin, H., and Hua, Z. (2011). Classification and prediction of karst collapse tendency grade based on Fisher discriminant method. China Saf. Sci. J. 21 (9), 70–76. doi:10.3969/j.issn.1003-3033.2011.09.012

CrossRef Full Text | Google Scholar

Jiang, C. L., and Jiang, Z. Q. (2012). Prediction of karst collapse based on Fisher discriminant analysis method. J. Earth Sci. Environ. 34 (1), 5. doi:10.3969/j.issn.1672-6561.2012.01.012

CrossRef Full Text | Google Scholar

Jiang, S. Q., and Shi, B. (2023). Prediction of failure pressure of pipelines with corrosion defects based on the ISSA-ELM model. Hot Work. Technol. 52 (12), 70–75 + 80. doi:10.14158/j.cnki.1001-3814.20221045

CrossRef Full Text | Google Scholar

Jiyuan, H., Mahdi, M., Jiayao, W., Qin, F., Zhang, J., Wu, W., et al. (2021). Karst collapse risk zonation and evaluation in wuhan, China based on analytic hierarchy process, logistic regression, and InSAR angular distortion approaches. Remote Sens. 13 (24), 5063. doi:10.3390/rs13245063

CrossRef Full Text | Google Scholar

Journal of Chemistry (2023). Retracted: study on early warning of karst collapse based on the BP neural network. 1. doi:10.1155/2023/9818621

CrossRef Full Text | Google Scholar

Lai, Y. B., and Qiao, C. S. (2008). An intelligent prediction model for karst collapse based on support vector machine. J. Beijing Jiaot. Univ. 32 (1), 5. doi:10.3969/j.issn.1673-0291.2008.01.009

CrossRef Full Text | Google Scholar

Liu, C. A., Feng, X. L., Sun, C. H., and Zhao, L. J. (2022). Maximum 2 - D entropy image segmentation method based on improved sparrow algorithm. Laser Technol. 46 (2), 274–282. doi:10.7510/jgjs.issn.1001-3806.2022.02.020

CrossRef Full Text | Google Scholar

Luo, X. J., and Shen, J. (2018). Research progress and prospect of karst ground collapse in China. Carsologica Sin. 37 (1): 101–111. doi:10.11932/karst20180106

CrossRef Full Text | Google Scholar

Lv, X., Mu, X. D., Zhang, J., and Wang, Z. (2021). Chaotic sparrow search optimization algorithm. J. Beijing Univ. Aeronautics Astronautics 47 (8), 1712–1720. doi:10.13700/j.bh.1001-5965.2020.0298

CrossRef Full Text | Google Scholar

Meng, Y., Huang, J. M., Lei, M. T., Li, Y., and Dai, J. L. (2009). Quantitative forecasting method of karst collapse based on grey Verhulst model. Carsologica Sin. (1), 17–22. doi:10.3969/j.issn.1001-4810.2009.01.004

CrossRef Full Text | Google Scholar

Ministry of Natural Resources of the People’s Republic of China (2023). DZ/T 0447-2023 specification for karst collapse survey. 1. Beijing: China Standard Press. 10–31.

Google Scholar

Pearson, K. (1901). LIII. On lines and planes of closest fit to systems of points in space. Philosophical Magazine Series 6. 2 (11), 559–572. doi:10.1080/14786440109462720

CrossRef Full Text | Google Scholar

Qiu, X. R. (2004). Grey - fuzzy comprehensive evaluation on the stability of karst collapse. Hydrogeology and Eng. Geol. 31 (4), 4. doi:10.3969/j.issn.1000-3665.2004.04.010

CrossRef Full Text | Google Scholar

Ren, T., Tian, G. L., Ning, Z. J., Zhou, A. H., Li, K., and Chen, S. (2023). Evaluation of karst collapse susceptibility based on geographical detector and random forest. J. Catastrophology 38 (3), 227–234. doi:10.3969/j.issn.1000-811X.2023.03.035

CrossRef Full Text | Google Scholar

Wang, G., Hao, J., Wen, H., and Cao, C. (2022). A random forest model of karst ground collapse susceptibility based on factor and parameter coupling optimization. Geocarto Int. 37 (27), 15548–15567. doi:10.1080/10106049.2022.2102216

CrossRef Full Text | Google Scholar

Wang, Z. Z., Zhuang, Z. H., Hu, F. Y., and Huang, W. L. (2024). Formation conditions and susceptibility assessment of karst collapses in the northern hilly area of Guangzhou City. J. China Geol. Hazard Control 35 (4), 163–172. doi:10.16031/j.cnki.issn.1003-8035.202311008

CrossRef Full Text | Google Scholar

Wei, A., Li, D., Zhou, Y., Deng, Q., and Yan, L. (2021). A novel combination approach for karst collapse susceptibility assessment using the analytic hierarchy process, catastrophe, and entropy model. Nat. Hazards 105, 405–430. doi:10.1007/s11069-020-04317-w

CrossRef Full Text | Google Scholar

Xiaozhen, J., Jianling, D., Zhiwen, Z., Li, X. J., Ma, X., Zhou, W., et al. (2024). An overview on karst collapse mechanism in China. Carbonates and Evaporites 39 (3), 71. doi:10.1007/s13146-024-00986-x

CrossRef Full Text | Google Scholar

Xie, J. F., Tan, F., Jiao, Y. Y., Zou, J., and Mao, Z. (2021). Prediction of karst ground collapse based on factor analysis-GA-ELM model. J. Eng. Geol. 29 (2), 236–544. doi:10.13544/j.cnki.jeg.2020-219

CrossRef Full Text | Google Scholar

Xue, J. K., and Shen, B. (2020). A novel swarm intelligence optimization approach: sparrow search algorithm. Systems Science and Control Engineering 8 (1), 22–34. doi:10.1080/21642583.2019.1708830

CrossRef Full Text | Google Scholar

Yang, Z., Li, B., Wu, H., Li, M., Fan, J., Chen, M., et al. (2023). Water consumption prediction and influencing factor analysis based on PCA-BP neural network in karst regions: a case study of Guizhou Province. Environmental Science and Pollution Research 30 (12), 33504–33515. doi:10.1007/s11356-022-24604-2

PubMed Abstract | CrossRef Full Text | Google Scholar

YanHua, X., BingHui, Z., YuXin, L., Liu, B. C., Zhang, C. F., and Lin, Y. S. (2022). Evaluation of the karst collapse susceptibility of subgrade based on the AHP method of ArcGIS and prevention measures: a case study of the quannan expressway, section K1379+300-K1471+920. Water 14 (9), 1432. doi:10.3390/w14091432

CrossRef Full Text | Google Scholar

Zhang, J., Bi, P., Wei, A. H., Tao, Z. B., and Zhu, H. C. (2021). Assessment of susceptibility to karst collapse in the Qixia Zhongqiao district of Yantai based on fuzzy comprehensive method. Carsologica Sinica (2), 215–220. doi:10.11932/karst2021y07

CrossRef Full Text | Google Scholar

Zhou, A. H., Niu, P. F., Yuan, Y., and Huang, H. C. (2020). Prediction of karst surface collapse risk in Fankou lead - zinc mine area based on PCA-PSO-SVM. Carsologica Sinica (4), 622–628. doi:10.11932/karst2020y30

CrossRef Full Text | Google Scholar

Zhuang, S. Y. (2022). Assessment of karst collapse susceptibility in yongding district, Longyan city using the fuzzy analytic hierarchy process. Geology of Fujian 41 (4), 323–331. doi:10.3969/j.issn.1001-3970.2022.04.008

CrossRef Full Text | Google Scholar