Time-domain electromagnetic inversion and application for VTI media based on convolutional neural networks

The distinct Vertical Transverse Isotropy (VTI) heterogeneity and anisotropic characteristics of shale are critical geophysical indicators for identifying shale gas sweet spots. To address the need for dynamic monitoring of the electrical properties of VTI shale reservoirs during hydraulic fracturing, this paper proposes a fast time-domain electromagnetic inversion method based on prior constraints and convolutional neural networks (CNN). Throughout the process, prior information from logging and magnetotelluric data is first integrated to construct a layered medium parameterization model. By fixing the electrical parameters of non-target layers and varying the vertical resistivity and anisotropy coefficient of the target layer, forward responses are generated to build the training dataset. A convolutional neural network (CNN) model is then designed to achieve the nonlinear mapping between the electromagnetic decay curve and the target parameters. During training, a dynamic learning rate scheduling strategy and Dropout regularization are applied to accelerate model convergence while avoiding overfitting. The results show that the convolutional neural network can effectively extract data features. Under noise-free conditions, the average relative inversion errors for the target layer’s resistivity and anisotropy coefficient are 2.26% and 2.32%, respectively, with an inversion time of less than one second per point. Tests on noisy data demonstrate the model’s noise resistance, with average relative errors remaining within an acceptable range when Gaussian noise below 5% is added. Application of field-measured transient electromagnetic data shows that the method effectively identifies changes in the target layer’s vertical resistivity and anisotropy coefficient induced by hydraulic fracturing, with the average resistivity decreasing from 11.49 to 7.27 (a 36.7% reduction) and the anisotropy coefficient decreasing from 3.21 to 1.58 (a 50.8% reduction). These trends are consistent with conclusions from laboratory core fracturing experiments. This study demonstrates that integrating prior constraints with deep learning can overcome the efficiency bottleneck of traditional inversion methods, providing a new approach for transient electromagnetic inversion in hydraulic fracturing monitoring.

1 Introduction

As the exploration and development of unconventional oil and gas resources such as shale gas gradually become an important part of the global energy strategy, how to efficiently and accurately assess the physical properties and fluid distribution of underground reservoirs has become a key issue in the field of oil and gas exploration (Fahad and Kamal, 2022). The significant VTI-type heterogeneity and anisotropic characteristics of shale reservoirs are key geophysical indicators for identifying shale gas sweet spots. Compared to seismic attributes (such as P-wave velocity and impedance), the electrical anisotropy of shale is more pronounced (Xiang et al., 2016). Especially during hydraulic fracturing, the injection of high-pressure fluid induces fracture propagation, causing significant changes in the electrical characteristics of the formation, particularly anisotropy (Heng et al., 2015). While magnetic source and electrical source magnetic component transient electromagnetic methods are also insensitive to electrical anisotropy, the electrical source electrical component transient electromagnetic method (TEM) shows unique advantages in this regard (Wang et al., 2015).

Traditional inversion methods often struggle to capture complex electrical variations in formations, especially in reservoirs with strong anisotropy. These methods typically assume that the subsurface medium is isotropic, which significantly affects the accuracy of inversion results in complex geological environments (Yin and Weidelt, 1999; Liu et al., 2018). To address this issue, deep learning methods such as Convolutional Neural Networks (CNN) provide new approaches for time-domain electromagnetic inversion. In recent years, the successful application of Convolutional Neural Networks (CNN) in fields such as image recognition, natural language processing, and physical inversion has demonstrated its advantages in handling high-dimensional complex data (Zhou et al., 2017; Vladimir, 2019). In electromagnetic inversion, Convolutional Neural Networks (CNN) can deeply mine data features through supervised learning and obtain effective inversion models through training, thereby overcoming the shortcomings of traditional methods in nonlinear and high-dimensional problems. Compared to traditional inversion methods, deep learning methods have the advantage of providing real-time inversion results once training is complete, effectively solving the problem of the long processing times associated with traditional inversion methods (Zhang et al., 2021). Among these, Liu et al. (2021) proposed a novel 18-layer residual fully convolutional neural network (18RFCN) for audio magnetotelluric (AMT) data inversion, and achieved excellent results when applied to field AMT data. Huang, (2021) implemented inversion in marine controlled-source electromagnetic detection using deep learning methods. Yan et al. (2023) achieved one-dimensional fast imaging of transient electromagnetics based on Convolutional Neural Networks (CNN), and introduced coordinate information as input parameters to enable rapid processing of area data. Yu et al. (2025) designed a ‘ResNet-50′residual neural network inversion model for two-dimensional magnetotelluric inversion. They tested the network with unfamiliar data and compared it with the NLCG inversion method, showing that the model not only achieves real-time accurate inversion but also has certain noise resistance. The aforementioned deep learning-based geophysical inversion methods are significantly more efficient than traditional regularization inversion methods, indicating that deep learning technology has broad application prospects in the field of electromagnetic inversion. However, there is a common issue that requires extensive coverage of the subsurface structure, which results in an exceptionally large training set, causing redundancy with a significant amount of invalid data. Therefore, this can significantly reduce the size of the training dataset, save computational resources, and improve efficiency. Additionally, by controlling variables, we can capture changes in the electrical properties of the target layer caused by fracturing during the inversion process, providing more reliable support for fracturing monitoring and decision-making.

Based on this scenario, this paper introduces a one-dimensional time-domain electromagnetic rapid inversion method based on CNN under VTI media, and discusses in detail the establishment of the training set, data preprocessing, deep learning model design and construction, network training, and hyperparameter design. First, fully utilize the existing prior geological data in the project to determine the physical property parameters of layers other than the target layer of interest. Then, set the range of variation for the physical property parameters of the target layer within a reasonable interval, and traverse the physical property parameters within the interval using logarithmic spacing to generate forward models. Use a data filtering algorithm to numerically simulate the transient electromagnetic response of the reservoir’s electrical anisotropy model to construct the sample dataset. Three datasets were generated to test the theoretical feasibility of the method by simulating low-resistivity target layers, high-resistivity target layers, and conventional target layers in a horizontally layered medium. Gaussian random noise with different proportions was added to the samples in the test set to evaluate the model’s noise resistance. Additionally, a learning rate scheduling strategy was introduced during training to accelerate the convergence of the model’s loss function. Finally, a set of formation model datasets was designed based on actual geological data combined with magnetotelluric inversion results. On the basis of inversion validation using synthetic data, real measured data from a survey line before and after fracturing was used for inversion. The results show that the network model constructed in this paper can invert the resistivity and anisotropy coefficients of the target layer. Especially in hydraulic fracturing scenarios, this method can efficiently capture the changes in subsurface resistivity and anisotropy coefficients, providing a new approach for transient electromagnetic inversion in hydraulic fracturing monitoring.

2 Methods

Inversion problems essentially involve deducing certain properties based on limited observations. In the hydraulic fracturing application scenario assumed in this paper, we simulate the formation conditions as a horizontally layered medium based on prior geological data. The forward process of the transient electromagnetic response can be represented by a function G (Equation 1):

$d=G\left(m,k\right)(1)$

where d represents the transient electromagnetic response data, m represents the physical parameters of the concerned target layer, including the anisotropy coefficient and the vertical resistivity, and k represents other parameters that can be constrained a priori, including non-target layer physical property parameters, transmitter output power, transmitter-receiver distance, survey point coordinates, etc. Given that the forward method’s correctness is validated, we control the variable k and set it consistent with the actual fracturing scenario. Then, we can attempt to establish the matrix mapping relationship g between response d and the concerned target layer’s physical parameters m for inversion, namely (Equation 2):

$g:\hspace{0.17em}d\to m(2)$

Due to the highly complex relationship between the electromagnetic field and the model parameters, it is difficult to express the mapping relationship g in simple mathematical terms. Therefore, we use supervised learning to train a convolutional neural network to extract the complex features embedded in the response data, in order to obtain the mapping relationship g_θ, that is (Equation 3):

$m=g_{\theta }\left(d\right)(3)$

where θ represents the hyperparameters and structural information of the neural network. To enable the neural network to learn the appropriate θ, a loss function L(θ) is introduced:

$L\left(\theta \right)=\frac{1}{N}{\displaystyle \sum _{i=1}^N}\Vert d_{obs}^i\left(\theta \right)-d_{pred}^i\left(\theta \right){\Vert }^2(4)$

where N is the number of samples, $d_{obs}^i\left(\theta \right)$ is the response data of the ith sample, and $d_{pred}^i\left(\theta \right)$ is the electromagnetic response predicted by the neural network. By optimizing this loss function, the network learns the best target layer parameter prediction model. Whether the loss function L(θ) can effectively converge to ensure the effectiveness and accuracy of the complex mapping g_θ mainly depends on the following parts: (1) Dataset construction, (2) Forward algorithm validation, (3) Data normalization, (4) Network structure optimization, (5) Inversion prediction model parameters. The flowchart of one-dimensional anisotropic transient electromagnetic inversion based on deep learning is shown in Figure 1.

Figure 1

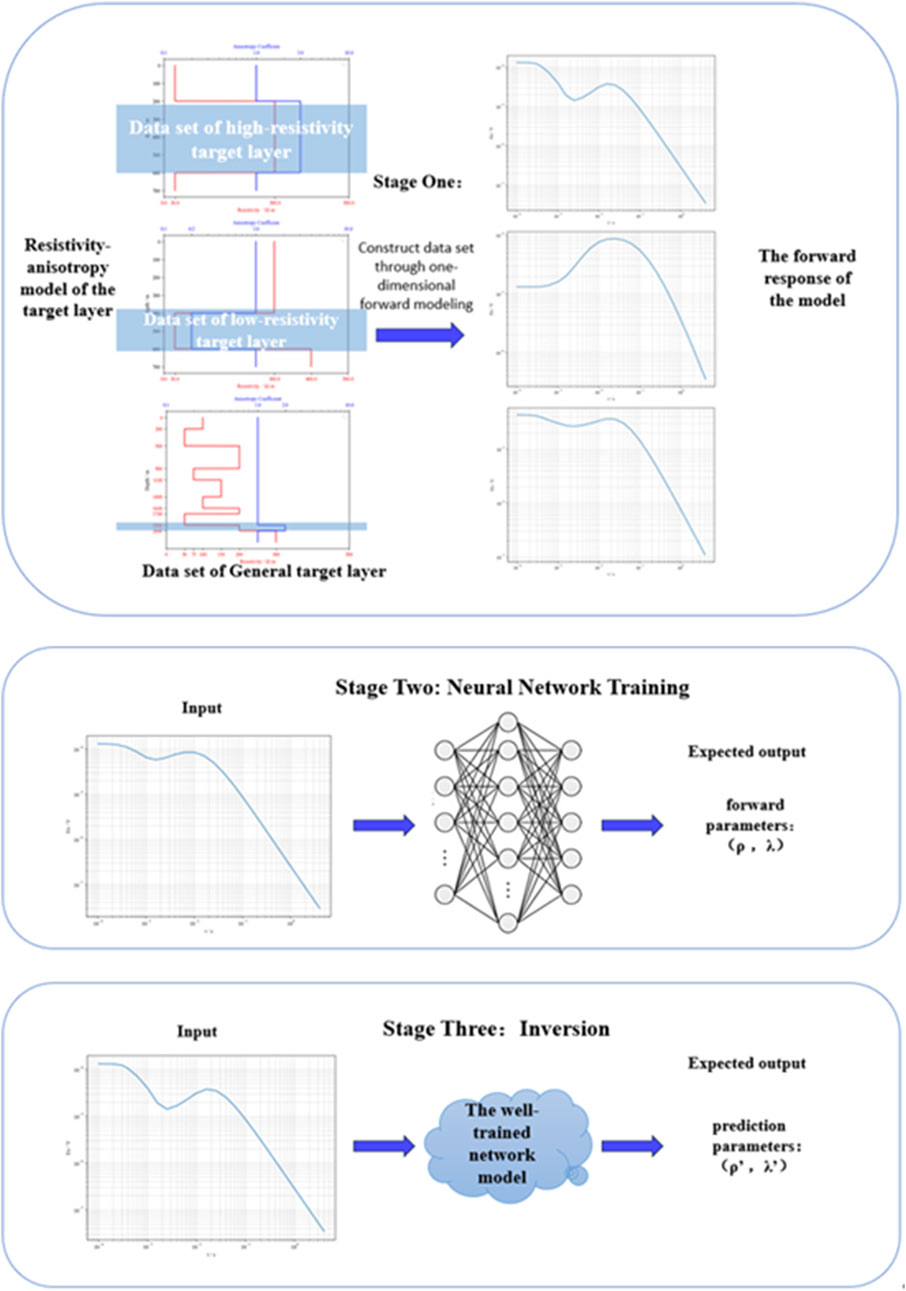
Figure 1. Steps of Transient Electromagnetic Deep Learning Inversion. Step 1 involves dataset construction, step 2 is neural network training, and step 3 performs the inversion.

2.1 Dataset construction

2.1.1 Anisotropic modeling and forward calculation

According to the study by Yan Liangjun on the transient electromagnetic response of the reservoir electrical anisotropy model, let the electric dipole be located at the coordinate origin, with its direction along the x-axis. In this case, the vector potential A has only $A_x$ and $A_z$ components. In cylindrical coordinates, the equations for $A_x$ and $A_z$ take the following forms (Yan et al., 2014) (Equations 5, 6):

$\frac{{\mathit{\partial }}^{\mathbf{2}}{\mathit{A}}_{\mathit{x}}}{\mathit{\partial }{\mathit{r}}^{\mathbf{2}}}+\frac{\mathbf{1}}{\mathit{r}}\frac{\mathit{\partial }{\mathit{A}}_{\mathit{x}}}{\mathit{\partial }\mathit{r}}+\frac{{\mathit{\partial }}^{\mathbf{2}}{\mathit{A}}_{\mathit{x}}}{\mathit{\partial }{\mathit{z}}^{\mathbf{2}}}-k_t^2{A}_x=0(5)$

$\frac{{\partial }^2{A}_z}{\partial r^2}+\frac{1}{r}\frac{\partial A_z}{\partial r}+\frac{1}{{\lambda }^2}\frac{{\partial }^2{A}_z}{\partial z^2}-k_n^2{A}_z=\left(1-\frac{1}{{\lambda }^2}\right)\frac{{\partial }^2{A}_x}{\partial x\partial z}(6)$

In the equation, the anisotropy coefficient is defined as $\lambda =\sqrt{\frac{{\rho }_n}{{\rho }_t}}$,where the resistivity in the parallel direction is ${\rho }_{xx}={\rho }_{yy}={\rho }_t$, and the resistivity in the vertical direction is ${\rho }_{zz}={\rho }_{nn}$, with units of Ω·m. The wavenumber in the vertical direction is $k_n=\sqrt{-\frac{iw\mu }{{\rho }_n}}$, while the wavenumber in the parallel direction is $k_t=\sqrt{-\frac{iw\mu }{{\rho }_t}}$ .

By applying the method of separation of variables and incorporating the continuous boundary conditions of the vector potential at the interface, the expressions for the electric and magnetic field components on the surface can be obtained (Vanyan et al., 1967). When the source is excited by a step current, the relationship between the electric field in the frequency domain and the time domain is given by (Niu, 2007) (Equation 7):

$e\left(t\right)=-\frac{\mathbf{2}}{\mathit{\pi }}{\int }_0^{\infty }\frac{ReE\left(w\right)}{w}\mathit{sin}\left(wt\right)dw(7)$

Among them:

$E_x\left(w\right)=\frac{iw{\mu }_{0}I}{2\pi }{\int }_0^{\infty }\frac{m}{m+\frac{n_1}{R^{*}}}{J}_0\left(mr\right)dm+\frac{iw{\mu }_{0}I}{2\pi }\times {\int }_0^{\infty }\left(\frac{\lambda \overline{n_1}}{{\overline{R}}^{*}{k}_{t1}^2}-\frac{1}{m+\frac{n_1}{R^{*}}}\right)\times \left[m{J}_0\left(mr\right){\mathit{cos}}^2\theta -J_1\left(mr\right)\frac{\mathit{cos}2\theta }{r}\right]dm(8)$

Equation 8 is the expression for the horizontal electric field component in the frequency domain, where $J_0$ and $J_1$ are the zeroth-order and first-order Bessel functions, respectively, $R^{*}$ and $\overline{R^{*}}$ is the reflection coefficient, And spatial frequency: $n_i^2=m^2+k_{ti}^2$; ${\overline{n}}_i^2=m^2+k_{ni}^2$.

To verify the accuracy of the forward modeling program, we first use a three-layer 1D isotropic model with the following parameters: ${\rho }_1=100\mathrm{\Omega }·m,h_1=2000m,{\rho }_2=10\mathrm{\Omega }·m,h_2=300m,$ and ${\rho }_3=100\mathrm{\Omega }·m$,When calculating with the anisotropic forward modeling program, the anisotropy coefficients are set as ${\lambda }_1={\lambda }_2={\lambda }_3=1.0$, representing an isotropic medium. The calculation results are shown in Figure 2. It can be observed that the electric field curves obtained from both the theoretical solution and the anisotropic forward modeling program fit well. This demonstrates that the forward modeling program based on the theory of electrical anisotropy is reliable.

Figure 2

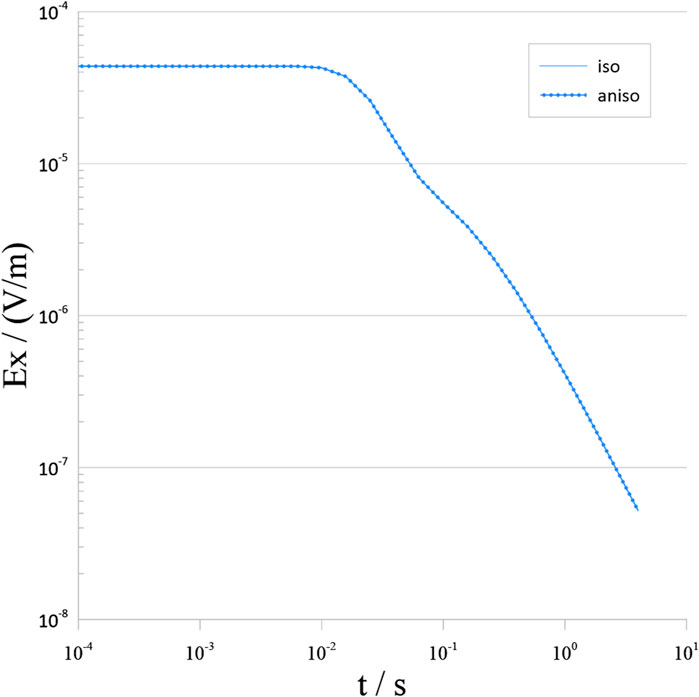
Figure 2. Forward modeling results of a one-dimensional isotropic model. “Aniso” shows results from the anisotropic modeling program developed in this study with anisotropy coefficients set to 1.0, while “iso” shows results from the isotropic modeling program.

2.1.2 Dataset construction

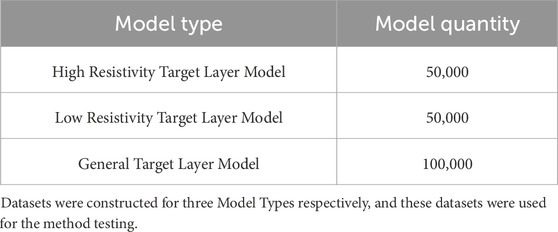
During the hydraulic fracturing process, the injection of high-pressure fluid promotes the expansion of fractures, which usually causes significant changes in the electrical properties of the target layer (Shen et al., 2009), while the physical parameters of the upper and lower layers remain relatively stable. Based on this background, this paper sets the parameters of the target layer as inversion variables and fixes the parameters of other layers to reduce the scale of the parameters. To ensure the effectiveness of the algorithm, we generated three datasets for testing. In the case of a three-layer horizontally layered medium, forward simulations were conducted for both high-resistivity and low-resistivity target layers, resulting in datasets D1 and D2. Additionally, a ten-layer underground model was forward simulated, with the target layer located in the ninth thin layer, generating dataset D3. The model parameters of each layer in these three datasets, as well as the changes in vertical resistivity and anisotropy coefficient of the target layer, are shown in Figure 3. In the high-resistivity target layer training set, the resistivity of the first and third layers is fixed at 30 Ω-meters, and the thickness of the first and second layers is 200 and 400 m, respectively. The resistivity range of the second layer (target layer) is 1–150 Ω m, with 250 resistivity values taken at logarithmic intervals, and the anisotropy coefficient (λ) ranges from 0.1 to 10.0, with 200 λ values taken at logarithmic intervals. In the low-resistivity target layer training set, the resistivity of the first and third layers is fixed at 300 Ω m, and the resistivity range of the second layer (target layer) is 150–1,000 Ω m, also with 250 resistivity values taken at logarithmic intervals and 200 λ values. In the general target layer training set, we refer to the actual prior data (from a specific location) to construct a ten-layer underground model, with the target layer located in the ninth layer. The resistivity range of the target layer is 1–1,000 Ω-meters, with 500 resistivity values taken at logarithmic intervals, and the λ range is 0.1–10.0, with 200 λ values. The distribution of the three sample sets ultimately used for testing is shown in Table 1.

Figure 3

Figure 3. Setting of physical property parameters of the target layer under three backgrounds. This figure illustrates the model settings of physical property parameters of the target layer under three background conditions: high-resistance target layer, low-resistance target layer, and conventional target layer.

Table 1

Table 1. Distribution of Sample Dataset.

2.2 Data normalization

As mentioned earlier, to enhance the nonlinear expression capability of the neural network, we need to introduce activation functions in the network layers. However, activation functions are most effective within a specific range, and their effectiveness diminishes when the input data exceeds this range. Therefore, we need to normalize the data to ensure that it is transformed to a reasonable magnitude range while retaining as much feature information as possible.

To this end, we tested the training effects of three normalization methods on the same dataset for the sample data: (Equation 9) Log Min-Max Normalization, (Equation 11) Early Apparent Resistivity * Time Normalization, and (Equation 12) Early Apparent Resistivity * Time + Log Min-Max Normalization. The effects are shown in Figure 4. Log Min-Max Normalization resulted in an excessive scaling range, losing the feature information of the sample data, which led to neuron inactivation in the neural network and caused the model to lose its predictive ability. The Early Apparent Resistivity * Time Normalization model converged well and did not exhibit severe overfitting. The Early Apparent Resistivity * Time + Log Min-Max Normalization method’s loss function also eventually converged, but overfitting occurred in the middle stages.

${\mathrm{x}}_{\text{norm}}=\frac{{\mathrm{x}}_{\log }-\mathit{min}\left({\mathrm{x}}_{\log }\right)}{\mathit{max}\left({\mathrm{x}}_{\log }\right)-\mathit{min}\left({\mathrm{x}}_{\log }\right)}(9)$

${\rho }_s=\frac{2\pi r^3{E}_x}{Idl}(10)$

${\rho }_s\times t=\frac{2\pi r^3{E}_{x}t}{Idl}(11)$

${\rho }_s=\frac{{\rho }_{slog}-{\rho }_{s{\mathit{log}}_{\mathit{min}}}}{{\rho }_{s{\mathit{log}}_{\mathit{max}}}-{\rho }_{s{\mathit{log}}_{\mathit{min}}}}(12)$

where ${\rho }_{\mathrm{s}}$ is the early-time apparent resistivity (Equation 10), r is the source-receiver distance, $E_x$ is the electric field response, I is the transmitting current, and dl is the length of the transmitting source.

Figure 4

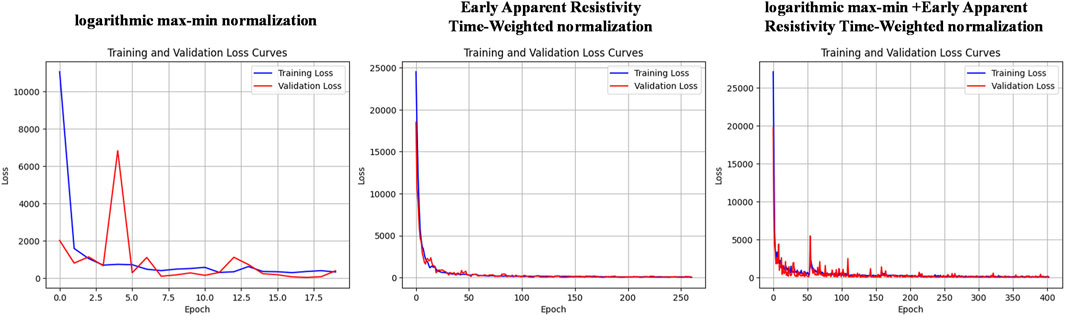
Figure 4. Decrease in the loss function under different normalization strategies. Among the three normalization strategies, the time-weighted normalization of early apparent resistivity yields the best performance.

Subsequently, to avoid excessive initial loss values, we also normalize the label data. To prevent the normalization amplitude from being too large and causing the differences between different label data to become too small, we scale both the resistivity and anisotropy coefficients within the range of 0–1,000. Then, we take the logarithm with base 10, so that the normalized label data for vertical resistivity and anisotropy coefficients are finally distributed within the range of (0, 3]. This helps the loss function converge effectively. After applying the above normalization strategy, the loss function decrease is shown in Figure 5.

Figure 5

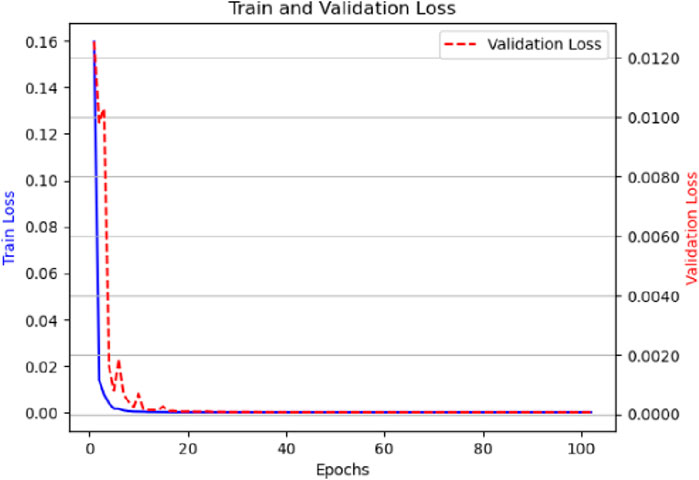
Figure 5. Training performance after normalizing both the sample data and labels. The figure shows the training results of the neural network after applying normalization to both input samples and output labels. The training process exhibits good convergence and stability.

2.3 Convolutional neural network model construction and training

2.3.1 Model construction

The classic convolutional neural network (CNN) structure typically includes an input layer, convolutional layers, activation functions, pooling layers, fully connected layers, and an output layer. The core idea is to extract features from the data using the convolutional layers, enhance the model’s non-linearity with activation functions, reduce dimensionality with pooling layers, and synthesize the features in the fully connected layers to complete classification or regression tasks. In the transient electromagnetic inversion process, unlike the two-dimensional CNN used for image processing, the one-dimensional CNN is more suitable for extracting features from time-series signals, and its computational scale is also much smaller than that of the two-dimensional CNN used for image processing (Chen et al., 2025). Therefore, we choose to adopt the one-dimensional convolutional neural network structure shown in Figure 6. The normalized response data d is used as input, and the normalized target layer resistivity and anisotropy coefficients m are used as the network’s output. Here, $d={\left[d_1,d_2,\dots ,d_{24},d_{25}\right]}^T,m={\left[p,\lambda \right]}^T$.

Figure 6

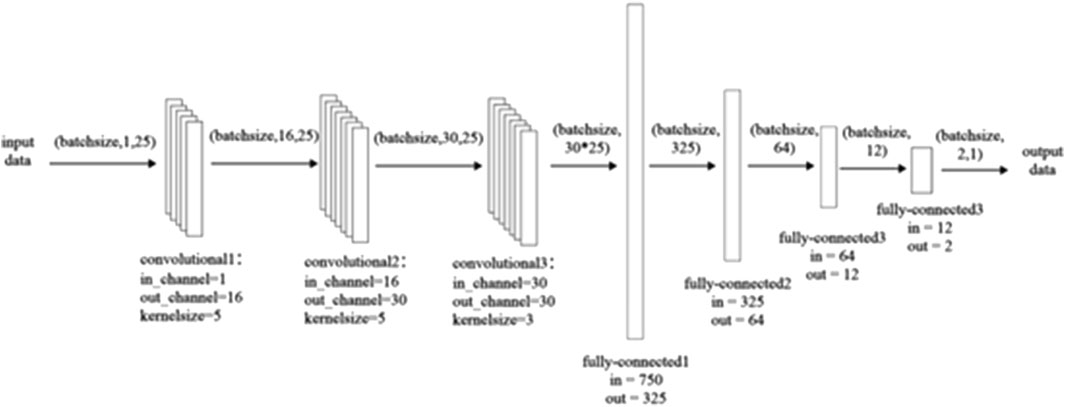
Figure 6. Convolutional Neural Network Architecture Diagram. The figure illustrates the structure of the convolutional neural network used in this study, including the arrangement of convolutional layers, and fully connected layers.

In this paper, we train the data using mini-batch gradient descent. In each iteration, a mini-batch of training data of size “batchsize” is used to calculate the gradient and update the model parameters. This method combines the advantages of batch gradient descent and stochastic gradient descent, offering high computational efficiency and good stability. The data flow during the training process is shown in Figure 6. First, the input data has the shape of (batchsize,1,25), where “batchsize” is the size of the mini-batch, one represents a single channel (indicating one-dimensional signal data), and 25 represents the number of time channels. The input data passes through three convolutional layers for feature extraction. The first convolutional layer uses 16 convolutional kernels, each with a size of 5; the second convolutional layer uses 30 convolutional kernels, each with a size of 5; the third convolutional layer also uses 30 convolutional kernels, each with a size of 3. After these three convolutional layers, the data shape becomes (batchsize,30,25), where 30 represents the number of feature channels and 25 is the number of time channels. To increase the network’s non-linear expressive power, the ReLU activation function is used in all layers. Additionally, to reduce data loss, zero-padding is used in the convolutional operations, and pooling layers are omitted to retain more spatial information. Then, the data processed by the convolutions is flattened into 30 × 25 features and passed into the fully connected layer. The fully connected layer contains three hidden layers. The first hidden layer has 325 neurons, the second hidden layer has 64 neurons, and the third hidden layer has 12 neurons. After the successive compression of the data, the final output is obtained, where the data shape is (batchsize,2,1), with 2 representing the number of predicted parameters and one indicating a single output feature.

2.3.2 Loss function

The network training process essentially involves minimizing the mathematical expectation of the loss function derived in Equation 4 to achieve optimal predictive performance of the model. During this process of minimizing the mathematical expectation of the loss function, the network obtains the model’s predicted output through forward propagation and compares it with the actual label values. Then, the backpropagation algorithm calculates the gradients of the error with respect to the network parameters (such as neuron weights and biases) and adjusts these parameters based on these gradients to optimize the loss function.

The mean squared error (MSE) loss function is one of the most commonly used loss functions in regression tasks. It is defined as (Equation 13):

$\text{MSE}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(y_i^{\prime }-y_i\right)}^2(13)$

Where N is the number of samples, $y_i$ represents the true label values, and $y_i^{\prime }$​ represents the predicted values from the model.

2.3.3 Learning rate

In deep learning, the learning rate is also a crucial hyperparameter. It represents the step size at which the model parameters are updated during each iteration. If the learning rate is too high, meaning the step size is too large, it may hinder the model’s convergence. On the other hand, if the learning rate is too low, meaning the step size is too small, it may cause the convergence to be too slow. Therefore, a reasonable learning rate schedule is essential for effective neural network training. After multiple tests, this paper finally adopts a learning rate adjustment strategy that changes with the number of iterations and the decrease in the loss function, which is represented by Equation 14:

$R=R_0\times {0.75}^{\alpha -1}(14)$

where $R_0$ is the initial learning rate, set to 0.01 in this study, and α represents the number of decay steps. Each time a specified condition is triggered during training, the learning rate is reduced to three-quarters of its previous value. The condition we set is that if the validation error does not decrease for 5 consecutive times, the decay step α is increased by 1. This method allows the model to dynamically reduce the learning rate during training, avoiding the drawbacks of a manually set learning rate that might be too high or too low. It significantly enhances the model’s performance and convergence speed, making it easier for the model to reach its optimal state.

2.3.4 Model training

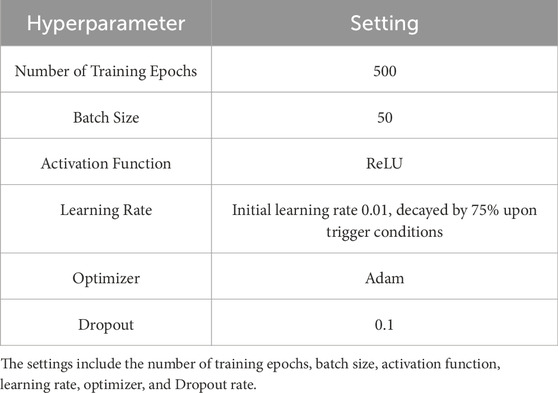
In this paper, a one-dimensional inversion neural network model for transient electromagnetic is built based on the PyTorch framework, and the network training and prediction are carried out in the GPU mode. The hardware configuration used is as follows: Intel(R) Xeon(R) Platinum 8352S CPU @ 2.20 GHz 3.40 GHz, NVIDIA GeForce RTX 4090 (24 GB) GPU, and the RAM is 256 GB (256 GB available). Under this hardware setup, the training efficiency of the model is reflected in a time consumption of 1.8 s per epoch. the complete hyperparameter settings for training the convolutional neural network model are shown in Table 2. The dataset is randomly split into training, validation, and test sets in an 8:1:1 ratio to ensure that after the network training is completed, the test set contains a sufficient number of unseen data to evaluate the inversion performance of the network model. Additionally, the ReLU activation function is used, and the Adam optimizer is employed for training. Apart from the aforementioned learning rate decay strategy, an “early stopping” strategy is also implemented. Training is halted early if the validation error does not decrease for 50 consecutive iterations, effectively preventing overfitting.

Table 2

Table 2. Hyperparameter Settings.

3 Results and testing

3.1 Inversion of synthetic data without noise

As shown in Figure 7, the inversion results of three models selected from the test samples (named a1b1, a2b2, and a3b3) under noiseless conditions are presented. From top to bottom, the first and second columns show the comparison between the true values and the predicted (inverted) values of the vertical resistivity and anisotropy coefficients of the target layer. The third column shows the forward modeling response fitting curves of the true geoelectric model and the inverted geoelectric model. The fourth column displays the absolute error curves of the forward response of the true model and the inverted model. For the high-resistivity target layer model a1b1, with layer thicknesses of 200, 400, and 5,000 m, vertical resistivities of 30.0, 280.17, and 30.0 Ω m, and anisotropy coefficients of 1.0, 5.62, and 1.0, the inversion results show that the second layer’s vertical resistivity is 297.05 Ω m, with a relative error of 6.02%, and the anisotropy coefficient is 5.51, with a relative error of 1.97%. For the low-resistivity target layer model a2b2, with layer thicknesses of 400, 200, and 5,000 m, vertical resistivities of 300, 60.65, and 300 Ω m, and anisotropy coefficients of 1.0, 1.66, and 1.0, the inversion results show that the second layer’s vertical resistivity is 64.23 Ω m, with a relative error of 5.94%, and the anisotropy coefficient is 1.55, with a relative error of 6.38%. For the general target layer model a3b3, with the target layer at the ninth layer and the settings of the underground 10 layers being consistent with Figure 3, the vertical resistivity of the target layer is 85.68 Ω m, and the anisotropy coefficient is 7.9. The inversion results show that the vertical resistivity of the ninth layer is 91.46 Ω m, with a relative error of 6.75%, and the anisotropy coefficient is 7.68, with a relative error of 2.78%.

Figure 7

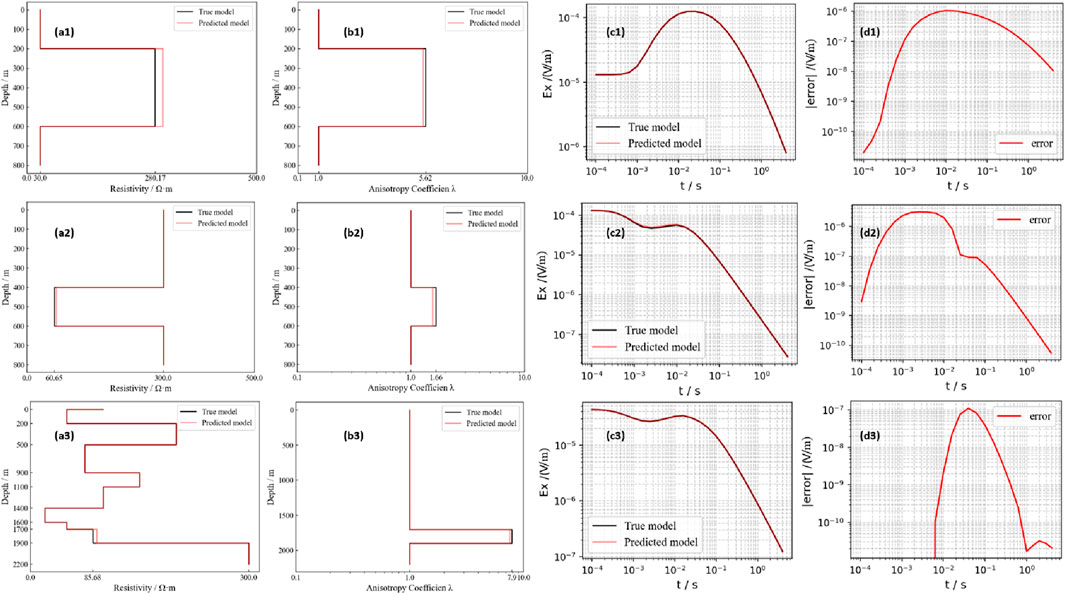
Figure 7. Inversion Results for Different Models. (a1–a3) are comparisons between the true values and predicted values of the vertical resistivity ρ for the target layer under different models. (b1–b3) are comparisons between the true values and predicted values of the anisotropy coefficient λ for the target layer under different models. (c1–c3) are comparisons of the forward modeling response curves for model parameters and predicted parameters. (d1–d3) are error absolute value curves comparing the forward modeling response of model parameters with the predicted parameter’s forward modeling response. The inversion results show that the predicted parameters closely match the true values, and the forward modeling responses based on predicted parameters exhibit high consistency with those from the true models, indicating the effectiveness of the proposed method.

From the three models and their inversion results, it can be seen that for the inversion of noise-free synthetic data, the vertical resistivity and anisotropy coefficient of the target layer can be well restored. The fitting error of the forward response curve is at least two orders of magnitude lower than the data itself. In terms of the prediction performance for special models, the inversion results are satisfactory, and the inversion time after network training is within 1 s, which is significantly shorter than the time required for traditional iterative inversion, perfectly meeting the real-time inversion requirements in practical scenarios. In addition, to verify the generalization performance of the model, all unseen data from the test set, which was not involved in model training, was used for inversion, and the relative error of the inversion parameters was calculated. The test results, as shown in Table 3, indicate that the average relative error is less than 5%, demonstrating that even for unfamiliar forward response curves, the convolutional neural network can effectively extract complex electromagnetic response features and accurately restore the vertical resistivity and anisotropy coefficient of the target layer.

Table 3

Table 3. Average Relative Inversion Error of the Test Set in Noise-Free Synthetic Data.

3.2 Inversion of synthetic data with noise

In this study, to evaluate the noise resistance of the convolutional neural network (CNN) inversion method under realistic conditions, Gaussian white noise—one of the most common types of noise—was introduced as the disturbance source. Gaussian white noise is characterized by a zero mean, flat power spectral density, and statistical independence, making it an effective representation of random disturbances encountered in practical electromagnetic measurements, such as instrument noise, atmospheric interference, and geological background noise. By introducing Gaussian noise, the complexity of real-world electromagnetic data can be more accurately simulated, enabling a more objective assessment of the CNN model’s robustness and generalization capability under varying noise levels.

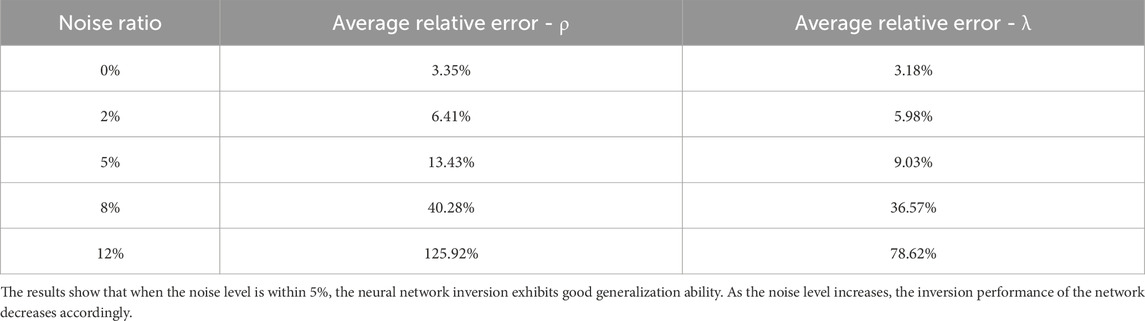
We calculated the average relative error of the inversion results for 5,000 noisy test samples from the D1 dataset without changing any other parameters, as shown in Table 4. This demonstrates that the convolutional neural network can still effectively capture data features when the noise level is not too severe. Subsequently, different levels of Gaussian noise (2%, 5%, 8%, and 12%) were added to the three sets of test samples used earlier, and the inversion was performed again. The results were compared with the true model and the noise-free inversion results, as shown in Figure 8. Specifically, e1, e2, and e3 represent the inversion results of the vertical resistivity of the target layer under different noise levels, while f1, f2, and f3 show the inversion results of the anisotropy coefficient. The results indicate that when the noise ratio is within 5%, the neural network inversion exhibits good generalization ability, and the error of the inversion parameters remains within an acceptable range. However, it is important to note that as the noise ratio increases, the inversion performance of the network deteriorates accordingly. Therefore, when applying this method to practical scenarios, it is still necessary to perform data cleaning and denoising in advance to ensure better inversion performance.

Table 4

Table 4. Inversion Results of Test Samples with Added Noise in Dataset D1.

Figure 8

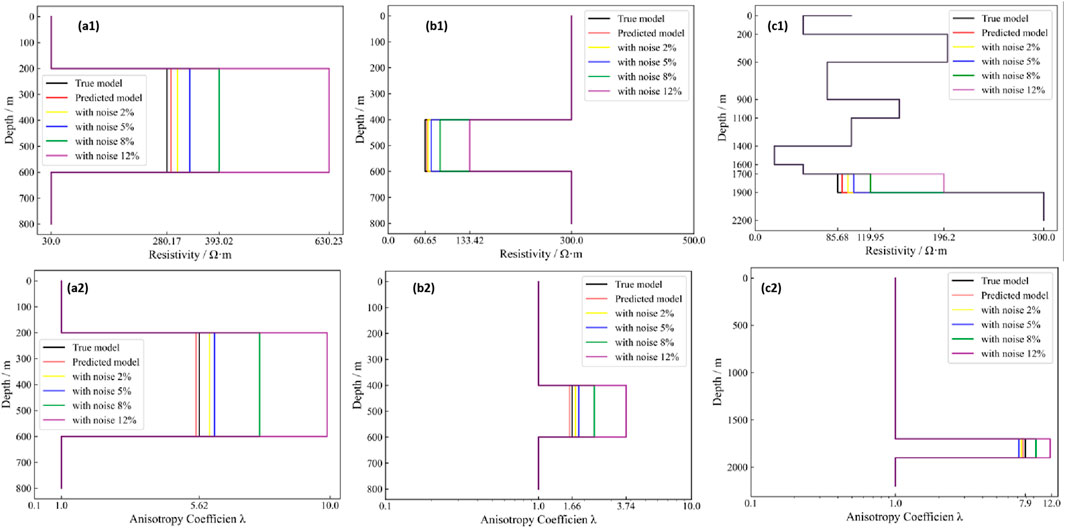
Figure 8. The Impact of Noise on Inversion Results. (a1,a2) show the effect of different levels of noise on the resistivity and anisotropy coefficient of the high-resistivity target layer. (b1,b2) show the effect of different levels of noise on the resistivity and anisotropy coefficient of the low-resistivity target layer. (c1,c2) show the effect of different levels of noise on the resistivity and anisotropy coefficient of the typical target layer. The results show that when the noise level is within 5%, the neural network inversion exhibits good generalization ability. As the noise level increases, the inversion performance of the network decreases accordingly.

3.3 Inversion comparison of field data before and after hydraulic fracturing

The method proposed in this paper focuses on the inversion of vertical resistivity and anisotropy coefficient of the target layer by fixing the electrical parameters of non-target layers. This strategy is often limited in conventional transient electromagnetic inversion, where complex unknown stratified structures require simultaneous inversion of multiple formation parameters, significantly increasing data dimensionality and computational complexity. However, in the context of hydraulic fracturing monitoring in shale reservoirs, this “parameter simplification” design becomes a unique advantage.

Firstly, prior to fracturing, an initial geoelectric model can be constructed using well-logging curves, 3D seismic interpretation, and magnetotelluric (MT) surveys, providing a reliable basis for fixing background layer parameters. Secondly, the resistivity anomalies caused by hydraulic fracturing are spatially constrained, mainly within the target reservoir around the horizontal wellbore (typically within a 200–300 m radius), while the electrical properties of non-target layers, such as the caprock and basement, remain relatively stable before and after fracturing. This physical constraint allows the proposed method to efficiently capture the dynamic changes in vertical resistivity and anisotropy of the target layer through inversion in a reduced parameter space, reducing the neural network training data by 2-3 orders of magnitude and meeting the computational efficiency required for fracturing monitoring.

This study is based on field data from a shale gas well in Zhongxian, Chongqing, using the ultra-long grounded source transient electromagnetic system. The transmission source has a total length of 4064m, with a peak current of 103.686A, and uses a TD50 bipolar trapezoidal waveform with a sampling rate of 1000 Hz. The field survey line layout relative to the horizontal well is shown in Figure 9. Based on well-logging interpretation, 3D seismic data, and MT inversion, a four-layer “low-high-low-high” resistivity structure model was constructed (target layer depth <2600 m), eight observation points were set along the main fracturing direction, and corresponding datasets were generated for the different coordinates of the eight observation points.

Figure 9

Figure 9. Schematic Diagram of Field Survey Line Design and the Relative Position of the Horizontal Well. The measured data were selected from the measurement points along 9 survey lines.

Taking the first observation point as an example (Figure 10), the early apparent resistivity curve (0.02–1.02s) before and after fracturing shows significant differences, with a maximum absolute change of Δρ_max = 23.95 Ω m and a relative change rate of up to 37.4%, far exceeding the system noise threshold (5%). This demonstrates the CNN’s ability to effectively extract characteristic signals from the fracturing process.

Figure 10

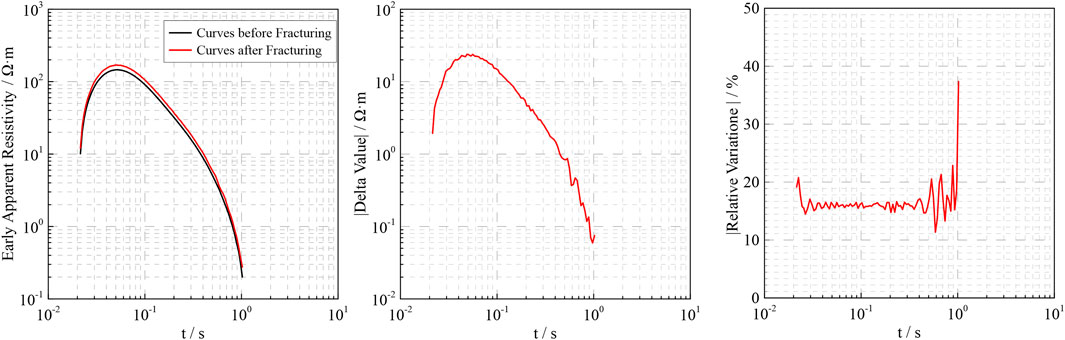
Figure 10. Early Apparent Resistivity Curves Before and After Fracturing and the Absolute and Relative Changes. This change in values can be effectively captured by the neural network.

According to the laboratory rock physics study by Tong et al. (2023), the replacement of original gas with conductive fluid in fracture pores leads to a significant decrease in the average resistivity of the formation, while the vertical resistivity decreases more significantly, further reducing the anisotropy coefficient. The inversion results for the entire survey line (Figures 11, 12) show that after fracturing, the average vertical resistivity of the target layer decreased from 11.49 Ω m to 7.27 Ω m (a 36.7% reduction), while the anisotropy coefficient decreased from 3.21 to 1.58 (a 50.8% reduction). The simultaneous decline in electrical parameters can be attributed to the formation of a conductive fluid network caused by the injection of proppant and low-resistivity fracturing fluid, which is consistent with the conclusions of laboratory core fracturing experiments.

Figure 11

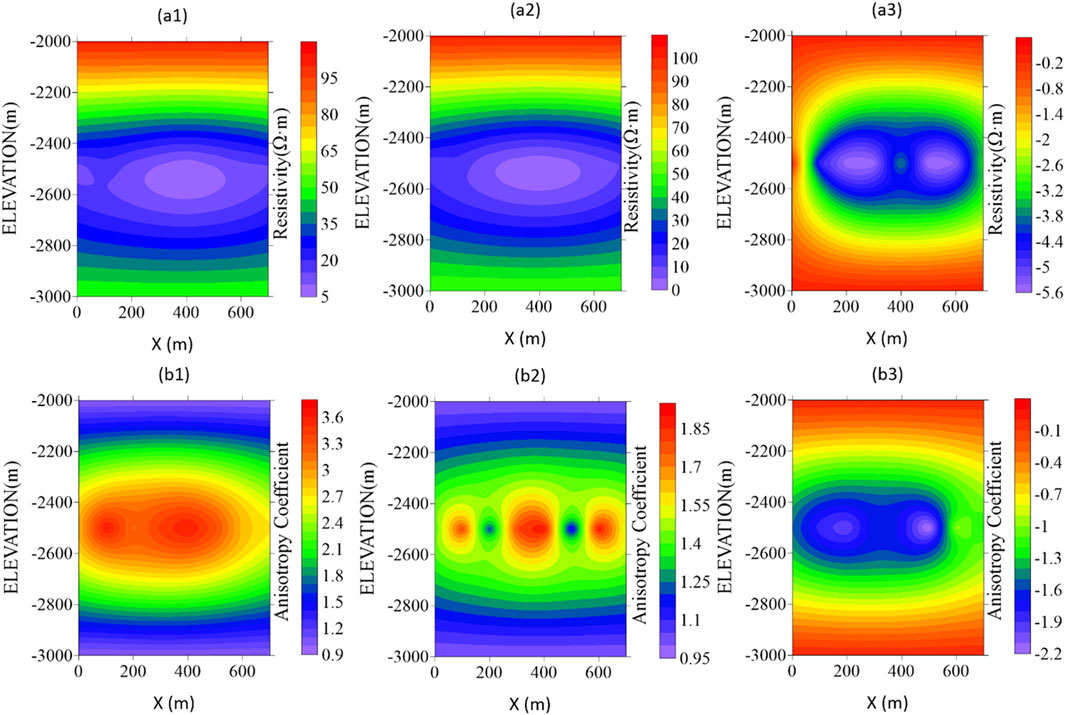
Figure 11. Electrical Property Parameters of the Target Layer Before and After Fracturing and Their Changes. (a1) Vertical resistivity distribution of the target layer before fracturing, (a2) Vertical resistivity distribution of the target layer after fracturing, (a3) Changes in vertical resistivity, (b1) Anisotropy coefficient distribution before fracturing, (b2) Anisotropy coefficient distribution after fracturing, (b3) Changes in anisotropy coefficient. Overall, after fracturing, both the resistivity and the anisotropy coefficient have generally decreased.

Figure 12

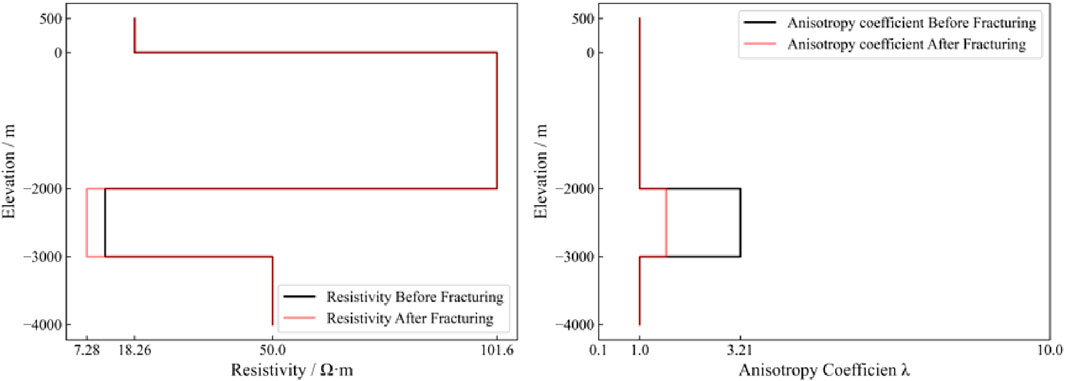
Figure 12. Changes in Average Resistivity and Average Anisotropy Coefficient of the Stratum. After fracturing of the target layer, the average value of vertical resistivity decreased from 11.49 Ω m to 7.27 Ω m, with a decrease of 36.7%; the average value of the anisotropy coefficient decreased from 3.21 to 1.58, representing a reduction of 50.8%.

4 Conclusion

This study proposes a CNN-driven anisotropic time-domain electromagnetic (TEM) inversion framework, which overcomes the limitations of traditional iterative inversion methods, such as long computation time and low efficiency. By leveraging an end-to-end deep extraction-regression architecture, the proposed method establishes a nonlinear mapping between multi-time window electromagnetic decay characteristics and the target layer’s electrical parameters (vertical resistivity ρ and anisotropy coefficient λ), successfully reducing the single-point inversion time to within 1 s, which is much lower than the 317 s used in the one-dimensional iterative inversion by Wang, (2024).

In the synthetic data tests, a standardized dataset containing 200,000 samples of three target layer types—high-resistivity (ρ > 100 Ω m), low-resistivity (ρ < 50 Ω m), and conventional (10 Ω m ≤ ρ ≤ 1,000 Ω m)—was constructed. The results verified the feasibility of the method, with an average relative error of less than 4% for both vertical resistivity (ρ) and anisotropy coefficient (λ), and no overfitting occurred (the loss between the validation set and the test set was less than 2%).

In the noisy data tests, the results showed that the CNN inversion maintained good generalization performance when the noise ratio was within 2%–5%, with inversion errors remaining within an acceptable range. However, as the noise level increased, the inversion performance gradually deteriorated.

In field data applications, this method has demonstrated remarkable practical potential. It successfully identified regions of reduced resistivity caused by the injection of fracturing fluid, with the average resistivity decreasing from 11.49 Ω m to 7.27 Ω m (a reduction of 36.7%), and the average anisotropy coefficient dropping from 3.21 to 1.58 (a reduction of 50.8%). The inversion time for a single point is less than 1 s, enabling the method to efficiently capture resistivity and anisotropy changes induced by hydraulic fracturing. This demonstrates that the integration of prior constraints and deep learning can overcome the timeliness bottleneck of traditional inversion, providing more reliable support for fracturing monitoring and decision-making.

However, it should be noted that while the method presented in this paper effectively reduces the size of the training dataset through sufficient prior constraints, and based on our analysis of field data, the trend of the inversion results is generally consistent with the laboratory rock physics experiments, we believe the prior information used is highly reliable. Nevertheless, due to the complexity of subsurface electrical structures, it is often difficult to fully match them with the prior model. If there is a significant discrepancy between the prior information and the actual subsurface electrical parameters, it may lead to substantial errors in the inversion results. At present, we are unable to precisely quantify the differences between the prior data and the true subsurface parameters. Therefore, the focus of our future research will be to further improve the inversion method, such as exploring whether it is possible to directly invert the changes in the electrical properties of the target layer by using the residual signal of the response before and after fracturing. This approach may help reduce the result bias caused by inaccurate prior information.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

PA: Writing – original draft. YL: Writing – review and editing. ZL: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was financially supported by the National Natural Science Foundation of China (NSFC) Key Project (Grant No. 42030805), titled “Research on Time-Domain Electromagnetic Monitoring Methods for Hydraulic Fracturing and Their Comprehensive Applications.”

Acknowledgments

Special thanks to the EMLAB laboratory at Yangtze University for their support in this research.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chen, C., Zhu, X. Y., Wang, F., Xu, Y. Q., and Zhang, W. (2025). A review of physics-guided deep learning: progress, challenges, and prospects. J. Front. Comput. Sci. Technol. 19 (02), 277–294. doi:10.3778/j.issn.1673-9418.2407056

CrossRef Full Text | Google Scholar

Fahad, A., and Kamal, A. (2022). Groundwater aquifer detection using the time-domain electromagnetic method: a case study in Harrat Ithnayn, northwestern Saudi Arabia. J. King Saud Univ. - Sci. 34 (01), 101684. doi:10.1016/j.jksus.2021.101684

CrossRef Full Text | Google Scholar

Heng, S., Yang, C. H., Zhang, B. P., Guo, Y. T., Wang, L., and Wei, Y. L. (2015). Experimental study on anisotropic characteristics of shale. Rock Soil Mech. 36 (03), 609–616. doi:10.16285/j.rsm.2015.03.001

CrossRef Full Text | Google Scholar

Huang, M. W. (2021). Research on marine controlled-source electromagnetic inversion based on deep learning. Henan Polytechnic University. doi:10.27116/d.cnki.gjzgc.2021.000219

CrossRef Full Text | Google Scholar

Liu, Y. H., Yin, C. C., Cai, J., Huang, W., Ben, F., Zhang, B., et al. (2018). Research status and prospects of anisotropy in electromagnetic exploration. Chin. J. Geophys. 61 (08), 3468–3487. doi:10.6038/cjg2018L0004

CrossRef Full Text | Google Scholar

Liu, Z., Chen, H., Ren, Z., Tang, J., Xu, Z., Chen, Y., et al. (2021). Deep learning audio magnetotellurics inversion using residual-based deep convolution neural network. J. Appl. Geophys. 188 (000), 104309. doi:10.1016/j.jappgeo.2021.104309

CrossRef Full Text | Google Scholar

Niu, Z. L. (2007). Principles of time-domain electromagnetic methods. Changsha: Central South University Press.

Google Scholar

Shen, J. S., Su, B. Y., and Guo, N. C. (2009). Electrical anisotropic response characteristics of fractured reservoirs. Chin. J. Geophys. 52 (11), 2903–2912. doi:10.3969/j.issn.0001-5733.2009.11.026

CrossRef Full Text | Google Scholar

Tong, X. L., Yan, L. J., Xiang, K., and Tan, G. X. (2023). IP characteristics and anisotropy experiment of hydraulic fracturing shale. Oil Geophys. Prospect. 58 (05), 1152–1163. doi:10.13810/j.cnki.issn.1000-7210.2023.05.012

CrossRef Full Text | Google Scholar

Vanyan, L. L., Bobrovnikov, L. Z., Davidov, V. M., Kuznetsov, A. N., Loshenitzina, V. L., Morozova, G. M., et al. (1967). Electromagnetic depth soundings. Boston, MA: Springer. doi:10.1007/978-1-4684-0670-2

CrossRef Full Text | Google Scholar

Vladimir, P. (2019). Deep learning electromagnetic inversion with convolutional neural networks. Geophys. J. Int. 218 (2), 817–832. doi:10.1093/gji/ggz204

CrossRef Full Text | Google Scholar

Wang, S. J. (2024). One-dimensional inversion and application of electric source transient electromagnetic method (Master’s thesis). Yangtze University. doi:10.26981/d.cnki.gjhsc.2024.001266

CrossRef Full Text | Google Scholar

Wang, X. X., Di, Q. Y., and Tang, J. (2015). Preliminary study on electrical source transient electromagnetic method. Prog. Geophys. 30 (02), 872–877. doi:10.6038/pg20150253

CrossRef Full Text | Google Scholar

Xiang, K., Hu, W. B., Yan, L. J., Tang, X. G., and Xie, X. B. (2016). Characteristics of shale gas reservoirs and geophysical prediction techniques. Spec. Oil Gas Reserv. 23 (02), 5–8+151. doi:10.3969/j.issn.1006-6535.2016.02.002

CrossRef Full Text | Google Scholar

Yan, L. J., Zhou, L., Xie, X. B., and Wang, Z. G. (2014). Transient electromagnetic response of electrically anisotropic reservoir models. Chin. J. Eng. Geophys. 11 (03), 346–350. doi:10.3969/j.issn.1672-7940.2014.03.013

CrossRef Full Text | Google Scholar

Yan, S., Yin, C. C., Su, Y., Ke, Z. Y., and Wang, L. Y. (2023). Fast imaging of transient electromagnetic data based on convolutional neural network. Chin. J. Geophys. 66 (10), 4290–4300. doi:10.6038/cjg2023Q0827

CrossRef Full Text | Google Scholar

Yin, C. C., and Weidelt, P. (1999). Geoelectrical fields in a layered earth with arbitrary anisotropy. Geophysics 64 (2), 426–434. doi:10.1190/1.1444547

CrossRef Full Text | Google Scholar

Yu, J. H., Tang, X. G., and Xiong, Z. T. (2025). 2D inversion of magnetotelluric data based on residual neural network. Chin. J. Geophys. 68 (01), 269–281. doi:10.6038/cjg2024R0859

CrossRef Full Text | Google Scholar

Zhang, Z. H., Liao, X. L., Cao, Y. Y., Hou, Z. L., Fan, X. T., Xu, Z. X., et al. (2021). Joint inversion of gravity and gravity gradient anomalies based on deep learning. Chin. J. Geophys. 64 (04), 1435–1452. doi:10.6038/cjg2021O0151

CrossRef Full Text | Google Scholar

Zhou, F. Y., Jin, L. P., and Dong, J. (2017). A survey of convolutional neural networks. Chin. J. Comput. 40 (06), 1229–1251. doi:10.11897/SP.J.1016.2017.01229

CrossRef Full Text | Google Scholar