A high-precision displacement prediction model for landslide geological hazards based on APSO-SVR-LSTM combination

The development of a high-precision displacement prediction model for landslide geological hazards is crucial for the early warning of such disasters. Landslide deformation typically exhibits a step-like curve pattern with implicit periodicity. Therefore, taking the Xintan landslide in the Baishui River of the Three Gorges Reservoir Area as a case study, this study proposes a novel displacement prediction approach that integrates the Adaptive Particle Swarm Optimization (APSO), Support Vector Regression (SVR), and Long Short-Term Memory (LSTM) network. The APSO is employed to optimize the hyperparameters of the SVR model, ensuring an optimal parameter combination. Subsequently, the Grey Wolf Optimizer is utilized to assign weights to the APSO-SVR and LSTM models, establishing an optimal hybrid model with an optimal weight ratio. Using the Baishui River landslide as the research object, cumulative displacement, rainfall, and reservoir water level are selected as influencing factors of periodic displacement for model training and validation. The results demonstrate that, in predicting the periodic displacement of the Baishui River landslide, the proposed APSO-SVR-LSTM hybrid model outperforms individual models in terms of both prediction accuracy and stability.

1 Introduction

Landslide geological hazards represent one of the most severe forms of geological disasters, causing significant economic losses and impeding societal development and progress (Cheng et al., 2018; Cui et al., 2019). Consequently, landslide disasters pose not only a global challenge but also a key research focus and difficulty within the academic domain of geological hazard studies. The destructive impact of landslides extends beyond the immediate threat to human life, encompassing substantial economic losses and infrastructure damage (Gbanie et al., 2018; Abd Majid and Rainis, 2019; Althuwaynee and Pradhan, 2017). However, such disasters are not entirely unavoidable. Effective monitoring and analysis of landslide displacement serve as crucial prerequisites for landslide disaster prevention and mitigation (Aristizábal and Sánchez, 2020).

As a dynamic evolutionary system, landslide deformation is influenced not only by its intrinsic geological structure but also by various natural and anthropogenic factors (Zhang et al., 2023; Kamal et al., 2023). To better characterize landslide evolution, researchers have developed models that decompose cumulative displacement into trend displacement and periodic displacement. Trend displacement exhibits apparent monotonicity, prompting researchers to employ mathematical functions such as quadratic, logarithmic, and exponential functions for predictive analysis. In contrast, periodic displacement is characterized by stochasticity and fluctuations, making it a central focus of landslide displacement prediction research (Batista et al., 2019; De Silva et al., 2017; Froude and Petley, 2018; Fu et al., 2020). Deng et al. extracted periodic displacement based on ensemble empirical mode decomposition of time series and applied a Particle Swarm Optimization (PSO)-optimized Support Vector Regression (SVR) model to enhance prediction accuracy. As research has progressed, Chen employed time series analysis techniques to capture the dynamic evolution of landslide displacement, successfully forecasting displacement trends. Similarly, Yang et al. addressed the limitations of SVR in periodic displacement prediction by introducing a Long Short-Term Memory (LSTM) neural network model. Compared with SVR, the dynamic LSTM model demonstrated superior predictive accuracy in periodic displacement forecasting (Görüm and Fidan, 2021; Kirschbaum et al., 2015; Klose et al., 2016). However, due to limited data availability and an extensive set of training parameters, LSTM models often suffer from prolonged training times and instability in output results.

The optimization of SVR model parameters and the application of deep learning algorithms in time-series analysis remain research hotspots. However, the SVR model fails to account for the long-term dependencies inherent in time series data, leading to reduced prediction accuracy for future periodic displacement trends (Lin and Wang, 2018). While deep learning algorithms such as LSTM offer high predictive accuracy, they are computationally intensive and have complex model architectures, resulting in extended training durations. In contrast, hybrid models overcome the limitations of individual models by reducing the impact of random fluctuations, thereby enhancing prediction accuracy, stability, and model generalization (Roy and Kshirsagar, 2020). Given the respective strengths of SVR and LSTM in periodic displacement forecasting, this study proposes a weighted ensemble model that integrates an Adaptive Particle Swarm Optimization (APSO)-optimized SVR model with an LSTM model for landslide periodic displacement prediction (Strouth and McDougall, 2020).

To validate the proposed model, monitoring data from ZG118 station at the Baishui River landslide in the Three Gorges region were analyzed. Following the principles of the additive time series model, the moving average method was employed to extract periodic displacement components. To mitigate the instability associated with individual predictive models, a hybrid modeling approach was adopted. The core concept involves assigning different weight coefficients to different models, effectively integrating their predictive capabilities. By leveraging the complementary strengths of multiple models, the proposed ensemble approach enhances prediction accuracy and generalization capacity, contributing to improved landslide early warning and disaster mitigation strategies.

2 Methodology

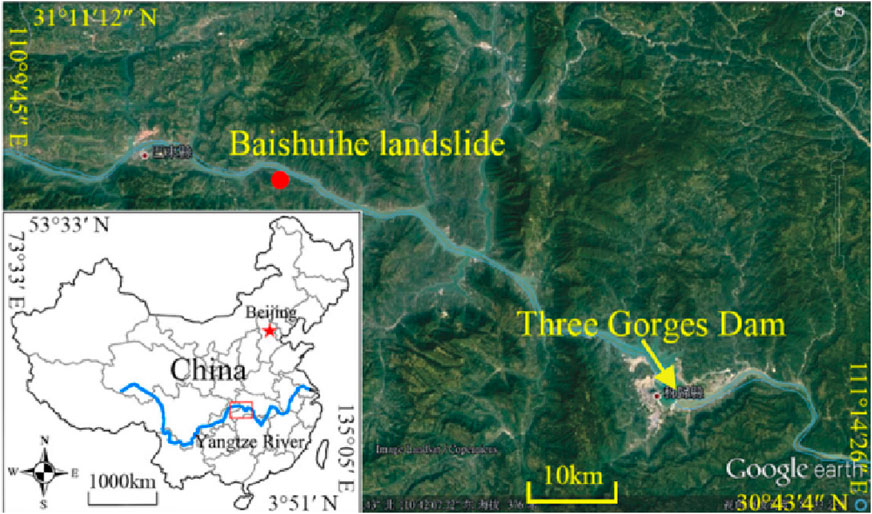
2.1 Research area

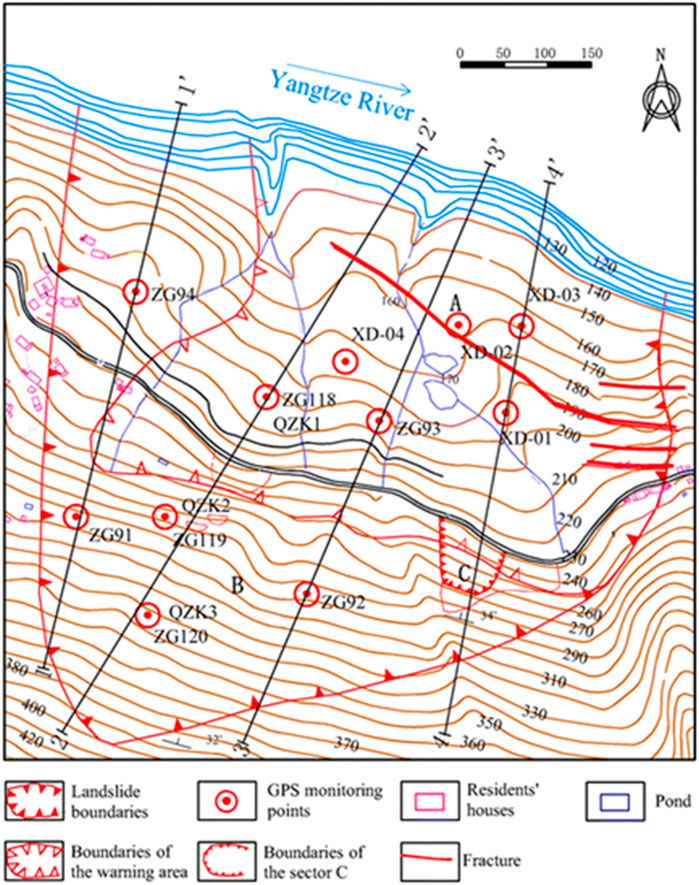
The Baishui River landslide is located on the southern bank of the Yangtze River, extending 600 m in the north-south direction and 700 m in the east-west direction, with an average landslide thickness of 30 m and a total volume of approximately 1.26 × 10⁷ m³. The elevation at the rear edge of the landslide is 410 m, with the boundary defined at the interface between soil and bedrock (Figure 1). The landslide front extends below the Yangtze River to an elevation of 135 m, while its eastern and western flanks are constrained by bedrock ridges. The overall slope inclination is approximately 30°. The sliding zone is primarily composed of silty clay containing gravels or breccia. Since the impoundment of the Three Gorges Project in 2003, the landslide mass has exhibited deformation due to the combined influences of seasonal rainfall and reservoir water level fluctuations. In 2004, based on the observed deformation characteristics, a landslide early warning zone was delineated. Landslide Early Warning Zone refers to a high-risk area for potential disasters, delineated based on geological conditions, hydro-meteorological data, and historical landslide activity. Its boundaries are determined by the extent of the landslide mass, rainfall-water level response relationships, and geotechnical stability. Taking the Baishuihe landslide as an example, the warning zone encompasses the main sliding body and downstream areas potentially affected by river blockage, while also accounting for the possibility of secondary landslides induced by rainfall infiltration. Key technical alert criteria include: Rainfall thresholds (Yellow alert triggered by ≥ 80 mm in 24 h; Red alert triggered by ≥150 mm in 72 h combined with a water level rise rate of ≥0.5 m/h); Water level-displacement linkage indicators (Secondary alert triggered by a water level rise of ≥2 m and slope displacement of ≥5 mm/day); Integrated monitoring (Emergency response initiated when InSAR and tiltmeter data detect crack propagation ≥10 mm/12 h, per the National Geological Hazard Prevention Manual, 2022). Threshold settings should be locally calibrated in accordance with “GB/T 38221-2019 Technical Specifications for Geological Hazard Warning” (Thapa et al., 2023; Salee et al., 2022). The eastern boundary of this zone is marked by the Loess Gully, while the western boundary is defined by the Goat Gully on the western side of the sliding mass. The rear boundary is set at an elevation of 297 m, and the shear outlet at the front extends below the Three Gorges Reservoir water level at 145 m. The early warning zone measures approximately 500 m in length (north-south) and 430 m in width (east-west), covering an area of 21.5 × 10⁴ m². The landslide body has an average thickness of 30 m and a total volume of 6.45 × 10⁶ m³. The primary sliding direction is approximately 20°, classifying it as a deep-seated, large-scale soil landslide.

Figure 1

Figure 1. Location map of the baishui river landslide.

Since 2003, the Baishui River landslide has undergone five significant deformation events, with the most severe occurring between June and September 2007. Based on the characteristics and extent of this deformation, an early warning zone was delineated (Lu et al., 2024). At present, deformation is primarily concentrated in the front section of the warning zone, while displacement at monitoring points in the rear section remains relatively stable. The overall deformation pattern of the landslide exhibits characteristics of a traction type failure. Currently, a total of 11 GPS displacement monitoring points have been installed on the Baishui River landslide, as illustrated in Figure 2.

Figure 2

Figure 2. Displacement monitoring arrangement of the baishui river landslide.

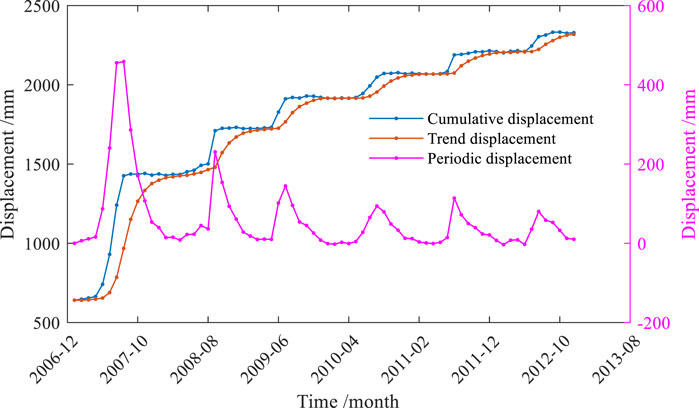
Since June 2003, the Baishui River landslide has been subjected to professional monitoring, with numerous monitoring stations established. Among these, the ZG118 station is located in the central part of the landslide body, providing a comprehensive reflection of the entire evolution process of the landslide. Additionally, the ZG118 station possesses relatively complete monitoring data, facilitating data-based modeling. Based on these two factors, the monitoring data from the ZG118 station were used to verify the effectiveness and superiority of the method proposed in this study. Figure 3 illustrates the cumulative displacement, reservoir water level, and rainfall data curves monitored at the ZG118 station from January 2007 to December 2012. It is evident that rapid displacement occurred at the onset of the rainy season (from May to September each year) and at the end of the reservoir water level drop (in June and July). The Baishuihe landslide area exhibits a pronounced positive correlation between precipitation and water level variations. Intense short-term rainfall or sustained precipitation events trigger rapid increases in surface runoff and subsurface infiltration, resulting in sharp water level rises throughout the watershed. Statistical analyses indicate a characteristic 1-3 h lag between rainfall peaks and corresponding water level responses, with channel water levels demonstrating nonlinear growth relative to rainfall intensity when cumulative precipitation exceeds 50 mm. This interdependent relationship stems from two primary mechanisms: direct rainfall recharge into channel systems, and reduced shear strength in soil masses due to saturation-induced pore water pressure, which promotes slope displacement and subsequent channel constriction. Historical records reveal that when 24-h rainfall accumulation reaches the 100 mm warning threshold, water level rise rates accelerate by more than 40%, corresponding to substantially elevated landslide risks. These coupled hydrologic-geotechnical dynamics establish the rainfall-water level interaction as a critical predictive parameter for landslide early warning systems in this region. Furthermore, the period of rapid displacement concluded before the end of the rainy season. Clearly, the fluctuations in the reservoir water level and rainfall have a profound impact on the cumulative displacement of the landslide, indicating that rainfall and reservoir water levels are the primary factors influencing the deformation and failure of the Baishui River landslide.

Figure 3

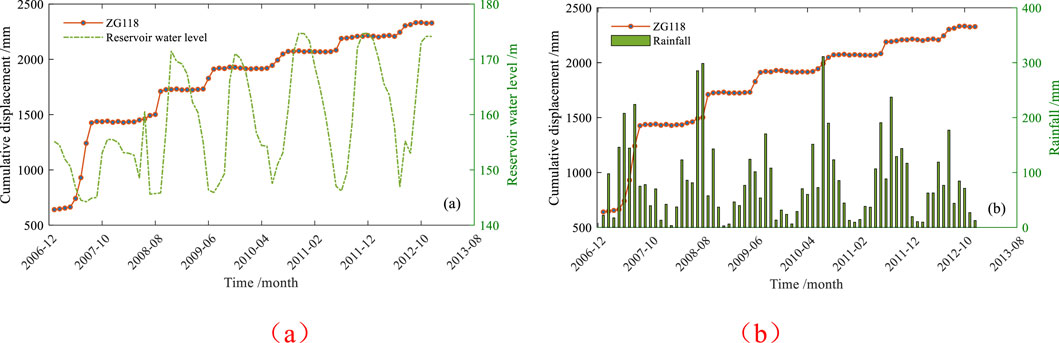
Figure 3. Monitoring curves of cumulative displacement, reservoir water level (a), and rainfall (b).

This study employs the Double Exponential Smoothing (DES) method to decompose displacement into trend displacement and periodic displacement components. Through multiple trials, an optimal exponential decay factor $\alpha$ of 0.4 was identified, effectively separating these displacement characteristics. The trend displacement component can therefore be expressed as:

$t_1=c_1(1)$

$t_i=0.4c_{i-1}+0.6t_{i-1}(2)$

$t_{i+1}=0.4c_i+0.24c_{i-1}+0.36t_{i-1}(3)$

The landslide's cumulative displacement was decomposed into trend displacement and periodic displacement using the Double Exponential Smoothing (DES) method, as illustrated in Figure 4. The results demonstrate that the trend displacement obtained through DES effectively captures the evolutionary pattern of the landslide's cumulative displacement. The periodic displacement component is primarily influenced by cyclical rainfall patterns and reservoir water level fluctuations. Consequently, prior to developing a predictive model for periodic displacement, it is necessary to extract the key factors governing the landslide's periodic displacement behavior.

Figure 4

Figure 4. Time series decomposition results of cumulative displacement.

2.2 APSO-SVR-LSTM displacement prediction model

2.2.1 APSO algorithm

The traditional Particle Swarm Optimization (PSO) algorithm suffers from issues such as premature convergence, low search accuracy, and inefficient late-stage iterations (Kennedy and Eberhart, 1995). To address these shortcomings, this study introduces an adaptive weight adjustment method and an asynchronous optimization approach for the learning factors, resulting in the Adaptive Particle Swarm Optimization (APSO) algorithm for parameter optimization. This modification allows the algorithm to balance both global and local optimization, effectively mitigating premature convergence (Rizvi et al., 2021). In the PSO algorithm, the weight factor is a critical parameter for balancing the global and local search capabilities of the algorithm. Therefore, an adaptive inertia weight adjustment method is introduced, with the following formula:

$\omega =\left\{\begin{array}{l}{\omega }_{\mathit{min}}+\frac{\left({\omega }_{\mathit{max}}-{\omega }_{\mathit{min}}\right)\left(f-f_{\mathit{min}}\right)}{f_{avg}-f_{\mathit{min}}},f\le f_{avg}\\ {\omega }_{\mathit{max}},f>f_{avg}\end{array}\right.(4)$

In the equation: ω_min, minimum weight value; ω_max maximum weight value; f, fitness value of the particle at any given time; f_min, minimum fitness value in the particle swarm; f_avg, average fitness value in the particle swarm.

The learning factors c₁ and c₂ primarily influence the optimization accuracy of the algorithm. A larger c₁ increases the iteration time, whereas a larger c₂ may lead to premature convergence of particles to local optima, resulting in early stagnation of the algorithm. Therefore, adaptively adjusting these two learning factors according to the number of iterations during the optimization process is beneficial for achieving global optimal convergence. The formula for the adaptive asynchronous learning factors is introduced as follows:

$c_1=c_{1,ini}+\frac{c_{1,fin}-c_{1,ini}}{k_{\mathit{max}}}·k(5)$

$c_2=c_{2,ini}+\frac{c_{2,fin}-c_{2,ini}}{k_{\mathit{max}}}·k(6)$

In the equation: c_1.ini, The initial value of c₁; c_2.ini, The initial value of c₂; c_1.fin, The final value of c₁; c_2.fin, The final value of c₂; k, Number of Iterations.

2.2.2 APSO-SVR algorithm

The Support Vector Regression (SVR) model (Szostek et al., 2024) employs a regression function $y_i=f\left(x_i\right)={\omega }^{*}\phi \left(x_i\right)+b$ to fit the sample points in the training set $\left\{x_i,y_i\right\}$, $i=1,2,...,n$, $x_i\in R_m$. Here, $\phi \left(x_i\right)$ represents the feature vector of the mapped influencing factors of periodic displacement; $y_i\in R_m$ denotes the periodic displacement value; ${\omega }^{*}$ is the dimensional weight vector of m; and b is the bias term. Based on the fundamental principles of SVR, the fitting process is ultimately transformed into a convex optimization problem, which is formulated as follows:

$\mathit{min}\frac{1}{2}\left({\omega }^{*},{\omega }^{*}\right)+C{\displaystyle \sum _{i=1}^n}\left({\zeta }_i+{\zeta }_i^{*}\right)(7)$

$\left\{\begin{array}{l}f\left(x_i\right)-y_i\le \epsilon +{\zeta }_i\\ y_i-f\left(x_i\right)\le \epsilon +{\zeta }_i^{*}\\ {\zeta }_i,{\zeta }_i^{*}\ge 0,i=1,2,...,m\end{array}\right.(8)$

In the equation: C is the penalty coefficient, which balances model accuracy and complexity; ξ_i and ξ^∗_i are slack variables used to prevent overfitting; ϵ is the insensitive loss function, representing the deviation between the predicted and actual displacement values.By introducing Lagrange multipliers, the original problem is transformed into its dual form, ultimately yielding the regression model for SVR as follows:

$f\left(x\right)={\displaystyle \sum _{i=1}^m}\left({\alpha }_i-{\alpha }_i^{*}\right)k\left(x,x_i\right)+b(9)$

$k\left(x,x_i\right)=\mathit{exp}\left(-\frac{{‖x-x_i‖}^2}{2{\sigma }^2}\right)(10)$

In the equation: α_i and α_i^∗ are Lagrange multipliers; The kernel function k (x_i,x_j) represents the inner product of x_i and x_j mapped into the feature space, which replaces complex computations within the feature space.

This study employs the Radial Basis Function (RBF) as the kernel function, requiring the determination of two key parameters: the penalty parameter C and the RBF kernel parameter γ (function center). The parameter optimization process follows these steps:

Step 1: Initialize Particle Swarm Optimization (PSO) parameters. Define the search ranges for SVR model parameters (C and γ), set population size, and specify maximum iteration count.

Step 2: Generate initial population. Randomly create the first generation of particles with positions and velocities represented as vectors (C, γ).

Step 3: Evaluate fitness function. Use mean squared error (MSE) of prediction results as the fitness criterion. Each particle's position (C, γ) is input into the SVR regression model to calculate its fitness value. The position with minimum fitness becomes the particle's personal best (pbest), while the global best (gbest) is identified by comparing all particles' optimal positions.

Step 4: Iterative updating. Update particle velocities and positions according to Equations, then recalculate fitness values for the new population. Update both pbest and gbest values for the current iteration.

Step 5: Termination and output. Upon reaching maximum iterations, the algorithm terminates and outputs the global best parameters (C, γ), which are then used to configure the final SVR model for prediction.

In the formula, the selection of the penalty coefficient C and the kernel function parameter $\gamma \left(\gamma =1/2{\sigma }^2\right)$ significantly affects the performance of the SVR model. Therefore, the APSO-SVR prediction model, constructed based on APSO, not only optimizes parameter selection during the prediction process—avoiding blind trial calculations—but also enhances the predictive accuracy of the SVR model. First, the influencing factors of landslide displacement are used as inputs, and the relevant parameters of the particle swarm are initialized. The initial search ranges for C and $\gamma$ are set, and the mean squared error (MSE) of the SVR model's prediction is used as the objective function to iteratively compute and identify the global optimum.

2.2.3 Long short-term memory network (LSTM)

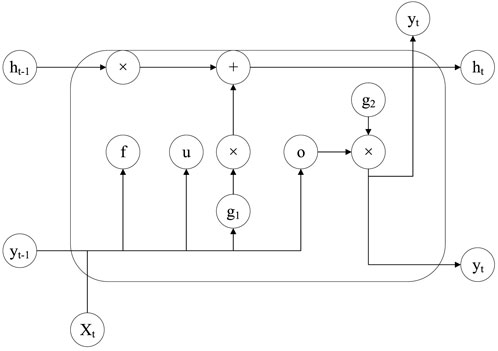
LSTM (Long Short-Term Memory) utilizes three gates to protect and control the information within the memory cells, which is achieved through the element-wise multiplication of an activation function. A series of parameters are trained using gradient descent to regulate the state of each gate (Huang et al., 2024).

Each gate in an LSTM has a specific and unique function. The forget gate (f) determines which information to discard from the previous state (h_t-1). The input gates (x_t and h_t-1) undergo an update gate (u) operation, and together with the modified forget gate (f), decide how much weight the candidate state (h_t) should contribute to the updated state. To generate the output (y_t), the current state is first filtered using a non-linear function (g₂), and then, after an operation with the output gate (o), the result (y_t) is produced. A portion of the state (y_t) is returned as the next input (y_t-1). Each gate depends on the current external input (x_t) and the previous output (y_t-1). Figure 4 provides a detailed illustration of the structural principles of LSTM. The update state equation of LSTM is given by Equation 8.

$\left\{\begin{array}{l}forgetgate:f_t=\sigma \left(W_f{x}_t+R_f{y}_{t-1}+b_f\right)\\ candidatestate:{\stackrel{\sim }{h}}_t=g_1\left(W_f{x}_t+R_f{y}_{t-1}+b_f\right)\\ updatestate:u_t=\sigma \left(W_u{x}_t+R_u{y}_{t-1}+b_u\right)\\ cellstate:h_t=u_t\otimes {\stackrel{\sim }{h}}_t+f_t\otimes h_{t-1}\\ outputgate:o_t=\sigma \left(W_o{x}_t+R_o{y}_{t-1}+b_o\right)\\ output:y_t=o_t\otimes g_2\left(h_t\right)\end{array}\right.(11)$

In the equation: x_t represents the input vector at time step t; W_f, W_h, W_u, and W_o are weight matrices associated with the input units; R_f, R_h, R_u, and R_o are weight matrices for hidden layer connections; b_f, b_h, b_u, and b_o denote bias vectors; the activation function σ is either a sigmoid function or another specified non-linear function; g₁ and g₂ represent non-linear activation functions; $\otimes$ denotes element-wise multiplication.

2.2.4 Establishing a hybrid model based on the grey wolf optimizer (GWO)

The Grey Wolf Optimization (GWO) algorithm is an effective approach for obtaining numerical solutions to optimization the problems (Balogun et al., 2020). This intelligent algorithm is inspired by the hierarchical structure and hunting behavior of grey wolves in nature. Compared with other swarm intelligence algorithms, GWO offers advantages such as conceptual simplicity, ease of implementation, and strong global search capability, leading to improved convergence speed and accuracy. At time step t, the Long Short-Term Memory (LSTM) model predicts displacement as L(t), while the Support Vector Regression (SVR) model predicts displacement as S(t). The hybrid model APSO-SVR-LSTM, which integrates LSTM with the Adaptive Particle Swarm Optimization (APSO)-optimized SVR, predicts displacement as M(t) at the same time step.

$M\left(t\right)={\omega }_1^{\prime }L\left(t\right)+{\omega }_2^{\prime }S\left(t\right),t=1,2,3...,N(12)$

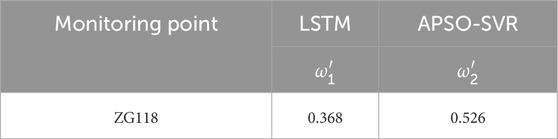
In the equation: ω₁' and ω₂' represent the weight coefficients of the LSTM model and the APSO-SVR model, respectively.

In the process of constructing the ensemble model, the weight coefficients are typically determined by minimizing the sum of squared fitting errors. Let m_t denote the prediction error of the ensemble model at time step t, and M_t represent the predicted displacement of the ensemble model at time step t. The actual displacement at time step t in the validation dataset is denoted as A(t).

$m_t=A\left(t\right)-M_t={\omega }_1^{\prime }{m}_{1t}+{\omega }_2^{\prime }{m}_{2t}(13)$

In the equation: m_1t, the periodic displacement prediction error of the LSTM model at time step t; m_2t, the periodic displacement prediction error of the APSO-SVR model at time step t; the weighting coefficients of the LSTM model ω₁' and the APSO-SVR model ω₂' satisfy the condition ω₁'+ω₂' = 1, with both ω₁' and ω₂' being greater than zero.

Let K represent the sum of squared errors of the ensemble model, and N denote the total training duration of the model. The corresponding formulation is established as follows:

$K={\displaystyle \sum _{i=1}^2}\left|m_t^2\right|={\displaystyle \sum _{t=1}^N}\left|{\displaystyle \sum _{i=1}^2}{\omega }_i^{\prime }{m}_{it}^2\right|(14)$

By transforming the problem into an optimization problem based on the criterion of minimizing the sum of squared errors, it can be expressed as:

$\mathit{min}K={\displaystyle \sum _{t=1}^N}\left|{\displaystyle \sum _{i=1}^2}{\omega }_i^{\prime }{m}_{it}^2\right|(15)$

In the equation: ω₁'+ω₂' = 1, with both ω₁' and ω₂' being greater than zero.

For the solution of Equation 12, the Lagrange multiplier λ is introduced to construct the objective function. Partial derivatives of the objective function are then computed to formulate a system of linear equations. By solving this system, the optimal weight coefficients of the model are obtained, and the combined model with the optimal weight ratio is trained and fitted accordingly.

2.2.5 Data normalization processing and model evaluation criteria

To evaluate the prediction accuracy of the model, the Root Mean Square Error (RMSE) and the Mean Absolute Percentage Error (MAPE) were selected as performance evaluation criteria. To enhance the prediction accuracy of the model, factors influencing periodic displacement, as mentioned in the literature, were selected as model inputs. These include the cumulative rainfall for the current month, cumulative rainfall for the previous month, cumulative rainfall for the two preceding months, current month's reservoir water level, monthly water level change, water level change over the past 2 months, cumulative displacement for the current month, cumulative displacement for the past 2 months, and cumulative displacement for the past 3 months. Due to the differing data types, all monitoring data were normalized to the range [0, 1] to eliminate the influence of dimensional differences between the variables. The formula for normalization is as follows:

$y=\frac{\left(x_i-x_{imin}\right)}{\left(x_{imax}-x_{imin}\right)}(16)$

In the equation: x_imax, the maximum value of variable i; x_imin, the minimum value of the variable i; x_i, the original value; y, the normalized value.

3 Results and discussion

In this study, a dataset consisting of 144 monitoring data points from the ZG118 monitoring stations at the Baishui River landslide, spanning from January 2007 to December 2012, was selected. This dataset includes reservoir water levels, rainfall, and displacement values, with rainfall and displacement values representing cumulative values for the respective months, and water level values representing the monthly averages. 80% of the data were used as the fitting dataset, while 20% of the data were reserved as the validation dataset to assess the model's prediction performance. The displacement monitoring data from the first 58 months is used as the training set, and the data from the last 14 months is used as the testing set.

After normalizing the data, it was used as the input parameters for the APSO-SVR-LSTM model. To verify its effectiveness, comparative experiments were conducted with the APSO-SVR model and the LSTM model. After continuous iterative calculations, for random displacement prediction, the number of hidden layer neurons is 22, the training times are 200, and the initial learning rate is 0.0001. Then, train the model and output the predicted values. First, the APSO algorithm was employed to optimize the penalty coefficient (C) and the RBF kernel function parameter in the SVR model. After multiple trials, the optimal parameter combination was obtained, as shown in Table 1. The weights of the hybrid model, calculated using the Grey Wolf Optimizer, are presented in Table 2. The prediction results of each model, validated using the test dataset, are illustrated in Figure 5, while the evaluation of the predictive performance of the three models is summarized in Table 3.

Table 1

Table 1. SVR combination parameter.

Table 2

Table 2. Weight distribution of combined models.

Figure 5

Figure 5. Structure of LSTM.

Table 3

Table 3. Prediction accuracy analysis of three models of monitoring point ZG118.

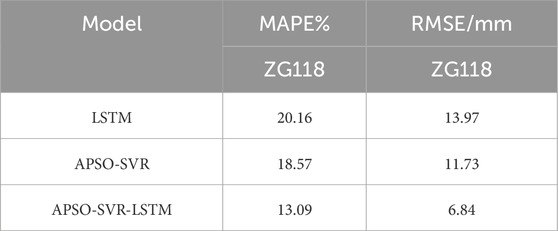
As shown in Table 3, the mean absolute percentage error (MAPE) of the ensemble model for periodic displacement prediction is reduced by 7% and 5% at monitoring point ZG118 compared to the LSTM and APSO-SVR models, respectively. Similarly, the root mean square error (RMSE) is reduced by 7.1 mm and 4.9 mm, respectively. These results indicate that, under the same training dataset, the ensemble model demonstrates superior stability and higher predictive accuracy compared to the individual models. As illustrated in Table 2 and Figure 5, the predictive accuracy of the LSTM and APSO-SVR models influences their weight distribution in the ensemble model. Given that the APSO-SVR model performs better overall at monitoring point ZG118, it holds a higher weight proportion in the ensemble model, thereby enhancing its predictive accuracy.

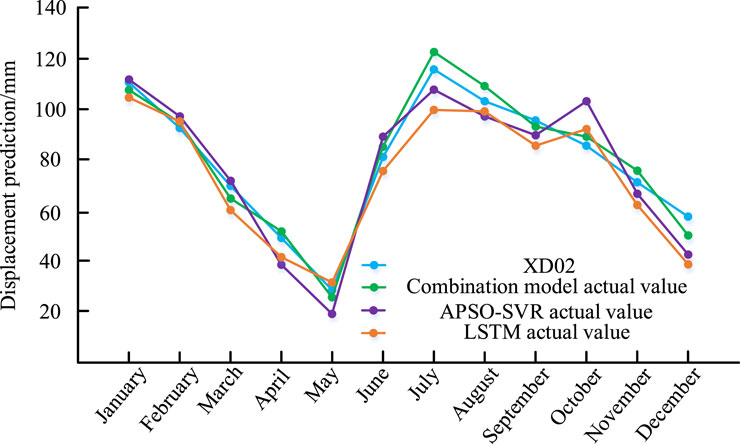
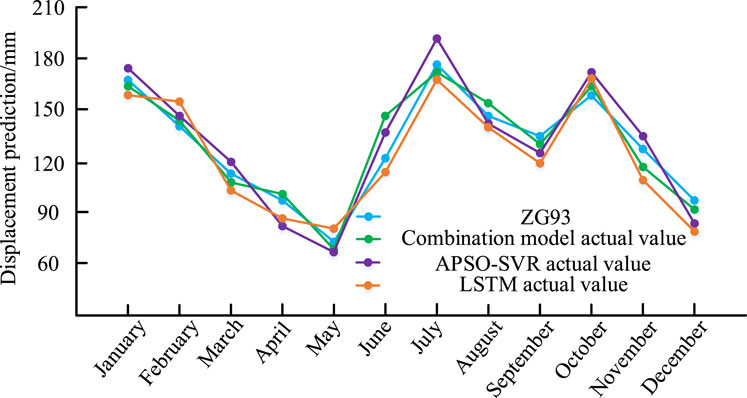
To further validate the superiority of the ensemble model, all three models were applied to two additional monitoring points, XD02 and ZG93, on the Baishuiihe landslide. The monitoring points XD02 and ZG93 exhibited the maximum cumulative deformation, with their displacement directions being essentially consistent. In contrast, the deformation directions of the remaining monitoring points showed certain angular deviations, indicating asynchronous displacement patterns (Pang et al., 2024). The objective was to predict the periodic displacement trends for these points in 2009, with the results presented in Figures 6, 7. The findings indicate that the ensemble model outperforms the two individual models in forecasting the periodic displacement of step-like landslides, demonstrating the robustness of the proposed approach.

Figure 6

Figure 6. Displacement prediction curve of periodic term at monitoring point ZG118 (in 2012 years).

Figure 7

Figure 7. Displacement prediction of period term of monitoring point XD02 (in 2009 years).

Figure 8

Figure 8. Displacement prediction of period term of monitoring point ZG93 (in 2009 years).

When performing periodic displacement predictions based on the same training dataset, the static SVR model exhibits higher predictive accuracy than the LSTM model. This is primarily because the SVR model demonstrates superior predictive performance when trained on small sample datasets. However, the SVR model can only learn information at the current time step, neglecting the fact that landslide displacement is a dynamic process that evolves over time. Due to the lagging effect of displacement-influencing factors, the accuracy of predictions deteriorates as the forecasting time extends, as long-term historical data introduces temporal dependencies that interfere with the results. Although some researchers have attempted to address the issue of data timeliness by improving the SVR predictive model, these methods still lack an effective quantitative evaluation criterion.

Given that recurrent neural networks (RNNs) can capture interdependencies in data and address data validity issues, this study integrates the dynamic LSTM model with the static SVR model to propose a novel predictive framework. This hybrid model fully leverages the LSTM model's capability to extract temporal dependencies from sequential data while maintaining the strong predictive performance of SVR in limited-sample scenarios. The results indicate that the ensemble model achieves RMSE values below 9 mm across all four monitoring points, with an average reduction of approximately 6% in MAPE compared to the two individual models. These findings highlight the high applicability of the propo3sed model in predicting periodic landslide displacements.

The experiments primarily focus on step-like landslides, with precipitation and water level fluctuations considered as the dominant influencing factors. However, geological structures vary across different landslides, and practical applications should first identify the key factors governing periodic displacement variations for each specific landslide to enhance the adaptability and generalization of the model.

4 Conclusion

Based on monitoring data of precipitation, water levels, and GPS displacement from the Baishuiihe landslide monitoring points, this study establishes a hybrid periodic displacement prediction model (APSO-SVR-LSTM) based on linear combination theory. The analysis of experimental results leads to the following conclusions:

(1) By integrating an adaptive inertia weight adjustment method with an asynchronous learning factor strategy, the adaptive particle swarm optimization (APSO) algorithm effectively balances global exploration and local exploitation, facilitating the rapid convergence of particles to the global optimum.

(2) Compared with traditional standalone models, the proposed APSO-SVR-LSTM model, developed based on the minimum variance criterion to determine optimal weight allocation, enhances predictive accuracy. The final prediction results demonstrate superior performance, indicating significant engineering application value.

(3) Landslides are highly complex systems with intricate internal structures. With the continuous advancement of information technology, deep displacement monitoring data can provide more comprehensive insights into internal landslide dynamics. Therefore, integrating surface and deep displacement measurements into predictive modeling represents a crucial direction for future research.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

NW: Data curation, Methodology, Conceptualization, Investigation, Writing – original draft. JZ: Visualization, Validation, Supervision, Writing – review and editing, Methodology. YX: Writing – review and editing, Methodology, Resources, Data curation, Visualization. SH: Validation, Formal Analysis, Conceptualization, Writing – review and editing, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by Excellent Science and Technology Innovation Team in Jiangsu Province's Universities, Research and Application of Industrial Safety Environment Technology and Equipment (BY20230482); Vice President of Science and Technology of Jiangsu Province (1781).

Acknowledgments

We would highly thank the Department of Surveying and Mapping of Huibei Province for providing relevant data.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abd Majid, N., and Rainis, R. (2019). Aplikasi Sistem Maklumat Geografi (GIS) dan Analisis Diskriminan dalam Pemodelan Kejadian Kegagalan Cerun di Pulau Pinang, Malaysia. Sains Malays 48, 1367–1381. doi:10.17576/jsm-2019-4807-06

CrossRef Full Text | Google Scholar

Althuwaynee, O. F., and Pradhan, B. (2017). Semi-quantitative landslide risk assessment using GIS-based exposure analysis in Kuala Lumpur City. Geom. Nat. Hazards Risk 8, 706–732. doi:10.1080/19475705.2016.1255670

CrossRef Full Text | Google Scholar

Aristizábal, E., and Sánchez, O. (2020). Spatial and temporal patterns and the socioeconomic impacts of landslides in the tropical and mountainous Colombian Andes. Disasters 44, 596–618. doi:10.1111/disa.12391

PubMed Abstract | CrossRef Full Text | Google Scholar

Balogun, A.-L., Rezaie, F., Pham, Q. B., Gigović, L., Drobnjak, S., Aina, Y. A., et al. (2020). Spatial prediction of landslide susceptibility in western Serbia using hybrid support vector regression (SVR) with GWO, BAT and COA algorithms. Geosci. Front. 12, 101104. doi:10.1016/j.gsf.2020.10.009

CrossRef Full Text | Google Scholar

Batista, E. F., Passini, L. D. B., and Kormann, A. C. M. (2019). Methodologies of economic measurement and vulnerability assessment for application in landslide risk analysis in a highway domain strip: a case study in the Serra Pelada Region (Brazil). Sustainability 11 (21), 6130. doi:10.3390/su11216130

CrossRef Full Text | Google Scholar

Cheng, D., Cui, Y., Su, F., Jia, Y., and Choi, C. E. (2018). The characteristics of the Mocoa compound disaster event, Colombia. Landslides 15, 1223–1232. doi:10.1007/s10346-018-0969-1

CrossRef Full Text | Google Scholar

Cui, Y., Cheng, D., and Chan, D. (2019). Investigation of post-fire debris flows in Montecito. ISPRS Int. J. Geo-Information 8 (1), 5. doi:10.3390/ijgi8010005

CrossRef Full Text | Google Scholar

De Silva, K., Gunasekera, M. Y., and Aap, D. A. (2017). Derivation of a societal risk acceptance criterion for major accident hazard installations in Sri Lanka. Process Saf. Environ. Prot. 111, 388–398. doi:10.1016/j.psep.2017.07.025

CrossRef Full Text | Google Scholar

Froude, M. J., and Petley, D. N. (2018). Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 18, 2161–2181. doi:10.5194/nhess-18-2161-2018

CrossRef Full Text | Google Scholar

Fu, S., Chen, L., Woldai, T., Yin, K., Gui, L., Li, D., et al. (2020). Landslide hazard probability and risk assessment at the community level: a case of western Hubei, China. Nat. Hazards Earth Syst. Sci. 20, 581–601. doi:10.5194/nhess-20-581-2020

CrossRef Full Text | Google Scholar

Gbanie, S. P., Griffin, A. L., and Thornton, A. (2018). Impacts on the urban environment: land cover change trajectories and landscape fragmentation in post-war Western area, Sierra Leone. Remote Sens. 10 (1), 129. doi:10.3390/rs10010129

CrossRef Full Text | Google Scholar

Görüm, T., and Fidan, S. (2021). Spatiotemporal variations of fatal landslides in Turkey. Landslides 18, 1691–1705. doi:10.1007/s10346-020-01580-7

CrossRef Full Text | Google Scholar

Huang, W., Zhao, J., and Wang, X. (2024). Model-driven multimodal LSTM-CNN for unbiased structural forecasting of European Union allowances open-high-low-close price. Energy Econ., 132.

Google Scholar

Kamal, A. M., Hossain, F., Ahmed, B., Rahman, M. Z., and Sammonds, P. (2023). Assessing the effectiveness of landslide slope stability by analysing structural mitigation measures and community risk perception. Nat. Hazards 117 (3), 2393–2418. doi:10.1007/s11069-023-05947-6

CrossRef Full Text | Google Scholar

Kennedy, J., and Eberhart, R. (1995). “Particle swarm optimization,” in Proceedings of ICNN'95 - International Conference on Neural Networks (IEEE), 1942–1948.

Google Scholar

Kirschbaum, D., Stanley, T., and Zhou, Y. (2015). Spatial and temporal analysis of a global landslide catalog. Geomorphology 249, 4–15. doi:10.1016/j.geomorph.2015.03.016

CrossRef Full Text | Google Scholar

Klose, M., Maurischat, P., and Damm, B. (2016). Landslide impacts in Germany: a historical and socioeconomic perspective. Landslides 13, 183–199. doi:10.1007/s10346-015-0643-9

CrossRef Full Text | Google Scholar

Lin, Q., and Wang, Y. (2018). Spatial and temporal analysis of a fatal landslide inventory in China from 1950 to 2016. Landslides 15, 2357–2372. doi:10.1007/s10346-018-1037-6

CrossRef Full Text | Google Scholar

Lu, K., Li, F., Pan, J., Li, K., Li, Z., and Wang, P. (2024). Structural characterization and attempted displacement interpretation of the Baishuihe landslide using integrated geophysical methods. Eng. Geol. 336, 107568. doi:10.1016/j.enggeo.2024.107568

CrossRef Full Text | Google Scholar

Pang, H., Chen, K., Geng, Y., Wu, L., Wang, F., and Liu, J. (2024). Accurate capacity and remaining useful life prediction of lithium-ion batteries based on improved particle swarm optimization and particle filter. Energy 293, 130555. doi:10.1016/j.energy.2024.130555

CrossRef Full Text | Google Scholar

Rizvi, A., Yang, D., and Khan, T. A. (2021). “Optimization of heliostat fields using advanced particle swarm optimization (APSO),” in 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering (REPE), 306–310.

Google Scholar

Roy, S., and Kshirsagar, R. (2020). Development of risk acceptance criteria in the Indian context. Process Saf. Environ. Prot. 148, 358–369. doi:10.1016/j.psep.2020.10.021

CrossRef Full Text | Google Scholar

Salee, R., Chinkulkijniwat, A., Yubonchit, S., Horpibulsuk, S., Wangfaoklang, C., and Soisompong, S. (2022). New threshold for landslide warning in the southern part of Thailand integrates cumulative rainfall with event rainfall depth-duration. Nat. Hazards 113 (1), 125–141. doi:10.1007/s11069-022-05292-0

CrossRef Full Text | Google Scholar

Strouth, A., and McDougall, S. (2020). Societal risk evaluation for landslides: historical synthesis and proposed tools. Landslides 18, 1071–1085. doi:10.1007/s10346-020-01547-8

CrossRef Full Text | Google Scholar

Szostek, K., Mazur, D., Drałus, G., and Kusznier, J. (2024). Analysis of the effectiveness of ARIMA, SARIMA, and SVR models in time series forecasting: a case study of wind farm energy production. Energies, 17(19), 4803. doi:10.3390/en17194803

CrossRef Full Text | Google Scholar

Thapa, P. S., Adhikari, B. R., Shaw, R., Bhattarai, D., and Yanai, S. (2023). Geomorphological analysis and early warning systems for landslide risk mitigation in Nepalese mid-hills. Nat. Hazards 117 (2), 1793–1812. doi:10.1007/s11069-023-05929-8

CrossRef Full Text | Google Scholar

Zhang, X., Ruan, Y., Xuan, W., Bao, H., and Du, Z. (2023). Risk assessment and spatial regulation on urban ground collapse based on geo-detector: a case study of Hangzhou urban area. Nat. Hazards 118 (1), 525–543. doi:10.1007/s11069-023-06016-8

CrossRef Full Text | Google Scholar