ChatGPT's perspectives on real numbers, straight lines, and probability—A quantitative study on the influence of prompting

Large language models like ChatGPT are currently a hot topic in mathematics education research. Various analyses are available on the correctness of mathematical responses and on performance in problem solving or proving contexts. However, the adequate representation of mathematical content in the responses has not yet been sufficiently considered in research. This article addresses this desideratum using the approach of belief systems about mathematics. For this purpose, four perspectives on mathematics are distinguished—the formal-abstract, the empirical-concrete, the application and the toolbox perspective. A qualitative content analysis of 450 ChatGPT responses to the mathematical concepts of real numbers, straight lines and probability and the subsequent quantitative evaluation with chi-square tests showed that the empirical-concrete perspective occurs much more frequently than the other perspectives and the formal-abstract perspective is found very rarely in comparison. The use of appropriate prompts can significantly increase or decrease the occurrence of perspectives. There are also significant differences between the mathematical concepts. The concept of a straight line is significantly more often defined in terms of the empirical-concrete and less often in terms of the formal-abstract perspective compared to the other concepts.

1 Introduction

The use of generative artificial intelligence (AI) in education is currently a hotly debated topic. In particular, large language models (LLMs) such as ChatGPT, Google Gemini or Microsoft Copilot are the focus of attention. LLMs are linguistic models that have been trained with a huge amount of text data and are intended to simulate natural communication via text. With the help of probability trees, answers (so-called responses) to user requests (so-called prompts) are generated. For this purpose, probabilities are assigned to the various words and smaller text parts, which describe the relation to the other words and text parts from the prompt and the responses already generated. Although the system was trained for linguistic knowledge, it can also contain rational knowledge from the training data (Petroni et al., 2019). Nevertheless, knowledge databases are not accessed directly for the responses; the knowledge comes solely from the trained linguistic model, which can also result in the output of incorrect information.

The AI-technology is expected to have a significant impact on education, with some authors even predicting a revolution (Wardat et al., 2023; Vandamme and Kaczmarski, 2023). Kasneci et al. (2023) describe the opportunities and challenges that they see arising from the new technology. On the one hand, there is the enhancement of assessment and evaluation, lesson planning, language learning, research and writing, and professional development of teachers. On the other hand, there are challenges such as copyright issues, bias and fairness, and the possibility that teachers and students become too reliant on generative AI. The use of generative AI is also being considered in mathematics education research, although the research is still in its early stages. However, it has been shown in various tests and studies that LLMs can generate mathematically correct responses in many cases and that this can be influenced by prompting (e.g., Wei, 2024; Schorcht et al., 2024). The rapid technical development in this sector suggests that mathematical errors will further decrease in future.

The mathematical correctness of the responses is certainly a prerequisite for LLMs to become an adequate tool for teaching mathematics. This issue did not need to be addressed at all with previous tools such as computer algebra systems, calculators, spreadsheets or dynamic geometry software. It was obvious, that these deterministic systems always provide a unique and mathematically correct solution. In addition to the generation of potentially incorrect answers, another aspect distinguishes LLMs from classic digital mathematics tools. The response does not only provide a solution given in the form of a number, a formula or a geometric drawing, but it is also interpreted, analyzed, explained or classified in the context of the prompt. LLMs are not limited to performing simple calculations or construction tasks; rather, they can also answer conceptual questions about mathematical concepts and situations. This means that they are not just a tool, but also a resource that can teach students new and already known knowledge, like a schoolbook, online learning videos or learning websites. In this context, it is also important to always check whether the information presented is mathematically correct. However, another crucial component is added with the adequate presentation of the mathematical situation. The same mathematical content can be presented quite differently in different contexts, for example, in a rather formal and abstract way in a university textbook, with a strong reference to the real world in a school textbook, or prototypically by emphasizing schematic aspects in an online learning video. All these forms of presentation can be mathematically correct and yet offer a different perspective on mathematics. These different perspectives can be described using the theoretical framework of belief systems about mathematics (e.g., Schoenfeld, 1985; see Section 2.2).

From this point of view, this article aims to investigate the perspectives on mathematics provided by the responses of the well-known LLM ChatGPT. To answer this, the next section first provides an insight into research on LLMs in mathematics education and belief systems about mathematics. Subsequently, an empirical study is presented in which responses to the three mathematical concepts real numbers, straight line, and probability are coded with regard to four previously defined perspectives on mathematics. A quantitative analysis of the codings reveals the influence of the used prompts and the mathematical concepts, as well as general differences in the occurrence of the four perspectives on mathematics. The results are discussed in the context of the state of research and a conclusion and an outlook are formulated.

2 Theoretical background

2.1 Large language models in mathematics education

Research on LLMs in mathematics education is still in its infancy and has largely emerged in the wake of the release of ChatGPT 3.5 and the resulting societal hype. However, the use of AI for mathematical learning has been discussed for several years, albeit more from the perspective of learning analytics or machine learning and with a strong developmental focus (Chen et al., 2020; bin Mohamed et al., 2022). The following discussion is focused on the use of LLMs and not AI in general. The discussion will be structured along the familiar model of the didactic tetrahedron. The didactic tetrahedron has been described in a similar way by many different authors and used to analyze empirical data (see the literature review in Ruthven, 2012). It consists of four corners, which stand for the fundamental elements of mathematics teaching: teacher, learner, mathematics and technology. Between these elements, there are many relationships, which are represented by the edges and triangular surfaces of the tetrahedron.

The theoretical discussions and empirical studies on LLMs in mathematics education that have been found so far relate to the use of LLMs by teachers (Technology-Mathematics-Teacher), the use of LLMs by students (Technology-Mathematics-Learner) and the analysis of LLMs with regard to mathematical capabilities (Technology-Mathematics).

Research on teachers' use of LLMs in mathematics (Technology-Mathematics-Teacher) focuses on LLMs as a tool for designing mathematics lessons. It can also be seen that pre-service teachers have been the focus of attention so far, rather than in-service teachers. Buchholtz and Huget (2024) have investigated how pre-service teachers use ChatGPT to develop mathematics lesson plans. For this purpose, the pre-service teachers were given initial prompts, which included a framework for planning lessons in five steps and specific instructions for the interaction between ChatGPT and the user. The results show that the pre-service teachers used ChatGPT in very different ways. The spectrum ranged from simply accepting the generated suggestions to consciously adapting them and making theoretically well-founded decisions. The quality of the developed lesson plans depended in particular on the adaptations made by the pre-service teachers, since the suggestions generated by ChatGPT mostly corresponded to a rather standardized teaching approach. The planning dialogue with ChatGPT was able to trigger reflection processes among the pre-service teachers in which they reconsidered their planning decisions.

Baumanns and Pohl (2024) address problem posing as a specific aspect of lesson planning. In a qualitative study, they examined the interaction processes of five pre-service teachers when creating a simple, a moderate and a difficult math problem based on a given problem on Hasse diagrams. The pre-service teachers worked with a special megaprompt, so that ChatGPT functioned more as an assistant and asked targeted impulse questions to the pre-service teachers. Baumanns and Pohl were able to reconstruct three ways of using ChatGPT. First, the pre-service teachers used ChatGPT as a collaboration partner to jointly develop ideas and reflect on them. A second way of using it was in discussions in the area of pedagogical content knowledge, in which ChatGPT asked for subject-specific justifications. The last reconstructed way of using ChatGPT was to support the linguistic formulation of the problems, for example by rephrasing them in simpler language.

Noster et al. (2024a) also studied pre-service teachers creating tasks. However, their study specifically focused on developing tasks in which ChatGPT is used as a tool. Although the results show that different ways of using ChatGPT appear in the tasks (e.g., generation of data sets, comparison of fractions, mathematical modeling), overall, the specific characteristics of the technology are not adequately considered by the pre-service teachers, e.g., that the responses of ChatGPT are not always correct.

Research on students' use of LLMs (Technology-Mathematics-Learner) tends to focus on university students and examines how they use technology in mathematical activities such as proving. Yoon et al. (2024) conducted three clinical interviews with undergraduate mathematics students in which the students were asked to prove six selected mathematical statements using ChatGPT. They found that the students' engagement with ChatGPT was significantly influenced by three factors: the students' different conceptions of mathematical proofs had particular effects on the evaluation of the responses and their integration into the final proof. The conceptions of ChatGPT influenced how ChatGPT was used (e.g., the revision of prompts). Finally, ethical considerations were relevant in determining whether and how ChatGPT should be integrated into the students' learning process.

Park and Manley (2024) have examined the proof-checking of university students with the help of ChatGPT. A sample of 29 students first independently developed statements and arguments to determine the area of a triangle from its side lengths. After that, the arguments were revised with the help of ChatGPT. By comparing the original and final arguments and analyzing the students' statements about using ChatGPT as a proof assistant, Park and Manley were able to show that the students mostly agreed with ChatGPT's suggestions and revised the arguments accordingly to improve clarity, provide additional justifications, and show the generality of their arguments.

Dilling and Herrmann (2024) have also investigated the use of ChatGPT as a proof assistant in geometry at university. By analyzing 162 chats of students on the proof of two well-known geometric theorems, nine different prompting types could be identified. Most commonly, students asked directly for the proof or asked follow-up questions to the previous responses. Other prompts included questions about specific mathematical concepts or theorems, requests for feedback on their own proof ideas, requests for a different proof, questions about the premises of the proof, or the output of a graphic visualization.

Noster et al. (2024b) also came to similar conclusions, observing 11 pre-service mathematics teachers while they worked on four mathematical tasks from the fields of arithmetic and probability theory with ChatGPT. They identified six different prompting techniques: the students most often formulated zero-shot prompts, frequently also by directly copying the task as a prompt. The repeating of prompts (regeneration of a response or using the same prompt again), the use of ChatGPT as a calculator for performing simple calculations, and the change of languages between German and English were also found quite frequently. Only occasionally, students used few-shot prompts (e.g., similar tasks with solutions) or asked for feedback on their own solution.

Dilling et al. (2024a) examined the use of ChatGPT by middle school students when proving the theorem of the sum of interior angles in a teaching experiment. They were able to determine various forms of communication and interaction with and about the LLM. The interaction with the LLM was used by the students to verify their own conclusions and to ask for visualizations, and typical for this form of communication was the regeneration of prompts and the reviewing of previous responses. The communication between the students about ChatGPT included reading out of the response, questioning the response, identifying errors, discussing responses and comparing the response to previous solutions. The role of the teacher was also considered in the teaching experiment. He particularly attracted attention by checking the ChatGPT responses for correctness and adequacy, highlighting incorrect aspects, and excluding too difficult mathematical topics that occurred in the chats. Overall, the teaching experiment showed that although ChatGPT produced many logical errors in the argumentation, this nevertheless provided an engaging learning opportunity for the students.

Most of the studies on Large Language Models in the field of mathematics directly examine the systems' mathematical capabilities without involving students or teachers (Technology-Mathematics). Many of these studies use publicly available tasks from well-known tests such as national or international final exams, comparative tests, or admission tests. As an example, the relatively current study by Wei (2024) should be mentioned here, which assessed the capabilities of ChatGPT-4 and ChatGPT-4o in solving mathematics problems from the National Assessment of Educational Progress (NAEP) in grades 4, 8, and 12. The results show that ChatGPT-4o performs slightly better overall than ChatGPT-4, and both systems perform better than the average U.S. student in the respective grades. Furthermore, the author notes that the LLMs perform significantly worse in geometry and measurement than in algebra and that more difficult mathematical tasks are generally solved worse by the LLMs.

In a systematic evaluation, Dilling (2024a) examined the potential of ChatGPT-4 as an assessment and feedback tool from a mathematics education perspective. The analysis of different sample tasks and solutions in the context of linear algebra and analytic geometry showed that ChatGPT offers a remarkable amount of potential for formative assessment and feedback in this field. All operations that can be performed by a computer algebra system can also be performed by ChatGPT by connecting to Python or Wolfram Alpha. Furthermore, the used prompt largely determines the form and content of the feedback, the correctness of the assessment and the extent to which the response is adapted to the feedback receiver. In general, the system was able to provide correct and didactically useful feedback in many but not all cases.

However, LLMs still have difficulty with more complex mathematical problem-solving, as can be seen, for example, from the studies by Getenet (2024) and Schorcht et al. (2024). However, the process-related and content-related quality could be increased in the study by Schorcht et al. (2024) by using appropriate prompting techniques (e.g., chain-of-thought prompting) and by using a suitable LLM version (ChatGPT-4 performed better than ChatGPT-3.5). Beside problem-solving, mathematical proofs generated by ChatGPT are not reliable and often contain logical errors (Dilling et al., 2024a; Dilling and Herrmann, 2024).

The mathematical correctness of LLM responses is thus being examined in detail in research and is also a key concern in the further development of the established LLMs. For example, in September 2024, OpenAI released the GPT-4o1 model, which was specifically trained for complex reasoning and implemented a chain-of-thought approach (OpenAI, 2024). However, the adequate presentation of (at best correct) mathematical content in LLM responses has only been considered in a few studies so far. Dilling (2024a) considered this aspect as briefly described above from the perspective of appropriate and individualized feedback. Another study that addresses appropriate presentation comes from Peters and Schorcht (2024). They examined how given mathematical tasks can be improved with the help of appropriately prompted ChatGPT agents. They considered the aspects of mathematical content, linguistic sensitivity, competence orientation, and differentiation. The tasks created with ChatGPT were evaluated by in-service teachers as human experts. It was found that AI-generated problem-based tasks were rated better than the original tasks in 61% of all cases, while tasks requiring basic competencies were rated better in only 28% of the cases. An important reason why teachers decided on the original tasks was their short length and concise presentation of information. Reasons for selecting the AI-generated tasks included the concrete call for action, the presentation of solution approaches and the motivational context.

Despite these initial studies, which consider the presentation of mathematical content in specific contexts such as giving feedback or generating tasks, there is a research gap in terms of which perspectives on mathematics and mathematical concepts are opened up by LLMs. This article aims to approach this fundamental question from the position of belief systems about mathematics.

2.2 Belief systems about mathematics

In this article, LLMs are analyzed in the context of the approach of beliefs systems about mathematics. Belief systems can be defined according to Schoenfeld (1985) as follows:

Belief systems are one's mathematical world view, the perspective with which one approaches mathematics and mathematical tasks. One's beliefs about mathematics can determine how one chooses to approach a problem, which techniques will be used or avoided, how long and how hard one will work on it, and so on. Beliefs establish the context within which resources, heuristics and control operate. (Schoenfeld, 1985, p. 45)

Beliefs and belief systems are a central subject of investigation in mathematics education research and they are assumed to have a significant influence on mathematical teaching and learning processes (Goldin et al., 2009). In a normative sense, Green (1971) considers the shaping of students' mathematical belief systems to be one of the key goals of teaching:

Teaching is an activity which has to do, among other things, with the modification and formation of belief systems. If belief systems were impervious to change, then teaching, as a fundamental method of education, would be a fruitful activity. (Green, 1971, p. 48)

The research literature often emphasizes the importance of teachers' beliefs, which significantly influence the development of students' beliefs (e.g., Grigutsch et al., 1998). The influence of teachers' beliefs on students' beliefs has been empirically proven in a number of empirical studies (e.g., Carter and Norwood, 2010; Muis and Foy, 2010). Other factors, such as the design of teaching materials, are less easy to measure directly in empirical studies—nevertheless, a long-term influence can be assumed. If LLMs will have a significant influence on the learning of mathematics in and outside the classroom in the future, it is also important to have a look on the perspectives on mathematics presented by this technology.

A basic assumption of research on belief systems about mathematics is that the belief systems of different individuals can be described as sufficiently similar and can therefore be categorized accordingly. Goldin (2002) uses the phrase “socially or culturally shared belief systems” (p. 64). Based on this assumption, theoretical and empirical approaches have been developed to categorize possible types of mathematical belief systems, each of which focuses on different characteristics.

Building on the research on the categorization of prototypical belief systems about mathematics, four perspectives will be described in more detail here (Dilling et al., 2024b; Dilling, 2024b). This is explicitly not an exhaustive description—many other belief systems or perspectives can be described by looking at other characteristics. Furthermore, the belief systems and perspectives are not mutually exclusive and combinations can occur.

The formal-abstract perspective (FA) corresponds to the commonly accepted scientific way of practicing and understanding mathematics. It is characterized by a strictly deductive and abstract approach. In addition, there is a complete separation of mathematics and reality, which can be achieved through the formulation of axioms as propositional patterns. The formal-abstract perspective can be found in particular at universities and was established with the work of David Hilbert on the foundations of geometry. A similar characterization of a formal-abstract belief system can be found in various places in the literature. For example, Schoenfeld (1985) compared the beliefs of mathematicians and students when solving problems, whereby the belief system of the mathematician describes the formal-abstract perspective. Grigutsch et al. (1998) characterized the formalism aspect with 12 different items and identified it as a frequently encountered perspective in a survey of teachers. Dionne (1984) distinguishes three views of mathematics on a theoretical basis, including the formalistic view, in which doing mathematics means developing rigorous proofs, using precise and exact terminology and standardizing concepts. In his framework of the three worlds of mathematics, Tall (2013) describes the world of axiomatic-formalism as “building formal knowledge in axiomatic systems specified by set-theoretic definition, whose properties are deduced by mathematical proof” (p. 133). Dilling (2022), Stoffels (2020), and Witzke and Spies (2016) emphasize the separation of mathematics from reality as a characteristic feature of a formal-abstract belief system.

The empirical-concrete perspective (EC) is a kind of opposite to the formal-abstract perspective. In this perspective, the objects of investigation in mathematics originate from empiricism (e.g., function graphs, drawing sheet figures, dice experiments) and the mathematical theory is ontologically bound to these. Mathematical propositions can be described within a theory, but the axioms and definitions refer directly to empirical objects. According to recent studies (e.g., Witzke and Spies, 2016), students at school and at the beginning of their university studies often hold such a belief system about mathematics, which can be attributed to the way mathematics is taught at school. In Schoenfeld's (1985) problem-solving case studies, the students' belief system corresponds to an empirical perspective on mathematics. However, Schoenfeld speaks of “pure empiricists,” as he did not observe any logical deductions or genuine theorizations. In Tall's (2013) three worlds framework, there is a world of conceptual embodiment, which describes the development of mathematical knowledge “building on human perceptions and actions” (p. 133). Dilling (2022), Stoffels (2020), and Witzke and Spies (2016) also describe an empirical-concrete belief system, which is about substantial mathematical theory development based on empirical objects.

The application perspective (A) is about the application of mathematical concepts and theorems in reality. This takes place, for instance, in applied sciences, but also in everyday life. Grigutsch et al. (1998) describe this in the so-called application aspect with items such as “Mathematics helps to solve everyday tasks and problems” or “Mathematics has a general, fundamental benefit for society” (p. 17). Witzke and Spies (2016) describe the application orientation, which focuses on extra-mathematical applications and mathematical modeling. As an anchor example, they cite the answer of a student who describes the concept of the inflection point in calculus with reference to the water level in a reservoir.

The toolbox perspective emphasizes the application of rules, formulas and procedures in a schematic way. Ernest (1989) describes this as the instrumentalist view (“mathematics is a useful but unrelated collection of facts, rules and skills”, p. 21)—Dionne (1984) uses the term traditional view. In the study by Grigutsch et al. (1998), the schema aspect is characterized, for example, with the item “Mathematics is a collection of procedures and rules that specify exactly how to solve tasks” (p. 19). Witzke and Spies (2016) cite the derivation of functions using derivation rules as an example of the toolbox orientation.

Brief descriptions of the four perspectives on mathematics, which also appear as definitions of the categories in the later analysis, can be seen in Table 1.

Table 1

Table 1. Definition of the four perspectives on mathematics considered in the empirical study.

At first glance, it may seem somewhat unusual to apply a psychological concept such as that of beliefs to the study of a technology like LLMs. It is not assumed that an LLM—such as ChatGPT in the present case—possesses human characteristics or an actual belief system. Rather, the premise is that certain perspectives are conveyed through its responses: the LLM represents mathematical concepts in a specific manner, for example by formulating axioms or referencing real-world situations. Whether this representation is consistent is one of the key questions addressed in this study.

This gives rise to the hypothesis that individuals who interact with the LLM in mathematical contexts (e.g., students in mathematics education) may develop or be supported in developing certain conceptions of mathematics. These, in turn, form the basis for the development or further development of their belief systems about mathematics. The concept of beliefs—extensively studied and well-established in mathematics education research—provides a useful framework for distinguishing between different perspectives on mathematics and for making them accessible to empirical investigation.

2.3 Research questions

On the basis of the literature review on LLMs in mathematics education, a research gap was identified with regard to the presentation of mathematical content, which can be addressed with the approach of belief systems about mathematics (see Table 1). Against this background, the following main research question is explored in this article:

Main RQ: Which perspectives on mathematics are presented in ChatGPT responses?

This research question can be subdivided into three sub-questions. First, differences in the occurrence of the four perspectives should be identified:

RQ 1: Are there significant differences in the occurrence of the perspectives on mathematics in ChatGPT responses?

This question is interesting because various empirical studies have examined the occurrence of typical belief systems in certain groups of individuals. For example, Grigutsch et al. (1998) found that teachers on average identify more strongly with the application perspective (or application aspect) and less with the toolbox perspective (or schema aspect). At the same time, they found that the toolbox perspective is often associated with a formalistic approach to mathematics, while the application perspective is associated with a process-oriented approach. Concerning students in school and early university studies, Dilling (2022), Stoffels (2020), and Witzke and Spies (2016) primarily identified the presence of the empirical-concrete perspective.

Another aspect to be investigated in this study is the influence of prompting on the occurrence of perspectives:

RQ 2: What influence do different prompt formulations have on the occurrence of perspectives on mathematics?

The literature review in Section 2.1 showed that prompting and the use of prompting techniques have a decisive influence on the responses generated by an LLM, for example in terms of mathematical correctness (e.g., Schorcht et al., 2024; Dilling, 2024a). In addition, research to date shows that students have so far only used very simple prompting strategies and that there is a great need for the development of meaningful prompting strategies for mathematics education (e.g., Dilling and Herrmann, 2024; Noster et al., 2024b).

Finally, the extent to which perspectives on mathematics differ in responses to different mathematical concepts will also be investigated:

RQ 3: What influence do different mathematical concepts have on the occurrence of perspectives on mathematics?

Since LLMs were primarily developed for communication in text form and are also mainly based on text data, it can be hypothesized that symbolically represented mathematical content can be processed more easily by LLMs. Actually, the study by Wei (2024) shows that ChatGPT performs significantly better on tasks in the field of algebra than in geometry and measurement. Therefore, with regard to perspectives on mathematics, one could also assume that these differ in different mathematical fields or for different mathematical concepts.

3 Methodology

3.1 Data sampling

A systematic analysis of the LLM ChatGPT-4 was carried out in February 2024 in order to investigate the above research questions. For data collection, a total of 450 inputs were made in English using 15 different prompts. The prompts were sent to ChatGPT within 3 days using three different ChatGPT accounts—no information was stored as metaprompts in the settings of the accounts. Each prompt was sent in a separate chat to avoid references to previous input. At the time the data was collected, ChatGPT was unable to reference or link information across separate chat sessions.

The 15 different prompts referred to three different mathematical concepts—real numbers, straight lines and probability. The use of basic concepts is a common approach in beliefs research, as these are particularly suitable for distinguishing between belief systems (see, e.g., Witzke and Spies, 2016). Furthermore, the three concepts come from different mathematical fields and thus represent a certain range of mathematics. The three basic prompts were formed by the questions: “What are/is a real number/straight line/probability in mathematics?” In subsequent entries, the basic prompts were expanded with four distinct additions, each designed to evoke one of the perspectives on mathematics, e.g., “rigorously formal” or “graphically.” The complete list of prompts can be seen in Table 2. Each of these prompts was entered 10 times by each account, which corresponds to 450 prompts. In the chats, there are 450 ChatGPT responses as answers to these prompts, which formed the database for the analysis. However, due to data losses, only 446 responses were accessible for the analysis.

Table 2

Table 2. List of prompts used for data collection.

3.2 Data evaluation

The data was analyzed using the deductive qualitative content analysis according to Mayring (2000). This method starts with the definition of research questions and the context of the study. This also includes the definition of the unit of analysis, which in the study presented here is a complete response. Based on the theoretical considerations, categories are distinguished and defined (see Sections 2.2, 2.3, and 3.1). Subsequently, characterizing examples are selected from the data material and, if necessary, further coding rules are developed to specify them. The examination of the data material can also lead to fundamental changes in the categories, but this was not the case in the presented study. With the final category system, the entire data material is coded once again.

Excerpts from ChatGPT responses to the three mathematical concepts, which are examples of the four perspectives on mathematics, can be seen in Table 3. The qualitative content analysis showed that all four perspectives occurred in relation to all three mathematical concepts in the data (Dilling, 2024b).

Table 3

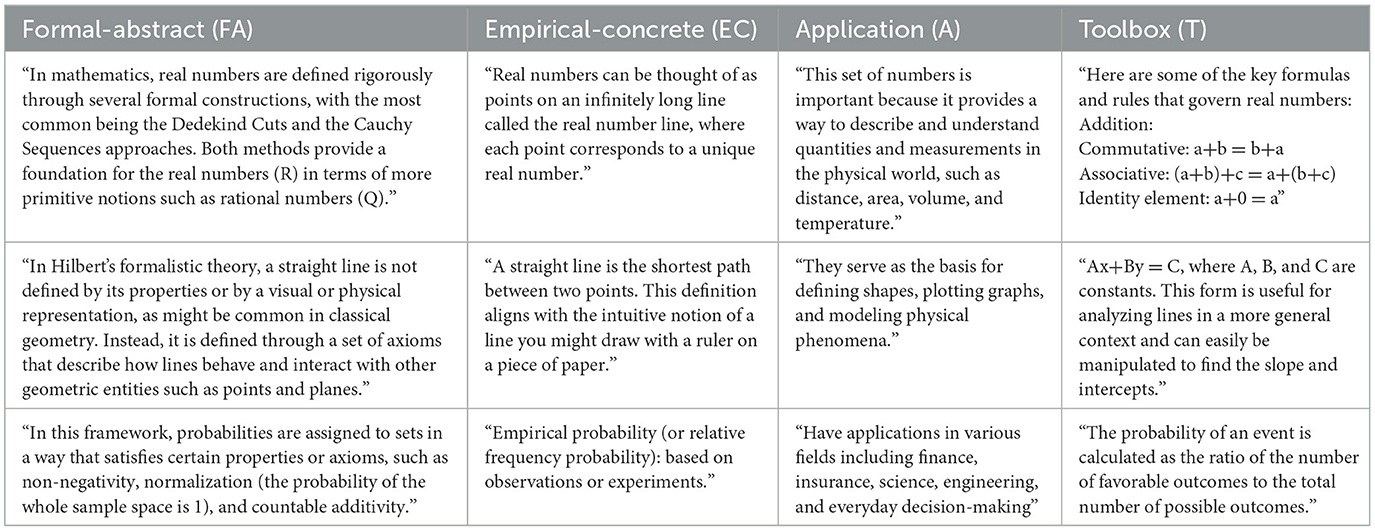
Table 3. Examples from the ChatGPT responses for the four perspectives and the three mathematical concepts.

As described earlier, the perspectives are not mutually exclusive and combinations can occur within one response. Therefore, in the deductive qualitative content analysis, a separate rating was made for each response in relation to each of the four perspectives. An example in which all four perspectives occur and which was rated accordingly for the data set can be seen in Figure 1.

Figure 1

Figure 1. ChatGPT response to the prompt “What is a probability in mathematics?”.

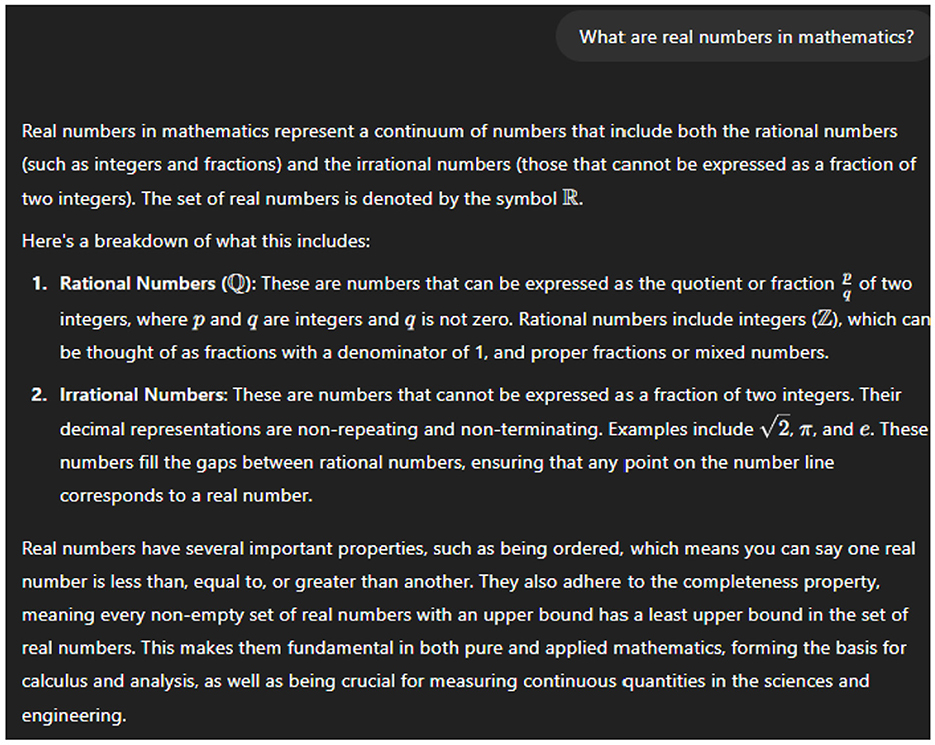
The entire data material consisting of 446 responses was coded independently by two experienced and specifically trained raters. The inter-rater reliabilities for the different perspectives range from substantial to almost perfect agreement (FA: κ = 0.92; EC: κ = 0.69; A: κ = 0.82; T: κ = 0.93). Based on these ratings, a quantitative study was conducted to examine the research questions. For this purpose, a code was only included in the analysis if both raters had evaluated a response with regard to one of the perspectives in the same way, i.e., either both decided that the perspective occurs or does not occur. As an illustrative example, the response to the prompt “How can real numbers be defined rigorously formal in mathematics?” from Figure 2 is considered. Both raters assigned the response to the formal-abstract and empirical-concrete perspectives. They also concurred that the application perspective was not present. Thus, the response was included in the analysis for these three perspectives. However, there was a discrepancy regarding the toolbox perspective: Rater 1 identified it—perhaps due to the explicit construction rule for a decimal number in point 3—while Rater 2 did not consider it applicable. Consequently, the response from Figure 2 was excluded from the analysis of the toolbox perspective.

Figure 2

Figure 2. ChatGPT response to the prompt “How can real numbers be defined rigorously formal in mathematics?” as an example for intercoder disagreement.

This procedure was adopted to minimize subjective interpretations and potential coding errors, especially in light of the large number of ChatGPT responses analyzed. This leads to different frequencies of coded responses in the four perspectives (Table 4 and following) although the number of inputs have been the same. The resulting frequency tables were then analyzed using a chi-square test. A significance level of p < 0.01 was selected for the chi-square tests. Cohen's ω was determined using the observed relative frequencies b_i,j and the expected relative frequencies e_i,j as a measure of the effect size:

$\begin{array}{l}\omega =\sqrt{{\displaystyle \sum _{i,j}}\frac{{(b_{i,j}-e_{i,j})}^2}{e_{i,j}}}\end{array}$

According to Cohen (1988), ω ≥ 0.5 characterize large effects, 0.5 > ω ≥ 0.3 medium effects, and 0.3 > ω ≥ 0.1 small effects. These thresholds are adopted for the present study, as there are no context-related recommendations for interpretation.

Table 4

Table 4. Frequencies of occurrence of the four perspectives on mathematics.

4 Results of the study

RQ 1: Perspectives on mathematics

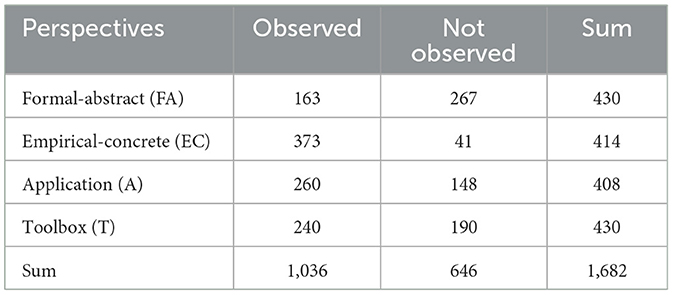
The first research question deals with differences in the occurrence of the four perspectives on mathematics. A total of 1682 codings was found in the study that were rated identically by both raters and that referred to the totality of the prompts used and the responses obtained from them. The number of identical ratings is highest for the formal-abstract and toolbox perspective with 430, while it is slightly lower for the empirical-concrete and application perspective with 414 and 408 identical ratings, respectively, which also explains the different interrater reliabilities.

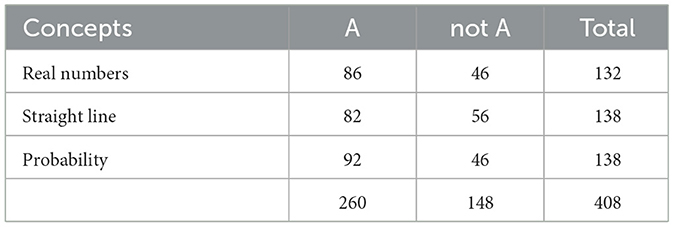
Looking at the individual categories in more detail, it is striking that the empirical-concrete perspective appears in 90% of the responses. The application perspective (64%) and the toolbox perspective (56%) are represented much less frequently, but still in a majority of the responses. By contrast, the formal-abstract perspective is not represented in most of the responses (only 37%). The chi-square test for the contingency table (Table 4) shows a significant difference in the occurrence of the perspectives with a medium effect size (ω = 0.39, p < 0.01).

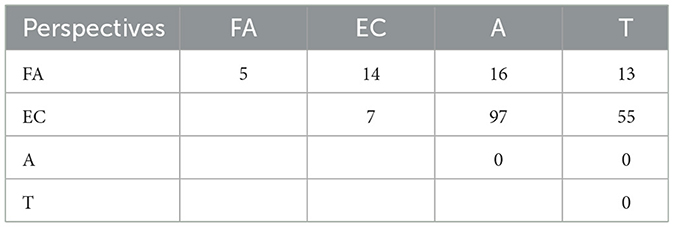
In addition to the occurrence of the individual perspectives on mathematics, it should also be examined at this point which perspectives occur together particularly frequently in a response. For this purpose, only the portion of responses could be used in which all four perspectives were assessed equally by both raters. This reduced the number of evaluable responses to 356, with the frequencies of occurrence remaining largely the same in the reduced data set (FA: 35%, EC: 90%, A: 64%, T: 56%). Combinations of different perspectives within a response occur very frequently. Only 12 responses were assigned to a single perspective (Table 5), of which 5 were only assigned to the formal-abstract perspective and 7 only to the empirical-concrete perspective. Combinations of two perspectives occur most frequently with a total of 195 responses (Table 5), whereby these are largely combinations of the empirical-concrete perspective with the application perspective (97) or the toolbox perspective (55). Figure 3 provides an example from the data illustrating the frequent combination of the empirical-concrete perspective and the application perspective. The example illustrates that when fields of application of a mathematical concept are described, this is usually accompanied by a definition of the concept that refers to real-world contexts, thereby aligning with the empirical-concrete perspective. Combinations of the formal-abstract perspective with one of the other perspectives can each be found in the low double digits. No response contains a combination exclusively of the application and toolbox perspectives.

Table 5

Table 5. Number of responses with exactly one (diagonal) or exactly two identified perspectives.

Figure 3

Figure 3. Example for the combination of the application perspective and the empirical-concrete perspective in a ChatGPT response.

The data clearly shows that the application and toolbox perspectives never occur alone but always in combination with the formal-abstract or empirical-concrete perspective. This is not really surprising, since a concept is either defined with an empirical reference (empirical-concrete) or without it (formal-abstract).

Combinations of three perspectives can also be found frequently in the data material. Of the 126 responses with three identified perspectives, 71 are without the formal-abstract, 35 without the application, 19 without the toolbox and one without the empirical-concrete perspective. In addition, further 23 responses show all four perspectives on mathematics, like the one that can be seen in Figure 1.

RQ 2: Influence of prompt formulations

The second research question was to examine the influence of the prompt formulations, i.e., the additions to the standard prompt. These were (1) the question of a rigorously formal definition, (2) a graphical definition, (3) the applications of the concept and (4) formulas and rules for the concept.

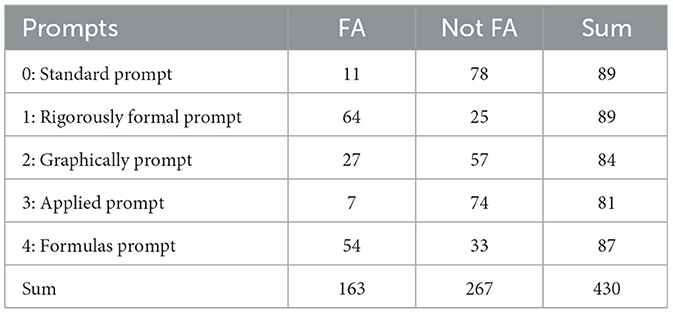
First, the effects of the prompt formulations on the formal-abstract perspective (FA) are to be examined (Table 6). It can be seen that the formal-abstract perspective occurs only very rarely (12% of responses) with the standard prompt (0), and with a significantly lower relative frequency than in the totality of all responses (see Section 4.1). The rigorously-formal prompt (1) leads to a significant increase in the frequency of occurrence to 72% of all responses, which corresponds to a significant difference with a large effect size (ω = 0.60, p < 0.01). An example of the differences in the responses using the standard and the rigorously-formal prompt can be seen in Figures 4, 5. Both responses address the concept of real numbers. In the standard prompt (Figure 4), there is a clear reference to the didactic model of the number line—an abstract definition of real numbers without reference to this visualization cannot be found. In contrast, the rigorously-formal prompt (Figure 5) clearly leads to an axiomatic definition without any connection to empirical aspects—in the section under consideration, this is done using Dedekind cuts.

Table 6

Table 6. Frequency of the formal-abstract perspective (FA) with different prompt formulations.

Figure 4

Figure 4. Part of a response on the standard prompt on real numbers (formal-abstract perspective not coded).

Figure 5

Figure 5. Part of a response on the rigorously-formal prompt on real numbers (formal-abstract perspective coded).

The appearance of the response was also significantly increased to 62% with the formulas prompt (ω = 0.51, p < 0.01). Even with the graphically prompt (2), the frequency of occurrence can still be increased to 32%, although this is only a small effect (ω = 0.24, p < 0.01). The applied prompt (3) slightly reduces the frequency to 9%, although this is not a significant difference compared to the frequency in the standard prompt.

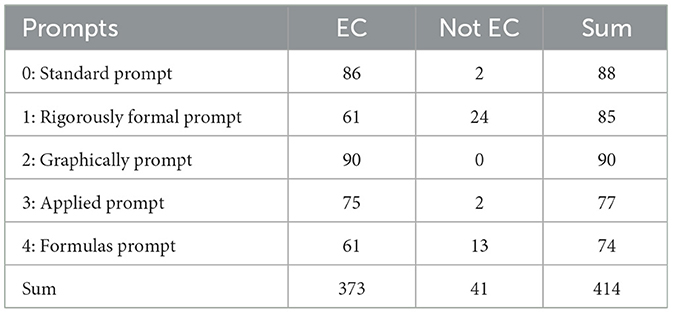
The empirical-concrete perspective (EC) is clearly different (Table 7). This occurs in almost all responses (98%) with the standard prompt (0). Accordingly, the frequency of occurrence can no longer be significantly increased, which leads to very similar percentages for the graphically prompt (100% of responses) and for the applied prompt (97% of responses). For the other two prompt formulations, the proportion of empirical-concrete responses is reduced, although in both cases it remains well above half. With the rigorously-formal prompt (1), the proportion is 72%, and with the formulas prompt it is 82%, which corresponds to significant differences with a medium effect (ω = 0.36, p < 0.01) and a small effect (ω = 0.26, p < 0.01).

Table 7

Table 7. Frequency of the empirical-concrete perspective (EC) with different prompt formulations.

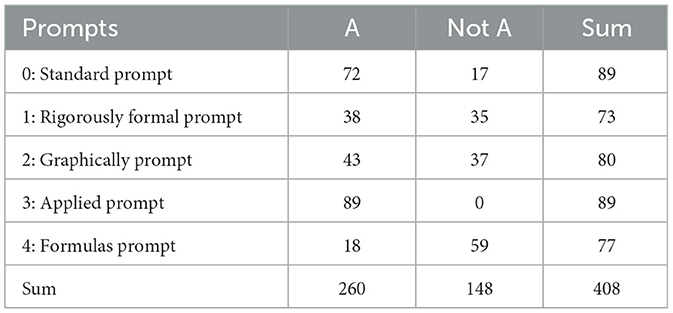
The application perspective (A) is represented in 81% of the responses when the standard prompt (0) is used, and is therefore present in a large proportion of responses, but not in all of them (Table 8). Accordingly, it is entirely possible to significantly increase the frequency of occurrence here. For example, the applied prompt (3) leads to a proportion of 100%, which means that in this case the application perspective was rated in all tests. This corresponds to a significant increase with a medium effect (ω = 0.32, p < 0.01). The other prompt formulations lead to a reduction in the occurrence of the application perspective. The effect (ω = 0.58, p < 0.01) is greatest for the formulas prompt (4), which leads to a proportion of 23%. For the rigorously-formal prompt (1) and the graphically prompt (2), the application perspective occurs in about half of the responses (52% and 54% of the responses, respectively), which is at the threshold from a small to a medium effect (ω = 0.31 and ω = 0.29, p < 0.01).

Table 8

Table 8. Frequency of the application perspective (A) in different prompt formulations.

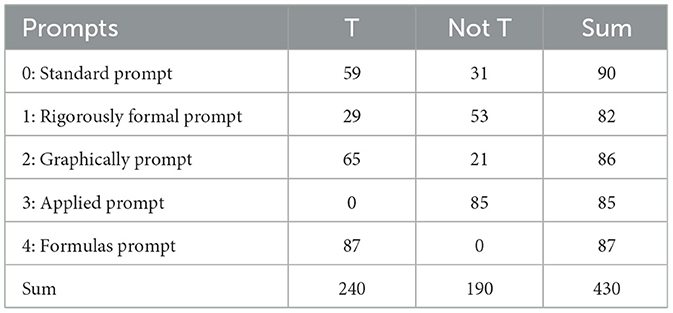
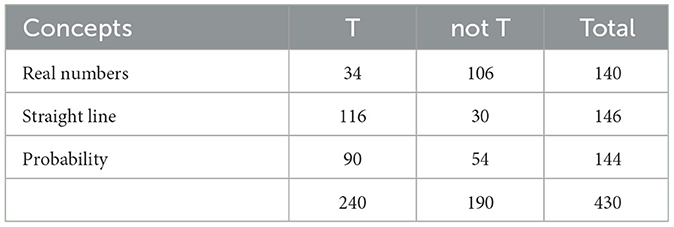
The toolbox perspective (P) occurs in 66% of responses to the standard prompt (0) (Table 9). Accordingly, the occurrence can be both increased and reduced by prompt formulations. The formulas prompt ensures a significant increase to 100%, which corresponds to a medium effect (ω = 0.45 p < 0.01). The graphically prompt also ensures a moderate increase, although the difference is not significant. The occurrence of the toolbox perspective can be reduced to 35% with the rigorously-formal prompt and to 0% with the applied prompt, which corresponds to a medium (ω = 0.30, p < 0.01) and a large effect (ω = 0.69, p < 0.01).

Table 9

Table 9. Frequency of the toolbox perspective (T) in different prompt formulations.

RQ 3: Influence of mathematical concepts

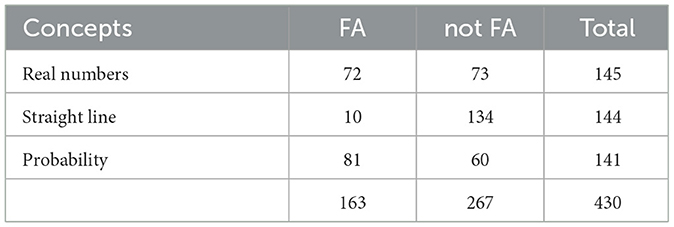
The third research question focuses on differences between the three mathematical concepts real numbers, straight lines and probability. Regarding the formal-abstract perspective, some differences arise (Table 10). Most of the attributions of the formal-abstract perspective occur with a relative frequency of 57% for probability. The formal-abstract perspective could also be identified in about half of the responses to real numbers. Almost no formal-abstract definitions occur with straight lines (only 7%). The chi-square test showed a significant difference between the mathematical concepts with a medium effect (ω = 0.46; p < 0.01).

Table 10

Table 10. Frequency of the formal-abstract perspective (FA) for different mathematical concepts.

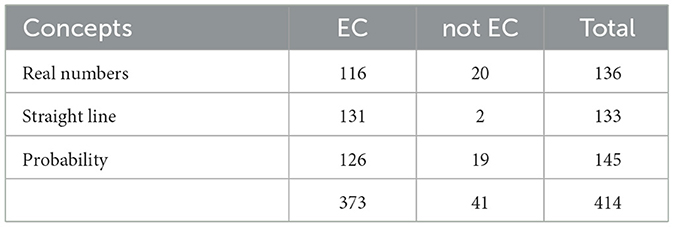
The empirical-concrete perspective is strongly represented in the responses on all three concepts (Table 11). The relative frequencies range from 85% and 87% for real numbers and probability to 98% for straight lines. The value for the term straight line is exceptionally high—the perspective was not identified in only two responses. The difference between the mathematical concepts is significant with a small effect (ω = 0.19; p < 0.01).

Table 11

Table 11. Frequency of the empirical-concrete perspective (EC) for different mathematical concepts.

The application perspective occurs in a very similar way for the three mathematical concepts (Table 12). For responses on straight lines, there is a relative frequency of 59%, for real numbers this is 65% and for probability it is 67%. The chi-square test could not find any significant difference.

Table 12

Table 12. Frequency of the application perspective (A) for different mathematical concepts.

The frequencies of the toolbox perspective are also quite different between the three concepts (Table 13). For straight lines, the toolbox perspective occurs quite frequently with 79% of responses. The percentage for the concept of probability is also quite large at 63%. The toolbox perspective occurs rather rarely with 24% for real numbers. The result of the chi-square test is a significant difference with a medium effect (ω = 0.46; p < 0.01). The variation in responses depending on the mathematical concept addressed is also illustrated in Figures 6, 7, both of which are based on the standard prompt. In Figure 6, the definition of a straight line highlights the formulation of linear equations in multiple forms. This response reflects not only the empirical-concrete and application perspectives but also includes the toolbox perspective. In contrast, the response on real numbers in Figure 7, while it similarly includes a definition aligned with the empirical-concrete perspective and references fields of application, contains no specific indications of rules or schemata related to real numbers—thus, the toolbox perspective is absent.

Table 13

Table 13. Frequency of the toolbox perspective (T) for different mathematical concepts.

Figure 6

Figure 6. Response on the standard prompt on straight lines (toolbox perspective coded).

Figure 7

Figure 7. Response on the standard prompt on real numbers (toolbox perspective not coded).

5 Discussion of the results

The results presented above allow us to answer the research questions posed at the beginning and thus contribute to our understanding of how mathematics is presented in LLMs. Research question 1 examined differences in the occurrence of the four perspectives on mathematics. Based on the quantitative analysis, significant differences with a medium effect size can be found. The empirical-concrete perspective occurs in almost every response, while the formal-abstract perspective was coded for only a few responses. The analysis of the combinations of perspectives showed that the application and toolbox perspectives never occur alone, but always in combination with the empirical-concrete or formal-abstract perspective. This is not surprising, since a concept is always defined either by reference to empiricism (empirical-concrete) or on an abstract level (formal-abstract); an application or the presentation of formulas and rules is not a complete and independent definition and more an addition.

The frequencies of the perspectives found in the study are not surprising in light of research on belief systems about mathematics. For example, Dilling (2022), Stoffels (2020), and Witzke and Spies (2016) have found in particular empirical-concrete belief systems among students at school and freshmen at university. The mathematics teaching at school is predominantly characterized by an empirical-concrete perspective with many references to empiricism. The formal-abstract perspective is largely restricted to university mathematics studies (Grigutsch et al., 1998; Schoenfeld, 1985) and is therefore presumably less common. The results could indicate that the version of ChatGPT tested is based in particular on mathematical training data, in which the empirical-concrete and not the formal-abstract perspective appears. This would not be surprising, because if you search in the internet for the mathematical concepts of real numbers, straight lines and probability, you will find mostly empirical-concrete definitions.

Research question 2 investigated differences in the occurrence of perspectives between the different prompt formulations. The effects of the prompts vary greatly depending on the perspective on mathematics. Since the formal-abstract perspective is only found in a small number of responses using the basic prompt, prompting (e.g., rigorously-formal prompt) can significantly increase its frequency. In contrast, the empirical-concrete perspective already occurs very frequently when using the standard prompt, and a significant change can only be made by a reduction with certain prompts (e.g., with the rigorously-formal prompt), whereby the empirical-concrete perspective remains very present in all cases. The frequencies of the application perspective and the toolbox perspective can be increased or decreased depending on the prompt formulation. Overall, the respective prompts lead to the expected change in perspectives on mathematics presented in the responses, for example an increase in the formal-abstract perspective with the rigorously-formal prompt or an increase in the application perspective with the application prompt. However, even with appropriate prompting, not all responses contain the respective perspective, as is particularly evident with the formal-abstract perspective, in which the proportion with the rigorously-formal prompt is still only 72%.

The results show that prompting can be used to control not only the correctness of mathematical responses (e.g., Schorcht et al., 2024; Dilling, 2024a), but also the presentation of mathematical content, considered in this study in terms of perspectives on mathematics. However, it also becomes clear that the LLMs do not always react the same way to the same mathematical prompt. LLMs are probabilistic systems, so that the responses are generated differently for each new input. There is no certainty that a given perspective will appear in the response for a given prompt. This is quite challenging for the design and implementation of learning scenarios using LLMs and emphasizes the role of the teacher as a learning guide who has to check the correctness and adequacy of the LLM responses (Dilling et al., 2024a).

Research question 3 examines differences in the occurrence of perspectives between the mathematical concepts of real numbers, straight lines and probability. When looking at the results, it becomes clear that the concept of a straight line is only rarely represented in formal-abstract terms in the responses compared to the other concepts, and very often in empirical-concrete terms. The toolbox perspective also occurs most frequently for the concept of a straight line and very rarely for real numbers. The application perspective is represented similarly frequently for all three concepts.

These results are in line with the results of the analysis by Wei (2024), who found significant differences between the fields of geometry and algebra regarding mathematical correctness. These differences also appear to exist with regard to the perspectives on mathematics. In addition, the strong presence of the empirical-concrete perspective in geometry can be well-explained by the fact that, outside of the university, geometry is usually associated with concrete operations on figures as objects of empiricism (Struve, 1990), while stochastics and calculus are usually described in a much more symbolic way.

6 Conclusion and outlook

This article has dealt with the presentation of mathematical content in responses of LLMs. An analysis of the current state of research on LLMs in mathematics education has shown that the mathematical correctness of responses and the possible way of controlling this via prompting has already been investigated in various places, but that the adequate presentation of mathematics has so far played a minor role. In view of the implementation of LLMs in mathematical learning processes, this is a clear desideratum, which the present article has approached with the notion of belief systems about mathematics. Based on research on belief systems, four perspectives on mathematics were distinguished. In the formal-abstract perspective, mathematical concepts are based exclusively on axioms and are strictly separated from reality. In contrast, the empirical-concrete perspective defines mathematical concepts with reference to empirical mathematical objects. The application perspective occurs when mathematical concepts are used to describe reality. The toolbox perspective involves the schematic application of rules, formulas, and procedures. These four perspectives on mathematics are neither exhaustive nor strictly separable, but they provide a good overview of different approaches to mathematics and mathematical learning.

The empirical study in this article examined ChatGPT-4 responses to 15 different mathematical prompts. Coding and subsequent quantitative analysis revealed that all four perspectives on mathematics were found in responses. This is not surprising, since ChatGPT is based on a wide range of different training data and is a conglomeration of the perspectives on mathematics described in it. The empirical-concrete perspective occurs particularly frequently, while the formal-abstract perspective is rather rare. The different perspectives can be effectively created or avoided by using suitable prompts—but there is no 100% certainty in the control, so that unexpected perspectives on mathematics can also appear for relatively targeted prompts. The study also revealed differences in the emergence of perspectives between different mathematical concepts. The concept of a straight line, which was used as an example in the study for the field of geometry, is more often defined in empirical-concrete terms and less often in formal-abstract terms in the responses compared to the concepts of real numbers and probability.

These results represent important initial findings on how mathematics is represented in LLM responses and how it can be controlled by prompting. For mathematics teaching, it is particularly noteworthy that ChatGPT responses to minimally specified prompts often offer multiple perspectives on mathematics. In this way, students are made aware of the breadth of aspects that mathematics encompasses. The strong presence of the empirical-concrete perspective suggests that mathematics, as represented in LLMs, is closely tied to real-world representations and concrete experiences—an alignment that resonates especially well with the goals of mathematics education in the early learning stages. At more advanced levels, however, students should also be introduced to a formal-abstract perspective. The findings show that in order to achieve this, educators must use LLMs strategically by crafting prompts that deliberately elicit the formal-abstract perspective. This can support the implementation of meta-level discussions about the nature of mathematics in the classroom and foster the development of more balanced belief systems about the discipline. From a curricular standpoint, the results suggest that explicit discussions and reflections on multiple mathematical perspectives should be embedded into instruction. This enables students to explore the potentials and limitations of different definitions of concepts such as real numbers, straight lines, or probability as they appear in AI-generated responses but also other mathematical resources. Teacher education programs should prepare pre-service teachers to identify and interpret the nature of mathematical conceptualizations and provide them with effective prompting strategies to guide AI tools toward responses that align with specific learning goals. Another crucial aspect is the ability to engage in reflective discussions about the epistemic framing of AI-generated content, in order to promote a critical and more strategic use of generative AI in mathematics classrooms by the students.

However, the study has several limitations, which should be reflected at this point. First, only three different mathematical concepts were considered in the study. To conduct a comprehensive study of ChatGPT's mathematical understanding, further mathematical concepts should also be included. A second limitation is that the current methodology does not allow for any conclusions to be drawn about the consistency and mathematical correctness of responses when the same prompt is used—an important factor for both the informative value of the results and their applicability in teaching. For example, Ling (2023) identified numerous inconsistencies and mathematical errors in ChatGPT responses. The third limitation is the restriction to the LLM ChatGPT-4. Although this was the most common LLM at the time of the survey and the other common LLMs are based on similar fundamental mechanisms, differences in the responses in terms of perspectives on mathematics cannot be ruled out. Furthermore, due to the rapid developments of large language models (LLMs), results may quickly become outdated. Another limitation lies in cultural and linguistic biases—mathematical terms may carry different connotations across languages or cultures, and diverse conceptualizations and procedures may be used. These differences could be reflected in the training data and, consequently, in the generated responses. Moreover, the analysis was limited to textual responses, even though generative AI is now capable of producing other forms of representation. This is a relevant restriction, as the multimodality of mathematical representations is a core principle of mathematics education, especially from an empirical-concrete perspective. Probably the most crucial limitation lies in the very simple design of the prompts used. Only one-shot prompts were used in separate chats, and there were no variations of prompt techniques or multi-step dialogues, which actually characterize LLM technology. This issue will be addressed in further studies by developing a survey tool that incorporates more complex and appropriate prompting. Moreover, the further studies will not only consider perspectives that occur indirectly in descriptions of mathematical concepts, but will also compare these with explicit descriptions of different perspectives on mathematics by LLMs. These explicit descriptions also provide students with an engaging learning opportunity in the sense of a mathematical nature of science education (see Lederman, 2013).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

FD: Conceptualization, Formal analysis, Methodology, Writing – original draft, Writing – review & editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Acknowledgments

I would like to thank Benedikt Heer and Lina-Marie Schlechting for participating in the rater training and coding the responses. I also wish to thank the reviewers of this article for their constructive feedback.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Gen AI was used in the creation of this manuscript. Generative AI was used solely for language refinement of the manuscript.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Baumanns, L., and Pohl, M. (2024). “Leveraging ChatGPT for problem posing: an exploratory study of pre-service teachers' professional use of AI,” in Proceedings of the 17th ERME Topic Conference MEDA 4, eds. E. Faggiano, A. Clark-Wilson, M. Tabach, and H.-G. Weigand (Bari: University of Bari Aldo Moro), 57–64.

Google Scholar

bin Mohamed, M. Z., Hidayat, R., binti Suhaizi, N. N., bin Mahmud, M. K. H., and binti Baharuddin, S. N. (2022). Artificial intelligence in mathematics education: a systematic literature review. Int. Electronic J. Math. Educ. 17:em0694. doi: 10.29333/iejme/12132

Crossref Full Text | Google Scholar

Buchholtz, N., and Huget, J. (2024). “ChatGPT as a reflection tool to promote the lesson planning competencies of pre-service teachers,” in Proceedings of the 17th ERME Topic Conference MEDA 4, eds. E. Faggiano, A. Clark-Wilson, M. Tabach, and H.-G. Weigand (Bari: University of Bari Aldo Moro), 129–136.

Google Scholar

Carter, G., and Norwood, K. S. (2010). The relationship between teacher and student beliefs about mathematics. Sch. Sci. Math. 97, 62–67. doi: 10.1111/j.1949-8594.1997.tb17344.x

Crossref Full Text | Google Scholar

Chen, L., Chen, P., and Lin, Z. (2020). Artificial intelligence in education: a review. IEEE Access 8, 75264–75278. doi: 10.1109/ACCESS.2020.2988510

Crossref Full Text | Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Hillside, NJ: Lawrence Erlbaum Associates.

Google Scholar

Dilling, F. (2022). Begründungsprozesse im Kontext von (digitalen) Medien im Mathematikunterricht [Reasoning Processes in the Context of (Digital) Technologies in Mathematics Education]. Wiesbaden: Springer Spektrum. doi: 10.1007/978-3-658-36636-0

Crossref Full Text | Google Scholar

Dilling, F. (2024a, accepted). “Large language models as formative assessment and feedback tools? – a systematic report,” in FAME 2024-Proceedings (Utrecht: University of Utrecht).

Google Scholar

Dilling, F. (2024b). “What is ChatGPT's belief system about math?” in Proceedings of the 17th ERME Topic Conference MEDA 4, eds. E. Faggiano, A. Clark-Wilson, M. Tabach, and H.-G. Weigand (Bari: University of Bari Aldo Moro), 137–144.

Google Scholar

Dilling, F., and Herrmann, M. (2024). Using large language models to support pre-service teachers mathematical reasoning. Front. Artif. Intell. 7, 1460337. doi: 10.3389/frai.2024.1460337

PubMed Abstract | Crossref Full Text | Google Scholar

Dilling, F., Herrmann, M., Müller, J., Pielsticker, F., and Witzke, I. (2024a). “Initiating interaction with and about ChatGPT – an exploratory study on the angle sum in triangles,” in Proceedings of the 17th ERME Topic Conference MEDA 4, eds. E. Faggiano, A. Clark-Wilson, M. Tabach, and H.-G. Weigand (Bari: University of Bari Aldo Moro), 145–152.

Google Scholar

Dilling, F., Stoffels, G., and Witzke, I. (2024b). Beliefs-oriented subject-matter didactics. Design of a seminar and a book on calculus education. LUMAT Int. J. Math Sci. Technol. Educ. 12, 4–14. doi: 10.31129/LUMAT.12.1.2125

Crossref Full Text | Google Scholar

Dionne, J. (1984). “The perception of mathematics among elementary school teachers,” in Proceedings of the 6th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education (PME), ed. J. Moser (Wisconsin: University of Wisconsin), 223–228.

Google Scholar

Ernest, P. (1989). The knowledge, beliefs and attitudes of the mathematics teacher: a model. J. Educ. Teach. 15, 12–33. doi: 10.1080/0260747890150102

Crossref Full Text | Google Scholar

Getenet, S. (2024). Pre-service teachers and ChatGPT in multistrategy problem-solving: implications for mathematics teaching in primary schools. Int. Electronic J. Math. Educ. 19:em0766. doi: 10.29333/iejme/14141

Crossref Full Text | Google Scholar

Goldin, G. (2002). “Affect, meta-affect, and mathematical belief structures,” in Beliefs: A Hidden Variable in Mathematics Education, eds. G. C. Leder, E. Pehkonen, and G. Törner (Dordrecht: Kluwer Academics Publishers), 59–72. doi: 10.1007/0-306-47958-3_4

Crossref Full Text | Google Scholar

Goldin, G., Rösken, B., and Törner, G. (2009). “Beliefs – no longer a hidden variable in mathematical teaching and learning processes,” in Beliefs and Attitudes in Mathematics Education: New Research Results, eds. J. Maaß, and W. Schlöglmann (Rotterdam: Sense Publishers), 1–18. doi: 10.1163/9789087907235_002

Crossref Full Text | Google Scholar

Green, T. F. (1971). The Activities of Teaching. New York, NY: McGraw-Hill.

Google Scholar

Grigutsch, S., Raatz, U., and Törner, G. (1998). Einstellungen gegenüber Mathematik bei Ma-thematiklehrern [Attitudes towards mathematics among mathematics teachers]. J. Mathematik-Didaktik 19, 3–45. doi: 10.1007/BF03338859

Crossref Full Text | Google Scholar

Kasneci, E., Seßler, K., Küchemann, S., Bannert, M., Dementieva, D., Fischer, F., et al. (2023). ChatGPT for good? On opportunities and challenges of large language models for education. Learn. Individ. Differ. 103:102274. doi: 10.1016/j.lindif.2023.102274

PubMed Abstract | Crossref Full Text | Google Scholar

Lederman, N. G. (2013). “Nature of science: past, present, and future,” in Handbook of Research on Science Education, eds. S. K. Abell and G. Lederman (New York, NY: Routledge), 831–879. doi: 10.4324/9780203097267

Crossref Full Text | Google Scholar

Ling, M. H. T. (2023). ChatGPT (Feb 13 version) is a chinese room. Novel Res. Sci. 14. doi: 10.48550/arXiv.2304.12411

Crossref Full Text | Google Scholar

Mayring, P. (2000). Qualitative content analysis. Forum Qualitative Soc. Res. 1:Art. 20. doi: 10.17169/fqs-1.2.1089

Crossref Full Text | Google Scholar

Muis, K. R., and Foy, M. J. (2010). “The effects of teachers' beliefs on elementary students' beliefs, motivation, and achievement in mathematics,” in Personal Epistemology in the Classroom: Theory, Research, and Implications for Practice, eds. L. D. Bendixen and F. C. Feucht (Cambridge: Cambridge University Press), 435–469. doi: 10.1017/CBO9780511691904.014

Crossref Full Text | Google Scholar

Noster, N., Gerber, S., and Siller, H.-S. (2024a). “Tasks incorporating the use of ChatGPT in mathematics education – designed by pre-service teachers,” in Proceedings of the 17th ERME Topic Conference MEDA 4, eds. E. Faggiano, A. Clark-Wilson, M. Tabach, and H.-G. Weigand (Bari: University of Bari Aldo Moro), 303–310.

Google Scholar

Noster, N., Gerber, S., and Siller, H.-S. (2024b). Pre-service Teachers' Approaches in Solving Mathematics Tasks with ChatGPT – A Qualitative Analysis of the Current Status Quo. doi: 10.21203/rs.3.rs-4182920/v1

Crossref Full Text | Google Scholar

OpenAI (2024). Learning to Reason with LLMs. Available online at: https://openai.com/index/learning-to-reason-with-llms/ (Accessed January 01, 2025).

Google Scholar

Park, H., and Manley, E. D. (2024). Using ChatGPT as a proof assistant in a mathematics pathways course. Math. Educ. 63, 139–163. doi: 10.63311/mathedu.2024.63.2.139

Crossref Full Text | Google Scholar

Peters, F., and Schorcht, S. (2024). “AI-supported mathematical task design with a GPT agent network,” in Proceedings of the 17th ERME Topic Conference MEDA 4, eds. E. Faggiano, A. Clark-Wilson, M. Tabach, and H.-G. Weigand (Bari: University of Bari Aldo Moro), 327–334.

Google Scholar

Petroni, F., Rocktäschel, T., Lewis, P., Bakhtin, A., Wu, Y., Miller, A. H., et al. (2019). Language models as knowledge bases? arXiv Preprint, arXiv:1909.01066. doi: 10.18653/v1/D19-1250

PubMed Abstract | Crossref Full Text | Google Scholar

Ruthven, K. (2012). The didactical tetrahedron as a heuristic for analysing the incorporation of digital technologies into classroom practice in support of investigative approaches to teaching mathematics. ZDM Math. Educ. 44, 627–640. doi: 10.1007/s11858-011-0376-8

Crossref Full Text | Google Scholar

Schoenfeld, A. H. (1985). Mathematical Problem Solving. Cambridge, MA: Academic Press.

Google Scholar

Schorcht, S., Buchholtz, N., and Baumanns, L. (2024). Prompt the problem – investigating the mathematics educational quality of AI-supported problem solving by comparing prompt techniques. Front. Educ. 9:1386075. doi: 10.3389/feduc.2024.1386075

Crossref Full Text | Google Scholar

Stoffels, G. (2020). (Re-)Konstruktion von Erfahrungsbereichen bei Übergängen von empirisch-gegenständlichen zu formal-abstrakten Auffassungen [(Re-)construction of Domains of Experience in the Transition from Empirical-Concrete to Formal-Abstract Belief Systems]. Siegen: Universi.

Google Scholar

Struve, H. (1990). Grundlagen einer Geometriedidaktik [Foundations of Geometry Education]. Leipzig: Bibliographisches Institut.

Google Scholar

Tall, D. (2013). How Humans Learn to Think Mathematically. Exploring the Three Worlds of Mathematics. Cambridge: Cambridge University Press. doi: 10.1017/CBO9781139565202

Crossref Full Text | Google Scholar

Vandamme, F., and Kaczmarski, P. (2023). ChatGPT: a tool towards an education revolution? Scientia Paedagogica Experimentalis 60, 95–135. doi: 10.57028/S60-095-Z1035

Crossref Full Text | Google Scholar

Wardat, Y., Tashtoush, M. A., AlAli, R., and Jarrah, A. M. (2023). ChatGPT: a revolutionary tool for teaching and learning mathematics. Eurasia J. Math. Sci. Technol. Educ. 19:em2286. doi: 10.29333/ejmste/13272

Crossref Full Text | Google Scholar

Wei, X. (2024). Evaluating chatGPT-4 and chatGPT-4o: performance insights from NAEP mathematics problem solving. Front. Educ. 9:1452570. doi: 10.3389/feduc.2024.1452570

Crossref Full Text | Google Scholar

Witzke, I., and Spies, S. (2016). Domain-specific beliefs of school calculus. J. Mathematik-Didaktik 37, 131–161. doi: 10.1007/s13138-016-0106-4

Crossref Full Text | Google Scholar

Yoon, H., Hwang, J., Lee, K., Roh, K. H., and Kwon, O. N. (2024). Students' use of generative artificial intelligence for proving mathematical statements. ZDM Math. Educ. 56, 1531–1551. doi: 10.1007/s11858-024-01629-0

Crossref Full Text | Google Scholar