- 1State Key Laboratory of Resources and Environmental Information System, Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing, China
- 2School of Sciences, Guangxi University of Science and Technology, Liuzhou, China
Introduction: In the field of wind power generation, short-term wind speed prediction plays an increasingly important role as the foundation for effective utilization of wind energy. However, accurately predicting wind speed is highly challenging due to its complexity and randomness in practical applications. Currently, single algorithms exhibit poor accuracy in short-term wind speed prediction, leading to the widespread adoption of hybrid wind speed prediction models based on deep learning techniques. To comprehensively enhance the predictive performance of short-term wind speed models, this study proposes a hybrid model, VMDAttention LSTM-ASSA, which consists of three stages: decomposition of the original wind speed sequence, prediction of each mode component, and weight optimization.
Methods: To comprehensively enhance the predictive performance of short-term wind speed models, this study proposes a hybrid model, VMDAttention LSTM-ASSA, which consists of three stages: decomposition of the original wind speed sequence, prediction of each mode component, and weight optimization. Firstly, the model incorporates an attention mechanism into the LSTM model to extract important temporal slices from each mode component, effectively improving the slice prediction accuracy. Secondly, two different search operators are introduced to enhance the original Salp Swarm Algorithm, addressing the issue of getting trapped in local optima and achieving globally optimal short-term wind speed predictions.
Result: Through comparative experiments using multiple-site short-term wind speed datasets, this study demonstrates that the proposed VMD-AtLSTM-ASSA model outperforms other hybrid prediction models (VMD-RNN, VMD-BPNN, VMD-GRU, VMD-LSTM) with a maximum reduction of 80.33% in MAPE values. The experimental results validate the high accuracy and stability of the VMD-AtLSTM-ASSA model.
Discussion: Short-term wind speed prediction is of paramount importance for the effective utilization of wind power generation, and our research provides strong support for enhancing the efficiency and reliability of wind power generation systems. Future research directions may include further improvements in model performance and extension into other meteorological and environmental application domains.
1 Introduction
Wind energy plays an important role in many new energy sources. According to the latest report released by the Global Wind Energy Council (GWEC) (Guliyev, 2020), the global installed capacity of wind power will reach 743 GW in 2020, with a 53% year-on-year growth in new installations. However, the stochastic, fluctuating and intermittent nature of wind farms poses significant challenges to the operation and control of the entire power system including wind farms (Lacal-Arantegui, 2019). Among them, short-term wind speed prediction is an indispensable factor for the development of daily scheduling plans. Therefore, proposing a method to accurately predict the short-term wind speed has an important impact on the economic and reliable operation of the power system (Rizwan-ul-Hassan et al., 2021).
Currently, short-term wind speed prediction methods are divided into two main categories: physical process-driven models (Higashiyama et al., 2018) and data-driven models (Yuan et al., 2017). Data-driven models are divided into statistical models (Liu et al., 2010) and artificial intelligence models (Khodayar et al., 2017). Physical process-driven models are mostly numerical weather prediction (NWP) models (Lowery and O’Malley, 2012), which make predictions based on local environmental information, such as, temperature, humidity, and geography. These methods are usually time-consuming and unsuitable for short-term and ultrashort-term wind speed forecasting due to excessive model considerations and model over-complexity (Wang and Li, 2018). In contrast, statistical models are more suitable for short-term wind speed forecasting. Statistical models learn the patterns of historical wind speed data and establish non-linear mapping relationships between the data, thus realizing time series forecasting (Rodrigues Moreno et al., 2020). Commonly used statistical methods are time series modeling (Liu et al., 2020b), Kalman filtering (Paliwal and Basu, 1987), Markov chain (Sahin and Sen, 2001), Bayesian method (Liu et al., 2020a) and so on. Statistical models have high prediction accuracy for static time series, but when facing highly nonlinear and complex wind speed data, these methods are less scalable and less effective in fitting.
In recent years, artificial intelligence models, including machine learning and deep learning models, have become increasingly popular in the field of short-term wind speed prediction (Scutaru et al., 2020). Compared with physical and statistical models, artificial intelligence models have greatly improved the accuracy of predicting wind speed. Among these, artificial neural network-based models seem to be the best choice because they can learn directly from historical data of wind speed without any a priori concepts and are more adaptable to practical applications (Tascikaraoglu and Uzunoglu, 2014). The most basic artificial neural network model is the back propagation neural network (BPNN) (Wang et al., 2015). Theoretically, as long as the number of neural units in the hidden layer of a BPNN reaches a certain number, then any nonlinear function can be fitted. However, BPNNs also have obvious shortcomings, firstly, it is easy to fall into the local optimum rather than obtaining the global optimal solution, and secondly, the learning efficiency caused by the need for too many trainings is low, and the convergence speed is not ideal. The other artificial neural network model, recurrent neural network (RNN) (Zaremba et al., 2015), is better at finding local correlations compared to BPNN. It can pass previous state information to neurons at the current time step. This mechanism allows the RNN to deal with dependencies in long sequences and also allows the same parameters to be shared between each time step, which gives it a smaller number of parameters and faster training speed, which fits well with the temporal continuum of wind speed prediction (Tanaka et al., 2015; Yu et al., 2018; Duan et al., 2021). However, the problem of backpropagation in the network architecture of RNNs leads to the problem of gradient vanishing and gradient explosion. This means that there are difficulties with very long sequences and the gradient decreases to near zero in hard-to-handle iterations. In order to overcome this problem, “gate control” techniques are used in RNN models, such as the long short-term memory (LSTM) (Hochreiter and Schmidhuber, 1997) and gate recurrent unit (GRU) (Niu et al., 2020), The GRU model adopts a simplified gating mechanism to prevent overfitting, but its prediction results are more logically correlated with recent time steps, which may lead to the loss of useful information from distant time steps. On the other hand, the LSTM model can effectively handle long-term dependencies, avoiding the issues of gradient vanishing or exploding. Experimental validation using multiple wind speed datasets has demonstrated the superior predictive performance of LSTM (Altan et al., 2021; Jaseena and Kovoor, 2021; Shahid et al., 2021). However, the computational structure of LSTM is relatively complex and it has a larger number of parameters, which could potentially lead to overfitting. Therefore, the key focus of research lies in effectively capturing important information based on the data conditions within the LSTM network, aiming to improve the prediction accuracy and robustness of wind speed forecasts.
Due to the distinct characteristics exhibited by various single models, hybrid models can effectively leverage the advantages of different individual models to achieve enhanced wind speed prediction performance. Consequently, hybrid prediction models based on decomposition and optimization have emerged as a research hotspot in the field of wind speed prediction in recent years. In order to ensure the sufficiency and integrity of feature decomposition and reconstruction, some scholars have proposed a novel hybrid model based on singular spectrum analysis and temporal convolutional attention network with adaptive receptive field (ARFTCAN). The results demonstrate that the proposed model effectively supports the adaptability of short-term wind power forecasting (WPF) across all four seasons (Shao et al., 2022). Furthermore, another group of researchers have introduced a wind speed prediction method that combines quaternion convolutional neural network (QCNN), Bi-LSTM, and adaptive decomposition techniques. This approach offers highly accurate forecasting results for long-term wind speed prediction (Neshat et al., 2022). Short-term hybrid wind speed prediction models usually include three steps: decomposition, prediction, and optimization (Ma et al., 2009). In the signal decomposition step, the unstable original wind speed sequence is decomposed into multiple IMF components with significant frequency characteristics by data decomposition methods, which reduces the complexity of the original data and performs noise reduction, e.g., empirical mode decomposition (EMD) (Ren et al., 2016) performs adaptive decomposition of nonlinear and highly fluctuating data in the original wind speed sequence to improve the prediction performance of wind speed prediction models (Naik et al., 2018). However, the EMD has the problems of large reconstruction error, poor decomposition completeness, and large noise residuals. Therefore, Literature (Hu et al., 2021) proposed a method using variational mode decomposition to mine the features of the wind speed sequence and eliminate the noise to predict each intrinsic mode function (IMF), which has obvious accuracy advantages over other decomposition methods in wind speed prediction.
In constructing the wind speed hybrid model, usually after signal decomposition of the data, a parameter optimization algorithm is also used to optimize the weights of each IMF to improve the performance of the prediction algorithm. Among the parameter optimization algorithms, the swarm intelligence optimization algorithm is the most commonly used algorithm for wind speed prediction. The swarm intelligence optimization algorithm is a number of algorithms proposed for solving optimization problems through the simulation study of the behavior of animal groups, which overcomes the limitations of the traditional algorithms when dealing with some complex problems such as, nonlinear, multi-constraint, multi-variable, etc., and demonstrates a better optimization ability. Some common ones are grey wolf optimizer (GWO) (Fu et al., 2019), differential evolution (DE) (Storn and Price, 1997), particle swarm optimization (PSO) (Kennedy, 2011), covariance matrix adaptation evolution strategy (CMAES) (Hansen and Ostermeier, 2001), whale optimization algorithm (WOA) (Mirjalili and Lewis, 2016), salp swarm algorithm (SSA) (Mirjalili et al., 2017), etc. These algorithms have their respective advantages, but the salp swarm algorithm (SSA), as an algorithm that achieves parameter optimization by simulating the behavior of salp populations, exhibits significant advantages in terms of parameter configuration, robustness, and convergence speed. For example, SSA only requires adjusting the position and velocity of salp individuals to update the search space. It utilizes information transmission and competition mechanisms among salp individuals to promote diversity and convergence during the search process (Mirjalili et al., 2017), achieving a balance between global and local search. Furthermore, SSA demonstrates superior robustness and faster convergence speed in solving complex optimization problems. However, like other heuristic algorithms, the algorithm also suffers from problems such as, a high likelihood of falling into local optimum, low optimization accuracy, and unstable solution results (Faris et al., 2018; Kang et al., 2019). Therefore, many scholars have improved the deficiencies of the salp swarm algorithm accordingly. For example, Literature (Faris et al., 2018) used adaptive operators to help the salp swarm algorithm break through the optimal local constraints in the process of follower position updating, so that the individual salp swarm has strong global convergence ability in the early stage, thus obtaining relatively accurate results in the later stage. Some researchers have also designed three new communication strategies, significantly improving the collaborative capability of SSA (Pan et al., 2021). Alternatively, starting from interval prediction, a novel prediction model based on wind speed distribution and multi-objective optimization is proposed by improving the SSA combination module (Wang and Cheng, 2021). The aforementioned studies by these scholars lay the foundation for the proposed multi-objective adaptive learning salp swarm algorithm (ASSA) in this paper.
In summary, this study proposes the VMD-Attention LSTM-ASSA (VMD-AtLSTM-ASSA) hybrid short-term wind speed prediction model containing decomposition, prediction, and optimization for short-term wind speed prediction. The variational mode decomposition (VMD), as a decomposition model in the hybrid model, decomposes the wind speed series data into a series of intrinsic mode functions (IMFs) that can adaptively update the optimal center frequency and bandwidth of each IMF component, which is helpful for the subsequent work of using the long short term memory networks (LSTM) prediction model to incorporate the attention mechanism effectively, which extracts the important slice information in each IMF component for high-precision prediction. Finally, the multi-objective adaptive learning rate salp swarm algorithm (ASSA) model is used to find the optimal weights for each IMF component, which is finally weighted to obtain the high-precision wind speed prediction value.
The main contributions and innovations of this paper are as follows.
(a) The use of long short term memory networks (LSTM) with the inclusion of an attention mechanism to individually predict the intrinsic mode functions (IMFs) obtained through variational mode decomposition (VMD). The Attention mechanism identifies the importance of slice information within each modal component, effectively improving the prediction accuracy and robustness of the LSTM network.
(b) On the basis of the salp swarm algorithm (SSA), improvements are made to address the problems of local optima trapping and premature convergence in the original salp swarm algorithm. This is achieved by proposing the adaptive learning operator and multi-objective operator in the multi-objective adaptive learning rate salp swarm optimization algorithm ASSA. Ultimately, this approach achieves global optimality and improves wind speed prediction accuracy.
(c) Through comprehensive comparisons with popular deep learning prediction models, decomposition models, and optimization models, this paper verifies the superiority of the proposed hybrid wind speed prediction model VMD-AtLSTM-ASSA in terms of individual components as well as overall predictive performance.
The structure of this paper is described as follows: Section 2 presents the algorithmic principles of the proposed model, including the model framework and execution process, and the model principles; Section 3 presents and discusses the case study; Section 4 gives the conclusions and future work.
2 Methodology
2.1 Overall framework and execution process of VMD-AtLSTM-ASSA
This section describes the framework structure of the proposed VMD-AtLSTM-ASSA combined model, and the specific flowchart is shown in Figure 1. The execution process of this study is in three phases, which are A. Wind speed sequence decomposition, B. Prediction of wind speed IMF components, and C. Weight optimization. In this study, the wind speed sequence decomposition stage utilizes the variational mode decomposition (VMD) model to decompose the complex original sequence into stable mode components, aiming to reduce the impact of non-stationarity and complexity of the original wind speed sequence on prediction accuracy. In the prediction stage, the LSTM model with attention mechanism (AtLSTM) is used to predict the wind speed from the decomposed IMF components. Since the predicted values of each IMF component are of differing importance to the actual values, the proposed multi-objective adaptive learning rate salp swarm algorithm (ASSA) algorithm is used to give the optimal weights to each component and then superimpose them to obtain the final highly accurate predicted values of wind speed.
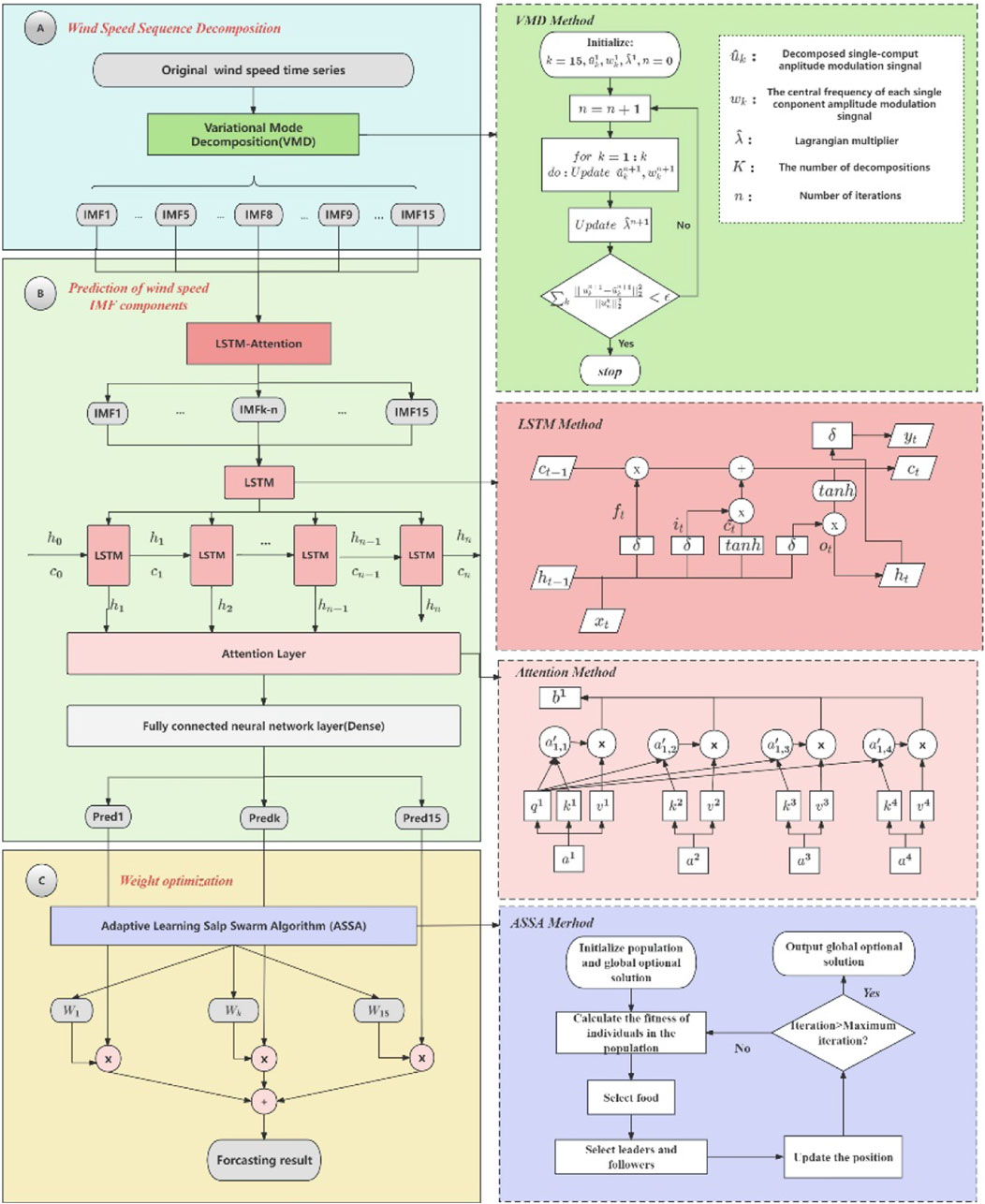
FIGURE 1. Framework and execution process of VMD-AtLSTM-ASSA model. This framework is divided into three steps, (A) is wind speed sequence decomposition, (B) is prediction of wind speed IMF conponents, and (C) is weight optimisation, and the three steps complete the prediction of the whole wind speed sequence in order.
2.2 Principle of VMD-AtLSTM-ASSA
2.2.1 Wind speed sequence decomposition—variational mode decomposition
The VMD is a signal decomposition method (Dragomiretskiy and Zosso, 2014), and the overall framework is a variational problem. That is, assuming that each “mode” is a finite bandwidth with different center frequencies, minimizing the sum of the estimated bandwidths of each mode becomes a problem. In order to solve this variational problem, the method adopts the alternating direction multiplier method, which constantly updates each mode and its center frequency, gradually demodulates each mode to the corresponding fundamental frequency band, and finally extracts each mode to the corresponding center frequency. Therefore, in this study, the VMD technique is employed to decompose the complex original wind speed sequence. The main objective is to decompose the original wind speed sequence, which exhibits nonlinearity and randomness, into a series of frequency-stable mode components, aiming to maximize the improvement in prediction accuracy. The specific process of VMD is as follows, and the results of the mode decomposition are shown in Figure 2.
Step 1. Assuming that each wind speed’s intrinsic mode functions have a finite bandwidth with a center frequency, now find the decomposed wind speed modes such that the sum of the estimated bandwidths of each wind speed mode is minimized. The specific model is as follows:
Where,
Step 2. In order to solve the above model, introduce the penalty factor
Step 3. Iteratively update the parameters,
Where
Step 4. For a given precision
The subsequent analysis focuses on the 15 intrinsic mode functions (IMFs) obtained through the variational mode decomposition (VMD), which are then utilized for short-term wind speed prediction using an Attention LSTM model. Additionally, the study investigates the optimization of weights associated with each IMF. The detailed process can be found in the flowchart depicted in Figure 1.
2.2.2 Prediction of wind speed IMF components—attention LSTM
The IMFs obtained by applying the variational mode decomposition (VMD) to the original wind speed sequence are individually predicted using an Attention LSTM model. LSTM network is a special type of recurrent neural network (RNN) (Hossain and Mahmood, 2020). Due to its special design, LSTM network memorizes long-term information by default, which can effectively solve the long-term and short-term dependence problem when dealing with nonlinear sequence data. Compared to RNN networks, LSTM networks overcome the problems of gradient vanishing and gradient explosion as well as long-term memory (Hochreiter and Schmidhuber, 1997), because the core of the LSTM network is a memory cell state that replaces the hidden layer of traditional neurons
First, each IMF after decomposition is used as an input to the LSTM
Step 1. Decide what information to discard from the memory cell state (calculate the “forget gate” state).
In the above equation,
Step 2. Decide which information is stored in the memory cell state (calculate the “input gate” state) and calculate the candidate values for the memory cell state.
In the above equation,
Step 3. Update the current moment memory cell state with the “forget gate” state, the “input gate” state, the previous moment memory cell state, and the candidate value of memory cell state:
In the above equation
Step 4. Determine what information to output from the memory cell state (calculate the “output gate” state):
In the above equation,
When predicting each wind speed IMF component, it is obviously not rigorous enough to assign the same weight to all input slice information. While the Attention mechanism can capture the important features of wind speed, the Attention mechanism evaluates the importance of different input features, focuses the important information with high weights, ignores the less relevant information with low weights, and finally assigns different weights to them reasonably. Therefore, the Attention mechanism is introduced into the LSTM prediction of each IMF component, and the specific implementation steps of the mechanism are as follows: firstly, the weight coefficients are calculated, i.e., the attention distribution of the slices inside each IMF component is calculated; secondly, the weighted summation of the calculated weight coefficients is carried out, i.e., the weighted average of the slices of each IMF component is calculated, and the calculation process is as follows:
Step 1. Multiply the sliced samples
Step 2. query and key perform similarity calculation to get the weights
Step 3. The weights
Step 4. The normalized weights are weighted and summed with VALUE to get the final output of a certain IMF component prediction
2.2.3 Weight optimisation - multi-objective adaptive learning rate salp swarm algorithm
After the prediction of each IMF component sequence, the salp swarm algorithm (SSA) will find the optimal weights of each component, and finally weigh the superposition to get the final short-term wind speed prediction. The salp swarm algorithm (SSA) simulates the group behavior of salp swarm chains, which is a novel swarm intelligence optimization algorithm (Mirjalili et al., 2017). In this study, the sum of IMF components represents the salp swarm, while the individual intrinsic mode function (IMF) represents the individual salp. During the foraging process, the salp swarm will move towards the food in a chain behavior, and the salp at the head of the chain becomes the leader, and the subsequent ones become the followers. During the movement process, the leader carries out global exploration, while the followers fully carry out local exploration, and this search pattern greatly increases the precision of optimization. This foraging process is the process of finding the optimal weights for each wind speed IMF component in this study, where important information is given high weights and information of low relevance is given ground weights.
However, in the SSA, the salp swarm leader is eager to reach the local optimum from the beginning, which leads to insufficient searching and sometimes the algorithm has a low convergence accuracy. Therefore, this paper proposes multi-objective adaptive learning rate salp swarm algorithm (ASSA). Aiming to solve the problem of a lack of global awareness in population updating, we add two different learning operators in leader position updating and follower position updating respectively, which effectively solves the problem of the SSA easily falling into local extremes and improves the optimization accuracy of the algorithm. The flowchart of multi-objective adaptive learning rate salp swarm algorithm (ASSA) is shown in Figure 1, The optimization steps are as follows (Mirjalili et al., 2017):
Step 1. Population initialization. Let the search space be the Euclidean space of
Step 2. Leader position update. During the movement and foraging process of the salp swarm chain, the position of the food source is the target position of all salp swarm individuals, so the leader’s position update formula is expressed as:
Where:
Where: l is the current iteration number; L is the maximum iteration number. The convergence factor is a decreasing function from 2 to 0. The control parameters c2, c3 are random numbers between 0 and 1, which are used to enhance the randomness of
Step 3. Follower position update. During the movement and foraging process of the salp swarm chain, the followers move forward sequentially in a chain by influencing each other between the front and back individuals. Their displacements conform to Newton’s laws of motion, and the equation for the follower’s motion displacement is:
Where: t is the time; a is the acceleration, calculated as
Where:
where
However, in the SSA algorithm, the salp swarm leader runs to the global optimum from the beginning of the iteration, which leads to insufficient global search, and an occasionally low convergence accuracy of the algorithm. To address this problem, this paper proposes the ASSA algorithm. For the problem of lack of global awareness in the population update, we add two different learning operators on the leader position update and follower position update respectively, which effectively solves the problem of the SSA algorithm easily falling into the local extreme value and improves the algorithm’s optimization accuracy.
The learning operator for leader position update is added to make the population search more biased towards large-scale search in the early stage and focused towards the global optimal solution in the late stage of the search. The improved salp swarm leader position update process is:
where
For the position update of a salp swarm follower, the individual position is always affected by the two individuals before and after it, and the fitness of the two individuals is unknown. Therefore, we propose that by calculating the fitness values of the two individuals and restricting the poorly adapted individual, we weaken the influence of the poorly adapted individual on the individual update at the current moment. The improved bottles sea squirt follower position update process is:
Where
This improved optimization algorithm has more than one objective function, thus the optimization problem is changed to a multi-objective optimization problem. We first de-measure the objective functions to ensure that the objective functions have the same measure; then average the objective functions, and then transform the multi-objective optimization problem into a simple single-objective optimization problem to solve the problem. As follows:
Step4: Judge whether the current iteration number count satisfies the maximum iteration number iter, if so, output the optimal weight results of each IMF component, otherwise return to Step2.
3 Case study
In this section, to verify the effectiveness of the proposed VMD-AtLSTM-ASSA model, we experimentally study the model using wind speed data collected from wind farms in three different regions. The VMD-AtLSTM-ASSA model is compared with popular models in the research field. All experiments are implemented under the deep learning framework under Python 3.7.3. The configuration of the emulated platform is Intel(R) Core(TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz with 8 GB memory capacity.
3.1 Dataset
The study collected wind speed datasets from three sites on https://data.nrel.gov/search-page, each with 3,000 data points. Site1 came from the St. Thomas Wind Station in the Virgin Islands, the United States; the site 2 wind speed dataset came from the St. Croix Wind Station, the United States Virgin Islands, and the site 3 wind speed dataset came from the Woodburn Wind Station in the United States. At each of the three sites, the wind speed was collected. The last 500 data points were taken as the test set in all datasets, while the rest was taken as the training set. The characteristics of the dataset are shown in Table 1 below.
3.2 Experiments and evaluation indicators
To validate the effectiveness and high accuracy performance of the proposed hybrid model, three sets of comparative experiments were conducted. Experiment 1 compared the predictive performance of AtLSTM with currently popular single deep learning models, verifying the superior predictive performance of Attention LSTM. Experiment 2 compared the prediction results of different wind speed sequence decomposition methods combined with Attention LSTM, demonstrating the superiority of VMD followed by Attention LSTM prediction. Experiment 3 compared the prediction results of different deep learning models combined with VMD, as well as the performance of models incorporating the optimization models SSA and ASSA. This experiment validated the superiority of the VMD-Attention LSTM hybrid model and the excellent predictive performance and stability of the VMD-AtLSTM-ASSA model. The details of these three sets of comparative experiments will be presented in Sections 3.4–3.6.
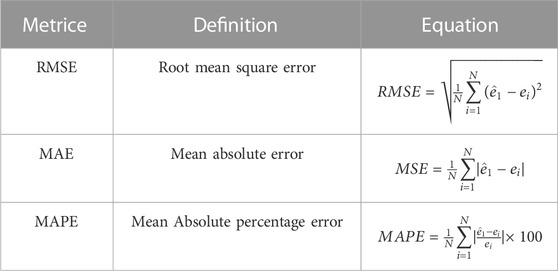
In the experiments, three different evaluation indicators, root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE), were used to present and analyze the experimental results, and according to the value of the evaluation Indicators, the model’s prediction performance was evaluated (Jiang et al., 2021). Their homologous expressions are shown in Table 2, it is worth noting that N represents the length of a predicted subsequence and ei and
3.3 Model parameter settings
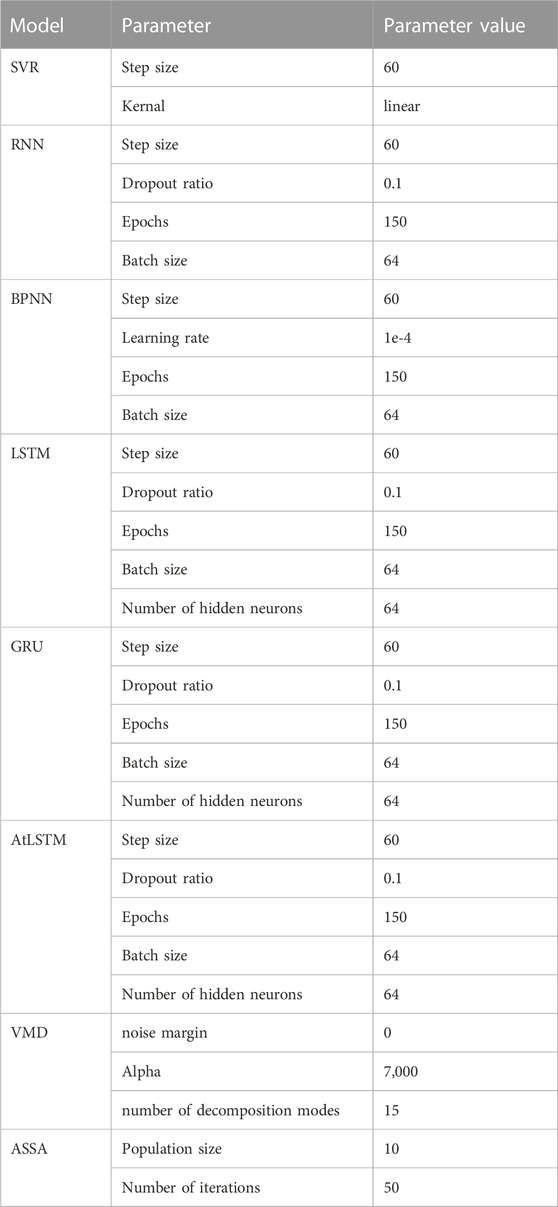
In order to verify the validity of the proposed model, the model parameters used in this study are the same, eliminating the influence of model parameter settings on experimental results. The Attention LSTM is commonly referred to as AtLSTM in the experimental setting. Table 3 shows the model parameter settings used.
3.4 Experiment 1: validating the accuracy advantage of the AtLSTM model over a single model
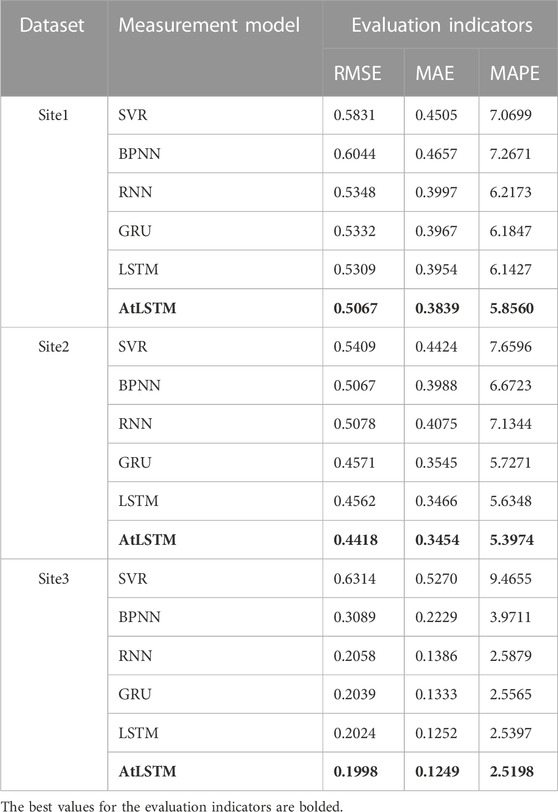
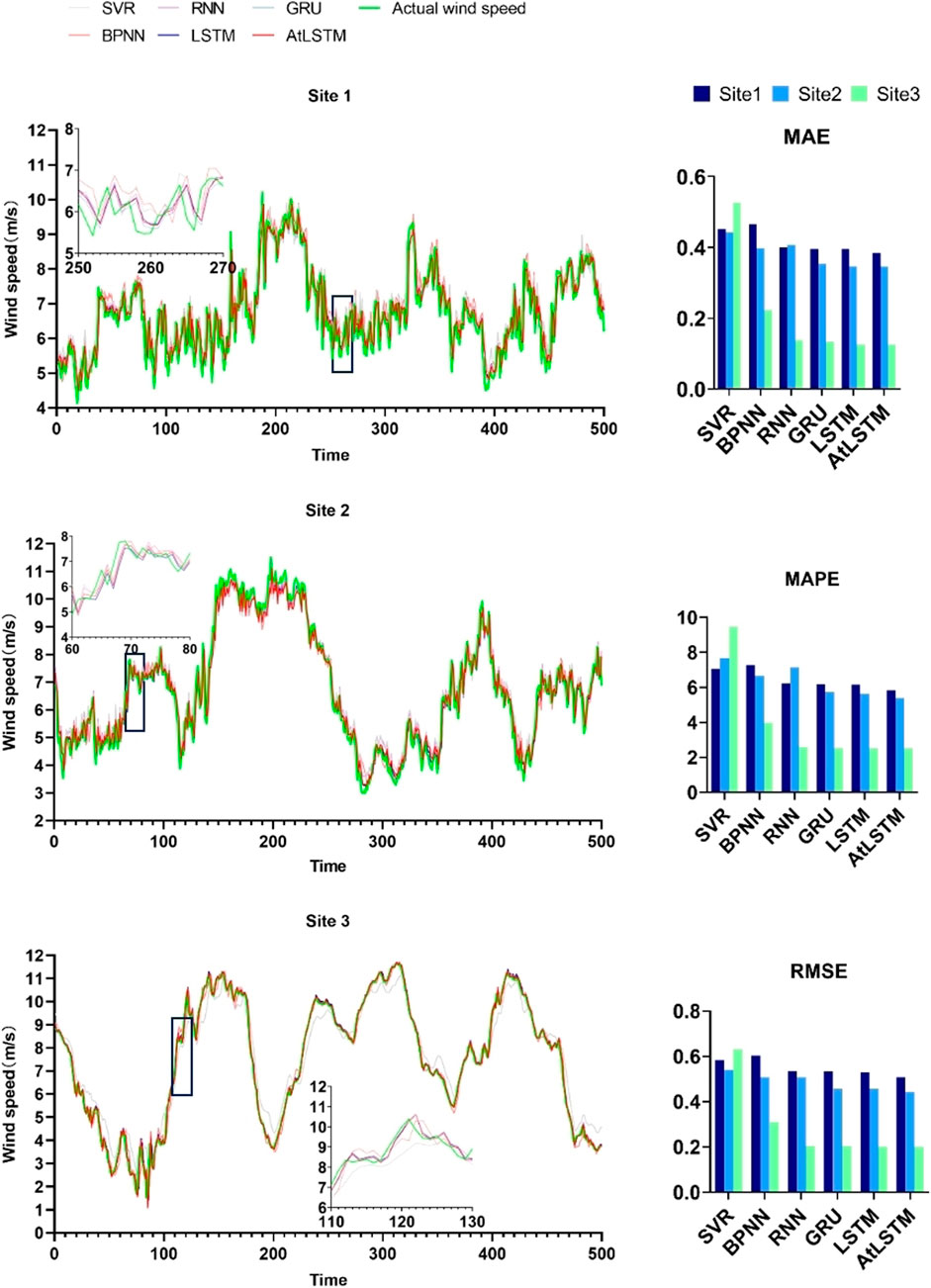
In this experiment, AtLSTM was compared with SVR, BPNN, RNN, GRU, and LSTM models to validate the exceptional predictive performance of the proposed model. The evaluation metrics for model prediction performance are presented in Table 4, with bold font used to indicate the metrics of the AtLSTM model. Figure 3 provides a visual representation of the differences in predictive performance between the proposed model and the four deep learning models.
From Table 4; Figure 3, it is evident that there are variations in the experimental results across the three stations. Both LSTM and GRU demonstrate excellent predictive performance, with LSTM slightly outperforming GRU. By incorporating the Attention mechanism, AtLSTM exhibits a significant improvement in predictive performance compared to LSTM. As shown in Table 4, for different datasets and the five models considered, AtLSTM consistently achieves lower error values, indicating its superior predictive ability. Specifically, in the experiments conducted on the three stations, AtLSTM demonstrates a maximum reduction of 16.16% in RMSE, 17.56% in MAE, and 19.42% in MAPE when compared to other prediction models, namely, SVR, BPNN, RNN, GRU, and LSTM. Therefore, it can be reasonably concluded that AtLSTM possesses superiority in improving the accuracy of prediction results.
3.5 Experiment 2: Validating the decomposition advantages of the VMD model over other decomposition models
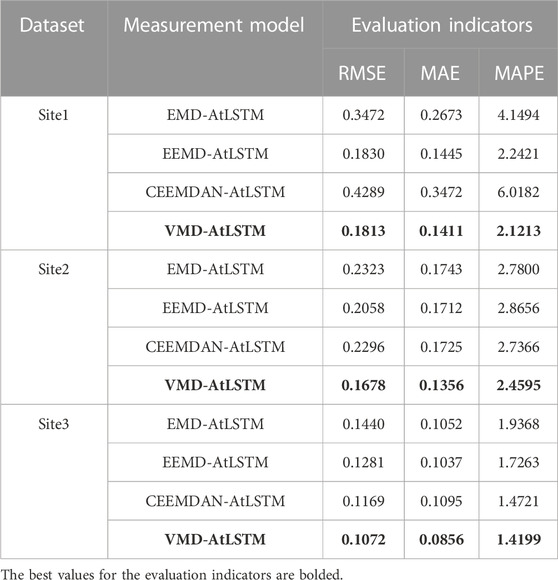
To demonstrate the superiority of AtLSTM based on the VMD decomposition model over other decomposition methods in improving wind speed prediction accuracy, we compared it with EMD-AtLSTM, EEMD-AtLSTM, and CEEMDAN-AtLSTM to validate the superior predictive performance of VMD-AtLSTM. The evaluation metrics for model prediction performance are presented in Table 5, with bold font used to indicate the metrics of the VMD-AtLSTM model. The fitting graph and circular bar chart in Figure 4 visually display the differences in predictive performance between VMD-AtLSTM and the other three decomposition models.
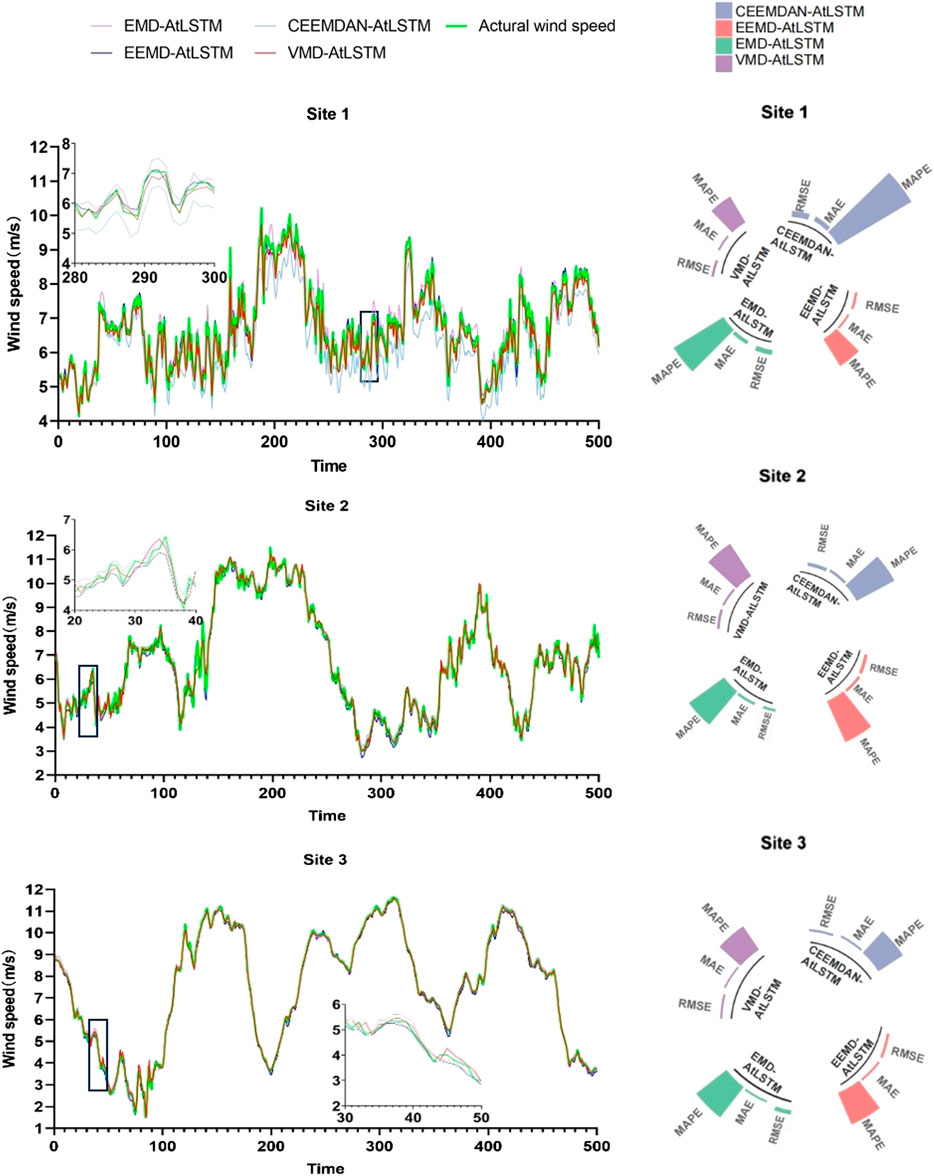
FIGURE 4. Circular bar charts comparing the fitting curves and error metrics of the four decomposition methods combined with AtLSTM.
From Table 5, it can be observed that VMD-AtLSTM achieves the lowest error values across the three locations. Compared to other decomposition models, namely, EMD-AtLSTM, EEMD-AtLSTM, and CEEMDAN-AtLSTM, VMD-AtLSTM exhibits maximum reductions of 57.73%, 59.36%, and 64.75% in RMSE, MAE, and MAPE values, respectively. In conclusion, it can be reasonably argued that combining VMD with AtLSTM for wind speed prediction demonstrates superiority in enhancing short-term wind speed prediction accuracy compared to other signal decomposition techniques.
3.6 Experiment 3: validating the predictive performance advantages of VMD-AtLSTM and VMD-AtLSTM-ASSA
In order to validate the superior predictive performance of the proposed VMD-AtLSTM-ASSA model, we first compared the prediction errors of VMD-SVR, VMD-BPNN, VMD-RNN, VMD-GRU, and VMD-LSTM models, and then evaluated the superiority of VMD-AtLSTM. Furthermore, we verified the effectiveness of incorporating SSA in improving the accuracy of VMD-AtLSTM. Subsequently, a comparison of prediction errors was conducted between the VMD-AtLSTM-SSA and VMD-AtLSTM-ASSA models, ultimately confirming the significant positive impact of the proposed VMD-AtLSTM-ASSA on prediction accuracy. Table 6 displays the prediction error metrics and computational time for the eight hybrid models, while Figure 5 further illustrates the prediction results obtained by each model at the three stations.
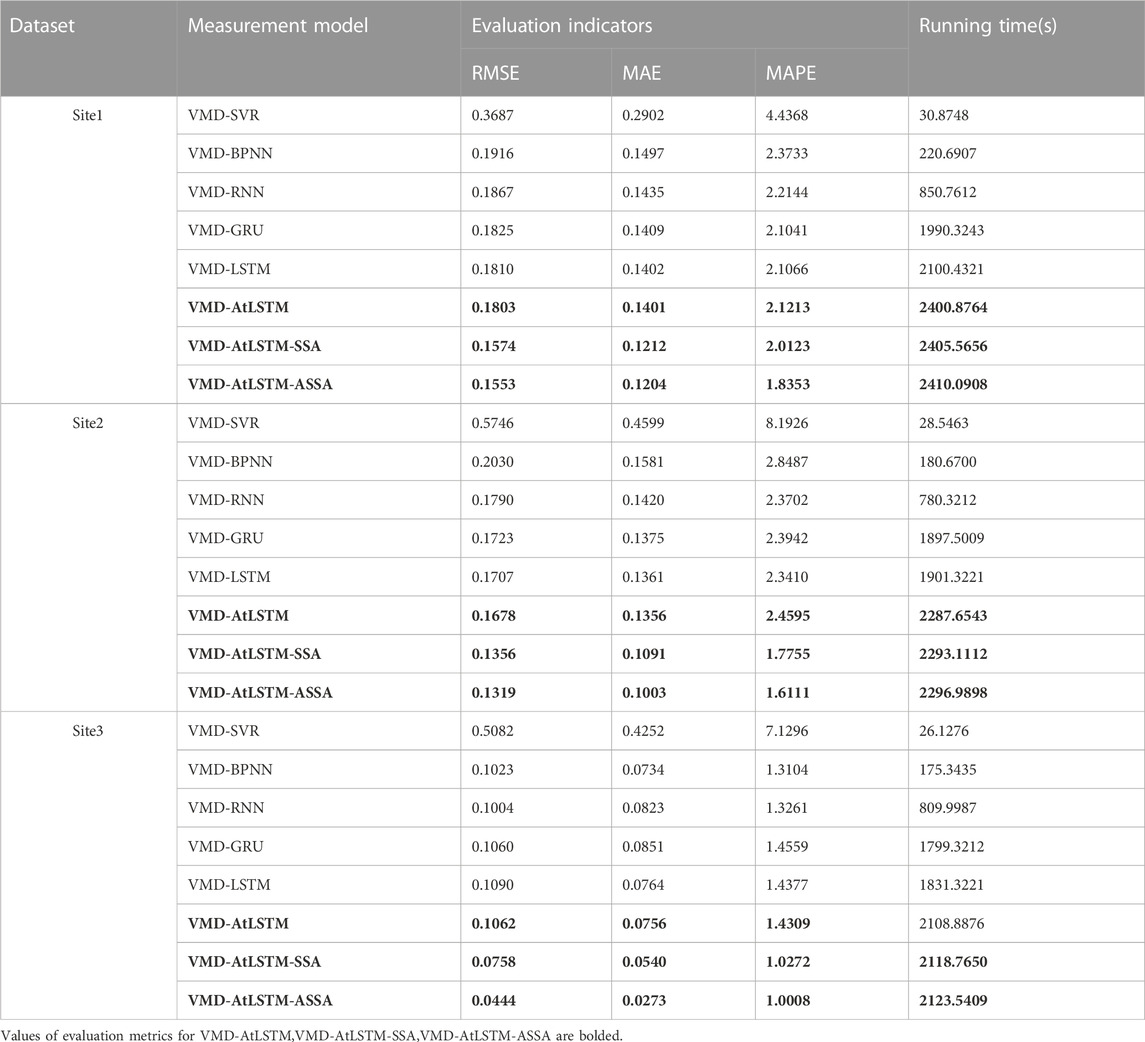
TABLE 6. Comparison of prediction errors based on VMD combined with various deep learning prediction models.
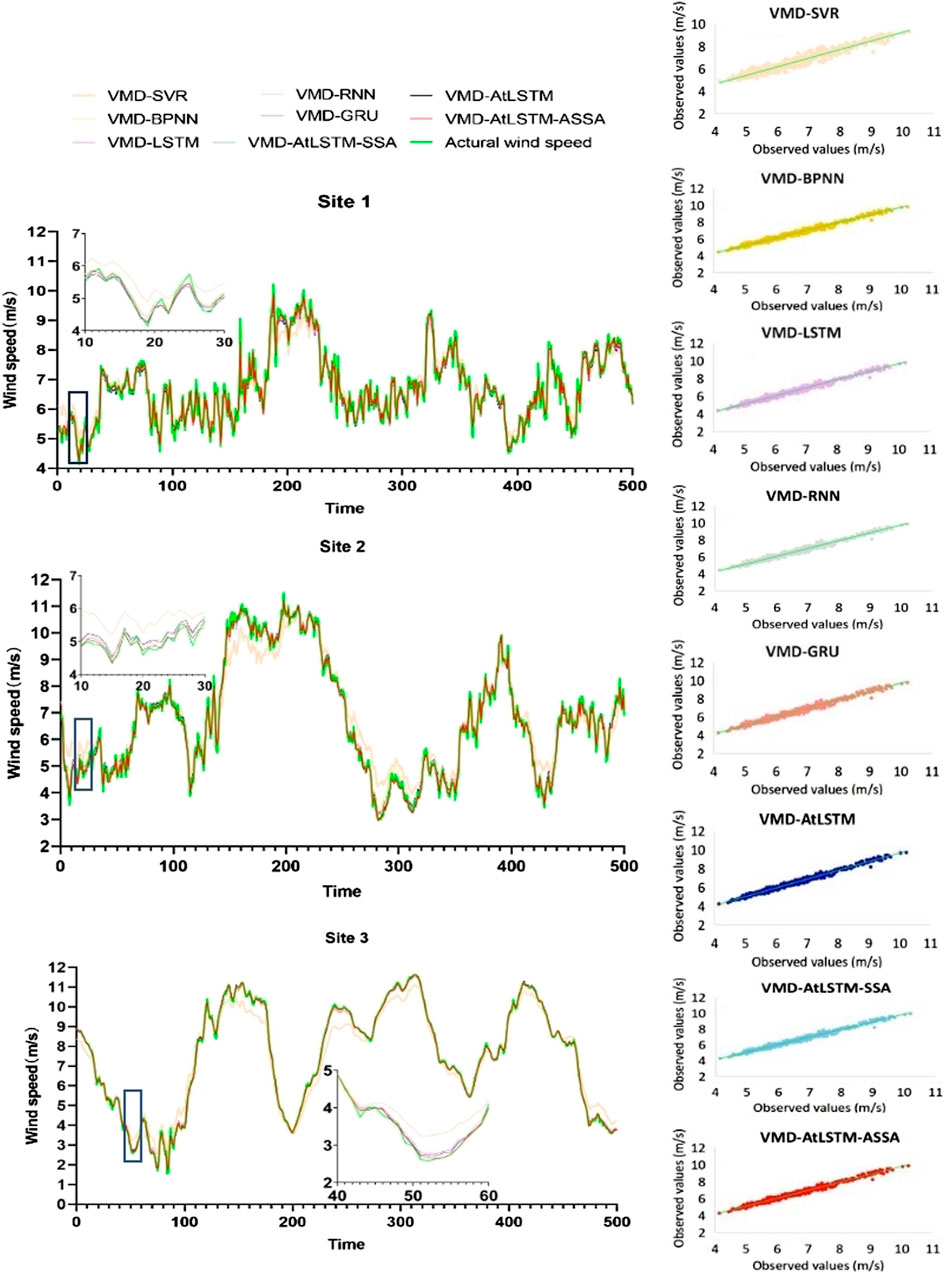
FIGURE 5. Curve fitting and regression fitting graphs of VMD combined with each model for prediction.
The results from Table 6; Figure 5 indicate that among the VMD-based hybrid models, VMD-LSTM performs the best in terms of prediction accuracy, followed by VMD-RNN and VMD-GRU. The VMD-AtLSTM model exhibits improved accuracy compared to VMD-LSTM, suggesting that incorporating attention mechanism enhances the predictive accuracy of the LSTM model. Additionally, it can be observed that VMD-AtLSTM-SSA reduces the RMSE value by 12.7% compared to VMD-AtLSTM, while VMD-AtLSTM-ASSA further reduces the RMSE value by 1.33% based on VMD-AtLSTM-SSA. The proposed model achieves maximum reductions of 57.88%, 58.51%, and 58.63% in RMSE, MAE, and MAPE values, respectively, compared to other prediction models. In summary, compared to other VMD-based hybrid models, VMD-AtLSTM improves prediction accuracy by incorporating attention mechanism into LSTM and adding ASSA effectively optimizes prediction accuracy. Figure 6 displays the results of weight searching for 15 IMF components after applying the ASSA algorithm at the three stations. It can be observed that the importance of IMF components varies across different datasets. IMF11 in Site1, IMF7 in Site2, and IMF6 in Site3 are identified as the dominant modes influencing the prediction results, and therefore assigned higher weights.
Generally, the complexity of a model is related to its computational time. Table 6 presents the running time of each model, revealing that AtLSTM model takes slightly more time to execute compared to the LSTM model due to the attention mechanism requiring importance calculation for each slice of the prediction sequence. However, the inclusion of the optimized model ASSA only requires approximately 10 seconds. Overall, the VMD-AtLSTM-ASSA model demonstrates superior predictive performance.
4 Conclusion and future work
With the rapid development of China’s economy, the consumption of traditional non-renewable resources (oil, coal, etc.) is huge, and wind energy, as a renewable and clean energy source, is becoming an important green power generation method for the modern power grid. However, due to the non-linear and non-stationary nature of wind speed, this trait seriously affects the safe and reliable operation of the power system, and finally leads to problems such as, difficult grid scheduling of wind farms. Therefore, the development of a high-precision and high-reliability short-term wind speed prediction model can, on the one hand, provide efficient and reliable planning for wind power, and on the other hand, stabilize the power grid and reduce the volatility. Numerous researchers have continuously invested in the study of wind speed prediction models, and a steady stream of wind speed prediction models have been proposed. Some examples of such models are, physical models based on meteorological data prediction; statistical models to establish the relationship with future wind speed function by calculating the historical wind speed; artificial intelligence prediction models based on training the model on training samples.
However, the above methods do not work well for fluctuating and complex data, so this paper proposes a short-term wind speed prediction model based on a mixture of the VMD model, the Attention LSTM prediction model, and an improved salp swarm algorithm (multi-objective adaptive learning rate salp swarm algorithm). In this study, the VMD model is employed to decompose the original wind speed sequence into multiple stable intrinsic mode functions (IMFs). Subsequently, the AtLSTM model is utilized to individually forecast each IMF component. Finally, the proposed ASSA algorithm is applied to assign weights to each IMF component, resulting in a weighted aggregation that yields highly accurate short-term wind speed predictions.
In this study, by simulating wind speed data from three wind farms and designing three aspects of comparison experiments, the experimental results illustrate that the data preprocessing strategy based on VMD technology can effectively reduce the volatility and complexity of the wind speed sequence, and significantly improve the accuracy of short-term high wind speed prediction. Furthermore, in the prediction module, the Attention LSTM (AtLSTM) with an incorporated attention mechanism is introduced. This attention mechanism enables the LSTM network to analyze the importance of each temporal slice of input data, assigning higher weight values to slices that have a significant impact on the prediction results. As a result, the predictive accuracy is enhanced. Finally, the multi-objective adaptive learning rate salp swarm algorithm (ASSA) proposed in the weight optimization part adds two operators on the basis of salp swarm algorithm (SSA) that effectively solve the problem of local optimal solution, which the original algorithm is prone to, so as to improve its accuracy in optimization searching. In summary, by setting up a large number of different comparison experiments, it has been verified that the hybrid short-term wind speed prediction model proposed in this paper based on the multi-objective adaptive learning rate salp swarm algorithm (ASSA), Attention LSTM, and VMD has fully demonstrated the accuracy advantage of the model.
In this study, a hybrid VMD-AtLSTM-ASSA short-term wind speed prediction model with decomposition algorithm and optimization algorithm is proposed to address the characteristics of short-term wind speed unsteadiness and nonlinearity and the lack of prediction accuracy of a single model for complex data. This proposed model shows excellent prediction performance. Nevertheless, this model still has more application scenarios and room for expansion. Firstly, this study mainly focuses on the processing and prediction of wind speed time series information, and other data inputs, such as, wind direction information, seasonal information, and spatial information between wind farms, can be considered to expand the model’s environmental adaptability. Secondly, the K value of the variational modal decomposition algorithm used in this study is determined by judging whether the center frequency of each IMF is aliased or omitted, also, the α value is limited to 7,000, so the K value in this paper is selected for the experimental data in this paper, and it is not adaptive, so the introduction of optimization algorithms can be considered to achieve adaptive modal decomposition. Furthermore, within this research, we have observed that VMD-GRU demonstrates remarkable predictive accuracy and computational efficiency. Therefore, in future studies, we plan to introduce additional advanced models for comparative analysis. Additionally, we aim to conduct comprehensive optimizations addressing both the accuracy and model complexity limitations identified in these models during our research. In addition, the optimization algorithm for the machine learning algorithm in this study is the salp swarm algorithm (SSA). Considering the rapid progress in the research of swarm intelligence algorithms, more efficient swarm intelligence optimization algorithms can be added to the future research, and other optimization algorithms can be replaced to improve the prediction performance of the model. Finally, the hybrid VMD-AtLSTM-ASSA short-term wind speed prediction model proposed in this paper is also suitable for other datasets with complex data, high volatility, and high accuracy requirements, such as, crude oil prices and nuclear energy consumption.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
LW: Conceptualization, Formal Analysis, Investigation, Methodology, Software, Visualization, Writing–original draft, Writing–review and editing. YL: Formal Analysis, Funding acquisition, Methodology, Project administration, Resources, Supervision, Writing–original draft, Writing–review and editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. The work was supported by a grant from the National Natural Science Foundation of China (Grant No: 42171419), awarded to YL.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Altan, A., Karasu, S., and Zio, E. (2021). A new hybrid model for wind speed forecasting combining long short-term memory neural network, decomposition methods and grey wolf optimizer. Appl. Soft Comput. 100, 106996. doi:10.1016/j.asoc.2020.106996
Duan, J., Zuo, H., Bai, Y., Duan, J., Chang, M., Chen, B., et al. (2021). Short-term wind speed forecasting using recurrent neural networks with error correction. Energy 217, 119397. doi:10.1016/j.energy.2020.119397
Dragomiretskiy, K., and Zosso, D. (2014). Variational mode decomposition. Ieee Trans. Signal Process. 62, 531–544. doi:10.1109/TSP.2013.2288675
Faris, H., Mafarja, M., Heidari, A., Aljarah, I., Al-Zoubi, A., Mirjalili, S., et al. (2018). An efficient binary Salp Swarm Algorithm with crossover scheme for feature selection problems. Knowledge-Based Syst. 154, 43–67. doi:10.1016/j.knosys.2018.05.009
Fu, W., Wang, K., Li, C., and Tan, J. (2019). Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis, improved hybrid GWO-SCA optimization and ELM. Energy Convers. And Manag. 187, 356–377. doi:10.1016/j.enconman.2019.02.086
Guliyev, F. (2020). Trump’s “America first” energy policy, contingency and the reconfiguration of the global energy order. Energy Policy 140, 111435. doi:10.1016/j.enpol.2020.111435
Hansen, N., and Ostermeier, A. (2001). Completely derandomized self-adaptation in evolution strategies. Evol. Comput. 9, 159–195. doi:10.1162/106365601750190398
Hassan, R. U., Li, C., and Liu, Y. (2021). Online dynamic security assessment of wind integrated power system using SDAE with SVM ensemble boosting learner. Int. J. Of Electr. Power and Energy Syst. 125, 106429. doi:10.1016/j.ijepes.2020.106429
Higashiyama, K., Fujimoto, Y., and Hayashi, Y. (2018). Feature extraction of NWP data for wind power forecasting using 3D-convolutional neural networks. in, ed. P. Droege, 350–358. doi:10.1016/j.egypro.2018.11.043
Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735
Hossain, M. S., and Mahmood, H. (2020). “Short-term load forecasting using an LSTM neural network,” in Proceeding of the 2020 IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, February 2020 (IEEE), 1–6. doi:10.1109/PECI48348.2020.9064654
Hu, H., Wang, L., and Tao, R. (2021). Wind speed forecasting based on variational mode decomposition and improved echo state network. Renew. Energy 164, 729–751. doi:10.1016/j.renene.2020.09.109
Jaseena, K., and Kovoor, B. (2021). Decomposition-based hybrid wind speed forecasting model using deep bidirectional LSTM networks. Energy Convers. And Manag. 234, 113944. doi:10.1016/j.enconman.2021.113944
Jiang, P., Liu, Z., Niu, X., and Zhang, L. (2021). A combined forecasting system based on statistical method, artificial neural networks, and deep learning methods for short-term wind speed forecasting. Energy 217, 119361. doi:10.1016/j.energy.2020.119361
Kang, F., Li, J., and Dai, J. (2019). Prediction of long-term temperature effect in structural health monitoring of concrete dams using support vector machines with Jaya optimizer and salp swarm algorithms. Adv. Eng. Softw. 131, 60–76. doi:10.1016/j.advengsoft.2019.03.003
Kennedy, J., and Eberhart, R. (2011). Particle swarm optimization. Proc. IEEE Int. Conf. Neural Netw. 4, 1942–1948. Perth, Australia. doi:10.1109/ICNN.1995.488968
Khodayar, M., Kaynak, O., and Khodayar, M. (2017). Rough deep neural architecture for short-term wind speed forecasting. Ieee Trans. Industrial Inf. 13, 2770–2779. doi:10.1109/TII.2017.2730846
Lacal-Arantegui, R. (2019). Globalization in the wind energy industry: contribution and economic impact of European companies. Renew. Energy 134, 612–628. doi:10.1016/j.renene.2018.10.087
Liu, H., Tian, H., Chen, C., and Li, Y. (2010). A hybrid statistical method to predict wind speed and wind power. Renew. Energy 35, 1857–1861. doi:10.1016/j.renene.2009.12.011
Liu, Y., Qin, H., Zhang, Z., Pei, S., Jiang, Z., Feng, Z., et al. (2020a). Probabilistic spatiotemporal wind speed forecasting based on a variational Bayesian deep learning model. Appl. Energy 260, 114259. doi:10.1016/j.apenergy.2019.114259
Liu, Z., Jiang, P., Zhang, L., and Niu, X. (2020b). A combined forecasting model for time series: application to short-term wind speed forecasting. Appl. Energy 259, 114137. doi:10.1016/j.apenergy.2019.114137
Lowery, C., and O’Malley, M. (2012). Impact of wind forecast error statistics upon unit commitment. Ieee Trans. Sustain. Energy 3, 760–768. doi:10.1109/TSTE.2012.2210150
Ma, L., Luan, S., Jiang, C., Liu, H., and Zhang, Y. (2009). A review on the forecasting of wind speed and generated power. Renew. Sustain. Energy Rev. 13, 915–920. doi:10.1016/j.rser.2008.02.002
Mirjalili, S., Gandomi, A., Mirjalili, S., Saremi, S., Faris, H., and Mirjalili, S. (2017). Salp Swarm Algorithm: a bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 114, 163–191. doi:10.1016/j.advengsoft.2017.07.002
Mirjalili, S., and Lewis, A. (2016). The whale optimization algorithm. Adv. Eng. Softw. 95, 51–67. doi:10.1016/j.advengsoft.2016.01.008
Naik, J., Satapathy, P., and Dash, P. (2018). Short-term wind speed and wind power prediction using hybrid empirical mode decomposition and kernel ridge regression. Appl. Soft Comput. 70, 1167–1188. doi:10.1016/j.asoc.2017.12.010
Neshat, M., Majidi Nezhad, M., Mirjalili, S., Piras, G., and Garcia, D. A. (2022). Quaternion convolutional long short-term memory neural model with an adaptive decomposition method for wind speed forecasting: north aegean islands case studies. Energy Convers. Manag. 259, 115590. doi:10.1016/j.enconman.2022.115590
Neshat, M., Nezhad, M. M., Abbasnejad, E., Mirjalili, S., Tjernberg, L. B., Garcia, D. A., et al. (2021). A deep learning-based evolutionary model for short-term wind speed forecasting: a case study of the Lillgrund offshore wind farm. Energy Convers. And Manag. 236, 114002. doi:10.1016/j.enconman.2021.114002
Niu, Z., Yu, Z., Tang, W., Wu, Q., and Reformat, M. (2020). Wind power forecasting using attention-based gated recurrent unit network. Energy 196, 117081. doi:10.1016/j.energy.2020.117081
Paliwal, K., and Basu, A. (1987). “A speech enhancement method based on Kalman filtering,” in ICASSP ’87. IEEE International Conference on Acoustics, Speech, and Signal Processing, Dallas, TX, USA, April 1987 (IEEE), 177–180. doi:10.1109/ICASSP.1987.1169756
Pan, J., Shan, J., Zheng, S., Chu, S., and Chang, C. (2021). Wind power prediction based on neural network with optimization of adaptive multi-group salp swarm algorithm. Clust. Computing-The J. Of Netw. Softw. Tools And Appl. 24, 2083–2098. doi:10.1007/s10586-021-03247-x
Potocnik, P., Skerl, P., and Govekar, E. (2021). Machine-learning-based multi-step heat demand forecasting in a district heating system. Energy And Build. 233, 110673. doi:10.1016/j.enbuild.2020.110673
Ren, Y., Suganthan, P., and Srikanth, N. (2016). A novel empirical mode decomposition with support vector regression for wind speed forecasting. Ieee Trans. Neural Netw. And Learn. Syst. 27, 1793–1798. doi:10.1109/TNNLS.2014.2351391
Rodrigues Moreno, S., Gomes da Silva, R., Cocco Mariani, V., and dos Santos Coelho, L. (2020). Multi-step wind speed forecasting based on hybrid multi-stage decomposition model and long short-term memory neural network. Energy Convers. Manag. 213, 112869. doi:10.1016/j.enconman.2020.112869
Sahin, A., and Sen, Z. (2001). First-order Markov chain approach to wind speed modelling. J. Of Wind Eng. And Industrial Aerodynamics 89, 263–269. doi:10.1016/S0167-6105(00)00081-7
Scutaru, M., Vlase, S., Marin, M., and Modrea, A. (2020). New analytical method based on dynamic response of planar mechanical elastic systems. Bound. Value Probl. 2020, 104. doi:10.1186/s13661-020-01401-9
Shahid, F., Zameer, A., and Muneeb, M. (2021). A novel genetic LSTM model for wind power forecast. Energy 223, 120069. doi:10.1016/j.energy.2021.120069
Shao, Z., Han, J., Zhao, W., Zhou, K., and Yang, S. (2022). Hybrid model for short-term wind power forecasting based on singular spectrum analysis and a temporal convolutional attention network with an adaptive receptive field. Energy Convers. And Manag. 269, 116138. doi:10.1016/j.enconman.2022.116138
Storn, R., and Price, K. (1997). Differential evolution - a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359. doi:10.1023/A:1008202821328
Tanaka, I., and Ohmori, H. (2015). “Method selection in different regions for short-term wind speed prediction in Japan,” in Proceeding of the 2015 54th Annual Conference of the Society of Instrument and Control Engineers of Japan (SICE), Hangzhou, China, July 2015 (IEEE), 189–194.
Tascikaraoglu, A., and Uzunoglu, M. (2014). A review of combined approaches for prediction of short-term wind speed and power. Renew. Sustain. Energy Rev. 34, 243–254. doi:10.1016/j.rser.2014.03.033
Wang, J., and Cheng, Z. (2021). Wind speed interval prediction model based on variational mode decomposition and multi-objective optimization. Appl. Soft Comput. 113, 107848. doi:10.1016/j.asoc.2021.107848
Wang, J., and Li, W. (2018). Ultra-short-term forecasting of wind speed based on CEEMD and GWO. Dianli Xit. Baohu yu Kongzhi/Power Syst. Prot. Control 46, 69–74. doi:10.7667/PSPC170590
Wang, L., Zeng, Y., and Chen, T. (2015). Back propagation neural network with adaptive differential evolution algorithm for time series forecasting. Expert Syst. Appl. 42, 855–863. doi:10.1016/j.eswa.2014.08.018
Yu, C., Li, Y., Bao, Y., Tang, H., and Zhai, G. (2018). A novel framework for wind speed prediction based on recurrent neural networks and support vector machine. Energy Convers. And Manag. 178, 137–145. doi:10.1016/j.enconman.2018.10.008
Yuan, X., Tan, Q., Lei, X., Yuan, Y., and Wu, X. (2017). Wind power prediction using hybrid autoregressive fractionally integrated moving average and least square support vector machine. Energy 129, 122–137. doi:10.1016/j.energy.2017.04.094
Keywords: variational modal decomposition, attention, long short-term memory, salp swarm algorithm, short-term wind speed prediction
Citation: Wang L and Liao Y (2023) A short-term hybrid wind speed prediction model based on decomposition and improved optimization algorithm. Front. Energy Res. 11:1298088. doi: 10.3389/fenrg.2023.1298088
Received: 21 September 2023; Accepted: 30 October 2023;
Published: 21 November 2023.
Edited by:
Linfei Yin, Guangxi University, ChinaReviewed by:
Ning Li, Xi’an University of Technology, ChinaMehdi Neshat, University of South Australia, Australia
Copyright © 2023 Wang and Liao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yilan Liao, bGlhb3lsQGxyZWlzLmFjLmNu
 Lu Wang
Lu Wang Yilan Liao
Yilan Liao