Assessment of Subsampling Strategies in Microspectroscopy of Environmental Microplastic Samples

The analysis of environmental occurrence of microplastic (MP) particles has gained notable attention within the past decade. An effective risk assessment of MP litter requires elucidating sources of MP particles, their pathways of distribution and, ultimately, sinks. Therefore, sampling has to be done in high frequency, both spatially and temporally, resulting in a high number of samples to analyze. Microspectroscopy techniques, such as FTIR imaging or Raman particle measurements allow an accurate analysis of MP particles regarding their chemical classification and size. However, these methods are time-consuming, which gives motivation to establish subsampling protocols that require measuring less particles, while still obtaining reliable results. The challenge regarding the subsampling of environmental MP samples lies in the heterogeneity of MP types and the relatively low numbers of target particles. Herein, we present a comprehensive assessment of different proposed subsampling methods on a selection of real-world samples from different environmental compartments. The methods are analyzed and compared with respect to resulting MP count errors, which eventually allows giving recommendations for staying within acceptable error margins. Our results are based on measurements with Raman microspectroscopy, but are applicable to any other analysis technique. We show that the subsampling-errors are mainly due to statistical counting errors (i.e., extrapolation from low numbers) and only in edge cases additionally impacted by inhomogeneous distribution of particles on the filters. Keeping the subsampling-errors low can mainly be realized by increasing the fraction of MP particles in the samples.

Introduction

The occurrence of microplastic (MP) particles in environmental compartments has gained notable interest in both scientific and mainstream media, a trend that is predicted to increase in the coming years (Halden 2015). A major cause of concern related to plastic materials is its accumulation potential due to their high persistence in the environment, while production rates further increase and concomitantly the plastic waste (Jambeck et al., 2015; Brandon et al., 2019; Borrelle et al., 2020). Assessments of the abundance of MP particles in various kinds of samples can be found throughout the literature e.g., in water (Lenz and Labrenz 2018; Liu et al., 2019; Karlsson et al., 2020), sediment or soil (Claessens et al., 2013; Vianello et al., 2013; Bergmann et al., 2017; Enders et al., 2019), wastewater treatment plants (Tagg et al., 2015; Murphy et al., 2016) as well as biota (Lusher et al., 2017). Understanding sources, pathways and sinks of MP particles is key to understand how to effectively limit further spreading of this pollutant (Halle et al., 2016; Geyer et al., 2017; Siegfried et al., 2017). Therefore, large numbers of environmental samples have to be analyzed quantitatively, as not only the spatial but also the temporal occurrence of MP particles at a given location is of high relevance. Methods suitable for comprehensive monitoring studies need to be fast, quantitative and automated to deal with the high number of samples to process.

The currently used analytical tools can be sorted into two categories: mass and particle-based methods. Mass based methods are pyrolysis gas chromatography and mass spectrometry (Py-GC-MS) (Fischer and Scholz-Böttcher, 2019; Logemann et al., 2018; Dierkes et al., 2019) or thermoextraction and desorption coupled with gas chromatography-mass spectroscopy (TED-GC-MS) (Fischer and Scholz-Böttcher, 2019; Duemichen et al., 2014; Dümichen et al., 2015; Dümichen et al., 2017). Their main advantages are short analysis times and straightforward application. Also challenging environmental samples can be processed in few hours (Fischer and Scholz-Böttcher, 2019; Dümichen et al., 2017), with only relatively little sample preparation. The better the removal of organic matter, however, the more robust the analysis results will be, as organic compounds can hamper the correct data interpretation (Primpke et al., 2020a). As a drawback, only the integral mass fraction of polymer within the sample is obtained, without giving details on particle numbers or size distribution. Furthermore, the techniques are destructive, which makes it impossible to reuse the samples after measurement. Particle-based methods, such as spectroscopic imaging by Fourier-Transform infrared (FTIR) spectroscopy (Löder et al., 2015; Käppler et al., 2016; Primpke et al., 2017; Primpke et al., 2019) or microspectroscopic particle measurement using FTIR (Browne et al., 2010; Vianello et al., 2013; Löder et al., 2015; Tagg et al., 2015; Wagner et al., 2017; Käppler et al., 2018; Poulain et al., 2019) or Raman (Lenz et al., 2015; Käppler et al., 2016; Anger et al., 2018; Schymanski et al., 2018), register size, morphology and chemical classification of each particle (mass fractions can be estimated by applying volume estimates and bulk density values (Simon et al., 2018)). Particles >500 µm are often picked and investigated manually. For particles <500 μm, a purified particle dispersion (i.e., after removal of non-MP particles) is typically filtered onto a suitable filter substrate and then subjected to either imaging or individual particle measurement. The imaging approach entails scanning the entire filter area without a-priori knowledge about particle locations. Each spectrum at each measured pixel is evaluated and particle information is obtained by grouping together adjacent pixels with identical spectral classification (Primpke et al., 2017; Primpke et al., 2019; Primpke et al., 2020b). The particle measurement approach is done in two passes. First, an optical image is acquired with a light microscope (LM) to identify particles. Then, spectra are only acquired where particles were detected. Figure 1 illustrates both approaches graphically.

FIGURE 1

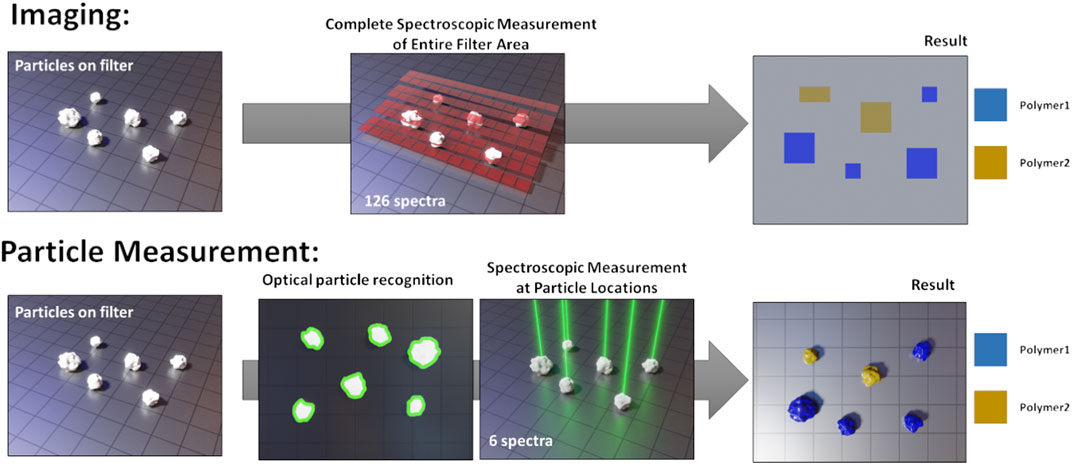
FIGURE 1. Schematic comparison of spectroscopic imaging and particle measurement. Reproduced from Brandt et al. (2020).

Both methods are inherently slower than the mass-based techniques and require elaborate sample purification steps to remove non-plastic particles (Enders et al., 2020). Increasing the fraction of MP particles per sample allows for a faster and more reliable analysis, as less particles have to be processed and overloaded filters are avoided, which can lead to erroneous results. The currently used microspectroscopic techniques cannot compete with mass-based techniques regarding their sample throughput rates. However, to assess the potential toxicological impacts on both biota and humans, knowledge about MP particle size distribution and numbers is critical (Masó et al., 2003; Zettler et al., 2013). Hence, microspectroscopic methods for MP analysis are of high current relevance and the acceleration of sample throughput rates is one of the major challenges.

One approach to speed up imaging and particle measurements is to measure only a certain fraction of any sample and to extrapolate the obtained results. This can be achieved in two ways: i) Subsampling before filtration: only a fraction of the entire sample is filtered onto the sample substrate which will be completely measured. This method requires very careful homogenization of the sample to avoid extrapolation errors. For homogenization, different densities and the fast sedimentation of the particles in aqueous suspensions pose challenges. The success of this splitting before filtration is largely influenced by the method and splitting tools applied. ii) Subsampling during analysis: The entire sample is filtered on one or multiple filters, but only a fraction of each filter is measured. This method circumvents the challenges of prior homogenization and sample splitting, but requires a robust strategy to select which areas or particles to measure. The main statistical problems therein arise from both, the inhomogeneous distribution of the particles on the filter and the low numbers of MP particles, of typically around 1%. The present study focuses on pathway ii) i.e., the statistical subsampling of particles that are already on the filter substrate. The results are applicable to any MP sampling technique probing particles spatially distributed on a filter substrate, irrespective of the exact measurement technique. However, we do not strive to determine hard numbers for potential speed gains, as these are highly dependent on the actually used method and measurement requirements. Speed optimization of each analysis technique is an important, yet difficult endeavor requiring careful balancing the runtime with result quality, which is highly specific for the respective methods.

Subsampling on a Substrate: Challenges

Filtering particles from an environmental sample onto a microscopy filter does not lead to a homogeneous distribution of particles on the filter area. Comprehensive guidelines explain the challenges and recommend strategies for successful filtrations. (Merck, 2018). The stream of water is usually not of a constant flow-rate, leading to different forces on the particles on the filter throughout the filtration process. Air bubbles can be present that introduce additional unpredictable forces. Often, the particle concentration on the filter follows a gradient with low concentrations around the filter center and higher concentrations closer to the filter perimeter (Thaysen et al., 2020). To minimize coagulation of particles on the filter, the flow rate can be reduced or tangential flow filtration can be performed (Buffle and Leppard 1995).

Further inhomogeneity is introduced by the nature of the environmental particles. Depending on the sample origin (e.g., rainwater or wastewater treatment sludge) and given the large range of MP types itself, the samples contain a broad variety of particles different in size, density and shape; properties that have a significant influence on particle distribution dynamics. In addition, particles that tend to aggregate easily clump together and can even incorporate particles of other types. The low fraction of MP particles per sample can lead to low statistical robustness of any deduced conclusions (Anger et al., 2018; Karlsson et al., 2020). All such factors make the selection of a representative subset an especially challenging task and have to be considered during the assessment.

Proposed Subsampling Strategies

The strategies proposed to select a representative subset during analysis can be sorted into two categories, corresponding to two different workflows.

The first category, the “area selection strategy,” does not need any a priori knowledge and distributes a number of box-shaped areas to measure over the entire filter area. It is mostly suitable for imaging protocols. Different layouts for distributing the measuring boxes can be considered to account for the inhomogeneous distribution of particles on the filter, such as a cross or a spiral layout (refer to Figure 2). (Huppertsberg and Knepper, 2018). The number and size of the boxes can be adjusted to cover a desired fraction of the filter. After the spectroscopic measurements within the box areas, the result is then extrapolated according to the fraction of filter area covered by the boxes. It is theoretically possible to design area-based subsampling approaches that do not rely on placing rectangular boxes, for instance dividing the filter in cake-piece shaped sections. Such a section accounts for a radial inhomogeneity by covering central and peripheral area of the filter. Their practical application could be limited, however, as most FTIR- or Raman-software packages are restricted to the selection of rectangular areas for measurement. The viability of the different layouts will be assessed practically later in this manuscript.

FIGURE 2

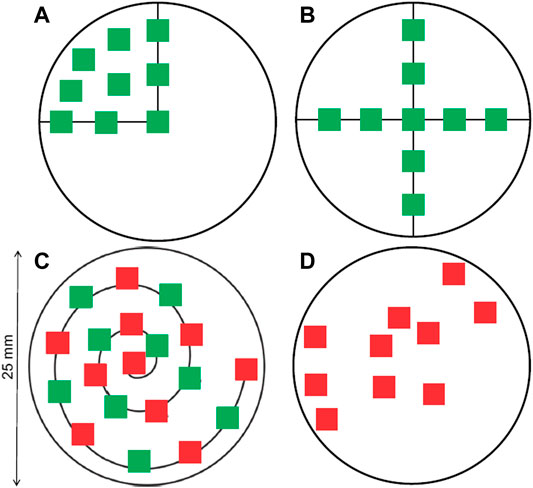
FIGURE 2. Distribution of measure areas on a circular filter, following different layouts. (A) Spreading on a quarter of the filter. (B) Forming a cross. (C) Following a spiral. (D) Random placement. The green squares correspond to 7.3% of the filter area and the red boxes to 8.2%, respectively. Both together represent 15.5% of the filter area (Huppertsberg and Knepper 2018).

The second category, the “particle selection strategy,” requires some a priori knowledge that is gained from first acquiring an overview optical image from the entire filter using a light microscope (LM). That image can be used to determine the number and location of each particle or even characterize the particles further regarding their size, shape and color (thereby decreasing the uncertainty about the particle location) and the actual fraction of particles measured can be adjusted more precisely. If further information per particle is derived, more sophisticated chemometric methods for finding representative subsamples can be engaged (Chaudhuri, 1994; Daszykowski et al., 2002; Rodionova and Pomerantsev, 2008).

It is also possible to combine both approaches. Imhof et al., for instance, chose to manually identify particles larger than 500 µm and to automatically measure all smaller particles based on an “area selection strategy,” measuring approx. 1.6% of the filter area (Imhof et al., 2016).

Different subsampling strategies are currently in use that usually measure about 1–10% of the filter area. Their use is in most cases justified by hypothetical considerations, but practical validations of the subsampling strategies are scarce. A recent study by Mintenting et al. assessed the subsampling and errors of riverine water samples and concluded that at least 50% filter coverage is needed for robust particle counts, which is substantially higher than most studies aim for (Mintenig et al., 2020).

With this publication, we revisited 27 MP samples from different environmental compartments that were measured by Raman microspectroscopy, without using any subsampling method. The GEPARD software was used for particle detection and automated Raman measurement, an appropriate tool to reduce analysis time and remove operator-bias (Brandt et al., 2020). As a side effect, all information about the filtered sample (e.g., particle count, coordinates, sizes and spectral identification) is stored in particle datasets. These datasets are used to re-evaluate the sample by simulating a measurement using a dedicated subsampling strategy and determining the subsampled result. Comparing subsampled to original result allowed us to draw quantitative conclusions about the statistical robustness and usability of the investigated subsampling strategies.

Materials and Methods

Sample Details and Filtration

27 fully analyzed samples from different environmental compartments were the basis for our analysis (Table 1). The samples underwent purification procedures identical to established schemes as presented by Enders et al. (Enders et al., 2020), a study which presents a flow chart of detailed protocols for the different sample conditions. Reproducibility of the applied purification methods is thereby ensured. An exception to the above are the rainwater samples that underwent a combination of oxidation with Fenton’s reagent, enzymatic digestion and density separation using ZnCl₂ (Löder et al., 2017). The final filtration was done using a tailor-made glass filtration device. After cleaning all glass parts with 3% H₂O₂ and sonication in MilliQ water (3 × 10 min, renewal of the MilliQ water after each 10 min interval), 10 × 10 mm silicon filters with 10 or 50 µm holes were inserted into the filtration device using red PTFE filter holders that also act as seals. During filtration, the flow rate of the water is observed to avoid overloading of the filters. The filtration is done in a laminar flow box (Telstar Aeolus V) to avoid contamination from air-borne particles. Full details about used filters and the filtration setup are already published and can be found elsewhere (Käppler et al., 2015; Brandt et al., 2020). Without prior homogenization, each sample was filtered onto several filters. Only one of these filters per sample was used in the following analyses, so the particle numbers and MP content are not representative for the actual environmental sample. Therefore, further information on the sample origin and the sampling is neglected. The analyzed samples counted between 1,500 and 33,000 particles per filter. In the following, both “sample” and “filter” refer to the single filter representing each environmental sample.

TABLE 1

TABLE 1. Summary of origin of analyzed samples (WWTP = wastewater treatment plant).

Particle Measurements

Full details about the measurement workflow using the GEPARD software are reported in a separate publication (Brandt et al., 2020); only a short summary is given here.

LM images were acquired directly in the Raman microscope (WITec® alpha 300R), which is also used for the spectroscopic measurements using a 532 nm laser and a 600 L/mm spectroscopic grating. The optical LM images were acquired in dark-field at adjustable focus heights, which allows constructing an image of optimal depth-of-field for both, small and large, particles. A watershed-based image segmentation algorithm was used to localize particles and determine their boundaries. Raman spectra were collected for each particle (typical conditions: 0.5 s integration time, five accumulations) and the TrueMatch® software (WITec®) was used for spectral evaluation. The results from spectra database matching were combined with the particle information from the particle recognition step to obtain complete information about particle type and size distributions.

Data Processing

The datasets generated by the GEPARD software contain all information about particle location, contour and chemical classification. This readily allows revisiting the datasets and selecting particles from the entirety of the particle list according to any desired subsampling strategy. The code for all calculations is realized in form of a Python script, the full source code can be found on https://gitlab.ipfdd.de/Brandt/subsampling.

To assess the performance of any considered subsampling model it is necessary to derive quantitative measures of its performance. We calculated the subsampling-error according to Equation 1. A subsampling model was applied to each fully measured dataset and the subsampled count of MP particles determined (SI chapter “Application of Subsampling Methods”). To estimate the total MP particle count, the subsampled count was extrapolated by dividing by the subsampling fraction. That estimated MP particle count was then divided by the original MP particle count.

$\mathit{subsamplingError}=\frac{\mathit{mpCoun}{\mathit{t}}_{\mathit{subsampled}}/\mathit{fraction}}{\mathit{mpCoun}{\mathit{t}}_{\mathit{original}}}\cdot \mathrm{100\%}(1)$

To reduce statistical deviations, each filter was processed 10 times. For each iteration, the filter was rotated about 36° around the filter center and then the subsampling is repeated. This increases the number of performed tests by 10-fold and reduces noise in the results, making data interpretation more robust.

Implemented Subsampling Methods

Hereafter, we describe the implemented subsampling methods. The first two followed the particle selection strategy, i.e., rely on knowledge about particle location, and the remaining methods follow the area selection strategy, i.e., they represent different approaches for placing rectangular areas (boxes) for conducting measurements. To test practically relevant fractions, we tested fractions from 2 to 90% in terms of particle count fractions, and from 2% to the maximum achievable fraction in terms of filter area coverage for the individual box selection methods.

Random Particle Subsampling

The method is based on a prior particle recognition step. Out of the list of detected particles, a given number is selected on a completely random basis to represent the desired fraction of particles measured.

SizeBin Particle Subsampling

The concept is the same as in the random particle subsampling with additional accounting for size distribution bias to reduce the uncertainty related to low number size fractions (as usually the case for larger particles). Therefore, the detected particles are first grouped into size bins. The chosen size limits in between the bins are 5 μm, 10 μm, 20 μm, 50 μm, 100 μm, 200 μm, and 500 µm. After sorting the particles into the bins, a certain number of particles is randomly drawn from each bin so that the measured fraction of particles is equal for all bins. At least one particle is taken from each bin (given, that the bin is not empty). For example, when 10% of all particles have to be measured, the algorithm will select 5 particles out of a bin with 50 particles, 20 out of a bin with 200 particles and 1 out of a bin with only 4 particles.

Box Selection Subsampling

Four different layouts were implemented for placing measuring boxes on the circular filter:

i. Cross layout with either 3 or 5 boxes across, respectively (Figure 2B)

ii. Spiral layout with 5, 10 or 20 boxes. The first box is located in the center and the last one touches the perimeter of the filter area. (Figure 2C).

iii. Random layout with 5, 10 or 20 boxes. The boxes are placed randomly on the filter area. Given this random character, the highest achievable fractions can vary slightly, also depending on how many tries the algorithm was allowed to perform to find a valid solution. The implemented algorithm sets the random number generator to a fixed seed prior to calculation to yield the same random pattern for each run (Figure 2D).

iv. Random layout on a quarter of the filter with 5, 10 or 20 boxes. Same as iii), but box placement is restricted to only a quarter of the filter (Figure 2A).

In all box selection approaches, the size of the (square) boxes is adjusted so that the desired fraction of filter area is covered, without having the individual boxes overlap or range over the filter perimeter. The maximum achievable fraction of filter to be covered is summarized in Table 2 (More details about box placement and the link to the code for interactive visualization can be found in SI chapter 1).

TABLE 2

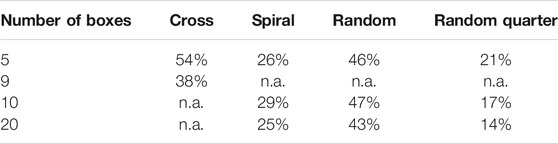
TABLE 2. Highest achievable filter coverage for the implemented patterns. By its pattern, the cross layout is only feasible with five or 9 boxes (3 or five boxes across, respectively). The other patterns were arbitrarily set to have either 5, 10 or 20 boxes.

Figure 3 shows a graphic user interface (gui) to visualize the implemented methods on real samples, measured by GEPARD. All the subsampling methods in Figure 3 are configured to select 10% of the sample i.e., 10% of the particles are measured by the “random” and the “size bin” selection, whereas 10% of the filter area is covered by the respective box selection methods. The gui allows adjusting the measured fraction of each method, as well as the number of boxes for the box sampling methods. Furthermore, the loaded sample can be rotated about a given angle. A text box above the filter scheme summarizes sample details (particle count, MP percentage) and displays the results from the respective subsampling method.

FIGURE 3

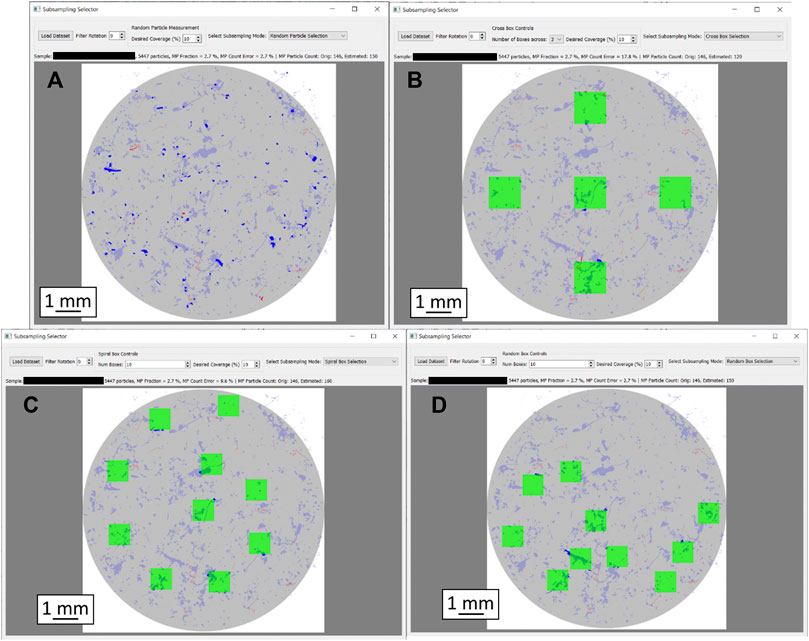
FIGURE 3. Graphic representation of the particle distribution heterogeneity as well as different subsampling approaches with 10% filter coverage each. Filter diameter is 10 mm in each case. (A): Random subsampling, (B): Box selection, cross layout, (C): Box selection, spiral layout, (D): Box selection, random layout. MP particles are shown in red, others in blue. Particles missed by the respective subsampling method are displayed in pale colors; only the particles in strong colors were captured.

Results and Discussion

Particle-Based Subsampling

At first, we investigated the subsampling-error (%) as a function of the measured fraction of particles (%) for the four respective sample categories (Figure 4), see SI chapter “Selected Images of Filters” for example images. We chose grouping the samples by their environmental origin because a sample’s origin is always known. Sorting samples into categories allows deduction of parameters influencing subsampling efficiency and, vice versa, allows estimating subsampling efficiency if a sample’s category was known. Hence, any correlation between environmental compartment and subsampling performance would allow for a better planning of the subsampling strategy without any further sample characterization. The averaged particle numbers per filter are given in the plot titles for each category, as well as the average MP percentage within these particles. Each data point in Figure 4 represents the average over all filters from the respective group of sample types (number of filters is given in plot title), where each filter was evaluated 10 times. The resulting subsampling-error exponentially decreases with increasing measured fraction and approaches 0 at 100% (note the logarithmic x-axis in Figure 4). Comparing the two different particle based subsampling methods shows that sorting particles into size bins (Figure 4, green) or not (Figure 4, orange) does not seem to have a systematic advantage across sample types.

FIGURE 4

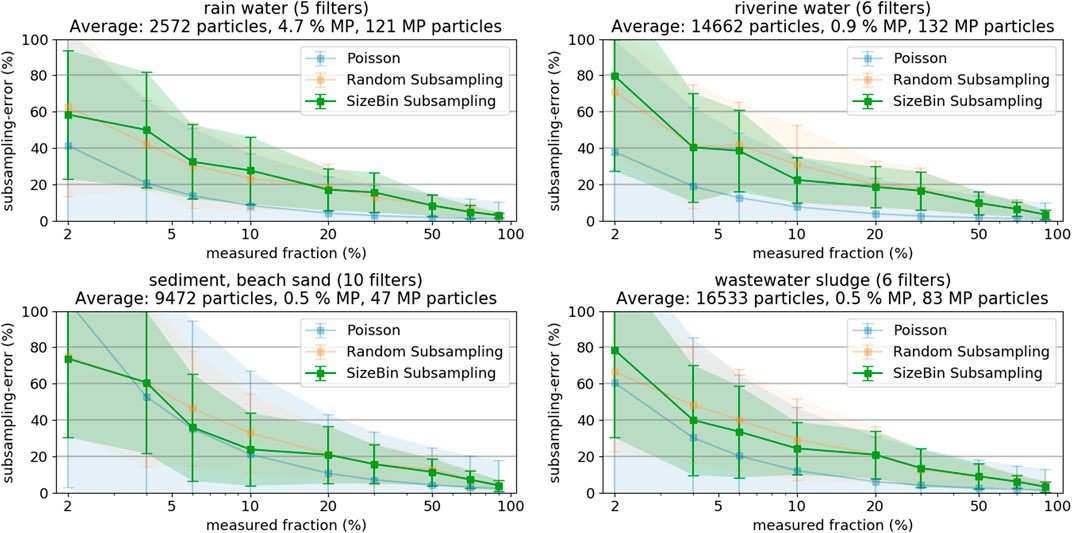
FIGURE 4. Subsampling-errors and their standard deviation of Random and SizeBin Subsampling, as derived from the different sample types (rainwater, river water, sediment, and sludge). As reference, the theoretical subsampling-error derived from the Poisson distribution.

The results illustrate that measuring only small filter fractions (both in terms of particle count or covered filter area) can lead to large counting errors. Measuring less than 5% of the entire particle population leads to errors exceeding 50%. Even worse, also the error margins increase with decreasing fraction measured in the plots in Figure 4. For example, at 5% measured fraction, the subsampling-error could be 20% or 80%. This large range of potential errors of a particular filter demonstrates that measuring such small fractions does not allow a sensible extrapolation of MP occurrences.

Comparing the results from the different compartments shows that the subsampling-errors are generally lower when the sample has more particles (i.e., higher number of particles is measured at a given fraction) or the sample has a higher content of MP particles. Especially the MP content is critical: The high MP content of the rainwater samples compensates the low particle count (at 10%, only about 300 particles are measured!) and the subsampling-errors are comparable to the sludge samples with a substantially higher particle count (at 10%, about 1,700 particles have to be measured) but low MP content.

Reliably predicting magnitude and standard deviation of the subsampling-error is a complicated task. Anger et al. used the normal distribution to estimate the number of particles to achieve a certain error, but applying the formula requires knowing MP fraction and the prediction interval (Anger et al., 2018). Karlsson et al. used the Poisson distribution to model the probability density functions of MP occurrence observations (Karlsson et al., 2020). The Poisson distribution is better suitable for smaller sample sizes and, for application to the present study results, only requires an estimate of the MP fraction (mean equals variance in the Poisson distribution). Figure 4 also shows the theoretically expected errors and error margins for the Poisson distribution, assuming the average MP count indicated in the plot titles. The agreement of theoretical and experimental subsampling-errors is good for the samples from sediment and beach sand, having the lowest absolute number of MP particles. However, the Poisson distribution more and more underestimates the subsampling-error with increasing number of MP particles. A more in-depth statistical discussion of the topic should be the scope of a separate study.

The estimation of the present MP content on a particular filter is difficult, but vital for the determination of the minimum subsampling fraction to measure. Based on the divers set of different sample types and applying the random particle subsampling, we found, that if we accept a maximum subsampling-error of 20%, the minimum fraction of particles to measure is either 50% of all particles, or a total of 7,000 particles (Figure 5). These thresholds are valid even for MP fractions approaching as low values as 0.1%. Note, the set of filters herein analyzed was characterized with relatively low total particle counts (maximum of 33,000), which hinders applying our findings to larger filters with substantially higher particle counts. These results furthermore show decreasing subsampling-errors with increasing MP content. This, in turn, highlights the tremendous importance of effective sample purification measures to increase the MP fraction. As a result, not only analysis times shorten by reducing the total number of particles to consider, but also the extrapolation of results becomes more reliable when applying subsampling methods.

FIGURE 5

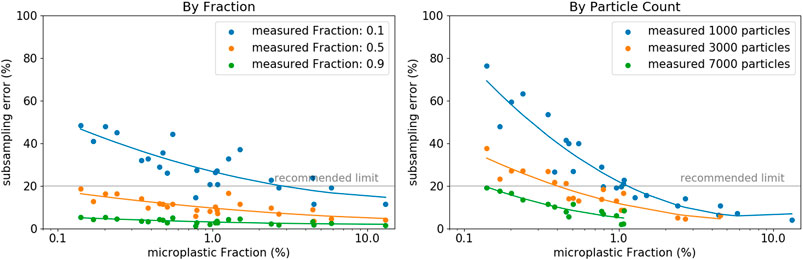
FIGURE 5. Compilation of the individual errors of each sample (each representing an average of 10 iterations per sample) as a function of the MP fraction with a color-coding representing (A) the measured fraction of particles or (B) a distinct particle count, respectively (random particle subsampling).

Measuring at least 5,000 particles per filter might be a realistic target for scientific purposes, but might also be impractical for monitoring applications with substantially higher sample counts. Measurement times can vary greatly depending on the exact parameters for optical scan and spectroscopic measurement. Our Raman microspectroscopy approach would require approximately 6 to 8 h for such a measurement, including optical scan (1–3 h), particle detection (several minutes) and spectroscopic measurement (approximately 5 h, a more comprehensive review of commonly used analysis times for Raman microspectroscopy is given by Anger et al. (2018)). The particle-based methods allow exploiting information from the optical microscope image to decrease the subsampling-errors at very low measured fractions. The image of the filter not only allows to precisely count and locate the particles, but also to analyze each particle in terms of its characteristics regarding shape, color, size and texture. A classifier that allows distinguishing MP from non-MP particles (with a certain level of confidence) based on these characteristics can be trained by running a feature extraction on a large number of particles of known type (i.e., MP and non-MP, respectively). This “artificial” up-concentration of MP particles post purification reduces the error-margins in subsampling and is especially useful when only low percentages of particles can be measured. Procedures for the classification of particles from microscopy can be found throughout literature and give valuable information about what kind of particle features to exploit (Xu et al., 1997; Xu et al., 2018; Peng and Kirk, 1998). Developing a machine-learning model for effective MP classification from microscopy images goes beyond the scope of this manuscript, due to the complexity of such an endeavor, especially due to the low content of MP particles i.e., the highly imbalanced datasets (Batista et al., 2004; Wei and Dunbrack 2013). Instead, we decided to assess the final reduction in subsampling-errors, given a classifier with a certain accuracy score would exist. That helps deciding on whether to actually start the efforts of developing a real classifier. As our datasets where already fully analyzed, a dummy classifier can be readily set up yielding any desired score from 0.5 (i.e., no actual knowledge, sampling is completely random) to 1.0 (i.e., perfect classifier). Three dummy classifiers with scores of 0.6, 0.7, and 0.8 were tested, respectively. The concept is to use the classifier to extract a subsample of all particles, which will have a higher MP fraction than the original set of particles. As discussed above, a higher fraction of MP has the highest potential to increase subsampling accuracy. Then, the desired number of particles is chosen on a random base from the subset with increased MP fraction. Details about the dummy classifier and the exact calculations can be found in SI chapter “Details on Trained Random Particle Subsampling”. Figure 6 shows the results of the three classifiers, as compared to the purely random particle subsampling.

FIGURE 6

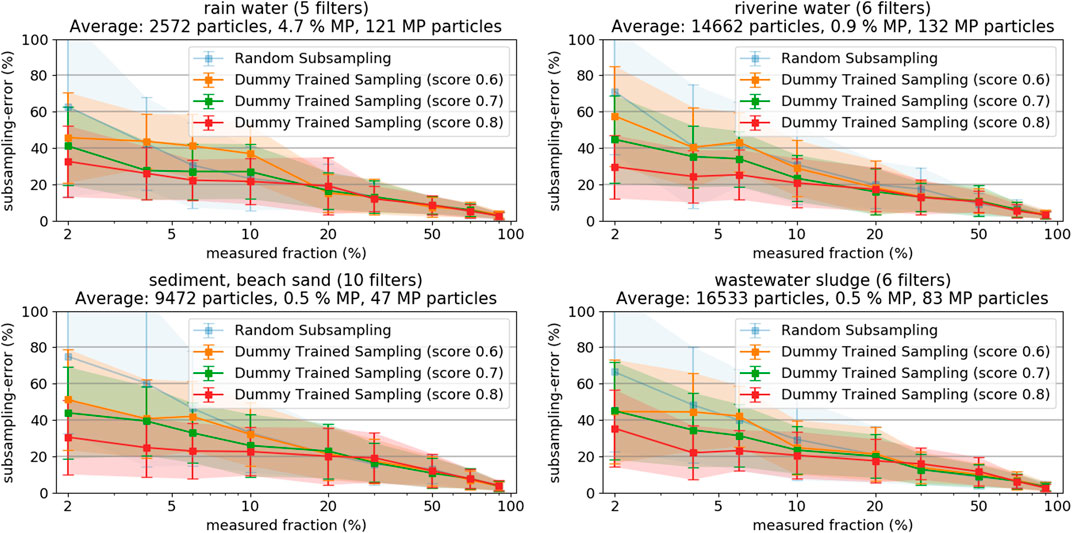
FIGURE 6. Resulting subsampling-errors and their standard deviation from random sampling based on trained classifiers with different scoring, as derived from samples from rainwater, river water, sediment, and sludge, respectively.

The subsampling-errors at low measured fractions decrease significantly when the score of the used classifier increases. The results clearly show that the application of a classifier substantially decreases the very high subsampling-errors below 10% measured fraction, even if their classification score is not higher than 0.6 to 0.8. The effect gets less pronounced at higher measured fractions wherefore it is most sensible to apply the methods if the measured fractions are lower than 10%. It is important to keep in mind that the final particle assignment is done according to the results of the spectroscopy measurement, regardless of the used classifier’s initial guess. Subsampling based on a classifier, however, complicates the step of extrapolation as the sample measured is no longer a random representative of the statistical universe of the filter. Refer to SI chapter 5 for more details on the calculations. The obtained findings are good reason for engaging in development of a real classifier suitable for MP classification on LM images. However, also other techniques, such as particle staining with fluorescent dyes, could be exploited for an according pre-selection of a subset with increased MP content (Shim et al., 2016).

Box-Based Subsampling

A closer investigation on distribution of the particles on the filters is necessary before reviewing the box-based subsampling method. The patchy and inhomogeneous distribution of the particles on the filter exemplifies the difficulty to design a pattern for a box selection subsampling (Figure 3, MP particles in red, others in blue). Analyzing the impact of particle distribution heterogeneity on the subsampling-error of the box-placement methods requires quantification of the heterogeneity, which is a difficult endeavor. Comparable literature studies are scarce but, fortunately, a recent study investigated the distribution of particles on filters (Thaysen et al., 2020). However, only examples from artificially produced model samples were included. They proposed plotting particle count as a function of particle distance to filter center to observe particle distribution patterns. They exhibited “starburst” particle distributions with highest particle density around the filter center. To compare our results of real environmental samples to their results we did the same calculations for filters from different environmental compartments. However, we converted “particle count” into “particle density”. Particle density is obtained by dividing particle count by the area of the filter section that is represented by the respective distances (intuitively, the section from 1 to 2 mm away from filter center is smaller than the section from 4 to 5 mm). Thereby, the differences in area of the filter sections is taken into account and patterns emerge more clearly (the original plots with particle count as function of distance from filter center (i.e., without correction for filter increasing area of filter sections) can be found in supporting information Supplementary Figure S1). However, the distance from the filter center distribution alone does not fully capture particle distribution inhomogeneity. For instance, the method would be insensitive to particles distributed only on one half, or quarter, of the filter. To overcome this potential error we developed and implemented an orthogonal approach to calculate the “average particle patchiness” value. The approach entails dividing the filter area in cells (e.g., 50 × 50), and calculating the number of particles in each cell. The average particle patchiness is then obtained by dividing standard deviation of the particle number per cell by its mean value. Supplementary Figure S2 in the SI shows example images of filters with low, medium and high particle patchiness and the respective (increasing) values.

In Figure 7, the filters are grouped again according to their environmental origin. Again, knowing if there was any correlation between particle distribution homogeneity and sample compartment would be useful (see SI chapter “Selected Images of Filters” for example images). In case of the rainwater filters, particle density on the filters peaks at around 5 mm, indicating a ring formation of particles at the perimeter of the filter (refer to Supplementary Figure S3); inhomogeneous particle distribution is also indicated by the high patchiness value of about 1.5. The samples from all other compartments show a similar pattern with almost constant particle density from center to the border of the filter, where particle density eventually decreases (refer to Supplementary Figures 4 - 6). The analyzed examples did not reveal any “starburst” pattern as to be expected from model samples (Thaysen et al., 2020), but drawing any conclusions is difficult, without taking into account details about sample workup and filtration procedures (Merck, 2018). Conversely, observing the averaged particle counts and the corresponding patchiness values indicates a correlation. Higher overall particle counts lead to a more homogeneous distribution of the particles on the filter. In fact, the observed patchiness of all investigated samples correlates well with the particle count, as shown in the left panel of Figure 8. It is important not to misunderstand that finding! The goal should not be to maximize the absolute particle count, but to increase the number of MP particles on a filter. The right panel of Figure 8 shows that the correlation between patchiness and particle count is the same if only MP particles on the filter are considered. The trend is the same, although the absolute values of the patchiness increase substantially. Refer to Supplementary Figure S2 in the SI for a visualization of different levels of patchiness.

FIGURE 7

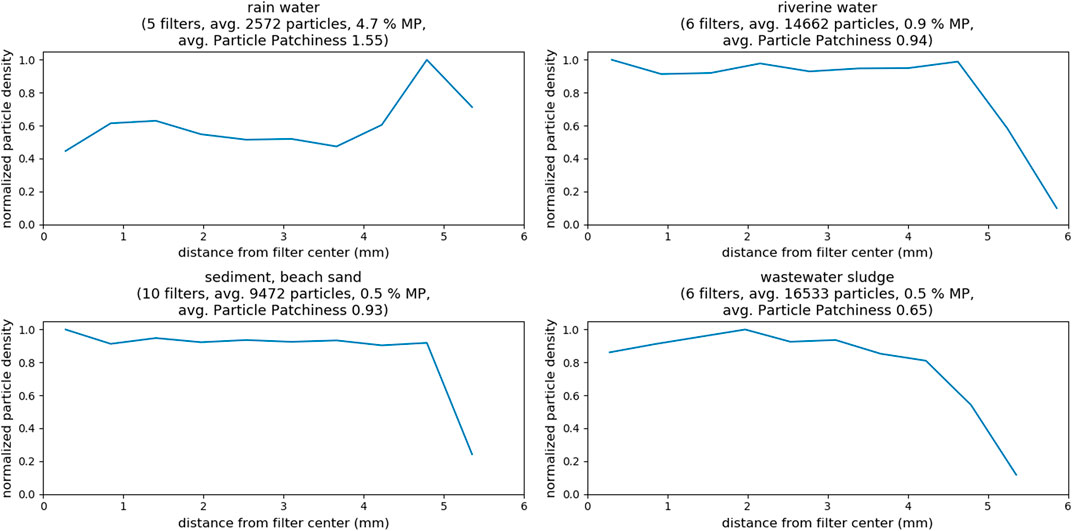
FIGURE 7. Total particle density as function of distance from filter center for samples of different compartments, as well as determined particle patchiness. All filtrations were done on 10 × 10 mm silicon filters.

FIGURE 8

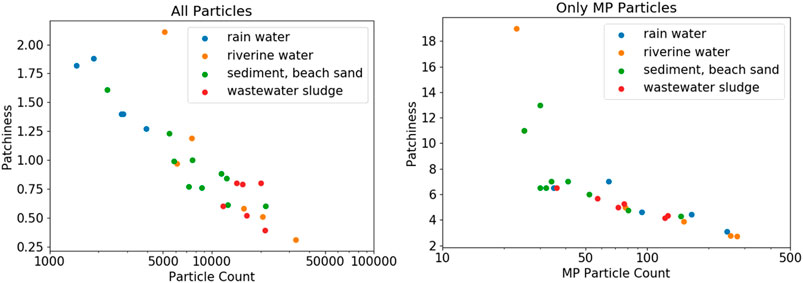
FIGURE 8. Particle patchiness as a function of total particle count and MP particle count, respectively. Note the logarithmic scale of the particle count. The patchiness is generally lower at higher particle counts.

Reviewing the subsampling-errors of the box subsampling methods, our investigations showed that the obtained subsampling-errors are very similar for the individual layouts when applied to the filters grouped according to their environmental origin (refer to Supplementary Figure S7–Supplementary Figure S10). The number of boxes to create the individual layouts does not seem to have a notable effect, although the cross layout shows slightly lower errors when using five, instead of three boxes across. Only in case of the rainwater samples with low particle counts and inhomogeneous particle distribution (resulting in many empty spaces on the filter i.e., high patchiness), the errors from box measurement subsampling exceed the errors from the random particle subsampling. Otherwise, the observed subsampling is dominated by the counting error, rather than an additional error resulting from inhomogeneous particle distribution.

Figure 9 shows the subsampling-error of the box-placement methods when sorting the filters into categories with different particle counts. Including the random particle subsampling-error, which is not affected by particle patchiness, allows distinguishing the pure counting error from errors resulting from inhomogeneous particle distribution on the filter. In case of very low particle numbers (≤2000) the subsampling-error from the box-based methods is substantially higher than for the random particle subsampling, which indicates an additional contribution of particle distribution inhomogeneity to the subsampling-error. At higher particle counts, the subsampling-errors from random particle subsampling and the box-placement methods come closer together, indicating a decreasing influence of the particle distribution inhomogeneity. At around 5,000 particles (corresponding to a patchiness of approximately 1.0, see Figure 8) the box-based sampling methods do not perform worse than the random particle subsampling.

FIGURE 9

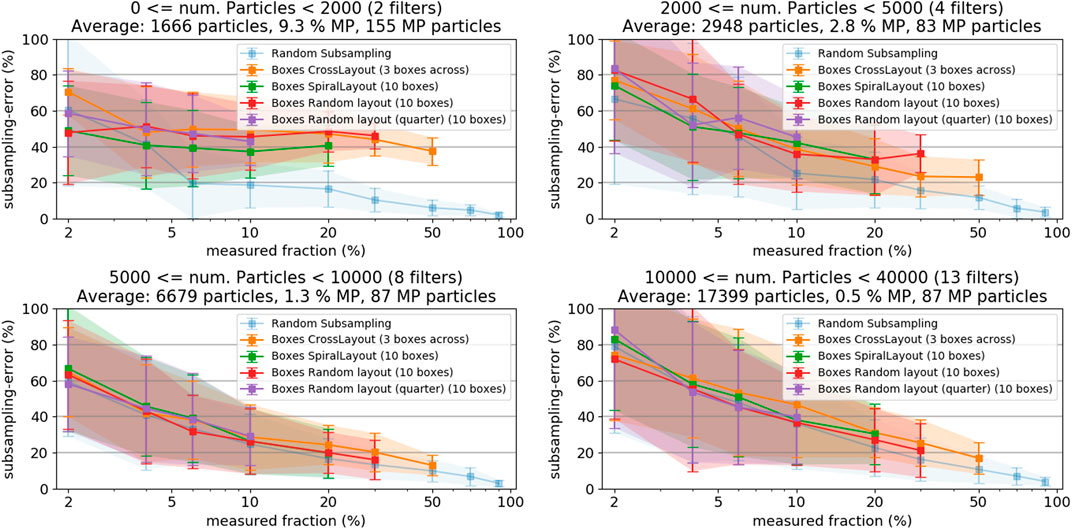
FIGURE 9. Subsampling-error of the box placement methods for filters with low (A) and high (B) particle patchiness, respectively. Both plots also show the random particle subsampling method, representing the count error, as reference.

In order to keep the subsampling-error and its deviation within one sigma below a 20% error margin, the covered area of the filter should be at least 50%. A 50% filter area coverage could only be fully realized with the cross layout with three boxes across and, near enough, the random box layout (with 47% coverage at 10 boxes, Table 2). In contrast to the particle-based subsampling, the box placement methods do not bear opportunities for exploiting machine-learning methods to increase accuracy at low measured fractions.

Counting all MP vs. Counting Particular MP Types

To simplify the quantitative assessment, herein only the integral MP particle numbers were considered without discrimination into different polymer types or morphological features. Most studies, however, require information of MP species such as chemical classification, color, size and shape. There are no standard categorization methods in place as it depends on the research question and the precise analytical tasks chosen. However, the issue shall be addressed with some general reflections.

Our study demonstrated the occurrence of high subsampling-errors and high error margins when measuring low fractions of particles on a filter. As a differentiation of different particle types would decrease the individual particle numbers, the subsampling-errors would increase accordingly. In other words, if particle types have to be distinguished, the overall number of particles to measure has to be increased. Thus, predicting which MP particle classes are present in a sample results in even larger uncertainties than estimating the integral MP content. A general recommendation about required particle numbers cannot be reliably given for such cases. A practical approach should entail measuring a certain fraction of all particles, counting the particles in all categories of interest and deciding if more particles need to be measured. As a consequence, already reducing the initial sample volumes prior to the purification steps can limit the final robustness of the results i.e., when yielding to small numbers of the target particles. Treated sample volumes should therefore be generously calculated. Karlsson et al. discussed how many particles have to be measured for having a statistically robust number (Karlsson et al., 2020). Their study concluded a reasonable number would be of about 30 particles per class. This is in agreement with the results of our analysis that revealed an error of about 20% (Figure 4) when having measured about 30 MP particles. Nevertheless, exceptions have to be made for “very rare” categories.

Conclusion and Outlook

Spectroscopic particle measurements are of high importance when it comes to MP analysis in environmental samples but need to be sped up to be established as monitoring tools. We compared the performance of different subsampling approaches, based on two different method categories: 1) particle-based methods and 2) measure box placement methods on 27 environmental samples from different compartments, such as rainwater, river water, sediment and wastewater sludge.

The results can be summarized in three general findings. First, none of the tested subsampling methods was identified to clearly outperform the others. The dependency of the subsampling-errors on the fraction measured was very similar for all methods; differences could only be seen in edge scenarios, as for instance in the case of filters with relatively low particle counts and inhomogeneous particle distribution on the filter. There, the particle-based subsampling proved to be more accurate than the box-based methods. In the majority of samples however, the observed subsampling-error was due to the counting error (i.e., extrapolating from a low number of measured particles) and particle distribution inhomogeneity is negligible.

Second, the magnitude of the averaged subsampling-error easily exceeded 50% if only 5% or less of the filter was measured. More critically, the standard deviation of the subsampling-error strongly increases when decreasing the measured fraction. If reliable particle counts with an error of less than 20% are required, the measured fraction should be at least 50% or, in the case of particle-based subsampling, at least 7,000 particles. However, if exact counts of particular types of MP particles are of interest, the measured fraction would have to be increased even further, thus reducing the time saving from the subsampling. It might be advisable to measure the entire filter in these cases.

Third, the best way to increase accuracy at low particle counts is to increase the fraction of MP particles in the sample. This can be done by further optimization of sample preprocessing steps or by implementing methods to identify possible MP particles prior to spectroscopic measurement (by specifically trained classification models or fluorescent staining). That finding seems trivial, but is important to keep in mind when designing workflows for workup and analysis of certain sample types. If only qualitative results are required (i.e., are MP particles present or not), higher error margins can be tolerated. Vice versa, if robust particle numbers are required, sample preprocessing should be optimized or, if not possible, higher fractions of the sample have to be measured.

To increase the validity of the herein gathered results to a larger diversity of filters, especially with higher particle counts, we encourage scientists in the field to critically reassess their measurements similarly as described here. Deeper statistical considerations would be beneficial for underpinning the observed effects.

The decision on the most appropriate subsampling strategy for a fast and proper quantification of specific objects from different environmental compartments is important for several scientific disciplines, going far beyond microplastic research. Only one example would be the microscopic quantification of specific prokaryotic groups via phylogenetic staining of cells e.g., by Fluorescence in situ hybridization (FISH). Therefore, we also understand this study as a general stimulus for a more extensive and interdisciplinary research on statistically relevant counting of small and less abundant objects in the environment.

Data Availability Statement

The datasets and calculations presented in this study can be found in online repositories. The repositories can be found under: https://gitlab.ipfdd.de/Brandt/subsampling.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This research was funded by the projects MicroCatch_Balt (03F0788A), PLASTRAT (02WPL1446 I) and PLAWES (03F0789A) supported by the Federal Ministry of Education and Research (BMBF Germany) and the BONUS MICROPOLL project supported by BONUS (Art 185), funded jointly by the European Union and BMBF (03F0775A).

Conflict of Interest

The authors declare that there the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Robin Lenz, Dr. Alexander Tagg and Juliana Ivar do Sul (IOW), Dr. Sarmite Kernchen, Dr. Martin Löder, and Prof. Christian Laforsch (University of Bayreuth), as well as Annett Mundane, Natalie Wick, and Prof. Christian Schaum (Universität der Bundeswehr München) for obtaining, treating and providing the samples.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2020.579676/full#supplementary-material.

References

Anger, P. M., Esch, E., Baumann, T., Elsner, M., Niessner, R., Ivleva, N. P., et al. (2018). Raman microspectroscopy as a tool for microplastic particle analysis. TrAC Trends Anal. Chem. 109, 214–226. doi:10.1016/j.trac.2018.10.010

CrossRef Full Text | Google Scholar

Batista, G. E. A. P. A., Prati, R. C., and Monard, M. C. (2004). A study of the behavior of several methods for balancing machine learning training data. ACM SIGKDD Explor. Newsl. 6, 20–29. doi:10.1145/1007730.1007735

CrossRef Full Text | Google Scholar

Bergmann, M., Wirzberger, V., Krumpen, T., Lorenz, C., Primpke, S., Tekman, M. B., et al. (2017). High quantities of microplastic in arctic deep-sea sediments from the HAUSGARTEN observatory. Environ. Sci. Technol. 51, 11000–11010. doi:10.1021/acs.est.7b03331

PubMed Abstract | CrossRef Full Text | Google Scholar

Borrelle, S. B., Ringma, J., Law, K. L., Monnahan, C. C., Lebreton, L., McGivern, A., et al. (2020). Predicted growth in plastic waste exceeds efforts to mitigate plastic pollution, Science. 369: 1515–1518. doi:10.1126/science.aba3656

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandon, J. A., Jones, W., and Ohman, M. D. (2019). Multidecadal increase in plastic particles in coastal ocean sediments. Sci. Adv. 5, eaax0587. doi:10.1126/sciadv.aax0587

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandt, J., Bittrich, L., Fischer, F., Kanaki, E., Tagg, A., Lenz, R., et al. (2020). High-throughput analyses of microplastic samples using fourier transform infrared and Raman spectrometry. Appl. Spectrosc. 74 (9), 1185–1197. doi:10.1177/0003702820932926

PubMed Abstract | CrossRef Full Text | Google Scholar

Browne, M. A., Galloway, T. S., and Thompson, R. C. (2010). Spatial patterns of plastic debris along estuarine shorelines. Environ. Sci. Technol. 44, 3404–3409. doi:10.1021/es903784e

PubMed Abstract | CrossRef Full Text | Google Scholar

Buffle, J., and Leppard, G. G. (1995). Characterization of aquatic colloids and macromolecules. 2. Key role of physical structures on analytical results. Environ. Sci. Technol. 29, 2176–2184. doi:10.1021/es00009a005

PubMed Abstract | CrossRef Full Text | Google Scholar

Chaudhuri, B. B. (1994). How to choose a representative subset from a set of data in multi-dimensional space. Pattern Recogn. Lett. 15, 893–899. doi:10.1016/0167-8655(94)90151-1

CrossRef Full Text | Google Scholar

Claessens, M., Van Cauwenberghe, L., Vandegehuchte, M. B., and Janssen, C. R. (2013). New techniques for the detection of microplastics in sediments and field collected organisms. Mar. Pollut. Bull. 70, 227–233. doi:10.1016/j.marpolbul.2013.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Daszykowski, M., Walczak, B., and Massart, D. L. (2002). Representative subset selection. Anal. Chim. Acta. 468, 91–103. doi:10.1016/S0003-2670(02)00651-7

CrossRef Full Text | Google Scholar

Dierkes, G., Lauschke, T., Becher, S., Schumacher, H., Földi, C., and Ternes, T. (2019). Quantification of microplastics in environmental samples via pressurized liqudslbid extraction and pyrolysis-gas chromatography. Anal. Bioanal. Chem. 411, 6959–6968. doi:10.1007/s00216-019-02066-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Duemichen, E., Braun, U., Senz, R., Fabian, G., and Sturm, H. (2014). Assessment of a new method for the analysis of decomposition gases of polymers by a combining thermogravimetric solid-phase extraction and thermal desorption gas chromatography mass spectrometry. J. Chromatogr. A. 1354, 117–128. doi:10.1016/j.chroma.2014.05.057

PubMed Abstract | CrossRef Full Text | Google Scholar

Dümichen, E., Barthel, A.-K., Braun, U., Bannick, C. G., Brand, K., Jekel, M., et al. (2015). Analysis of polyethylene microplastics in environmental samples, using a thermal decomposition method. Water Res. 85, 451–457. doi:10.1016/j.watres.2015.09.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Dümichen, E., Eisentraut, P., Bannick, C. G., Barthel, A.-K., Senz, R., Brau, U., et al. (2017). Fast identification of microplastics in complex environmental samples by a thermal degradation method. Chemosphere. 174, 572–584. doi:10.1016/j.chemosphere.2017.02.010

PubMed Abstract | CrossRef Full Text | Google Scholar

Enders, K., Käppler, A., Biniasch, O., Feldens, P., Stollberg, N., Lange, X., et al. (2019). Tracing microplastics in aquatic environments based on sediment analogies. Sci. Rep. 9, 15207. doi:10.1038/s41598-019-50508-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Enders, K., Lenz, R., Ivar do Sul, J. A., Tagg, A. S., and Labrenz, M. (2020). When every particle matters: a QuEChERS approach to extract microplastics from environmental samples. Methods. 7, 100784. doi:10.1016/j.mex.2020.100784

CrossRef Full Text | Google Scholar

Fischer, M., and Scholz-Böttcher, B. M. (2019). Microplastics analysis in environmental samples-recent pyrolysis-gas chromatography-mass spectrometry method improvements to increase the reliability of mass-related data. Anal. Methods. 11: 2489–2497. doi:10.1039/C9AY00600A

CrossRef Full Text | Google Scholar

Geyer, R., Jambeck, J. R., and Law, K. L. (2017). Production, use, and fate of all plastics ever made. Sci. Adv. 3, e1700782. doi:10.1126/sciadv.1700782

PubMed Abstract | CrossRef Full Text | Google Scholar

Halden, R. U. (2015). Epistemology of contaminants of emerging concern and literature meta-analysis. J. Hazard Mater. 282, 2–9. doi:10.1016/j.jhazmat.2014.08.074

PubMed Abstract | CrossRef Full Text | Google Scholar

Halle, A. T., Ladirat, L., Gendre, X., Goudouneche, D., Pusineri, C., Routaboul, C., et al. (2016). Understanding the fragmentation pattern of marine plastic debris. Environ. Sci. Technol. 50, 5668–5675. doi:10.1021/acs.est.6b00594

PubMed Abstract | CrossRef Full Text | Google Scholar

Logemann, J., Oveland, E., Bjorøy, Ø., Peters, W., Cojocariu, C., and Kögel, T. (2018). “Pyrolysis-GC-Orbitrap MS-a powerful analytical tool for identification and quantification of microplastics in a biological matrix”. (2018), application note 10643.

CrossRef Full Text | Google Scholar

Huppertsberg, S., and Knepper, T. P. (2018). Instrumental analysis of microplastics-benefits and challenges. Anal. Bioanal. Chem. 410, 6343–6352. doi:10.1007/s00216-018-1210-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Imhof, H. K., Laforsch, C., Wiesheu, A. C., Schmid, J., Anger, P. M., Niessner, R., et al. (2016). Pigments and plastic in limnetic ecosystems: a qualitative and quantitative study on microparticles of different size classes. Water Res. 98, 64–74. doi:10.1016/j.watres.2016.03.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Jambeck, J. R., Geyer, R., Wilcox, C., Siegler, T. R., Perryman, M., Andrady, A., et al. (2015). Marine pollution. Plastic waste inputs from land into the ocean. Science. 347, 768–771. doi:10.1126/science.1260352

PubMed Abstract | CrossRef Full Text | Google Scholar

Käppler, A., Fischer, D., Oberbeckmann, S., Schernewsk, G., Labrenz, M., Eichhorn, K.- J., et al. (2016). Analysis of environmental microplastics by vibrational microspectroscopy: FTIR, Raman or both?. Anal. Bioanal. Chem. 408, 8377–8391. doi:10.1007/s00216-016-9956-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Käppler, A., Fischer, M., Scholz-Böttcher, B. M., Oberbeckmann, S., Labrenz, M., Fischer, D., et al. (2018). Comparison of μ-ATR-FTIR spectroscopy and py-GCMS as identification tools for microplastic particles and fibers isolated from river sediments. Anal. Bioanal. Chem. 410, 5313–5327. doi:10.1007/s00216-018-1185-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Käppler, A., Windrich, F., Löder, M. G. J., Malanin, M., Fischer, D., Labrenz, M., et al. (2015). Identification of microplastics by FTIR and Raman microscopy: a novel silicon filter substrate opens the important spectral range below 1300 cm⁻¹ for FTIR transmission measurements. Anal. Bioanal. Chem. 407, 6791–6801. doi:10.1007/s00216-015-8850-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Karlsson, T. M., Kärrman, A., Rotander, A., and Hassellöv, M. (2020). Comparison between manta trawl and in situ pump filtration methods, and guidance for visual identification of microplastics in surface waters. Environ. Sci. Pollut. Res. Int. 27, 5559–5571. doi:10.1007/s11356-019-07274-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Lenz, R., Enders, K., Stedmon, C. A., Mackenzie, D. M., and Nielsen, T. G. (2015). A critical assessment of visual identification of marine microplastic using Raman spectroscopy for analysis improvement. Mar. Pollut. Bull. 100, 82–91. doi:10.1016/j.marpolbul.2015.09.026

PubMed Abstract | CrossRef Full Text | Google Scholar

Lenz, R., and Labrenz, M. (2018). Small microplastic sampling in water: development of an encapsulated filtration device. Water. 10, 1055. doi:10.3390/w10081055

CrossRef Full Text | Google Scholar

Liu, F., Olesen, K. B., Borregaard, A. R., and Vollertsen, J. (2019). Microplastics in urban and highway stormwater retention ponds. Sci. Total Environ. 671, 992–1000. doi:10.1016/j.scitotenv.2019.03.416

CrossRef Full Text | Google Scholar

Löder, M. G. J., Imhof, H. K., Ladehoff, M., Löschel, L. A., Lorenz, C., Mintenig, S., et al. (2017). Enzymatic purification of microplastics in environmental samples. Environ. Sci. Technol. 51, 14283–14292. doi:10.1021/acs.est.7b03055

PubMed Abstract | CrossRef Full Text | Google Scholar

Löder, M. G. J., Kuczera, M., Mintenig, S., Lorenz, C., and Gerdts, G. (2015). Focal plane array detector-based micro-Fourier-transform infrared imaging for the analysis of microplastics in environmental samples. Environ. Chem. 12, 563–581. doi:10.1071/en14205

CrossRef Full Text | Google Scholar

Lusher, A. L., Welden, N. A., Sobral, P., and Cole, M. (2017). Sampling, isolating and identifying microplastics ingested by fish and invertebrates. Anal. Methods. 9, 1346–1360. doi:10.1039/c6ay02415g

CrossRef Full Text | Google Scholar

Masó, M., Garcés, E., Pagès, F., and Camp, J. (2003). Drifting plastic debris as a potential vector for dispersing Harmful Algal Bloom (HAB) species. Sci. Mar. 67, 107–111. doi:10.3989/scimar.2003.67n1107

CrossRef Full Text | Google Scholar

Merck (2018). AD030 Air and fluid particle monitoring guide, Darstamdt, Germany: MerckKGaA.

CrossRef Full Text | Google Scholar

Mintenig, S. M., Kooi, M., Erich, M. W., Primpke, S., Redondo-Hasselerharm, P. E., Dekker, S. C., et al. (2020). A systems approach to understand microplastic occurrence and variability in Dutch riverine surface waters. Water Res. 176, 115723. doi:10.1016/j.watres.2020.115723

PubMed Abstract | CrossRef Full Text | Google Scholar

Murphy, F., Ewins, C., Carbonnier, F., and Quinn, B. (2016). Wastewater Treatment Works (WwTW) as a source of microplastics in the aquatic environment. Environ. Sci. Technol. 50, 5800–5808. doi:10.1021/acs.est.5b05416

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Z., and Kirk, T. B. (1998). Automatic wear-particle classification using neural networks. Tribol. Lett. 5, 249–257. doi:10.1023/A:1019126732337

CrossRef Full Text | Google Scholar

Poulain, M., Mercier, M. J., Brach, L., Martignac, M., Routaboul, C., Perez, E., et al. (2019). Small microplastics as a main contributor to plastic mass balance in the North Atlantic subtropical Gyre. Environ. Sci. Technol. 53, 1157–1164. doi:10.1021/acs.est.8b05458

PubMed Abstract | CrossRef Full Text | Google Scholar

Primpke, S., Christiansen, S. H., Cowger, W., Frond, H. D., Deshpande, A., Fischer, M., et al. (2020a). Critical assessment of analytical methods for the harmonized and cost-efficient analysis of microplastics. Appl. Spectrosc. 74, 1012–1047. doi:10.1177/0003702820921465

PubMed Abstract | CrossRef Full Text | Google Scholar

Primpke, S., Cross, R. K., Mintenig, S. M., Simon, M., Vianello, A., Gerdts, G., et al. (2020b). Toward the systematic identification of microplastics in the environment: evaluation of a new Independent software tool (siMPle) for spectroscopic analysis. Appl. Spectrosc. 74 (9), 1127–1138. doi:10.1177/0003702820917760

PubMed Abstract | CrossRef Full Text | Google Scholar

Primpke, S., Dias, P. A., and Gerdts, G. (2019). Automated identification and quantification of microfibres and microplastics. Anal. Methods. 11, 2138–2147. doi:10.1039/C9AY00126C

CrossRef Full Text | Google Scholar

Primpke, S., Lorenz, C., Rascher-Friesenhausen, R., and Gerdts, G. (2017). An automated approach for microplastics analysis using focal plane array (FPA) FTIR microscopy and image analysis. Anal. Methods. 9, 1499–1511. doi:10.1039/c6ay02476a

CrossRef Full Text | Google Scholar

Rodionova, O. Y., and Pomerantsev, A. L. (2008). Subset selection strategy. J. Chemom. 22, 674–685. doi:10.1002/cem.1103

CrossRef Full Text | Google Scholar

Schymanski, D., Goldbeck, C., Humpf, H. U., and Fürst, P. (2018). Analysis of microplastics in water by micro-Raman spectroscopy: release of plastic particles from different packaging into mineral water. Water Res. 129, 154–162. doi:10.1016/j.watres.2017.11.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Shim, W. J., Song, Y. K., Hong, S. H., and Jang, M. (2016). Identification and quantification of microplastics using Nile Red staining. Mar. Pollut. Bull. 113, 469–476. doi:10.1016/j.marpolbul.2016.10.049

PubMed Abstract | CrossRef Full Text | Google Scholar

Siegfried, M., Koelmans, A. A., Besseling, E., and Kroeze, C. (2017). Export of microplastics from land to sea. A modelling approach. Water Res. 127, 249–257. doi:10.1016/j.watres.2017.10.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Simon, M., van Alst, N., and Vollertsen, J. (2018). Quantification of microplastic mass and removal rates at wastewater treatment plants applying Focal Plane Array (FPA)-based Fourier Transform Infrared (FT-IR) imaging. Water Res. 142, 1–9. doi:10.1016/j.watres.2018.05.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Tagg, A. S., Sapp, M., Harrison, J. P., and Ojeda, J. J. (2015). Identification and quantification of microplastics in wastewater using focal plane array-based reflectance micro-FT-IR imaging. Anal. Chem. 87, 6032–6040. doi:10.1021/acs.analchem.5b00495

PubMed Abstract | CrossRef Full Text | Google Scholar

Thaysen, C., Munno, K., Hermabessiere, L., and Rochman, C. (2020). EXPRESS: toward Raman automation for microplastics: developing strategies for particle adhesion and filter subsampling. Appl. Spectrosc. 74, 000370282092290. doi:10.1177/0003702820922900

CrossRef Full Text | Google Scholar

Vianello, A., Boldrin, A., Guerriero, P., Moschino, V., Rella, R., Sturaro, A., et al. (2013). Microplastic particles in sediments of Lagoon of Venice, Italy: first observations on occurrence, spatial patterns and identification. Estuar. Coast. Shelf Sci. 130, 54–61. doi:10.1016/j.ecss.2013.03.022

CrossRef Full Text | Google Scholar

Wagner, J., Wang, Z. M., Ghosal, S., Rochman, C., Gassel, M., and Wall, S. (2017). Novel method for the extraction and identification of microplastics in ocean trawl and fish gut matrices. Anal. Methods. 9, 1479–1490. doi:10.1039/C6AY02396G

CrossRef Full Text | Google Scholar

Wei, Q., and Dunbrack, R. L. (2013). The role of balanced training and testing data sets for binary classifiers in bioinformatics. PLoS One. 8, e67863. doi:10.1371/journal.pone.0067863

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, B., Wen, G., Zhang, Z., and Chen, F. (2018). Wear particle classification using genetic programming evolved features. Lubric. Sci. 30, 229–246. 10.1002/ls.1411

CrossRef Full Text | Google Scholar

Xu, K., Luxmoore, A. R., and Deravi, F. (1997). Comparison of shape features for the classification of wear particles. Eng. Appl. Artif. Intell. 10, 485–493. doi:10.1016/S0952-1976(97)00017-1

CrossRef Full Text | Google Scholar

Zettler, E. R., Mincer, T. J., and Amaral-Zettler, L. A. (2013). Life in the “plastisphere”: microbial communities on plastic marine debris. Environ. Sci. Technol. 47, 7137–7146. doi:10.1021/es401288x

PubMed Abstract | CrossRef Full Text | Google Scholar