Fuzzy-based group decision-making approach utilizing a 2-tuple linguistic -rung orthopair set for the selection of optimal watershed system model

Watershed system models are tools used to study and simulate the behavior of watersheds, which are areas of land where all the water drains to a common outlet, typically a river, lake, or ocean. These models are essential for understanding and managing water resources, predicting flood events, and assessing the impact of land use and climate changes on the environment. Moreover, these advanced models should also help in making better decisions about the watersheds. This paper presents an integrated novel approach for decision-making in the selection of a watershed system model called decision-making trial and evaluation laboratory (DEMATEL)-multi-objective optimization based on the ratio analysis (MOORA) framework. The proposed method employs the 2-tuple linguistic $q$-rung orthopair fuzzy set (2TL$q$-ROFS) and enables the integration of new knowledge into models through dynamic data-sharing mechanisms. The weights of attributes are determined by the application of the 2TL$q$-ROF-DEMATEL technique, while the 2TL$q$-ROF-MOORA approach is employed to establish the ranking of the alternatives. The weighted power Muirhead mean (WPMM) aggregation operator is subsequently expanded to incorporate the 2TL$q$-ROF information for aggregating data. Finally, in order to assess the feasibility of the given methodology, an illustration is employed to choose the most suitable watershed system model. Moreover, we establish the soundness and feasibility of our methodology through a comprehensive comparison with several existing methodologies. Finally, findings of the study are reviewed, and potential directions for future research are discussed.

1 Introduction

In hydrology and environmental research, a watershed system model (WSM) is a complex and all-encompassing analytical framework. It is a useful resource for figuring out how water moves around a certain area, or watershed, where all the precipitation and runoff from that region eventually meets up and empties into a larger body of water. The purpose of this model is to simulate and anticipate how water will behave throughout the watershed given a variety of conditions. The WSM, at its heart, incorporates multiple critical components to provide a comprehensive analysis of the hydrological cycle in a specific area. Among these factors is meteorological information, such as rainfall and temperature patterns, which is crucial for comprehending the system’s water supply. Things like land use and land cover have a significant impact on how water moves through the landscape. Urban areas, farms, woods, and wetlands all have different impacts on water penetration, surface runoff, and pollution transfer. Because soil type and features effect water retention and infiltration rates, which in turn effect groundwater recharge and the water balance within the watershed, they are also accounted for in the model. Variations in runoff rates and possible flood-risk areas are directly influenced by the topography of the area, which includes slopes and elevation changes. Additionally, agriculture, industry, and urban expansion within the watershed can introduce toxins and change the natural flow of water. The WSM must take into account these human-caused issues because of their significant effects on water quality, habitat protection, and ecosystem health. The WSM is used primarily to anticipate and analyze the flow of water within the system under varying conditions. This data is crucial for numerous uses, such as flood forecasting and management, water resource administration, pollution avoidance, and urban development strategies. It equips politicians, environmental scientists, and other decision-makers (DMs) with the fundamental information they require to make educated decisions on land use, conservation, and infrastructure development. The WSM is essentially a potent instrument that connects a theoretical understanding of environmental processes with real-world decision-making.

It helps us safeguard and sustainably manage our essential water resources while reducing our overall environmental impact by modeling the interplay between natural and human-induced elements within a watershed. The WSM continues to be an invaluable tool in our fight to preserve the world’s water supplies and secure a sustainable future for future generations in the face of mounting environmental problems and climate change. Earth system modeling, a fundamental research approach in Earth system science, is considered as the second Copernican revolution. Modeling may be seen of as a synthesis strategy to formalizing existing knowledge in Earth system science. The only way to simulate the evolution and interactions between the spheres of the complex and massive Earth system is through numerical modeling. The qualitative understanding of the Earth system may be transformed into a quantitative understanding via numerical modeling. Models can reproduce the previous state of the Earth system and anticipate its future condition. Moreover, models can assist academics, stakeholders, and DMs in proposing responses in advance of potential future changes based on real and hypothetical circumstances. In this light, numerical modeling is a critical tool for attaining sustainability. The watershed is the fundamental unit of the land-surface system on Earth. To better understand complex watershed processes and to promote the implementation of integrated river basin management, scientists have developed what is known as a watershed model, which is an all-encompassing Earth system model at the basin measurement. Similar to Earth system modeling, watershed modeling necessitates the simulation of energy, water, and geochemical cycles within the natural system. A watershed model must also be adequately detailed because the size of watershed research is significantly smaller than that of the entire Earth system. A wide range of phenomena, which are typically not accounted for in global-scale models, need to be incorporated into a WSM. These include three-dimensional groundwater dynamics, variations in plant distribution, seasonal changes in land use, and patterns of water demand. A WSM should also contain human activity simulation to better understand human impacts on hydrologic and biological processes and to propose solutions for river basin management.

1.1 Motivation

Although multiple multi-attribute decision-making strategies are employed to handle different decision-making problems, there is no study in which 2TL$q$-ROF-DEMATEL and 2TL$q$-ROF-MOORA methods are utilized simultaneously to solve the problem related to WSM. To identify the linkages between attributes and priorities, as well as the impacts of the attributes on each other in order of priority, the DEMATEL approach can be utilized. The MOORA technique was used for rating the WSM because it takes into account all interactions between alternatives and targets as a whole. 2TL$q$-ROF-DEMATEL and 2TL$q$-ROF-MOORA techniques are utilized here since it is difficult to represent the interaction between attributes numerically. The purpose of this paper is to introduce a unique methodology, namely, the 2TL$q$-ROF-DEMATEL-MOORA method based on the WPMM aggregation operator (AO). Our suggested approach is capable of representing the language judgments of DMs. Additionally, the presence of a $q$-rung orthopair fuzzy set (FS) ($q$-ROFS) allows them to make judgments while taking into account the varying powers of $q$. As a result, the provided technique triumphs over the current frameworks.

The proposed study is driven by the following motivations:

1. The 2TL$q$-ROFS is a wider structure that integrates the notable properties of several structures accessible in the researchers’ prior work. Furthermore, the flexibility of 2TL$q$-ROFS to incorporate additional data allows decision-making specialists to use this structure to reflect their early judgments. The suggested model is a more generic framework for capturing uncertainty in multi-attribute group decision-making (MAGDM) situations due to its helpful qualities and flexible structure for representing qualitative and quantitative data. As a result of these characteristics, we want to create this model.

2. The WPMM AO is a versatile and effective decision-making tool. This operator is very useful for aggregating data in MAGDM problems. As a result of these assertions, we are inspired to utilize WPMM AO for the 2TL$q$-ROFS.

3. The DEMATEL-MOORA approach is capable of handling various MAGDM situations and provides a unique way to compute attribute weights and alternatives’ ranking values. This integrated method has received very little attention thus far. Apart from that, it has been noted to be a highly thorough, easy, and reliable way to determine the optimal choice in decision-making with the calculation of attribute weights. Nevertheless, this integrated method has not yet been expanded in the context of 2TL$q$-ROFS. As a result, we want to expand its use to 2TL$q$-ROFS.

1.2 Contribution

We begin our study by utilizing some fundamental WPMM AO for 2TL$q$-ROFS. Next, within the environment of 2TL$q$-ROFS, we develop an expanded MAGDM methodology based on the DEMATEL-MOORA method. Moreover, we use the 2TL$q$-ROFWPMM operator to aggregate all expert judgments to create a combined decision matrix. A numerical example is then used to demonstrate the effectiveness of the proposed method. We investigate the ranking outcomes by changing the value of the parameter $q$. A comparison study is used to assess the validity of the offered approach.

The contributions of this study are as follows:

• The objective of this study is to employ the WPMM AO methodology within the context of the 2TL$q$-ROFS framework. Our objective was accomplished by employing the WPMM AO methodology, with a specific focus on the 2TL$q$-ROFWPMM operator, and conducting an in-depth analysis of its characteristics.

• The subsequent objective is to formulate an enhanced DEMATEL-MOORA methodology in order to tackle the MAGDM problem. The DEMATEL-MOORA approach is implemented within the framework of 2TL$q$-ROFS, and the WPMM AO is employed for aggregation purposes. We intend to develop a 2TL$q$-ROF-DEMATEL-MOORA approach based on the generalized properties of 2TL$q$-ROFS. A graphic description of the major steps of the established approach is also provided. The suggested extension of the DEMATEL-MOORA approach can be used to solve complicated MAGDM issues.

• To show the efficacy of the proposed method, it is applied to the problem of choosing a WSM. In addition, we analyze how varying inputs affect the outcomes.

• We compare the proposed technique to other existing approaches in order to demonstrate the reliability of the proposed method.

1.3 Structure

The article is structured as follows: In Section 2, a brief literature review is provided. Section 3 goes through some fundamental notions and definitions of existing concepts. Based on the 2TL$q$-ROFWPMM operator, we describe the DEMATEL-MOORA technique for MAGDM using 2TL$q$-ROF information in Section 4. In Section 5, a numerical example is provided to demonstrate the efficiency and the benefits of the suggested technique. The impact of factors on ranking outcomes, a comparison study with existing methodologies are also explored. Section 6 has some conclusion remarks.

2 Literature review

In this section, we discuss about the literature review of $q$-ROFS, 2-tuple linguistic (2TL) representation model, PMM operator, DEMATEL method, and MOORA method.

2.1 $q$-rung orthopair fuzzy set

A key challenge is defining assessment values in decision-making due to unclear and unpredictable information. As a result, the FS was defined by Zadeh (1965). Later that year, FS extensions and FS-based MAGDM approaches were created (He and Wang, 2023; Denoeux, 2023; Al-shami and Mhemdi, 2023). However, FS only identifies the membership degree (MD) when representing uncertain information and completely ignores the non-membership degree (NMD). In order to characterize each element by two elements of MD $(\mu )$ and NMD $(\nu )$, Atanassov (1986) developed the notion of the intuitionistic FS (IFS). Since then, several researchers Namburu et al. (2023), Ihsan et al. (2023), Yue et al. (2023) have conducted in-depth research on the IFS. Yager (2013) proposed the Pythagorean FS (PFS) with $\mu +\nu \ge 1$ but ${\mu }^2+{\nu }^2\le 1$ to overcome the IFS’s limitation since $\mu +\nu \le 1$ is a constraint of the IFS. Following that, other authors Akram et al. (2023a), Saeed et al. (2023), Pan et al. (2023) modified the PFS. Furthermore, Yager (2013) defined the $q$-ROFS, which is superior to PFS and IFS in terms of information space representation and satisfies ${\mu }^q+{\nu }^q\le 1$ and $q\ge 1$. Compared to IFS and PFS, the $q$-ROFS is capable of relaxing restrictions more and dynamically defining the space of uncertain information. Hence, $q$-ROFS is more capable of handling uncertain information suitably and flexibly. Many researchers have been interested in the $q$-ROFS and have produced various beneficial results. At the evaluation stage, Guneri and Deveci (2023) proposed the $q$-ROFS-based EDAS method. That study offered a novel method for determining supplier selection in the defense industry that can be extended to many other industries. To evaluate the system’s quality under the interval-valued $q$-ROFS, Wan et al. (2023) designed a novel integrated group decision-making method. The design of their evaluation indices was determined by the characteristics of the hypertension follow-up system, which in turn represent the evaluation requirements of typical software applications and reflect the uniqueness of the system. The mass assignment of features based on bidirectional encoder representations using transformers and $q$-ROFS theory was utilized by Yin et al. [? ] to present a novel method for product ranking. In that study, the $q$-ROF generalized weighted Heronian mean operator was used to combine the $q$-ROFNs and rank the products. Arora et al. (2023) designed a novel TOPSIS plan to tackle the MAGDM problems in the context of $q$-ROF numbers. To evaluate the fuzziness of the $q$-ROFS, they suggested a new Entropy measure. Razzaque et al. (2023) developed the idea of $q$-ROF cosets of a $q$-ROF ideal and demonstrated that, in the scenario of particular binary operations, the collection of all $q$-ROF cosets of a $q$-ROF ideal forms a ring. They offered an analogue of the basic ring homomorphism theorem for $q$-rung orthopairs. Sarkar et al. (2023) proposed the idea of a weighted dual hesitant $q$-ROFS which helps DMs precisely assign different weights to different possible arguments. In that article, they investigated various operational principles for weighted dual hesitant $q$-ROFS using Hamacher t-norms and t-conorms as a combination of algebraic and Einstein operations.

2.2 2-Tuple linguistic representation model

It is common practice to consider multiple alternatives to a problem and pick the best one based on the results of these comparisons. MAGDM is a cutting-edge field of study in the field of management science. The ability to make decisions is crucial in many contexts. The majority of individuals are obliged to convey their opinions in language because qualitative attributes are subjective or because exact numerical data collection is expensive. Significant improvements have been achieved in a variety of fields, including business strategy planning, quality evaluation, investment strategy selection, and linguistic decision-making, which evaluates linguistic data as the values of linguistic variables. DMs can communicate their preferences for different options in real-world decision-making situations. This can be done through the use of linguistic phrases such as good, fair, or poor. By employing appropriate decision-making processes, DMs can then identify and choose the most optimal alternative. In the context of analyzing the viability of a company’s investment strategy, professionals may articulate their assessments by employing a set of seven linguistic phrases derived from the linguistic term set (LTS) S = {${\mathit{\pounds }}_0$: extremely poor, ${\mathit{\pounds }}_1$: poor, ${\mathit{\pounds }}_2$: slightly poor, ${\mathit{\pounds }}_3$: fair, ${\mathit{\pounds }}_4$: slightly good, ${\mathit{\pounds }}_5$: good, ${\mathit{\pounds }}_6$: extremely good}. If an expert judges the company’s profit performance to be slightly good, it may be displayed as {${\mathit{\pounds }}_4$}. The experts may have different evaluation values for the same problem in the actual decision-making problem due to the cognitive differences between them and the complexity of the decision-making environment. In the realm of mathematical sets, the symbols 0 and 1 are utilized to denote the absence or presence, respectively, of a certain entity. Conversely, when attempting to depict real-world phenomena, the depiction often entails a degree of uncertainty. The effective representation of assessment values throughout the decision-making process is a critical issue that needs resolution, as information often exhibits qualities of fuzziness and uncertainty. Herrera and Martinez (2001) proposed a 2TL representation approach which achieved advancements in information extraction. The core element of this construct comprises a verbal phrase and a numerical number and is grounded in the concept of symbolic translation.

Owing to its advanced linguistic information processing capability, the language model effectively mitigates the issues of data loss and misrepresentations that were prevalent in previous models of language. According to Herrera and Martinez, a 2TL information processing method can successfully prevent information loss and deformation. To deal with scenarios where linguistic labels are applied to given data, Akram et al. (2023b) created a novel decision-making technique based on the 2TL Fermatean FS. That study’s key objective was to explore and clarify the use of the ELECTRE II method for group decision-making in a 2TL Fermatean fuzzy context. They investigated and expanded the 2TL $q$-rung picture FS as a context for evaluating and ranking alternatives by the compromise solution. Akram et al. (2023c) came up with the idea of a 2TL $q$-rung picture FS because of how flexible $q$-rung picture FS is and how useful 2TL term sets are for managing qualitative data. Akram et al. (2023a) proposed a method for handling challenging $q$-ROF2TL set in MAGDM issues. In that study, the concepts of a 2TL set and complex $q$-ROFS were combined to present a complex $q$-ROF2TL set. In order to handle decision-making problems where the DMs are disposed to apply linguistic variables to represent assessment information, Jin et al. (2023) developed the 2TL preference relations, which are effective tools. Rao and Xiao (2023) proposed the generalized 2TL neutrosophic power Heronian mean operator, which combined the generalized Heronian mean operator and power average with 2TL neutrosophic set. For MAGDM, the generalized 2TL neutrosophic power Heronian mean operator was developed. To resolve MAGDM problems, Akram et al. (2023d) designed the extended MABAC approach. The study presented a comprehensive framework for the expression and computation of qualitative evaluation. This framework utilized a mix of $T$-spherical FS and 2TL representation. The concept of the complex interval-valued $q$-rung orthopair 2TL set was proposed by Zeng et al. (2022). This novel approach offers a robust solution for handling unstable and uncertain data in real-world decision-making contexts. They also investigated some of its essential characteristics and rules. Naz et al. (2022a) established the 2TL bipolar FS, a novel approach to handling uncertainty that combines a 2TL term into a bipolar FS. The 2TL bipolar FS is a more effective method for handling ambiguous and inaccurate information in a decision-making environment.

2.3 Power Muirhead mean aggregation operator

In the field of mathematical aggregation, the PMM operator is a strong synthesis of elegance and adaptability. Using its power parameter to add a dynamic twist on top of the classical Muirhead mean (MM), the PMM operator lets it naturally adapt to many situations. See it as a symphony conductor harmonizing individual parts to capture their interconnections and produce a balanced and subtle result. In multi-attribute decision-making, where complexity abounds and easily balances importance and correlation among inputs, this operator shines the most. The PMM operator creates a real masterpiece of mathematical creativity by combining the individual and group traits of data, transforming complex problems into clear, practical insights. Li et al. (2018) introduced new operators for aggregating PF information, including the PMM operator. These operators considered relationships between fused data and aggregated values, providing more information for multi-attribute decision-making. Linguistic $q$-rung orthopair fuzzy numbers were presented as a qualitative form of $q$-ROFNs able of flexible descriptions of a wider range of linguistic assessment data. Two AOs for aggregating assessment data the power average and MM were proposed by Liu and Liu (2019). Designed to handle linguistic $q$-ROFNs, a new MAGDM approach was developed using real-world scenarios to show its efficiency and superiority. Liu et al. (2019a) developed new AOs for aggregating single-valued neutrosophic information and applied them to MAGDM. While considering the correlation among input data, the proposed AOs removed the influence of inconvenient data. A new method for solving MAGDM problems was presented and a numerical example was given to show its simplicity and efficiency. They examined particular case studies and covered the fundamental characteristics of the AOs. Liu et al. (2019b) presented a strong mathematical tool for managing uncertain, inconsistent, and vague information, the $T$-spherical FS. The need for effective decision-making strategies for businesses, particularly for managers and experts, was emphasized by Mahmood et al. (2021). The study investigated the use of interval-valued linear Diophantine FS with the development of PMM and weighted PMM operators, and the advantages of the multi-attribute decision-making technique. Additionally, geometric interpretations and a comparative analysis were provided.

2.4 DEMATEL method

In order to more effectively boost the competency development of global managers, Wu and Lee (2007) created an efficient method combining fuzzy logic and the DEMATEL method. To evaluate the relationships between factors in different areas in an uncertain and fuzzy environment, the fuzzy DEMATEL approach is widely used. Zhang et al. (2023) developed a novel fuzzy DEMATEL approach based on alpha-level sets for managing fuzzy information, as well as recognizing experts’ hesitation from the qualitative context in an uncertain and fuzzy environment. Most modern DEMATEL approaches are only appropriate for small and simple systems, and they do not determine whether expert consensus has been reached. For achieving consensus in complex systems, Du and Shen (2023) proposed a group hierarchical DEMATEL approach. The decision-making process of the hierarchical DEMATEL approach was examined as it was expanded from individual decisions to group decisions. Based on a fuzzy DEMATEL approach, Priyanka et al. (2023) studied the critical challenges in selecting the best human resources practices for start-ups. Because the DEMATEL method on human assessments is inaccurate and subjective, the fuzzy DEMATEL approach was proposed to investigate the significance of identified challenges and the cause-effect relationships between them. Yilmaz et al. (2023) proposed the fuzzy DEMATEL approach to improve performance. The proposed approach evaluated and ranked the most important indicators for boosting an enterprise’s overall maintenance performance. Using a $T$-spherical fuzzy DEMATEL called TOP-DEMATEL, Ozdemirci et al. (2023) created a MAGDM model for assessing alternative social banking systems (with no interest charges). Komsiyah and Balqis (2023) used the DEMATEL approach to determine the weights of each criterion and the MABAC method to determine which industrial sub-districts are the best. The purpose of that paper was to develop a decision support system application for selecting industrial locations in Serang Regency by mathematical calculations using the hybrid DEMATEL and MABAC. Eti et al. (2023) investigated methods for reducing energy inflation in the healthcare industry. Both the AHP and the DEMATEL approaches have been used in the investigation in that context. The ideal criterion was the same for both the AHP and DEMATEL results since it provided information on the study’s coherence and reliability.

2.5 MOORA method

Several objectives are handled through multi-objective optimization, with each objective maintaining its units. It is suggested to use a ratio system’s internal mechanical solution, which generates dimensionless numbers. The ratio system makes it possible to use a second method called a Reference Point Theory, which makes use of the ratios in the ratio system. Brauers and Zavadskas (2012) were the creators of the general theory known as the MOORA method. Sevim and Kurtaran (2023) used MOORA, a MAGDM method based on ratio analysis, to evaluate Turkey’s performance in the field of health tourism and to show the current situation in the interest of improving the field. In that study, the MOORA-Ratio method and the MOORA-Reference Point method were combined. To choose the best alternatives, Kumar et al. (2023) applied the decision-making methods AHP and MOORA, which combined minimization and maximization attributes. AHP and MOORA have been merged and used in that study to optimize the outcomes. When selecting phase change materials, Wankhede et al. (2023) used the GRA, COPRAS, and MOORA approaches while considering the technical requirements of the materials. The failure mode and effects analysis method have some disadvantages, including incomplete prioritization and the lack of ability to assess the relative importance of risk factors in an uncertain environment. To solve these problems, Ghiaci and Ghoushchi (2023) developed a new integrated approach based on SWARA and MOORA in the field of PFS. Shahzadi et al. (2022) explored the intelligent manufacturing system, a framework that boosted productivity by integrating the logical aspects of manufacturing. The applicability of the MOORA method has been investigated in that paper to choose the intelligent manufacturing system utilizing Fermatean FS. For the contemporary era’s growing energy demand, a movement towards clean and natural energy sources is essential. Basaran and Tarhan (2022) used the MOORA approach, one of the MAGDM methods, to determine the best location for offshore wind turbines. Due to the Dombi generalized structure, the Dombi operators provide a versatile structure with their adjustable parameters. On $q$-ROFS, Aydemir and Yilmaz Gunduz (2020) built Dombi and prioritized aggregations. The MULTIMOORA method employed the suggested operators. Based on a numerical example, the proposed methods with new AOs were evaluated using the $q$ parameter of $q$-ROFS and the Dombi parameter.

2.6 Abbreviations and descriptions

Different abbreviations and their descriptions used in this article are given in Table 1.

Table 1

Table 1. Abbreviations and descriptions.

3 Review of fundamental concepts

To facilitate a better understanding of the subject matter, this section presents a concise summary of fundamental principles, encompassing the $q$-ROFS, the 2TL$q$-ROFS, and the WPMM operator.

Definition 1. (Yager, 2016) Let $L$ be a universal set. Objects with the structure of a $q$-ROFS can be characterized in Equations 1:

$T=\left\{⟨♭,\left(p\left(♭\right),l\left(♭\right)\right)⟩|♭\in L\right\},(1)$

in which $p(♭):L\to [\mathrm{0,1}]$ represents the MD and $l(♭):L\to [\mathrm{0,1}]$ represents the NMD of the factor $♭\in L$ to T, and for each $♭\in L$, $({(p(♭))}^q+{(l(♭))}^q)\le 1,q\ge 1$. $\upsilon (♭)=\sqrt{1-{(p(♭))}^q-{(l(♭))}^q}$ represents as indeterminacy degree. For convenience, $\mathfrak{t}=(p,l)$ is known as a $q$-ROFN.

Definition 2. (Naz et al., 2022a) Consider a LTS denoted as $\mathcal{S}$, which consists of terms ${\mathit{\pounds }}_t$ for $t$ ranging from 0 to $k$ with an odd cardinality. Let ${\mathit{\pounds }}_p(\vartheta ),{\mathit{\pounds }}_l(\vartheta )\in \mathcal{S}$, and $\wp (\vartheta ),\xi (\vartheta )\in [-0.5,0.5)$ such that $(({\mathit{\pounds }}_p(\vartheta ),\wp (\vartheta )),({\mathit{\pounds }}_l(\vartheta ),\xi (\vartheta )))$ is defined. The terms $({\mathit{\pounds }}_p(\vartheta ),\wp (\vartheta ))$ and $({\mathit{\pounds }}_l(\vartheta ),\xi (\vartheta ))$ denote the MD and NMD, respectively, using 2TL expressions. The 2TL$q$-ROFS can be defined in Equations 2:

$\aleph =\left\{⟨\vartheta ,\left(\left({\mathit{\pounds }}_p\left(\vartheta \right),\wp \left(\vartheta \right)\right),\left({\mathit{\pounds }}_l\left(\vartheta \right),\xi \left(\vartheta \right)\right)\right)⟩|\vartheta \in L\right\}(2)$

where $0\le {\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_p(\vartheta ),\wp (\vartheta ))\le k,0\le {\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_l(\vartheta ),\xi (\vartheta ))\le k$, and $0\le {({\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_p(\vartheta ),\wp (\vartheta )))}^q+{({\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_l(\vartheta ),\xi (\vartheta )))}^q\le k^q$.

Definition 3. (Naz et al., 2022a) Consider the 2TL$q$-ROFN denoted by $\aleph =(({\mathit{\pounds }}_p,\wp ),({\mathit{\pounds }}_l,\xi ))$. The score function $\mathcal{F}$ for a 2TL$q$-ROFN can be expressed as:

$\mathcal{F}\left(\aleph \right)=\mathrm{\Delta }\left(\frac{k}{2}\left(1+{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_p,\wp \right)}{k}\right)}^q-{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_l,\xi \right)}{k}\right)}^q\right)\right),{\mathrm{\Delta }}^{-1}\left(\mathcal{F}\left(\aleph \right)\right)\in \left[0,k\right],(3)$

and its accuracy function $\beth$ can be defined in Equations 4:

$\beth \left(\aleph \right)=\mathrm{\Delta }\left(k\left({\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_p,\wp \right)}{k}\right)}^q+{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_l,\xi \right)}{k}\right)}^q\right)\right),{\mathrm{\Delta }}^{-1}\left(\beth \left(\aleph \right)\right)\in \left[0,k\right].(4)$

Definition 4. (Naz et al., 2022a) Let ${\aleph }_1=(({\mathit{\pounds }}_{p_1},{\wp }_1),({\mathit{\pounds }}_{l_1},{\xi }_1))$ and ${\aleph }_2=(({\mathit{\pounds }}_{p_2},{\wp }_2),({\mathit{\pounds }}_{l_2},{\xi }_2))$ represent two 2TL$q$-ROFNs. The comparison between these two 2TL$q$-ROFNs can be conducted based on the following rules:

(1) If $\mathcal{F}({\aleph }_1)>\mathcal{F}({\aleph }_2)$, then ${\aleph }_1\succ {\aleph }_2$;

(2) If $\mathcal{F}({\aleph }_1)<\mathcal{F}({\aleph }_2)$, then ${\aleph }_1\prec {\aleph }_2$;

(3) If $\mathcal{F}({\aleph }_1)=\mathcal{F}({\aleph }_2)$, then

• If $\beth ({\aleph }_1)>\beth ({\aleph }_2)$, then ${\aleph }_1\succ {\aleph }_2$;

• If $\beth ({\aleph }_1)<\beth ({\aleph }_2)$, then ${\aleph }_1\prec {\aleph }_2$;

• If $\beth ({\aleph }_1)=\beth ({\aleph }_2)$, then ${\aleph }_1\sim {\aleph }_2$.

Definition 5. (Naz et al., 2022a) Let $\aleph =(({\mathit{\pounds }}_p,\wp ),({\mathit{\pounds }}_l,\xi ))$, ${\aleph }_1=(({\mathit{\pounds }}_{p_1},{\wp }_1),({\mathit{\pounds }}_{l_1},{\xi }_1))$, and ${\aleph }_2=(({\mathit{\pounds }}_{p_2},{\wp }_2),({\mathit{\pounds }}_{l_2},{\xi }_2))$ be three 2TL$q$-ROFNs, where $q\ge 1$, then.

1. ${\aleph }_1\oplus {\aleph }_2=\left(\begin{array}{c}\hfill \mathrm{\Delta }\left(k\sqrt[q]{1-\left(1-{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{p_1},{\wp }_1)}{k}\right)}^q\right)\left(1-{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{p_2},{\wp }_2)}{k}\right)}^q\right)}\right),\hfill \\ \mathrm{\Delta }\left(k\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{l_1},{\xi }_1)}{k}\right)\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{l_2},{\xi }_2)}{k}\right)\right)\end{array}\right)$;

2. ${\aleph }_1\otimes {\aleph }_2=\left(\begin{array}{c}\hfill \mathrm{\Delta }\left(k\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{p_1},{\wp }_1)}{k}\right)\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{p_2},{\wp }_2)}{k}\right)\right),\hfill \\ \mathrm{\Delta }\left(k\sqrt[q]{1-\left(1-{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{l_1},{\xi }_1)}{k}\right)}^q\right)\left(1-{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_{l_2},{\xi }_2)}{k}\right)}^q\right)}\right)\end{array}\right)$;

3. $\lambda \aleph =\left(\begin{array}{c}\hfill \mathrm{\Delta }\left(k\sqrt[q]{1-{\left(1-{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_p,\wp )}{k}\right)}^q\right)}^{\lambda }}\right),\mathrm{\Delta }\left(k{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_l,\xi )}{k}\right)}^{\lambda }\right)\hfill \end{array}\right),\lambda >0$;

4. ${\aleph }^{\lambda }=\left(\begin{array}{c}\hfill \mathrm{\Delta }\left(k{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_p,\wp )}{k}\right)}^{\lambda }\right),\mathrm{\Delta }\left(k\sqrt[q]{1-{\left(1-{\left(\frac{{\mathrm{\Delta }}^{-1}({\mathit{\pounds }}_l,\xi )}{k}\right)}^q\right)}^{\lambda }}\right)\hfill \end{array}\right),\lambda >0$.

Definition 6. (Naz et al., 2022a) Let ${\aleph }_1=(({\mathit{\pounds }}_{p_1},{\wp }_1),({\mathit{\pounds }}_{l_1},{\xi }_1))$ and ${\aleph }_2=(({\mathit{\pounds }}_{p_2},{\wp }_2),({\mathit{\pounds }}_{l_2},{\xi }_2))$ be two 2TL$q$-ROFNs. The 2TL$q$-ROF normalized Hamming distance can be described as:

$d\left({\aleph }_1,{\aleph }_2\right)=\mathrm{\Delta }\left(\frac{k}{2}\left(\begin{array}{c}\hfill \left|{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_{p_1},{\wp }_1\right)}{k}\right)}^q-{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_{p_2},{\wp }_2\right)}{k}\right)}^q\right|+\left|{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_{l_1},{\xi }_1\right)}{k}\right)}^q-{\left(\frac{{\mathrm{\Delta }}^{-1}\left({\mathit{\pounds }}_{l_2},{\xi }_2\right)}{k}\right)}^q\right|\hfill \end{array}\right)\right).(5)$

Definition 7. (Muirhead, 1902) Let $[\mathfrak{b}]=\{\mathrm{1,2},\dots ,\mathfrak{b}\}$, $ð=({ð}_1,{ð}_2,\dots ,{ð}_{\mathfrak{b}})$ and $\{{\mathfrak{a}}_{\varsigma }\mid \varsigma \in [\mathfrak{b}]\}$ be a set of non-negative numbers. Then the WPMM operator can be define in Equations 6:

${\mathrm{W}\mathrm{M}\mathrm{M}}_{\omega }^{\overrightarrow{ð}}\left({\mathfrak{a}}_1,{\mathfrak{a}}_2,\dots ,{\mathfrak{a}}_{\mathfrak{b}}\right)={\left(\frac{1}{\mathfrak{b}!}{\displaystyle \sum _{\mathrm{\Phi }\in {\mathbb{S}}_{\mathfrak{b}}}}\prod _{\varsigma =1}^{\mathfrak{b}}{\left(\mathfrak{b}{\omega }_{\mathrm{\Phi }\left(\varsigma \right)}{\mathfrak{a}}_{\mathrm{\Phi }\left(\varsigma \right)}\right)}^{{\overrightarrow{ð}}_{\varsigma }}\right)}^{\frac{1}{{\displaystyle \sum _{\varsigma =1}^{\mathfrak{b}}}{ð}_{\varsigma }}}(6)$

where $\mathrm{\Phi }=\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 2\hfill & \hfill \cdots \hfill & \hfill \mathfrak{b}\hfill \\ \hfill \mathrm{\Phi }(1)\hfill & \hfill \mathrm{\Phi }(2)\hfill & \hfill \cdots \hfill & \hfill \mathrm{\Phi }(\mathfrak{b})\hfill \end{array}\right)$ denotes any permutation of $[\mathfrak{b}]$ and ${\mathbb{S}}_{\mathfrak{b}}$ is the symmetric group on $\mathfrak{b}$ symbols.

3.1 Terminologies and notations

The terminologies and notations used in this article are listed in Table 2.

Table 2

Table 2. Notations and terminologies.

4 Decision analysis with a 2TL$q$-ROF-DEMATEL-MOORA approach in MAGDM environment

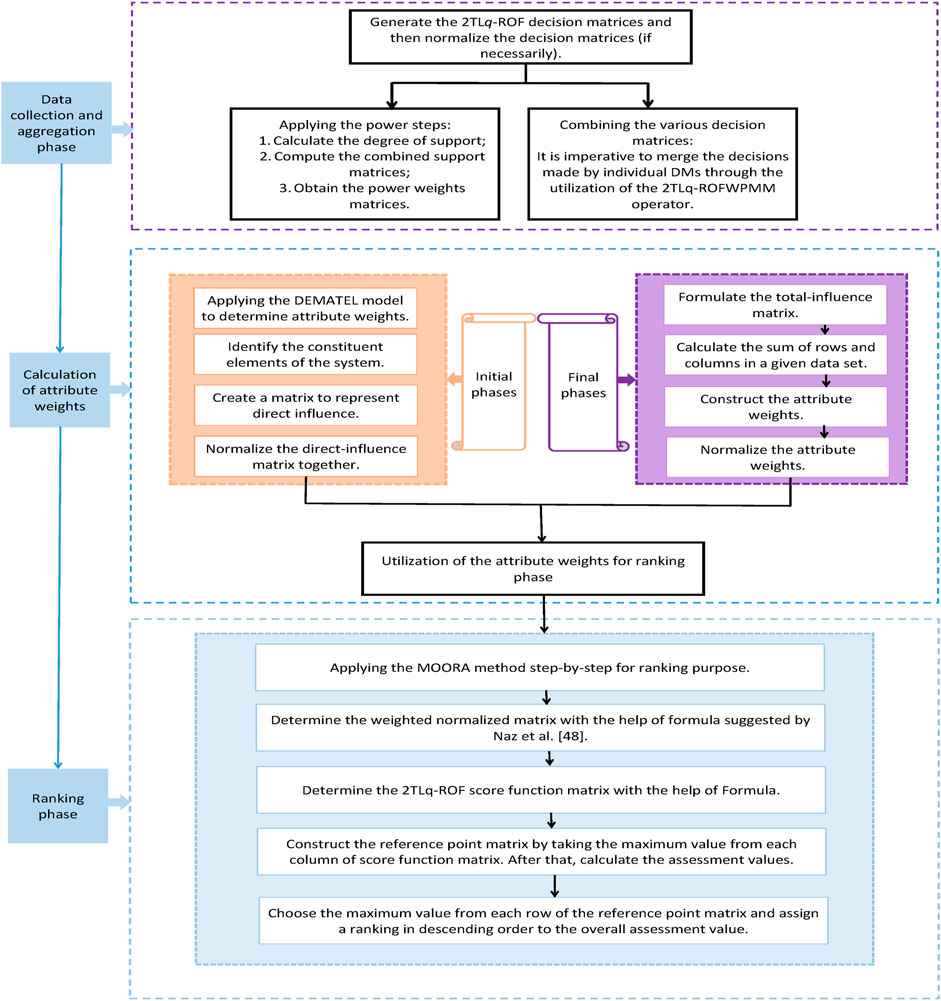
Research methodology plays a crucial role in scientific investigations as it provides a systematic framework for conducting research and generating reliable results. The combination of 2TL$q$-ROFS, WPMM operator, and DEMATEL-MOORA method in research methodology can offer several benefits and enhance the quality of the research. By using 2TL$q$-ROFS, WPMM operator, and DEMATEL-MOORA method, researchers can capture complex real-world phenomena, account for uncertainty, and make informed decisions based on comprehensive evaluations. This methodology promotes robustness, transparency, and accuracy in research, facilitating the generation of valuable insights and supporting evidence-based decision-making. This section presents a novel 2TL$q$-ROF-DEMATEL-MOORA-MAGDM approach that utilizes the 2TL$q$-ROFWPMM operator to address group decision-making difficulties within the context of 2TL$q$-ROFNs. Here is a detailed description of the suggested approach:

Step 1. Establish the 2TL$q$-ROF decision matrix.

Let us consider a set of $\mathfrak{a}$ alternatives denoted as $\gimel =\{{\gimel }_1,{\gimel }_2,\dots ,{\gimel }_{\mathfrak{a}}\}$, along with a collection of $\mathfrak{b}$ attributes labelled as $\mathcal{N}=\{{\mathcal{N}}_1,{\mathcal{N}}_2,\dots ,{\mathcal{N}}_{\mathfrak{b}}\}$. A collection of DMs, represented as $\mathcal{D}=\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_{\mathfrak{e}}\}$, is formed. Each decision-maker and attribute are associated with a weight vector ${\omega }^{\prime }={({\omega }_1^{\prime },{\omega }_2^{\prime },\dots ,{\omega }_{\mathfrak{e}}^{\prime })}^T$ and $\omega ={({\omega }_1,{\omega }_2,\dots ,{\omega }_{\mathfrak{e}})}^T$, where ${\omega }^{\prime }\in [\mathrm{0,1}]$ and $\omega \in [\mathrm{0,1}]$ and the sum of these weights across all DMs and attributes are constrained to be equal to 1. The primary purpose of this group is to express their perspectives on each alternative ${\gimel }_{\varrho }$ concerning the attributes in ${\mathcal{N}}_{\varsigma }$ using the framework of 2TL$q$-ROFNs. It is important to note that each decision-maker, labeled as ${\mathcal{D}}_{\kappa }$, contributes their evaluative insights using a 2TL$q$-ROF decision matrix referred to as ${\hslash }^{\kappa }={[{\aleph }_{\varrho \varsigma }^{\kappa }]}_{\mathfrak{a}\times \mathfrak{b}}$. This matrix encapsulates the assessments provided by ${\mathcal{D}}_{\kappa }$ for each combination of alternative ${\gimel }_{\varrho }$ and attribute ${\mathcal{N}}_{\varsigma }$ in terms of 2TL$q$-ROFNs. The structure of ${\hslash }^{\kappa }$ is defined as a tuple comprising the MD and NMD components, i.e., $(({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }),({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }))$, where $\varrho =\mathrm{1,2},\dots ,\mathfrak{a}$, $\varsigma =\mathrm{1,2},\dots ,\mathfrak{b}$, and $\kappa =\mathrm{1,2},\dots ,\mathfrak{e}$.

Step 2. Normalize the decision matrices:

${\aleph }_{\varrho \varsigma }^{\kappa }=\left\{\begin{array}{c}\left(\left({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }\right),\left({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }\right)\right)\in I_1,\hfill \\ \left(\left({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }\right),\left({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }\right)\right)\in I_2,\hfill \end{array}\right.(7)$

where $I_1$ stands for the benefit index and $I_2$ for the cost index.

Step 3. Calculate the degree of support denoted as $\mathbb{S}({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d)$:

$\mathbb{S}\left({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d\right)=1-d\left({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d\right)\left(\kappa ,d=\mathrm{1,2},\dots ,\mathfrak{e};\kappa \ne d\right).(8)$

The dissimilarity between ${\aleph }_{\varrho \varsigma }^{\kappa }$ and ${\aleph }_{\varrho \varsigma }^d$ is quantified by the normalized Hamming distance, which is computed using Formula 5.

Step 4. Compute the combined support matrices ${[\mathbb{T}({\aleph }_{\varrho \varsigma }^{\kappa })]}_{\mathfrak{a}\times \mathfrak{b}}$:

$\mathbb{T}\left({\aleph }_{\varrho \varsigma }^{\kappa }\right)={\displaystyle \sum _{\kappa ,d=1;d\ne \kappa }^{\mathfrak{e}}}\mathbb{S}\left({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d\right).(9)$

Step 5. The power weights matrices, denoted as ${[{\zeta }_{\varrho \varsigma }^{\kappa }]}_{\mathfrak{a}\times \mathfrak{b}}(\kappa =\mathrm{1,2},\dots ,\mathfrak{e})$ can be established as follows:

${\zeta }_{\varrho \varsigma }^{\kappa }=\frac{{\omega }^{\prime }\left(1+\mathbb{T}\left({\aleph }_{\varrho \varsigma }^{\kappa }\right)\right)}{{\displaystyle \sum _{\kappa =1}^{\mathfrak{e}}}{\omega }^{\prime }\left(1+\mathbb{T}\left({\aleph }_{\varrho \varsigma }^{\kappa }\right)\right)}.(10)$

Step 6. Combining the various decision matrices.

In order to construct an aggregated 2TL$q$-ROF decision matrix, it is imperative to merge the decisions made by individual DMs through the utilization of the 2TL$q$-ROFWPMM operator (Naz et al., 2024).

Step 7. Applying the DEMATEL model to determine attribute weights.

Step 7.1. Identify the constituent elements of the system. This approach can be achieved through several methodologies, such as conducting a comprehensive review of pertinent scholarly sources, engaging in collaborative group deliberations regarding practical obstacles, and seeking insights from authoritative subject matter specialists. Let ${\mathcal{N}}_1$, ${\mathcal{N}}_2$, …, ${\mathcal{N}}_{\mathfrak{b}}$ be represent the $\mathfrak{b}$ elements.

Step 7.2. Create a matrix to represent direct influence by conducting pairwise assessments of the causal impact among $\mathfrak{b}$ elements with input from a panel of experts denoted as $\mathcal{D}=\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_{\mathfrak{e}}\}$. This results in the formation of individual direct-influence matrices, denoted as $X^{\kappa }$ = ${(v_{\varrho \varsigma }^{\kappa })}_{\mathfrak{b}\times \mathfrak{b}}$ for each of the ${\kappa }^{th}$ experts, where $\kappa =\mathrm{1,2},\dots ,\mathcal{D}$. Here, $v_{\varrho \varsigma }$ signifies the causal influence of element ${\mathcal{N}}_{\varrho }$ on element ${\mathcal{N}}_{\varsigma }$, and this influence is assessed using a scale ranging from 0 (no influence) to 4 (very high influence), covering the spectrum of no, low, medium, high, and very high influences, respectively. The combined direct-influence matrix, denoted as $X$, is then formed by aggregating all individual $X^{\kappa }$ matrices, where $\kappa =\mathrm{1,2},\dots ,\mathfrak{e}$. Additionally, each element $w_{\kappa ,\varsigma }$ represents the assigned importance weight for the ${\kappa }^{th}$ expert are written in Equation 11.

$X={\left(v_{\varrho \varsigma }\right)}_{\mathfrak{b}\times \mathfrak{b}}={\left(\frac{{\displaystyle \sum _{\kappa =1}^{\mathfrak{e}}}{w}_{\kappa }{v}_{\varrho \varsigma }^{\kappa }}{{\displaystyle \sum _{\kappa =1}^{\mathfrak{e}}}{w}_{\kappa }}\right)}_{\mathfrak{b}\times \mathfrak{b}}.(11)$

Step 7.3. Normalize the direction-influence matrix together. The formula for calculating the normalized direct-influence matrix in Equations 12:

$G=gX,(12)$

where in Equations 13

$g=\max \left\{\frac{1}{{\max }_{1\le \varrho \le \mathfrak{b}}{\displaystyle \sum _{\varsigma =1}^{\mathfrak{b}}}{v}_{\varrho \varsigma }},\frac{1}{{\max }_{1\le \varsigma \le \mathfrak{b}}{\displaystyle \sum _{\varrho =1}^{\mathfrak{b}}}{v}_{\varrho \varsigma }}\right\}.(13)$

And,

$G=\left[\begin{array}{ccccccccccccccccc}\hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{12}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{13}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \dots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{1\mathfrak{b}}\hfill \\ \hfill g_{21}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{23}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \dots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{2\mathfrak{b}}\hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \ddots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill ⋮\hfill \\ \hfill g_{\mathfrak{b}1}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{\mathfrak{b}2}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill g_{\mathfrak{b}3}\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \dots \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill 0\hfill \end{array}\right],1\le g_{\varrho \varsigma }\le 0.(14)$

Step 7.4. Use an iterative method to compute the complete influence matrix. Matrix inversion converges if and only if the system’s indirect effects, as well as the powers of $G$ (i.e., $G+G^2+G^3+\cdots$), decrease with increasing $G$. Utilizing Equation 15, compute the complete influence matrix $T={(t_{\varrho \varsigma })}_{\mathfrak{b}\times \mathfrak{b}}$. Formulate the total-influence matrix $T$ as defined by the following equation.

$T={\left(t_{\varrho \varsigma }\right)}_{\mathfrak{b}\times \mathfrak{b}}=G{\left(I-G\right)}^{-1}.(15)$

Step 7.5. Use the following formulas to find the total number of rows $(R)$ and columns $(C)$ in Equations 16 and 17.

$R={\left[r_{\varrho }\right]}_{\mathfrak{b}\times 1}={\left[\begin{array}{c}\hfill {\displaystyle \sum _{\varsigma =1}^{\mathfrak{b}}}{t}_{\varrho \varsigma }\hfill \end{array}\right]}_{\mathfrak{b}\times 1},\varrho =\mathrm{1,2},\dots ,\mathfrak{b},(16)$

$C={\left[c_{\varsigma }\right]}_{1\times \mathfrak{b}}^{\prime }={\left[\begin{array}{c}\hfill {\displaystyle \sum _{\varrho =1}^{\mathfrak{b}}}{t}_{\varrho \varsigma }\hfill \end{array}\right]}_{1\times \mathfrak{b}}^{\prime },\varsigma =\mathrm{1,2},\dots ,\mathfrak{b}.(17)$

The transposed value of the $\varsigma$-th column is represented as ${[c_{\varsigma }]}_{1\times \mathfrak{b}}^{\prime }$. Here, $c_{\varsigma }$ signifies the total values within the $\varsigma$-th column, indicating the impact of the $\varsigma$-th attribute on the other attributes. Similarly, the summation of values within the $\varrho$-th row, denoted as $r_{\varrho }$, demonstrates the influence of the $\varrho$-th attribute on other attributes.

Step 7.6. The construction of attribute weights is determined by the following Equation 18:

$w_{\varsigma }=\left[\begin{array}{c}\hfill \sqrt[q]{{\left(r_{\varsigma }+c_{\varsigma }\right)}^q+{\left(r_{\varsigma }-c_{\varsigma }\right)}^q}\hfill \end{array}\right],\varsigma =\mathrm{1,2},\dots ,\mathfrak{b}.(18)$

Finally, the normalized attribute weights are defined in Equation 19:

$\omega =\frac{w_{\varsigma }}{{\displaystyle \sum _{\varsigma =1}^{\mathfrak{b}}}{w}_{\varsigma }}.(19)$

Step 8. Determine the weighted normalized matrix $(\mathbb{W}\mathbb{N})$ with the help of formula suggested by Naz et al. (2023).

Step 9. Determine the 2TL$q$-ROF score function matrix $(\mathbb{P})$ with the help of Formula 3.

Step 10. Construct the reference point matrix $\mathrm{\Omega }$ by taking the maximum value $\delta$ from each column of score function matrix calculated from Step 8. After that calculate the assessment values utilizing Equation 20.

$\mathrm{\Omega }=\mathrm{a}\mathrm{b}\mathrm{s}\left(\frac{\mathbb{P}-\delta }{\mathfrak{b}}\right).(20)$

Step 11. Choose the maximum value from each row of the reference point matrix $\mathrm{\Omega }$ and assign a ranking in descending order to the overall assessment value.

4.1 Pseudocode framework

The pseudocode framework of the proposed approach is as follows:

Step 1. Establish the 2TL$q$-ROF decision matrix.

     Let us consider a set of $\mathfrak{a}$ alternatives denoted as $\gimel =\{{\gimel }_1,{\gimel }_2,\dots ,{\gimel }_{\mathfrak{a}}\}$, along with a collection of $\mathfrak{b}$ attributes labelled as $\mathcal{N}=\{{\mathcal{N}}_1,{\mathcal{N}}_2,\dots ,{\mathcal{N}}_{\mathfrak{b}}\}$. A collection of decision-makers (DMs), represented as $\mathcal{D}=\{{\mathcal{D}}_1,{\mathcal{D}}_2,\dots ,{\mathcal{D}}_{\mathfrak{e}}\}$, is formed. Each decision-maker is associated with a weight vector ${\omega }^{\prime }={({\omega }_1^{\prime },{\omega }_2^{\prime },\dots ,{\omega }_{\mathfrak{e}}^{\prime })}^T$, where ${\omega }^{\prime }\in [\mathrm{0,1}]$, and the sum of these weights across all DMs is constrained to be equal to 1. Each decision-maker, labeled as ${\mathcal{D}}_{\kappa }$, contributes their evaluative insights using a 2TL$q$-ROF decision matrix referred to as ${\hslash }^{\kappa }={[{\aleph }_{\varrho \varsigma }^{\kappa }]}_{\mathfrak{a}\times \mathfrak{b}}$. This matrix encapsulates the assessments provided by ${\mathcal{D}}_{\kappa }$ for each combination of alternative ${\gimel }_{\varrho }$ and attribute ${\mathcal{N}}_{\varsigma }$ in terms of 2TL$q$-ROFNs. The structure of ${\hslash }^{\kappa }$ is defined as a tuple comprising the MD and NMD components, i.e.,

${\hslash }^{\kappa }=\left(\left({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }\right),\left({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }\right)\right),\varrho =\mathrm{1,2},\dots ,\mathfrak{a},\varsigma =\mathrm{1,2},\dots ,\mathfrak{b},\kappa =\mathrm{1,2},\dots ,\mathfrak{e}.$

>

Step 2. Normalize the decision matrices:

${\aleph }_{\varrho \varsigma }^{\kappa }=\left\{\begin{array}{cc}\left(\left({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }\right),\left({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }\right)\right)\hfill & \text{if\hspace{0.17em}}{I}_1\left(\text{benefit\hspace{0.17em}index}\right),\hfill \\ \left(\left({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }\right),\left({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }\right)\right)\hfill & \text{if\hspace{0.17em}}{I}_2\left(\text{cost\hspace{0.17em}index}\right).\hfill \end{array}\right.$

Step 3. Calculate the degree of support $\mathbb{S}({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d)$:

$\mathbb{S}\left({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d\right)=1-d\left({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d\right),\left(\kappa ,d=\mathrm{1,2},\dots ,\mathfrak{e};\kappa \ne d\right).$

The dissimilarity is quantified by the normalized Hamming distance.

Step 4. Compute the combined support matrices:

$\mathbb{T}\left({\aleph }_{\varrho \varsigma }^{\kappa }\right)={\displaystyle \sum _{\kappa ,d=1;d\ne \kappa }^{\mathfrak{e}}}\mathbb{S}\left({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d\right).$

Step 5. Compute the power weight matrices:

${\zeta }_{\varrho \varsigma }^{\kappa }=\frac{{\omega }^{\prime }\left(1+\mathbb{T}\left({\aleph }_{\varrho \varsigma }^{\kappa }\right)\right)}{{\sum }_{\kappa =1}^{\mathfrak{e}}{\omega }^{\prime }\left(1+\mathbb{T}\left({\aleph }_{\varrho \varsigma }^{\kappa }\right)\right)}.$

Step 6. Combine the decision matrices using the 2TL$q$-ROFWPMM operator.

Step 7. Apply the DEMATEL model to determine attribute weights. Perform the following sub-steps:

7.1. Identify the constituent elements of the system.

7.2. Create and aggregate direct influence matrices:

$X={\left(v_{\varrho \varsigma }\right)}_{\mathfrak{b}\times \mathfrak{b}}=\left(\frac{{\sum }_{\kappa =1}^{\mathfrak{e}}{w}_{\kappa }{v}_{\varrho \varsigma }^{\kappa }}{{\sum }_{\kappa =1}^{\mathfrak{e}}{w}_{\kappa }}\right).$

7.3. Normalize the direct influence matrix:

$G=gX,g=\max \left\{\frac{1}{{\max }_{1\le \varrho \le \mathfrak{b}}{\sum }_{\varsigma =1}^{\mathfrak{b}}{v}_{\varrho \varsigma }},\frac{1}{{\max }_{1\le \varsigma \le \mathfrak{b}}{\sum }_{\varrho =1}^{\mathfrak{b}}{v}_{\varrho \varsigma }}\right\}.$

7.4. Compute the total influence matrix:

$T=G{\left(I-G\right)}^{-1}.$

7.5. Calculate row and column sums:

$R={\displaystyle \sum _{\varsigma =1}^{\mathfrak{b}}}{t}_{\varrho \varsigma },C={\displaystyle \sum _{\varrho =1}^{\mathfrak{b}}}{t}_{\varrho \varsigma }.$

7.6. Construct normalized attribute weights:

$w_{\varsigma }=\frac{\sqrt[q]{{\left(r_{\varsigma }+c_{\varsigma }\right)}^q+{\left(r_{\varsigma }-c_{\varsigma }\right)}^q}}{{\sum }_{\varsigma =1}^{\mathfrak{b}}{w}_{\varsigma }}.$

Step 8. Compute the weighted normalized matrix $(\mathbb{W}\mathbb{N})$.

Step 9. Determine the 2TL$q$-ROF score function matrix $(\mathbb{P})$.

Step 10. Construct the reference point matrix $\mathrm{\Omega }$:

$\mathrm{\Omega }=\text{abs}\left(\frac{\mathbb{P}-\delta }{\mathfrak{b}}\right),$

where $\delta$ is the maximum value from each column of $(\mathbb{P})$.

Step 11. Rank alternatives based on the maximum values from $\mathrm{\Omega }$ in descending order.

The steps of the proposed approach are visually depicted in Figure 1.

Figure 1

Figure 1. Visual depiction of the framework.

4.2 Complexity analysis

The complexity of the proposed approach is analyzed as follows:

The complexity analysis of the proposed approach involves evaluating each step in the decision-making process. Constructing the decision matrix for all DMs and normalizing it has a time complexity that grows linearly with the number of alternatives, attributes, and DMs. The calculation of the degree of support involves pairwise comparisons, which adds a quadratic factor concerning the number of DMs. Aggregating these support values and computing power weights also scale linearly. The DEMATEL model, used to analyze relationships among attributes, includes matrix inversion and multiplication, leading to a cubic complexity with respect to the number of attributes. Ranking alternatives requires sorting, which is logarithmic in complexity relative to the number of alternatives. Combining all steps, the dominant factors are the quadratic dependency on the number of DMs for degree of support and the cubic dependency on the number of attributes in the DEMATEL model, resulting in the overall complexity being the sum of these terms.

5 Numerical illustration

WSMs are highly advanced instruments that serve a crucial function in comprehending, evaluating, and governing the intricate hydrological and environmental dynamics within watersheds, which are fundamental constituents of our natural ecosystems. These models function as comprehensive frameworks for analyzing the complex interrelationships among different elements of a watershed, encompassing precipitation, surface water, groundwater, soil, vegetation, and human activities. WSMs offer significant insights into the dynamics of water movement, pollutant dispersion, and the influence of factors such as land use alterations, climate fluctuations, and infrastructure advancements on the overall wellbeing and sustainability of a watershed. These models effectively simulate intricate interactions within the system, thereby facilitating a comprehensive understanding of the aforementioned processes. One of the principal purposes of these models is to accurately forecast and efficiently administer water resources. Water resource managers can make well-informed decisions regarding the allocation, distribution, and conservation of water by utilizing estimates of both the quantity and quality of water present within a given watershed. Moreover, watershed models provide significant value in the realm of flood prediction and management. In addition, WSMs are critical resources for these aims. Water quality and ecosystem health can be evaluated concerning human activities, including agriculture, urbanization, and industrial development. This data is crucial for planning strategies that reduce pollution and maintain watershed ecosystem health. WSMs are becoming increasingly important in a fast-evolving world where climate change presents formidable threats to water resources and ecosystems. They help us learn more about the possible implications of climate change on rainfall, temperature, and hydrological cycles, which is crucial for planning adaptation methods to lessen the severity of these effects. Models of the watershed system are multi-purpose tools that help bridge the gap between theoretical knowledge and real-world watershed management. Ultimately, they ensure the sustainable use and protection of one of our most precious natural resources, water, by equipping scientists, policymakers, and stakeholders to make educated decisions about water resource management, environmental conservation, and disaster preparedness. For the sake of present and future generations, these models are vital parts of our toolset for creating sustainable and robust communities.

A concise overview of the alternatives that have to be assessed is provided below: (1) Physically-based models $({\gimel }_1)$: These models simulate the physical processes occurring in the watershed, such as rainfall-runoff, evapotranspiration, and soil infiltration, based on the principles of physics and hydrology. Examples include soil and water assessment tools and hydrologic modeling systems. (2) Conceptual models $({\gimel }_2)$: These models simplify the complex processes in a watershed by using conceptual representations of hydrological components, such as lumped parameter models. The HBV hydrology model is an example of this approach. (3) Distributed models $({\gimel }_3)$: These models divide the watershed into smaller spatial units and simulate processes separately for each unit. This allows for capturing spatial variability in climate, soil, and land use. MIKE-SHE hydrological model and distributed hydrology-soil-vegetation model are examples of distributed models. (4) Semi-distributed models $({\gimel }_4)$: These models strike a balance between conceptual and distributed approaches by dividing the watershed into several sub-basins and applying conceptual models to each sub-basin. These models are computationally more efficient than fully distributed models. The SWAT model can also be used in a semi-distributed configuration. (5) Data-driven models $({\gimel }_5)$: These models use machine learning techniques to learn patterns and relationships from observed data without explicit physical equations. Examples include artificial neural networks, support vector machines, and random forests applied to hydrological modeling. (6) Hybrid models $({\gimel }_6)$: Hybrid models combine different modeling approaches to take advantage of their strengths. For instance, a physically-based model could be combined with a data-driven model to improve predictive accuracy. (7) Climate change impact models $({\gimel }_7)$: These models focus on assessing the potential impacts of climate change on watershed processes. They involve scenarios of altered temperature, precipitation, and other climatic variables to predict how the watershed’s behavior might change. (8) Decision support systems models $({\gimel }_8)$: These models provide a platform for DMs to evaluate various management strategies and their impacts on the watershed. These models often incorporate multiple components, including hydrological, ecological, and socioeconomic factors.

WSMs can simulate the potential impacts of excessive precipitation or snowmelt on downstream regions, thereby facilitating the provision of timely warnings and the implementation of effective disaster preparedness measures. Therefore, WSMs in the environment could be categorized as a classical MAGDM problem. Based on the discussion above, the 2TL$q$-ROF-DEMATEL-MOORA method is suggested to evaluate the WSMs. In this particular scenario, a collection of eight WSMs, denoted as $\gimel =\{{\gimel }_1,{\gimel }_2,{\gimel }_3,\dots ,{\gimel }_8\}$, is evaluated by a panel of five DMs represented as $\mathcal{D}=\{{\mathcal{D}}_1,{\mathcal{D}}_2,{\mathcal{D}}_3,{\mathcal{D}}_4,{\mathcal{D}}_5\}$. These DMs assign weights ${\omega }^{\prime }={(0.2192,0.2134,0.1930,0.1906,0.1838)}^T$ to address the specific problem at hand. The group of five DMs is responsible for choosing the most suitable option from a set of eight alternatives. Their decision-making process involves evaluating four attributes, denoted as $\mathcal{N}=\{{\mathcal{N}}_1,{\mathcal{N}}_2,{\mathcal{N}}_3,{\mathcal{N}}_4\}$, which are defined as follows: (1) Accuracy and reliability ${\mathcal{N}}_1$: Models should accurately represent real-world processes and produce reliable results under various conditions. Calibration and validation are crucial for ensuring accuracy. (2) Spatial and temporal resolution ${\mathcal{N}}_2$: The complexity of spatial (related to space) and temporal (related to time) intricacies directly affects a model’s effectiveness and appropriateness. Models that incorporate a finer spatial and temporal resolution typically produce more precise results. (3) Data requirements ${\mathcal{N}}_3$: Models vary in their data needs, ranging from basic meteorological data to detailed land cover, soil properties, and topography. The availability and quality of data influence model accuracy. (4) Computational efficiency ${\mathcal{N}}_4$: Some models require extensive computational resources due to their complexity and detailed spatial discrimination. Computational efficiency is essential for large-scale applications and real-time simulations. All the attributes have a weight vector being $\omega ={(0.2962,0.1403,0.2669,0.2967)}^T$ which is computed utilizing the 2TL$q$-ROF-DEMATEL method. Five individuals express their viewpoints in order to assign numerical values to each LTS $\mathcal{S}$ = {${\mathit{\pounds }}_0$: extraordinarily poor, ${\mathit{\pounds }}_1$: extremely poor, ${\mathit{\pounds }}_2$: poor, ${\mathit{\pounds }}_3$: slightly poor, ${\mathit{\pounds }}_4$: moderate, ${\mathit{\pounds }}_5$: slightly excellent, ${\mathit{\pounds }}_6$: excellent, ${\mathit{\pounds }}_7$: extremely excellent, ${\mathit{\pounds }}_8$: extraordinarily excellent}. Table 3 provides a detailed summary of the assessment values that are provided by the five DMs to each alternative.

Table 3

Table 3. Evaluation matrix by five DMs with 2TL$q$-ROFNs.

5.1 Decision analysis

This subsection outlines the evaluation approach employed for the selection of WSMs. The 2TL$q$-ROF-DEMATEL-MOORA method, which utilizes the 2TL$q$-ROFWPMM operator, is used for this purpose.

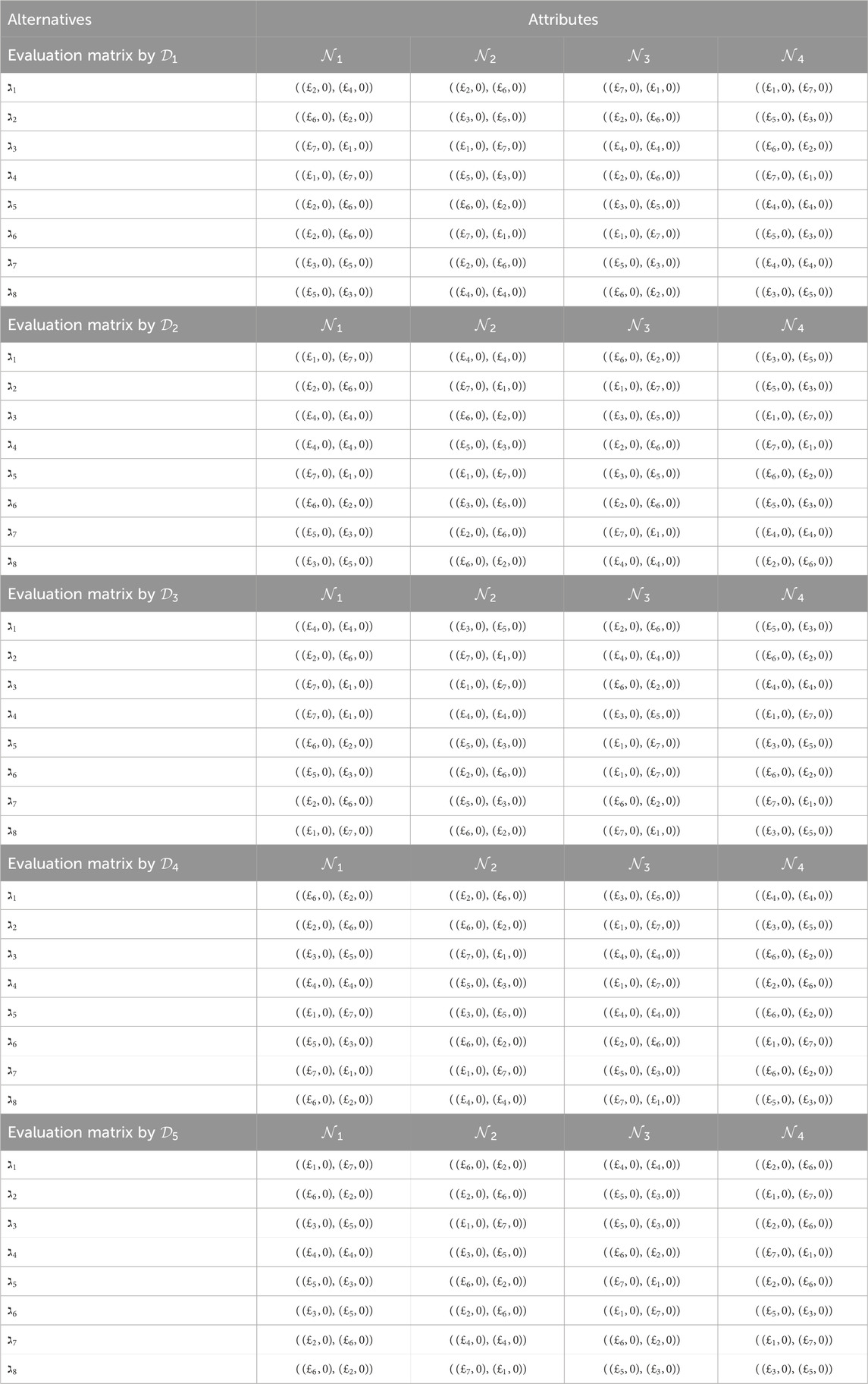
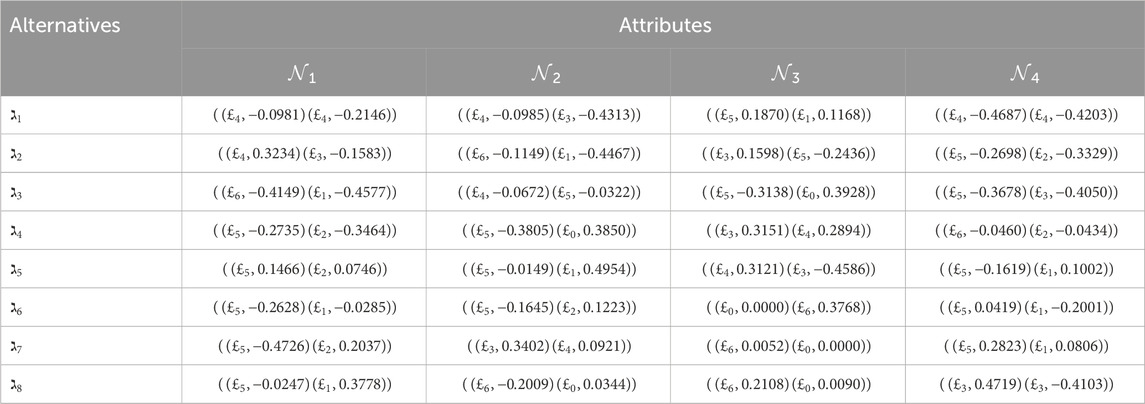
Step 1. Formulate the 2TL$q$-ROF evaluation matrix ${\hslash }^{\kappa }={[{\aleph }_{\varrho \varsigma }^{\kappa }]}_{8\times 4}={(({\mathit{\pounds }}_{p_{\varrho \varsigma }}^{\kappa },{\wp }_{\varrho \varsigma }^{\kappa }),({\mathit{\pounds }}_{l_{\varrho \varsigma }}^{\kappa },{\xi }_{\varrho \varsigma }^{\kappa }))}_{8\times 4}(\varrho =\mathrm{1,2,3},\dots ,8,\varsigma =\mathrm{1,2,3,4}$, and $\kappa =\mathrm{1,2,3,4,5})$, encapsulating the evaluations provided by five DMs, as computed in Table 3.

Step 2. The utilization of Equation 7 serves the goal of normalizing the decision matrices. Given that all attributes exhibit advantageous characteristics, it can be shown that the five choice matrices remain unaltered.

Step 3. Using Equation 8, we can compute the support $\mathbb{S}({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d)$. For the sake of simplicity, we can denote $\mathbb{S}({\aleph }_{\varrho \varsigma }^{\kappa },{\aleph }_{\varrho \varsigma }^d)$ as ${\mathbb{S}}^{\kappa d}$. The computed results of ${\mathbb{S}}^{\kappa d}$ are presented as follows:

Step 4. Utilizing Equation 9, we can determine the comprehensive support matrices $\mathbb{T}({\aleph }_{\varrho \varsigma }^{\kappa })$ for the 2TL$q$-ROFN $\mathbb{T}({\aleph }_{\varrho \varsigma }^{\kappa })$. To facilitate convenience, we can symbolize $\mathbb{T}({\aleph }_{\varrho \varsigma }^{\kappa })$ as a matrix $\mathbb{T}({\aleph }^{\kappa })$. The computed results of $\mathbb{T}({\aleph }^{\kappa })$ are presented as follows:

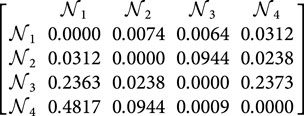
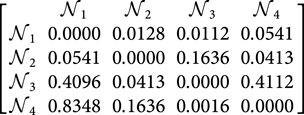
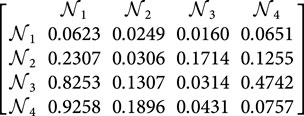
Step 5. By utilizing Equation 10, we are able to calculate the power weight matrix for the judgment ${\mathcal{D}}_{\kappa }$ associated with the 2TL$q$-ROFN $\mathbb{T}({\aleph }_{\varrho \varsigma }^{\kappa })$. To improve its usability, we can represent $\zeta ({\aleph }_{\varrho \varsigma }^{\kappa })$ as a matrix denoted by $\zeta ({\aleph }^{\kappa })$. The computed results of $\zeta ({\aleph }^{\kappa })$ are presented as follows:

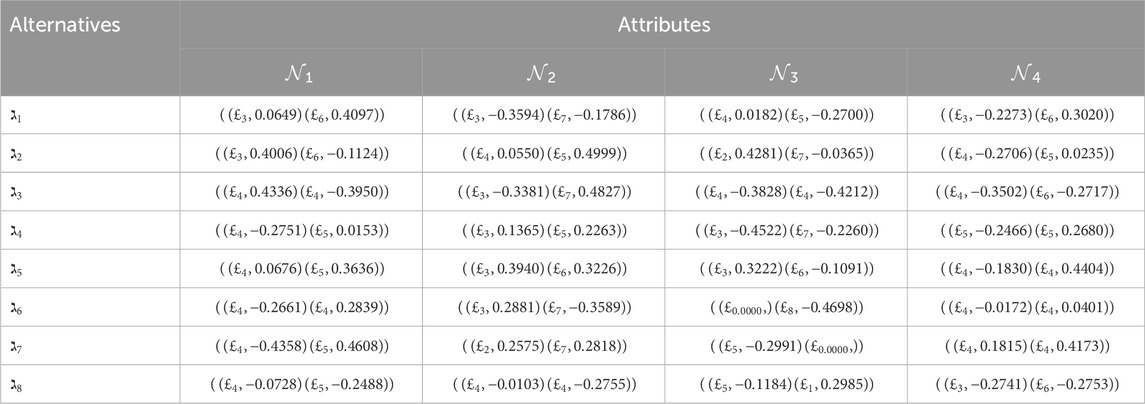
Step 6. To aggregate the values from the overall $[{\aleph }_{\varrho \varsigma }^{\kappa }]$ to form $[{\aleph }_{\varrho \varsigma }]$, the 2TL$q$-ROFWPMM operator, as described in Naz et al. (2024), is employed. The resulting merged 2TL$q$-ROFNs matrix, denoted as: $\hslash ={[{\aleph }_{\varrho \varsigma }]}_{\mathfrak{a}\times \mathfrak{b}}$, is presented in Table 4.

Step 7. The DEMATEL model is utilized for the determination of attribute weights.

Step 7.1. The identification of the system’s components can be accomplished by several methods, such as conducting a comprehensive review of pertinent literature, engaging in group deliberations focused on practical obstacles encountered in real-life scenarios, and seeking input from domain experts.

Step 7.2. The construction of the direct influence matrix involves conducting pairwise comparisons of qualities with DMs, as seen in Table 5.

Step 7.3. Acquire a matrix that represents the direction and influence of a single value. The matrix values are presented below:

$\left[\begin{array}{ccccc}\hfill \hfill & \hfill {\mathcal{N}}_1\hfill & \hfill {\mathcal{N}}_2\hfill & \hfill {\mathcal{N}}_3\hfill & \hfill {\mathcal{N}}_4\hfill \\ \hfill {\mathcal{N}}_1\hfill & \hfill 0.0000\hfill & \hfill 0.0074\hfill & \hfill 0.0064\hfill & \hfill 0.0312\hfill \\ \hfill {\mathcal{N}}_2\hfill & \hfill 0.0312\hfill & \hfill 0.0000\hfill & \hfill 0.0944\hfill & \hfill 0.0238\hfill \\ \hfill {\mathcal{N}}_3\hfill & \hfill 0.2363\hfill & \hfill 0.0238\hfill & \hfill 0.0000\hfill & \hfill 0.2373\hfill \\ \hfill {\mathcal{N}}_4\hfill & \hfill 0.4817\hfill & \hfill 0.0944\hfill & \hfill 0.0009\hfill & \hfill 0.0000\hfill \end{array}\right]$

Table 4

Table 4. Collective evaluation matrix utilizing the 2TL$q$-ROFWPMM operator.

Table 5

Table 5. Direct influence matrix $X$.

Then normalized the single valued direct-influence matrix. Normalized direct-influence matrix is given below:

$\left[\begin{array}{ccccc}\hfill \hfill & \hfill {\mathcal{N}}_1\hfill & \hfill {\mathcal{N}}_2\hfill & \hfill {\mathcal{N}}_3\hfill & \hfill {\mathcal{N}}_4\hfill \\ \hfill {\mathcal{N}}_1\hfill & \hfill 0.0000\hfill & \hfill 0.0128\hfill & \hfill 0.0112\hfill & \hfill 0.0541\hfill \\ \hfill {\mathcal{N}}_2\hfill & \hfill 0.0541\hfill & \hfill 0.0000\hfill & \hfill 0.1636\hfill & \hfill 0.0413\hfill \\ \hfill {\mathcal{N}}_3\hfill & \hfill 0.4096\hfill & \hfill 0.0413\hfill & \hfill 0.0000\hfill & \hfill 0.4112\hfill \\ \hfill {\mathcal{N}}_4\hfill & \hfill 0.8348\hfill & \hfill 0.1636\hfill & \hfill 0.0016\hfill & \hfill 0.0000\hfill \end{array}\right]$

Step 7.4. The total influence matrix is constructed according to the format presented below:

$\left[\begin{array}{ccccc}\hfill \hfill & \hfill {\mathcal{N}}_1\hfill & \hfill {\mathcal{N}}_2\hfill & \hfill {\mathcal{N}}_3\hfill & \hfill {\mathcal{N}}_4\hfill \\ \hfill {\mathcal{N}}_1\hfill & \hfill 0.0623\hfill & \hfill 0.0249\hfill & \hfill 0.0160\hfill & \hfill 0.0651\hfill \\ \hfill {\mathcal{N}}_2\hfill & \hfill 0.2307\hfill & \hfill 0.0306\hfill & \hfill 0.1714\hfill & \hfill 0.1255\hfill \\ \hfill {\mathcal{N}}_3\hfill & \hfill 0.8253\hfill & \hfill 0.1307\hfill & \hfill 0.0314\hfill & \hfill 0.4742\hfill \\ \hfill {\mathcal{N}}_4\hfill & \hfill 0.9258\hfill & \hfill 0.1896\hfill & \hfill 0.0431\hfill & \hfill 0.0757\hfill \end{array}\right]$

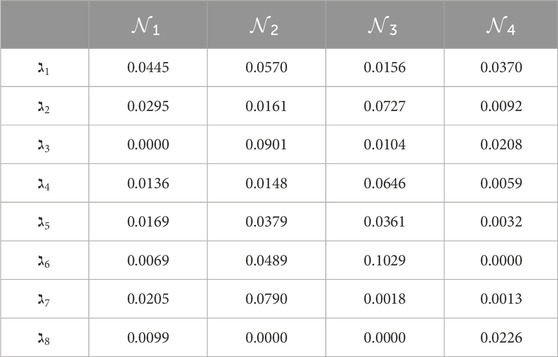
Step 7.5. The calculation of the row sums $(R_{\mathfrak{b}})$ and column sums $(C_{\mathfrak{b}})$ is displayed in Table 6.

Step 7.6. So, the normalized representation of the weight vector is as follows:

$\omega ={\left(0.2962,0.1403,0.2669,0.2967\right)}^T.$

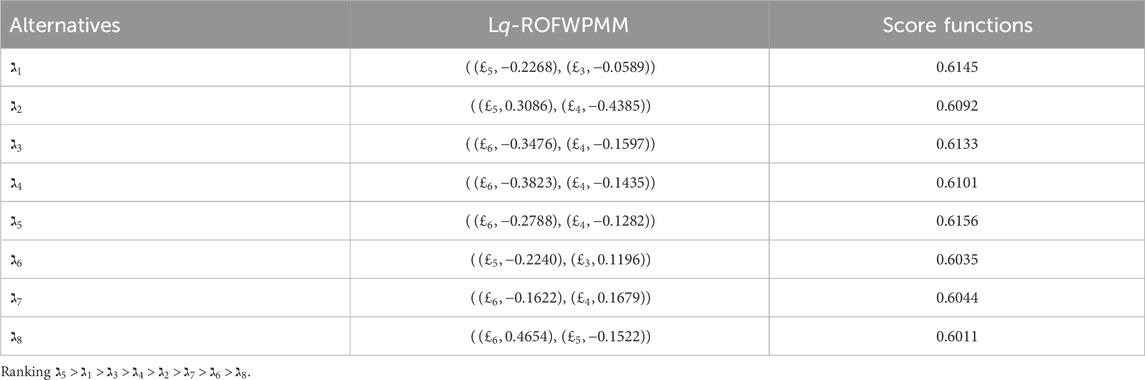
Step 8. Determine $\mathbb{W}\mathbb{N}$ with the help of formula suggested by Naz et al. (2023) and the results are shown in Table 7.

Step 9. Determine the 2TL$q$-ROF-$\mathbb{P}$ matrix with the help of Formula 3 and the results are shown in Table 8.

Step 10. Construct $\mathrm{\Omega }$ matrix (tabulated in Table 9) by taking $\delta$ from each column of $\mathbb{P}$ matrix calculated from Step 8. After that calculate the assessment values are tabulated in Table 10.

Step 11. Choose the maximum value from each row of $\mathrm{\Omega }$ matrix (tabulated in Table 11) and assign a ranking in descending order to the overall assessment value.

Table 6

Table 6. Values of $R_{\mathfrak{b}}$ and $C_{\mathfrak{b}}$.

Table 7

Table 7. 2TL$q$-ROF-$\mathbb{W}\mathbb{N}$ matrix.

Table 8

Table 8. Score values of normalize decision matrix.

Table 9

Table 9. Reference points.

Table 10

Table 10. Assessment matrix.

Table 11

Table 11. Overall assessment value.

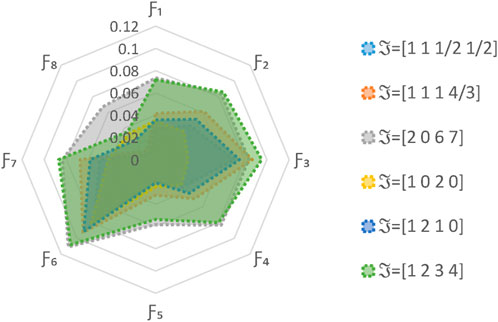
And the ranking of alternatives is as follows:

${\gimel }_6>{\gimel }_3>{\gimel }_7>{\gimel }_2>{\gimel }_4>{\gimel }_1>{\gimel }_5>{\gimel }_8$

Therefore, ${\gimel }_6$ is the best WSM.

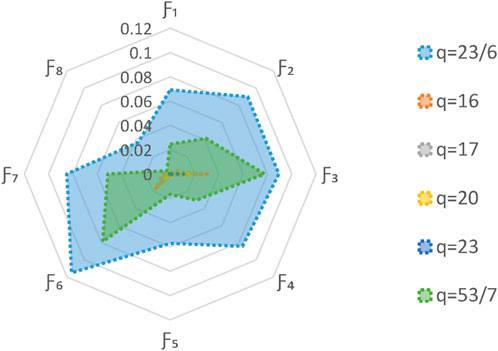
5.2 Parameter analysis

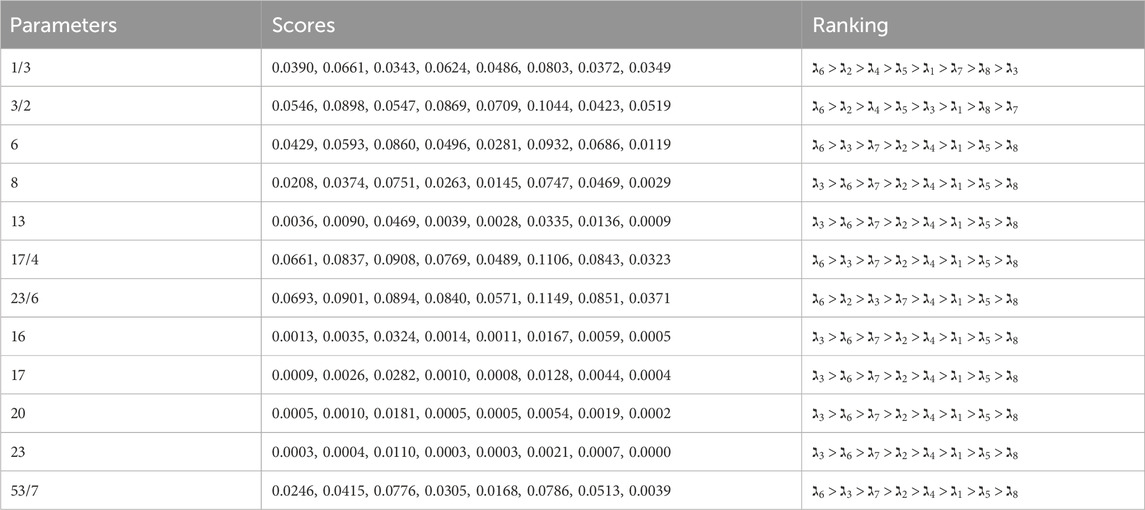
In this subsection, a thorough parameter analysis is conducted utilizing the parameters $q$ and $\mathfrak{I}$ to evaluate the stability and effectiveness of the suggested technique. The approach is based on the 2TL$q$-ROFWPMM operator. The objective of this analysis is to investigate how different values of the parameters $q$ and $\mathfrak{I}$ influence the obtained scores and rankings within our approach. To achieve this, we systematically vary the values of the parameters $q$ and $\mathfrak{I}$ and closely examine their impact on the outcomes, particularly on the scores and rankings generated by the 2TL$q$-ROFWPMM operator and the results are displayed in Tables 12 and 13. The visual depiction of parameter analysis is given in Figures 2–5.

Table 12

Table 12. Parameter analysis with the parameter $q$ by the 2TL$q$-ROFWPMM operator.

Table 13

Table 13. Parameter analysis with the parameter $\mathfrak{I}$ by the 2TL$q$-ROFWPMM operator.

Figure 2

Figure 2. Parameter analysis with $q(q=1/33/2681317/4)$ parameter.

Figure 3

Figure 3. Parameter analysis with $q(q=23/61617202353/7)$ parameter.

Figure 4

Figure 4. Parameter analysis with $\mathfrak{I}(\mathfrak{I}=[111/21/2],[1114/3],[2067],$$[1020],[1210],[1234])$ parameter.

Figure 5

Figure 5. Parameter analysis with $\mathfrak{I}(\mathfrak{I}=[227/37/3],[035/29/4],$$[2305],[2045],[1/213/22],[8/34017/5])$ parameter.

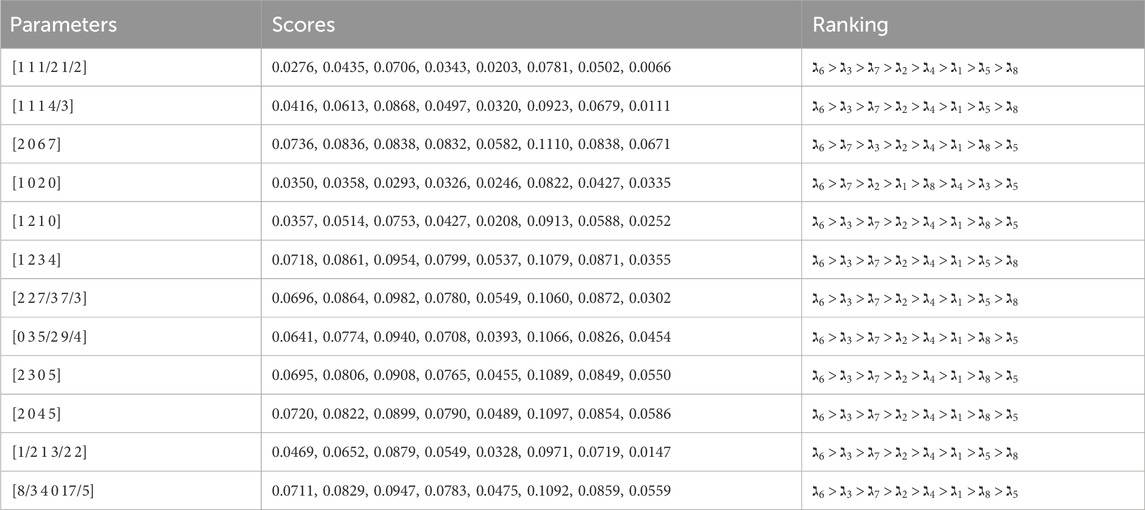
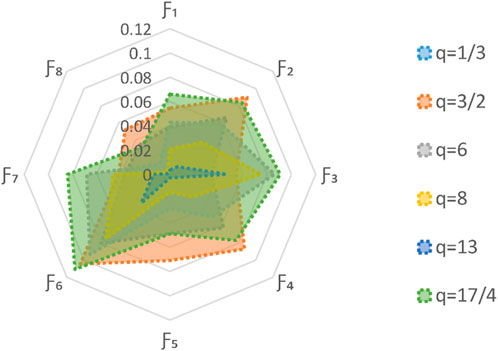
5.2.1 The effect of parameter $q$ on the solution ranking

The parameter $q$ in the 2TL$q$-ROFWPMM operator enables DMs to adjust the balance between different attributes when evaluating alternatives. This parameter influences how much importance is assigned to favorable or unfavorable attributes. For this purpose, we assign different values to parameter $q$ in order to rank and identify the best one. Furthermore, it has been determined that the outcome values of the alternatives in various evaluations exhibit minimal differences. However, it is consistently seen that the optimal choice remains always the same. For instance, when considering $q=1/\mathrm{3,2}/\mathrm{3,6,17}/\mathrm{4,23}/\mathrm{6,53}/7$, the calculated scores consistently ranked alternative ${\gimel }_6$ as the best choice. Similarly, for $q=\mathrm{8,13,16,17,20,23}$, the analysis consistently pointed to ${\gimel }_3$ as the optimal alternative. This remarkable consistency in the optimal choice, despite varying $q$ values and minor discrepancies in scores, underscores the robustness of our approach. It highlights that while parameter $q$ influences the scores and rankings, the best alternative remains stable, demonstrating the reliability of our decision-making process based on the 2TL$q$-ROFWPMM operator.

5.2.2 The effect of parameter $\mathfrak{I}$ on the solution ranking

The present study evaluates the impact of parameter $\mathfrak{I}$ on the ultimate results and then prioritizes alternatives using the suggested methodology. To assess the outcomes of the comprehensive aggregation, we establish fixed values for the various parameters of $\mathfrak{I}$. The final decision outcomes are subsequently employed to evaluate the available choices. The final findings are given in Table 13 by modifying $\mathfrak{I}$ based on the 2TL$q$-ROFWPMM operator. Subsequently, the outcomes of these decisions are employed to establish a hierarchical order among the available possibilities. The selection of the optimal alternative is determined by the ranking outcomes, and it is consistently identified as the best option by the 2TL$q$-ROFWPMM operator. Changes in the values of the $\mathfrak{I}$ parameter have a considerable impact on the outcomes of the alternative ranking. The ranking results exhibit consistency even when the imaginary component is altered, and the optimal alternative remains unchanged, as depicted in Table 13. The selection of the optimal alternative is determined by the ranking outcomes, with the ${\gimel }_6$ option being identified as the most favorable according to the 2TL$q$-ROFWPMM operator. By manipulating the values of $\mathfrak{I}$ in order to get the most favorable choice outcome, the decision preference can be effectively articulated within the context of the decision-making process.

This consistency in the optimal choice, regardless of different $q$ and $\mathfrak{I}$ values and small score differences, highlights the robustness and reliability of our decision-making approach using the 2TL$q$-ROFWPMM operator. It demonstrates that while the parameter $q$ and $\mathfrak{I}$ influences the scores and rankings of alternatives, the best choice remains stable. This emphasizes that the decision-making process is dependable and not overly sensitive to variations in $q$ and $\mathfrak{I}$ values.

5.3 Comparative analysis

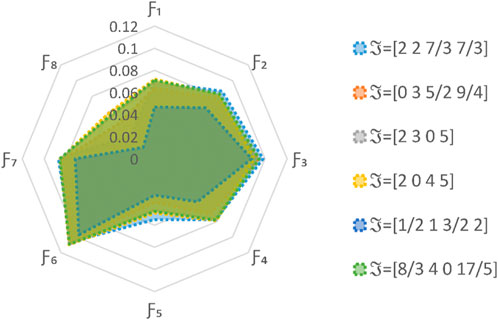
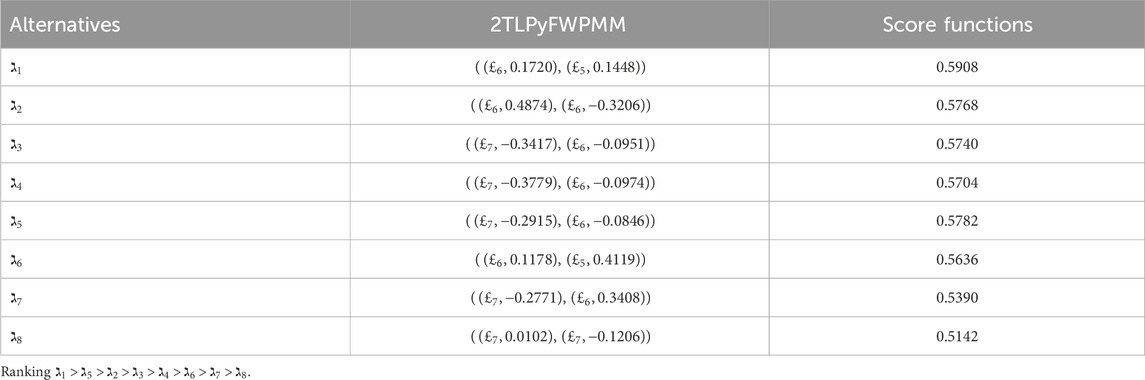
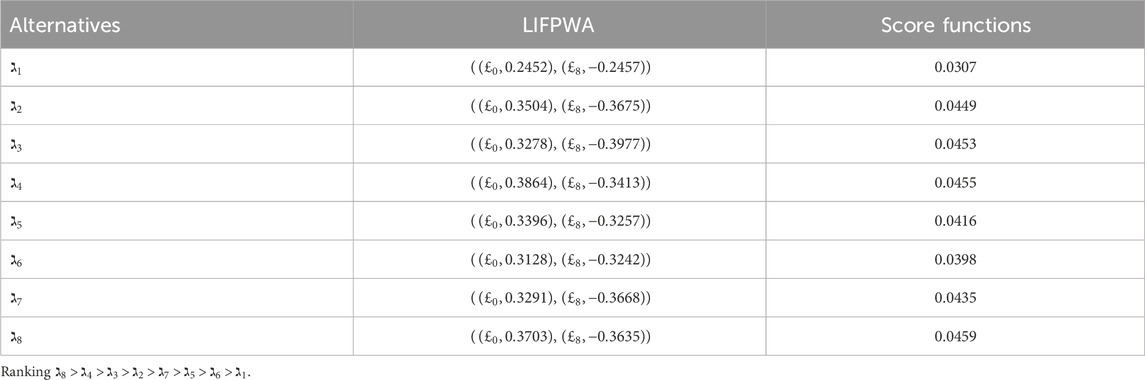
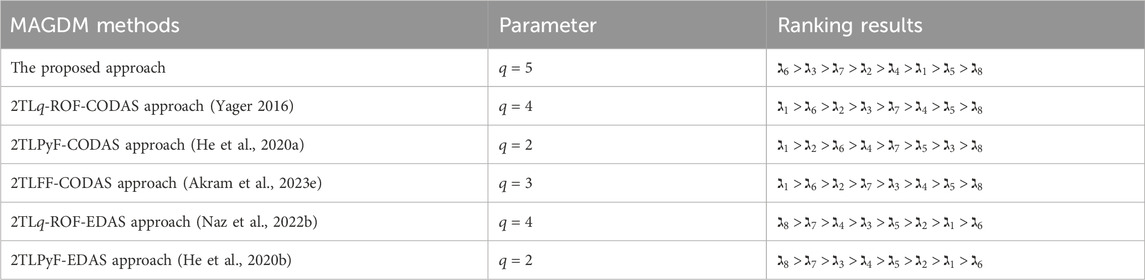
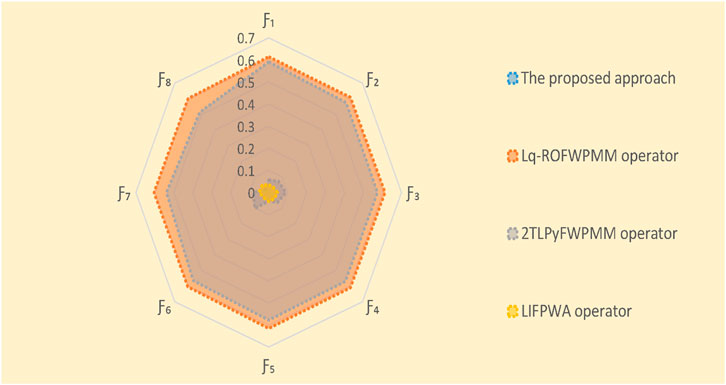
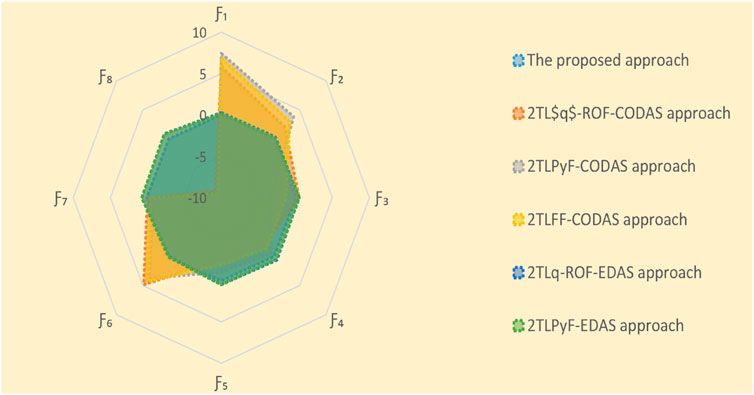
In this subsection, we employ validated methodologies to address the proposed MAGDM problem and evaluate the results using our framework to assess its practicality and efficacy. The proposed technique is subjected to a comparative study using several AOs and ranking systems. The evaluation outcomes for the selection of the best choice are computed meticulously through the implementation of these procedures. Hence, we solve the concerned problem for these approaches and ranked the results in Tables 14–17. The visual depiction of comparative analysis is given in Figures 6, 7.

Table 14

Table 14. The outcomes about L$q$-ROFWPMM operator.

Table 15

Table 15. The outcomes about 2TLPyFWPMM operator.

Table 16

Table 16. The outcomes about LIFPWA operator.

Table 17

Table 17. Ranking results of comparative analysis with different methods.

Figure 6

Figure 6. Comparative analysis with different existing AOs.

Figure 7

Figure 7. Comparative analysis with different existing ranking methods.

5.3.1 Comparative analysis with different AOs

In this study, we compare our proposed method to three existing AOs: the L$q$-ROFWPMM operator developed by Liu and Liu (2019), the 2TLPyFWPMM operator developed by Deng et al. (2020), and the LIFPWA operator developed by Liu and Qin (2017). This evaluation is meant to determine whether or not the innovative approach described in this study is reliable and useful. Based on this computation, the alternatives are ranked to identify the best one. Furthermore, it has been determined that the outcome values of the alternatives in various evaluations exhibit maximal differences. However, it is consistently seen that the optimal choice remains always changed. When we make a comparison with the L$q$-ROFWPMM operator then the ranking is ${\gimel }_5>{\gimel }_1>{\gimel }_3>{\gimel }_4>{\gimel }_2>{\gimel }_7>{\gimel }_6>{\gimel }_8$, and the best one is ${\gimel }_5$. When we make a comparison with the 2TLPyFWPMM operator then the ranking is ${\gimel }_1>{\gimel }_5>{\gimel }_2>{\gimel }_3>{\gimel }_4>{\gimel }_6>{\gimel }_7>{\gimel }_8$, and the best one is ${\gimel }_1$. Lastly, when we make a comparison with the LIFPWA operator then the ranking is ${\gimel }_8>{\gimel }_4>{\gimel }_3>{\gimel }_2>{\gimel }_7>{\gimel }_5>{\gimel }_6>{\gimel }_1$, and the best one is ${\gimel }_8$. The numerical results are shown in Tables 14–16.

5.3.2 Comparative analysis with different ranking methods

In this analysis, we compare our proposed approach with the 2TL$q$-ROF-CODAS approach (Yager, 2016), the 2TLPyF-CODAS approach (He et al., 2020a), the 2TLFF-CODAS approach (Akram et al., 2023e), 2TL$q$-ROF-EDAS approach (Naz et al., 2022b), and the 2TLPyF-EDAS approach (He et al., 2020b) to properly represent the innovative approach presented in this study’s reasonableness and efficiency. Based on this computation, the alternatives are ranked to identify the best one. Furthermore, it has been determined that the outcome values of the alternatives in various evaluations exhibit minimal differences. However, it is consistently seen that the optimal choice remains slightly changed. When we make a comparison with the 2TL$q$-ROF-CODAS approach then the ranking is ${\gimel }_1>{\gimel }_6>{\gimel }_2>{\gimel }_3>{\gimel }_7>{\gimel }_4>{\gimel }_5>{\gimel }_8$, and the best one is ${\gimel }_1$. When we make a comparison with the 2TLPyF-CODAS approach then the ranking is ${\gimel }_1>{\gimel }_2>{\gimel }_6>{\gimel }_4>{\gimel }_7>{\gimel }_5>{\gimel }_3>{\gimel }_8$, and the best one is ${\gimel }_1$. When we make a comparison with the 2TLFF-CODAS approach then the ranking is ${\gimel }_1>{\gimel }_6>{\gimel }_2>{\gimel }_7>{\gimel }_3>{\gimel }_4>{\gimel }_5>{\gimel }_8$, and the best one is ${\gimel }_1$. When we make a comparison with the 2TL$q$-ROF-EDAS approach then the ranking is ${\gimel }_8>{\gimel }_7>{\gimel }_4>{\gimel }_3>{\gimel }_5>{\gimel }_2>{\gimel }_1>{\gimel }_6$, and the best one is ${\gimel }_8$. Lastly, when we make a comparison with the 2TLPyF-EDAS approach then the ranking is ${\gimel }_8>{\gimel }_7>{\gimel }_3>{\gimel }_4>{\gimel }_5>{\gimel }_2>{\gimel }_1>{\gimel }_6$, and the best one is ${\gimel }_8$. The numerical results are shown in Table 17.

Our analysis involves a comprehensive comparison of our proposed methodology with different AOs and ranking methods. The primary objective is to rigorously validate the effectiveness and rationale of our novel approach presented in this research paper. By conducting thorough computations and rankings, we aim to discern the most optimal alternative. To achieve this, we employed a range of datasets and scenarios to test the adaptability and robustness of our method under various conditions. Ultimately, this comprehensive evaluation seeks to establish the reliability and practical utility of our approach in addressing real-world decision-making problems.

6 Conclusion

To better understand the complex dynamics of watersheds, which are vital parts of our natural landscape, hydrologists and environmental scientists rely on WSMs. A WSM is a computational depiction of the complex processes that occur within a watershed, such as the flow of water, the distribution of precipitation, the actions of soil and plants, and the effects of human activities. These models are based on the idea of simulating a watershed’s behavior under different conditions, which provides researchers, scientists, and policymakers with invaluable insights into water flow across the landscape, the transport of pollutants, and the impact of factors like land use change, climate variation, or infrastructure development on the watershed’s health and sustainability. Management of water supplies is a fundamental use case for WSMs. They allow for accurate forecasting and control of a watershed’s water supply. This is of critical importance in areas where water is scarce or when water is used for multiple purposes. These models help with water allocation, conservation policies, and infrastructure construction by providing realistic estimates of water availability and demand. In addition, watershed models assume a critical role in the prediction and management of floods. Through the simulation of a watershed’s reaction to intense precipitation or the melting of snow, these models can offer early notification of the likelihood of flooding occurrences. This aids communities in their preparedness and enables them to respond efficiently, thereby mitigating harm and safeguarding human lives. WSMs are also highly advantageous for environmental conservation and protection.

These tools provide an evaluation of the influence of human activities, such as agriculture, urbanization, or industrial operations, on the quality of water and the overall wellbeing of ecosystems within a given watershed. Understanding this information is crucial for formulating policies and implementing strategies that effectively address pollution and uphold the integrity of ecological equilibrium. In the context of a dynamic climate, the significance of WSMs is progressively escalating. These studies aid in comprehending the influence of climate change on precipitation patterns, temperature variations, and hydrological cycles within a specific watershed. Consequently, they furnish useful empirical evidence for the formulation of policies aimed at adapting to and mitigating the aforementioned impacts. WSMs are highly adaptable and essential instruments that serve to connect the divide between scientific comprehension and the implementation of effective watershed management strategies. These tools provide individuals with the ability to make well-informed choices regarding water resources, environmental preservation, and readiness for disasters, guaranteeing the sustainable utilization and safeguarding of one of the Earth’s most valuable assets water. These models play a crucial role in our repertoire for constructing resilient and ecologically sustainable communities that cater to the needs of both current and future generations. The use of integrated watershed models to examine complex watershed systems and facilitate integrated river basin management is on the rise. We think that improved watershed management and scientific understanding can both benefit from integrated watershed modeling.

The water, land, air, plant, and human nexus within the watershed should be modeled to accurately reflect its dynamics and coevolution. As a stand-in for models of watershed systems that incorporate decision-making algorithms, the management-focused model is useful. The explicit linkage of attribute values in the modern environment means that the generalized WPMM AO can address problems in MAGDM that arise in the real-world. So, we suggested forming a group AO to combine 2TL$q$-ROFNs. This article considered the DEMATEL-MOORA method’s stability, feasibility, and simplicity in the calculation process and proposed a new tool, the 2TL$q$-ROF-DEMATEL-MOORA method, built on the 2TL$q$-ROFWPMM AO, that can be used to express DMs’ complex and uncertain decision information in the MAGDM setting. In order to produce results that are consistent with real-world scenarios, the proposed method can assign different weights to the attributes depending on the nature of the problem at hand. The numerical example supports the claim that our proposed method is more flexible than existing approaches. Our proposed method is still vital for dealing with real-world MAGDM scenarios because of its advantages and benefits. In comparison to alternative methodologies, the recently developed decision-making algorithm exhibits a higher prevalence of adoption and effectively mitigates the loss of knowledge. While the proposed 2TL$q$-ROF-DEMATEL-MOORA method offers flexibility and enhanced decision-making capabilities in MAGDM settings, it does have some limitations. First, the model’s complexity can increase significantly with the inclusion of multiple attributes and DMs, potentially leading to computational challenges in large-scale applications. Additionally, the accuracy of the model’s results depends heavily on the quality and reliability of the input data, which can vary in real-world scenarios.

Moreover, the method’s effectiveness in predicting real-world watershed dynamics may be influenced by the limitations of the available data and the assumptions made during model development, such as the simplification of environmental processes and human behaviors. Furthermore, the approach may require more extensive validation under diverse environmental and socio-economic conditions to fully establish its generalizability and robustness across different geographical regions. In the future, we will plan to broaden our scope to encompass cases involving two variables. Our initial goal is to see if the method we have proposed can be applied to other typical MAGDM situations, such as supplier selection, medical diagnostics, and so on. The rest of the study will examine prospective alternative AOs for 2TL$q$-ROFS and discuss their use in MAGDM environments. Additionally, more comprehensive case studies and field validations are necessary to assess the model’s performance in various real-world watershed management scenarios, including diverse climate conditions and land-use practices. Extending the model to incorporate real-time data from remote sensing and Internet of Things devices could enhance its predictive power and adaptability. Future work could also explore the integration of machine learning techniques to further improve the model’s ability to handle uncertainty and dynamic changes in watershed systems. Furthermore, incorporating a wider range of socio-economic factors, such as population growth or economic activities, into the decision-making process could provide more holistic solutions for integrated watershed management.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JL: Writing–original draft, Writing–review and editing. HS: Writing–original draft, Writing–review and editing. AS: Writing–original draft, Writing–review and editing. MR: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. MB: Writing–original draft, Writing–review and editing. NS: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Educational Fund: Doctoral, and Scientific Research Start up Fund (Project No: 2019jb25).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akram, M., Bibi, R., and Deveci, M. (2023b). An outranking approach with 2-tuple linguistic Fermatean fuzzy sets for multi-attribute group decision-making. Eng. Appl. Artif. Intell. 121, 105992–992. doi:10.1016/j.engappai.2023.105992

CrossRef Full Text | Google Scholar

Akram, M., Khan, A., Luqman, A., Senapati, T., and Pamucar, D. (2023c). An extended MARCOS method for MCGDM under 2-tuple linguistic q-rung picture fuzzy environment. Eng. Appl. Artif. Intell. 120, 105892. doi:10.1016/j.engappai.2023.105892

CrossRef Full Text | Google Scholar

Akram, M., Muhammad, G., and Ahmad, D. (2023a). Analytical solution of the Atangana-Baleanu-Caputo fractional differential equations using Pythagorean fuzzy sets. Granul. Comput. 8 (4), 667–687. doi:10.1007/s41066-023-00364-3

CrossRef Full Text | Google Scholar

Akram, M., Naz, S., Feng, F., Ali, G., and Shafiq, A. (2023d). Extended MABAC method based on 2-tuple linguistic T-spherical fuzzy sets and Heronian mean operators: an application to alternative fuel selection. AIMS Math. 8 (5), 10619–10653. doi:10.3934/math.2023539

CrossRef Full Text | Google Scholar

Akram, M., Niaz, Z., and Feng, F. (2023e). Extended CODAS method for multi-attribute group decision-making based on 2-tuple linguistic Fermatean fuzzy Hamacher aggregation operators. Granul. Comput. 8 (3), 441–466. doi:10.1007/s41066-022-00332-3

CrossRef Full Text | Google Scholar

Al-shami, T. M., and Mhemdi, A. (2023). Generalized frame for orthopair fuzzy sets: (m, n)-fuzzy sets and their applications to multi-criteria decision-making methods. Information 14 (1), 56. doi:10.3390/info14010056

CrossRef Full Text | Google Scholar

Arora, R., Dhankhar, C., Yadav, A. K., and Kumar, K. (2023). “A TOPSIS method based on Entropy measure for q-rung orthopair fuzzy sets and its application in MADM,” in In soft computing for problem solving: proceedings of the SocProS. Singapore: springer nature Singapore, 709–718. doi:10.1007/978-981-19-6525-8-54

CrossRef Full Text | Google Scholar

Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20 (1), 87–96. doi:10.1016/s0165-0114(86)80034-3

CrossRef Full Text | Google Scholar

Aydemir, S. B., and Yilmaz Gunduz, S. (2020). Extension of multi-Moora method with some q-rung orthopair fuzzy Dombi prioritized weighted aggregation operators for multi-attribute decision making. Soft Comput. 24 (24), 18545–18563. doi:10.1007/s00500-020-05091-4

CrossRef Full Text | Google Scholar

Basaran, H. H., and Tarhan, I. (2022). Investigation of offshore wind characteristics for the northwest of Turkiye region by using multi-criteria decision-making method (MOORA). Results Eng. 16, 100–757.

CrossRef Full Text | Google Scholar

Brauers, W. K. M., and Zavadskas, E. K. (2012). Robustness of MULTIMOORA: a method for multi-objective optimization. Informatica 23 (1), 1–25. doi:10.15388/informatica.2012.346

CrossRef Full Text | Google Scholar

Deng, X., Wang, J., and Wei, G. (2020). Multiple attribute decision making based on power muirhead mean operators under 2-tuple linguistic pythagorean fuzzy environment. Cogn. Comput. 12 (6), 1276–1298. doi:10.1007/s12559-020-09756-y

CrossRef Full Text | Google Scholar

Denoeux, T. (2023). Reasoning with fuzzy and uncertain evidence using epistemic random fuzzy sets: general framework and practical models. Fuzzy Sets Syst. 453, 1–36. doi:10.1016/j.fss.2022.06.004

CrossRef Full Text | Google Scholar

Du, Y. W., and Shen, X. L. (2023). Group hierarchical DEMATEL method for reaching consensus. Comput. and Industrial Eng. 175, 108842–842. doi:10.1016/j.cie.2022.108842

CrossRef Full Text | Google Scholar

Eti, S., Dincer, H., Gokalp, Y., Yuksel, S., and Kararoglu, D. (2023). Identifying key issues to handle the inflation problem in the health care industry caused by energy prices: an evaluation with decision-making models. Manag. Inflat. Supply Chain Disruptions Glob. Econ., 162–178. doi:10.4018/978-1-6684-5876-1.ch011

CrossRef Full Text | Google Scholar

Ghiaci, A. M., and Ghoushchi, S. J. (2023). Assessment of barriers to IoT-enabled circular economy using an extended decision-making-based FMEA model under uncertain environment. Internet Things 22, 100–719.

Google Scholar

Guneri, B., and Deveci, M. (2023). Evaluation of supplier selection in the defense industry using q-rung orthopair fuzzy set based EDAS approach. Expert Syst. Appl. 222, 119846–846. doi:10.1016/j.eswa.2023.119846

CrossRef Full Text | Google Scholar

He, S., and Wang, Y. (2023). Evaluating new energy vehicles by picture fuzzy sets based on sentiment analysis from online reviews. Artif. Intell. Rev. 56 (3), 2171–2192. doi:10.1007/s10462-022-10217-1

CrossRef Full Text | Google Scholar

He, T., Wei, G., Lu, J., Wu, J., Wei, C., and Guo, Y. (2020b). A novel EDAS based method for multiple attribute group decision making with Pythagorean 2-tuple linguistic information. Technol. Econ. Dev. Econ. 26 (6), 1125–1138. doi:10.3846/tede.2020.12733

CrossRef Full Text | Google Scholar

He, T., Zhang, S., Wei, G., Wang, R., Wu, J., and Wei, C. (2020a). CODAS method for 2-tuple linguistic Pythagorean fuzzy multiple attribute group decision making and its application to financial management performance assessment. Technol. Econ. Dev. Econ. 26 (4), 920–932. doi:10.3846/tede.2020.11970

CrossRef Full Text | Google Scholar

Herrera, F., and Martinez, L. (2001). A model based on linguistic 2-tuples for dealing with multigranular hierarchical linguistic contexts in multi-expert decision-making. IEEE Trans. Syst. Man, Cybern. Part B Cybern. 31 (2), 227–234. doi:10.1109/3477.915345

PubMed Abstract | CrossRef Full Text | Google Scholar

Ihsan, M., Saeed, M., Khan, K. A., and Nosheen, A. (2023). An algebraic approach to the variants of convexity for soft expert approximate function with intuitionistic fuzzy setting. J. Taibah Univ. Sci. 17 (1), 2182144. doi:10.1080/16583655.2023.2182144

CrossRef Full Text | Google Scholar

Jin, F., Guo, S., Cai, Y., Liu, J., and Zhou, L. (2023). 2-Tuple linguistic decision-making with consistency adjustment strategy and data envelopment analysis. Eng. Appl. Artif. Intell. 118, 105671. doi:10.1016/j.engappai.2022.105671

CrossRef Full Text | Google Scholar

Komsiyah, S., and Balqis, D. A. (2023). Analysis of decision support system for determining industrial sub-district using DEMATEL-MABAC methods. Procedia Comput. Sci. 216, 499–509. doi:10.1016/j.procs.2022.12.162

CrossRef Full Text | Google Scholar

Kumar, R., Mishra, A. K., Dutta, S., Singh, A. K., and Kumar Singh, A. (2023). Optimization and prediction of response characteristics of electrical discharge machining using AHP-MOORA and RSM. Mater. Today Proc. 80, 333–338. doi:10.1016/j.matpr.2023.02.138

CrossRef Full Text | Google Scholar

Li, L., Zhang, R., Wang, J., Zhu, X., and Xing, Y. (2018). Pythagorean fuzzy power Muirhead mean operators with their application to multi-attribute decision making. J. Intelligent and Fuzzy Syst. 35 (2), 2035–2050. doi:10.3233/jifs-171907

CrossRef Full Text | Google Scholar

Liu, P., Khan, Q., and Mahmood, T. (2019a). Some single-valued neutrosophic power muirhead mean operators and their application to group decision making. J. Intelligent and Fuzzy Syst. 37 (2), 2515–2537. doi:10.3233/jifs-182774

CrossRef Full Text | Google Scholar

Liu, P., Khan, Q., Mahmood, T., and Hassan, N. (2019b). T-spherical fuzzy power Muirhead mean operator based on novel operational laws and their application in multi-attribute group decision making. IEEE Access 7, 22613–22632. doi:10.1109/access.2019.2896107

CrossRef Full Text | Google Scholar

Liu, P., and Liu, W. (2019). Multiple-attribute group decision-making method of linguistic q-rung orthopair fuzzy power Muirhead mean operators based on entropy weight. Int. J. Intelligent Syst. 34 (8), 1755–1794. doi:10.1002/int.22114

CrossRef Full Text | Google Scholar

Liu, P., and Qin, X. (2017). Power average operators of linguistic intuitionistic fuzzy numbers and their application to multiple-attribute decision making. J. Intelligent and Fuzzy Syst. 32 (1), 1029–1043. doi:10.3233/jifs-16231

CrossRef Full Text | Google Scholar

Mahmood, T., Haleemzai, I., Ali, Z., Pamucar, D., and Marinkovic, D. (2021). Power Muirhead mean operators for interval-valued linear Diophantine fuzzy sets and their application in decision-making strategies. Mathematics 10 (1), 70. doi:10.3390/math10010070

CrossRef Full Text | Google Scholar

Muirhead, R. F. (1902). Some methods applicable to identities and inequalities of symmetric algebraic functions of n letters. Proc. Edinb. Math. Soc. 21, 144–162. doi:10.1017/s001309150003460x

CrossRef Full Text | Google Scholar

Namburu, A., Mohan, S., Chakkaravarthy, S., and Selvaraj, P. (2023). Skin Cancer segmentation based on triangular intuitionistic fuzzy sets. SN Comput. Sci. 4 (3), 228. doi:10.1007/s42979-023-01701-8

CrossRef Full Text | Google Scholar

Naz, S., Akram, M., Al-Shamiri, M. M. A., Khalaf, M. M., and Yousaf, G. (2022a). A new MAGDM method with 2-tuple linguistic bipolar fuzzy Heronian mean operators. Math. Biosci. Eng. 19 (4), 3843–3878. doi:10.3934/mbe.2022177

PubMed Abstract | CrossRef Full Text | Google Scholar

Naz, S., Akram, M., Fatima, A., and Nadeem, A. (2022b). Q-rung orthopair fuzzy 2-tuple linguistic hamy mean operators for MAGDM with modified EDAS method. In real life applications of multiple criteria decision making techniques in fuzzy domain. Singap. Springer Nat. Singap., 369–415. doi:10.1007/978-981-19-4929−618

CrossRef Full Text | Google Scholar

Naz, S., Akram, M., Shafiq, A., and Akhtar, K. (2024). Optimal airport selection utilizing power Muirhead mean based group decision model with 2-tuple linguistic q-rung orthopair fuzzy information. Int. J. Mach. Learn. Cybern. 15 (2), 303–340. doi:10.1007/s13042-023-01911-9

CrossRef Full Text | Google Scholar

Naz, S., Shafiq, A., Butt, S. A., and Ijaz, R. (2023). A new approach to sentiment analysis algorithms: extended SWARA-MABAC method with 2-tuple linguistic q-rung orthopair fuzzy information. Eng. Appl. Artif. Intell. 126, 106943–943. doi:10.1016/j.engappai.2023.106943

CrossRef Full Text | Google Scholar

Ozdemirci, F., Yuksel, S., Dincer, H., and Eti, S. (2023). An assessment of alternative social banking systems using T-spherical fuzzy TOP-DEMATEL approach. Decis. Anal. J. 6, 100184–184. doi:10.1016/j.dajour.2023.100184

CrossRef Full Text | Google Scholar

Pan, L., Deng, Y., and Cheong, K. H. (2023). Quaternion model of Pythagorean fuzzy sets and its distance measure. Expert Syst. Appl. 213, 119222–222. doi:10.1016/j.eswa.2022.119222

CrossRef Full Text | Google Scholar

Priyanka, R., Ravindran, K., Sankaranarayanan, B., and Ali, S. M. (2023). A fuzzy DEMATEL decision modeling framework for identifying key human resources challenges in start-up companies: implications for sustainable development. Decis. Anal. J. 6, 100192–192. doi:10.1016/j.dajour.2023.100192

CrossRef Full Text | Google Scholar

Rao, F., and Xiao, M. (2023). A novel MADM algorithm for physical education teaching quality evaluation based on 2-tuple linguistic neutrosophic numbers power Heronian mean operators. Plos One 18 (2), e0279534. doi:10.1371/journal.pone.0279534

PubMed Abstract | CrossRef Full Text | Google Scholar

Razzaque, A., Razaq, A., Alhamzi, G., Garg, H., and Faraz, M. I. (2023). A detailed study of mathematical rings in q-rung orthopair fuzzy framework. Symmetry. 15 (3), 697. doi:10.3390/sym15030697

CrossRef Full Text | Google Scholar

Saeed, M., Ahmad, M. R., and Rahman, A. U. (2023). Refined Pythagorean fuzzy sets: properties, set-theoretic operations and axiomatic results. J. Comput. Cognitive Eng. 2 (1), 10–16. doi:10.47852/bonviewjcce2023512225

CrossRef Full Text | Google Scholar

Sarkar, A., Deb, N., and Biswas, A. (2023). Weighted dual hesitant $$q$$-rung orthopair fuzzy sets and their application in multicriteria group decision making based on Hamacher operations. Comput. Appl. Math. 42 (1), 40. doi:10.1007/s40314-022-02160-2

CrossRef Full Text | Google Scholar

Sevim, F., and Kurtaran, A. T. (2023). Evaluation of Turkey’s health tourism performance with the MOORA method. Gumushane Univ. Sos. Bilim. Derg. 14 (1), 99–109.

Google Scholar

Shahzadi, G., Luqman, A., and Ali Al-Shamiri, M. M. (2022). The extended MOORA method based on Fermatean fuzzy information. Math. Problems Eng. 2022 (1), 7595872.

Google Scholar

Wan, B., Hu, Z., Garg, H., Cheng, Y., and Han, M. (2023). An integrated group decision-making method for the evaluation of hypertension follow-up systems using interval-valued q-rung orthopair fuzzy sets. Complex and Intelligent Syst. 9 (4), 4521–4554. doi:10.1007/s40747-022-00953-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wankhede, S., Pesode, P., Pawar, S., and Lobo, R. (2023). Comparison study of GRA, COPRAS and MOORA for ranking of phase change material for cooling system. Mater. Today Proc. doi:10.1016/j.matpr.2023.02.437

CrossRef Full Text | Google Scholar

Wu, W. W., and Lee, Y. T. (2007). Developing global managers’ competencies using the fuzzy DEMATEL method. Expert Syst. Appl. 32 (2), 499–507. doi:10.1016/j.eswa.2005.12.005

CrossRef Full Text | Google Scholar

Yager, R. R. (2013). Pythagorean membership grades in multicriteria decision making. IEEE Trans. Fuzzy Syst. 22 (4), 958–965. doi:10.1109/tfuzz.2013.2278989

CrossRef Full Text | Google Scholar

Yager, R. R. (2016). Generalized orthopair fuzzy sets. IEEE trans. Fuzzy syst., IEEE transactions on fuzzy systems, 25(5), 1222–1230. doi:10.1109/tfuzz.2016.2604005

CrossRef Full Text | Google Scholar

Yilmaz, I., Erdebilli, B., Naji, M. A., and Mousrij, A. (2023). A fuzzy DEMATEL framework for maintenance performance improvement: a case of Moroccan chemical industry. J. Eng. Res. 11 (1), 100019–019. doi:10.1016/j.jer.2023.100019

CrossRef Full Text | Google Scholar

Yue, Q., Zou, W., and Hu, W. (2023). A new theory of triangular intuitionistic fuzzy sets to solve the two-sided matching problem. Alexandria Eng. J. 63, 57–73. doi:10.1016/j.aej.2022.07.018

CrossRef Full Text | Google Scholar

Zadeh, L. A. (1965). Fuzzy sets. Inf. Control 8 (3), 338–353. doi:10.1016/s0019-9958(65)90241-x

CrossRef Full Text | Google Scholar

Zeng, S., Ali, Z., Mahmood, T., and Jin, H. (2022). Complex interval-valued q-rung orthopair 2-tuple linguistic aggregation operators and their application in multi-attribute decision-making. Appl. Artif. Intell. 36 (1), 2033471. doi:10.1080/08839514.2022.2033471

CrossRef Full Text | Google Scholar

Zhang, Z. X., Wang, L., Wang, Y. M., and Martinez, L. (2023). A novel alpha-level sets based fuzzy DEMATEL method considering experts’ hesitant information. Expert Syst. Appl. 213, 118925–925. doi:10.1016/j.eswa.2022.118925

CrossRef Full Text | Google Scholar