- 1Human Sciences Research Council (HSRC), Pretoria, South Africa
- 2Department of Biomedical Engineering, College of Biomedical Engineering, Taiyuan University of Technology, Taiyuan, China
- 3Department of Mathematics, Taiyuan University of Technology, Taiyuan, China
- 4Department of Mathematics, Tshwane University of Technology, Pretoria, South Africa
- 5Department of Mathematics, Federal University, Dutse, Nigeria
- 6AGEIS Laboratory, University Grenoble Alpes, Saint Martin d'Hères, France
In this study, a mathematical model for studying the dynamics of monkeypox virus transmission with non-pharmaceutical intervention is created, examined, and simulated using real-time data. Positiveness, invariance, and boundedness of the solutions are thus examined as fundamental features of mathematical models. The equilibrium points and the prerequisites for their stability are achieved. The basic reproduction number and thus the virus transmission coefficient ℜ0 were determined and quantitatively used to study the global stability of the model's steady state. Furthermore, this study considered the sensitivity analysis of the parameters according to ℜ0. The most sensitive variables that are important for infection control are determined using the normalized forward sensitivity index. Data from the United Kingdom collected between May and August 2022, which also aid in demonstrating the usefulness and practical application of the model to the spread of the disease in the United Kingdom, were used. In addition, using the Caputo–Fabrizio operator, Krasnoselskii's fixed point theorem has been used to analyze the existence and uniqueness of the solutions to the suggested model. The numerical simulations are presented to assess the system dynamic behavior. More vulnerability was observed when monkeypox virus cases first appeared recently as a result of numerical calculations. We advise the policymakers to consider these elements to control monkeypox transmission. Based on these findings, we hypothesized that another control parameter could be the memory index or fractional order.
1. Introduction
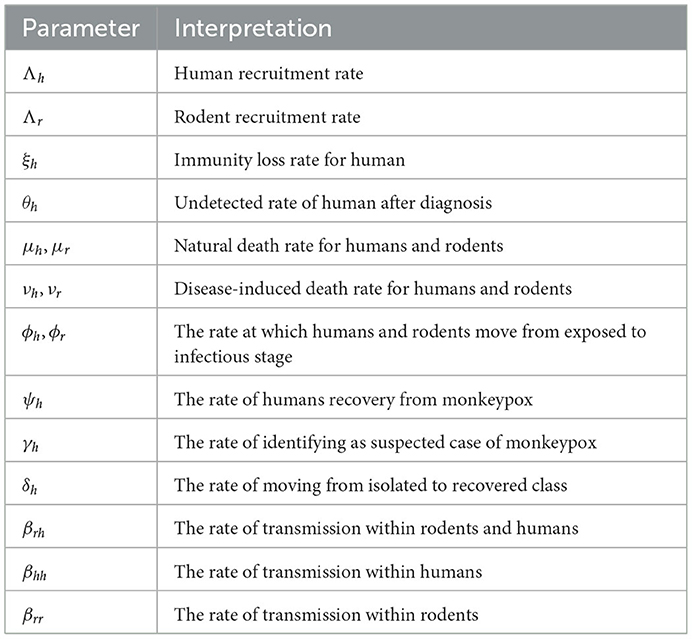
The unexpected breakout and global spread of monkeypox have drawn the attention of scientists due to the continuing COVID-19 pandemic. The prevalence of the largest and most pervasive monkeypox pandemic outside of Africa as of 22 June 2022, is 3,340 confirmed cases reported across the world. In addition to mother-to-child vertical transmission, the monkeypox virus can spread from person to person by direct contact with infectious skin or mucosal skin lesions, respiratory droplets, or indirect contact with contaminated objects or materials. The possibility of community transmission cannot be ruled out, and it may also be sexually transferred by semen or vaginal fluid. The virus that causes monkeypox is called the monkeypox virus, and it is an enveloped, linear, double-stranded DNA virus that belongs to the Chordopoxvirinae subfamily of the Poxviridae family. With symptoms of the disease lasting 2–4 weeks and a death rate that previously ranged from 0 to 11 deaths, monkeypox is often a self-limiting sickness. Intense headaches, fever, lesions, and lymphadenopathy are some of the symptoms of monkeypox. Antiviral medications and smallpox vaccines have been approved for use in various nations in response to the monkeypox outbreak, despite the fact that there is no specific treatment or vaccine for monkeypox virus infection. Before allowing the virus to successfully establish person-to-person transmission, quick action is required to stop the local development of the disease and, consequently, the global monkeypox outbreak (1–11). In Peter et al. (12), modeling and optimal control were used to study monkeypox and the cost-effective strategies were investigated. This study shows that, among all competing measures, combining preventative measures to reduce rodent-to-human disease transmission is the most practical and cost-effective option.
Numerous research articles have been published where both classical and fractional models were constructed, and there is a plethora of literature on modeling infectious diseases. Because fractional-order derivative has unique properties such as heredity and memory that enable it to fully comprehend the dynamics of real phenomena, an analysis based on fractional-order derivative is more advantageous and practical than an analysis based on classical derivative (13, 14). At two separate closed locations, the phenomenon is indistinguishable by the standard derivatives. A generalized derivative known as the fractional order was proposed to address the problems with ordinary derivatives (15). Many researchers used fractional- order derivatives in many fields, as shown in Kumar et al. (16), Higazy et al. (17), Djida and Atangana (18), Baba (19), Owolabi and Atangana (20), Mohammadi et al. (21), Baleanu et al. (22), and Wutiphol and Turab (23). In the realm of mathematical biology, the Mittag–Leffler-type kernel has been used continuously over other derivatives, and numerous epidemiological models, such as for dengue fever, smoking, tuberculosis, measles, Ebola, and other diseases, have been studied using this operator as shown in Asamoah et al. (24), Peter et al. (25, 26), Kumar et al. (27), Morales-Delgadoa et al. (28), Atangana and Baleanu (29), and Atangana et al. (30). Most notably, in Zhang et al. (31), the Mittag–Leffler-type kernel modeling for Ebola–malaria co-infection was investigated by the authors with the best possible control. They strongly recommended the Mittag–Leffler-type kernel. In Kumar et al. (32), investigated the COVID-19 model using singular and non-singular fractional operators and compared the results of these operators. In Aslam et al. (33), the authors examined a recent study on the mathematical modeling of HIV/AIDS using the Mittag–Leffler-type kernel and came to the conclusion that the infection rate decreases with decreasing operator. In Evirgen (34), the authors studied the transmission dynamics of the Nipah virus using the Caputo derivative. One of the interesting segments of their study was to focus on tracing the influence of fractional-order derivatives on the manner in which the model responds. In Ucar (35), the authors investigated a fractional SAIDR model within the framework of the Mittag–Leffler-type kernel. The effectiveness of the fractional operator is shown through a numerical simulation.
Considering the characteristics of exponential decay, the Caputo–Fabrizio fractional-order operator has been preferred over Atangana–Beleanu beta derivatives and a few other operators in the field of mathematical biology with more information (17–19, 24, 36–39). For instance, in Addai et al. (40), the authors studied a novel model of COVID-19 incorporating Alzheimer's disease using the Caputo–Fabrizio fractional-order operator. The results of the aforementioned study revealed that the two diseases have a link and the authors also concluded that the fractional operator is related to the rate of infection. In Shaikh and Nisar (41), the authors also considered the transmission dynamics of a fractional-order typhoid fever model using the Caputo–Fabrizio operator and the existence theory and achieved numerical solutions. In Shah et al. (42), Shah and his co-authors conducted a semi-analytical study of the Pine Wilt Disease (PWD) model with a convex rate via fractional order involving a non-singular kernel. To comprehend the trade-off between the lockdown and the transmission of the virus, Ahmed and his co-authors devised a five-term dynamical system (43). Another use of the Caputo–Fabrizio fractional-order operator was indicated, for instance, in Addai et al. (40), Shaikh and Nisar (41), Shah et al. (42), Ahmed et al. (43), Ullah et al. (44), Abboubakar et al. (45).
Furthermore, in Peter et al. (46), the authors used real data from Nigeria to study the dynamics of the transmission of the monkeypox virus using fractional calculus. The authors presented an argument on the modeling system by studying the infection control policies that will help the public to better understand the significance of control parameters in the eradication of the virus in the studied population. Furthermore, the transmission dynamics of the monkeypox virus was studied using a mathematical modeling approach in Peter et al. (47). In their findings, the authors indicated that the isolation of infected individuals in the human population helps reduce the transmission of the disease, which can serve as a form of intervention to control the spread of the virus.
We observed that none of the studies on the monkeypox virus and its modes of transmission took into account the interaction between the isolated and exposed compartments in the human subpopulation and the results of that contact rate with the rodent population and applied the modeling approach to real data from the United Kingdom. The major goals of this research are to calculate the exponential growth rate of the monkeypox virus, to forecast what might occur in future and how to stop it from spreading, and to understand the effects of non-pharmaceutical intervention on infected individuals, which will be able to guide us on how to deploy intervention resources to contain the spread of the disease. The remaining sections of the article are structured as follows: Section 2 presents some basic definitions and preliminary information, Section 3 presents the model formulation, Sections 4 deals with the dynamism of the model, Section 5 computes the basic reproduction number and some basic mathematical analysis, Section 6 present the endemic equilibrium of the model, Section 7 proves the existence and uniqueness of our model, Section 8 deals with the fitting of the model to real data from the United Kingdom, Section 9 presents numerical schemes and numerical simulations, Section 10 deals with sensitivity analysis, and Section 11 provides some perspectives, discussion, and conclusion.
2. Preliminaries
In this section, we review several key definitions, lemmas, and concepts that are necessary to understand the suggested model.
Definition 2.1 Let f ∈ Q1(p, q), q > p, and α∗ ∈ (0, 1) (17), (40). Then, the Caputo–Fabrizio fractional-order derivative can be defined as
Here, G(α) is a normalization function, where G(0) = G(1) = 1. The fractional integral of the Caputo–Fabrizio fractional order is defined by:
Lemma 2.2 Assuming there is a function u(t) ∈ Wl[0, η], then the solution of fractional differential equation
is given by
Lemma 2.3 Suppose A ⊂ B be a closed convex non-empty subset of A and there exist two operators, T1 and T2, then it is Krasnoselskii's fixed point theorem (40) and it follows that:
(i) T1u + T1u ∈ A, ∀u ∈ A;
(ii) T1 is contraction and T2 continuous and compact. Then quantify at least one solution u ∈ A such that
3. Model formulation
Using a system of differential equations, we studied both human and rodent populations in a closed homogeneous environment. There are five compartments in a human population of size Nh(t): Susceptible Sh(t); Exposed Eh(t); Infected Ih(t); Isolation/Quarantine Qh(t); and Recovered Rh(t); where Nh(t) = Sh(t) + Eh(t) + Ih(t) + Qh(t) + Rh(t). The rodent population Nr(t) is split into Sr(t) Susceptible; Er(t) Exposed; and Ir(t) Infected. Let Nr(t) = Sr(t) + Er(t) + Ir(t). From the aforementioned description, using the ideas in Yinka-Ogunleye et al. (5), we extend the studies of Peter et al. (46) and (47), then the ordinary differential equations in system (1) describe the dynamics of monkeypox transmission incorporating non-pharmaceutical intervention;
where . To capture the memory in the predictions of the monkeypox virus transmission model and also to verify that both sides of the fractional equations have exact dimensions, the time-dependent kernel is defined by the power law correlation function, as in Tilahuna et al. (48); therefore, we propose the following fractional-order model for the monkeypox virus transmission model using the Caputo–Fabrizio fractional-order derivative;
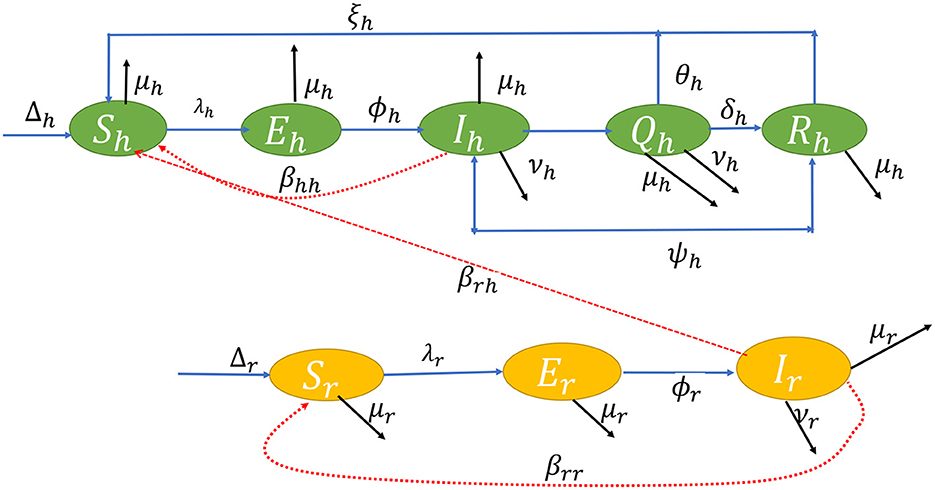
The flow diagram of the model equation is presented in Figure 1 while the parameters used in the model and their signification is presented in Table 1.
4. Dynamics of the model
In this section, we focus on the dynamics of the solutions for the suggested models (1) and (2) that are positive, bounded, and invariant. In an epidemiological model, it is important to evaluate the population survival and the expansion that is naturally constrained by scarce resources. As a result, we demonstrate the following theorem.
Theorem 1. The solution of (1) along with initial conditions is positively invariant and bounded in . Therefore,
Proof. Using the results in Lin (49) and taking into account the initial values given, from model (2), we obtain
From Equation (4), we can see that Sh(0) > 0, Eh(0) > 0, Ih(0) > 0, Rh(0) > 0, Sv(0) > 0, Ev(0) > 0, Iv(0) > 0, for all t > 0. From Equation (2), the first equation gives
Then, by applying the fractional comparison technique, we obtain the first estimate of Equation (4). We continue for the second equation of the system of Equation (2), we obtain
Therefore, we get the second estimate of Equation (1). We continue again for the third equation of the system of Equation (2), we obtain
and, consequently, we obtain the third estimate of Equation (4). Similarly, for the fourth to eighth equation, we obtain the estimate of Equation (4). Hence, Theorem 1 is complete.
4.1. Monkeypox equilibrium state
The monkeypox model is studied by obtaining the equilibrium states. To verify the existence of the equilibrium points, the derivatives of the model on the right-hand side are set to zero, which provides the monkeypox disease free equilibrium points.
We assume Eh, Er, Ih, Ir, Qh, Rh, Sh, Sr be the solution to the monkeypox model with the initial condition in a feasible region such that
where the human population is represented as
and the rodent population, respectively,
To achieve the disease-free equilibrium state, the derivatives are set to zero as seen in (10) to obtain
By setting the derivatives to zero, we obtain
hence, Equation (9) is represented as
This equation describes a population free of monkeypox infection and is denoted as E*
5. The basic reproduction number
We derive the basic reproduction number ℜ0 by using the next-generation matrix approach (25). Since Eh, Ih, Qh, and Ir are the disease-infected classes, hence,
The next-generation matrix (G) is given by
The basic reproduction number is the dominant eigenvalue (spectral radius) of the next-generation matrix G, that is, ℜ0 = ρ(G)
5.1. Stability of monkeypox-free equilibrium (MFE)
Investigating the stability of the monkeypox disease-free equilibrium, we compute the Jacobian matrix of the system at the disease-free equilibrium by obtaining the eigenvalues, which will be used to determine the stability of the model.
where ζ1 and ζ2 are represented in Equations (17) and (18)
Evaluating at the monkeypox-free equilibrium (MFE), we obtain
We compute the eigenvalues from the using the characteristic polynomial of O8, which will not be represented as a result of its lengthiness. The eigenvalues and characteristic polynomial are calculated by , where I is an 8 × 8 unit matrix, and the values of λ are obtained:
Let Δ1 and Δ2 be well represented from Equation (20) in Equations (21) and (22)
Then,
From the calculated eigenvalues, we obtain negative real parts, that is, the monkeypox-free equilibrium is asymptotically stable if
Upon simplification, we obtain Equation (31):
Therefore, the monkeypox-free equilibrium state is asymptotically stable.
5.2. Global stability of the equilibrium state
If ℜ0 < 1, then the monkeypox-free equilibrium is globally asymptotically stable; otherwise, it is unstable. This is proven by the Lyapunov function such that
Differentiating, we obtain
At the disease-free equilibrium state as seen in Equation (11),
From the result obtained in Equation (39), we can see that provided ℜ0 ≤ 0 as well as provided that ℜ0 = 0 or Eh = 0. Global stability of the disease-free equilibrium is asymptotically stable, if ℜ0 ≤ 0; otherwise, it is unstable.
6. Endemic equilibrium state
The endemic equilibrium state occurs when the rate of infection persists in the population and it is represented in Equations (40 - 47) by
where
7. Existence and uniqueness results for the monkeypox transmission model with non-pharmaceutical intervention
We reformulate Equation (2) as follows:
From Equation (10), the developed model of Equation (1) can be written in the form
therefore,
With the help of Lemma 2.4, Equation (49) yields
Furthermore, let ussay E = C([0, η]) is the Banach space, and supposing that the following assumptions hold;
(H1), there exists a non-negative constant Q, W, and k ∈ [0, 1) such that
(H2) There exists a nonnegative constant Cρ > 0 for all , then
Furthermore, let us define operator Am : E → E such that
therefore, we can see that
From this knowledge, Equation (52) can be written as
Theorem 2. Suppose that (H1) and (H2) hold, such that , then, the monkeypox transmission model with non-pharmaceutical intervention has at least one solution.
Proof. For simplicity, we divide the proof into two steps.
Step 1. We prove that operator M1 is contraction. Then, let , where Ω = {Φ ∈ Z : ||Φ|| ≤ ϑ, ϑ > 0} is a close convex set, thus
Thus,
Hence, M1 is contraction since .
Step 2. We also prove that M2 is compact and also continuous; for all Φ ∈ Ω, then M2 will be continuous as Φ is continuous, thus
Hence, M2 is boundedness. For equicontinuous, let t1, t2 ∈ [0, η] such that
As t1 → t2, then |(M2Φ)(t1) − (M2Φ)(t2)| → 0, which makes operator M2 equicontinuous and compact by the Arzela–Ascoli theorem. Therefore, by Lemma 2.3, the existence for the monkeypox transmission model with non-pharmaceutical intervention has at least one solution. □
Theorem 3. Suppose that ∃ is a nonnegative integer Λρ is > 0 such that
then operator Am has a unique fixed point.
Proof. Let , then we say
Hence, by the Banach contraction principle, Am has a unique fixed point. Consequently, the monkeypox transmission model with non-pharmaceutical intervention has a unique solution. □
8. Fitting of model to data
We used the available public database to collect our data while the formulated model of Equation (1) includes 16 parameters. To treat the waggliness of the reported daily new cases, we smoothed the data to remove noise from the data set so as to make it suitable for our analysis. The total population of the United Kingdom is 68,530,739 (1), which was used for calculating the initial number of susceptible humans, while the initial value for the number of infected humans was calculated from the reported daily new cases. Other initial values were assumed.
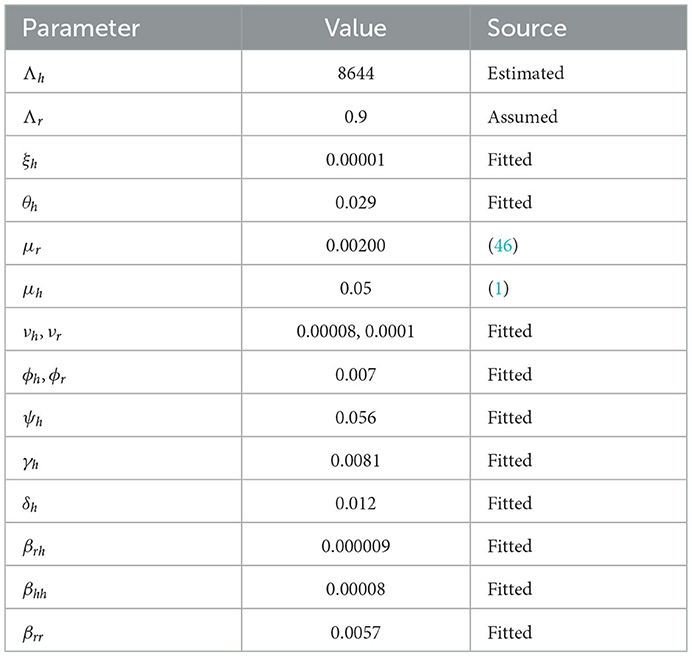
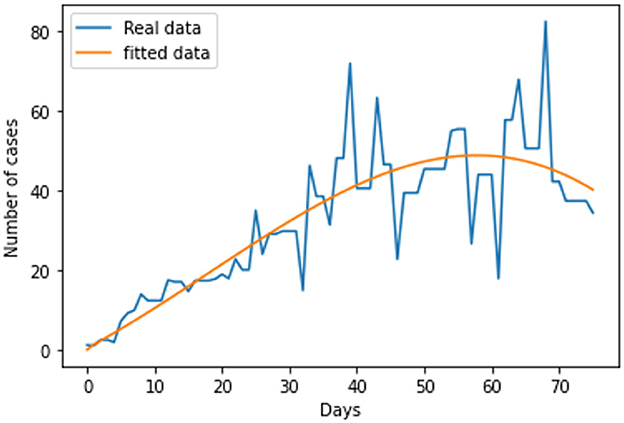
The link to the data used for this research and the initial values; Sh(t) = 68530739; Eh(t) = 0; Ih(t) = 31412; Qh(t) = 0; Sr(t) = 1074103; Er(t) = 1074103; and Ir(t) = 1074103; can be found in the Data Availability section. The parameters are fitted based on the smoothed reported daily new cases of infected humans from May to August 2022. This information was taken from the United Kingdom public health database (1). The nonlinear least square technique was used to fit the model using python programming. Table 2 shows all of the parameter values that were fitted, and Figure 2 shows the data fitting of the observed smoothed daily new cases.
9. Numerical scheme
In this section, we present the numerical results for the monkeypox transmission model with non-pharmaceutical intervention based on the Lagrange interpolation. Details about the numerical scheme is presented in Atangana and Owolabi (50). The Cauchy problem of the CF fractional derivative can be given as:
On the other hand, we can express Equation (60) as
Taking Equation (61) at the point tn+1 = (n + 1)h and tn = nh, n = 0, 1, 2, 3, …, with h being the time step, we have
Taking the results of Equations (62)-(63) in
Equation (64) in the two-step Lagrange polynomial gives
The aforementioned Equation (65) leads to
Solving the integrals in Equation (66) yields
Substituting Equation (67) into Equation (66), then generalizing the numerical scheme of CF is as follows:
Thus, in terms of our CF-fractional monkeypox transmission model with non-pharmaceutical intervention, we obtain;
10. Sensitivity analysis
Since an epidemiological system's parameters are either estimated or fitted, there is some degree of uncertainty in the numbers that are utilized to derive conclusions about the underlying epidemic. It is crucial to evaluate the individual effects of each parameter on the dynamics of the epidemic to identify those effects that have the greatest impact on the epidemic's spread or contraction. For biological factors included in the proposed monkeypox model, we perform the sensitivity analysis in this section. This analysis is investigated analytically by computing , where, p = (βhh, Λh, ϕh, μh, γh, νh, and ψh). The sensitivity of ℜ0 to each parameter is as follows:
thus,
The sensitivity index technique will help measure the most sensitive parameters for the fundamental reproductive number ℜ0 (Borgonovo et al. (51) for details about the method). The fundamental reproduction number's normalized sensitivity index is provided by , where p is a parameter as defined earlier. We obtain
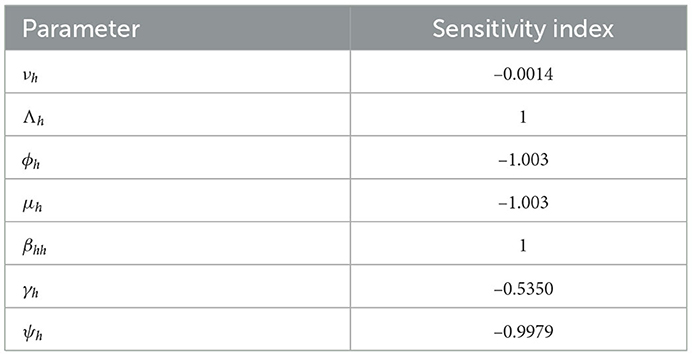
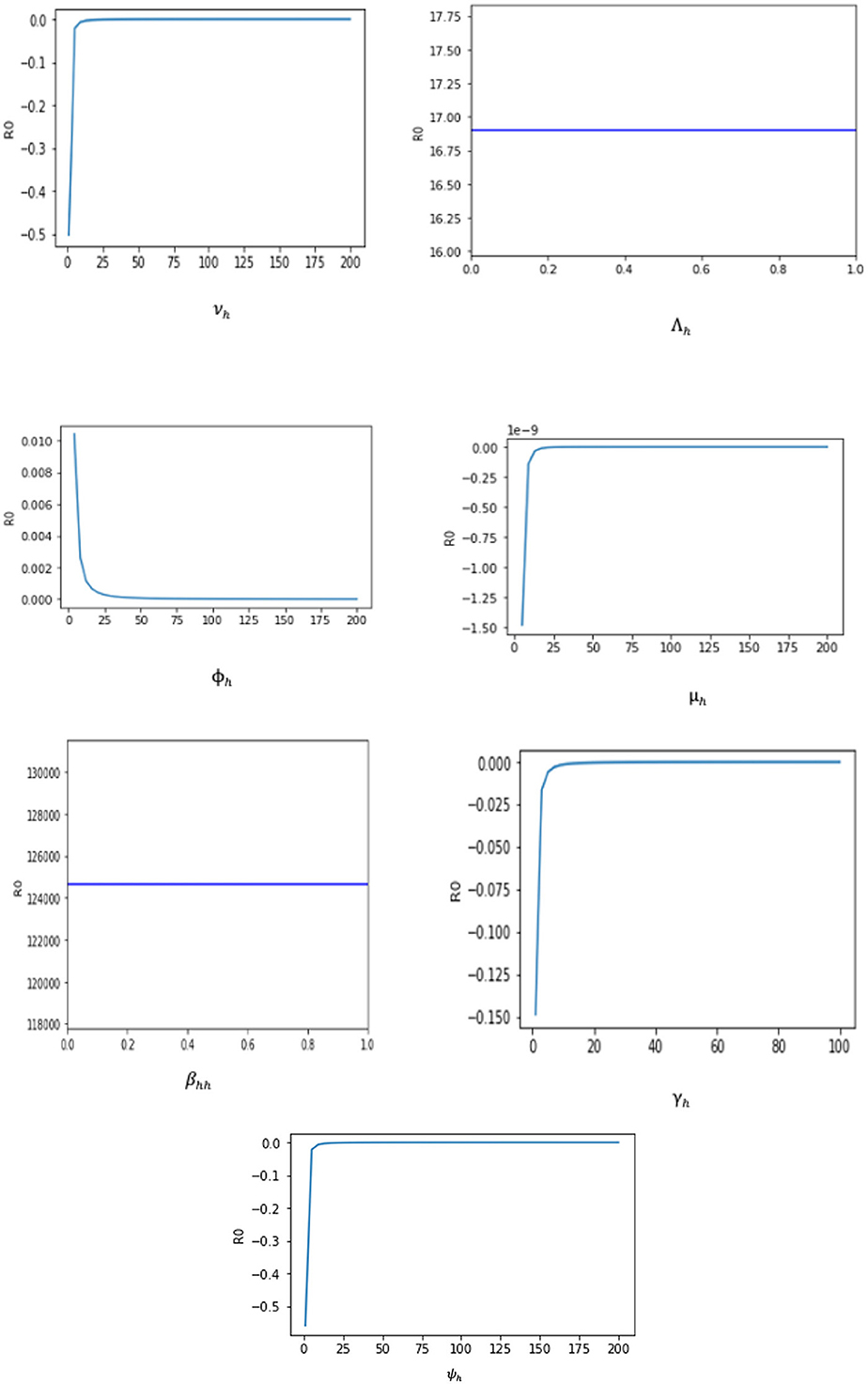
The sensitivity indices using the parameter values given in Table 2 are presented in Table 3. The sensitivity analysis of βhh, Λh, ϕh, ψh, νh, γh, and μh with respect to ℜ0 and their graphs are presented in Figure 3.
Two of the sensitivity indices are positive while others are negative, as can be seen in Table 3. Additionally, the majority of these indices are functions of the Caputo–Fabrizio fractional monkeypox model parameters. This implies that changing one of the parameters slightly will alter the dynamics of the epidemic. The basic reproductive number ℜ0 normalized sensitivity indices to the Caputo–Fabrizio fractional monkeypox model parameters are calculated. We conclude that increasing the rate of recovery and the rate of identifying suspected cases, that is, isolation and quarantining of the monkeypox virus carrier will aid in decreasing the ℜ0, which is an affirmation of the effect of non-pharmaceutical intervention to combat the spread of the virus.
11. Discussion and conclusion
Following the estimation of parameter values and data fitting, we simulate the Caputo–Fabrizio fractional monkeypox virus model using the parameter values, as presented in Table 2. The fitted Caputo–Fabrizio curve and ℜ0 are given in Figure 2. Figures 4, 5 show dynamic behavior for all the nine compartments involved in the proposed Caputo–Fabrizio fractional monkeypox virus model. We observed a significantly high susceptibility and infection in the solution pathways of individual species. The work of Hammouch et al. (52), Bonyah et al. (53), Peter (54), and Sene (55) have provided a strong basis for the discussion of our results. This indicates that, whenever the memory index increases, the rate at which people get infected with monkeypox virus reduces and vice versa, which then indicates that, using fractional order, we can obtain clear qualitative information on monkeypox virus transmission. In Figure 6, we varied the input parameter γh on quarantine and exposed, respectively, to observe variation in the system dynamics. We noticed the contribution of this parameter in the transmission pathways of infected individuals. In a similar way, we varied the input parameters δh and ψh on individual recovery and noticed the variation in the trajectory of monkeypox recovery. We discovered that the rate at which humans and rodents move from exposed to infectious stage is also important and potentially dangerous in terms of increasing the level of monkeypox infection.
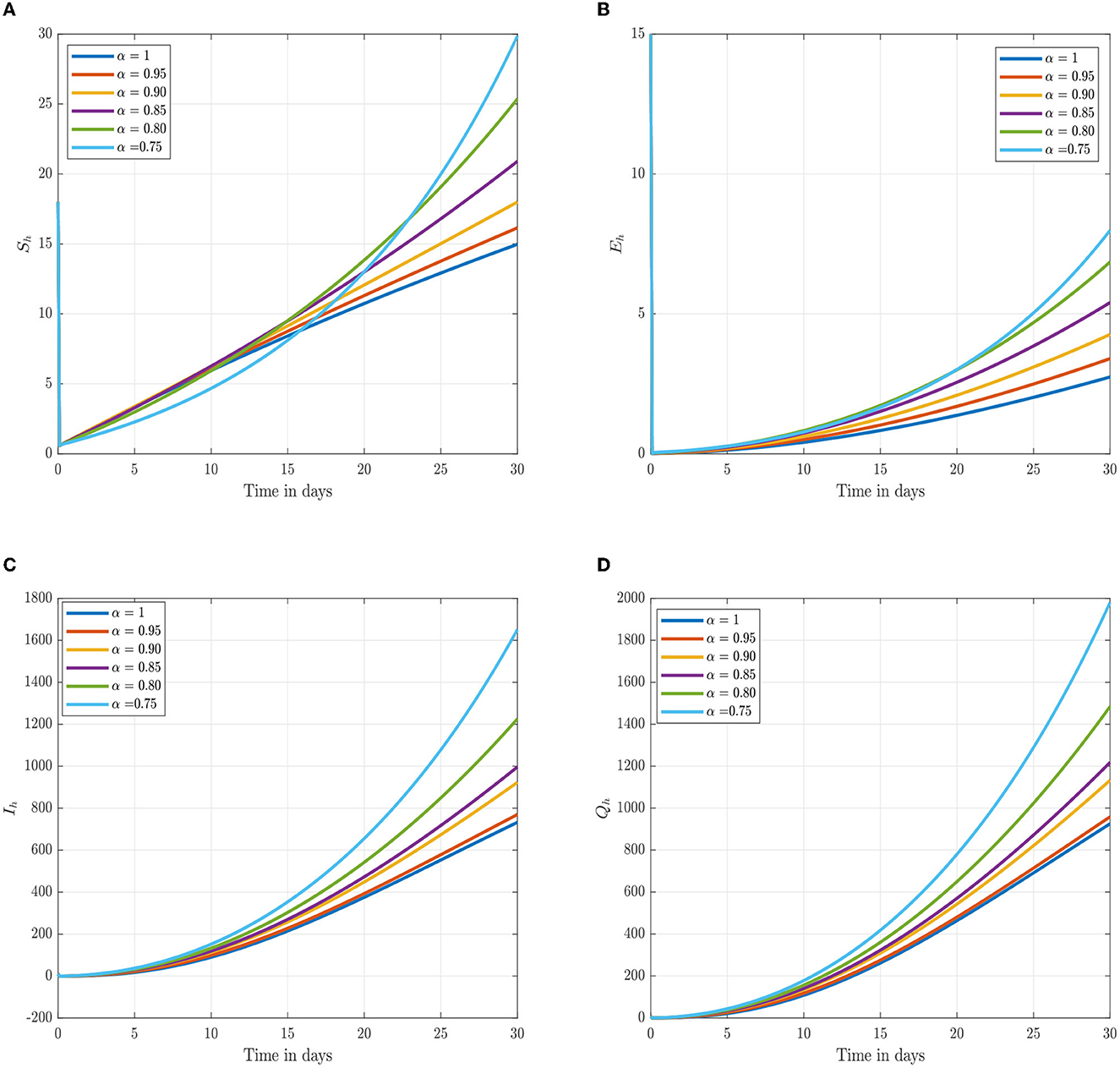
Figure 4. Numerical trajectory of the CF-fractional-order derivative, α, of Equation (2). (A) Dynamics of susceptible (Sh) humans class. (B) Dynamics of expose (Eh) humans class. (C) Dynamics of infected (Ih) humans class. (D) Dynamics of quarantine (Qh) class.
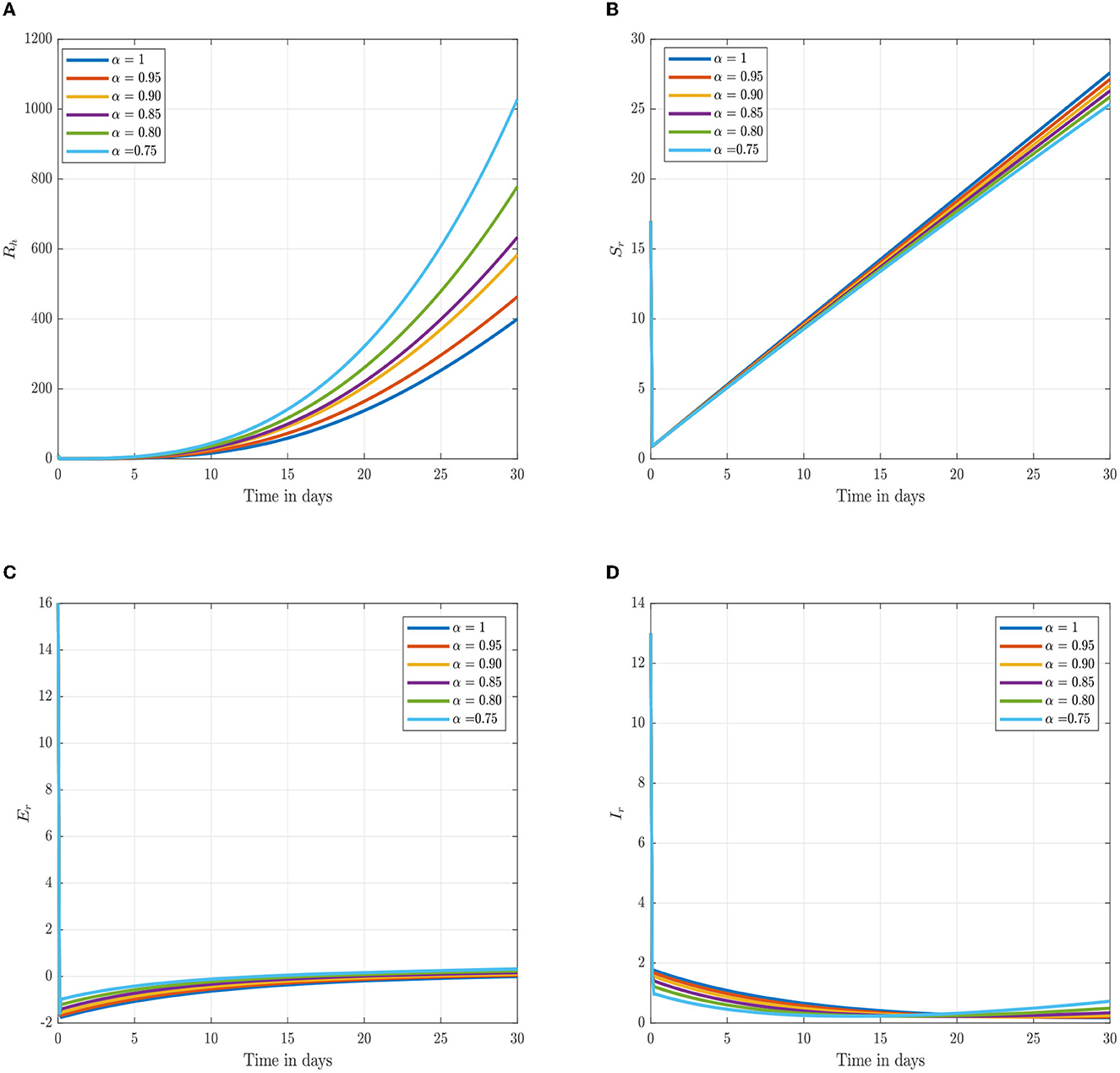
Figure 5. Numerical trajectory of the CF-fractional-order derivative, α, of Equation (2). (A) Dynamics of recovery (Rh) class. (B) Dynamics of susceptible (Sr) rodents class. (C) Dynamics of exposed (Er) rodents class. (D) Dynamics of asymptomatic infected (Ir) rodents class.
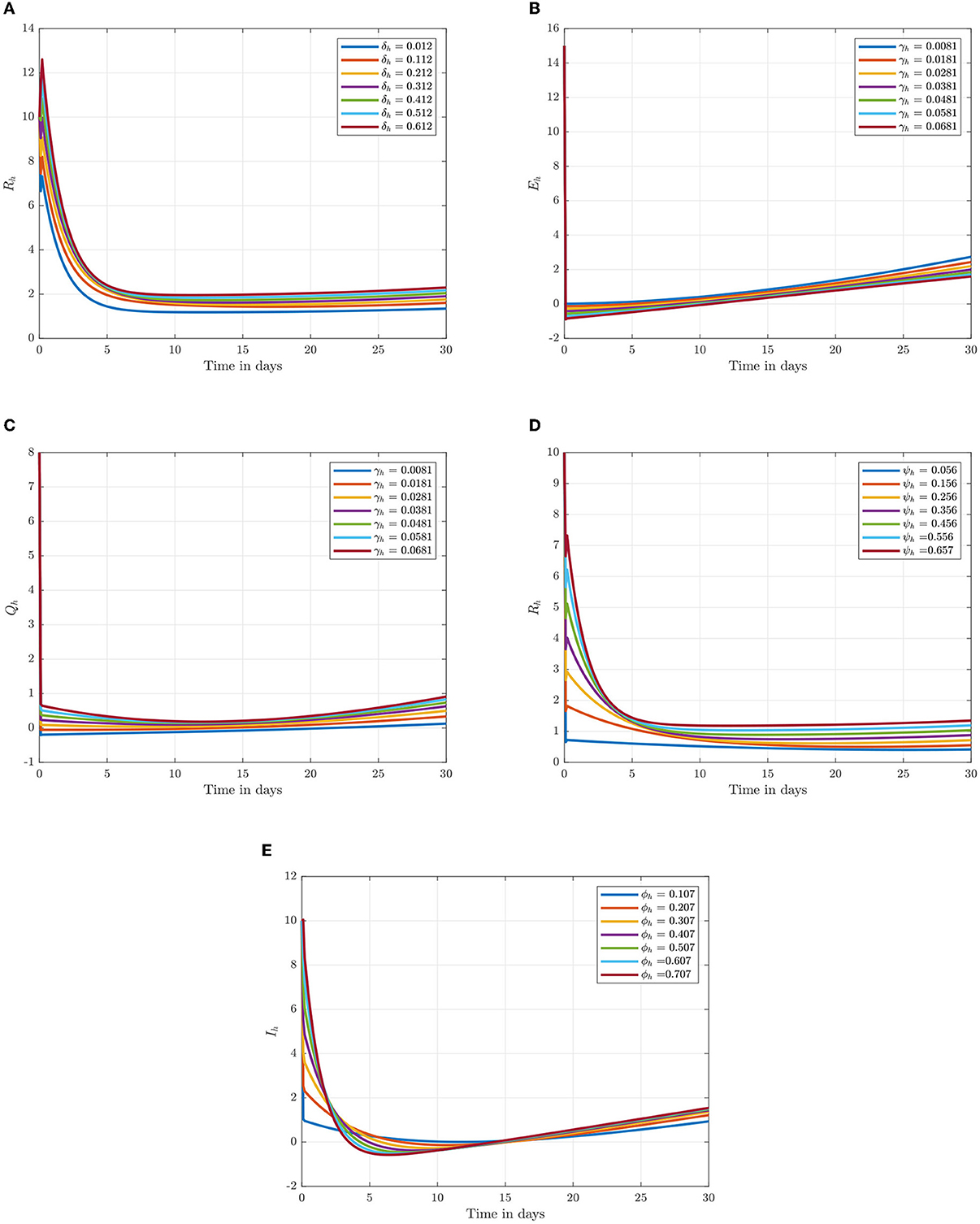
Figure 6. Numerical trajectory of varying δh, γh, ψh, and ϕh when α = 0.95. (A) Variation of δh on recovery class. (B) Variation of γh on expose class. (C) Variation of γh on quarantine class. (D) Variation of ψh on recovery class. (E) Variation of ϕh on infected class.
In conclusion, we provided a brief overview of the monkeypox virus and the dynamics of its transmission in this study. We investigated the spread of monkeypox virus and its effect on non-pharmaceutical intervention, thus quarantine. Positiveness, invariance, boundedness, and equilibrium points of the solutions are thus examined as fundamental features of mathematical models. We considered real data of the monkeypox virus from the United Kingdom, and the best fit curve has been obtained (see Figure 2). As a result, we created a novel, dimensionally consistent Caputo–Fabrizio fractional-order model. Krasnoselskii's fixed point theorem has been used to demonstrate that the system has a solution. The Adams–Bashforth method has been used to display numerical simulations of the suggested pandemic model for various fractional orders and parameter values. We looked into the impact of factors on the expansion and contraction of the quarantine compartment, recovery compartment, and infected compartment on the spread and regression of the pandemic with the use of numerical simulations. As can be inferred from the data, it is clear that the fractional-order equations can help explain this unique effect of the monkeypox. Real-world data can be used to test the accuracy of a mathematical model that has been created. The key challenge, however, is where to find these data and/or how to obtain the right curve for the collected data. The mathematical representation of the monkeypox has been the subject of numerous studies. To the best of our knowledge, there is still no research on fractional modeling that uses actual data on the monkeypox in the United Kingdom. Using actual data on the monkeypox from the United Kingdom, a fractional-order modeling has been shown in this study. The numerical results of this study show that the spread of monkeypox can be stopped if the number of contacts with infected people can be decreased through methods such as effective mass education, improved quarantine facilities, or increased testing of the general population, that is, performing routine tests not only on exposed individuals but also on those who have come into contact with infected patients. As a result, these studies offer other professionals and scientists who focus on infectious diseases insight that may help them in future to control the outbreak of monkeypox and contribute to the development of further treatment options. This study may provide insight into potential future research projects in this regard. Future study of the monkeypox can take into account other fractional operator types, both with and without single kernels. Furthermore, data imputation techniques can be used to fit rodent population parameters from the number of monkeypox disease since the number of rodents cannot be determined.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
KO, EA, and MN: conceptualization. EA, AA, UA, and KO: methodology, software, and formal analysis. EA, UA, and KO: validation, investigation, and visualization. MN and AA: resources. EA, MN, UA, and KO: data curation. EA and KO: writing and original draft preparation, writing, reviewing, and editing. KO and MN: supervision and project administration. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
Authors would like to appreciate the Black in Mathematics Association (BMA) and the Human Sciences Research Council (HSRC) for giving us the platform to collaborate as young researchers to carry out this work.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Monkeypox Cases Confirmed in England–Latest Updates. UK Health Security Agency (2022). Available online at: https://www.gov.uk/government/news/monkeypox-cases-confirmed-in-england-latest-updates (accessed August 29, 2022).
2. Multi-country Monkeypox Outbreak: Situation Update. World Health Organization (2022). Available online at: https://www.who.int/emergencies/disease-outbreak-news/item/2022-DON392 (accessed August 10, 2022).
3. Mathieu E, Spooner F, Dattani S, Ritchie H, Roser M. Mpox (monkeypox). Our World Data. (2022). Available online at: https://ourworldindata.org/monkeypox (accessed August 28, 2022).
4. Public Health Agencies Issue Monkeypox Guidance to Control Transmission. UK Health Security Agency (2022). Available online at: https://www.gov.uk/government/news/public-health-agencies-issue-monkeypox-guidance-to-control-transmission (accessed August 13, 2022).
5. Yinka-Ogunleye A, Aruna O, Dalhat M, Ogoina D, McCollum A, Disu Y, et al. Outbreak of human monkeypox in Nigeria in 2017-18: a clinical and epidemiological report. Lancet Infect Dis. (2019) 19:872–9. doi: 10.1016/S1473-3099(19)30294-4
6. Hobson G, Adamson J, Adler H, Firth R, Gould S, Houlihan C, et al. Family cluster of three cases of monkeypox imported from Nigeria to the United Kingdom, May 2021. Euro Surveill. (2021) 26:2100745. doi: 10.2807/1560-7917.ES.2021.26.32.2100745
7. Factsheet for Health Professionals on Monkeypox. UK Health Security Agency (2022). Available online at: https://www.ecdc.europa.eu/en/publications-data/data-mpox-monkeypox-cases-eueea (accessed August 27, 2022).
9. Reynolds MG, Doty JB, McCollum AM, Olson VA, Nakazawa Y. Monkeypox re-emergence in Africa: a call to expand the concept and practice of one health. Expert Rev Anti Infect Ther. (2019) 17:129–39. doi: 10.1080/14787210.2019.1567330
10. Durski KN, McCollum AM, Nakazawa Y, Petersen BW, Reynolds MG, Briand S, et al. Emergence of monkeypox - West and Central Africa, 1970-2017. MMWR Morb Mortal Wkly Rep. (2018) 67:306–10. doi: 10.15585/mmwr.mm6710a5
11. Usman S, Adamu II. Modeling the transmission dynamics of the monkeypox virus infection with treatment and vaccination interventions. J Appl Math Phys. (2017) 5:2335. doi: 10.4236/jamp.2017.512191
12. Peter OJ, Madubueze CE, Ojo MM, Oguntolu FA, Ayoola TA. Modeling and optimal control of monkeypox with cost-effective strategies. Model Earth Syst Environ. (2022) 1–19. doi: 10.1007/s40808-022-01607-z
13. Samko SG, Kilbas AA, Marichev OI. Fractional Integrals and Derivatives, Theory and Applications. Yverdon: Gordon and Breach (1993).
14. Katugampola UN. A new approach to generalized fractional derivatives. Bull Math Anal Appl. (2014) 6:1–15. doi: 10.48550/arXiv.1106.0965
15. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:1–13. doi: 10.18576/pfda/020101
16. Kumar S, Ahmadian A, Kumar R, Kumar D, Singh J, Baleanu D, et al. An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets. Mathematics. (2020) 8:558. doi: 10.3390/math8040558
17. Higazy M, Alyami MA. New Caputo-Fabrizio fractional order SEIASqEqHR model for COVID-19 epidemic transmission with genetic algorithm based control strategy. Alex Eng J. (2020) 59:4719–36. doi: 10.1016/j.aej.2020.08.034
18. Djida JD, Atangana A. More generalized groundwater model with space-time Caputo Fabrizio fractional differentiation. Numer Methods Partial Differ Equ. (2017) 33:1616–27. doi: 10.1002/num.22156
19. Baba IA. Existence and uniqueness of a fractional order tuberculosis model. Eur Phys J. (2019) 134:489. doi: 10.1140/epjp/i2019-13009-1
20. Owolabi KM, Atangana A. Mathematical modelling and analysis of fractional epidemic models using derivative with exponential kernel. In: Fractional Calculus in Medical and Health Science. London: CRC Press (2020). p. 109–128.
21. Mohammadi H, Kumar S, Rezapour S, Etemad, S. A theoretical study of the Caputo-Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control. Chaos Solit Fract. (2021) 144:110668. doi: 10.1016/j.chaos.2021.110668
22. Baleanu D, Jajarmi A, Mohammad H, Rezapour S. A new study on the mathematical modelling of human liver with Caputo-Fabrizio fractional derivative. Chaos Solit Fract. (2020) 134:109705. doi: 10.1016/j.chaos.2020.109705
23. Wutiphol S, Turab A. Mathematical analysis of an extended SEIR model of COVID-19 using the ABC-Fractional operator. Math Comput Simul. (2022) 198:65–84. doi: 10.1016/j.matcom.2022.02.009
24. Asamoah JKK, Okyere E, Yankson E, Opoku AA, Adom-Konadu A, Acheampong E, et al. Non-fractional and fractional mathematical analysis and simulations for Q fever. Chaos Solit Fract. (2022) 156:111821. doi: 10.1016/j.chaos.2022.111821
25. Peter OJ, Yusuf A, Ojo MM, Kumar S, Kumari N, Oguntolu FA. A mathematical model analysis of meningitis with treatment and vaccination in fractional derivatives. Int J Appl Comput Math. (2022) 8:117. doi: 10.1007/s40819-022-01317-1
26. Peter OJ, Shaikh AS, Ibrahim MO, Nisar KS, Baleanu D, Khan I, et al. Analysis and dynamics of fractional order mathematical model of covid-19 in nigeria using atangana-baleanu operator. Comput Mater Continua. (2021) 66:1823–48. doi: 10.32604/cmc.2020.012314
27. Kumar S, Ghosh S, Kumar R, Jleli M. A fractional model for population dynamics of two interacting species by using spectral and hermite wavelets methods. Numer Methods Part Diff Equ. (2020) 37:1652–72. doi: 10.1002/num.22602
28. Morales-Delgadoa VF, Gómez-Aguilar JF, Taneco-Hernández MA, Escobar Jiménez RF, Olivares Peregrino VH. Mathematical modeling of the smoking dynamics using fractional differential equations with local and nonlocal kernel. J Nonlinear Sci Appl. (2018) 11:1004–14. doi: 10.22436/jnsa.011.08.06
29. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci. (2016) 220:763–9. doi: 10.2298/TSCI160111018A
30. Atangana A, Gomez-Aguilar JF. A new derivative with normal distribution kernel: theory, methods and applications. Physica A Stat Mech Appl. (2017) 476:1–14. doi: 10.1016/j.physa.2017.02.016
31. Zhang L, Addai E, Ackora-Prah J, Arthur YD, Asamoah JKK. F. Fractional-order ebola-malaria coinfection model with a focus on detection and treatment rate Comput Math Methods Med. (2022) 2022:6502598. doi: 10.1155/2022/6502598
32. Kumar S, Chauhan RP, Momani S, Hadid S. Numerical investigations on COVID-19 model through singular and non-singular fractional operators. Numer Methods Part Diff Equ. (2020) 2020:1–27. doi: 10.1002/num.22707
33. Aslam M, Murtaza R, Abdeljawad T, Rahman, G, Khan A, et al. A fractional order HIV/AIDS epidemic model with Mittag-Leffler kernel. Adv Diff Equ. (2021) 2021:1–5. doi: 10.1186/s13662-021-03340-w
34. Evirgen F. Transmission of Nipah virus dynamics under Caputo fractional derivative. J Comput Appl Math. (2023) 419:114654. doi: 10.1016/j.cam.2022.114654
35. Ucar S. Analysis of hepatitis B disease with fractal fractional Caputo derivative using real data from Turkey. J Comput Appl Math. (2023) 419:114692. doi: 10.1016/j.cam.2022.114692
36. Khan Y, Khan MA, Fatmawati, Faraz N. A fractional bank competition model in Caputo-Fabrizio derivative through newton polynomial approach. Alexandria Eng J. (2021) 60:711–8. doi: 10.1016/j.aej.2020.10.003
37. Fatmawati, Khan MA, Alfiniyah C, Alzahrani E. Analysis of dengue model with fractal-fractional Caputo-Fabrizio operator. Adv Diff Equ. (2020) 2020:1–23. doi: 10.1186/s13662-020-02881-w
38. Qureshi S, Yusuf A, Shaikh AA, Inc M, Baleanu D. Mathematical modeling for adsorption process of dye removal nonlinear equation using power law and exponentially decaying kernels. Chaos. (2020) 30:043106. doi: 10.1063/1.5121845
39. Sher M, Shah K, Khan ZA, Khan H, Khan A. Computational and theoretical modeling of the transmission dynamics of novel COVID-19 under Mittag-Leffler Power Law. Alexandria Eng J. (2020) 59:3133–7. doi: 10.1016/j.aej.2020.07.014
40. Addai E, Zhang LL, Preko AK, Asamoah JKK. Fractional order epidemiological model of SARS-CoV-2 dynamism involving Alzheimer's disease. Healthc Analyt. (2022) 2:100114. doi: 10.1016/j.health.2022.100114
41. Shaikh AS, Nisar KS. Transmission dynamics of fractional order Typhoid fever model using Caputo-Fabrizio operator. Chaos Solit Fract. (2019) 128:355–65. doi: 10.1016/j.chaos.2019.08.012
42. Shah K, Alqudah MA, Jarad F, Abdeljawad T. Semi-analytical study of Pine Wilt Disease model with convex rate under Caputo-Febrizio fractional order derivative. Chaos Solit Fract. (2020) 135:109754. doi: 10.1016/j.chaos.2020.109754
43. Ahmed I, Baba IA, Yusuf A, Kumam P, Kumam W. Analysis of Caputo fractional-order model for COVID-19 with lockdown. Adv Differ Equ. (2020) 2020:110007. doi: 10.1186/s13662-020-02853-0
44. Ullah S, Khan MA, Farooq M, Hammouch Z, Baleanu D. A fractional model for the dynamics of tuberculosis infection using Caputo-Fabrizio derivative. Discrete Cont Dyn Syst. (2020) 13:975–93. doi: 10.3934/dcdss.2020057
45. Abboubakar H, Kumar P, Rangaig NA, Kumar S. A malaria model with Caputo-Fabrizio and Atangana-Baleanu derivatives. Int J Mod Simul Sci Comput. (2021) 12:2150013. doi: 10.1142/S1793962321500136
46. Peter OJ, Oguntolu FA, Ojo MM, Oyeniyi AO, Jan R, Khan I. Fractional order mathematical model of monkeypox transmission dynamics. Phys Script. (2022) 97:084005. doi: 10.1088/1402-4896/ac7ebc
47. Peter OJ, Kumar S, Kumari N, Oguntolu FA, Oshinubi K, Musa R. Transmission dynamics of Monkeypox virus: a mathematical modelling approach. Model Earth Syst Environ. (2022) 8:3423–34. doi: 10.1007/s40808-021-01313-2
48. Tilahuna GT, Woldegerimab WA, Mohammed N. A fractional order model for transmission dynamics of hepatitis B virus with two-age structure in the presence of vaccination. Arab J Basic Appl Sci. (2022) 28:87–106. doi: 10.1080/25765299.2021.1896423
49. Lin W. Global existence theory and chaos control of fractional differential equations. J Math Anal Appl. (2007) 332:709726. doi: 10.1016/j.jmaa.2006.10.040
50. Atangana A, Owolabi KM. New numerical approach for fractional differential equations. Math Model Nat Phenom. (2018) 13:3. doi: 10.1051/mmnp/2018010
51. Borgonovo E, Plischke E. Sensitivity analysis: a review of recent advances. Eur J Oper Res. (2016) 248:869–87. doi: 10.1016/j.ejor.2015.06.032
52. Hammouch Z, Yavuz M, Özdemir N. Numerical solutions and synchronization of avariable-order fractional chaotic system. Math Model Numer Simul Appl. (2021) 1:11–23. doi: 10.53391/mmnsa.2021.01.002
53. Bonyah E, Juga M, Fatmawati. Fractional dynamics of coronavirus with comorbidity via Caputo-Fabrizio derivative. Commun Math Biol Neurosci. (2022) 2022:12.
54. Peter OJ. Transmission dynamics of fractional order brucellosis model using Caputo-Fabrizio operator. Int J Differ Equ. (2020) 2020:2791380. doi: 10.1155/2020/2791380
Keywords: Caputo-Fabrizio fractional derivative, reproduction number, parameter estimation, numerical scheme, data fitting
Citation: Ngungu M, Addai E, Adeniji A, Adam UM and Oshinubi K (2023) Mathematical epidemiological modeling and analysis of monkeypox dynamism with non-pharmaceutical intervention using real data from United Kingdom. Front. Public Health 11:1101436. doi: 10.3389/fpubh.2023.1101436
Received: 17 November 2022; Accepted: 16 January 2023;
Published: 17 February 2023.
Edited by:
Nicola Luigi Bragazzi, York University, CanadaReviewed by:
Necati Özdemir, Balıkesir University, TurkeyOlumuyiwa James Peter, University of Medical Sciences, Nigeria
Maryam Shafaati, Tehran University of Medical Sciences, Iran
Copyright © 2023 Ngungu, Addai, Adeniji, Adam and Oshinubi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kayode Oshinubi,  a2F5b2RlLm9zaGludWJpQHVuaXYtZ3Jlbm9ibGUtYWxwZXMuZnI=
a2F5b2RlLm9zaGludWJpQHVuaXYtZ3Jlbm9ibGUtYWxwZXMuZnI=
 Mercy Ngungu1
Mercy Ngungu1 Kayode Oshinubi
Kayode Oshinubi