- 1Applied Physiology Laboratory, Department of Kinesiology, Health Promotion and Recreation, University of North Texas, Denton, TX, United States
- 2Department of Business Economics, Health and Social Care, University of Applied Sciences and Arts of Southern Switzerland, Manno, Switzerland
- 3Independent Consultant, Atlanta, GA, United States
- 4Department of Health Behavior, School of Public Health, University of Alabama at Birmingham, Birmingham, AL, United States
- 5Children's Nutrition Research Center, Baylor College of Medicine, Houston, TX, United States
- 6School of Public Health, Indiana University, Bloomington, IN, United States
by Wang, Q., Xiao, W. S., Danaee, M., Geok, S. K., Gan, W. Y., Zhu, W. L., and Mai, Y. Q. (2025). Front. Public Health 13:1589036. doi: 10.3389/fpubh.2025.1589036
Introduction
Cluster randomized controlled trials (cRCTs) are multilevel experimental designs in which groups of participants are randomly assigned to a condition (e.g., an exercise intervention) such that all individuals nested in a naturally occurring group (i.e., cluster) receive the same treatment (1–3). This design is often utilized when individual randomization is not feasible for various reasons (e.g., concerns about contamination of study conditions, logistical difficulties). There are several factors to consider when selecting this design (1, 4, 5); one of the most important is the number of clusters per experimental arm (6, 7). At a minimum, at least two clusters must be randomized to each condition (1), just as more than one participant must be assigned to a condition during traditional individually randomized RCTs. Many investigators experience resource constraints (e.g., funding), leading to fewer clusters. However, resources may be wasted if spent on severely underpowered studies, and regardless of the number of resources, results from cRCTs assigning <2 clusters per condition are uninterpretable as randomized experiments because cluster membership is perfectly confounded with treatment assignment. The optimal number of clusters depends on many factors, including intra-class correlation coefficients, effect sizes, and analysis method (7, 8). Based on our interest in cRCTs (9, 10), we read the Wang et al. investigation (11). We commend this research team for coordinating a 12-week exercise intervention. An investigation of this size requires high effort and dedication. However, we have identified a fundamental flaw in the experimental design, including the statistical approach, which invalidates the corresponding interpretations.
Experimental and statistical approach considerations
Wang et al. (11) aimed to examine the effects of three different resistance training loads versus a control on body composition and nutritional intake in a sample of women who were overweight or had obesity. The twelve-week resistance programs were designed to be completed using loads defined as the following: (a) Low-intensity (LI): 45–50% one-repetition maximum (1RM), (b) Moderate-intensity (MI): 60–65% 1RM, and (c) High-intensity (HI): 75–80% 1RM. The manuscript (11) defined four campuses in Yichen, Jiangxi, China, which were used to complete this trial, with each campus representing a single cluster: LI was completed at the “new campus” of Early Childhood Teachers College, while MI was completed at the “new campus” and HI was completed at the “old campus” of Yichun College. The control group (CG) was conducted at the Early Childhood Teachers College Gaoan campus. Therefore, the participants were not randomly assigned to a particular campus or group, but instead, each naturally occurring group (i.e., cluster) was assigned a resistance training protocol. To illustrate, Table 1 was created with the data in the manuscript and the data provided in Supplementary material, specifically with the change in percent (%) body fat. We thank the authors for their transparency and for making their raw data publicly accessible. Our intent with Table 1 is to clearly show that one cannot separate whether the differences in mean responses are due to the treatment (e.g., high vs. low loads) or the unique characteristics of the clusters (i.e., campuses) themselves. Said differently, there is no within-cluster variation in treatment assignment; group (treatment) is perfectly collinear with cluster.
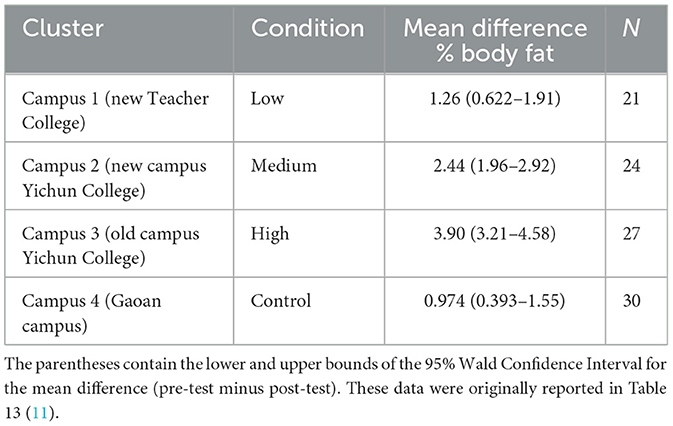
Table 1. Data depicting the mean change in body fat percentage (%) resulting from 12 weeks of resistance training or control.
The reported values were generated using a generalized estimating equation (GEE) approach (11) that relies on asymptotic properties, and this can be problematic with a small number of clusters because GEE requires a large sample to calculate accurate standard errors (i.e., sandwich estimator biased downward; underestimates true variability of parameter estimates) (12). Even if a correction is applied to rectify issues with the number of clusters, there is no suitable method to analyze one cluster per condition (13). Thus, the reported values reflect a misapplication of the statistical approach, and their use to justify any conclusions is erroneous (11). Our analysis of the provided data does match the authors' results (11); but, importantly, under these conditions, the analysis does not consider (1) the number of clusters per group, (2) validate whether the design is randomized appropriately, or (3) alert that group-level inference is invalid with a single cluster per condition. Therefore, the results are invalid. Below, we further highlight this.
Consider the following GEE model:
Where:
• Yijt: outcome for individual i in cluster j at time t,
• μ: grand mean,
• ß1: time effect,
• ß2: group (condition) effect,
• ß3: time × group interaction (treatment effect),
• uj: random (or correlated) cluster effect,
• ϵijt: individual-level error.
In a situation of two campuses and two conditions, if the control is only at the Gaoan campus and the low load is only at the new Teacher College campus, then Groupj = Clusterj (i.e., condition = cluster) and the uj parameter cannot be estimated. Thus, what provokes the change cannot be determined. To correct this, multiple clusters would be needed per condition. We also suggest using a random effects model with an appropriate number of clusters for future cRTC analyses because there are meaningful distinctions between the approaches (i.e., random effects vs. GEE modeling).
Discussion
The identified fatal flaw of the investigation (11) is that the unit of randomization is the cluster, such that the treatment is being applied at the cluster level, and there is only one cluster per treatment. There is no reported replication of the treatment at the cluster level, no ability to distinguish treatment effects from cluster effects, and zero degrees of freedom for estimating variance between clusters. Varnell et al. (14) have provided a strong warning against one-group-per-condition designs, summarized as “Trials with one cluster per arm should be avoided as they cannot give a valid analysis, as the intervention effect is completely confounded with the cluster effect [(8), p. 2].” Thus, this investigation should be considered an exploratory quasi-experiment, relabeled as such, and no causal inferences should be drawn. An emphasis must also be placed on the fact that any apparent difference between groups needs to be interpreted with substantial caution. Accordingly, per the Committee on Publication Ethics guidelines for handling post-publication critiques (15), a published correction or a retraction and replacement is essential.
Public health implications
As Wang et al. (11) appropriately described, overweight and obesity continue to contribute substantially to global mortality and the development of chronic diseases, including cardiovascular disease. There is a broad consensus that physical activity, like structured exercise, mitigates the incidence and severity of many adverse health outcomes associated with unhealthy body composition. However, despite its inclusion as a core component of the U.S. Physical Activity Guidelines, the specific benefits of resistance training, particularly in comparison to aerobic training, remain substantially understudied. Evidence from the Aerobic Center Longitudinal Study, which included nearly 12,000 participants at the Cooper Clinic in Dallas, TX, suggested that participation in resistance training was associated with a 20–30% reduction in obesity-related risk (16). These findings highlight the value of conducting randomized controlled trials that investigate resistance exercise as a targeted intervention to combat obesity. Wang et al. (11) sought to contribute to this research agenda by examining how varying resistance training load (e.g., 75–80% 1RM) influenced percent fat and nutritional intake. In addition, and perhaps most importantly, their study focused on female human participants, a population that has been historically underrepresented in biomedical and exercise science research. Collecting data from such groups is essential for developing evidence-based, individualized clinical guidelines for exercise prescription. Although the methodological limitations of Wang et al.'s study preclude its current use in inferences about causal effects, their efforts to investigate this topic are commendable. Their study reflects a growing and necessary interest in understanding how resistance training can be utilized to address obesity, while simultaneously highlighting the need for rigorously designed, randomized controlled trials.
Author contributions
JK: Writing – original draft, Writing – review & editing. SD: Methodology, Validation, Writing – review & editing. GD: Validation, Formal analysis, Writing – review & editing, Conceptualization. SP: Conceptualization, Validation, Writing – review & editing, Formal analysis. KF: Validation, Conceptualization, Writing – review & editing. DA: Writing – review & editing, Supervision, Conceptualization, Investigation, Validation, Funding acquisition.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. The work was supported by NIH grants R25DK099080 and R25HL124208.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Gen AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Author disclaimer
The opinions expressed are those of the authors and do not necessarily represent those of the NIH or any other organization.
References
1. Jamshidi-Naeini Y, Brown AW, Mehta T, Glueck DH, Golzarri-Arroyo L, Muller KE, et al. A practical decision tree to support editorial adjudication of submitted parallel cluster randomized controlled trials. Obesity (Silver Spring). (2022) 30:565–70. doi: 10.1002/oby.23373
2. Murray DM, Varnell SP, Blitstein JL. Design and analysis of group-randomized trials: a review of recent methodological developments. Am J Public Health. (2004) 94:423–32. doi: 10.2105/AJPH.94.3.423
3. Sedgwick P. Clinical trials: units of randomisation. BMJ. (2014) 348:g3297. doi: 10.1136/bmj.g3297
4. Murray DM. Design and Analysis of Group-randomized Trials. New York, NY: Oxford University Press Inc. (1998).
5. Donner A, Klar N. Design and Analysis of Cluster Randomization Trials in Health Research. Wiley (2000).
6. Leyrat C, Morgan KE, Leurent B, Kahan BC. Cluster randomized trials with a small number of clusters: which analyses should be used? Int J Epidemiol. (2018) 47:321–31. doi: 10.1093/ije/dyx169
7. Hayes RJ, Moulton LH. Cluster Randomised Trials. 2nd ed. New York, NY: Chapman and Hall/CRC (2017). p. 424
8. Campbell MK, Piaggio G, Elbourne DR, Altman DG. Consort 2010 statement: extension to cluster randomised trials. BMJ. (2012) 345:e5661. doi: 10.1136/bmj.e5661
9. Jamshidi-Naeini Y, Golzarri-Arroyo L, Thapa DK, Brown AW, Kpormegbey DE, Allison DB. Ambiguity in statistical analysis methods and nonconformity with prespecified commitment to data sharing in a cluster randomized controlled trial. J Med Internet Res. (2024) 26:e54090. doi: 10.2196/54090
10. Hefner M, Jamshidi-Naeini Y, Vorland CJ, Golzarri-Arroyo L, Shaw BP, Allison DB. Inappropriate analysis of a cluster randomized controlled trial due to not accounting for nesting and clustering: comment on “a home-based dyadic music-with-movement intervention for people with dementia and caregivers: a hybrid type 2 cluster-randomized effectiveness-implementation design” ClinIntervAging. (2023) 18:141–2. doi: 10.2147/CIA.S400881
11. Wang Q, Xiao WS, Danaee M, Geok SK, Gan WY, Zhu WL, et al. Impact of resistance training intensity on body composition and nutritional intake among college women with overweight and obesity: a cluster randomized controlled trial. Front Public Health. (2025) 13:1589036 doi: 10.3389/fpubh.2025.1589036
12. Carroll RJ, Wang S, Simpson D, Stromberg A, Ruppert D. The sandwich (robust covariance matrix) estimator. Unpublished manuscript (1998).
13. Thompson JA, Hemming K, Forbes A, Fielding K, Hayes R. Comparison of small-sample standard-error corrections for generalised estimating equations in stepped wedge cluster randomised trials with a binary outcome: a simulation study. Stat Methods Med Res. (2021) 30:425–39. doi: 10.1177/0962280220958735
14. Varnell SP, Murray DM, Baker WL. An evaluation of analysis options for the one-group-per-condition design: can any of the alternatives overcome the problems inherent in this design? Eval Rev. (2001) 25:440–53. doi: 10.1177/0193841X0102500402
15. COPE Council. Handling of post-publication critiques. COPE Flowcharts Infographics. (2021). doi: 10.24318/o1VgCAih
Keywords: statistics, cluster randomized controlled trials, generalized estimating equation, random effects model, experimental design
Citation: Keller JL, Deemer SE, Di Tanna GL, Pals SL, Fontaine KR and Allison DB (2025) Commentary: Impact of resistance training intensity on body composition and nutritional intake among college women with overweight and obesity: a cluster randomized controlled trial. Front. Public Health 13:1653392. doi: 10.3389/fpubh.2025.1653392
Received: 24 June 2025; Accepted: 09 September 2025;
Published: 29 September 2025.
Edited by:
Terry Huang, City University of New York, United StatesReviewed by:
Hugo Luca Corrêa, Catholic University of Brasilia (UCB), BrazilSamara Sezana Costa, Universidade Católica de Brasília (UCB), Brazil, in collaboration with reviewer HC
Copyright © 2025 Keller, Deemer, Di Tanna, Pals, Fontaine and Allison. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David B. Allison, RGF2aWQuQWxsaXNvbkBiY20uZWR1
 Joshua L. Keller
Joshua L. Keller Sarah E. Deemer
Sarah E. Deemer Gian Luca Di Tanna
Gian Luca Di Tanna Sherri L. Pals3
Sherri L. Pals3 Kevin R. Fontaine
Kevin R. Fontaine David B. Allison
David B. Allison