A New Numerical Method for Time Fractional Non-linear Sharma-Tasso-Oliver Equation and Klein-Gordon Equation With Exponential Kernel Law

In this work, we derived a novel numerical scheme to find out the numerical solution of fractional PDEs having Caputo-Fabrizio (C-F) fractional derivatives. We first find out the formula of approximation for the C-F derivative of the function f(t) = t^k. We approximate the C-F derivative in time direction with the help of Legendre spectral method and approximation formula of t^k. The unknown function and their derivatives in spatial direction are approximated with the help of the method which is based on a quasi wavelet. We implement this newly derived method to solve the non-linear Sharma-Tasso-Oliver equation and non-linear Klein-Gordon equation in which time-fractional derivative is of C-F type. The accuracy and validity of this new method are depicted by giving the numerical solution of some numerical examples. The numerical results for the particular cases of Klein-Gordon equation are compared with the existing exact solutions and from the obtained error we can conclude that our proposed numerical method achieves accurate results. The effect of time-fractional exponent α on the solution profile is characterized by figures. The comparison of solution profile u(x, t) for different type time-fractional derivative (C-F vs. Caputo) is depicted by figures.

1. Introduction

In the recent years fractional differential equations have received more attention of the researchers due to its exact description of the physical phenomenon. Many physical phenomenons have been described through fractional diffusion equation viz., transport in porous medium, ground water contamination problem through porous medium etc. As we know as far as fractional calculus is a classical branch of mathematics whose have history like as integer calculus [1]. Its progress is still increasing with day to day. N. H. Abel and J. Liouville have developed the theory of this fractional calculus. We can find wide details of fractional calculus in Kilbas et al. [2] and Podlubny [3]. We are allowed to generalize integer integrals and derivatives to arbitrary and real order with the help of fractional calculus. It is that branch of mathematical analysis that permit us to study operators and equations having integral are singular and convolution type. Many application of this calculus are found in special functions, control theory, computational complexity [4] and stochastic process. Fractional calculus was assumed to esoteric theory having no applications but a lot of applications to finance, control system and economics have been discovered in last few years.

In literature many types of differential operators have discovered like as Grunwald-Letnikov, Hadamard, Caputo, Riesz, Riemann-Liouville, Caputo-Fabrizio [5, 6] and Atangana-Baleanu derivatives [7–9]. The variable form of above operators have also been introduced. The application of fractional differential equation is go on increasing so researchers started to develop new methods to solve these differential equation numerically as they have to face many problems solve these equations analytically. The methods which are available in literature are as predictor-corrector method [10], Adomain decomposition method [11], homotopy perturbation method [12], generalized block pulse operational matrix method [13], eigen-vector expansion, Adams-Bashforth scheme [14], and fractional differential transform method [15], etc. The operational matrix method is easy and efficient method which is so widely used now a days. This method based on some polynomials and wavelets are available in literature. Haar wavelets [16], Chebyshev wavelets [17], sine wavelets, Legendre wavelets [18] is used to develop for the numerical solutions of integral equations, integro-differential equations and FPDEs. Some polynomials which can be utilized derive the operational matrix are Laguerre polynomial [19], Chebyshev polynomial, Legendre polynomial [20], and Genocchi polynomial [21] which is semi-orthogonal.

The process of diffusion and reaction has been studied from last some years. In the diffusion process the molecules or any other quantity is transferred from the higher concentration region to low concentration region. When the reaction process is happened together with the process of diffusion then combined process is called reaction-diffusion process. In the reaction process more molecules is consumed or created and this term mathematically denoted by adding a reaction term in classical diffusion equation

$\begin{array}{ll}\frac{\partial \varrho }{\partial t}=D{\nabla }^2\varrho +R(\varrho ,t),& (1)\end{array}$

where first term on the right hand side presents diffusion process with D diffusion coefficient while R(ϱ, t) characterize the reaction term at space point ϱ and time t. We can extend this reaction -diffusion equation to advection-reaction-diffusion equation where advection term denotes the movement of particle or molecules due to the bulk flow of fluid. Many beautiful an curious phenomena in nature as chemistry, physics, biology, and medical sciences could be depicted by reaction diffusion equation.

A heat transfer analysis in sodium alginate based nanofluid using MoS2 nanoparticles is studied in article [22]. The behavior of normal and tumor cells with the effect of radiotherapy in fractional derivative environment is investigated in Farayola et al. [23]. The De-Levie's model is studied by researchers in Abro et al. [24]. The investigation of heat dissipation in transmission line of electrical circuit is given in Abro et al. [25]. A analysis of generalized Jeffery nanofluid in a rotating frame with non-singular fractional derivative is given in Ali et al. [26]. The behavior of heat transfer in different model with singular and non-singular is given in articles [27–31]. The study of electro-osmotic flow of viscoelastic fluids with non-singular Mittag-Leffler fractional derivative is given in Ali et al. [32]. The Drinfeld-Sokolov-Wilson model with exponential fractional derivative is investigated in article [33]. An analysis of fractional vibration equation with ABC fractional derivative is studied in Kumar et al. [34]. The study of FDEs equations occurring in ion acoustic waves in plasma is done in Goswami et al. [35]. The FDEs is very useful in biological model as SIRS-SI malaria disease model with application of vaccines [36] and fractional equal width equations describing hydro-magnetic waves in cold plasma [37].

We organized our article as follows. The definition of R-L, Caputo, and Caputo-Fabrizio is given in section 2. We also discussed about quasi wavelet and quasi wavelet-based numerical method. In section 3, we derived the general formula of C-F derivative of the function x^k. Some properties of Legendre polynomial is also included in this section. In section 4, we described the proposed method for solving FPDEs with C-F derivative. In section 5, some numerical examples and results are presents including the variation of different parameters. The conclusion of all over the article is given in the last section.

2. Preliminary Definitions

In the last few years, many definitions of fractional integration and differentiation have come into the light. All of them have own special properties and applications. Caputo's definition is more reliable as compare to Riemann-Liouville's definition as an application point of view. These definitions are with power or singular kernel law. Nowadays many generalized definitions of the fractional derivative with exponential and Mittag-Leffler kernel law have been introduced. We discussed brief definitions and properties of R-L, Caputo and recently developed Caputo-Fabrizio derivative.

2.1. Riemann-Liouville Order Derivative and Integration

The R-L integration of order ϱ > 0 of a function h(t) is given by

$\begin{array}{ll}{I}^{\vartheta }h(z)=\frac{1}{\Gamma (\varrho )}{\displaystyle {\int }_0^z}{(z-\varpi )}^{\varrho -1}h(\varpi )d\varpi ,z>0,\vartheta \in R^{+}.& (2)\end{array}$

Now Riemann-Liouville fractional order differentiation of a function h(t) with order ϑ > 0 is defined as

$\begin{array}{ll}{D}_l^{\vartheta }h(t)={(\frac{d}{dt})}^m(I^{m-\vartheta }h)(t),(m-1<\vartheta <m,\vartheta >0).& (3)\end{array}$

2.2. Definition of Caputo Derivative

The Caputo derivative of a function h(t) having order ϑ > 0 is given as follows

$\begin{array}{ll}{D}_c^{\vartheta }h(t)=\{\begin{array}{ll}\frac{1}{\Gamma (\vartheta )}{\int }_0^t{(-\eta +t)}^{-\vartheta -1+l}{h}^l(\eta )d\eta & l-1<\vartheta <l,\\ \frac{d^l}{d{t}^l}h(t)& \vartheta =l\in N.\end{array}& (4)\end{array}$

with l an integer and time interval t > 0.

Some important properties of Caputo differentiation are given as follows

$\begin{array}{ll}{D}_c^{\vartheta }C=0,& (5)\end{array}$

where C is a constant. The fractional differentiation operator $D_c^{\vartheta }$ follow the linear property so we have

$\begin{array}{ll}{D}_c^{\vartheta }(c_{1}h(t)+c_{2}g(t))=c_1{D}_c^{\vartheta }h(t)+c_2{D}_c^{\vartheta }g(t),& (6)\end{array}$

where c₁ and c₂ denotes constants. We can relate the Caputo differential operator and R-L operator as

$\begin{array}{ll}(I^{\vartheta }{D}_c^{\vartheta }g)(t)=g(t)-{\displaystyle \sum _{k=0}^{l-1}}{g}^k(0^{+})\frac{t^k}{k!},l-1<\vartheta \le l.& (7)\end{array}$

2.3. Definition of Caputo-Fabrizio Derivative [38, 39]

Consider a function g(t) which is a element of Sobolev space H¹(a, b), b > a then C-F derivative of order n < ϑ < n + 1 is given as [40]

$\begin{array}{l}{}_0^{CF}{D}_t^{\vartheta }g(t)=\frac{B(\vartheta )}{\lceil \vartheta \rceil -\vartheta }{\displaystyle {\int }_0^t\exp }[\frac{-\vartheta (x,t)}{\lceil \vartheta \rceil -\vartheta }(t-s)]\\ \times \frac{{\partial }^{n+1}g(s)}{\partial t^{n+1}}ds,n<\vartheta \le n+1.& (8)\end{array}$

Here B(ϑ) denotes the normalization function. In all our calculations we have taken B(ϑ) = 1.

2.4. Definition of Caputo-Fabrizio Integral

The C-F integral of order n < ϑ < n + 1 associated with the function g(t) is defined as follows

$\begin{array}{l}{}_0^{CF}{I}_t^{\vartheta }g(t)={\displaystyle \sum _{i=0}^n\frac{t^i}{i!}}{g}^{(i)}(0)+\frac{(1-\eta )}{B(\eta )(n-1)!}{\displaystyle {\int }_0^t{(t-s)}^{n-1}}g(s)ds\\ +\frac{\eta }{M(\eta )n!}{\displaystyle {\int }_0^t{(t-s)}^n}g(u)du,& (9)\end{array}$

where η denotes the fractional part of the order ϑ. If the fractional part η = 0 then CF integral is given by

$\begin{array}{ll}{}_0^{CF}{I}_x^{\vartheta }g(x)=\frac{(1-\eta )}{B(\eta )}g(x)+\frac{\eta }{M(\eta )}{\displaystyle {\int }_0^t}g(u)du.& (10)\end{array}$

2.5. Why We Are Using C-F Derivative?

The operators play an important role in science and the interchange of these operators is an important property. Let us consider two operators A and B we say these two commutes if they follow the property AB = BA. Many operators arising in physics, biology, statistics, and mathematics do not follow the property of commutativity and are called non-commutative operators. We give some examples of non-commutative operators:

• Product of two matrices.

• Division operator on real numbers as $\frac{3}{4}\ne \frac{4}{3}$.

• Linear operators like z and $\frac{d}{dz}$ do not follow the commutative property on wave function Ψ(y) in the case when we formulate the Schrodinger equation in quantum mechanics.

• Lie bracket of Lie ring.

• Lie bracket of a Lie algebra.

The general form of fractional type derivatives in Caputo and Riemann-Liouville form are defined as

$\begin{array}{l}\begin{array}{l}{}_0^{RL}{D}_z^{\vartheta }g(z)=\frac{d}{dz}{\displaystyle {\int }_0^z}\kappa (z-x)g(z)dz\frac{d}{dz}\kappa \ast g,\\ {}_0^C{D}_z^{\vartheta }g(z)={\displaystyle {\int }_0^z}\kappa (z-x)\frac{d}{dz}g(z)dz=\kappa \ast \frac{d}{dz}g.\end{array}\end{array}$

In fractional calculus, many form of kernel is discovered as $\kappa (z-x)=\frac{1}{\Gamma (1-\vartheta )}{(z-x)}^{-\vartheta }$ and $\kappa (z-x)=\frac{M(\vartheta )}{(1-\vartheta )}exp\left(\frac{-\vartheta }{1-\vartheta }{(z-x)}^{-\vartheta }\right)$. The kernel $\kappa (z-x)=\frac{1}{\Gamma (1-\vartheta )}{(z-x)}^{-\vartheta }$ is known as power kernel law which has been used in classical fractional calculus and the kernel $\kappa (z-x)=\frac{M(\vartheta )}{(1-\vartheta )}exp\left(\frac{-\vartheta }{1-\vartheta }{(z-x)}^{-\vartheta }\right)$ is exponential kernel law which is newly discovered. The general derivatives having exponential kernel known as Caputo-Fabrizio derivative. In statistics, Pareto distribution which describes the fitting of the shape of a large portion of wealth for a small portion of the population and the wealth in our society has corresponded to the power-law kernel. The negative exponential distribution is mainly used in statistics as a probability distribution. This type of distribution is used to characterize the time between events between Poisson point distribution. The important property of this distribution is that it depicts infinite divisibility and infinite divisible distribution shows an important role in the context of limit theorem and Levy process. This type of derivatives is beneficial when the distribution of waiting time is not dependent upon elapsed time [41]. Here we give some properties of C-F derivative:

1. The mean square displacement associated with Caputo-Fabrizio fraction derivative is a usual to sub-diffusion crossover.

2. The Caputo-Fabrizio distribution follow the rule from Gaussian to non-Gaussian crossover.

3. The asymptotic behavior of Caputo-Fabrizio satisfies the power law behavior and connect the theory of fading memory concept with kernels which are non-singular [42].

Nowadays the derivative with exponential kernel law has become so popular and capture the attention of researchers. This derivative has many applications which can be found in elasticity, Keller Segel equation, flow of complex rheological medium and flow of ground water in mass-spring damped system [43].

2.6. Approximation of Function by Quasi-Wavelets

In literature there are many polynomial and wavelets which are used to approximate an arbitrary function. But the procedure based upon the quasi-wavelets is growing rapidly as spectral collocation method which is local. It is very useful to solve different type of space-time fractional FPDEs and partial integro-differential equation of different order. We define a mathematical transformation known as the singular discrete convolution in distribution theory

$\begin{array}{ll}\Phi (v)=(F*s)(z)={\displaystyle {\int }_{-\infty }^{\infty }}F(-t+z)s(t)dt,& (11)\end{array}$

where s(t) is called a test function and F is recognized as singular kernel. We can find a family of wavelet by a function which is known as mother wavelet ς using operations of dilation and translation.

$\begin{array}{ll}{\varsigma }_{\beta ,\delta }(z)={\beta }^{\frac{-1}{2}}\varsigma \left(\frac{z-\delta }{\beta }\right).& (12)\end{array}$

The parameter δ represents the translation process while β represents the process of dilation. An orthonormal wavelet base generates any arbitrary subspace by using orthogonal scaling functions. A Shannon's delta sequence kernel is used in our work which is defined as

$\begin{array}{ll}{\delta }_{\alpha }(z)=\frac{1}{\pi }{\displaystyle {\int }_0^{\pi }}cos(zy)dy=\frac{sin(\alpha z)}{\pi z},& (13)\end{array}$

where ${lim}_{\alpha \to {\alpha }_0}{\delta }_{\alpha }(z)=\delta (z).$ δ is discussed by Dirac and so known as Dirac delta function. For a α > 0, Shannon's delta sequence kernel generates a basis for the Paley-Wiener reproducing kernel Hilbert space ${\mathbf{\text{B}}}_{\alpha }^2$[44] which is a subspace of L²(R). We can reproduce the function $g(z)\in {\mathbf{\text{B}}}_{\alpha }^2$ as follows

$\begin{array}{ll}g(z)={\displaystyle {\int }_{-\infty }^{\infty }}g(z){\delta }_{\alpha }(z-t)dt={\displaystyle {\int }_{-\infty }^{\infty }}g(z)\frac{sin((z-t)\alpha )}{(z-t)\pi }dt,\forall g(z)\in B_{\alpha }^2.& (14)\end{array}$

This sampling scaling function can be put in another form in reproducing kernel of Paley-Wiener

$\begin{array}{ll}{\delta }_{\alpha ,k}={\delta }_{\alpha }(z-z_k)=\frac{sin((z-z_k)\alpha )}{(z-z_k)\pi },& (15)\end{array}$

the points {x_k} is known as collection of sampling points which is placed around x. We can put all functions $\forall g\in {\mathbf{\text{B}}}_{\alpha }^2$ in discrete form using Equations (11) and (12)

$\begin{array}{ll}g(z)={\displaystyle \sum _{k=-\infty }^{\infty }}g(z_k){\delta }_{\alpha }(z-z_k).& (16)\end{array}$

According to Shannnon sampling theorem the uniformly spatial discrete samples for a given band-limited signal in $B_{\gamma }^2$ can depicted the sampling at the Nyquist frequency γ. We represent Δ by grid size in spatial direction and $\gamma =\frac{\pi }{\Delta }$. So

$\begin{array}{ll}g(z)={\displaystyle \sum _{k=-\infty }^{\infty }}g(z_k){\delta }_{\alpha }(z-z_k)={\displaystyle \sum _{k=-\infty }^{\infty }}g(z_k)\frac{sin(\frac{\pi (z-z_k)}{\Delta })}{\frac{\pi (z-z_k)}{\Delta }}& (17)\end{array}$

A method for the improvement of Dirichlet's delta kernel is given by Wan. If we introduce a regularizer R_σ(y) then we can increases its regularity

$\begin{array}{ll}{\delta }_{\alpha }(z)\to {\delta }_{\alpha ,\sigma }={\delta }_{\alpha }(z)R_{\sigma }(z).& (18)\end{array}$

here R_σ satisfies

$\begin{array}{l}{\displaystyle \underset{\sigma \to \infty }{lim}}{R}_{\sigma }(z)=1\end{array}$

and

$\begin{array}{l}{\displaystyle {\int }_{-\infty }^{\infty }}{\displaystyle \underset{\sigma \to \infty }{lim}}{R}_{\sigma }(y){\delta }_{\alpha }(y)dy=R_{\sigma }(0)=1.\end{array}$

Many regularizers satisfies the two conditions which is given as above. But Gaussian type regularizer is so commonly used

$\begin{array}{ll}{R}_{\sigma }(z)=e\left(\frac{-z^2}{2{\sigma }^2}\right),\sigma >0,& (19)\end{array}$

where σ represents the width parameter. The relation between Δ and σis σ = r × Δ, where r is a computation parameter. We can define regularized orthogonal sampling scaling function which are Gaussian type as

$\begin{array}{ll}{\delta }_{\Delta ,\sigma }(z)=\frac{sin(\frac{\pi z}{\Delta })}{\frac{\pi z}{\Delta }}exp\left(\frac{-z^2}{2{\sigma }^2}\right).& (20)\end{array}$

Here

$\begin{array}{l}{\displaystyle \underset{\sigma \to \infty }{lim}}{\delta }_{\Delta ,\sigma }(x)=\frac{sin(\frac{\pi x}{\Delta })}{\frac{\pi x}{\Delta }},\end{array}$

Gaussian regularized sampling scaling function has no property of orthonormal wavelet scaling function so it is called a quasi scaling function.

By using quasi scaling function, we can approximate a function $\theta \in {\mathbf{\text{B}}}_{\alpha }^2$

$\begin{array}{ll}\theta (z)={\displaystyle \sum _{k=-\infty }^{\infty }}\theta (z_k){\delta }_{\alpha }(z-z_k)={\displaystyle \sum _{k=-\infty }^{\infty }}\theta (z_k){\delta }_{\alpha }(z-z_k)R_{\alpha }(z-z_k).& (21)\end{array}$

For computation purpose we have to take finite sampling points as infinite sampling points is not possible in computer computation. We choose 2W + 1 sampling points in our work. All sampling points are chosen close to x. We can rewrite Equation (18) as

$\begin{array}{ll}\theta (z)={\displaystyle \sum _{k=-W}^W}\theta (z_k){\delta }_{\Delta ,\sigma }(z-z_k),& (22)\end{array}$

The n^th order derivatives of a function θ(z)

$\begin{array}{ll}{\theta }^n(z)={\displaystyle \sum _{k=-W}^W}\theta (z_k){\delta }_{\Delta ,\sigma }^n(z-z_k),n=1,2,\cdots .& (23)\end{array}$

We have chosen the computational width equal to 2W + 1. We present the description of formulas of ${\delta }_{\Delta ,\sigma },{\delta }_{\Delta ,\sigma }^1$ and ${\delta }_{\Delta ,\sigma }^2$ [45] which are helpful in calculation as follows

$\begin{array}{ll}{\delta }_{\Delta ,\sigma }(y)=\{\begin{array}{ll}\frac{exp\{-\frac{y^2}{2{\sigma }^2}\}sin\left(\frac{\pi y}{\Delta }\right)}{\frac{\pi y}{\Delta }},& y\ne 0\\ 1& y=0.\end{array}& (24)\end{array}$

$\begin{array}{ll}{\delta }_{\Delta ,\sigma }^1(y)=\{\begin{array}{l}\left(-\frac{sin\left(\frac{\pi y}{\Delta }\right)}{\frac{\pi y^2}{\Delta }}-\frac{\Delta sin\left(\frac{\pi y}{\Delta }\right)}{\frac{\pi {\sigma }^2}{\Delta }}+\frac{cos\left(\frac{\pi y}{\Delta }\right)}{y}\right)\\ exp\left(-\frac{y^2}{2{\sigma }^2}\right)& y\ne 0,\\ \hfill 0\hfill & y=0.\end{array}& (25)\end{array}$

$\begin{array}{ll}{\delta }_{\Delta ,\sigma }^2(y)=\{\begin{array}{ll}\begin{array}{l}(\frac{2\Delta sin\left(\frac{y\pi }{\Delta }\right)}{\pi y^3}-\frac{2cos\left(\frac{\pi y}{\Delta }\right)}{y^2}+\frac{\Delta ysin\left(\frac{y\pi }{\Delta }\right)}{\pi {\sigma }^4}\\ +\frac{\Delta sin\left(\frac{\pi y}{\Delta }\right)}{\pi {\sigma }^{2}y}-\frac{2cos\left(\frac{\pi y}{\Delta }\right)}{{\sigma }^2}-\frac{\pi sin\left(\frac{y\pi }{\Delta }\right)}{y\Delta })\\ \hfill exp\left(-\frac{y^2}{2{\sigma }^2}\right)\hfill \\ \end{array}& y\ne 0,\\ \hfill 0\hfill & y=0.\end{array}& (26)\end{array}$

3. Approximation of Caputo-Fabrizio Derivative

In the following theorem, we will find out an approximate expression of Caputo-Fabrizio derivative of the function f(t) = t^k

Theorem 1: The C-F derivative of function f(t) = t^k having order n < α < n + 1 with k ≥ ⌈α⌉ is given by

$\begin{array}{r}{}_0^{CF}{D}_t^{\alpha }{t}^k=\frac{B(\alpha )\Gamma (1+k)}{\lceil \alpha \rceil -\alpha }({\displaystyle \sum _{r=0}^{k-n-1}}\frac{{(-1)}^r{t}^{k-n-1-r}}{\Gamma (k-n-r){(\frac{-\alpha }{\lceil \alpha \rceil -\alpha })}^{r+1}}\\ +\frac{{(-1)}^{k-n}}{{(\frac{-\alpha }{\lceil \alpha \rceil -\alpha })}^{k-n}}\exp (\frac{-\alpha }{\lceil \alpha \rceil -\alpha }t)).& (27)\end{array}$

Proof: By the definition of CF derivative Dⁿt^k = 0, k = 0, 1, …, ⌈α⌉ − 1. Now for k ≥ ⌈α⌉ we have

$\begin{array}{l}{}_0^{CF}{D}_t^{\alpha }{t}^k=\frac{B(\alpha )}{\lceil \alpha \rceil -\alpha }{\displaystyle {\int }_0^t{D}^{n+1}}{s}^k\exp \left(\frac{-\alpha }{\lceil \alpha \rceil -\alpha }(t-s)\right)ds\\ =\frac{B(\alpha )}{\lceil \alpha \rceil -\alpha }{\displaystyle {\int }_0^t\frac{\Gamma (k+1)}{\Gamma (k-n)}}{s}^{k-n-1}\exp \left(\frac{-\alpha }{\lceil \alpha \rceil -\alpha }(t-s)\right)ds\\ =\frac{B(\alpha )}{\lceil \alpha \rceil -\alpha }\frac{\Gamma (k+1)}{\Gamma (k-n)}\exp \left(\frac{-\alpha }{\lceil \alpha \rceil -\alpha }t\right)\\ {\displaystyle {\int }_0^t{s}^{k-n-1}}\exp \left(\frac{\alpha }{\lceil \alpha \rceil -\alpha }s\right)ds\\ =\frac{B(\alpha )}{\lceil \alpha \rceil -\alpha }\times \frac{\Gamma (k+1)}{\Gamma (k-n)}\exp \left(\frac{-\alpha }{\lceil \alpha \rceil -\alpha }t\right)\times \\ [\exp \left(\frac{\alpha }{\lceil \alpha \rceil -\alpha }t\right){\displaystyle \sum _{r=0}^{k-n-1}{(-1)}^r}\frac{\Gamma (k-n)t^{k-n-1-r}}{\Gamma (k-n-r){(\frac{\alpha }{1-\alpha })}^{r+1}}\\ -\frac{{(-1)}^{k-n-1}\Gamma (k-n)}{{(\frac{\alpha }{1-\alpha })}^{k-n}}]\\ =\frac{B(\alpha )\Gamma (k+1)}{\lceil \alpha \rceil -\alpha }[{\displaystyle \sum _{r=0}^{k-n-1}\frac{{(-1)}^r{t}^{k-n-1-r}}{\Gamma (k-n-r){(\frac{\alpha }{1-\alpha })}^{r+1}}}\\ -\frac{{(-1)}^{k-n-1}}{{(\frac{\alpha }{1-\alpha })}^{k-n}}\exp \left(\frac{-\alpha }{\lceil \alpha \rceil -\alpha }t\right)].\end{array}$

3.1. Legendre Polynomials

Now we discussed here about Legendre polynomials and their some properties. We shifted Legendre polynomials on the [0, 1] from the interval [−1, 1] by the transformation z = 2x − 1. The analytical form of these polynomials of degree i are given as follows

$\begin{array}{ll}{\psi }_i(x)={\displaystyle \sum _{k=0}^i}\frac{{(-1)}^{i+k}(i+k)!}{{(k!)}^2(l-k)!}{x}^k& (28)\end{array}$

where i = 0, 1, ….

The Legendre polynomials follows the orthogonality property with weight function 1 and orthogonality condition can be described as

$\begin{array}{ll}{\displaystyle {\int }_0^1}{\psi }_j(x){\psi }_i(x)=\{\begin{array}{ll}\frac{1}{2i+1},& j=i,\\ 0& j\ne i.\end{array}& (29)\end{array}$

A function u(x) which belongs to the L²[0, 1] can be approximated by a linear sum of shifted Legendre polynomials as

$\begin{array}{ll}u(x)=u_m(x)={\displaystyle \sum _{j=0}^m}{a}_j{\psi }_i(x),& (30)\end{array}$

where the linear coefficients are given by

$\begin{array}{ll}{a}_j=(2j+1){\displaystyle {\int }_0^1}u(x){\psi }_j(x).& (31)\end{array}$

Similarly, a function u(x, t) of two variable can be approximated as

$\begin{array}{ll}u(x,t)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(x){\psi }_l(t),& (32)\end{array}$

where a_il are unknown coefficient.

4. Proposed New Method

In this section, we develop a new algorithm with the combination of Legendre spectral method and quasi wavelet method and then apply it to derive the numerical solution of C-F time fractional non-linear Sharma-Tasso-Oliver equation and C-F time-fractional non-linear Klein-Gordon equation. We approximate the C-F time fractional derivative by using Legendre spectral method. On the other hand spatial derivatives and unknown functions are approximated with the help of quasi wavelet based numerical method. We have used fractional derivative in our model as they are better than the integer ones. The fractional differential equations are more comprehensive and depict the memory effect of physical process as compare to ordinary differential equation. Recent study shows that the fractional model perfectly describe the test data of various memory phenomena at different fields. Sharma-Tasso-Oliver C-F fractional model is as follows

$\begin{array}{ll}\begin{array}{l}{}_0^{CF}{D}_t^{\alpha }u(t,x)+3\mu (\frac{\partial u(x,t)}{\partial x}{)}^2+3\mu {(u(x,t))}^2\frac{\partial u(x,t)}{\partial x}\\ +3\mu (u(x,t))\frac{{\partial }^{2}u(x,t)}{\partial x^2}+\mu \frac{{\partial }^{2}u(x,t)}{\partial x^2}=f(x,t).\end{array}& (33)\end{array}$

The prescribed initial and boundary conditions for this model are taken as follows

$\begin{array}{ll}\begin{array}{c}u(0,x)=f_1(x),\\ u(t,0)=f_2(t),\\ u(t,1)=f_3(t).\end{array}& (34)\end{array}$

where 0 < α ≤ 1, 0 ≤ x ≤ 1, and 0 ≤ t ≤ 1.

The model of Klein-Gordon equation is

$\begin{array}{ll}\begin{array}{c}{}_0^{CF}{D}_t^{\alpha }u(t,x)+a\frac{\partial u(x,t)}{\partial t}+bu(x,t)=\frac{{\partial }^{2}u(x,t)}{\partial x^2}\\ +c{(u)}^2+d{(u)}^3+f(x,t),\end{array}& (35)\end{array}$

where 1 < α ≤ 2, 0 ≤ x ≤ 1, and 0 ≤ t ≤ 1.

The initial and boundary conditions for above model are

$\begin{array}{ll}\begin{array}{l}u(0,x)=g_1(x),\\ u(t,0)=g_2(t),\\ u(1,t)=g_3(t),\\ \frac{\partial u(x,0)}{\partial t}=g_4(x).\end{array}& (36)\end{array}$

Now we develop the method with the help of Legendre spectral and a method which is based on quasi wavelet to investigate the models (34) and (36).

Approximating the unknown function in terms of shifted Legendre polynomial

$\begin{array}{ll}u(x,t)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{c}_{il}{\psi }_i(x){\psi }_l(t),& (37)\end{array}$

where c_il are unknown coefficients for i = 0, 2, …; and l = 0, 1, 2, ….

Now operating the C-F time fractional operator and using Equation (38) we get

$\begin{array}{ll}\begin{array}{l}{}_0^{CF}{D}_t^{\alpha }u(t,x)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{c}_{il}{\psi }_i(x)({}_0^{CF}{D}_t^{\alpha }{\psi }_l(t)),\\ ={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x)\left({}_0^{CF}{D}_t^{\alpha }{t}^k\right),\\ ={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x),{\Pi }_{k,t,\alpha },\end{array}& (38)\end{array}$

where

$\begin{array}{ll}\begin{array}{c}{\Pi }_{k,t,\alpha }=\frac{B(\alpha )\Gamma (1+k)}{\lceil \alpha \rceil -\alpha }({\displaystyle \underset{r=0}{\overset{k-n-1}{{\sum }^{\text{}}}}}\frac{{(-1)}^r{t}^{k-n-1-r}}{\Gamma (k-n-r){(\gamma )}^{r+1}}\\ +\frac{{(-1)}^{k-n}}{{(\gamma )}^{k-n}}{e}^{-\gamma t})\end{array}\hfill & (39)\end{array}$

with $\gamma =\frac{\alpha }{\lceil \alpha \rceil -\alpha }$. Similarly, we can find the value of time fractional derivative ${}_0^C{D}_t^{\alpha }u(t,x)$ when its type is Caputo.

Differentiating Equation (38) with respect to t we get the following

$\begin{array}{ll}\begin{array}{l}\frac{\partial u(x,t)}{\partial t}={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{c}_{il}{\psi }_i(x)\left(\frac{\partial {\psi }_l(t)}{\partial t}\right),\\ ={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}k{t}^{k-1}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x).\end{array}& (40)\end{array}$

We have approximated derivative in the time direction with the help of Legendre spectral method. To approximate the unknown function u(x, t) and derivative in time direction we take the help of quasi wavelet based numerical method. We know a function and its all derivatives can be approximated by

$\begin{array}{ll}{u}^{(n)}(x)={\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^n(x-x_k)u(x_k),n=0,1,\cdots & (41)\end{array}$

where the superscript (n) denotes the n^th order derivative with respect to x. At spatial point x = x_j we can rewrite above equation as

$\begin{array}{ll}{u}^{(n)}(x_j,t)={\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^n(-s\Delta x)u(x_{j+s}),n=0,1,\cdots & (42)\end{array}$

where Δx is the spatial step. Putting the value of u(x, t) and their space and time derivatives in model (34) we get the following residual

$\begin{array}{ll}\begin{array}{l}{\xi }_1(x,t)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x),{\Pi }_{k,t,\alpha }\\ +3\mu ({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^1(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t){)}^2\\ +3\mu ({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^0(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t){)}^2\\ \times \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^1(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t)\right)\\ +3\mu \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^0(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t)\right)\\ \times \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^2(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t)\right)\\ +\mu \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^2(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t)\right)-f(x,t)\end{array}& (43)\end{array}$

The initial and boundary conditions takes the following form in view of Equation (33)

$\begin{array}{ll}\begin{array}{l}{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(x){\psi }_l(0)=f_1(x),\\ {\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(0){\psi }_l(t)=f_2(t),\\ {\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(1){\psi }_l(t)=f_3(t).\end{array}& (44)\end{array}$

Similarly the residual of model (36) with initial and boundary conditions (37) is given by

$\begin{array}{ll}\begin{array}{l}{\xi }_2(x,t)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x),{\Pi }_{k,t,\alpha }\\ +a{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}k{t}^{k-1}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x)\\ +b{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^0(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t)\\ -{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^2(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t)\\ -c({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^0(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t){)}^2\\ -d({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=-W}^W}{\delta }_{\Delta ,\sigma }^0(x-x_k){\psi }_i(x_k)a_{il}{\psi }_l(t){)}^3-f(x,t).\end{array}& (45)\end{array}$

$\begin{array}{ll}\begin{array}{l}{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(x){\psi }_l(0)=g_1(x)\\ {\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(0){\psi }_l(t)=g_2(t),\\ {\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(1){\psi }_l(t)=g_3(t),\\ {\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{a}_{il}{\psi }_i(x)\frac{\partial {\psi }_l(0)}{\partial t}=g_4(x).\end{array}& (46)\end{array}$

Now collocating Equations (44) and (45) at suitable collocation points (x_j, t_j) and in Equation (44) considering the discrete sampling points x_k = x_j equal to the collocation points and using Equation (43) an non-linear system of algebraic equations is obtained.

$\begin{array}{ll}\begin{array}{l}{\xi }_1(x_j,t_j)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x_j),{\Pi }_{k,t_j,\alpha }\\ +3\mu ({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^1(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j){)}^2\\ +3\mu ({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^0(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j){)}^2\\ \times \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^1(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j)\right)\\ +3\mu \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^0(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j)\right)\\ \times \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^2(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j)\right)\\ +\mu \left({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^2(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j)\right)-f(x,t).\end{array}& (47)\end{array}$

Similarly collocating Equations (46) and (47) we get the following system of non-linear algebraic equation

$\begin{array}{ll}\begin{array}{l}{\xi }_2(x_j,t_j)={\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x_j),{\Pi }_{k,t_j,\alpha }\\ +a{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{k=0}^l}\frac{c_{il}k{t}^{k-1}{(-1)}^{l+k}(l+k)!}{{(k!)}^2(l-k)!}{\psi }_i(x)\\ +b{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^0(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j)\\ -{\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^2(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j)\\ -c({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^0(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j){)}^2\\ -d({\displaystyle \sum _{i=0}^{m-1}}{\displaystyle \sum _{l=0}^{m-1}}{\displaystyle \sum _{s=-W}^W}{\delta }_{\Delta ,\sigma }^0(-s\Delta x){\psi }_i(x_{j+s})a_{il}{\psi }_l(t_j){)}^3-f(x,t).\end{array}& (48)\end{array}$

By Solving that system of non-linear algebraic Equations (48) and (49) in the addition of Equations (35) and (37), respectively and finding a_ij we obtained numerical solution of our proposed models.

5. Numerical Results

Our motive in this section is to depict accuracy and the validity of our new derived method by solving some examples which have C − F time fractional derivative. We perform all our numerical simulations with the help of Wolfram Mathematica version-11.3.

Example 1: If we consider the following Sharma-Tasso-Oliver equation with μ = 1 and α = 0.9

$\begin{array}{ll}\begin{array}{l}{}_0^{CF}{D}_t^{\alpha }u(t,x)+3(\frac{\partial u(x,t)}{\partial x}{)}^2+3{(u(x,t))}^2\frac{\partial u(x,t)}{\partial x}\\ +3(u(x,t))\frac{{\partial }^{2}u(x,t)}{\partial x^2}+\frac{{\partial }^{2}u(x,t)}{\partial x^2}=f(x,t).\end{array}& (49)\end{array}$

The initial and boundary conditions are considered as

$\begin{array}{ll}u(t,0)=0,u(t,1)=t,u(0,x)=0.& (50)\end{array}$

We take exact solution as u(x, t) = x²t with suitable force function f(x, t). the exact analytical solution of above problem is u(x, t) = x²t.

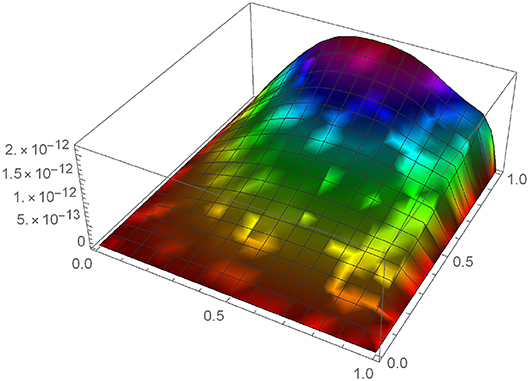
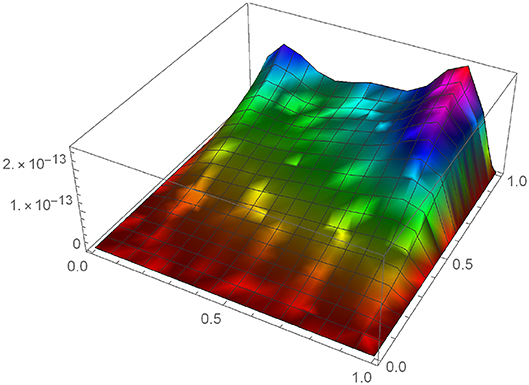
To show the accuracy and validity of our proposed method we draw the 3D graph of absolute error between exact and numerical solution for m = 10 represented by Figure 1. The representation of absolute error for various m at time t = 0.1 is shown by Table 1.

FIGURE 1

Figure 1. 3D-plot of absolute error for m = 10.

TABLE 1

Table 1. Deviation of absolute error at time t = 0.1.

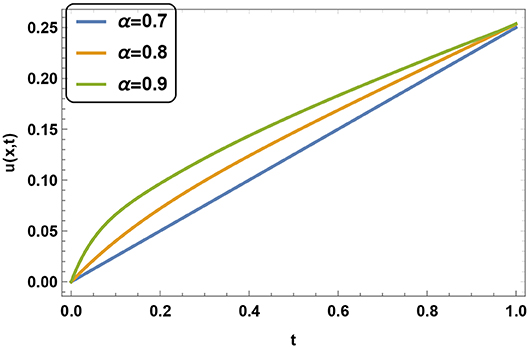
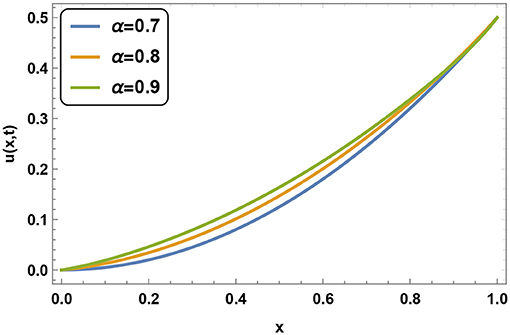
Figures 2, 3 shows the variation of u(x, t) at different value of α in t and x direction, respectively. We can conclude that at a fixed space point value of u(x, t) increases with in increment in α. Same nature can be found at a fixed time but this time rate of growth of u(x, t) is very slow. We compare the values of u(x, t) in Figures 4, 5 when time fractional derivative is Caputo-Fabrizio and Caputo type in space and time direction, respectively.

FIGURE 2

Figure 2. Plots of u at space position x = 0.1 for m = 4 at different value of α.

FIGURE 3

Figure 3. Plots of u at time t = 0.1 for m = 4 at different value of α.

FIGURE 4

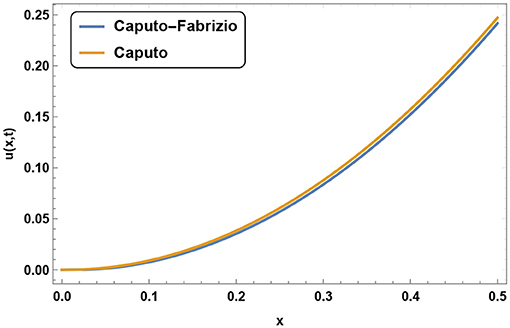
Figure 4. Variation of u for α = 0.9, m = 4, and t = 0.1 in case when time-fractional derivative is of Caputo Fabrizio and Caputo type.

FIGURE 5

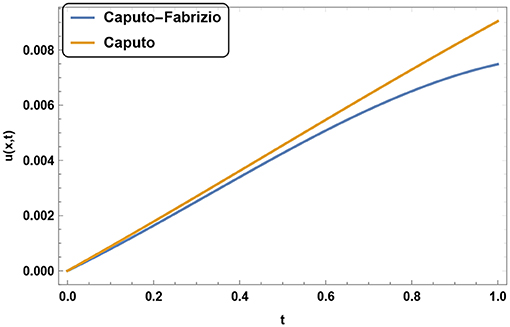
Figure 5. Variation of u for α = 0.9, m = 4, and t = 0.1 in case when time-fractional derivative is of Caputo Fabrizio and Caputo type.

Example 2: Considering C-F time fractional reaction-diffusion equation

$\begin{array}{ll}{}_0^{CF}{D}_t^{0.9}u(x,t)=\frac{{\partial }^{2}u(x,t)}{\partial x^2}+c{u}^2(x,t)+f(x,t).& (51)\end{array}$

We take the following equations as initial-boundary conditions

$\begin{array}{ll}u(0,x)=x^2,u(t,0)=0,u(t,1)=e^t.& (52)\end{array}$

We take u(x, t) = x²e^t as the exact solution where f(x, t) is suitable force function.

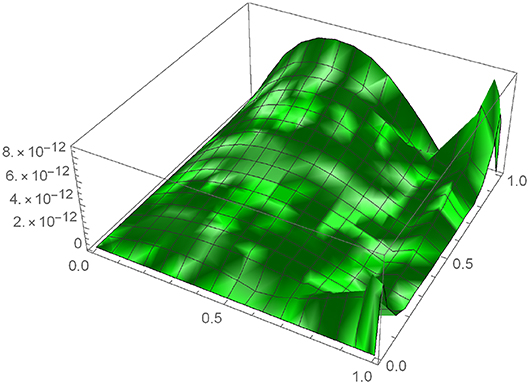
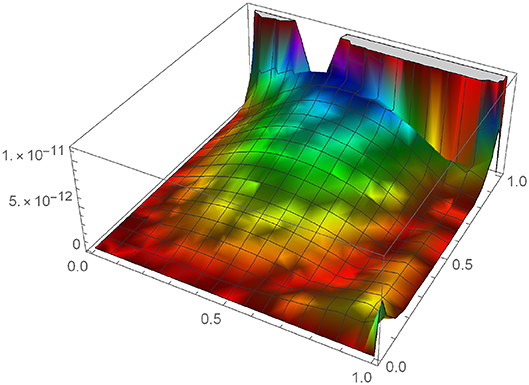
To show the accuracy and validity of our proposed method we draw the 3D graph of absolute error between exact and numerical solution for m = 10 which is depict by Figure 6. Table 2 present the variations of absolute error for different value of m.

FIGURE 6

Figure 6. 3D-plot of absolute error for m = 10.

TABLE 2

Table 2. Deviation of absolute error at time t = 0.1.

Example 3: Considering d = 0, a = 1, b = 1, c = 1, and α = 1.5 we get the following C-F time fractional Klein-Gordon equation

$\begin{array}{ll}{}_0^{CF}{D}_t^{\alpha }u(t,x)+\frac{\partial u(x,t)}{\partial t}+u(t,x)=\frac{{\partial }^{2}u(t,x)}{\partial x^2}+{(u)}^2+f(t,x).& (53)\end{array}$

The initial and boundary conditions are taken as follows

$\begin{array}{ll}\begin{array}{l}u(x,0)=0,\\ u(0,t)=0,\\ u(1,t)=t^2,\\ \frac{\partial u(x,0)}{\partial t}=0.\end{array}& (54)\end{array}$

The exact solution is taken as u(x, t) = t²x² with force function f(x, t).

To show the accuracy and validity of our proposed method we draw the 3D graph of absolute error between exact and numerical solution for m = 10 which is depict by Figure 7. The representation of absolute error at t = 0.1 is shown by Table 3. Our results clearly shown the complete agreement of obtained results.

FIGURE 7

Figure 7. 3D-plot of absolute error for m = 10.

TABLE 3

Table 3. Deviation of absolute error for different m at time t = 0.1.

Example 4: Considering a = 1, b = 1 and c = 1, d = 1 α = 1.5 we get the following non-linear C-F time fractional Klein-Gordon equation

$\begin{array}{ll}{}_0^{CF}{D}_t^{\alpha }u(t,x)+\frac{\partial u(x,t)}{\partial t}+u(x,t)=\frac{{\partial }^{2}u(x,t)}{\partial x^2}+{(u)}^2+u^3+f(x,t),& (55)\end{array}$

The Equation (55) with the initial-boundary conditions

$\begin{array}{ll}\begin{array}{l}u(0,t)=0,\\ u(1,t)=e^t+t,\\ \frac{\partial u(x,0)}{\partial t}=x^2+x,\\ u(x,0)=x^2.\end{array}& (56)\end{array}$

We chose forced function f(x, t) such that the exact solution of above problem is u(x, t) = e^tx² + xt.

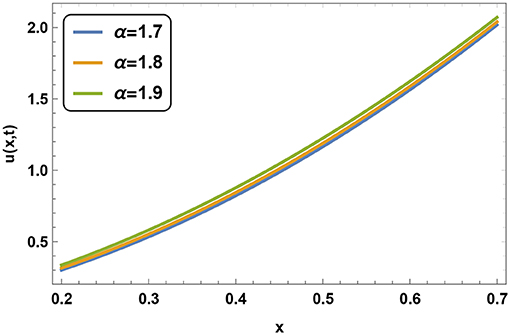
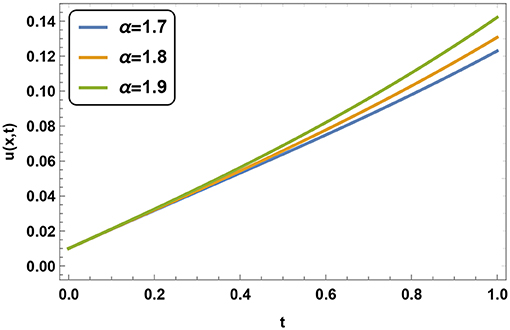
Figure 8 represents the absolute error for this problem between exact and numerical solution. We have taken m = 10 at the time of plotting the absolute error graph. The variation of absolute error for various m at time t = 0.1 is depicted by Table 4. We have plotted the Figures 9, 10 of u(x, t) for α = 1.7, α = 1.8 and α = 1.9 at fixed t and x, respectively. We can conclude that at a fixed space point value of u(x, t) increases with in increment in α. Same nature can be found at a fixed time but this time, rate of growth of u(x, t) is slow and increases as time increases to t = 1.

FIGURE 8

Figure 8. 3D-plot of absolute error for m = 10.

TABLE 4

Table 4. Deviation of absolute error at time t = 0.1.

FIGURE 9

Figure 9. Variation of u with m = 10 and t = 0.1 at different value of α.

FIGURE 10

Figure 10. Variation of u withm = 10 and x = 0.1 at different value of α.

6. Conclusion

In this work, first, we find out the approximate expression of C-F fractional derivative of the function t^k. We developed a new numerical algorithm with the combination of the Legendre spectral method and quasi wavelet-based numerical method to solve fractional PDEs having a C-F fractional derivative. We implement this new algorithm to solve the C-F time-fractional Sharma-Tasso-Oliver equation and Klein-Gordon equation. We have shown the successful implementation of this method to solve the C-F time-fractional FPDEs. This implies that our proposed method has reasonable accuracy and valid different type of FPDEs. The 3D graphs of absolute error depicted the validity and effectiveness of our proposed method. The behavior of u(x, t) in the diffusion equation with the variation in α at space and time direction is also shown by figures. We see the comparative behavior of the solution profile for C-F and Caputo derivatives. In future work, our new algorithm can be applied to another type of non-singular fractional models as Mittag-Leffler kernel derivative. It can also be applied to the system of a fractional differential equations and to investigate a different types of models.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Baleanu D, Machado JAT, Luo AC. Fractional Dynamics and Control. Berlin: Springer Science & Business Media (2011).

Google Scholar

2. Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of the Fractional Differential Equations. Vol. 204. Amsterdam: Elsevier (North-Holland) (2006).

Google Scholar

3. Podlubny I. Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications. Fractional Differential Equations: An Introduction to Fractional Derivatives. San Diego, CA: Academic Press (1998).

4. Xiao-Jun Y, Zhang ZZ, Machado J, Baleanu D. On local fractional operators view of computational complexity. Thermal Sci. (2016) 20:S755–67. doi: 10.2298/TSCI16S3755Y

CrossRef Full Text | Google Scholar

5. Aydoğan SM, Baleanu D, Mousalou A, Rezapour S. On approximate solutions for two higher-order Caputo-Fabrizio fractional integro-differential equations. Adv Differ Equat. (2017) 2017:221. doi: 10.1186/s13662-017-1088-3

CrossRef Full Text | Google Scholar

6. Baleanu D, Mousalou A, Rezapour S. On the existence of solutions for some infinite coefficient-symmetric Caputo-Fabrizio fractional integro-differential equations. Bound Value Probl. (2017) 2017:145. doi: 10.1186/s13661-017-0867-9

CrossRef Full Text | Google Scholar

7. Atangana A, Baleanu D. New fractional derivatives with nonlocal and non-singular kernel: theory and application to heat transfer model. arXiv. (2016) 160203408. doi: 10.2298/TSCI160111018A

CrossRef Full Text | Google Scholar

8. Atangana A, Koca I. Chaos in a simple nonlinear system with Atangana-Baleanu derivatives with fractional order. Chaos Solit Fract. (2016) 89:447–54. doi: 10.1016/j.chaos.2016.02.012

CrossRef Full Text | Google Scholar

9. Korpinar Z, Inc M, Baleanu D, Bayram M. Theory and application for the time fractional Gardner equation with Mittag-Leffler kernel. J Taibah Univ Sci. (2019) 13:813–9. doi: 10.1080/16583655.2019.1640446

CrossRef Full Text | Google Scholar

10. Diethelm K, Ford NJ, Freed AD. A predictor-corrector approach for the numerical solution of fractional differential equations. Nonlin Dyn. (2002) 29:3–22. doi: 10.1023/A:1016592219341

CrossRef Full Text | Google Scholar

11. Suarez L, Shokooh A. An eigenvector expansion method for the solution of motion containing fractional derivatives. J Appl Mech. (1997) 64:629–35. doi: 10.1115/1.2788939

CrossRef Full Text | Google Scholar

12. Hashim I, Abdulaziz O, Momani S. Homotopy analysis method for fractional IVPs. Commun Nonlin Sci Numer Simul. (2009) 14:674–84. doi: 10.1016/j.cnsns.2007.09.014

CrossRef Full Text | Google Scholar

13. Li Y, Sun N. Numerical solution of fractional differential equations using the generalized block pulse operational matrix. Comput Math Appl. (2011) 62:1046–54. doi: 10.1016/j.camwa.2011.03.032

CrossRef Full Text | Google Scholar

14. Owolabi KM, Atangana A. Analysis and application of new fractional Adams-Bashforth scheme with Caputo-Fabrizio derivative. Chaos Solit Fract. (2017) 105:111–9. doi: 10.1016/j.chaos.2017.10.020

CrossRef Full Text | Google Scholar

15. Darania P, Ebadian A. A method for the numerical solution of the integro-differential equations. Appl Math Comput. (2007) 188:657–68. doi: 10.1016/j.amc.2006.10.046

CrossRef Full Text | Google Scholar

16. Li Y, Zhao W. Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations. Appl Math Comput. (2010) 216:2276–85. doi: 10.1016/j.amc.2010.03.063

CrossRef Full Text | Google Scholar

17. Yuanlu L. Solving a nonlinear fractional differential equation using Chebyshev wavelets. Commun Nonlin Sci Numer Simul. (2010) 15:2284–92. doi: 10.1016/j.cnsns.2009.09.020

CrossRef Full Text | Google Scholar

18. Jafari H, Yousefi S, Firoozjaee M, Momani S, Khalique CM. Application of Legendre wavelets for solving fractional differential equations. Comput Math Appl. (2011) 62:1038–45. doi: 10.1016/j.camwa.2011.04.024

CrossRef Full Text | Google Scholar

19. Gürbüz B, Sezer M. Laguerre polynomial solutions of a class of initial and boundary value problems arising in science and engineering fields. Acta Phys Pol A. (2016) 130:194–7. doi: 10.12693/APhysPolA.130.194

CrossRef Full Text | Google Scholar

20. Odibat Z. On Legendre polynomial approximation with the VIM or HAM for numerical treatment of nonlinear fractional differential equations. J Comput Appl Math. (2011) 235:2956–68. doi: 10.1016/j.cam.2010.12.013

CrossRef Full Text | Google Scholar

21. Araci S. Novel identities for q-Genocchi numbers and polynomials. J Funct Spaces Appl. (2012) 2012:214961. doi: 10.1155/2012/214961

CrossRef Full Text | Google Scholar

22. Tassaddiq A, Khan I, Nisar K. Heat transfer analysis in sodium alginate based nanofluid using MoS2 nanoparticles: Atangana-Baleanu fractional model. Chaos Solit Fract. (2020) 130:109445. doi: 10.1016/j.chaos.2019.109445

CrossRef Full Text | Google Scholar

23. Farayola MF, Shafie S, Siam FM, Khan I. Numerical simulation of normal and cancer cells' populations with fractional derivative under radiotherapy. Comput Methods Prog Biomed. (2020) 187:105202. doi: 10.1016/j.cmpb.2019.105202

CrossRef Full Text | Google Scholar

24. Abro KA, Shaikh PH, Gómez-Aguilar J, Khan I. Analysis of De-Levie's model via modern fractional differentiations: an application to supercapacitor. Alexandr Eng J. (2019) 58:1375–84. doi: 10.1016/j.aej.2019.11.009

CrossRef Full Text | Google Scholar

25. Abro KA, Khan I, Nisar KS. Novel technique of Atangana and Baleanu for heat dissipation in transmission line of electrical circuit. Chaos Solit Fract. (2019) 129:40–5. doi: 10.1016/j.chaos.2019.08.001

CrossRef Full Text | Google Scholar

26. Ali F, Murtaza S, Sheikh NA, Khan I. Heat transfer analysis of generalized Jeffery nanofluid in a rotating frame: Atangana-Balaenu and Caputo-Fabrizio fractional models. Chaos Solit Fract. (2019) 129:1–15. doi: 10.1016/j.chaos.2019.08.013

CrossRef Full Text | Google Scholar

27. Saqib M, Khan I, Shafie S. Application of fractional differential equations to heat transfer in hybrid nanofluid: modeling and solution via integral transforms. Adv Differ Equat. (2019) 2019:52. doi: 10.1186/s13662-019-1988-5

CrossRef Full Text | Google Scholar

28. Abro KA, Memon AA, Abro SH, Khan I, Tlili I. Enhancement of heat transfer rate of solar energy via rotating Jeffrey nanofluids using Caputo-Fabrizio fractional operator: an application to solar energy. Energy Rep. (2019) 5:41–9. doi: 10.1016/j.egyr.2018.09.009

CrossRef Full Text | Google Scholar

29. Khan A, Khan D, Khan I, Taj M, Ullah I, Aldawsari AM, et al. MHD flow and heat transfer in sodium alginate fluid with thermal radiation and porosity effects: fractional model of Atangana-Baleanu derivative of non-local and non-singular kernel. Symmetry. (2019) 11:1295. doi: 10.3390/sym11101295

CrossRef Full Text | Google Scholar

30. Ali F, Khan N, Imtiaz A, Khan I, Sheikh NA. The impact of magnetohydrodynamics and heat transfer on the unsteady flow of Casson fluid in an oscillating cylinder via integral transform: a Caputo-Fabrizio fractional model. Pramana. (2019) 93:47. doi: 10.1007/s12043-019-1805-4

CrossRef Full Text | Google Scholar

31. Arif M, Ali F, Sheikh NA, Khan I, Nisar KS. Fractional model of couple stress fluid for generalized couette flow: a comparative analysis of Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. IEEE Access. (2019) 7:88643–55. doi: 10.1109/ACCESS.2019.2925699

CrossRef Full Text | Google Scholar

32. Ali F, Iftikhar M, Khan I, Sheikh NA. Atangana-Baleanu fractional model for electro-osmotic flow of viscoelastic fluids. Chaos Solit Fract. (2019) 124:125–33. doi: 10.1016/j.chaos.2019.05.001

CrossRef Full Text | Google Scholar

33. Bhatter S, Mathur A, Kumar D, Singh J. A new analysis of fractional Drinfeld-Sokolov-Wilson model with exponential memory. Phys A Stat Mech Appl. (2020) 537:122578. doi: 10.1016/j.physa.2019.122578

CrossRef Full Text | Google Scholar

34. Kumar D, Singh J, Baleanu D. On the analysis of vibration equation involving a fractional derivative with Mittag-Leffler law. Math Methods Appl Sci. (2019) 43:443–57. doi: 10.1002/mma.5903

CrossRef Full Text | Google Scholar

35. Goswami A, Singh J, Kumar D, Gupta S, Sushila. An efficient analytical technique for fractional partial differential equations occurring in ion acoustic waves in plasma. J Ocean Eng Sci. (2019) 4:85–99. doi: 10.1016/j.joes.2019.01.003

CrossRef Full Text | Google Scholar

36. Kumar D, Singh J, Al Qurashi M, Baleanu D. A new fractional SIRS-SI malaria disease model with application of vaccines, antimalarial drugs, and spraying. Adv Differ Equat. (2019) 2019:278. doi: 10.1186/s13662-019-2199-9

CrossRef Full Text | Google Scholar

37. Goswami A, Singh J, Kumar D, Sushila. An efficient analytical approach for fractional equal width equations describing hydro-magnetic waves in cold plasma. Phys A Stat Mech Appl. (2019) 524:563–75. doi: 10.1016/j.physa.2019.04.058

CrossRef Full Text | Google Scholar

38. Qureshi S, Rangaig NA, Baleanu D. New numerical aspects of Caputo-Fabrizio fractional derivative operator. Mathematics. (2019) 7:374. doi: 10.3390/math7040374

CrossRef Full Text | Google Scholar

39. Caputo M, Fabrizio M. A new definition of fractional derivative without singular kernel. Progr Fract Differ Appl. (2015) 1:1–13. doi: 10.18576/pfda/020101

CrossRef Full Text | Google Scholar

40. Loh JR, Isah A, Phang C, Toh YT. On the new properties of Caputo-Fabrizio operator and its application in deriving shifted Legendre operational matrix. Appl Numer Math. (2018) 132:138–53. doi: 10.1016/j.apnum.2018.05.016

CrossRef Full Text | Google Scholar

41. Atangana A, Gómez-Aguilar J. Fractional derivatives with no-index law property: application to chaos and statistics. Chaos Solit Fract. (2018) 114:516–35. doi: 10.1016/j.chaos.2018.07.033

CrossRef Full Text | Google Scholar

42. Hristov J. On the Atangana-Baleanu derivative and its relation to the fading memory concept: the diffusion equation formulation. In: J. F. Gómez, L. Torres, R. F. Escobar eds Fractional Derivatives with Mittag-Leffler Kernel. New York, NY: Springer (2019). p. 175–93. doi: 10.1007/978-3-030-11662-0_11

CrossRef Full Text | Google Scholar

43. Hristov J. Derivatives with non-singular kernels from the Caputo-Fabrizio definition and beyond: appraising analysis with emphasis on diffusion models. Front Fract Calc. (2017) 1:270–342. doi: 10.2174/9781681085999118010013

CrossRef Full Text | Google Scholar

44. Wei G. Discrete singular convolution for the solution of the Fokker-Planck equation. J Chem Phys. (1999) 110:8930–42. doi: 10.1063/1.478812

CrossRef Full Text | Google Scholar

45. Yang X, Xu D, Zhang H. Quasi-wavelet based numerical method for fourth-order partial integro-differential equations with a weakly singular kernel. Int J Comput Math. (2011) 88:3236–54. doi: 10.1080/00207160.2011.587003

CrossRef Full Text | Google Scholar