- 1Institute for Solid State Physics, Vienna University of Technology, Vienna, Austria
- 2School of Physics, Northwest University, Xi’an, China
- 3Institute for Theoretical Solid State Physics, Leibniz IFW Dresden, Dresden, Germany
- 4RIKEN Center for Emergent Matter Sciences (CEMS), Wako, Japan
- 5Department of Applied Physics, the University of Tokyo, Bunkyo, Japan
- 6Key Laboratory of Magnetic Materials and Devices and Zhejiang Province Key Laboratory of Magnetic Materials and Application Technology, Ningbo Institute of Materials Technology and Engineering (NIMTE), Chinese Academy of Sciences, Ningbo, China
We review the electronic structure of nickelate superconductors with and without effects of electronic correlations. As a minimal model, we identify the one-band Hubbard model for the Ni 3
1 Introduction
Twenty years ago, Anisimov, Bukhvalov, and Rice [1] suggested high-temperature (Tc) superconductivity in nickelates based on material calculations that showed apparent similarities to cuprates. Subsequent calculations [2–4] demonstrated the potential to further engineer the nickelate Fermi surface by heterostructuring. Two years ago, Li, Hwang et al. [5] discovered superconductivity in Sr-doped NdNiO2 films grown on a SrTiO3 substrate and protected by a SrTiO3 capping layer. These novel SrxNd1–xNiO2 films are isostructural and formally isoelectric to the arguably simplest, but certainly not the best superconducting cuprate: infinite layer CaCuO2 [6–9].
However, the devil is in the details, and here cuprates and nickelates differ. For revealing such material-specific differences, band-structure calculations based on density functional theory (DFT) are the method of choice. They serve as a starting point for understanding the electronic structure and, subsequently, the phase diagram of nickelate superconductors. Following the experimental discovery of nickelate superconductivity, and even before that, numerous DFT studies have been published [10–20]. Based on these DFT calculations, various models for the low-energy electronic structure for nickelates and the observed superconductivity have been proposed. Besides the cuprate-like Ni 3
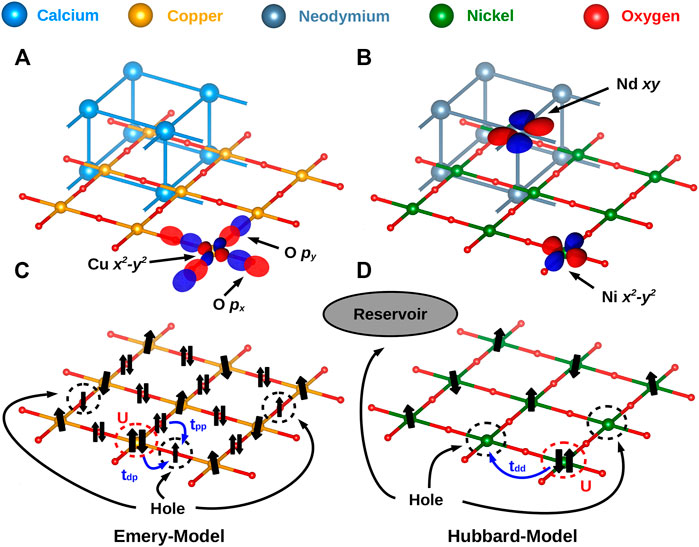
FIGURE 1. Crystal lattice and most important orbitals for (A) cuprates and (B) nickelates. (C) For cuprates, the arguably simplest model is the Emery model with a half-filled copper 3
At first glance, nickelates appear to be much more complicated with more relevant orbitals than in the case of the cuprates. In this article, we review the electronic structure of nickelates in comparison to that of cuprates and the arguments for a simpler description of nickelate superconductors, namely, a Hubbard model for the Ni 3
The outline of this article is as follows: In Section 2,we first compare the electronic structure of nickelates to that of cuprates, starting from DFT but also discussing effects of electronic correlations as described, for example, by DMFT. Subsequently, we argue in Section 3, orbital-by-orbital, that the other orbitals besides the Ni 3
2 Electronic Structure: Nickelates vs. Cuprates
Let us start by looking into the electronic structure in more detail and start with the DFT results. On a technical note, the calculations presented have been performed using the wien2k [43, 44], VASP [45], and FPLO [46] program packages, with the PBE [47] version of the generalized gradient approximation (GGA). For further details, see the original work [33]. Figure 2 compares the bandstructure of the two simple materials: CaCuO2 and NdNiO2. Here, we restrict ourselves to only the Brillouin zone path along the most relevant momenta for these compounds: Γ (0, 0, 0), X (π, 0, 0), and A (π, π, π). In DFT, both the cuprate and nickelate parent compounds are metals with a prominent Cu or Ni 3
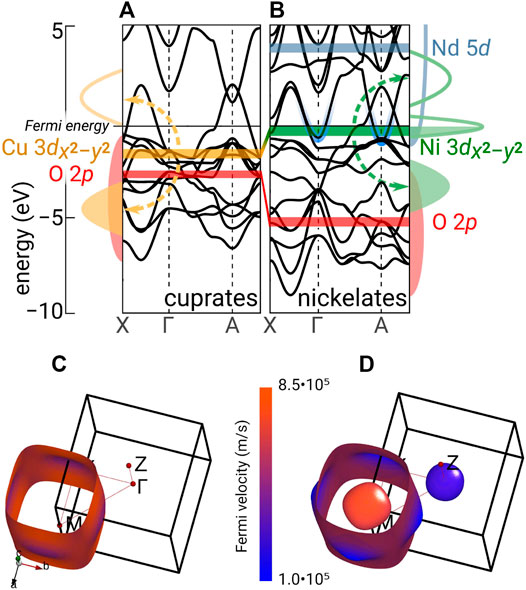
FIGURE 2. Electronic structures of CaCuO2 (A) and NdNiO2 (B) exemplifying superconducting cuprates and nickelates. Top: The bars indicate the center of energy for the most important DFT bands. The dashed arrows indicate the correlation-induced splitting of the Cu or Ni 3
Because cuprates are charge-transfer insulators, the one-band Hubbard model can only be considered an effective Hamiltonian mimicking the Zhang–Rice singlet [31]. As already pointed out in the Introduction, more appropriate is the Emery model of Figure 1. The correlation-induced splitting into the Hubbard bands [40], as well as the Zhang–Rice singlet [49], can be described already by DMFT [39, 40, 42]. Two-dimensional spin-fluctuations and superconductivity, however, cannot be described. For describing such physics, non-local correlations beyond DMFT are needed.
For the nickelates, the oxygen bands are at a much lower energy. Hence, as indicated in the right side panel of Figure 2, the lower Ni 3
3 Irrelevance of Various Orbitals
Next, we turn to various orbitals that may appear relevant at first glance but turn out to be irrelevant for the low-energy physics when taking electronic correlations properly into account. To account for the latter, we use DFT + DMFT [50–54], which is the state of the art for calculating correlated materials.
Oxygen Orbitals
For nickelates, the oxygen 2p orbitals are approximately 3 eV lower in energy than in cuprates within DFT. Hence, some DFT + DMFT calculations did not include these from the beginning [32, 33], and those that did [22] also found the oxygen 2p orbitals at a lower energy than the lower Ni 3
Ni 3
Instead of the oxygen 2p orbitals, the DFT calculation in Figure 2 and elsewhere [10, 11, 17, 48] show other Ni 3d orbitals closely below the Ni 3
Figure 3 shows the DFT + DMFT spectral function for SrxLa1−xNiO2 from 0 to 25% Sr-doping. In these calculations [33], all Ni 3d and all La 5d orbitals have been taken into account in a wien2wannier [56] projection supplemented by interactions calculated within the constrained random phase approximation (cRPA) [55] to be U′ = 3.10 eV (2.00 eV) and Hund’s exchange J = 0.65 eV (0.25 eV) for Ni (La). On a technical note, the DMFT self-consistency equations [39] have been solved here at room temperature (300 K) by continuous-time quantum Monte Carlo simulations in the hybridization expansions [57] using the w2dynamics implementation [58, 59] and the maximum entropy code of ana_cont [60] for analytic continuation.
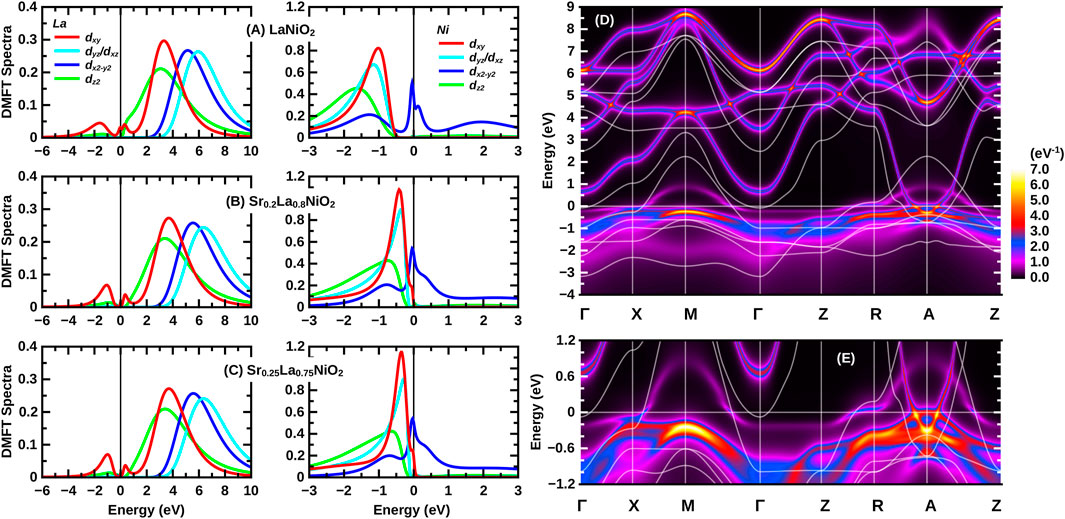
FIGURE 3. DMFT k-integrated (A–C) and k-resolved (D,E) spectral functions A(ω) and A (k, ω) of undoped LaNiO2 (A), 20% Sr-doped LaNiO2 (Sr0.2La0.8NiO2) (B), and 25% Sr-doped LaNiO2 (Sr0.25La0.75NiO2) (C). The k-resolved spectral function A (k, ω) of La0.8Sr0.2NiO2 is shown in (D); (E) is a zoom-in of (D). Data partially obtained from [33, 55].
Clearly, Figure 3 indicates that for up to 20% Sr-doping, the other Ni 3d orbitals besides the 3
DFT + DMFT calculations by Lechermann [22, 23] stress, on the other hand, the relevance of the 3
First experimental hints on the (ir) relevance of the 3
Γ Pocket
A feature clearly present in DFT calculations for the nickelate parent compounds LaNiO2 and NdNiO2 is the Γ pocket, see Figure 2D. However, when the Coulomb interaction on the La or Nd sites is included, it is shifted upward in energy. Furthermore, Sr-doping depopulates the Ni 3
Briefly after the discovery of superconductivity in nickelates, it has also been suggested that the Nd 5d orbitals of the pockets couple to the Ni 3

TABLE 1. Hybridization (hopping amplitude in eV) between the partially occupied Ni 3
Nd 4f Orbitals
Finally, the importance of the Nd 4f orbitals has been suggested in the literature. Treating these 4f orbitals in DFT is not trivial because DFT puts them in the vicinity of the Fermi level. This neglects that electronic correlations split the Nd 4f into upper and lower Hubbard bands as they form a local spin. This effect is beyond DFT. One way to circumvent this difficulty is to put the Nd 4f orbitals in the core instead of having them as valence states close to the Fermi energy. This is denoted as “GGA open core” instead of standard “GGA” in Table 1. The localized Nd 4f spins might, in principle, be screened through a Kondo effect. However, the hybridization of the Nd 4f with the Ni 3

TABLE 2. Hybridization (hopping amplitude in eV) between the Ni 3
4 One-Band Hubbard model Plus Reservoir
Altogether, this leaves us with Figures 1B,D as the arguably simplest model for nickelate superconductors, consisting of a strongly correlated Ni 3
On the other hand, the A pocket does not interact with the Ni 3
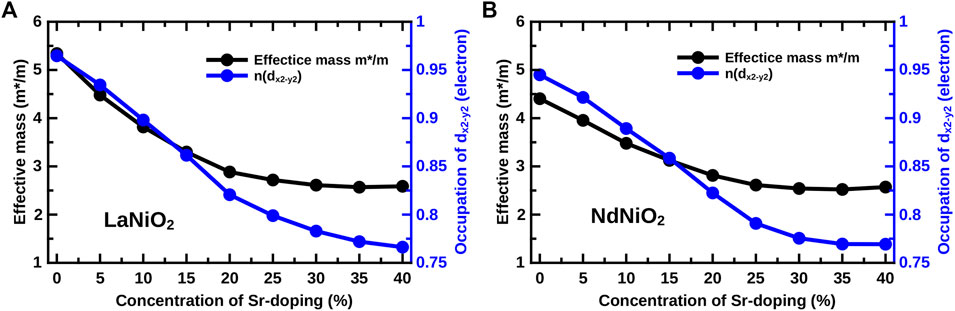
FIGURE 4. Occupation of the Ni 3
It is noted that NdNiO2 shows for Sr-doping below about 10% more holes in the Ni 3
In the subsequent one-band calculation, presented in the next paragraph, we employ the occupation from the Ni 3
The hopping parameters for the Ni-3

TABLE 3. Major hopping elements (in units of eV) of the Ni-3
Besides the doping from Figure 4 and the hopping for the one-band Wannier projection from Table 3, we only need the interaction parameter for doing realistic one-band Hubbard model calculations for nickelates. In cRPA for a single 3
5 Non-Local Correlations and Superconducting Phase Diagram
DFT provides a first picture of the relevant orbitals, and DMFT adds to this effect of strong local correlations, such as the splitting into Hubbard bands, the formation of a quasiparticle peak, and correlation-induced orbital shifts, such as the upshift of the Γ pocket. However, at low temperatures, non-local correlations give rise to additional effects. Relevant factors are as follows: the emergence of strong spin fluctuations and their impact on the spectral function and superconductivity.
For including such non-local correlations, diagrammatic extensions of DMFT, such as the dynamical vertex approximation (DΓA) [36–38, 70], have been proven extremely powerful. Such calculations are possible down to the temperatures of the superconducting phase transition in the correlated regime and for very large lattices so that the long-range correlations close to a phase transition can be properly described. Even (quantum) critical exponents can be calculated [71–74]. DΓA has proven reliable compared with the numerically exact calculations where these are possible [75] and, in particular, provide for a more accurate determination of Tc [76] since the full local frequency dependence of the two-particle vertex is included. Such local frequency dependence can affect even the non-local pairing through spin fluctuations. In, for example, RPA, this frequency dependence and the suppression of the pairing vertex for small frequencies can only be improperly mimicked by (quite arbitrarily) adjusting the static U.
This simple one-band Hubbard model in DΓA has been the basis for calculating the phase diagram Tc vs. Sr-doping in Figure 5 [33]. At the time of the calculation, only a single experimental Tc at 20% Sr-doping was available [5]. The physical origin of the superconductivity in these calculations is strong spin fluctuations which form the pairing glue for high-temperature superconductivity. Charge fluctuations are much weaker; the electron–phonon coupling has not been considered and is also too weak for transition metal oxides to yield high-temperature superconductivity. The theoretical Tc in Figure 5 at 20% doping was from the very beginning slightly larger than in the experiment. Most likely, this is because in the ladder DΓA [36, 37] calculation of Tc, the spin fluctuations are first calculated and then enter the superconducting particle–particle channel [76]. This neglects the feedback effect of these particle–particle fluctuations on the self-energy and the spin fluctuations, which may, in turn, suppress the tendency toward superconductivity somewhat. Such effects would be only included in a more complete parquet DΓA calculation [77–79]. Also, the ignored weak three-dimensional dispersion will suppress Tc. Let us note that antiferromagnetic spin fluctuations have recently been observed experimentally [64, 80].
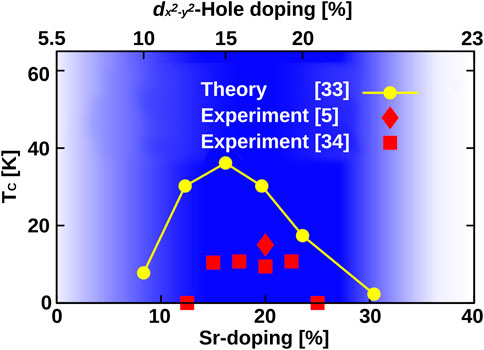
FIGURE 5. Superconducting phase diagram Tc vs. x for SrxNd1−xNiO2 as predicted by DΓA [33] and experimentally confirmed a posteriori in [34, 35]. A priori, that is, at the time of the calculation, only one experimental data point [5] was available. For such a difficult to determine quantity as the superconducting Tc and without adjusting parameters, the accuracy is astonishing. The bottom x-axis shows the Sr-doping and the top x-axis the calculated hole doping of the 3
Given the slight overestimation of Tc from the very beginning, the agreement with the subsequently obtained experimental Tc vs. Sr-doping x phase diagram [34, 35] in Figure 5 is astonishingly good. We further see that the superconducting doping regime also concurs with the doping regime where a one-band Hubbard model description is possible for SrxNd1−xNiO2, as concluded from a full DFT + DMFT calculation for 5 Ni plus 5 Nd bands. This regime is marked dark blue in Figure 5 and, as already noted, extends to somewhat larger dopings [33] than for SrxLa1−xNiO2 shown in Figure 3. Concomitant with this is the fact that the experimental superconducting doping range for SrxLa1−xNiO2 extends to a larger x than for SrxNd1−xNiO2. For dopings larger than the dark blue regime in Figure 5, two Ni 3d bands need to be included. As we will show in the next section, this completely changes the physics and is not favorable for superconductivity. For dopings smaller than the dark blue regime in Figure 5, on the other hand, the Γ pocket may become relevant for SrxNd1−xNiO2, as well as its exchange coupling to the 4f moments.
Our theoretical calculations also reveal ways to enhance Tc. Particularly promising is to enhance the hopping parameter t. This enhances Tc because (i) t sets the energy scale of the problem, and a larger t means a larger Tc if U/t, t′/t, and t″/t and doping are kept fixed. Furthermore, the ratio U/t = 8 for nickelates is not yet optimal. Indeed, (ii) a somewhat smaller ratio U/t would imply a larger Tc at fixed t [33]. Since the interaction U is local, it typically varies much more slowly when, for example, applying compressive strain or pressure and can be assumed to be constant as a first approximation (for secondary effects, see [81, 82]). Thus, compressive strain or pressure enhance (i) t and reduce (ii) U/t. Both effects enhance Tc. This prediction made in [33] has been confirmed experimentally: applying a pressure of 12 GPa increases Tc from 18K to 31 K in Sr0.18Pr0.82NiO2 [83]. This is so far the record Tc for nickelates, and there are yet no signs for saturation or maximum, indicating that even higher Tc’s are possible at higher pressures.
Alternatives to enhance t are 1) to substitute the SrTiO3 substrate by a substrate with smaller in-plane lattice constants since the nickelate film in-plane axis parameters will be locked to that of the substrate. Furthermore, one can 2) replace 3d Ni by 4d Pd, that is, try to synthesize Nd (La)PdO2 [11]. Since the Pd 4d orbitals are more extended than the 3d Ni orbitals, this should enhance t as well.
Next, we turn to the DΓA spectra, more precisely Fermi surfaces, in Figure 6. Here, beyond quasiparticle renormalizations of DMFT, non-local spin fluctuations can further impact the spectrum. Only the spectral function of the Hubbard model is shown, describing the 3
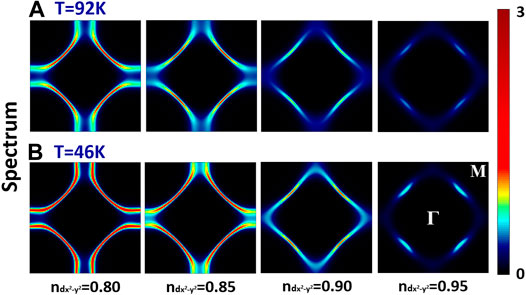
FIGURE 6. DΓA k-resolved spectrum at the Fermi energy for T = 0.02t = 92 K (A) and T = 0.01t = 46 K (B) and four different dopings
6 Topotactic Hydrogen: Turning the Electronic Structure Upside Down
The fact that it took 20 years from the theoretical prediction of superconductivity in rare-earth nickelates to the experimental realization already suggests that the synthesis is far from trivial. This is because nickel has to be in the unusually low oxidation state Ni+1. The recipe of success for nickelate superconductors is a two-step process [85]: First, doped perovskite films Sr (Ca)xNd (La,Pr)1−xNiO3 films are deposited on a SrTiO3 substrate by pulsed laser deposition. Already, this first step is far from trivial, not least because the doped material has to be deposited with homogenous Sr (Ca) concentration. Second, Sr(Ca)xNd(La,Pr)1−xNiO3 needs to be reduced to Sr(Ca)xNd(La,Pr)1−xNiO2. To this end, the reducing agent CaH2 is used. Here, the problem is that this reduction might be incomplete with excess oxygen remaining or that hydrogen from CaH2 is topotactically intercalated in the Sr (Ca)xNd (La,Pr)1−xNiO2 structure. A particular difficulty is that the light hydrogen is experimentally hard to detect, for example, it evades conventional X-ray structural detection.
In [55], we studied the possibility to intercalate hydrogen, that is, to synthesize unintendedly SrxNd(La)1−xNiO2H instead of SrxNd(La)1−xNiO2. For the reduction of, for example, SrVO3 with CaH2, it is well-established that SrVO2H may be obtained as the end product [86]. Both possible end products are visualized in Figure 7. The extra H takes away one more electron from the Ni sites. Hence, we have two holes on the Ni sites which in a local picture are distributed to two orbitals and form a spin-1, due to Hund’s exchange.
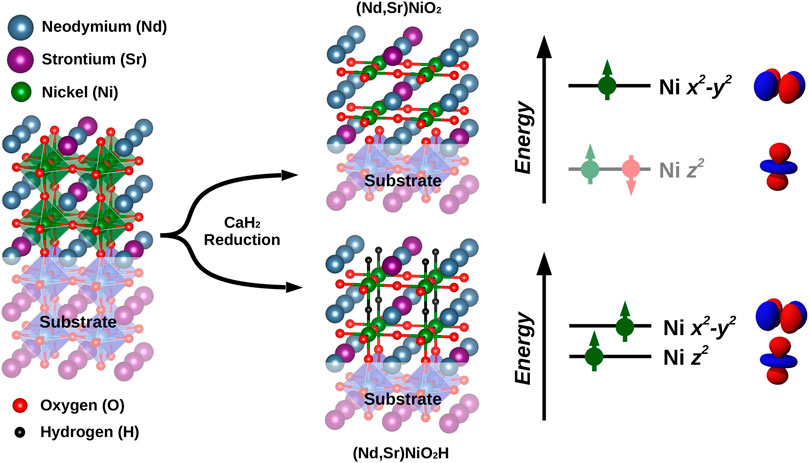
FIGURE 7. Reduction of SrxNd(La)1−xNiO3 with CaH2 may result not only in the pursued end product SrxNd(La)1−xNiO2 but also in SrxNd(La)1−xNiO2H, where H atoms occupy the vacant O sites between the layers. This has dramatic consequences for the electronic structure. In a first, purely local picture, visualized on the right side, there is instead of Ni 3d9 with one-hole in the 3
The first question is how susceptible the material is to bind topotactic H. To answer this question, one can calculate the binding energy E (ABNiO2) + 1/2 E (H2)- E (ABNiO2H) in DFT [55, 87]. The result is shown in Figure 8, which clearly shows that early transition metal oxides are prone to intercalate hydrogen, whereas for cuprates, the infinite layer compound without H is more stable. Nickelates are in-between. For the undoped compounds NdNiO2, and even a bit more for LaNiO2, it is favorable to intercalate H. However, for the Sr-doped nickelates, the energy balance is inverted. Here, it is unfavorable to bind hydrogen.
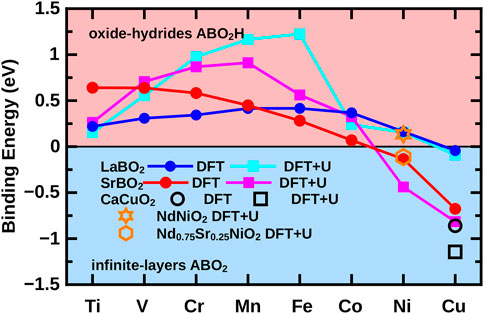
FIGURE 8. Binding energy for topotactical H as calculated by non–spin-polarized DFT and spin-polarized DFT + U for various transition metals B (x-axis). Positive binding energies indicate that ABNiO2H is energetically favored; for negative binding energies, ABNiO2 is more stable. The data for non–spin-polarized DFT calculations are from [55].
Let us emphasize that this is only the enthalpy balance. In the actual synthesis also the reaction kinetics matter, and the entropy which is large for the H2 gas. Nonetheless, this shows that undoped nickelates are very susceptible to topotactic H. This possibly means that, experimentally, not a complete H-coverage as in ABNiO2H of Figure 8 is realized, but some hydrogen may remain in the nickelates because of an incomplete reduction with CaH2. Indeed, hydrogen remainders have later been detected experimentally by nuclear magnetic resonance (NMR) spectroscopy, and they have even been used to analyze the antiferromagnetic spin fluctuations [80].
Now that we have established that remainders of hydrogen can be expected for nickelates at low doping, the question is how this affects the electronic structure. The local picture of Figure 7 already suggested a very different electronic configuration. This is further corroborated by DFT + DMFT calculations for LaNiO2H presented in Figure 9. Here, the DFT band structure shows a metallic behavior with two orbitals, Ni 3
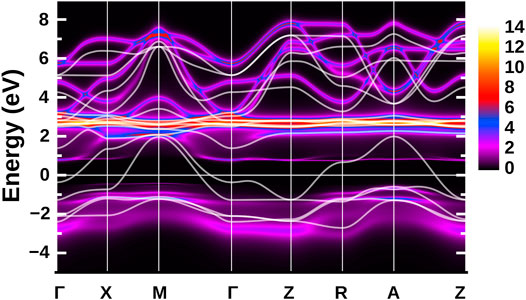
FIGURE 9. DFT (white lines) and DMFT (color bar) k-resolved spectral function for LaNiO2H. Here, a model with La-d + La-f + Ni-d was used, which is beyond the Ni-d only and La-d + Ni-d models shown in [55].
Even if we dope LaNiO2H, this electronic structure is not particularly promising for superconductivity. First, it is not two-dimensional because of the 3
7 Conclusion
In this article, we have discussed the physics of nickelate superconductors from the perspective of a one-band Hubbard model for the Ni 3
The one-band Hubbard model picture for nickelates was put forward early on for nickelates [11, 19, 32, 33], and its proper doping, including correlation effects, has been calculated in [33]. This picture has been confirmed by many experimental observations so far. The Nd 4f states are, from the theoretical perspective, irrelevant because they form a local spin and barely hybridize with the 3
Strong evidence for the one-band Hubbard model picture is the prediction of the superconducting phase diagram [33], confirmed experimentally in [34, 35]. A further prediction was the increase of Tc with pressure or compressive strain [33], which was subsequently found in the experiment with a record Tc = 31 K for nickelates under pressure [83]. The strength of antiferromagnetic spin-fluctuations as obtained in RIXS [64] also roughly agrees with that of the calculation [33]. Altogether, this gives us quite some confidence in the one-band Hubbard model scenario, which even allowed for a rough calculation of Tc. Notwithstanding, further theoretical calculations, in particular including non-local correlations also in a realistic multi-orbital setting [37, 70, 88], are eligible. On the experimental side more detailed, for example, k-resolved information is desirable as are further close comparisons between the experiment and theory.
A good analysis of the quality of the samples is also mandatory, especially against the background that superconducting nickelates have been extremely difficult to synthesize. Incomplete oxygen reduction and topotactic hydrogen [55, 87] are theoretically expected to be present because this is energetically favored, at least for low Sr-doping. This leads to two holes in two orbitals forming a high-spin state and a three-dimensional electronic structure, thus obstructing the intrinsic physics of superconducting nickelates.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the study and approved it for publication.
Funding
We acknowledge funding through the Austrian Science Funds (FWF), Project numbers P 32044 and P 30213, and Grant-in-Aids for Scientific Research (JSPS KAKENHI), Grant numbers 19H05825, JP20K22342, and JP21K13887. OJ was supported by the Leibniz Association through the Leibniz Competition. Calculations were partially performed on the Vienna Scientific Cluster (VSC).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We thank Atsushi Hariki, Motoaki Hirayama, Josef Kaufmann, Yusuke Nomura, and Terumasa Tadano for valuable discussions.
References
1. Anisimov VI, Bukhvalov D, Rice TM. Electronic Structure of Possible Nickelate Analogs to the Cuprates. Phys Rev B (1999) 59:7901–6. doi:10.1103/PhysRevB.59.7901
2. Chaloupka J, Khaliullin G. Orbital Order and Possible Superconductivity in LaNiO3/LaMO3 Superlattices. Phys Rev Lett (2008) 100:016404. doi:10.1103/PhysRevLett.100.016404
3. Hansmann P, Toschi A, Yang X, Andersen O, Held K. Electronic Structure of Nickelates: From Two-Dimensional Heterostructures to Three-Dimensional Bulk Materials. Phys Rev B (2010) 82:235123. doi:10.1103/PhysRevB.82.235123
4. Hansmann P, Yang X, Toschi A, Khaliullin G, Andersen OK, Held K. Turning a Nickelate Fermi Surface into a Cupratelike One through Heterostructuring. Phys Rev Lett (2009) 103:016401. doi:10.1103/PhysRevLett.103.016401
5. Li D, Lee K, Wang BY, Osada M, Crossley S, Lee HR, et al. Superconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. doi:10.1038/s41586-019-1496-5
6. Balestrino G, Medaglia PG, Orgiani P, Tebano A, Aruta C, Lavanga S, et al. Very Large Purely Intralayer Critical Current Density in Ultrathin Cuprate Artificial Structures. Phys Rev Lett (2002) 89:156402. doi:10.1103/physrevlett.89.156402
7. Di Castro D, Cantoni C, Ridolfi F, Aruta C, Tebano A, Yang N, et al. High-Tc Superconductivity at the Interface between the CaCuO2 and SrTiO3 Insulating Oxides. Phys Rev Lett (2015) 115:147001. doi:10.1103/PhysRevLett.115.147001
8. Orgiani P, Aruta C, Balestrino G, Born D, Maritato L, Medaglia PG, et al. Direct Measurement of Sheet Resistance R□ in Cuprate Systems: Evidence of a Fermionic Scenario in a Metal-Insulator Transition. Phys Rev Lett (2007) 98:036401. doi:10.1103/PhysRevLett.98.036401
9. Siegrist T, Zahurak S, Murphy D, Roth R. The Parent Structure of the Layered High-Temperature Superconductors. Nature (1988) 334:231–2. doi:10.1038/334231a0
10. Botana AS, Norman MR. Similarities and Differences between LaNiO2 and CaCuO2 and Implications for Superconductivity. Phys Rev X (2020) 10:011024. doi:10.1103/PhysRevX.10.011024
11. Hirayama M, Tadano T, Nomura Y, Arita R. Materials Design of Dynamically Stable D9 Layered Nickelates. Phys Rev B (2020) 101:075107. doi:10.1103/PhysRevB.101.075107
12. Hu L-H, Wu C. Two-band Model for Magnetism and Superconductivity in Nickelates. Phys Rev Res (2019) 1:032046. doi:10.1103/PhysRevResearch.1.032046
13. Jiang M, Berciu M, Sawatzky GA. Critical Nature of the Ni Spin State in Doped NdNiO2. Phys Rev Lett (2020) 124:207004. doi:10.1103/PhysRevLett.124.207004
14. Lee K-W, Pickett W. Infinite-layer LaNiO2: Ni1+ Is Not Cu2+. Phys Rev B (2004) 70:165109. doi:10.1103/PhysRevB.70.165109
15. Nomura Y, Hirayama M, Tadano T, Yoshimoto Y, Nakamura K, Arita R. Formation of a Two-Dimensional Single-Component Correlated Electron System and Band Engineering in the Nickelate Superconductor NdNiO2. Phys Rev B (2019) 100:205138. doi:10.1103/PhysRevB.100.205138
16. Pavarini E, Dasgupta I, Saha-Dasgupta T, Jepsen O, Andersen OK. Band-structure Trend in Hole-Doped Cuprates and Correlation with T (C max). Phys Rev Lett (2001) 87:047003. doi:10.1103/PhysRevLett.87.047003
17. Sakakibara H, Usui H, Suzuki K, Kotani T, Aoki H, Kuroki K. Model Construction and a Possibility of Cupratelike Pairing in a New D9 Nickelate Superconductor (Nd, Sr)NiO2. Phys Rev Lett (2020) 125:077003. doi:10.1103/PhysRevLett.125.077003
18. Werner P, Hoshino S. Nickelate Superconductors: Multiorbital Nature and Spin Freezing. Phys Rev B (2020) 101:041104. doi:10.1103/PhysRevB.101.041104
19. Wu X, Di Sante D, Schwemmer T, Hanke W, Hwang HY, Raghu S, et al. Robust Dx2-y2 -wave Superconductivity of Infinite-Layer Nickelates. Phys Rev B (2020) 101:060504. doi:10.1103/PhysRevB.101.060504
20. Zhang G-M, Yang Y-F, Zhang F-C. Self-Doped Mott Insulator for Parent Compounds of Nickelate Superconductors. Phys Rev B (2020) 101:020501. doi:10.1103/PhysRevB.101.020501
21. Adhikary P, Bandyopadhyay S, Das T, Dasgupta I, Saha-Dasgupta T. Orbital-selective Superconductivity in a Two-Band Model of Infinite-Layer Nickelates. Phys Rev B (2020) 102:100501. doi:10.1103/PhysRevB.102.100501
22. Lechermann F. Late Transition Metal Oxides with Infinite-Layer Structure: Nickelates versus Cuprates. Phys Rev B (2020) 101:081110. doi:10.1103/PhysRevB.101.081110
23. Lechermann F. Multiorbital Processes Rule the Nd1−xSrxNiO2 normal State. Phys Rev X (2020) 10:041002. doi:10.1103/PhysRevX.10.041002
24. Petocchi F, Christiansson V, Nilsson F, Aryasetiawan F, Werner P. Normal State of Nd1−xSrxNiO2 from Self-Consistent GW + EDMFT. Phys Rev X (2020) 10:041047. doi:10.1103/PhysRevX.10.041047
25. Bandyopadhyay S, Adhikary P, Das T, Dasgupta I, Saha-Dasgupta T. Superconductivity in Infinite-Layer Nickelates: Role of F Orbitals. Phys Rev B (2020) 102:220502. doi:10.1103/PhysRevB.102.220502
26. Zaanen J, Sawatzky GA, Allen JW. Band Gaps and Electronic Structure of Transition-Metal Compounds. Phys Rev Lett (1985) 55:418–21. doi:10.1103/PhysRevLett.55.418
27. Emery VJ. Theory of High–Tc Superconductivity in Oxides. Phys Rev Lett (1987) 58:2794–7. doi:10.1103/PhysRevLett.58.2794
28. Gutzwiller MC. Effect of Correlation on the Ferromagnetism of Transition Metals. Phys Rev Lett (1963) 10:159–62. doi:10.1103/PhysRevLett.10.159
29. Hubbard J. Electron Correlations in Narrow Energy Bands. Proc R Soc Lond Ser A, Math Phys Sci (1963) 276:238–57. doi:10.1098/rspa.1963.0204
30. Kanamori J. Electron Correlation and Ferromagnetism of Transition Metals. Prog Theor Phys (1963) 30:275–89. doi:10.1143/ptp.30.275
31. Zhang FC, Rice TM. Effective Hamiltonian for the Superconducting Cu Oxides. Phys Rev B (1988) 37:3759–61. doi:10.1103/PhysRevB.37.3759
32. Karp J, Botana AS, Norman MR, Park H, Zingl M, Millis A. Many-Body Electronic Structure of NdNiO2 and CaCuO2. Phys Rev X (2020) 10:021061. doi:10.1103/PhysRevX.10.021061
33. Kitatani M, Si L, Janson O, Arita R, Zhong Z, Held K. Nickelate Superconductors – a Renaissance of the One-Band Hubbard Model. npj Quan Mater (2020) 5:59. arXiv:2002.12230. doi:10.1038/s41535-020-00260-y
34. Li D, Wang BY, Lee K, Harvey SP, Osada M, Goodge BH, et al. Superconducting Dome in Nd1−xSrxNiO2 Infinite Layer Films. Phys Rev Lett (2020) 125:027001. arxiv:2003.08506. doi:10.1103/PhysRevLett.125.027001
35. Zeng S, Tang CS, Yin X, Li C, Li M, Huang Z, et al. Phase Diagram and Superconducting Dome of Infinite-Layer Nd1−xSrxNiO2 Thin Films, arxiv:2004.11281. Phys Rev Lett (2020) 125:147003. doi:10.1103/physrevlett.125.147003
36. Katanin AA, Toschi A, Held K. Comparing Pertinent Effects of Antiferromagnetic Fluctuations in the Two- and Three-Dimensional Hubbard Model. Phys Rev B (2009) 80:075104. doi:10.1103/PhysRevB.80.075104
37. Rohringer G, Hafermann H, Toschi A, Katanin AA, Antipov AE, Katsnelson MI, et al. Diagrammatic Routes to Nonlocal Correlations beyond Dynamical Mean Field Theory. Rev Mod Phys (2018) 90:025003. doi:10.1103/revmodphys.90.025003
38. Toschi A, Katanin AA, Held K. Dynamical Vertex Approximation; a Step Beyond Dynamical Mean-Field Theory. Phys Rev B (2007) 75:045118. doi:10.1103/PhysRevB.75.045118
39. Georges A, Kotliar G, Krauth W, Rozenberg MJ. Dynamical Mean-Field Theory of Strongly Correlated Fermion Systems and the Limit of Infinite Dimensions. Rev Mod Phys (1996) 68:13. doi:10.1103/RevModPhys.68.13
40. Georges A, Krauth W. Numerical Solution of the D = ∞ Hubbard Model: Evidence for a Mott Transition. Phys Rev Lett (1992) 69:1240–3. doi:10.1103/PhysRevLett.69.1240
41. Jarrell M. Hubbard Model in Infinite Dimensions: A Quantum Monte Carlo Study. Phys Rev Lett (1992) 69:168–71. doi:10.1103/PhysRevLett.69.168
42. Metzner W, Vollhardt D. Correlated Lattice Fermions in D = ∞ Dimensions. Phys Rev Lett (1989) 62:324–7. doi:10.1103/PhysRevLett.62.324
43. Blaha P, Schwarz K, Madsen G, Kvasnicka D, Luitz J. wien2k: An Augmented Plane Wave+ Local Orbitals Program for Calculating crystal Properties (2001). Wien: TU Wien.
44. Schwarz K, Blaha P, Madsen GKH (2002). Electronic Structure Calculations of Solids Using the Wien2k Package for Material Sciences. Comp Phys Comm 147:71–6. doi:10.1016/S0010-4655(02)00206-0
45. Kresse G, Hafner J. Ab Initio molecular Dynamics for Open-Shell Transition Metals. Phys Rev B (1993) 48:13115–8. doi:10.1103/PhysRevB.48.13115
46. Koepernik K, Eschrig H. Full-potential Nonorthogonal Local-Orbital Minimum-Basis Band-Structure Scheme. Phys Rev B (1999) 59:1743–57. doi:10.1103/PhysRevB.59.1743
47. Perdew JP, Burke K, Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys Rev Lett (1996) 77:3865–8. doi:10.1103/PhysRevLett.77.3865
49. Hansmann P, Parragh N, Toschi A, Sangiovanni G, Held K. Importance of D–P Coulomb Interaction for High Tc Cuprates and Other Oxides. New J Phys (2014) 16:033009. doi:10.1088/1367-2630/16/3/033009
50. Anisimov VI, Poteryaev AI, Korotin MA, Anokhin AO, Kotliar G. First-principles Calculations of the Electronic Structure and Spectra of Strongly Correlated Systems: Dynamical Mean-Field Theory. J Phys Condens Matter (1997) 9:7359–67. doi:10.1088/0953-8984/9/35/010
51. Held K. Electronic Structure Calculations Using Dynamical Mean Field Theory. Adv Phys (2007) 56:829–926. doi:10.1080/00018730701619647
52. Held K, Nekrasov IA, Keller G, Eyert V, Blümer N, McMahan AK, et al. Realistic Investigations of Correlated Electron Systems with LDA+DMFT. physica status solidi (b) (2006) 243:2599–631. Previously appeared as Psi-k Newsletter No. 56 (April 2003). doi:10.1002/pssb.200642053
53. Kotliar G, Savrasov SY, Haule K, Oudovenko VS, Parcollet O, Marianetti CA. Electronic Structure Calculations with Dynamical Mean-Field Theory. Rev Mod Phys (2006) 78:865. doi:10.1103/RevModPhys.78.865
54. Lichtenstein AI, Katsnelson MI. Ab Initio calculations of Quasiparticle Band Structure in Correlated Systems: LDA++ Approach. Phys Rev B (1998) 57:6884–95. doi:10.1103/PhysRevB.57.6884
55. Si L, Xiao W, Kaufmann J, Tomczak JM, Lu Y, Zhong Z, et al. Topotactic Hydrogen in Nickelate Superconductors and Akin Infinite-Layer Oxides ABO2. Phys Rev Lett (2020) 124:166402. doi:10.1103/PhysRevLett.124.166402
56. Kuneš J, Arita R, Wissgott P, Toschi A, Ikeda H, Held K. Wien2wannier: From Linearized Augmented Plane Waves to Maximally Localized Wannier Functions. Comput Phys Commun (2010) 181:1888–95. doi:10.1016/j.cpc.2010.08.005
57. Gull E, Millis AJ, Lichtenstein AI, Rubtsov AN, Troyer M, Werner P. Continuous-time Monte Carlo Methods for Quantum Impurity Models. Rev Mod Phys (2011) 83:349–404. doi:10.1103/RevModPhys.83.349
58. Parragh N, Toschi A, Held K, Sangiovanni G. Conserved Quantities of SU(2)-Invariant Interactions for Correlated Fermions and the Advantages for Quantum Monte Carlo Simulations. Phys Rev B (2012) 86:155158. doi:10.1103/PhysRevB.86.155158
59. Wallerberger M, Hausoel A, Gunacker P, Kowalski A, Parragh N, Goth F, et al. w2dynamics: Local One- and Two-Particle Quantities from Dynamical Mean Field Theory. Comp Phys Comm (2019) 235:388–99. doi:10.1016/j.cpc.2018.09.007
60. Kaufmann J, Held K. ana_cont: Python Package for Analytic Continuation (2021). arXiv:2105.11211.
61. Osada M, Wang BY, Goodge BH, Harvey SP, Lee K, Li D, et al. Nickelate Superconductivity without Rare-Earth Magnetism: (La,Sr)NiO2. Adv Mater (2021) 33:2104083. doi:10.1002/adma.202104083
62. Worm P, Si L, Kitatani M, Arita R, Tomczak JM, Held K. Correlations Turn Electronic Structure of Finite-Layer Nickelates Upside Down (2021). arXiv:2111.12697.
63. Hepting M, Li D, Jia CJ, Lu H, Paris E, Tseng Y, et al. Electronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381. doi:10.1038/s41563-019-0585-z
64. Lu H, Rossi M, Nag A, Osada M, Li DF, Lee K, et al. Magnetic Excitations in Infinite-Layer Nickelates. Science (2021) 373:213–6. doi:10.1126/science.abd7726
65. Higashi K, Winder M, Kuneš J, Hariki A. Core-level X-ray Spectroscopy of Infinite-Layer Nickelate: LDA + DMFT Study. Phys Rev X (2021) 11:041009. doi:10.1103/PhysRevX.11.041009
66. Gu Y, Zhu S, Wang X, Hu J, Chen H. A Substantial Hybridization between Correlated Ni-D Orbital and Itinerant Electrons in Infinite-Layer Nickelates. Commun Phy (2020) 3:84. doi:10.1038/s42005-020-0347-x
67. Jiang P, Si L, Liao Z, Zhong Z. Electronic Structure of Rare-Earth Infinite-Layer RNiO2 (R = La, Nd). Phys Rev B (2019) 100:201106. doi:10.1103/PhysRevB.100.201106
68. Choi M-Y, Lee K-W, Pickett WE. Role of 4f States in Infinite-Layer NdNiO2. Phys Rev B (2020) 101:020503. doi:10.1103/PhysRevB.101.020503
69. Zeng SW, Li CJ, Chow LE, Cao Y, Zhang ZT, Tang CS, et al. Superconductivity in Infinite-Layer Lanthanide Nickelates (2021). arXiv:2105.13492.
70. Galler A, Thunström P, Gunacker P, Tomczak JM, Held K. Ab Initio dynamical Vertex Approximation. Phys Rev B (2017) 95:115107. doi:10.1103/PhysRevB.95.115107
71. Antipov AE, Gull E, Kirchner S. Critical Exponents of Strongly Correlated Fermion Systems from Diagrammatic Multiscale Methods. Phys Rev Lett (2014) 112:226401. doi:10.1103/PhysRevLett.112.226401
72. Rohringer G, Toschi A, Katanin A, Held K. Critical Properties of the Half-Filled Hubbard Model in Three Dimensions. Phys Rev Lett (2011) 107:256402. doi:10.1103/PhysRevLett.107.256402
73. Schäfer T, Katanin AA, Held K, Toschi A. Interplay of Correlations and Kohn Anomalies in Three Dimensions: Quantum Criticality with a Twist. Phys Rev Lett (2017) 119:046402. doi:10.1103/PhysRevLett.119.046402
74. Schäfer T, Katanin AA, Kitatani M, Toschi A, Held K. Quantum Criticality in the Two-Dimensional Periodic anderson Model. Phys Rev Lett (2019) 122:227201. doi:10.1103/PhysRevLett.122.227201
75. Schäfer T, Wentzell N, Šimkovic F, He Y-Y, Hille C, Klett M, et al. Tracking the Footprints of Spin Fluctuations: A Multimethod, Multimessenger Study of the Two-Dimensional Hubbard Model. Phys Rev X (2021) 11:011058. doi:10.1103/PhysRevX.11.011058
76. Kitatani M, Schäfer T, Aoki H, Held K. Why the Critical Temperature of High-Tc Cuprate Superconductors Is So Low: The Importance of the Dynamical Vertex Structure. Phys Rev B (2019) 99:041115. doi:10.1103/PhysRevB.99.041115
77. Li G, Kauch A, Pudleiner P, Held K. The Victory Project v1.0: An Efficient Parquet Equations Solver. Comp Phys Comm (2019) 241:146–54. doi:10.1016/j.cpc.2019.03.008
78. Li G, Wentzell N, Pudleiner P, Thunström P, Held K. Efficient Implementation of the Parquet Equations: Role of the Reducible Vertex Function and its Kernel Approximation. Phys Rev B (2016) 93:165103. doi:10.1103/physrevb.93.165103
79. Valli A, Schäfer T, Thunström P, Rohringer G, Andergassen S, Sangiovanni G, et al. Dynamical Vertex Approximation in its Parquet Implementation: Application to Hubbard Nanorings. Phys Rev B (2015) 91:115115. doi:10.1103/PhysRevB.91.115115
80. Cui Y, Li C, Li Q, Zhu X, Hu Z, feng Yang Y, et al. NMR Evidence of Antiferromagnetic Spin Fluctuations in Nd0.85Sr0.15NiO2. Chin Phys Lett (2021) 38:067401. doi:10.1088/0256-307x/38/6/067401
81. Ivashko O, Horio W, Wan M, Christensen N, McNally D, Paris E, et al. Strain-engineering Mott-insulating La2CuO4. Nat Comm (2019) 10:786. doi:10.1038/s41467-019-08664-6
82. Tomczak JM, Miyake T, Sakuma R, Aryasetiawan F. Effective Coulomb Interactions in Solids under Pressure. Phys Rev B (2009) 79:235133. doi:10.1103/PhysRevB.79.235133
83. Wang NN, Yang MW, Chen KY, Yang Z, Zhang H, Zhu ZH, et al. Pressure-induced Monotonic Enhancement of Tc to over 30 K in the Superconducting Pr0.82Sr0.18NiO2 Thin Films (2021). arXiv:2109.12811.
84. Chen Z, Osada M, Li D, Been EM, Chen S-D, Hashimoto M, et al. Electronic Structure of Superconducting Nickelates Probed by Resonant Photoemission Spectroscopy (2021). arXiv:2106.03963.
85. Lee K, Goodge BH, Li D, Osada M, Wang BY, Cui Y, et al. Aspects of the Synthesis of Thin Film Superconducting Infinite-Layer Nickelates. APL Mater (2020) 8:041107. doi:10.1063/5.0005103
86. Katayama T, Chikamatsu A, Yamada K, Shigematsu K, Onozuka T, Minohara M, et al. Epitaxial Growth and Electronic Structure of Oxyhydride SrVO2H Thin Films. J Appl Phys (2016) 120:085305. doi:10.1063/1.4961446
87. Malyi OI, Varignon J, Zunger A. Bulk NdNiO2 Is Thermodynamically Unstable with Respect to Decomposition while Hydrogenation Reduces the Instability and Transforms it from Metal to Insulator (2021). arXiv:2107.01790.
Keywords: electronic structure calculations, dynamical mean field theory, electronic correlation, high-temperature superconductivity, solid state theory
Citation: Held K, Si L, Worm P, Janson O, Arita R, Zhong Z, Tomczak JM and Kitatani M (2022) Phase Diagram of Nickelate Superconductors Calculated by Dynamical Vertex Approximation. Front. Phys. 9:810394. doi: 10.3389/fphy.2021.810394
Received: 06 November 2021; Accepted: 10 December 2021;
Published: 21 January 2022.
Edited by:
Matthias Hepting, Max Planck Institute for Solid State Research, GermanyReviewed by:
Fabio Bernardini, University of Cagliari, ItalyLiviu Chioncel, University of Augsburg, Germany
Copyright © 2022 Held, Si, Worm, Janson, Arita, Zhong, Tomczak and Kitatani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Karsten Held, aGVsZEBpZnAudHV3aWVuLmFjLmF0; Liang Si, bGlhbmcuc2lAaWZwLnR1d2llbi5hYy5hdA==; Motoharu Kitatani, bW90b2hhcnUua2l0YXRhbmlAcmlrZW4uanA=
 Karsten Held
Karsten Held Liang Si
Liang Si Paul Worm
Paul Worm Oleg Janson3
Oleg Janson3 Ryotaro Arita
Ryotaro Arita Zhicheng Zhong
Zhicheng Zhong Jan M. Tomczak
Jan M. Tomczak Motoharu Kitatani
Motoharu Kitatani