- 1Faculty of Chemistry, University of Isfahan, Isfahan, Iran
- 2Department of Cognitive Neuroscience, University of Tabriz, Tabriz, Iran
- 3Faculty of Engineering, Shahrekord University, Shahrekord, Iran
- 4Department of Chemistry, Isfahan University of Technology, Isfahan, Iran
Background: The thermal conductivity of fluids can be calculated by several computational methods. However, these methods are reliable only at the confined levels of density, and there is no specific computational method for calculating thermal conductivity in the wide ranges of density.
Methods: In this paper, two methods, an Artificial Neural Network (ANN) approach and a computational method established upon the Rainwater-Friend theory, were used to predict the value of thermal conductivity in all ranges of density. The thermal conductivity of six refrigerants, R12, R14, R32, R115, R143, and R152 was predicted by these methods and the effectiveness of models was specified and compared.
Results: The results show that the computational method is a usable method for predicting thermal conductivity at low levels of density. However, the efficiency of this model is considerably reduced in the mid-range of density. It means that this model cannot be used at density levels which are higher than 6. On the other hand, the ANN approach is a reliable method for thermal conductivity prediction in all ranges of density. The best accuracy of ANN is achieved when the number of units is increased in the hidden layer.
Conclusion: The results of the computational method indicate that the regular dependence between thermal conductivity and density at higher densities is eliminated. It can develop a nonlinear problem. Therefore, analytical approaches are not able to predict thermal conductivity in wide ranges of density. Instead, a nonlinear approach such as, ANN is a valuable method for this purpose.
Introduction
Fluids, containing gases and liquids, have a wide range of applications in daily life and play an important role in modern industrial processes. Since refrigerants are crucial in the refrigeration industry, we must have a scientific knowledge about their transport properties. Computational methods that allow for the prediction of transport properties serve as valuable tools due to their time efficiency when compared to the time it would take to conduct the work in a laboratory. The effect of microscopic motions and the interactions of molecules on the transport properties of gases are considered to form the basis of these methods.
The transport properties of refrigerants have been investigated in numerous studies. Kandlikar et al. (1975) predicted the transport properties of R12 and R22 (Kandlikar et al., 1975). Assael at al. performed the absolute thermal conductivity measurement of liquid refrigerants R11 and R12 at the temperature range of 250–340 K and pressures from saturation to 30 MPa (Assael et al., 1992). In another study, the thermal conductivity of R134a, R152a, and R123 was evaluated using the transient hot-wire method (Gross et al., 1992). The viscosity coefficient of R152 was investigated by Krauss et al. (1996). A practical representation for the transport coefficients of pure refrigerants R32, R125, R134a, and R125 + R32 mixtures was presented by Kiselev et al. and was valid in the vapor-liquid critical region (Kiselev et al., 1999). Also, the transport properties of R14 have been examined in some studies (Smith and Pace, 1969; Rubio et al., 1985).
In 1917, Sydney Chapman and David Enskog solved the accurate equation for the transport properties of gases that had been presented by Maxwell and Boltzmann in 1860–1870 (Levine, 1995). Chapman-Enskog relations for monatomic gases and mixtures of these gases are expressed through the use of inter-atomic potential and temperature. In this theory, each coefficient of transport properties in gases is related to the collision integral (Ω) that depends on the value of potential, the nature of the interaction, and the reduced temperature (T*). The basis of the calculation of (Ω) in this work was the expansion of corresponding states presented by Najafi et al. (1983).
The Chapman-Enskog theory relates the effect of local binary molecular collisions. Furthermore, the role of higher-order molecular collisions is considered in the regions of higher density in gases. The existence of the internal degree of freedom in polyatomic gases has a considerable influence on thermal conductivity (λ), and thus thermal conductivity cannot be definitely calculated by the Chapman-Enskog theory (Maitland et al., 1978). In 1980, Rainwater and Friend proposed a microscopic theoretical methodology for calculating the second transport virial coefficients of moderately dense gases (up to 2 mol.dm−3; Friend and Rainwater, 1984; Rainwater and Friend, 1987). In this theory, thermal conductivity is described according to the second thermal conductivity virial coefficient (Bλ) and depends on interatomic potential and temperature. Rainwater and Friend calculated Bλ by utilizing the Lennard-Jones potential (Rainwater and Friend, 1987). Bich and Vogel then presented correlation functions for B*λ (reduced second virial coefficient of thermal conductivity; Millat et al., 1996). Since the Lennard-Jones potential is a rough approximation of reality, Najafi et al. (1998) calculated the thermal conductivity of some gases at moderate density by applying a highly accurate and realistic potential known as Aziz potential (Aziz and Slaman, 1990; Aziz, 1993).
Husseinnejad and Behnejad estimated the thermal conductivity of a number of refrigerants via Bich and Vogel potential scaling parameters (Hosseinnejad and Behnejad, 2008). In 2014, Geller et al. calculated the viscosity and thermal conductivity of refrigerant mixtures using a set of models. They utilized a corresponding states method to anticipate thermal conductivity in refrigerant mixtures (Geller et al., 2014). Huber and Assael used Chapman-Enskog method to predict the transport properties of (R1234yf) and [R1234ze(E)] as refrigerant replacements (Huber and Assael, 2016). Perkins et al. represented the thermal conductivity of (R245fa) as a sum of three contributions in a range of temperatures and pressures (Perkins et al., 2016).
At densities higher than the moderate range of the RF theory, new residual correction functions were offered by Najafi et al. (1998, 2000). These functions are density-dependent. However, at higher levels of density, these methods are defeated and, thus, an appropriate method is required to solve this problem.
Recently, some nonlinear methods have been presented to classify and predict the behavior of nonlinear systems. One of the most famous approaches in these contexts is the artificial neural network (ANN). The ANN prediction method is employed in many areas including climate (Ghaderi and Darooneh, 2012; Abdellatif et al., 2015) and economy (Aydin et al., 2015) as well as in thermodynamic and thermophysics applications (Di Nicola et al., 2016; Rostamian et al., 2016).
The thermodynamic characteristics of an alternative refrigerant (R407c) have been examined by Sozen et al. They used an ANN to determine the specific volume, enthalpy, entropy, viscosity, and thermal conductivity of R407c. Promising results were obtained from the thermodynamic specifications of this refrigerant in acceptable error (Sozen et al., 2009).
The determination of thermophysical properties in the case of refrigerants was accomplished by Sencan et al. using ANN. R413A, R417a, R422a, R422d, and R423a were considered while the liquid and vapor thermophysical properties of refrigerants were obtained by ANN (Sencan et al., 2011). The thermodynamic analyses of R12, R22, and R502 using ANNs were performed by Arcaklioglu et al. (2004). In some studies, ANN has been used for predicting the viscosity of refrigerants (Cristofoli et al., 2002; Ghaderi et al., 2013). Thermodynamic properties such as enthalpy, entropy, and specific volume of R413a, R417a, R422d, and R423a were predicted using ANN and the adaptive neuro-fuzzy approach by Sahin et al. (2012). Furthermore, Sozen et al. utilized ANN method for estimating the thermodynamic properties of an environmentally friendly refrigerant (R404a) in both superheated vapor region and saturated liquid-vapor region (wet vapor) as numerical equations. In this study, the calculated thermodynamic properties had an acceptable uncertainty (Sozen et al., 2010). A three-layer feed-forward neural network was employed to predict the thermal conductivity of pure gases, and the performance of ANN was compared with those of several commonly used models. The results indicated that the commonly used regular conductivity correlations are used for a limited range of temperatures and components, while the network method can cover a wide range of temperatures and substances (Eslamloueyan and Khademi, 2009). In the case of refrigerants, the viscosity of six refrigerants was predicted by ANN and computational methods. The ANN method shows a very good accuracy at high levels of density, while computational methods are defeated in the case of density levels higher than 8 (Ghaderi et al., 2013).
In the present study, the thermal conductivity of six refrigerants containing R12 (dichlorodifluoromethane), R14 (carbontetrafluoride), R32 (diflouromethane), R143a (1, 1, 1trifluoroethane), R115 (chloropentafluoroethane), and R152a (1, 1difluoroethane) was calculated by the RF method at low and moderate levels of density. For higher ranges of density, a modified RF theory was applied which stretched beyond the validity range of the RF theory and allowed for the development of corresponding states correction functions. Residual thermal conductivity was also computed. Then, the graphs of Δλ vs. ρ were drawn. The principle of corresponding states was used to confirm the graphs. The parameters λ* and ρ* of refrigerants were also found.
The results of thermal conductivity calculation were compared with the existing experimental data (Keyes, 1954; Oshen et al., 1967; Rosenbaum and Thodos, 1967; Rodgers et al., 1974; Makita et al., 1981; Yata et al., 1984; Imaishi et al., 1985; Millat et al., 1988; Hahne and Song, 1989; Tanaka et al., 1991; Assael et al., 1992, 2000; Gross et al., 1992; Assael and Karagiannidis, 1993; Kim et al., 1993; Papadaki and Wakeham, 1993; Vargaftik, 1994; Gao et al., 1995; Hammerschmidt, 1995; Ro et al., 1995; Zaporozhan and Geller, 1995; Gross and Song, 1996; Krauss et al., 1996; Tsvetkov et al., 1996; McLinden et al., 2000; Le and Garrabos, 2001). After that, a feed forward ANN was used to predict the thermal conductivity of six refrigerants in the entire range of densities. The ANN training data were collected from the National Institute of Standards and Technology (NIST) (http://webbook.nist.gov/chemistry/). The NIST Chemistry Web Book has provided a great online database of chemical and physical properties for chemical species. The NIST also introduces many useful references and experiments that contain practical and experimental data.
Since there is no established method for determining the thermal conductivity of refrigerants in a wide range of densities, the ANN's efficiency was investigated. It is proposed that ANN as a nonlinear approach can successfully predict thermal conductivity. Finally, the two methods were compared. According to the results, the computational method is a reliable method only at low levels of density, while ANN is a valuable method at moderate and high levels of density where the computational method fails.
This paper is organized as follows: Computational methods for predicting thermal conductivity are described in first section. The feed-forward ANN and the learning algorithm are explained in second section. Applications of the computational method and the ANN approach for predicting thermal conductivity are stated in third and fourth sections. Finally, fifth and sixth sections are devoted to the expression of results, discussion, and conclusions.
Computational Method for Predicting Thermal Conductivity Over a Wide Range of Densities
Refrigerant Thermal Conductivity at Low and Moderate Levels of Density
Since polyatomic gas refrigerants have internal degrees of freedom, the unity between translational and internal modes has a significant influence on the thermal conductivity of these gases. The Chapman-Enskog theory is applicable only to monatomic gases with a symmetrical and spherical intermolecular potential. Therefore, the thermal conductivity of the refrigerants cannot be calculated with this theory (Felder et al., 1964).
The thermal conductivity of refrigerants in the moderate density (up to 2 mol.dm−3) has been calculated using the Rainwater-Friend theory. In this method, the thermal conductivity has been considered as a function of second virial coefficients (Rainwater, 1981; Rainwater and Friend, 1987):
In the RF method, the Lennard-Jones potential has been used to calculate Bλ over the reduced temperature (T*). In this equation, λ0 is the thermal conductivity in zero density limits, ρ is the molar density, NA is Avogadro's constant, and σ is the collision diameter. RF theory deals with realistic potentials and the reduced second thermal conductivity virial coefficient (B*) (Rainwater, 1981; Rainwater and Friend, 1987). B* is composed of three statements:
where are monomer-monomer collisions, triple molecular collisions and monomer-dimer collisions, respectively. B*(T*) of a gas is dependent on the potential and the reduced temperature and is presented as:
where the coefficients are:
T* is the reduced temperature and equals to , where k is the Boltzmann constant, T is the absolute temperature and ϵ is the potential well depth. In this section, RF theory is developed to calculate the thermal conductivity of refrigerants. Furthermore, by applying the Mason-Monchick theory (Mason and Monchick, 1962), an appropriate correction is applied for computing the internal contribution of thermal conductivity. In the Mason-Monchick theory, the thermal conductivity of polyatomic gases is expressed as the sum of two private contributions. (Bich and Vogel, 1991):
With an acceptable approximation, these two statements of contributions are assumed to be separate. Combining the Mason-Monchick theory and Enskog hard sphere theory, the expansion of the RF theory is written as: (Vesovic and Wakeham, 1992; Heck et al., 1995)
where D is the diffusion coefficient and Cint is the contribution of internal states of heat capacity. The self-diffusion coefficient is density dependent and in the Enskog theory, it is defined as (Bennett and Curtiss, 1969):
where D0 is the self-diffusion coefficient in zero density and ρ* is the reduced density that is expressed as:
so the Equation (5) rearranges as:
by combining Equations (1, 8), the density dependence of the thermal conductivity is defined as (Mason and Monchick, 1962):
where bλ is presented as the extended RF second thermal conductivity virial coefficient for polyatomic gases. bλ is then calculated as follows:
and
where kB is the Boltzmann constant, M is molecular weight and η0 is viscosity at zero density (Bennett and Curtiss, 1969).
Thermal Conductivity of Refrigerants at Higher Levels of Density
At the high levels of density, residual thermal conductivity is presented as Dλ. This term is a function of both temperature and density. At density levels beyond the range of the RF theory, there is a regular dependence between thermal conductivity and density which can be presented as: (Millat et al., 1996)
where λc(ρ,T) is the thermal conductivity critical enhancement. The refrigerants are not considered at their critical range. Therefore, λc(ρ,T) can be ignored in the discussion of the refrigerants' behavior. It means that the residual thermal conductivity can be defined as:
Dλ for aforesaid refrigerants is calculated via the following relation:
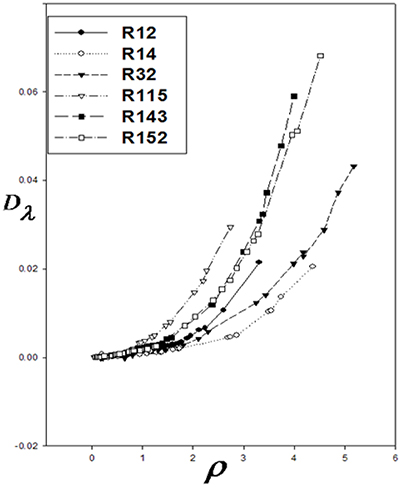
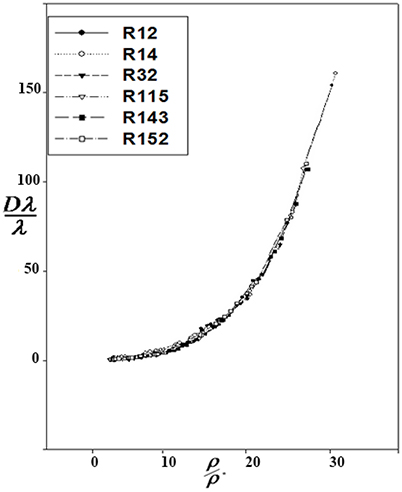
Correction functions have been used for the corresponding states offered by Najafi et al. (2000). The curves of Dλ vs. ρ for six refrigerants are used to show Dλ/λ* vs. ρ/ρ*:
where expansion coefficients are:
Thermal conductivity for each of the refrigerants has been obtained by a simple equation:
ANN, MLPs, and Back-Propagation Algorithm
ANNs are models of the cognitive process of the brain with an incredible potential for advancing the types of problems solved by computers (Steeb, 2005). The neuron is the basic processor in these models. Each neuron receives several inputs from other neurons. In 1958, perceptron was suggested as the simplest model of computational neuron by Rosenblatt. Perceptron is used for classifying linearly separable patterns. The network which consists of a set of perceptrons in a layer-by-layer structure is known as Multi-Layer Perceptrons (MLPs). In layered architectures, the first-layer perceptrons (input layer) are only connected to the second-layer units (first hidden layer) and so on (Ghaderi and Darooneh, 2012). The input signal propagates through the network in a forward direction and there is no recurrent connection in these networks. Consequently, these networks are called multi-layer feedforward ANNs. The model of each neuron in the MLP includes a nonlinear activation function. Therefore, the output of each perceptron is:
where wik is synaptic weight of the neuron k, xi is input to the each neuron and n is the number of inputs. sig is a nonlinear sigmoid function. The output of these functions is in the range of −1 to +1 or 0 to +1.
In a multilayer feed-forward network, several learning algorithms can be applied for network training. The back-propagation algorithm is a powerful method which is operated based on the gradient descent rule in the weight space. Three stages are implemented in this algorithm: (1) the feed-forward of input signals, (2) the calculations of the associated error and back-propagations of the error signal, and (3) the improvement of synaptic weights [79]. The error signal is calculated by subtracting the desired output from the network output. Using the error signal, the instantaneous value of error energy for neuron j is indicated by:
where n is the number of neurons in the output layer. The associated error in the back-propagation algorithm is calculated using average squared error energy:
where E(n) is error energy for neuron j.
Application of Computational Method for Predicting of Thermal Conductivity
The six refrigerants including R12, R14, R32, R115, R143, and R152 are polyatomic. As a result, available experimental data should be used to obtain λ0 (thermal conductivity in the zero density). Rainwater-Friend theory was employed for moderate density range (Equation 1). In addition, the value of η0 (Equation 11) was calculated for these six refrigerants in Ghaderi et al. (2013).
At the high densities, Dλ is dependent on density. Therefore, different isotherms of the residual thermal conductivity will confirm on a single curve. Dλ was calculated using Equation 14, and Dλ vs. ρ were drawn for the aforementioned refrigerants (Figure 1). Using the Sigma-Plot software, adjust quantities λ* and ρ* were found. The corresponding states principle was applicable for the thermal conductivity as a transport property. It means that the six curves were fitted on, as shown in Figure 2. The values obtained by the computational method are compared with the experimental values in Table 1. The calculated values of the noted refrigerants are in good agreement with the experimental values. Adjust quantities and predicted values for thermal conductivity are compared with the experimental data for six refrigerants in Table 1. The results are in agreement with the experimental data outside the critical area.

Table 1. Values obtained by computational method were compared with the experimental data of λ for 6 refrigerants in low and low-moderate density.
Predicting Thermal Conductivity by ANN at Low, Moderate, and High Levels of Density
A three-layer feed-forward ANN was constructed using MATLAB neural network toolbox. Three neurons were considered in the input layer and one neuron in the output layer. The three input variables were temperature, density, and pressure, while the output variable was thermal conductivity. These variables proved to be effective parameters on the thermal conductivity value.
The ANN structure is illustrated in Figure 3. Resilient back-propagation algorithm was used as the training algorithm and a nonlinear sigmoid function (logsig), which showed better results than the other sigmoid function (tansig), was employed as the activation function in the hidden and output layers. The logsig function is defined as:
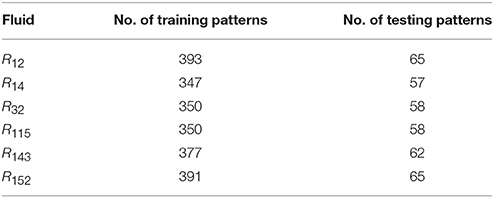
where n is the input value. Additional data about this network are presented in Table 2. NIST data were used as the training data, while the testing data were obtained from experimental references. The number of training and testing patterns of the six refrigerants is indicated in Table 3.
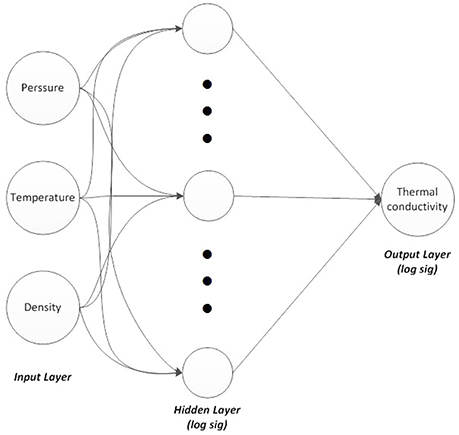
Figure 3. Three-layers neural network, three neurons in input, 10, 20, and 30 nodes in hidden layer and one node in output.
Networks with 10, 20, and 30 neurons in the hidden layer were tested and the performances of each network in low, mid, and high densities are represented in Tables 4–6, respectively. The efficiency of the ANN method for predicting the thermal conductivity of the six refrigerants and a comparison of this method with computational method are depicted in Figures 4–9 and Tables 4–6.
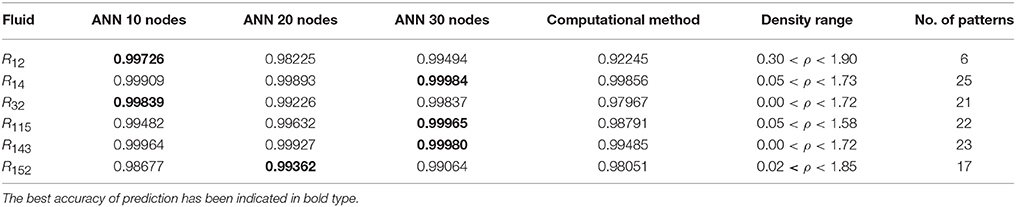
Table 4. The R values of computational method and ANN with 10, 20, and 30 hidden neurons, for thermal conductivity prediction in low density.
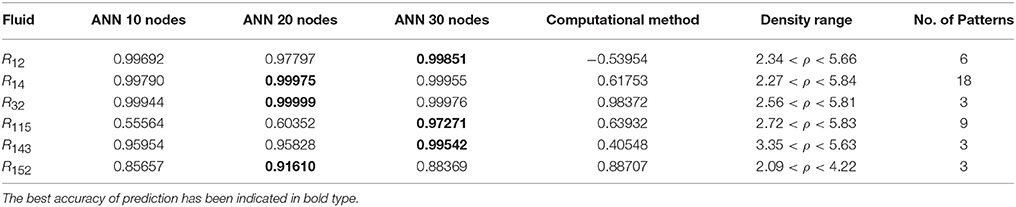
Table 5. The R values of computational method and ANN with 10, 20, and 30 hidden neurons, for thermal conductivity prediction in mid density.
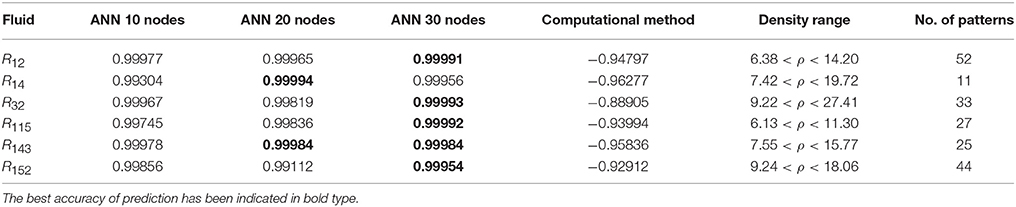
Table 6. The R-values of computational method and ANN with 10, 20, and 30 hidden neurons, for thermal conductivity prediction in high density.
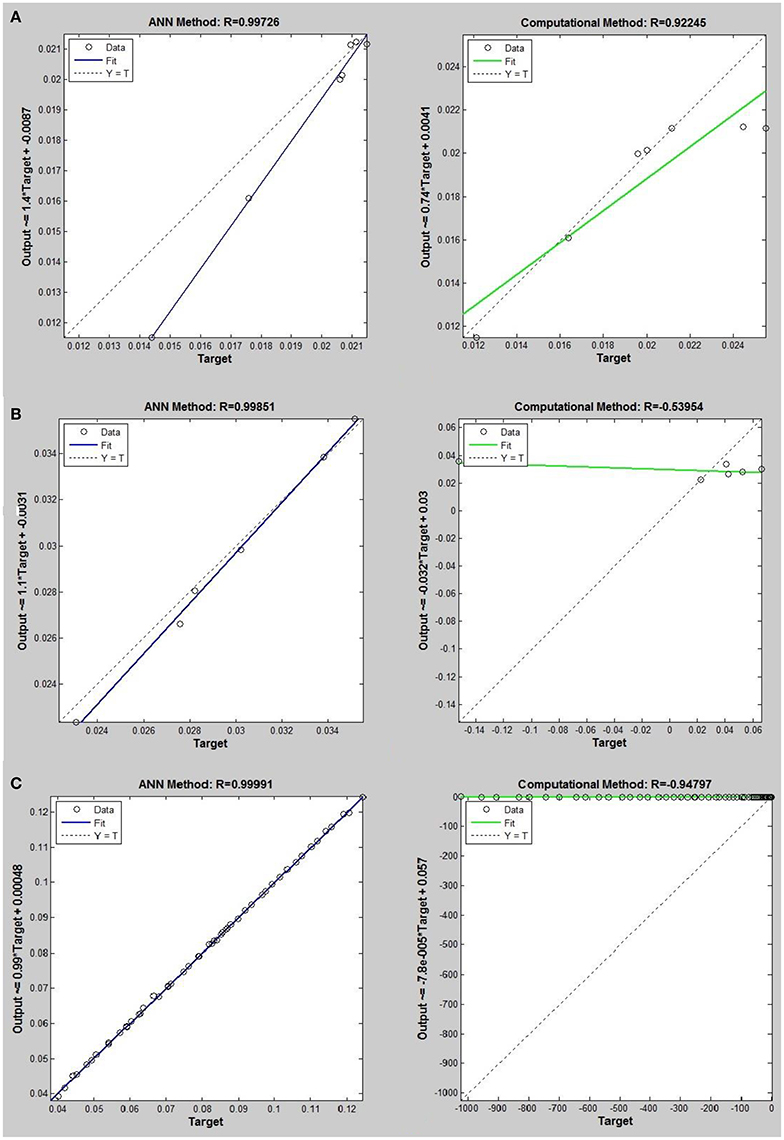
Figure 4. Thermal conductivity regression. Comparison between computational and ANN Methods for R12. (A) Comparition in low density (ρ < 2). (B) Comparison in moderate density (2 < ρ < 6). (C) Comparison in high density (ρ > 6).
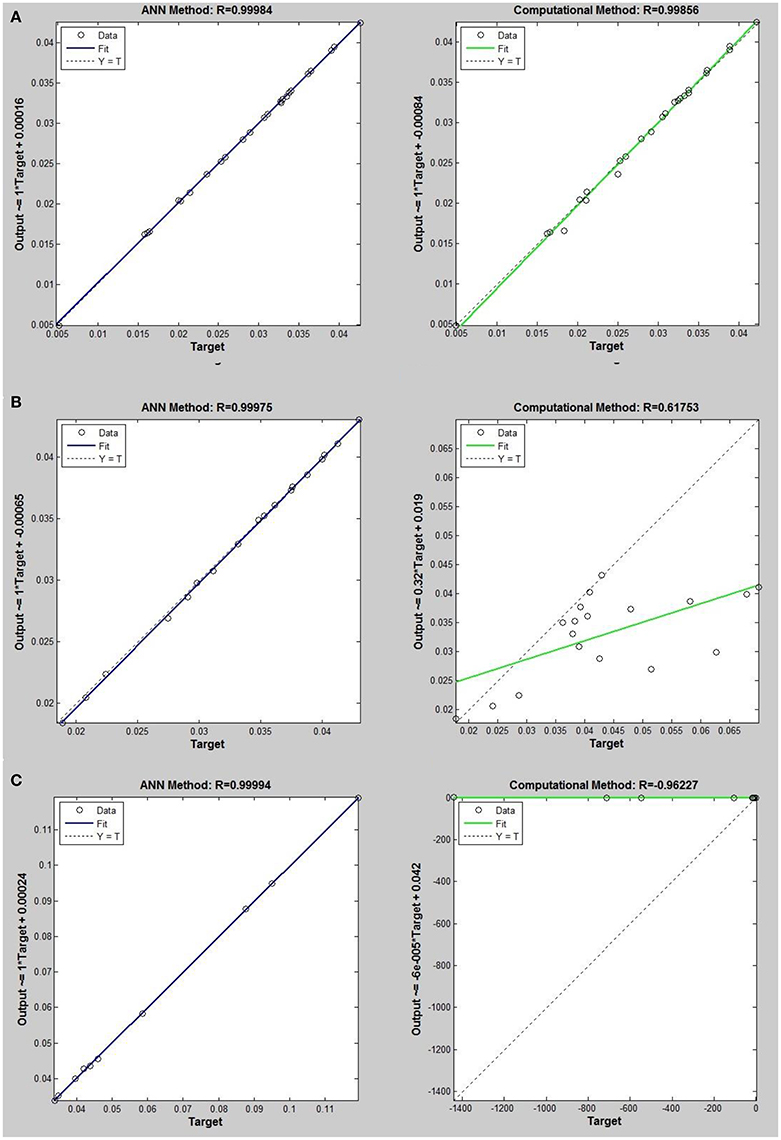
Figure 5. Thermal conductivity regression. Comparison between computational and ANN Methods for R14. (A) Comparison in low density (ρ < 2). (B) Comparison in moderate density (2 < ρ < 6). (C) Comparison in high density (ρ > 6).
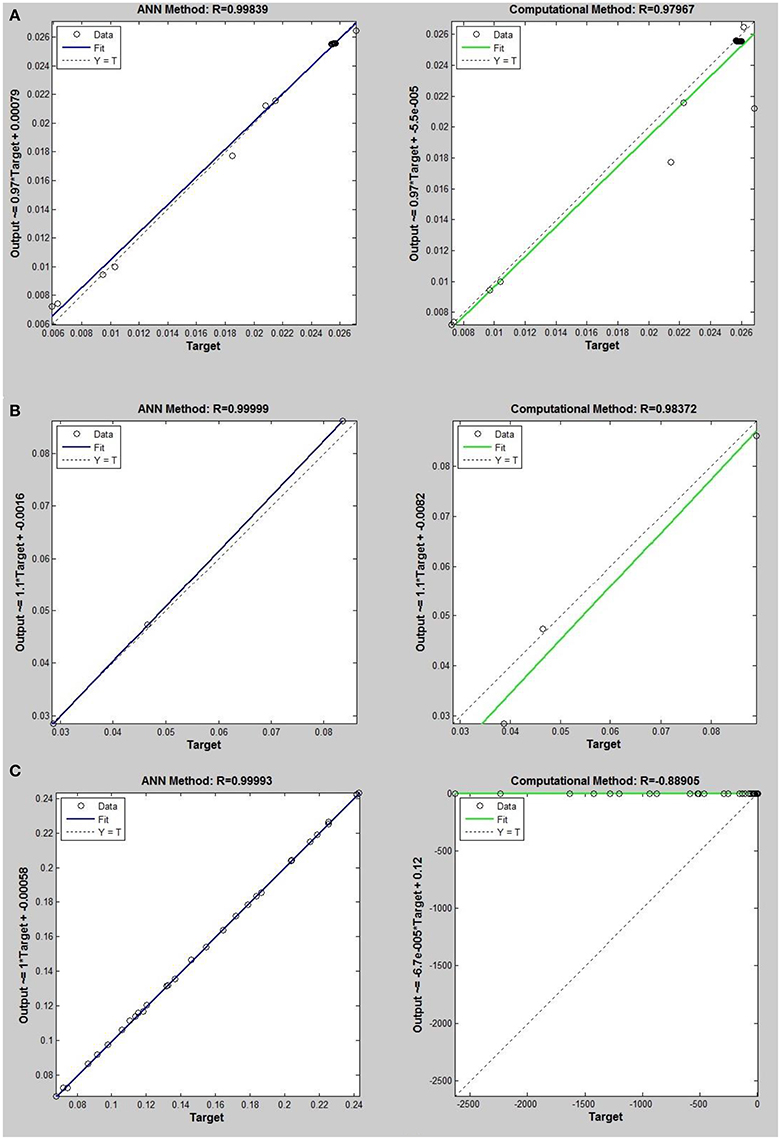
Figure 6. Thermal conductivity regression. Comparison between computational and ANN Methods for R32. (A) Comparison in low density (ρ < 2). (B) Comparison in moderate density (2 < ρ < 6). (C) Comparison in high density (ρ > 6).
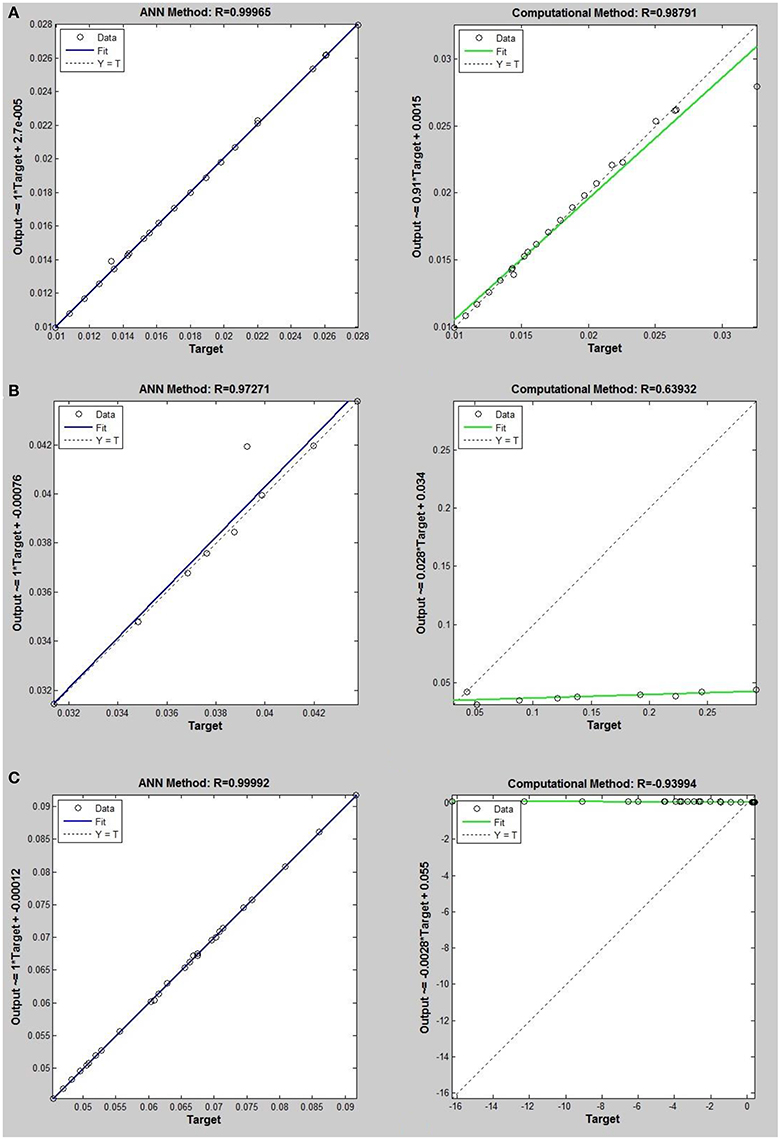
Figure 7. Thermal conductivity regression. Comparison between computational and ANN Methods for R115. (A) Comparison in low density (ρ < 2). (B) Comparison in moderate density (2 < ρ < 6). (C) Comparison in high density (ρ > 6).
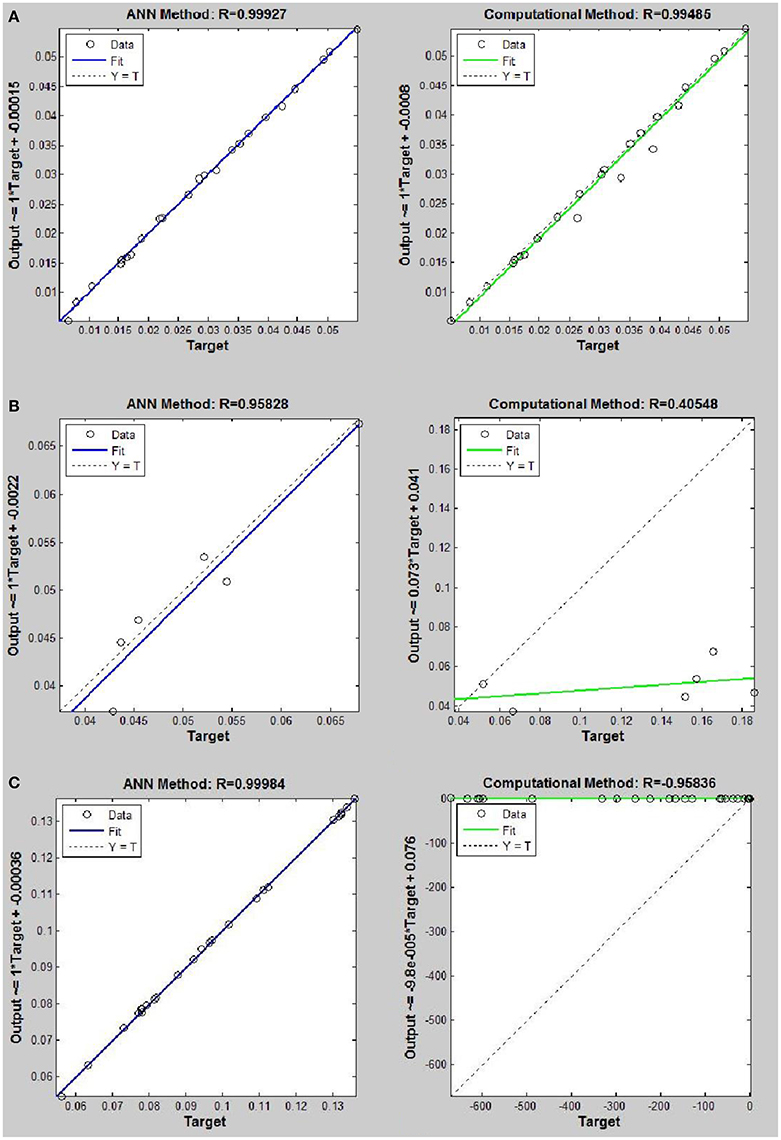
Figure 8. Thermal conductivity regression. Comparison between computational and ANN Methods for R143. (A) Comparison in low density (ρ < 2). (B) Comparison in moderate density (2 < ρ < 6). (C) Comparison in high density (ρ > 6).
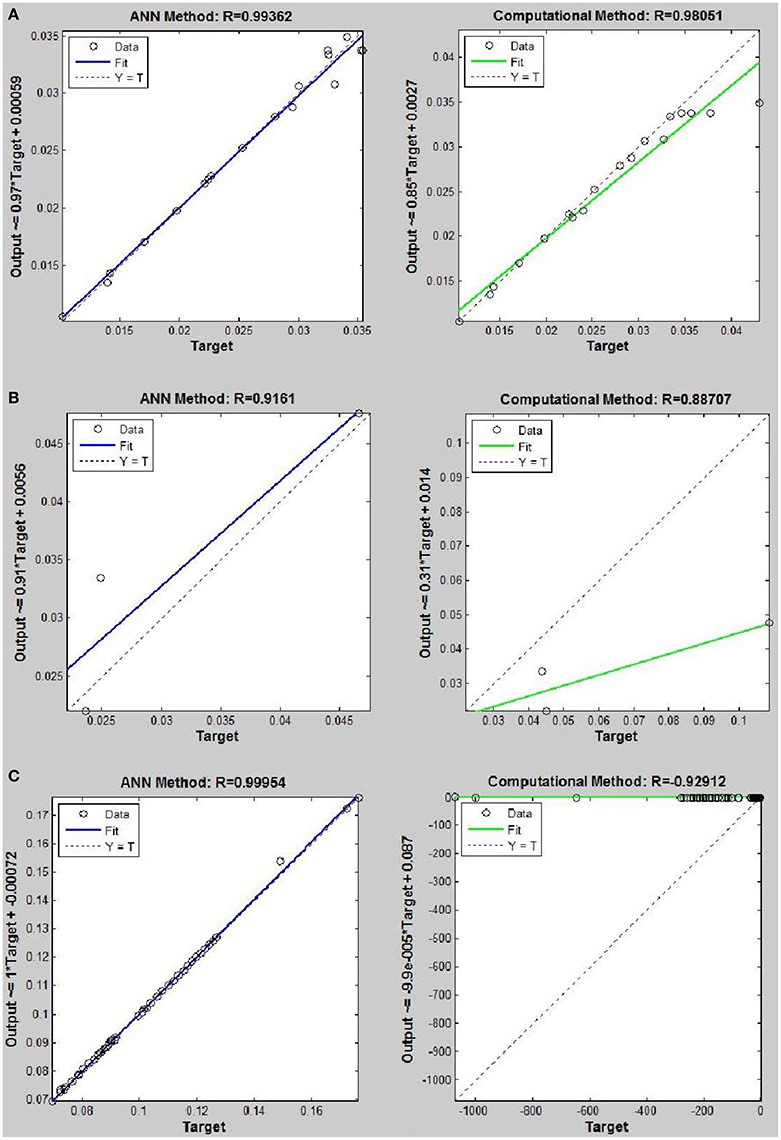
Figure 9. Thermal conductivity regression. Comparison between computational and ANN Methods for R152. (A) Comparison in low density (ρ < 2). (B) Comparison in moderate density (2 < ρ < 6). (C) Comparison in high density (ρ > 6).
Results and Discussion
In the case of calculating the thermal conductivity of the six refrigerants, the efficiency of the two methods (ANN and the computational approach) was compared. The RF theory is a statistical method for predicting the thermal conductivity of refrigerants in low densities (Rainwater, 1981; Rainwater and Friend, 1987). Nevertheless, this model fails at higher levels of density. To predict thermal conductivity at higher densities, the RF theory can be used (Najafi et al., 2000).
On the other hand, the ANN approach is a nonlinear method which can be applied for predicting thermal conductivity in all ranges of density (Sencan et al., 2011; Ghaderi et al., 2013). The performances of the ANN approach and the computational method were compared at low, mid, and high levels of density, with the results presented in Tables 4–6, respectively. At the low densities (<2), the two methods were reliable. However, the ANN approach had better results (Table 4). These results show that, in the case of R14, R32, R115, R143, R153, all of the three ANNs represented slightly better predictions than the computational method. In the moderate range of density, (Tables 1, 5 and Figures 4–9), the computational method could be used only for R32 and was defeated in other cases. In another study, however, the computational method showed reliable results in this range of density for predicting the viscosity of the same fluids (Ghaderi et al., 2013). Furthermore, the thermal conductivity of the six refrigerants was precisely predicted by ANN in the mid-density range.
In the high range of density, the computational method was invalid for the six refrigerants, while the ANN approach proved to be a reliable method for predicting thermal conductivity at density levels up to 27. These results are consistent with the results of another study on viscosity prediction (Ghaderi et al., 2013).
The number of hidden neurons in the ANN structure is selected as 10, 20, and 30. Based on the results, a network with 30 hidden neurons has the best prediction at higher levels of density. On the other hand, the results of the computational method indicate that the regular dependence between thermal conductivity and density at higher densities is eliminated. It can develop a nonlinear problem. Therefore more nodes in hidden layer are needed to solve the nonlinearity problem.
Conclusion
The ANN approach proved to be a reliable method for predicting thermal conductivity in all ranges of density, while the computational method was restricted to low densities (Figures 4–9 and Tables 1, 4–6). In the low levels of density (ρ < 2), the computational method based on RF theory was usable (R > 0.92) (Tables 1, 4 and Figures 4–9). However, in the moderate and high levels of density (ρ > 2), this model often failed.
On the other hand, the results showed that, in the case of R32, this model succeeded at moderate levels of density (R = 0.98372). Thus, according to the results, we concluded that the computational method is an accurate model at low levels of density for predicting thermal conductivity prediction. Nevertheless, since the accuracy of computational method based on RF theory is reduced at higher levels of density, the ANN with MLPs as a nonlinear method is proposed for solving this problem. There is a nonlinear relationship between the thermal conductivity and other thermodynamical properties such as, pressure and density. As a result, analytical approaches are unable to predict thermal conductivity in a wide range of densities. Instead, a nonlinear approach such as, ANN is a valuable method for this purpose.
Other thermodynamic properties may be predicted by the ANN approach and the accuracy of predictions can be compared with those of computational methods. Moreover, other nonlinear methods may be used for prediction in this context.
Author Contributions
FG worked on theoretical concept of chemical aspects and computational method and wrote a considerable volume of manuscript. AG worked on artificial neural network model, compared results of two methods, and wrote a part of manuscript. NG wrote a part of manuscript and helped in data analyzing. BN conducted group in all procedures.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors of this article thank NIST Chemistry Web Book at http://webbook.nist.gov/chemistry/ because of the references and useful data provided for training neural networks.
References
Abdellatif, M., Atherton, W., Alkhaddar, R., and Osman, Y. (2015). Flood risk assessment for urban water system in a changing climate using artificial neural network. Nat. Hazards 79, 1059–1077. doi: 10.1007/s11069-015-1892-6
Arcaklioglu, E., Cavusoglu, A., and Erisen, A. (2004). Thermodynamic analyses of refrigerant mixtures using artificial neural networks. Appl. Energy 78, 219–230. doi: 10.1016/j.apenergy.2003.08.001
Assael, M. J., Dalaouti, N. K., Dymond, J. H., and Feleki, E. P. (2000). Correlation for viscosity and thermal conductivity of liquid halogenated ethane refrigerants. Int. J. Thermophys. 21, 367–375. doi: 10.1023/A:100662741
Assael, M. J., Karagiannidis, E., and Wakeham, W. A. (1992). Measurements of the thermal conductivity of R11 and R12 in the temperature range 250340 K at pressures up to 30 MPa. Int. J. Thermophys. 13, 735–751. doi: 10.1007/BF00503903
Assael, M. J., and Karagiannidis, L. (1993). Measurements of the thermal conductivity of R22, R123, and R134a in the temperature range 250340 K at pressures up to 30 MPa. Int. J. Thermophys. 14, 183–197. doi: 10.1007/BF00507807
Aydin, A. D., Dilek, A., and Cavdar, S. C. (2015). Prediction of financial crisis with artificial neural network: an empirical analysis on Turkey. Int. J. Financ. Res. 6:36. doi: 10.5430/ijfr.v6n4p36
Aziz, R. A. (1993). A highly accurate interatomic potential for argon. J. Chem. Phys. 99, 4518–4525.
Aziz, R. A., and Slaman, M. J. (1990). The repulsive wall of the ArAr interatomic potential reexamined. J. Chem. Phys. 92, 10–30. doi: 10.1063/1.458165
Bennett, D. E., and Curtiss, C. F. (1969). Density effects on the transport coeficients of gaseous mixtures. J. Chem. Phys. 51, 2811–2825.
Bich, E., and Vogel, E. (1991). The initial density dependence of transport properties: noble gases. Int. J. Thermophys. 27–42. doi: 10.1007/BF00506120
Cristofoli, G., Piazza, L., and Scalabrin, G. (2002). A viscosity equation of state for R134a through a multi-layer feedforward neural network technique. Fluid Phase Equilib. 199, 223–236. doi: 10.1016/S0378-3812(02)00004-3
Di Nicola, G., Pierantozzi, M., Petrucci, G., and Stryjek, R. (2016). Equation for the thermal conductivity of liquids and an artificial neural network. J. Thermophys. Heat Transfer, 30, 651–660. doi: 10.2514/1.T4863
Eslamloueyan, R., and Khademi, M. H. (2009). Estimation of thermal conductivity of pure gases by using Artificial neural networks. Int. J. Therm. Sci. 48, 1094–1101. doi: 10.1016/j.ijthermalsci.2008.08.013
Felder, J. O., Curtiss, C. F., and Bird, R. B. (1964). Molecular Theory of Gases and Liquids. New York, NY: Wiley.
Friend, D. G., and Rainwater, C. J. (1984). Transport properties of a moderately dense gas. Chem. Phys. Lett. 107, 590–594. doi: 10.1016/S0009-2614(84)85163-5
Gao, X., Iojima, H., Nagasaka, Y., and Nagashima, A. (1995). “Thermal conductivity of HFC-32 in the liquid phase, in Proceedings 4th Asian Thermophysical Properties Conference (Paper C1c4) (Tokyo).
Geller, V., Shimchuk, N., and Plokhotnyuk, M. (2014). Transport Properties for Refrigerant Mixtures. Odessa National Academy of Food Technologies. 149.
Ghaderi, A. H., and Darooneh, A. H. (2012). Artificial neural network with regular graph formaximum air temperature forecasting: the effect of decrease in nedes degreeon learning. Int. J. Mod. Phys. C 23, 1–10. doi: 10.1142/S0129183112500088
Ghaderi, F., AGhaderi, H., Najafi, B., and Ghaderi, N. (2013). Viscosity prediction by computational method and artificial neural network approach: the case of six refrigerants. J. Supercritical Fluids 81, 67–78. doi: 10.1016/j.supflu.2013.04.017
Gross, U., and Song, Y. W. (1996). Thermal conductivities of new refrigerants R125 and R32 measured by the transient hot-wire method. Int. J. Thermophys. 17, 607–619. doi: 10.1007/BF01441507
Gross, U., Song, Y. W., and Hahne, E. (1992). Thermal conductivity of the new refrigerants R134a, R152a, and R123 measured by the transient hot-wire method. Int. J. Thermophys. 13, 957–983. doi: 10.1007/BF01141209
Hahne, E., and Song, Y. (1989). The thermal conductivity of R115 in the critical region. Int. J. Thermophys. 10, 687–700. doi: 10.1007/BF00507989
Hammerschmidt, U. (1995). Thermal conductivity of a wide range of alternative refrigerants measured with an improved guarded hot-plate apparatus. Int. J. Thermophys. 16, 1203–1211. doi: 10.1007/BF02081288
Heck, E. L., Dickinson, A. S., and Vesovic, V. (1995). Testing the mason-monchick approximation for transport properties of CO. Chem. Phys. Letters. 240, 151–156.
Hosseinnejad, T., and Behnejad, H. (2008). Viscosity and thermal conductivity of some refrigerants at moderate and high densities on the basis of rainwater friend theory and the corresponding states principle. Fluid Phase Equilib. 263, 85–95. doi: 10.1016/j.fluid.2007.09.024
Huber, M. L., and Assael, M. J. (2016). Correlations for the viscosity of 2, 3, 3, 3-tetrafluoroprop-1-ene (R1234yf) and trans-1, 3, 3, 3-tetrafluoropropene (R1234ze (E)). Int. J. Refrigerat. 71, 39–45. doi: 10.1016/j.ijrefrig.2016.08.007
Imaishi, N., Kestin, J., and Paul, R. (1985). Thermal conductivity of carbon tetrauoride withargon and helium. Int. J. Thermophys. 6, 320. doi: 10.1007/BF00505789
Kandlikar, S., Bijlani, C., and Sukhatme, S. (1975). Predicting the properties of mixtures of R22 and R12 part II-Transport properties. Am. Soc. Heat. Refrigerating Air Cond. Eng. 2343, 285–294.
Kim, S., Kim, D., Kim, M., and Ro, S. (1993). The thermal conductivity of R22, R142b, R152a, and their mixtures in the liquid state. Int. J. Thermophys. 14, 937–950. doi: 10.1007/BF00502116
Kiselev, S. B., Perkins, R. A., and Huber, M. L. (1999). Transport properties of refrigerants R32, R125, R134a, and R125+ R32 mixtures in and beyond the critical region. Int. J. Refrigeration 22, 509–520. doi: 10.1016/S0140-7007(99)00007-9
Krauss, R., Weiss, V. C., Edison, T. A., Sengers, J. V., and Stephan, K. (1996). Transport proper-ties of 1,1-diuoroethane (R152a). Int. J. Thermophys. 17, 731757. doi: 10.1007/BF01439187
Le Neindre, B., and Garrabos, Y. (2001). Measurement of thermal conductivity of HFC-32 (diuoromethane) in the temperature rante from 300 to 465 K atpressures up to 50 MPa. Int. J. Thermophys. 22, 701–722. doi: 10.1023/A:1010766730306
Maitland, G. C., Rigby, M., Smith, E. B., and Wakeham, W. A. (1978). Intermolecular Forces, their Origin and Determination. Oxford: Clarendon Press.
Makita, T., Tanaka, Y., Morimoto, Y., Noguchi, M., and Kubota, H. (1981). Thermal conductivityof gaseous uoro carbon refrigerants R12, R13, R22, and R23 under pressure. Int. J. Thermophys. 2, 249–268. doi: 10.1007/BF00504188
Mason, E. A., and Monchick, L. (1962). Heat conductivity of polyatomic and polar gases. J. Chem. Phys. 36, 1622–1639. doi: 10.1063/1.1732790
McLinden, M. O., Klein, S. A., and Perkins, R. A. (2000). An extended corresponding states model for the thermal conductivity of refrigerants and refrigerant mixtures. Int. J. Refrigeration 23, 43–63. doi: 10.1016/S0140-7007(99)00024-9
Millat, J., Dymond, J. H., and Nieto de Castro, C. (1996). Transport Properties of Fluid. Cambridge: Cambridge University Press.
Millat, J., Ross, M., Wakeham, W. A., and Zalaf, M. (1988). The thermal conductivity of neon,methane and tetrau oromethane. Physica 148A, 124–152. doi: 10.1016/0378-4371(88)90138-0
Najafi, B., Araghi, R., Rainwater, J. C., Alavi, S., and Snider, R. F. (2000). Prediction of the thermal conductivity of gases based on the RainwaterFriend theory and a new corresponding states function. Physica A 275, 48–69. doi: 10.1016/S0378-4371(99)00413-6
Najafi, B., Ghayeb, Y., Rainwater, J. C., Alavi, S., and Snider, R. F. (1998). Improved initial density dependence of the viscosity and a corresponding states function for highpressures. Physica A 260, 31–48.
Najafi, B., Mason, E. A., and Kestin, J. (1983). Improved corresponding states principle for thenoble gases. Physica A 119, 387–440. doi: 10.1016/0378-4371(83)90101-2
Oshen, S., Rosenblum, B., and Thodos, G. (1967). Thermal conductivity of carbon tetrau-oride in the dense gaseous region. J. Chem. Phys. 46, 2939–2944.
Papadaki, M., and Wakeham, W. (1993). Thermal conductivity of R32 and R125 in the liquid phase at the saturation vapor pressure. Int. J. Thermophys. 14, 1215–1220. doi: 10.1007/BF02431285
Perkins, R. A., Huber, M., and Assael, J. M. (2016). Measurements of the thermal conductivity of 1, 1, 1, 3, 3-Pentafluoropropane (R245fa) and correlations for the viscosity and thermal conductivity surfaces. J. Chem. Eng. Data 61, 3286–3294. doi: 10.1021/acs.jced.6b00350
Rainwater, J. C. (1981). Softness expansion of gaseous transport properties. II. Moder-ately dense gases. J. Chem. Phys. 74, 4130–4144. doi: 10.1063/1.441542
Rainwater, J. C., and Friend, D. G. (1987). Second viscosity and thermal-conductivity virialcoe_cients of gases: ex tension to low reduced temperature. Phys. Rev. A 36, 4062–4066.
Ro, S., Kim, J., and Kim, D. (1995). Thermal conductivity of R32 and its mixture with R134a. Int. J. Thermophys. 16, 1193–1201. doi: 10.1007/BF02081287
Rodgers, A., Chao, J., Wilhoit, R. C., and Zwolinski, B. J. (1974). Ideal gas thermodynamic prop-erties of eight chloro- and uoromethanes. J. Phys. Chem. Ref. Data 3, 117–140.
Rosenbaum, M., and Thodos, G. (1967). Thermal conductivity of mixtures in the densegaseous state: the methanecarbon tetrauoride system. Physica 37, 442–456. doi: 10.1016/0031-8914(67)90199-1
Rostamian, S. H., Esfe, M. H., Mohammad Had, H. M., Toghraie, D., Sarsam, W. S., and Dahari, M. (2016). Optimization, modeling and accurate prediction of thermal conductivity and dynamic viscosity of stabilized ethylene glycol and water mixture Al2 O3 nanofluids by NSGA-II using ANN. Int. Commun. Heat Mass Transfer 82, 154–160. doi: 10.1016/j.icheatmasstransfer.2016.08.015
Rubio, R. G., Calado, J. C. G., Clancy, P., and Streett, W. B. (1985). A theoretical and experimen-tal study of the equation of state of tetrauoromethane. J. Phys. Chem. 89, 4637–4646.
Sahin, A. S., Kose, I., and Selbas, R. (2012). Comparative analysis of neural network and neuro-fuzzy system for thermodynamic properties of refrigerants. Appl. Artif. Intell. 26, 662–672. doi: 10.1080/08839514.2012.701427
Sencan, A., Kose, I., and Selbas, R. (2011). Prediction of thermophysical properties of mixed refrigerants using Artificial neural network. Energy Conversion Manage. 52, 958–974. doi: 10.1016/j.enconman.2010.08.024
Smith, J. H., and Pace, E. L. (1969). Thermodynamic properties of carbon tetrauoride from 12.deg. K to its boiling point. Significance of the parameter. J. Phys. Chem. 73, 4232–4236.
Sozen, A., Arcaklioglu, E., and Menlik, T. (2010). Derivation of empirical equations for thermodynamic properties of a ozone safe refrigerant (R404a) using artificial neural network. Expert Syst. Appl. 37, 1158–1168. doi: 10.1016/j.eswa.2009.06.016
Sozen, A., Arcaklioglu, E., and Ozalp, M. (2009). Determination of thermodynamic properties of an alternative refrigerant (R407c) using artificial neural network. Expert Syst. Appl. 36, 4346–4356. doi: 10.1016/j.eswa.2008.05.023
Tanaka, Y., Nakata, M., and Makita, T. (1991). Thermal conductivity of gaseous HFC-134a, HFC-143a, HCFC 141b, and HCFC-142b. Int. J. Thermophys. 12, 949–963. doi: 10.1007/BF00503512
Tsvetkov, O., Laptev, Y. A., and Asambaev, A. G. (1996). The thermal conductivity of binary mixtures of liquid R22 with R142b and R152a at low temperatures. Int. J. Thermophys. 17, 597–606. doi: 10.1007/BF01441506
Vargaftik, N. B. (1994). Handbook of Thermal Conductivity of Liquids and Gases. New York, NY: CRC press.
Vesovic, W., and Wakeham, A. (1992). Transport cross-sections for polyatomic gases. Int. Rev. Phys. Chem. 11, 161–194. doi: 10.1080/01442359209353269
Yata, J., Minamiyama, T., and Tanaka, S. (1984). Measurement of thermal conductivity of liquid uorocarbons. Int. J. Thermophys. 5, 209–218. doi: 10.1007/BF00505501
Keywords: thermal conductivity, transport properties, refrigerant, RF theory, ANN
Citation: Ghaderi F, Ghaderi AH, Ghaderi N and Najafi B (2017) Prediction of the Thermal Conductivity of Refrigerants by Computational Methods and Artificial Neural Network. Front. Chem. 5:99. doi: 10.3389/fchem.2017.00099
Received: 10 August 2017; Accepted: 30 October 2017;
Published: 15 November 2017.
Edited by:
Ramesh L. Gardas, Indian Institute of Technology Madras, IndiaReviewed by:
Sugata Chowdhury, National Institute of Standards and Technology, United StatesMiguel Rubi, University of Barcelona, Spain
Copyright © 2017 Ghaderi, Ghaderi, Ghaderi and Najafi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Amir H. Ghaderi, YW1pcmhvc2VpbmdoYWRlcmlAZ21haWwuY29t
 Forouzan Ghaderi1
Forouzan Ghaderi1 Amir H. Ghaderi
Amir H. Ghaderi