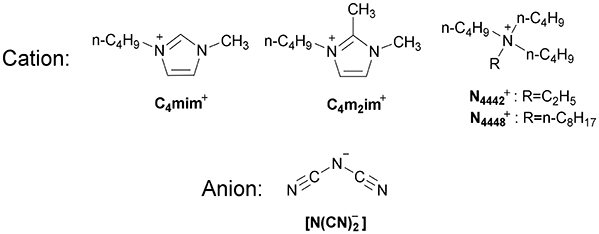
- College of Chemistry, Sichuan University, Chengdu, China
The instructive structure-property relationships of ionic liquids (ILs) can be put to task-specific design of new functionalized ILs. The dicyanamide (DCA) ILs are typical CHN type ILs which are halogen free, chemical stable, low-viscous, and fuel-rich. The transport properties of DCA ionic liquids are significant for their applications as solvents, electrolytes, and hypergolic propellants. This work systematically investigates several important transport properties of four DCA ILs ([C4mim][N(CN)2], [C4m2im][N(CN)2], N4442[N(CN)2], and N8444[N(CN)2]) including viscosity, conductivity, and electrochemical property at different temperatures. The melting points, temperature-dependent viscosities and conductivities reveal the structure-activity relationship of four DCA ILs. From the Walden plots, the imidazolium cations exhibit stronger cation–anion attraction than the ammonium cations. DCA ILs have relatively high values of electrochemical windows (EWs), which indicates that the DCA ILs are potential candidates for electrolytes in electrochemical applications. The cyclic voltammograms of Eu(III) in these DCA ILs at GC working electrode at various temperatures 303–333 K consists of quasi-reversible waves. The electrochemical properties of the DCA ILs are also dominated by the cationic structures. The current intensity (ip), the diffusion coefficients (Do), the charge transfer rate constants (ks) of Eu(III) in DCA ILs all increased with the molar conductivities increased. The cationic structure-transport property relationships of DCA ILs were constructed for designing novel functionalized ILs to fulfill specific demands.
Introduction
Ionic liquids (ILs) have many desirable properties to serve as soft functional materials including solvents (Rogers and Seddon, 2003), catalysts (Hallett and Welton, 2011), lubricants (Fan et al., 2014), electrolytes (Armand et al., 2009), extractants (Wieszczycka et al., 2013), absorbents (Brennecke and Gurkan, 2010), magnetic fluids (Nacham et al., 2015), optical fluids (He et al., 2015; Zhao et al., 2015), and propellants (Tao et al., 2008; He et al., 2010; Gao et al., 2015; Yin et al., 2016). In comparison with traditional molecular solvents, ILs have many unique physical properties such as negligible vapor pressure, large liquidus range, high thermal stability, and wide electrochemical window (Galinski et al., 2006; Andriyko et al., 2009). Functionalized ILs/task-specific ILs have already become general pattern to prepare new ionic liquid materials based on the remarkable “design” capacity of ILs (Muller et al., 2013). The design processes of novel materials sorely depend on empirical rules. Therefore, researchers are always on the lookout for the instructive structure-property relationships of ILs that can be put to task-specific design of new functionalized ILs.
Dicyanamide (DCA) ILs are good nonaqueous solvents of transition metal salts because of the ligand ability of DCA anion as a Lewis base (Simons et al., 2014). Most of the metal chlorides are insoluble in tetrafluoroborate, hexafluorophosphate, and bis(trifluoromethylsulfonyl)imide ILs, but well dissolved into DCA ILs due to the high complexing ability of DCA anion (Schmeissera and Eldik, 2014). Furthermore, the structure of DCA anion is much easier to be oxidize by fuming nitric acid, which can be used as new hypergolic propellants. DCA ILs possess lower viscosity than most of common ILs such as tetrafluoroborate, hexafluorophosphate, and bis(trifluoromethylsulfonyl)imide counterparts (MacFarlane et al., 2002). Lower viscosity implies higher conductivity and more efficient mass transport for the applications of electrochemical and rocket bipropellant system (Yoshida et al., 2007). Meanwhile, the CHN component of DCA anion gives these ILs an inbuilt advantage over other halogen-containing ILs to the facility and environment. These features would highly benefit the electrochemical studies. Transport properties are very important for electrochemical solvents. However, in fact, some DCA ILs may be a little viscous. Then their physicochemical properties would be much different with the conventional DCA ILs. The structure-property relationships of DCA ILs, especially the effects of cationic structures on the transport properties including viscosity, conductivity, and electrochemical properties, are still not clear enough.
Herein, a series of DCA ILs was designed and synthesized to find the structure-activity relationship of different cation structures, including 1-butyl-3-methylimidazolium dicyanamide ([C4mim][N(CN)2]), 1-butyl-2,3-dimethylimidazolium dicyanamide ([C4m2im][N(CN)2]), N-ethyl-N,N,N-tributylammonium dicyanamide (N4442[N(CN)2]), and N-octyl-N,N,N-tributylammonium dicyanamide (N8444[N(CN)2]), (Scheme 1). Besides the basic characterization, the electrochemical behaviors of Eu(III) in DCA ILs were also investigated by cyclic voltammetry method. The diffusion coefficients, charge transfer rate constants, formal potentials and Gibbs energy were estimated based on cyclic voltammetry curves, from which we can find the effects of cation structures on the transport properties in DCA ILs.
Materials and Methods
All chemicals were commercially available with analytical grade. 1-Butyl-3-methylimidazolium bromide ([C4mim]Br), 1-butyl-2,3-dimethylimidazolium bromide ([C4m2im]Br), N-ethyl-N,N,N-tributylammonium bromide (N4442Br), and N-octyl-N,N,N-tributylammonium bromide (N8444Br) were synthesized by the Menschutkin reaction of corresponding imidazole or N,N,N-tributylamine with the appropriate alkyl halides according to the literature method (Gordon, 2002). Silver dicyanamide (Ag[N(CN)2]) was prepared by the metathesis of Na[N(CN)2] with AgNO3 in the dark in distilled water.
[C4mim][N(CN)2]
[C4mim]Br (4.39 g, 20 mmol) were dissolved in 50 mL distilled water, and then Ag[N(CN)2] (3.68 g, 21 mmol) was added. The resulting suspension was stirred overnight in the dark at room temperature. The byproduct AgBr along with the unreacted Ag[N(CN)2] were removed by filtration. The filtrate was collected and dried under vacuum at 373 K to yield [C4mim][N(CN)2] as a colorless liquid. Yield: 3.96 g (96%). IR (KBr, cm−1): 3148 (w), 3102 (w), 2962 (m), 2937 (w), 2873 (w), 2232 (s), 2194 (s), 2132 (vs.), 1570 (s), 1464 (s), 1380 (w), 1310 (s), 1169 (s), 1113 (w), 1024 (w), 948 (w), 903 (w), 846 (w), 754 (m), 652 (m), 622 (s). 1H-NMR (DMSO-d6, δ/ppm): 0.89 (t, 3H, J = 7.2 Hz), 1.27 (m, 2H), 1.77 (m, 2H), 3.85 (s, 3H), 4.16 (t, 2H, J = 7.2 Hz), 7.68 (s, 1H), 7.75 (s, 1H), 9.11 (s, 1H). 13C-NMR (DMSO-d6, δ/ppm): 13.12, 18.68, 31.25, 35.63, 48.44, 122.13, 123.48, 136.41. Anal. Calcd for C10H15N5 (205.26): C, 58.51; H, 7.37; N, 34.12; found: C, 58.32; H, 7.56; N, 33.97.
[C4m2im][N(CN)2]
A similar procedure was followed as that described for [C4mim][N(CN)2]. [C4m2im]Br (4.66 g, 20 mmol) and Ag[N(CN)2] (3.68 g, 21 mmol) were reacted in 50 mL distilled water to obtain a light yellow liquid. Yield: 4.03 g (92%). IR (KBr, cm−1): 3178 (vw), 3134 (w), 3016 (vw), 2963 (m), 2937 (w), 2229 (s), 2192 (s), 2132 (vs.), 1588 (s), 1538 (s), 1417 (s), 1251 (w), 1185 (m), 1134 (m), 1044 (w), 903 (m), 828 (w), 755 (s), 665 (s), 626 (w). 1H-NMR (DMSO-d6, δ/ppm): 0.89 (t, 3H, J = 7.2 Hz), 1.29 (m, 2H), 1.69 (m, 2H), 2.60 (s, 3H), 3.77 (s, 3H), 4.12 (t, 2H, J = 7.2 Hz), 7.63 (s, 1H), 7.66 (s, 1H). 13C-NMR (DMSO-d6, δ/ppm): 9.14, 13.24, 18.77, 31.07, 34.58, 47.23, 120.71, 122.14, 144.06. Anal. Calcd for C11H17N5 (219.29): C, 60.25; H, 7.81; N, 31.94; found: C, 60.13; H, 7.88; N, 31.84.
N4442[N(CN)2]
A similar procedure was followed as that described for [C4mim][N(CN)2]. N4442Br (5.87 g, 20 mmol) and Ag[N(CN)2] (3.68 g, 21 mmol) were reacted in 50 mL distilled water to obtain a yellow liquid. Yield: 4.76 g (85%). IR (KBr, cm−1): 3134 (w), 2964 (s), 2933 (s), 2875 (s), 2226 (s), 2190 (s), 2130 (vs.), 1638 (w), 1568 (w), 1467 (s), 1386 (m), 1306 (s), 1158 (w), 1096 (w), 1062 (w), 1032 (w), 898 (w), 804 (w), 739 (w). 1H-NMR (DMSO-d6, δ/ppm): 0.93 (t, 3H, J = 7.2 Hz), 1.18 (t, 3H, J = 7.2 Hz), 1.32 (m, 2H), 1.58 (m, 2H), 3.18 (s, 2H), 3.29 (s, 2H). 13C-NMR (DMSO-d6, δ/ppm): 7.03, 13.16, 18.95, 22.79, 56.79, 118.85. Anal. Calcd for C16H32N4 (280.45): C, 68.52; H, 11.50; N, 19.98; found: C, 68.74; H, 11.58; N, 19.62.
N8444[N(CN)2]
A similar procedure was followed as that described for [C4mim][N(CN)2]. N8444Br (7.54 g, 20 mmol) and Ag[N(CN)2] (3.68 g, 21 mmol) were reacted in 50 mL distilled water to obtain a yellow liquid. Yield: 6.47 g (89%). IR (KBr, cm−1): 3132 (w), 2961 (s), 2930 (s), 2872 (s), 2225 (s), 2189 (s), 2130 (vs.), 1637 (w), 1569 (w), 1466 (m), 1381 (w), 1306 (m), 1152 (w), 1110 (w), 1067 (w), 1032 (w), 895 (w), 799 (w), 740 (w). 1H-NMR (DMSO-d6, δ/ppm): 0.87 (t, 3H, J = 7.2 Hz), 0.94 (t, 3H, J = 7.2 Hz), 1.31 (m, 2H), 1.58 (m, 2H), 3.01 (s, 2H), 3.20 (s, 2H). 13C-NMR (DMSO-d6, δ/ppm): 13.27, 19.08, 20.85, 21.94, 22.96, 25.11, 25.62, 28.30, 31.01, 51.78, 57.47, 118.97. Anal. Calcd for C22H44N4 (364.61): C, 72.47; H, 12.16; N, 15.37; found: C, 72.36; H, 12.45; N, 15.14.
Measurements Methods
Infrared spectra (IR) were recorded using KBr plates on a Bruker ALPHA-ATR spectrophotometer. 1H and 13C NMR spectra were recorded on a Bruker AVANCE III HD nuclear magnetic resonance spectrometer with DMSO-d6 as locking solvent. 1H and 13C chemical shifts are reported in ppm from TMS with the solvent resonance as the internal standard (DMSO, δ = 2.50). Thermogravimetric analysis (TGA) measurements were accomplished on a NETZSCH TG 209F1 instrument by heating samples at 10 K min−1 from 298 to 873 K in a dynamic nitrogen atmosphere at flow rate of 70 mL min−1. Differential scanning calorimetry (DSC) measurements were performed on a TA Q20 calorimeter equipped with a cool accessory and calibrated with pure indium. Measurements were performed at a heating rate of 10 K min−1 in sealed aluminum pans with a nitrogen flow rate of 20 mL min−1. Elemental analyses (C, H, N) were performed on an Flash 1112 Series EA elemental analyzer. Densities were measured by pycnometer method. Viscosities were measured with a NDJ-1B-1 viscometer. Conductivity measurements were recorded on a DDSJ-308A conductivity meter with a Q/YXLG133 conductance electrode. Cyclic voltammetry measurements were carried out in a standard three-electrode electrochemical cell with a platinum rod counter electrode and a silver/silver ion (0.1 M Ag+ in CH3CN) acted as the quasi-reference electrode. The working electrode was a glassy carbon (GC) rod with the area of 0.1256 cm2. Experiments were took from 303 to 333K under the nitrogen atmosphere. The electrochemical cell had a single leak-tight compartment and all the electrodes were placed in the same compartment. The ionic liquid solutions were prepared by dissolving EuCl3 (anhydrous, 99.9% Eu, purchased from Jiangxi Xinzheng Chemicals) into the ILs, and dried in vacuum for 12 h at 373 K.
Results and Discussion
Thermal Behaviors
The glass transition temperatures (Tg), crystallization temperatures (Tc), melting points (Tm), and decomposition temperatures (Td) of four DCA ILs are summarized in Table 1. These DCA ILs are thermally stable, with Td over 500 K. The structural differences in their cations could give the changes in their decomposition temperatures. Imidazolium cation could yield DCA ILs with higher thermal stability than quaternary ammonium cation. Furthermore, the highest decomposition temperature was found from [C4m2im][N(CN)2] than [C4mim][N(CN)2]. The reason for the increased thermal stability is most likely the presence of methyl group relative to active hydrogen attached to the C(2) position of imidazolium framework.
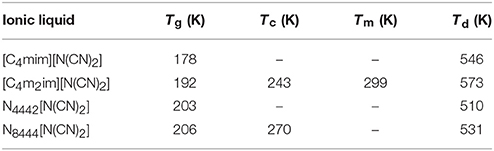
Table 1. Thermal properties of DCA ILs: [C4mim][N(CN)2], [C4m2im][N(CN)2], N4442[N(CN)2], and N8444[N(CN)2].
Viscosity
Viscosity of ILs is a key feature associated with their liquid characteristic, and thus clearly affects their charge transport capacity. Change in viscosity of ILs can give intimate changes in their transport properties, including conductivity, diffusion coefficient, and charge transfer rate etc. The viscosities of four DCA ILs were recorded at different temperatures and summarized in Figure 1. The combination of 1-butyl-3-methylimidazolium cation with DCA anion yields room-temperature IL [C4mim][N(CN)2] with viscosity as low as 29 cP at 298 K. The viscosity of [C4m2im][N(CN)2], with a methyl group attached to C2, increases to 68 cP. While, N4442[N(CN)2] and N8444[N(CN)2] with quaternary ammonium cation produce DCA ILs in higher viscosity. The viscosity values shows the salts with imidazolium cations are less viscous than the quaternary ammonium-based ILs. Asymmetric N-subsitituted imidazolium cations have been noted to be suitable for the design of low-viscous, room-temperature ILs. In these cases, the synergistic effect of the charge delocalization and planarity leads to low viscous ILs.
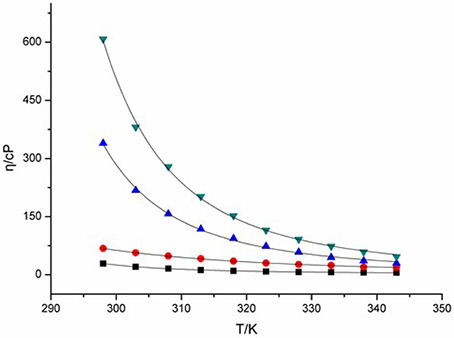
Figure 1. Viscosities (η) of [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green) at different temperatures.
Hydrogen bonding is an important factor affected the viscosity of ILs. Fewer hydrogen bonds may lead to lower viscosity of IL (Kowsari et al., 2014). However, the DCA IL [C4mim][N(CN)2] with active hydrogen on C(2) exhibits lower viscosity than [C4m2im][N(CN)2]. For the quaternary ammonium DCA ILs, less hydrogen bonds in N4442[N(CN)2] and N8444[N(CN)2] are not give descent in their viscosity, relative to the imidazolium DCA ILs. The C(2) methyl of [C4m2im][N(CN)2] may increase the van der Waals interactions and decrease the entropy, leading to its viscosity bigger than that of C4mim[N(CN)2]. Meanwhile, the lengthening of alkyl chain also increases the van der Waals interactions, resulting in that N8444[N(CN)2] is more viscous than N4442[N(CN)2]. On the other hand, the imidazolium cation contains a conjugated cation structure. The positive charge of imidazolium cation is well distributed, which remarkably weakens the Coulomb interactions among ions. As a result, the viscosity of imidazolium DCA ILs are lower than that of quaternary ammonium DCA ILs. Therefore, the cationic structures may influence the viscosity of ILs through the synergistic effect of hydrogen-bond, van der Waals (vdW) attractive force, entropy and charge distribution.
Normally, the viscosity and the melting point have positive correlations. Low melting ILs should have lower viscosity and better fluidity (He et al., 2009). The DCA ILs with similar structure such as [C4m2im][N(CN)2] and [C4mim][N(CN)2] are in well accord with this feature. However, no positive correlation of viscosity vs. melting point was found for the DCA ILs with different cationic frameworks.
The relation between the viscosity and temperature for [C4m2im][N(CN)2], [C4m2im][N(CN)2], N4442[N(CN)2], and N8444[N(CN)2] is described in Figure 1. A rapid decrease in the viscosities is found in the DCA ILs as the temperature increases. A glassy or supercooled feature of the DCA ILs was observed. A rapid increase in the viscosity and a slowing descent of the structural relaxation occurs, on approaching the glass transition temperature. Such feature is also noted in other ILs (Tao et al., 2012). This temperature dependence of the viscosity η can be well described by the Vogel-Fulcher-Tammann (VFT) empirical equation suitable for glass-forming liquids (Equation 1; He et al., 2011; Smith et al., 2013):
where η is the viscosity, T is the temperature, T0 corresponds to the characteristic temperature at which η is infinite, η0 is a reference viscosity, and D is a constant presenting the structural “strength” of the system. The VFT fit curves in the equation are also shown in Figure 1. The viscosity vs. temperature graphs can be fit well to the VFT model, with a fit R2 > 0.999. The T0 values of [C4mim][N(CN)2], [C4m2im][N(CN)2], N4442[N(CN)2] and N8444[N(CN)2] ILs are estimated to be 249, 136, 123, and 187 K, respectively. The Arrhenius plot of the viscosity vs. temperature was also fitted. However, lower R2 > 0.99 was obtained. This plot of viscosity indicates that these DCA ILs display no-Arrhenius temperature behavior.
From Figure 1, a rapid decrease in the viscosities is found in the DCA ILs as the temperature increases. The influence of temperature is very significant on the viscosity at lower temperature. At a higher temperature 343 K, the viscosity of [C4mim][N(CN)2] is only 6.1 cP and that of [C4m2im][N(CN)2] is 18.8 cP, which are lower than that of N4442[N(CN)2] (29.6 cP) and N8444[N(CN)2] (46.4 cP). The strength of the momentum transfer of quaternary ammonium DCA ILs is more temperature-dependent than imidazolium DCA ILs.
Conductivity
Conductivity of ILs originates from the inherent motion of cations and anions in ILs under electric potential difference, which is of great importance as an electrolyte for electrochemical application (Jin et al., 2008). The cationic structure has a remarkable influence on the conductivities of the four DCA ILs. At 298 K, the value of conductivity for [C4mim][N(CN)2] reaches 10.09 mS cm−1, which is comparable to the best non-aqueous solvent/electrolyte systems (Hapiot and Lagrost, 2008). A reduce in conductivity is found for [C4m2im][N(CN)2] (2.88 mS cm−1). Compared with the imidazolium DCA ILs, N4442[N(CN)2] and N8444[N(CN)2] exhibit much less conductivities, with the values of 50.8 μS cm−1 and 10.77 μS cm−1, respectively. The four DCA ILs have similar electrical charge, and would be all expected to possess high conductivities because they are composed of entirely of ions. However, the hundreds times difference of the conductivities indicates the available charge carries is not the only factor to high conductivities. Because of the ion aggregation/pairing, the large ion size could cause the reduction of ion mobility and then the reduction of available charge carries. Although low conductivity is not a general expectative property for ILs, it is still very interesting for studying the structure-property relationships. The conductivity of the quaternary ammonium DCA ILs are lower than other common room temperature ILs (Hapiot and Lagrost, 2008). It is predictable that N8444[N(CN)2] is not the one that owns the lowest conductivity in DCA ILs. The lower one may be expected if a quaternary ammonium with larger ion size is introduced.
The temperature and the viscosity of ILs inevitably affect the conductivity of ILs. The plots of temperature-dependent conductivity for the DCA ILs are shown in Figure 2. These curves of temperature dependence the conductivity (σ) also can be fit well by the VFT equation with the variance R2 > 0.999. (Equation 2):
where σ is conductivity, T is the temperature, T0 corresponds to the characteristic temperature when σ is infinite, σ0 is a reference viscosity, and D is a structural constant depend on each ionic liquid. From Figure 2, an obvious influence of the temperature on the conductivity is observed.
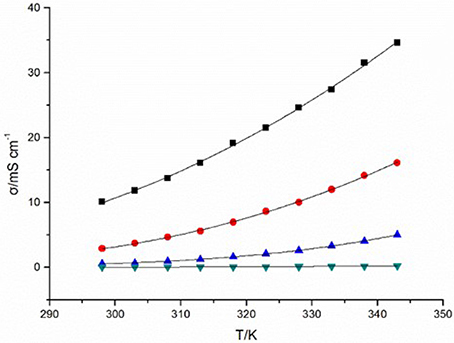
Figure 2. Conductivities (σ) of [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green) at different temperatures.
The alternation of conductivities of the four studied ILs in this paper is not linear correlation with the decreasing of viscosities. The higher viscosities of ILs, the slower increase of conductivities. Then becoming quicker due to continuously decrease of viscosities with the temperatures increased. This illustrates that high viscosity will hinder the diffusion and transfer rate of charge, thus lead to the low conductivity of IL. The cationic structure, including ionic size, formula weight and conjugated structure of imidazolium ring will also influence the conductivities of ILs. The conductivity of ILs can be described as Equation (3) (Rüther et al., 2013):
where uc, ua are the cation and anion mobilities, F is the Faraday constant, C is the molar concentration, y is the degree of dissociation and 0 < y < 1, d is the density, and FW is the formula weight.
The Stokes-Einstein relation correlates self-diffusivity (D) to viscosity is depicted of the medium even in an ionic medium. The equations are following: (Equation 4)
where ξa and ξc are the anion and cation microviscosity factors, respectively. The self-diffusivity of the ions can be also associated with ion mobility: (Equation 5)
Based on Equations (3–5), the relationship of conductivity and viscosity can be shown in Equation (6):
where NA is the Avogadro's number, ra and rc are the anion and cation radius. The microviscosity factor ξc and ξa relates to the specific interactions between the mobile ions in the ILs, of which is governed by interionic hydrogen-bonding and Coulombic interactions.
According to Equation (6), the conductivities of the ILs can get a reasonable degree of approximation related to their viscosities (η), formula weight (FW), densities (d), and radii of their ions (ra and rc). Qualitatively, the relationship between conductivity and other physical parameters in Equation (6) was verified. Besides the obvious influence of the viscosity, the effect of ion size and formula weight must be stressed.
According to the combination of the Nernst-Einstein equation for the relationship between the self-diffusivity in a liquid and its ionic conductivity, and the Stokes–Einstein equation, the relationship of the molar conductivity (Λ) and viscosity (η) can be shown in Equation (7):
The conductivity and viscosity of an IL is often combined into what is termed Walden's rule (Equation 8) (Ueno et al., 2010):
where Λ is the molar conductivity of the IL, and it is given by Equation (9):
where M is the molecular weight and d is the density of the IL. Ideally, the Walden product (Λη) remains constant for a given IL regardless of temperature. The magnitude of the Walden product for different ILs has been shown to vary inversely with ion size. This inverse relationship between ion size and the magnitude of Λη is generally followed for the cations. Figure 3 shows the Walden plot of log(molar conductivity, Λ) against log(reciprocal viscosity η−1) graphs.
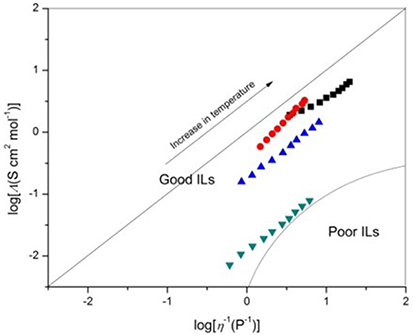
Figure 3. Walden plots of log(molar conductivity, Λ) against log(reciprocal viscosity η−1), [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green).
The magnitude of the deviation below the ideal line is presumably a result of ion aggregation, which suggests that Coulombic interactions between ions can strongly influence ionicity. Increasing cation size tends to give rise to lower conductivity, most probably due to the lower mobility of the larger cations. Moreover, the formula weight increase with the alkyl chain elongated, then increasing the van der Waals attractive forces. The bigger van der Waals forces will present an obstacle to the migration of charge, resulting in the decrease of conductivity. Although all of the DCA ILs has the same charge, the apparent Coulombic interactions are much different. Compared with quaternary ammonium cation, the synergistic effect of charge delocalization and ion size and of imidazolium cation is bigger. The π electron of the conjugated structure in imidazolium ring along with a smaller ion size gives advantage of higher mobility of the imidazolium cation and lower Coulombic interactions. A strong cation–anion attraction causes poor IL ionicity. From the deviations from the reference line in the Walden plot, [C4mim][N(CN)2], [C4m2im][N(CN)2] and N4442[N(CN)2] which have slight deviation can be classified as “good” ILs. Obviously, the plots of N8444[N(CN)2] have larger deviation that located at the edge of “poor” ILs as Angell et al. suggested (Xu et al., 2003) (Figure 3). In particular, the imidazolium cations exhibit clear superiority than the ammonium cations.
Electrochemical Windows (EWs)
Electrochemical behavior was performed by cyclic voltammetry using three-electrode cell with a glassy carbon (GC) rod working electrode at different temperatures. The redox potentials were recorded relative to a stable (Ag/Ag+) reference electrode. Figure 4 shows the representative voltammograms measured for the DCA ILs. Electrochemical window (EW, ΔE), associated with the electrochemical stabilities of ILs, is determined from the curve described in Figure 4. The EWs ΔE for [C4mim][N(CN)2] and [C4m2im][N(CN)2] are similar, with values of 3.63 and 3.56 V, respectively. These ΔE values are lower than the ΔE values observed for [C4mim][BF4] (4.1 V) and [C4mim][PF6] (4.2 V) (Schröder et al., 2000; Zhang et al., 2014). However, the ILs consisted of fluorine component are environmentally unfriendly because of their fluorine release. In fact, the ΔE value of [C4mim][N(CN)2] is higher than many ILs normally about 2–3 V (Wicelinski et al., 1987). The ΔE value ~4.5 V is observed for N4442[N(CN)2] (4.47 V). A further increase in the ΔE is found for N8444[N(CN)2], with the value up to 4.80 V. The data clearly indicates N8444[N(CN)2] exhibits the highest electrochemical stability among the four DCA ILs. The cation provides better protection against electrochemical oxidation and reduction. The ΔE values of the DCA ILs are relatively wide, which give potential feasibility as electrolytes in some electrochemical applications.
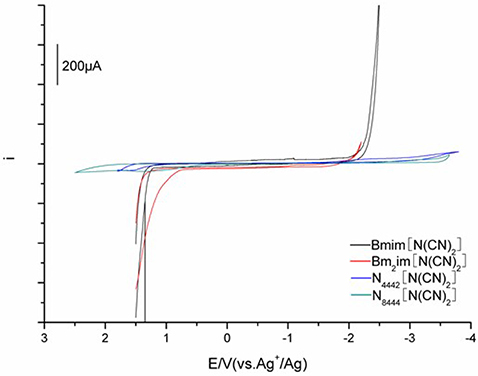
Figure 4. Cyclic voltammograms of [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green) measured at 303 K.
Cyclic voltammetry of Eu(III) in DCA ILs. The cyclic voltammograms of a solution of 50 mM Eu(III) in these ILs recorded at GC electrode are shown in Figure 5. The cyclic voltammograms of Eu(III) in [C4mim][N(CN)2], [C4m2im][N(CN)2], N4442[N(CN)2], N8444[N(CN)2] consists of quasi-reversible waves. At 303 K, a cathodic peak and an anode peak potentials of Eu(III) in [C4mim][N(CN)2], are observed around −1.39 V and −0.71 V owing to the reduction and oxidation of Eu(III). What's more, there is no deposition of elemental europium during the potentiostatic reduction. Therefore, the reduced product in this system is probably the divalent europium complex, Eu(II). The cyclic voltammetry analysis of the Eu(III)/Eu(II) in [C4mim][N(CN)2] is a quasi-reversible. Similar cyclic voltammograms determined in other three DCA ILs were also assembled, with an anode peak potentials of −0.79 V ([C4m2im][N(CN)2]), −0.64 V (N4442[N(CN)2]) and −0.59 V (N8444[N(CN)2]), respectively.
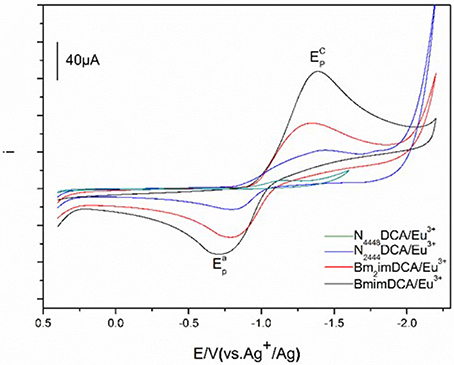
Figure 5. Cyclic voltammograms of Eu(III) measured in [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green) at 303 K.
The cyclic voltammograms of 50 mM Eu(III) at various temperatures were assembled in Figure 6. The temperatures were controlled in accuracy and selected as 303, 313, 323, and 333 K, respectively. An increase of the current intensities for Eu(III) is found in [C4mim][N(CN)2] along with the rise of temperature. A cathodic peak potentials of Eu(III) are significantly higher than the values observed at lower temperature. While, a slight reduce is recorded for an anode peak potential at higher temperature. For example, at 303 K the cathodic peak potential for Eu(III) is −1.42 V whereas the value is significantly less negtive, reaching ~ −1.02 V. The tendency of Eu(III)/Eu(II) redox reaction shows more quasi-reversible with the increase of temperature. A similar tendency is also found in [C4m2im][N(CN)2], N4442[N(CN)2], and N8444[N(CN)2]. This feature is associated with the mass transition caused by the viscosity and conductivity of the solvent, which depends on temperature closely (Nockemann et al., 2006). For these ILs, their viscosities decreased and the conductivities increased with the increasement of temperature, which are contributed to the diffusion of trivalent lanthanide ion Eu(III). Thus, many parameters related to transport properties are also temperature-dependent for the variation of the viscosity of ILs, such as conductivity, diffusion coefficient, and charge transfer rate. The diffusion rate became faster as the temperature increased.
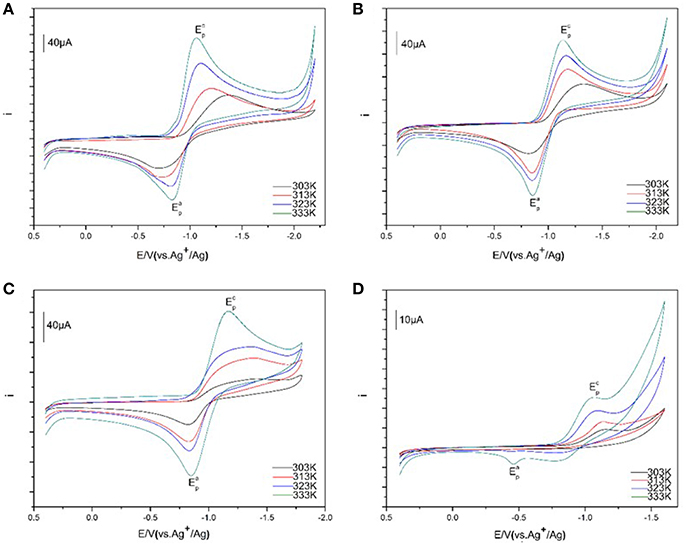
Figure 6. Cyclic voltammograms of Eu(III) in [C4mim][N(CN)2] (A), [C4m2im][N(CN)2] (B), N4442[N(CN)2] (C), and N8444[N(CN)2] (D) with Ag/AgCl as reference electrode at the scan rate of 100 mV/s from 303 to 333 K.
The relation between the current intensities of cathodic peak (ip) and the square-root of the potential scan rate (ν1/2) is shown in Figure 7 at 303 and 333 K. The plots show that there exist a positive correlation between the cathodic peak current intensity and the square-root of the potential scan rate. Good linear relationships were obtained for Eu(III) in the four DCA ILs. In addition, the value of the cathodic current densities increased as the temperature raised, which might be generated from the diffusion coefficients and charge transfer rates of the Eu(III) in DCA ILs. These results indicate that the electrode reaction kinetics is controlled by the mass transport under semi-infinitive linear diffusion conditions.
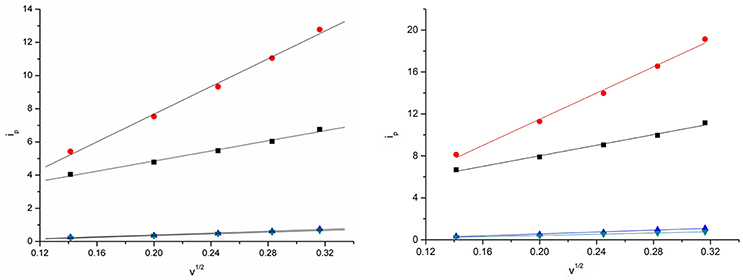
Figure 7. Cathodic peak current intensities as a function of ν1/2 of Eu(III) measured in [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green) at 303 K (left) and 333 K (right).
Figure 8 described the cyclic voltammograms and the peak potential separation values of Eu(III) at various scan rates. The redox peak potentials of Eu(III) in these ILs at various scan rates are obviously observed. Along with the scan rate change, both current intensity and peak potential are moved. The Eu(III)/Eu(II) redox reaction shows more reversible at the low scan rate, and the separation of the cathodic and anodic peak potentials would be shift to cathode and anode, respectively, as the scan rate raised.
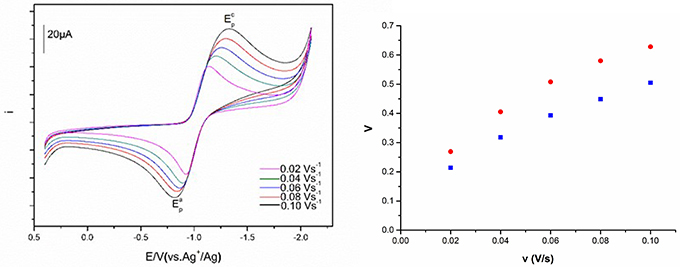
Figure 8. Cyclic voltammograms of Eu(III) measured in [C4m2im][N(CN)2] and the peak potential separation values of [C4m2im][N(CN)2] (blue) and N8444[N(CN)2] (red) at different scan rates.
Diffusion coefficients and energy of activation (Ea) of Eu(III) in DCA ILs. The diffusion coefficients of Eu(III) in DCA ILs were measured by series of electrochemical analyses. The relationship between cathodic peak current and diffusion coefficient (Do) for a quasi-reversible system can be predicted as Equation (10) (Bard and Faulkner, 1980; Molina et al., 2013):
where A is the electrode area in cm2, is the Eu(III) concentration in mmol·L−1, Do is the diffusion coefficient in cm2·s−1, ν is the potential scan rate in V·s−1, F is the Faraday constant, α is the charge transfer coefficient, n is the number of electron transfer, nα is the number of electron transfer in the rate determining step, and T is the absolute temperature in K. The value of αnα can be determined using Equation (11) (Matsumiya et al., 2008):
where is the cathodic potentials, is the half wave potentials, and |-| is the absolute value of the difference between and . The data of cathodic peak (), anodic peak () potentials and the average of cathodic and anodic peak potential, ()/2, at various temperatures are summarized in Table 2.
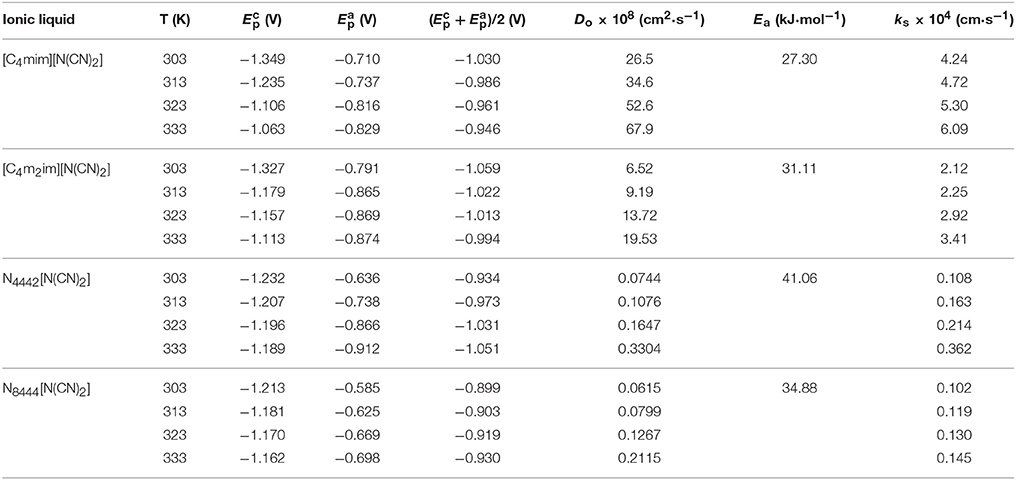
Table 2. Peak potentials ( and ), average of cathodic and anodic peak potentials [()/2], diffusion coefficients (Do), electron transfer rate constant (ks), and energy of activation (Ea) of Eu(III) measured in the DCA ILs at different temperatures.
From the Equations (10, 11), the diffusion coefficients of Eu(III) in these ILs can be determined, the values are shown in Table 2. The diffusion coefficients can be regarded as a function of T. Changes of temperature gives an increase or decrease of the diffusion coefficients and the charge transfer coefficients. The diffusion coefficient of Eu(III) in [C4mim][N(CN)2] is about 26.5 × 10−8 cm2·s−1 at 303 K, and as high as 67.9 × 10−8 cm2·s−1 at higher temperature. Low viscosity and high conductivity at high temperature result in more efficient mass transport with high value of diffusion coefficient. The viscosity and conductivity of IL are of importance to influent the application of IL as a solvent because that they will influence the transport properties of IL for some metal ions, including diffusion coefficient and charge transfer rate etc. Similar trends are also found for Eu(III) in other DCA ILs. The magnitude of diffusion coefficients for Eu(III) in [C4mim][N(CN)2] and [C4m2im][N(CN)2] are around ~10−7 cm2·s−1, while the values for Eu(III) recorded in N4442[N(CN)2] and N8444[N(CN)2] are ~10−10 cm2·s−1 at 303 K, then being ~10−9 cm2·s−1 at higher temperature. Such values performed in the imidazolium DCA ILs are 102–103 times larger than those of Eu(III) in N4442[N(CN)2] and N8444[N(CN)2], which are attributed to their higher viscosity and lower conductivity of the quaternary ammonium-based ILs relative to the imidazolium-based ILs. A reduce in the transport properties of quaternary ammonium DCA ILs hinders the diffusion of Eu(III) in ILs. This phenomenon shows that the electrostatic interaction around Eu(III) in the quaternary ammonium DCA ILs may be weaker than those of Eu(III) in the imidazolium-based ILs.
Figure 9 shows the plots of the diffusion coefficients (logDo) of Eu(III) in four DCA ILs and the molar conductivities (logΛ) of these ILs. A linear relationship is observed, which indicates that the diffusion coefficients are correlative with molar conductivity. Although the mechanism how the friction on the translational motion affects the relaxation of the ionic atmosphere around the Eu ion is still unknown, based on the plots, the diffusion coefficients may be predicted as a function of molar conductivity. Thus, for ILs, molar conductivity is a valuable quantity to construct linear relationship with the transport properties. The calculated data of diffusion coefficients may not be accurate and can be used as reference data.
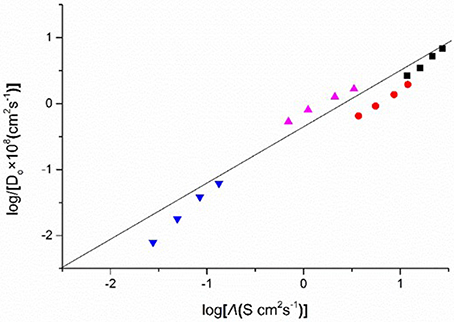
Figure 9. Logarithm of diffusion coefficients (Do) of Eu(III), against as a function of log(molar conductivity, Λ), measured in [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (violet).
The energy of activation (Ea) of the reduction of Eu(III) to Eu(II) can be determined from the slope of lnDo against 1/T (Figure 10) and the data were also given in Table 2. The raise of the Ea magnitude is parallel to the increase of the conductivities of these ILs. The reduction of Eu(III) to Eu(II) exhibits the values of Ea DCA ILs around 27.30 to 41.06 kJ·mol−1.
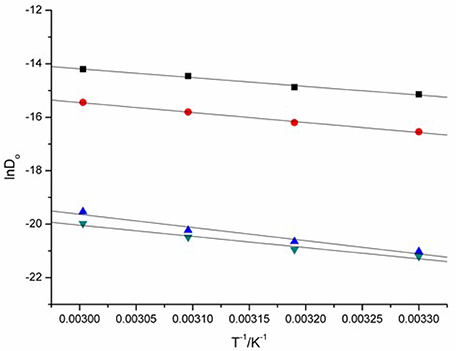
Figure 10. lnDo of Eu(III), as a function of T−1 measured in [C4mim][N(CN)2] (black), [C4m2im][N(CN)2] (red), N4442[N(CN)2] (blue), and N8444[N(CN)2] (green).
Charge transfer rate constants (ks) of Eu(III) in ILs. The major factors that affect the reduction process of Eu(III) to Eu(II) in DCA ILs relate to both diffusion and charge transfer kinetics. For a quasi-reversible system, the charge transfer rate constant (ks), depended on both diffusion coefficient and transfer coefficient, can be described as Equation (12) (Brown and Sandifer, 1986; Rao et al., 2010):
The data of charge transfer rate constants (ks), the cathodic and anodic peak potentials of Eu(III) are summarized in Table 2. The charge transfer rate constants of Eu(III) in [C4mim][N(CN)2] and [C4m2im][N(CN)2] are higher than the values recorded in N4442[N(CN)2] and N8444[N(CN)2]. The magnitude of charge transfer rate constants of Eu(III) in [C4mim][N(CN)2] and [C4m2im][N(CN)2] are observed to be the order of 10−4 cm·s−1, while those determined in N4442[N(CN)2] and N8444[N(CN)2] are of the order of ~10−5 cm·s−1. Such data increased when the temperature increased. The lower viscosity and higher conductivity of ILs at higher temperatures may facilitate electron transfer at electrode-electrolyte interphase. Thus, an increase of the ks for Eu(III) in BmimBr can be found at higher temperature. The electrode reaction can be classified as, reversible when ks ≥ 0.3v1/2 cm·s−1, quasi-reversible when 0.3v1/2 ≥ ks ≥2 × 10−5v1/2 cm·s−1, and irreversible when ks ≤ 2 × 10−5v1/2 cm·s−1. Based on the ks values determined using Equation (12), the electrode reactions of Eu(III) to Eu(II) in DCA ILs are confirmed as quasi-reversible reactions.
Determination of Gibbs energy change of Eu(III) in ILs. Gibbs energy, ΔG, is of central importance to reaction. The reductions of Eu(III) to Eu(II) in [C4mim][N(CN)2] and [C4m2im][N(CN)2] are just expressed as:
The apparent standard potential, , is related to the cathodic and anodic peak potentials and their relation are given:
Because the number of electrons transfer (n) in the reduction of Eu(III) equals to 1, the expression of , a function of temperature, can be predicted as Equations (14, 15).
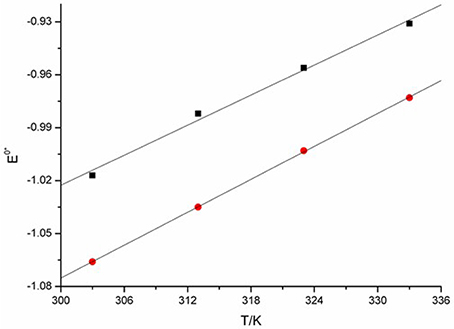
The relation between and temperature can be obtained from linear regression of the experimental data. The plots were shown in Figure 11. The alternation of are linear correlation with the increasing of T. Thus, the apparent standard potential can be further simplified and expressed as Equations (17, 18).
From the expression we see, the can be recognized as a function of T. In this work, a linear correlation of with temperature is found.
Assuming the solutions of Eu(III) in the DCA ILs are dilute and the activity coefficient are negligible, the standard Gibbs energy of the reaction EuCl2 + 1/2Cl2 → EuCl3 can be estimated using the expression (19).
where is the apparent standard potential of oxidation of Eu(II) to Eu(III). The relationships of the standard Gibbs energy of the reaction in [C4mim][N(CN)2] and [C4m2im][N(CN)2] and T just as given below expressions (20, 21), respectively.
Based on Equations (17–19), the standard Gibbs energy expression is to be a linear function of temperature.
The expressions of Equations (20, 21) show that the standard entropy (Δ) of the reaction EuCl2 + 1/2 Cl2 → EuCl3. According to the expression ΔG = ΔH – TΔS, the values of Δ are found to be negative around −0.3. The result shows that there is a decrease entropy during the reaction process, accompanied by the generation of more ordered EuCl3 from less ordered substrates. The results indicate that the entropy of reaction decrease, which are accord with the stoichiometric number of substances of the reaction reduced.
Conclusions
Four DCA ILs, [C4mim][N(CN)2], [C4m2im][N(CN)2], N4442[N(CN)2], and N8444[N(CN)2], were prepared and characterized. Except for [C4m2im][N(CN)2] with a melting point 299 K, other DCA ILs are all room temperature ILs with good thermal stability. Their transport properties including viscosities, conductivities, and electrochemical properties, were studied in detail at different temperatures. The influence factors on the viscosity and ionic conductivity of these ILs have been discussed. A decrease of the viscosity and increase of ionic conductivity of these ILs are recorded as the temperature increase. Besides temperature, hydrogen-bond, van der Waals force, entropy and charge distribution of cations are all possible affecting factors on the viscosity. Although the effect of viscosity on the conductivity is very significant, the cationic structure, including ionic size, formula weight, and conjugated structure of imidazolium ring could not be ignored. Based on the Walden plots, the cation–anion attraction among IL could be estimated. [C4mim][N(CN)2], [C4m2im][N(CN)2], and N4442[N(CN)2] can be classified as “good” ILs. While N8444[N(CN)2] locates at the edge of “poor” ILs. So in order to design low viscous and high conductive ILs, the importance of the cationic structure must be kept in mind.
A series of electrochemical analyses of the DCA ILs have been performed. These ILs give relatively high values of EWs, with the order of N8444[N(CN)2] > N4442[N(CN)2] > [C4mim][N(CN)2] ≈ [C4m2im][N(CN)2]. Such feature indicates that the DCA ILs are potential candidates for electrolytes in electrochemical applications. Meanwhile, the electrochemical behaviors of Eu(III) in these DCA ILs at GC working electrode at various temperatures 303–333 K were found. A series of quasi-reversible waves of Eu(III) were recorded by cyclic voltammetry. The electrochemical properties of the DCA ILs are also dominated by the cationic structures. The current intensity (ip), the diffusion coefficients (Do), the charge transfer rate constants (ks) of Eu(III) in DCA ILs all increased with the molar conductivities increased. Moreover, the apparent standard potentials [] and the standard Gibbs energy of the reduction of Eu(III) to Eu(II) were also determined.
In summary, the effect of the cationic structures including ionic size, formula weight and conjugated structure of imidazolium ring on the transport properties is very significant. The structure-property relationships of DCA ILs will be very useful to help us to understand other IL families and design novel functionalized ILs fulfilling specific demand.
Author Contributions
LH and G-HT: designed the research; W-LY, XY, and SQ: prepared the samples and did determinations; W-LY, XY, YX, and G-HT: were involved in the data analysis; W-LY, XY, LH, and G-HT: wrote the manuscript.
Funding
National Natural Science Foundation of China (No. 21303108, J1210004), and the Fundamental Research Funds for the Central Universities (No. 2015SCU04A21).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank the Comprehensive training platform of specialized laboratory, College of chemistry, Sichuan University for instrumental measurement.
References
Andriyko, Y. O., Reischl, W., and Nauer, G. E. (2009). Trialkyl-substituted imidazolium-based ionic liquids for electrochemical applications: basic physicochemical properties. J. Chem. Eng. Data 54, 855–860. doi: 10.1021/je800636k
Armand, M., Endres, F., MacFarlane, D. R., Ohno, H., and Scrosati, B. (2009). Ionic-liquid materials for the electrochemical challenges of the future. Nat. Mater. 8, 621–629. doi: 10.1038/nmat2448
Bard, A. J., and Faulkner, L. R. (1980). Electrochemical Methods-Fundamentals and Applications, 2nd Edn. New York, NY: Wiley.
Brennecke, J. F., and Gurkan, B. E. (2010). Ionic liquids for CO2 capture and emission reduction. J. Phys. Chem. Lett. 1, 3459–3464. doi: 10.1021/jz1014828
Brown, E. R., and Sandifer, J. R. (1986). “Cyclic voltammetry, AC polorography and related techniques,” in Physical Methods of Chemistry, Electrochemical Methods, Vol. 2, eds B. W. Rossiter and J. F. Hamilton (New York, NY: Wiley), 273–432.
Fan, M., Song, Z., Liang, Y., Zhou, F., and Liu, W. (2014). Laxative inspired ionic liquid lubricants with good detergency and no corrosion. ACS Appl. Mater. Interfaces 6, 3233–3241. doi: 10.1021/am4049332
Galinski, M., Lewandowski, A., and Stepniak, I. (2006). Ionic liquids as electrolytes. Electrochim. Acta 51, 5567–5580. doi: 10.1016/j.electacta.2006.03.016
Gao, Y. F., Zhang, L., He, L., Zhao, Y., Tang, N., Yuan, Y. L., et al. (2015). Insensitive energetic 5-nitroaminotetrazolate ionic liquids. RSC Adv. 5, 54527–54534. doi: 10.1039/C5RA07415K
Hallett, J. P., and Welton, T. (2011). Room-temperature ionic liquids: solvents for synthesis and catalysis. Chem. Rev. 111, 3508–3576. doi: 10.1021/cr1003248
Hapiot, P., and Lagrost, C. (2008). Electrochemical reactivity in room-temperature ionic liquids. Chem. Rev. 108, 2238–2264. doi: 10.1021/cr0680686
He, L., Ji, S. P., Tang, N., Zhao, Y., and Tao, G. H. (2015). Synthesis, structure and near-infrared photoluminescence of hexanitratoneodymate ionic liquids. Dalton Trans. 44, 2325–2332. doi: 10.1039/C4DT03294B
He, L., Tao, G. H., Parrish, D. A., and Shreeve, J. M. (2009). Slightly viscous amino acid ionic liquids: synthesis, properties, and calculations. J. Phys. Chem. B 113, 15162–15169. doi: 10.1021/jp905079e
He, L., Tao, G. H., Parrish, D. A., and Shreeve, J. M. (2010). Nitrocyanamide-based ionic liquids and their potential applications as hypergolic fuels. Chem. Eur. J. 16, 5736–5743. doi: 10.1002/chem.200902651
He, L., Tao, G. H., Parrish, D. A., and Shreeve, J. M. (2011). Liquid dinitromethanide salts. Inorg. Chem. 50, 679–685. doi: 10.1021/ic101959r
Jin, H., O'Hare, B., Dong, J., Arzhantsev, S., Baker, G. A., Wishart, J. F., et al. (2008). Physical properties of ionic liquids consisting of the 1-butyl-3-methylimidazolium cation with various anions and the bis(trifluoromethylsulfonyl)imide anion with various cations. J. Phys. Chem. B 112, 81–92. doi: 10.1021/jp076462h
Kowsari, M. H., Fakhraee, M., Alavi, S., and Najafi, B. (2014). Molecular dynamics and ab initio studies of the effects of substituent groups on the thermodynamic properties and structure of four selected imidazolium-based [Tf2N–] ionic liquids. J. Chem. Eng. Data 59, 2834–2849. doi: 10.1021/je5004675
MacFarlane, D. R., Forsyth, S. A., Golding, J., and Deacon, G. B. (2002). Ionic liquids based on imidazolium, ammonium and pyrrolidinium salts of the dicyanamide anion. Green Chem. 4, 444–448. doi: 10.1039/b205641k
Matsumiya, M., Suda, S., Tsunashima, K., Sugiya, M., Kishioka, S. Y., and Matsuura, H. (2008). Electrochemical behaviors of multivalent complexes in room temperature ionic liquids based on quaternary phosphonium cations. J. Electroanal. Chem. 622, 129–135. doi: 10.1016/j.jelechem.2008.04.021
Molina, A., Laborda, E., González, J., and Compton, R. G. (2013). Effects of convergent diffusion and charge transfer kinetics on the diffusion layer thickness of spherical micro- and nanoelectrodes. Phys. Chem. Chem. Phys. 15, 7106–7113. doi: 10.1039/c3cp50290b
Muller, E. A., Strader, M. L., Johns, J. E., Yang, A., Caplins, B. W., Shearer, A. J., et al. (2013). Femtosecond electron solvation at the ionic liquid/metal electrode interface. J. Am. Chem. Soc. 135, 10646–10653. doi: 10.1021/ja3108593
Nacham, O., Clark, K. D., Yu, H. L., and Anderson, J. L. (2015). Synthetic strategies for tailoring the physicochemical and magnetic properties of hydrophobic magnetic ionic liquids. Chem. Mater. 27, 923–931. doi: 10.1021/cm504202v
Nockemann, P., Thijs, B., Pittois, S., Thoen, J., Glorieux, C., Van Hecke, K., et al. (2006). Task-specific ionic liquid for solubilizing metal oxides. J. Phys. Chem. B 110, 20978–20992. doi: 10.1021/jp0642995
Rao, C. J., Venkatesan, K. A., Nagarajan, K., Srinivasan, T. G., and Rao, P. R. V. (2010). Electrochemical and thermodynamic properties of europium(III), samarium(III) and cerium(III) in 1-butyl-3-methylimidazolium chloride ionic liquid. J. Nucleic Mater. 399, 81–86. doi: 10.1016/j.jnucmat.2010.01.005
Rogers, R. D., and Seddon, K. R. (2003). Ionic liquids-solvents of the future? Science 302, 792–793. doi: 10.1126/science.1090313
Rüther, T., Harris, K. R., Horne, M. D., Kanakubo, M., Rodopoulos, T., Veder, J. P., et al. (2013). Transport, electrochemical and thermophysical properties of two N-donor-functionalised ionic liquids. Chem. Eur. J. 19, 17733–17744. doi: 10.1002/chem.201302258
Schmeissera, M., and van Eldik, R. (2014). Elucidation of inorganic reaction mechanisms in ionic liquids: the important role of solvent donor and acceptor properties. Dalton Trans. 43, 15675–15692. doi: 10.1039/C4DT01239A
Schröder, U., Wadhawan, J. D., Compton, R. G., Marken, F., Suarez, P. A. Z., Consorti, C. S., et al. (2000). Water-induced accelerated ion diffusion: voltammetric studies in 1-methyl-3-[2,6-(S)-dimethylocten-2-yl]imidazolium tetrafluoroborate, 1-butyl-3-methylimidazolium tetrafluoroborate and hexafluorophosphate ionic liquids. J. New J. Chem. 24, 1009–1015. doi: 10.1039/b007172m
Simons, T. J., Bayley, P. M., Zhang, Z., Howlett, P. C., MacFarlane, D. R., Madsen, L. A., et al. (2014). Influence of Zn2+ and water on the transport properties of a pyrrolidinium dicyanamide ionic liquid. J. Phys. Chem. B 118, 4895–4905. doi: 10.1021/jp501665g
Smith, J. A., Webber, G. B., Warr, G. G., and Atkin, R. (2013). Rheology of protic ionic liquids and their mixtures. J. Phys. Chem. B 117, 13930–13935. doi: 10.1021/jp407715e
Tao, G. H., Guo, Y., Joo, Y. H., Twamley, B., and Shreeve, J. M. (2008). Energetic nitrogen-rich salts and ionic liquids: 5-aminotetrazole (AT) as a weak acid. J. Mater. Chem. 18, 5524–5530. doi: 10.1039/b811506k
Tao, G. H., Tang, M., He, L., Ji, S. P., Nie, F. D., and Huang, M. (2012). Synthesis, structure and property of 5-aminotetrazolate room-temperature ionic liquids. Eur. J. Inorg. Chem. 2012, 3070–3078. doi: 10.1002/ejic.201200065
Ueno, K., Tokuda, H., and Watanabe, M. (2010). Ionicity in ionic liquids: correlation with ionic structure and physicochemical properties. Phys. Chem. Chem. Phys. 12, 1649–1658. doi: 10.1039/b921462n
Wicelinski, S. P., Gale, R. J., and Wilkes, J. S. (1987). Low temperature chlorogallate molten salt systems. J. Electrochem. Soc. 134, 262–263. doi: 10.1149/1.2100425
Wieszczycka, K., Wojciechowska, A., Krupa, M., and Kordala-Markiewicz, R. (2013). Quaternary pyridinium ketoximes as zinc extractants from chloride solutions. J. Chem. Eng. Data 58, 3207–3215. doi: 10.1021/je400646z
Xu, W., Cooper, E. I., and Angell, C. A. (2003). Ionic liquids: ion mobilities, glass temperatures, and fragilities. J. Phys. Chem. B 107, 6170–6178. doi: 10.1021/jp0275894
Yin, P., Zhang, Q. H., and Shreeve, J. M. (2016). Dancing with energetic nitrogen atoms: versatile N-functionalization strategies for N-heterocyclic frameworks in high energy density materials. Acc. Chem. Res. 49, 4–16. doi: 10.1021/acs.accounts.5b00477
Yoshida, Y., Baba, O., Larriba, C., and Saito, G. (2007). Imidazolium-based ionic liquids formed with dicyanamide anion: influence of cationic structure on ionic conductivity. J. Phys. Chem. B 111, 12204–12210. doi: 10.1021/jp0745236
Zhang, Y., Shi, C. J., Brennecke, J. F., and Maginn, E. J. (2014). Refined method for predicting electrochemical windows of ionic liquids and experimental validation studies. J. Phys. Chem. B 118, 6250–6255. doi: 10.1021/jp5034257
Keywords: dicyanamide ionic liquids, electrochemistry, viscosity, Walden plots, diffusion coefficients
Citation: Yuan W-L, Yang X, He L, Xue Y, Qin S and Tao G-H (2018) Viscosity, Conductivity, and Electrochemical Property of Dicyanamide Ionic Liquids. Front. Chem. 6:59. doi: 10.3389/fchem.2018.00059
Received: 05 October 2017; Accepted: 23 February 2018;
Published: 15 March 2018.
Edited by:
Sotiris Sotiropoulos, Aristotle University of Thessaloniki, GreeceReviewed by:
Evgeni B. Starikov, Karlsruhe Institute of Technology, Germany and Chalmers University of Technology, SwedenLinpo Yu, The University of Nottingham Ningbo China, China
Vedagiri Lakshminarayanan, Raman Research Institute, India
Copyright © 2018 Yuan, Yang, He, Xue, Qin and Tao. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ling He, bGhlQHNjdS5lZHUuY24=
Guo-Hong Tao, dGFvZ2hAc2N1LmVkdS5jbg==
 Wen-Li Yuan
Wen-Li Yuan Guo-Hong Tao
Guo-Hong Tao