Progress of Research in Negative Thermal Expansion Materials: Paradigm Shift in the Control of Thermal Expansion

To meet strong demands for the control of thermal expansion necessary because of the advanced development of industrial technology, widely various giant negative thermal expansion (NTE) materials have been developed during the last decade. Discovery of large isotropic NTE in ZrW₂O₈ has greatly advanced research on NTE deriving from its characteristic crystal structure, which is now classified as conventional NTE. Materials classified in this category have increased rapidly. In addition to development of conventional NTE materials, remarkable progress has been made in phase-transition-type NTE materials using a phase transition accompanied by volume contraction upon heating. These giant NTE materials have brought a paradigm shift in the control of thermal expansion. This report classifies and reviews mechanisms and materials of NTE to suggest means of improving their functionality and of developing new materials. A subsequent summary presents some recent activities related to how these giant NTE materials are used as practical thermal expansion compensators, with some examples of composites containing these NTE materials.

Introduction

Control of thermal expansion, an urgent demand in modern industrial technology, is making remarkable progress. Even a minute change of 10⁻⁵ in linear distortion fatally degrades the performance of high-precision devices and instruments. Furthermore, for a device comprising multiple materials, mismatched thermal expansion between the constituents themselves can cause severe damage such as exfoliation of interfaces and breakage of wires. In addition to work in fields that have traditionally avoided the adverse influence of thermal expansion such as optical instruments and precise machining equipment, control of thermal expansion has been strongly sought in recent years for advanced electronics such as power semiconductor devices, thermoelectric conversion systems, and fuel cells. Difficulties attributable to thermal expansion control are universal and are difficult to resolve.

The core technology of thermal expansion control is negative thermal expansion (NTE) materials: substances that contract when heated (Chu et al., 1987; Sleight, 1998; Evans, 1999; Barrera et al., 2005; Lind, 2012; Takenaka, 2012; Chen et al., 2015). After discovery of the large isotropic NTE of ZrW₂O₈ in 1996, for which the coefficient of linear thermal expansion α_L (subscript L signifying “linear”) reaches −9 × 10⁻⁶ K⁻¹ (Mary et al., 1996), the successive discovery of giant NTE materials has encouraged remarkable progress of research in this field, particularly during the last decade. Such development has brought a paradigm shift for the control of thermal expansion. For further improvement of the NTE functions and for the development of new materials, the achievements of the last two decades in this field are summarized briefly, particularly addressing recently discovered giant NTE materials (Figure 1).

FIGURE 1

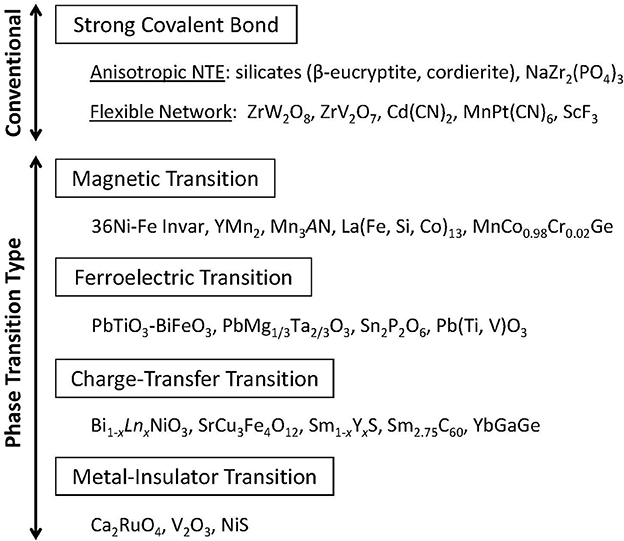
Figure 1. Classification of negative thermal expansion materials. Materials are divisible into two categories: conventional and phase-transition-type materials.

Positive and Negative Thermal Expansion

Thermal Expansion of Solids

The origin of thermal expansion of solids can be summarized briefly (Cochran, 1973). One might consider atoms connected together by springs as a model of solids, but these springs are anharmonic and do not exactly and simply obey Hooke's law. The atoms are prevented from becoming extremely close to one another because of Pauli's exclusion principle. As a result, excursions to longer interatomic distances occur more readily than those to shorter interatomic distances. Consequently, the average interatomic distance increases concomitantly with increasing temperature T. More intuitively, one can generally infer from Pauli's exclusion principle that as the temperature rises and the thermal vibration of an atom increases, it tries to maintain its distance from other atoms to avoid mutual collision. This increasing distance with vibration explains thermal expansion.

Conventional NTE Materials

In stark contrast to ordinary materials, some materials contract upon heating. Some examples are those of a silicon oxide family including β-eucryptite (LiAlSiO₄) and cordierite (Mg₂Al₂Si₅O₁₈), which were reported in the 1950s (Gillery and Bush, 1959). These silicates have strong covalent bonds such as Al–O and Si–O bonds, and not so strong ionic bonds such as Li–O and Mg–O bonds. The ionic bonds expand on heating, resulting in the expansion of two-dimensional sheets in β-eucryptite, for example. Thermal expansion of these ionic bonds pulls the two-dimensional sheets closer together because these two-dimensional sheets are joined by strong covalent bonds that do not expand when heated (Figure 2). For β-eucryptite with a hexagonal crystal lattice, on warming from 293 K to 1073 K, the in-plane (a axis) direction in which the Li–O bond is dominant expands 0.62%, whereas the out-of-plane (c axis) direction, in which the Si–O bond is dominant, contracts 1.39%. This thermal distortion causes unit-cell volume contraction of 0.15%. From another viewpoint, open spaces are filled by the thermal distortion of strong covalent bonds. This concept is exemplified more clearly in the open-framework or flexible-network materials described next. Readers might doubt that the NTE of β-eucryptite is much larger. Details of the discrepancy between the unit-cell volumetric NTE and the bulk NTE are discussed in Chapter 4.

FIGURE 2

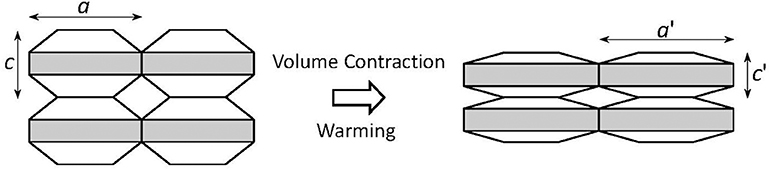
Figure 2. Schematic of anisotropic thermal expansion in the silicates. As the shaded layers undergo thermal expansion, they are pulled closer together in the direction perpendicular to the layer, which causes significant thermal contraction in this direction and yields slight net volumetric thermal contraction.

Flexible-network materials are a well-known family of NTE materials that includes ZrW₂O₈ and vanadates and phosphates of certain kinds (Mary et al., 1996; Pryde et al., 1996; Evans et al., 1997). This network consists of rigid units connected by soft linkages. The rigid units are formed by strong covalent bonds. For ZrW₂O₈, W–O covalent bonds are strong. Therefore WO₄ units are rigid. They do not expand on heating. By contrast, although the W–O and Zr–O bond distances are not changed, the Zr–O–W linkages are soft. Transverse oxygen displacement is induced easily on heating. These displacements consume open spaces in the crystal structure, resulting in volumetric NTE (Figure 3). Different from the silicates, anisotropic lattice thermal expansion is unimportant. The volume change related to NTE is much greater. In fact, ZrW₂O₈ has attracted great attention because of its large and isotropic NTE of α_L = −9 × 10⁻⁶ K⁻¹ (Mary et al., 1996). NTE appears at the whole T range below 1443 K. The total volume change related to NTE, ΔV/V, reaches 2.7% (Evans, 1999).

FIGURE 3

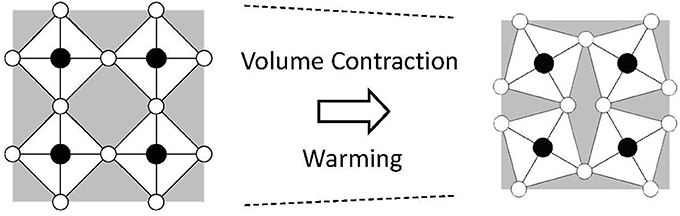
Figure 3. Schematic of negative thermal expansion in a flexible network. A vibrational mode consuming an open space in a crystal lattice is thermally excited, which yields net volumetric thermal contraction.

Negative thermal expansion that is explainable from the concept that strong atomic bonds and thermally induced deformation fill open spaces in the crystal lattice explains conventional NTE materials (Figure 1), which include widely diverse materials. In addition to cyanides (Chapman et al., 2006; Phillips et al., 2008), the fluoride group (Greve et al., 2010; Attfield, 2011; Chatterji et al., 2011; Chen et al., 2017), such as ScF₃ and ZnF₂, has attracted attention recently. Particularly, Cd(CN)₂·xCCl₄ shows large NTE of α_L = −34 × 10⁻⁶ K⁻¹ and ΔV/V = 2.1% at T = 175–375 K (Phillips et al., 2008).

At present, most industrial thermal-expansion compensators, including β-eucryptite, belong to the group of conventional type oxides. This type of NTE has a structural origin for its phenomena. Therefore, NTE appears in almost the entire T range, which is extremely important industrially. However, when discussing practically used materials, their NTE magnitude, at most α_L = −7 × 10⁻⁶ K⁻¹, is not large from today's perspective. Because the coexistence of strong and not strong chemical bonds is fundamentally important for conventional NTE, low thermal conductivity and low stiffness are unavoidable in these materials. Low thermal conductivity and low stiffness are weak points even for some phase-transition-type NTE materials described in the next chapter. Diligent efforts are continuing toward overcoming them. For example, high thermal conductivity is indispensable for rapid heat dissipation of devices. Development of NTE materials with high thermal conductivity is desired.

Phase-Transition Type NTE Materials

Various attempts have been made to overcome the shortcomings of the conventional NTE materials presented in the preceding chapter. The current trend of NTE material development is to use the phase transition accompanied by volume contraction upon heating. The effectiveness of this approach was recognized widely by discovery of the giant NTE of α_L = −25 × 10⁻⁶ K⁻¹ in antiferromagnetic antiperovskite Mn₃Zn_1−xGe_xN, which uses magnetovolume effects (Takenaka and Takagi, 2005). The giant NTE of manganese nitride strongly influenced subsequent NTE research, leading to the discovery of many NTE materials using magnetic, ferroelectric, charge-transfer, and metal–insulator phase transitions. The phase-transition type NTE concept became dominant in the field (Figure 1). The relation between phase transition and NTE might not be a modern concept because NTE accompanying the magnetic transition (Fe-Pt Invar alloy, Wasserman, 1990) and the ferroelectric transition (PbTiO₃, Shirane and Hoshino, 1951) has been known for a long time. The novelty of the present method is the modification of the properties of “mother” materials showing a phase transition (in many cases, first-order phase transition), intentionally using chemical approaches such as element substitution (Figure 4).

FIGURE 4

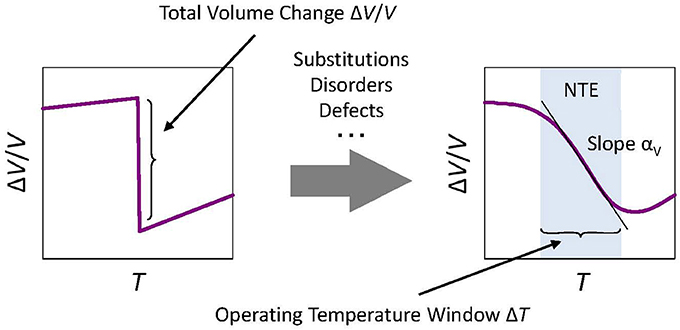
Figure 4. Concept of total volume change ΔV/V related to negative thermal expansion (NTE). In the case of phase-transition-type NTE materials, “slope” α_V (coefficient of volumetric thermal expansion) shares a tradeoff relation with the width of the operating-temperature window ΔT, roughly described as ΔV/V~|α_V|ΔT. As an isotropic material, a coefficient of linear thermal expansion α_L is related to α_V as α_V = 3α_L. Therefore, coefficients α_V and α_L are not intrinsic for such phase-transition-type materials. Instead, the total volume change ΔV/V is the intrinsic index indicating the potential of NTE.

Specifications of the recently discovered giant NTE materials are presented in Table 1. Phase-transition type materials have an operating temperature that is limited to several tens to 100 K around the phase transition, but they have a negative α_L that is several times to 10 times larger than those of conventional type materials. Although a wide operating temperature window ΔT is generally suitable for practical applications, limited ΔT presents no difficulty in many cases, such as precision equipment that is expected to operate at room temperatures. Bi_0.95La_0.05NiO₃ exhibits large negative α_L of −82 × 10⁻⁶ K⁻¹ (Azuma et al., 2015), which is comparable to the magnitude of positive α_L of epoxy resin, although the operating-temperature window ΔT is not so wide (60 K). Despite that operating temperature window limitation, it is of great importance that it suppresses the thermal expansion of plastics, which has heretofore been difficult.

TABLE 1

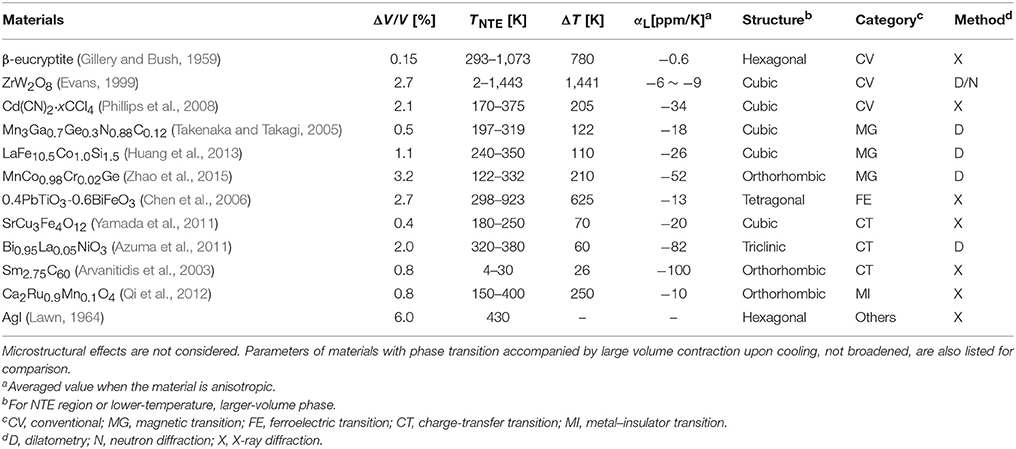
Table 1. Parameters related to crystallographic negative thermal expansion for prototypical materials.

For phase-transition-type NTE materials, a certain mechanism causes excessive shrinkage that can overcome positive lattice thermal expansion. The mechanisms of prototypical phase-transition-type NTE are described in this chapter. It is noteworthy that the mode of classification, including the conventional type, is not absolute. For example, ferroelectric transition and charge-transfer transition have a common point of charge disproportionation. Other phase transitions such as structural phase transition are often coupled with the magnetic transition.

It is noteworthy that slope α_L presents a tradeoff relation with the width of operating-temperature window ΔT in the case of phase-transition-type NTE materials (Figure 4). The total volume change ΔV/V is a value that is peculiar to the substance. It is difficult to increase it artificially. As a result, the wider the operating-temperature window ΔT becomes, the smaller the negative slope α_L becomes. For isotropic materials, we obtain the simple relation of ΔV/V = 3α_LΔT. Therefore, slope α_L is not intrinsic for such phase-transition-type materials. Instead, ΔV/V is the intrinsic and the most important index indicating the potential of NTE. The word “giant” is customarily used in the field, but no clear definition exists. One important turning point was the discovery of ZrW₂O₈ in 1996, and a material that surpasses it by the negative coefficient of linear thermal expansion and/or the total volume change related to NTE: a so-called giant NTE material.

Magnetic Transition

The magnetovolume effect is a phenomenon by which the volume changes according to the amplitude of the magnetic moment in itinerant systems. The relative volume change attributable to magnetism is known as the spontaneous volume magnetostriction ω_s. Generally speaking, less-itinerant electrons are necessary for magnetism. Electronic spins are aligned via the exchange interaction. That exchange interaction does not work well when electrons are itinerant. Volume expansion decreases the overlap of electronic orbitals and makes electrons less itinerant. This effect is explainable by the electronic theory of solids as follows: volume expansion suppresses the bandwidth and condenses the density of states near the Fermi level E_F, which is helpful for magnetism (Figure 5). Therefore, if possible, the system expands the volume to assist magnetism when the magnetic order sets in. This expansion is the magnetovolume effect, which is intimately related with the origin of magnetism in metals. Therefore, it has persisted as a central topic in the field of condensed-matter physics.

FIGURE 5

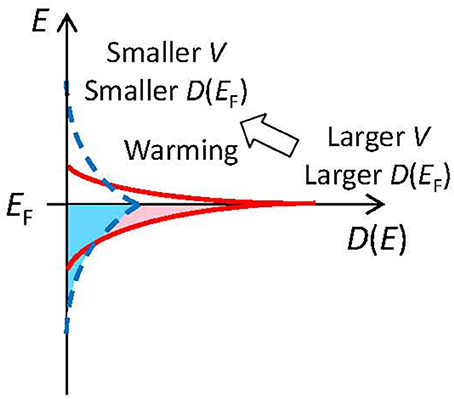
Figure 5. Relation between volume and density of states at the Fermi level D(E_F) (schematic). Volume expansion shrinks the electronic band width and therefore enhances D(E_F), which is favorable for the magnetic state. It also strengthens the electronic repulsion effects.

The materials classified into this category include 36Ni-Fe alloy (Invar alloy, which has low thermal expansion rather than negative thermal expansion) (Wasserman, 1990), Fe₃Pt (Sumiyama et al., 1979), YMn₂ (Nakamura et al., 1988) in the past, and Mn₃AN (where A is a transition metal or semiconducting elements, Takenaka and Takagi, 2005; Hamada and Takenaka, 2011; Wang et al., 2012; Takenaka et al., 2014), La(Fe, Si, Co)₁₃ (Fujita et al., 2001; Huang et al., 2013), and MnCo_0.98Cr_0.02Ge (Zhao et al., 2015) in recent years. Mass production technology developed in 2012 for manganese nitrides has made them commercially available (Smartec^®; Kojundo Chemical Lab. Co. Ltd., Japan, Kawahara et al., 2017).

The low thermal expansion of 36Ni-Fe Invar alloy was reportedly explained by the difference in atomic radius in the early stages of research. The concept of the 2γ model (Weiss, 1963) is that upon heating, the spin configuration of Fe changes gradually from a high-spin state with a larger radius to a low-spin state with a smaller radius. A controversy has long persisted (van Schilfgaarde et al., 1999) between this atomic picture and the itinerant-electron picture described in earlier paragraphs, which emphasizes the contribution from electronic density anomaly near E_F (Wohlfarth, 1977; Moriya and Usami, 1980). Although details are not included herein, metallic electronic images are regarded as superior in the sense that they can universally explain the magnetovolume effect of various materials, not merely Invar alloys. Nevertheless, differences in atomic radius between high-spin and low-spin states can play an important role in volume change in real materials such as cobalt oxides (Burley et al., 2004). The 2γ model, which still holds importance as a possible mechanism of NTE, is closely related to NTE caused by charge transfer in the sense that NTE is induced by a change in the atomic radius.

Negative thermal expansion is reported also for localized-moment magnets of certain kinds. Actually, NTE is known to appear in the T range of several tens of degrees on the high T side of the magnetic transition with a compound having a certain spinel or breathing pyrochlore structure (Hemberger et al., 2007; Okamoto et al., 2018; Pokharel et al., 2018). In these materials, NTE disappears below the critical temperature at which the magnetic long-range order is formed. From the localized-moment picture, the magnetovolume effect is attributed to the peculiar volume dependence of the magnetic exchange interaction J, ∂J/∂ω (ω = ΔV/V) (Hausch, 1973). The generalized framework extended to the strain derivative of J is also discussed (Filippetti and Hill, 2000). The argument based on the Bethe–Slater curve of single J discussed previously is too naive to explain the diverse phenomena of real materials. However, if there exist multiple (e.g., ferromagnetic and antiferromagnetic) J and competition between them, then the once discarded localized-moment picture might be revived as worthy of consideration.

Ferroelectric Transition

Actually, NTE is widely known to appear in ferroelectric materials with charge disproportionation such as PbTiO₃ (Shirane and Hoshino, 1951), 0.4PbTiO₃-0.6BiFeO₃ (Chen et al., 2006), Sn₂P₂S₆ (Rong et al., 2016), and Pb(Ti,V)O₃ (Pan et al., 2017). From general consideration of the relation between valence and bond length, the averaged bond length in the charge disproportionate case is greater than the bond length in the charge uniform case (Evans, 1999, Figure 6). Atomic bonds are readily expanded, but they are difficult to shrink. We can regard that fact as representing a kind of anharmonicity of atomic bonds. It is noteworthy that anisotropy is fundamentally important for NTE materials of this type. Phenomenologically, dielectric polarization corresponds to volume change (Chen et al., 2015), similar to magnetic NTE materials in which magnetic moments are intimately related to the volume change, but their physical origin differs greatly.

FIGURE 6

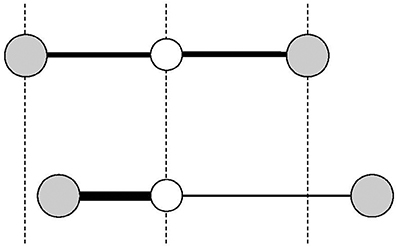
Figure 6. Schematic of negative thermal expansion in a ferroelectric material with charge disproportionation. When charge disproportionation occurs, because the higher-valence interatomic bond length does not shrink as much as the lower-valence one expands (Bottom), the bond length becomes longer than that of the averaged case (Upper).

Charge-Transfer Transition

When charge transfer occurs between the constituent elements, atoms with an increasing number of valence electrons become larger. On the other hand, those with a decreasing number of valence electrons become smaller. However, the change in the atomic radius varies according to the atomic species, electronic configuration, etc. In addition, the effect of the atomic radius on the crystal size depends on the atom's position in the crystal structure. If the contribution from atoms with a decreasing number of valence electrons upon heating is greater, then one can expect net NTE.

A famous example of charge-transfer-type NTE materials, bismuth-nickel oxides (Azuma et al., 2011, 2015), is discussed next. When these oxides are warmed, charges are transferred from Ni to Bi. Therefore, the atomic radius of Ni contracts and that of bismuth expands on warming, but the atomic radius of nickel dominates the lattice volume because the Ni–O octahedron dominates the lattice volume. For that reason, the net volumetric NTE occurs in the bismuth-nickel oxide. A similar mechanism functions for NTE of LaCu₃Fe₄O₁₂ (Yamada et al., 2011).

Negative thermal expansion is also induced by intra-atomic charge transfer that increases the 4f electron number with decreasing temperature. For example, Sm_1−xY_xS (Jayaraman et al., 1975; Alekseev et al., 2006), Sm_2.75C₆₀ (Arvanitidis et al., 2003), and YbGaGe (Salvador et al., 2003; Sleight, 2003) are known for negative or low thermal expansion by such a mechanism. In the case of Sm, two electronic configurations of (4f)⁵(5d)¹ and (4f)⁶ compete energetically, but the atomic radius is determined mainly by the 4f electron number. Therefore, NTE appears if the electrons are transferred from the 5d to the 4f orbitals with decreasing temperature.

Metal–Insulator Transition

An example in which the effect of electronic repulsion manifests as an apparent physical property is a Mott insulator (Mott, 1990). In transition metal compounds of a certain kind, the metallic state is often lost because of electronic correlations at low temperatures and the system becomes an insulating state. This transition is called a Mott transition. Generally, a Mott insulating state appears at the lower-T side. The volume of the low-T insulating phase is known to expand upon Mott transition for V₂O₃ (1.5%) (McWhan and Remeika, 1970) and NiS (1.8%) (Matoba et al., 1991). The mechanism of volume expansion in the insulating state might resemble a magnetovolume effect in the itinerant-electron magnets (Figure 5). It can be understood that volume expansion suppresses the bandwidth and that it therefore enhances electronic-correlation effects, which stabilizes the low-T Mott insulating state. Furthermore, Ca₂RuO₄ (Takenaka et al., 2017a) is classified into this category, as explained in the next chapter.

Other Factors

Some materials are also known to have volume of the low-T phase which becomes greater than that of the high-T phase with the phase transition because of mechanisms other than the four explained above. They are not understood so systematically as the four above, but they are suggestive for the development of new materials. They are therefore explained here. Silver iodide, AgI (Lawn, 1964; Kumar et al., 2006), which is known as a superionic conductor, undergoes a structural phase transition from β and γ phases with larger volume at low temperatures to α phase and smaller volume at high temperatures near 400 K. The volume change is known to reach 5%. The fact that the relation between NTE and ionic conductivity is discussed (Sleight, 1998) also for the famous NTE material β-eucryptite is suggestive of its importance for future development.

Related to a structural phase transition, certain martensitic transformations accompany volume expansion on cooling. For example, MnCoGe is known to expand by 3.9% in the martensitic transformation from high-T hexagonal phase to low-T orthorhombic phase at around 370 K (Johnson, 1975). Actually, MnCo_0.98Cr_0.02Ge, with one of the largest total volume change related to NTE found to date, belongs to the same family and shows the same martensitic transformation simultaneously with the magnetic transition (Zhao et al., 2015). Correlation between magnetism and structure in these materials is an interesting subject that has yet to be explored (Kanomata et al., 1995).

Although the relation between NTE and superconductivity is not well understood, Ca_0.85La_0.15Fe₂As₂ with the superconducting transition temperature of 43 K exhibits a marked NTE of α_L = −16 × 10⁻⁶ K⁻¹ and ΔV/V = 1.4% at almost all temperatures below 300 K (Robello et al., 2012). Orbital ordering is regarded as involving the Mott transition in Ca₂RuO₄ (Mizokawa et al., 2001; Qi et al., 2010) and, although weak, NTE appears just above the Verwey transition (ca. 110 K) in Fe₃O₄ (Wright et al., 2000). These results suggest that an orbital-ordering transition might be a universal mechanism of NTE.

Mechanism of Broadening Volume Change

From the viewpoint of the mechanism of how the sharp volume change accompanying the first-order phase transition becomes a gradual change with temperature, the phase-transition-type NTE materials are broadly divisible into two categories: “phase-separation” type and “second-order-transition” type. In the former category, which includes bismuth-nickel oxides (Azuma et al., 2011, 2015), the system separates into the larger-unit-cell L phase and the smaller-unit-cell S phase, while preserving the first-order phase transition. NTE is induced because the volume fraction of the L phase increases concomitantly with decreasing T. In the latter category, which includes magnetic NTE materials such as antiperovskite manganese nitrides (Takenaka and Takagi, 2005; Hamada and Takenaka, 2011; Wang et al., 2012; Takenaka et al., 2014), the phase transition changes from first-order-like to second-order-like. Negative thermal expansion of these materials is characterized by a gradual increase in the unit-cell volume of a single phase with decreasing T without phase separation. For manganese nitrides, a detailed neutron diffraction study (Iikubo et al., 2008) demonstrated that the evolution of the amplitude of the magnetic moment is in one-to-one correspondence with the volume increase due to NTE. For the phase-transition-type materials, the mechanism of broadening the volume change is a key issue dominating the operating-temperatures of NTE. To elucidate the broadening mechanism, a certain kind of diffraction study and microscopic observations are required in addition to dilatometry.

Anisotropic Thermal Expansion and Microstructural Effects

Negative thermal expansion discussed in the former chapters is associated with NTE of the crystallographic unit cell. For these materials, NTE of the unit cell found using a crystallographic technique such as x-ray diffraction and NTE of the bulk measured using a dilatometric technique are fundamentally equal. However, in some cases, the crystallographic NTE and the dilatometric NTE do not coincide. Actually, β-eucryptite, which is a representative practical thermal-expansion compensator, is one example. The colossal NTE measured in the sintered body of layered ruthenium oxide Ca₂RuO₄ (Takenaka et al., 2017a) reaffirmed this discrepancy as an important subject in NTE research (Figure 7). The total volume change ΔV/V related to NTE reaches a maximum of 6.7%, exceeding twice the former maximum (3.2%) obtained with MnCo_0.98Cr_0.02Ge (Zhao et al., 2015). Despite the wide operating-temperature window of 135–345 K (ΔT = 210 K), α_L shows a remarkable size of −115 × 10⁻⁶ K⁻¹ because of this large total volume change.

FIGURE 7

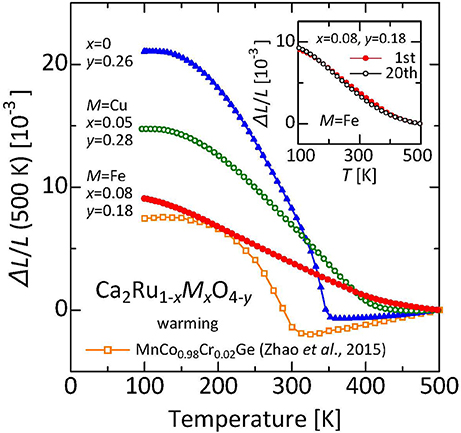
Figure 7. Linear thermal expansion of Ca₂Ru_1−xM_xO_4−y (M = Fe, Cu). Reference temperature: 500 K. Inset: Linear thermal expansion ΔL/L of Ca₂Ru_0.92Fe_0.08O_3.82 before and after 20 iterations of thermal cycling (reference temperature: 500 K). Data related to the warming process were collected using a laser interference dilatometer. Referred from earlier reports (Takenaka et al., 2017a,b). For comparison, data of MnCo_0.98Cr_0.02Ge (Zhao et al., 2015) are also shown.

Originally, Ca₂RuO₄ was known for unit-cell volume expansion of about 1% at the onset of high-T metallic to low-T insulating phase transition at 360 K (Friedt et al., 2001; Qi et al., 2012). Therefore, Ca₂RuO₄ is classified as the metal–insulator transition category of NTE described in the preceding chapter. Even in our sample showing a huge bulk NTE, during warming from 150 to 340 K, the c axis expands by 4.6%, whereas the a axis and the b axis shrink respectively by 0.6 and 5.0%. As a result, the unit cell shrinks by 1%. The anisotropic thermal expansion of this unit cell and the fairly large NTE with volume change of ΔV/V = 1% are regarded as attributable to the Mott transition coupled with electronic orbital ordering, although the details remain to be explored.

The colossal NTE of Ca₂RuO₄ ceramics is proposed as explainable by anisotropic thermal deformation of the crystal grain which fills in the volume of pores that are contained in the sintered body (Figure 8). Such deformation is trivial in the field of ceramics. Moreover, it is not limited to β-eucryptite, for example, also known as MgTi₂O₅ (Kuszyk and Bradt, 1973; Ohya et al., 1987; Yamai and Ota, 1993). In most cases, however, it is a “one-time” phenomenon that induces microcracks, which is useless as a practical thermal-expansion compensator. One well-known exception is β-eucryptite, the practical use of which was achieved by overcoming the difficulty of advanced control of microcracks (Pelletant et al., 2012; Benavente et al., 2016). Although the NTE characteristics of β-eucryptite vary according to fabrication conditions, the total volume change of the bulk specimen (1.7%) reaches 10 times that of the unit cell (0.15%); also, α_L is −7 × 10⁻⁶ K⁻¹.

FIGURE 8

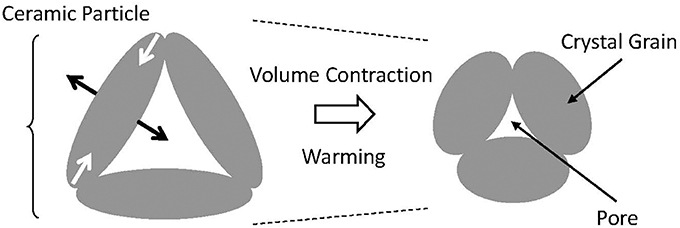
Figure 8. Schematic explanation ΔL/L of microstructural effect for bulk negative thermal expansion. The ceramic body consists of crystal grains with anisotropic thermal expansion and pores. When the temperature increases, the crystal grain expands in one direction and contracts in a perpendicular direction. If there exists open space in the direction in which the crystal grain expands, then this ceramic body contracts.

The ruthenium oxides are characterized by rather low onset temperatures of anisotropic thermal expansion of the unit cell, which is about 500 K. For many other materials including β-eucryptite and MgTi₂O₅, the onset temperature is close to the sintering temperature, typically over 1,300 K. Therefore, the inner stress accumulates greatly during cooling to room temperature. Compared with those, the accumulated inner stresses are expected to be much smaller for the ruthenates. Indeed, the linear thermal expansion ΔL(T)/L of Ca₂Ru_0.92Fe_0.08O_3.82 is reproducible after 20 repetitions of thermal cycling of 300 K → 500 K → 300 K (inset of Figure 7), which suggests that possible degradation of the characteristics because of the thermal history is avoidable. Recently reported theoretical calculations indicate that the microstructural effects without cracks can reproduce the gigantic NTE observed in the ruthenate sintered body (Takezawa et al., 2018). Enhancement of NTE in the ruthenates occurs at a scale of 10 times that of β-eucryptite. Examples for which the material structure is deeply involved in the bulk function of NTE do not exist among recently discovered NTE materials. The concept of microstructural effects provides a strategy for realizing giant NTE. Control of thermal expansion using specific characteristics of materials, particularly in a negative α region, are highly limited in an operating temperature and/or a magnitude of α because of the severe constraints of available materials. To overcome these difficulties, designated structures consisting of two materials having different (positive) thermal expansions and voids are proposed as an artificial materials showing NTE (Takezawa et al., 2015; Wang et al., 2016). The present result is expected to stimulate those activities as a “natural” counterpart of the artificial structures. Structures composed of Structures composed of crystal grains exhibiting anisotropic thermal expansion and voids are expected to be important subjects of future NTE research.

Composites Containing Giant NTE Materials

Forming a composite using a NTE material as a thermal-expansion compensator is an effective method of controlling the thermal expansion of a material. Many commercial materials exist such as zero-expansion glass used for precision optical equipment and a zero-expansion ceramic material used for semiconductor device manufacturing. Many earlier studies have examined composites containing NTE materials, particularly β-eucryptite (Xue et al., 2010; Borrell et al., 2012) and ZrW₂O₈ (Holzer and Dunand, 1999; Matsumoto et al., 2003; Sullivan and Lukehart, 2005; Lind et al., 2011), as thermal expansion compensating fillers. Regarding phase-transition-type giant NTE materials, composites containing Mn₃AN (Ding et al., 2011; Takenaka et al., 2012, 2015; Takenaka and Ichigo, 2014; Lin et al., 2017), BiNi_1−xFe_xO₃ (Nabetani et al., 2015), La(Fe, Si, Co)₁₃ (Shan et al., 2015), and Ca₂Ru_0.92Fe_0.08O_3.82 (Takenaka et al., 2017b) have been reported. Because their chemical reactivity is higher at high temperatures than those of conventional NTE materials, phase-transition-type NTE materials are difficult to use as thermal expansion compensating filler, particularly in cases of metal matrix composites (MMCs). However, powder metallurgy, which enables us to form MMCs at lower temperatures and in a shorter time than when using the conventional method, produced MMCs containing manganese nitrides (Ding et al., 2011; Takenaka et al., 2012, 2015). Some concern arose about difficulties arising from a large thermal expansion difference at the interface between the matrix and the gigantic NTE material. Additional research on the interfaces is expected to be indispensable for the development of industrial materials with high reliability, although this difficulty has not arisen for some composites at present (Takenaka and Ichigo, 2014). Here, plastic matrix composites (PMCs) containing manganese nitrides and ruthenium oxides are discussed.

Generally, the operating temperatures of phase-transition-type NTE materials are not high (ca. 600 K at highest). Therefore, plastics for which the operating temperature range and composite processing temperature are low are indeed the most compatible matrices. In electronic devices, plastics are used in various components such as printed circuit boards, sealing materials, and substrate-chip bonding films. As miniaturization and high integration of integrated circuits progress, problems originating from thermal expansion mismatch between these plastics and inorganic materials such as semiconductors have become more severe. To suppress the large thermal expansion of plastics, conventional thermal expansion compensators such as silica are insufficient. The use of large NTE of phase-transition-type NTE materials is indispensable. Furthermore, control of thermal expansion at a local region at the micrometer level in an integrated circuit, such as underfill of a three-dimensional integrated circuit (3DIC) is strongly demanded (Kino et al., 2017). It is technically important to miniaturize the particle diameter of a giant NTE material to submicrometer size, or less (Lin et al., 2016; Yang et al., 2016).

Before presenting scientific arguments, to summarize briefly how to evaluate the thermal expansion of composites, the author presents discussion of a simple case in which particles of an isotropic reinforcement are dispersed uniformly in an isotropic matrix for analyzing PMCs containing thermal expansion compensating particles. In that case, thermal expansion of the composite falls between the two bounds: The rule of mixture (ROM) and Turner's model (Takenaka, 2012). A bound, ROM, is given, assuming that thermally induced stress is uniform throughout a composite, which is equivalent to saying that the matrix and the filler exhibit their own thermal expansion independently. Consequently, the thermal expansion of a composite is given as the volume-weighted sum of contributions from the matrix and the dispersed filler.

$\begin{array}{ll}{\alpha }_{\text{c}}={\mathit{\text{v}}}_{\text{m}}{\alpha }_{\text{m}}+{\mathit{\text{v}}}_{\text{t}}{\alpha }_{\text{t}}& (1)\end{array}$

Another bound, that of Turner's model, is given as the approximation that strain is uniform throughout a composite as a result of elastic interactions between the matrix and the filler at the interfaces. It gives the following estimation.

$\begin{array}{ll}{\alpha }_{\text{c}}=({\mathit{\text{v}}}_{\text{m}}{\mathit{\text{E}}}_{\text{m}}{\alpha }_{\text{m}}+{\mathit{\text{v}}}_{\text{t}}{\mathit{\text{E}}}_{\text{t}}{\alpha }_{\text{t}})/({\mathit{\text{v}}}_{\text{m}}{\mathit{\text{E}}}_{\text{m}}+{\mathit{\text{v}}}_{\text{t}}{\mathit{\text{E}}}_{\text{t}})& (2)\end{array}$

In the equations above, subscripts c, m, and t respectively denote a composite, matrix, and thermal-expansion compensator. Also, v_m and v_t respectively represent the volume fractions of the matrix and thermal-expansion compensator; v_m + v_t = 1. E represents Young's modulus. In Equation (2), the constituent with the larger elastic modulus contributes more to α_c beyond the volume fraction. In the case of PMCs containing NTE filler, the relations α_m > α_t and E_m < E_t are always fulfilled. Therefore, Equation (1), ROM, gives the upper bound; Equation (2), Turner's model, gives the lower bound for α_c.

Figure 9 displays a plot of the ΔL(T)/L experimental values along with curves calculated assuming ROM and Turner's moles for 38 vol%-Mn_3.25Zn_0.5Sn_0.25N/polyamide-imide composite (Takenaka and Ichigo, 2014). The typical grain size of the nitride filler is 30–50 μm. This nitride thermal expansion compensating filler shows a huge NTE of α_L = −45 × 10⁻⁶ K⁻¹ at T = 305–340 K, resulting in NTE (α_L = −3 × 10⁻⁶ K⁻¹ at T = 315–327 K) for the composite. Displacement in ΔL/L is less than 160 ppm at T = 303–333 K, equivalent to the averaged α_L of 5.3 × 10⁻⁶ K⁻¹. The obtained ΔL(T)/L of the composite is between the ROM and Turner's estimates. This result reflects much larger E of the nitride filler (200 GPa, Nakamura et al., 2009) than the matrix (5 GPa, Reinecke et al., 1996), demonstrating the excellent thermal expansion compensating capability of the manganese nitride.

FIGURE 9

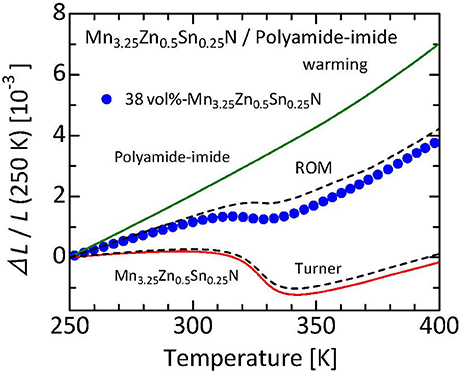
Figure 9. Linear thermal expansion ΔL/L of 38 vol%-Mn_3.25Zn_0.5Sn_0.25N/polyamide-imide composite. Reference temperature: 250 K. Data were collected on a warming process using a laser interference dilatometer. Curves calculated by assuming the ROM and Turner's model are also displayed for comparison. Referred from an earlier report (Takenaka and Ichigo, 2014).

The results of bis-phenol epoxy resin matrix composite in which the ruthenium oxide particles are dispersed (Takenaka et al., 2017b) can be discussed next. The filler is Ca₂Ru_0.92Fe_0.08O_3.82. Although Fe doping somewhat suppresses negative α_L to −28 × 10⁻⁶ K⁻¹, the operating temperature window is expanded to 100–500 K. Furthermore, T-linearity of ΔL(T)/L is improved. Thermal expansion exhibits almost T-linear behavior, even near the lowest temperature used for the present dilatometry measurements. Therefore, NTE apparently continues down to the lower temperature. In that case, the total volume change ΔV/V might become greater than the present estimate of 2.8% (T = 100–500 K). Unfortunately, thermal expansion below 100 K was not measured successfully because of exfoliation of the strain gage. Nevertheless, the composite exhibits low thermal expansion down to 4 K, suggesting NTE of the ruthenate below 100 K.

Figure 10A presents a plot of the ΔL(T)/L experimental values for the 56 vol%- Ca₂Ru_0.92Fe_0.08O_3.82/bis-phenol epoxy resin composite (Takenaka et al., 2017b). For the epoxy resin and the composite, ΔL(T)/L was measured down to 5 K using a strain gage. Figure 10B depicts an SEM image of the composite. Dark-gray and light-gray regions respectively represent the epoxy-resin matrix and the ruthenate filler. The ruthenate filler particles, with average size of 20–30 μm, are dispersed uniformly. Each particle is regarded as consisting of smaller crystal grains (ca. 80vol%) and pores (ca. 20vol%). Here, Young's modulus of the epoxy resin is 3.2 GPa (Nabetani et al., 2015). Young's modulus of the ruthenate ceramics particle is estimated as 100 GPa considering the Young's modulus of the related substance Sr₂RuO₄ of 160 GPa (Hao et al., 2014) and sample porosity of 0.2 (Wagh et al., 1991). The obtained linear thermal expansion of the composite falls between Equations (1, 2), similar to reports of many earlier studies (Sullivan and Lukehart, 2005; Takenaka and Ichigo, 2014; Nabetani et al., 2015). Therefore, the ruthenium oxide particles dispersed in the composite have sufficient stiffness and negative α_L. They suppress thermal expansion of the matrix effectively via elastic interactions at the interfaces.

FIGURE 10

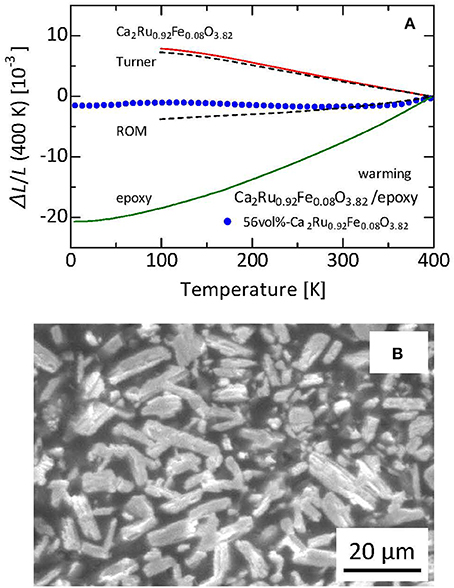
Figure 10. (A) Linear thermal expansion (a) and microscopic image (B) of 56 vol%-Ca₂Ru_0.92Fe_0.08O_3.82/epoxy composite. Reference temperature: 400 K. Curves calculated by assuming the ROM and Turner's model are also displayed for comparison. Reproduced from an earlier report (Takenaka et al., 2017b). Copyright (2017) The Japan Society of Applied Physics.

Concluding Remarks

Because of the phase transition accompanied by large volume contraction on heating, giant NTE beyond that of conventional materials has been realized. That achievement has enabled us to compensate the large thermal expansion of plastics, which has been difficult to date, although the operating temperature ranges of the accomplishments have remained limited. The conventional wisdom of materials science, which has held that “negative CTE cannot be so large,” has been rejected. Concepts and technologies related to thermal expansion control are about to change dramatically. One remarkable achievement in recent years is the huge NTE observed for ruthenium oxide sintered bodies. A structure comprising crystal grains exhibiting anisotropic thermal expansion and pores presents fertile ground for the development of new NTE materials. Today, thermal expansion adjustable composites are being fabricated using recently discovered giant NTE materials including the ruthenates.

Author Contributions

The author confirms being the sole contributor of this work and approved it for publication.

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The author is grateful to M. Azuma, Y. Okamoto, N, Katayama, A. Takezawa, and S. Mori for many fruitful discussions and to his students for their enthusiastic conduct of experiments. This work was partly supported by Grants-in-Aid for Scientific Research (Nos. 17H02763 and 18H01351) from MEXT, Japan and by Adaptable and Seamless Technology Transfer Program (A-STEP; No. AS2911907T) from JST, Japan.

References

Alekseev, P. A., Mignot, J.-M., Nefeodova, E. V., Nemkovski, K. S., Lazukov, V. N., Tiden, N. N., et al. (2006). Magnetic spectral response and lattice properties in mixed-valence Sm_1−xY_xS solid solutions studied with X-ray diffraction, X-ray absorption spectroscopy, and inelastic neutron scattering. Phys. Rev. B 74:035114. doi: 10.1103/PhysRevB.74.035114

CrossRef Full Text | Google Scholar

Arvanitidis, J., Papagelis, K., Margadonna, S., Prassides, K., and Fitch, A. N. (2003). Temperature-induced valence transition and associated lattice collapse in samarium fulleride. Nature 425, 599–602. doi: 10.1038/nature01994

PubMed Abstract | CrossRef Full Text | Google Scholar

Attfield, J. P. (2011). A fresh twist on shrinking materials. Nature 480, 465–466. doi: 10.1038/480465a

PubMed Abstract | CrossRef Full Text | Google Scholar

Azuma, M., Chen, W.-T., Seki, H., Czapski, M., Olga, S., Oka, K., et al. (2011). Colossal negative thermal expansion in BiNiO₃ induced by intermetallic charge transfer. Nat. Commun. 2, 347. doi: 10.1038/ncomms1361

PubMed Abstract | CrossRef Full Text | Google Scholar

Azuma, M., Oka, K., and Nabetani, K. (2015). Negative thermal expansion induced by intermetallic charge transfer. Sci. Technol. Adv. Mater. 16:034904. doi: 10.1088/1468-6996/16/3/034904

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrera, G. D., Bruno, J. A. O., Barron, T. H. K., and Allan, N. L. (2005). Negative thermal expansion. J. Phys. 17, R217–R252. doi: 10.1088/0953-8984/17/4/R03

CrossRef Full Text | Google Scholar

Benavente, R., Salvador, M. D., Martinez-Amesti, A., Fernandez, A., and Borrell, A. (2016). Effect of sintering technology in β-eucryptite ceramics: influence on fatigue life and effect of microcracks. Mater. Sci. Eng. A 651, 668–674. doi: 10.1016/j.msea.2015.11.013

CrossRef Full Text | Google Scholar

Borrell, A., Garcia-Moreno, O., Torrecillas, R., Garcia-Rocha, V., and Fernandez, A. (2012). Lithium aluminosilicate reinforced with carbon nanofiber and alumina for controlled-thermal-expansion materials. Sci. Technol. Adv. Mater. 13:015007. doi: 10.1088/1468-6996/13/1/015007

PubMed Abstract | CrossRef Full Text | Google Scholar

Burley, J. C., Mitchell, J. F., and Short, S. (2004). Competing electronic ground states in La_1−xSr_xCoO₃. Phys. Rev. B 69:054401. doi: 10.1103/PhysRevB.69.054401

CrossRef Full Text | Google Scholar

Chapman, K. W., Chupas, P. J., and Kepart, C. J. (2006). Compositional dependence of negative thermal expansion in the Prussian blue analogues M^IIPt^IV(CN)₆ (M = Mn, Fe, Co, Ni, Cu, Zn, Cd). J. Am. Chem. Soc. 128, 7009–7014. doi: 10.1021/ja060916r

PubMed Abstract | CrossRef Full Text | Google Scholar

Chatterji, T., Zbiri, M., and Hansen, T. C. (2011). Negative thermal expansion in ZnF₂. Appl. Phys. Lett. 98:181911. doi: 10.1063/1.3588414

CrossRef Full Text | Google Scholar

Chen, J., Gao, Q., Sanson, A., Jiang, X., Huang, Q., Carnera, A., et al. (2017). Tunable thermal expansion in framework materials through redox intercalation. Nat. Commun. 8:14441. doi: 10.1038/ncomms14441

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Hu, L., Deng, J. X., and Xing, X. R. (2015). Negative thermal expansion in functional materials: controllable thermal expansion by chemical modifications. Chem. Soc. Rev. 44, 3522–3567. doi: 10.1039/C4CS00461B

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Xing, X. R., Liu, G. R., Li, J. H., and Liu, Y. T. (2006). Structure and negative thermal expansion in the PbTiO₃-BiFeO₃ system. Appl. Phys. Lett. 89:101914. doi: 10.1063/1.2347279

CrossRef Full Text | Google Scholar

Chu, C. N., Saka, N., and Suh, N. P. (1987). Negative thermal expansion ceramics: a review. Mater. Sci. Eng. 95, 303–308. doi: 10.1016/0025-5416(87)90523-4

CrossRef Full Text | Google Scholar

Cochran, W. (1973). The Dynamics of Atoms in Crystals (Edward Arnold). London.

Google Scholar

Ding, L., Wang, C., Na, Y. Y., Chu, L. H., Yan, J., and Yan, J. (2011). Preparation and near zero thermal expansion property of Mn₃Cu_0.5A₀₅N/Cu (A = Ni, Sn) composites. Scripta Mater. 65, 687–690. doi: 10.1016/j.scriptamat.2011.07.008

CrossRef Full Text | Google Scholar

Evans, J. S. O. (1999). Negative thermal expansion materials. J. Chem. Dalton Trans. 3317–3326. doi: 10.1039/a904297k

CrossRef Full Text | Google Scholar

Evans, J. S. O., Mary, T. A., and Sleight, A. W. (1997). Negative thermal expansion in a large molybdate and tungstate family. J. Solid State Chem. 13, 580–583. doi: 10.1006/jssc.1997.7605

CrossRef Full Text | Google Scholar

Filippetti, A., and Hill, N. A. (2000). Magnetic stress as a driving force of structural disorders: the case of CrN. Phys. Rev. Lett. 85, 5166–5169. doi: 10.1103/PhysRevLett.85.5166

CrossRef Full Text | Google Scholar

Friedt, O., Braden, M., Andre, G., Adelmann, P., Nahatsuji, S., and Maeno, Y. (2001). Structural and magnetic aspects of the metal–insulator transition in Ca_2−xSr_xRuO₄. Phys. Rev. B 63:174432. doi: 10.1103/PhysRevB.63.174432

CrossRef Full Text | Google Scholar

Fujita, A., Fujieda, S., Fukamichi, K., Mitamura, H., and Goto, T. (2001). Itinerant-electron metamagnetic transition and large magnetovolume effects in La(Fe_xSi_1−x)₁₃ compounds. Phys. Rev. B 65:014410. doi: 10.1103/PhysRevB.65.014410

CrossRef Full Text | Google Scholar

Gillery, F. H., and Bush, E. A. (1959). Thermal contraction of β-eucryptite (Li₂O·Al₂O₃·2SiO₂) by X-ray and Dilatometer Methods. J. Am. Ceram. Soc. 42, 175–177. doi: 10.1111/j.1151-2916.1959.tb12942.x

CrossRef Full Text | Google Scholar

Greve, B. K., Martin, K. L., Lee, P. L., Chupas, P. J., Chapman, K. W., and Wilkinson, A. P. (2010). Pronounced negative thermal expansion from a simple structure: cubic ScF₃. J. Am. Chem. Soc. 132, 15496–15498. doi: 10.1021/ja106711v

CrossRef Full Text | Google Scholar

Hamada, T., and Takenaka, K. (2011). Giant negative thermal expansion in antiperovskite manganese nitrides. J. Appl. Phys. 109:07E309. doi: 10.1063/1.3540604

CrossRef Full Text | Google Scholar

Hao, X. P., Cui, H. L., Lv, Z. L., and Ji, G. F. (2014). Electronic and elastic properties of Sr₂RuO₄ with pressure effects by first principles calculation. Phys. B 441, 62–67. doi: 10.1016/j.physb.2014.02.009

CrossRef Full Text | Google Scholar

Hausch, G. (1973). Magnetovolume effects in invar alloys: spontaneous and forced volume magnetostriction. Phys. Stat. Sol. 18, 735–740. doi: 10.1002/pssa.2210180236

CrossRef Full Text | Google Scholar

Hemberger, J., Krug von Nidda, H. A., Tsurkan, V., and Loidl, A. (2007). Large magnetostriction and negative thermal expansion in the frustrated antiferromagnet ZnCr₂Se₄. Phys. Rev. Lett. 98:147203. doi: 10.1103/PhysRevLett.98.147203

PubMed Abstract | CrossRef Full Text | Google Scholar

Holzer, H., and Dunand, D. C. (1999). Phase transformation and thermal expansion of Cu/ZrW₂O₈ metal matrix composites. J. Mater. Res. 14, 780–789. doi: 10.1557/JMR.1999.0104

CrossRef Full Text | Google Scholar

Huang, R. J., Liu, Y. Y., Fan, W., Tan, J., Xiao, F. R., Qian, L. H., et al. (2013). Giant negative thermal expansion in NaZn₁₃-type La(Fe, Si, Co)₁₃ compounds. J. Am. Chem. Soc. 135, 11469–11472. doi: 10.1021/ja405161z

PubMed Abstract | CrossRef Full Text | Google Scholar

Iikubo, S., Kodama, K., Takenaka, K., Takagi, H., and Shamoto, S. (2008). Magnetovolume effect in Mn₃Cu_1−xGe_xN related to the magnetic structure: neutron powder diffraction measurements. Phys. Rev. B 77:020409. doi: 10.1103/PhysRevB.77.020409

CrossRef Full Text | Google Scholar

Jayaraman, A., Dernier, P., and Longinotti, L. D. (1975). Study of valence transition in SmS induced by alloying, temperature, and pressure. Phys. Rev. B 11:2783–2794. doi: 10.1103/PhysRevB.11.2783

CrossRef Full Text | Google Scholar

Johnson, V. (1975). Diffusionless orthorhombic to hexagonal transitions in ternary silicides and germanides. Inorg. Chem. 14, 1117–1120. doi: 10.1021/ic50147a032

CrossRef Full Text | Google Scholar

Kanomata, T., Ishigaki, H., Suzuki, T., Yoshida, H., Abe, S., and Kaneko, T. (1995). Magneto-volume effects of MnCo_1−xGe (0 ≤ x ≤ 0.2). J. Magn. Magn. Mater. 140–144, 131–132. doi: 10.1016/0304-8853(94)00833-7

CrossRef Full Text | Google Scholar

Kawahara, M., Matsumoto, H., and Takenaka, K. (2017). “Performance of plastic composites by antiperovskite manganese nitrides with giant negative thermal expansion,” in Proceedings of the Second Internastional Symposium on Negative Thermal Expansion and Related Materials (ISNTE-II), Vol. 61, (Yokohama).

Kino, H., Fukushima, T., and Tanaka, T. (2017). “Remarkable suppression of local stress in 3D IC by manganese nitride-based filler with large negative CTE,” in Proceedings of 2017 IEEE 67th Electronic Components and Technology Conference (Lake Buena Vista, FL), 1523–1528.

Google Scholar

Kumar, P. S., Kini, N. S., Umarji, A. M., and Sunandana, C. S. (2006). Search for a novel zero thermal expansion material: dilatometry of the AgI-CuI system. J. Mater. Sci. 41, 3861–3865. doi: 10.1007/s10853-006-6657-x

CrossRef Full Text | Google Scholar

Kuszyk, J. A., and Bradt, R. C. (1973). Influence of grain size effects of thermal expansion anisotropy in MgTi₂O₅. J. Am. Ceram. Soc. 56, 420–423. doi: 10.1111/j.1151-2916.1973.tb12714.x

CrossRef Full Text | Google Scholar

Lawn, B. R. (1964). The thermal expansion of silver iodide and the cuprous halides. Acta Cryst. 17, 1341–1347. doi: 10.1107/S0365110X64003401

CrossRef Full Text | Google Scholar

Lin, J. C., Tong, P., Zhang, K., Ma, X., Tong, H., Guo, X., et al. (2017). The GaNMn₃-epoxy composites with tunable coefficient of thermal expansion and good dielectric performance. Compos. Sci. Technol. 146, 177–182. doi: 10.1016/j.compscitech.2017.04.028

CrossRef Full Text | Google Scholar

Lin, J. C., Tong, P., Zhang, K., Tong, H., Guo, X., Yang, C., et al. (2016). Colossal negative thermal expansion with an extended temperature interval covering room temperature in fine-powdered Mn_0.98CoGe. Appl. Phys. Lett. 109:241903. doi: 10.1063/1.4972234

CrossRef Full Text | Google Scholar

Lind, C. (2012). Two decades of negative thermal expansion research: where do we stand? Materials (Basel) 5, 1125–1154. doi: 10.3390/ma5061125

PubMed Abstract | CrossRef Full Text | Google Scholar

Lind, C., Coleman, M. R., Kozy, L. C., and Sharma, G. R. (2011). Zirconium tungstate/polymer nanocomposites: challenges and opportunities. Phys. Status Solid B 248, 123–129. doi: 10.1002/pssb.201083967

CrossRef Full Text | Google Scholar

Mary, T. A., Evans, J. S. O., Vogt, T., and Sleight, A. W. (1996). Negative thermal expansion from 0.3 to 1050 Kelvin in ZrW₂O₈. Science 272, 90–92. doi: 10.1126/science.272.5258.90

CrossRef Full Text | Google Scholar

Matoba, M., Anzai, S., and Fujimori, A. (1991). Thermal expansion, thermoelectric power, and XPS study of the nonmetal-metal transition in Ni_1−xS_1−ySey. J. Phys. Soc. Jpn. 60, 4230–4244. doi: 10.1143/JPSJ.60.4230

CrossRef Full Text | Google Scholar

Matsumoto, A., Kobayashi, K., Nishio, T., and Ozaki, K. (2003). Fabrication and thermal expansion of Al-ZrW₂O₈ composites by pulse current sintering process. Mater. Sci. Forum 426–432, 2279–2284. doi: 10.4028/www.scientific.net/MSF.426-432.2279

CrossRef Full Text | Google Scholar

McWhan, D. B., and Remeika, J. P. (1970). Metal-insulator transition in (V_1−xCr_x)₂O₃. Phys. Rev. B 2, 3734–3750. doi: 10.1103/PhysRevB.2.3734

CrossRef Full Text | Google Scholar

Mizokawa, T., Tjeng, L. H., Sawatzky, G. A., Ghiringhelli, G., Tjernberg, O., Brookes, N. B., et al. (2001). Spin–Orbit coupling in the Mott insulator Ca₂RuO₄. Phys. Rev. Lett. 87:077202. doi: 10.1103/PhysRevLett.87.077202

CrossRef Full Text | Google Scholar

Moriya, T., and Usami, K. (1980). Magneto-volume effect and Invar phenomena in ferromagnetic metals. Solid State Commun. 34, 95–99. doi: 10.1016/0038-1098(80)91241-7

CrossRef Full Text | Google Scholar

Mott, N. F. (1990). Metal–Insulator Transitions, 2nd Edn. London: Taylor and Francis.

Nabetani, K., Muramatsu, Y., Oka, K., Nakano, K., Hojo, H., Mizumaki, M., et al. (2015). Suppression of temperature hysteresis in negative thermal expansion compound BiNi_1−xFe_xO₃ and zero-thermal expansion composite. Appl. Phys. Lett. 106:061912. doi: 10.1063/1.4908258

CrossRef Full Text | Google Scholar

Nakamura, H., Wada, H., Yoshimura, K., Shiga, M., Nakamura, Y., Sakurai, J., et al. (1988). Effect of chemical pressure on the magnetism of YMn₂: magnetic properties of Y_1−xSc_xMn₂ and Y_1−xLa_xMn₂. J. Phys. F Metal Phys. 18, 981–991. doi: 10.1088/0305-4608/18/5/015

CrossRef Full Text | Google Scholar

Nakamura, Y., Takenaka, K., Kishimoto, A., and Takagi, H. (2009). Mechanical properties of metallic perovskite Mn₃Cu_0.5Ge_0.5N: high-stiffness isotropic negative thermal expansion material. J. Am. Ceram. Soc. 92, 2999–3003. doi: 10.1111/j.1551-2916.2009.03297.x

CrossRef Full Text | Google Scholar

Ohya, Y., Nakagawa, Z., and Hamano, K. (1987). Grain-boundary microcracking due to thermal expansion anisotropy in aluminum titanate ceramics. J. Am. Ceram. Soc. 70, C184–C186. doi: 10.1111/j.1151-2916.1987.tb05720.x

CrossRef Full Text | Google Scholar

Okamoto, Y., Mori, M., Katayama, N., Miyake, A., Tokunaga, M., Matsuo, A., et al. (2018). Magnetic and structural properties of A-site ordered chromium spinel sulfides: alternating antiferromagnetic and ferromagnetic interactions in the breathing pyrochlore lattice. J. Phys. Soc. Jpn. 87:034709. doi: 10.7566/JPSJ.87.034709

CrossRef Full Text | Google Scholar

Pan, Z., Chen, J., Jiang, X., Hu, L., Yu, R., Yamamoto, H., et al. (2017). Colossal volume contraction in strong polar perovskites of Pb(Ti, V)O₃. J. Am. Chem. Soc. 139, 14865–14868. doi: 10.1021/jacs.7b08625

PubMed Abstract | CrossRef Full Text | Google Scholar

Pelletant, A., Reveron, H., Chevalier, J., Fantozzi, G., Blanchard, L., Guinot, F., et al. (2012). Grain size dependence of pure β-eucryptite thermal expansion coefficient. Mater. Lett. 66, 68–71. doi: 10.1016/j.matlet.2011.07.107

CrossRef Full Text | Google Scholar

Phillips, A. E., Goodwin, A. L., Halder, G. J., Southon, P. D., and Kepert, C. J. (2008). Nanoporosity and exceptional negative thermal expansion in single-network cadmium cyanide. Angew. Chem. Int. Ed. 47, 1396–1399. doi: 10.1002/anie.200704421

PubMed Abstract | CrossRef Full Text | Google Scholar

Pokharel, G., May, A. F., Parker, D. S., Calder, S., Ehlers, G., Huq, A., et al. (2018). Negative thermal expansion and magnetoelastic coupling in the breathing pyrochlore lattice material LiGaCr₄S₈. Phys. Rev. B 97:134117 doi: 10.1103/PhysRevB.97.134117

CrossRef Full Text | Google Scholar

Pryde, A. K. A., Hammonds, K. D., Dove, M. T., Heine, V., Gale, J. D., and Warren, M. C. (1996). Origin of the negative thermal expansion in ZrW₂O₈ and ZrV₂O₇. J. Phys. 8, 10973–10982. doi: 10.1088/0953-8984/8/50/023

CrossRef Full Text | Google Scholar

Qi, T. F., Korneta, O. B., Parkin, S., De Long, L. E., Schlottmann, P., and Cao, G. (2010). Negative volume thermal expansion via orbital and magnetic orders in Ca₂Ru_1−xCr_xO₄ (0 < x < 0.13). Phys. Rev. Lett. 105:177203. doi: 10.1103/PhysRevLett.105.177203

CrossRef Full Text | Google Scholar

Qi, T. F., Korneta, O. B., Parkin, S., Hu, J. P., and Cao, G. (2012). Magnetic and orbital orders coupled to negative thermal expansion in Mott insulators Ca₂M_1−xCr_xO₄ (M = Mn and Fe). Phys. Rev. B 85:165143. doi: 10.1103/PhysRevB.85.165143

CrossRef Full Text | Google Scholar

Reinecke, H., DelaCampa, J. G., and DeAbajo, J. (1996). Synthesis and characterization of novel poly(amide imide)s. J. Appl. Polym. Sci. 61, 923–928. doi: 10.1002/(SICI)1097-4628(19960808)61:6<923::AID-APP5>3.0.CO;2-J

CrossRef Full Text | Google Scholar

Robello, A., Neumeier, J. J., Gao, Z. S., Qi, Y. P., and Ma, Y. W. (2012). Giant negative thermal expansion in La-doped CaFe₂As₂. Phys. Rev. B 86:104303. doi: 10.1103/PhysRevB.86.104303

CrossRef Full Text | Google Scholar

Rong, Y. C., Li, M. L., Chen, J., Zhou, M., Lin, K., Hu, L., et al. (2016). Large negative thermal expansion in non-perovskite lead-free ferroelectric Sn₂P₂S₆. Phys. Chem. Chem. Phys. 18, 6247–6251. doi: 10.1039/C6CP00011H

PubMed Abstract | CrossRef Full Text | Google Scholar

Salvador, J. R., Guo, F., Hogan, T., and Kantzidis, M. G. (2003). Zero thermal expansion in YbGaGe due to an electronic valence transition. Nature 425, 702–705. doi: 10.1038/nature02011

PubMed Abstract | CrossRef Full Text | Google Scholar

Shan, X. R., Huang, R. J., Han, Y. M., Huang, C. J., and Li, L. F. (2015). Preparation and property study of La(Fe, Si, Co)₁₃/Cu composite with nearly zero thermal expansion behavior. J. Alloy. Compd. 648, 463–466. doi: 10.1016/j.jallcom.2015.06.139

CrossRef Full Text | Google Scholar

Shirane, G., and Hoshino, S. (1951). On the phase transition in lead titanate. J. Phys. Soc. Jpn. 6, 265–270. doi: 10.1143/JPSJ.6.265

CrossRef Full Text | Google Scholar

Sleight, A. (2003). Zero-expansion plan. Nature 425, 674–676. doi: 10.1038/425674a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sleight, A. W. (1998). Compounds that contract on heating. Inorg. Chem. 37, 2854–2860. doi: 10.1021/ic980253h

CrossRef Full Text | Google Scholar

Sullivan, L. M., and Lukehart, C. M. (2005). Zirconium tungstate (ZrW₂O₈)/polyimide nanocomposites exhibiting reduced coefficient of thermal expansion. Chem. Mater. 17, 2136–2141. doi: 10.1021/cm0482737

CrossRef Full Text | Google Scholar

Sumiyama, K., Shiga, M., Morioka, M., and Nakamura, Y. (1979). Characteristic magnetovolume effects in Invar type Fe-Pt alloys. J. Phys. F Metal Phys. 9, 1665–1677. doi: 10.1088/0305-4608/9/8/017

CrossRef Full Text | Google Scholar

Takenaka, K. (2012). Negative thermal expansion materials: technological key for control of thermal expansion. Sci. Technol. Adv. Mater. 13:013001. doi: 10.1088/1468-6996/13/1/013001

PubMed Abstract | CrossRef Full Text | Google Scholar

Takenaka, K., and Ichigo, M. (2014). Thermal expansion adjustable polymer matrix composites with giant negative thermal expansion. Compos. Sci. Technol. 104, 47–51. doi: 10.1016/j.compscitech.2014.08.029

CrossRef Full Text | Google Scholar

Takenaka, K., and Takagi, H. (2005). Giant negative thermal expansion in Ge-doped antiperovskite manganese nitrides. Appl. Phys. Lett. 87:261902. doi: 10.1063/1.2147726

CrossRef Full Text | Google Scholar

Takenaka, K., Hamada, T., Kasugai, D., and Sugimoto, N. (2012). Tailoring thermal expansion in metal matrix composites blended by antiperovskite manganese nitrides exhibiting giant negative thermal expansion. J. Appl. Phys. 112:083517. doi: 10.1063/1.4759121

CrossRef Full Text | Google Scholar

Takenaka, K., Ichigo, M., Hamada, T., Ozawa, A., Shibayama, T., Inagaki, T., et al. (2014). Magnetovolume effects in manganese nitrides with antiperovskite structure. Sci. Technol. Adv. Mater. 15:015009. doi: 10.1088/1468-6996/15/1/015009

PubMed Abstract | CrossRef Full Text | Google Scholar

Takenaka, K., Kuzuoka, K., and Sugimoto, N. (2015). Matrix-filler interfaces and physical properties of metal matrix composites with negative thermal expansion manganese nitride. J. Appl. Phys. 118:084902. doi: 10.1063/1.4929363

CrossRef Full Text | Google Scholar

Takenaka, K., Okamoto, Y., Shinoda, T., Katayama, N., and Sakai, Y. (2017a). Colossal negative thermal expansion in reduced layered ruthenate. Nat. Commun. 8:14102. doi: 10.1038/ncomms14102

PubMed Abstract | CrossRef Full Text | Google Scholar

Takenaka, K., Shinoda, T., Inoue, N., Okamoto, Y., Katayama, N., Sakai, Y., et al. (2017b). Giant negative thermal expansion in Fe-doped layered-ruthenate ceramics. Appl. Phys. Express 10:115501. doi: 10.7567/APEX.10.115501

CrossRef Full Text | Google Scholar

Takezawa, A., Kobashi, M., and Kitamura, M. (2015). Porous composite with negative thermal expansion obtained by photopolymer additive manufacturing. APL Mater. 3:076103. doi: 10.1063/1.4926759

CrossRef Full Text | Google Scholar

Takezawa, A., Takenaka, K., and Zhang, X. P. (2018). Inverse analysis of giant macroscopic negative thermal expansion of Ca₂RuO_y−4 ceramics based on elastic mechanics and structural topology optimization. Appl. Phys. Expr. 11:055801. doi: 10.7567/APEX.11.055801

CrossRef Full Text | Google Scholar

van Schilfgaarde, M., Abrikosov, I. A., and Johansson, B. (1999). Origin of the Invar effect in iron-nickel alloys. Nature 400, 46–49. doi: 10.1038/21848

CrossRef Full Text | Google Scholar

Wagh, A. S., Poeppel, R. B., and Singh, J. P. (1991). Open pore description of mechanical properties of ceramics. J. Mater. Sci. 26, 3862–3868.

Google Scholar

Wang, C., Chu, L., Yao, Q., Sun, Y., Wu, M., Ding, L., et al. (2012). Tuning the range, magnitude, and sign of the thermal expansion in intermetallic Mn₃(Zn, M)_xN (M = Ag, Ge). Phys. Rev. B 85:220103R. doi: 10.1103/PhysRevB.85.220103

CrossRef Full Text | Google Scholar

Wang, Q. M., Jackson, J. A., Ge, Q., Hopkin, J. B., Spadaccini, C. M., and Fang, N. X. (2016). Lightweight mechanical metamaterials with tunable negative thermal expansion. Phys. Rev. Lett. 117:175901. doi: 10.1103/PhysRevLett.117.175901

PubMed Abstract | CrossRef Full Text | Google Scholar

Wasserman, E. F. (1990). Invar: moment-volume instabilities in transition metals and alloys. Ferromagn. Mater. 5, 237–322. doi: 10.1016/S1574-9304(05)80063-X

CrossRef Full Text | Google Scholar

Weiss, R. J. (1963). The origin of the ‘Invar’ effect. Proc. Phys. Soc. 82, 281–288.

Google Scholar

Wohlfarth, E. P. (1977). Thermodynamic aspects of itinerant electron magnetism. Physica 91B, 305–314. doi: 10.1016/0378-4363(77)90199-1

CrossRef Full Text | Google Scholar

Wright, J. P., Bell, A. M. T., and Attfield, J. P. (2000). Variable temperature powder neutron diffraction study of the Verwey transition in magnetite Fe₃O₄. Solid State Sci. 2, 747–753. doi: 10.1016/S1293-2558(00)01107-9

CrossRef Full Text | Google Scholar

Xue, Z. W., Wang, L. D., Liu, Z., and Fei, W. D. (2010). Effect of interfacial state on thermal expansion behaviors of β-eucryptite particle-reinforced Cu compounds. Scripta Mater. 62, 867–870. doi: 10.1016/j.scriptamat.2010.02.022

CrossRef Full Text | Google Scholar

Yamada, I., Tsuchida, K., Ohgushi, K., Hayashi, N., Kim, J., Tsuji, N., et al. (2011). Giant negative thermal expansion in the iron perovskite SrCu₃Fe₄O₁₂. Angew. Chem. Int. Ed. 50, 6579–6582. doi: 10.1002/anie.201102228

PubMed Abstract | CrossRef Full Text | Google Scholar

Yamai, I., and Ota, T. (1993). Grain size-microcracking relation for NaZr₂(PO₄)₃ family ceramics. J. Am. Ceram. Soc. 76, 487–491. doi: 10.1111/j.1151-2916.1993.tb03811.x

CrossRef Full Text | Google Scholar

Yang, C., Tong, P., Lin, J. C., Guo, X. G., Zhang, K., Wang, M., et al. (2016). Size effects on negative thermal expansion in cubic ScF₃. Appl. Phys. Lett. 109:023110. doi: 10.1063/1.4959083

CrossRef Full Text | Google Scholar

Zhao, Y. Y., Hu, F.-X., Bao, L.-F., Wang, J., Wu, H., Huang, Q.-Z., et al. (2015). Giant negative thermal expansion in bonded MnCoGe-based compounds with Ni₂In-type hexagonal structure. J. Am. Chem. Soc. 137, 1746–1749. doi: 10.1021/ja510693a

PubMed Abstract | CrossRef Full Text | Google Scholar