Non-adiabatic Quantum Dynamics of the Dissociative Charge Transfer He++H2 → He+H+H+

Introduction

Atomic Hydrogen and Helium are the dominant chemical species of the early Universe (Galli and Palla, 2013) and of the interstellar medium, and are easily ionized by cosmic rays. Therefore, these atoms and their ions are the astrochemical fundamental reactants (Lepp et al., 2002), together with ubiquitous photons, giving first simple diatoms as H₂, ${\text{H}}_2^{+}$ (Stancil et al., 1993), and HeH⁺ (Zygelman et al., 1998) and then atom+diatom bimolecular collisions as He+${\text{H}}_2^{+}$ (De Fazio et al., 2012), H+HeH⁺ (De Fazio, 2014; Gamallo et al., 2015), and He⁺+H₂.

When all chemical species are in the ground electronic states, the He+${\text{H}}_2^{+}$ reaction is endothermic and rather slow, but the other two are exothermic by about ~0.7 and 6.2 eV, respectively, as many ion+neutral astrochemical reactions (Herbst and Klemperer, 1973). H+HeH⁺ is barrierless and gives quickly the He+${\text{H}}_2^{+}$ products, but the collision-induced dissociative charge transfer (DCT) He⁺(²S)+H₂(X¹Σ${}_g^{+}$) → He(¹S)+H(²S)+H⁺ is very slow at low collision energy E_coll and at room temperature, if H₂ is in the ground vibro-rotational state. In fact, H+HeH⁺↔He⁺+H₂ occurs on the ground potential energy surface (PES) $\tilde{X}$²A' of ${\text{HeH}}_2^{+}$, which is well-separated from the excited electronic species, but the low-E_coll DCT involves the first two excited adiabatic electronic states òA' and $\tilde{B}$²A' of ${\text{HeH}}_2^{+}$, which differ by a two-electron excitation and are coupled by a C_2v conical intersection (CI) (Preston et al., 1978; McLaughlin and Thompson, 1979). In the latter case the non-adiabatic coupling is weak and the lower, dissociative cone of the intersection seam gives rise to an adiabatic barrier with diabatic character, that is the DCT tends to follow the diabatic PESs without changing the electronic configuration. This strongly inhibits the reactivity that is associated with the tunneling through the barrier (Preston et al., 1978).

This is schematically shown in the correlation diagram of Figure 1 for the òA' and $\tilde{B}$²A' adiabatic and (1)²A₁ and (2)²B₂ diabatic PESs V of ${\text{HeH}}_2^{+}$, where all chemical species are in the ground electronic states, save ${\text{H}}_2^{+}$(A²Σ${}_u^{+}$) that is unbound, and the energy is referred to the reactant minimum. This diagram is obtained from the ab initio Multi-Reference Configuration-Interaction results of McLaughlin and Thompson (1979), changing the label of the reactant diabatic state ²A₁ from (5) to (1), and from the analytical fits of the associated diabatic PESs V₁₁ and V₂₂ by Aguado et al. (1993). In the scheme of Figure 1 we omit the ground adiabatic PES, well below the excited PESs and with too small non-adiabatic couplings. However, all three adiabatic PESs are strongly coupled by intense laser pulses (Szidarovszky and Yamanouchi, 2016) when the ground PES becomes populated (Schauer et al., 1989). A more complete description of the reaction dynamics in presence of electric and magnetic fields is out of the scope of the present article. Note in the figure the small ion-induced dipole minimum in the C_2v entrance channel at R(He-H₂) = 4.45 a₀, r(H-H) = 1.42 a₀, and V = −0.08 eV and the CI C_2v minimum at R = 4.89 a₀, r = 2.18 a₀, and V = 1.34 eV, owing to the intersection (Preston et al., 1978) between the H₂(X¹Σ${}_g^{+}$) and ${\text{H}}_2^{+}$(A²Σ${}_u^{+}$) curves at r = 2.19 a₀ and V = 1.28 eV.

FIGURE 1

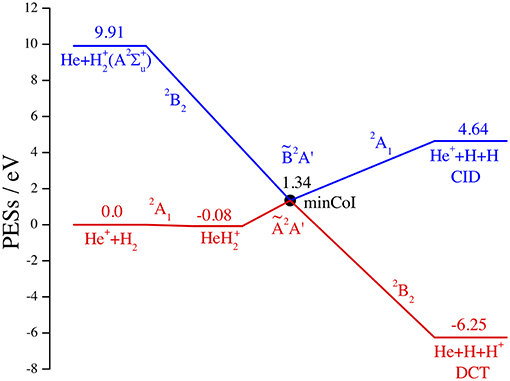
Figure 1. Dissociative charge transfer (DCT) and collision induced dissociation (CID) of He⁺+H₂. Schematic correlation diagram in eV of the adiabatic òA′ (red) and $\tilde{B}$²A′ (blue) and of the diabatic (1)²A₁ and (2)²B₂ PESs. All reactants and products are in the ground electronic state, save ${\text{H}}_2^{+}$(A²Σ${}_u^{+}$, unbound).

Experimental studies on the He⁺+H₂ → He+H+H⁺ DCT dynamics date back to 1955 (Stedeford and Hasted, 1955) and 1961 (Giese and Maier, 1961), when the integral cross sections (ICSs) were measured at E_coll = 4 eV and found <0.05 Ų. ICSs as functions of E_coll were then measured in many works up to 1996 (Dhuicq et al., 1996), finding values from 0.01 up to ~2 Ų, for E_coll between 3 and 100 eV, by considering H₂ in the ground vibro-rotational state and all ground and excited open states of H. Below 3 eV, the H product is in the ground 1s state and the ICSs are so small and so difficult to measure that experimental values present large discrepancies (Reinig et al., 1992). However, the ICSs increase by one/two orders of magnitude if H₂ is excited by one vibrational quantum (Preston et al., 1978) or E_coll grows up to ~100 eV. Differential cross sections were also measured (Dhuicq et al., 1998) at E_coll > 9 eV, that is for the formation of the H* excited product. Accordingly, small rate constants were observed (Johnsen et al., 1980), with values of (1.5 ± 0.15) × 10⁻¹³ and (1.1 ± 0.1) × 10⁻¹³cm³s⁻¹ at 78 and 330 K, respectively, that is nearly four order of magnitude lower than the Langevin (Gioumousis and Stevenson, 1958) estimates for ion+neutral barrierless and exothermic reactions.

A few works have also theoretically investigated the dynamics of the DCT collision since 1994, when Aguillon (1994) employed a semiclassical coupled wavepacket (WP) method and the analytical diabatic PESs of Aguado et al. (1993) for computing ICSs for ground and excited vibrational states v₀ of H₂, up to v₀ = 4 and in the E_coll range from 2 to 10 eV. He found total-ICS values from ~0.001 Ų (v₀ = 0, E_coll = 2 eV) to ~1 Ų (v₀ = 3, E_coll = 10 eV), in agreement with the most recent measurements (Dhuicq et al., 1996). In a subsequent work (Aguillon, 1998), an improved version of this semiclassical method was used for obtaining new ICS values and differential cross sections. Approximated theoretical models were also employed (Dhuicq et al., 1996) for explaining observed cross sections above 9 eV, when excited H*(n = 2) was produced. Finally, quantum infinite-order-sudden cross sections were calculated (Martínez et al., 2000) for He⁺+H₂ → He+H*(n ≥ 2)+H⁺ at E_coll ≥ 10 eV, using the accurate diabatic representation of Aguado et al. (1993) and six more approximated diabatic electronic states (Sidis, 1996).

As far as we know, no further studies of the title reaction have been published and its collision dynamics below ~2 eV is unknown. In particular, only semiclassical or approximated quantum theoretical studies were carried out, although both conical intersection and barrier tunneling are purely quantum effects. We thus here report a rigorous time-dependent quantum study of the DCT He⁺+H₂(v₀ = 0,1) → He+H+H⁺ with all species in the ground electronic state, at thermal and hyperthermal collision energy up to 3 eV, using the diabatic PESs of Aguado et al. (1993) and WP and flux formalisms. In section Theory and Calculations we present the theoretical method and its numerical details. Section Collision Results reports initial-state-resolved total reaction probabilities, ICSs, and thermal rate constants. Finally, we present our conclusions in section Conclusions.

Theory and Calculations

Potential Energy Surfaces and Non-adiabatic Coupling

As we said in the Introduction, the ${\text{HeH}}_2^{+}$ adiabatic and diabatic electronic states relevant in the present work were obtained ab initio in McLaughlin and Thompson (1979), fitted analytically in Aguado et al. (1993), and they are schematically plotted in Figure 1. We label the adiabatic species and PESs by òA' and $\tilde{B}$²A' and by V_A and V_B, respectively. As already discussed (Aguado et al., 1993), these states belong to the fully symmetric irreducible representation for linear (C_∞v) and non-symmetric (C_S) geometries, while Figure 1 shows that they transform as A₁/B₂ and B₂/A₁ for perpendicular geometries (C_2v), before/after the CI, respectively, which rules the title reaction. On the other hand, we label the associated diabatic electronic states and PESs by (1)A₁ and (2)B₂ and by V₁₁, V₂₂, and V₁₂, respectively, where the third surface describes the CI non-adiabatic coupling in the diabatic representation.

In order to simultaneously describe these electronic species and take into account the CI, a fit of the diabatic PESs and coupling V₁₁, V₂₂, and V₁₂ was made in Aguado et al. (1993). The description of the adiabatic states is obtained as the eigenvalues V_A and V_B of a 2 × 2 matrix $\left(\begin{array}{cc}{V}_{11}& V_{12}\\ V_{12}& V_{22}\end{array}\right)$, in which the interaction term V₁₂ must have the correct symmetry, being anti-symmetric with respect to the permutation of the H atoms and thus vanishing identically for equal He–H distances. This coupling term V₁₂ was fitted in Aguado et al. (1993) to reproduce the CI between the òA' and $\tilde{B}$²A' adiabatic states.

The diabatic surfaces where fitted in Aguado et al. (1993) using the Aguado-Paniagua functional form (Aguado and Paniagua, 1992; Aguado et al., 1998) that expands the energy as a multidimensional permutationally invariant polynomial (Aguado et al., 1994, 2001) in Rydberg type variables (Rydberg, 1931) of the form ρ_AB = R_ABexp(−β_ABR_AB), where A and B are two nuclei and R_AB is their distance. For the interaction term, a simple expansion in Rydberg functions,

$\begin{array}{l}{V}_{12}\left(R_{\text{HeH}},R_{\text{He}{\text{H}}^{\prime }},R_{\text{H}{\text{H}}^{\prime }}\right)=C_{12}{\rho }_{\text{H}{\text{H}}^{\prime }}\left({\rho }_{\text{HeH}}-{\rho }_{\text{He}{\text{H}}^{\prime }}\right),\\ & (1)\end{array}$

fulfills the anti-symmetric requirement.

The DCT is produced through the CI, as shown in Figure 2 using nuclear Jacobi coordinates R, r = R${}_{\text{H}{\text{H}}^{\text{′}}}$, and γ , at R = 4 a₀ and γ = 0. The top panel shows the adiabatic òA' and $\tilde{B}$²A' PESs of ${\text{HeH}}_2^{+}$ in the reactant channel, obtained from the diabatic V_ij surfaces, where òA' correlates with He⁺(²S)+H₂(X¹Σ${}_g^{+}$) for r < 2 a₀ and with He(¹S)+${\text{H}}_2^{+}$($A^2{\Sigma }_u^{+}$, unbound) for r > 2 a₀. To analyze the accuracy of the fit, we compare the analytical non-adiabatic coupling matrix elements (NACMEs) in the adiabatic representation, obtained from the fitted diabatic energies and coupling, with the ab initio results calculated using the MOLPRO program package (Werner et al., 2018). As done previously for ${\text{H}}_4^{+}$ and ${\text{H}}_5^{+}$ in Sanz-Sanz et al. (2015), the analytical NACMEs can be calculated from the generalized Hellmann-Feynman theorem,

$\begin{array}{cc}\langle {\tilde{A}}^2{A}^{\prime }|\frac{\partial }{\partial R_{\text{AB}}}|{\tilde{B}}^2{A}^{\prime }\rangle =\frac{1}{V_B-V_A}\langle {\tilde{A}}^2{A}^{\prime }|\frac{\partial {\widehat{H}}^{el}}{\partial R_{\text{AB}}}|{\tilde{B}}^2{A}^{\prime }\rangle ,& (2)\end{array}$

where Ĥ^el is the electronic Hamiltonian and the rhsm is obtained from the derivatives of the diabatic energies V_ij (Sanz-Sanz et al., 2015). Ab initio calculations have been performed using the Multi-Reference Configuration-Interaction method, with the aug-cc-pVTZ basis set of Dunning (1989) and Woon and Dunning (1994). The ab initio NACMEs are obtained using a first order difference method with an interval of 0.01 a₀, and that for R_AB = r is compared with the fitted one in the bottom panel of Figure 2. The agreement, in form and in position, between both is excellent, indicating that the equation used for the interaction term V₁₂ is also appropriate to reproduce the NACMEs. The probability density of the first two vibrational states of H₂(X¹Σ${}_g^{+}$) has been included in the top panel of Figure 2, in order to analyze the reason why the reaction is faster when H₂ is vibrationally excited (Aguillon, 1994, 1998). While the maximum of the probability density of the vibrational state v₀ = 0 is found at 1.4 a₀, those in the first excited vibrational state v₀ = 1 are at 1.25 and 1.73 a₀. The latter is close to the region in which the NACME has is maximum, that explains the enhancement of the reactivity as we shall see in section Reaction Probabilities.

FIGURE 2

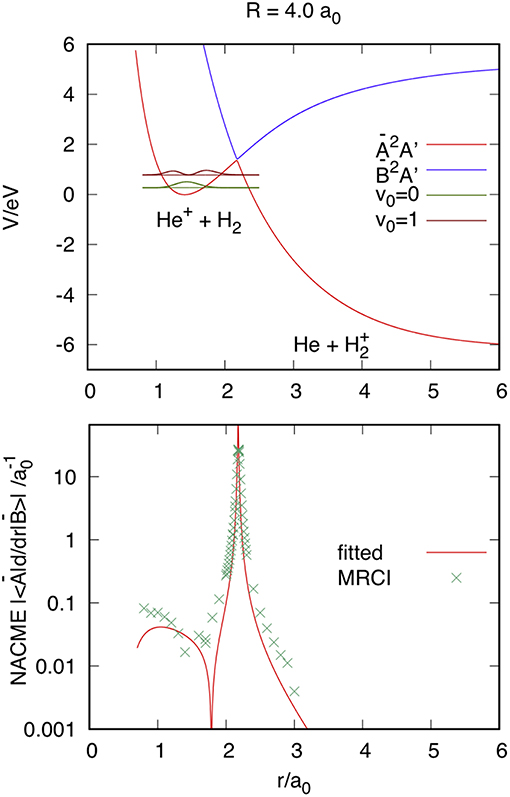
Figure 2. Top panel: òA' and $\tilde{B}$²A' adiabatic PESs at reactant Jacobi coordinates R = 4 a₀, r, and γ = 0. The vibrational v₀ = 0 and 1 probability density is plotted at the corresponding vibrational energy. Bottom panel: Comparison of the absolute values of the fitted and ab initio Multi-Reference Configuration-Interaction (MRCI) NACME.

In Figure 3 the ratio between the interaction term and the energy difference of the diabatic states, V₁₂/(V₂₂-V₁₁), is plotted as a function of the R_HeH and R${}_{\text{H}{\text{H}}^{\text{′}}}$ distances, for several values of the angle θ ≤ 180° between these distances. This ratio is important for the calculation of the adiabatic PESs from the fitted diabatic ones, according to:

$\begin{array}{cc}{V}_{A/B}=\frac{1}{2}\left\{V_{11}+V_{22}-/+\left[{\left(V_{11}-V_{22}\right)}^2+4V_{12}^2\right]{}^{1/2}\right\}.& (3)\end{array}$

As expected, V₁₂/(V₂₂-V₁₁) changes sign and its absolute value is maximum in the region of the diabatic crossing line shown in Figures 2, 3 of Aguado et al. (1993).

FIGURE 3

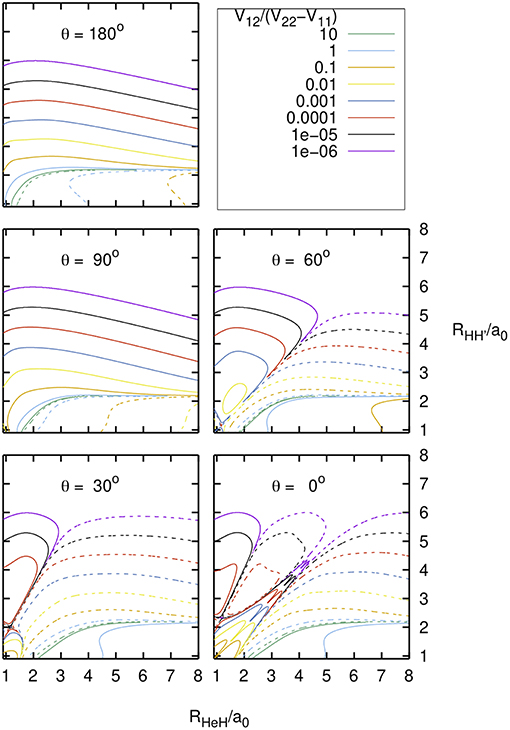
Figure 3. Diabatic PESs: V₁₂/(V₂₂-V₁₁) as function of the nuclear distances R_HeH and R_HH' = r, and of the included angle θ . Solid/dashed curves correspond to positive/negative values.

In conclusion, these results show that the collisional dynamics of DCT He⁺(²S)+H₂(X¹Σ${}_g^{+}$)→ He(¹S)+H(²S)+H⁺ can be investigated with high accuracy in the present diabatic electronic representation, using the V₁₁, V₂₂, and V₁₂ PESs.

Collision Dynamics

Since many years we are presenting our quantum theory (Petrongolo, 1988) and results of non-adiabatic effects in spectroscopy of triatomics and dynamics of atom+diatom collisions and we here report a brief summary, following our work on the CI dynamics of the OH(A²Σ⁺)+H(²S) reaction (Gamallo et al., 2013).

The He⁺+H₂ collision is described by reactant Jacobi coordinates R, r, and γ , by a body-fixed reference frame with the z axis along R, and by a ${\text{HeH}}_2^{+}$ spinless rovibronic Hamiltonian Ĥ, which contains the electronic Ĥ^el and the total angular momentum $\widehat{J}$ operators. Ĥ is represented in an orthonormal basis of diabatic electronic states (1)²A₁ and (2)²B₂, radial grid |Rr>, associated Legendre |jK>, and symmetry Wigner states |K+p>. Here (1)²A₁ and (2)²B₂ are coupled by Ĥ^el owing to the CI, ℏ K is the Ĵ_z eigenvalue, and we omit J and its space-fixed Z component in |K+p>, where the total parity is $p={(-)}^{J+K_{min}}$ with K_min = 0 or 1. The 2J+1 values of K are thus factorized in two non-interacting groups, with K_min ≤ K ≤ J, of dimensions J+1 or J according to K_min = 0 or 1, respectively.

Initial-state-resolved reaction probabilities are computed through the quantum, real WP formalism of Gray and Balint-Kurti (1998) and Meijer et al. (1998), essentially equal to the Chebyshev approach of Guo (2012). Shortly, an arccos mapping of the ${\text{HeH}}_2^{+}$ time-dependent Schrödinger equation is solved recursively, using a scaled and shifted Hamiltonian Ĥ_s and starting from an initial and complex WP |ψ₀ > = |a₀ > +i|b₀ > (Gray and Balint-Kurti, 1998). This initial WP describes the entrance channel He⁺(²S)+H₂(X¹Σ${}_g^{+}$), with the diabatic electronic state (1)²A₁ and the R-dependent term

$\begin{array}{l}{g}_0(R)={\text{π}}^{-1/4}{\text{α}}^{-1/2}exp\left[-\left(R-R_0{)}^2/2{\text{α}}^2\right)\right]\hfill \\ exp{[-i\left(2{\text{μ}}_{\text{R}}{E}_0\right)}^{1/2}\hfill \\ \left(R-R_0\right)],\text{ in atomic units},\hfill & (4)\end{array}$

where μ_R is the He⁺+H₂ reduced mass. The r and angular terms of |ψ₀ > are the vibrational |v₀ > and rotational |j₀K₀ > states of H₂(X¹Σ${}_g^{+}$), and finally |K₀+p> is the initial overall rotational species. The recursions are

$\begin{array}{l}|a_1\rangle ={\widehat{H}}_{\text{s}}|a_0\rangle -{\left(1-{\widehat{H}}_s^2\right)}^{1/2}|b_0\rangle ,\\ \text{ first complex propagation},& (5)\end{array}$

$\begin{array}{l}|a_{\text{n}+\text{2}}\rangle =2{\widehat{H}}_{\text{s}}|a_{\text{n}+1}\rangle -|a_{\text{n}}\rangle ,\\ \text{ other real propagations,}& (6)\end{array}$

where the square root in Equation (5) is evaluated with a Chebyshev expansion, and Equation (6) is a standard Chebyshev propagation of just a real WP, which is also absorbed at R > R_abs and r > r_abs by the Gaussians exp[–$C_{abs}^R$(R–R_abs)²] and $exp[C_{abs}^r{(r-r_{\text{abs}})}^2]$, respectively. At the end of the propagation, we obtain the probability via a time-to-energy Fourier transform and a flux analysis (Meijer et al., 1998) on the (2)²B₂ PES.

We compute non-adiabatic initial-state-resolved reaction probabilities $P_{v_0}^J$(E_coll), with the initial WP on the ${\text{HeH}}_2^{+}$ (1)²A₁ diabatic PES and H₂(X¹Σ${}_g^{+}$) in the ground and first excited vibrational state, v₀ = 0 and 1, and in the ground rotational state j₀ = 0. Then the initial K₀ is equal to K_min = 0 and the total parity p is (–)^J. Here we have

$\begin{array}{cc}{P}_{v_0}^J\left(E_{coll}\right)={{\displaystyle \sum _{v^{\prime }{j}^{\prime }{K}^{\prime }}\left|S_{2v^{\prime }{j}^{\prime }{K}^{\prime }\leftarrow 1v_{0}00}^J\left(E_{coll}\right)\right|}}^2,& (7)\end{array}$

where (1) and (2) are the diabatic electronic states, v′, j′, and K′ label open vibrational, rotational, and helicity states of the products, respectively, and S^J is the state-to-state parity adapted S-matrix at J. The total ICS is then defined by

$\begin{array}{cc}{\sigma }_{v_0}\left(E_{coll}\right)=\frac{\pi }{2{\text{μ}}_R{E}_{coll}}{\displaystyle \sum _J\left(2J+1\right)}{P}_{v_0}^J\left(E_{coll}\right),& (8)\end{array}$

and the initial-state-resolved rate constant is

$\begin{array}{cc}{k}_{v_0}\left(T\right)={\left(\frac{8}{\pi {\text{μ}}_R{k}_B^3{T}^3}\right)}^{1/2}{\displaystyle \underset{0}{\overset{\infty }{\int }}{E}_{coll}}{\sigma }_{v_0}\exp \left(-E_{coll}/k_{B}T\right)d{E}_{coll},& (9)\end{array}$

where T is the temperature and k_B is the Boltzmann constant.

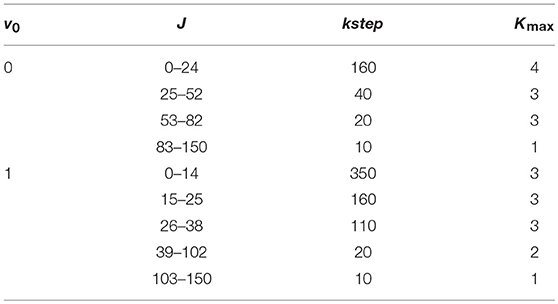
The calculations are done up to J = 150, using the coupled-channel formalism with Coriolis couplings among the K values, up to K_max, that are necessary for converging the probabilities. Considering the H–H permutation symmetry, the numerical parameters of the WP propagations are listed in Table 1: they correspond to 7,053,300 basis states at K = 0, including two coupled electronic states. These parameters span the whole range of E_coll from 0.0002 to 3 eV, with ΔE_coll = 0.0001 or 0.001 eV below or above 0.2 eV, respectively. The most important parameters that affect the convergence of the calculations are the number of the propagation kilo-steps, kstep, the maximum K value, K_max, and the dimension of the R grid, nR. We shall see in the next sections some convergence results with respect to kstep and K_max. The probabilities obtained with nR = 461 of Table 1 are practically indistinguishable by those corresponding to nR = 559. All calculations are done with our J-K-parallelized Open MPI codes.

TABLE 1

Table 1. Parameters of the quantum dynamics calculations.

Collision Results

Reaction Probabilities

We plot in Figure 4 the opacities functions (2J+1)$P_{v_0}^J$(E_coll) at J = 20 and 40, v₀ = 0 and 1, E_coll ≤ 3 eV, and K_max = 0, 1, and 2, with kstep = 5, which converges the probabilities within 0.1% above ~0.5 eV. The curves at v₀ = 0 and 1 present a similar behavior, namely narrow resonance features at J = 20 and E_coll ≤ 0.5 eV and a smooth, fast increase above. From the comparison among lower and upper panels we see that v₀ = 1 is more reactive than v₀ = 0 by ~one order of magnitude. Of course, this finding reflects the ${\text{HeH}}_2^{+}$(òA′) early potential barrier of 1.34 eV and the v₀ = 1 density maximum at 1.73 a₀ (Figure 2), close to the NACME maximum. Comparing the curves inside each panel, we observe a very fast convergence in K_max, so that the Coupled-State approximation (McGuire and Kouri, 1974; Pack, 1974) at K_max = 0 gives already reasonable results. Just two Ks converge the plots within the graphical accuracy, implying that the Coriolis couplings between K and K ± 1 vanish quickly when the initial K₀ is equal to zero. To reach the high accuracy claimed above at all the partial waves required to give convergent ICSs in all the collision energy range considered, we employ K_max = 2 and 3 for v₀ = 0 and 1, respectively. In the J = 20 left panels, the dashed lines show the convergent results below 0.5 eV and the weight of the resonances with respect to the background. The resonance features are probably due to rotational metastable states of the C_2v ion-induced dipole minimum in the entrance channel. These states, embedded in the collisional continuum, are particular Feshbach resonances induced by the CI (Cederbaum and Friedman, 2003), with lifetimes of the order of the nano-second. The v₀ = 0 opacities then increase in a monotonic way above 0.6 eV up to a maximum value of ~0.06 at 3 eV, that is one-two orders of magnitude larger than the strongest resonance. The v₀ = 1 opacities show the same behavior, but the value at 3 eV is just two times larger than the resonance maximum. However, to converge the resonance energy pattern very different values of the convergent parameters K_max and kstep are required.

FIGURE 4

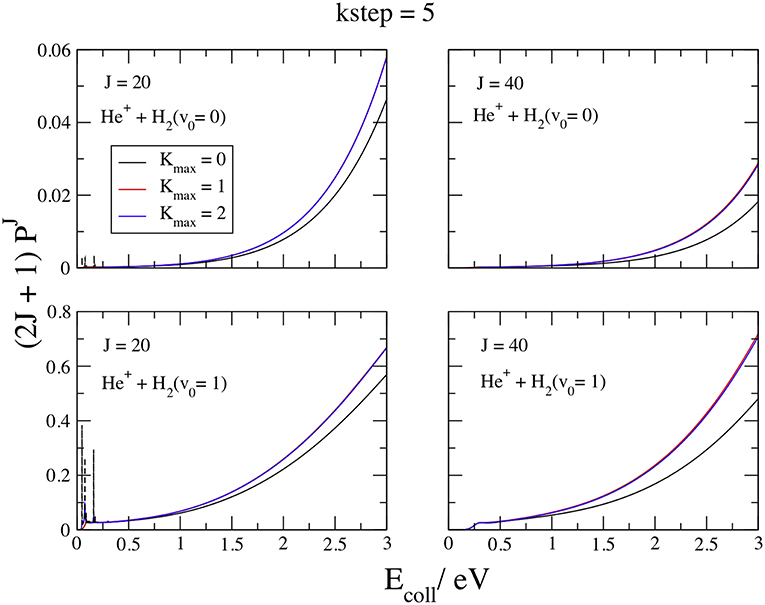
Figure 4. v₀ = 0, 1; J = 20, 40; kstep = 5. Convergence of the opacities (2J+1)$P_{v_0}^J$ with respect to K_max.

We show in Figure 5 the opacities at J = 10 and 20, for v₀ = 0, E_coll ≤ 0.3 V, K_max = 0, 3, and 4, and kstep = 120. In the upper panels a blow up of 0.05 eV also shows the details of the resonance features. From this figure we can observe that the convergence in K_max is slower than for high energies. The curves at K_max = 0 exhibit less peaks and the resonances shift in energy by increasing this parameter. Three main groups of resonances could be identified, decreasing and then disappearing at high E_coll. This result suggests that the different peaks inside each group correspond to different bending energies of the collision complex (Aquilanti et al., 2005) while different groups correspond to different energies of the symmetric stretching motion. The v₀ = 1 curves have a similar behavior, with the K_max convergence slightly faster and the resonances at lower energies.

FIGURE 5

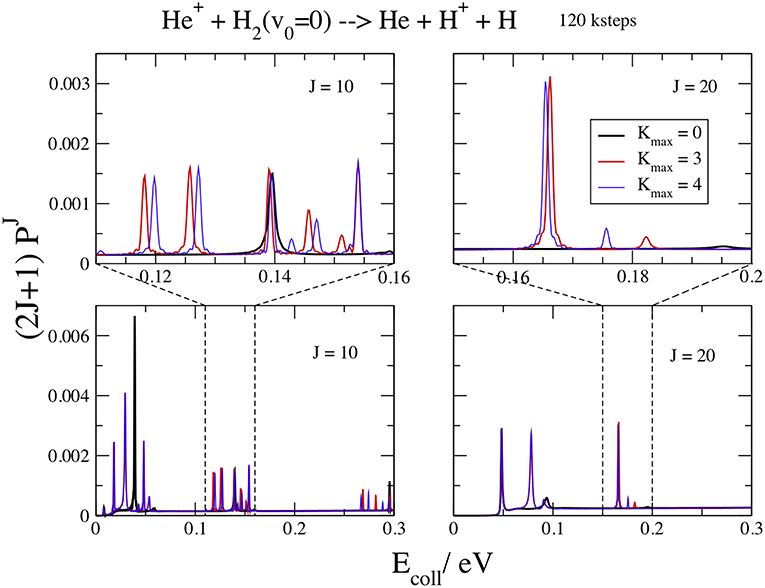
Figure 5. v₀ = 0; J = 10, 20; kstep = 120. Convergence of the opacities (2J+1)$P_{v_0}^J$ with respect to K_max.

In Figure 6 the resonance energy patterns at J = 5, 10, 15, and 20, v₀ = 1, and K_max = 3 are plotted for E_coll ≤ 0.11 eV at different kstep values. The K_max value gives a graphical convergence to the curves and the logarithmic scale of the energy points out the resonance details. Here kstep is much greater than for the background and changes markedly with J and E_coll. In fact, kstep = 350 is still not enough to converge all the J = 5 and 10 features, especially below 0.01 eV, but kstep = 160 perfectly converges the resonances at J = 15 and 20. As expected, the slowest convergent resonances are the narrowest ones, with largest lifetimes (Aquilanti et al., 2004). Moreover, the lifetimes of the collision complexes decrease at high J and E_coll, because the centrifugal barrier increases and the resonances are less trapped inside the shallower well. Above J = 25 the well is so shallow that it does not support any resonance and the features disappear. Of course, increasing kstep means increase the collision time that must be of the same order of magnitude of the lifetime of the resonance intermediate to give convergent results.

FIGURE 6

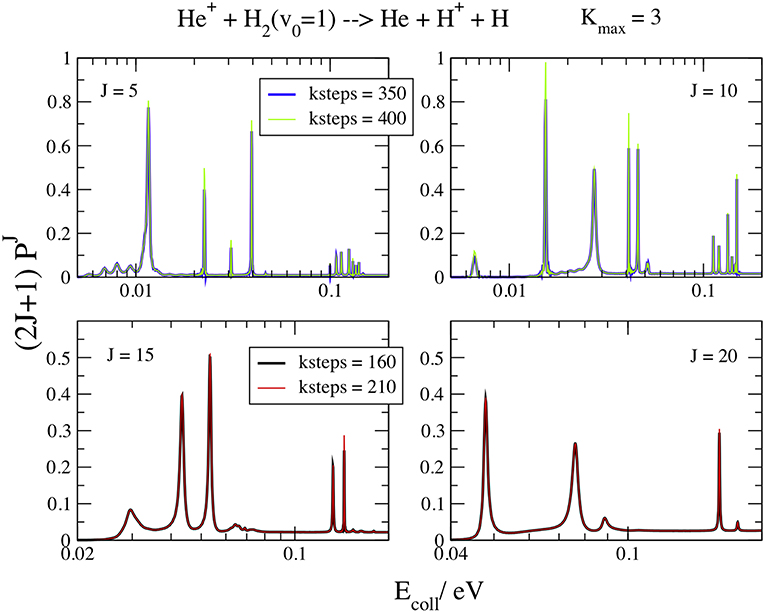
Figure 6. v₀ = 1; J = 5, 10, 15, 20; K_max = 3. Convergence of the opacities (2J+1)$P_{v_0}^J$ with respect to kstep.

Integral Cross Sections and Rate Constants

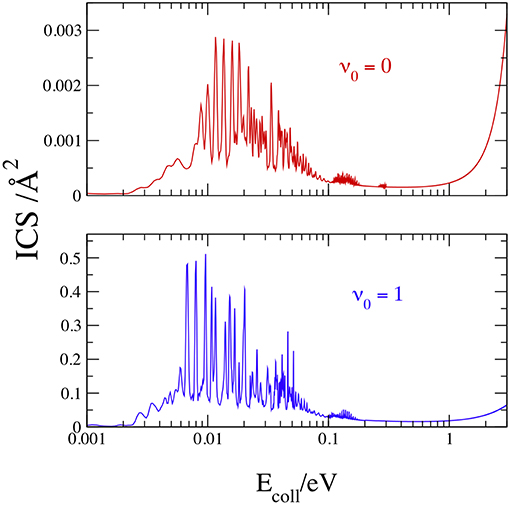
We plot in Figure 7 the total ICS at v₀ = 0 and 1, with J ≤ 150 to obtain convergent results up to 3 eV, noting that the convergent requirements change markedly with E_coll and J. To minimize the computational effort, the total number of partial waves was therefore shared in different groups, and different values of K_max and kstep were employed in each group, as shown in Table 2.

FIGURE 7

Figure 7. Initial-state-resolved ICSs at v₀ = 0 (red) and 1 (blue).

TABLE 2

Table 2. Parameters of ICS calculations.

Notwithstanding the large kstep used for the lowest partial waves, test calculations show that some narrow ICS peak slightly increases with more steps. With these input data, a convergence within 0.1% is reached only by the resonance peaks above 0.05 eV. The results in Figure 7 confirm the general scenario of the opacities: sharp resonances below 0.3 eV and a monotonic increase at larger E_coll. The J sum now merges the resonances in two main groups, the first and stronger below 0.1 eV, and the latter and weaker from 0.1 to 0.3 eV. At v₀ = 0, the strongest resonance is equal to 0.003 Ų at 0.0116 eV and the maximum at 3 eV has nearly the same value. At v₀ = 1, the strongest resonance is larger than the value at 3 eV by ~one order of magnitude, and is equal to 0.455 Ų at 0.0096 eV. In conclusion, the one-quantum vibrational excitation of H₂(X¹Σ${}_g^{+}$) increases the cross section by more than two orders of magnitude at ~0.01–0.02 eV and by ~20 times at 3 eV.

As said in the Introduction, only the semiclassical theoretical works by Aguillon (1994, 1998) have obtained ICSs at or below 3 eV. We present in Table 3 a comparison between our quantum ICSs and those estimated from Figure 4 of Aguillon (1998), showing the good agreement between the results that differ at the most by ~24% at v₀ = 0 and E_coll = 2 eV. Taking into account the different theoretical treatment and the small reactivity at these conditions, this implies that the Aguillon semiclassical treatment of the DCT reaction works remarkably well at this collision energies, where the ICSs do not present any quantum resonance.

TABLE 3

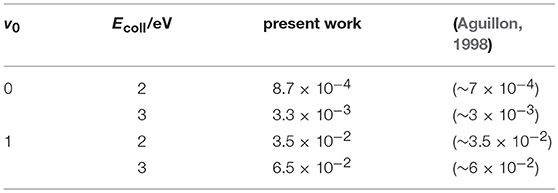
Table 3. Present quantum ICSs/Ų vs. those semiclassical (Aguillon, 1998).

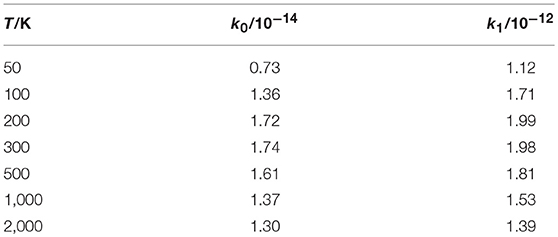
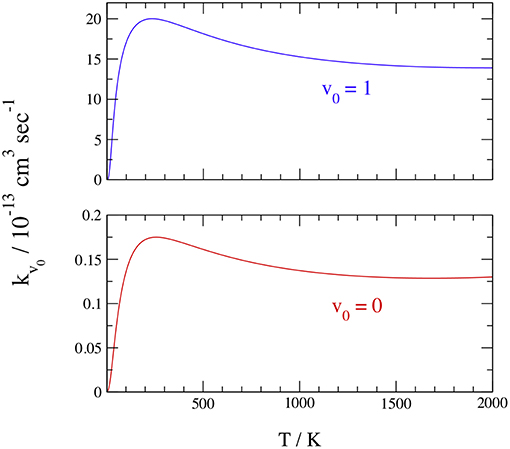
Finally, we report in Table 4 and Figure 8 the initial-state-resolved rate constants k_v0(T), at v₀ = 0 and 1, as functions of the temperature T up to 2,000 K. Their accuracy is ~2%, considering the slow convergence of the resonances, and the rates are stable with respect to changes of the parameters in Tables 1, 2. Both rates increase quickly by a factor of ~30 from 20 to 200 K, with a maximum at ~250 K equal to 1.75 10⁻¹⁴ and 1.97 10⁻¹² cm³ sec⁻¹ for v₀ = 0 and 1, respectively. This behavior is associated with the sharp ICS resonances above ~0.006 eV and is similar to that of H+HeH⁺ (De Fazio, 2014). Note that a rate-constant maximum was also found in the adiabatic ground PES dynamics of H+HeH⁺ (Esposito et al., 2015) using the PES of Ramachandran et al. (2009), but it was at ~10,000 K and due to a complete different mechanism. Then the rates slowly decrease with T and become nearly constant above 1,500 K, where they differ by two orders of magnitude. On the overall, this behavior is due to the ICS resonances shown in Figure 7 overlapped to a nearly Langevin decrease of the associated cross sections up to ~0.5 eV.

TABLE 4

Table 4. Rate constants k₀ and k₁/cm³ s⁻¹.

FIGURE 8

Figure 8. Initial-state-resolved rate constants at v₀ = 0 (red) and 1 (blue).

Because we have considered just the ground rotational state of H₂(X¹Σ${}_g^{+}$), j₀ = 0, the present rate constant at v₀ = 0 and 300 K underestimates by a factor of ~6 the thermal experimental k(330) = (1.1 ± 0.1) × 10⁻¹³cm³s⁻¹ (Johnsen et al., 1980), which is however 39 years old. The agreement increases if we consider H₂ in the excited rotational states that are open at 300 K, because test calculations suggest that the reactivity can be enhanced by ~33% when j₀ = 1. Taking into account the H₂(X¹Σ${}_g^{+}$) Fermi-Dirac nuclear spin statistics, the room-temperature populations of j₀ = 0 and 1 are ~0.13 and 0.66, respectively, and this implies a rotational enhancement of the rate constant by a factor of ~7. Owing to the room-temperature branching ratio of para- and ortho-H₂ and the rotational effects on the reactivity, we can roughly estimate than ortho-H₂ is ~4 times more reactive than the para species.

In closing this section, we have also done some test calculations of the reaction probabilities in the adiabatic approximation, on the òA' PES of ${\text{HeH}}_2^{+}$ (see Figure 1). Without reaching the accuracy and the stability of the results in section Reaction Probabilities, we present an example at v₀ = 0, J = 0, and kstep = 120, contrasting in Figure 9 adiabatic òA' and non-adiabatic CI (1)²A₁/(2)²B₂ results. Although both probabilities present a resonance structure at low E_coll and increase above ~1 eV, the reactivity is dramatically different, with the òA′ probability hugely larger than the CI one, from 6 orders of magnitude at 0.001 eV to 2 orders at 3 eV. This finding shows that the òA′ adiabatic PES drives the WP into the exothermic product channel, following a C_s pathway that avoids the C_2v barrier of the CI. On the contrary, the non-adiabatic CI WP remains essentially on the initial and repulsive (1)²A₁ diabatic PES V₁₁, owing to the weak non-adiabatic interaction. As expected, only at energies larger than 3 eV the two probabilities seem to merge and the adiabatic approximation is probably less worse. We roughly estimate that the adiabatic òA′ rate constants at 330 K is ~1,000 times larger than the experimental value (Johnsen et al., 1980).

FIGURE 9

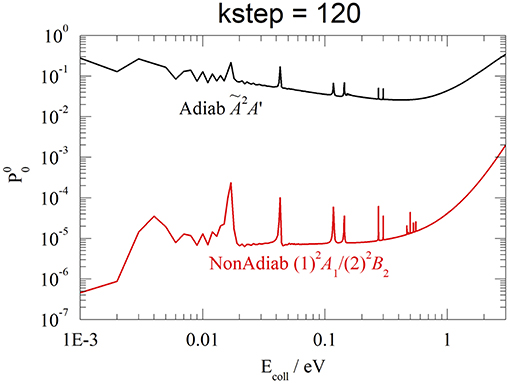
Figure 9. v₀ = 0, J = 0, kstep = 120. Adiabatic òA' (black) and non-adiabatic (1)A₁/(2)B₂ (red) probabilities.

Conclusions

In this article we have presented quantum non-adiabatic DCT results of the He⁺+H₂ collision, employing an electronic diabatic representation, previously computed by Aguado et al. (1993), a WP time dependent formalism, and a flux analysis. Specifically, we have taken into account the non-adiabatic CI coupling between the first two excited diabatic PESs of ${\text{HeH}}_2^{+}$. Dynamical calculations are performed for the ground and first excited vibrational states of H₂, for investigating vibrational effects on the DCT dynamics, and collision energies up to 3 eV are considered. Reaction probabilities and ICSs present strong and narrow resonance features up to 0.5 eV, due to quasi-bound molecular states embedded in the continuum and trapped in the ion-induced dipole minimum of the reactant channel, near the CI. These features are very hard to converge and affect all the DCT dynamics. These intense resonance features have a determinant role in the radiative charge-transfer formation (Mrugala et al., 2013) of stable ${\text{HeH}}_2^{+}$, probably present in the interstellar medium (Tennyson and Miller, 1987). At higher collision energies the computational load reduces drastically owing to a near conservation of the helicity quantum number. Our results are in reasonable agreement with previous experimental and theoretical studies of this reaction, confirming the strong vibrational enhancement previously founded. In fact, rate constants increase of about two orders of magnitude just adding one vibrational quantum to the H₂ reactants.

At the best of our knowledge, these are the first rigorous quantum DCT calculations presented for a chemical system, made possible by the joint implementation of time-dependent WP, time-to-energy Fourier transform, and flux methods. On the other hand, a more rigorous approach, as time independent close coupling calculations, cannot be attempted at the present state-of-the-art of the reaction dynamics theories, because of the difficulty of these methods to treat the three-bodies breakup (see e.g., (Pack et al., 1998), and references therein). The results achieved could have relevant consequences in astrophysics and in particular in the early Universe evolution models (Bovino et al., 2011). Although the reaction is probably negligible when the molecular hydrogen is relaxed in its ground vibrational state, the strong increase with the vibrational energy suggests that it could have a role during the early stages of the adiabatic expansion at high redshift, destroying the molecular hydrogen formed and slowing down further cooling of the primordial gas. Of course, to determinate its role, evolution Universe models with at least a vibrational resolution of the chemical network (Coppola et al., 2011, 2012) are required. Moreover, this reaction could be also relevant in other different astrophysical environments, as for example in the study of the Sun atmosphere where the temperature is very high and hydrogen and helium are very abundant species.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are very grateful to P. Gamallo and to the Dipartimento di Biotecnologie, Chimica, e Farmacia, Universita' di Siena, Italy, for the availability of essential computer resources. We want also to thank O. Roncero for fruitful discussions. The research leading to these result has received funding from the European Research Council under the European Union's Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement n. 610256 (NANOCOSMOS), the HPC Europa3 Project (INFRAIA-2013-1-730897) with the support of the EC Research Innovation Action under H2020 Programme and the COST Action CM1401 (Our Astrochemical History). Also, we acknowledge support by the Ministerio de Economía y Competitividad under grants No. FIS2014-52172-C2-2-P and FIS2017-83473-C2-2-P. CINECA is also acknowledged for computer time awarded via the ISCRA programme.

References

Aguado, A., and Paniagua, M. (1992). A new functional form to obtain analytical potentials of triatomic molecules. J. Chem. Phys. 96, 1265–1275. doi: 10.1063/1.462163

CrossRef Full Text | Google Scholar

Aguado, A., Suárez, C., and Paniagua, M. (1993). Accurate fit of the two lowest excited-state potential-energy surfaces for doublet ${\text{HeH}}_2^{+}$. J. Chem. Phys. 98, 308–315.

Google Scholar

Aguado, A., Suárez, C., and Paniagua, M. (1994). Accurate global fit of the H₄ potential energy surface. J. Chem. Phys. 101, 4004–4010. doi: 10.1063/1.467518

CrossRef Full Text | Google Scholar

Aguado, A., Tablero, C., and Paniagua, M. (1998). Global fit of ab initio potential energy surfaces I. Triatomic systems. Comp. Phys. Comm. 108, 259–266. doi: 10.1016/S0010-4655(97)00135-5

CrossRef Full Text | Google Scholar

Aguado, A., Tablero, C., and Paniagua, M. (2001). Global fit of ab initio potential energy surfaces: II.1. Tetraatomic systems ABCD. Comp. Phys. Comm. 134, 97–109. doi: 10.1016/S0010-4655(00)00181-8

CrossRef Full Text | Google Scholar

Aguillon, F. (1994). Semi-classical coupled wavepacket study of the dissociative charge exchange He⁺+H₂→ He+H+H⁺. Chem. Phys. Lett. 222, 69–74. doi: 10.1016/0009-2614(94)00330-0

CrossRef Full Text | Google Scholar

Aguillon, F. (1998). A new treatment of nonadiabatic dynamics: application to the determination of the He⁺+H₂ → He+H+H⁺ differential cross section. J. Chem. Phys. 109, 560–571. doi: 10.1063/1.476592

CrossRef Full Text | Google Scholar

Aquilanti, V., Cavalli, S., De Fazio, D., Simoni, A., and Tscherbul, T. V. (2005). Direct evaluation of the lifetime matrix by the hyperquantization algorithm: narrow resonances in the F+H₂ reaction dynamics and their splitting for nonzero angular momentum. J. Chem. Phys. 123:054314. doi: 10.1063/1.1988311

PubMed Abstract | CrossRef Full Text | Google Scholar

Aquilanti, V., Cavalli, S., Simoni, A., Aguilar, A., Lucas, J. M., and De Fazio, D. (2004). Lifetime of reactive scattering resonances: Q-matrix analysis and angular momentum dependence for the F+H₂ reaction by the hyperquantization algorithm. J. Chem. Phys. 121, 11675–11690. doi: 10.1063/1.1814096

PubMed Abstract | CrossRef Full Text | Google Scholar

Bovino, S., Tacconi, M., Gianturco, F. A., and Galli, D. (2011). Ion chemistry in the early unverse: revisiting the role of HeH⁺ with new quantum calculations. Astronomy Astrophys. 529:A150. doi: 10.1051/0004-6361/201116740

CrossRef Full Text | Google Scholar

Cederbaum, L. S., and Friedman, R. S. (2003). Conical intersections and bound molecular states embedded in the continuum. Phys. Rev. Lett. 90:013001. doi: 10.1103/PhysRevLett.90.013001

PubMed Abstract | CrossRef Full Text | Google Scholar

Coppola, M., D'Introno, R., Galli, D., Tennyson, J., and Longo, S. (2012). Non-equilibrium H₂ formation in the early universe: energy exchanges, rate coefficients, and spectral distortions. Astrophys. J. Suppl. Ser. 199:16. doi: 10.1088/0067-0049/199/1/16

CrossRef Full Text | Google Scholar

Coppola, M., Longo, S., Capitelli, M., Palla, F., and Galli, D. (2011). Vibrational level population of H₂ and ${\text{H}}_2^{+}$ in the early universe. Astrophys. J. Suppl. Ser. 193:7. doi: 10.1088/0067-0049/193/1/7

CrossRef Full Text | Google Scholar

De Fazio, D. (2014). The H+HeH⁺ → He+${\text{H}}_2^{+}$ reaction from the ultra-cold regime to the three-body breakup: exact quantum mechanical integral cross sections and rate constants. Phys. Chem. Chem. Phys. 16, 11662–11672. doi: 10.1039/C4CP00502C

CrossRef Full Text | Google Scholar

De Fazio, D. M., de Castro-Vitores, M., Aquilanti, V., and Cavalli, S. (2012). The He+${\text{H}}_2^{+}$ → HeH⁺+H reaction: Ab initio studies of the potential energy surface, benchmark time-independent quantum dynamics in an extended energy range and comparison with experiments. J. Chem. Phys. 137:244306. doi: 10.1063/1.4772651

CrossRef Full Text | Google Scholar

Dhuicq, D., Jugi, B., Benoit, C., and Sidis, V. (1998). The He⁺+H₂ → HeH⁺+H*(2s,2p)+H₂ reaction: study of the s and p contributions in a coincidence-correlation experiment. J. Chem. Phys. 109, 512–524. doi: 10.1063/1.476588

CrossRef Full Text | Google Scholar

Dhuicq, D., Lehner, O., Linder, F., and Sidis, V. (1996). Angular and energy analysis of HeH⁺ products from the charge exchange excitation reaction He⁺+H₂ → HeH⁺+H*. Chem. Phys. 206, 139–159. doi: 10.1016/0301-0104(96)00014-6

CrossRef Full Text | Google Scholar

Dunning, T. H. Jr. (1989). Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen. J. Chem. Phys. 90, 1007–1023.

Google Scholar

Esposito, F., Coppola, C. M., and De Fazio, D. (2015). Complementarity between quantum and classical mechanics in chemical modeling. The H+HeH⁺ → ${\text{H}}_2^{+}$+He reaction: a rigourous test for reaction dynamics methods. J. Phys. Chem. A 119, 12615–12626. doi: 10.1021/acs.jpca.5b09660

CrossRef Full Text | Google Scholar

Galli, D., and Palla, F. (2013). The dawn of chemistry. Annu. Rev. Astron. Astrophys. 51:163. doi: 10.1146/annurev-astro-082812-141029

CrossRef Full Text | Google Scholar

Gamallo, P., Akpinar, S., Defazio, P., and Petrongolo, C. (2013). Conical-intersection quantum dynamics of OH(A²Σ⁺)+H(²S) collisions. J. Chem. Phys. 139:94303. doi: 10.1063/1.4819355

PubMed Abstract | CrossRef Full Text | Google Scholar

Gamallo, P., Akpinar, S., Defazio, P., and Petrongolo, C. (2015). Born–Oppenheimer and Renner–Teller quantum dynamics of CH(X²Π)+D(²S) reactions on three CHD potential surfaces. J. Phys. Chem. A 119, 11254–11264. doi: 10.1021/acs.jpca.5b08891

CrossRef Full Text | Google Scholar

Giese, C. F., and Maier, W. M. I. I. (1961). Ion-molecule reactions studied with mass analysis of primary ion beam. J. Chem. Phys. 35, 1913–1914. doi: 10.1063/1.1732184

CrossRef Full Text | Google Scholar

Gioumousis, G., and Stevenson, D. P. (1958). Reactions of gaseous molecule ions with gaseous molecules. V. Theory. J. Chem. Phys. 29, 294–299. doi: 10.1063/1.1744477

CrossRef Full Text | Google Scholar

Gray, S. K., and Balint-Kurti, G. G. (1998). Quantum dynamics with real wave packets, including application to three-dimensional (J = 0)D+H2 → HD+H(J = 0) reactive scattering. J. Chem. Phys. 108, 950–962. doi: 10.1063/1.475495

CrossRef Full Text | Google Scholar

Guo, H. (2012). Quantum dynamics of complex-forming bimolecular reactions. Int. Rev. Phys. Chem. 31, 1–68. doi: 10.1080/0144235X.2011.649999

CrossRef Full Text | Google Scholar

Herbst, E., and Klemperer, W. (1973). The formation and depletion of molecules in dense interstellar clouds. Ap. J. 185:505. doi: 10.1086/152436

CrossRef Full Text | Google Scholar

Johnsen, R., Chen, A., and Biondi, M. A. (1980). Dissociative charge transfer of He⁺ ions with H₂ and D₂ molecules from 78 to 330 K. J. Chem. Phys. 72, 3085–3088. doi: 10.1063/1.439512

CrossRef Full Text | Google Scholar

Lepp, S., Stancil, P. C., and Dalgarno, A. (2002). Atomic and molecular processes in the early universe. J. Phys. B At. Mol. Opt. Phys. 35, R57–R80. doi: 10.1088/0953-4075/35/10/201

CrossRef Full Text | Google Scholar

Martínez, E., Grimbert, D., Aguillon, F., and Sidis, V. (2000). Calculations of quantum cross-sections for dissociative charge transfer in the He⁺+H₂ collision in the 10–50 eV center of mass energy range. Chem. Phys. Lett. 322, 103–110. doi: 10.1016/S0009-2614(00)00363-8

CrossRef Full Text | Google Scholar

McGuire, P., and Kouri, D. J. (1974). Quantum mechanical close coupling approach to molecular collisions. jz-conserving coupled states approximation. J. Chem. Phys. 60, 2488–2499.

Google Scholar

McLaughlin, D. R., and Thompson, D. L. (1979). Ground- and lower excited-state discrete ab initio electronic potential energy surfaces for doublet ${\text{HeH}}_2^{+}$. J. Chem. Phys. 70, 2748–2769.

Google Scholar

Meijer, J. H. M., Goldfield, E. M., Gray, S. K., and Balint-Kurti, G. G. (1998). Flux analysis for calculating reaction probabilities with real wave packets. Chem. Phys. Lett. 293, 270–276. doi: 10.1016/S0009-2614(98)00743-X

CrossRef Full Text | Google Scholar

Mrugala, F., and Kraemer, W. P (2013). Radiative charge transfer in He⁺ +H₂ collisions in the milli- to nano-electron-volt range: a theoretical study within state-to-state and optical potential approaches. J. Chem. Phys. 138:104315. doi: 10.1063/1.4793986

PubMed Abstract | CrossRef Full Text | Google Scholar

Pack, R., Walker, R., and Kendrick, B. (1998). Three-body collision contributions to recombination and collision-induced dissociation. I. Cross sections. J. Chem. Phys. 109, 6701–6713. doi: 10.1063/1.477349

CrossRef Full Text | Google Scholar

Pack, R. T. (1974). Space-fixed vs body-fixed axes in atom-diatomic molecule scattering. Sudden approximations. J. Chem. Phys. 60, 633–639. doi: 10.1063/1.1681085

CrossRef Full Text | Google Scholar

Petrongolo, C. (1988). Nonadiabatic theory of triatomics: general formalism and application to Renner-Teller and conical-intersection effects. J. Chem. Phys. 89, 1297–1308. doi: 10.1063/1.455181

CrossRef Full Text | Google Scholar

Preston, R. K., Thompson, D. L., and McLaughlin, D. R. (1978). A theoretical prediction of vibrational enhancement for dissociative charge transfer in the ${\text{HeH}}_2^{+}$ system. J. Chem. Phys. 68:13.

Google Scholar

Ramachandran, N., De Fazio, D., Cavalli, S., Tarantelli, F., and Aquilanti, V. (2009). Revisiting the potential energy surface for the He+${\text{H}}_2^{+}$ → HeH⁺+H reaction at the full configuration interaction level. Chem. Phys. Lett. 469, 26–30. doi: 10.1016/j.cplett.2008.12.035

CrossRef Full Text | Google Scholar

Reinig, P., Zimmer, M., and Linder, F. (1992). Nucl. Fusion A&M Suppl. Wien: IAEA.

Google Scholar

Rydberg, R. (1931). Rydberg-Klein-Rees method for determining potential energy curves of diatomic molecules from band spectra. Ann. Phys. 73:376.

Google Scholar

Sanz-Sanz, C., Aguado, A., Roncero, O., and Naumkin, F. (2015). Non-adiabatic couplings and dynamics in proton transfer reactions of ${\text{H}}_n^{+}$systems: application to H₂+${\text{H}}_2^{+}$→H+H${}_3^{+}$ collisions. J. Chem. Phys. 143:234303. doi: 10.1063/1.4937138

CrossRef Full Text | Google Scholar

Schauer, M., Jefferts, S. R., Barlow, S. E., and Dunn, G. H. (1989). Reactions of H₂ with He⁺ at temperatures below 40 K. J. Chem. Phys. 91, 4593–4596. doi: 10.1063/1.456748

CrossRef Full Text | Google Scholar

Sidis, V. (1996). Diabatic excited states of the (HeH2)⁺ molecular ion for the charge exchange-excitation reaction: He⁺+H₂ → HeH⁺+H*. Chem. Phys. 209, 313–326. doi: 10.1016/0301-0104(96)00060-2

CrossRef Full Text | Google Scholar

Stancil, P. C., Babb, J. F., and Dalgarno, A. (1993). The radiative association of He⁺ and He and H⁺ and H. Ap. J. 414:672. doi: 10.1086/173113

CrossRef Full Text | Google Scholar

Stedeford, J. B. H., and Hasted, J. B. (1955). Further investigations of charge exchange and electron detachment—I. Ion energies 3 to 40 keV. Proc. Royal Soc. A 227, 466–486.

Google Scholar

Szidarovszky, T., and Yamanouchi, K. (2016). Photodissociation dynamics of weakly bound ${\text{HeH}}_2^{+}$ in intense light fields. Phys. Rev. A 94:063405. doi: 10.1103/physreva.94.063405

CrossRef Full Text | Google Scholar

Tennyson, J., and Miller, S. (1987). Predicted vibrational-rotation levels of H₂He⁺ and its isotopomers. J. Chem. Phys. 87, 6648–6652. doi: 10.1063/1.453399

CrossRef Full Text | Google Scholar

Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R., Schütz, M., Celani, P., et al. (2018). MOLPRO, Version 2015.1, a Package of ab initio Programs. Available online at: http://www.molpro.net

Woon, E., and Dunning, T. H. Jr. (1994). Gaussian basis sets for use in correlated molecular calculations. IV. Calculation of static electrical response properties. J. Chem. Phys. 100, 2975–2988.

Google Scholar

Zygelman, B., Stancil, P. C., and Dalgarno, A. (1998). Stimulated radiative association of He and H⁺. Ap. J. 508:121. doi: 10.1086/306399

CrossRef Full Text | Google Scholar