- 1Grupo de Química Teórica e Estrutural de Anápolis, Campus de Ciências Exatas e Tecnológicas, Universidade Estadual de Goiás, Anápolis, Brazil
- 2Dipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, Perugia, Italy
- 3Istituto di Struttura della Materia, Consiglio Nazionale delle Ricerche, Rome, Italy
Advances in the understanding of the dependence of reaction rates from temperature, as motivated from progress in experiments and theoretical tools (e. g., molecular dynamics), are needed for the modeling of extreme environmental conditions (e.g., in astrochemistry and in the chemistry of plasmas). While investigating statistical mechanics perspectives (Aquilanti et al., 2017b, 2018), the concept of transitivity was introduced as a measure for the propensity for a reaction to occur. The Transitivity plot is here defined as the reciprocal of the apparent activation energy vs. reciprocal absolute temperature. Since the transitivity function regulates transit in physicochemical transformations, not necessarily involving reference to transition-state hypothesis of Eyring, an extended version is here proposed to cope with general types of transformations. The transitivity plot permits a representation where deviations from Arrhenius behavior are given a geometrical meaning and make explicit a positive or negative linear dependence of transitivity for sub- and super-Arrhenius cases, respectively. To first-order in reciprocal temperature, the transitivity function models deviations from linearity in Arrhenius plots as originally proposed by Aquilanti and Mundim: when deviations are increasingly larger, other phenomenological formulas, such as Vogel-Fulcher-Tammann, Nakamura-Takayanagi-Sato, and Aquilanti-Sanches-Coutinho-Carvalho are here rediscussed from the transitivity concept perspective and with in a general context. Emphasized is the interest of introducing into this context modifications to a very successful tool of theoretical kinetics, Eyring's Transition-State Theory: considering the behavior of the transitivity function at low temperatures, in order to describe deviation from Arrhenius behavior under the quantum tunneling regime, a “d-TST” formulation was previously introduced (Carvalho-Silva et al., 2017). In this paper, a special attention is dedicated to a derivation of the temperature dependence of viscosity, making explicit reference to feature of the transitivity function, which in this case generally exhibits a super-Arrhenius behavior. This is of relevance also for advantages of using the transitivity function for diffusion-controlled phenomena.
Introduction
To understand and control the physical chemistry of materials in an ample variety of environments that may be encountered in basic and applied scientific research, information on the kinetics of the involved elementary processes and their role in global mechanisms is needed: of particular interest are the rates, and often in a wide range of conditions—specifically of temperature. Theoretical and computational studies are of increasing utility, especially in the cases where experimental results are difficult to obtain, or the measurements are difficult to interpret. Examples span all of chemistry: from the long list that is continuously updated, we refer here to some selected cases from: combustion chemistry (Atkinson, 1986); condensed-phase (Limbach et al., 2006), atmospheric and astrochemical reactions (Smith, 2008; Sims, 2013); processes involved in preservation and aging of food and drugs (Darrington and Jiao, 2004; Peleg et al., 2012) as well as in basic geochemical (e.g., Giordano and Russell, 2018) and biochemical environments (e.g., Klinman and Kohen, 2013; Warshel and Bora, 2016).
A variety of techniques has been applied with remarkable success in several scenarios to investigate the mechanisms to both calculate and interpret the kinetics of reactive processes at a microscopic level (Sikorski et al., 2004; Pu et al., 2006; Wang et al., 2012; Hassanali et al., 2014; Coutinho et al., 2015a; Santin et al., 2016; Roy et al., 2017). From the early Arrhenius (1889) and Eyring (1935) formulations, demands emerge for interpretative theoretical tools to study the kinetics of chemical reactions and to phenomenological account of reaction rate data as generated from exact quantum benchmarks or from approximate semi-classical and classical trajectory approaches.
The seminal phenomenological description of the reaction rate constants, date of birth of theoretical chemical kinetics as a science, can be traced back to 1889 with the empirical formulation of the Arrhenius formula (Arrhenius, 1889; Laidler, 1987).
where R is the gas constant and T is the absolute temperature. The pre-factor A (often found to be temperature independent) has sometimes been given the meaning and the name of a “frequency factor.” The quantity Ea is termed the “energy of activation” of the reaction; according to the Arrhenius interpretation, it represents the energy that the molecule in the initial state of the process must acquire before it can take part in the reaction, whether it be a physical or a chemical process. In the Arrhenius plane prompted by Equation (1) the logarithm of a reaction rate constant, ln k(T) is plotted against reciprocal temperature, : for systems that obey the Arrhenius law, Equation (1), a linear behavior is observed.
Formulations from first principles of theoretical reaction rates only became realistic after the advent of quantum and statistical mechanics. The Eyring formulation (~1935) proposes a consistent and predictive theory for the kinetic reaction rate constant: the celebrated Transition-State Theory (TST) (Eyring, 1935; Glasstone et al., 1941) provided the basis for the understanding of many phenomena and triggered most of the subsequent proposals for the understanding of physicochemical rate processes. However, as traditionally implemented, TST is unable to cope with systems with strong deviation from Arrhenius behavior (Masgrau et al., 2003). The chemical reactions for which quantum tunneling effects play an important role are those where Arrhenius plots show a concave curvature (Limbach et al., 2006; Silva et al., 2013; Sanches-Neto et al., 2017): this is the most important case of sub-Arrhenius kinetics for elementary reactions, but in complex processes it may show up, e.g., when concurrent reactions contribute to the mechanism (Hulett, 1964; Perlmutter-Hayman, 1976; Vyazovkin, 2016).
Eyring himself amplified the scope of his TST beyond elementary reactions proposing a formulation for including the description of viscosity and diffusion of fluids in physicochemical rate processes (Glasstone et al., 1941). However, an ample set of old and more recent data in wide ranges of temperature has been showing again and again a strong convex curvature in Arrhenius plot for both viscosity and diffusion in fluids (Angell, 1995; Coutinho et al., 2015b; Giordano and Russell, 2018). There are examples of super-Arrhenius kinetics, rare for elementary processes (Truhlar and Kohen, 2001), but that in complex processes are common, in particular when consecutive reactions contribute to the mechanism (Hulett, 1964; Perlmutter-Hayman, 1976; Vyazovkin, 2016): these are characteristic cases of super-Arrhenius kinetics for which the traditional Eyring's transition-state formulation fails. However, the TST connection between the potential energy surface profile with the phenomenological apparent activation energy through Tolman Theorem (Tolman, 1920), serves as a guide toward an interpretation of deviation from Arrhenius behavior.
In previous work (Aquilanti et al., 2017b, 2018) evidence emerged for introducing the phenomenological Transitivity function γ(T) which regulates transit in physicochemical transformations and can be put into a relationship with traditional and recent reaction rate constant formulas available in the literature. With respect to other popular phenomenological approaches, ours arguably offers flexibility for the description of the experimental data over a wide range of temperature alternative to other formulas, that were applied to various sets of problems, ranging from particle diffusion and viscosity in supercooled liquids and glasses (Angell, 2002; Stillinger and Debenedetti, 2013) to food and drug preservation and aging processes (Peleg et al., 2012).
The still popular Kooij formula (Kooij, 1893) involving an arbitrary Tn parameter multiplying the pre-factor A has no justification and is often unable to reproduce observations. Kooij formulation has to be discouraged and is physically unrealistic. It should be abandoned because: (i) at high temperature, the Arrhenius Activation energy is not recovered; (ii) at intermediate temperatures, the non-Arrhenius description is illusory valid only in extremely narrow ranges and is mathematically arbitrary; (iii) at low and ultra-low temperatures, there is consensus that non-Arrhenius behavior is pronounced, and the Kooij formula tends to Arrhenius law in clear disagreement with transitivity concept. Also, the Arrhenius-Break Temperature (ABT) formulation (Kumamoto et al., 1971; Kubo, 1985) is often one commonly used: it involves two additional parameters beyond Arrhenius and may turn out misleading from an interpretative viewpoint—when possible, it should be avoided in compacting data for modeling.
The suitability of the transitivity function is being checked against a variety of phenomenological examples with respect to its power to account for deviation from Arrhenius behavior. Here, we will show details on the treatment for amplifying the insight in various directions (section Transitivity Defined). In the subsequent section, specifically regarding the super-Arrhenius case, we establish the connections with the Vogel-Fulcher-Tammann treatments (VFT) (see Vogel, 1921; Fulcher, 1925; Tammann and Hesse, 1926) via the transitivity function. We also generalize the sub-Arrhenius case discussing in a uniform way the trend toward Wigner' limit (Wigner, 1948), yielding Nakamura-Takayanagi-Sato (NTS) formula (Nakamura et al., 1989) and Aquilanti-Sanches-Coutinho-Carvalho (ASCC) (Coutinho et al., 2018b) at low temperature. In section Transition-State Theory Extended to Moderate Tunneling (d-TST), the sub-Arrhenius case appropriate for extending the Transition-State Theory of Eyring (the d-TST formalism) is accounted for, as introduced and applied recently (Claudino et al., 2016; Carvalho-Silva et al., 2017; Sanches-Neto et al., 2017). A special attention will be devoted in section Viscosity and Diffusion From the Transitivity Function to a derivation of the temperature dependence of viscosity of fluids from the transitivity function γ according for the super-Arrhenius behavior and establishing the connection with the diffusion coefficient through the Stokes-Einstein equation. The final section is devoted to additional and concluding remarks.
Transitivity Defined
The Transitivity Plot
In this section, we will show how the properly defined “Transitivity” function γ(T) regulates the transit in physicochemical transformations: in other words, it controls the rate of passage with no bias from the transition-state hypothesis. In the 1976 article of Berta Perlmutter-Hayman (Perlmutter-Hayman, 1976) the concept of apparent activation energy Ea has been considered in a very deep detail: in her spirit 20 years later, the International Union of Pure and Applied Chemistry (Laidler, 1996) recommended the now accepted definition:
To be consistent with Equation (1), the assumption of constancy for Ea can be taken as valid for physicochemical processes, at least for the temperature range of interest but deviation occur. According to our classification of d-Arrhenius cases (Silva et al., 2013; Aquilanti et al., 2017a), the deviations are considered as exhibiting sub-, super-, or anti-types of behavior.
An initial step in order to find out how to account in a simple form for these deviations, we search for a functional dependence of Ea according to a large variety of cases accumulated from experiments and simulations. In her thorough study, a few decades-old, Perlmutter-Hayman (Perlmutter-Hayman, 1976) considered a large body of documentation where the dependence were regarded either as
the latter form clearly inspired by the Arrhenius plot. We have been showing ample phenomenological evidence and deep theoretical motivation (Aquilanti et al., 2017b) of the insight to be gained by studying
i.e., to study the behavior of the reciprocal the activation energy studied against reciprocal of absolute temperature. Therefore, from now on, we find convenient to adopt the usual definition in statistical mechanics, of the parameter sometime referred to as “the coldness” (e.g., Müller, 1971) and often referred as to the Lagrange parameter, because of its ubiquitous role in statistical mechanics where it occurs in optimization procedures involving the Lagrange multipliers.
From a decade-old work (Aquilanti et al., 2010), the observation arose that the reciprocal of Ea vs. the reciprocal of absolute temperature yielded an approximate linearization by the d parameter (italic symbol for the linearization parameter should not be confused with the roman d denoting differentials). Writing as customary the Arrhenius-Eyring energy barrier, ε‡, as essentially an energetic obstacle toward reaction, we have
Introducing the “transitivity” function through the identifications
and also putting
Equation (5) takes the simple form
In general, as discussed in preceding work (Aquilanti et al., 2017b), a linear γ dependence from β may be only valid in a specific range around a value β0; on a wider range, we can always assume that the function is well-behaved, namely that it has a Laurent power expansion,
where the cn coefficients are related to n-order derivatives of γ(β) with respect to β, taken at β0.
The task of a theory of the kinetics of chemical reactions is therefore focused at that of providing a set of such coefficients to connect to experimental or computationally generated k(T) via Equations (2 and 6). Advantages now are shown for the introduction of the “Transitivity Plot,” defining as the plane γ vs. β, which gives insight into the idea of the “canonical” dependence of the γ function in regulating transitions in physicochemical processes (see Figure 1).
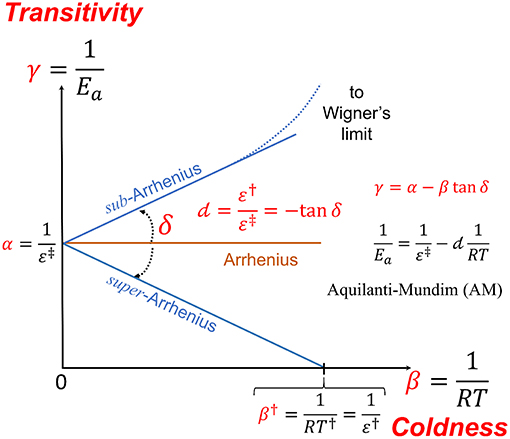
Figure 1. The transitivity plane, vs. serves to give a geometrical meaning to the phenomenological parameters occurring in the study of non-linear Arrhenius plots. The Arrhenius behavior is given as corresponding to a line parallel to the β axis starting at and corresponds to a constant apparent activation energy Ea. The well-known double dagger notation was introduced by Eyring (Eyring, 1935; Glasstone et al., 1941). Deviations from Arrhenius behavior gives to the γ function straight line dependence at small β a direction forming the δ angle, which it is connected to the d parameter of the Aquilanti-Mundim (AM) law. At low temperatures as the “coldness” variable β increases, the transitivity function tends to characteristic ultra-cold limiting values: (i) for d < 0 (sub-Arrhenius) it tends to the Wigner limit and (ii) for d > 0 (super-Arrhenius), γ, namely the propensity for reaction to occur, vanishes in β†, γ(β†) = 0: the corresponding energy and temperature parameters are denoted by a single dagger, ε†and T†, respectively, as detailed below.
Consistently with the established nomenclature, one gets a positive linear dependence of γ(β) for sub-Arrhenius (and negative for super-Arrhenius, d > 0): this according to experimental and theoretical evidence from many sources (Aquilanti et al., 2010; Silva et al., 2013). Defining in the transitivity plot , Equation (7), as a horizontal line (the Arrhenius line), the line of deviations from Arrhenius around β0 forms δ angle which can show sub- or super-Arrhenius-type of behavior, corresponding to anticlock—and clockwise direction from the β axis, respectively, yielding an expression corresponding to Equation (8),
where d < 0 (δ > 0) corresponds to the sub- case while d > 0 (δ < 0) corresponds to the super-Arrhenius case. Rarer cases are found for which d > 0 and α < 0, and are referred as corresponding to anti-Arrhenius behavior (e.g., Coutinho et al., 2015a).
The expression for the rate constant can be retrieved, integrating (10) from Equation (2). Introducing an integrating factor, A that accounts for a value for γ at the reference value, e.g., β = 0: we obtain the Aquilanti-Mundim (AM) or d-Arrhenius formula in the form:
Through Equations (7, 10) and introducing the Lagrange parameter, we finally obtain the AM formula
in the usual notation (Aquilanti et al., 2010). The Arrhenius law is obtained in two well-defined cases at β → 0 (high temperature limit) and at d → 0 (the “thermodynamic” limit) (Aquilanti et al., 2018).
Limiting Behaviors for the Transitivity Function at Low and High Temperature
In the AM formulation for k, Equation (12), when d or tan δ tends to zero, one gets the exponential Arrhenius behavior through the Euler limit as detailed in Aquilanti et al. (2018). In this limit, to first order, the transitivity function deviate linearly from constancy (the Arrhenius behavior) as described by the AM formula. When β increases (low temperature):
i) in the super-Arrhenius cases, continuing the straight-line behavior one encounters the β axis and gets for γ a zero value for a maximum attainable value of β, denoted β†. Here, one consequently gets a minimum value for the allowed temperature to be denoted T†. However, in generic super-Arrhenius behavior, sometimes high-order terms in the transitivity function are to be introduced to describe a sequence of processes, yielding concavities in the transitivity plot and moving the minimum temperature T† at lower values (Figure 2);
ii) in sub-Arrhenius cases, the linear growth of γ as β increases may be accelerated at low temperatures: actual experimental information (Limbach et al., 2006; Tizniti et al., 2014; Meng et al., 2015) is confirmed by computations (Aquilanti et al., 2005; De Fazio et al., 2006; Cavalli et al., 2014; De Fazio, 2014; Coutinho et al., 2018b) and is eventually governed by Wigner's limit (Wigner, 1948): before the latter limit is accessed interference effects may superimpose to quantum tunneling effects, which can be studied through microcanonical exact computations (Aquilanti et al., 2005; De Fazio et al., 2006; Coutinho et al., 2018b).
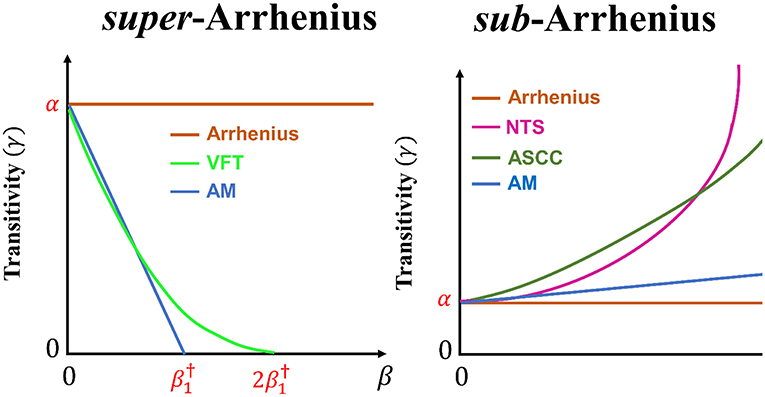
Figure 2. The transitivity plot is presented for venerable and recent phenomenological reaction rate constant model to account for super-Arrhenius behavior (Arrhenius, AM, and VFT) and sub-Arrhenius behavior (Arrhenius, AM, ASCC, and NTS). The comparison of the behavior of the transitivity between AM and VFT is exhibited assuming in Equation (26).
We are now in the position to look at the d-parameter from alternative perspectives. For super-Arrhenius cases, the β endpoint, β†, marks the final low-temperature range for the system to be “active”: energetically, the introduction of the corresponding energy ε† = RT†, permits the identification
For sub-Arrhenius, the connection of d with features of the potential energy barrier permits to describe quantum tunneling in elementary chemical reactions (see e.g., Silva et al., 2013 and next section).
Additional insight to the AM formula in Equation (5) for d < 0 is obtained when β tends to infinity yielding,
Going back to the rate constant, integrating (14) from Equation (2), we obtain
formally appearing as the venerable Esson-Harcourt formula (Laidler, 1984), and in consonance with the Wigner limit restricted to the case of thermoneutral reactions at ultra-low temperature (Takayanagi, 2004). Nevertheless, for d > 0 a minimum and constant reactivity is obtained for β†,
In Equation (16), when ε† tends to infinity, k(β) = A respecting the Arrhenius limit (most other formulations do not).
After the description of the sub- and super-Arrhenius cases in the limit d → 0 at large β, we turn now to consider the limiting behavior as β → 0, namely at high temperature. In most cases, the generic behavior is considered to be the tendency to the Arrhenius as a limit: situations may occur where this assumption has been relaxed [important examples are protein folding (Chan and Dill, 1998; Wallace et al., 2002) and reactions in sub- or super-critical solvent (Christensen and Sehested, 1983; Lukac, 1989; Marin et al., 2003)]. We can take advantage of the following useful expansion (Abe and Okamoto, 2008; Tsallis, 2009):
Therefore, Arrhenius behavior is recovered both as β and d tend to zero independently:
Phenomenological Models of Temperature Dependence of Reaction Rate Constants through the Transitivity Function
The previous development opens the way to the next step of our study, the examination and classification through the transitivity concept of previous phenomenological proposals, assessing relationships between them and also attempting at giving a physicochemical meaning to their empirical parameters. As a bonus, more physically motivated formulas can be generated.
From Equations (2, 6), it is possible to build up the theoretical apparatus to connect experimental or computationally generated reaction rate constants to the transitivity function and vice-versa. Below traditional and recent phenomenological reaction rate constant formulas and transitivity function are presented to deal with sub- and super-Arrhenius behavior with larger deviations than those not accounted for the AM d-Arrhenius formula (see Figure 2): VFT, ASCC, and NTS. The basic expression
Can be employed, where clearly, A = k(β0) represents the initial condition (again, the differential under the integral sign is denoted by the roman letter d to avoid confusion with d in italic for the deviation parameters).
Vogel–Fulcher–Tammann (VFT) Formula
It is insightful to obtain the expression for the transitivity function for perhaps the most popular equation for modeling super-Arrhenius behavior, the Vogel–Fulcher–Tammann (VFT) formula (Vogel, 1921; Fulcher, 1925; Tammann and Hesse, 1926), here written as a rate constant in an Arrhenius-like fashion, but involving one additional parameter:
where A, B, and T0 are the fitting parameters: they are often designated, respectively being often denoted as the pre-factor, pseudo-activation energy and VFT-temperature, respectively. It is noteworthy, that in the polymer and food science community (Angell, 1997; Peleg et al., 2002; Coutinho et al., 2015b) Equation (20) is also known as the Williams-Landel-Ferry (WLF) equation: see (Williams et al., 1955; Dudowicz et al., 2015) where the equivalence among the respective parameters is demonstrated explicitly.
The VFT transitivity function is obtained directly from the definition through the analytical logarithmic differentiation of Equation (20) with respect to β: The result is
That can be worked out in a more compact representation,
Here, formula (22) adds insight on the VFT parametrization for γ by a summarizing comparison with the Arrhenius and with the AM formulations for the transitivity function: the following general expression,
covers three cases for different values of n: (i) for n = 0 one recovers Arrhenius formula, (ii) for n = 1 the AM formula is obtained, and (iii) for n = 2 one gets the VFT (and WLF) formula. From Figure 1, in the transitivity plane, a geometrical interpretation can be given and leads to
in limiting case of β tending to zero,
and the comparison between n = 1 (AM) and n = 2 (VFT) parametrizations is shown to be
See details in Figure 2, where the ASCC and NTS formulas, to be discussed next, are also considered.
Deep Tunneling and the ASCC Formula
As reported in the earlier literature (Bell, 1980; Christov, 1997), the degree of concavity in the Arrhenius plot can be correlated with the assessment of the role of tunneling in chemical reactions: the definition of a “crossover temperature,”
permits to conventionally establish (within some arbitrariness) the ranges of tunneling regimes for a specific imaginary frequency at the top of the barrier point, consistently denoted by a double dagger, ν‡: classical (T > 4Tc), negligible(4Tc > T > 2Tc), moderate (2Tc > T > Tc) and deep (Tc > T) regimes. The ranges of tunneling regimes are indicative of the importance of quantum tunneling to affect rate constants in particular cases. From a mathematical viewpoint, the AM formulation has clear limitations in the description of the deep tunneling regime toward the Wigner limit (Wigner, 1948)
Details pertinent to the present discussion can be found in a very useful reference (Takayanagi et al., 1987).
As a counterpart for sub-Arrhenius behavior of the super-Arrhenius VFT formula, it is argued that cases of deep tunneling can be dealt by introducing a modified form of the AM formula (Coutinho et al., 2018b), defined as Aquilanti-Sanches-Coutinho-Carvalho (ASCC) expression:
where as reported in Silva et al. (2013) and references therein. Here, the formulation introduces the three A, ε‡ and ν‡ parameters and reproduces the Wigner limit at low temperature, β → ∞. The ASCC transitivity function can be worked out considering the logarithmic differentiation of Equation (29) with respect to β and the result is
or in a more compact representation,
For small values of dε‡, an analogous to VFT formula is recovered, see Equation (22). The ASCC formula was initially applied in Coutinho et al. (2018b) for astrochemical reactions in extremely cold environments generated by “exact” benchmark quantum dynamics. More results of applications will be given elsewhere for a variety of processes that involve deep tunneling.
Nakamura-Takayanagi-Sato (NTS) Formula
A flexible approach to describe the deep tunneling phenomenology was proposed 30 years ago by Nakamura et al. (1989) and Sato (2005): their formula evolves smoothly behavior down to low temperature and with respect to the tendency toward the Wigner limit (Wigner, 1948):
where A, ε‡ and T0 are the parameters. Again, ε‡ is essentially the fitting parameter bearing connection with the barrier height along the minimum energy pathway to reaction.
Also, in this case, we can work out the Nakamura-Takayanagi-Sato transitivity function
Beyond Eyring
Transition-State Theory Extended to Moderate Tunneling (d-TST)
Eyring's Transition-State Theory (TST) and its variants are frequently used to compute rates of chemical reactions typically assuming a well-defined activated complex. The theory has been the object of a number of studies yielding a variety of formulations based on the concept of an equilibrium between the reactants and the activated complex, all assumed with Boltzmann distributions of the internal degrees of freedom. The rate of transformation is, then, obtained by a combining of thermodynamics, kinetics, quantum chemistry, and statistical mechanics arguments. The authoritative textbook is (Glasstone et al., 1941). For a general bimolecular reaction, such as , it is necessary to compute the Q1, Q2, and Q‡ partition functions of R1, R2 and of the transition state, respectively. However, the conventional TST is not able to account for low temperature curvatures in the Arrhenius plot, particularly when due to quantum tunneling through the reaction barriers (for the viscosity of fluids see next section). To account for the quantum tunneling in chemical reactions, the transitivity function is modeled in analogy with the AM formula, yielding the deformed-Transition-State Theory (d-TST) (Carvalho-Silva et al., 2017):
where h is the Planck's constant and ε‡ is the effective height of the energy barrier, given by the sum of the harmonic zero-point energy correction and the height of the potential energy barrier. This formulation uniformly covers the range from classical to moderate tunneling regimes but is inadequate for deep tunneling. The proposed variant of transition-state theory permits comparison with experiments and tests against alternative formulations (see e.g., Claudino et al., 2016; Santin et al., 2016; Sanches-Neto et al., 2017).
Viscosity and Diffusion From the Transitivity Function
Eyring's proposal of a kinetic rate theory was also amplified toward the description of viscosity and diffusion of fluids in physicochemical processes (Eyring, 1936; Glasstone et al., 1941). Eventually, it turned out that the theory was unable to describe processes in a wide temperature range, in particular when presenting a convex curvature in the Arrhenius plot. In the present context, this is a manifestation of super-Arrhenius kinetics (Truhlar and Kohen, 2001; Coutinho et al., 2015b; Giordano and Russell, 2018). To describe deviations from Arrhenius of the rates of reaction in fluids, we take into account later developments by Kramers (1940) and Collins and Kimball (1949), involving viscosity and diffusion.
To account for the temperature dependence of viscosity in cases clearly exhibiting super-Arrhenius behavior, we introduce a treatment using the transitivity function concept. From the defining, Equations (2) and (6) we obtain the differential equation,
For β0 = 0 as the lower limit of integration range and the restriction to only two terms of the Taylor–McLaurin series of Equation (9), we obtain the AM transitivity function, where α < 0 represents an energetic propensity toward to evolution of the fluid. The d is again the deformation parameter, playing an analogous role to that amply discussed previously: the result is an AM-like formula for viscosity (Aquilanti et al., 2017b),
here ηo is introduced as a counterpart of Arrhenius pre-factor A and is the viscosity when the temperature tends to infinity (β → 0). At low temperature, in viscous processes the apparent activation energy turns out to increase indefinitely and consequently the propensity to proceed to a kinetic transition approaches zero, γ → 0: so we establish a direct relationship for the d parameter (analogous to the cases dealt in section Limiting Behaviors for the Transitivity Function at Low and High Temperature):
and T† is identified as a phenomenological “freezing” temperature of the process, namely the critical temperature (to be connected with that of glass transition, see Aquilanti et al., 2017b), where the kinetic energy of the fluid particles is too low for the process to be turned on. In the early approach by Eyring (1936) and Glasstone et al. (1941), it was argued that the ε‡ parameter be empirically put into relationship with the energy of vaporization of the fluid, ΔHvap, and intuitively connected with the work required to make a hole of molecular size.
Using the Kauzmann-Eyring pre-factor (Kauzmann and Eyring, 1940; Glasstone et al., 1941), where Na is the Avogadro number and is the molar volume, and Equation (37) for d, we finally obtain,
when T† tends to zero, the Arrhenius-Eyring exponential formula for viscosity is recovered, through the Euler limit.
The deviation from Arrhenius behavior in the temperature dependence of diffusion can now be evaluated from Equation (39) through the Stokes-Einstein equation(Einstein, 1905).
where r is the hydrodynamic radius (Henriksen and Hansen, 2008). This treatment of course does not provide further insight into these amply investigated issues, but points at a simple and perhaps useful physical interpretation of a long-standing as well recent intriguing rate phenomena. From a general perspective, the theory encourages considering wide ranges of available data on geochemistry (Giordano and Russell, 2018), supercooled liquids science (Angell, 1995) and biochemistry (Kohen et al., 1999) and digging for hidden insights. Preliminary searches, to be published, turned on successful.
Additional and Final Remarks
This paper applies thoroughly the transitivity concept to a set of topics, completing the presentation of the theory outlined in Aquilanti et al. (2017b). A separated paper (Machado et al., submitted) presents the code developed for the implementation to a set of cases of interest in physicochemical kinetics where the need for deviation from Arrhenius behavior is demanded: applications of our formulation can be accessed in the homepage of our computational code—Transitivity (www.vhcsgroup.com/transitivity), where manual, installation video, and specific examples are provided. Further remarks follow:
Ab initio “Exact” Quantum Dynamics
In principle, this is the most valuable source of kinetics data but still limited to simple benchmark cases. For full formulations of the reaction kinetics, following the microcanonical path along a quantum chemically or empirically generated potential energy surface, high-level computational effort is demanded. It typically proceeds according to these steps: a) calculation of the intermolecular interactions involved in a reactive process with a high-level of accuracy, b) dynamical evolution in phase-space configurations from the solution of quantum equations of motion, c) identification of reactive trajectories, with consequent calculation of the quantum scattering matrix, cumulative reaction probability and cross sections. Finally, the Boltzmann weight averaging over a large span of kinetics energies yields the canonical expressions of kinetic variables as a function of temperature. These severe prescriptions have been able to provide the exact calculation over a given potential energy surface for reaction rate constants of only a limited number of reactive systems: in fact, the complexity of the programming and the computationally demanding requirements and computational demand strongly limit the study of reactive processes involving only a few atoms. Additional reactions involving isotopic exchange among three hydrogen atoms, exemplary benchmarks to be cited are the three-body reactions: F + H2 (Aquilanti et al., 2005), F + HD (De Fazio et al., 2006; Cavalli et al., 2014), H + HeH+ (De Fazio, 2014) see also and references therein.
First-Principles Molecular Dynamics
Another viable path is becoming possible thanks to improvements in computational facilities, in order to access at kinetic information through first-principles molecular dynamics simulations. However, computationally severe storing and time constraints permitting to obtain myriads of “on-the-fly trajectories” require a great effort toward the aim of generating realistic reactive kinetic data: this in spite of the fact that a wide research activity has been pursued, aiming at developing techniques capable of accurately predicting kinetic reaction rate constants from molecular dynamics simulations. Among examples that have been tackled in recent years, we cite (Pomerantz et al., 2005; Coutinho et al., 2015a; Döntgen et al., 2015; Fleming et al., 2016; Wu et al., 2019) and references therein. However, calculation of reaction rate constants has been limited by the arduous procedures both to accurately characterize reactive activated complexes of many body systems and to overcome the inherent difficulties of producing a number of trajectories with statistical consistency and reasonable completeness in the filling of the dynamically relevant parts of the phase-space. Recently, several works have been yielding values with reliable accuracy: overestimates due to limited sampling of phase-space, when experimental values are available for comparison, may exploit empirical calibration (Coutinho et al., 2016, 2017, 2018a).
Phenomenological Considerations and the Role of the Transitivity Concept
Experimentally and computationally generated kinetic data for polyatomic molecules provide reaction rate constants with the implicit fingerprint of the microscopical variables at work in the reactive process (Angell, 1995; Kohen et al., 1999; Limbach et al., 2006; Giordano and Russell, 2018; Capitelli and Pietanza, 2019, and references therein). Application of the techniques discussed in previous remarks is tremendously laborious for many-body systems: when the Arrhenius law is not obeyed at low temperature transitivity function guides us to an as a fruitful and consistent approach. As discussed in this article the approach turns out to be a powerful tool, capable of establishing a connection between canonical data and microcanonical information, permitting comparisons among apparently uncorrelated formulations: it also allows interpretation of empirical parameters, for example for the AM, ASCC, VFT and NTS formulas considered in this paper. Previous (Tsallis and Bukman, 1996; Lenzi et al., 2001; JiangLin et al., 2006; Zhou and Du, 2013) and concomitant (Zhou and Du, 2014; Guo and Du, 2015; Rosa et al., 2016; Junior et al., 2019) efforts have been dedicated to provide also a connection of anomalous kinetic diffusion effects while surmounting a potential barrier via variants of Fokker-Planck equation, tackling a class of phenomenologically physicochemical diffusion process.
Conclusion and Perspectives
In order to extend the validity of the Arrhenius rate law, the introduction of the deformation parameter d not only phenomenologically mimics the low temperature dependence of rate constants, but its relevance in producing physical insight is now amply demonstrated. The statistical mechanics aspects are now firmly established (Aquilanti et al., 2017b, 2018) capitalizing on various investigations inspired openly or implicitly on a Maxwellian approach: several examples in the literature have been inspiring the transfer from thermodynamics to the field of kinetics assuming procedures for taking the “thermodynamic limit.” Venerable papers are (Jeans, 1913; Condon, 1938; Kennard, 1938; Landau and Lifshitz, 1958), and recent ones (Tsallis, 1999; Biró et al., 2014; Aquilanti et al., 2017b).
Data Availability
The raw data supporting the conclusions of this manuscript will be made available by the authors, without undue reservation, to any qualified researcher.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
VHC-S thanks Brazilian agency CNPq for the research funding programs [Universal 01/2016—Faixa A−406063/2016-8] and Organizzazione Internazionale Italo-Latino Americana (IILA) for Biotechnology Sector-2019 scholarship. VA and NDC acknowledge the Italian Ministry for Education, University and Research, MIUR, for financial support: SIR 2014 Scientific Independence for young Researchers (RBSI14U3VF).
References
Abe, S., and Okamoto, Y. (2008). Nonextensive Statistical Mechanics and Its Applications. Springer Berlin Heidelberg. Available online at: https://books.google.com.br/books?id=caNqCQAAQBAJ
Angell, C. A. (1995). Formation of glasses from liquids and biopolymers. Science 267, 1924–1935. doi: 10.1126/science.267.5206.1924
Angell, C. A. (1997). Why C1 = 16–17 in the WLF equation is physical—and the fragility of polymers. Polymer (Guildf). 38, 6261–6266. doi: 10.1016/S0032-3861(97)00201-2
Angell, C. A. (2002). Liquid fragility and the glass transition in water and aqueous solutions. Chem. Rev. 102, 2627–2650. doi: 10.1021/cr000689q
Aquilanti, V., Arruda, M. S., Coletti, C., Littlejohn, R., and Santos, R. F. (2017a). Combinatorial and Geometrical Origins of Regge Symmetries: Their Manifestations From Spin-Networks to Classical Mechanisms, and Beyond (Trieste; Cham: Springer). doi: 10.1007/978-3-319-62404-4_23
Aquilanti, V., Borges, E. P., Coutinho, N. D., Mundim, K. C., and Carvalho-Silva, V. H. (2018). From statistical thermodynamics to molecular kinetics: the change, the chance and the choice. Rend. Lincei. Sci. Fis. Nat. 28, 787–802. doi: 10.1007/s12210-018-0749-9
Aquilanti, V., Cavalli, S., De Fazio, D., Volpi, A., Aguilar, A., and Lucas, J. M. (2005). Benchmark rate constants by the hyperquantization algorithm. The F + H2 reaction for various potential energy surfaces: features of the entrance channel and of the transition state, and low temperature reactivity. Chem. Phys. 308, 237–253. doi: 10.1016/j.chemphys.2004.03.027
Aquilanti, V., Coutinho, N. D., and Carvalho-Silva, V. H. (2017b). Kinetics of low-temperature transitions and reaction rate theory from non-equilibrium distributions. Philos. Trans. R. Soc. London A 375:20160204. doi: 10.1098/rsta.2016.0201
Aquilanti, V., Mundim, K. C., Elango, M., Kleijn, S., and Kasai, T. (2010). Temperature dependence of chemical and biophysical rate processes: phenomenological approach to deviations from Arrhenius law. Chem. Phys. Lett. 498, 209–213. doi: 10.1016/j.cplett.2010.08.035
Arrhenius, S. (1889). On the reaction rate of the inversion of non-refined sugar upon souring. Z. Phys. Chem. 4, 226–248.
Atkinson, R. (1986). Kinetics and mechanisms of the gas-phase reactions of the hydroxyl radical with organic compounds under atmospheric conditions. Chem. Rev. 86, 69–201. doi: 10.1021/cr00071a004
Biró, T., Ván, P., Barnaföldi, G., and Ürmössy, K. (2014). Statistical power law due to reservoir fluctuations and the universal thermostat independence principle. Entropy 16, 6497–6514. doi: 10.3390/e16126497
Capitelli, M., and Pietanza, L. D. (2019). Past and present aspects of Italian plasma chemistry. Rend. Lincei. Sci. Fis. Nat. 30, 31–48. doi: 10.1007/s12210-019-00781-0
Carvalho-Silva, V. H., Aquilanti, V., de Oliveira, H. C., and Mundim, K. C. (2017). Deformed transition-state theory: deviation from Arrhenius behavior and application to bimolecular hydrogen transfer reaction rates in the tunneling regime. J. Comput. Chem. 38, 178–188. doi: 10.1002/jcc.24529
Cavalli, S., Aquilanti, V., Mundim, K. C., and De Fazio, D. (2014). Theoretical reaction kinetics astride the transition between moderate and deep tunneling regimes: the F + HD case. J. Phys. Chem. A 118, 6632–6641. doi: 10.1021/jp503463w
Chan, H. S., and Dill, K. A. (1998). Protein folding in the landscape perspective: Chevron plots and non-Arrhenius kinetics. Proteins Struct. Funct. Genet. 30, 2–23. doi: 10.1002/(SICI)1097-0134(19980101)30:1<2::AID-PROT2>3.0.CO;2-R
Christensen, H., and Sehested, K. (1983). Reaction of hydroxyl radicals with hydrogen at elevated temperatures. Determination of the activation energy. J. Phys. Chem. 87, 118–120. doi: 10.1021/j100224a027
Christov, S. G. (1997). The characteristic (crossover) temperature in the theory of thermally activated tunneling processes. Mol. Eng. 7, 109–147. doi: 10.1023/A:1008274213168
Claudino, D., Gargano, R., Carvalho-Silva, V. H., E Silva, G. M., and Da Cunha, W. F. (2016). Investigation of the abstraction and dissociation mechanism in the nitrogen trifluoride channels: combined post-hartree-fock and transition state theory approaches. J. Phys. Chem. A 120, 5464–5473. doi: 10.1021/acs.jpca.6b04947
Collins, F. C., and Kimball, G. E. (1949). Diffusion-controlled reaction rates. J. Colloid Sci. 4, 425–437. doi: 10.1016/0095-8522(49)90023-9
Condon, E. U. (1938). A simple derivation of the Maxwell-Boltzmann Law. Phys. Rev. 54, 937–940. doi: 10.1103/PhysRev.54.937
Coutinho, N. D., Aquilanti, V., Silva, V. H. C., Camargo, A. J., Mundim, K. C., and Oliveira, H. C. B. de (2016). Stereodirectional origin of anti-Arrhenius kinetics for a tetra-atomic hydrogen exchange reaction: Born-Oppenheimer molecular dynamics for OH + HBr. J. Phys. Chem. 120, 5408–5417. doi: 10.1021/acs.jpca.6b03958
Coutinho, N. D., Carvalho-Silva, V. H., de Oliveira, H. C. B., and Aquilanti, V. (2017). “The HI + OH → H2O + I reaction by first-principles molecular dynamics: stereodirectional and anti-Arrhenius kinetics,” in Computational Science and Its Applications—ICCSA 2017, eds O. Gervasi, B. Murgante, S. Misra, G. Borruso, C. M. Torre, A. M. A. C. Rocha, D. Taniar, B. O. Apduhan, and E. S. A. Cuzzocrea (Trieste: Springer International Publishing), 297–313. doi: 10.1007/978-3-319-62404-4_22
Coutinho, N. D., Sanches-Neto, F. O., Carvalho-Silva, V. H., de Oliveira, H. C. B., Ribeiro, L. A., and Aquilanti, V. (2018a). Kinetics of the OH + HCl → H2O + Cl reaction: rate determining roles of stereodynamics and roaming and of quantum tunneling. J. Comput. Chem. 39, 2508–2516. doi: 10.1002/jcc.25597
Coutinho, N. D., Silva, V. H. C., De Oliveira, H. C., Camargo, A. J., Mundim, K. C., and Aquilanti, V. (2015a). Stereodynamical origin of anti-arrhenius kinetics: negative activation energy and roaming for a four-atom reaction. J. Phys. Chem. Lett. 6, 1553–1558. doi: 10.1021/acs.jpclett.5b00384
Coutinho, N. D., Silva, V. H. C., Mundim, K. C., and de Oliveira, H. C. B. (2015b). Description of the effect of temperature on food systems using the deformed Arrhenius rate law: deviations from linearity in logarithmic plots vs. inverse temperature. Rend. Lincei 26, 141–149. doi: 10.1007/s12210-015-0407-4
Coutinho, N. D., Silva, Y. S., Fazio, D. de Cavalli, S., Carvalho-Silva, V. H., and Aquilanti, V. (2018b). “Chemical kinetics under extreme conditions: exact, phenomenological and first-principles computational approaches,” in Rendiconti Accademia Nazionale delle Scienze detta dei XL (Rome), 1–15.
Darrington, R. T., and Jiao, J. (2004). Rapid and accurate prediction of degradant formation rates in pharmaceutical formulations using high-performance liquid chromatography-mass spectrometry. J. Pharm. Sci. 93, 838–846. doi: 10.1002/jps.20006
De Fazio, D. (2014). The H + HeH+ → He+ H2+ reaction from the ultra-cold regime to the three-body breakup: exact quantum mechanical integral cross sections and rate constants. Phys. Chem. Chem. Phys. 16, 11662–11672. doi: 10.1039/c4cp00502c
De Fazio, D., Aquilanti, V., Cavalli, S., Aguilar, A., and Lucas, J. M. (2006). Exact quantum calculations of the kinetic isotope effect: cross sections and rate constants for the F + HD reaction and role of tunneling. J. Chem. Phys. 125:133109. doi: 10.1063/1.2221695
Döntgen, M., Przybylski-Freund, M. D., Kröger, L. C., Kopp, W. A., Ismail, A. E., and Leonhard, K. (2015). Automated discovery of reaction pathways, rate constants, and transition states using reactive molecular dynamics simulations. J. Chem. Theory Comput. 11, 2517–2524. doi: 10.1021/acs.jctc.5b00201
Dudowicz, J., Douglas, J. F., and Freed, K. F. (2015). The meaning of the “universal” WLF parameters of glass-forming polymer liquids. J. Chem. Phys. 142:014905. doi: 10.1063/1.4905216
Einstein, A. (1905). Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Phys. 322, 549–560. doi: 10.1002/andp.19053220806
Eyring, H. (1935). The activated complex in chemical reactions. J. Chem. Phys. 3, 107–115. doi: 10.1063/1.1749604
Eyring, H. (1936). Viscosity, plasticity, and diffusion as examples of absolute reaction rates. J. Chem. Phys. 4, 283–291. doi: 10.1063/1.1749836
Fleming, K. L., Tiwary, P., and Pfaendtner, J. (2016). New approach for investigating reaction dynamics and rates with ab initio calculations. J. Phys. Chem. A 120, 299–305. doi: 10.1021/acs.jpca.5b10667
Fulcher, G. S. (1925). Analysis of recent measurements of the viscosity of glasses. J. Am. Ceram. Soc. 8, 339–355. doi: 10.1111/j.1151-2916.1925.tb16731.x
Giordano, D., and Russell, J. K. (2018). Towards a structural model for the viscosity of geological melts. Earth Planet. Sci. Lett. 501, 202–212. doi: 10.1016/j.epsl.2018.08.031
Glasstone, S., Laidler, K. J., and Eyring, H. (1941). The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion and Electrochemical Phenomena. McGraw-Hill. Available online at: https://books.google.com.br/books?id=7zwGAQAAIAAJ
Guo, R., and Du, J. (2015). The precise time-dependent solution of the Fokker–Planck equation with anomalous diffusion. Ann. Phys. 359, 187–197. doi: 10.1016/J.AOP.2015.04.019
Hassanali, A. A., Cuny, J., Verdolino, V., and Parrinello, M. (2014). Aqueous solutions: state of the art in ab initio molecular dynamics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 372, 20120482–20120482. doi: 10.1098/rsta.2012.0482
Henriksen, N. E., and Hansen, F. Y. (2008). Theories of Molecular Reaction Dynamics: The Microscopic Foundation of Chemical Kinetics. New York, NY: Oxford University Press. doi: 10.1093/acprof:oso/9780199203864.001.0001
Hulett, J. R. (1964). Deviations from the Arrhenius equation. Q. Rev. Chem. Soc. 18, 227–242. doi: 10.1039/qr9641800227
Jeans, J. (1913). The Dynamical Theory of Gases. Dover Publications Incorporated. Available online at: https://books.google.com.br/books?id=UhJfawEACAAJ
JiangLin, Z., Bao, J. D., and Wenping, G. (2006). Kramers escape rate in nonlinear diffusive media. J. Chem. Phys. 124:024112. doi: 10.1063/1.2150433
Junior, A. C. do P. R., Cruz, C., Santana, W. S., and Moret, M. A. (2019). Characterization of the non-Arrhenius behavior of supercooled liquids by modeling non-additive stochastic systems. Available online at: http://arxiv.org/abs/1903.03156 (accessed March 24, 2019).
Kauzmann, W., and Eyring, H. (1940). The viscous flow of large molecules. J. Am. Chem. Soc. 62, 3113–3125.
Kennard, E. H. (1938). Kinetic Theory of Gases: With an Introduction to Statistical Mechanics. McGraw-Hill. Available online at: https://books.google.com.br/books?id=uP4gAAAAMAAJ
Klinman, J. P., and Kohen, A. (2013). Hydrogen tunneling links protein dynamics to enzyme catalysis. Annu. Rev. Biochem. 82, 471–496. doi: 10.1146/annurev-biochem-051710-133623
Kohen, A., Cannio, R., Bartolucci, S., and Klinman, J. P. (1999). Enzyme dynamics and hydrogen tunnelling in a thermophilic alcohol dehydrogenase. Nature 399, 496–499. doi: 10.1038/20981
Kooij, D. M. (1893). Über die Zersetzung des gasförmigen Phosphorwasserstoffs. Zeitschrift für Phys. Chemie 12, 155–161. doi: 10.1515/zpch-1893-1214
Kramers, H. A. (1940). Brownian motion in a field of force and the diffusion model of chemical reactions. Phys. 7, 284–304. doi: 10.1016/S0031-8914(40)90098-2
Kubo, K. (1985). A view on the break in the Arrhenius plots. J. Theor. Biol. 115, 551–569. doi: 10.1016/S0022-5193(85)80140-5
Kumamoto, J., Raison, J. K., and Lyons, J. M. (1971). Temperature “breaks” in Arrhenius plots: a thermodynamic consequence of a phase change. J. Theor. Biol. 31, 47–51. doi: 10.1016/0022-5193(71)90120-2
Laidler, K. J. (1984). The development of the Arrhenius equation. J. Chem. Educ. 61:494. doi: 10.1021/ed061p494
Laidler, K. J. (1996). A glossary of terms used in chemical kinetics, including reaction dynamics. Pure Appl. Chem. 68, 149–192.
Lenzi, E. K., Anteneodo, C., and Borland, L. (2001). Escape time in anomalous diffusive media. Phys. Rev. E 63, 51105–51109. doi: 10.1103/PhysRevE.63.051109
Limbach, H. H., Miguel Lopez, J., and Kohen, A. (2006). Arrhenius curves of hydrogen transfers: tunnel effects, isotope effects and effects of pre-equilibria. Philos. Trans. R. Soc. Lond. B. Biol. Sci. 361, 1399–1415. doi: 10.1098/rstb.2006.1872
Lukac, S. R. (1989). Modelling of radiolysis of reactor cooling water—a comparative study. Int. J. Radiat. Appl. Instrumentation. Part C. Radiat. Phys. Chem. 33, 223–230. doi: 10.1016/1359-0197(89)90143-4
Marin, T. W., Jonah, C. D., and Bartels, D. M. (2003). Reaction of OH* radicals with H2 in sub-critical water. Chem. Phys. Lett. 371, 144–149. doi: 10.1016/S0009-2614(03)00064-2
Masgrau, L., Gonzalez-Lafont, A., and Lluch, J. M. (2003). The curvature of the Arrhenius plots predicted by conventional canonical transition-state theory in the absence of tunneling. Theor. Chem. Accounts Theory, Comput. Model. 110, 352–357. doi: 10.1007/s00214-003-0484-9
Meng, X., Guo, J., Peng, J., Chen, J., Wang, Z., Shi, J.-R., et al. (2015). Direct visualization of concerted proton tunnelling in a water nanocluster. Nat. Phys. 11, 235–239. doi: 10.1038/nphys3225
Müller, I. (1971). The coldness, a universal function in thermoelastic bodies. Arch. Ration. Mech. Anal. 41, 319–332. doi: 10.1007/BF00281870
Nakamura, K., Takayanagi, T., and Sato, S. (1989). A modified arrhenius equation. Chem. Phys. Lett. 160, 295–298. doi: 10.1016/0009-2614(89)87599-2
Peleg, M., Engel, R., Gonzalez-Martinez, C., and Corradini, M. G. (2002). Non-Arrhenius and non-WLF kinetics in food systems. J. Sci. Food Agric. 82, 1346–1355. doi: 10.1002/Jsfa.1175
Peleg, M., Normand, M. D., and Corradini, M. G. (2012). The Arrhenius equation revisited. Crit. Rev. Food Sci. Nutr. 52, 830–851. doi: 10.1080/10408398.2012.667460
Perlmutter-Hayman, B. (1976). “Progress in inorganic chemistry: on the temperature dependence of Ea,” in Progress in Inorganic Chemistry, ed. S. J. Lippard (New York, NY: John Wiley & Sons, Inc.), 229–297.
Pomerantz, A. E., Camden, J. P., Chiou, A. S., Ausfelder, F., Chawla, N., Hase, W. L., et al. (2005). Reaction products with internal energy beyond the kinematic limit result from trajectories far from the minimum energy path: an example from H + HBr → H 2 + Br. J. Am. Chem. Soc. 127, 16368–16369. doi: 10.1021/ja055440a
Pu, J., Gao, J., and Truhlar, D. G. (2006). Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chem. Rev. 106, 3140–3169. doi: 10.1021/cr050308e
Rosa, A. C. P., Vaveliuk, P., Mundim, K. C., and Moret, M. A. (2016). A model for diffusive systems: beyond the Arrhenius mechanism. Phys. A Stat. Mech. its Appl. 450, 317–322. doi: 10.1016/j.physa.2015.12.122
Roy, S., Schopf, P., and Warshel, A. (2017). Origin of the non-Arrhenius behavior of the rates of enzymatic reactions. J. Phys. Chem. B 121, 6520–6526. doi: 10.1021/acs.jpcb.7b03698
Sanches-Neto, F. O., Coutinho, N. D., and Carvalho-Silva, V. H. (2017). A novel assessment of the role of the methyl radical and water formation channel in the CH3OH + H reaction. Phys. Chem.Chem. Phys. 19, 24467–24477. doi: 10.1039/C7CP03806B
Santin, L. G., Toledo, E. M., Carvalho-Silva, V. H., Camargo, A. J., Gargano, R., and Oliveira, S. S. (2016). Methanol solvation effect on the proton rearrangement of Curcumin's Enol forms: an ab initio molecular dynamics and electronic structure viewpoint. J. Phys. Chem. C 120, 19923–19931. doi: 10.1021/acs.jpcc.6b02393
Sato, S. (2005). Tunneling in bimolecular reactions. Chem. Phys. 315, 65–75. doi: 10.1016/J.CHEMPHYS.2005.01.034
Sikorski, R. S., Wang, L., Markham, K. A., Rajagopalan, P. T., Benkovic, S. J., and Kohen, A. (2004). Tunneling and coupled motion in the Escherichia coli dihydrofolate reductase catalysis. J. Am. Chem. Soc. 126, 4778–4779. doi: 10.1021/ja031683w
Silva, V. H. C., Aquilanti, V., De Oliveira, H. C. B., and Mundim, K. C. (2013). Uniform description of non-Arrhenius temperature dependence of reaction rates, and a heuristic criterion for quantum tunneling vs classical non-extensive distribution. Chem. Phys. Lett. 590, 201–207. doi: 10.1016/j.cplett.2013.10.051
Sims, I. R. (2013). Low-temperature reactions: tunnelling in space. Nat. Chem. 5, 734–736. doi: 10.1038/nchem.1736
Smith, I. W. (2008). The temperature-dependence of elementary reaction rates: beyond Arrhenius. Chem. Soc. Rev. 37, 812–826. doi: 10.1039/B704257B
Stillinger, F. H., and Debenedetti, P. G. (2013). Glass transition thermodynamics and kinetics. Annu. Rev. 4, 263–285. doi: 10.1146/annurev-conmatphys-030212-184329
Takayanagi, T. (2004). Theory of Atom Tunneling Reactions in the Gas Phase. Berlin; Heidelberg: Springer, 15–31. doi: 10.1007/978-3-662-05900-5_2
Takayanagi, T., Masaki, N., Nakamura, K., Okamoto, M., Sato, S., and Schatz, G. C. (1987). The rate constants for the H + H2 reaction and its isotopic analogs at low temperatures: Wigner threshold law behavior. J. Chem. Phys. 86:6133. doi: 10.1063/1.452453
Tammann, G., and Hesse, W. (1926). Die Abhängigkeit der Viscosität von der Temperatur bie unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 156, 245–257. doi: 10.1002/zaac.19261560121
Tizniti, M., Le Picard, S. D., Lique, F., Berteloite, C., Canosa, A., Alexander, M. H., et al. (2014). The rate of the F + H2 reaction at very low temperatures. Nat. Chem. 6, 141–145. doi: 10.1038/nchem.1835
Tolman, R. C. (1920). Statistical mechanics applied to chemical kinetics. J. Amer. Chem. Soc. 42, 2506–2528.
Truhlar, D., and Kohen, A. (2001). Convex Arrhenius plots and their interpretation. Proc. Nat. Acad. Sci. U.S.A. 98, 848–851. doi: 10.1073/pnas.98.3.848
Tsallis, C. (1999). Nonextensive statistics: theoretical, experimental and computational evidences and connections. Braz. J. Phys. 29, 1–35. doi: 10.1590/S0103-97331999000100002
Tsallis, C. (2009). Introduction to Nonextensive Statistical Mechanics: Approaching a Complex World. New York, NY: Springer.
Tsallis, C., and Bukman, D. J. (1996). Anomalous diffusion in the presence of external forces: Exact time-dependent solutions and their thermostatistical basis. Phys. Rev. E 54, R2197–R2200. doi: 10.1103/PhysRevE.54.R2197
Vogel, H. (1921). Das temperature-abhangigketsgesetz der viskositat von flussigkeiten. Phys. Z. 22, 645–646.
Vyazovkin, S. (2016). A time to search: finding the meaning of variable activation energy. Phys. Chem. Chem. Phys. 18, 18643–18656. doi: 10.1039/C6CP02491B
Wallace, M. I., Ying, L., Balasubramanian, S., and Klenerman, D. (2002). Non-Arrhenius kinetics for the loop closure of a DNA hairpin. Proc. Natl. Acad. Sci. U.S.A. 98, 5584–5589. doi: 10.1073/pnas.101523498
Wang, Y., Babin, V., Bowman, J. M., and Paesani, F. (2012). The water hexamer: cage, prism, or both. Full dimensional quantum simulations say both. J. Am. Chem. Soc. 134, 11116–11119. doi: 10.1021/ja304528m
Warshel, A., and Bora, R. P. (2016). Perspective: Defining and quantifying the role of dynamics in enzyme catalysis. J. Chem. Phys. 144:180901. doi: 10.1063/1.4947037
Wigner, E. P. (1948). On the behavior of cross sections near thresholds. Phys. Rev. 73, 1002–1009. doi: 10.1103/PhysRev.73.1002
Williams, M. L., Landel, R. F., and Ferry, J. D. (1955). The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 77, 3701–3707.
Wu, Y., Sun, H., Wu, L., and Deetz, J. D. (2019). Extracting the mechanisms and kinetic models of complex reactions from atomistic simulation data. J. Comput. Chem. 40, 1586–1592. doi: 10.1002/jcc.25809
Zhou, Y., and Du, J. (2013). The mean first passage time in an energy-diffusion controlled regime with power-law distributions. J. Stat. Mech. 11005:P11005. doi: 10.1088/1742-5468/2013/11/P11005
Keywords: transitivity plot, Aquilanti-Mundim (AM) formula, Nakamura-Takayanagi-Sato (NTS) formula, Volgel-Fulcher-Tammann (VFT) formula, viscosity and diffusion
Citation: Carvalho-Silva VH, Coutinho ND and Aquilanti V (2019) Temperature Dependence of Rate Processes Beyond Arrhenius and Eyring: Activation and Transitivity. Front. Chem. 7:380. doi: 10.3389/fchem.2019.00380
Received: 26 March 2019; Accepted: 10 May 2019;
Published: 29 May 2019.
Edited by:
Antonio Aguilar, University of Barcelona, SpainReviewed by:
Luca Evangelisti, University of Bologna, ItalyErnesto Garcia, University of the Basque Country, Spain
Copyright © 2019 Carvalho-Silva, Coutinho and Aquilanti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Valter H. Carvalho-Silva, ZmF0aW9sZWdAZ21haWwuY29t; Nayara D. Coutinho, bmF5YXJhZGNvdXRpbmhvQGdtYWlsLmNvbQ==; Vincenzo Aquilanti, dmluY2Vuem9hcXVpbGFudGlAeWFob28uaXQ=
 Valter H. Carvalho-Silva
Valter H. Carvalho-Silva Nayara D. Coutinho2*
Nayara D. Coutinho2* Vincenzo Aquilanti
Vincenzo Aquilanti