- 1Beijing National Laboratory for Molecular Sciences, Institute of Chemistry, Chinese Academy of Sciences, Beijing, China
- 2School of Chemical Sciences, University of Chinese Academy of Sciences, Beijing, China
Double proton transfer plays an important role in biology and chemistry, such as with DNA base pairs, proteins and molecular clusters, and direct information about these processes can be obtained from tunneling splittings. Carboxylic acid dimers are prototypes for multiple proton transfer, of which the formic acid dimer is the simplest one. Here, we present efficient quantum dynamics calculations of ground-state and fundamental excitation tunneling splittings in the formic acid dimer and its deuterium isotopologues. These are achieved with a multidimensional scheme developed by us, in which the saddle-point normal coordinates are chosen, the basis functions are customized for the proton transfer process, and the preconditioned inexact spectral transform method is used to solve the resultant eigenvalue problem. Our computational results are in excellent agreement with the most recent experiments (Zhang et al., 2017; Li et al., 2019).
1. Introduction
Proton transfer plays important roles in various chemical and biological processes (Mayer, 2011; Weinberg et al., 2012; Layfield and Hammes-Schiffer, 2014; Salamone and Bietti, 2015). Multiple proton transfer is nearly ubiquitous in living organisms, such as in DNA mutation reactions (Jacquemin et al., 2014) or enzyme catalysis reactions (Klinman and Kohen, 2013). In particular, the hydrogen bond is crucial and omnipresent in many chemical and biological reactions, and in case that more than one hydrogen bond exist, different multiple proton transfer processes along the corresponding hydrogen bonds would appear, either in a concerted or stepwise way. In this field, the double proton transfer systems are of extraordinary importance as they can serve as the template for DNA base pairs (Barnes et al., 2008; Smedarchina et al., 2018). The carboxylic acid dimers are often used as models for multiple proton concerted transfer (Arabi and Matta, 2011; Daly et al., 2011; Evangelisti et al., 2012; Feng et al., 2012; Zhou et al., 2019), of which the formic acid dimer (FAD) is the smallest one. Therefore, the FAD system has long been considered as the prototype for multiple proton transfer studies (Li et al., 2019). Of course, it should be noted that a realistic simulation of the proton transfer processes in the real biological environment would require a more complex model, since such factors as the surrounding water molecules (Cerón-Carrasco et al., 2010; Cerón-Carrasco and Jacquemin, 2015) and the local electric field (Arabi and Matta, 2011) have been shown to play important roles.
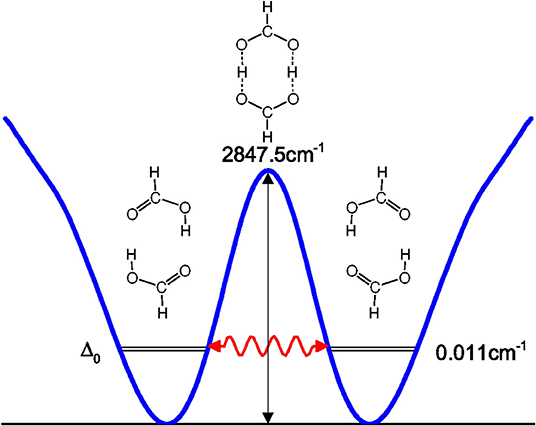
Tunneling splittings can provide direct information about dynamics of proton transfer, and it can be detected by high-resolution spectroscopic techniques (Zielke and Suhm, 2007; Daly et al., 2011; Goroya et al., 2014; MacKenzie et al., 2014; Zhang et al., 2017; Li et al., 2019). As shown in Figure 1, hydrogen (protons) in FAD can transfer between oxygen via tunneling, resulting in vibrational energy level splitting. Experimentally, Li et al. (2019) have just performed the most accurate measurement of ground-state tunneling splitting of FAD with microwave spectroscopy, with the splitting value reported as 334.9 MHz (0.01117 cm−1). In 2002, Havenith's group (Madeja and Havenith, 2002) first successfully employed high-resolution spectroscopy to measure tunneling splitting in (DCOOH)2. More recently, Havenith's group (Ortlieb and Havenith, 2007) and Duan's group (Goroya et al., 2014) measured ground-state tunneling splitting(Δ0) of (HCOOH)2 as 0.0158 and 0.01649 cm−1, respectively. In 2017, Duan's group (Zhang et al., 2017) improved their experimental accuracy, getting an updated Δ0 of 0.011367(92) cm−1 for (HCOOH)2, and they also reported a new experimental Δ0 of 0.00113 cm−1 for HCOOD-HCOOH. Theoretically, several researchers studied the tunneling splittings in the FAD system using approximate methods, such as instanton theory (Mil'nikov et al., 2005; Smedarchina et al., 2005, 2013; Richardson, 2017) and reduced-dimensionality quantum dynamics (QD) (Luckhaus, 2006, 2010; Barnes et al., 2008; Jain and Sibert, 2015; Qu and Bowman, 2016). In 2016, Qu and Bowman successfully constructed a full-dimensional potential-energy surface (PES) for FAD (Qu and Bowman, 2016), which provides us the basis for further dynamical calculations. Based on this PES, two kinds of dynamical calculations have been reported, which are reduced-dimensional quantum calculations with the multi-mode method (Qu and Bowman, 2016) and semiclassical calculations with the instanton approach by Richardson (Richardson, 2017). However, the agreement of the reported theoretical values for the ground-state tunneling splittings with the most recent experiments (Zhang et al., 2017; Li et al., 2019) is still not satisfactory. The ground-state tunneling splitting for FAD is very small (only 0.01 cm−1 or so), which causes problems for some approximate approaches such as diffusion Monte Carlo (Qu and Bowman, 2016), and in some cases the numerical errors may be larger than the splitting value. In addition, although great efforts have been made in full-dimensional exact QD calculations (Wu et al., 2016; Pandey and Poirier, 2019), the full-dimensional exact QD calculations are still prohibitive for the title 10-atom system.
In this work, we present efficient QD calculations of ground-state and fundamental excitation tunneling splittings in FAD using the PES of Bowman's group (Qu and Bowman, 2016), and as for the ground-state tunneling splitting, our calculations yield much better agreement with experiments (Zhang et al., 2017; Li et al., 2019) than previous theoretical calculations. These are achieved with a multidimensional scheme developed by us, in which the saddle-point normal coordinates are chosen and vibrational modes that are strongly coupled to the proton transfer are included. The basis functions are customized for the proton transfer process using the process-oriented basis function customization (PBFC) strategy proposed by us (Ren and Bian, 2015; Wu et al., 2016), and the preconditioned inexact spectral transform (PIST) method (Huang and Carrington, 2000; Poirier and Carrington, 2001, 2002; Ren et al., 2011; Yang et al., 2011) is used to solve the resultant eigenvalue problem. The main idea of our PBFC strategy is to customize basis functions for specific chemical processes or those desired states by optimizing and adjusting the 1D or nD effective potential (EP).
2. Methods and Computational Details
2.1. Normal Mode Hamiltonian
The exact normal mode Hamiltonian of a non-linear system for total angular momentum J = 0 reads (Kamarchik et al., 2009)
where Q denotes a collection of the 3N−6 normal coordinates, μαβ is the inverse of the effective moment of inertia tensor, and are the Coriolis coupling coefficients. The four terms are the standard kinetic energy operator, the vibrational angular momentum (VAM) term, the so-called “Watson” term, and the potential term in order. As VAM and Watson are inverse with the moment of inertia, we can neglect them in this 10-atom system. Therefore, the expression of multidimensional effective Hamiltonian reads (Ren et al., 2011; Wu, 2016)
where M is the number of modes included in this calculation. V(Q1, …, QM) is the EP obtained by customized according the reaction process or simply minimizing the remaining degrees of freedom (DOF). The criterion for choosing normal modes will be discussed later in the article.
For facilitating description of proton tunneling in FAD, the Hamiltonian is represented in the saddle-point normal coordinates as the saddle point has the highest symmetry. Normal mode analysis is performed employing the PES constructed by Bowman's group (Qu and Bowman, 2016). We chose the direction of the saddle point painstakingly to avoid the symmetrical error caused by the numerical problem. The mass-scaled normal modes obtained at the saddle point and global minimum are provided in Table 1, in which the imaginary frequency Q1 is the reaction coordinate.
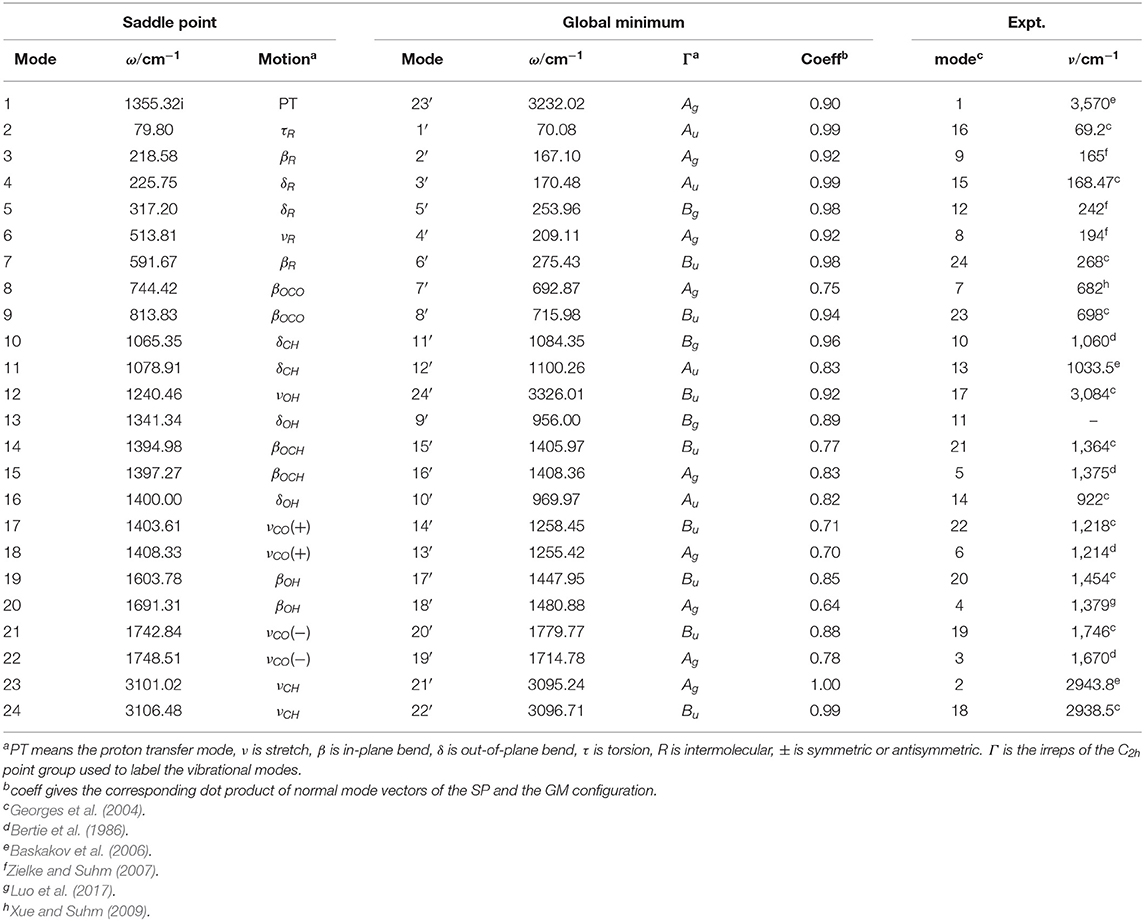
Table 1. Correspondence between the normal modes of the saddle point (SP) and the global minimum (GM).
2.2. Basis Function Representation
The wave function is expanded by the direct product of 1D discrete variable representation (DVR) basis functions
where πij(Qj) is the 1D DVR basis function for Qj with basis size of Nj. The 1D DVR basis functions are obtained by a designed 1D effective Hamiltonian with a unitary transformation from the truncated eigenfunctions
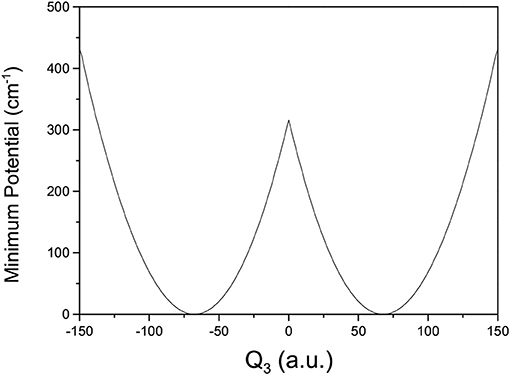
where V(Qj) is the 1D EP (Li et al., 2011; Ren et al., 2011; Zhang et al., 2012). The two protons in FAD transfer between the two equivalent wells results in ground-state tunneling splitting (Figure 1), and in normal coordinates at the saddle point, Q1 is identified as the proton transfer reaction coordinate as shown in Table 1. The PBFC strategy is used to customize the 1D EP for the proton tunneling process attracting our interest, and the four 1D EPs used in this work are shown in Figure 2. In particular, the 1D EP for Q3 is obtained by smoothly connecting three parts: the central part is yielded by following the steepest descending path starting from the saddle point, whereas the parts on the two sides are produced by minimizing all the remaining DOF. It is clear that the obtained 1D EP for Q3 is proton-transfer-process oriented, which includes the reactant and product equilibrium geometries and the transition-state geometry. If the EP for Q3 is generated by minimizing all the remaining DOF, a segmented point or cusp at Q3 = 0 will appear (see Figure 3), and on the two sides of the cusp the relaxed coordinate Q1 has the opposite sign, indicating that it just describes the well regions but omits the barrier region. In the following we will show that the coupling between Q1 and Q3 is anti-symmetric, and generally speaking, whenever this kind of strong anti-symmetric coupling is encountered, the above problem would appear. In addition, the 1D EP for the mode Q1 can be obtained in a similar way to that for Q3. The 1D EPs for the modes Q6 and Q8 are generated from the full-dimensional PES by minimizing the potential with all the remaining DOF, respectively, which is in accordance with the spirit of the PBFC strategy, since the minimum potential is energetically favored in the process of proton transfer. It should be noted that the minimal potentials have been shown to give rise to nearly optimal effective Hamiltonians using the phase space optimizing (PSO) theory (Poirier and Light, 1999, 2001; Poirier, 2001; Bian and Poirier, 2003).
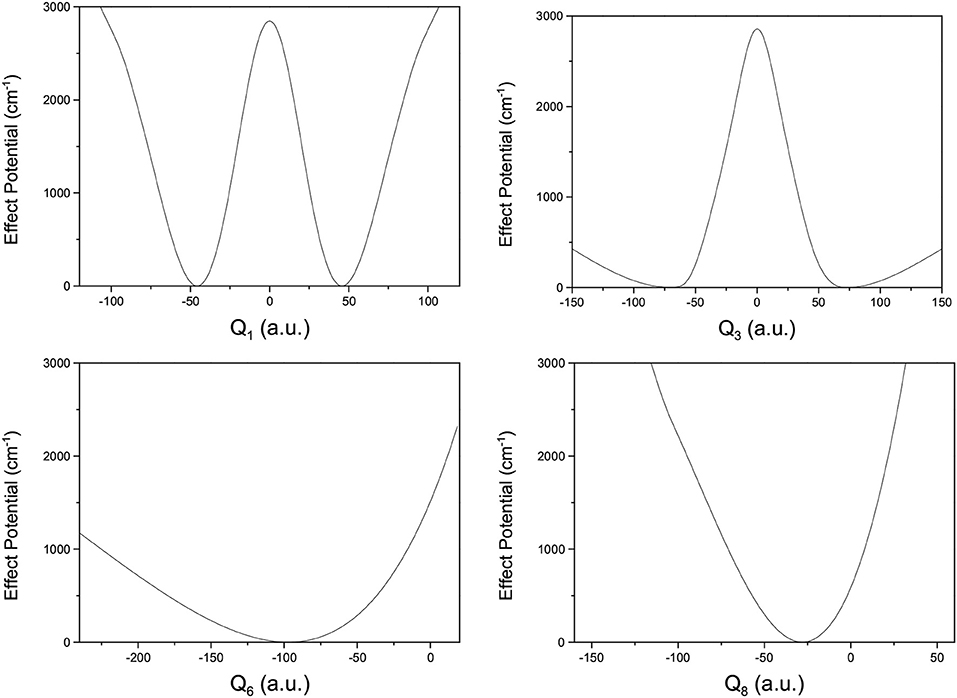
Figure 2. 1D effective potentials for Qi(i = 1, 6, 3, 8) in formic acid dimer, where Qi is in the mass-rescaled unit.
Figure 2 shows that the 1D EP for Q1 has a double-well structure, as does that for Q3, indicating that the Q1 and Q3 modes may be the most important in the study of tunneling splitting. Furthermore, the elements in the Hamiltonian matrix we use for this work are the following,
where refers to the kinetic energy matrix in DVRs for Qj, M = (1, 2, 3, 4).
2.3. Hamiltonian Martix Solution
The essence of the PIST method is to transform the original H−1 into matrix (H−EI)−1 before the Lanczos algorithm is applied, such that states close to energy E converge first and fast to reduce the number of Lanczos iterations needed. In each Lanczos iteration, the matrix-vector multiplication is equivalent to the linear equations (H − EI)xi+1 = xi, which are solved with the quasi-minimal residual (QMR) algorithm. Wyatt preconditioner (Wyatt, 1995a,b), P, is employed to improve the efficiency of the QMR iterative convergence by transforming the linear equations into , as the matrix P−1(H − EI) is more close to a diagonal matrix. QMR convergence criteria can be loosened to a certain extent, as the exact eigenvalues and eigenvectors are given by the Lanczos step. However, loosening it too much will highly increase the number of steps for Lanczos iteration, which is much slower than QMR iteration. The PIST method has also been employed in other applications (Bian and Poirier, 2004; Li and Bian, 2008; Brandon and Poirier, 2014; Petty and Poirier, 2014).
3. Results and Discussion
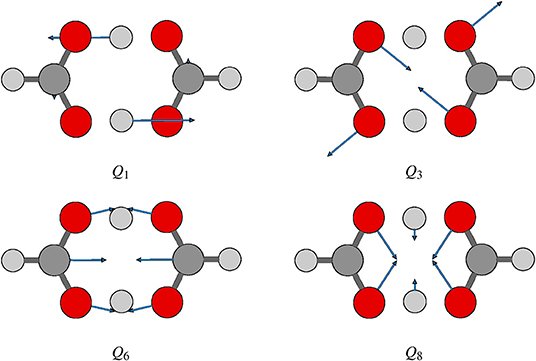
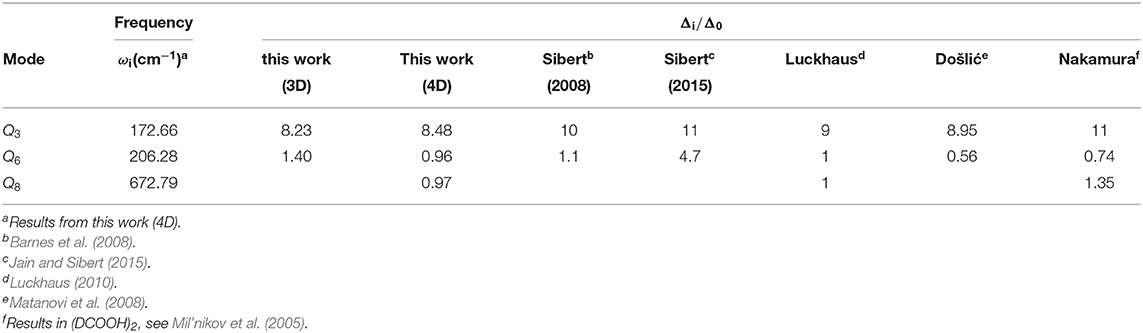
Proton transfer in FAD is a multidimensional process. In order to identify important normal coordinates related to the proton transfer of FAD and incorporate them into the current multidimensional research, we first inspect the magnitude of the displacement [|ΔQi| (i = 1, …, 24)] for each normal coordinate from the saddle point to the global minimum. As shown in Figure 4, the |ΔQi|s of four modes, modes 1, 3, 6, and 8 (Figure 5), are substantially larger than those of the other modes. The contour plots of the PES cut along Qi(i = 3, 6, 8, 10) and Q1 are shown in Figure 6, as seen, the coupling between modes 3 and 1 and that between modes 6 and 1 are extremely strong, while the coupling between modes 10 and 1 is very small. The contour plot of the PES cut along Q22 and Q1 is similar to that along Q3 and Q1, but the coupling between modes 22 and 1 is much smaller. That confirms the importance of Q6, Q3, Q8, which are used as the main mode in the previous work (Barnes et al., 2008; Jain and Sibert, 2015; Qu and Bowman, 2016; Richardson, 2017). The only replacement may be using Q22 instead of Q8 (Matanovi et al., 2008).
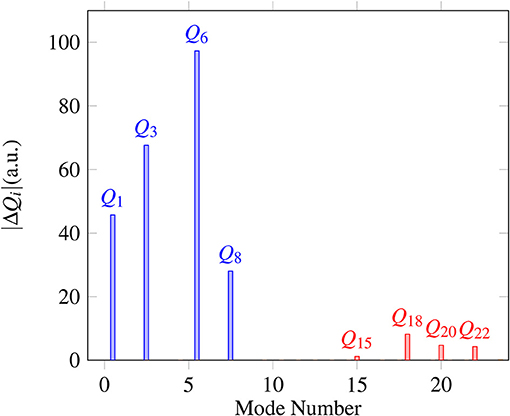
Figure 4. Magnitudes of the displacement for 24 normal coordinates from the saddle point to the global minimum, where |ΔQi|(i = 1, 2, …, 24) is in the mass-rescaled unit.
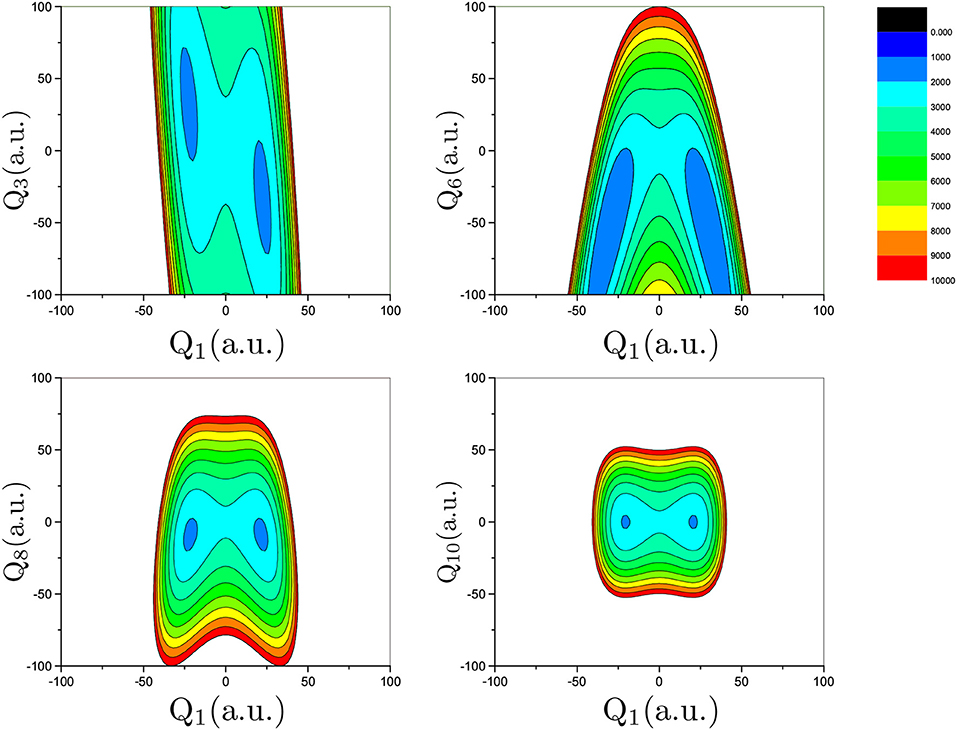
Figure 6. Contour plot of the PES cut along Qi (i = 3, 6, 8, 10) and Q1 by fixing the remaining modes at zero. The potential energy is in cm−1 and Qi is in the mass-rescaled unit.
As what written above, for the calculation of ground-state splitting (Δ0), Q6, Q3, and Q8 are extracted from the 4D (Q1, Q6, Q3, Q8) model. Converged ground-state splittings are obtained with the basis set of (NQ1 = 32, NQ6 = 13, NQ3 = 13, NQ8 = 11) which is denoted as (32, 13, 13, 11) for simplicity. In analyzing the EPs, we find that the coordinate with |ΔQi| ≈ 0 (Figure 4) leaves from 0 only in the region where the FAD breaks into two monomers. Thus, when making multidimensional EPs, we relax the modes shown in Figure 4 and keep the others near 0 to make our calculations focus on the process of isomerization.
Because the theoretical splittings are computed with the saddle point coordinates whereas the experiments are measured as a property of the global minimum, we establish the corresponding relations between the saddle-point modes and the global minimum ones to compare our splittings of each mode with experiment. The relations of the different mode numbers are shown in Table 1.
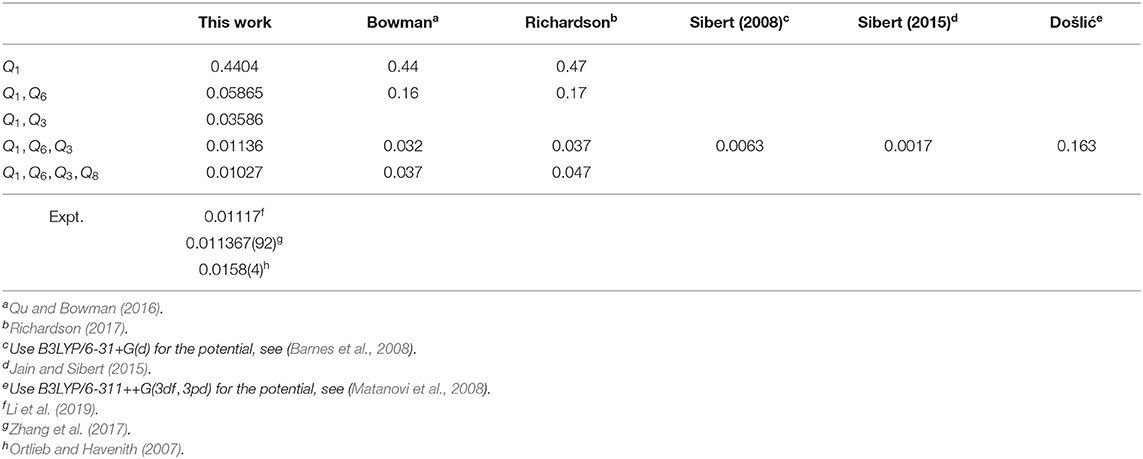
The calculated ground-state tunneling splitting results for (HCOOH)2 are listed in Table 2. As shown, the present 3-4D results agree well with the experimental measurements, which are superior to the previous 3-4D results (Qu and Bowman, 2016; Richardson, 2017). The good performance of the present calculations may be attributed to two reasons. First, the potential energies used in the calculations of Sibert's group (Barnes et al., 2008; Jain and Sibert, 2015) and Došlić's group (Matanovi et al., 2008) are only at the B3LYP level and not accurate enough, and similar problem is also found in the 7D calculation of Luckhaus (Luckhaus, 2010) which reported a value of 0.008 cm−1. Second, although we use the same PES as that used in Bowman's calculations, we treat the symmetry problem in calculations with great care and obtain more reliable results. We find that the symmetry of PES breaks while converting the coordinate from Cartesian coordinate to normal coordinate. When the two wells are not in symmetry with each other, the wave-functions of the doublets that one state splits into will be independently bonded in one well instead of spreading in both wells, so the two doublets are broken into two states. Although this symmetry problem is not obvious in 1D calculation, it does affect the 2-4D results.
We find that the computer's numerical precision does affect the transformation from the Cartesian coordinates to the normal coordinates, leading to errors, which needs careful treatment to ensure that the zero elements in the coordinate transfer matrix are as expected and the PES in normal coordinates is symmetric. The 4D result is in very good agreement with the experiments (Zhang et al., 2017; Li et al., 2019), and the Δ0 in different basis size varies by around 0.0005 cm−1 (see Figure 7) which is much smaller than that in Bowman's calculation of 0.003 cm−1. In addition, the present computational scheme is efficient. For instance, the calculation with the 4D basis size of (24, 13, 13, 11) takes only 100 s for the PIST part on our workstation with Intel Xeon E5645@2.4GHz, and the most time-consuming part for constructing multidimensional EPs has been parallelized.
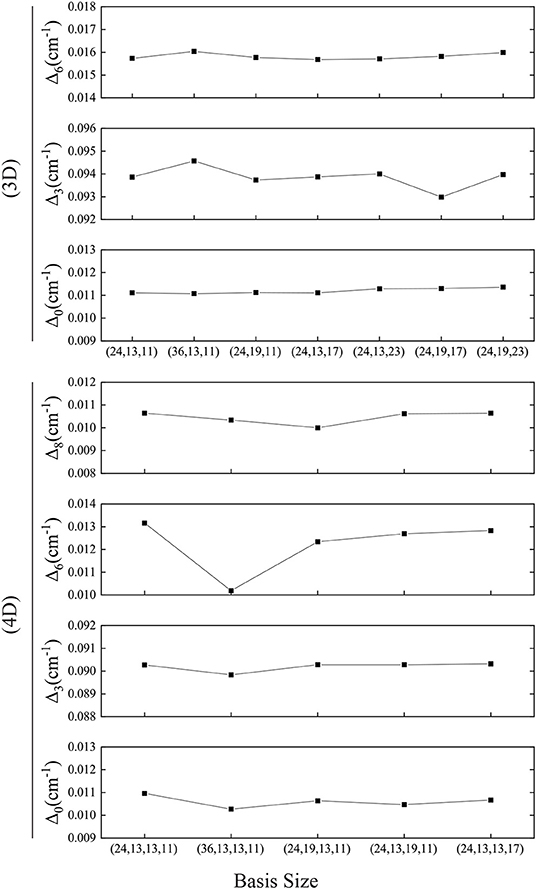
Figure 7. Convergence of the tunneling splittings in 3D or 4D calculations. Basis size is (Q1, Q6, Q3) or (Q1, Q6, Q3, Q8).
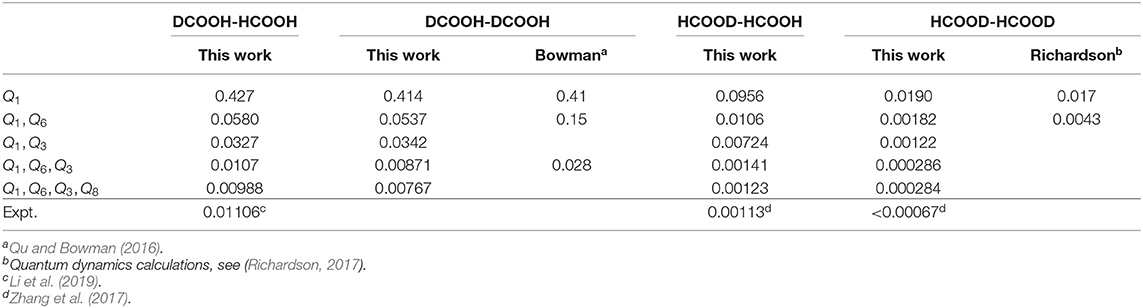
We also use the same scheme to calculate the ground-state tunneling splitting of various deuterium isotopologues, and the results for DCOOH-HCOOH (DCOOH)2, HCOOD-HCOOH and (HCOOD)2 are presented in Table 3. As can be seen, the ground-state tunneling splittings of the four deuterium isotopologues are smaller than that of (HCOOH)2, meaning that substituting the hydrogen atoms with the deuterium atom would slow down the tunneling. In particular, for the 4D results, the calculated splitting for DCOOH-HCOOH and HCOOD-HCOOH are 0.00988 and 0.00123 cm−1, respectively, which is in very good agreement with the experimental values of 0.01106 cm−1 (Li et al., 2019) and 0.00113 cm−1 (Zhang et al., 2017). As for (DCOOH)2, the present calculated ratio of the tunneling splitting for (HCOOH)2/(DCOOH)2 of 1.25 is in excellent agreement with the experimental value of 1.21 (Ortlieb and Havenith, 2007). The calculated tunneling splitting of (HCOOD)2 is 0.000284 cm−1, which is consistent with the reported theoretical results of 0.00022 cm−1 (Smedarchina et al., 2005) and 0.00021 cm−1 (Richardson, 2017) based on the instanton method; unfortunately, there has been no available experimental data, and further experimental studies are desired.
The doublets of splittings are assigned according to the nodal structure of wave function probability density against each coordinate, with the other coordinates integrated over. As illustrated in Figure 8 concerning a 4D (Q1, Q6, Q3, Q8) calculation, Figures 8A–D is the wave function probability density curve of the energy doublets of splittings for the ground state, fundamentals (Q6, Q3, Q8), respectively. There are two potential wells separated by a barrier along Q3 (Figure 2); considering that the ZPE of Q3 is about 90 cm−1, the wave-functions of Q3 are divided into the two wells. The number of nodes in wave function of vibrational state of Q3(ν = n) is 2n+1, whereas this number of single-well modes like Q3 or Q8 is n.
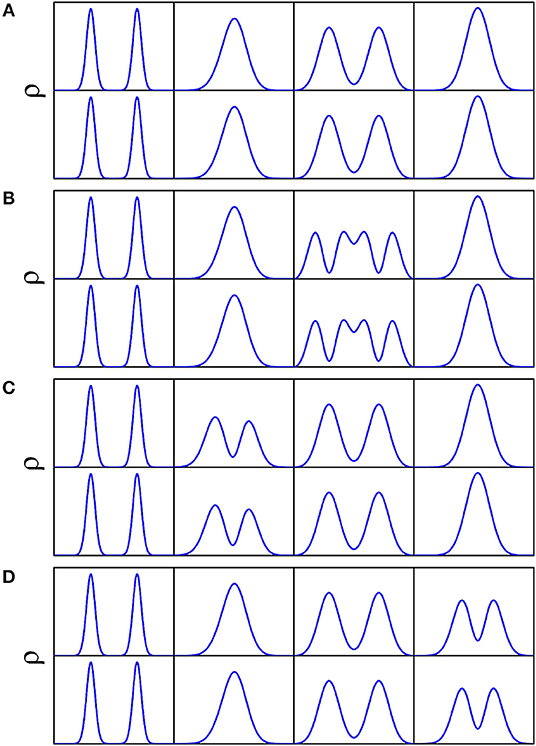
Figure 8. Wave function probability density for the ground state (A), fundamentals Q3 (B), Q6 (C), and Q8 (D) against each coordinate with the other coordinates integrated over in the 4D (Q1, Q6, Q3, Q8) calculation. Top and bottom panels of (A–D) correspond to lower and upper doublets of respective tunneling splittings.
One can notice that in Table 4, the effect of the vibrational excitation in mode Q3 is significantly larger than that in mode Q6 and Q8, though the Q6 has larger displacement and higher frequency. This selective can be found in many systems such as malonaldehyde (Wu et al., 2016). The reason may be that in the tunneling dynamic, the reaction path does not go through the saddle point. For the two global minimums of FAD, Q6 and Q8 are nearly the same, while Q3 has a significant change. Which means that when the protons transfer below the barrier the other atoms will have movement along the mode Q3 but not along Q6 and Q8.
In addition, we perform a series of 2D calculations for (Q1, Q3) with a basis size up to (48,31); the results are also listed in Table 2. The smaller Δ0 indicates that Q3 does play the second important role in the tunneling; however, being 3 times higher than Δ0 in 3D mode shows that Q6 still shows significant influence to the calculation. For both the 2D cases, we also checked the ratios of Δ6/Δ0 and Δ3/Δ0. The results are Δ6/Δ0 ≈ 4.5, Δ3/Δ0 ≈ 7.0. Our testing calculation using mode (Q1, Q3, Q8) with a basis size of (24,13,11) gives the result Δ6/Δ0 ≈ 4.4, far from 1.0, which shows that ignoring Q3 will affect both the ground state and fundamental excitation tunneling splitting and also reconfirms that Q3 plays a more important role than Q6 in the tunneling splitting of FAD.
4. Summary
Using a multidimensional scheme developed by us, we achieve much better agreement with experiments than those reported in previous theoretical calculations for the ground-state tunneling splitting in FAD. The obtained ground-state tunneling splitting of 0.010 cm−1 is in excellent agreement with the most recent experimental values of 0.011 cm−1. This is achieved with a 4-dimensional PBFC-PIST theoretical scheme, in which the saddle-point normal coordinates are chosen, the basis functions are customized for the proton transfer process, and the PIST method is used to solve the resultant eigenvalue problem. Our scheme is also used to study the ground-state tunneling splittings of various deuterium isotopologues of FAD, and the obtained results are in very good agreement with experiment.
The roles of various vibrational modes in the process of proton transfer are also studied, and our analysis and calculations indicate that the Q3 and Q6 are strongly coupled to the proton transfer process, whereas Q3 plays a more important role than Q6 in the tunneling dynamics. The present work demonstrates the feasibility of our multidimensional PBFC-PIST scheme, which may be extended to the study of multiple proton transfer dynamics in even larger molecular systems or using more complex models, although in the latter case further refinements are required to take into account such factors as the solvent effects by including several explicit water molecules into the model (Cerón-Carrasco et al., 2010).
Data Availability Statement
All datasets generated for this study are available within the article and from the corresponding author on request.
Author Contributions
HL carried out the QD calculations. HL, JC, and WB analyzed the data, interpreted the results, developed the theoretical scheme, and wrote the paper. WB supervised the research.
Funding
This work was supported by the National Natural Science Foundation of China (Nos. 21973098, 21773251), the Beijing National Laboratory for Molecular Sciences and the Chinese Academy of Sciences.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Arabi, A. A., and Matta, C. F. (2011). Effects of external electric fields on double proton transfer kinetics in the formic acid dimer. Phys. Chem. Chem. Phys. 13, 13738–13748. doi: 10.1039/c1cp20175a
Barnes, G. L., Squires, S. M., and Sibert, E. L. (2008). Symmetric double proton tunneling in formic acid dimer: a diabatic basis approach. J. Phys. Chem. B 112, 595–603. doi: 10.1021/jp075376e
Baskakov, O. I., Markov, I. A., Alekseev, E. A., Motiyenko, R. A., Lohilahti, J., Horneman, V.-M., et al. (2006). Simultaneous analysis of rovibrational and rotational data for the 41, 51, 61, 72, 81, 7191 and 92 states of HCOOH. J. Mol. Struct. 795, 54–77. doi: 10.1016/j.molstruc.2006.02.052
Bertie, J. E., Michaelian, K. H., Eysel, H. H., and Hager, D. (1986). The Raman-active O-H and O-D stretching vibrations and Raman spectra of gaseous formic acid-d1 and -OD. J. Chem. Phys. 85, 4779–4789. doi: 10.1063/1.451737
Bian, W., and Poirier, B. (2003). Accurate and highly efficient calculation of the O(1D)HCl vibtational bound states, using a combination of methods. J. Theor. Comput. Chem. 2, 583–597. doi: 10.1142/S0219633603000768
Bian, W., and Poirier, B. (2004). Accurate and highly efficient calculation of the highly excited pure OH stretching resonances of O(1D)HCl, using a combination of methods. J. Chem. Phys. 121, 4467–4478. doi: 10.1063/1.1779577
Brandon, D., and Poirier, B. (2014). Accurate calculations of bound rovibrational states for argon trimer. J. Chem. Phys. 141:034302. doi: 10.1063/1.4887459
Cerón-Carrasco, J. P., and Jacquemin, D. (2015). DNA spontaneous mutation and its role in the evolution of GC-content: assessing the impact of the genetic sequence. Phys. Chem. Chem. Phys. 17, 7754–7760. doi: 10.1039/C4CP05806B
Cerón-Carrasco, J. P., Requena, A., Perpète, E. A., Michaux, C., and Jacquemin, D. (2010). Theoretical study of the tautomerism in the one-electron oxidized guanine-cytosine base pair. J. Phys. Chem. B 114, 13439–13445. doi: 10.1021/jp101711z
Daly, A. M., Douglass, K. O., Sarkozy, L. C., Neill, J. L., Muckle, M. T., Zaleski, D. P., et al. (2011). Microwave measurements of proton tunneling and structural parameters for the propiolic acid-formic acid dimer. J. Chem. Phys. 135:154304. doi: 10.1063/1.3643720
Evangelisti, L., Écija, P., Cocinero, E. J., Castaño, F., Lesarri, A., Caminati, W., et al. (2012). Proton tunneling in heterodimers of carboxylic acids: a rotational study of the benzoic acid-formic acid bimolecule. J. Phys. Chem. Lett. 3, 3770–3775. doi: 10.1021/jz3018489
Feng, G., Favero, L. B., Maris, A., Vigorito, A., Caminati, W., and Meyer, R. (2012). Spectrum of the dimer of acrylic acid. J. Am. Chem. Soc. 134, 19281–19286. doi: 10.1021/ja309627m
Georges, R., Freytes, M., and Herman, M. (2004). Jet-cooled and room temperature FTIR spectra of the dimer of formic acid in the gas phase. Chem. Phys. 305, 187–196. doi: 10.1016/j.chemphys.2004.06.027
Goroya, K. G., Zhu, Y., Sun, P., and Duan, C. (2014). High resolution jet-cooled infrared absorption spectra of the formic acid dimer: a reinvestigation of the C-O stretch region. J. Chem. Phys. 140:164311. doi: 10.1063/1.4872367
Huang, S.-W., and Carrington, T. (2000). A new iterative method for calculating energy levels and wave functions. J. Chem. Phys. 112, 8765–8771. doi: 10.1063/1.481492
Jacquemin, D., Zúñiga, J., Requena, A., and Céron-Carrasco, J. P. (2014). Assessing the importance of proton transfer reactions in DNA. Accounts Chem. Res. 47, 2467–2474. doi: 10.1021/ar500148c
Jain, A., and Sibert, E. L. (2015). Tunneling splittings in formic acid dimer: an adiabatic approximation to the Herring formula. J. Chem. Phys. 142:084115. doi: 10.1063/1.4908565
Kamarchik, E., Wang, Y., and Bowman, J. (2009). Reduced-dimensional quantum approach to tunneling splittings using saddle-point normal coordinates. J. Phys. Chem. A 113, 7556–7562. doi: 10.1021/jp901027g
Klinman, J. P., and Kohen, A. (2013). Hydrogen tunneling links protein dynamics to enzyme catalysis. Annu. Rev. Biochem. 82, 471–496. doi: 10.1146/annurev-biochem-051710-133623
Layfield, J. P., and Hammes-Schiffer, S. (2014). Hydrogen tunneling in enzymes and biomimetic models. Chem. Rev. 114, 3466–3494. doi: 10.1021/cr400400p
Li, B., and Bian, W. (2008). Efficient quantum calculations of vibrational states of vinylidene in full dimensionality: a scheme with combination of methods. J. Chem. Phys. 129:024111. doi: 10.1063/1.2953706
Li, B., Ren, Y., and Bian, W. (2011). Accurate quantum dynamics study on the resonance decay of vinylidene. ChemPhysChem 12, 2419–2422. doi: 10.1002/cphc.201100144
Li, W., Evangelisti, L., Gou, Q., Caminati, W., and Meyer, R. (2019). The Barrier to proton transfer in the dimer of formic acid: a pure rotational study. Angew. Chem. Int. Ed. 58, 859–865. doi: 10.1002/anie.201812754
Luckhaus, D. (2006). Concerted hydrogen exchange tunneling in formic acid dimer. J. Phys. Chem. A 110, 3151–3158. doi: 10.1021/jp054558a
Luckhaus, D. (2010). Hydrogen exchange in formic acid dimer: tunnelling above the barrier. Phys. Chem. Chem. Phys. 12, 8357–8361. doi: 10.1039/c001253j
Luo, W., Zhang, Y., Li, W., and Duan, C. (2017). Jet-cooled infrared absorption spectrum of the v 4 fundamental band of HCOOH and HCOOD. J. Mol. Spectrosc. 334, 22–25. doi: 10.1016/j.jms.2017.03.005
MacKenzie, R. B., Dewberry, C. T., and Leopold, K. R. (2014). The formic acid-nitric acid complex: microwave spectrum, structure, and proton transfer. J. Phys. Chem. A 118, 7975–7985. doi: 10.1021/jp507060w
Madeja, F., and Havenith, M. (2002). High resolution spectroscopy of carboxylic acid in the gas phase: observation of proton transfer in (DCOOH)2. J. Chem. Phys. 117:7162. doi: 10.1063/1.1507581
Matanović, I., Doslić, N., and Johnson, B. R. (2008). Generalized approximation to the reaction path: the formic acid dimer case. J. Chem. Phys. 128:084103. doi: 10.1063/1.2833978
Mayer, J. M. (2011). Understanding hydrogen atom transfer: from bond strengths to marcus theory. Accounts Chem. Res. 44, 36–46. doi: 10.1021/ar100093z
Mil'nikov, G. V., Kühn, O., and Nakamura, H. (2005). Ground-state and vibrationally assisted tunneling in the formic acid dimer. J. Chem. Phys. 123:074308. doi: 10.1063/1.2000257
Ortlieb, M., and Havenith, M. (2007). Proton transfer in (HCOOH)2: an IR high-resolution spectroscopic study of the antisymmetric C-O stretch. J. Phys. Chem. A 111, 7355–7363. doi: 10.1021/jp070763+
Pandey, A., and Poirier, B. (2019). Using phase-space Gaussians to compute the vibrational states of OCHCO+. J. Chem. Phys. 151:014114. doi: 10.1063/1.5096770
Petty, C., and Poirier, B. (2014). Using scalIT for performing accurate rovibrational spectroscopy calculations for triatomic molecules: a practical guide. Appl. Math. 5:2756. doi: 10.4236/am.2014.517263
Poirier, B. (2001). Phase space optimization of quantum representations: non-cartesian coordinate spaces. Found. Phys. 31, 1581–1610. doi: 10.1023/A:1012642832253
Poirier, B., and Carrington, T. (2001). Accelerating the calculation of energy levels and wave functions using an efficient preconditioner with the inexact spectral transform method. J. Chem. Phys. 114, 9254–9264. doi: 10.1063/1.1367396
Poirier, B., and Carrington, T. (2002). A preconditioned inexact spectral transform method for calculating resonance energies and widths, as applied to HCO. J. Chem. Phys. 116, 1215–1227. doi: 10.1063/1.1428752
Poirier, B., and Light, J. C. (1999). Phase space optimization of quantum representations: direct-product basis sets. J. Chem. Phys. 111, 4869–4885. doi: 10.1063/1.479747
Poirier, B., and Light, J. C. (2001). Phase space optimization of quantum representations: three-body systems and the bound states of HCO. J. Chem. Phys. 114, 6562–6571. doi: 10.1063/1.1354181
Qu, C., and Bowman, J. M. (2016). An ab initio potential energy surface for the formic acid dimer: zero-point energy, selected anharmonic fundamental energies, and ground-state tunneling splitting calculated in relaxed 1–4-mode subspaces. Phys. Chem. Chem. Phys. 18, 24835–24840. doi: 10.1039/C6CP03073D
Ren, Y., and Bian, W. (2015). Mode-specific tunneling splittings for a sequential double-hydrogen transfer case: an accurate quantum mechanical scheme. J. Phys. Chem. Lett. 6, 1824–1829. doi: 10.1021/acs.jpclett.5b00672
Ren, Y., Li, B., and Bian, W. (2011). Full-dimensional quantum dynamics study of vinylidene – acetylene isomerization: a scheme using the normal mode Hamiltonian. Phys. Chem. Chem. Phys. 13, 2052–2061. doi: 10.1039/C0CP01186J
Richardson, J. O. (2017). Full- and reduced-dimensionality instanton calculations of the tunnelling splitting in the formic acid dimer. Phys. Chem. Chem. Phys. 19, 966–970. doi: 10.1039/C6CP07808G
Salamone, M., and Bietti, M. (2015). Tuning reactivity and selectivity in hydrogen atom transfer from aliphatic C–H bonds to alkoxyl radicals: role of structural and medium effects. Accounts Chem. Res. 48, 2895–2903. doi: 10.1021/acs.accounts.5b00348
Smedarchina, Z., Fernández-Ramos, A., and Siebrand, W. (2005). Tunneling dynamics of double proton transfer in formic acid and benzoic acid dimers. J. Chem. Phys. 122:134309. doi: 10.1063/1.1868552
Smedarchina, Z., Siebrand, W., and Fernández-Ramos, A. (2013). Zero-point tunneling splittings in compounds with multiple hydrogen bonds calculated by the rainbow instanton method. J. Phys. Chem. A 117, 11086–11100. doi: 10.1021/jp4073608
Smedarchina, Z., Siebrand, W., and Fernández-Ramos, A. (2018). Entanglement and co-tunneling of two equivalent protons in hydrogen bond pairs. J. Chem. Phys. 148:102307. doi: 10.1063/1.5000681
Weinberg, D. R., Gagliardi, C. J., Hull, J. F., Murphy, C. F., Kent, C. A., Westlake, B. C., et al. (2012). Proton-coupled electron transfer. Chem. Rev. 112, 4016–4093. doi: 10.1021/cr200177j
Wu, F. (2016). Quantum mechanical investigation of mode-specific tunneling upon fundamental excitation in malonaldehyde. J. Phys. Chem. A 120, 3849–3854. doi: 10.1021/acs.jpca.6b00340
Wu, F., Ren, Y., and Bian, W. (2016). The hydrogen tunneling splitting in malonaldehyde: a full-dimensional time-independent quantum mechanical method. J. Chem. Phys. 145:074309. doi: 10.1063/1.4960789
Wyatt, R. E. (1995a). Computation of high–energy vibrational eigenstates: application to C6H5D. J. Chem. Phys. 103, 8433–8443. doi: 10.1063/1.470154
Wyatt, R. E. (1995b). Matrix spectroscopy: computation of interior eigenstates of large matrices using layered iteration. Phys. Rev. E 51, 3643–3658. doi: 10.1103/PhysRevE.51.3643
Xue, Z., and Suhm, M. A. (2009). Probing the stiffness of the simplest double hydrogen bond: the symmetric hydrogen bond modes of jet-cooled formic acid dimer. J. Chem. Phys. 131:054301. doi: 10.1063/1.3191728
Yang, B., Chen, W., and Poirier, B. (2011). Rovibrational bound states of neon trimer: quantum dynamical calculation of all eigenstate energy levels and wavefunctions. J. Chem. Phys. 135:094306. doi: 10.1063/1.3630922
Zhang, Y., Li, W., Luo, W., Zhu, Y., and Duan, C. (2017). High resolution jet-cooled infrared absorption spectra of (HCOOH)2, (HCOOD)2, and HCOOH-HCOOD complexes in 7.2 μ m region. J. Chem. Phys. 146:244306. doi: 10.1063/1.4989863
Zhang, Z., Li, B., Shen, Z., Ren, Y., and Bian, W. (2012). Efficient quantum calculation of the vibrational states of acetylene. Chem. Phys. 400, 1–7. doi: 10.1016/j.chemphys.2012.01.010
Zhou, Z., Aitken, R. A., Cardinaud, C., Slawin, A. M. Z., Wang, H., Daly, A. M., et al. (2019). Synthesis, microwave spectra, x-ray structure, and high-level theoretical calculations for formamidinium formate. J. Chem. Phys. 150:094305. doi: 10.1063/1.5081683
Keywords: tunneling splitting, proton transfer, quantum dynamics, formic acid dimer, normal coordinates
Citation: Liu H, Cao J and Bian W (2019) Double Proton Transfer in the Dimer of Formic Acid: An Efficient Quantum Mechanical Scheme. Front. Chem. 7:676. doi: 10.3389/fchem.2019.00676
Received: 19 July 2019; Accepted: 30 September 2019;
Published: 23 October 2019.
Edited by:
Ol'ha Brovarets', National Academy of Sciences of Ukraine, UkraineReviewed by:
Luca Evangelisti, University of Bologna, ItalyJosé Pedro Cerón-Carrasco, Catholic University San Antonio of Murcia, Spain
Bill Poirier, Texas Tech University, United States
Copyright © 2019 Liu, Cao and Bian. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wensheng Bian, YmlhbkBpY2Nhcy5hYy5jbg==
 Hao Liu
Hao Liu Jianwei Cao
Jianwei Cao Wensheng Bian
Wensheng Bian