Irreverent Nature of Dissymmetry Factor and Quantum Yield in Circularly Polarized Luminescence of Small Organic Molecules

Introduction

An increasingly considerable attention has been paid recently to circularly polarized luminescence (CPL) behavior (Riehl and Muller, 2011; Longhi et al., 2016). Not only their potential applications in chemical sensors (Bradberry et al., 2014), biological probes (Muller, 2009), and three-dimensional displays (Schadt, 1997), but also the exclusive chiroptical and photophysical property of CPL reflects the structural information of chiral molecules or molecules in chiral environment in their excited states (Richardson and Riehl, 1977; Riehl and Richardson, 1986). Every so often, the CPL signal is relatively weak but can be unique and selective; accordingly, the CPL materials are believed to be applicable to various smarter photonic materials and discerning biological censors (Han et al., 2018; Ma et al., 2019). At an early stage, the materials had been developed for derivatives of lanthanoids, due to their intrinsic characteristics that electronic forbidden f–f transitions commonly afford better dissymmetry factor (or a degree of chirality, g_lum, vide infra) (Carr et al., 2012; Zinna and Di Bari, 2015). Recent advance in supramolecular chirality is another trend in the CPL chemistry, where improved responses have been frequently reported through molecular aggregation, agglomeration, flocculation, as well as their combinations (Kumar et al., 2015; Sang et al., 2020). However, systematic investigations to pursue a so-called structure–property relationship to attain a reliable strategy and a design principle for the superior CPL materials, even for more simple isolated molecular systems, have been quite limited. As such, current studies on the CPL materials are mostly based on a cut-and-try basis. Further discussions and many examples are available in recent review articles (Sanchez-Carnerero et al., 2015; Tanaka et al., 2018b).

Naturally, an observed difference between emission intensities of left- and right-handed circularly polarized light (I_L-I_R) at a given frequency ν in the CPL measurement on chiral substance depends on an intensity of an incident excitation light. Therefore, a degree of chirality in the CPL response is generally discussed with the polarization efficiency, or the dissymmetry factor of luminescence (g_lum). Thus, the g_lum value is a difference emission intensity divided by an averaged intensity at a given frequency ν, which is defined as follows:

$\begin{array}{ll}{g}_{\text{lum}}(\nu )=2\frac{I_L(\nu )-I_R(\nu )}{I_L(\nu )+I_R(\nu )}& (1)\end{array}$

By definition, minimum and maximum g_lum factors are −2 and +2. Most of the studies that explore better CPL molecules thus pursue molecules with larger absolute g_lum value (i.e., |g_lum|), as this parameter is frequently the most limiting factor, particularly in small organic molecules where g_lum factors are typically as low as in an order of 10⁻⁵ to 10⁻³ range.

In the 1960s and 1970s, the CPL chemistry on small organic molecules had been limited to constraint cyclic ketones, where relatively larger g_lum values were obtained due to the electronically forbidden n–π* transition. In most of these molecules, chiral distortion of carbonyl moiety is usually released in their excited states, the degree of which is highly dependent on the nature of the molecule. Accordingly, g_lum prediction of chiral ketones is specifically challenging. Recent emphasis has been rather placed on electronically allowed π-π* transition of rigid aromatic systems, for reasons such as below. Firstly, these systems often afford much improved fluorescence probability. Second, a facile structural modification is conceivable that can fine-tune absorption and emission wavelengths and bandwidths, and possibly the degree of dissymmetry as well. Also, the degree of excited-state relaxation in such systems has been found surprisingly systematic, although slightly dependent on the structural motifs or types of chirality. Such statistical analyses afforded empirical linear correlations between the dissymmetry factors of luminescence and absorption, allowing us an empirical yet a rational design (Tanaka et al., 2018b).

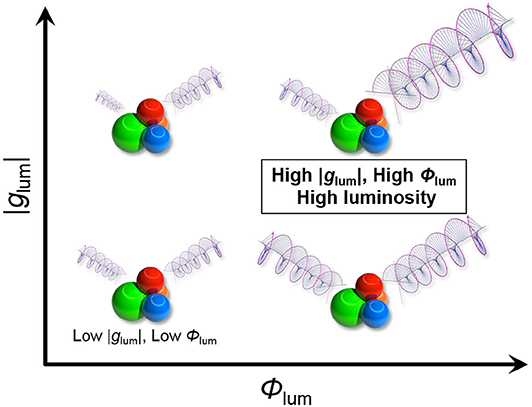
In order to fully understand the overall CPL efficiency, other photophysical parameters beside the dissymmetry factor (g_lum) should be also taken into consideration (Figure 1). As more materials-oriented intrinsic index of CPL efficiency, we propose a circular polarization luminosity (Λ_CPL) per single chiral molecule in the excited state, which is defined as follows:

$\begin{array}{ll}{\Lambda }_{\text{CPL}}=f\times {\Phi }_{\text{lum}}\times \frac{\left|g_{lum}\right|}{2}& (2)\end{array}$

where f and Φ_lum are efficiencies of light absorption (oscillator strength) and emission intensity (quantum yield), respectively. By definition, minimum and maximum Λ_CPL values are 0 and 1. Hypothetically, molecules with larger Λ_CPL values at desired excitation and emission wavelengths are considered as satisfactory chiroptical materials. In the following discussion, we made an effort to understand a possible relationship among the photophysical parameters in the CPL behavior, particularly that between g_lum and Φ_lum.

FIGURE 1

Figure 1. Conceptual diagram for two-dimensional improvement of CPL materials.

Theoretical Consideration

In real spectra, the CPL and fluorescence bands are characterized by distinct parameters, which are called rotational (R) and dipole (D) strengths, respectively. In isotropic solution, the following equations generally fold (in cgs unit) for the CPL (I_L-I_R) and total (I_L + I_R) emission intensities from chiral substance as a function of ν:

$\begin{array}{ll}{I}_L(\nu )-I_R(\nu )=\frac{16{\nu }^3\rho (\nu )}{3c^3{\hslash }^4}R& (3)\end{array}$

$\begin{array}{ll}{I}_L(\nu )+I_R(\nu )=\frac{8{\nu }^3\rho (\nu )}{3c^3{\hslash }^4}D& (4)\end{array}$

where h is the reduced Planck's constant, c is the speed of light, and ρ(ν) is a Gaussian band shape.

Theoretically, the value D is defined as the square of an electric transition dipole moment (μ) for an electronic transition between an emissive state j and a ground state i:

$\begin{array}{ll}D={\langle {\text{Ψ}}_j\left|\mu \right|{\text{Ψ}}_i\rangle }^2& (5)\end{array}$

According to Rosenfeld (Rosenfeld, 1929), the value R can be expressed as a product of wavefunction overlap integrals between the electric (μ) and magnetic (m) transition dipole moments, as follows:

$\begin{array}{ll}R=\text{lm}\left[\langle {\text{Ψ}}_j\left|\mu \right|{\text{Ψ}}_i\rangle ·\langle {\text{Ψ}}_i\left|m\right|{\text{Ψ}}_j\rangle \right]& (6)\end{array}$

where Im refers to an imaginary component of the scalar product between real vector μ and imaginary vector m. In most situations, this is also expressed as:

$\begin{array}{ll}R=\left|\mu \right|\left|m\right|cos\theta & (7)\end{array}$

where θ is the angle between the two dipole moments. This obviously demonstrates a non-orthogonal nature of μ and m of chiral materials. By substituting Equations (3) and (4) for Equation (1), the dissymmetry factor can be simplified with R and D as follows:

$\begin{array}{ll}{g}_{lum}=4\times \frac{R}{D}& (8)\end{array}$

Equation (8) clearly suggests the linear correlation between the g_lum value against the inverse of D. That is, g_lum should be reciprocally proportional to the square of transition probability, if the value R is independent to D. This is empirically in accord with the fact that classical examples of CPL responsive materials were based on the molecules with forbidden transitions, in which better g_lum factors were frequently reported. In a different expression, Equation (8) is also stated as:

$\begin{array}{ll}{g}_{lum}=4\times \frac{\left|m\right|cos\theta }{\left|\mu \right|}& (9)\end{array}$

Thus, g_lum is proportional to reciprocal amplitude of μ, under conditions that μ is independent to m. For further details on the relevant theoretical consideration and numerical expressions, see refs (Richardson and Riehl, 1977) and (Riehl and Richardson, 1986).

The quantum yield of emission Φ_lum is determined by the rate of radiative and non-radiative decays, as follows:

$\begin{array}{ll}{\Phi }_{\text{lum}}=\frac{k_r}{k_r+k_{nr}}=\frac{1}{1-\left(-\frac{k_{nr}}{k_r}\right)}& (10)\end{array}$

In order to assess a possible correlation between g_lum and Φ_lum values, we may consider the following relations (Carr et al., 2012; Kumar et al., 2015; Tanaka et al., 2018b; Sang et al., 2020) that are valid only at the condition of k_nr/k_f ≪ 1, for which the molecules have relatively good emission properties. This allows to expand the Equation (10) to:

$\begin{array}{ll}{\Phi }_{\text{lum}}\approx 1-\frac{k_{nr}}{k_r},\text{ in the limit of }\frac{k_{nr}}{k_r}\ll 1& (11)\end{array}$

The rate of emission is dependent on f and the square of the frequency of the electronic transition ν. Here, we ignore the difference between absorption and emission processes as structural relaxation in the excited state can be negligible in rigid aromatic systems. Also, the experimental emission and absorption intensities are proportional to the square of corresponding electric transition dipole moments. Thus, Φ_lum is related to the electronic transition dipole moment μ as follows:

$\begin{array}{ll}{1-\Phi }_{lum}\propto |\mu {|}^{-2}& (12)\end{array}$

Subsequently, Equations (9) and (12) can be rearranged to:

$\begin{array}{ll}{g}_{lum}\propto \left|m\right|cos\theta \times \sqrt{{1-\Phi }_{\text{lum}}}& (13)\end{array}$

Therefore, under the condition that Φ_lum and m can be regarded independent, g_lum values are dependent to the square of (1 – Φ_lum). That is:

$\begin{array}{ll}{g}_{lum}\propto \sqrt{{1-\Phi }_{\text{lum}}},\text{ in the limit of }\frac{k_{nr}}{k_r}\ll 1& (14)\end{array}$

Finally, Equation (2) can be also reorganized into:

$\begin{array}{l}{\Lambda }_{\text{CPL}}\propto |\mu {|}^2\times {\Phi }_{\text{lum}}\times \frac{\left|m\right|cos\theta }{\left|\mu \right|}=|\mu \left|\right|m|cos\theta \times {\Phi }_{\text{lum}}\\ =R\times {\Phi }_{\text{lum}}& (15)\end{array}$

Thus, as the first approximation, the circular polarization luminosity (Λ_CPL), a key parameter for the excellent CPL materials, is eventually related to the rotational strength (R) and the emission quantum yield (Φ_lum). Note that this equation holds without the condition of k_nr/k_f ≪ 1.

Statistical Analyses

We have recently collected all the reported CPL data that were associated with circular dichroisms (CDs) for small organic molecules up to the year 2017 (Tanaka et al., 2018b). We found the direct correlation between dissymmetry factors of luminescence and absorption, affording an empirical linear correlation of |g_lum| = 0.81 × |g_abs| (r² = 0.60) as a global fit for all the CPL and CD data of the electronically allowed π-π* transition of rigid aromatic systems. For comparison and clarity, the same data were plotted in log–log format depicted in Figure 2A. Although some scattered data were apparent, statistical analysis led to the same conclusion that there is a linear correlation between two dissymmetry factors with a slop of ≈1. As discussed above, the g_lum value will be correlated to the square of (1 – Φ_lum), unless there is extensive bias. Such an analysis was performed as shown in Figure 2B, utilizing all the chiral molecules used in the same review (Tanaka et al., 2018b). As clearly seen, data were more dispersed and direct correlation was not obtained between g_lum and Φ_lum, at least among these samples, both in global plot and among sub-class of chirality, which was categorized in different colors.

FIGURE 2

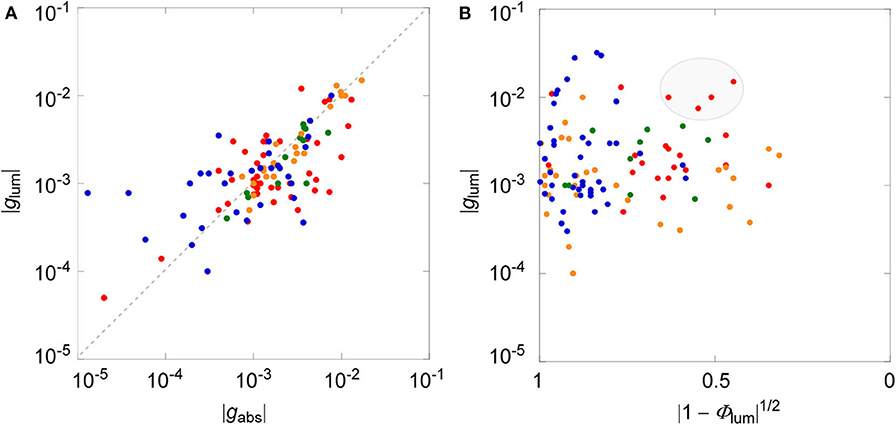
Figure 2. (A) Log–log plot between luminescence (g_lum) and absorption (g_abs) dissymmetry factors. (B) Log plot between g_lum and square of 1—luminescence quantum yield (Φ_lum). Blue, helicenes and derivatives; red, planar chiral cyclophanes; orange, binaphthyls with axial chirality; green chiral BODIPY derivatives. Data are taken from Tanaka et al. (2018b).

Discussion

Before providing our supposition on the above observations, we better comment on a limitation of our evaluations. Possible issues on reliability of our data analyses may include the following: (1) Limiting examples: Our analyses were rather limited in terms of numbers of available data (N ≈ 100) in indefectible statistical point of view. (2) Exclusion of negative data: In particular, data with low Φ_lum values (<10⁻³) are almost completely neglected as such systems have been rarely published. Such trend is also true for those with low g_lum values (<10⁻⁵). (3) Measurement conditions: Measurements to be compared are better to be identical. Also, both the CPL and luminescence experiments should be executed under the comparable conditions. From time to time, Φ_lum and g_lum were evaluated at specific peak wavelengths that were not always matching each other (e.g., g_lum was reported at a relatively feeble shoulder position of emission). In such cases, both parameters are maximized at individual wavelengths, but the correlation may be lost, or at least deteriorated. In other instances, very wide slit widths are employed in the CPL experiment. The g_lum values tend to be observed smaller as widths of slit (window of light propagation) in the CPL spectroscopy are increased. This is often inevitable, however, for samples of weak signal (i.e., low luminescence and/or dissymmetry factor). (4) Sample quality: As well as the purity and optical purity of the chiral samples, additional experimental issues such as aggregation, band overlap, and vibronic contribution should be carefully considered and possibly be eliminated or corrected. Such propositions, however, have been overlooked in most of the reports.

Although we admit that more studies are certainly needed to have a definite relevancy between g_lum and Φ_lum values, we may deduce the following (tentative) suppositions.

(1) The plots between g_lum and Φ_lum values, even among the sub-class of different types of chiral molecules, provided substantially dispersed ones (Figure 2B). They did not provide a linear (or any meaningful) relationship, as has been expected by theory or by intuition from the classical examples. This immediately indicates that there is some bias between these values. We believe that this is due, at least in part, to the fact that the data of low Φ_lum values were missing simply because such numbers were reluctant to be included in a publication. In fact, the plots based on the reported values were widely dispersed with the exception of a region with low Φ_lum values (right-hand side).

(2) At a first glance, the fact that there was no immediate correlation between g_lum and Φ_lum values was somewhat disappointing. However, it was also realized that the g_lum values were still expanded in a whole range between 10⁻⁵ and 10⁻¹ within the selected Φ_lum domain. This observation clearly infers that the g_lum values may be improved irrespective to the emission property, in spite of possible correlation in Equation (14). As such, we suggest the rather straightforward strategy for designing superior CPL materials having better circular polarization luminosity (Λ_CPL), that is, to inspect a systematic structural modification on certain molecules already demonstrating high Φ_lum value in a trial-and-error manner.

(3) In this regard, we can point to some data located at the top-middle position in Figure 2B (highlighted in a gray ellipse), those simultaneously possessing relatively larger g_lum and Φ_lum values. These include some planar chiral rigid cyclophane derivatives that may be quite promising as the starting points for more improved CPL materials with larger g_lum value concomitantly keeping high Φ_lum value. In another respect, it is worth noting that there have been substantially growing numbers of investigations recently that report the improved CPL responses based on molecular symmetry with helicene derivatives (Tanaka et al., 2018a,c; Isla et al., 2019; Schaack et al., 2019; Zhao et al., 2019).

Concluding Remarks

Although the number of reported examples of CPL active small organic molecules has been rapidly increasing, mostly being explored in a cut-and-try basis, a structure–property relationship that can guide the design principle has not been established. Thus, to design desired CPL response in molecular systems is still challenging. In most of the CPL studies in organic molecules, the dissymmetry factor of luminescence (g_lum) is the limiting factor because the reported values are considerably smaller, usually in several orders of magnitude than the limiting value. Alternatively, other photophysical parameters, in particular the luminescence quantum yields (Φ_lum), are also an important factor to develop the truly useful CPL materials.

In this contribution, we tried to determine the possible correlation between g_lum and Φ_lum values, both in theoretical formula and experimental observations. It was a little surprise that the observed g_lum values of π-π* transition of rigid aromatic molecules are independent to their Φ_lum values, despite the expected correlation derived from Equation (14). Rather, a direct relationship between the circular polarization luminosity (Λ_CPL) and rotational strength (R) found in Equation (15) seems more substantial. Our analyses also advocate that the g_lum values can be improved irrespective to Φ_lum. Therefore, the most straightforward means to develop the improved CPL materials could be a methodical structural modification of aromatic systems that already enjoy the high Φ_lum values, which will directly maximize the circular polarization luminosity (Λ_CPL), the real measure for the superior CPL materials. We hope our analyses and suppositions may be of benefit for future design of materials of better CPL responses.

Author Contributions

TM wrote the first draft of the manuscript. Both authors contributed to manuscript revision, and read and approved the submitted version.

Funding

Financial support for TM by Grant-in-Aids for Scientific Research, Challenging Exploratory Research, and Promotion of Joint International Research (Fostering Joint International Research) (Grant Numbers JP16H06041, JP16KK0111, JP17H05261, JP18K19077, and JP18H01964) from JSPS, by the Asahi Glass Foundation and the Murata Science Foundation, Tonen General Sekiyu Research/Development Encouragement & Scholarship Foundation, and by the Cooperative Research Program of Network Joint Research Center for Materials and Devices are greatly acknowledged.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer CY declared a past co-authorship with one of the author TM to the handling editor.

Acknowledgments

TM thanks Emeritus Prof. Yoshihisa Inoue for a fruitful discussion.

References

Bradberry, S. J., Savyasachi, A. J., Martinez-Calvo, M., and Gunnlaugsson, T. (2014). Development of responsive visibly and NIR luminescent and supramolecular coordination self-assemblies using lanthanide ion directed synthesis. Coord. Chem. Rev. 273, 226–241. doi: 10.1016/j.ccr.2014.03.023

CrossRef Full Text | Google Scholar

Carr, R., Evans, N. H., and Parker, D. (2012). Lanthanide complexes as chiral probes exploiting circularly polarized luminescence. Chem. Soc. Rev. 41, 7673–7686. doi: 10.1039/c2cs35242g

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, J., Guo, S., Lu, H., Liu, S., Zhao, Q., and Huang, W. (2018). Recent progress on circularly polarized luminescent materials for organic optoelectronic devices. Adv. Optic. Mater. 6:1800538. doi: 10.1002/adom.201800538

CrossRef Full Text | Google Scholar

Isla, H., Saleh, N., Ou-Yang, J.-K., Dhbaibi, K., Jean, M., Dziurka, M., et al. (2019). Bis-4-aza(6)helicene: a bis-helicenic 2,2'-bipyridine with chemically triggered chiroptical switching activity. J. Org. Chem. 84, 5383–5393. doi: 10.1021/acs.joc.9b00389

PubMed Abstract | CrossRef Full Text | Google Scholar

Kumar, J., Nakashima, T., and Kawai, T. (2015). Circularly polarized luminescence in chiral molecules and supramolecular assemblies. J. Phys. Chem. Lett. 6, 3445–3452. doi: 10.1021/acs.jpclett.5b01452

PubMed Abstract | CrossRef Full Text | Google Scholar

Longhi, G., Castiglioni, E., Koshoubu, J., Mazzeo, G., and Abbate, S. (2016). Circularly polarized luminescence: a review of experimental and theoretical aspects. Chirality 28, 696–707. doi: 10.1002/chir.22647

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, J.-L., Peng, Q., and Zhao, C.-H. (2019). Circularly polarized luminescence switching in small organic molecules. Chem. Eur. J. 25, 15441–15454. doi: 10.1002/chem.201903252

PubMed Abstract | CrossRef Full Text | Google Scholar

Muller, G. (2009). Luminescent chiral lanthanide(III) complexes as potential molecular probes. Dalton Trans. 9692–9707. doi: 10.1039/b909430j

PubMed Abstract | CrossRef Full Text | Google Scholar

Richardson, F. S., and Riehl, J. P. (1977). Circularly Polarized Luminescence Spectroscopy. Chem. Rev. 77, 773–792. doi: 10.1021/cr60310a001

CrossRef Full Text | Google Scholar

Riehl, J. P., and Muller, G. (2011). Circularly polarized luminescence spectroscopy and emission-detected circular dichroism. Compreh. Chiropt. Spectr. 65–90. doi: 10.1002/9781118120187.ch3

CrossRef Full Text | Google Scholar

Riehl, J. P., and Richardson, F. S. (1986). Circularly polarized luminescence spectroscopy. Chem. Rev. 86, 1–16. doi: 10.1021/cr00071a001

CrossRef Full Text | Google Scholar

Rosenfeld, L. (1929). Quantenmechanische theorie der natürlichen optischen aktivität von flüssigkeiten und gasen. Z. Phys. 52, 161–174. doi: 10.1007/BF01342393

CrossRef Full Text | Google Scholar

Sanchez-Carnerero, E. M., Agarrabeitia, A. R., Moreno, F., Maroto, B. L., Muller, G., Ortiz, M. J., et al. (2015). Circularly Polarized Luminescence from Simple Organic Molecules. Chem. Eur. J. 21, 13488–13500. doi: 10.1002/chem.201501178

PubMed Abstract | CrossRef Full Text | Google Scholar

Sang, Y., Han, J., Zhao, T., Duan, P., and Liu, M. (2020). Circularly polarized luminescence in nanoassemblies: generation, amplification, and application. Adv. Mater. 32. doi: 10.1002/adma.201900110

PubMed Abstract | CrossRef Full Text | Google Scholar

Schaack, C., Arrico, L., Sidler, E., Gorecki, M., Di Bari, L., and Diederich, F. (2019). Helicene monomers and dimers: chiral chromophores featuring strong circularly polarized luminescence. Chem. Eur. J. 25, 8003–8007. doi: 10.1002/chem.201901248

PubMed Abstract | CrossRef Full Text | Google Scholar

Schadt, M. (1997). Liquid crystal materials and liquid crystal displays. Annu. Rev. Mater. Sci. 27, 305–379. doi: 10.1146/annurev.matsci.27.1.305

CrossRef Full Text | Google Scholar

Tanaka, H., Ikenosako, M., Kato, Y., Fujiki, M., Inoue, Y., and Mori, T. (2018a). Symmetry-based rational design for boosting chiroptical responses. Comms. Chem. 1, 38. doi: 10.1038/s42004-018-0035-x

CrossRef Full Text | Google Scholar

Tanaka, H., Inoue, Y., and Mori, T. (2018b). Circularly polarized luminescence and circular dichroisms in small organic molecules: correlation between excitation and emission dissymmetry factors. ChemPhotoChem 2, 386–402. doi: 10.1002/cptc.201800015

CrossRef Full Text | Google Scholar

Tanaka, H., Kato, Y., Fujiki, M., Inoue, Y., and Mori, T. (2018c). Combined experimental and theoretical study on circular dichroism and circularly polarized luminescence of configurationally robust D₃-symmetric triple pentahelicene. J. Phys. Chem. A 122, 7378–7384. doi: 10.1021/acs.jpca.8b05247

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, W.-L., Li, M., Lu, H.-Y., and Chen, C.-F. (2019). Advances in helicene derivatives with circularly polarized luminescence. Chem. Commun. 55, 13793–13803. doi: 10.1039/C9CC06861A

PubMed Abstract | CrossRef Full Text | Google Scholar

Zinna, F., and Di Bari, L. (2015). Lanthanide circularly polarized luminescence: bases and applications. Chirality 27, 1–13. doi: 10.1002/chir.22382

PubMed Abstract | CrossRef Full Text | Google Scholar