Sulfate, Bisulfate, and Hydrogen Co-adsorption on Pt(111) and Au(111) in an Electrochemical Environment

1. Introduction

Electrochemistry is concerned with the processes at the interface between an electron conductor, the electrode, and an ion conductor, the electrolyte (Schmickler and Santos, 2010). At this interface, an electric double layer (EDL) forms (Groß and Sakong, 2019). Charged electrodes attract counterions from the electrolyte, but ions might also specifically adsorb at the electrode due to a strong chemical interaction (Tripkovic et al., 2009). These adsorbed ions can significantly modify the chemical and catalytic properties of the electrode surface (Magnussen, 2002; Marković and Ross, 2002). Hence a detailed knowledge of the coverage and structure of electrode surfaces under electrochemical conditions is crucial for a true understanding of the processes occurring at electrochemical electrode/electrolyte interfaces (Magnussen and Groß, 2019).

On this account, the interaction of electrolytes with catalytic surfaces was studied intensively in the last decades (Groß, 2020; Nowicki and Wandelt, 2020). One of the best studied systems is sulfate adsorption on platinum (Shingaya and Ito, 1996; Kolics and Wieckowski, 2001; Herrero et al., 2002; Braunschweig et al., 2010; Garcia-Araez et al., 2010; Santana et al., 2010; Comas-Vives et al., 2013), but despite various investigations the surface structure of the ad-layer is still controversially discussed. The origin of this problem can be traced back to the fact that both sulfate and bisulfate can exist in equilibrium at the electrode/electrolyte interface, but experimentally it is hard to differentiate between these two anions by most electrochemical technics. From a theoretical point of view (Santana et al., 2010; Comas-Vives et al., 2013), it is important to realize that the (bi)sulfate ions are rather large and do form close packed layers. Hence water molecules penetrate the (bi)sulfate layers, so that in the theoretical treatment the presence of the water molecules needs to be taken into account, in contrast to the specific adsorption of small ions such as halides for which experimental observations (Magnussen, 2002; Garcia-Araez et al., 2005a,b) can be well-reproduced by density functional theory calculations (Groß et al., 2014; Gossenberger et al., 2015, 2016) that do not explicitly consider the presence of the aqueous electrolyte.

Results from cyclic voltammetry of (bi)sulfate on Pt(111) indicate the existence of four dominant regions, distinct from each other by significant structural changes (Herrero et al., 2002; Braunschweig et al., 2010; Garcia-Araez et al., 2010). At low electrode potentials favoring the presence of cations, platinum is covered by hydrogen (Jerkiewicz, 2010). The stability window of the hydrogen adsorbate layers depends on the pH of the solvent. A lower pH shifts the onset potential for hydrogen adsorption regime in the anodic scan to higher potentials, but it is always below 0.4 V (Herrero et al., 2002; Braunschweig et al., 2010; Garcia-Araez et al., 2010).

After hydrogen desorption at about 0.5 V, the adsorption of (bi)sulfate takes place according to cyclic voltammograms. This region is governed by the adsorption of mobile species, since STM experiments do not show a particular adsorbate pattern on the surface (Funtikov et al., 1997). Density functional studies by Santana et al. (2010) suggest that bisulfate ions adsorb in this regime with three oxygen atoms down, stabilized by hydrogen bonds to the surrounding water molecules.

In the region of 0.5 V–0.6 V, a sharp feature appears in the cyclic voltammogram, sometimes called the “spike” (Funtikov et al., 1997). At this potential, a serious rearrangement in the adsorbate structure occurs, a highly ordered $\sqrt{3}\times \sqrt{7}$ structure appears, as observed in STM experiments (Funtikov et al., 1995, 1997). The surface coverage corresponds to 0.2 ML (Funtikov et al., 1995; Herrero et al., 2002; Santana et al., 2010). From the vibrational analysis of ab initio molecular dynamics simulations it has been proposed that the adsorption geometry of the (bi)sulfate ions changes to a three-point adsorption at the spike (Qian et al., 2014). Theoretical studies show that the resulting row-like $\sqrt{3}\times \sqrt{7}$ structure is stabilized by the presence of water molecules situated in-between the sulfate rows (Santana et al., 2010; Comas-Vives et al., 2013). The precise position of the spike in cyclic voltammograms is shifted slightly to more negative potentials when the sulfate concentration (Herrero et al., 2002; Garcia-Araez et al., 2010) or the pH (Garcia-Araez et al., 2010) are increased. However, for a pH value of larger than 4, the spike is no longer observed in the cyclic voltammograms.

Garcia-Araez et al. (2010) clarified in an extensive analysis, that in the pH-range of 0.8-4.5 rather sulfate than bisulfate is present on the surface. DFT calculations also support the conclusion that for electrode potentials larger than 0.48 V sulfate is the favored adsorbate species (Jinnouchi et al., 2012). Thus, the origin of the spike is assumed to be the result of the deprotonation of the previously adsorbed bisulfate ions. However, this assumption is still debated, as linear sweep voltammetry simulations and DFT calculations by Yeh et al. (2013) suggest that the spike is actually the result of a rapid coverage change rather than deprotonation. This disorder-order transition was also the subject of a generic kinetic Monte Carlo study of bridge-bonded anions on fcc(111) surfaces (Hermse et al., 2004) which found a strong dependence of this transition on the nature of the lateral interactions between the adsorbed anions.

The row-like $(\sqrt{3}\times \sqrt{7})$ structure is then stable up to potentials of about 0.7 V (Funtikov et al., 1995), for higher potentials the STM images become noisy and any clear structure disappears. At this point obviously a phase transition occurs, the surface becomes oxidized by additional sulfate adsorbates if the pH is below 2. At higher pH values, the surface gets rather oxidized by competitive OH⁻ adsorption (Funtikov et al., 1997; Braunschweig et al., 2010). However, if the spike feature is not present, the phase transition at 0.7 V is also not observable. Thus, both structure changes are closely related (Garcia-Araez et al., 2008).

For the case of (bi)sulfate adsorption on Au(111), the situation is comparable. There also a “spike” appears, but at a potential of about 1.0 V (Cuesta et al., 2000; Sato et al., 2006). At the spike a serious restructuring of the adlayer occurs, which proceeds in a similar way. A unordered structure of preadsorbed (bi)sulfate becomes ordered and the long ranged periodic $(\sqrt{3}\times \sqrt{7})$ structure appears on the gold surface (Sato et al., 2006). IR studies have indicated that in this structure the (bi)sulfate ions also, as on Pt(111), bind to the surface via three oxygen atoms (Ataka and Osawa, 1998).

Here we present a quantum-chemical study based on density functional theory to calculate phase-diagrams and Pourbaix diagrams of hydrogen and (bi)sulfate adsorption on Pt(111) and Au(111). The electrode potential is taken into account in a grand-canonical approach (Nørskov et al., 2004; Peterson et al., 2010). We demonstrate the fundamental importance of a proper solvation scheme for theoretical models and show in detail, how both explicit and implicit solvation impact the adsorbates in theoretical calculations. Finally, we discuss the equilibrium of bisulfate and sulfate at the surface of both metals.

2. Theoretical Background and Computational Details

All the calculations were performed using the periodic density functional theory (DFT) program Vienna ab initio simulation package (VASP) (Kresse and Furthmüller, 1996). The exchange and correlation energy was taken into account within the generalized gradient approximation (GGA) as suggested by Hammer and Nørskov, known as a revised version of the Perdew-Burke-Ernzerhof (RPBE) functional (Hammer et al., 1999). To include van-der-Waals interactions we used the D3 correction scheme by Grimme et al. (2010). It has been shown that the RPBE-D3 approach reliably yields properties of liquid water (Tonigold and Groß, 2012; Forster-Tonigold and Groß, 2014; Morawietz et al., 2016; Sakong et al., 2016; Schienbein and Marx, 2018), the interaction of water with surfaces (Tonigold and Groß, 2012; Forster-Tonigold and Groß, 2014; Sakong et al., 2016; Sakong and Groß, 2018; Mahlberg et al., 2019; Ruiz-Barragan et al., 2019), and the interaction of organic molecules with metal surfaces (Koslowski et al., 2013; Sakong and Groß, 2016). The electron-core interaction was described by the projector augmented wave method (PAW) (Blöchl, 1994), as constructed by Kresse and Joubert (1999). The electronic wave functions were expanded in a plane wave basis set with an energy of at least 500 eV.

For the calculations we constructed several different supercells with metal slab having a thickness of 4 atomic layers and a distance of approximately 20 Å vacuum. To get reliable phase diagrams it is crucial to consider all configurations of the adsorbate structure which might exist on the electrode surface. The most important cells are those that allow the formation of row-like structures. We considered the following surface unit cells with increasing separation between the rows: $(2\sqrt{3}\times 2\sqrt{3})R30^{\circ }$, $(\sqrt{3}\times \sqrt{13})R13.1^{\circ }$, and $(2\sqrt{3}\times 2\sqrt{7})R19.1^{\circ }$. We also used other surface unit cells that allowed the adsorbates to be accommodated in different configurations and reach various coverages, e.g., (3 × 3), (4 × 2), and $(\sqrt{7}\times \sqrt{13})R13.1^{\circ }$. In this manner we were able to construct (bi)sulfate adsorbate configurations with coverages between 0.05 and 0.33.

To consider solvent effects we used an implicit solvation model (Petrosyan et al., 2005, 2007; Letchworth-Weaver and Arias, 2012; Gunceler et al., 2013; Sakong et al., 2015; Bramley et al., 2020; Heenen et al., 2020) as implemented in the VASP code (Mathew et al., 2014). For the permittivity of the solvent we used the one of clean water ($80\frac{As}{Vm}$). Moreover, for these calculations we raised the energy cutoff to 700 eV to guarantee an accurate electronic density, since this is crucial for the solvent model.

3. Gibbs Energy of Adsorption

We will first present the basic formalism entering the grand-canonical determination of stable adsorbate phases. The Gibbs energy of adsorption Δγ is the thermodynamic magnitude that determines the most stable structure of an adsorbate on an electrode surface under certain electrochemical conditions, such as temperature T, concentrations c_i or rather activities a_i of species i, and electrode potential U. It is defined by the expression

$\begin{array}{ll}\Delta \gamma =\frac{1}{A_{\text{S}}}(G_{\text{surf},\text{ads}}-G_{\text{surf},0}-{\displaystyle \sum _i}{n}_i{\tilde{\mu }}_i(T,a_i,U)),& (1)\end{array}$

where G_{surf, ads} and G_{surf, 0} are the Gibbs energies of the surface with and without the adsorbate, respectively, A_S is the area of the supercell, and ${\tilde{\mu }}_i$ and n_i are the electrochemical potentials and number of the adsorbates. Unfortunately, it is quite demanding to derive thermodynamic properties directly from abinitio simulations, since statistical averages need to be obtained (Schnur and Groß, 2011). An efficient way to avoid these problems is to use the concept of the computational hydrogen electrode (CHE) introduced by Nørskov et al. (2004) and Peterson et al. (2010). This scheme is related to the abinitio atomistic thermodynamics approach for heterogeneous catalysis (Reuter and Scheffler, 2001) and allows to obtain thermodynamic quantities from abinitio calculations by coupling them to grand-canonical reservoirs.

In this work, we considered as adsorbate protons (H⁺), sulfate (${\text{SO}}_4^{2-}$) and bisulfate (${\text{HSO}}_4^{-}$) anions. Note that still all calculations have been performed with charge-neutral super cells as the metal slab acts as an electron reservoir supplying necessary excess charges. Furthermore, anions often do not remain strongly negatively charged upon specific adsorption on metal electrodes (Roman and Groß, 2013; Gossenberger et al., 2014). We will briefly explain how we obtained expressions of their electrochemical potentials in terms of total energies derived from DFT calculations and appropriate redox equilibria. We begin with the chemical potential of the proton. Assuming that protons and electrons in the solution are in equilibrium with the hydrogen molecule through the redox half-reaction: $2{\text{H}}^{+}+2{\text{e}}^{-}\rightleftharpoons {\text{H}}_2$, the following equation is obtained,

$\begin{array}{ll}{\tilde{\mu }}_{{\text{H}}^{+}}+{\tilde{\mu }}_{{\text{e}}^{-}}=\frac{1}{2}{\mu }_{{\text{H}}_2}-e{U}_{SHE}-k_{B}Tln(10)\text{pH},& (2)\end{array}$

where μ_H2 is the chemical potential of hydrogen in the gas phase, ${\tilde{\mu }}_{{\text{H}}^{+}}$ and ${\tilde{\mu }}_{{\text{e}}^{-}}$ are the electrochemical potentials of protons and electrons in the solution, respectively, e is the charge of the electron, and U_SHE is the electrode potential on the standard hydrogen scale (SHE). We regroup all the therms related to the electrode potential and pH in the expression

$\begin{array}{ll}\Delta {\tilde{\mu }}_{{\text{H}}^{+}}=-e{U}_{SHE}-k_{B}Tln(10)\text{pH}.& (3)\end{array}$

In the case of sulfate we used the half-reaction: $\text{S}{\text{O}}_4^{2-}+4{\text{H}}^{+}+2{\text{e}}^{-}\rightleftharpoons \text{S}{\text{O}}_2+2{\text{H}}_2\text{O}$ (at a standard redox potential of $U_{\text{S}{\text{O}}_4^{2-}/\text{S}{\text{O}}_2}^0$ = 0.17 V) to establish the equilibrium between the different species. The electrochemical potential of sulfate at this particular electrode potential and standard conditions is given by

$\begin{array}{ll}{\tilde{\mu }}_{\text{S}{\text{O}}_4^{2-}}+2{\tilde{\mu }}_{{\text{e}}^{-}}={\mu }_{\text{S}{\text{O}}_2}+2{\mu }_{{\text{H}}_2\text{O}}-4{\tilde{\mu }}_{{\text{H}}^{+}},& (4)\end{array}$

where μ_SO2 is the chemical potential of SO₂ in aqueous solution, and ${\tilde{\mu }}_{{\text{SO}}_{\text{4}}{}^{2-}}$ is the electrochemical potential of sulfate ions in the solution. Allowing arbitrary electrode potentials U_SHE on the SHE scale yields

$\begin{array}{l}{\tilde{\mu }}_{{\text{SO}}_{\text{4}}{}^{2-}}+2{\tilde{\mu }}_{{\text{e}}^{-}}={\mu }_{{\text{SO}}_2}+2{\mu }_{{\text{H}}_2\text{O}}-4{\tilde{\mu }}_{{\text{H}}^{+}}\\ +2e(U_{{\text{SO}}_4^{2-}/{\text{SO}}_2}-U_{\text{SHE}}).& (5)\end{array}$

Finally, taking different concentrations of sulfate anions into account and replacing ${\tilde{\mu }}_{{\text{H}}^{+}}$ from Equation (2) gives, using the Nernst equation and assuming an activity coefficient a_SO2 = 1,

$\begin{array}{l}{\tilde{\mu }}_{{\text{SO}}_{\text{4}}{}^{2-}}-2{\tilde{\mu }}_{{\text{e}}^{-}}={\mu }_{{\text{SO}}_2}+2{\mu }_{{\text{H}}_2\text{O}}-2{\mu }_{{\text{H}}_2}+2e{U}_{SHE}\\ +2e{U}_{{\text{SO}}_4^{2-}/{\text{SO}}_2}^0+k_{B}T\ln ({\alpha }_{{\text{SO}}_4^{2-}}),& (6)\end{array}$

where ${\alpha }_{\text{S}{\text{O}}_4^{2-}}$ is the activity of sulfate in the solution which for ideal solutions corresponds to the concentration. Note, that the pH dependence does not appear in the formula, since it has been canceled out because of the equilibrium with protons. We now collect again all the terms related to the experimental conditions in the expression

$\begin{array}{ll}\Delta {\tilde{\mu }}_{\text{S}{\text{O}}_4^{2-}}=2e{U}_{SHE}+2e{U}_{\text{S}{\text{O}}_4^{2-}/\text{S}{\text{O}}_2}^0+k_{B}Tln(a_{\text{S}{\text{O}}_4^{2-}}).& (7)\end{array}$

Following the same methodology a similar expression can be derived for bisulfate:

$\begin{array}{ll}\Delta {\tilde{\mu }}_{\text{HS}{\text{O}}_4^{-}}=e{U}_{SHE}+2e{U}_{\text{HS}{\text{O}}_4^{-}/\text{S}{\text{O}}_2}^0+k_{B}Tln(a_{\text{HS}{\text{O}}_4^{-}})& (8)\end{array}$

where $U_{\text{HS}{\text{O}}_4^{-}/\text{S}{\text{O}}_2}^0$ = 0.11 V is the redox potential of the couple bisulfate/sulfur dioxide.

Usually two-dimensional phase diagrams are plotted displaying the phases that have the lowest Gibbs energies of adsorption as a function of the chemical potentials of two species. In our case we have to consider three possible adsorbates. Still, note that there is an acid/base equilibrium between protons, sulfate and bisulfate anions that connects the three electrochemical potentials according to

$\begin{array}{ll}{\tilde{\mu }}_{\text{HS}{\text{O}}_4^{-}}={\tilde{\mu }}_{\text{S}{\text{O}}_4^{2-}}+{\tilde{\mu }}_{{\text{H}}^{+}}.& (9)\end{array}$

This equation allows to express the electrochemical potential of bisulfate as a function of the other two electrochemical potentials.

Inserting these relations into Equation (1), one arrives at the final expression of the Gibbs energy of adsorption per area as a function of the electrochemical potentials of protons and sulfate anions:

$\begin{array}{l}\Delta \gamma =\frac{1}{A_{\text{S}}}(G_{\text{surf},\text{ads}}-G_{\text{surf},\text{0}}-n_{{\text{H}}^{+}}{\tilde{\mu }}_{{\text{H}}^{+}}-n_{{\text{SO}}_4^{2-}}{\tilde{\mu }}_{{\text{SO}}_4^{2-}}\\ -n_{{\text{HSO}}_4^{-}}{\tilde{\mu }}_{{\text{HSO}}_4^{-}})\\ =\frac{1}{A_{\text{S}}}(G_{ads}-{n^{\prime }}_{{\text{H}}^{+}}\Delta {\tilde{\mu }}_{{\text{H}}^{+}}-{n^{\prime }}_{{\text{SO}}_4^{2-}}\Delta {\tilde{\mu }}_{{\text{SO}}_4^{2-}})& (10)\end{array}$

where $n_{{\text{H}}^{+}}^{\prime }=n_{{\text{H}}^{+}}+n_{\text{HS}{\text{O}}_4^{-}}$, and $n_{\text{S}{\text{O}}_4^{2-}}^{\prime }=n_{\text{S}{\text{O}}_4^{2-}}+n_{\text{HS}{\text{O}}_4^{-}}$. Furthermore, we have introduced the adsorption energy G_ads defined by

$\begin{array}{ll}{G}_{ads}=G_{\text{surf},\text{ads}}-G_{\text{surf},\text{0}}-\frac{{n^{\prime }}_{{\text{H}}^{+}}}{2}{\mu }_{H_2}-{n^{\prime }}_{{\text{SO}}_4^{2-}}({\mu }_{{\text{SO}}_2}+2{\mu }_{{\text{H}}_2\text{O}}-2{\mu }_{{\text{H}}_2}).& (11)\end{array}$

It can be written as

$\begin{array}{ll}{G}_{ads}=E_{ads}+\Delta ZP{E}_{ads}-T\Delta S_{ads}& (12)\end{array}$

where E_ads is the total energy of adsorption

$\begin{array}{ll}{E}_{ads}=E_{\text{surf},\text{ads}}-E_{\text{surf},\text{0}}-\frac{{n^{\prime }}_{{\text{H}}^{+}}}{2}{E}_{{\text{H}}_2}-{n^{\prime }}_{{\text{SO}}_4^{2-}}(E_{{\text{SO}}_2}+2E_{{\text{H}}_2\text{O}}-2E_{{\text{H}}_2}).& (13)\end{array}$

that can be derived from DFT calculations. E_{surf, ads} is the total energy of the slab representing the electrode plus the adsorbates per surface unit cell and E_{surf, 0} is the corresponding total energy of the slab without any adsorbates. The total energies of the molecules have been calculated with respect to the phase that enters the redox equilibria in Equations (2) and (4). E_H2 is the total energy of the H₂ molecule in the gas-phase or rather in vacuum. E_SO2 and E_H2O have been calculated for these molecules in an aqueous electrolyte by determining their total energy in an implicit solvent with the dielectric constant of water. Finally, ΔZPE_ads and ΔS_ads are the change of the molecular zero-point energies and the entropy, respectively, upon adsorption.

In the expression Equation (12) for the adsorption energy G_ads, entropic contributions enter. Often these contributions are neglected, as entropic changes upon adsorption can be small (Reuter and Scheffler, 2001). Still, for a higher reliability of the results it is desirable to include entropic corrections. Here we follow the approach also suggested by Nørskov et al. (2004). We have used tabulated entropies of the molecules taken from experiment (Chase, 1998) and neglected entropic changes of the surface with and without adsorbates. The corresponding values are presented in Table 1. Changes of the molecular zero-point energies upon adsorption have not been considered in this study, as changes in the vibrational properties often only yield a small contribution to the adsorption energy (Reuter and Scheffler, 2001).

TABLE 1

Table 1. Entropy and entropic energy of the molecules.

As already mentioned, we assume that in the bulk solvent the concentration of protons, sulfate, and bisulfate ions are in equilibrium (according to an acid/base reaction). In order to calculate the Pourbaix diagrams we have to keep the total concentration of anions c_i in the electrolyte fixed and to calculate the molar fraction x_i of ${\text{SO}}_4^{2-}$ at each pH according to

$\begin{array}{ll}{x}_{\text{S}{\text{O}}_4^{2-}}=\frac{1}{1+10^{-pH}/10^{-p{K}_a}}& (14)\end{array}$

4. Results

4.1. Adsorption in Vacuum

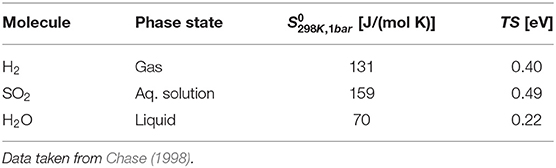
In the first step, we neglected the presence of the electrolyte in the calculation of the adsorption energy, i.e., we performed the calculations at the electrode-vacuum interface. Figure 1 collects the adsorption energies G_ads as a function of the coverage of H, sulfate or bisulfate adsorbed separately on both Au(111) and Pt(111), OH adsorption was not considered in this study. Note that in order to be consistent with the further results for the adsorption energies, we have used as a reference for the energies of the adsorbates those given in Equation (13), namely H₂ in vacuum and SO₂ and H₂O embedded in implicit water. This makes adsorption of (bi)sulfate on the electrode-vacuum interface energetically unfavorable, as SO₂ and H₂O are stabilized in an aqueous electrolyte. With respect to the radicals in vacuum, in fact the interaction between the surface and (bi)sulfate anions is attractive, as already found in previous studies (Venkatachalam and Jacob, 2007; Comas-Vives et al., 2013). For instance, we find that the adsorption of SO₄ on Au(111) within the $(\sqrt{3}\times \sqrt{7})$ structure from the vacuum is associated with an energy gain of −2.48 eV, in a rather nice agreement with previously calculated values (Venkatachalam and Jacob, 2007).

FIGURE 1

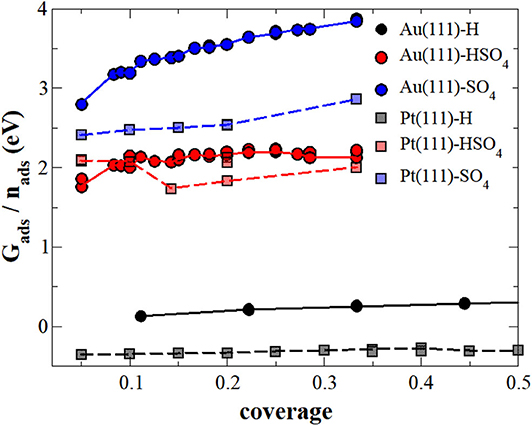
Figure 1. Adsorption energy (G_ads) of sulfate (blue), bisulfate (red) or hydrogen (black) per molecule or atom, respectively, on Au(111) (continuous lines) and Pt(111) (dashed lines) surfaces under vacuum conditions. The lines serve as a visual guidance.

The (bi)sulfate adsorption energies in general increase with coverage, i.e., adsorption becomes energetically less favorable, indicating that there is a repulsive interaction between sulfate and bisulfate adsorbates on these surfaces. Such a behavior is not unexpected. Both adsorbates are still partially charged upon adsorption which leads to coulombic repulsion. Sulfate adsorption is energetically less favorable than bisulfate adsorption on both Au(111) and Pt(111). However, whereas bisulfate adsorption energies are rather similar on both surfaces, sulfate adsorption is significantly less favorable on Au(111) than on Pt(111), and its mutual repulsion also increases more strongly with coverage.

4.2. Adding Solvent I: Using Implicit Water Model

In a second step, we included the presence of an aqueous electrolyte through an implicit solvent model in which water is represented by a polarizable dielectricum. By studying the same systems as in the previous section, we found that the adsorption energy of hydrogen is only weakly changed (≤ 0.05 eV) through the presence of the implicit solvent, as found before (Sakong et al., 2015; Sakong and Groß, 2016). However, due to the fact that (bi)sulfate is larger, adsorbs in an upright fashion, and carries a partial charge, its adsorption energy changes more significantly upon the inclusion of the implicit solvent with respect to the molecule in the gas phase. On Pt(111), adsorption of both species becomes more favorable by up to a value of 0.4 eV (at a coverage of 0.33). On Au(111), the addition of the solvent has the opposite effect, adsorption becomes energetically less favorable by up to 0.2 and 0.3 eV for bisulfate and sulfate, respectively.

Using the adsorption energies obtained in the presence of the implicit solvent, we derived the phase diagrams for Au(111) and Pt(111), that are shown in Figures 2A,B, respectively. One important difference is that on Au(111) the clean surface is stable in a wide range of conditions whereas on Pt(111) hydrogen adsorption sets in already at rather low proton electrochemical potentials $\Delta {\tilde{\mu }}_{{\text{H}}^{+}}$ (note the different range of $\Delta {\tilde{\mu }}_{{\text{H}}^{+}}$ in both panels of Figure 2). This is caused by the strong interaction of Pt(111) with hydrogen whereas Au(111) is only weakly interacting with hydrogen. The coverage of bisulfate/sulfate depends on both electrochemical potentials $\Delta {\tilde{\mu }}_{\text{S}{\text{O}}_4^{2-}}$ and $\Delta {\tilde{\mu }}_{{\text{H}}^{+}}$. For proton electrochemical potentials $\Delta {\tilde{\mu }}_{{\text{H}}^{+}}$ larger than about −0.8 eV, bisulfate adsorbs at lower potentials $\Delta {\tilde{\mu }}_{\text{S}{\text{O}}_4^{2-}}$ than sulfate on both surfaces. Bisulfate coverages of up to 0.33 can be achieved.

FIGURE 2

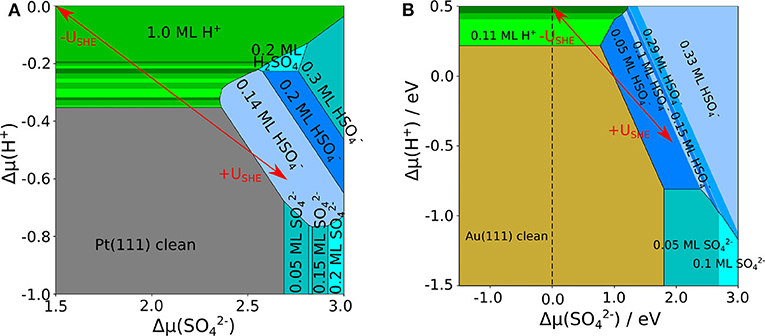
Figure 2. Phase diagram of sulfate, bisulfate, and hydrogen adsorption on (A) Pt(111) and (B) Au(111), as a function of the electrochemical potential of protons and of sulfate anions, using an implicit water model. The uncovered metal electrodes are indicated in gray [Pt(111)] or in brown [Au(111)], respectively; green: pure hydrogen coverage; blue: pure sulfate or bisulfate coverage. The red arrows indicate the effect of varying the electrode potential for fixed concentrations of the species.

The most stable adsorption position of sulfate is always with the three oxygen atoms located on top of the metal atoms so that the sulfur atom is positioned above a three-fold hollow site. The bisulfate ions adsorb in a similar manner with the hydrogen atom attached to the atom that it is not bound to the surface. Only the sulfuric acid molecule H₂SO₄ adsorbs in a different configuration. The molecule adopts a bicoordinate structure with two oxygen on top of two metal atoms. One of the hydrogen atoms is located at the oxygen atom on the metal surface, the remaining is located at a top oxygen atom, where it builds up inter-molecular hydrogen bonds to neighboring sulfuric acid molecules.

There are distinct differences in the stable adsorption structures of bisulfate/sulfate on Pt(111) and Au(111), but also serious discrepancies with respect to experimental observations. The most striking one is related to the formation of row-like structures. On both Pt(111) and Au(111), according to experiments (Funtikov et al., 1995; Cuesta et al., 2000; Herrero et al., 2002; Sato et al., 2006) after the adsorption of disordered structures a phase transition to a $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ row-like structure with a coverage of sulfate/bisulfate of θ = 0.2 ML occurs, in which the adsorbate rows are separated by 7.4 Å. In contrast, our calculations for Au(111) considering only implicit solvation do not yield the experimentally observed $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ structure to be stable at any conditions. Instead, adsorption starts at a lower coverage and then shows two other structures at high coverages of ${\theta }_{\text{HS}{\text{O}}_4^{-}}=0.28$ ML and 0.33 ML, in which complete rows are present. Yet, the separation between the rows is only 5.9 and 4.4 Å, respectively, which is distinctively smaller than the experimentally observed separation.

As far as Pt(111) is concerned, our calculations correctly yield row-like structures to be more stable than other homogeneous configurations. At low coverage, the adsorption of bisulfate starts with the formation of row-like structures with a separation between them of 10.4 Å. Increasing the sulfate electrochemical potential, the $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ structure appears in the phase diagram. However, this structure is only stable in a reduced range of conditions that are far from those observed experimentally. Furthermore, converting the electrochemical potentials to an electrode potential scale using Equations (3), (7), (8), and (9) yields that the onset potentials of sulfate adsorption are significantly higher than those observed in the experiments. Obviously, on both surfaces the simple addition of a continuous dielectric simulating the presence of an aqueous electrolyte is not sufficient to reproduce the experimental findings. As was pointed out before (Santana et al., 2010; Comas-Vives et al., 2013), the unusual separation between the ion rows can only be explained by the presence of water or hydronium molecules in between the anion rows. Therefore we will in the next section present results of calculations which considered both implicit and explicit solvent.

4.3. Adding Solvent II: Adsorption Model Including Both Implicit and Explicit Solvent

In order to determine the effect of the presence of explicit water on the stability of the (bi)sulfate structures, we added one, two, and three water molecules per sulfate molecule to the $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ row-like sulfate structure both on Pt(111) and on Au(111). The explicit values of the water adsorption energies are listed in Table 2. On Pt(111) the first addition of a water molecule to the sulfate rows has an adsorption energy of −0.82 eV with respect to the solvated water molecule in bulk water, for the bisulfate row the energy gain is −0.71 eV. On Au(111), the absolute values are a little bit smaller. For comparison, the adsorption energy of a water molecule in a solvated bilayer structure is just −0.19 eV. This significant difference indicates that implicit solvent models are not capable of properly describing localized, strongly bonded solvent molecules. To be fair, these implicit solvent models are not made for such situations.

TABLE 2

Table 2. Water adsorption energies with respect to bulk water on Pt(111) and Au(111) covered by 0.2 ML of sulfate or bisulfate.

The adsorption energy of a second water molecule in the row-like structure is somewhat smaller on Pt(111), but on Au(111) the energy gain for the second water molecule is higher. The resulting stable structure is illustrated in Figure 3. The water molecules form a string that fits very well into the space between the sulfate molecules and which is also hydrogen-bonded to oxygen atoms of the adsorbed sulfate molecules, thus strongly stabilizing the row-like structure.

FIGURE 3

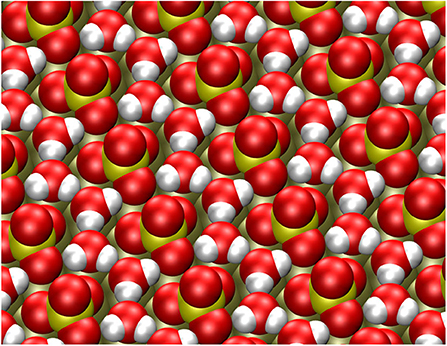
Figure 3. Stable configuration of the $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ sulfate structure together with two explicit water molecules per sulfate adsorbate.

However, the addition of a third water molecule is only associated with an energy gain of −0.17 eV, which is less favorable than addition to a bilayer. This energy gain is so small because the third molecule does not fit any more into the row-like sulfate structure like the first and the second water molecules did. The energetically most stable position for the water rows is rather robust, the first and the second water molecule always ended up in the same energy minimum structure in spite of rather different initial configurations in the energy minimization scheme. Note that the strong interaction of (bi)sulfate and water in the $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ structure was also indicated in TPD (Shingaya and Ito, 1996) and radioactive labeling studies (Kolics and Wieckowski, 2001).

Comparing the phase diagrams without and with the presence of explicit water molecules in Figures 2, 4, it is obvious that the portion of stable sulfate and bisulfate phases has become significantly larger. The consideration of additional explicit water molecules in the (bi)sulfate structures has changed the stability of these phases dramatically. Low coverage (bi)sulfate phases do not appear anymore in the phase diagrams. Furthermore, high-coverage phases with θ = 0.3 ML have become less dominant. The stability of the phases with coverage of 0.2 ML has been significantly increased, especially in the case of Au(111). An important distinction between both diagrams of Au(111) and Pt(111) is the dominant species on the surface. In the case of Pt(111), sulfate is the predominant species whereas it is bisulfate on Au(111). On Pt(111) the amount of bisulfate is rather small, one can only identify one mixed structure with 25% of bisulfate. Even at a low pH values or low electrode potentials, higher concentrations of the acidic species are thermodynamical not stable. Note, however, that we could only consider a limited amount of mixing ratios bisulfate to sulfate because of the finite size of the surface unit cells. Hence we can not exclude that mixed structure with other bisulfate/sulfate mixing ratios might also show up as stable phases in the phase diagram.

FIGURE 4

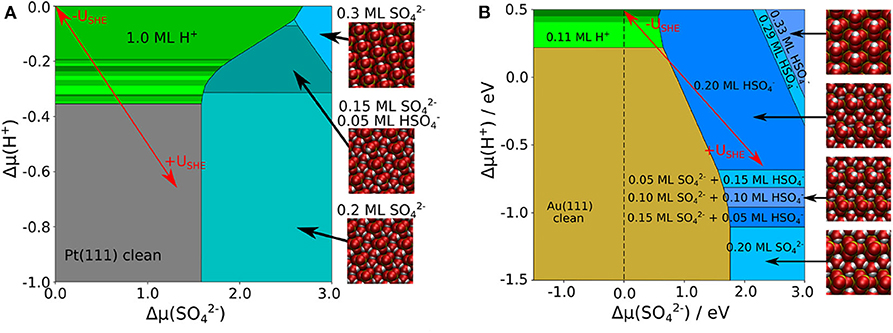
Figure 4. Phase diagram of co-adsorbed sulfate, bisulfate, and water on Pt(111) (A) and Au(111) (B), including a combination of implicit and explicit solvent. The uncovered metal electrodes are indicated in gray [Pt(111)] or in brown [Au(111)], respectively; green: pure hydrogen coverage; blue: pure 0.3 ML sulfate or bisulfate coverages; cyan: sulfate or bisulfate row structures in 0.2 ML coverage with additional 0.4 ML explicit water.

4.4. Pourbaix Diagrams

So far we have discussed phase diagrams as a function of the electrochemical potentials of protons and sulfate anions. However, electrochemical potentials typically do not correspond to experimental input parameters. Pourbaix diagrams, on the other hand, are phase diagrams as a function of electrode potential and pH which are both experimental observables. Thus, they allow a direct comparison with experimental observations such as cyclovoltammetry. As both the electrode potential and the pH enter the expressions for the electrochemical potential, through a coordinate transformations Pourbaix diagrams can be directly derived from the phase diagrams as a function of electrochemical potentials. The Pourbaix diagrams plotted in Figure 5 have been obtained in that way. Note, however, that further parameters such as temperature and the activities of the solvated species except for the protons also enter the electrochemical potentials. For the construction of the Pourbaix diagram, one has to choose specific values for these parameters. We have chosen a temperature of T = 298K and a sulfate activity of $a(S{O}_4^{2-})+a(HS{O}_4^{-})=0.1$.

FIGURE 5

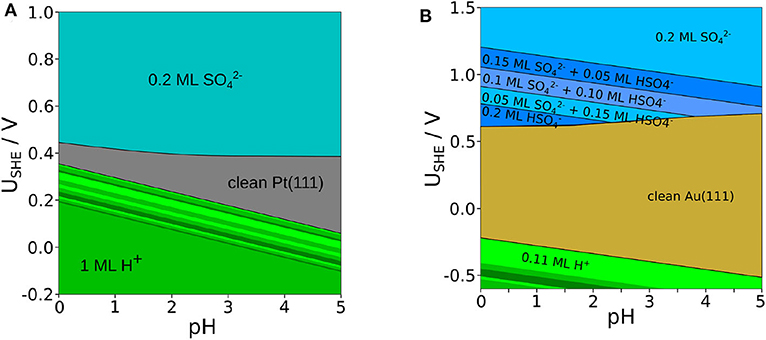
Figure 5. Pourbaix diagram of adsorbed ${\text{SO}}_4^{2-}$, ${\text{HSO}}_4^{-}$, and H⁺ on Pt(111) (A) and Au(111) (B) for a temperature of T = 298K and a fixed sulfate activity of a(${\text{SO}}_4^{2-})=0.1$. The green area denotes a pure coverage of H⁺, whereas the blueish areas denote different structures of ${\text{SO}}_4^{2-}$ and ${\text{HSO}}_4^{-}$.

At low electrode potentials where the electrode surface is negatively charged, the adsorption of the positively charged protons becomes stable in both the Pourbaix diagrams for Pt(111) and Au(111). Still, due to the weak interaction of hydrogen with Au(111), hydrogen adsorption becomes only stable at potentials below −0.2 V, i.e., at potentials at which water is in principle no longer stable. On Pt(111), in contrast, hydrogen adsorption is stable at positive potentials in the so-called under potential deposition (upd) regime (Jerkiewicz, 2010). There is a large portion of the Pourbaix diagram of Pt(111) for which our calculations predict a full monolayer of adsorbed hydrogen. Yet, according to experiments (Marković and Ross, 2002; Strmcnik et al., 2008) such a full monolayer does not form on Pt(111) at positive electrode potentials (Marković and Ross, 2002; Strmcnik et al., 2008). Note that a recent joint experimental/theoretical study has indicated that entropic effects could lead to the fact that a full monolayer hydrogen coverage can not be reached on Pt(111) under electrochemical conditions (Yang et al., 2019). As this effect is not fully included in the present study, we can not reproduce these findings.

Due to the fact that the Au(111) surface is much less reactive than Pt(111), on Au(111) the hydrogen coverage is significantly smaller and desorption occurs at much lower potentials. The boundaries of the hydrogen adsorption phases exhibit a slope of −59 meV per change of the pH by 1. This is simply due to the way the pH value enters the electrochemical potential of the protons in Equation (3). After hydrogen desorption, there is a regime for both surfaces in which the clean metal electrode is thermodynamically stable. As mentioned in the introduction, in this regime the adsorption of mobile (bi)sulfate species is inferred from cyclic voltammograms. As apparently in this regime no ordered structure is formed, it does not show up in our calculated Pourbaix diagram.

At electrode potentials above 0.4 V, on Pt(111) the adsorption of sulfate in the $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ structure sets in, in good agreement with the position of the corresponding spike obtained by cyclic voltammetry (Herrero et al., 2002; Garcia-Araez et al., 2010). It is also gratifying that the experimentally derived displacement of sulfate adsorption to higher potentials for decreasing pH, in particular for pH ≤ 2 (Garcia-Araez et al., 2010), is well-reproduced by our calculations. There are no stable bisulfate phases according to our calculations on Pt(111), even at low pH values, although the experimental derivation of electrosorption valencies (Kolics and Wieckowski, 2001) suggests that there could be bisulfate adsorption before the onset of sulfate adsorption as mobile species. On the one hand, there is a debate about how electrosorption valencies can be related to charge transfer (Schmickler and Guidelli, 2014) and thus to the identification of adsorbed particles based on the electrosorption valency. On the other hand, one has to note that we did not consider bisulfate to sulfate ratios below 1/4, hence we cannot exclude that phases with a lower bisulfate concentration might be stable. Furthermore, the sulfate $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ structure remains stable also for the highest considered electrode potentials, in contrast to experimental observations (Funtikov et al., 1995). This is simply due to the fact that we did not consider the adsorption of OH in our study which might occur at about 0.7 V (Garcia-Araez et al., 2008). However, the inclusion of OH adsorption would have increased the computational effort substantially, therefore we have rather concentrated on the onset of (bi)sulfate adsorption.

On Au(111), a broader variety of different stable structures at electrode potentials above 0.6-0.7 V is visible in our calculated Pourbaix diagram. At pH values below 2, first a 0.2 ML structure entirely consisting of bisulfate is obtained, but for higher potentials structures with a decreasing amount of bisulfate become stable until the pure sulfate $(\sqrt{3}\times \sqrt{7})R19.1^{\circ }$ layer forms at about 1 V. This potential for the formation of the pure sulfate phase agrees rather satisfactorily with the experimental observation of disorder-order transition at this potential (Cuesta et al., 2000; Sato et al., 2006). The different bisulfate phases are also separated by boundaries that exhibit a slope of −59 meV per change of the pH by 1, again indicating that this is a effect purely caused by the changing proton concentration in the electrolyte. Furthermore, due to the finite size of our surface unit cells we could only model a limited amount of different bisulfate to sulfate ratio. Hence it might well be that there is a more gradual transition from bisulfate to sulfate phases, as also suggested by the featureless cyclovoltammograms in this region (Cuesta et al., 2000; Sato et al., 2006). Finally note that our calculations do not yield any dense bisulfate or sulfate phases with coverage of 0.3 ML or higher in the considered range of electrochemical conditions presented in Figure 5.

5. Conclusion

The specific adsorption of anions at electrochemical electrode/electrolyte interfaces significantly alters the structural and chemical properties of electrode surfaces. Hence a detailed atomistic understanding of the stable anion adsorbate phases as a function of electrochemical control parameters is crucial for, e.g., an assessment of the electrocatalytic activity of a particular electrode/electrolyte interface. In this theoretical and computational study we addressed the structure of Pt(111) and Au(111) in the presence of a (bi)sulfate containing electrolyte which correspond to benchmark systems in electrochemistry. From a computational point of view, the stability of adsorbate phases in an electrochemical environment can be conveniently evaluated in a grand-canonical approach using the concept of the computational hydrogen electrode. For small anions such as halides that adsorb close to the surface, the presence of the electrolyte can even be neglected in the determination of the stable phases.

In contrast, (bi)sulfate anions adsorb in an upright fashion thus interacting more strongly with the water molecules of the electrolyte. In a first step, we included the presence of the aqueous electrolyte in our calculations using an implicit solvent model, i.e., by representing the electrolyte through a polarizable dielectricum. Using this approach, we were not able to reproduce the experimental findings with respect to the stable (bi)sulfate phases on Pt(111) and Au(111). Only after additional introducing some explicit water molecules that in particular stabilize the row-like sulfate adsorption structures, we have succeeded in achieving a satisfactorily agreement with the experiment. Our calculated Pourbaix diagrams nicely reproduce features that can be derived from measured cyclovoltammograms of (bi)sulfate adsorption on Pt(111) and Au(111). Our study demonstrates that quantum chemical calculations based on the computational hydrogen electrode that include the presence of the electrochemical environment in an appropriate way can reliably yield stable adsorbate phases at electrochemical electrode/electrolyte interfaces as a function of electrochemical control parameters.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

FG performed all DFT calculations for sulfate adsorption on Pt(111), FJ those for sulfate adsorption on Au(111). FG and FJ wrote the first version of manuscript. AG designed and supervised the project. All authors revised the manuscript, read, and approved the submitted version.

Funding

This research has been supported by the German Science Foundation (DFG) through the research unit FOR 1376 (DFG contract GR 1503/21-1) and by the Baden-Württemberg Foundation within the Network of Excellence Functional Nanostructures.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors furthermore acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 40/467-1 FUGG (JUSTUS cluster). This work contributes to the research performed at CELEST (Center for Electrochemical Energy Storage Ulm-Karlsruhe).

References

Ataka, K.-I., and Osawa, M. (1998). In situ infrared study of water-sulfate coadsorption on gold(111) in sulfuric acid solutions. Langmuir 14, 951–959. doi: 10.1021/la971110v

CrossRef Full Text | Google Scholar

Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50:17953. doi: 10.1103/PhysRevB.50.17953

PubMed Abstract | CrossRef Full Text | Google Scholar

Bramley, G., Nguyen, M.-T., Glezakou, V.-A., Rousseau, R., and Skylaris, C.-K. (2020). Reconciling work functions and adsorption enthalpies for implicit solvent models: a Pt(111)/water interface case study. J. Chem. Theory Comput. 16, 2703–2715. doi: 10.1021/acs.jctc.0c00034

CrossRef Full Text | Google Scholar

Braunschweig, B., Mukherjee, P., Dlott, D. D., and Wieckowski, A. (2010). Real-time investigations of Pt(111) surface transformations in sulfuric acid solutions. J. Am. Chem. Soc. 132, 14036–14038. doi: 10.1021/ja106618z

PubMed Abstract | CrossRef Full Text | Google Scholar

Chase, M. J. (1998). NIST-JANAF Thermochemical Tables, 4th Edn. Washington, DC: American Chemical Society.

Google Scholar

Comas-Vives, A., Bandlow, J., and Jacob, T. (2013). Ab initio study of the electrochemical H₂SO₄/Pt(111) interface. Phys. Chem. Chem. Phys. 15, 992–997. doi: 10.1039/C2CP43054A

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuesta, A., Kleinert, M., and Kolb, D. M. (2000). The adsorption of sulfate and phosphate on Au(111) and Au(100) electrodes: an in situ STM study. Phys. Chem. Chem. Phys. 2, 5684–5690. doi: 10.1039/b006464p

CrossRef Full Text | Google Scholar

Forster-Tonigold, K., and Groß, A. (2014). Dispersion corrected RPBE studies of liquid water. J. Chem. Phys. 141:064501. doi: 10.1063/1.4892400

PubMed Abstract | CrossRef Full Text | Google Scholar

Funtikov, A., Linke, U., Stimming, U., and Vogel, R. (1995). An in-situ STM study of anion adsorption on Pt(111) from sulfuric acid solutions. Surf. Sci. 324, L343–L348. doi: 10.1016/0039-6028(94)00774-8

CrossRef Full Text | Google Scholar

Funtikov, A., Stimming, U., and Vogel, R. (1997). Anion adsorption from sulfuric acid solutions on Pt(111) single crystal electrodes. J. Electroanal. Chem. 428, 147–153. doi: 10.1016/S0022-0728(96)05051-6

CrossRef Full Text | Google Scholar

Garcia-Araez, N., Climent, V., Herrero, E., Feliu, J., and Lipkowski, J. (2005a). Thermodynamic studies of chloride adsorption at the Pt(111) electrode surface from 0.1 M HClO₄ solution. J. Electroanal. Chem. 576, 33–41. doi: 10.1016/j.jelechem.2004.10.003

CrossRef Full Text | Google Scholar

Garcia-Araez, N., Climent, V., Herrero, E., Feliu, J. M., and Lipkowski, J. (2005b). Determination of the Gibbs excess of H adsorbed at a Pt(111) electrode surface in the presence of co-adsorbed chloride. J. Electroanal. Chem. 582, 76–84. doi: 10.1016/j.jelechem.2005.01.031

CrossRef Full Text | Google Scholar

Garcia-Araez, N., Climent, V., Rodriguez, P., and Feliu, J. M. (2008). Thermodynamic analysis of (bi)sulphate adsorption on a Pt(111) electrode as a function of pH. Electrochim. Acta 53, 6793–6806. doi: 10.1016/j.electacta.2007.12.086

CrossRef Full Text | Google Scholar

Garcia-Araez, N., Climent, V., Rodriguez, P., and Feliu, J. M. (2010). Elucidation of the chemical nature of adsorbed species for Pt(111) in H₂SO₄ solutions by thermodynamic analysis. Langmuir 26, 12408–12417. doi: 10.1021/la101112b

PubMed Abstract | CrossRef Full Text | Google Scholar

Gossenberger, F., Roman, T., Forster-Tonigold, K., and Groß, A. (2014). Adsorbate coverage-dependent work function changes on platinum. Beilstein J. Nanotechnol. 5:152. doi: 10.3762/bjnano.5.15

PubMed Abstract | CrossRef Full Text | Google Scholar

Gossenberger, F., Roman, T., and Groß, A. (2015). Equilibrium coverage of halides on metal electrodes. Surf. Sci. 631, 17–22. doi: 10.1016/j.susc.2014.01.021

CrossRef Full Text | Google Scholar

Gossenberger, F., Roman, T., and Groß, A. (2016). Hydrogen and halide co-adsorption on Pt(111) in an electrochemical environment: a computational perspective. Electrochim. Acta 216, 152–159. doi: 10.1016/j.electacta.2016.08.117

CrossRef Full Text | Google Scholar

Grimme, S., Antony, J., Ehrlich, S., and Krieg, H. (2010). A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 132:154104. doi: 10.1063/1.3382344

PubMed Abstract | CrossRef Full Text | Google Scholar

Groß, A. (2020). “Theory of solid/electrolyte interfaces– in Surface and Interface Science: Volume 8: Interfacial Electrochemistry, Vol. 8, ed K. Wandelt (Weinheim: John Wiley & Sons, Ltd.), 471–515. doi: 10.1002/9783527680603.ch56

CrossRef Full Text | Google Scholar

Groß, A., Gossenberger, F., Lin, X., Naderian, M., Sakong, S., and Roman, T. (2014). Water structures at metal electrodes studied by ab initio molecular dynamics simulations. J. Electrochem. Soc. 161, E3015–E3020. doi: 10.1149/2.003408jes

PubMed Abstract | CrossRef Full Text | Google Scholar

Groß, A., and Sakong, S. (2019). Modelling the electric double layer at electrode/electrolyte interfaces. Curr. Opin. Electrochem. 14, 1–6. doi: 10.1016/j.coelec.2018.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Gunceler, D., Letchworth-Weaver, K., Sundararaman, R., Schwarz, K. A., and Arias, T. A. (2013). The importance of nonlinear fluid response in joint density-functional theory studies of battery systems. Modell. Simul. Mater. Sci. Eng. 21:074005. doi: 10.1088/0965-0393/21/7/074005

CrossRef Full Text | Google Scholar

Hammer, B., Hansen, L. B., and Nørskov, J. K. (1999). Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 59, 7413–7421. doi: 10.1103/PhysRevB.59.7413

CrossRef Full Text | Google Scholar

Heenen, H. H., Gauthier, J. A., Kristoffersen, H. H., Ludwig, T., and Chan, K. (2020). Solvation at metal/water interfaces: an ab initio molecular dynamics benchmark of common computational approaches. J. Chem. Phys. 152:144703. doi: 10.1063/1.5144912

PubMed Abstract | CrossRef Full Text | Google Scholar

Hermse, C., van Bavel, A., Koper, M., Lukkien, J., van Santen, R., and Jansen, A. (2004). Modelling the butterfly: (3 × 7) ordering on fcc(111) surfaces. Surf. Sci. 572, 247–260. doi: 10.1016/j.susc.2004.08.038

CrossRef Full Text | Google Scholar

Herrero, E., Mostany, J., Feliu, J. M., and Lipkowski, J. (2002). Thermodynamic studies of anion adsorption at the Pt(111) electrode surface in sulfuric acid solutions. J. Electroanal. Chem. 534, 79–89. doi: 10.1016/S0022-0728(02)01101-4

CrossRef Full Text | Google Scholar

Jerkiewicz, G. (2010). Electrochemical hydrogen adsorption and absorption. part 1: under-potential deposition of hydrogen. Electrocatalysis 1, 179–199. doi: 10.1007/s12678-010-0022-1

CrossRef Full Text | Google Scholar

Jinnouchi, R., Hatanaka, T., Morimoto, Y., and Osawa, M. (2012). First principles study of sulfuric acid anion adsorption on a Pt(111) electrode. Phys. Chem. Chem. Phys. 14, 3208–3218. doi: 10.1039/c2cp23172g

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolics, A., and Wieckowski, A. (2001). Adsorption of bisulfate and sulfate anions on a Pt(111) electrode. J. Phys. Chem. B 105, 2588–2595. doi: 10.1021/jp003536f

CrossRef Full Text | Google Scholar

Koslowski, B., Tschetschetkin, A., Maurer, N., Ziemann, P., Kucera, J., and Groß, A. (2013). 4,4'-dithiodipyridine on Au(111): a combined STM, STS, and DFT study. J. Phys. Chem. C 117, 20060–20067. doi: 10.1021/jp4071289

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54:11169. doi: 10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59:1758. doi: 10.1103/PhysRevB.59.1758

CrossRef Full Text | Google Scholar

Letchworth-Weaver, K., and Arias, T. A. (2012). Joint density functional theory of the electrode-electrolyte interface: application to fixed electrode potentials, interfacial capacitances, and potentials of zero charge. Phys. Rev. B 86:075140. doi: 10.1103/PhysRevB.86.075140

CrossRef Full Text | Google Scholar

Magnussen, O. M. (2002). Ordered anion adlayers on metal electrode surfaces. Chem. Rev. 107, 679–725. doi: 10.1021/cr000069p

PubMed Abstract | CrossRef Full Text | Google Scholar

Magnussen, O. M., and Groß, A. (2019). Toward an atomic-scale understanding of electrochemical interface structure and dynamics. J. Am. Chem. Soc. 141, 4777–4790. doi: 10.1021/jacs.8b13188

PubMed Abstract | CrossRef Full Text | Google Scholar

Mahlberg, D., Sakong, S., Forster-Tonigold, K., and Groß, A. (2019). Improved DFT adsorption energies with semiempirical dispersion corrections. J. Chem. Theory Comput. 15, 3250–3259. doi: 10.1021/acs.jctc.9b00035

PubMed Abstract | CrossRef Full Text | Google Scholar

Marković, N. M., and Ross, P. N. Jr (2002). Surface science studies of model fuel cell electrocatalysts. Surf. Sci. Rep. 45:117. doi: 10.1016/S0167-5729(01)00022-X

CrossRef Full Text | Google Scholar

Mathew, K., Sundararaman, R., Letchworth-Weaver, K., Arias, T. A., and Hennig, R. G. (2014). Implicit solvation model for density-functional study of nanocrystal surfaces and reaction pathways. J. Chem. Phys. 140:084106. doi: 10.1063/1.4865107

PubMed Abstract | CrossRef Full Text | Google Scholar

Morawietz, T., Singraber, A., Dellago, C., and Behler, J. (2016). How van der waals interactions determine the unique properties of water. Proc. Natl. Acad. Sci. U.S.A. 113, 8368–8373. doi: 10.1073/pnas.1602375113

PubMed Abstract | CrossRef Full Text | Google Scholar

Nørskov, J. K., Rossmeisl, J., Logadottir, A., Lindqvist, L., Kitchin, J. R., Bligaard, T., et al. (2004). Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892. doi: 10.1021/jp047349j

CrossRef Full Text | Google Scholar

Nowicki, M., and Wandelt, K. (2020). “Chapter 57: Metal-electrolyte interfaces, in Surface and Interface Science: Volume 8: Interfacial Electrochemistry, Vol. 8, ed K. Wandelt (Weinheim: John Wiley & Sons, Ltd.), 517–731. doi: 10.1002/9783527680603.ch57

CrossRef Full Text | Google Scholar

Peterson, A. A., Abild-Pedersen, F., Studt, F., Rossmeisl, J., and Nørskov, J. K. (2010). How copper catalyzes the electroreduction of carbon dioxide into hydrocarbon fuels. Energy Environ. Sci. 3, 1311–1315. doi: 10.1039/c0ee00071j

CrossRef Full Text | Google Scholar

Petrosyan, S. A., Briere, J.-F., Roundy, D., and Arias, T. A. (2007). Joint density-functional theory for electronic structure of solvated systems. Phys. Rev. B 75:205105. doi: 10.1103/PhysRevB.75.205105

CrossRef Full Text | Google Scholar

Petrosyan, S. A., Rigos, A. A., and Arias, T. A. (2005). Joint density-functional theory: ab initio study of Cr₂O₃ surface chemistry in solution. J. Phys. Chem. B 109, 15436–15444. doi: 10.1021/jp044822k

PubMed Abstract | CrossRef Full Text | Google Scholar

Qian, Y., Ikeshoji, T., Zhao, Y.-Y., and Otani, M. (2014). Vibrational dynamics of sulfate anion adsorption on Pt(111) surface: ab initio molecular dynamics simulations. ChemElectroChem 1, 1632–1635. doi: 10.1002/celc.201402205

CrossRef Full Text | Google Scholar

Reuter, K., and Scheffler, M. (2001). Composition, structure, and stability of RuO₂(110) as a function of oxygen pressure. Phys. Rev. B 65:035406. doi: 10.1103/PhysRevB.65.035406

CrossRef Full Text | Google Scholar

Roman, T., and Groß, A. (2013). Periodic density-functional calculations on work function change induced by adsorption of halogens on Cu(111). Phys. Rev. Lett. 110:156804. doi: 10.1103/PhysRevLett.110.156804

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruiz-Barragan, S., Munoz-Santiburcio, D., and Marx, D. (2019). Nanoconfined water within graphene slit pores adopts distinct confinement-dependent regimes. J. Phys. Chem. Lett. 10, 329–334. doi: 10.1021/acs.jpclett.8b03530

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakong, S., Forster-Tonigold, K., and Groß, A. (2016). The structure of water at a Pt(111) electrode and the potential of zero charge studied from first principles. J. Chem. Phys. 144:194701. doi: 10.1063/1.4948638

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakong, S., and Groß, A. (2016). The importance of the electrochemical environment in the electro-oxidation of methanol on Pt(111). ACS Catal. 6, 5575–5586. doi: 10.1021/acscatal.6b00931

CrossRef Full Text | Google Scholar

Sakong, S., and Groß, A. (2018). The electric double layer at metal-water interfaces revisited based on a charge polarization scheme. J. Chem. Phys. 149:084705. doi: 10.1063/1.5040056

PubMed Abstract | CrossRef Full Text | Google Scholar

Sakong, S., Naderian, M., Mathew, K., Hennig, R. G., and Groß, A. (2015). Density functional theory study of the electrochemical interface between a pt electrode and an aqueous electrolyte using an implicit solvent method. J. Chem. Phys. 142:234107. doi: 10.1063/1.4922615

PubMed Abstract | CrossRef Full Text | Google Scholar

Santana, J. A., Cabrera, C. R., and Ishikawa, Y. (2010). A density-functional theory study of electrochemical adsorption of sulfuric acid anions on Pt(111). Phys. Chem. Chem. Phys. 12, 9526–9534. doi: 10.1039/c000981d

PubMed Abstract | CrossRef Full Text | Google Scholar

Sato, K., Yoshimoto, S., Inukai, J., and Itaya, K. (2006). Effect of sulfuric acid concentration on the structure of sulfate adlayer on Au(111) electrode. Electrochem. Comm. 8, 725–730. doi: 10.1016/j.elecom.2006.03.001

CrossRef Full Text | Google Scholar

Schienbein, P., and Marx, D. (2018). Liquid-vapor phase diagram of RPBE-D3 water: electronic properties along the coexistence curve and in the supercritical phase. J. Phys. Chem. B 122, 3318–3329. doi: 10.1021/acs.jpcb.7b09761

PubMed Abstract | CrossRef Full Text | Google Scholar

Schmickler, W., and Guidelli, R. (2014). The partial charge transfer. Electrochim. Acta 127, 489–505. doi: 10.1016/j.electacta.2014.02.057

CrossRef Full Text | Google Scholar

Schmickler, W., and Santos, E. (2010). Interfacial Electrochemistry, 2nd Edn. Berlin: Springer. doi: 10.1007/978-3-642-04937-8

CrossRef Full Text | Google Scholar

Schnur, S., and Groß, A. (2011). Challenges in the first-principles description of reactions in electrocatalysis. Catal. Tdy. 165, 129–137. doi: 10.1016/j.cattod.2010.11.071

CrossRef Full Text | Google Scholar

Shingaya, Y., and Ito, M. (1996). Interconversion of a bisulfate anion into a sulfuric acid molecule on a Pt(111) electrode in a 0.5 M H₂SO₄ solution. Chem. Phys. Lett. 256, 438–444. doi: 10.1016/0009-2614(96)00465-4

CrossRef Full Text | Google Scholar

Strmcnik, D., Tripkovic, D., van der Vliet, D., Stamenkovic, V., and Markovic, N. (2008). Adsorption of hydrogen on Pt(111) and Pt(100) surfaces and its role in the HOR. Electrochem. Commun. 10, 1602–1605. doi: 10.1016/j.elecom.2008.08.019

CrossRef Full Text | Google Scholar

Tonigold, K., and Groß, A. (2012). Dispersive interactions in water bilayers at metallic surfaces: a comparison of the PBE and RPBE functional including semiempirical dispersion corrections. J. Comput. Chem. 33, 695–701. doi: 10.1002/jcc.22900

PubMed Abstract | CrossRef Full Text | Google Scholar

Tripkovic, D. V., Strmcnik, D., van der Vliet, D., Stamenkovic, V., and Markovic, N. M. (2009). The role of anions in surface electrochemistry. Faraday Discuss. 140, 25–40. doi: 10.1039/B803714K

PubMed Abstract | CrossRef Full Text | Google Scholar

Venkatachalam, S., and Jacob, T. (2007). DFT studies on the nature of coadsorbates on ${\text{SO}}_4^{2-}$/Au(111). Z. Phys. Chem. 221, 1393–1406. doi: 10.1524/zpch.2007.221.9-10.1393

CrossRef Full Text | Google Scholar

Yang, G., Akhade, S. A., Chen, X., Liu, Y., Lee, M.-S., Glezakou, V.-A., et al. (2019). The nature of hydrogen adsorption on platinum in the aqueous phase. Angew. Chem. Int. Ed. 58, 3527–3532. doi: 10.1002/anie.201813958

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeh, K.-Y., Restaino, N. A., Esopi, M. R., Maranas, J. K., and Janik, M. J. (2013). The adsorption of bisulfate and sulfate anions over a Pt(111) electrode: a first principle study of adsorption configurations, vibrational frequencies and linear sweep voltammogram simulations. Catal. Tdy 202, 20–35. Electrocatalysis. doi: 10.1016/j.cattod.2012.03.011

CrossRef Full Text | Google Scholar