The Model of the Extraction Process of Rare Metals Under Condition of Filtration Combustion Wave

To study the mass transfer of metal compounds, a model of filtration combustion of metal-containing combustible mixtures is developed. Using cadmium-containing mixture as an example, the main characteristics of filtration combustion are determined when the gas pressure at the reactor inlet is constant. It is shown that under the conditions of a filtration combustion wave, a metal can evaporate into the gas phase and be transferred with gas through the reactor. Due to the evaporation and condensation of cadmium, it is transported and accumulated before the combustion front. The possibility of controlling the mass transfer of metal compounds under the conditions of a filtration combustion wave with the aim of concentrating them is shown. It is revealed that a 4-fold increase in the pressure difference at the open boundaries of the reactor can lead to a decrease in the maximum metal concentration by about 1.5 times. An increase in the concentration of metals due to mass transfer will subsequently make it economically feasible to extract them by traditional methods.

Introduction

Rare metals have actively entered the scope of industrial applications: electronics, aviation, superconductors, mobile power sources, etc. (Frohlich et al., 2017). As a rule, they are not widespread in the earth's crust; therefore, the volume of production and use of rare metals is relatively small due to the high degree of dispersion and complexity of extraction methods. However, without the use of rare and precious metals, the sustainable development of new technologies and the production of materials with necessary properties are impossible. Rare metals do not have their own large deposits and are associated elements of the ore layers (Jowitt et al., 2018). With the development of more accurate analysis methods and more efficient extraction technologies, the raw material base of rare and valuable metals began to expand. Currently, waste from metallurgical industries (Johnson, 2014), waste electronics (Sthiannopkao and Wong, 2013), as well as coal and oil are considered as an alternative raw material base for rare and precious metals. The content of some metals in coal and oil can reach several hundred grams per ton, and in their ash residue it can reach several kilograms per ton (Dai and Finkelman, 2017; Salgansky et al., 2019).

The main technologies for the extraction of rare metals are the following: metallurgical methods (Jha et al., 2001), extraction methods (Kuang and Liao, 2018), methods of mechanical separation (Frohlich et al., 2017). Biological methods for the extraction of rare and precious metals are being actively developed: biohydrometallurgical (Erüst et al., 2013), bioelectrochemical (Nancharaiah et al., 2016), bioextraction (Watling et al., 2010). As a rule, these methods are used for the extraction of metals from ores. As for the metals contained in oils and coals, it is rational to remove the organics (for example, by burning) and leave the metals in the ash residue to extract them. In this case, due to the low ash content of oils and coals, the concentration of metals in the ash will significantly increase. The method of filtration combustion with super-adiabatic heating is a way of efficiently burning of various combustible materials (Manelis et al., 2011; Toledo et al., 2018). The possibility of concentrating and separation of molybdenum compounds (Manelis et al., 2016), zinc (Rozenberg et al., 2009) in a laboratory reactor has been experimentally shown. The theory of filtration combustion of solid fuels is well developed (Aldushin, 1997). Mathematical models have been developed that describe the filtration combustion of solid fuels both in the one-dimensional (Salganskii et al., 2003; Lutsenko, 2013) and two-dimensional approaches (Levin and Lutsenko, 2017; Lutsenko, 2018). However, up to date, the models of filtration combustion of solid fuels have not taken into account the presence of metal compounds in porous combustible media.

The aim of this work is to develop a mathematical model that allows studying the behavior of metal compounds under conditions of a filtration combustion wave. The proposed model is a development of the one described in (Lutsenko and Salgansky, 2019).

Mathematical Model and Numerical Method

Consider vertical packed bed reactor, which has impermeable side walls and is opened to an atmosphere at a bottom and at a top. Gas is pumped through the lower open boundary (inlet) of the object, passes through the porous medium and flows through the upper boundary (outlet) (Figure 1).

FIGURE 1

Figure 1. Sketch of the porous object.

Suppose that a condensed porous matter consists of combustible component (fuel), inert component, solid products of reaction and metal-containing substance. The gas phase can include evaporated metal. The solid fuel transforms into gaseous and solid products in the reaction with gaseous oxidizer, so we have the following expression:

$\begin{array}{l}\text{Solid fuel}+({\mu }_g)\text{Oxidizer}\to (1+{\mu }_g-{\mu }_p)\text{Gaseous product}\\ +({\mu }_p)\text{Solid product},& (1)\end{array}$

where μ_g and μ_p are the mass stoichiometric coefficients for gaseous oxidizer and solid products, respectively.

Suppose that only a solid combustible component and an oxidizing agent from the gas phase (oxygen) are chemically reacted. The metal-containing substance does not chemically react and undergoes two phase transitions: when heated, it can melt and then evaporate with transforming to gaseous products. The evaporated metal can condense when the gas phase is cooled. The liquid phase of the metal remains immovable and associated with the solid (due to adsorption); when it cools, it solidifies. We assume that the melting and solidification of the metal occur at a fixed temperature T_melt, the evaporation and condensation of the metal also occur at a fixed temperature T_evap, and the phase transitions occur so quickly that their rates are completely determined by the heat fluxes.

The mathematical model is based on the methods of multicomponent continuum mechanics (Nigmatulin, 1990) using classical approaches of the theory of filtration combustion (Aldushin, 1997). To describe the phase transitions, we introduce the following notation: F – is the fraction of the liquid phase in the metal, ρ′_cm is the decrease in the effective density of the condensed metal due to evaporation (in average: mass of the condensed metal per unit volume that evaporates), ρ′_gm is the decrease in the effective density of the evaporated metal due to condensation (in average: mass of evaporated metal per unit volume that condenses). So, we can write the following mathematical model of the investigated process:

Energy equation for condensed phase:

$\begin{array}{l}\left({\rho }_{cf}{c}_{cf}+{\rho }_{ci}{c}_{ci}+{\rho }_{cp}{c}_{cp}+{\rho }_{cm}{c}_{cm}\right)\frac{\partial T_c}{\partial t}=\\ =-\alpha \left(T_c-T_g\right)+{\rho }_{cf0}{Q}_{comb}W+\left(1-a_g\right){\lambda }_c\Delta T_c\\ -{\rho }_{cm}{Q}_{melt}\frac{\partial F}{\partial t}-Q_{evap}\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t},& (2)\end{array}$

Energy equation for gas phase:

$\begin{array}{l}{\rho }_g{c}_g\left(\frac{\partial T_g}{\partial t}+\left({\nu }_g·\nabla \right)T_g\right)=\alpha \left(T_c-T_g\right)+a_g{\lambda }_g\Delta T_g\\ +Q_{evap}\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t},& (3)\end{array}$

Equations of continuity and state for gas:

$\begin{array}{l}\frac{\partial {\rho }_g}{\partial t}+\nabla ·\left({\rho }_g{\nu }_g\right)=\left(1-{\mu }_p\right){\rho }_{cf0}W+\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}-\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t},\\ p=\frac{{\rho }_{g}R{T}_g}{a_{g}M},& (4)\end{array}$

Momentum conservation equation for gas:

$\begin{array}{l}{\rho }_g\left(1+\chi \left(1-a_g\right)\right)\left(\frac{\partial {\nu }_g}{\partial t}+\left({\nu }_g·\nabla \right){\nu }_g\right)=-a_g\nabla p\\ +{\rho }_{g}g-a_g^2\frac{\mu }{k_1}{\nu }_g-\\ -\left[\left(1-{\mu }_p\right){\rho }_{cf0}W+\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}-\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t}\right]{\nu }_g,& (5)\end{array}$

Equation for oxidizer concentration:

$\begin{array}{l}{\rho }_g\left(\frac{\partial C}{\partial t}+\left({\nu }_g·\nabla \right)C\right)=\nabla ·\left({\rho }_g{D}_g\nabla C\right)-{\mu }_g{\rho }_{cf0}W-\\ -\left[\left(1-{\mu }_p\right){\rho }_{cf0}W+\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}-\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t}\right]C,& (6)\end{array}$

Equations of chemical kinetics:

$\begin{array}{ll}W=(1-\eta )Ckexp(-E/(R{T}_c)),\frac{\partial \eta }{\partial t}=W,& (7)\end{array}$

Equation of mass conservation for evaporated metal in gas:

$\begin{array}{ll}\frac{\partial {\rho }_{gm}}{\partial t}+\nabla \left({\rho }_{gm}{\nu }_g\right)=-\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t}+\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}& (8)\end{array}$

Equations of mass conservation for components of condensed phase:

$\begin{array}{l}{\rho }_{cf}=\left(1-\eta \right){\rho }_{cf0},{\rho }_{cp}={\mu }_p{\rho }_{cf0}\eta ,\frac{\partial {\rho }_{cm}}{\partial t}=\\ -\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}+\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t},& (9)\end{array}$

Equations for porosity:

$\begin{array}{ll}{a}_g=a_{g0}+\left(a_{cf0}-a_{cpEnd}\right)\eta +\frac{{\rho }_{cm0}-{\rho }_{cm}}{{\rho }_{cm0}}{a}_{cm0},& (10)\end{array}$

Equations for oxidizer diffusion and gas viscosity:

$\begin{array}{ll}{D}_g=D_{g0}{\left(T_g/273\right)}^b,\mu =c_{s1}\frac{T_g^{1.5}}{c_{s2}+T_g}.& (11)\end{array}$

Here a is the volume concentration, b is the exponent in the expression for diffusion coefficient, C is the mass concentration of oxidizer, c is the specific heat capacity, c_s1 and c_s2 are the constants in Sutherland's formula, D_g is the diffusion coefficient of gas, E is the activation energy, g is the gravity acceleration, k is the pre-exponential factor in the expression for the rate of reaction, k₁ is the permeability coefficient, M is the molar mass of gas, p is the gas pressure, Q is the heat release, R is the universal gas constant, t is the time, T is the temperature, v is the velocity, W is the rate of chemical reaction, α is the constant determining the interphase heat transfer intensity, η is the degree of conversion of the solid combustible component, λ is the thermal conductivity (including radiation heat transfer according to diffusion approximation), μ is the dynamic viscosity of gas, ρ is the effective (or bulk) density (i.e., the product of phase density and volume concentration), χ is the coefficient, taking into account the inertial interaction of the phases in their relative motion (Nigmatulin, 1990), ∇ is the del (nabla) operator, Δ is the Laplace operator; subscripts: “0” denotes the initial moment, “c” denotes the condensed phase, “comb” denotes the combustion, “End” denotes the end point of time, “evap” denotes the evaporation, “f ” denotes the combustible component (fuel), “g” denotes the gas, “i" denotes the inert component, “m” denotes the metal substance, “melt” denotes the melting, “p” denotes the product of reaction.

We will use dimensionless quantities and dimensionless similarity parameters; therefore, we introduce dimensionless variables as follows: $\tilde{x}=x/H$, $\tilde{t}=t/t_{*}$, ${\tilde{v}}_g=v_g/{ṽ}_{*}$, where H is the characteristic size of the simulated reactor (unless otherwise specified, this is its height), t_* are v_* are the characteristic values of time and gas velocity, x is the Eulerian coordinate; $\tilde{p}=p/p_{*}$, ${\tilde{\rho }}_g={\rho }_g/{\rho }_{*}$, ${\tilde{T}}_c=T_c/T_{*}$, ${\tilde{T}}_g=T_g/T_{*}$, where p_*, ρ_*, T_* are the pressure, density and temperature of the gas under “normal” conditions; ${\tilde{\rho }}_{cf}={\rho }_{cf}/{\rho }_{sf0}$; ${\tilde{\rho }}_{cp}={\rho }_{cp}/{\rho }_{cf0}$; $\tilde{W}=W/k$; ${\tilde{D}}_g={(T_{*}/273)}^{-b}{D}_g/D_{g0}$; ${\tilde{\rho }}_{cm}={\rho }_{cm}/{\rho }_{cf0}$; ${\tilde{\rho }}_{gm}={\rho }_{gm}/{\rho }_{*}$; $\frac{\partial {{\tilde{\rho }}^{\prime }}_{cm}}{\partial \tilde{t}}=\frac{\partial \rho {\prime }_{cm}}{\partial t}\frac{t_{*}}{{\rho }_{sf0}}$; $\frac{\partial {{\tilde{\rho }}^{\prime }}_{gm}}{\partial \tilde{t}}=\frac{\partial \rho {\prime }_{gm}}{\partial t}\frac{t_{*}}{{\rho }_{*}}$.

The following similarity parameters will be used:

$\begin{array}{l}\text{Sh}=\frac{v_{*}{t}_{*}}{H},\text{S}{\text{t}}_1=\frac{\alpha H}{{\rho }_{cf0}{c}_{cf}{v}_{*}},\text{S}{\text{t}}_2=\frac{\alpha H}{{\rho }_{*}{c}_g{v}_{*}},\\ \text{Eu}=\frac{p_{*}}{{\rho }_{*}{v}_{*}^2},\text{Re}=\frac{{\rho }_{*}{v}_{*}H}{c_{s1}\sqrt{T_{*}}},\\ \text{Fr}=\frac{v_{*}^2}{gH},\text{P}{\text{e}}_1=\frac{v_{*}{\rho }_{cf0}{c}_{cf}H}{{\lambda }_c},\text{P}{\text{e}}_2=\frac{v_{*}{\rho }_{*}{c}_{g}H}{{\lambda }_g},\\ \text{Sc}=\frac{c_{s1}\sqrt{T_{*}}}{{\rho }_{*}{D}_{g0}{(T_{*}/273)}^b},{\tilde{Q}}_{comb}=\frac{Q_{comb}}{c_{cf}{T}_{*}},\\ Ẽ=\frac{E}{R{T}_{*}},\pi =\frac{k_1}{H^2},{\pi }_1=\frac{{\rho }_{ci}{c}_{ci}}{{\rho }_{cf0}{c}_{cf}},{\pi }_2=k{t}_{*},{\pi }_3\\ =\frac{{\rho }_{cf0}}{{\rho }_{*}},{\pi }_4=\frac{c_{cp}}{c_{cf}},{\stackrel{⌢}{c}}_{s2}=\frac{c_{s2}}{T_{*}},\\ {\pi }_5=\frac{c_{cm}}{c_{cf}},{\pi }_6=\frac{{\rho }_{cf0}}{{\rho }_{cmIst}},{\tilde{Q}}_{melt}=\frac{Q_{melt}}{c_{cf}{T}_{*}},{\tilde{Q}}_{evap1}\\ =\frac{Q_{evap}}{c_{cf}{T}_{*}},{\tilde{Q}}_{evap2}=\frac{Q_{evap}}{c_g{T}_{*}}.\end{array}$

We can rewrite Equations (2)–(11) in dimensionless variables omitting the tilde sign:

$\begin{array}{l}\left({\rho }_{sf}+{\pi }_1+{\pi }_4{\rho }_{cp}+{\pi }_5{\rho }_{cm}\right)\frac{\partial T_c}{\partial t}=\\ =-{\text{Sh St}}_1\left(T_c-T_g\right)+Q_{comb}{\pi }_{2}W+\frac{\text{Sh}}{{\text{Pe}}_1}\left(1-a_g\right)\Delta T_c\\ -{\rho }_{cm}{Q}_{melt1}\frac{\partial F}{\partial t}-Q_{evap1}\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t},& (12)\end{array}$

$\begin{array}{l}{\rho }_g\left(\frac{\partial T_g}{\partial t}+\text{Sh}\left({\nu }_g·\nabla \right)T_g\right)=\text{Sh}{\text{St}}_2\left(T_c-T_g\right)+\frac{\text{Sh}}{{\text{Pe}}_2}{a}_g\Delta T_g\\ +Q_{evap2}\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t},& (13)\end{array}$

$\begin{array}{l}{\rho }_g\left(1+\chi \left(1-a_g\right)\right)\left(\frac{\partial {\nu }_g}{\partial t}+\text{Sh }\left({\nu }_g·\nabla \right){\nu }_g\right)=\\ -a_g\text{Eu Sh}\nabla p-\frac{a_g^2\text{Sh}}{\text{Re }\pi }{\nu }_g\frac{T_g^{1.5}}{{\stackrel{⌢}{c}}_{s2}+T_g}-\\ -\frac{\text{Sh}}{\text{Fr}}{\rho }_g\frac{g}{\left|g\right|}-\left[\left(1-{\mu }_p\right){\pi }_2{\pi }_{3}W+{\pi }_3\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}-\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t}\right]{\nu }_g,& (14)\end{array}$

$\begin{array}{l}\frac{\partial {\rho }_g}{\partial t}+\text{Sh}\nabla ·\left({\rho }_g{\nu }_g\right)=\left(1-{\mu }_p\right){\pi }_2{\pi }_{3}W+{\pi }_3\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}\\ -\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t}{,}_p=\frac{{\rho }_g{T}_g}{a_g},& (15)\end{array}$

$\begin{array}{l}{\rho }_g\left(\frac{\partial C}{\partial t}+\text{Sh }({\nu }_g·\nabla )C\right)=\frac{\text{Sh}}{\text{Re Sc}}\nabla ·({\rho }_g{D}_g\nabla C)\\ -{\mu }_g{\pi }_2{\pi }_{3}W-& (16)\end{array}$

$\begin{array}{l}-\left[\left(1-{\mu }_p\right){\pi }_2{\pi }_{3}W+{\pi }_3\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}-\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}\right]C,\\ W=\left(1-\eta \right)C\exp \left(-E/T_c\right),\frac{\partial \eta }{\partial t}={\pi }_{2}W,& (17)\end{array}$

$\begin{array}{ll}\frac{\partial {\rho }_{gm}}{\partial t}+\text{Sh}\nabla ·\left({\rho }_{gm}{\nu }_g\right)={\pi }_3\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}-\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t},& (18)\end{array}$

$\begin{array}{ll}{\rho }_{cf}=1-\eta ,{\rho }_{cp}={\mu }_p\eta ,\frac{\partial {\rho }_{cm}}{\partial t}=-\frac{\partial {{\rho }^{\prime }}_{cm}}{\partial t}+\frac{1}{{\pi }_3}\frac{\partial {{\rho }^{\prime }}_{gm}}{\partial t},& (19)\end{array}$

$\begin{array}{l}{a}_g=a_{g0}+\left(a_{cf0}-a_{cpEnd}\right)\eta +({\rho }_{cm0}-{\rho }_{cm}){\pi }_6,\\ D_g=T_g^b.& (20)\end{array}$

The boundary conditions for system (12)–(20) are the following. At the inlet of the reactor the gas velocity or the gas pressure is known, also the gas temperature, the mass concentration for the oxidizer and effective density of metal in gas are known. At the outlet of the reactor the gas pressure and conditions for gas temperature, oxidizer concentration and effective density of metal in gas are known. Also, we specify the conditions of heat exchange at the open boundaries and impermeable walls of the reactor. Thus, the boundary conditions for system of Equations (12)–(20) can be written in the following form:

$\begin{array}{l}p{|}_{x\in G_1}=p_0(x)or{\nu }_g{|}_{x\in G_1}={\nu }_{g0}(x),T_g{|}_{x\in G_1}=T_{g0},C{|}_{x\in G_1}=C_0\\ \text{ and }{\rho }_{gm}{|}_{x\in G_1}=0,\text{if }{\nu }_g{|}_{x\in G_1}·n{|}_{x\in G_1}\le 0,& (21)\end{array}$

$\begin{array}{l}p{|}_{x\in G_1}=p_0(x),\partial T_g/\partial n{|}_{x\in G_1}=0,\partial C/\partial n{|}_{x\in G_1}=0\\ \text{ and }\partial {\rho }_{gm}/\partial n{|}_{x\in G_1}=0,\text{if }{\nu }_g{|}_{x\in G_1}·n{|}_{x\in G_1}>0,& (22)\end{array}$

$\begin{array}{ll}\partial T_c/\partial n{|}_{x\in G_1}=\text{Bi}\left(T_{g0}-T_c{|}_{x\in G_1}\right),& (23)\end{array}$

$\begin{array}{ll}\partial T_c/\partial n{|}_{x\in G_2}=0,\partial T_g/\partial n{|}_{x\in G_2}=0,{\nu }_g{|}_{x\in G_2}·n{|}_{x\in G_2}=0.& (24)\end{array}$

Here G₁ is the object boundary opened to an atmosphere, G₂ is the impermeable walls of the object, n is the outward vector directed normally to G₁ or to G₂; C₀, p₀, T_g0 are the mass concentration of the oxidizer, the gas pressure and the gas temperature in the vicinity of the object, and Bi = $\frac{\beta H}{{\lambda }_c}$, where β is the heat removal coefficient.

In the calculation, Equation (12) splits into three equations, from which three functions are determined—T_c, F ρ′_cm–as follows:

(a) when T_c ≠ T_melt and T_c ≠ T_evap, then ∂ρ′_cm/∂t = 0, ∂F/∂t = 0, and we can determine T_c,

(b) when T_c = T_melt, then ∂T_c/∂t = 0 and ∂ρ′_cm/∂t = 0, and we can determine F;

(c) when T_c = T_evap, then ∂T_c/∂t = 0 and ∂F/∂t = 0, and we can determine ρ′_cm.

Equation (13) splits into two equations, from which two functions are determined—T_g and ρ′_gm–as follows:

(a) when T_g ≠ T_evap, then ∂ρ′_gm/∂t = 0, and we can determine T_g,

(b) when T_g = T_evap, then ∂T_g/∂t = 0, and we can determine ρ′_gm.

Note that the system of Equations (12)–(20) with boundary conditions (21)–(24) is based on two models previously developed and tested: model of heterogeneous combustion of porous media (Levin and Lutsenko, 2017; Lutsenko, 2018) and model of gas flow through granular materials with phase changes (Levin et al., 2018; Lutsenko and Fetsov, 2019). The computational algorithms used for these models have formed the basis of the numerical method for solving the system of Equations (12)–(20). According to the method the energy equations, momentum conservation equation, equation for oxidizer concentration and equation of mass conservation for evaporated metal in gas are transformed into explicit finite difference equations. The condensed phase temperature, the liquid fraction in the metal, the decrease in the effective density of the condensed metal due to evaporation, the gas temperature, the decrease in the effective density of the evaporated metal due to condensation, the gas filtration velocity, the oxidizer concentration and the effective density of metal in gas phase are determined from these equations. The continuity equation is transformed into implicit finite difference equation, from which the gas pressure is determined using Thomas algorithm (Tannehill et al., 1997) and taking into account the perfect gas equation of state. The effective gas density and the remaining unknown quantities are determined trivially from the perfect gas equation of state and other closure equations.

Results and Discussion

To study the mass transfer of metal compounds under conditions of filtration combustion, we consider a cylindrical reactor with a porous medium consisting of a mixture of particles of birch coal (fuel), chamotte bricks (inert material) and cadmium (metal). Thus, the characteristics of a combustible, inert material and metal were assumed to be equal to the characteristics of birch coal, chamotte and cadmium, respectively. It should be noted that the selected characteristics of the materials are close to those of coal gasification in the works of other researchers (Aldushin, 1997; Rozenberg et al., 2009; Manelis et al., 2016; Antonov et al., 2017). We suppose that the solid phase is premixed, its properties at each point in the reactor at the initial time are constant and equal. To carry out combustion, air is supplied into the reactor; the flow in the reactor is assumed to be one-dimensional. At the time of ignition, the pressure at the object bottom rapidly increases up to p₀₁and remains constant; the pressure at the object top p_h does not change. To initiate the combustion, the temperature of the solid phase in ignition zone, which is located near the inlet of the reactor and has a width of H₁, becomes instantly equal to T_c0 that is much higher than the initial temperature. After ignition of the fuel, the combustion wave passes through the reactor. The initial characteristics of the system are presented in the Table 1.

TABLE 1

Table 1. The initial characteristics of the system.

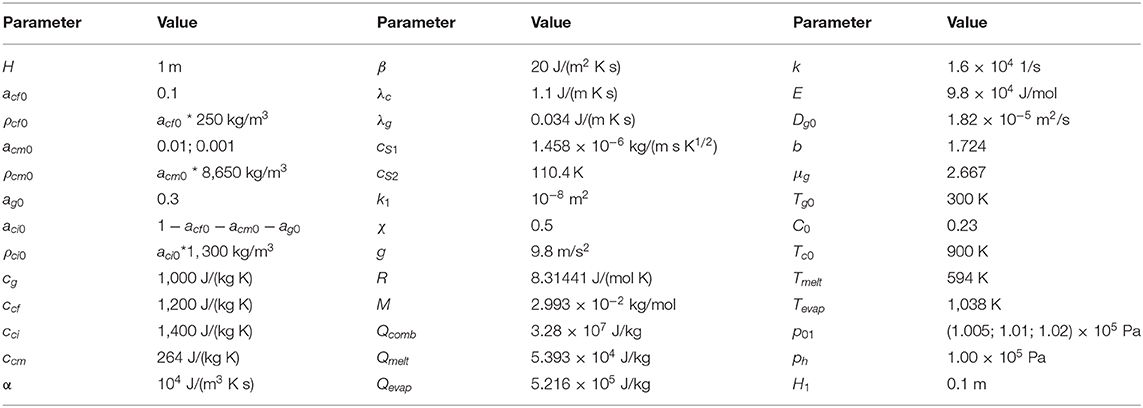
In Figure 2 the distribution of the temperature of the condensed phase along the length of the reactor is shown at various points in time. The initial volumetric concentration of cadmium is equal to 0.001 or 0.01, the pressure at the inlet of the reactor is equal to 1.005 atm. Hereinafter, the presented calculations results were obtained using a uniform grid with mesh size 1/800. As seen from the figure, the combustion front moves through the reactor from its inlet to outlet. The maximum temperatures are close to 1,500 K. It can be seen that for same compositions (curves 1, 3 or 2, 4) the temperature profiles practically coincide, which indicates the achievement of a quasistationary state. Before the combustion front, there is the zone of cadmium evaporation. The zone of evaporation of the metal into gas expands (curves 1 and 3), which indicates the accumulation of cadmium before the combustion front. The initial cadmium concentration of 0.001 has almost no effect on the type of temperature profiles. Such a low metal concentration makes a negligible contribution to the thermal state of the system. An increase in cadmium concentration leads to a decrease in the velocity of the combustion front (curves 1, 2 or 3, 4). This can be explained by the fact that the higher the initial cadmium concentration, the more vaporized cadmium is transferred to the zone in front of the combustion wave, and this increases the temperature in this zone. The higher temperature in front of the combustion wave, the higher temperature in the combustion wave. At a constant gas pressure at the reactor inlet, increase in temperature of porous medium leads to a decrease in the gas velocity, that leads to a decrease in the velocity of the combustion wave. The evaporation of the metal into the gas phase makes it more difficult to filter the gas through the porous medium.

FIGURE 2

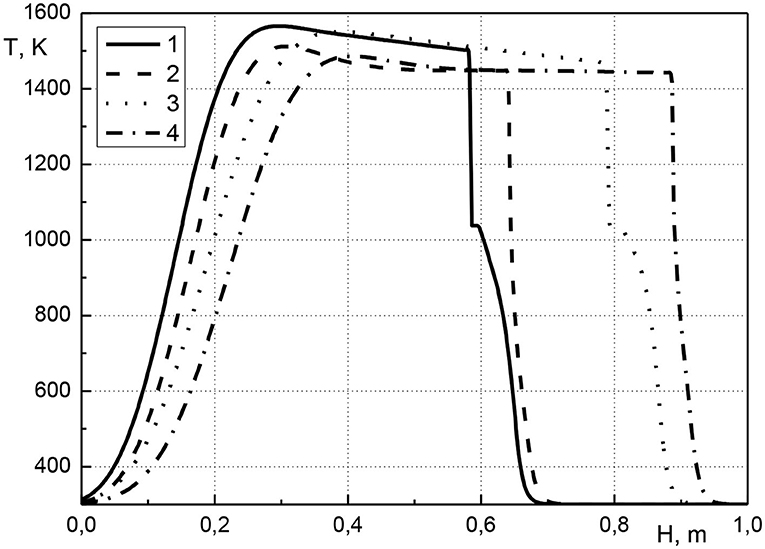
Figure 2. Condensed phase temperature profiles at various points in time. 1–t = 2,700 s, a_cm0 = 0.01; 2–t = 2,700 s, a_cm0 = 0.001; 3–t = 4,500 s, a_cm0 = 0.01; 4–t = 4,500 s, a_cm0 = 0.001.

In Figure 3 the distribution of condensed cadmium effective density along the length of the reactor is shown at various points in time. The calculations are performed for the same parameters as in Figure 2. It should be noted that the effective density of substance is equal to the product of its volume concentration and true density, therefore, changes in the effective density of the condensed cadmium and its concentration are equivalent. The distribution of metal along the length of the reactor is as follows. At the beginning of the reactor, the cadmium concentration is zero, i.e., the metal is missing. Next is a narrow zone with a high metal content, which is located directly before the combustion front (see Figure 2). After this zone, the cadmium concentration is constant until the end of the reactor and is equal to the initial value. Over time, the maximum metal concentration increases (curves 1, 3 or 2, 4). It can be noted that the width of the zone with a high metal content remains almost constant (curves 1, 3 or 2, 4). Thus, we can conclude that the metal is transported through the reactor due to the continuous evaporation and condensation of the metal before the combustion front.

FIGURE 3

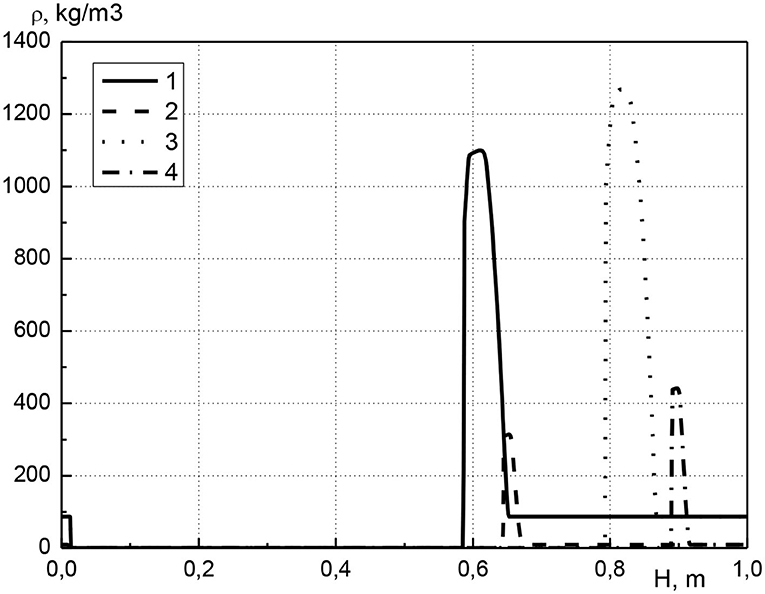
Figure 3. Profiles of condensed cadmium effective density at various points in time. 1–t = 2,700 s, a_cm0 = 0.01; 2–t = 2,700 s, a_cm0 = 0.001; 3–t = 4,500 s, a_cm0 = 0.01; 4–t = 4,500 s, a_cm0 = 0.001.

In Figure 4 the distribution of the temperature of the condensed phase along the length of the reactor is shown for various pressure values at the inlet of the reactor for a point in time of 1,500 s from the start of the process. The pressure at the inlet of the reactor ranges from 1.005 to 1.02 atm; the initial volume concentration of cadmium is equal to 0.01. It can be seen that an increase in pressure at the inlet of the reactor leads to an increase in the maximum temperature. The maximum temperature value is realized in the combustion front where the main heat release occurs (curves 2 and 3). For curve 1, this is not observed due to the influence of the ignition stage. At the beginning of the process, the mixture ignites due to the heating of a part of the solid phase. In this case, a sharp rise in temperature occurs both due to the heat release of chemical reactions of fuel oxidation, and due to the preliminary heating of the solid phase. For the first case (curve 1), as the combustion front moves, the temperature in the front decreases slightly, and the temperature profile has convex. Over time, this convexity of the profile decreases due to thermal conductivity (see Figure 2, curves 2 and 4). An increase in pressure at the inlet of the reactor leads to an increase in gas flow and, as a consequence, to an increase in the velocity of the combustion front. With increasing the inlet gas pressure, an increase in the width of transition zone of the metal into the gas phase is observed, which indicates the accumulation of metal before the combustion front.

FIGURE 4

Figure 4. Condensed phase temperature profiles at time t = 1,500 s. 1–p₀₁ = 1.005 atm; 2–p₀₁ = 1.01 atm; 3–p₀₁ = 1.02 atm.

In Figure 5 the distribution of condensed cadmium effective density along the length of the reactor is shown for various pressure values at the inlet to the reactor. Profiles are presented at various points in time in increments of 500 s. The calculations were performed for the same parameters as in Figure 4. For each pressure value at the inlet of the reactor, metal is transferred along the length of the reactor and accumulates before the combustion front. Moreover, as in Figure 3, the maximum concentration of the metal increases over time, and the width of the high metal content zone remains almost constant. When the pressure values at the inlet of the reactor is equal to 1.005, 1.01, and 1.02 atm, the maximal achievable concentration of cadmium is about 1,350, 1,150, and 900 kg/m³, respectively. The increase in pressure at the inlet of the reactor leads to the fact that the zone of high cadmium content decreases in height and increases in width, that is, the accumulation of metal occurs in a wider area. This is due to an increase in the velocity of the gas phase with increasing the gas pressure at the inlet of the reactor. Due to the increase in gas velocity, a particle of the evaporated metal, moving into an area with a low temperature, flies a greater distance until it completely condensed, this leads to the expansion of the metal-containing zone.

FIGURE 5

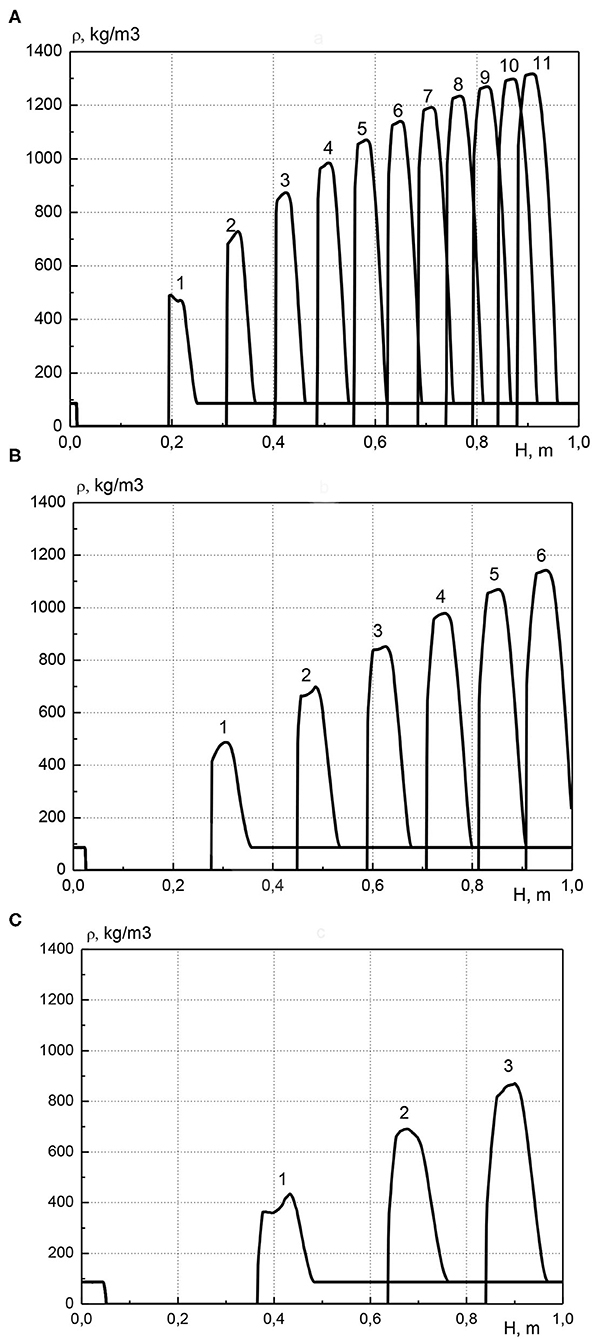
Figure 5. Profiles of condensed cadmium effective density at various points in time, curve number corresponds to time t = (curve number) × 500 s. (A) p₀₁ = 1.005 atm; (B) p₀₁ = 1.01 atm; (C) p₀₁ = 1.02 atm.

Conclusions

To study the mass transfer of metal compounds, a model of filtration combustion of metal-containing combustible mixtures is developed. A system of dimensionless equations is obtained, and a solution method is briefly described. Using cadmium-containing mixture as an example, the main characteristics of filtration combustion are determined when the gas pressure at the reactor inlet is constant. It is shown that under the conditions of a filtration combustion wave, cadmium can evaporate into the gas phase and be transferred with gas through the reactor. Due to the evaporation and condensation of cadmium, it is transported and accumulated before the combustion front. It is shown that an increase in the initial concentration of the metal, as well as its accumulation before the combustion front, can affect the temperature profile. At a high initial concentration of cadmium, a zone before the combustion front is substantially heated due to the condensation of the evaporated metal, and the condensed metal begins to evaporate in this zone. As a result, the zone expanding with time with a constant temperature equal to the phase transition temperature is clearly visible on the profile of the condensed medium temperature. An increase in pressure at the inlet of the reactor leads to an increase in the maximum temperature and velocity of the combustion front, due to an increase in gas flow. The increase in pressure at the inlet of the reactor leads to the fact that the high cadmium content zone decreases in height and increases in width, that is, the accumulation of metal occurs in a wider area. It is shown that a 4-fold increase in the pressure difference at the open boundaries of the reactor leads to a decrease in the maximum metal concentration by about 1.5 times. The possibility of controlling the mass transfer of metal compounds under the conditions of a filtration combustion wave with the aim of concentrating them is shown. An increase in the concentration of metals due to mass transfer will subsequently make it economically feasible to extract them by traditional methods.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

ES and NL: substantial contributions to the design of the work and model investigated and resolved. MT: analysis and interpretation of data for the work and provide approval for publication of the content. All authors contributed to the article and approved the submitted version.

Funding

The reported study was partially funded by RFBR (project number 18-29-24029-mk) and by ANID-Chile (FONDECYT Project N° 1190654). The results were obtained using the equipment of Shared Resource Center Far Eastern Computing Resource IACP FEB RAS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor is currently organizing a Research Topic with one of the authors MT.

References

Aldushin, A. P. (1997). “Filtration combustion, in Advances in combustion science,” in Progress in Astronautics and Aeronautics 173. Eds Y. B. Zeldovich, W.A. Sirignano, A.G. Merzhanov, and L. De Luka (Reston: AIAA), 95–115.

Google Scholar

Antonov, D. V., Valiullin, T. R., Iegorov, R. I., and Strizhak, P. A. (2017). Effect of macroscopic porosity onto the ignition of the waste-derived fuel droplets. Energy 119, 1152–1158. doi: 10.1016/j.energy.2016.11.074

CrossRef Full Text | Google Scholar

Dai, S., and Finkelman, R. (2017). Coal as a promising source of critical elements: progress and future prospects. Int. J. Coal Geol. 186, 155–164. doi: 10.1016/j.coal.2017.06.005

CrossRef Full Text | Google Scholar

Erüst, C., Akcil, A., Gahan, C. S., Tuncuk, A., and Deveci, H. (2013). Biohydrometallurgy of secondary metal resources: a potential alternative approach for metal recovery. J. Chem. Technol. Biotechnol. 88, 2115–2132. doi: 10.1002/jctb.4164

CrossRef Full Text | Google Scholar

Frohlich, P., Lorenz, T., Martin, G., Brett, B., and Bertau, M. (2017). Valuable metals-recovery processes, current trends, and recycling strategies. Angew. Chem. Int. Ed. 10, 2544–2580. doi: 10.1002/anie.201605417

PubMed Abstract | CrossRef Full Text | Google Scholar

Jha, M. K., Kumar, V., and Singh, R. J. (2001). Review of hydrometallurgical recovery of zinc from industrial wastes. Resour. Conserv. Recycl. 33, 1–22. doi: 10.1016/S0921-3449(00)00095-1

CrossRef Full Text | Google Scholar

Johnson, D. B. (2014). Biomining - biotechnologies for extracting and recovering metals from ores and waste materials. Curr. Opin. Biotechnol. 30:24e31. doi: 10.1016/j.copbio.2014.04.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Jowitt, S. M., Werner, T. T., Weng, Z., and Mudd, G. M. (2018). Recycling of the rare earth elements. Curr. Opin. Green Sust. Chem. 13, 1–7. doi: 10.1016/j.cogsc.2018.02.008

CrossRef Full Text | Google Scholar

Kuang, S. T., and Liao, W. P. (2018). Progress in the extraction and separation of rare earths and related metals with novel extractants: a review. Sci. China Tech. Sci. 61, 1319–1328. doi: 10.1007/s11431-018-9295-0

CrossRef Full Text | Google Scholar

Levin, V. A., and Lutsenko, N. A. (2017). Two-dimensional gas flows under heterogeneous combustion of solid porous media. Doklady Phys. 62, 425–429. doi: 10.1134/S1028335817090014

CrossRef Full Text | Google Scholar

Levin, V. A., Lutsenko, N. A., and Fetsov, S. S. (2018). Modeling of gas flow through a granular bed of a thermal storage phase-change material. Doklady Phys. 63, 158–160. doi: 10.1134/S102833581804002X

CrossRef Full Text | Google Scholar

Lutsenko, N. A. (2013). Modeling of heterogeneous combustion in porous media under free convection. Proc. Combust. Inst. 34, 2289–2294. doi: 10.1016/j.proci.2012.06.147

CrossRef Full Text | Google Scholar

Lutsenko, N. A. (2018). Numerical model of two-dimensional heterogeneous combustion in porous media under natural convection or forced filtration. Combust. Theory Model. 22, 359–377. doi: 10.1080/13647830.2017.1406617

CrossRef Full Text | Google Scholar

Lutsenko, N. A., and Fetsov, S. S. (2019). Influence of gas compressibility on gas flow through bed of granular phase change material. Int. J. Heat Mass Transf. 130, 693–699. doi: 10.1016/j.ijheatmasstransfer.2018.10.100

CrossRef Full Text | Google Scholar

Lutsenko, N. A., and Salgansky, E. A. (2019). On the modelling of the extraction process of rare metals from metal-containing systems by the method of filtration combustion. IOP Conf. Ser. J. Phys. Conf. Ser. 1268:012044. doi: 10.1088/1742-6596/1268/1/012044

CrossRef Full Text | Google Scholar

Manelis, G. B., Glazov, S. V., Lempert, D. B., and Salgansky, E. A. (2011). Salgansky Filtration combustion of solid fuel in countercurrent reactors. Russ. Chem. Bull. Int. Ed. 60, 1301–1317. doi: 10.1007/s11172-011-0198-4

CrossRef Full Text | Google Scholar

Manelis, G. B., Glazov, S. V., Salgansky, E. A., Lempert, D. B., Gudkova, I. Y., and Domashnev, I. A. (2016). Extraction of molybdenum-containing species from heavy oil residues using the filtration combustion method. Int. J. Heat Mass Transf. 92, 744–750. doi: 10.1016/j.ijheatmasstransfer.2015.09.056

CrossRef Full Text | Google Scholar

Nancharaiah, Y. V., Mohan, S. V., and Lens, P. N. L. (2016). Biological and bioelectrochemical recovery of critical and scarce metals. Trends Biotechnol. 34:137e155. doi: 10.1016/j.tibtech.2015.11.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Nigmatulin, R. I. (1990). Dynamics of Multiphase Media. New York, NY: Hemisphere Publ. Corp.

Google Scholar

Rozenberg, A. S., Grigor'Yan, L. A., Gudkova, I. Y., Lempert, D. B., and Manelis, G. B. (2009). Mass transfer of zinc-containing compounds during filtration combustion in the counterflow regime: 3. Mass transfer at a low content of the zinc-containing component in the initial stock. Russ. J. Phys. Chem. 3, 802–806. doi: 10.1134/S1990793109050157

CrossRef Full Text | Google Scholar

Salganskii, E. A., Fursov, V. P., Glazov, S. V., Salganskaya, M. V., and Manelis, G. B. (2003). Model of air gasification of a solid fuel in a filtration regime. Combust. Explo. Shock Waves. 39, 37–42. doi: 10.1023/A:1022193117840

CrossRef Full Text | Google Scholar

Salgansky, E. A., Tsvetkov, M. V., Kadiev, K. M., Visaliev, M. Y., and Zekel, L. A. (2019). Rare and valuable metals in oils and coals of the Russian Federation: content and methods of extraction. Russ. J. Appl. Chem. 92, 1616–1633. doi: 10.1134/S1070427219120024

CrossRef Full Text | Google Scholar

Sthiannopkao, S., and Wong, M. H. (2013). Handling e-waste in developed and developing countries: initiatives, practices, and consequences. Sci. Total Environ. 463–464, 1147–1153. doi: 10.1016/j.scitotenv.2012.06.088

PubMed Abstract | CrossRef Full Text | Google Scholar

Tannehill, J. C., Anderson, D. A., and Pletcher, R. H. (1997). Computational Fluid Mechanics and Heat Transfer, 2nd Edn. Washington, DC: Taylor & Francis.

Google Scholar

Toledo, M., Ripoll, N., Céspedes, J., Zbogar-Rasic, A., Fedorova, N., Jovicic, V., et al. (2018). Syngas production from waste tires using a hybrid filtration reactor under different gasifier agents. Energy Convers. Manag. 172, 381–390. doi: 10.1016/j.enconman.2018.07.046

CrossRef Full Text | Google Scholar

Watling, H., Watkin, E., and Ralph, D. (2010). The resilience and versatility of acidophiles that contribute to the bio-assisted extraction of metals from mineral sulphides. Environ. Technol. 31, 915–933. doi: 10.1080/09593331003646646

CrossRef Full Text | Google Scholar