Phase Transition and Electronic Structures of All-d-Metal Heusler-Type X2MnTi Compounds (X = Pd, Pt, Ag, Au, Cu, and Ni)

In this work, we investigated the phase transition and electronic structures of some newly designed all-d-metal Heusler compounds, X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni), by means of the first principles. The competition between the XA and L2₁ structures of these materials was studied, and we found that X₂MnTi favors to feature the L2₁-type structure, which is consistent with the well-known site-preference rule (SPR). Under the L2₁ structure, we have studied the most stable magnetic state of these materials, and we found that the ferromagnetic state is the most stable due to its lower energy. Through tetragonal deformation, we found that the L2₁ structure is no longer the most stable structure, and a more stable tetragonal L1₀ structure appeared. That is, under the tetragonal strain, the material enjoys a tetragonal phase transformation (i.e., from cubic L2₁ to tetragonal L1₀ structure). This mechanism of L2₁-L1₀ structure transition is discussed in detail based on the calculated density of states. Moreover, we found that the energy difference between the most stable phases of L1₀ and L2₁, defined as ΔE_M (ΔE_M = E_Cubic-E_Tetragonal), can be adjusted by the uniform strain. Finally, the phonon spectra of all tetragonal X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) phases are exhibited, which provides a powerful evidence for the stability of the tetragonal L1₀ state. We hope that our research can provide a theoretical guidance for future experimental investigations.

Introduction

Magnetic shape memory compounds (MSMAs) (O'Handley, 1998) are a new type of intelligent materials which integrates magnetic controlled shape memory and magnetic field-induced strain simultaneously. It can be used as key components of sensors and brakes in the future. MSMAs have both thermoplastic martensitic transformation (Oikawa et al., 2001) and magnetic transformation (Oikawa et al., 2002), and their shape memory effect can be controlled by the magnetic field. That is to say, under the effect of magnetic field, their size or volume will be changed, resulting in a great strain, i.e., the magnetostrictive effect (Populoh et al., 2012). In addition, MSMAs enjoy magnetoresistance (Ullakko et al., 1996) and magnetocaloric (GschneidnerJr et al., 2005) effects, so they have been regarded as a research hot spot in recent years.

Heusler (Graf et al., 2011; Birkel et al., 2013; Ahmadian and Salary, 2014; Kirievsky et al., 2014; Xue et al., 2016; Miranda and Gruhn, 2017; Ghunaim et al., 2018; Li et al., 2019, 2020) compounds belong to intermetallic compounds. Heusler compounds naturally have many excellent properties, such as high Curie temperature (T_C) (Wurmehl et al., 2005), adjustable electronic structure, suitable semiconductor lattice constants, and various magnetic properties. Therefore, Heusler compounds can be seen as good candidates for spin gapless semiconductors (SGSs) (Gao and Yao, 2013; Skaftouros et al., 2013; Wang et al., 2016; Wang X. et al., 2017), thermoelectric materials (Downie et al., 2013; Huang et al., 2018; Mallick and Vitta, 2018), shape memory compounds (SMAs) (Aksoy et al., 2009; Li et al., 2018), half metals (Shigeta et al., 2018; Singh and Gupta, 2019; Hao et al., 2020), and topological insulators (Hou et al., 2015; Lin et al., 2015). Because Heusler compounds possess excellent properties, they have been regarded as a research hot spot over the past 100 years. To date, researchers have discovered thousands of Heusler compounds. Heusler compounds roughly can be divided into three structures, namely, full Heusler (Wang X. T. et al., 2017), half Heusler (Silpawilawan et al., 2017), and quaternary Heusler (Cui et al., 2019), whose stoichiometric compositions are X₂YZ, XYZ, and XYMZ, respectively. X, Y, and M are usually transition elements, while the Z atom is a main group element. In recent years, a new type of Heusler compounds has been found by researchers, and this type of Heusler compounds is named as all-d-metal Heusler compounds (Wei et al., 2015).

In the early 1990s, all-d-metal Heusler compounds Zn₂AuAg and Zn₂CuAu (Muldawer, 1966) were synthesized experimentally, which proved that all-d-metal Heusler compounds can be successfully prepared. This interesting study opened up a new direction for the research of Heusler compounds. All-d-metal Heusler compounds are different from common Heusler compounds in that they are composed of transition metal elements without the participation of main group elements. Compared with common Heusler compounds, all-d-metal Heusler compounds have the following advantages: (1) all-d-metal Heusler compounds do have not many restrictions on atomic site preference, so they can show more phase space and versatility than traditional materials; (2) they have high strength and toughness; and (3) in addition to magnetic phase transitions, all-d-metal Heusler compounds also have many untouched physical properties, such as spintronics properties.

Recently, an effective method, i.e., adjusting composition, was proposed by Tan et al. (2019) to make regular the phase transition of all-d-metal Heusler compounds. In their work, the atomic ordering, structural stability, tetragonal deformation, magnetism, and electronic structures of the Mn–Ni–V system, including Mn_2−xNi_1.5+xV_0.5, Mn_2−xNi_1+xV, and Mn_2−xNi_0.5+xV_1.5 compounds, are studied by employing the first principles. They stated that the tetragonal phase is more stable than the cubic phase for these all-d-metal Heusler compounds: MnNi₂V, Mn_1.25Ni_1.75V, MnNi_2.5V_0.5, and Mn_0.5Ni₂V_1.5.

Based on the above information, we focus on the electronic structures and phase transition of all-d-metal Heusler compounds X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) with the help of the first principles. To the best of knowledge, the physical properties of the X₂MnTi system have not been studied yet by other researchers up to now. We will reflect that a L2₁-L1₀ phase transition can be found in all-d-metal Heusler compounds X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) under the tetragonal distortion. The effect of uniform strain on the cubic–tetragonal transition for this X₂MnTi system was also discussed in detail in this work. The mechanism of the L2₁-L1₀ phase transition is discussed according to the calculated density of states in both cubic and tetragonal phases, and finally, we will further prove the stability of the tetragonal phase by calculating the phonon spectrum of the tetragonal L1₀ phase.

Computational Methods

Electronic structure calculations were performed using density functional theory (DFT), within the VASP code (Hafner, 2007). The exchange–correlation potential is treated by using the generalized gradient approximation (GGA) (Perdew et al., 1996) with the Perdew–Burke–Ernzerhof (PBE) (Perdew et al., 1998) functional. We also use the projection enhanced wave (PAW) (Kresse and Furthmüller, 1996) method to deal with the interaction between the ion nucleus and valence electron. In the calculations, the cutoff energy was set at 450 eV. A Monkhorst-Pack special 12 × 12 × 12 k-point mesh was used in the Brillouin zone (BZ) integration. The unit cell was optimized until the force and total energy were <0.001 eV/Å and 1 × 10⁻⁵ eV, respectively. The crystal models of cubic L2₁ phase and tetragonal L1₀ phase of Heusler alloys are built via VESTA. To calculate the dynamical stabilities of these alloys, phonon dispersion is obtained by means of the force-constants method using Nanodcal code. For the L2₁-type X₂MnTi alloys, two magnetic states are considered: one is the ferromagnetic state with spin orderings of X-1, X-2, Mn, and Ti that are ↑↑↑↑; the other one is the antiferromagnetic state with spin orderings of X-1, X-2, Mn, and Ti that are ↓↓↑↓, respectively.

Results and Discussion

The Crystal and Magnetic Structures of the X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) Heusler Compounds

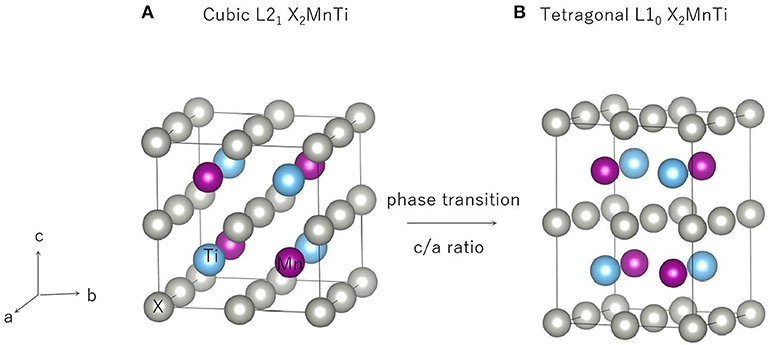
Heusler compounds, X₂YZ, enjoy a highly ordered cubic structure (Han et al., 2019a). There are generally four different positions in a primitive cell, namely, A (0, 0, 0), B (0.25, 0.25, 0.25), C (0.5, 0.5, 0.5), and D (0.75, 0.75, 0.75), respectively. The transition metal elements X and Y occupy the A, B, and C positions, and the main group element Z is preferred to occupy the D position. Different occupation positions of X and Y atoms will lead to different structures, namely, L2₁ and XA structures (Suzuki and Kyono, 2004) (as shown in Figures 1A,B). In the former, two X atoms occupy A and C positions, and Y and Z atoms enter B and D positions, respectively; in the latter, two X atoms occupy A and B positions, and Y and Z atoms are located at C and D positions, respectively.

FIGURE 1

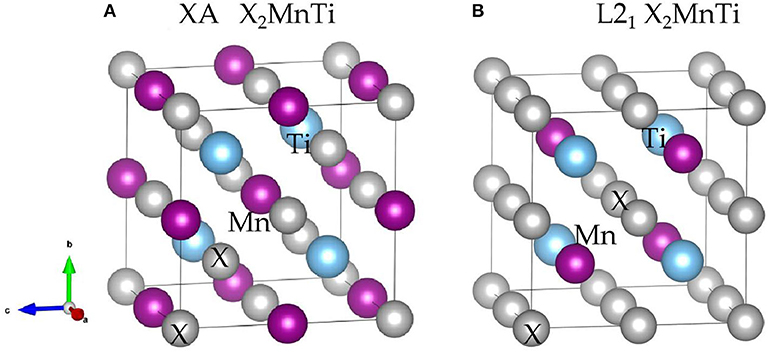
Figure 1. Crystal structure of the (A) XA-type X₂MnTi and (B) L2₁-type X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni); X is highlighted by gray balls, Ti is marked by blue balls, and Mn is marked by purple balls, respectively.

Next, we studied the competition between the XA structure and the L2₁ structure of X₂MnTi. In Figure 2, the total energy of X₂MnTi at the ground state with different structures (L2₁ and XA) is determined, and we set the ground state energy of the L2₁ structure as 0 eV as reference. One can clearly see that, for X₂MnTi, the total energy of XA is higher than L2₁, reflecting that the most stable ordered structure is L2₁ for the X₂MnTi system. In Figure 3, we further give a comparison of the total energy of two magnetic states [ferromagnetic (FM) and antiferromagnetic (AFM)] for the L2₁-type X₂MnTi. We set the total energy of AFM to 0 eV as reference. As shown in Figure 3, the energy of X₂MnTi in the FM structure is lower than 0, which indicates that the X₂MnTi tends to exhibit the FM magnetic state.

FIGURE 2

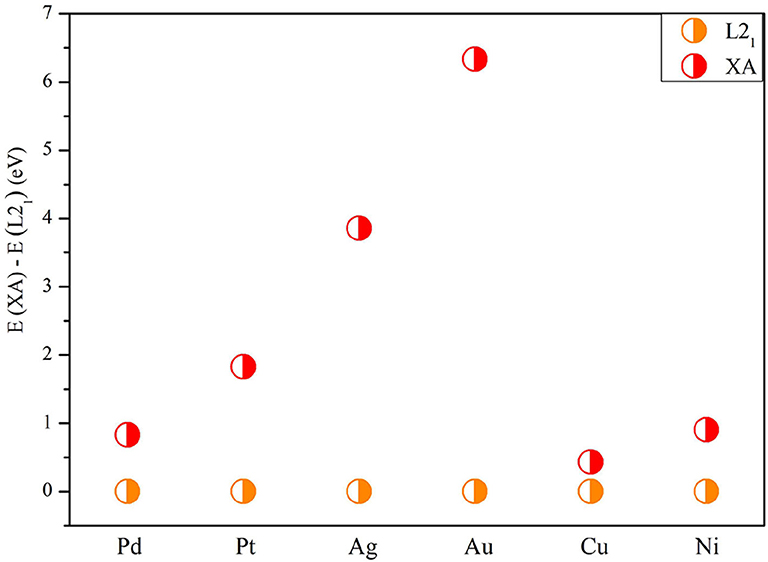
Figure 2. Total energy difference E(XA) – E(L2₁) of X₂MnTi under the L2₁ and XA structure (in FM state) with the energy of L2₁ set as 0 eV for reference.

FIGURE 3

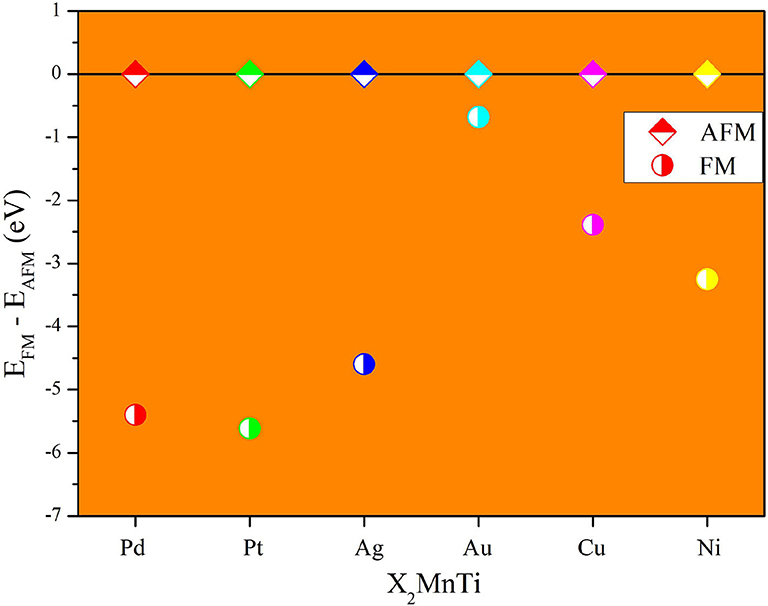
Figure 3. Total energy difference (E_FM – E_AFM) of different magnetic states (AFM and FM) of X₂MnTi (L2₁ structure) with the total energy of AFM set as 0 eV.

The L2₁-L1₀ Phase Transition of All-d-Metal Heusler-Type X₂MnTi

In this section, our research goal is to explore the possible competition between the L2₁ (see Figure 4A) and L1₀ (see Figure 4B) of the all-d-metal Heusler compounds X₂MnTi. We used Bain paths to investigate the reversible transformation between the ordered L2₁ and L1₀ phases during tetragonal distortion. Bain paths (Alippi et al., 1997) have tetragonal states along the geometries which connect the bcc and fcc phases of a material. It is assumed that there is no cell volume change after applying deformation on the cubic phase, then the energy difference ΔE in respect to c/a ratios is calculated to estimate whether it is a stable or metastable phase. It is a commonly used method to predict reversible transformation, and a number of literature (Barman et al., 2007; Özdemir Kart et al., 2008; Qawasmeh and Bothina, 2012; Zeleny et al., 2014) have used this method to estimate shape memory effect in Heusler FSMAs, such as Ni₂MnGa and Mn₂NiGa.

FIGURE 4

Figure 4. Cubic phase (L2₁) (A) and tetragonal phase (L1₀) (B) of X₂MnTi compounds.

In Figure 5, we can see that all X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) compounds present a L2₁-L1₀ (possible martensitic transformation) under the effect of tetragonal distortion. In detail, we found that X₂MnTi (except for X = Au) compounds have two local minimum energies, one locates at c/a < 1 and the other locates at c/a > 1. The value of the local minimum energy with c/a > 1 is lower than that of the local minimum energy with c/a < 1, which means that the local minimum energy with c/a > 1 is the most stable state. Moreover, when c/a < 1, the local minimum energy of X₂MnTi (except for X = Au) is a metastable phase. For the Au₂MnTi compound, there is only one local minimum energy, which locates at c/a >1. This local minimum energy is the most stable phase and there is no metastable structure during the cubic–tetragonal transformation. The c/a ratio values of the most stable tetragonal L1₀ structure of these materials are summarized in Table 2.

FIGURE 5

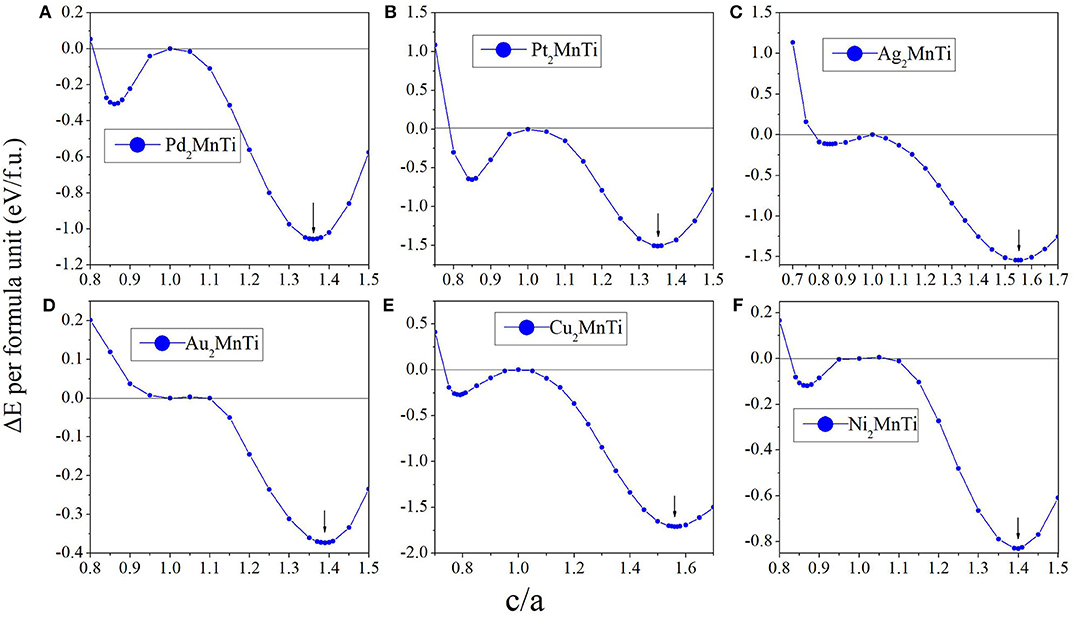
Figure 5. (A–F) Relationship between the c/a ratio and ΔE (ΔE = E_T – E_C) for X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) compounds.

Next, we studied the influence of uniform strain on the competitiveness of the L2₁ and L1₀ structures. We give Cu₂MnTi and Ni₂MnTi as examples in Figure 6 for a detailed discussion.

FIGURE 6

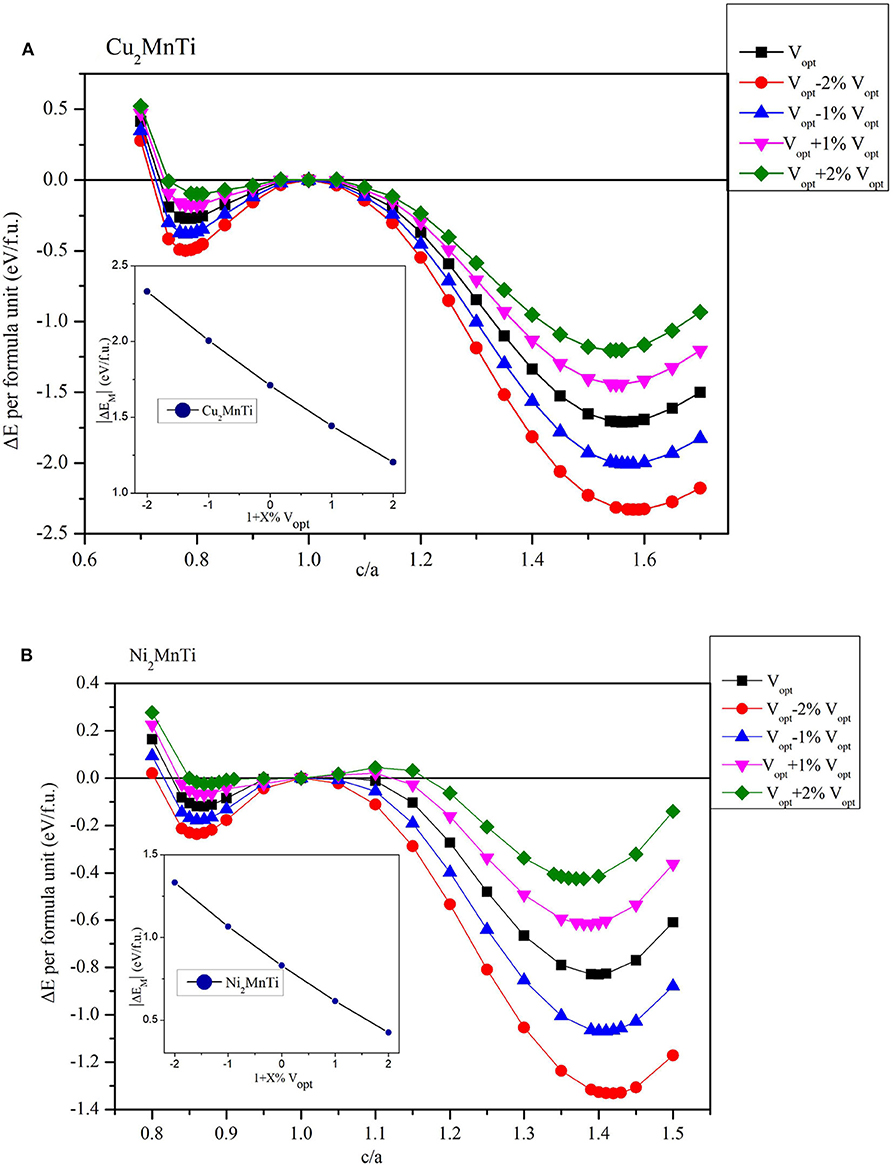
Figure 6. Relationship between c/a ratio and ΔE (ΔE = E_T – E_C) with different volumes (insert figures: the relationship between the |ΔE_M| and 1 + X%V_opt) for (A) the Cu₂MnTi compound and (B) the Ni₂MnTi compound.

By adjusting the lattice parameters of X₂MnTi (X = Cu, Ni), their volume was changed between −2 and +2%, and then tetragonal distortion is applied to the cubic crystal structures. As shown in Figure 6, under the effect of tetragonal distortion, we can see that all substances with a volume of −2 and +2% still have two local energy minimums, which is the same as the optimized volume (V_opt). However, the difference is that during the volume changes from +2 to −2%, the minimum value of local energy gradually becomes lower, that is, the L1₀ state becomes more and more stable as the volume decreases.

In addition, it can be seen that the value of the c/a ratio for the most stable L1₀ phase also changes with the volume changes. During the volume changes from −2% to +2%, the c/a ratio (for the most stable L1₀ phase) gradually decreases. A smaller c/a ratio means a smaller degree of tetragonal distortion.

The Calculated Density of States of All-d-Metal Heusler-Type Compounds X₂MnTi

We calculated their total density of states (TDOSs) and partial state density of states (PDOSs) (Han et al., 2019b) in cubic and tetragonal states, respectively, and we plotted them in Figures 7, 8.

FIGURE 7

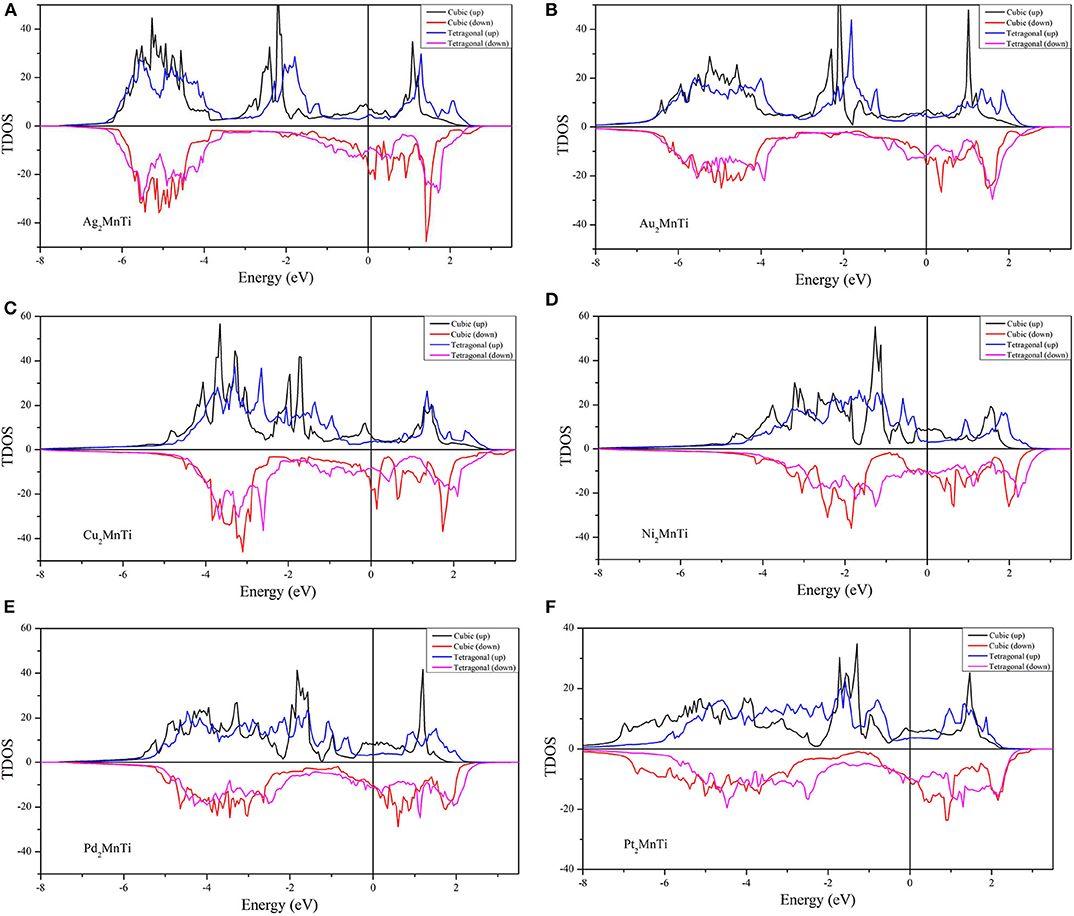
Figure 7. (A–F) Calculated TDOSs of X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) compounds in cubic and tetragonal phases.

FIGURE 8

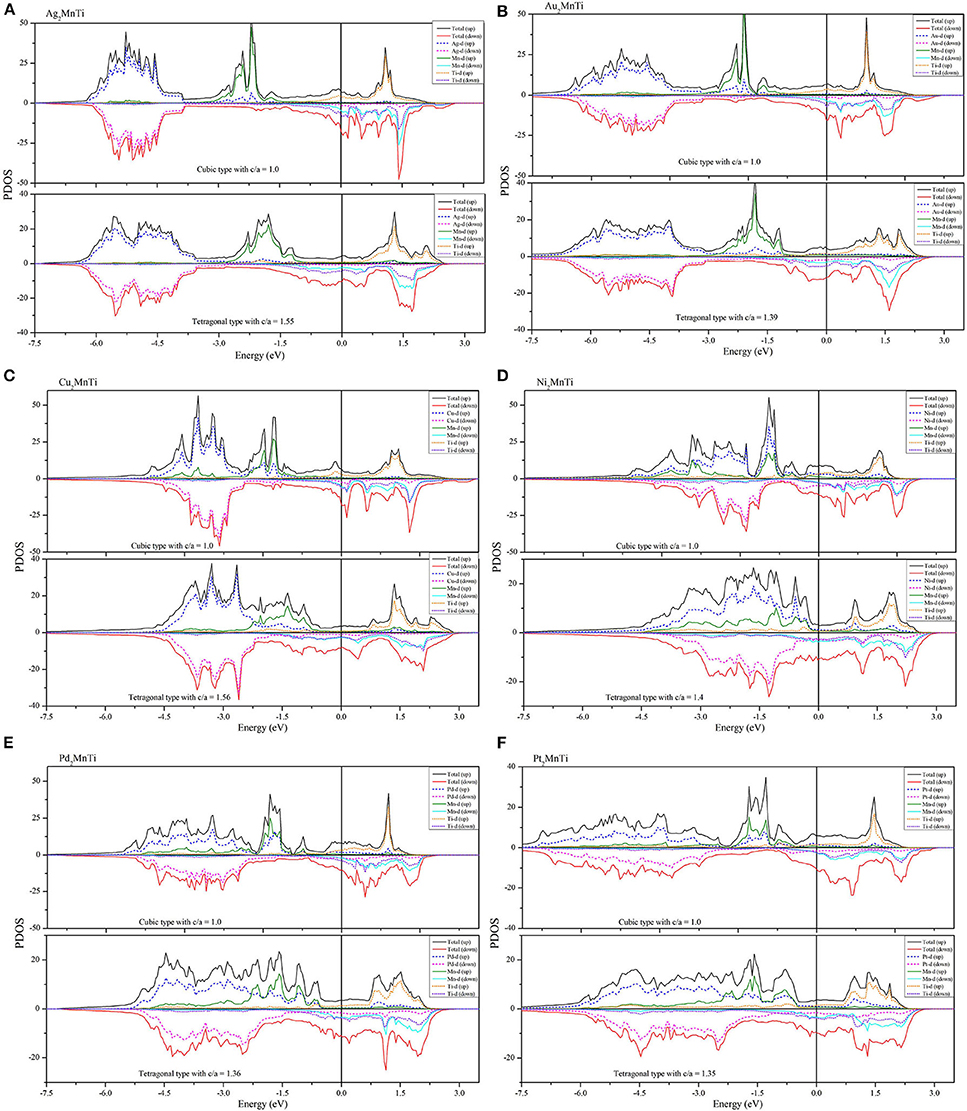
Figure 8. (A–F) PDOS diagrams of X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) compounds in cubic and tetragonal phases.

We found that the TDOS of tetragonal structure around the Fermi level is softer than the cubic TDOS. For example, we can find some strong peaks (see the red lines) near the Fermi level in the spin-down direction and some small peaks in the spin-up direction (see the black line) for the cubic phase (see Figure 7A). Note that one of the contributions to the total energy is the band energy $E_{\mathrm{\text{band}}}={\int }_{E_{min}}^{E_{\mathrm{\text{F}}}}\mathrm{\text{d}}E\mathrm{\text{DOS}}(E)E$; a reduction of the DOS near E_F in a tetragonal phase, in conjunction with the conservation of the integral for the number of valence electrons $N_{\mathrm{\text{V}}}={\int }_{E_{min}}^{E_{\mathrm{\text{F}}}}\mathrm{\text{d}}E\mathrm{\text{DOS}}(E)$, often leads to a lower band energy and, thus, to a lower total energy for the tetragonal phase than for the cubic phase. As shown in Figure 7, we can find that, under the effect of the tetragonal strain, the energy states near E_F tend to decrease or move to a high energy level. We give two more detailed explanations as follows: (1) as shown in Figures 7A,C–F, we can clearly observe that the local energy states (blue lines) near the Fermi level of the tetragonal L1₀ phase are significantly lower than those of the cubic L2₁ phase (black lines). Thanks to the TDOSs above, the total energy of the system will be released, resulting in cubic–tetragonal transformation; (2) as shown in Figures 7A,C, we find that the peaks (red line) of the cubic structure near the Fermi level disappeared in the tetragonal structure; however, a very small valley at the same energy (see the pink line) occurred. The peak to valley transition of TDOS near the Fermi level also proves that the tetragonal L1₀ structure is more stable for X₂MnTi compounds.

In Figure 8, we also show the PDOSs of each atom in the cubic and tetragonal phases. As shown in Figure 8A, the PDOS of the L2₁-type Ag orbitals is almost located in the energy areas of −4.5 to −6 eV. In this region, the spin-up and spin-down PDOSs of Ag-d are almost symmetrical, reflecting that the contribution of Ag atoms to the total magnetism is relatively small. In the energy range from −1.5 to −4 eV, two large energy peaks, which come from the Mn-d orbitals, can be found in the spin-up channel; however, the DOS in the spin-down is nearly flat. Above the Fermi level, the TDOS in the spin-up channel is coming from the Ti-d orbital, and the TDOS in the spin-down channel is arising from the hybridization between the Ti-d and Mn-d orbitals. A similar phenomenon can also be found in L2₁-type Au₂MnTi as shown in Figure 8B.

As shown in Figures 8C–F, some large peaks can be obviously found below the Fermi level in the spin-up channel for the L2₁-type X₂MnTi (X = Ni, Cu, Pd, Pt) alloys. The formation of these peaks owes to the hybridization between X-d and Mn-d orbitals. For Ni₂MnTi, the energy peak of the Ni-d orbital is larger than that of the Mn-d orbital around −1.2 eV; however, for the other three cases, the energy peaks of the X-d orbital are smaller than those of the X-d orbitals. Above the Fermi level, the TDOS is mainly coming from the Mn-d orbital in the spin-up channel and from the Mn-d and X-d orbitals in the spin-down channel.

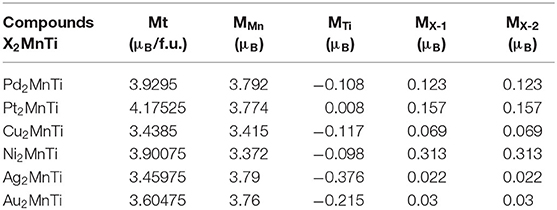
As shown in Figure 8, near the Fermi level, PDOSs of the Mn atom will produce a strong spin splitting in two spin channels, and then result in strong magnetism. Thus, the total magnetism of X₂MnTi is mainly coming from the Mn atoms. We also exhibit the total and atomic magnetic moments in Tables 1, 2.

TABLE 1

Table 1. Total and atomic magnetic moments for cubic L2₁ type X₂MnTi (X = Pd, Pt, Cu, Ni, Ag, Au).

TABLE 2

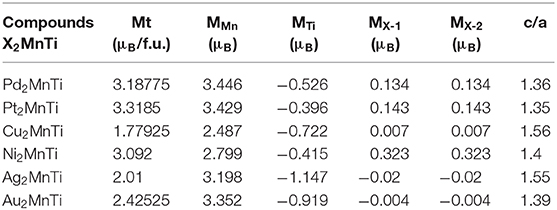
Table 2. Total and atomic magnetic moments, and c / a ratio for tetragonal L1₀ type X₂MnTi (X = Pd, Pt, Cu, Ni, Ag, Au).

Finally, we calculated the phonon spectrum of the X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) tetragonal L1₀ phase by means of the force-constants method using Nanodcal code and the results are collected in Figure 9. In Figure 9, we can clearly see that there are no virtual frequencies in the phonon spectrum of the X₂MnTi, and the absence of virtual frequencies further confirms that their tetragonal L1₀ states are theoretically stable. Unfortunately, the possible L2₁-L1₀ phase transition of X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) has not been studied experimentally, and therefore, a comparison between the theoretical and experimental results cannot be shown in the current work. However, this investigation can help in understanding the physics in all-d-metal alloys. Moreover, we would like to point out that Bain paths are a sophisticated way to investigate the reversible transformation between the L2₁ and L1₀ phases during the tetragonal distortion. This method has been widely used to design new MSMAs, and some designed MSMAs have been experimentally verified, such as the Mn–Ni–Co–Ti system.

FIGURE 9

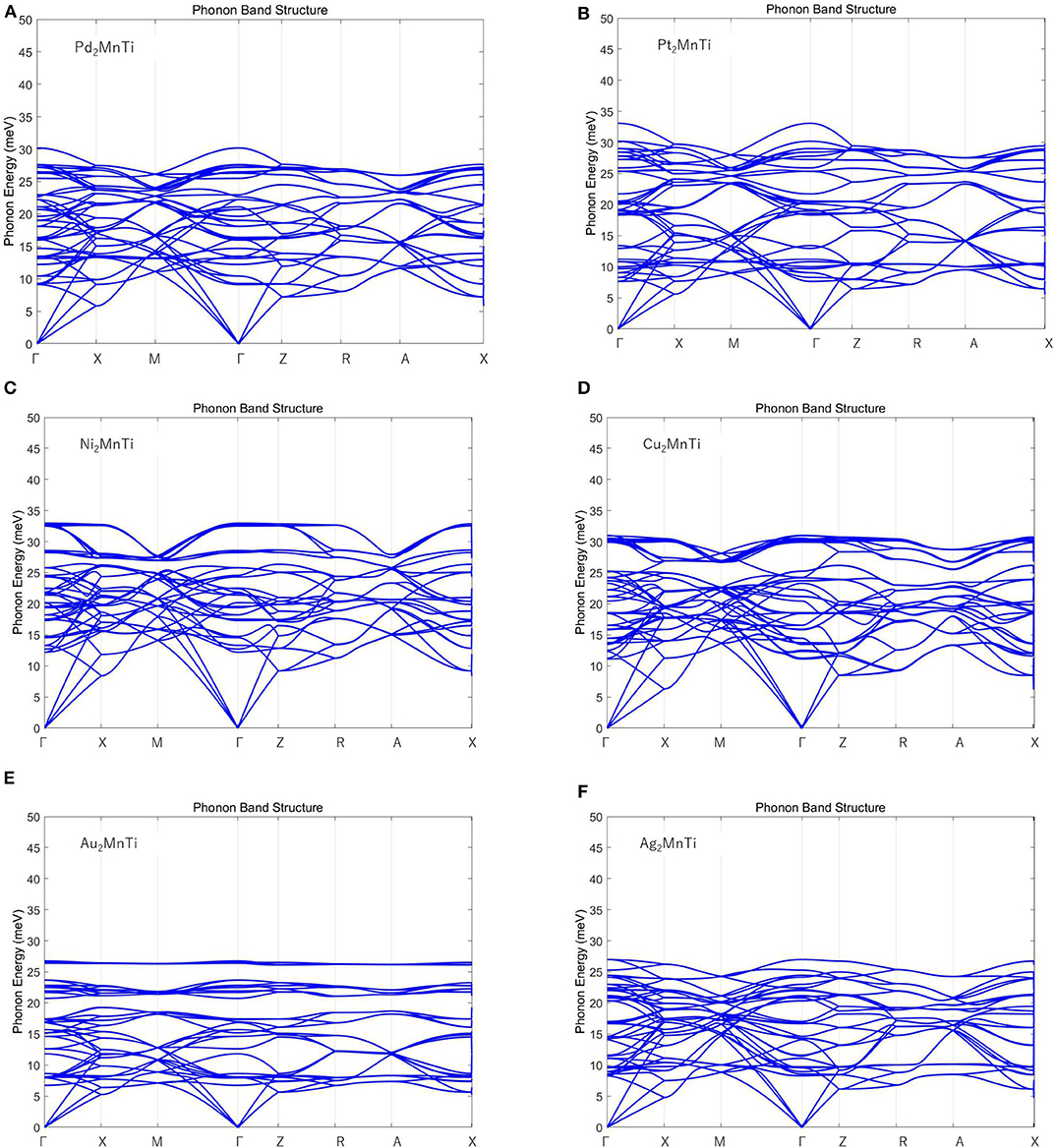
Figure 9. (A–F) Calculated phonon energy of X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) with tetragonal L1₀ phase.

Conclusions

In this study, we investigated the phase transition and electronic structures of X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) compounds based on first-principle calculations. First, we examined the L2₁ and XA competition of Heusler compounds X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni). The results show that the L2₁ type is the most stable ordered structure for these newly designed materials. Based on the L2₁ structure, we also compared the total energies of the L2₁ X₂MnTi system with different magnetic states, i.e., FM and AFM. We found that these compounds have lower ground state energy when in the FM state, that is, the most stable state of X₂MnTi is the FM state under the L2₁ structure. Subsequently, we studied the possible tetragonal transformation of Heusler compounds X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) and found that these materials all feature a stable L1₀ tetragonal phase. The energy difference ΔE_M (E_T – E_C) in X₂MnTi can be adjusted by a uniform strain. By analyzing the DOS diagram, it can be found that the magnetic moment of X₂MnTi mainly comes from Mn atoms, which is due to their strong spin splitting around E_F. The lower TDOS of the tetragonal L1₀ state near the Fermi level can be used to explain the stability of the tetragonal L1₀ state of X₂MnTi. Finally, we gave the phonon spectra of the tetragonal L1₀ phase of X₂MnTi (X = Pd, Pt, Ag, Au, Cu, and Ni) to further prove their stability.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

MW: conceptualization, methodology, software, and writing—original draft preparation. FZ and RK: software and writing—original draft preparation. MK and XW: supervision. All authors contributed to the article and approved the submitted version.

Funding

This study has been funded by the National Natural Science Foundation of China (Grant No. 11704315) and the Fundamental Research Funds for the Central Universities (Grant No. XDJK2019C112).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ahmadian, F., and Salary, A. (2014). Half-metallicity in the Inverse Heusler compounds Sc₂MnZ (Z = C, Si, Ge, and Sn). Intermetallics. 46, 243–249. doi: 10.1016/j.intermet.2013.11.021

CrossRef Full Text | Google Scholar

Aksoy, S., Acet, M., Deen, P. P., Manosa, L., and Planes, A. (2009). Magnetic correlations in martensitic Ni-Mn-based Heusler shape-memory compounds: neutron polarization analysis. Phys. Rev. B. 79:212401. doi: 10.1103/PhysRevB.79.212401

CrossRef Full Text | Google Scholar

Alippi, P., Marcus, P. M., and Scheffler, M. (1997). Strained tetragonal states and Bain paths in metals. Phys. Rev. Lett. 78:3892. doi: 10.1103/PhysRevLett.78.3892

CrossRef Full Text | Google Scholar

Barman, S. R., Banik, S., Shukla, A. K., Kamal, C., and Chakrabarti, A. (2007). Martensitic transition, ferrimagnetism and Fermi surface nesting in Mn₂NiGa. EPL 80:57002. doi: 10.1209/0295-5075/80/57002

CrossRef Full Text | Google Scholar

Birkel, C. S., Douglas, J. E., Lettiere, B. R., Seward, G., Verma, N., Zhang, Y., et al. (2013). Improving the thermoelectric properties of half-Heusler TiNiSn through inclusion of a second full-Heusler phase: microwave preparation and spark plasma sintering of TiNi_1+xSn. Phys. Chem. Chem. Phys. 15:6990. doi: 10.1039/c3cp50918d

PubMed Abstract | CrossRef Full Text | Google Scholar

Cui, Z., Wu, B., Xin, R., Zhou, Q., and Feng, Y. (2019). Enhancing the half-metallicity of equiatomic quaternary Heusler compound CoFeCrGe via atomic doping. Results Phys. 15:102533. doi: 10.1016/j.rinp.2019.102533

CrossRef Full Text | Google Scholar

Downie, R. A., Maclaren, D. A., Smith, R. I., and Bos, J. W. G. (2013). Enhanced thermoelectric performance in TiNiSn-based half-Heuslers. Chem. Commun. 49:4184 doi: 10.1039/c2cc37121a

PubMed Abstract | CrossRef Full Text | Google Scholar

Gao, G. Y., and Yao, K. L. (2013). Antiferromagnetic half-metals, gapless half-metals, and spin gapless semiconductors: The DO₃-type Heusler compounds. Appl. Phys. Lett. 103:232409. doi: 10.1063/1.4840318

CrossRef Full Text | Google Scholar

Ghunaim, R., Ecker, V., Scholz, M., Gellesch, S., and Wurmehl, D. (2018). Carbon nanotube-assisted synthesis of ferromagnetic Heusler nanoparticles of Fe3Ga (Nano-Galfenol). J. Mater. Chem. C 6:1255. doi: 10.1039/C7TC04618A

CrossRef Full Text | Google Scholar

Graf, T., Felser, C., and Parkin, S. S. P. (2011). Simple rules for the understanding of Heusler compounds. Progr. Solid State Chem. 39, 1–50. doi: 10.1016/j.progsolidstchem.2011.02.001

CrossRef Full Text | Google Scholar

GschneidnerJr, K. A., Pecharsky, V. K., and Tsokol, A. O. (2005). Recent developments in magnetocaloric materials. Rep. Progr. Phys. 68:1479. doi: 10.1088/0034-4885/68/6/R04

CrossRef Full Text | Google Scholar

Hafner, J. (2007). Materials simulations using VASP—a quantum perspective to materials science. Comput. Phys. Commun. 177, 6–13. doi: 10.1016/j.cpc.2007.02.045

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, Y., Chen, Z., Kuang, M., Liu, Z., Wang, X., and Wang, X. (2019a). 171 Scandium-based full Heusler compounds: A comprehensive study of competition between XA and L2₁ atomic ordering. Results Phys. 12, 435–446. doi: 10.1016/j.rinp.2018.11.079

CrossRef Full Text | Google Scholar

Han, Y., Wu, M., Feng, Y., Cheng, Z. X., and Wang, X. T. (2019b). Competition between cubic and tetragonal phases in all-d-metal Heusler compounds, X_2−−xMn_1+xV (X = Pd, Ni, Pt, Ag, Au, Ir, Co; x = 1, 0): a new potential direction of the Heusler family. IUCrJ. 6, 465–472 doi: 10.1107/S2052252519004007

PubMed Abstract | CrossRef Full Text | Google Scholar

Hao, Z. P., Liu, R., Fan, Y. H., and Wang, L. L. (2020). First-principles calculations of a new half-metallic Heusler compound FeCrAs. J. Comp Comp. 820:153118. doi: 10.1016/j.jallcom.2019.153118

CrossRef Full Text | Google Scholar

Hou, Z., Wang, W., Xu, G., Zhang, X., Wei, Z., Shen, S., et al. (2015). High electron mobility and large magnetoresistance in the half-Heusler semimetal LuPtBi. Phys. Rev. B. 92:235134. doi: 10.1103/PhysRevB.92.235134

CrossRef Full Text | Google Scholar

Huang, S., Liu, X., Zheng, W., Guo, J., Xiong, R., Wang, Z., et al. (2018). Dramatically improving thermoelectric performance of topological half-Heusler compound LuPtSb via hydrostatic pressure. J. Mater. Chem. A. 6:20069. doi: 10.1039/C8TA07350C

CrossRef Full Text | Google Scholar

Kirievsky, K., Shlimovich, M., Fuks, D., and Gelbstein, Y. (2014). An ab initio study of the thermoelectric enhancement potential in nano-grained TiNiSn. Phys. Chemi. Chem. Phys. 16:20023. doi: 10.1039/C4CP02868F

PubMed Abstract | CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys RevB. 54:11169. doi: 10.1103/PhysRevB.54.11169

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, F., Yang, B., Zhang, J., Han, X., and Yan, Y. (2020). Interface-induced perpendicular magnetic anisotropy in Co₂FeAl/NiFe₂O₄ superlattice: first-principles study. Phys. Chemi. Chem. Phys. 22:716. doi: 10.1039/C9CP05703J

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, J., Zhang, G., Peng, C., Wang, W., and Yang, J. (2019). Magneto-Seebeck effect in Co₂FeAl/MgO/Co₂FeAl: First-principles calculations. Phys. Chemi. Chem. Phys. 21:5803. doi: 10.1039/C8CP07697A

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Z., Jiang, Y., Li, Z., Valdés, C. F. S., and Liang, Z. (2018). Phase transition and magnetocaloric properties of Mn₅₀Ni_42−−xCo_xSn₈ (0 ≤ x ≤ 10) melt-spun ribbons. IUCrJ. 5, 54–66. doi: 10.1107/S2052252517016220

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, S. Y., Chen, M., Yang, X. B., Zhao, Y. J., Wu, S. C., Felser, C., et al. (2015). Theoretical search for half-Heusler topological insulators. Phys. Rev. B. 91:094107. doi: 10.1103/PhysRevB.91.094107

CrossRef Full Text | Google Scholar

Mallick, M. M., and Vitta, S. (2018). Enhancing the thermoelectric performance of a p-type half-Heusler alloy, HfCoSb by incorporation of a band-matched chalcogenide, Cu₂Te. J. Mater. Chem. A. 6:14709. doi: 10.1039/C8TA04372H

CrossRef Full Text | Google Scholar

Miranda, J., and Gruhn, T. (2017). Demixing and ordering in Ni(Ti,Zr)(Sb,Sn) Half-Huesler materials. Phys. Chemi. Chem. Phys. 19:30695. doi: 10.1039/C7CP05513G

PubMed Abstract | CrossRef Full Text | Google Scholar

Muldawer, L. (1966). X-ray Study of Ternary Ordering of the Noble Metals in AgAuZn₂ and CuAuZn₂. J. Appl. Phys. 37, 2062–2066. doi: 10.1063/1.1708670

CrossRef Full Text | Google Scholar

O'Handley, R. C. (1998). Model for strain and magnetization in magnetic shape-memory compounds. J. Appl. Phys. 83, 3263–3270. doi: 10.1063/1.367094

CrossRef Full Text | Google Scholar

Oikawa, K., Ota, T., Ohmori, T., Tanaka, Y., Morito, H., Fujita, A., et al. (2002). Magnetic and martensitic phase transitions in ferromagnetic Ni–Ga–Fe shape memory compounds. Appl. Phys. Lett. 81, 5201–5203. doi: 10.1063/1.1532105

CrossRef Full Text | Google Scholar

Oikawa, K., Wulff, L., Iijima, T., Gejima, F., Ohmori, T., Fujita, A., et al. (2001). Promising ferromagnetic Ni–Co–Al shape memory compound system. Appl. Phys. Lett. 79, 3290–3292. doi: 10.1063/1.1418259

CrossRef Full Text | Google Scholar

Özdemir Kart, S., Uludogan, M., Karaman, I., and Cagin, T. (2008). DFT studies on structure, mechanics and phase behavior of magnetic shape memory alloys: Ni₂MnGa. Phys. Status Solidi (a). 205, 1026–1035. doi: 10.1002/pssa.200776453

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77:3865. doi: 10.1103/PhysRevLett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1998). Perdew, burke, and ernzerhof reply. Phys. Rev. Lett. 80:891. doi: 10.1103/PhysRevLett.80.891

CrossRef Full Text | Google Scholar

Populoh, S., Aguirre, M. H., Brunko, O. C., Galazka, K., Lu, Y., and Weidenkaff, A. (2012). High figure of merit in (Ti, Zr, Hf)NiSn half-Heusler compounds. Scr. Mater. 66, 1073–1076. doi: 10.1016/j.scriptamat.2012.03.002

CrossRef Full Text | Google Scholar

Qawasmeh, Y., and Bothina, H. (2012). Investigation of the structural, electronic, and magnetic properties of Ni-based Heusler alloys from first principles. J. Appl. Phys 111:033905. doi: 10.1063/1.3681286

CrossRef Full Text | Google Scholar

Shigeta, I., Kubota, T., Sakuraba, Y., Kimura, S., and Awaji, S. (2018). Transport properties of epitaxial films for superconductor NbN and half-metallic Heusler compound Co₂MnSi under high magnetic fields. Phys B Cond. Matt. 536, 310–313. doi: 10.1016/j.physb.2017.09.074

CrossRef Full Text | Google Scholar

Silpawilawan, W., Kurosaki, K., Ohishi, Y., Muta, H., and Yamanaka, S. (2017). FeNbSb p-type half-heusler compound: beneficial thermomechanical properties and high-temperature stability for thermoelectrics. J. Mater. Chem. C. 5:6677. doi: 10.1039/C7TC01570D

CrossRef Full Text | Google Scholar

Singh, S., and Gupta, D. C. (2019). Lanthanum based quaternary Heusler compounds LaCoCrX (X = Al, Ga): Hunt for half-metallicity and high thermoelectric efficiency. Results Phys. 13:102300. doi: 10.1016/j.rinp.2019.102300

CrossRef Full Text | Google Scholar

Skaftouros, S., Ozdogan, K., Sasioglu, E., and Galanakis, I. (2013). Search for spin gapless semiconductors: The case of inverse Heusler compounds. Appl. Phys. Lett. 102:022402. doi: 10.1063/1.4775599

CrossRef Full Text | Google Scholar

Suzuki, R. O., and Kyono, T. (2004). Thermoelectric properties of Fe₂TiAl Heusler compounds. J. Comp. Comp. 377, 38–42. doi: 10.1016/j.jallcom.2004.01.035

CrossRef Full Text | Google Scholar

Tan, J. G., Liu, Z. H., Zhang, Y. J., Li, G. T., Zhang, H. G., Liu, G. D., et al. (2019). Site preference and tetragonal distortion of Heusler compound Mn-Ni-V. Results Phys. 12, 1182–1189. doi: 10.1016/j.rinp.2018.12.096

CrossRef Full Text | Google Scholar

Ullakko, K., Huang, J. K., Kantner, C., Ohandley, R. C., and Kokorin, V. V. (1996). Large magnetic-field-induced strains in Ni₂MnGa single crystals. Appl. Phys. Lett. 69, 1966–1968. doi: 10.1063/1.117637

CrossRef Full Text | Google Scholar

Wang, X., Cheng, Z., Liu, G., Dai, X., and Bouhemadou, A. (2017). Rare earth-based quaternary Heusler compounds MCoVZ (M = Lu, Y; Z= Si, Ge) with tunable band characteristics for potential spintronic applications. IUCrJ. 4, 758–768. doi: 10.1107/S2052252517013264

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X., Cheng, Z., Wang, J., Wang, X., and Liu, G. (2016). Recent advances in the Heusler based spin-gapless semiconductors. J. Mater. Chem. C. 4, 7176–7192. doi: 10.1039/C6TC01343K

CrossRef Full Text | Google Scholar

Wang, X. T., Cheng, Z. X., Yuan, H. K., and Khenata, R. (2017). L2₁ and XA ordering competition in titanium-based full-heusler alloys. J. Mater. Chem. C. 5:11559. doi: 10.1039/C7TC03909C

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z. Y., Liu, E. K., Chen, J. H., Li, Y., Liu, G. D., Luo, H. Z., et al. (2015). Realization of multifunctional shape-memory ferromagnets in all-d-metal Heusler phases. Appl. Phys. Lett. 107:022406. doi: 10.1063/1.4927058

CrossRef Full Text | Google Scholar

Wurmehl, S., Fecher, G. H., Kandpal, H. C., Ksenofontov, V., Felser, C., Lin, H. J., et al. (2005). Geometric, electronic, and magnetic structure of Co₂FeSi: Curie temperature and magnetic moment measurements and calculations. Phys. Rev. B. 72:184434. doi: 10.1103/PhysRevB.72.184434

CrossRef Full Text | Google Scholar

Xue, Q. Y., Liu, H. J., Fan, D. D., Cheng, L., Zhao, B. Y., and Shi, J. (2016). LaPtSb: a half-Heusler compound with high thermoelectric performance. Phys. Chemi. Chem. Phys. 18:17912. doi: 10.1039/C6CP03211G

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeleny, M., Sozinov, A., Straka, L., Björkman, T., and Nieminen, R. M. (2014). First-principles study of Co-and Cu-doped Ni₂MnGa along the tetragonal deformation path. Phys. Rev. B. 89:184103. doi: 10.1103/PhysRevB.89.184103

CrossRef Full Text | Google Scholar