- 1Department of Mathematics, University of Seoul, Seoul, South Korea
- 2Department of Mathematics and Statistics, The University of Lahore, Lahore, Pakistan
- 3Department of Humanities and Basic Sciences, Military College of Signals, National University of Science and Technology, Islamabad, Pakistan
- 4Research Institute for Natural Sciences, Hanyang University, Seoul, South Korea
- 5Department of Mathematics, Iran University of Science and Technology, Tehran, Iran
In this article, we provide new formulas to compute the reduced reciprocal randić index, Arithmetic geometric1 index, SK index, SK1 index, SK2 index, edge version of the first zagreb index, sum connectivity index, general sum connectivity index, and the forgotten index using the M-polynomial and finding these topological indices for a boron triangular nanotube. We also elaborate the results with graphical representations.
1. Introduction
A chemical molecular structure is composed of atoms that join together with chemical bonds. This molecular structure is responsible for the chemical, physical, and biological properties of the chemical compound. A chemical graph theory is an important field of science, in which we study the formation and behavior of a chemical structure with the help of graph theory tools.
In graph theory a set of points is referred as graph G. These points are known as vertices. An edge is a line joining the two vertices. The number of edges that coincide at a vertex is considered to be the degree of the vertex and is represented as dj and the degree of the edge is defined as djk = dj + dk − 2. E(G) represents the set of edges and V(G) shows the set of vertices. In the chemical graph, an atom of the molecule is represented with the vertex of the graph, and the bond is considered as an edge.
There are many uses of chemical graph theory in different subjects, such as quantum chemistry, computer sciences, biology, stereochemistry, and engineering, which is explained by Gutman and Trinajstić (1972), Balaban (1985), Trinajstiéc (1992), Shirinivas et al. (2010), and Vergniory et al. (2017). With the help of chemical graph theory techniques, we convert a chemical molecule into a real number, which is referred to as a topological index and the molecular structure is examined through the topological indices. In this study, we try to develop mathematical methods for the calculation of topological indices. With the help of topological indices, Hosamani et al. (2017) studied the different physical properties like the molar volume, boiling points, and molar refraction, of the molecular structure. Rouvray (1986) and Ramakrishnan et al. (2013) describe the biological behavior, such as nutritive, stimulation of cell growth, toxicity, and pH regulation, of the chemical species, which are also characterized through topological indices.
These topological indices are widely used in chemical graph theory to explain the different properties of the chemical structure. The carbon-hydrogen bond is not considered during the computation of topological indices because this bond does not have a serious effect on the properties of the chemical compound. During the QSAR and QSPR analysis, topological indices are widely used.
Gutman et al. (2014) formulated a reduced reciprocal randić index defined as . Shigehalli and Kanabur (2015) presented the arithmetic geometric1 index defined as . Shigehalli and Kanabur (2016) also introduced the new indices defined as SK index = , SK1 index = , and SK2 index = . Miličević et al. (2004) presented the first Zagreb index in term of edge degree defined as . Du et al. (2011) formulated the general sum-connectivity index defined as and . Gutman and Furtula (2015) presented the forgotten index represented with F and defined as .
2. Boron Triangular Nanotube
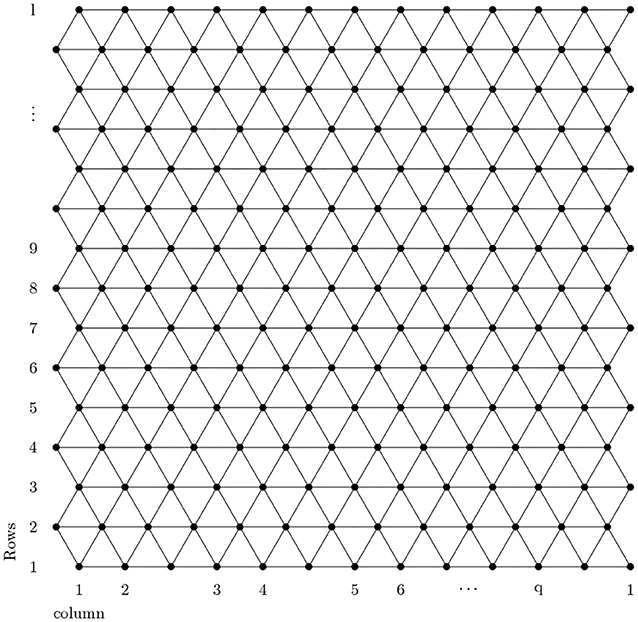
The analysis of a chemical molecular structure smaller than 100 nm is known as nanotechnology. Nanomaterials have many applications in different fields of nanoscience. The boron triangular nanotube BTntlq is a well-known structure in nanomaterials with a wide range of applications in medicine, electronics, and computers as discussed by Menuel (2010), Bezugly et al. (2011), and Liu et al. (2018). With the help of this, experts are expected to revolutionize the world. The formation of the boron triangular nanotube is formed by a 2-D boron triangular nanosheet consisting of l rows and q columns. The first and the last column of the 2-D boron triangular nanosheet are connected to form a boron triangular nanotube.
A detailed analysis of Figures 1, 2 shows that there are only two types of vertex present in BTntlq. One which has a degree of four and the other has a degree of six. Now count the edges with smaller dimension and then by generalization and we obtain Table 1.
3. M-Polynomial
An algebraic polynomial has the ability to elaborate the chemical molecular structure. M-polynomial is such a polynomial that represents the graph. Deutsch and Klawzar (2015) formulated the M-polynomial and defined as . Where δ represents the minimum degree of the vertex belonging to the vertex set V(G), Δ represents the maximum degree of the vertex belonging to the vertex set V(G) and mυv(G) is the total number of edges jk ∈ E(G) such that {dj, dk} = {u, υ}.
Deutsch and Klawzar (2015) introduced M-polynomial and in the same article nine topological indices closed formulas are given via m-polynomial. Some indices are calculated by Munir et al. (2016). In the past, Kang et al. (2018), Afzal et al. (2020a,b), Cancan et al. (2020a,b), and Khalaf et al. (2020) used these formulas to compute topological indices via M-polynomial and a lot of work has been done in this area. One more set of nine topological indices has been computed by Afzal et al. (2020c). The F-index is also computed by Mondal et al. (2020). In this article, we formulated a new set of nine topological indices shown in Table 2. These formulas are used to compute the topological indices via M-polynomial for the chemical structure. This formulation is a useful achievement in the field the topological indices and opens a new research field. We apply the newly formulated indices on BTntlq.
4. M-Polynomial of Boron Triangular Nanotube
Theorem 4.1. Let BTntlq be a Boron triangular nanotube where lq is the dimension of the BTntlq then M-polynomial of BTntlq is
Proof. Let BTntlq be a boron triangular nanotube then by using Figures 1, 2 and Table 1 the edge partition of boron triangular nanotube is consisting of three type of sets. The first edge partition represented with E1 contains 3q edges, in which dj and dk have the same value equal to 4. The second edge partition referred to as E2 consists of 6q edges jk, in which the value of dj is 4 and value of dk is 6. The third edge partition named as E3 contains edges jk, in which dj = dk = 6. Now, by using the definition of M-polynomial, we have
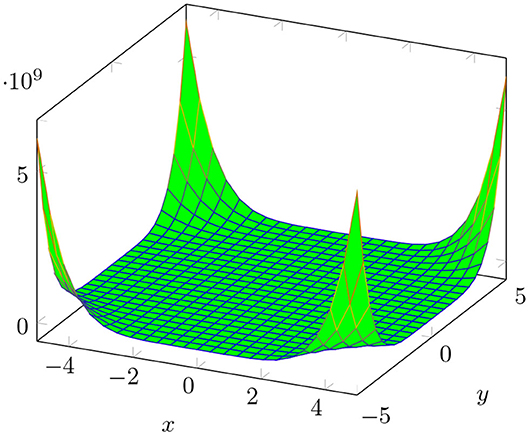
The plot of M[BTntlq; x, y] is shown in Figure 3.
5. Topological Indices of Boron Triangular Nanotube
Theorem 5.1. Let BTntlq be a boron triangular nanotube and
then
1.
2.
3. SK[BTntlq] = 27ql − 30q,
4. SK1[BTntlq] = 81ql − 120q,
5. SK2[BTntlq] = 162ql − 234q,
6. EM1[BTntlq] = 450ql − 708q,
7.
8.
9. F[BTntlq] = 324ql − 456q.
Proof. Let M[BTntlq; x,y] = g(x,y)
1.
2.
3.
SK[BTntlq] = 27ql − 30q.
4.
SK1[BTntlq] = 81ql − 120q.
5.
SK2[BTntlq] = 162ql − 234q.
6.
EM1[BTntlq] = 450ql − 708q.
7.
8.
9.
F[BTntlq] = 324ql − 456q.
Figure 4 shows a graphical analysis of topological indices of BTntlq. With the help of these graphs, we observe the behavior of the topological indices regarding the different parameters involved. These visualizations are shown to be identical but have different gradients.
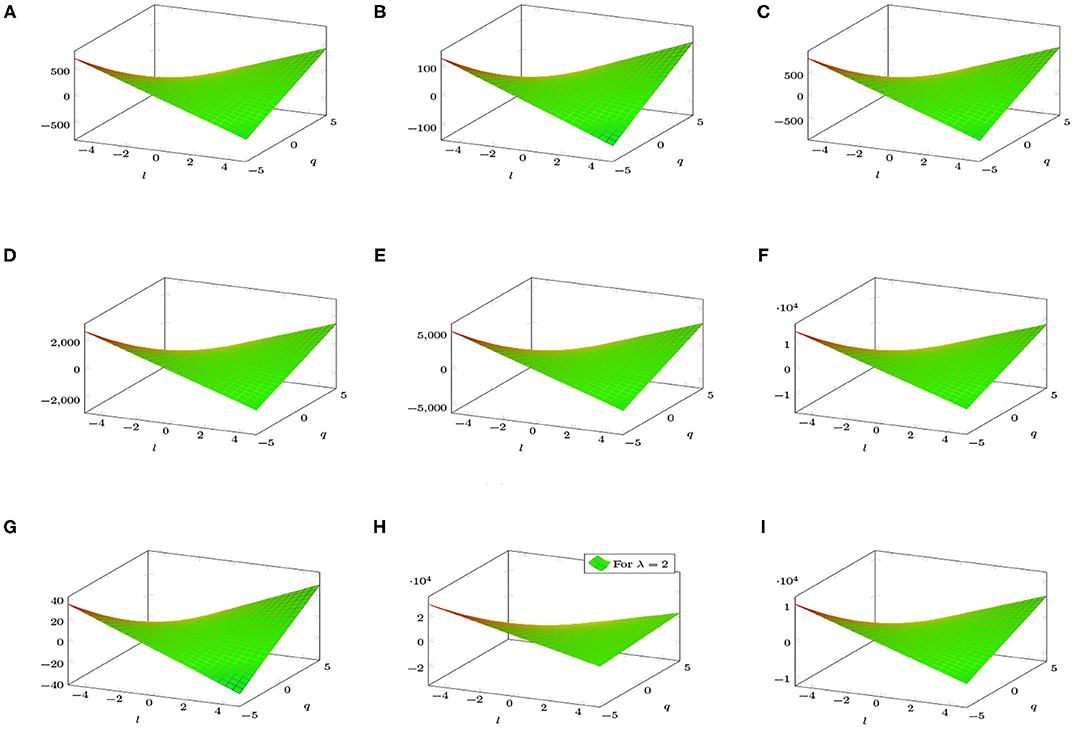
Figure 4. 3D plots of topological indices of BTntlq. (A) Reduced reciprocal randić index. (B) Arithmetic geometric1 index. (C) SK index. (D) SK1 index. (E) SK2 index. (F) Edge version of first Zagreb index. (G) Sum connectivity index. (H) General sum connectivity index. (I) Forgotten index.
6. Conclusion
The formulation of new formulas, placed in Table 2, to compute the topological indices for the molecular structure via M-polynomial lead to a new era in the computational field. In this research work, we compute M(BTntlq; x, y) and with the help of this polynomial, we find the various topological invariants given in Table 2. We also presented the graphical presentation of M-Polynomial and topological indices. This visualization helps us to understand results against parameters.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
DS: supervision, resources, and funding. SH: writing original draft, computations, and graphs. FA: editing, proof reading, and methodology. CP: investigation, validation, and funding. DA: conceptualization, supervision, and programming. MF: resources, proof reading, and validation. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Afzal, D., Hussain, S., Aldemir, M., Farahani, M., and Afzal, F. (2020a). New degree-based topological descriptors via m-polynomial of boron α-nanotube. Eurasian Chem. Commun. 2, 1117–1125. doi: 10.22034/ecc.2020.254614.1092
Afzal, F., Hussain, S., Afzal, D., and Hameed, S. (2020b). M-polynomial and topological indices of zigzag edge coronoid fused by starphene. Open Chem. 18, 1362–1369. doi: 10.1515/chem-2020-0161
Afzal, F., Hussain, S., Afzal, D., and Razaq, S. (2020c). Some new degree based topological indices via M-polynomial. J. Inform. Optimiz. Sci. 41, 1061–1076. doi: 10.1080/02522667.2020.1744307
Balaban, A. T. (1985). Applications of graph theory in chemistry. J. Chem. Inform. Model. 25, 334–343. doi: 10.1021/ci00047a033
Bezugly, V., Kunstmann, J., Grundkötter-Stock, B., Frauenheim, T., Niehaus, T., and Cuniberti, G. (2011). Highly conductive boron nanotubes: transport properties, work functions, and structural stabilities. ACS Nano 5, 4997–5005. doi: 10.1021/nn201099a
Cancan, M., Afzal, D., Hussain, S., Maqbool, A., and Afzal, F. (2020a). Some new topological indices of silicate network via M-polynomial. J. Discrete Math. Sci. Cryptogr. 23, 1157–1171. doi: 10.1080/09720529.2020.1809776
Cancan, M., Ediz, S., Mutee-Ur-Rehman, H., and Afzal, D. (2020b). M-polynomial and topological indices poly (EThyleneAmidoAmine) dendrimers. J. Inform. Optimiz. Sci. 41, 1117–1131. doi: 10.1080/02522667.2020.1745383
Deutsch, E., and Klawzar, S. (2015). M-polynomial and degree-based topological indices. Iran. J. Math. Chem. 6, 93–102.
Du, Z., Zhou, B., and Trinajstić, N. (2011). On the general sum-connectivity index of trees. Appl. Math. Lett. 24, 402–405. doi: 10.1016/j.aml.2010.10.038
Gutman, I., and Furtula, B. (2015). A forgotten topological index. J. Math. Chem. 53, 1184–1190. doi: 10.1007/s10910-015-0480-z
Gutman, I., Furtula, B., and Elphick, C. (2014). Three new/old vertex–degree–based topological indices. MATCH Commun. Math. Comput. Chem. 72, 617–632.
Gutman, I., and Trinajstić, N. (1972). Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem. Phys. Lett. 17, 535–538. doi: 10.1016/0009-2614(72)85099-1
Hosamani, S., Perigidad, D., Jamagoud, S., Maled, Y., and Gavade, S. (2017). QSPR analysis of certain degree based topological indices. J. Stat. Appl. Probabil. 6, 361–371. doi: 10.18576/jsap/060211
Kang, S. M., Nazeer, W., Gao, W., Afzal, D., and Gillani, S. N. (2018). M-polynomials and topological indices of dominating David derived networks. Open Chem. 16, 201–213. doi: 10.1515/chem-2018-0023
Khalaf, A. J. M., Hussain, S., Afzal, D., Afzal, F., and Maqbool, A. (2020). M-polynomial and topological indices of book graph. J. Discrete Math. Sci. Cryptogr. 23, 1217–1237. doi: 10.1080/09720529.2020.1809115
Liu, J.-B., Shaker, H., Nadeem, I., and Hussain, M. (2018). Topological aspects of boron nanotubes. Adv. Mater. Sci. Eng. 12:134. doi: 10.1155/2018/5729291
Menuel, P. (2010). Computational aspects of carbon and boron nanotubes. Molecules 15, 8709–8722. doi: 10.3390/molecules15128709
Miličević, A., Nikolić, S., and Trinajstić, N. (2004). On reformulated Zagreb indices. Mol. Divers 8, 393–399. doi: 10.1023/B:MODI.0000047504.14261.2a
Mondal, S., De, N., and Pal, A. (2020). Topological properties of networks using M-polynomial approach. Konuralp J. Math. 8, 97–105.
Munir, M., Nazeer, W., Rafique, S., and Kang, S. M. (2016). M-polynomial and related topological indices of nanostar dendrimets. Symmetry 8:97. doi: 10.3390/sym8090097
Ramakrishnan, S., Senbagamalar, J., and Babujee, J. B. (2013). Topological indices of molecular graphs under specific chemical reactions. Int. J. Comput. Algorithm 2, 68–74. doi: 10.20894/IJCOA.101.002.001.019
Rouvray, D. H. (1986). The prediction of biological activity using molecular connectivity indices. Acta Pharma. Jugoslavica 36, 239–252.
Shigehalli, V., and Kanabur, R. (2015). Arithmetic-geometric indices of path graph. J. Comp. Math. Sci. 6, 19–24.
Shigehalli, V., and Kanabur, R. (2016). Computing degree based topological indices of polyhex nanotube. J. Math. Nanosci. 6, 47–55. doi: 10.22061/JMNS.2016.525
Shirinivas, S. G., Vetrivel, S., and Elango, N. M. (2010). Applications of graph theory in computer science an overview. Int. J. Eng. Sci. Technol. 2, 4610–4621.
Keywords: graph, chemical graph theory, M-polynomial, boron triangular nanotube, topological indices
Citation: Shin DY, Hussain S, Afzal F, Park C, Afzal D and Farahani MR (2021) Closed Formulas for Some New Degree Based Topological Descriptors Using M-polynomial and Boron Triangular Nanotube. Front. Chem. 8:613873. doi: 10.3389/fchem.2020.613873
Received: 05 October 2020; Accepted: 09 December 2020;
Published: 03 February 2021.
Edited by:
Nino Russo, University of Calabria, ItalyReviewed by:
Muhammad Jamil, Riphah International University, PakistanSk. Md. Abu Nayeem, Aliah University, India
Copyright © 2021 Shin, Hussain, Afzal, Park, Afzal and Farahani. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Farkhanda Afzal, ZmFya2hhbmRhQG1jcy5lZHUucGs=
 Dong Yun Shin1
Dong Yun Shin1 Farkhanda Afzal
Farkhanda Afzal Choonkil Park
Choonkil Park Deeba Afzal
Deeba Afzal Mohammad R. Farahani
Mohammad R. Farahani