Bandgap Engineering and Near-Infrared-II Optical Properties of Monolayer MoS2: A First-Principle Study

The fluorescence-based optical imaging in the second near-infrared region (NIR-II, 1,000–1,700 nm) has broad applications in the biomedical field, but it is still difficult to find new NIR-II fluorescence materials in the two dimension. As a crucial characteristic of the electronic structure, the band structure determines the fundamental properties of two-dimensional materials, such as their optical excitations and electronic transportation. Therefore, we calculated the electronic structures and optical properties of different crystalline phases (1T phase and 2H phase) of pure monolayer MoS₂ films and found that the 1T phase has better absorption and thus better fluorescence in the NIR-II window. However, its poor stability makes the 1T-phase MoS₂ less useful in vivo bioimaging. By introducing vacancy defects and doping with foreign atoms, we successfully tuned the bandgap of the monolayer 2H-MoS₂ and activated it in the NIR-II. Our results show that by engineering the vacancy defects, the bandgap of the 2H phase can be tailored to around 1 eV, and there are three candidates of vacancy structures that exhibit strong absorption in the NIR-II.

Introduction

The NIR-II fluorescence probe has attracted much attention in recent years. Compared with the visible light (400–700 nm) and the NIR-I (700–900 nm) imaging, the NIR-II (1,000–1,700 nm) imaging has longer fluorescence wavelength and stronger penetrating ability, which has shown great potential in tumor diagnosis and in vivo in situ imaging. Since Dai et al. discovered that carbon nanotubes (Jiao et al., 2009; Welsher et al., 2009), fluorescent quantum dots (Hong et al., 2012), small molecules (Antaris et al., 2016), and rare earth metals have good fluorescence and biocompatibility in the NIR-II window (Sun et al., 2019), the development of this technology has been widely promoted (Hong et al., 2012; Fan et al., 2018). With the rapid development of imaging equipment and technology in the NIR-II (Zhang et al., 2016; Liu et al., 2019), finding new fluorescence material in the NIR-II is still a pressing task, which requires us to find semiconductor materials with a bandgap less than 1.0 eV. It is well-known that two-dimensional materials have obvious advantages in bandgap modulation; however, in recent years, there have been very few theoretical works studying the fluorescence materials in the NIR-II. As a result, searching for the well-behaved two-dimensional materials relies more on perceptions and arduous experiments. Among these efforts, layered transition metal dichalcogenides (TMDs) (Soares et al., 2020) have been widely studied in recent years due to their unique atomic structure, band structure, and optical properties (Wang et al., 2012). Thereinto, MoS₂ with natural bandgap (1.2∼1.8 eV) come to the fore. In the benefit of that, all the TMDs₂-MX₂ (M = Mo, W; X = S, Se) possess similar electronic structures and thus similar properties in photoelectric and catalytic processes; MoS₂ is usually studied as a representative for TMDs (Hong et al., 2017).

MoS₂ has three types of crystal structures: 1T (trigonal), 2H (hexagonal), and 3R (rhombohedral). The 1T phase is metallic, while the 2H and the 3R are semiconductors. Besides, the 2H phase is the most stable one (Xu et al., 2016). 1T and 3R are metastable and can be converted back to the 2H phase (Chaste et al., 2020) under the conditions of heating and annealing (Geng et al., 2016; Byrley et al., 2019). As shown in Figure 1, a monolayer MoS₂ film is composed of two layers of sulfur atoms sandwiched by one layer of Mo atoms (Helveg et al., 2000). The atoms of different layers are bonded by strong covalent bonds. The thickness of the monolayer MoS₂ is about 6.5 Å. The upper and lower S atoms of the 2H phase overlap completely in the direction perpendicular to the film, while the upper and lower S atoms of the 1T phase do not overlap at all.

FIGURE 1

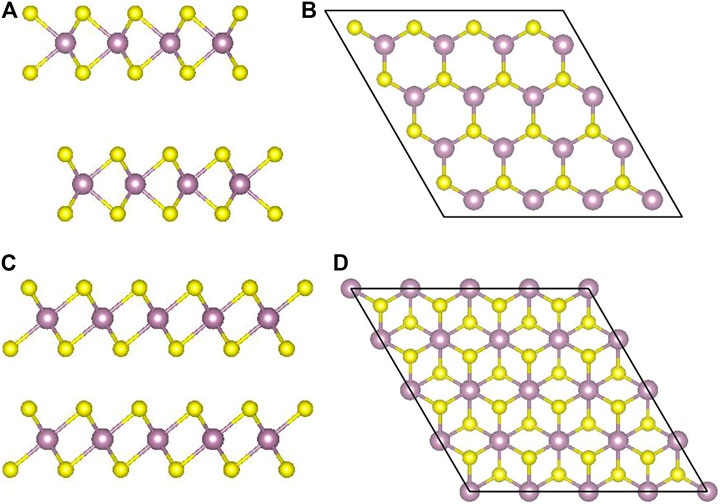
FIGURE 1. 1T- and 2H-phase MoS₂: (A) and (B) the layered structure of 2H-MoS₂ and the top view in z direction; (C) and (D) the same for 1T-MoS₂.

The layered nature of bulk MoS₂ makes it easy to slide subjected to external friction (Zhang et al., 2009). Therefore, 2H-MoS₂ has been widely used in the field of lubricants (Lahouij et al., 2012) and hydrodesulfurization catalysts (Gutiérrez et al., 2014). When reducing to single-layer structures, the bandgap of MoS₂ increases from ∼1.2 to ∼1.8 eV and changes from indirect bandgap to direct, which indicates that the layered MoS₂ bandgap is adjustable and has potential applications in optoelectronics (Steinhoff et al., 2015). Because of a direct bandgap of ∼1.8 eV, monolayer MoS₂ has great applications in photodetectors and plasma devices. Moreover, as an attractive nanomaterial for photothermal cancer therapy, 1T-phase MoS₂ is a highly effective reagent in photoacoustic imaging (PAI)–guided photothermal therapy (PTT) in the NIR-II window (Zhou et al., 2020). Under 1,064 nm laser irradiation, it can effectively ablate cancer cells in vitro and tumors in vivo. However, monolayer 1T-MoS₂ is less stable than the 1H phase. Therefore, it is necessary to find a way to engineer 1H-MoS₂, so that it can be used for fluorescence in the NIR-II. At present, different point defects and antisite defects (Nakayasu et al., 2019) have been observed experimentally. In the study of Zhou et al., point vacancies are more common than antisite defects, which is consistent with their DFT calculations, and mono-vacancy V_S (only one S atom missing from the sulfur sublattice site) has the lowest formation energy. And V_MoS2 (containing a V_Mo and V_S2 pair), V_MoS3 (vacancy complex of Mo atom and nearby three S atoms), and V_MoS6 (vacancy complex of Mo atom nearby three S pairs) have relatively poor structural stability due to its higher formation energy (Zhou et al., 2013). Mann et al. studied MoS_2(1-x) Se_2x doped with different concentrations of Se and concluded that the bandgap decreases linearly with increasing Se-doping concentration with the tuning window ranging from 1.85 eV (pure MoS₂) to 1.55 eV (pure MoSe₂) (Li et al., 2014), which provides a feasible way to manipulate of the bandgap of MoS₂ (Mann et al., 2014). Dumcenco et al. reported single-layer Mo_1-xW_xS₂ semiconductor alloy with a bandgap ranging from 1.82 eV to 1.99 eV, not significantly depending on the concentration of W (Dumcenco et al., 2013). Inspired by previous studies (Zeng et al., 2020), we calculated the electronic structures and optical properties of 1T and 2H phases of monolayer MoS₂ films by the first-principle method. By adjusting the position of the vacancy defects and dopings, we predict three possible structures that can be applied in the NIR-II, which provides a potential direction for experimentally studying NIR-II fluorescence of single-layer MoS₂ films.

The article is organized as below. Theories reviews basic steps in calculating the optical properties from the first-principal methods. Results and Discussion presents our results and discussions on band structures, ground-state energies, and absorption spectra for different defects and dopings. The technique details are listed in Methods.

Theories

In this section, we will discuss the basic concepts of how to get the absorption spectra of two-dimension materials from the first-principle calculations. Although one can get the plasma frequency and the dynamic dielectric function from VASP directly and the absorption spectra seem to be obtained straightforwardly from the imaginary part of the dielectric function, special attention should be paid to the metallic phase. According to the band structure as shown in Figure 2B, 1T-phase monolayer MoS₂ behaves like a metal. Therefore, its dynamic dielectric function consists of two parts: one from the interband transition, which can be obtained from the optical calculation module in VASP, the other from the intraband transition, which requires some extra steps recapitulated as below.

FIGURE 2

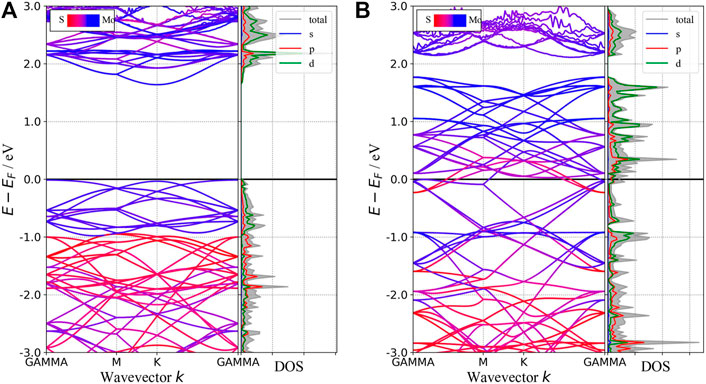
FIGURE 2. Band structures and pDOS of 2H-MoS₂(A) and 1T-MoS₂(B). The blue (red) curves are mainly contributed by atom Mo (S) in the band structure. The shadow area in the pDOS refers to the total DOS, and the solid lines of different colors refer to the projection on different orbitals indicated by the legend inside the figure.

For metals, the optical complex dielectric function consists of interband and Drude-like intraband contributions (Guan et al., 2015):

$\epsilon \left(\omega \right)={\epsilon }^{\mathrm{int}ra}\left(\omega \right)+{\epsilon }^{\mathrm{int}er}\left(\omega \right).(1)$

The imaginary part of the interband dielectric function is given by the first-principle calculations as follows (Gajdoš et al., 2006)

${\epsilon }_{\alpha \beta }^{\left(2\right)}\left(\omega \right)=\frac{4{\pi }^2{e}^2}{\Omega }\underset{q\to 0}{\lim }\frac{1}{q^2}\times {\displaystyle \sum _{c,v,\overrightarrow{k}}2w_k\delta \left(E_c-E_v-\omega \right){\left|\langle c|\widehat{e}\cdot \overrightarrow{q}|v\rangle \right|}^2},(2)$

where $\widehat{e}$ is the polarization direction of the photon, $\overrightarrow{q}$ is the electron momentum operator, and the $\langle c|\widehat{e}\cdot \overrightarrow{p}|v\rangle$ is the optical transition amplitude from the valence bands $\left(v\right)$ to the conduction bands $\left(c\right)$. $\alpha$ and $\beta$ refer to Cartesian coordinates, $\Omega$ is the volume of the unit cell, and the integration over $\overrightarrow{k}$ is performed by summation over special k-points with a corresponding weighting factor $w_k$. The real part of the interband dielectric function ${\epsilon }_1\left(\omega \right)$ is obtained from the imaginary part ${\epsilon }_2\left(\omega \right)$ based on the usual Kramers–Kronig transformation,

${\epsilon }_1\left(\omega \right)=1+\frac{2}{\pi }P{\displaystyle {\int }_{\text{0}}^{\infty }\frac{{\epsilon }_{\alpha \beta }^{\left(2\right)}\left(\omega \prime \right)\omega \prime }{\omega {\prime }^2-{\omega }^2+i\eta }d\omega \prime },(3)$

where $P$ denotes the principal value and $\eta$ is the complex shift parameter. The intraband contribution is usually modeled by the Drude model (Olmon et al., 2012):

$\begin{array}{l}{\epsilon }_1\left(\omega \right)=1-\frac{{\omega }_p^2{\tau }_D^2}{1+{\omega }^2{\tau }_D^2},\\ {\epsilon }_2\left(\omega \right)=\frac{{\omega }_p^2{\tau }_D}{\omega \left(1+{\omega }^2{\tau }_D^2\right)},\end{array}(4)$

where ${\tau }_D$ is electron relaxation time and ${\omega }_p$ is intraband plasma frequency. ${\omega }_{p,\alpha \beta }$ is the plasma frequency tensor which can be calculated using (Harl, 2008):

${\omega }_{p,\alpha \beta }^2=-\frac{4\pi e^2}{\Omega }{\displaystyle \sum _{nk}2\frac{\partial f\left({\epsilon }_n\right)}{\partial {\epsilon }_n}}\left(e_{\alpha }\frac{\partial {\epsilon }_n\left(k\right)}{\partial k}\right)\left(e_{\beta }\frac{\partial {\epsilon }_n\left(k\right)}{\partial k}\right).(5)$

In this study, we took into account the electron–electron scattering only (${\tau }_D={\tau }_{ee}$) and neglected the other scattering processes, such as those involving phonon, impurity, and defects. After the GW approximation (Shishkin and Kresse, 2006; Shishkin and Kresse, 2007), the inverse of the electron relaxation time (electron relaxation rate) (Ogawa and Petek, 1996) can be obtained from the imaginary part of the electron self-energy $\mathrm{Im}\sum \left({\epsilon }_j\right)$ (Schöne, 2007; Cazzaniga, 2012):

${\tau }_{ee}^{-1}\left(j\right)=2\left|\langle j|\mathrm{Im}\sum \left(E_j\right)|j\rangle \right|=2Z_j\left|\langle j|\mathrm{Im}\sum \left({\epsilon }_j\right)|j\rangle \right|\text{,}(6)$

where $j$ represents the Kohn–Sham eigenstate, and $Z_j$ is the quasi particle correction factor given by GW calculation, $Z_j^{-1}=1-\langle j|{\left|\frac{\partial \sum \left(\omega \right)}{\partial \omega }\right|}_{\omega ={\epsilon }_j}|j\rangle$.

Different from bulk materials, the absorbance of two-dimensional materials is defined by (Wang et al., 2019):

$A\left(\omega \right)=\mathrm{Re}{\sigma }_{2D}\left(\omega \right)/{\epsilon }_{0}c\text{.}(7)$

The in-plane 2D optical conductivity is directly related to the corresponding ${\sigma }_{3D}\left(\omega \right)$ component through ${\sigma }_{2D}\left(\omega \right)=L{\sigma }_{3D}\left(\omega \right)$, where $L$ is the slab thickness in the simulation cell. Based on the Maxwell’s equations, the 3D optical conductivity can be expressed as below:

${\sigma }_{3D}\left(\omega \right)=i\left[1-\epsilon \left(\omega \right)\right]{\epsilon }_0\omega \text{.}(8)$

Combining with the above equation, we obtained the absorption spectra $A\left(\omega \right)$ of two-dimensional materials by $A\left(\omega \right)=\frac{L\omega {\epsilon }_2}{c}$.

Results and Discussion

1T-MoS₂ and 2H-MoS₂

In this subsection, we will compare the band structures and the optical properties of monolayers 1T-MoS₂ and 2H-MoS₂ without defects and doping. The band structures and density of states (DOS) of 1T and 2H phases are shown in Figure 2. It shows that monolayer 2H-MoS₂ remains a semiconductor as the bulk MoS₂, while monolayer 1T-MoS₂ turns into a metal, whose states near the Fermi surface mainly come from the Mo–d orbit and the S–p orbit. The 2H-phase monolayer shows a direct bandgap of 1.65 eV, close to the calculated result of Kan et al. (1.67 eV) and Johari et al. (1.68 eV) (Johari and Shenoy, 2012; Kan et al., 2014). The results are in the same bandgap as GGA-PBE predicts (Komsa and Krasheninnikov, 2015), and this ensures the rationality of the calculated parameters in this study. However, since the DFT-GGA tends to underestimate the bandgap, our result is lower than the experimental value ∼1.8 eV (Kam and Parkinson, 1982; Mak et al., 2010).

The optical properties of the two phases are shown in Figure 3. 2H-MoS₂ shows peaks at 1.89 eV and 2.82 eV in the imaginary part of the complex dielectric functions (Figure 3A), which is mainly due to the electron transition between the highest valence band Mo–3d orbit and the conduction bands Mo–3d and S–p orbitals, according to the partial density of states (pDOS) as shown in Figure 2. The monolayer 2H-MoS₂ imaginary part of the dielectric functions peaks at 1.89 eV and matches the lower absorption resonance in both its position and width. Therefore, we attribute the photoluminescence of monolayer MoS₂ to direct-gap luminescence. These findings are in good agreement with the experimental results of Mak et al. (Mak et al., 2010) and previous calculations (Zeng et al., 2020) for monolayer MoS₂ (Kumar and Ahluwalia, 2012). The transition of the 1T phase occurs at a lower energy of 1.12 eV, corresponding to the Mo–d and S–p transitions. The characteristic peaks in the dielectric functions for each phase lead to the distinct absorption spectra in Figure 3B. The 2H phase mainly absorbs light with a wavelength below 700 nm, while the 1T phase shows a strong absorption in the NIR-II window and an absorption peak at 1050 nm, which is consistent with the experimental conclusion of Zhou et al. (Zhou et al., 2020). However, the 1T phase is less stable than the 2H phase. Therefore, it will be useful to find a way to modify the band structure of the 2H phase while keeping its stability. We found that the introduction of vacancy defects or doping of foreign atoms into the 2H phase shows great promise for its application in the NIR-II window. The results will be presented in rest of the article.

FIGURE 3

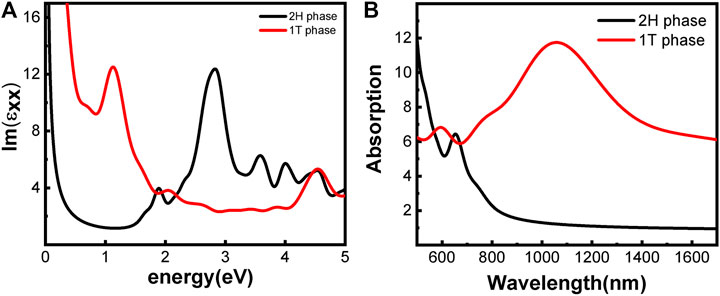
FIGURE 3. Optical properties of monolayer MoS₂ without defect and doping: (A) imaginary part of the dielectric function; (B) absorption spectra. The phases are indicated by color.

2H-MoS₂ With Vacancy and Doping

S-Vacancy Structures

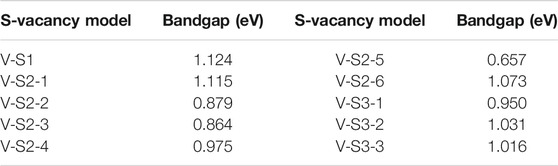
Point defects in monolayer MoS₂ are attractive because defects play a crucial role in manipulating its electrical and optical properties. Therefore, we designed the supercell of 2H-MoS₂ with different numbers of S-vacancy, whose configurations have been plotted in Figure 4. Figure 4A shows single S-vacancy structure, and Figures 4C,D,F show two S-vacancies in the same atomic plane. Figures 4B,G,H show two S-vacancy structures in different atomic planes. Figure 4E compares the ground-state energy of the six configurations of double S-vacancies, demonstrating the structure stability, indicating that configurations V-S2-1, V-S2-2, and V-S2-6 are relatively stable, compared to V-S2-3, V-S2-4, and V-S2-5. Figure 4J shows triple S-vacancy structures in the same plane. Figures 4K,L show the triple S-vacancy structures in different planes. Figure 4I compares the ground-state energy of the three configurations of triple S-vacancies and indicates configuration V-S3-2 is the most stable among the three, while V-S3-1 is the worst. To explore the influence of S-vacancy on the electronic structure of the system, we calculated the band and pDOS, as shown in Figure 5, and found that different S-vacancy defects induce different energy levels contributed by Mo–d and S–p in the bandgap relative to the pure MoS₂, which are distributed around 1 eV above the Fermi energy. In addition, it is noted that the density of states of the defect states in the bandgap increases with the increasing number of vacancies. The introduction of vacancies significantly reduces the bandgap. We also summarized the width of bandgap and the number of vacancies in Table 1 but found there is no direct relation between the two.

FIGURE 4

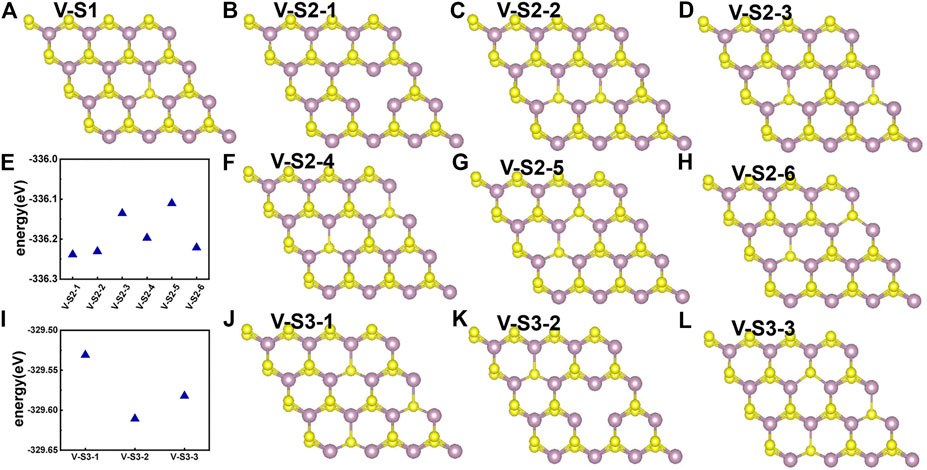
FIGURE 4. Different S-vacancy defect structures of 2H-MoS₂, rotated by an angle to distinguish the two S layers: (A) single S-vacancy; (B–D) and (F–H) six types of configuration for double S-vacancies; (J–L) three types of configuration for triple S-vacancies; (E) and (I) compares the ground-state energy of double and triple S-vacancies.

FIGURE 5

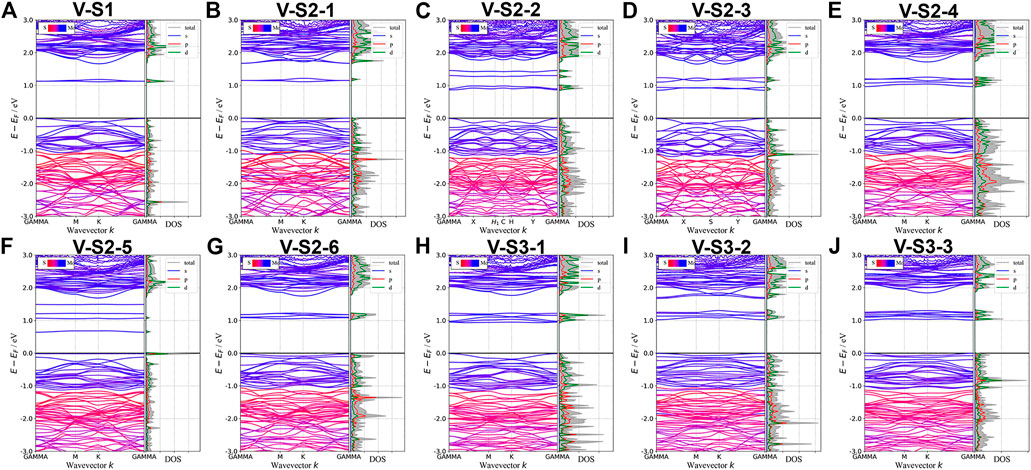
FIGURE 5. Band structures and pDOS of monolayer 2H-MoS₂ with different S-vacancy defects. The labels of different vacancy structures are denoted above each figure. The corresponding atomic configurations can be referred to Figure 4.

TABLE 1

TABLE 1. Bandgap of different S-vacancy model.

Next, we studied the effects of S-vacancies on the optical properties. The imaginary part of the dielectric function is highly related to the absorption coefficient of the material. As shown in Figure 6A, in the presence of S-vacancy, the imaginary part of the dielectric function appears at a transition peak around 1 eV due to the energy levels between the bandgap of pure MoS₂ (Figure 5), but the transition peak around 1 eV is lower than the peak at the higher energy. Rai et al. studied the optical properties of the S-vacancy concentration from 0 to 50% (0, 12.5, 25, 37.5, and 50%) and found a transition peak at a lower energy range, which would significantly increase with the increasing vacancy concentration (Rai et al., 2020). However, our calculations show that as the number of vacancies increases, the stability of the structure becomes worse. Although the density of defect states is small, it enhances the absorption in the NIR-II window significantly, as shown in Figure 6B. Taken together, the stability of the ground-state energy and absorbance, configurations V-S2-2, V-S2-3, and V-S2-6 are the best whose peaks are at 1,150 nm, 1,240 nm, and 980 nm, respectively.

FIGURE 6

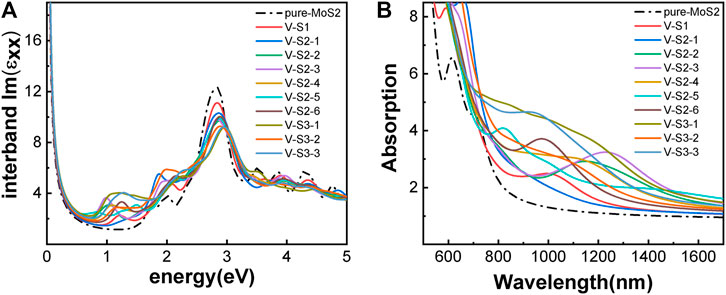
FIGURE 6. Optical properties of monolayer 2H-MoS₂ with different S-vacancy defects: (A) the imaginary part of the dynamic dielectric function; (B) absorption spectra. The black dotted line is for pure monolayer 2H-MoS₂. The labels in the legend refer to different vacancy structures as shown in Figure 4.

Mo-Vacancy Structures

Figures 7A–D,F give the different Mo-vacancy structures. In analogy to the S-vacancy structures, we considered the configurations of single, double, and triple Mo-vacancies. Judging from the ground-state energy, as shown in Figure 7E, V-Mo2-2 is the most stable among the configurations of double Mo-vacancies. With introducing Mo-vacancy, monolayer 2H-MoS₂ tends to be a metal; as shown in Figure 8, except for the configurations of V-Mo1 and V-Mo2-2 whose bandgaps are 0.26 eV and 0.04 eV, respectively. The occupied states at the Fermi level are mainly contributed by the S–p and Mo–d orbitals. Figure 9 shows the dynamic dielectric function and the absorption spectra of the series of configurations of Mo-vacancy. It can be seen from the imaginary part of the dielectric function that the peak at 2.81 eV is quenching with the increasing number of Mo-vacancy, which is consistent with the band structure analysis in previous sections. In the first-principle calculations of Feng et al. (Feng et al., 2018), for monolayer MoS₂ with lower Mo-vacancy concentration (4%), the imaginary part of the complex dielectric function has a slight blue shift, while for monolayer MoS₂ with higher Mo-vacancy concentration (6.25 and 11%), the imaginary part of the complex dielectric function has a significant red shift. Our calculation results are consistent with the conclusion of Feng et al. that when Mo-vacancy concentration is high (6.26, 12.5, and 18.75%), the imaginary part of complex dielectric function of defective monolayer MoS₂ appears obvious red shift. At low energy, V-Mo1 and V-Mo2-1 have an obvious transition peak at 0.93 eV, and V-Mo3 has a small transition peak at 1.56 eV. The red shift explains the dramatical improvement of the absorption in the NIR-II window, as shown in Figure 9B, where both V-Mo1 and V-Mo2-1 have an absorption peak at 1,270 nm. Considering the structure instability of V-Mo2-1 compared with the other two configurations of double Mo-vacancies, V-Mo1 may be a better choice for NIR-II applications.

FIGURE 7

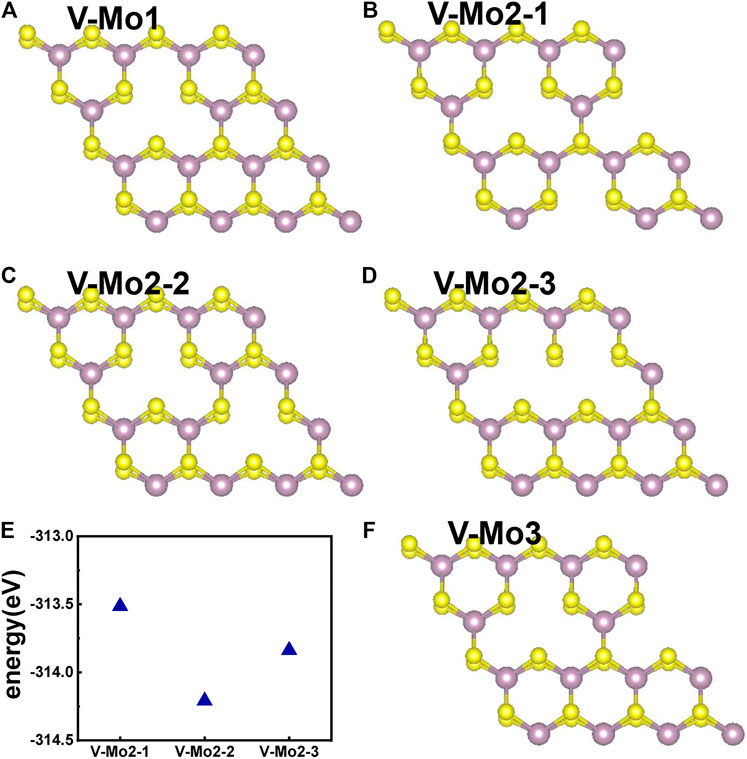
FIGURE 7. Different Mo-vacancy defect structures of 2H-MoS₂, rotated by an angle to distinguish the two S layers: (A) single Mo-vacancy; (B–D) three configurations of double Mo-vacancies; (F) one configuration of triple Mo-vacancies; (E) comparison of the ground-state energies of different configurations of double Mo-vacancies.

FIGURE 8

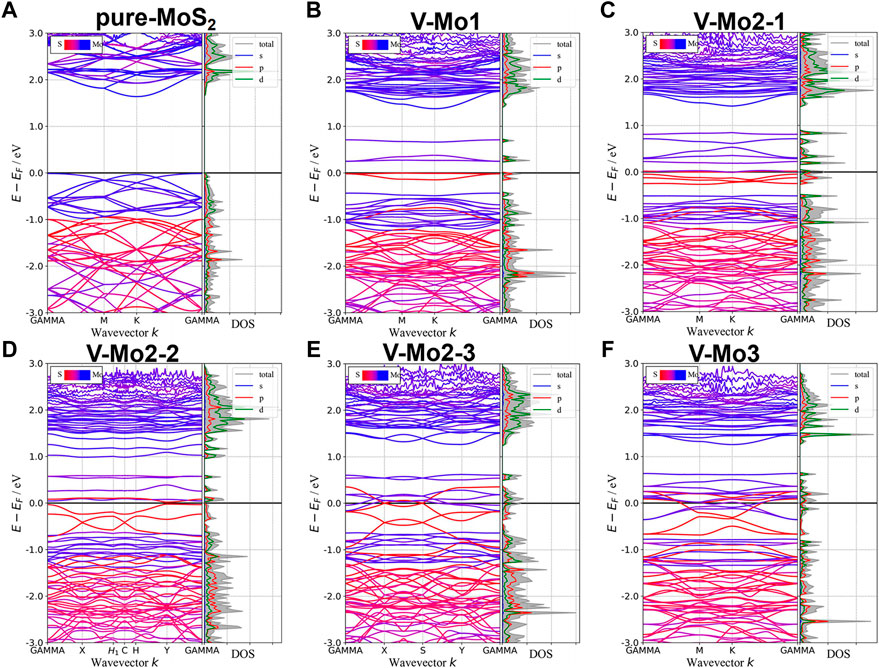
FIGURE 8. Band structures and pDOS of monolayer 2H-MoS₂ with different Mo-vacancy defects. The labels of different vacancy structures are denoted above each figure. The corresponding atomic configurations can be referred to Figure 7.

FIGURE 9

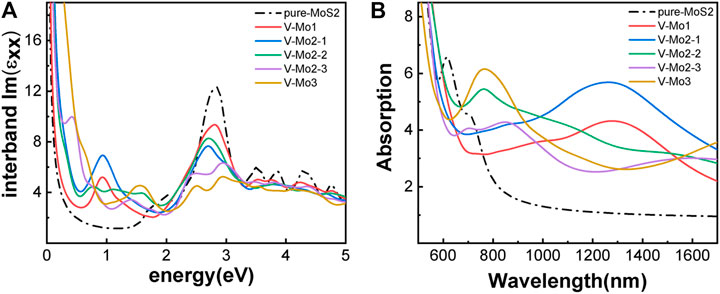
FIGURE 9. Optical properties of monolayer 2H-MoS₂ with different Mo-vacancy defects: (A) the imaginary part of the dynamic dielectric function; (B) absorption spectra. The black dotted line is for pure monolayer 2H-MoS₂. The labels in the legend refer to different vacancy structures, as shown in Figure 7.

Foreign Atom–Doped Structures

Besides introducing vacancies, foreign atom doping is also a common method to manipulate the bandgap. As shown in Figure 10, we studied the substitution of atom S with C, Si, and Se and atom Mo with designed structures in which different elements replaced single S atom or single Mo atom with Ag, Au, Cr, Pd, Ru, and Sb. C, Si, and Se to replace S, respectively, and Ag, Au, Cr, Pd, Ru, and Sb to replace Mo, respectively. For dopants that fill single S-vacancy, C and Si have energy levels in the middle of the gap, while Se does not produce any localized states, as Komsa et al. expected in their work (Komsa et al., 2012). As shown in Figure 11, the doping of C and Si produces energy levels at 0.99 eV and 0.86 eV above the Fermi energy, respectively, and the doping of Se makes the bandgap increase to 1.73 eV, and our calculation result is in accordance with their findings. The doping of Ag, Au, Ru, and Sb turns the monolayer 2H-MoS₂ into a metal. The doping of Cr and Ru leads to an impurity level within the original bandgap reduces the bandgap to 1.48 eV and 0.32 eV, respectively, which is consistent with those of Komsa et al., who observed vacancies filling and discussed the prospects for electron beam–mediated doping of TMDs (Komsa et al., 2012). Figure 12 shows the dynamic dielectric function and the absorption spectra of the doped structures. For the S substitution, doped Se leads to a sharp increase in the transition peak of the imaginary part of the dielectric function at 2.81 eV, but there is basically no change in the absorption in the NIR-II window, while doped C presents a small absorption peak at 1,020 nm. As for the Mo substitution, only Ag shows some improvement in the NIR-II absorption. In general, doping with foreign atoms is not as effective as introducing vacancies in the respect of improving the NIR-II absorption of monolayer 2H-MoS₂.

FIGURE 10

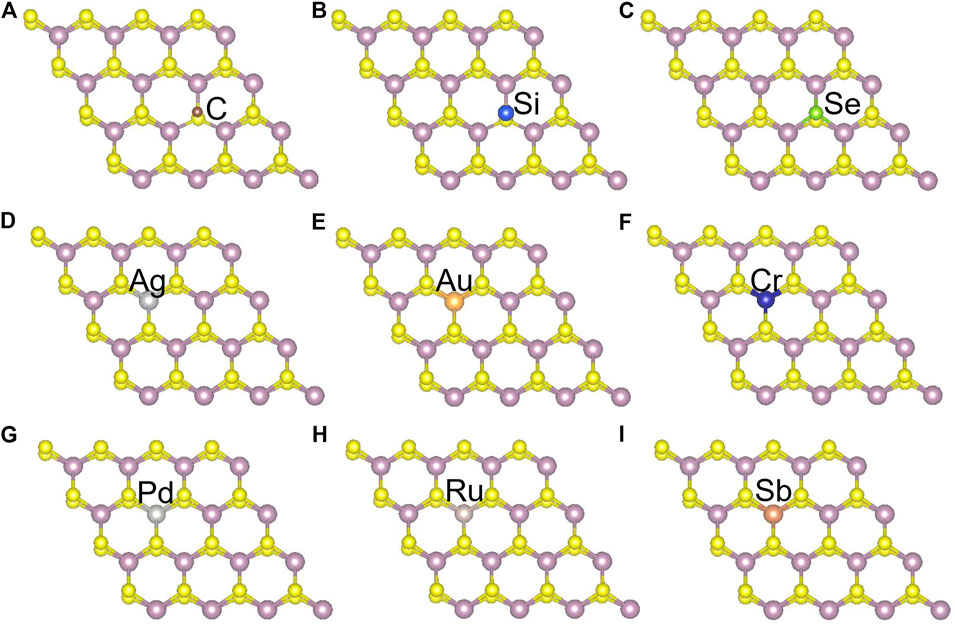
FIGURE 10. Monolayer 2H-MoS2 structure doped with different foreign atoms: (A–C) the substitution of a S atom with C, Si, and Se atoms, respectively; (D–I) the substitution of a Mo atom with Ag, Au, Cr, Pd, Ru, and Sb atoms, respectively.

FIGURE 11

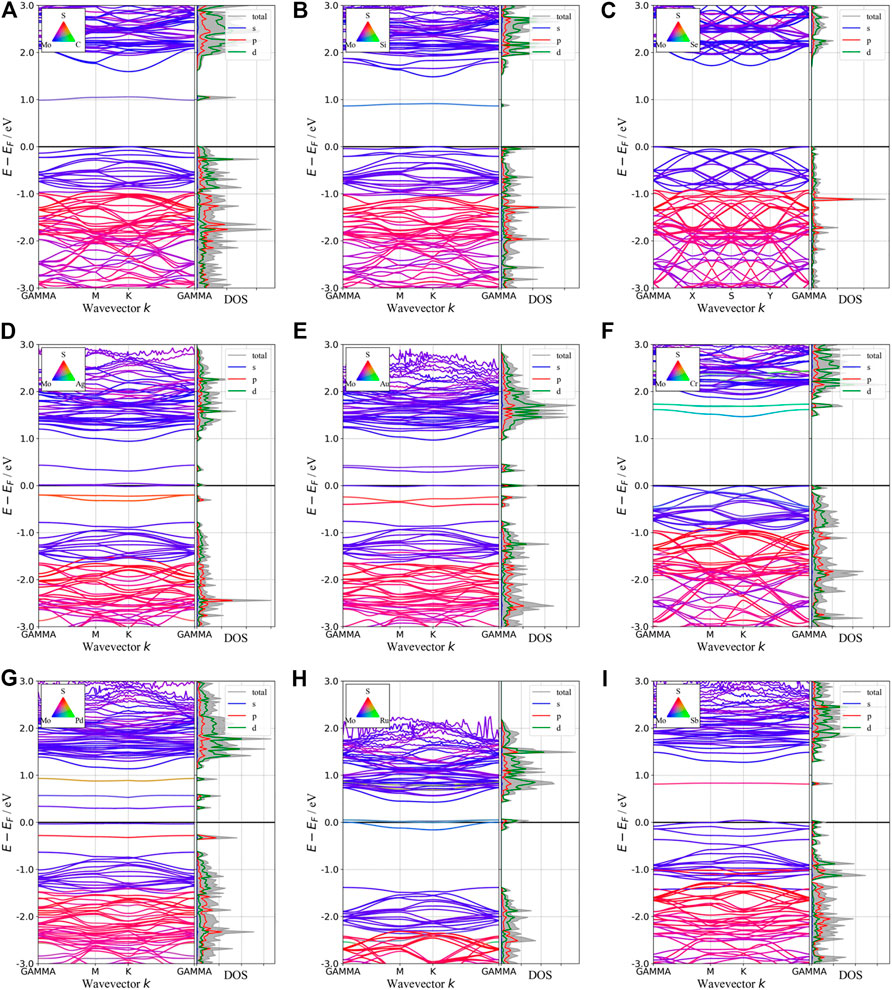
FIGURE 11. Band structures and pDOS of monolayer 2H-MoS₂ after doping with different foreign atoms. The type of doped atoms is indicated by the color map in the upper left corner of each plot.

FIGURE 12

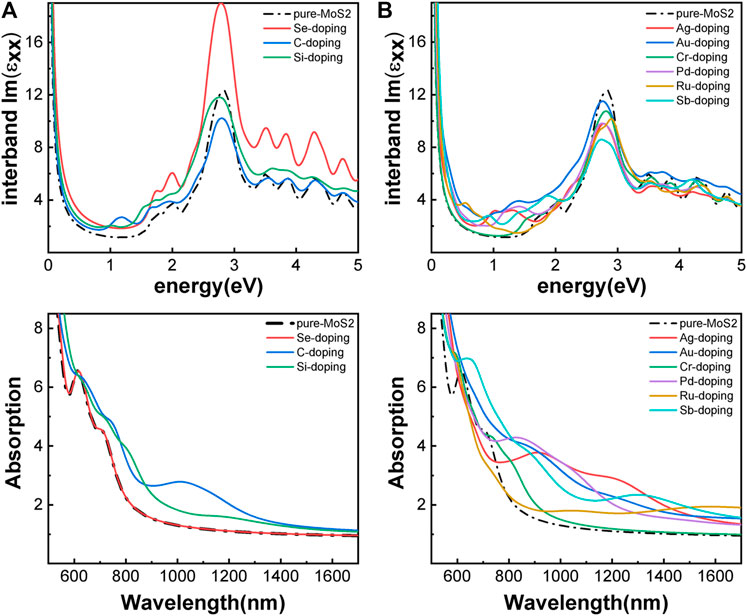
FIGURE 12. Optical properties of monolayer 2H-MoS₂ after doping with different foreign atoms: (A) the imaginary part of the dynamic dielectric function; (B) absorption spectra. The left column is plotted for the substitution of S atom and the right for Mo atom. The black dotted line is for pure monolayer 2H-MoS₂. The solid lines of different color refer to different doped atoms as shown in the legends.

Formation Energy and Stiffness Matrix

Usually, the formation energy and the elastic stiffness constants are used to investigate the thermodynamic and mechanical stabilities of the system, respectively. To investigate the stability of the structure, we calculated the formation energy of all the structures with defects and those doping with foreign atoms, and the stiffness matrices of the three structures with defects that have good absorption performance in the NIR-II window, as shown in Figure 13. Considering that V-S1 has the lowest formation energy, it is the most common defect, which is consistent with the previous experiments (Zhou et al., 2013). Missing of the same number of S atoms is more stable than Mo atoms. Our calculations also show that the stability of the system becomes worse as the number of vacancies increases. In all the vacancies proposed in this study, single S, two S, and single Mo vacancies are relatively stable in either S-rich or Mo-rich environments. But Mo-vacancy is prone and easier to form under the condition of S-rich, and our calculation is the same as Feng’s conclusion (Feng et al., 2018). Combined with the ground-state energy, this indicates that V-S2-2, V-S2-6, and V-Mo1 are thermodynamically stable. As shown in Figure 13B, the foreign atoms doped on the monolayer MoS₂ substrate are C, Si, and Se and Ag, Au, Cr, Pd, Ru, and Sb, respectively. However, in the case of Au, Ag, Pd, and Sb doping, substitutive doping has very high formation energy, so it is speculated that they may be more inclined to act as adsorbed atoms on the surface, which is consistent with the research of Wu et al (Wu et al., 2017). In addition, we found that the formation energy of different dopants substitution S-vacancy was lower than that substitution Mo-vacancy, which was consistent with our conclusion that the formation energy of Mo-vacancies was higher than that of S-vacancies.

FIGURE 13

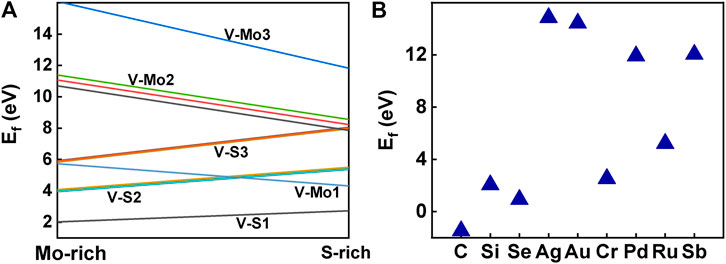
FIGURE 13. (A) Formation energies of different point defects, plot in Mo-rich and S-rich, which correspond to the chemical potential of its body-centered cubic bulk Mo and the S8 ring, respectively. (B) The doping formation energies of different foreign atoms.

In order to evaluate the mechanical stability of the point defects V-S2-2, V-S2-6, and V-Mo1, the elastic stiffness constants of the unit cell of the defects were calculated. For 2D materials, a necessary but not a sufficient condition for mechanical stability must be satisfied: $C_{66}>0$ and $C_{11}{C}_{22}-C_{12}^2>0$ (Maździarz, 2019; Imani Yengejeh et al., 2020). The calculated elastic stiffness constants of V-S2-2 are $C_{11}=69.66GP\text{a}$, $C_{22}=68.76GP\text{a}$, $C_{12}=16.58GP\text{a}$, and $C_{66}=26.15GP\text{a}$ , which satisfy the criterion of mechanical stability. In particular, $C_{12}\approx C_{21}$, this is due to the symmetric stiffness matrix. The elastic constants of V-S2-6 and V-Mo1 are $C_{11}=68.94GP\text{a}$, $C_{22}=69.05GP\text{a}$, $C_{12}=17.03GP\text{a}$, and $C_{66}=25.91GP\text{a}$ and $C_{11}=59.05GP\text{a}$, $C_{22}=58.98GP\text{a}$, $C_{12}=15.84GP\text{a}$, and$C_{66}=21.62GP\text{a}$, respectively. All of them satisfy the criterion of mechanical stability. According to the work by Akhter et al., with increasing the doping and vacancy defect ratio, the elastic property of MoS₂ film decreases, and when the defect ratio exceeds 10%, the elastic property decreases significantly (Akhter et al., 2020). It indicates that the structures in our work are mechanically stable because the proportion of defects under consideration is relatively low.

Conclusion

In conclusion, based on the first-principle calculations, we found that monolayer 1T-MoS₂ has a better performance in the NIR-II absorption than that of the 2H phase. However, monolayer 2H-MoS₂ has the advantage of stability over the 1T phase, and its NIR-II absorption can be improved by introducing vacancies, while doping with foreign atoms is less effective. Our results show that there exist stable double-S-vacancy configurations (V-S2-2 and V-S2-6) and single-Mo-vacancy configuration (V-Mo1) that can be applied in the NIR-II absorption. Our calculations provide a useful guideline for the fabrication of monolayer MoS₂ for the purpose of photothermal therapy guided by photoacoustic imaging.

Methods

In this study, Vienna Ab initio Simulation Package (VASP) (Kresse and Furthmüller, 1996; Kresse and Furthmüller, 1996) has been used to calculate the electronic structure and optical properties of monolayer MoS₂ films based on the projector augmented wave and Perdew–Burke–Ernzerhof (PAW-PBE) pseudopotential (Perdew et al., 1996; Kresse and Joubert, 1999). The numbers of valence electrons of each atom used in the calculation are listed in Table 2. The cutoff energy for plane wave expansion is set to be 500 eV. The generalized gradient approximation (GGA) is used for the exchange correlation energy functional to consider the nonuniformity of electron density. A vacuum layer of 15Å is taken in the z direction to avoid the interaction between the layers due to periodicity. The Brillouin zone integrations were carried out on the $\Gamma$-centered k-mesh (Monkhorst and Pack, 1976). For the 2H-phase monolayer MoS₂ film, in order to better study the influence of different vacancy models and doping on its electronic structure, we first carried out $4\times 4\times 1$ cell expansion on monolayer MoS₂, which was a supercell with 48 atoms in total (16 Mo atoms, 32 S atoms). In the structural optimization, Monkhorst–Pack k-point meshes with size of $5\times 5\times 1$ and $18\times 18\times 1$ were used for supercell and primitive cell, respectively. The convergence standard of energy was 10⁻⁶ eV, and the convergence standard of force in the relaxation process was 0.02eV/Å. Ionic positions, cell volume, and cell shape were optimized by the conjugate gradient algorithm. In the self-consistent calculation, the method of Methfessel–Paxton (Gordienko and Filippov, 2009) order 1 is used in single-layer 1T phase MoS₂, and the width of the smearing is 0.2, while the Gaussian smearing with the width of 0.05 is used for the single-layer 2H-MoS₂. The tetrahedron method (Blöchl et al., 1994) with Blöchl corrections (use a $\Gamma$-centered k-mesh) was adopted in all the density-of-state calculations, and the width of the smearing was so small that it could be ignored. The (small) complex shift $\eta$ in the Kramers–Kronig transformation is 0.1 when calculating the dielectric function.

TABLE 2

TABLE 2. Valence electrons of the atoms used in the calculation.

In addition, GW approximation (Shishkin and Kresse, 2006; Fuchs et al., 2007) is used to calculate the electron–electron scattering relaxation rate of 1T–metal phase monolayer MoS₂. Combined with Drude-like intraband dielectric function contributions (Brendel and Bormann, 1992), the total dielectric function of 1T–metal phase MoS₂ can be obtained. In the GW approximate calculation, the cutoff energy is set to be 300 eV, and 80eV is enough for the number of empty bands after the convergence test.

To investigate the formation of defects, the formation energy for defects can be calculated using the expression as follows (Persson et al., 2005):

$E_f=E_D-E_H+{\displaystyle \sum _{\alpha }{n}_{\alpha }{\mu }_{\alpha }}\text{,}(9)$

where $E_D$ and $E_H$ are the total energies of the supercells with and without defects, respectively; $n_{\alpha }$ is the number of $\alpha$ atoms added ($n_{\alpha }<0$) or removed ($n_{\alpha }>0$); and ${\mu }_{\alpha }$ is the chemical potential of atom $\alpha$. The chemical potential ${\mu }_{Mo}$ and ${\mu }_S$ satisfy the equation ${\mu }_{Mo{S}_2}={\mu }_{Mo}+2{\mu }_S$, where ${\mu }_{Mo{S}_2}$ is the chemical potential of MoS₂ unit in a pristine sheet. The formation for doped energies are defined as (Pan et al., 2015)

$E_f=E\left(M{o}_{16-m}{S}_{32-n}{X}_{m+n}\right)-E\left(M{o}_{16}{S}_{32}\right)+mE\left(Mo\right)+nE\left(S\right)-\left(m+n\right)E\left(X\right)\text{,}(10)$

where $m$ and $n$ are the number of foreign-doped atoms, and $E\left(M{o}_{16}{S}_{32}\right)$ and $E\left(M{o}_{16-m}{S}_{32-n}{X}_{m+n}\right)$ represent the total energy of the system before and after doping. $E\left(Mo\right)$, $E\left(S\right)$, and $E\left(X\right)$ are energy per atom for Mo, S, and foreign atoms X.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

TL and XZ contributed to conception and design to the study. KY processed the calculation. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The calculation was conducted on the High Performance Cluster at the Center for Joint Quantum Studies. This work was financially supported by the NSF of China (Nos. 11904256, 91859101, 81971744, U1932107, 82001952, and 81471786) and the Foundation of Tianjin University (1801).

References

Akhter, M. J., Kuś, W., Mrozek, A., and Burczyński, T. (2020). Mechanical Properties of Monolayer MoS2 with Randomly Distributed Defects. Materials 13 (6), 1307. doi:10.3390/ma13061307

PubMed Abstract | CrossRef Full Text | Google Scholar

Antaris, A. L., Chen, H., Cheng, K., Sun, Y., Hong, G., Qu, C., et al. (2016). A Small-Molecule Dye for NIR-II Imaging. Nat. Mater 15 (2), 235–242. doi:10.1038/nmat4476

PubMed Abstract | CrossRef Full Text | Google Scholar

Blöchl, P. E., Jepsen, O., and Andersen, O. K. (1994). Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 49 (23), 16223–16233. doi:10.1103/physrevb.49.16223

CrossRef Full Text | Google Scholar

Brendel, R., and Bormann, D. (1992). An Infrared Dielectric Function Model for Amorphous Solids. J. Appl. Phys. 71 (1), 1–6. doi:10.1063/1.350737

CrossRef Full Text | Google Scholar

Byrley, P., Liu, M., and Yan, R. (2019). Photochemically Induced Phase Change in Monolayer Molybdenum Disulfide. Front. Chem. 7, 442. doi:10.3389/fchem.2019.00442

PubMed Abstract | CrossRef Full Text | Google Scholar

Cazzaniga, M. (2012). GW and beyond Approaches to Quasiparticle Properties in Metals. Phys. Rev. B 86 (3), 035120. doi:10.1103/physrevb.86.035120

CrossRef Full Text | Google Scholar

Chaste, J., Hnid, I., Khalil, L., Si, C., Durnez, A., Lafosse, X., et al. (2020). Phase Transition in a Memristive Suspended MoS2 Monolayer Probed by Opto- and Electro-Mechanics. ACS nano 14 (10), 13611–13618. doi:10.1021/acsnano.0c05721

PubMed Abstract | CrossRef Full Text | Google Scholar

Dumcenco, D. O., Kobayashi, H., Liu, Z., Huang, Y-S., and Suenaga, K. (2013). Visualization and Quantification of Transition Metal Atomic Mixing in Mo_{1− x}W_xS₂ Single Layers. Nat. Commun. 4 (1), 1–5. doi:10.1038/ncomms2351

CrossRef Full Text | Google Scholar

Fan, Y., Wang, P., Lu, Y., Wang, R., Zhou, L., Zheng, X., et al. (2018). Lifetime-engineered NIR-II Nanoparticles Unlock Multiplexed In Vivo Imaging. Nat. Nanotech 13 (10), 941–946. doi:10.1038/s41565-018-0221-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Feng, L.-p., Sun, H.-q., Li, A., Su, J., Zhang, Y., and Liu, Z.-t. (2018). Influence of Mo-Vacancy Concentration on the Structural, Electronic and Optical Properties of Monolayer MoS2: A First-Principles Study. Mater. Chem. Phys. 209, 146–151. doi:10.1016/j.matchemphys.2018.01.015

CrossRef Full Text | Google Scholar

Fuchs, F., Furthmüller, J., Bechstedt, F., Shishkin, M., and Kresse, G. (2007). Quasiparticle Band Structure Based on a Generalized Kohn-Sham Scheme. Phys. Rev. B 76 (11), 115109. doi:10.1103/physrevb.76.115109

CrossRef Full Text | Google Scholar

Gajdoš, M., Hummer, K., Kresse, G., Furthmüller, J., and Bechstedt, F. (2006). Linear Optical Properties in the Projector-Augmented Wave Methodology. Phys. Rev. B 73 (4), 045112.

Google Scholar

Geng, X., Sun, W., Wu, W., Chen, B., Al-Hilo, A., Benamara, M., et al. (2016). Pure and Stable Metallic Phase Molybdenum Disulfide Nanosheets for Hydrogen Evolution Reaction. Nat. Commun. 7 (1), 1–7. doi:10.1038/ncomms10672

CrossRef Full Text | Google Scholar

Gordienko, A. B., and Filippov, S. I. (2009). A Modified Version of the Methfessel‒Paxton Method. Russ. Phys. J. 52 (7), 668–673. doi:10.1007/s11182-009-9281-9

CrossRef Full Text | Google Scholar

Guan, S., Yang, S. A., Zhu, L., Hu, J., and Yao, Y. (2015). Electronic, Dielectric and Plasmonic Properties of Two-Dimensional Electride Materials X₂N (X= Ca, Sr): A First-Principles Study. Sci. Rep. 5 (1), 1–14. doi:10.1038/srep12285

PubMed Abstract | CrossRef Full Text | Google Scholar

Gutiérrez, O. Y., Singh, S., Schachtl, E., Kim, J., Kondratieva, E., Hein, J., et al. (2014). Effects of the Support on the Performance and Promotion of (Ni)MoS2 Catalysts for Simultaneous Hydrodenitrogenation and Hydrodesulfurization. ACS Catal. 4 (5), 1487–1499. doi:10.1021/cs500034d

CrossRef Full Text | Google Scholar

Harl, J. (2008). The Linear Response Function in Density Functional Theory: Optical Spectra and Improved Description of the Electron Correlation: Na.

Helveg, S., Lauritsen, J. V., Lægsgaard, E., Stensgaard, I., Nørskov, J. K., Clausen, B. S., et al. (2000). Atomic-Scale Structure of Single-LayerMoS2Nanoclusters. Phys. Rev. Lett. 84 (5), 951–954. doi:10.1103/physrevlett.84.951

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, G., Lee, J. C., Robinson, J. T., Raaz, U., Xie, L., Huang, N. F., et al. (2012). Multifunctional In Vivo Vascular Imaging Using Near-Infrared II Fluorescence. Nat. Med. 18 (12), 1841–1846. doi:10.1038/nm.2995

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, G., Robinson, J. T., Zhang, Y., Diao, S., Antaris, A. L., Wang, Q., et al. (2012). In Vivo Fluorescence Imaging with Ag2S Quantum Dots in the Second Near-Infrared Region. Angew. Chem. Int. Ed. 51 (39), 9818–9821. doi:10.1002/anie.201206059

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, J., Jin, C., Yuan, J., and Zhang, Z. (2017). Atomic Defects in Two-Dimensional Materials: From Single-Atom Spectroscopy to Functionalities in Opto-/Electronics, Nanomagnetism, and Catalysis. Adv. Mater. 29 (14), 1606434. doi:10.1002/adma.201606434

PubMed Abstract | CrossRef Full Text | Google Scholar

Imani Yengejeh, S., Liu, J., Kazemi, S. A., Wen, W., and Wang, Y. (2020). Effect of Structural Phases on Mechanical Properties of Molybdenum Disulfide. ACS omega 5 (11), 5994–6002. doi:10.1021/acsomega.9b04360

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiao, L., Zhang, L., Wang, X., Diankov, G., and Dai, H. (2009). Narrow Graphene Nanoribbons from Carbon Nanotubes. Nature 458 (7240), 877–880. doi:10.1038/nature07919

PubMed Abstract | CrossRef Full Text | Google Scholar

Johari, P., and Shenoy, V. B. (2012). Tuning the Electronic Properties of Semiconducting Transition Metal Dichalcogenides by Applying Mechanical Strains. ACS nano 6 (6), 5449–5456. doi:10.1021/nn301320r

PubMed Abstract | CrossRef Full Text | Google Scholar

Kam, K. K., and Parkinson, B. A. (1982). Detailed Photocurrent Spectroscopy of the Semiconducting Group VIB Transition Metal Dichalcogenides. J. Phys. Chem. 86 (4), 463–467. doi:10.1021/j100393a010

CrossRef Full Text | Google Scholar

Kan, M., Wang, J. Y., Li, X. W., Zhang, S. H., Li, Y. W., Kawazoe, Y., et al. (2014). Structures and Phase Transition of a MoS2 Monolayer. J. Phys. Chem. C 118 (3), 1515–1522. doi:10.1021/jp4076355

CrossRef Full Text | Google Scholar

Komsa, H-P., Kotakoski, J., Kurasch, S., Lehtinen, O., Kaiser, U., and Krasheninnikov, A. V. (2012). Two-dimensional Transition Metal Dichalcogenides under Electron Irradiation: Defect Production and Doping. Phys. Rev. Lett. 109 (3), 035503. doi:10.1103/physrevlett.109.035503

PubMed Abstract | CrossRef Full Text | Google Scholar

Komsa, H-P., and Krasheninnikov, A. V. (2015). Native Defects in Bulk and Monolayer MoS₂ from First Principles. Phys. Rev. B 91 (12), 125304. doi:10.1103/physrevb.91.125304

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set. Comput. Mater. Sci. 6 (1), 15–50. doi:10.1016/0927-0256(96)00008-0

CrossRef Full Text | Google Scholar

Kresse, G., and Furthmüller, J. (1996). Efficient Iterative Schemes Forab Initiototal-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 54 (16), 11169–11186. doi:10.1103/physrevb.54.11169

CrossRef Full Text | Google Scholar

Kresse, G., and Joubert, D. (1999). From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 59 (3), 1758–1775. doi:10.1103/physrevb.59.1758

CrossRef Full Text | Google Scholar

Kumar, A., and Ahluwalia, P. (2012). A First Principle Comparative Study of Electronic and Optical Properties of 1H–MoS₂ and 2H–MoS₂. Mater. Chem. Phys. 135 (2-3), 755–761. doi:10.1016/j.matchemphys.2012.05.055

CrossRef Full Text | Google Scholar

Lahouij, I., Vacher, B., Martin, J-M., and Dassenoy, F. (2012). IF-MoS₂ Based Lubricants: Influence of Size, Shape and crystal Structure. Wear 296 (1-2), 558–567. doi:10.1016/j.wear.2012.07.016

CrossRef Full Text | Google Scholar

Li, H., Duan, X., Wu, X., Zhuang, X., Zhou, H., Zhang, Q., et al. (2014). Growth of Alloy MoS2xSe2(1-x)Nanosheets with Fully Tunable Chemical Compositions and Optical Properties. J. Am. Chem. Soc. 136 (10), 3756–3759. doi:10.1021/ja500069b

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, H., Hong, G., Luo, Z., Chen, J., Chang, J., Gong, M., et al. (2019). Atomic‐Precision Gold Clusters for NIR‐II Imaging. Adv. Mater. 31 (46), 1901015. doi:10.1002/adma.201901015

PubMed Abstract | CrossRef Full Text | Google Scholar

Mak, K. F., Lee, C., Hone, J., Shan, J., and Heinz, T. F. (2010). Atomically Thin MoS₂: a New Direct-gap Semiconductor. Phys. Rev. Lett. 105 (13), 136805. doi:10.1103/physrevlett.105.136805

PubMed Abstract | CrossRef Full Text | Google Scholar

Mann, J., Ma, Q., Odenthal, P. M., Isarraraz, M., Le, D., Preciado, E., et al. (2014). 2-Dimensional Transition Metal Dichalcogenides with Tunable Direct Band Gaps: MoS2(1-x)Se2xMonolayers. Adv. Mater. 26 (9), 1399–1404. doi:10.1002/adma.201304389

PubMed Abstract | CrossRef Full Text | Google Scholar

Maździarz, M. (2019). Comment on ‘The Computational 2D Materials Database: High-Throughput Modeling and Discovery of Atomically Thin Crystals’. 2D Mater. 6 (4), 048001.

Google Scholar

Monkhorst, H. J., and Pack, J. D. (1976). Special Points for Brillouin-Zone Integrations. Phys. Rev. B 13 (12), 5188–5192. doi:10.1103/physrevb.13.5188

CrossRef Full Text | Google Scholar

Nakayasu, Y., Bradley, S., Kobayashi, H., Nayuki, K., Sasaki, Y., Tomai, T., et al. (2019). Rapid Synthesis of Defective and Composition-Controlled Metal Chalcogenide Nanosheets by Supercritical Hydrothermal Processing. Nanoscale Adv. 1 (9), 3383–3387. doi:10.1039/c9na00435a

CrossRef Full Text | Google Scholar

Ogawa, S., and Petek, H. (1996). Femtosecond Dynamics of Hot-Electron Relaxation in Cu(110) and Cu(100). Surf. Sci. 357-358, 585–594. doi:10.1016/0039-6028(96)00228-2

CrossRef Full Text | Google Scholar

Olmon, R. L., Slovick, B., Johnson, T. W., Shelton, D., Oh, S-H., Boreman, G. D., et al. (2012). Optical Dielectric Function of Gold. Phys. Rev. B 86 (23), 235147. doi:10.1103/physrevb.86.235147

CrossRef Full Text | Google Scholar

Pan, J. W., Li, C., Zhao, Y. F., Liu, R. X., Gong, Y. Y., Niu, L. Y., et al. (2015). Electronic Properties of TiO2 Doped with Sc, Y, La, Zr, Hf, V, Nb and Ta. Chem. Phys. Lett. 628, 43–48. doi:10.1016/j.cplett.2015.03.056

CrossRef Full Text | Google Scholar

Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77 (18), 3865–3868. doi:10.1103/physrevlett.77.3865

PubMed Abstract | CrossRef Full Text | Google Scholar

Persson, C., Zhao, Y-J., Lany, S., and Zunger, A. (2005). n-Type Doping of CuInSe₂ and CuGaSe₂. Phys. Rev. B 72 (3), 035211. doi:10.1103/physrevb.72.035211

CrossRef Full Text | Google Scholar

Rai, D. P., Vu, T. V., Laref, A., Ghimire, M. P., Patra, P. K., Srivastava, S., et al. (2020). Electronic and Optical Properties of 2D Monolayer (ML) MoS2 with Vacancy Defect at S Sites. Nano-Structures & Nano-Objects 21, 100404. doi:10.1016/j.nanoso.2019.100404

CrossRef Full Text | Google Scholar

Schöne, W-D. (2007). Theoretical Determination of Electronic Lifetimes in Metals. Prog. Surf. Sci. 82 (4-6), 161–192. doi:10.1016/j.progsurf.2007.03.004

CrossRef Full Text | Google Scholar

Shishkin, M., and Kresse, G. (2006). Implementation and Performance of the Frequency-dependent GW Method within the PAW Framework. Phys. Rev. B 74 (3), 035101. doi:10.1103/physrevb.74.035101

CrossRef Full Text | Google Scholar

Shishkin, M., and Kresse, G. (2007). Self-consistent G W Calculations for Semiconductors and Insulators. Phys. Rev. B 75 (23), 235102. doi:10.1103/physrevb.75.235102

CrossRef Full Text | Google Scholar

Soares, D. M., Mukherjee, S., and Singh, G. (2020). TMDs beyond MoS 2 for Electrochemical Energy Storage. Chem. Eur. J. 26 (29), 6320–6341. doi:10.1002/chem.202000147

PubMed Abstract | CrossRef Full Text | Google Scholar

Steinhoff, A., Kim, J.-H., Jahnke, F., Rösner, M., Kim, D.-S., Lee, C., et al. (2015). Efficient Excitonic Photoluminescence in Direct and Indirect Band Gap Monolayer MoS2. Nano Lett. 15 (10), 6841–6847. doi:10.1021/acs.nanolett.5b02719

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, C., Li, B., Zhao, M., Wang, S., Lei, Z., Lu, L., et al. (2019). J-aggregates of Cyanine Dye for NIR-II In Vivo Dynamic Vascular Imaging beyond 1500 Nm. J. Am. Chem. Soc. 141 (49), 19221–19225. doi:10.1021/jacs.9b10043

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Q. H., Kalantar-Zadeh, K., Kis, A., Coleman, J. N., and Strano, M. S. (2012). Electronics and Optoelectronics of Two-Dimensional Transition Metal Dichalcogenides. Nat. Nanotech 7 (11), 699–712. doi:10.1038/nnano.2012.193

CrossRef Full Text | Google Scholar

Wang, V., Xu, N., Liu, J. C., Tang, G., and Geng, W-T. (2019). VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using VASP Code. doi:10.1002/leap.1229arXiv preprint arXiv:08269

CrossRef Full Text

Welsher, K., Liu, Z., Sherlock, S. P., Robinson, J. T., Chen, Z., Daranciang, D., et al. (2009). A Route to Brightly Fluorescent Carbon Nanotubes for Near-Infrared Imaging in Mice. Nat. Nanotech 4 (11), 773–780. doi:10.1038/nnano.2009.294

CrossRef Full Text | Google Scholar

Wu, P., Yin, N., Li, P., Cheng, W., and Huang, M. (2017). The Adsorption and Diffusion Behavior of noble Metal Adatoms (Pd, Pt, Cu, Ag and Au) on a MoS2 Monolayer: a First-Principles Study. Phys. Chem. Chem. Phys. 19 (31), 20713–20722. doi:10.1039/c7cp04021k

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, D., Zhu, Y., Liu, J., Li, Y., Peng, W., Zhang, G., et al. (2016). Microwave-assisted 1T to 2H Phase Reversion of MoS2in Solution: a Fast Route to Processable Dispersions of 2H-MoS2nanosheets and Nanocomposites. Nanotechnology 27 (38), 385604. doi:10.1088/0957-4484/27/38/385604

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, M., Liu, J., Zhou, L., Mendes, R. G., Dong, Y., Zhang, M.-Y., et al. (2020). Bandgap Tuning of Two-Dimensional Materials by Sphere Diameter Engineering. Nat. Mater. 19 (5), 528–533. doi:10.1038/s41563-020-0622-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X.-D., Wang, H., Antaris, A. L., Li, L., Diao, S., Ma, R., et al. (2016). Traumatic Brain Injury Imaging in the Second Near-Infrared Window with a Molecular Fluorophore. Adv. Mater. 28 (32), 6872–6879. doi:10.1002/adma.201600706

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, X., Luster, B., Church, A., Muratore, C., Voevodin, A. A., Kohli, P., et al. (2009). Carbon Nanotube−MoS2 Composites as Solid Lubricants. ACS Appl. Mater. Inter. 1 (3), 735–739. doi:10.1021/am800240e

CrossRef Full Text | Google Scholar

Zhou, W., Zou, X., Najmaei, S., Liu, Z., Shi, Y., Kong, J., et al. (2013). Intrinsic Structural Defects in Monolayer Molybdenum Disulfide. Nano Lett. 13 (6), 2615–2622. doi:10.1021/nl4007479

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z., Li, B., Shen, C., Wu, D., Fan, H., Zhao, J., et al. (2020). Metallic 1T Phase Enabling MoS 2 Nanodots as an Efficient Agent for Photoacoustic Imaging Guided Photothermal Therapy in the Near‐Infrared‐II Window. Small 16 (43), 2004173. doi:10.1002/smll.202004173

PubMed Abstract | CrossRef Full Text | Google Scholar