Equation-of-Motion Coupled-Cluster Cumulant Green’s Function for Excited States and X-Ray Spectra

1 Introduction

The core-level x-ray absorption spectra (XAS) μ(ω) is typically described formally by Fermi’s golden rule. However, this formulation requires calculations of and summations over eigenstates of the many-body Hamiltonian H and is computationally intractable. Simplifications such as the determinantal ΔSCF approach, in terms of Slater determinants (Liang et al., 2017; Liang and Prendergast, 2019; Nozieres and Combescot, 1971) have similar limitations. Although still computationally demanding, Green’s function methods provide an attractive alternative since summation over final states is implicit (Lee et al., 2012; Bertsch and Lee, 2014; Rehr et al., 2009). Real-time approaches can also be advantageous as they avoid explicit calculations of eigenstates. Our treatment here exploits real-time approaches, following several recent developments: 1) Equation of motion coupled-cluster (EOM-CC) approaches for molecular systems have been formulated for the Green’s function in energy-space (Peng and Kowalski, 2016; Peng and Kowalski, 2018a), 2) An approach has also been developed (Rehr et al., 2020) for calculations of many-body XAS μ(ω) in terms of the convolution of a one-body XAS μ₁(ω) and the spectral function of the core-hole A_c(ω)

$\mu (\omega )=\int dt{e}^{-i\omega t}\mu (t)=\int d{\omega }^{\prime }{\mu }_1({\omega }^{\prime })A_c(\omega -{\omega }^{\prime }).(1)$

This result originates from the time-correlation approach (Nozieres and de Dominicis, 1969) that was used to solve the x-ray edge-singularity problem. In this approach the time-domain XAS transition amplitude μ(t) is given by the factorization

$\mu (t)=⟨\mathrm{\Psi }|D(0)D(t)|\mathrm{\Psi }⟩=L(t)G_c(t).(2)$

Here L(t) is an effective one-body transition amplitude and A_c(ω) = −(1/π)Im G_c(t). 3) A real-time EOM-CC approach for the cumulant core Green’s function G_c has been developed including excitations up to CC-singles (CCS). Intrinsic losses induced by the sudden creation of the core hole lead to shake-up effects, characterized by satellites in A_c(ω), as observed in x-ray photoemission spectra (XPS). The effective one-body XAS μ₁(ω) also builds in orthogonality corrections leading to edge enhancements, as predicted by Mahan, Nozieres and de Dominicis (Mahan, 1967). Our goal here is to review these developments and to combine the one-particle absorption spectrum with a more accurate treatment of the core Green’s function, including the complete form of the CCS cumulant, as well as the full single, doubles and triple cluster excitations in the cluster amplitude equations.

In the rest of this review, Section 2 describes the theoretical approaches used, in particular a brief introduction to the cumulant approach (Section 2.1), the real-time equation of motion, coupled cluster (RT-EOM-CC) approach (Section 2.2), the frequency space implementation of the Green’s Function coupled clusters (GFCC) approach (Section 2.3), and the application to XAS (Section 2.4). Section 3 presents results for the core binding energies of small molecules, and a comparison of the theory to XPS and XAS experimental results for NH₃. Finally, Section 4 presents a summary and discusses future developments.

2 Theory

2.1 Cumulant Approach

Within the cumulant approximation, the core-level Green’s function is defined by an exponential expression

$G_c(t)=G_c^0(t)e^{C(t)},(3)$

where $G_c^0(t)=-i\theta (t)e^{-i{ϵ}_{c}t}$ is the independent particle Green’s function (Hartree-Fock in this paper), with single particle energy ε_c, and denotes the core-level in question. C(t) is the cumulant function, which builds the correlation into the Green’s function. This cumulant can be expressed in Landau form (Landau, 1944), in terms of an excitation spectrum β(ω),

$C(t)=\int d\omega \frac{\beta (\omega )}{{\omega }^2}\left[e^{-i\omega t}+i\omega t-1\right].(4)$

As a consequence, the cumulant Green’s function is naturally normalized, with an occupation G_c(t = 0) = 1. One can also analyze A(ω) = −(1/π)Im G_c(ω), which is the natural quantity to compare to experimental x-ray photoemission spectra, and to assess the quality of many-body correlation approximations since satellites appearing in spectral quantities such as XPS are directly related to those seen in the spectral function. The above form of the cumulant also permits a natural separation into quasiparticle and satellite contributions. Separating the terms in the expression for the cumulant above, we have

$C(t)=-a+i\mathrm{\Delta }t+\tilde{C}(t),(5)$

where a = ∫dωβ(ω)/ω² is the net satellite strength, Δ = ∫dωβ(ω)/ω is the quasiparticle shift, or core-level “relaxation energy”, and $\tilde{C}(t)$ is the remainder of the cumulant, which contains the information about the satellites. By expanding about small $\tilde{C}$, the spectral function can be obtained analytically in terms of β(ω), i.e.,

$A_c(\omega )=Z_c\delta (\omega -E_c)\ast \left[1+A_{\text{sat}}(\omega )+\frac{1}{2}{A}_{\text{sat}}(\omega )\ast A_{\text{sat}}(\omega )+\cdots \right],(6)$

where Z_c = e^−a is the quasiparticle renormalization, E_c = ϵ_c −Δ is the quasiparticle energy, and A_sat(ω) = β(ω)/ω² is the satellite spectral function (Aryasetiawan et al., 1996).

The cumulant kernel or excitation spectrum β(ω) can be approximated in a variety of ways. The most common approximation is to expand the Green’s function to low order either in the bare Coulomb interaction, giving β(ω) in terms of the second order self-energy (Vila et al., 2020), or by expanding in terms of the screened Coulomb interaction, which produces an approximation in terms of the GW self-energy (Hedin, 1999; Guzzo et al., 2011; Zhou et al., 2015). Approximate non-linear corrections can be included using real-time TDDFT (Tzavala et al., 2020). Here, as described in the next section, we calculate the cumulant including non-linear corrections within a non-perturbative approach, by expressing the Green’s function in terms of the time-dependent EOM-CC states.

2.2 RT-EOM-CC Theory

Our treatment of the core-hole Green’s function G_c(t) is based on the CC-ansatz for the time-evolved initial state of the system with a core-hole created at t = 0⁺: |Ψ_c (0)⟩ ≡|Ψ_c⟩ = c_c|Ψ⟩ where c_c is the core annihilation operator and |Ψ⟩ is the ground state Hartree-Fock Slater determinant:

$|{\mathrm{\Psi }}_c(t)\rangle \equiv N_c(t)e^{T(t)}|{\mathrm{\Psi }}_c\rangle .(7)$

Then $G_c(t)=-i⟨{\mathrm{\Psi }}_c|e^{i(H-E_0)t}|{\mathrm{\Psi }}_c⟩\theta (t)$ simply becomes

$G_c(t)=-i{N}_c(t)e^{-i{E}_{0}t}\theta (t).(8)$

Calculations of G_c(t) are based on the real-time equation of motion coupled cluster (RT-EOM-CC) ansatz of Schönhammer and Gunnarsson (SG) (Schönhammer and Gunnarsson, 1978), in which the time-evolution of |Ψ_c(t)⟩ is carried out using an initial value problem and propagation via the Schrödinger equation of motion i ∂|Ψ_c(t)⟩/∂t = H|Ψ_c(t)⟩. The time-evolved wave-function |Ψ_c(t)⟩ can then be expressed using the CC ansatz in Eq. 7. The use of a single-excitations CC ansatz is justified for a single-determinant reference state approximation due to Thouless’ theorem (Thouless, 1961). In Eq. 7N_c(t) is a normalization factor, while the CC operator T(t) is defined in terms of single, double, etc., excitation creation operators $a_n^{†}$, i.e.,

$T(t)=\sum _n{t}_n(t)a_n^{†}.(9)$

For example, for single excitations n = (i, a) and $a_n^{†}=c_a^{†}{c}_i$; for double excitations n = i, j, a, b and $a_n^{†}=c_a^{†}{c}_b^{†}{c}_j{c}_i$; etc. As is conventional in CC, the indices i, j… refer to occupied single-particle states, a, b, … to unoccupied, and p, q, … to either occupied or unoccupied ones. Projecting the EOM with either the ground state, or with singly-excited versions of it, the equations decouple naturally, i.e.,

$\begin{array}{c}\hfill i\partial \ln N_c(t)/\partial t=\langle {\mathrm{\Psi }}_c|\bar{H}(t)|{\mathrm{\Psi }}_c\rangle ,\end{array}(10)$

$\begin{array}{c}\hfill i\partial t_n(t)/\partial t=\langle n|\bar{H}(t)|{\mathrm{\Psi }}_c\rangle ,\end{array}(11)$

where $|n\rangle =a_n^{†}|{\mathrm{\Psi }}_c\rangle$ and $\bar{H}=e^{-T}H{e}^T$ is the similarity-transformed Hamiltonian. The first of these results shows that the normalization factor N_c(t) is a pure exponential, so that the core Green’s function G_c(t) has a natural cumulant representation $G_c(t)=G_c^0(t)e^{C(t)}$ with a cumulant defined as

$C(t)=-i{\int }_0^{t}d{t}^{\prime }⟨{\mathrm{\Psi }}_c|(\bar{H}(t^{\prime })-E_0^{\prime })|{\mathrm{\Psi }}_c⟩,(12)$

where $E_0^{\prime }=E_0-{ϵ}_c$, and E₀ is the ground state energy. As noted above, the EOM-CC cumulant can have a Landau form (Eq. 4) (Landau, 1944) that simplifies analysis of its spectrum. The cumulant kernel or excitation spectrum β(ω) from the EOM-CC approach is given by

$\beta (\omega )=\frac{1}{\pi }\mathrm{R}\mathrm{e}{\int }_0^{\infty }dt{e}^{-i\omega t}\frac{d}{dt}⟨{\mathrm{\Psi }}_c|\bar{H}(t)|{\mathrm{\Psi }}_c⟩(13)$

This amplitude accounts for the transfer of oscillator strength from the main peak in XPS to the satellite excitations at frequencies ω. The cumulant initial conditions C (0) = C′(0) = 0 guarantee the normalization of the spectral function. In addition, they ensure that its centroid remains invariant at the Koopmans’ energy −ϵ_c. After some straightforward diagrammatic analysis to compute the matrix elements in Eqs. 10, 12, we obtain a compact expression for the time-derivative of the cumulant

$-i\frac{dC(t)}{dt}=\sum _{ia}{f}_{ia}{t}_i^a+\frac{1}{2}\sum _{ijab}{v}_{ij}^{ab}{t}_j^b{t}_i^a,(14)$

where $t_i^a=t_n(t)$ when n = (i, a), and the f_ia and $v_{ij}^{ab}$ coefficients correspond, respectively, to the one- and two-particle elements that define the second-quantized Hamiltonian in a core-hole reference (Vila et al., 2020). The terms on the rhs of Eq. 14 correspond to the linear- (L) and non-linear (NL) CC diagrams (Crawford and Schaefer, 2000; Brandow, 1967) shown in Figure 1. The linear term arises from the coupling of the core-hole to the i → a excitation, while the second term [which is quadratic in the amplitudes t (NL)] represents valence polarization effects that screen the core-hole.

FIGURE 1

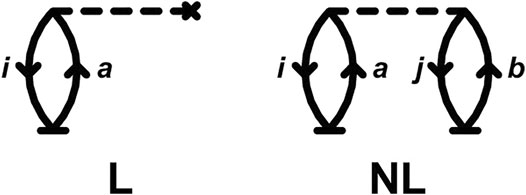
FIGURE 1. Linear (L) and non-linear (NL) CC diagrams (Crawford and Schaefer, 2000; Brandow, 1967) for the time-derivative of the cumulant in Eq. 14. Unlike in traditional EOM-CC diagrams, the base vertices (t) are time-dependent.

Remarkably, these diagrams are completely analogous to the time-independent diagrams for the CCSD energy if only single excitations (T₁) are included. It is interesting to note that only one more diagram is needed to obtain the complete CC cumulant for the core-hole Green's function, namely that from double excitations similar to the NL diagram in Figure 1, but with a cluster line joining the base vertices representing the T₂ operator.

The EOM for the matrix elements of the CC amplitudes in Eq. 11 can be calculated using similar diagrammatic analysis which yield a set of coupled first-order differential equations.

$\begin{array}{l}\hfill -i{\dot{t}}_i^a=-v_{ac}^{ic}+\left({ϵ}_a-{ϵ}_i\right)t_i^a\end{array}(\mathrm{15a})$

$\begin{array}{l}+\sum _j{v}_{jc}^{ic}{t}_j^a-\sum _b{v}_{ac}^{bc}{t}_i^b+\sum _{jb}{v}_{ja}^{bi}{t}_j^b+\sum _{jb}{v}_{jc}^{bc}{t}_i^b{t}_j^a\hfill \end{array}(\mathrm{15b})$

$\begin{array}{l}+\sum _{jbd}{v}_{aj}^{bd}{t}_i^b{t}_j^d-\sum _{jkb}{v}_{jk}^{ib}{t}_j^a{t}_k^b\hfill \end{array}(\mathrm{15c})$

$\begin{array}{l}-\sum _{jkbd}{v}_{jk}^{bd}{t}_i^b{t}_j^a{t}_k^d,\hfill \end{array}(\mathrm{15d})$

where ϵ_p are the bare single-particle energies. The low order terms are identical to those in our original paper (Rehr et al., 2020). However, now the complete CCS T₁ approximation is used, including terms up to third order in $t_i^a$. The similarity in the form of Eq. 14 and Eq. 15 to the time-independent matrix elements used in standard CC theory implies that the overall scaling of the RT-EOM-CC approach per time step is equivalent to that of the standard CC equations of the same order per solution iteration (i.e. N⁴ for CCS, N⁶ for CCSD, etc.). The main difference arises in that while for the latter only a few tens of iterations are needed for convergences, RT-EOM-CC requires hundreds to thousands of steps to described the core dynamics. One final difference arises from the complex nature of the time-dependent CC amplitudes, which doubles the computational demands. Thus, approximations are highly desirable and here we review four possible levels of approximation:

1) Lowest order approximation, with only the leading terms, i.e., Eq. 15a: At this level the EOM is exactly solvable giving $t_i^a(t)=-v_{ac}^{ic}[\exp (i{\omega }_{ia}t)-1]$, with ω_ia = ϵ_a−ϵ_i. Moreover, the second-order self-energy cumulant (Vila et al., 2020) is obtained if only the linear part in Eq. 14 is kept. However this low level of approximation produced mean absolute errors for the core binding energies an order of magnitude larger than those with the next higher levels of approximation to Eq. 15 (2–4, as summarized below) which we have used for the results presented in Section 3.

2) Core-valence approximation: Eq. 15a together with the dominant, first four sums in Eq. 15b. This approximation includes the linear core- and valence-valence contributions and a non-linear term corresponding to excitations linked to the core-hole.

3) Full second order approximation: Keeping all terms of level 2, and the non-linear valence-valence excitations from the two sums in Eq. 15c. This gives corrections that close the gap between the QP peak and the satellites.

4) Full third order T₁ level: This approximation retains all the terms in the T₁ EOM in Eq. 15, including the cubic term in Eq. 15d.

Each of the approximation levels to Eq. 15 can be combined with either the linear (L), or both the linear and non-linear (NL) components of C(t) defined in Eq. 14. As we have demonstrated previously (Vila et al., 2020), the NL component is key for obtaining accurate core binding energies. Consequently it is useful to focus on the 2_NL, 3_NL and 4_NL results only. For comparison results are also shown for the solution of the Dyson equation (DSE2) (Linderberg and Öhrn, 2004; Szabo and Ostlund, 1996)

$G_c(\omega )={[1-G_c^0(\omega ){\mathrm{\Sigma }}^{(2)}(\omega )]}^{-1}{G}_c^0(\omega )(16)$

where Σ⁽²⁾(ω) is the second order self-energy (Szabo and Ostlund, 1996); and for the frequency space Green’s function GFCCSD and GFCC-i (2, 3) methods (Peng and Kowalski, 2018a; Peng and Kowalski, 2018b).

2.3 GFCC Theory

In this section we briefly review the GFCC formalism introduced by Nooijen et al. (Nooijen and Snijders, 1992; Nooijen and Snijders, 1993; Nooijen and Snijders, 1995, see also Meissner and Bartlett, 1993; Kowalski et al., 2014; Bhaskaran-Nair et al., 2016; Peng and Kowalski, 2016; Peng and Kowalski, 2018a), which draws heavily on the bi-variational CC formalism (Arponen, 1983; Stanton and Bartlett, 1993) where the ground-state bra- ket (〈Ψ_g|) and (|Ψ_g〉) states are parametrized in a different way.

$\begin{array}{c}\hfill \langle {\mathrm{\Psi }}_g|=\langle \mathrm{\Phi }|(1+\mathrm{\Lambda })e^{-T}\end{array}(17)$

$\begin{array}{c}\hfill |{\mathrm{\Psi }}_g\rangle =e^T|\mathrm{\Phi }\rangle ,\end{array}(18)$

where the reference function |Φ⟩ is typically chosen as a Hartree-Fock Slater determinant (for the original papers on the CC ansatz see Coester, 1958; Coester and Kümmel, 1960; Čížek, 1966; Paldus et al., 1972; Purvis and Bartlett, 1982; Paldus and Li, 1999; Bartlett and Musiał, 2007). In the above equations the T and Λ operators refer to the so-called cluster and de-excitation operators, respectively, which can be obtained by solving canonical CC equations for the N-electron system. For simplicity, in this review we will discuss the algebraic form of the retarded part of the frequency dependent CC Green’s function defined by matrix elements $G_{pq}^R(\omega )$:

$G_{pq}^R(\omega )=⟨{\mathrm{\Psi }}_g|c_q^{†}{(\omega +(H-E_0)-i\eta )}^{-1}{c}_p|{\mathrm{\Psi }}_g⟩.(19)$

Here H is the electronic Hamiltonian for the N-electron system, E₀ the corresponding ground-state energy, η is a broadening factor, and c_p ($c_q^{†}$) operator is an annihilation (creation) operator for an electron in the q-th spin-orbital. The bi-variational CC formalism then leads to a formula for the general matrix element $G_{pq}^R(\omega )$ given by:

$G_{pq}^R(\omega )=⟨\mathrm{\Phi }|(1+\mathrm{\Lambda })\overline{c_q^{†}}{(\omega +{\bar{H}}_N-\text{i}\eta )}^{-1}{\bar{c}}_p|\mathrm{\Phi }⟩,(20)$

The similarity transformed operators here $\bar{A}$ ($A=H,c_p,c_q^{†}$) are defined as $\bar{A}=e^{-T}A{e}^T$. By defining ω-dependent auxiliary operators X_p(ω)

$\begin{array}{c}\hfill X_p(\omega )=X_{p,1}(\omega )+X_{p,2}(\omega )+\dots \\ =\sum _i{x}^i{(\omega )}_p{c}_i+\sum _{i<j,a}{x}_a^{ij}{(\omega )}_p{c}_a^{†}{c}_j{c}_i+\dots ,{\forall }_p\hfill \end{array}(21)$

that satisfy equations

$(\omega +{\bar{H}}_N-\text{i}\eta )X_p(\omega )|\mathrm{\Phi }\rangle ={\bar{c}}_p|\mathrm{\Phi }\rangle ,(22)$

Equation 20 can then be re-expressed compactly as

$G_{pq}^R(\omega )=⟨\mathrm{\Phi }|(1+\mathrm{\Lambda })\overline{c_q^{†}}{X}_p(\omega )|\mathrm{\Phi }⟩.(23)$

The X_p(ω) operators can be effectively solved using a parallel implementation of the GFCC formalism based on the approximate forms of T, Λ, and X_p(ω) (Peng et al., 2021).

The RT-EOM-CC Green’s function differs from the frequency-space GFCC approaches (Peng and Kowalski, 2016; Peng and Kowalski, 2018b) in several respects. In particular RT-EOM-CC is based on a transformation to an initial value problem with the propagation of the N − 1 particle system carried out after the creation of the core-hole; in contrast the GFCC methods are implemented in frequency-space. In addition, RT-EOM-CC assumes an uncorrelated N-particle single-determinant ground state, while the GFCC approaches calculate this ground state using the CC ansatz (Eq. 17 and Eq. 18). Finally, the RT-EOM-CC cumulant treats the N − 1 particle excited states at the CCS level, while the GFCCSD approximation solves for the excitations of the N − 1 particle system at the approximate CCSD level, keeping only single and double excitations, as discussed near Eq. 14 of Peng and Kowalski, 2018a. Thus high order diagrams are implicitly built in the RT-EOM-CC GF from the exponential form of the cumulant (Gunnarsson et al., 1994; Lange and Berkelbach, 2018). While the RT-EOM-CC utilizes a unique approximation for the time-dependent T(t) operator, the GFCC formalisms permit the use of several levels of approximation for the T, Λ and X_p(ω) operators (for assuring size-extensivity of diagrams defining the $G_{pq}^R(\omega )$ matrix elements, the “n+1” rule of Peng and Kowalski, 2018b has to be followed). The numerical complexities of the RT-EOM-CC and GFCC methods, aside from complicated tensor contractions, originate in the time propagation algorithms, and the need for solving a large number of linear equations for frequency domain, respectively. Efficient algorithms have already been tested to alleviate possible numerical problems and instabilities (Peng et al., 2019; Peng et al., 2021).

2.4 X-Ray Spectra

Our treatment here is adapted from that in our original EOM-CC paper (Rehr et al., 2020), but updated here with a more detailed treatment of the EOM discussed above. As outlined in the introduction, the contribution from a deep core level |c⟩ to the XAS is given by the time-correlation function μ(t) = L(t)G_c(t) in Eq. 2, as in Nozieres and de Dominicis, 1969 and Rehr et al., 2020. The core-hole Green’s function G_c can be obtained from the RT-EOM-CC Eq. 8. Calculations of L(t), the one-body time-dependent transition amplitude, can be carried out using coupled equation of motion or equivalent integral equations (Langreth, 1969; Grebennikov et al., 1977; Privalov et al., 2001). Alternatively, propagation based on the overlap integrals u_ij(t) can also be used, as done by Nozieres and Combescot (NC) (Nozieres and Combescot, 1971). However, it is more convenient to replace the sums over k with the complete set of eigenstates κ of the final state one-particle Hamiltonian $h^{\prime }={\sum }_{\kappa }{ϵ}_{\kappa }{c}_{\kappa }^{†}{c}_{\kappa }$. Then, defining the core transition operator D in terms of the transition matrix elements M_cκ = ⟨c|d|κ⟩, $D={\mathrm{\Sigma }}_{\kappa }{M}_{c\kappa }{c}_{\kappa }^{†}{c}_c$, the single-particle XAS amplitude L(t) becomes.

$\begin{array}{c}\hfill L(t)=\sum _{\kappa ,{\kappa }^{\prime }}{M}_{c\kappa }^{*}{M}_{c{\kappa }^{\prime }}{L}_{\kappa ,{\kappa }^{\prime }}(t),\end{array}(24)$

$\begin{array}{c}\hfill L_{\kappa ,{\kappa }^{\prime }}(t)=e^{i{ϵ}_{\kappa }t}\left[u_{\kappa ,{\kappa }^{\prime }}(t)-\sum _{ij}^{occ}{u}_{\kappa i}(t)u_{ij}^{-1}(t)u_{j{\kappa }^{\prime }}(t)\right].\end{array}(25)$

The leading term on the rhs of Eq. 25 can be interpreted as a contribution to L_κ,κ′(t) from the independent particle transition amplitude for the final state when the core-hole is present L₀(t) = Σ_κ|M_cκ|²  exp(iϵ_κt), consistent with the final-state rule of von Barth and Grossman (von Barth and Grossmann, 1982). The diagonal terms κ = κ′ in Eq. 25 suppress transitions to the occupied states κ < k_F by yielding the theta function θ(k_F − k). The off-diagonal terms in L_κ,κ′(t) are controlled by states with either κ (or κ′) > k_F or κ′ (or κ) < k_F. Interestingly the net result can be approximated accurately by the expression

$L(t)\approx \sum _{\kappa }|{\tilde{M}}_{c\kappa }{|}^2{e}^{i{ϵ}_{\kappa }t},(26)$

equivalent to the one derived by Friedel (Friedel, 1969), where ${\tilde{M}}_{c\kappa }=⟨c|d\bar{P}|\kappa ⟩$, and $\bar{P}=1-{\mathrm{\Sigma }}_{i=1}^N|i\rangle \langle i|$ projects out the occupied valence states in the ground state. Note that the sum-rule ∫dω μ(ω) = πL(0) for the XAS is also preserved by this formula. The additional terms −Σ_i⟨c|d|i⟩⟨i|κ⟩ from $\bar{P}$ are termed replacement transitions (Friedel, 1969). Physically, these terms are necessary to remove transitions into the initial occupied levels. First order perturbation theory shows that, for an attractive core-hole potential and κ > i, the integral for the overlap⟨i|κ⟩ ≈ −v_ik/ω_ik < 0. Thus these terms imply an intrinsic edge enhancement factor L/L₀ = (1 + χ_κ) for each photoelectron level κ in the XAS where ${\chi }_{\kappa }\approx -2{\mathrm{\Sigma }}_{i=1}^N(M_{ci}/M_{c\kappa })⟨i|\kappa ⟩$. Though this edge-enhancement effect is non-singular in molecular systems, it is consistent with the power-law singularity ${\mu }_1\sim |(ϵ-{ϵ}_F)/{ϵ}_F{|}^{-2{\delta }_l/\pi }$ predicted by Mahan for metallic systems (Mahan, 1967). The XAS in Eq. 1 is finally given by a convolution of μ₁(ω) with the spectral function A_c(ω). It is convenient to shift μ₁(ω) and A_c(ω) by ϵ_c, the energy of the core level, with ω = ϵ−ϵ_c, so that for the non-interacting system, μ₁(ω) reduces to the independent particle XAS. The shifted A_c(ω) then accounts for the shake-up excitation spectrum

$A_c(\omega )=\sum _n|S_n{|}^2\delta (\omega -{ϵ}_n).(27)$

Here $S_n=⟨{\mathrm{\Psi }}_c|{\mathrm{\Psi }}_n^{\prime }⟩$ is the N − 1, many-body overlap integral, and ${ϵ}_n=E_n^{\prime }-E_0$ is the shake-up energy. The net effect of the spectral function A_c(ω) is to broaden the XAS and significantly reduce its magnitude near the edge, transferring the weight to the satellite peaks. For metallic systems this yields an Anderson power-law singularity ${\left[\left(ϵ-{ϵ}_F\right)/{ϵ}_F\left.\right)\right]}^{\alpha }$ (Nozieres and de Dominicis, 1969). This reduction effect has opposite sign to and competes with the Mahan enhancement L/L₀ in μ₁(ω). However, the above formulation neglects extrinsic losses and interference effects, which will likely lessen these effects. The net result, however, is a many-body amplitude correction to the independent particle XAS visible in experimental XPS. This spectrum is proportional to the spectral function J_k(ω) ∼ A_c (ω − ϵ_k), and usually measured vs photoelectron energy ϵ_k at fixed photon energy ω. Thus the peaks in the XPS correspond to a quasiparticle peak as well as satellite excitations at higher binding energies, as discussed in more detail below.

3 Results and Discussion

As an example of the accuracy of the RT-EOM-CCS method for core ionization energies we show results for CH₄, NH₃, H₂O, HF and Ne, i.e. the ten-electron series, using the experimental geometries (NIST, 2019) for all systems (r_CH = 1.087 Å, r_NH = 1.012 Å, a_HNH = 106.67 degree, r_OH = 0.958 Å, a_HOH = 104.48 degree, r_FH = 0.917 Å), and the aug-cc-pVDZ basis set (Kendall et al., 1992). We also show spectral function and XAS results for NH₃ for which experimental values are available in the literature. The ground state single-particle states and molecular orbitals integrals for the RT-EOM-CCS approach and the ΔSCF method were calculated from a Hartree-Fock (HF) reference, while those for the core-excited ΔSCF were derived from a spin-symmetric and occupation-constrained HF reference. The final spectra were broadened to compare with experiment as in Rehr et al., 2020 and Vila et al., 2020 with varying (1–6 eV) broadening to account for the limited basis set for the continuum; similarly XAS used constant broadening consistent with experimental broadening below and 3.5 eV above the binding energy.

Figure 2 shows a comparison of errors vs experiment for the core binding energies of the ten-electron series molecules. The RT-EOM-CCS method shows small errors even at the simplest non-linear level of approximation (2_NL), with a mean-absolute error (MAE) across systems of only 0.5 eV, significantly smaller than for the other methods tested. Although better core-optimized basis sets need to be tested to ensure full convergence with basis set size, we find (Vila et al., 2020) similar errors even for smaller basis sets (e.g. DZVP and cc-pVDZ). We emphasize that these accurate results arise from the non-linear terms in $v_{ij}^{ab}$ in the expression of the cumulant (Eq. 14), which reduce the error typically by an order of magnitude. Of the ten-electron systems, the Ne atom has the smallest MAE across the methods (0.3 eV), while for the molecules the MAE increases systematically from CH₄ (0.4 eV) to HF (0.8 eV). It should be noted that these results do not include contributions from changes in the vibrational zero point energy (which are expected to be an order of magnitude smaller) or from relativistic effects. The latter can be significant even for these light elements (Keller et al., 2020). For instance, the inclusion of relativistic effects in the calculation of the C, N, O and F atoms increases the 1s core binding energies by 0.1, 0.3, 0.5 and 0.8 eV, respectively (Pueyo Bellafont et al., 2016). If these corrections are applied to our results the MAE are reduced by 50%.

FIGURE 2

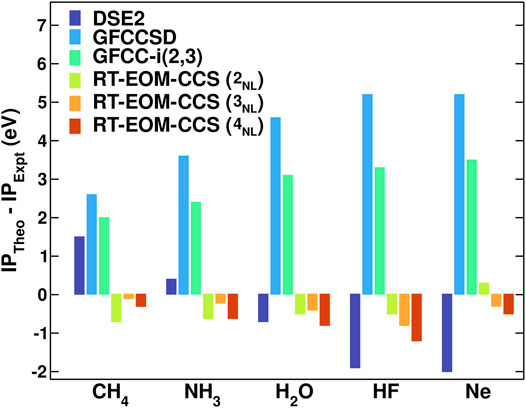
FIGURE 2. Comparison of the theory errors vs experiment (Karlsen et al., 2002; Buttersack et al., 2019; Viñes et al., 2018; Jolly et al., 1984; Williams, 2009) for the core binding energies. The theoretical calculations were performed with the 2-4_NL RT-EOM-CCS approximations with the aug-cc-pVDZ basis set. Also shown are results from the second order Dyson equation (DSE2) and the standard GFCCSD and GFCC-i (2, 3) coupled-cluster Green’s function methods (Peng and Kowalski, 2016; Peng and Kowalski, 2018a).

Figure 3 shows results for the spectral function A_c(ω) and the cumulant kernel β(ω). These are shown vs. binding energy to compare more readily to the experimental XPS. β(ω) is dominated by shake-up excitation peaks about 20–30 eV above the quasiparticle peak that correspond precisely with the inelastic losses in A_c(ω). The satellites structure is in reasonable agreement with that observed in XPS (Sankari et al., 2006) once scissors corrections are included, despite the fact that our HF-based Hamiltonian overestimates the excitation energies. From the Landau form in Eq. 4, the strength of the quasi-particle peak is defined by the renormalization constant Z, where for the 4_NL approximation to the EOM-CC cumulant Z = exp (−a) = 0.70. The satellite strength is a = ∫dω β(ω)/ω² = 0.35. This matches the numerical integration over the QP peak that yields Z = 0.70, in good agreement with the ΔSCF value Z = 0.76. The renormalization constant Z is also partly responsible for the amplitude reduction factor $S_0^2$ for the XAS fine structure (Rehr et al., 1978). We also find that the RT-EOM-CCS values for Z agree with those obtained using the frequency-space CC Green’s function methods (Peng and Kowalski, 2016; Peng and Kowalski, 2018a). Moreover, the energy shift Δ from the middle term in Eq. 5 is the “relaxation energy,” that introduces electron-electron correlations corrections to the Koopmans’ theorem approximation of the core binding energy. Here we find that Δ = ∫dω β(ω)/ω = 17.1 eV, with a core binding energy E_b = |ϵ_c|−Δ = 406.1 eV, in good agreement with the experimental value of 405.52 eV, and the position of the quasiparticle peak in A_c(ω) at 404.9 eV.

FIGURE 3

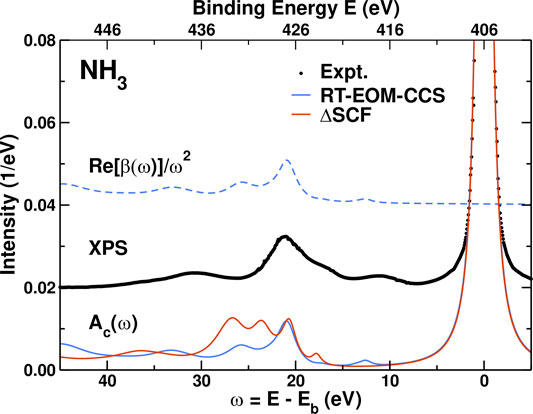
FIGURE 3. Comparison of the 4_NL RT-EOM-CCS and ΔSCF core spectral functions A_c(ω) (full lines) and cumulant kernel β(ω) (dashed lines, shown only for the RT-EOM-CC method) for the NH₃ molecule, to the experimental XPS (dots) (Sankari et al., 2006). Energies are shows in either absolute binding energy E or versus excitation energy ω = E−E_b with respect to the experimental core binding energy E_b = 405.52 eV (Sankari et al., 2006). All the theoretical results were obtained with the aug-cc-pVDZ basis set. The theoretical A_c(ω) were broadened and include a scissors shift of 3.9 eV.

Results for the XAS, including experiment (Wight and Brion, 1974), are shown in Figure 4. The overall agreement between theory and experiment is quite good for the positions and relative intensities of the first two peaks. The third peak, at 403.5 eV, is almost in the continuum and is more difficult to describe with our limited basis set. For this molecule, the corrections to the independent particle XAS (L₀(ϵ)) are clearly visible: First, the edge enhancement factor 1 + χ increases the intensity to L(ϵ). Second, the amplitude reduction factor from the spectral function A_c(ϵ), which has opposite sign and is approximately twice as strong, reduces the intensity to the final μ(ϵ). Since the leading satellites peaks in A_c(ϵ) are 20–30 eV above the QP peak, the corresponding XAS satellite features fall in the continuum and are thus not visible.

FIGURE 4

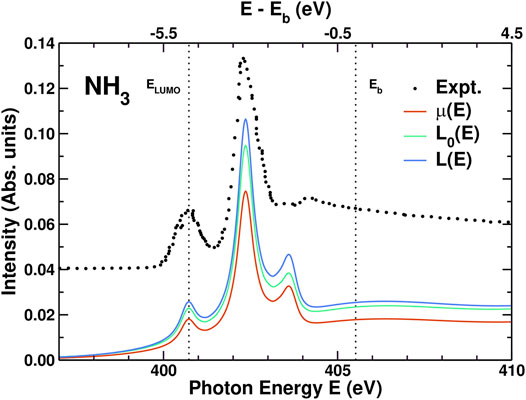
FIGURE 4. Comparison of the experimental XAS μ(E) for NH₃ (Wight and Brion, 1974) vs photon energy E to those calculated from the convolution in Eq. 2, the effective one-body XAS L(E) = μ₁(E) and the independent particle XAS L₀(E) = μ₀(E) from Eq. 25. The N x-ray K edge lies just under E_LUMO while E_b is the ionization threshold. In order to account for the sparsity of the Gaussian-type orbital basis set in the continuum region above E_b, the comparison to experiment includes variable broadening (see text) that increases to a maximum of 3.5 eV above E_b.

4 Conclusions

This review describes a combined equation of motion coupled cluster approach in real-time to calculate excitations corresponding to intrinsic losses in XAS and XPS. The approach is based on the cumulant form of the Green’s function representation for the core-hole spectral function that arises naturally from the coupled cluster ansatz. This theoretical connection between the cumulant approach, a powerful tool for computing satellites in solid state physics, to the coupled cluster approach which is the gold standard for accuracy in quantum chemistry brings together two previously mostly unrelated fields, thus opening new areas of research. Unlike our previous treatment of the XAS, where an approximate, effective single-particle Hamiltonian was used, here we use the full two-particle one, yet for simplicity we still limit the representation of the reference wavefunctions functions to single-determinants. We show that the cumulant form aids in both the physical interpretation of many-body effects observed in the spectra as well as the numerical simulations. We find that, for the XAS, a convolution form in terms of an effective single-particle spectrum and the core-hole spectral function is key to accounting for two types of many-body effects: First, inelastic losses caused by shake up excitations, accounted for the spectral function. Second the edge enhancement due to orthogonality. Both effects modulate the XAS amplitude in opposite direction near threshold, despite being non-singular for molecular systems. Interference terms and extrinsic losses from the coupling between the core-hole and the photoelectron are ignored. Nevertheless, these effects tend to cancel due to their opposite signs. The formal behavior of the RT-EOM-CC cumulant Green’s function is similar to that in other approaches, e.g., field-theoretic methods such as the linked-cluster theorem, or the quasi-boson approximation (Nozieres and de Dominicis, 1969; Langreth, 1970; Hedin, 1999). For condensed matter systems, the cumulant kernel function β(ω) is directly connected to the loss function or the screened Coulomb interaction, and represents collective excitations such as density fluctuations arising from the sudden creation of the core-hole (Langreth, 1970; Kas and Rehr, 2017). Other extensions to the approach reviewed here are feasible. For instance, an analogous treatment is possible to study x-ray emission spectra instead of XAS (Nozieres and Combescot, 1971) by changing the unoccupied single-particle states for the occupied ones. Finally, bigger systems computed with a more user-friendly and efficient implementation, including higher excitations, will be presented elsewhere.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author Contributions

All authors contributed to the derivation of the theory described in this work and to the writing of the manuscript. FV developed the EOM-CC code and performed all the calculations behind the results presented except for the GFCCSD and GFCC-i(2,3) which were performed by BP.

Funding

This work was supported by the Computational Chemical Sciences Program of the U.S. Department of Energy, Office of Science, BES, Chemical Sciences, Geosciences and Biosciences Division in the Center for Scalable and Predictive methods for Excitations and Correlated phenomena (SPEC) at the Pacific Northwest National Laboratory. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a U.S. Department of Energy Office of Science User Facility located at Lawrence Berkeley National Laboratory, operated under Contract No. DE-AC02-05CH11231.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank N. Hirshberg, X. Li, J. Lisschner, D. Prendergast, K. Schönhammer, and M. Tzavala, for comments. BP also acknowledges the support of Laboratory Directed Research and Development (LDRD) program from PNNL.

References

Arponen, J. (1983). Variational Principles and Linked-Cluster Exp S Expansions for Static and Dynamic many-body Problems. Ann. Phys. 151, 311–382. doi:10.1016/0003-4916(83)90284-1

CrossRef Full Text | Google Scholar

Aryasetiawan, F., Hedin, L., and Karlsson, K. (1996). Multiple Plasmon Satellites in Na and Al Spectral Functions from Ab Initio Cumulant Expansion. Phys. Rev. Lett. 77, 2268–2271. doi:10.1103/physrevlett.77.2268

PubMed Abstract | CrossRef Full Text | Google Scholar

Bartlett, R. J., and Musiał, M. (2007). Coupled-cluster Theory in Quantum Chemistry. Rev. Mod. Phys. 79, 291–352. doi:10.1103/revmodphys.79.291

CrossRef Full Text | Google Scholar

Bertsch, G. F., and Lee, A. J. (2014). Time-dependent Mean-Field Theory for X-ray Near-Edge Spectroscopy. Phys. Rev. B 89, 075135. doi:10.1103/physrevb.89.075135

CrossRef Full Text | Google Scholar

Bhaskaran-Nair, K., Kowalski, K., and Shelton, W. A. (2016). Coupled Cluster Green Function: Model Involving Single and Double Excitations. J. Chem. Phys. 144, 144101. doi:10.1063/1.4944960

CrossRef Full Text | Google Scholar

Brandow, B. H. (1967). Linked-cluster Expansions for the Nuclear many-body Problem. Rev. Mod. Phys. 39, 771–828. doi:10.1103/revmodphys.39.771

CrossRef Full Text | Google Scholar

Buttersack, T., Mason, P. E., McMullen, R. S., Martinek, T., Brezina, K., Hein, D., et al. (2019). Valence and Core-Level X-ray Photoelectron Spectroscopy of a Liquid Ammonia Microjet. J. Am. Chem. Soc. 141, 1838–1841. doi:10.1021/jacs.8b10942

PubMed Abstract | CrossRef Full Text | Google Scholar

Čížek, J. (1966). On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 45, 4256–4266.

Google Scholar

Coester, F. (1958). Bound States of a many-particle System. Nucl. Phys. 7, 421–424. doi:10.1016/0029-5582(58)90280-3

CrossRef Full Text | Google Scholar

Coester, F., and Kümmel, H. (1960). Short-range Correlations in Nuclear Wave Functions. Nucl. Phys. 17, 477–485. doi:10.1016/0029-5582(60)90140-1

CrossRef Full Text | Google Scholar

Crawford, T. D., and Schaefer, H. F. (2000). An Introduction to Coupled Cluster Theory for Computational Chemists. Rev. Comp. Ch. 14, 33–136.

Google Scholar

Friedel, J. (1969). X-ray Absorption and Emission Edges in Metals. Comments Solid State. Phys. 2, 21.

Google Scholar

Grebennikov, V., Babanov, Y., and Sokolov, O. (1977). Extra-atomic Relaxation and X-ray Spectra of Narrow-Band Metals. I. Formalism. Phys. Stat. Sol. (B) 79, 423. doi:10.1002/pssb.2220790204

CrossRef Full Text | Google Scholar

Gunnarsson, O., Meden, V., and Schönhammer, K. (1994). Corrections to Migdal’s Theorem for Spectral Functions: A Cumulant Treatment of the Time-dependent Green’s Function. Phys. Rev. B 50, 10462–10473. doi:10.1103/physrevb.50.10462

PubMed Abstract | CrossRef Full Text | Google Scholar

Guzzo, M., Lani, G., Sottile, F., Romaniello, P., Gatti, M., Kas, J. J., et al. (2011). Valence Electron Photoemission Spectrum of Semiconductors: Ab Initio Description of Multiple Satellites. Phys. Rev. Lett. 107, 166401. doi:10.1103/physrevlett.107.166401

PubMed Abstract | CrossRef Full Text | Google Scholar

Hedin, L. (1999). On Correlation Effects in Electron Spectroscopies and the GW Approximation. J. Phys. Condens. Matter 11, R489. doi:10.1088/0953-8984/11/42/201

CrossRef Full Text | Google Scholar

Jolly, W., Bomben, K., and Eyermann, C. (1984). Core-electron Binding Energies for Gaseous Atoms and Molecules. Atom. Data Nucl. Data 31, 433–493. doi:10.1016/0092-640x(84)90011-1

CrossRef Full Text | Google Scholar

Karlsen, T., Børve, K. J., Sæthre, L. J., Wiesner, K., Bässler, M., and Svensson, S. (2002). Toward the Spectrum of Free Polyethylene: Linear Alkanes Studied by Carbon 1s Photoelectron Spectroscopy and Theory. J. Am. Chem. Soc. 124, 7866–7873. doi:10.1021/ja010649j

CrossRef Full Text | Google Scholar

Kas, J. J., and Rehr, J. J. (2017). Finite Temperature Green’s Function Approach for Excited State and Thermodynamic Properties of Cool to Warm Dense Matter. Phys. Rev. Lett. 119, 176403. doi:10.1103/physrevlett.119.176403

PubMed Abstract | CrossRef Full Text | Google Scholar

Keller, L., Blum, V., Rinke, P., and Golze, D. (2020). Relativistic Correction Scheme for Core-Level Binding Energies from GW. J. Chem. Phys. 153, 114110. doi:10.1063/5.0018231

CrossRef Full Text | Google Scholar

Kendall, R. A., Dunning, T. H., and Harrison, R. J. (1992). Electron Affinities of the First-Row Atoms Revisited. Systematic Basis Sets and Wave Functions. J. Chem. Phys. 96, 6796–6806. doi:10.1063/1.462569

CrossRef Full Text | Google Scholar

Kowalski, K., Bhaskaran-Nair, K., and Shelton, W. A. (2014). Coupled-cluster Representation of Green Function Employing Modified Spectral Resolutions of Similarity Transformed Hamiltonians. J. Chem. Phys. 141, 094102. doi:10.1063/1.4893527

PubMed Abstract | CrossRef Full Text | Google Scholar

Landau, L. (1944). On the Energy Loss of Fast Particles by Ionization. J. Phys. USSR 8, 201–205.

Google Scholar

Lange, M. F., and Berkelbach, T. C. (2018). On the Relation between Equation-Of-Motion Coupled-Cluster Theory and the GW Approximation. J. Chem. Theor. Comput. 14, 4224–4236. doi:10.1021/acs.jctc.8b00455

PubMed Abstract | CrossRef Full Text | Google Scholar

Langreth, D. C. (1969). Singularities in the X-ray Absorption and Emission of Metals. Phys. Rev. 182, 973–974. doi:10.1103/physrev.182.973

CrossRef Full Text | Google Scholar

Langreth, D. C. (1970). Singularities in the X-ray Spectra of Metals. Phys. Rev. B 1, 471–477. doi:10.1103/physrevb.1.471

CrossRef Full Text | Google Scholar

Lee, A. J., Vila, F. D., and Rehr, J. J. (2012). Local Time-Correlation Approach for Calculations of X-ray Spectra. Phys. Rev. B 86, 115107. doi:10.1103/physrevb.86.115107

CrossRef Full Text | Google Scholar

Liang, Y., and Prendergast, D. (2019). Taming Convergence in the Determinant Approach for X-ray Excitation Spectra. ArXiv:1905.00542v1.

Liang, Y., Vinson, J., Pemmaraju, S., Drisdell, W. S., Shirley, E. L., and Prendergast, D. (2017). Accurate X-ray Spectral Predictions: An Advanced Self-Consistent-Field Approach Inspired by many-body Perturbation Theory. Phys. Rev. Lett. 118, 096402. doi:10.1103/PhysRevLett.118.096402

PubMed Abstract | CrossRef Full Text | Google Scholar

Linderberg, J., and Öhrn, Y. (2004). Propagators in Quantum Chemistry. Wiley. Theoretical chemistry.

Mahan, G. D. (1967). Excitons in Metals: Infinite Hole Mass. Phys. Rev. 163, 612. doi:10.1103/physrev.163.612

CrossRef Full Text | Google Scholar

Meissner, L., and Bartlett, R. J. (1993). Electron Propagator Theory with the Ground State Correlated by the Coupled-Cluster Method. Int. J. Quan. Chem. 48, 67–80. doi:10.1002/qua.560480810

CrossRef Full Text | Google Scholar

Nist, (2019). in NIST Computational Chemistry Comparison and Benchmark Database. Editor R. D. Johnson III (NIST). vol. Release 20 of NIST Standard Reference Database Number 101. doi:10.18434/T47C7Z

CrossRef Full Text

Nooijen, M., and Snijders, J. G. (1992). Coupled Cluster Approach to the Single-Particle Green’s Function. Int. J. Quan. Chem. 44, 55–83. doi:10.1002/qua.560440808

CrossRef Full Text | Google Scholar

Nooijen, M., and Snijders, J. G. (1993). Coupled Cluster Green’s Function Method: Working Equations and Applications. Int. J. Quan. Chem. 48, 15–48. doi:10.1002/qua.560480103

CrossRef Full Text | Google Scholar

Nooijen, M., and Snijders, J. G. (1995). Second Order many-body Perturbation Approximations to the Coupled Cluster Green’s Function. J. Chem. Phys. 102, 1681–1688. doi:10.1063/1.468900

CrossRef Full Text | Google Scholar

Nozieres, P., and Combescot, M. (1971). Infrared Catastrophy and Excitons in the X-ray Spectra of Metals. J. de Physique 32, 11.

CrossRef Full Text | Google Scholar

Nozieres, P., and de Dominicis, C. (1969). Singularities in the X-ray Absorption and Emission of Metals. III. One-Body Theory Exact Solution. Phys. Rev. 178, 1097. doi:10.1103/physrev.178.1097

CrossRef Full Text | Google Scholar

Paldus, J., Čížek, J., and Shavitt, I. (1972). Correlation Problems in Atomic and Molecular Systems. IV. Extended Coupled-Pair many-electron Theory and its Application to the BH₃ Molecule. Phys. Rev. A. 5, 50–67. doi:10.1103/physreva.5.50

CrossRef Full Text | Google Scholar

Paldus, J., and Li, X. (1999). A Critical Assessment of Coupled Cluster Method in Quantum Chemistry. Adv. Chem. Phys. 110, 1–175.

Google Scholar

Peng, B., and Kowalski, K. (2016). Coupled-cluster Green’s Function: Analysis of Properties Originating in the Exponential Parametrization of the Ground-State Wave Function. Phys. Rev. A. 94, 062512. doi:10.1103/physreva.94.062512

CrossRef Full Text | Google Scholar

Peng, B., and Kowalski, K. (2018b). Green’s Function Coupled Cluster Formulations Utilizing Extended Inner Excitations. J. Chem. Phys. 149, 214102. doi:10.1063/1.5046529

CrossRef Full Text | Google Scholar

Peng, B., and Kowalski, K. (2018a). Green’s Function Coupled-Cluster Approach: Simulating Photoelectron Spectra for Realistic Molecular Systems. J. Chem. Theor. Comput. 14, 4335–4352. doi:10.1021/acs.jctc.8b00313

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, B., Panyala, A., Kowalski, K., and Krishnamoorthy, S. (2021). GFCCLib: Scalable and Efficient Coupled-Cluster Green’s Function Library for Accurately Tackling many-body Electronic Structure Problems. Computphys. Commun. 265, 108000. doi:10.1016/j.cpc.2021.108000

CrossRef Full Text | Google Scholar

Peng, B., Van Beeumen, R., Williams-Young, D. B., Kowalski, K., and Yang, C. (2019). Approximate Green’s Function Coupled Cluster Method Employing Effective Dimension Reduction. J. Chem. Theor. Comput. 15, 3185–3196. doi:10.1021/acs.jctc.9b00172

PubMed Abstract | CrossRef Full Text | Google Scholar

Privalov, T., Gel’mukhanov, F., and Ågren, H. (2001). Role of Relaxation and Time-dependent Formation of X-ray Spectra. Phys. Rev. B 64, 165115. doi:10.1103/physrevb.64.165115

CrossRef Full Text | Google Scholar

Pueyo Bellafont, N., Viñes, F., and Illas, F. (2016). Performance of the Tpss Functional on Predicting Core Level Binding Energies of Main Group Elements Containing Molecules: A Good Choice for Molecules Adsorbed on Metal Surfaces. J. Chem. Theor. Comput. 12, 324–331. doi:10.1021/acs.jctc.5b00998

CrossRef Full Text | Google Scholar

Purvis, G., and Bartlett, R. (1982). A Full Coupled-Cluster Singles and Doubles Model: The Inclusion of Disconnected Triples. J. Chem. Phys. 76, 1910–1918. doi:10.1063/1.443164

CrossRef Full Text | Google Scholar

Rehr, J. J., Kas, J. J., Prange, M. P., Sorini, A. P., Takimoto, Y., and Vila, F. (2009). Ab Initio theory and Calculations of X-ray Spectra. CR Phys. 10, 548–559. doi:10.1016/j.crhy.2008.08.004

CrossRef Full Text | Google Scholar

Rehr, J. J., Stern, E. A., Martin, R. L., and Davidson, E. R. (1978). Extended x-ray-absorption fine-structure Amplitudes—Wave-Function Relaxation and Chemical Effects. Phys. Rev. B 17, 560–565. doi:10.1103/physrevb.17.560

CrossRef Full Text | Google Scholar

Rehr, J. J., Vila, F. D., Kas, J. J., Hirshberg, N., Kowalski, K., and Peng, B. (2020). Equation of Motion Coupled-Cluster Cumulant Approach for Intrinsic Losses in X-ray Spectra. J. Chem. Phys. 152, 174113. doi:10.1063/5.0004865

CrossRef Full Text | Google Scholar

Sankari, R., Ehara, M., Nakatsuji, H., Fanis, A. D., Aksela, H., Sorensen, S., et al. (2006). High Resolution O 1s Photoelectron Shake-Up Satellite Spectrum of H₂O. Chem. Phys. Lett. 422, 51–57. doi:10.1016/j.cplett.2006.02.018

CrossRef Full Text | Google Scholar

Schönhammer, K., and Gunnarsson, O. (1978). Time-dependent Approach to the Calculation of Spectral Functions. Phys. Rev. B 18, 6606–6614. doi:10.1103/physrevb.18.6606

CrossRef Full Text | Google Scholar

Stanton, J. F., and Bartlett, R. J. (1993). The Equation of Motion Coupled-Cluster Method. A Systematic Biorthogonal Approach to Molecular Excitation Energies, Transition Probabilities, and Excited State Properties. J. Chem. Phys. 98, 7029–7039. doi:10.1063/1.464746

CrossRef Full Text | Google Scholar

Szabo, A., and Ostlund, N. (1996). Modern Quantum Chemistry: Introduction to Advanced Electronic Structure Theory. Dover Publications). Dover Books on Chemistry.

Thouless, D. (1961). The Quantum Mechanics of Many-Body Systems. (New York: Academic).

Tzavala, M., Kas, J. J., Reining, L., and Rehr, J. J. (2020). Nonlinear Response in the Cumulant Expansion for Core-Level Photoemission. Phys. Rev. Res. 2, 033147. doi:10.1103/PhysRevResearch.2.033147

CrossRef Full Text | Google Scholar

Vila, F. D., Rehr, J. J., Kas, J. J., Kowalski, K., and Peng, B. (2020). Real-time Coupled-Cluster Approach for the Cumulant Green’s Function. J. Chem. Theor. Comput. 16, 6983–6992. doi:10.1021/acs.jctc.0c00639

PubMed Abstract | CrossRef Full Text | Google Scholar

Viñes, F., Sousa, C., and Illas, F. (2018). On the Prediction of Core Level Binding Energies in Molecules, Surfaces and Solids. Phys. Chem. Chem. Phys. 20, 8403–8410. doi:10.1039/c7cp08503f

PubMed Abstract | CrossRef Full Text | Google Scholar

von Barth, U., and Grossmann, G. (1982). Dynamical Effects in X-ray Spectra and the Final-State Rule. Phys. Rev. B 25, 5150–5179. doi:10.1103/physrevb.25.5150

CrossRef Full Text | Google Scholar

Wight, G., and Brion, C. (1974). K-shell Excitation of CH₄, NH₃, H₂O, CH₃OH, CH₃OCH₃ and CH₃NH₂ by 2.5 keV Electron Impact. J. Electron. Spectrosc. Relat. Phenom. 4, 25–42. doi:10.1016/0368-2048(74)80040-x

CrossRef Full Text | Google Scholar

Williams, G. P. (2009). X-Ray Data Booklet: Section 1.1 ELECTRON BINDING ENERGIES. Berkeley): Lawrence Berkeley National Laboratory.

Zhou, J., Kas, J., Sponza, L., Reshetnyak, I., Guzzo, M., Giorgetti, C., et al. (2015). Dynamical Effects in Electron Spectroscopy. J. Chem. Phys. 143, 184109. doi:10.1063/1.4934965

CrossRef Full Text | Google Scholar