- 1Geophysical Institute, University of Alaska Fairbanks, Fairbanks, AK, United States
- 2Department of Civil and Environmental Engineering, University of Washington, Seattle, WA, United States
Glaciers in High Mountain Asia are an important freshwater resource for large populations living downstream who rely on runoff for hydropower, irrigation, and municipal use. Projections of glacier mass change and runoff therefore have important socio-economic impacts. In this study, we use a new dataset of geodetic mass balance observations of almost all glaciers in the region to calibrate the Python Glacier Evolution Model (PyGEM) using Bayesian inference. The new dataset enables the model to capture spatial variations in mass balance and the Bayesian inference enables the uncertainty associated with the model parameters to be quantified. Validation with historical mass balance observations shows the model performs well and the uncertainty is well captured. Projections of glacier mass change for 22 General Circulation Models (GCMs) and four Representative Concentration Pathways (RCPs) estimate that by the end of the century glaciers in High Mountain Asia will lose between 29 ± 12% (RCP 2.6) and 67 ± 10% (RCP 8.5) of their total mass relative to 2015. Considerable spatial and temporal variability exists between regions due to the climate forcing and glacier characteristics (hypsometry, ice thickness, elevation range). Projections of annual glacier runoff reveal most monsoon-fed river basins (Ganges, Brahmaputra) will hit a maximum (peak water) prior to 2050, while the Indus and other westerlies-fed river basins will likely hit peak water after 2050 due to significant contributions from excess glacier meltwater. Monsoon-fed watersheds are projected to experience large reductions in end-of-summer glacier runoff. Uncertainties in projections at regional scales are dominated by the uncertainty associated with the climate forcing, while at the individual glacier level, uncertainties associated with model parameters can be significant.
1. Introduction
High Mountain Asia has the largest coverage of glaciers outside of the polar regions. The meltwater from these glaciers provides valuable freshwater for hydropower, irrigation, and municipal use to people living downstream (Biemans et al., 2019; Pritchard, 2019). Projections of glacier mass change in this region from up to five global glacier evolution models for an ensemble of General Circulation Models (GCMs) and Representative Concentration Pathways (RCPs) estimate by 2100 the glaciers could lose 45 ± 8% (RCP 2.6) to 69 ± 14% (RCP 8.5) of their total mass relative to 2015 (Hock et al., 2019). These results are consistent with projections from Kraaijenbrink et al. (2017). As a result of glacier mass loss, glacier runoff typically first increases as glacier melt intensifies, but then reaches a peak beyond which annual runoff declines (Jansson et al., 2003). Most river basins in High Mountain Asia are expected to experience maximum glacier runoff (“peak water”) by the middle of the century (Bliss et al., 2014; Lutz et al., 2014; Huss and Hock, 2018). River basins in Southwest and Central Asia will be more adversely affected since the glacier runoff is a significant component of total runoff especially in the dry season (Huss and Hock, 2018). Given the large, growing populations living downstream of these glaciers are already considered to be water stressed, the importance of glacier meltwater is expected to grow in the future, especially in times of drought (Pritchard, 2019). Advancing our understanding of the timing and quantity of peak water is therefore crucial for assisting regional water resources planning and management.
Despite the general consensus that High Mountain Asia is expected to experience significant glacier mass loss by 2100, there is considerable spatial variability and uncertainty associated with these mass loss projections. The spatial variability is predominantly driven by the complex interactions between the summer monsoon and the winter westerly disturbances, which fundamentally alter the timing and amount of precipitation (Kapnick et al., 2014). For example, the balanced/positive mass budgets observed in the Karakoram and Kunlun Shan (Brun et al., 2017; Berthier and Brun, 2019; Shean et al., 2020) are consistent with increasing trends in snow accumulation attributed to stronger winter westerly disturbances (Forsythe et al., 2017; Smith and Bookhagen, 2018). Unfortunately, existing climate datasets are too coarse to accurately resolve precipitation at high altitudes (Immerzeel et al., 2015; Dahri et al., 2016; Wortmann et al., 2018), so most glacier evolution models calibrate a model parameter that adjusts the precipitation (Radić and Hock, 2014). As a result, a model’s ability to resolve spatial variability in precipitation, and consequently mass change, is strongly dependent on the calibration data (Rounce et al., 2020).
Previous models have been calibrated with sparse measurements from less than 100 glaciers (e.g., Marzeion et al., 2012) and/or regional-scale mass balance estimates from a combination of glaciological, geodetic, gravimetric, and altimetric data (e.g., Huss and Hock, 2015; Kraaijenbrink et al., 2017). New datasets of systematic geodetic mass balance observations of nearly all glaciers in High Mountain Asia (Brun et al., 2017; Shean et al., 2020) provide unique opportunities to more accurately resolve the spatial variations in mass balance to inform future projections.
The dominant source of uncertainty in these future projections of mass change comes from the GCMs (Hock et al., 2019). Models quantify this uncertainty by running simulations for an ensemble of GCMs and reporting the mean and variability. The other main sources of uncertainty are simplified model physics and inaccuracies in input data. Uncertainties associated with model physics are difficult to quantify since all existing glacier evolution models are over-parameterized due to the use of limited calibration data. Hence, even if a specific process is not included or poorly represented in a model, the model parameters will likely compensate for it through the calibration. For example, Kraaijenbrink et al. (2017) is the first study that explicitly accounts for the changes in ablation rates due to debris cover, supraglacial ponds, and ice cliffs, yet their projections of glacier mass change are similar to previous studies (Hock et al., 2019). Since the calibration data used in previous studies includes debris-covered glaciers, these surface processes are inherently compensated for by the model parameters. Previous studies have sought to quantify uncertainty associated with model physics by performing sensitivity analyses on the model parameters (e.g., Kraaijenbrink et al., 2017) or on specific components of the model (e.g., Huss and Hock, 2015).
The purpose of this study is to project the mass changes of all glaciers in High Mountain Asia and quantify spatial variations and the resulting impacts on glacier runoff. We use the global Python Glacier Evolution Model (PyGEM) and a new dataset of geodetic glacier mass balances to more accurately resolve the spatial variability of glacier mass change and runoff projections and to quantify the uncertainty associated with model parameters. The calibrated model is validated against available historical direct observations. The calibrated parameter sets are used to run simulations from 2015 to 2100 for an ensemble of GCMs and RCPs. The spatial variability in mass change and runoff are discussed, the timing and quantity of peak water are investigated in detail, and the various sources of uncertainties are evaluated.
2. Data
2.1. Study Area and Glacier Inventory Data
Our study region includes the three primary regions in High Mountain Asia (Central Asia, South Asia West, and South Asia East) from the Randolph Glacier Inventory (RGI; RGI Consortium, 2017) spanning from 65–105°E and 26–46°N (Figure 1). The entire region comprises 95,536 glaciers that cover an area of 97,606 km2 (RGI Consortium, 2017). Meltwater from these glaciers supplies upwards of 40% of the runoff in major river basins (Immerzeel et al., 2010; Armstrong et al., 2019; Zhang et al., 2019), which include the Brahmaputra, Ganges, Indus, Amu Darya, and Tarim. Given the complex topography and large-scale climate systems that affect the glaciers, studies have reported the spatial variability in glacier mass change using 15 RGI subregions (Kraaijenbrink et al., 2017), 12 subregions (Gardelle et al., 2013; Kääb et al., 2015) or 22 subregions (Bolch et al., 2019). Our study uses the 22 subregions from Bolch et al. (2019) for mass change and 14 major river basins for glacier runoff. These river basins are defined based on Vörösmarty et al. (2000) at a 6-min spatial resolution. The percent of the total basin area that is glacierized ranges from less than 0.1 to 3.2% with a mean of 1.2% (Huss and Hock, 2018).
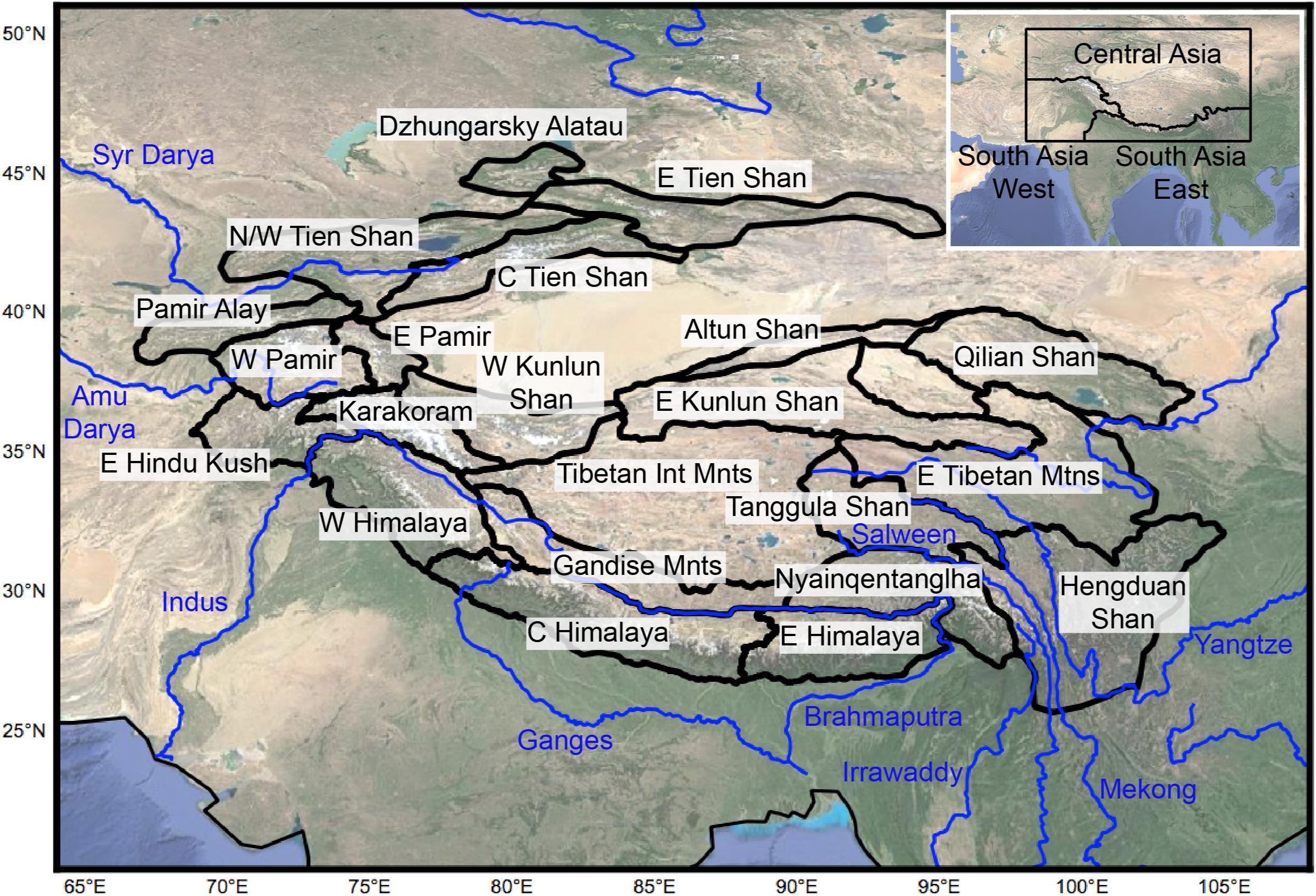
Figure 1. Map of High Mountain Asia showing subregions according to Bolch et al. (2019) (black) and some of the major rivers (blue). Inset shows the location of High Mountain Asia with the three primary RGI regions (RGI Consortium, 2017). Background map data: Google, Digital Globe.
RGIv6.0 is the starting point for PyGEM as it provides general information about each glacier including its glacier Id (RGIId), region, subregion, center latitude, center longitude, and terminus type (RGI Consortium, 2017). Glacier area, ice thickness, and width for every 10 m elevation bin of each glacier is estimated by Huss and Farinotti (2012, updated to RGIv6.0). The total volume for all glaciers in High Mountain Asia is estimated to be 7590 km3, which is well within the uncertainty associated with the recent estimate of 7020 ± 1150 km3 by Farinotti et al. (2019). Compared to all the glaciers in the world excluding the Antarctic and Greenland ice sheets, glaciers in High Mountain Asia account for 44% of the total number of glaciers, 14% of the glacier area, and 4% of the glacier volume (Farinotti et al., 2019). Roughly 11% of this glacier area and 18% of the volume is debris-covered, and if one only considers the ablation area, 30% of the total glacier volume is debris-covered (Kraaijenbrink et al., 2017).
2.2. Climate Data
The glacier evolution model is forced with monthly air temperature, precipitation, and temperature lapse rate data from gridded global climate data. For each glacier, the model uses climate data from the nearest neighboring pixel relative to the glacier’s center latitude and longitude. ERA-Interim reanalysis data from the European Centre for Medium Range Weather Forecasts is used as the reference climate data for model calibration over the period 2000–2018. GCMs from the Coupled Model Intercomparison Project Phase 5 (CMIP5) (Taylor et al., 2012) are used for future simulations over the period 2000–2100.
ERA-Interim reanalysis data provide monthly near-surface (2 m) air temperature (monthly means of daily means), air temperature at various pressure levels (300–1000 hPa), and precipitation (monthly totals of daily data) from 1979 to present at a native resolution of ∼0.7°, which is bilinearly interpolated to a resolution of 0.5° (Dee et al., 2011). The near-surface air temperature is used to calculate the positive degree days and distinguish snow from rain (see Section 3.1), while the pressure level data are used to calculate the monthly temperature lapse rates in the free atmosphere. Precipitation data are converted to monthly precipitation by multiplying the precipitation by the number of days in each month.
Data from 22 GCMs and several RCPs (RCP 2.6, RCP 4.5, RCP 6.0, and RCP 8.5) are used to quantify uncertainty in projections due to the climate model and emission scenario (Supplementary Table S1). The RCP is an emission scenario that is named after the approximate increase in radiative forcing relative to pre-industrial levels that is reached before (RCP 2.6, RCP 4.5), after (RCP 6.0), or near (RCP 8.5) the end of the 21st century. In total, 81 combinations of models and RCP scenarios are used. The resolution of these GCMs ranges from 0.94 to 3.75°. All simulations use the r1i1p1 ensemble member. Monthly temperature lapse rates for the GCMs are estimated from the mean monthly lapse rate from the reference climate data (ERA-Interim) over the calibration period.
Since the model is calibrated with ERA-Interim climate data (see Section 4.1), the GCM temperature and precipitation data are adjusted for each glacier to account for any biases between the two datasets over the calibration period (2000–2018). GCM temperatures from 2000–2100 are adjusted using an additive correction factor ensuring the mean monthly temperature for the period 2000–2018 is equal and the interannual variability in temperature for each month is similar to ERA-Interim following Huss and Hock (2015). Precipitation is adjusted using a multiplicative correction factor ensuring that the monthly mean precipitation is equal and the variability in the monthly mean precipitation is similar. For some glaciers, the mean monthly GCM precipitation is near zero (<10–3 m), which can result in large multiplicative correction factors that cause unrealistic values of monthly precipitation (>10 m). Since precipitation may increase or decrease in the future, the maximum adjusted precipitation in any given month is considered to be the maximum monthly precipitation from the reference period adjusted for future increases or decreases based on the normalized interannual variations. If the monthly precipitation exceeds this maximum adjusted precipitation, the value is replaced by the monthly mean precipitation from the reference period adjusted by the normalized interannual variation for that given year.
3. Glacier Evolution Model
The Python Glacier Evolution Model (PyGEM; Rounce et al., 2020) is an open-source glacier evolution model coded in Python1 that estimates the transient evolution of glaciers. PyGEM has a modular framework that allows different schemes to be used for model calibration or model physics (e.g., climatic mass balance, glacier dynamics). The user-specified schemes and parameterizations selected to run the model depend on data availability, computational resources available, and the focus of the study. The minimum data required to run the model is a glacier inventory (glacier attributes, area, and ice thickness) and climate data (temperature and precipitation). This study also uses glacier thickness, area, and width data for the glacier dynamics scheme. Model parameters need to be calibrated and results should be validated using some form of mass balance (altimetric, glaciological, geodetic, or gravimetric), runoff, snowline, or equilibrium line altitude data. The model has been developed to seamlessly integrate with publicly available glaciological and geodetic measurements (WGMS, 2018), although we have opted to use geodetic measurements from Shean et al. (2020) as they provide an unprecedented level of spatial coverage at a high resolution in the study region.
Here we present an application of PyGEM using model parameterizations for the mass balance and glaciers dynamics that rely heavily on Radić and Hock (2011) and Huss and Hock (2015). Each glacier is modeled independently using a monthly timestep using 10 m elevation bins. The major advance in this study is the application of a Bayesian model (Rounce et al., 2020) to calibrate every glacier in High Mountain Asia and quantify the uncertainty associated with the model parameters. Furthermore, the model is open-source and the bias correction for the precipitation has been modified to avoid unreasonably high values for glaciers located in dry regions. Details of the model parameterizations are described below.
3.1. Mass Balance Components
The specific climatic mass balance (m w.e.) for each elevation bin (10 m) is computed each month as the sum of the ablation, accumulation, and refreezing. Mass loss is negative, while mass gain is positive. Ablation is calculated using a degree-day model based on the monthly mean temperature and number of days per month. The degree-day factors for snow, ice, and firn are assumed to be related to one another to reduce the number of model parameters. The ratio of the degree-day factor for snow to the degree-day factor of ice is 0.7 (Kayastha et al., 2000; Singh et al., 2000; Yong et al., 2006; Huss and Hock, 2015; Lutz et al., 2016), and the degree-day factor of firn is assumed to be the mean of the degree-day factors for snow and ice. This study does not explicitly account for debris cover, but rather treats such surfaces as clean ice.
Temperature for each elevation bin is assigned by selecting the temperature from the gridded climate data (see Section 2.2) based on the nearest neighbor, which is adjusted based on the calibrated temperature bias and then downscaled to each elevation bin based on the temperature lapse rate (Huss and Hock, 2015). As the glacier evolves, the ice thickness in a bin may increase or decrease thereby changing the bins elevation and air temperature. This feedback may greatly alter the glacier’s evolution, so the bin temperature is further adjusted based on the temperature lapse rate derived from ERA-Interim air temperatures at various pressure levels, and the difference between the present ice thickness and the initial ice thickness.
Precipitation at each elevation bin of the glacier is computed using the scheme from Huss and Hock (2015). Precipitation from the gridded climate data (see Section 2.2) based on the nearest neighbors downscaled to each elevation bin using a calibrated precipitation factor and a precipitation gradient on the glacier. The precipitation gradient is assumed to be 0.01% m–1. Additionally, for glaciers with an elevation range that exceeds 1000 m, the precipitation in the uppermost 25% of the glacier’s elevation is reduced using an exponential function to account for reduced air moisture and wind erosion. Accumulation is calculated by partitioning the precipitation into liquid and solid based on the air temperature and snow temperature threshold (assumed to be 1°C). Within ±1°C of the snow temperature threshold, the liquid and solid precipitation ratio is linearly interpolated.
Following Radić and Hock (2011), refreezing is calculated as a function of its weighted annual mean air temperature according to Woodward et al. (1997) and cannot be negative. The model assumes that refreezing occurs in the snow pack as opposed to being superimposed ice, so refreezing cannot exceed the snow depth. In October of each year, any melt is assumed to refreeze up to the maximum refreeze potential; after which the snow and refreezing completely melts and the model can melt the underlying ice or firn.
3.2. Surface Type
The glacier surface is classified as snow, firn, or ice. Initially, the surface type is defined based on the glacier’s median elevation (Braithwaite and Raper, 2009), with higher elevations classified as firn and lower elevations classified as ice. The surface type evolves based on the 5-year running average of the glacier bin’s annual climatic mass balance (Huss and Hock, 2015). If the 5-year running average is positive, the surface is classified as firn; if negative, the surface is classified as ice. The surface type is classified as snow when snow accumulates on the surface.
3.3. Glacier Area and Elevation Changes
Glacier geometry changes in large-scale glacier evolution models typically rely on volume-area-length scaling (e.g., Radić and Hock, 2011), mass redistribution using empirical equations (e.g., Huss and Hock, 2015), or simplified glacier flow models (e.g., Maussion et al., 2019; Zekollari et al., 2019). These methods all allow the glacier to evolve over time in response to the total glacier-wide mass balance. The benefit of volume-area-length scaling and mass redistribution is that they are computationally inexpensive.
This study uses the mass redistribution curves developed by Huss and Hock (2015) based on Huss et al. (2010). The approach is only applied to glaciers that have at least three elevation bins. At the end of each mass-balance year the glacier-wide annual mass change is redistributed over the glacier using empirical equations that set the normalized surface elevation change as a function of the glacier’s elevation bins. The glacier bed is assumed to be parabolic. Here, we explicitly solve for the updated glacier area (A), width (W), and ice thickness (H) based on mass conservation and similar shapes as follows:
This avoids any mass loss or gain that can result from not solving for the area and ice thickness simultaneously, which was the case for Huss and Hock (2015) and required them to perform an additional correction of the ice thickness after updating the area in order to enforce mass conservation.
Modeled glacier retreat occurs when the volume change in an elevation bin causes the ice thickness for the next time step to be less than zero. In this case, the ice thickness is set to zero and the remaining volume change is redistributed over the entire glacier according to the mass redistribution described above.
Following Huss and Hock (2015), modeled glacier advance occurs when the ice thickness change exceeds the ice thickness advance threshold of 5 m. When this occurs, the ice thickness change is set to 5 m, the area and width of the bin are calculated accordingly, and the excess volume is recorded. The model then calculates the average area and thickness associated with the bins located in the glacier’s terminus, which is defined by the lowest 20% of glacier area. Another minor modification to our implementation of Huss and Hock (2015) is that our calculation of the average area and thickness excludes the bin located at the terminus because prior to adding a new elevation bin, the model checks that the bin located at the terminus is “full.” Specifically, the area and ice thickness of the lowermost bin are compared to the terminus’ average, and if the area and ice thickness is less than the average, then the lowermost bin is first filled until it reaches the terminus average. This ensures that the lowermost bin is full and prevents adding new bins to a glacier that may only have a relatively small excess volume in consecutive years. In other words, if this criterion did not exist, then it would be possible to add new bins over multiple years that had small areas, which would appear as though the glacier was moving down a steep slope.
If there is still excess volume remaining after filling the lowermost bin to the terminus average, then a new bin is added below the terminus. The ice thickness in this new bin is set to be equal to the terminus average and the area is computed based on the excess volume. If the area of this bin would be greater than the average area of the terminus, this indicates that an additional bin needs to be added. However, prior to adding an additional bin the excess volume is redistributed over the glacier again. This allows the glacier’s area and thickness to increase and prevents the glacier from having a thin layer of ice that advances down-valley without thickening. The one exception for when a glacier is not allowed to advance to a particular bin is if the bin is over a known discontinuous section of the glacier, which is determined based on the initial glacier area. For example, it is possible, albeit unlikely, that a glacier could retreat over a discontinuous section and then advance in the future. This discontinuous area is assumed to be a steep vertical drop, hence why a glacier currently does not exist, so a glacier is not allowed to form there in the future. The glacier instead skips over this discontinuous bin and a new bin is added below it.
3.4. Glacier Runoff
Following Huss and Hock (2018), we define glacier runoff, Q, as all water that leaves the initial glacierized area, which is computed from rain (pliquid), ablation (a), and refreezing (R) as follows:
This is equivalent to the runoff that would be measured at a fixed-gauge station at the initial glacier terminus. For clarity we use the term “fixed-gauge” glacier runoff throughout the text. When discussing fixed-gauge glacier runoff, we separate it into two components: (i) the runoff from the changing glacierized area, which we refer to as “moving-gauge” glacier runoff as this is equivalent to the runoff that would be measured at a gauging station that moved with the terminus (Bliss et al., 2014), and (ii) the runoff from the ice-free portion of the initially glacierized area once the glacier has retreated, which we refer to as “off-glacier” runoff.
The off-glacier runoff is computed as the sum of rain, seasonal snow melt, and refreezing from the non-glacierized portion of the initial glacier area. No other processes, e.g., evapotranspiration or groundwater recharge, are accounted for in these off-glacier areas. In the case of glacier advance, runoff is computed over the present glacier area, which may exceed the initial glacierized area. Given that most glaciers are retreating, the increase in glacier runoff due to the additional glacier area is considered to be negligible.
Excess meltwater is defined as the runoff caused by the net glacier mass loss. A glacier that melts completely contributes its entire mass as excess meltwater, while a glacier in equilibrium or with consistently positive mass balances produces no excess meltwater. First, we compute the total excess meltwater for each glacier over the period 2000–2100, which is equivalent to the total net mass change over this period or the sum of all (positive and negative) annual mass balances. Since interannual glacier mass change is highly variable, i.e., a glacier can lose, gain, and then lose mass again, we determine the amount of excess meltwater for each individual mass-balance year retroactively (Supplementary Figure S1). We distribute the total amount of excess meltwater in sequential order, starting from the first year, to all mass-balance years that are negative and where the lost mass is not regained in the future. This way the amount of excess meltwater over the entire period is maintained, even when the glacier experiences some positive mass-balance years. If the total mass change is zero or positive, excess meltwater is zero for all years.
From the projected time series of annual glacier runoff, peak water is calculated based on 11-year moving averages following Huss and Hock (2018).
4. Model Calibration and Validation
4.1. Model Calibration
Geodetic mass balance observations from 2000 to 2018 of 95,086 glaciers (99.6% of the total glacier area) from Shean et al. (2020) are used for model calibration. These mass balance observations were primarily derived from time series of Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEMs. They were quality controlled by identifying outliers using a 3-sigma filter for (a) the uncertainty of the glacier mass balance compared to the uncertainty of all glacier mass balances, and (b) the glacier mass balance compared to its corresponding regional mass balance (Rounce et al., 2020). Any glaciers that were not initially observed or were deemed outliers (1401 glaciers; 0.5% of the total glacier area) were replaced with the regional specific mass balance and uncertainty. This dataset was used instead of Brun et al. (2017), since it has fewer data gaps, integrates an additional 2 years of ASTER DEMs and more than 2 years of high-resolution DEMs from WorldView/GeoEye imagery, and calculates the mass balance for nearly every glacier in High Mountain Asia regardless of its size (Shean et al., 2020).
The three model parameters that require calibration are the temperature bias, precipitation factor, and degree-day factor of snow. The temperature bias and precipitation factor are meant to account for any biases or inability of the climate data to properly resolve the temperature and precipitation on the glacier, while the degree-day factor of snow is meant to account for any variations in the relation between the temperature and ablation. In reality, these three model parameters also compensate for any physical processes that are poorly accounted for or missing in PyGEM (e.g., debris cover, firn development, glacier dynamics).
Calibration is performed using a Bayesian model (Rounce et al., 2020), which combines mass balance observations with prior information of the model parameters to estimate the model parameters and their uncertainty for every glacier. The Bayesian model is applied using Markov chain Monte Carlo methods. These methods produce a chain of model parameter sets that is formed by iteratively sampling combinations of model parameters (Carlin and Louis, 2008). Sets of model parameters that agree well with the mass balance observations are more frequently accepted than those that agree poorly; however, some of the poorer sets are also accepted such that the chain of model parameters properly reflects the uncertainty associated with the observations. The theory behind Markov chain Monte Carlo methods is that if the chain is long enough, i.e., enough iterations are performed, the chain will converge to a unique stationary distribution such that the model parameters in the chain are from the joint posterior distribution (Carlin and Louis, 2008). In other words, once the chains are sufficiently long, we can be confident that the parameter sets are representative of the true distribution of potential sets of model parameters based on the observations and prior information. A detailed description of the calibration methods is presented in Rounce et al. (2020).
We calibrate each glacier independently using the geodetic mass balance observations from 2000 to 2018 (Shean et al., 2020) and the calibration scheme described above. The calibration scheme generates at least 100 independent sets of model parameters, which are used in the model simulations to quantify the uncertainty associated with the model parameters. For each GCM and RCP scenario, 100 simulations are run based on these sets of model parameters.
4.2. Model Validation
Model performance is evaluated at both a regional and glacier level comparing simulations forced by ERA-Interim from 1980 to 2017 with available observations not used in the calibration. Since the glacier volume at the start of the simulation in 1980 is not known (the input ice volumes refer approximately to the year 2000) the period 1980–2017 is split into two periods. For the period 1980-2000 the model is run in reverse (2000, 1999,…, 1980), and for the period 2000–2017 the model is run normally (2000, 2001,…, 2017), and both simulations are then merged. This ensures that the modeled glacier volume and area at year 2000 is consistent between the simulations used for validation (1980–2017) and calibration (2000–2018) and thus avoid any uncertainty that could be introduced from changes in glacier geometry between 1980 and 2000.
At the regional scale, the model is compared to regionally averaged time series of annual mass balance from 1980 to 2016 for each of the three primary RGI regions (Zemp et al., 2019) derived primarily from geodetic mass balances covering 51–72% of the total glacier area in each region, but also from glaciological mass balances covering 1–3% of the total glacier area in each region. At the glacier scale, the model is compared to all publicly available glacier-wide geodetic and glaciological observations (WGMS, 2018) between 1980 and 2017. This includes 41 observations of 17 different glaciers for the geodetic data and 112 annual, 154 winter, and 158 summer observations of 24 different glaciers for the glaciological data. In addition, model results are compared with observed equilibrium line altitudes from approximately year 2000 derived from end-of-summer snow lines averaged over 15–26 glaciers in various subregions (Gardelle et al., 2013).
All modeled and observed values are compared using the root-mean-square-error (RMSE) and regression analysis, where perfect agreement would result in a correlation coefficient (r) of 1.0 and a slope of 1. Geodetic mass balance data from Brun et al. (2017) are not used for validation because these mass balances agree well with the calibration data (Shean et al., 2020). Hence, good agreement would merely reflect the similarities between datasets, i.e., both were derived using time series of ASTER DEMs from 2000 to 2016 or 2018, and not properly evaluate model performance.
4.3. Propagation of Model Parameter Uncertainty
While the model generates output for every glacier in High Mountain Asia, the model results are typically aggregated to regions or river basins. When the root sum of squares method is used to estimate regional uncertainties based on the individual glaciers, the uncertainties are unrealistically low (e.g., <0.01 m w.e. yr–1) due to the large sample size. Shean et al. (2020) performed an analysis of the spatial autocorrelation of the glacier elevation change uncertainty and found a characteristic length of 32 km. For their regional estimates, they first aggregated the elevation change uncertainty into 55 km hexagonal cells assuming the glaciers are perfectly correlated. The regional elevation change uncertainty was then estimated by aggregating the uncertainty of each hexagon within a given region using the root sum of squares method, i.e., assuming the hexagons are independent. Lastly, the regional mass balance uncertainty was estimated by aggregating the regional elevation change uncertainty with the density and area uncertainty in quadrature. For consistency with the calibration data, we apply the same methods to propagate the glacier mass balance uncertainty to regional scales. Since PyGEM outputs the glacier mass balance and uncertainty, we first isolate the elevation change uncertainty by assuming the dimensionless fractional uncertainty is 0.10 for the area and 0.071 for the density according to Shean et al. (2020, eq. (4)).
The propagation of uncertainty is also important for comparisons with the mass balance observations, since monthly mass balances must be aggregated. In these cases, the uncertainty associated with the two extreme cases is reported, i.e., assuming each month is independent or perfectly correlated. The actual uncertainty is likely somewhere between these two end members. Note that for projections we report the uncertainty as the multi-GCM mean ± standard deviation instead of the model parameter uncertainty (see Section 6.3.1 for a comparison of the two sources of uncertainties).
5. Results
5.1. Model Performance
The calibration of the glacier evolution model using geodetic mass balance observations of more than 95,000 glaciers enables the model to resolve spatial variability in mass balance at an unprecedented level of detail. Regional mass balances, aggregated by the three RGI regions, show the model and observations agree reasonably well between 1980 and 2016, especially when uncertainty is considered (Zemp et al., 2019) (Figures 2A–C). By comparison, the uncertainty associated with the modeled results is much less due to the large sample size. Agreement is best in Central Asia (RMSE = 0.18 m w.e. yr–1, r = 0.44) followed by South Asia West (RMSE = 0.24 m w.e. yr–1, r = 0.40) and South Asia East (RMSE = 0.31 m w.e. yr–1, r = 0.44) (Supplementary Table S2). This reflects the methods used to extrapolate long-term trends in High Mountain Asia, which were solely based on glaciological measurements in Central Asia (Zemp et al., 2019).
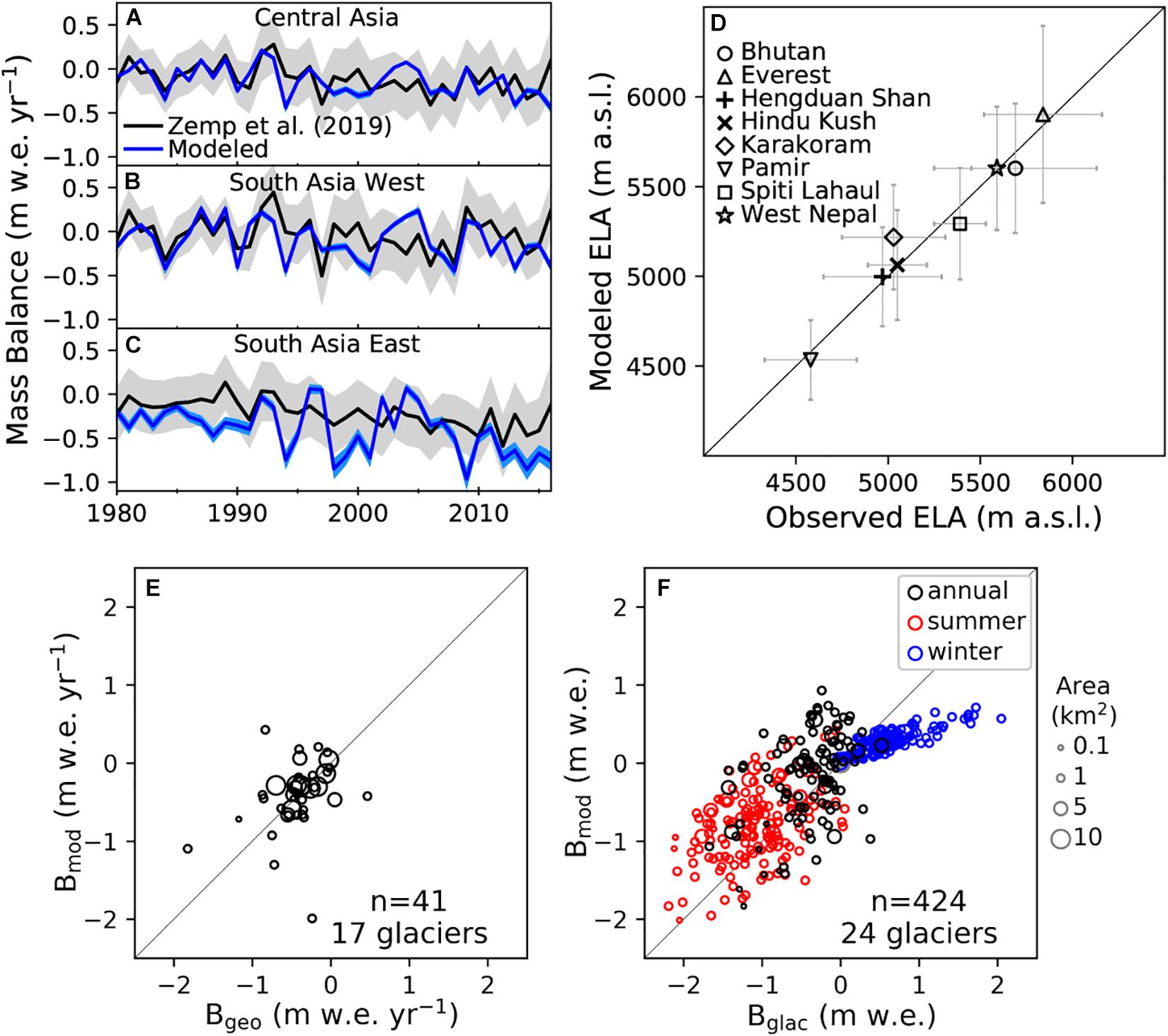
Figure 2. Validation of model performance via comparison of (A–C) RGI regional annual specific mass balances (m w.e. yr– 1) from 1980 to 2016 with Zemp et al. (2019), (D) equilibrium line altitudes (ELA, m a.s.l.) with Gardelle et al. (2013), and mass balances from (E) geodetic (Bgeo, m w.e. yr– 1) and (F) annual, winter, and summer glaciological balances (Bglac, m w.e.) (WGMS, 2018). Uncertainty reported by the observations and for the model (standard deviation) are shown for (A–D).
Comparison with equilibrium line altitudes (Gardelle et al., 2013) shows good agreement (RMSE = 86 m, r = 0.98; Supplementary Table S2) with all regions lying close to the 1:1 line (Figure 2D). The good agreement provides confidence that the modeled accumulation and ablation areas are well represented in the model, which suggests the sets of model parameters generated by the calibration procedure are good.
The comparison of mass balances derived from geodetic and glaciological measurements (WGMS, 2018) show relatively good agreement around the 1:1 line with a fair amount of scatter (Figures 2E,F and Supplementary Table S3). For all geodetic and glaciological measurements, the mean ± standard deviation of the difference between the observed and modeled annual and seasonal mass balances is −0.12 ± 1.00 m w.e. yr–1. The agreement is much better when only considering the geodetic mass balances (−0.01 ± 0.46 m w.e. yr–1) or only the annual glaciological balances (−0.21 ± 0.52 m w.e. yr–1). The mean uncertainty (expressed as the standard deviation) of the modeled mass balances ranges from 0.35–0.74 m w.e. yr–1 assuming that the monthly modeled values are uncorrelated or perfectly correlated, respectively. In other words, the modeled uncertainty derived from the sets of calibrated model parameters is comparable to the differences between the observed and modeled mass balances, which suggests that the model’s uncertainty at the glacier scale is reasonably quantified.
The model performed poorly at the seasonal scale and typically had less negative summer balances (−0.71 ± 1.3 m w.e. yr–1) and less positive winter balances (0.53 ± 0.50 m w.e. yr–1). Hence, the good agreement with annual observations provides confidence that the model can reasonably resolve interannual variability in the mass balance, while the poorer agreement with seasonal observations suggests caution should be used when interpreting results on a sub-annual time scale. While the model’s intended use is for large-scale applications, the relatively good agreement on a glacier scale when considering model uncertainty highlights the unprecedented level of detail that is resolved by calibrating every glacier with a mass balance observation. At the regional level, the comparison with equilibrium line altitudes and historic mass balance estimates also suggest the model performs well at this scale.
5.2. Projections
The calibrated model parameters were used to estimate the glacier mass change and runoff of every glacier in High Mountain Asia from 2015 to 2100 for 22 GCMs forced by three to four RCPs each. All GCMs were run for RCP 2.6, RCP 4.5, and RCP 8.5, while only 15 of the GCMs had input data for RCP 6.0. Since projections are heavily dependent on the climate forcing, results are reported as multi-GCM means ± standard deviation of all the GCMs for a given RCP scenario.
5.2.1. Mass Change Projections
Projections estimate that from 2015 to 2100, glaciers in High Mountain Asia will lose 1900 ± 748 Gt (29 ± 12%, RCP 2.6), 3003 ± 705 Gt (46 ± 11%, RCP 4.5), 3200 ± 698 Gt (50 ± 11%, RCP 6.0), and 4327 ± 648 Gt (67 ± 10%, RCP 8.5). As expected, mass loss by 2100 increases for higher emission scenarios. While all regions are projected to experience significant mass loss, the relative mass loss (fraction of initial glacier mass) varies greatly by region (Figure 3). Some of the smallest regions (Dzhungarsky Alatau, Gangdise Mountains, and Tanggula Shan) are expected to experience the most relative mass loss (more than 67% even for RCP 2.6), while Karakoram and Western Kunlun Shan are projected to experience the least relative mass loss (less than 55% for RCP 8.5). Despite experiencing the least relative mass loss, Karakoram and Western Kunlun Shan contribute 24–34% of the total mass loss depending on the RCP scenario due to their large initial glacier mass. Mass change for 12 regions from Kääb et al. (2015) and the three primary RGI regions are provided in Supplementary Figures S2, S3, respectively.
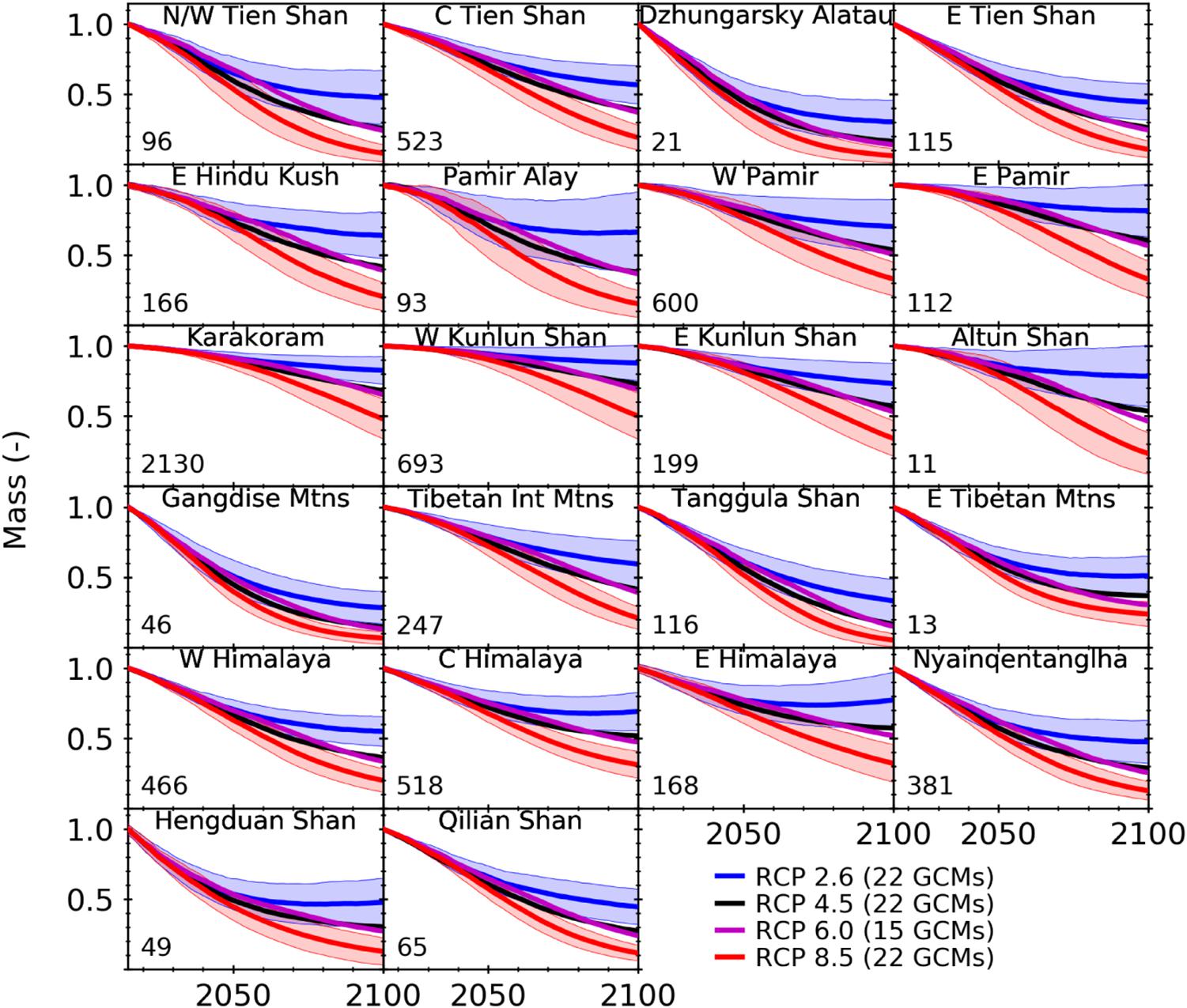
Figure 3. Regional multi-GCM means (±1 standard deviation) of normalized mass remaining, relative to 2015, for up to 22 GCMs and 4 RCP scenarios from 2015 to 2100. Uncertainty only shown for RCP 2.6 and RCP 8.5 for clarity. Numbers in lower left corner of each subplot refer to the region’s initial glacier mass (Gt). Subplots of regions from Bolch et al. (2019) are roughly ordered by geographic location. C, Central; E, Eastern; N, Northern; W, Western; Int, Interior; Mtns, Mountains.
The spatial variability in projected mass loss is dependent on present-day mass balance, projected changes in air temperature and precipitation, and various glacier attributes (e.g., glacier hypsometry, ice thickness). Since the model was calibrated with mass balance data for every glacier, the model is able to resolve subregional variations. The mass balance evolution of every glacier greater than 1 km2 for RCP 4.5 shows significant spatial and temporal variability exists due to spatial variations in the temperature and precipitation projections (Figure 4). By the end of the century, temperature in all regions is projected to increase by 2–3°C, relative to the 2000–2015 mean, with Eastern Hindu Kush and Gandise Mountains experiencing the greatest increase closer to 3°C. Changes to precipitation are more variable with some regions projected to increase by ∼10% (Altun Shan, Eastern Kunlun Shan, Gandise Mountains, Qilian Shan), while others show no significant change (Eastern Hindu Kush, Western Himalaya).
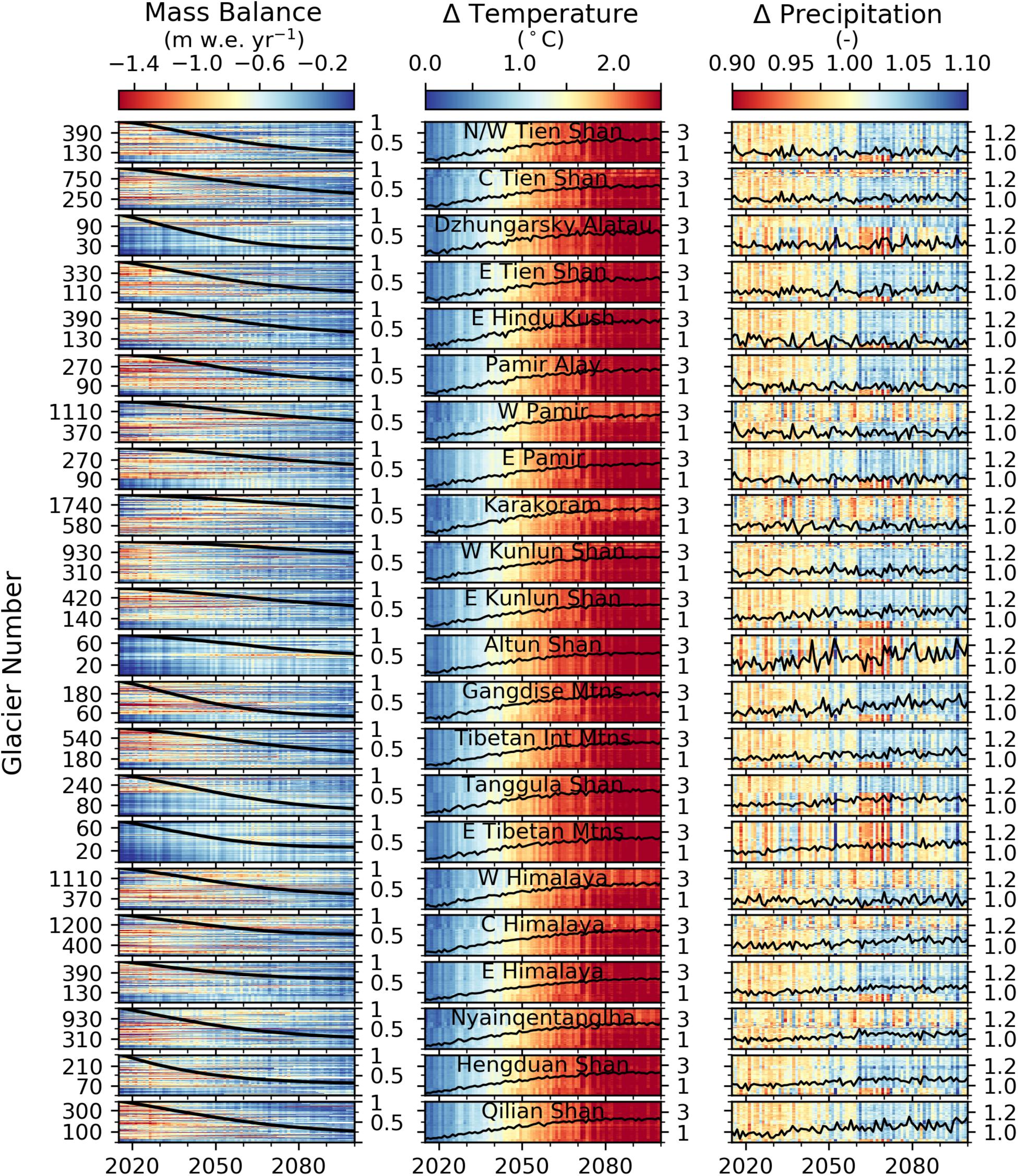
Figure 4. Mass balance and bias adjusted temperature and precipitation changes relative to the mean from 2000 to 2015 for each glacier greater than 1 km2 from 2015 to 2100 for RCP 4.5. Each row is a glacier and glacier number refers to the number greater than 1 km2 in each region. Glaciers are ordered according to the RGIId in each subregion. Lines show the normalized regional mass remaining relative to 2015, and the area-weighted bias adjusted temperature and precipitation changes relative to the mean from 2000 to 2015. White color for the mass balance indicates the glacier has completely melted. Regions are from Bolch et al. (2019). C, Central; E, Eastern; N, Northern; W, Western; Int, Interior; Mtns, Mountains. RCP 2.6, RCP 6.0, and RCP 8.5 are shown in the Supplementary Figures S2–S4.
The glaciers’ response to temperature and precipitation is complex. For example, Eastern Himalaya, which had the most negative specific mass balance from 2000 to 2018 (Shean et al., 2020), is projected to experience less relative mass loss by 2100 for RCP 4.5 compared to other regions in part due to increases in precipitation and comparatively smaller increases in temperature (Figures 4, 5). Conversely, Pamir Alay, which had an almost balanced present-day mass budget, is projected to experience more mass loss than other regions as it gets warmer but not wetter. While the climate forcing is likely responsible for a significant amount of these changes, the glacier’s hypsometry, ice thickness, and elevation range will also impact how quickly the glacier is able to retreat in search of a new equilibrium. Hence, mass balance and overall mass change may significantly differ between regions even if they appear to have similar climate forcing (e.g., Eastern Kunlun Shun and Gandise Mountains).
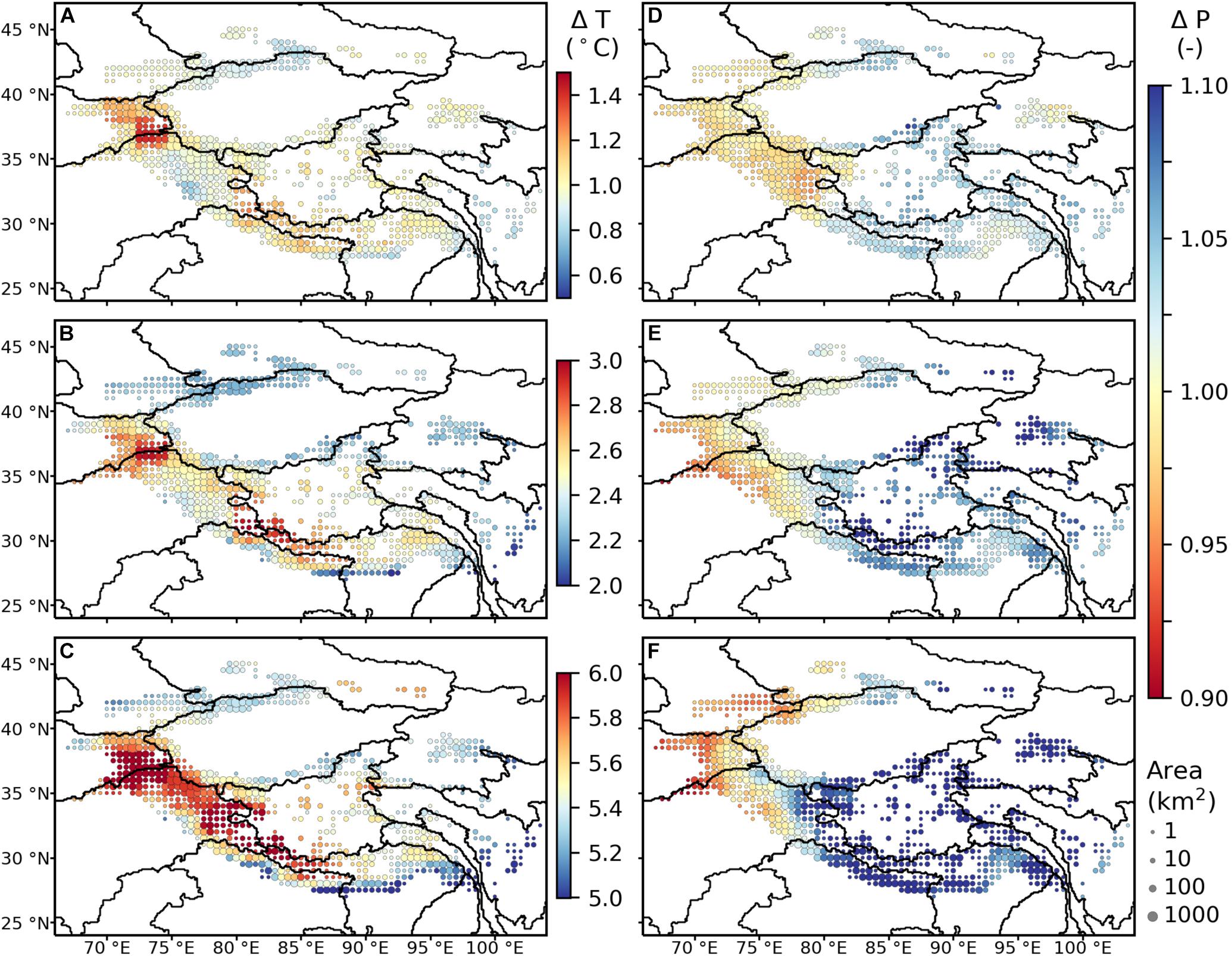
Figure 5. Spatial distribution of bias adjusted (see Section 2.2), multi-GCM mean temperature change (ΔT) (A–C) and precipitation change (ΔP) (D–F) from 2085–2100, relative to 2000–2015, aggregated by 0.5° grid cells for (A,D) RCP 2.6, (B,E) RCP 4.5, and (C,F) RCP 8.5. Note the difference in the colorbar scales for the temperature change subplots. The circles are scaled by the initial glacier area (km2) within the cell. Outlines of major river basins are shown for reference.
Figure 4 also shows substantial variations in specific mass balance projections within a region due to differences in changes to the temperature and precipitation. This is most apparent in Karakoram, Nyainqentangla, Western Himalaya, and Western Pamir, where parts of these regions experience an increase in precipitation that coincides with a strong increase in temperature, while other parts of these regions experience a decrease in precipitation that coincides with a smaller temperature increase. Interestingly, the parts of these regions that appear to become warmer and wetter appear to have less negative mass balances near the end of the century compared to the beginning of the century (Figure 4). In most subregions the individual glaciers’ specific mass balances tend to become considerably less negative throughout the 21st century, indicating that glaciers retreat to higher elevations. However, in some regions (e.g., Dzhungarsky Alatau, Altun Shan, Tanggula Shan, and the Eastern Tibetan Mountains) the trend is reversed with increasingly negative specific mass balances.
The same regional and subregional variations are also apparent in the projections of mass balance, temperature, and precipitation for RCP 2.6, RCP 6.0, and RCP 8.5 (Figure 5 and Supplementary Figures S4–S6). For RCP 2.6, the temperature is projected to increase ∼1°C by the middle of the century and stabilize, which allows many glaciers to reach a new equilibrium (Supplementary Figure S4). RCP 6.0 projects a relatively steady temperature increase of 3–4°C by 2100, while precipitation change is highly variable by region, leading to higher rates of total mass loss by 2100 compared to RCP 4.5 (Supplementary Figure S5). Lastly, RCP 8.5 projects a constant increase in temperature throughout the century such that all regions increase by 5–6°C. While the precipitation is also projected to increase in most regions, it does not compensate for the severe mass loss rates (<−1.5 m w.e. yr–1) and many glaciers subsequently melt completely by 2100 (Supplementary Figure S6). For glaciers that do not completely melt, the mass balance at the end of the century is very negative (<1 m w.e. yr–1) indicating these glaciers are still far from equilibrating with the new climate and continue to rapidly retreat.
5.2.2. Glacier Runoff Projections
Similar to the regional variations in the mass balance projections, projected peak water varies significantly among large-scale river basins (Figure 6). The projections of fixed-gauge annual glacier runoff indicate that, on average, a peak has already been reached or will be reached within approximately two decades, followed by declining glacier runoff, in several major river basins (Brahmaputra, Ganges, Ili, Salween, and Syr Darya) regardless of the RCP scenario. Glacier runoff in all river basins will have reached peak water by ∼2080 for all RCP scenarios.
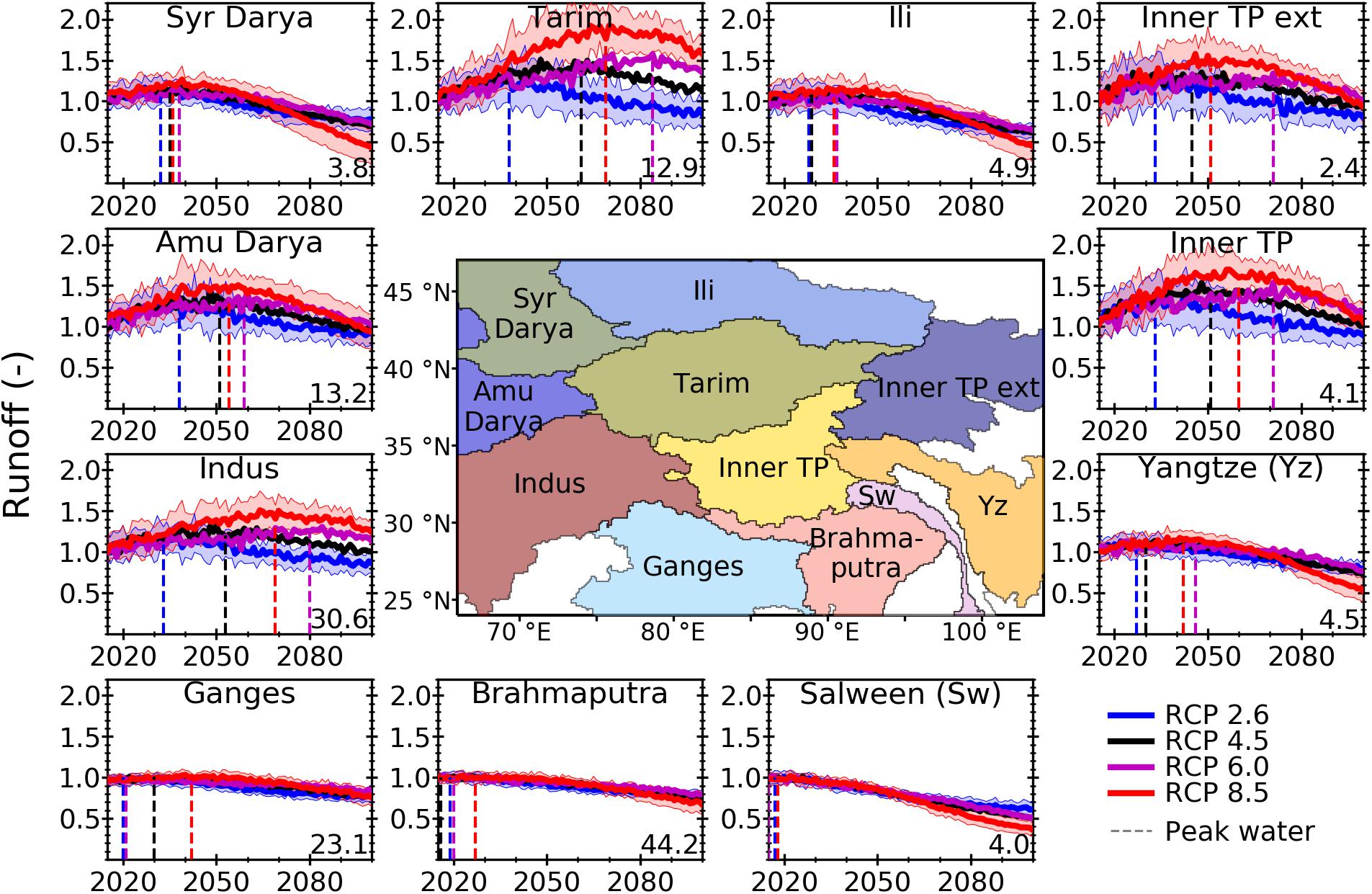
Figure 6. Time series of multi-GCM means (±1 standard deviation) of annual fixed-gauge glacier runoff (i.e., the runoff from the initially glacierized area) in eleven river basins for each RCP scenario from 2015 to 2100, relative to the mean annual fixed-gauge glacier runoff from 2000 to 2015 (given in bottom right in Gt yr– 1). Uncertainty only shown for RCP 2.6 and RCP 8.5 for clarity. Dashed lines show peak water for each RCP. Center map shows major river basins in study area (Vörösmarty et al., 2000). Abbreviations in center map are Sw, Salween; TP, Tibetan Plateau; Yz, Yangtze.
Higher RCP scenarios will delay peak water due to increasing excess glacier melt, while lower RCP scenarios will allow many glaciers to approach a new equilibrium and therefore reduce glacier runoff earlier in the century. In some basins (e.g., Indus and Tarim), the timing of glacier melt is projected to cause peak water to be later for RCP 6.0 than RCP 8.5, but the percentage increase in total runoff at the time of peak water will be less for RCP 6.0 than RCP 8.5. The later timing may also be a consequence of the smaller sample of GCMs for RCP 6.0 (15 instead of 22). The basin averaged increases in annual glacier runoff when peak water occurs can be substantial, e.g., in the Tarim basin glacier runoff increases by ∼80% of the initial glacier runoff, while glacier runoff on the Tibetan Plateau and Amu Darya increase by more than 50% (multi-GCM mean for RCP 8.5). The relative increases in glacier runoff tend to be more pronounced for higher emission scenarios in most basins, and in basins where peak water is later.
Spatial variations within these large-scale drainage basins are most apparent in the Indus and Tarim (Figure 7), where some sub-basins have already reached peak water for all emission scenarios, while others (Karakoram and Kunlun) will reach peak water much later, e.g., after 2080 for RCP 8.5 (Figure 7C). Given that these latter subregions contain ∼42% of the total glacier mass in High Mountain Asia, mass loss from these regions drives the peak water within their river basins. In general, these sub-basins are located in the interior (e.g., Karakoram) and their bias adjusted, multi-GCM mean temperature change from 2085–2100, relative to 2000–2015, is projected to be higher than the exterior (e.g., Western Himalaya) sub-basins for all emission scenarios (Figures 5A–C). The differences in precipitation are much less pronounced, although the interior appears to become slightly wetter than the exterior (e.g., Western Himalaya and Eastern Hindu Kush) sub-basins for RCP 8.5 (Figure 5F). Given that temperature drives both the ablation rates and accumulation rates (since the temperature dictates whether precipitation falls as rain or snow), these higher temperature changes promote more negative mass balances.
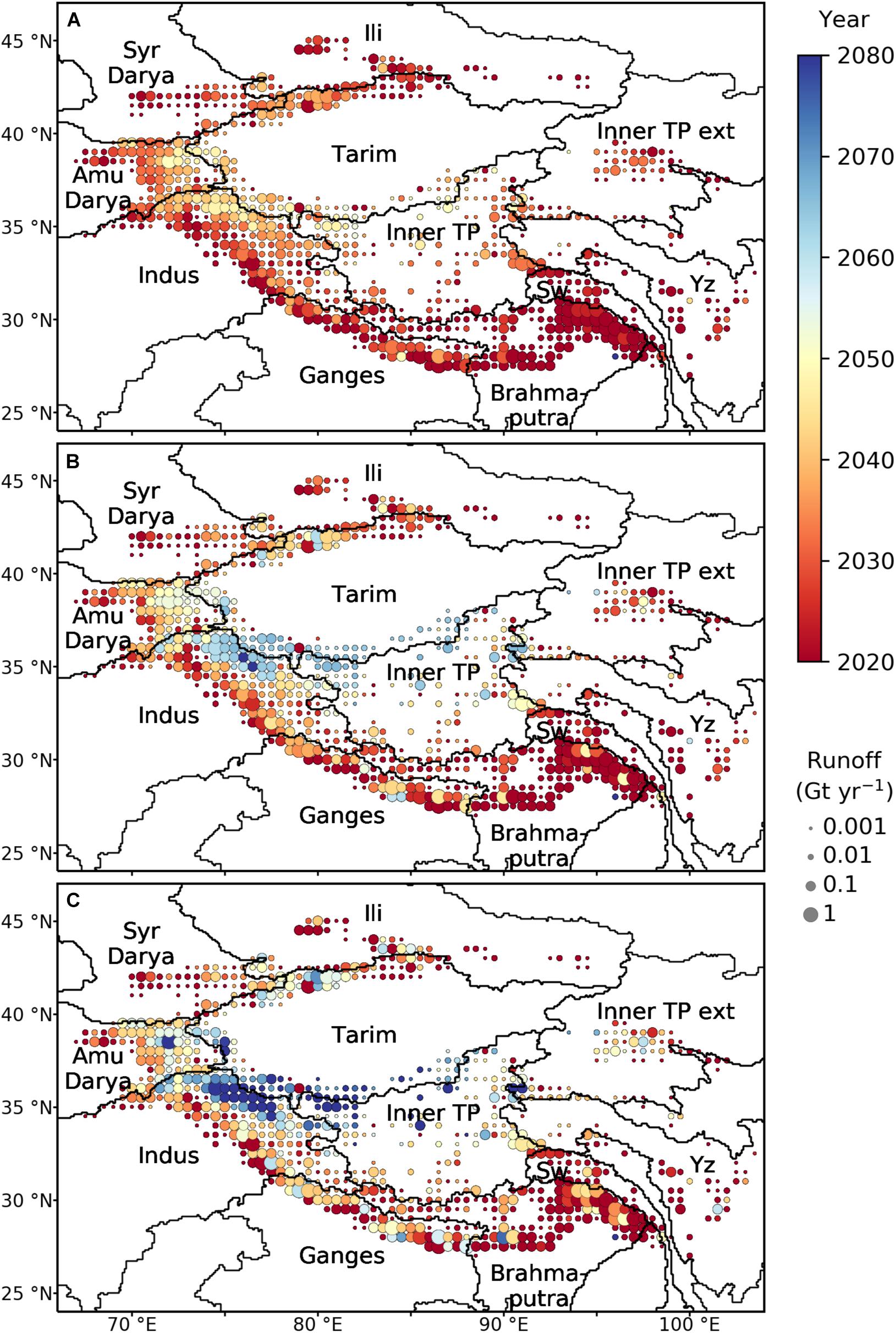
Figure 7. Spatial distribution of peak water (i.e., the year of maximum annual fixed-gauge glacier runoff) aggregated by 0.5° grid cells for (A) RCP 2.6, (B) RCP 4.5, and (C) RCP 8.5. The circles are scaled by the multi-GCM mean annual glacier runoff (Gt yr– 1) from 2000 to 2015 within the cell. Major river basins are shown (Sw, Salween; TP, Tibetan Plateau; Yz, Yangtze).
Conversely, peak water in Southeast Asia (e.g., Ganges and Brahmaputra) shows significantly less variability with almost all sub-basins reaching peak water by 2050 for all emission scenarios (Figure 7). This may reflect that glaciers in these river basins have already been experiencing high mass loss rates since 2000 (Shean et al., 2020). The subregional spatial variations in the timing of peak water are consistent for the various emission scenarios, although the spatial variations are more pronounced for the higher emission scenarios (Figure 7).
The spatial variability and timing of peak water is driven by the amount of excess meltwater, i.e., the additional runoff due to annual glacier net mass loss, and the relative importance of meltwater compared to other components of the fixed-gauge glacier runoff in each river basin (Figure 8). Excess meltwater is essentially the release of a long-term water supply that is not replenished. River basins that have significant amounts of excess meltwater (e.g., Amu Darya, Indus, Tarim) cause peak water to occur later in the century. As these glaciers continue to melt, the excess meltwater becomes depleted thereby reducing the amount of glacier runoff. Unsurprisingly, glacier meltwater in these river basins is the largest contributor to the fixed-gauge glacier runoff (upwards of 80%) as they receive most of their precipitation as snow from the winter westerlies.
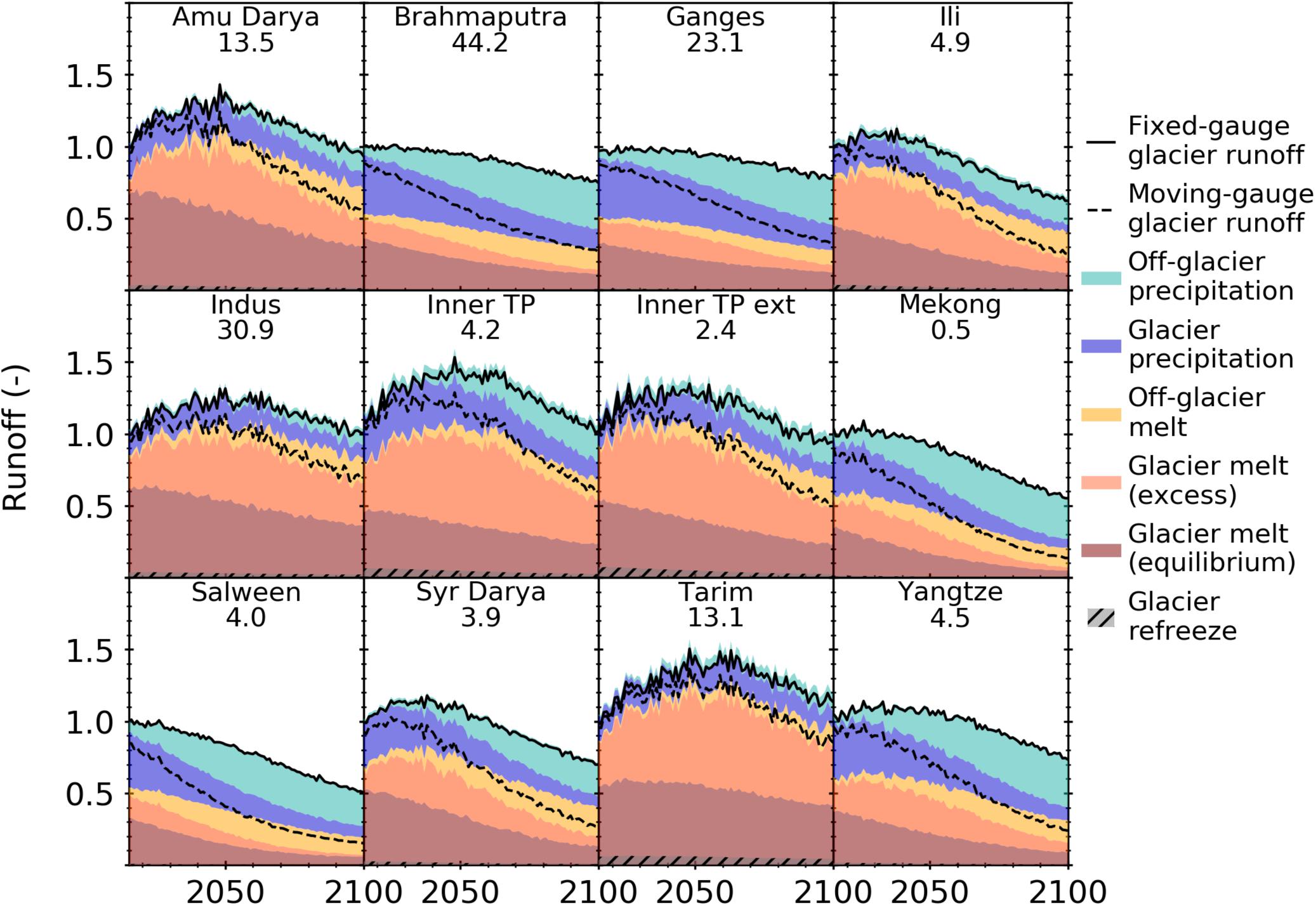
Figure 8. Multi-GCM mean of annual fixed-gauge glacier runoff and the relative contribution from various components for RCP 4.5 from 2015 to 2100 relative to the mean annual fixed-gauge glacier runoff from 2000 to 2015 (given below region name in Gt yr– 1). Results for RCP 2.6, RCP 6.0, and RCP 8.5 are shown in the Supplementary Figures S7–S9.
River basins fed by the summer monsoons (e.g., Brahmaputra and Ganges) receive 50% or more of their fixed-gauge glacier runoff from precipitation (Figure 8 and Supplementary Figures S7–S9) and their annual runoff only decreases a little by 2100 regardless of the emission scenario (Figure 6). Excess meltwater in these river basins appears to have already peaked and therefore does not drive the timing of peak water to the same extent.
For all river basins, as the glaciers retreat the glacier melt is replaced by off-glacier (seasonal snow) melt, which becomes an increasingly important component of the fixed-gauge glacier runoff (Figure 9 and Supplementary Figures S10–S12). Since these off-glacier areas replace portions of the glaciers that have already retreated, they are inherently located at lower elevations and will be the first to experience snow melt each year. Figure 9 shows the relative components of fixed-gauge glacier runoff for each month near the end of the century (2085–2100) for RCP 4.5 relative to the monthly runoff from 2000 to 2015. All river basins show a clear lag in the timing of snow melt followed by glacier melt later in the summer. The relative importance of the glacier melt varies based on the climate system.
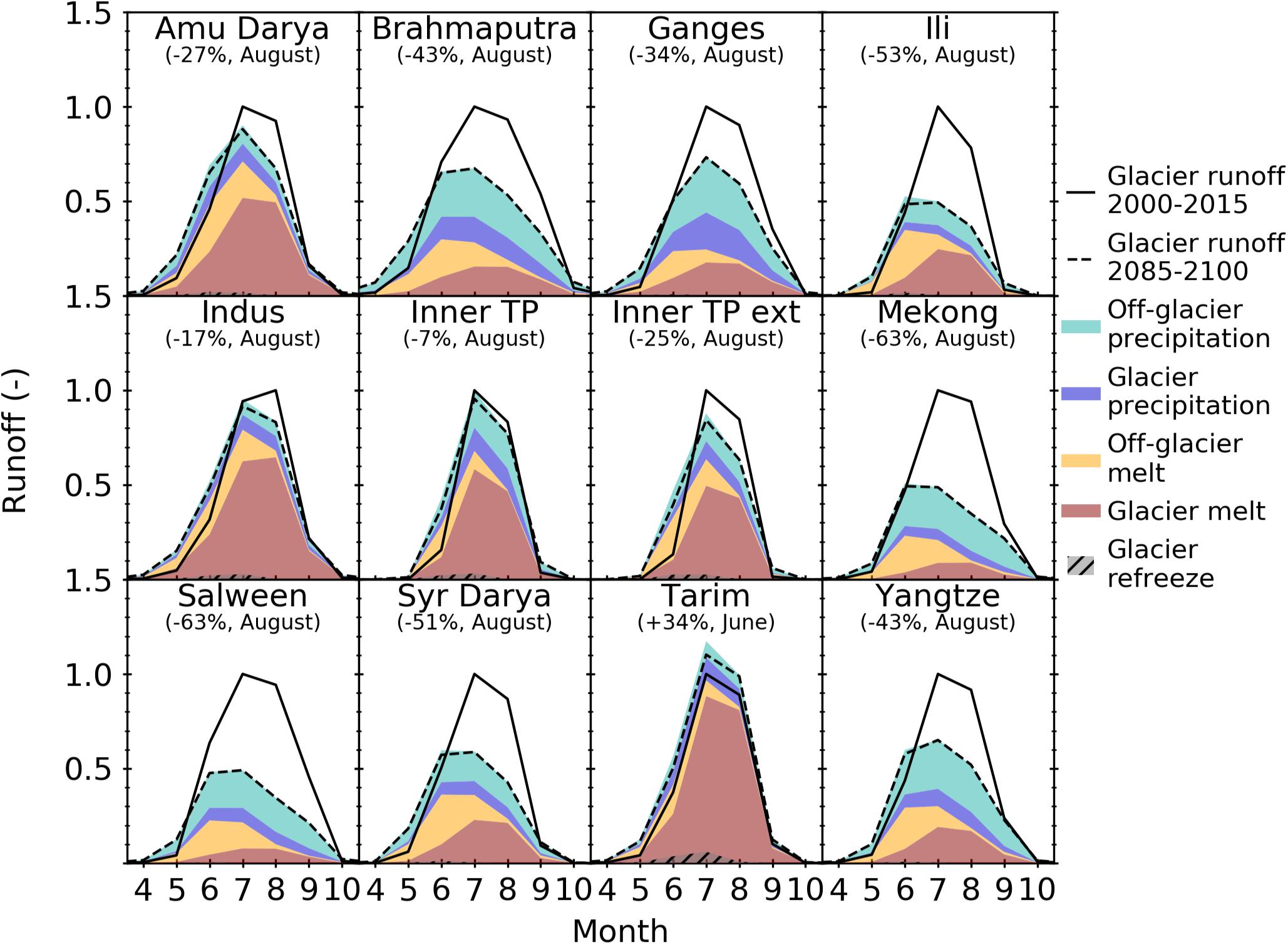
Figure 9. Mean monthly fixed-gauge glacier runoff averaged over 2000–2015 and 2085–2100 for RCP 4.5. Runoff for both period averages is normalized relative to the maximum monthly runoff from 2000 to 2015. Relative contribution from various components are shown for the runoff from 2085 to 2100. Maximum monthly decrease (or, when all months show an increase, maximum increase) of runoff between June and September is given in parentheses. Results for RCP 2.6, RCP 6.0, and RCP 8.5 are shown in the Supplementary Figures S10–S12.
For RCP 4.5, in monsoon-fed river basins (e.g., Brahmaputra and Ganges), glacier melt contributes ∼20% in August, while precipitation contributes ∼70% of the fixed-gauge glacier runoff (Figure 9). In westerlies-fed river basins (e.g., Amu Darya and Tarim), glacier melt is a much greater contributor (50% or more). Interestingly, despite relying on glacier runoff less, monsoon-fed river basins are expected to experience the most significant reductions in fixed-gauge monthly glacier runoff (∼40% in August). Conversely, some westerlies-fed river basins are projected to be reduced by ∼20% (Amu Darya), while the Tarim basin is expected to see an increase in fixed-gauge glacier runoff by the end of the century due to contributions from excess meltwater despite its steady decrease after peak water around 2060 (Figure 8). In general, monthly runoff reductions are considerably higher for RCP 8.5 reaching 65% or more in four basins (Ili, Mekong, Salween, Syr Darya; Supplementary Figure S12).
6. Discussion
6.1. Mass Change Projections
Glaciers in High Mountain Asia are projected to lose 29 ± 12% (RCP 2.6), 46 ± 11% (RCP 4.5), 50 ± 11% (RCP 6.0), and 67 ± 10% (RCP 8.5) of their total mass by 2100. These projections generally fall within the range of those from previous studies considering uncertainties (Kraaijenbrink et al., 2017; Hock et al., 2019). The major advance in this study is the availability of geodetic mass balance data for almost every glacier to calibrate each glacier individually. Given that the model physics are almost identical to those from Huss and Hock (2015), a comparison shows the added value of the calibration data.
Huss and Hock (2015) was calibrated using regional data from Gardner et al. (2013). A comparison between Shean et al. (2020) and Gardner et al. (2013) reveal there are significant differences in the present-day mass balance. For example, in Eastern Himalaya, the specific mass balance used in our study is half as negative as that used by Huss and Hock (2015). Unsurprisingly, the mass loss in South Asia East (RGI region 15) was 18–31% less in our study (Supplementary Figure S3). Similarly, in Karakoram and Tien Shan, where the most mass in High Mountain Asia resides, Gardner et al. (2013) is significantly more negative than Shean et al. (2020). Consequently, we project 15–30% less mass loss in Central Asia (RGI region 13) and South Asia West (RGI region 14). These differences illustrate that advances in the systematic measurement of indirect glacier mass balance (e.g., Brun et al., 2017; Shean et al., 2020) are important for future projections.
The calibration of every glacier enabled the model to capture the spatial variability that is present within subregions (Figure 4). While quantifying mass change for large regions is helpful for water resources planning at the scale of major river basins, our model’s ability to resolve subregional differences provides important data for much smaller river basins such as those containing hydropower plants. The comparison with geodetic and annual glaciological measurements from WGMS (2018) showed that the model agreed well with observations (Figure 2). Since PyGEM is currently designed for large-scale applications and its model physics are consequently relatively simple to enable rapid calculations over large areas (e.g., use of mass redistribution curves), caution should be used when analyzing the results of individual glaciers, especially for smaller glaciers (see Section 6.3; Figure 10C).
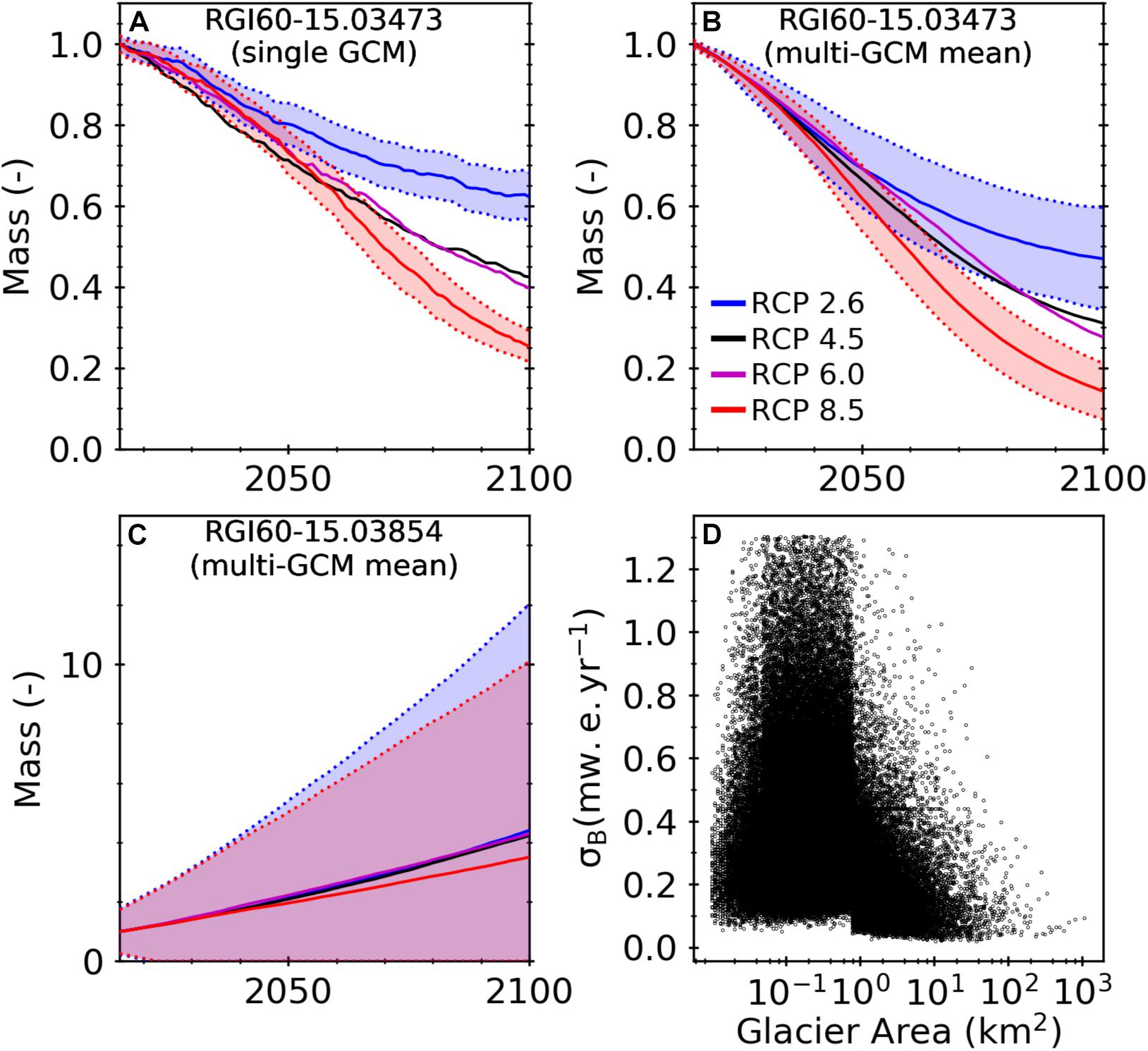
Figure 10. (A–C) Examples of the normalized mass remaining from 2015 to 2100, relative to 2015, for various RCP scenarios for a large (61 km2) glacier (A,B) and a small (0.4 km2) glacier (C) showing the uncertainty for RCP 2.6 and RCP 8.5 (shaded colors) associated with the model parameters and GCMs for various RCP scenarios, and (D) the uncertainty associated with the mass balance data (σB) used for calibration (Shean et al., 2020) versus glacier area.
6.2. Glacier Runoff Projections
Glacier runoff projections provide critical information for the planning and management of water resources. Two approaches have been used for projecting glacier runoff: (1) using an imaginary fixed-gauge station at the initial glacier terminus (e.g., Huss and Hock, 2018) or (2) using a moving-gauge station that tracks the glacier terminus over time (e.g., Bliss et al., 2014). Figure 8 shows the difference in fixed-gauge glacier runoff (solid line) versus the moving-gauge glacier runoff that does not account for off-glacier runoff (dashed line). If off-glacier runoff is not included, both the timing and amount of peak water is severely underestimated, indicating that glacier runoff calculations should always use a fixed-gauge station approach. The major limitation for the fixed-gauged station approach starting with the initial glacierized area is how to account for glaciers that advance, since theoretically the glacier runoff associated with the glacier area that exceeds the initial area should not be counted. In this study, we have not removed any runoff for advancing glaciers, which is considered to have negligible implications on the total runoff since projections show glaciers are rapidly retreating (Figure 3).
The spatial distribution of the timing of peak water in this study for RCP 4.5 (Figure 7) is fairly consistent with Huss and Hock (2018, Figure 2), which estimates peak water to be later in the Karakoram and Kunlun and much earlier in Southeast Asia. However, the exact timing of peak water does show significant variations. For the major monsoon-fed river basins (Ganges, Brahmaputra, Salween, and Mekong), our study estimates peak water will occur in 2030, 2016, 2015, and 2023, respectively, which is 14, 33, 34, and 26 years prior than Huss and Hock (2018), respectively. For westerlies-fed river basins, our study estimates peak water will occur in 2053 for the Indus, 2061 for the Tarim, and 2047 for the Aral Sea (the combination of Amu Darya and Syr Darya). The timing of peak water in the Indus and Tarim are 8 and 10 years later than Huss and Hock (2018), respectively, while the Aral Sea is 2 years earlier.
Given the nearly identical model physics between our study and Huss and Hock (2015), we attribute the differences in the timing of peak water to differences in the calibration data. The use of mass balance data for every glacier to calibrate our study enables us to resolve subregional variations in mass change and provides improved estimates of the timing and amount of peak water. Kraaijenbrink et al. (2017), who used subregional mass balance data for calibration, mention meltwater peaks around 2050 for RCP 8.5 and earlier around 2030 for the other RCPs, but did not account for any other components of the fixed-gauge glacier runoff. Our study finds for RCP 8.5 meltwater can peak as late as 2080 (Supplementary Figure S9) and as early as 2020 for RCP 2.6 (Supplementary Figure S7), although this varies considerably based on the river basin. Given our study does not account for debris cover, future work should assess how the response of debris-covered glaciers affects the timing of glacier runoff.
The timing of peak water, which is driven by excess meltwater, is more important in westerlies-fed river basins than monsoon-fed river basins, since glacier meltwater contributes a significantly higher percentage of the fixed-gauge glacier runoff (Figure 8). Consequently, the annual glacier runoff in the two major monsoon-fed river basins (Brahmaputra and Ganges) only declines by ∼20% (−10.4 Gt yr–1 and −4.3 Gt yr–1, respectively) by the end of the century relative to the mean over 2000–2015. As Huss and Hock (2018) highlighted, the glacier melt contribution to end-of-summer (August, September) fixed-gauge glacier runoff is significant (Supplementary Table S4). The Brahmaputra and Ganges are projected to experience a decline in the end-of-summer glacier runoff of 35–54% and 32–41% (RCP 2.6 – RCP 8.5), respectively (Supplementary Figures S10–S12). These declines are much higher than those projected by Huss and Hock (2018), which varied from 21 to 35% and 19 to 23%, respectively.
The Indus and Amu Darya are also expected to experience declines in August fixed-gauge glacier runoff ranging from 23–7% and 22–33% (RCP 2.6 – RCP 8.5), respectively. The Tarim differs from other river basins as excess meltwater will actually cause an increase in glacier runoff in all months by the end of the century relative to 2000–2015 by at least 11% for RCPs 4.5, 6.0, and 8.5 (Figure 8, Supplementary Figures S11, S12, and Supplementary Table S4) despite steady declines following peak water; however, for RCP 2.6 many glaciers would reach an equilibrium (Supplementary Figure S7) and cause a decline in end-of-summer months of up to 24% (Supplementary Figure S10). These projections for the Tarim for RCP 4.5 and RCP 8.5 are much different than Huss and Hock (2018) who report glacier runoff will decline in August by 18–24%. Nonetheless, while these increases in glacier runoff may be beneficial in the short-term, projections show glacier melt and excess meltwater significantly decline toward the end of the century, so these increases will likely not remain after 2100.
6.3. Uncertainties
6.3.1. Uncertainties Associated With Model Parameters and Climate Forcing
One of the major advances in this study is the use of Markov chain Monte Carlo methods, which enable the uncertainty associated with the model parameters to be quantified for every glacier based on the uncertainty associated with the mass balance data used for calibration. This uncertainty was used to assess the model performance (see Section 5.1). The model projections on the other hand reported the multi-GCM mean ± standard deviation, which we refer to as the uncertainty associated with the climate forcing (see Section 5.2). Figure 10 shows that for a large glacier, RGI60-15.03473, the uncertainty in future projections associated with the model parameters for a single GCM (±10%) is approximately half as much as the uncertainty in future projections associated with the climate forcing (±20%) (Figures 10A,B). However, for a small glacier, RGI60-15.03854, the uncertainty associated with the model parameters is much greater than the uncertainty associated with the climate forcing (Figure 10C).
The considerable difference in the sources of uncertainty is due to the glacier’s initial mass and the uncertainty associated with the mass balance data used for calibration. Since the mass change is shown relative to 2015, glaciers with more initial mass are inherently less sensitive to uncertainty associated with the model parameters. Additionally, the uncertainty associated with the mass balance data is larger for smaller glaciers (<1 km2) (Figure 10D). For example, the mass balance of the smaller glacier, RGI60-15.03854, is −0.39 ± 1.09 m w.e. yr–1. Since the Markov chain Monte Carlo methods generate parameter sets corresponding to the 99.7% confidence interval (−3.66 to 2.88 m w.e. yr–1) and the initial mass is small (8.8 × 10–3 Gt), the uncertainty associated with the model parameters will cause the glacier to completely melt or experience tremendous growth.
One issue caused by these large uncertainties is that the mean mass change is inherently skewed toward these positive values because a glacier’s maximum mass loss is limited by its initial mass, while there is no limit for how large a glacier can grow. Hence, reporting mass or runoff change and its corresponding uncertainty for model parameters and/or climate forcing would be better represented using the median and normalized median absolute deviation. Fortunately, when these smaller glaciers are aggregated with other glaciers to subregions, the regional mass change signal and its uncertainty are dominated by larger glaciers, so these issues associated with the uncertainty of smaller glaciers become minor.
6.3.2. Other Sources of Uncertainty
Uncertainty associated with glacier projections comes from the climate forcing (GCM and RCP scenarios), calibration data/scheme, model physics, and input data. The dominant source of uncertainty in this study is the climate forcing. Even at large-scales, the uncertainty associated with the climate forcing, expressed by the standard deviation of multiple GCMs, can range from 10 to 15% of the initial volume. Given the difference in multi-GCM means for RCP 2.6 and RCP 8.5 ranges from 20 to 50% depending on the region (Figure 3), this amount of uncertainty is considerable.
While the uncertainty associated with the model parameters is smaller than the uncertainty associated with the climate forcing, it is considerable for individual glaciers (Figure 10). The use of Bayesian inference to quantify the uncertainty associated with the model parameters (Rounce et al., 2020) is a major advance for large-scale glacier evolution models and provides a framework to integrate multiple datasets in the future. As more systematic observations of mass balance are performed, it is likely that every glacier in the world will be able to be calibrated independently. While these systematic observations of mass change (e.g., Brun et al., 2017; Shean et al., 2020) are an excellent source of data that enable models to resolve the spatial variability in projections (Figure 4) and can significantly improve those projections (see Section 5.2.1), all existing models are still over-parameterized. Until this over-parameterization issue is solved, glacier projections will likely only be as good as their model physics and calibration data.
For example, Kraaijenbrink et al. (2017) is the first study to incorporate debris cover. Our study projects 7% less net mass loss by 2100 for RCP 2.6, 3% less for RCP 4.5, 1% less for RCP 6.0, and 3% more mass loss for RCP 8.5. While these differences are well within the range of reported uncertainties, the change from estimating less net mass loss for RCP 2.6 to estimating more net mass loss for RCP 8.5 may be because we did not account for debris and therefore do not capture the delayed response of debris-covered glaciers (Kraaijenbrink et al., 2017). If true, this suggests that accounting for debris is more important for higher emission scenarios. One possible explanation could be that glaciers are able to reach a new equilibrium for lower emission scenarios (e.g., RCP 2.6; Supplementary Figure S4), but are unable to do so for higher emission scenarios (e.g., RCP 8.5; Supplementary Figure S6); hence, the lag in the response of debris-covered glaciers becomes more important. However, given the differences in model physics, calibration data, GCMs used, and bias correction methods applied to the GCMs by each study, this is highly speculative. Future work should seek to quantify the impact debris-covered glaciers have on projections of glacier mass change and runoff. This type of analysis requires accurate debris thickness estimates that can resolve thick (>0.5 m) debris (e.g., Rounce et al., 2018), and advanced glacier dynamic modules (e.g., Maussion et al., 2019; Zekollari et al., 2019) that can capture feedbacks between spatial variations in subdebris melt and reduced driving stresses (Kraaijenbrink et al., 2017).
Model intercomparisons like GlacierMIP (Hock et al., 2019) can help identify sources of uncertainty and develop additional controlled experiments to quantify these uncertainties. However, as long as models are over-parameterized, it will remain difficult to assess the relative importance of a specific physical process because calibration schemes may inherently account for them. This issue applies to glacier dynamics, firn development, avalanching, and any other physical processes that may be missing or poorly represented in models. Until the over-parameterization issue is resolved, the only way to definitively quantify these uncertainties will be to control all input data (e.g., glacier inventories, climate data, calibration data) and methods (e.g., calibration scheme, model physics, GCM bias adjustments), which is albeit impossible to coordinate amongst multiple research groups. As more glacier evolution models become open-source like PyGEM and the Open Global Glacier Model (OGGM; Maussion et al., 2019), these controlled experiments will be easier to perform.
Fortunately, recent advances in systematic observations of elevation change (Brun et al., 2017; Shean et al., 2020) and surface velocities (Dehecq et al., 2019) that could be paired with consensus ice thickness estimates (Farinotti et al., 2019), provide unique opportunities to estimate climatic mass balance (e.g., Brun et al., 2018; Rounce et al., 2018) and potentially minimize the over-parameterization issue in the near future. Given that changes in glacier velocities in High Mountain Asia are mainly driven by changes in ice thickness (Dehecq et al., 2019), combining these new observations with new schemes for glacier dynamics (e.g., Maussion et al., 2019; Zekollari et al., 2019) and modules accounting for debris cover (e.g., Kraaijenbrink et al., 2017) may greatly improve future projections.
7. Conclusion
This study used a new dataset of glacier mass balances in conjunction with Bayesian inference to calibrate every glacier in High Mountain Asia independently and quantify the uncertainty associated with the model parameters. This enabled us to resolve spatial and temporal variability in mass change and glacier runoff with an unprecedented level of detail. The comparison with historical mass balance observations shows the model captures regional variations well and even agrees well at the glacier-level with longer (>1 year) observations when one considers the uncertainty associated with the model parameters.
Projections of mass change show glaciers in High Mountain Asia are expected to lose between 29 ± 12% for RCP 2.6 and 67 ± 10% for RCP 8.5 by 2100 relative to 2015. While the Karakoram and Western Kunlun Shan will contribute the most mass loss due to their large initial glacier volume, significant regional variability exists and the smallest glacierized regions are projected to experience the most mass loss in terms of percent of their initial mass. The glaciers’ response to future climate forcing is complex as considerable variability in the temperature and precipitation changes, and glacier attributes (thickness, hypsometry, elevation range) will alter how each glacier responds.
Projections of glacier runoff show the timing of peak water is driven by excess meltwater, especially in river basins fed by the winter westerlies. These river basins are expected to hit peak water in the latter half of the century, while most monsoon-fed river basins are expected to hit peak water before 2050. Interestingly, these monsoon-fed river basins that appear to rely on glacier meltwater the least are expected to be most negatively impacted in the future due to declining estimates of runoff in the end-of-summer months. This could have major implications for future water resources and is an important area of future work.
The new calibration scheme used in this study shows that at regional scales the uncertainty associated with GCMs dominates the uncertainty associated with model parameters. While the use of this new mass balance dataset enabled the model to resolve spatial variations in mass change, the model is still over-parameterized. Future work should seek to continue generating systematic datasets that may be used to solve this issue. Once this issue is resolved, models will be able to assess how much of an impact accurately accounting for various physical processes (e.g., debris cover, glacier dynamics) have on projections, which will likely greatly improve these projections as well.
Data Availability Statement
The datasets generated for this study can be found in the National Snow and Ice Data Center (NSIDC) (https://nsidc.org/data/highmountainasia). The model code is publicly available at https://github.com/drounce/PyGEM (PyGEMv0.1.0).
Author Contributions
DR lead the study, performed the calculations, and wrote the manuscript. DR and RH developed the methodology and design of the study. RH initiated the study. DS provided the mass balance data. All authors commented on the manuscript.
Funding
DR and RH received support from NASA-ROSES program grants NNX17AB27G and 80NSSC17K0566. DS was supported by NASA-ROSES program grant NNX16AQ88G.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported in part by the high-performance computing and data storage resources operated by the Research Computing Systems Group at the University of Alaska Fairbanks Geophysical Institute. Matthias Huss provided ice thickness data. Etienne Berthier provided ELA data.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2019.00331/full#supplementary-material
Footnotes
References
Armstrong, R. L., Rittger, K., Brodzik, M. J., Racoviteanu, A., Barrett, A. P., Khalsa, S.-J. S., et al. (2019). Runoff from glacier ice and seasonal snow in High Asia: separating melt water sources in river flow. Reg. Environ. Change 19, 1249–1261. doi: 10.1007/s10113-018-1429-0
Berthier, E., and Brun, F. (2019). Karakoram geodetic glacier mass balances between 2008 and 2016: persistence of the anomaly and influence of a large rock avalanche on siachen glacier. J. Glaciol. 65, 494–507. doi: 10.1017/jog.2019.32
Biemans, H., Siderius, C., Lutz, A. F., Nepal, S., Ahmad, B., Hassan, T., et al. (2019). Importance of snow and glacier meltwater for agriculture on the Indo-Gangetic Plain. Nat. Sustainabil. 2, 594–601. doi: 10.1038/s41893-019-0305-303
Bliss, A., Hock, R., and Radić, V. (2014). Global response of glacier runoff to twenty-first century climate change. J. Geophys. Res. 119, 717–730. doi: 10.1002/2013JF002931
Bolch, T., Shea, J. M., Liu, S., Azam, F. M., Gao, Y., Gruber, S., et al. (2019). “Status and change of the cryosphere in the extended Hindu Kush Himalaya Region,” in The Hindu Kush Himalaya Assessment: Mountains, Climate Change, Sustainability and People, eds P. Wester, A. Mishra, A. Mukherji, and A. B. Shrestha (Lalitpur: ICIMOD).
Braithwaite, R. J., and Raper, S. C. B. (2009). Estimating equilibrium-line altitude (ELA) from glacier inventory data. Ann. Glaciol. 50, 127–132. doi: 10.3189/172756410790595930
Brun, F., Berthier, E., Wagnon, P., Kääb, A., and Treichler, D. (2017). A Spatially resolved estimate of high mountain asia glacier mass balances from 2000 to 2016. Nat. Geosci. 10, 668–673. doi: 10.1038/ngeo2999
Brun, F., Wagnon, P., Berthier, E., Shea, J. M., Immerzeel, W. W., Kraaijenbrink, P. D. A., et al. (2018). Ice cliff contribution to the tongue-wide ablation of Changri Nup glacier, Nepal, central Himalaya. Cryosphere 12, 3439–3457. doi: 10.5194/tc-12-3439-2018
Carlin, B. P., and Louis, T. A. (2008). Bayesian Methods for Data Analysis, 3rd Edn, Boca Rato: Taylor & Francis.
Dahri, Z. H., Khan, A., Ahmad, B., Moors, E., Kabat, P., and Ludwig, F. (2016). An appraisal of precipitation distribution in the high-altitude catchments of the indus basin. Sci. Total Environ. 54, 289–306. doi: 10.1016/j.scitotenv.2016.01.001
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., et al. (2011). The ERA-interim reanalysis: configuration and performance of the data assimilation system. Quar. J. R. Meteorol. Soc. 137, 553–597. doi: 10.1002/qj.828
Dehecq, A., Gourmelen, N., Gardner, A. S., Brun, F., Goldberg, D., Nienow, P. W., et al. (2019). Twenty-first century glacier slowdown driven by mass loss in High Mountain Asia. Nat. Geosci. 12, 22–27. doi: 10.1038/s41561-018-0271-9
Farinotti, D., Huss, M., Fürst, J. J., Landmann, J., Machguth, H., Maussion, F., et al. (2019). A consensus estimate for the ice thickness distribution of all glaciers on Earth. Nat. Geosci. 12, 168–173. doi: 10.1038/s41561-019-0300-3
Forsythe, N., Fowler, H. J., Li, X. F., Blenkinsop, S., and Pritchard, D. (2017). Karakoram temperature and glacial melt driven by regional atmospheric circulation variability. Nat. Clim. Change. 7, 664–670. doi: 10.1038/NCLIMATE3361
Gardelle, J., Berthier, E., Arnaud, Y., and Kääb, A. (2013). Region-wide glacier mass balances over the Pamir-Karakoram-Himalaya during 1999-2011. Cryosphere 7, 1263–1286. doi: 10.5194/tc-7-1263-2013
Gardner, A. S., Moholdt, G., Cogley, J. G., Wouters, B., Arendt, A. A., Wahr, J., et al. (2013). A reconciled estimate of glacier contributions to sea level rise: 2003 to 2009. Science 340, 852–857. doi: 10.1126/science.1234532
Hock, R., Marzeion, B., Bliss, A., Giesen, R., Hirabayashi, Y., Huss, M., et al. (2019). GlacierMIP - a model intercomparison of global-scale glacier mass-balance models and projections. J. Glaciol. 65, 453–467. doi: 10.1017/jog.2019.22
Huss, M., and Farinotti, D. (2012). Distributed ice thickness and volume of all glaciers around the globe. J. Geophys. Res. 117, 1–10. doi: 10.1029/2012JF002523
Huss, M., and Hock, R. (2015). A new model for global glacier change and sea-level rise. Front. Earth Sci. 3:1–22. doi: 10.3389/feart.2015.00054
Huss, M., and Hock, R. (2018). Global-scale hydrological response to future glacier mass loss. Nat. Clim. Change 8, 135–140. doi: 10.1038/s41558-017-0049-x
Huss, M., Jouvet, G., Farinotti, D., and Bauder, A. (2010). Future High-Mountain hydrology: a new parameterization of glacier retreat. Hydrol. Earth Syst. Sci. 14, 815–829. doi: 10.5194/hess-14-815-2010
Immerzeel, W. W., van Beek, L. P. H., and Bierkens, M. F. P. (2010). Climate change will affect the Asian water towers. Science 328, 1382–1385. doi: 10.1126/science.1183188
Immerzeel, W. W., Wanders, N., Lutz, A. F., Shea, J. M., and Bierkens, M. F. P. (2015). Reconciling high-altitude precipitation in the upper indus basin with glacier mass balances and runoff. Hydrol. Earth Syst. Sci. 19, 4673–4687. doi: 10.5194/hess-19-4673-2015
Jansson, P., Hock, R., and Schneider, T. (2003). The concept of glacier storage: a review. J. Hydrol. 282, 116–129. doi: 10.1016/S0022-1694(03)00258-0
Kääb, A., Treichler, D., Nuth, C., and Berthier, E. (2015). Brief Communication: contending Estimates of 2003-2008 glacier mass balance over the Pamir-Karakoram-Himalaya. Cryosphere 9, 557–564. doi: 10.5194/tc-9-557-2015
Kapnick, S. B., Delworth, T. L., Ashfaq, M., Malyshev, S., and Milly, P. C. D. (2014). Snowfall less sensitive to warming in Karakoram Than in Himalayas Due to a unique seasonal cycle. Nat. Geosci. 7, 834–840. doi: 10.1038/NGEO2269
Kayastha, R. B., Ageta, Y., and Nakawo, M. (2000). Positive degree-day factors for ablation on glaciers in the Nepalese Himalayas: case study on Glacier AX010 in Shorong Himal, Nepal. Bull. Glaciol. Res. 17, 1–10.
Kraaijenbrink, P. D. A., Bierkens, M. F. P., Lutz, A. F., and Immerzeel, W. W. (2017). Impact of a global temperature Rise of 1.5 degrees celsius on Asia’s Glaciers. Nature 549, 257–260. doi: 10.1038/nature23878
Lutz, A. F., Immerzeel, W. W., Kraaijenbrink, P. D. A., Shrestha, A. B., and Bierkens, M. F. P. (2016). Climate change impacts on the Upper Indus hydrology: sources, shifts and extremes. PLoS One 11:e0165630. doi: 10.1371/journal.pone.0165630
Lutz, A. F., Immerzeel, W. W., Shrestha, A. B., and Bierkens, M. F. P. (2014). Consistent increase in High Asia’s Runoff Due to increasing glacier melt and precipitation. Nat. Clim. Change 4, 587–592. doi: 10.1038/nclimate2237
Marzeion, B., Jarosch, A. H., and Hofer, M. (2012). Past and future sea-level change from the surface mass balance of Glaciers. Cryosphere 6, 1295–1322. doi: 10.5194/tc-6-1295-2012
Maussion, F., Butenko, A., Champollion, N., Dusch, M., Eis, J., Fourteau, K., et al. (2019). The open global glacier model (OGGM) v1.0. Geosci. Model Dev. 12, 909–931. doi: 10.5194/gmd-12-909-2019
Pritchard, H. D. (2019). Asia’s shrinking glaciers protect large populations from drought stress. Nature 569, 649–654. doi: 10.1033/s41586-019-1240
Radić, V., and Hock, R. (2011). Regionally differentiated contribution of mountain glaciers and ice caps to future sea-level rise. Nat. Geosci. 4, 91–94. doi: 10.1038/ngeo1052
Radić, V., and Hock, R. (2014). Glaciers in the earth’s hydrological cycle: assessments of glacier mass and runoff changes on global and regional scales. Surv. Geophys. 35, 813–837. doi: 10.1007/s10712-013-9262-y
RGI Consortium. (2017). Randolph Glacier Inventory-A Dataset of Global Glacier Outlines: Version 6.0. Technical Report, Global Land Ice Measurements from Space, Colorado: Digital Media.
Rounce, D. R., Khurana, T., Short, M. B., Hock, R., Shean, D. E., and Brinkerhoff, D. J. (2020). Quantifying parameter uncertainty in a large-scale glacier evolution model using Bayesian inference: application to High Mountain Asia. J. Glaciol. doi: 10.1017/jog.2019.91
Rounce, D. R., King, O., McCarthy, M., Shean, D. E., and Salerno, F. (2018). Quantifying debris thickness of debris-covered glaciers in the Everest region of Nepal through invesion of a subdebris melt model. J. Geophys. Res. 123, 1094–1115. doi: 10.1029/2017JF004395
Shean, D. E., Bhushan, S., Montesano, P., Rounce, D. R., Arendt, A., and Osmanoglu, B. (2020). A systematic, regional assessment of High-Mountain Asia glacier mass balance. Front. Earth Sci. 7:331. doi: 10.3389/feart.2019.00363
Singh, P., Kumar, N., and Arora, M. (2000). Degree-day factors for snow and ice for Dokriani Glacier, Garhwal Himalayas. J. Hydrol. 235, 1–11. doi: 10.1016/s0022-1694(00)00249-3
Smith, T., and Bookhagen, B. (2018). Changes in seasonal snow water equivalent distribution in High Mountain Asia (1987 to 2009). Sci. Adv. 4:e1701550. doi: 10.1126/sciadv.1701550
Taylor, K. E., Stouffer, R. J., and Meehl, G. A. (2012). An overview of CMIP5 and the experiment design. Bull. Am. Meterol. Soc. 93, 485–498. doi: 10.1175/BAMS-D-11-00094.1
Vörösmarty, C. J., Fekete, B. M., Meybeck, M., and Lammers, R. B. (2000). Geomorphometric attributes of the global system of Rivers at 30-minute spatial resolution. J. Hydrol. 237, 17–39. doi: 10.1016/s0022-1694(00)00282-1
Woodward, J., Sharp, M., and Arendt, A. (1997). The Influence of Superimposed-Ice formation on the sensitivity of glacier mass balance to climate change. Ann. Glaciol. 24, 186–190. doi: 10.1038/s41598-019-50398-4
Wortmann, M., Bolch, T., Menz, C., Tong, J., and Krysanova, V. (2018). Comparison and correction of high-mountain precipitation data based on glacio-hydrological modeling in the tarim River Headwaters (High Asia). J. Hydrometeorol. 19, 777–801. doi: 10.1175/jhm-d-17-0106.1
Yong, Z., Shiyin, L., and Yongjian, D. (2006). Observed degree-day factors and their spatial variation on glaciers in western China. Ann. Glaciol. 43, 301–306. doi: 10.3189/172756406781811952
Zekollari, H., Huss, M., and Farinotti, D. (2019). Modelling the future evolution of glaciers in the European Alps under the EURO-CORDEX RCM ensemble. Cryosphere 13, 1125–1146. doi: 10.5194/tc-13-1125-2019
Zemp, M., Huss, M., Thibert, E., Eckert, N., McNabb, R., Huber, J., et al. (2019). Global glacier mass changes and their contributions to sea-level rise from 1961 to 2016. Nature 568, 382–386. doi: 10.1038/s41586-019-1071-0
Keywords: glaciers, mass change, glacier runoff, High Mountain Asia, projections
Citation: Rounce DR, Hock R and Shean DE (2020) Glacier Mass Change in High Mountain Asia Through 2100 Using the Open-Source Python Glacier Evolution Model (PyGEM). Front. Earth Sci. 7:331. doi: 10.3389/feart.2019.00331
Received: 31 May 2019; Accepted: 29 November 2019;
Published: 23 January 2020.
Edited by:
Walter W. Immerzeel, Utrecht University, NetherlandsReviewed by:
Shichang Kang, State Key Laboratory of Cryospheric Science (CAS), ChinaAdina Elena Racoviteanu, Aberystwyth University, United Kingdom
Copyright © 2020 Rounce, Hock and Shean. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: David R. Rounce, ZHJvdW5jZUBhbGFza2EuZWR1
 David R. Rounce
David R. Rounce Regine Hock
Regine Hock David E. Shean
David E. Shean