Geological Carbon Sequestration by Reactive Infiltration Instability

We study carbon capture and sequestration (CCS) over time scales of 2000 years by implementing a numerical model of reactive infiltration instability caused by reactive porous flow. Our model focuses on the mineralization of CO₂ dissolved in the pore water—the geological carbon sequestration phase of a CCS operation—starting 10–100 years after the injection of CO₂ in the subsurface. We test the influence of three parameters: porosity, mass fraction of the Ca-rich feldspar mineral anorthite in the solid, and the chemical reaction rate, on the mode of fluid flow and efficiency of CaCO₃ precipitation during geological carbon sequestration. We demonstrate that the mode of porous flow switches from propagation of a planar front at low porosities to propagation of channels at porosities exceeding 10%. The channels develop earlier for more porous aquifers. Both high anorthite mass fraction in the solid phase and high reaction rates aid greater amounts of carbonate precipitation, with the reaction rate exerting the stronger influence of the two. Our calculations indicate that an aquifer with dimensions 500 m $\times$ 2 km $\times$ 2 km can sequester over 350 Mt solid CaCO₃ after 2000 years. To precipitate 50 Mt CaCO₃ after 2000 years in this aquifer, we suggest selecting a target aquifer with more than 10 wt% of reactive minerals. We recommend that the aquifer porosity, abundance of reactive aluminosilicate minerals such as anorthite, and reaction rates are taken into consideration while selecting future CCS sites.

1. Introduction

Carbon capture and permanent sequestration in the subsurface is becoming an important mechanism in carbon neutralization (Hosa et al., 2011; Odenberger et al., 2013; Celia, 2017). Current anthropogenic CO₂ emissions (42 Gt/yr, Le Quéré et al., 2018; Friedlingstein et al., 2019) are three orders of magnitude higher than the current combined global CCS injection rate (35–40 Mt/yr, Celia, 2017). Recognizing the importance of CCS in mitigating global carbon emissions, a number of different incentives are offered. For example, the 2018 US Bipartisan Budget Act (26 U.S.C. § 45Q) provided a tax credit of $20 per ton of CO₂ sequestered permanently. To encourage CCS using existing infrastructure, a number of locations—Sleipner site in the Norwegian North Sea (1 Mt/yr, Hosa et al., 2011), Kimberlina site in the western US (0.25 Mt over 4 years, Doughty, 2010), and Goldeneye reservoir in the North Sea (10 Mt CO₂ over 10 years, Spence et al., 2014)—are either targeted for future operations or are being used as permanent CO₂ storage sites. Hosa et al. (2011) provided an overview of the storage capacity, reservoir characteristics, and injection rates of 20 active CCS sites over the world. This article identifies a number of controls on the efficiency of CCS in potential future sites and testing facilities. Kingdon et al. (2019) provided details of such planned experimental facilities at the United Kingdom Geoenergy Observatory Cheshire Energy Research Facility Site, which will be used for in-situ testing of these controls.

Carbon capture and storage can broadly be envisioned as a two-step process (Bachu, 2000; Friedmann, 2007; Jiang, 2011; Aminu et al., 2017). During the early phase, supercritical CO₂ is injected into the subsurface (Doughty, 2010; Bacci et al., 2011; Emami-Meybodi et al., 2015). Following subsurface injection, the supercritical CO₂ remains a separate, migrating phase before slowly reacting with the connate water in the saline aquifer. This slow phase of reaction with saline groundwater leads to the formation of carbonic acid by the reaction.

${\text{H}}_2\text{O}+{\text{CO}}_2\rightleftharpoons {\text{H}}_2{\text{CO}}_3\rightleftharpoons {\text{HCO}}_3^{-}+{\text{H}}^{+}(1)$

We assume that the target aquifer has minimal buffering capacity, which leads to lower pH values. Therefore, given the time frame of the model used in this paper, H₂CO₃ will be dominant over bicarbonate species. Once the solution of CO₂ is completed, the process of geological carbon sequestration (GCS), or mineralization of carbon, ensues. During this phase, dense, carbonic acid-rich groundwater descends into the porous host formation, reacting with the aluminosilicate and silicate minerals to form solid carbon deposits in the form of carbonate minerals, which takes place over time scales of 1,000 years. In this article, we focus on the mechanisms involved in this stage.

The process of carbonate mineralization by assimilation of dissolved H₂CO₃ takes place through a combination of density-driven porous flow, chemical reaction, and diffusion. The combination of these processes leads to a mechanism known as the reactive infiltration instability (RII) (Chadam et al., 1986), which has been associated with subsurface cavern or “wormhole” formation (Hinch and Bhatt, 1990; Szymczak and Ladd, 2013; Szymczak and Ladd, 2011) and chemical reaction between magmatic melts and mantle rocks (Aharonov et al., 1995; Spiegelman et al., 2001; Takei and Hier-Majumder, 2009; Sun et al., 2020a). An important manifestation of RII is the propagation of the reactive fluids into the aquifer through transient “channels” or “fingers”, which merge and interact with each other during the penetration of the reactive fluid into the saline aquifer (Riaz et al., 2006; Soltanian et al., 2016). Laboratory experiments on reactive porous flow of basaltic melt into olivine (Pec et al., 2015) and dense brine injection into a porous medium also support this observation (Kneafsey and Pruess, 2010; Vosper et al., 2014).

In addition to the flow regime, the physical and chemical characteristics of the saline aquifer or subsurface reservoir also exert an influence on the efficiency of GCS. Previous models of porous flow and laboratory experiments studied the efficiency of mass transfer as a function of two important dimensionless numbers: the Damköhler number ($\mathcal{D}a$), representing the ratio between the rates of reaction and advection, and the Péclet number ($\mathcal{P}e$), representing the ratio between rates of advection and diffusion (Chadam et al., 1986; Riaz et al., 2006; Ghesmat et al., 2011; Szymczak and Ladd, 2013). These studies, however, ignored the crucial role of parameters such as the lithology and porosity of the aquifer on the efficiency of GCS. These parameters can be potentially important in identifying CCS sites and quantifying the amount of long term carbon sequestration in currently active sites. They can also vary significantly across different sites. For example, Hosa et al. (2011) showed that currently active sites of CCS can be characterized by a low porosity of 3% and a permeability of 0.1 mD (MRCSP R.E. Burger project, Ohio, USA) to a high porosity of 37% and a permeability of 5 D (Sleipner site, Norwegian N. Sea). The role of porosity and permeability variations is generally incorporated into models of supercritical CO₂ injection over periods of time spanning over a few years (Class et al., 2009; Doughty, 2010; Soltanian et al., 2016). Systematic analyses of the efficiency of GCS as a function of porosity, formation lithology, and fundamental dimensionless numbers still remain scarce.

In this work, we bridge this gap by studying the influence of formation porosity and the mineral composition on the efficiency of GCS in a porous saline aquifer. Our model begins after the supercritical CO₂ has been injected into the aquifer and has reacted with the brine in the pore space to create a dense, H₂CO₃ rich pore fluid. In our numerical simulations, this dense pore fluid sinks into the unaffected formation by reactive porous flow. To model the deposition of solid carbonate resulting from the reaction between the H₂CO₃ rich fluid and the solid matrix, we carry out a series of 2D finite element simulations using a massively parallel open source software MuPoPP 1.2 (Hier-Majumder, 2020) running on the Oracle cloud computing platform. In these simulations, we vary the dimensionless Damköhler ($\mathcal{D}a$) and Péclet ($\mathcal{P}e$) numbers, aquifer porosity, and the initial concentration of the Ca bearing $\mathcal{D}a$ feldspar mineral phase anorthite (An) in the aquifer. As we demonstrate, these parameters influence (a) the mode of fluid transport by a transition from propagation of a planar front to channelized flow and (b) the amount of carbonate deposited in the solid phase after 2000 years of fluid flow.

2. Model

2.1. Governing Equations and Boundary Conditions

We model the porous flow of a reactive, H₂CO₃ rich fluid as a reactive infiltration instability problem. As discussed above, this model focuses on the long term GCS process and begins after the supercritical CO₂ has been pumped into the subsurface and equilibrated with the groundwater to create a dense, H₂CO₃ rich pore fluid. The density of the pore fluid, ρ, depends on the concentration of the dissolved H₂CO₃ in the pore water, $c_0$, and is related to the concentration by $\rho ={\rho }_0\left(1+\gamma c_0\right)$, where ${\rho }_0$ is the density of H₂CO₃ free water, and γ is a dimensionless constant. Driven by the concentration dependent density, pore fluid from the aquifer percolates through the porous medium reacting with the aluminosilicate minerals to precipitate CaCO₃. In our model, we use the chemical reaction between anorthite (An CaAl₂Si₂O₈) in the solid with H₂CO₃ in the pore fluid, leading to the precipitation of CaCO₃ and kaolinite ($\text{Ka}{\text{Al}}_2{\text{Si}}_2{\text{O}}_5{\text{(OH)}}_4$), given by the reaction.

${\text{CaAl}}_2{\text{Si}}_2{\text{O}}_8\left(\text{s}\right)+{\text{H}}_2\text{O}\left(\text{l}\right)+{\text{H}}_2{\text{CO}}_3\left(\text{l}\right)\rightleftharpoons {\text{CaCO}}_3\left(\text{s}\right)+{\text{Al}}_2{\text{Si}}_2{\text{O}}_5{\left(\text{OH}\right)}_4\left(\text{s}\right)(2)$

While a number of chemical reactions can take place between H₂CO₃ and subsurface minerals, the most common set of reactions involves aluminosilicates in the rock (Ghesmat et al., 2011; Zhang and Song, 2014). In this article, we focus on the influence on GCS driven by this chemical reaction between the solid and the pore fluid. We discuss the assumptions made in our model in detail in Section 2.2.

We provide the full set of dimensional equations, nondimensionalization schemes, and details of the numerical methods in the Supplementary Material. For brevity, here we present the final, dimensionless equations. In this set‐up, the velocity, $\mathit{u}$, of the pore fluid is governed by Darcy flow,

$\varphi \mathit{u}=-k\left[\nabla p+\left(1+\gamma c_0\right)\widehat{\mathit{z}}\right](3)$

where ϕ is the constant porosity of the rock, $k={\left(\varphi /{\varphi }_0\right)}^3$ is the permeability, ${\varphi }_0=0.1$ is a reference porosity, p is the fluid pressure, and $\widehat{\mathit{z}}$ is a unit vector in the vertically upward direction (Sun et al., 2020a). The last term arises from the concentration dependent density of the fluid, where we set $\gamma =1$. In addition to Darcy flow, the continuity equation requires that the velocity is nondivergent.

$\nabla \cdot \mathit{u}=0(4)$

The rate of transport of dissolved H₂CO₃ in the pore fluid is controlled by advection via porous flow, chemical diffusion, and chemical reaction,

$\frac{\partial c_0}{\partial t}+\mathit{u}\cdot \nabla c_0=\frac{1}{\mathcal{P}e}{\nabla }^2{c}_0-X_0\frac{\mathcal{D}a{c}_0{c}_1}{\varphi }(5)$

where $X_0$ is the stoichiometric mass fraction of H₂CO₃ in Eq. (2), and the dimensionless quantities $\mathcal{P}e$ and $\mathcal{D}a$ are defined below in Eq. 8. We consider a second order chemical reaction driven by the rate of the forward reaction (Ghesmat et al., 2011). As a result, the rate of consumption and production of reactants and products depend on the concentrations of H₂CO₃ in the pore fluid, $c_0$, and mass fraction of anorthite in the system, $c_1$, as evidenced by the second term on the right hand side.

Finally, the rate of consumption of anorthite in the rock and the rate of production of CaCO₃ are given by the two equations

$\frac{\partial c_1}{\partial t}=-X_1\frac{\mathcal{D}a{c}_0{c}_1}{1-\varphi }(6)$

$\frac{\partial c_2}{\partial t}=X_2\frac{\mathcal{D}a{c}_0{c}_1}{1-\varphi }(7)$

where $X_1$ and $X_2$ are the mass fractions of anorthite and CaCO₃ in the chemical reaction (Eq. 2), and $c_2$ is the mass fraction of CaCO₃ produced by GCS.

The dimensionless quantities are defined by the relations

$\mathcal{P}e=\frac{u_{0}H}{D},\mathcal{D}a=\frac{{\text{Γ}}_{0}H}{u_0}(8)$

where $u_0$ is a characteristic fluid velocity, H is the height of the domain (thickness of the aquifer), D is the chemical diffusivity, and ${\text{Γ}}_0$ is a characteristic rate of chemical reaction. In this work, we chose to carry out a number of simulations over a range of plausible values of these dimensionless quantities, which allows us to quantify the influence of not only the dimensionless numbers, but also the aquifer characteristics on the efficiency of GCS. We discuss the rationale behind selecting these ranges in the following subsection.

We solved the five governing Eq. 3–7 for the five unknowns—$\mathit{u}$, p, $c_0$, $c_1$, and $c_2$—subject to a set of Dirichlet and Neumann boundary conditions (BCs) and initial conditions (ICs). These BCs and ICs are illustrated in the schematic diagram in Figure 1. On the top boundary, $\partial {\text{Ω}}_t$, we assume a Dirichlet boundary condition, namely a uniformed constant downward velocity $w_0\widehat{\mathit{z}}$. On the vertical boundaries, $\partial {\text{Ω}}_v$, the fluid velocity and concentrations are defined to be periodic. On the top and bottom boundaries, a Neumann boundary condition is applied on $\partial {\text{Ω}}_N$.

$\mathit{u}=w_0\widehat{\mathit{z}}\text{on}\partial {\text{Ω}}_t(9)$

$\mathit{u},c_0=\text{periodic}\text{on}\partial {\text{Ω}}_v(10)$

$\nabla c_0\cdot \widehat{\mathit{n}}=0\text{on}\partial {\text{Ω}}_N(11)$

In addition, we impose the initial conditions,

$c_0\left(x,z,0\right)=0,c_1\left(x,z,0\right)=\left[\text{An}\right],c_2\left(x,z,0\right)=0(12)$

where [An] is a constant value of initial anorthite mass fraction in the aquifer. In order to explore the influence of aquifer composition on the efficiency of the GCS, we carried out a number of simulations with different values of [An].

FIGURE 1

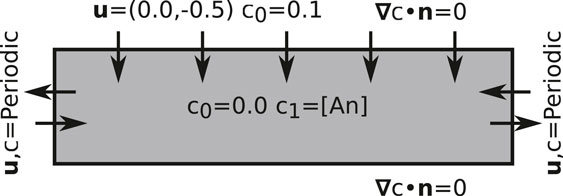
FIGURE 1. A schematic diagram outlining the domain of the numerical model with the boundary conditions.

The unknown $c_2\left(x,z,t\right)$ gives the concentration of CaCO₃ at each point within the domain at a given time. It is useful to also have an estimate for the mass of CaCO₃ that can be sequestered by the process. To calculate the cumulative CaCO₃ mass M over time, we use the definition of production rate of CaCO₃ in Eq. 7. Using the right hand side of the equations from the known quantities at each time step and integrating, we get

$M\left(t\right)={\rho }_{sst}H{L}^2\left(1-\varphi \right){{\displaystyle \int }}_0^t{{\displaystyle \int }}_{\text{Ω}}\frac{\partial c_2}{\partial t}\text{dΩ}\text{d}t={\rho }_{sst}H{L}^2{{\displaystyle \int }}_0^t{{\displaystyle \int }}_{\text{Ω}}{X}_2\mathcal{D}a{c}_0{c}_1\text{dΩ}\text{d}t(13)$

where $M\left(t\right)$ is the transient mass of CaCO₃ deposited over the time period $0-t$ within the domain $\text{Ω}$ (the aquifer), of height H and depth L. Since our simulations are 2D, we assume that the length of the domain in the third dimension is also L. Finally, the density of sandstone in the aquifer is given by ${\rho }_{sst}$. The dimensional values of these constants are listed in Table 1.

TABLE 1

TABLE 1. Nondimensional numbers and dimensional constants used in this article. See Section 2.3 for more detailed description.

2.2. Model Assumptions

In this model, we focus on the influence of three parameters: aquifer porosity, initial abundance of Anorthite in the aquifer, and the chemical reaction rate on the structure of the fluid percolation and the amount of solid carbonate precipitation. To address the complex, nonlinear interplay among these factors, we made a few assumptions in our model.

First, we only consider the chemical reaction given in Eq. 2 and test the outputs of our models over a range of $\mathcal{D}\text{a}$, a method followed by previous numerical studies (Aharonov et al., 1995; Ghesmat et al., 2011). In addition to the reaction between H₂CO₃ rich fluid and anorthite, reactions between the fluid and CaCO₃ and, although much slower, reactions between the fluid and quartz are possible (Espinoza et al., 2011). By ignoring these possible reactions, especially the dissolution of CaCO₃, we assume that the pH level of the pore fluid is buffered such that the fluid is saturated with CaCO₃. While we do not explicitly include such buffering reactions in our model, Snæbjörnsdóttir et al. (2017) reported that samples of injected fluid reached CaCO₃ saturation within months of injection at the CarbFix site in Iceland. Given the substantially longer timescale of our simulations, this observation of Snæbjörnsdóttir et al. (2017) suggests that our assumption of CaCO₃ buffering in the pore fluid is likely reasonable.

Second, we ignore the influence of calcite precipitates on reducing the porosity and permeability of the aquifer. Within the timescale of our simulations, this effect is likely to play an insignificant role. As we show in Figure 6, the highest concentration of precipitated CaCO₃ in our simulations is less than 0.5%. Recent microtomographic studies on permeability reduction by cementation show that porosity and permeability reduction by precipitates is negligible for cement volume fractions less than 3–5% (Thomson et al., 2019; Thomson et al., 2020). The assumption of constant porosity, therefore, is reasonable for the range of time considered in these simulations. With these caveats, we next discuss the range of parameters explored in this work.

2.3. Parameter Ranges

In this study, we focus on the influence of a number of factors on the modes and efficiency of GCS by reactive infiltration instability. These parameters are highlighted on Table 1. As discussed below, it is often difficult to assign a particular value of a characteristic dimensionless number such as $\mathcal{D}a$ and $\mathcal{P}e$. In addition, aquifer features such as porosity and the anorthite content can vary between sites. It is, therefore, useful to have the information on the influence of these factors on the efficiency of GCS, which can be used for selection and planning of sites such as those associated with the UKGEOS initiative. In this section, we discuss the range of values of these parameters discussed in literature and the rationale behind the ranges selected in this study.

Despite a number of reports on the second order reaction rate for dissolution of silicate and aluminosilicate minerals (Oelkers and Schott, 1995; Palandri and Kharaka, 2004; Espinoza et al., 2011), direct estimates of $\mathcal{D}a$ from experimental measurements remain scarce. Here, we present a range of most likely natural values of $\mathcal{D}a$ relevant to the CCS problem. Following previous works on reactive infiltration instability (Steefel and Lasaga, 1994; Aharonov et al., 1995), we notice that the rate of mass fraction ${\text{Γ}}_0$ can be expressed as a function of dissolution rate, R, specific surface area A, and the density of anorthite ${\rho }^{\prime }=2750$ kg/m³, as

${\text{Γ}}_0=\frac{M_{An}RA}{{\rho }^{\prime }}(14)$

where $M_{An}=0.28$ kg/mol is the mass of anorthite per mole. Using the dissolution rate of anorthite from Espinoza et al. (2011), we calculate a lower and an upper limit of $R=4.3\times {10}^{-12}$ and $R=1.3\times {10}^{-10}$ mol/m²/s, respectively. Following the argument outlined by Steefel and Lasaga (1994), we take the specific surface area as the area of contact between the pore fluid and grains per unit volume. We use the microstructural model of Hier-Majumder and Abbott (2010) to obtain this specific surface area (unit of m²/m³). Next, we combine the value of A with reaction rate R in Eq. 14, yielding values of ${\text{Γ}}_0$ ranging between $1.0\times {10}^{-11}$ and $3.1\times {10}^{-10}$ ${\text{s}}^{-1}$. Using the values of characteristic velocities and length scales listed in Table 1, these lead to values of $\mathcal{D}a$ ranging between 0.3 and 9.7. We ran the simulations for a more conservative range of $\mathcal{D}a$ ranging between 0.1 and 5. It is possible that the value of $\mathcal{D}a$ is higher than our estimates, in this case the mass of deposited CaCO₃ will be higher than the amount reported here.

For the range of $\mathcal{P}e$, we used a range of values between 0, completely diffusion dominated transport, to ${10}^4$, convection dominated transport (Chadam et al., 1986; Hinch and Bhatt, 1990). Of these two regimes of flow, the latter, convection dominated mode is more dominant in natural reactive infiltration instability problems (Chadam et al., 1986; Hinch and Bhatt, 1990; Riaz et al., 2006; Ghesmat et al., 2011; Soltanian et al., 2016). Consequently, we show the results from a run of $\mathcal{P}e=500$ in this article. Using the definition of $\mathcal{P}e$ from Eq. 8 and using the values of the dimensional constants in the table, we get $\mathcal{P}e=3963$. Thus, the results shown here depict a more conservative estimate of the flow rate than natural conditions. Finally, we use a range of values of aquifer porosity and anorthite concentration in the solid, as shown in Table 1.

3. Result

Our simulations identify the modes of penetration of dense H₂CO₃ rich fluid into the porous aquifer as a function of various parameters controlling the process. Some of these factors, such as porosity and aquifer composition, are potentially critical in GCS site selection. In Figures 2–4 we show sets of three snapshots of the concentration map of H₂CO₃ dissolved in the pore water $\left(c_0\left(x,z,t\right)\right)$. To isolate the effect of one controlling parameter in each figure, we kept the other three constant and show the concentration map for four different values of the controlling parameter. A number of previous studies on reactive infiltration instability focused on the role of $\mathcal{P}e$ and $\mathcal{D}a$ (Aharonov et al., 1995; Riaz et al., 2006; Ghesmat et al., 2011; Szymczak and Ladd, 2013; Sun et al., 2020a), as we show here, the aquifer properties such as porosity and composition exert equally important controls on the mode and efficiency of GCS by reactive infiltration instablity. The source code for the simulation, MuPoPP1.2.0 (Multiphase Porous flow and Physical Properties) is publicly available (Hier‐Majumder et al., 2020). Simulation data is also available for download through the Royal Holloway Figshare repository (Sun et al., 2020b).

FIGURE 2

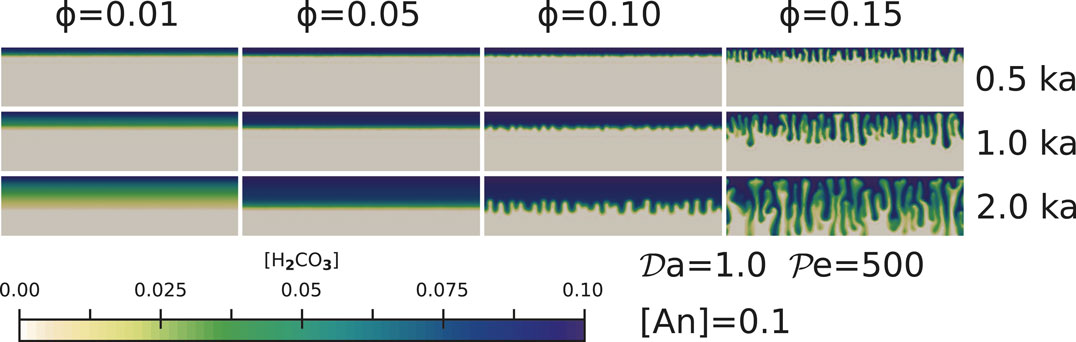
FIGURE 2. The effect of porosity on pore fluid percolation for simulations with $\mathcal{D}a=1.0$, $\mathcal{P}e=500$, and [An] = 0.1. The time corresponding to each snapshot is annotated to the right of the panels, while the values of porosity, ϕ, are shown at the top of each block of panels. The colormap depicts the concentration of H₂CO₃ in the solid $c_0\left(x,z,t\right)$. The snapshots show that the porosity of sandstone controls the distribution form and the internal structure of H₂CO₃ rich domain.

FIGURE 3

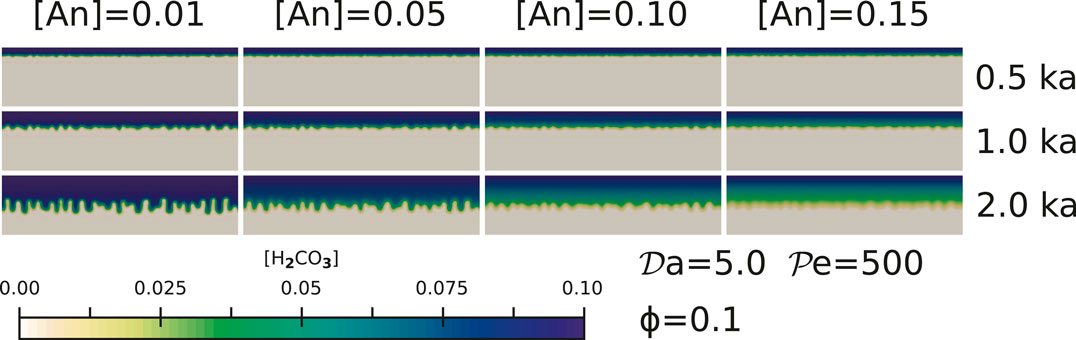
FIGURE 3. The effect of Anorthite concentrations for simulations with $\mathcal{D}a=5.0$, $\mathcal{P}e=500$, and $\varphi =0.1$. Each of the four columns is marked by a different initial anorthite content in the solid, annotated at the top. The values of dimensional time at each step are annotated on the right. The snapshots show that a higher mass fraction of anorthite in sandstone weakens the propagation of H₂CO₃.

FIGURE 4

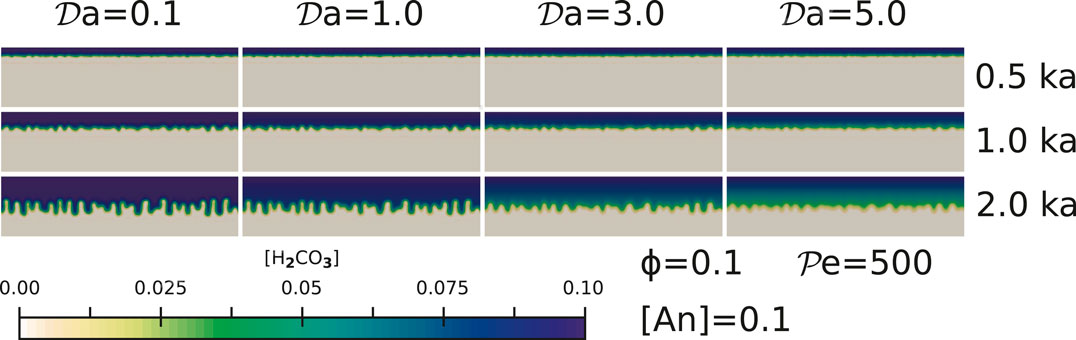
FIGURE 4. The effect of reaction rates for simulations with $\varphi =0.1$, $\mathcal{P}e=500$, and $\left[An\right]=0.1$, and $\alpha ={10}^{-8}$. The snapshots show that efficient reactions (higher $\mathcal{D}a$) will constrain the propagation of dissolved CO₂, namely H₂CO₃ in groundwater.

3.1. The Effect of Porosity

Rock porosity exerts a strong influence on the mode of invasion of H₂CO₃ rich pore fluid into the aquifer, by controlling the shape of the reaction front. As outlined in Figure 2, for small values of porosity $\left(\varphi =0.01\text{or}\text{0}\text{.}05\right)$, the H₂CO₃ rich pore fluid descends slowly, as a planar front. In contrast, simulations with higher values of porosity $\left(\varphi =0.10\text{or}\text{0}\text{.}15\right)$ depict the propagation of H₂CO₃ rich fluid as growing channels, characteristic of reactive infiltration instability. We also notice that the channels for $\varphi =0.15$ begin forming earlier, grow faster, and are characterized by the thinnest top boundary layer for all four sets of simulations reported here. The rate of infiltration of the H₂CO₃ rich fluid into the aquifer is also much faster with the presence of channels. The snapshots in Figure 2 illustrate that while the H₂CO₃ rich channels penetrate the aquifer (500 m) by 2000 years for $\varphi =0.15$, the planar interface traverses only half of the aquifer after the same time for $\varphi =0.01$. We also notice that for $\varphi =0.15$, the onset of channelization is marked by a large number of small wavelength channels, which later merge into fewer, larger wavelength channels. This behavior of reactive infiltration instability arises from the fundamentally nonlinear nature of the process and interaction between channels (Aharonov et al., 1995; Riaz et al., 2006) and indicates that—at least within the parameter space explored in this work—GCS is dominated by processes far from equilibrium. Vosper et al. (2014) tested the formation of channels in a nonreactive Hele-Shaw cell experiment containing close packed glass beads. The porosity of close-packed systems, typically exceeding 25% (Wimert and Hier-Majumder, 2012), is much higher than the range tested here. Qualitatively, their observation of channel growth and low spacing between the channels are similar to the trend we report at higher porosities.

While previous studies of reaction infiltration instability noticed the formation of channels (Hinch and Bhatt, 1990; Aharonov et al., 1995; Ghesmat et al., 2011; Sun et al., 2020a) and evolution of the channels (Riaz et al., 2006; Soltanian et al., 2016), none of these studies reported the transition of the flow from a slow planar front to a highly nonliner channeling instability with an increase in the porosity of the aquifer. The transition of the flow model from a planar front to channels indicates that GCS models need to incorporate the nonlinear effects arising from reactive infiltration instability. The spatial distribution of fluid flow rate is apparently heterogeneous, especially with the formation of channels. Therefore, if we use a parameterized, one-dimensional fluid flow rate when calculating CaCO₃ precipitation, the efficiency of the GCS can be significantly under or over estimated.

3.2. The Effect of Anorthite Concentration and Reaction Rate

The extent of reaction between H₂CO₃ rich pore fluid and the aquifer matrix depends on both the availability of reactants (in this case, An) and the rate of chemical reactions. These two factors, while controlled by two different parameters, have a similar effect on the channel propagation.

A higher anorthite concentration [An] in the solid leads to more rapid consumption of the dissolved H₂CO₃ in the pore fluid, as observed in the series of simulations with increasing anorthite content in Figure 3. With an increasing consumption of the H₂CO₃ in the pore fluid, formation of the channeling instabilities at the reaction front are more subdued, as evidenced during each time step of the comparative snapshots. We observe the strongest channel formation after 2 ka in the simulations with [An] = 0.01. In contrast, the simulations with [An] = 0.15 (15 wt% anorthite in the initial solid composition) display weak channels containing lower concentrations of the dissolved H₂CO₃ as evidenced by the colormap. While these channels penetrate into the aquifer, the dissolved H₂CO₃ in the channels are quickly consumed by the high concentration of anorthite in the surrounding, unreacted rock. As a result, the amount of CaCO₃ precipitation is much higher in these cases, an issue we discuss in Section 4.1.

High reaction rates, represented by high values of $\mathcal{D}a$, also reduce the concentration and the propagation rate of H₂CO₃ rich pore fluid. The images in Figure 4 display that in the simulations with higher $\mathcal{D}a$, the concentration of H₂CO₃ in the channels is lower compared to simulations with a lower $\mathcal{D}a$. Similar to high initial anorthite abundance, a high reaction rate also aids rapid consumption of the acidic pore fluid and CaCO₃ precipitation. Although arising from two separate mechanisms, the influence of initial anorthite abundance in the solid and the rate of chemical reaction both exert a similar kind of control on the propagation of channels during GCS.

4. Discussion

The results presented in Section 3 demonstrate the influence of the control parameters on the structure of the RII. In this section, we summarize the influence of porosity, initial abundance of anorthite, and the rate of reaction on the mass of ${\text{CaCO}}_3$ precipitated during GCS. For an aquifer with a given porosity, the reaction rate exerts a stronger influence than the initial anorthite concentration, while an increase in any of the three parameters leads to an increase in the amount of carbonate mineralization. Based on the structure of the porous flow and magnitude of carbonate mineralization, we present our recommendations for selecting future sites of CCS.

4.1. Capacity of Deep Saline Aquifers as GCS Sites

An important outcome of numerical modeling of GCS is an estimate for the amount of carbon permanently sequestered in solid mineral phases. The formulation in Eq. 13 provides the dimensional form of this time-dependent mass. As discussed earlier, we integrate the CaCO₃ deposition rate over a volume of 500 m thick and 2 km wide aquifer over 2000 years. The resultant values of permanently sequestered CaCO₃ mass are strongly dependent on the parameters studied in this work, as illustrated by the plots in Figures 5A,B.

FIGURE 5

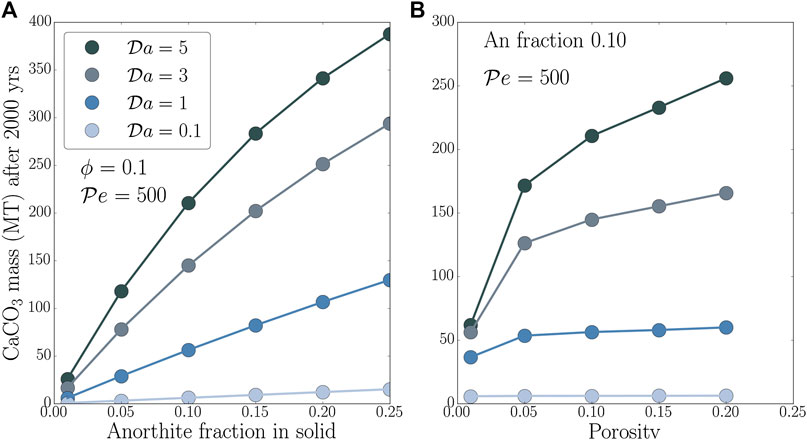
FIGURE 5. Mass of precipitated CaCO₃ after 2000 years as a function of (A) anorthite mass fraction in sandstone $\left[An\right]$ or (B) porosity ϕ.

Aquifer properties characterized by initial anorthite mass fraction and porosity strongly influence the sequestered CaCO₃ mass. The plot in Figure 5A shows that this mass increases with the initial mass fraction of anorthite in the solid. Moreover, the trend of the growth is greatly modulated by the value of the $\mathcal{D}a$, with a more strongly nonlinear trend evident at higher values of $\mathcal{D}a$. Of the four cases shown in Figure 5A, the flattest curve corresponding to $\mathcal{D}a=0.1$ shows that the CaCO₃ mass varies approximately between 1 and 15 Mt, while for a value of $\mathcal{D}a=5$, the same increase in An concentration in the solid leads to a nonlinear increase of mass from 30 to 390 Mt. The comparison between these two influencing factors—chemical reactivity ($\mathcal{D}a$) and abundance of reactant [An]—demonstrates that the chemical reactivity exerts a stronger influence on the amount of carbon permanently sequestered in minerals.

Porosity of the aquifer exerts a similar, but slightly more moderate influence on the mass of precipitated CaCO₃. The plot in Figure 5B demonstrates this influence for values of $\mathcal{D}a$ exceeding 0.1. For $\mathcal{D}a=1$, the mass increases from 35 to 60 Mt by increasing the porosity from 0.01 to 0.2. For a value of $\mathcal{D}a=5$, this effect is more pronounced, as the mass increases from 65 to 260 Mt for the same increase in aquifer porosity. Porosity influences the flow by controlling the magnitude of permeability. A more porous aquifer permits faster transport of H₂CO₃ rich fluid, which, subject to the reaction rate, can increase the precipitation of CaCO₃.

The cumulative mass fraction of CaCO₃ sequestered by GCS varies with time. The plot in Figure 6 shows the evolution of the volume-averaged CaCO₃ mass fraction with time for four different aquifers. The top curves, shaded in gray, correspond to an aquifer containing 20% anorthite in the bulk, and the upper and lower limits are fixed by porosity values of 15 and 5% respectively. The bottom set of curves correspond to an aquifer containing 10% anorthite in the bulk. While following the conclusions drawn from the previous results, this plot also outlines that the process of GCS starts to produce appreciable CaCO₃ deposition at least after 500 years, but gains pace with time. This increase in rate is related to the penetration of the channels to the bottom of the aquifer and reacting with a larger amount of unreacted anorthite.

FIGURE 6

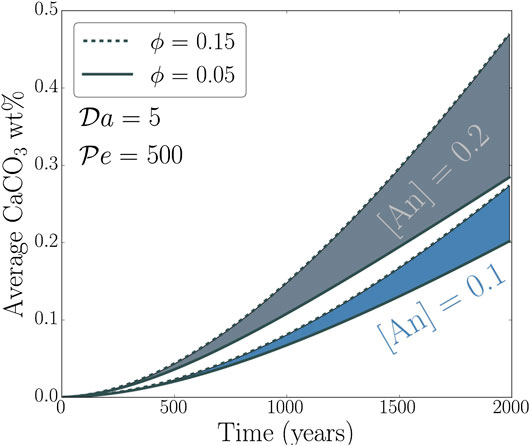
FIGURE 6. Volume averaged concentration of precipitated CaCO₃ in the aquifer as a function of time with different anorthite fractions and porosities.

4.2. Geological Criteria for Future CCS Site Selection

As discussed by Hosa et al. (2011) and Celia (2017), current CCS sites contain rocks with a wide range of porosity values. To meet the challenge of carbon neutralization, and increase the current global injection rate of $\sim$40 Mt/yr (Celia, 2017), more CCS sites need to be identified. In identifying these sites, a number of factors such as the existence of a cap rock, cost of CO₂ transport to the site, and public perception need to be weighed against the geological criteria. Keeping these mitigating factors in mind, we use the results from our study to suggest parameter ranges that can ensure efficient GCS by CaCO₃ precipitation.

The amount of immobilized CO₂, namely precipitated CaCO₃, is influenced by initial anorthite amount and the reaction rate, as shown in Figure 5A. For a moderate reaction rate ($\mathcal{D}a=1$), in order to sequester at least 50 Mt CaCO₃ after 2000 years, we suggest choosing an aquifer with more than 10 wt% of reactive minerals, such as anorthite. However, when the reaction rate is high $\left(\mathcal{D}a=3-5\right)$, an amount of 5 wt% anorthite in the target formation is sufficient to sequester 50 Mt CaCO₃ after 2000 years.

We observe that in deep saline aquifers containing $>10\text{\%}$ porosity, the mode of fluid propagation shows the transition from a planar front to channels. Our simulations indicate that the channels are faster and more efficient in transferring H₂CO₃ rich pore fluid into the aquifer, and as the curves in Figure 6 demonstrate, channels also lead to larger amounts of CaCO₃ precipitation. Thus, to ensure GCS by channel formation, we recommend selection of future sites containing $>10\text{\%}$ porosity. Additionally, CaCO₃ precipitation increases with an increase in anorthite concentration in the solid. Comparison of experimentally determined reaction rates indicates that anorthite or anorthite-rich members of the feldspar solid solution group are more reactive than the albite end member (Palandri and Kharaka, 2004). If the composition of the aquifer rock is known, we recommend selecting an aquifer containing anorthite or other reactive aluminosilicate minerals (Oelkers and Schott, 1995; Espinoza et al., 2011) over one containing primarily unreactive quartz.

5. Conclusion

Our simulations demonstrate the presence of two distinct regimes of porous flow: planar front propagation at porosities less than 10% and channel formation at higher porosities. When comparing percolation rates into the aquifer, H₂CO₃ rich pore fluids percolate faster along channels than planar reaction fronts. The amount of CaCO₃ precipitation by GCS increases with both an increase in the $\mathcal{D}a$ andgrows with an increase in the reaction rate or the initial anorthite concentration of the aquifer. Of these two, the former exerts a stronger influence on the mass of CaCO₃ deposited after 2000 years. Under the most reactive conditions considered in this study, up to 390 Mt CaCO₃ is sequestered in the aquifer over a period of 2000 years. Also in order to sequester at least 50 Mt CaCO₃ after 2000 years, the amount of reactive minerals should exceed 10 wt%. While an increase in porosity also leads to an increase in the amount of CaCO₃ deposition, the effect of the reaction rate$\mathcal{D}a$ is stronger than the influence of porosity on the cumulative mass of CaCO₃. Based on the results of the numerical models, we suggest the selection of future GCS sites containing $>10\text{\%}$ porosity and characterized by the presence of anorthite or similarly reactive aluminosilicate minerals in the solid.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author. The source code for the simulation, MuPoPP1.2.0 (Multiphase Porous flow and Physical Properties) is publicly available (Hier‐Majumder et al., 2020). Simulation data is also available for download through the Royal Holloway Figshare repository (Sun et al., 2020b).

Author Contributions

YS, RP, and SH-M developed the source code. YS carried out the simulations. AK provided information about the parameters around the planned UKGEOS observatory. All authors contributed toward writing the manuscript.

Funding

The computational resources for this work was provided by a computational grant from Oracle Research. RP was funded by the NERC London Doctoral Training Partnership, grant number NE/L002485/1 and matching case funding grant from the BGS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors wish to thank Frank Lehane (RHUL) for his support. Anirban Basu (RHUL) and Andy Kilpatrick (BGS) provided insightful suggestions on the manuscript. This manuscript was published with the permission of the Executive Director of the British Geological Survey (UKRI).

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.533588/full#supplementary-material

References

Aharonov, E., Whitehead, J. P., Kelemen, P. B., and Spiegelman, M. (1995). Chanelling instability of upwelling melt in the mantle. J. Geophys. Res. Solid Earth 100, 20433–20450. 10.1029/95JB01307

Google Scholar

Aminu, M. D., Nabavi, S. A., Rochelle, C. A., and Manovic, V. (2017). A review of developments in carbon dioxide storage. Appl. Energy 208, 1389–1419. doi:10.1016/j.apenergy.2017.09.015

CrossRef Full Text | Google Scholar

Bacci, G., Korre, A., and Durucan, S. (2011). An experimental and numerical investigation into the impact of dissolution/precipitation mechanisms on CO₂ injectivity in the wellbore and far field regions. Int. J. Greenh. Gas Control 5, 579–588. doi:10.1016/j.ijggc.2010.05.007

CrossRef Full Text | Google Scholar

Bachu, S. (2000). Sequestration of CO₂ in geological media: criteria and approach for site selection in response to climate change. Energy Convers. Manag. 41, 953–970. doi:10.1016/s0196-8904(99)00149-1

CrossRef Full Text | Google Scholar

Celia, M. A. (2017). Geological storage of captured carbon dioxide as a large-scale carbon mitigation option. Water Resour. Res. 53, 3527–3533. doi:10.1002/2017WR020841

CrossRef Full Text | Google Scholar

Chadam, J., Hoff, D., Merino, E., Ortoleva, P., and Sen, A. (1986). Reactive infiltration instabilities. IMA J. Appl. Math. 36, 207–221. doi:10.1093/imamat/36.3.207

CrossRef Full Text | Google Scholar

Class, H., Ebigbo, A., Helmig, R., Dahle, H. K., Nordbotten, J. M., Celia, M. A., et al. (2009). A benchmark study on problems related to CO₂ storage in geologic formations. Comput. Geosci. 13, 409. doi:10.1007/s10596-009-9146-x

CrossRef Full Text | Google Scholar

Doughty, C., (2010). Investigation of CO2 plume behavior for a large-scale pilot test of geologic carbon storage in a saline formation. Transp. Porous Media 82, 49–76. doi:10.1007/s11242-009-9396-z

CrossRef Full Text | Google Scholar

Emami-Meybodi, H., Hassanzadeh, H., and Ennis-King, J. (2015). CO₂ dissolution in the presence of background flow of deep saline aquifers. Water Resour. Res. 51, 2595–2615. 10.1002/2014WR016659

Google Scholar

Espinoza, D. N., Kim, S. H., and Santamarina, J. C. (2011). CO2 geological storage—geotechnical implications. KSCE J. Civ. Eng. 15, 707–719. doi:10.1007/s12205-011-0011-9

CrossRef Full Text | Google Scholar

Friedlingstein, P., Jones, M. W., O’Sullivan, M., Andrew, R. M., Hauck, J., Peters, G. P., et al. (2019). Global carbon budget 2019. Earth Syst. Sci. Data 11, 1783–1838. doi:10.5194/essd-11-1783-2019

Google Scholar

Friedmann, S. J. (2007). Geological carbon dioxide sequestration. Elements 3, 179–184. doi:10.2113/gselements.3.3.179

CrossRef Full Text | Google Scholar

Ghesmat, K., Hassanzadeh, H., and Abedi, J. (2011). The impact of geochemistry on convective mixing in a gravitationally unstable diffusive boundary layer in porous media: CO₂ storage in saline aquifers. J. Fluid Mech. 673, 480–512. doi:10.1017/s0022112010006282

CrossRef Full Text | Google Scholar

Hassanzadeh, H., Pooladi-Darvish, M., and Keith, D. W. (2007). Scaling behavior of convective mixing, with application to geological storage of CO₂. AIChE J. 53, 1121–1131. doi:10.1002/aic.11157

CrossRef Full Text | Google Scholar

Hier-Majumder, S.,, and Abbott, M. E. (2010). Influence of dihedral angle on the seismic velocities in partially molten rocks. Earth Planet Sci. Lett. 299, 23–32. doi:10.1016/j.epsl.2010.08.007

CrossRef Full Text | Google Scholar

Hier-Majumder, S. [Dataset] (2020). MuPoPP 1.2.0: a finite elements solver for multiphase flow problems. Available at: https://github.com/sashgeophysics/MuPoPP/tree/v1.2.0 (Accessed January 30, 2020).

Google Scholar

Hinch, E. J.,, and Bhatt, B. S. (1990). Stability of an acid front moving through porous rock. J. Fluid Mech. 212, 279–288. doi:10.1017/S0022112090001963

CrossRef Full Text | Google Scholar

Hosa, A., Esentia, M., Stewart, J., and Haszeldine, S. (2011). Injection of CO₂ into saline formations: benchmarking worldwide projects. Chem. Eng. Res. Des. 89, 1855–1864. doi:10.1016/j.cherd.2011.04.003

CrossRef Full Text | Google Scholar

Jiang, X. (2011). A review of physical modelling and numerical simulation of long-term geological storage of CO₂. Appl. Energy 88, 3557–3566. doi:10.1016/j.apenergy.2011.05.004

CrossRef Full Text | Google Scholar

Kingdon, A., Fellgett, M., and Spence, M. (2019). Open Report OR/18/055. UKGEOS Cheshire energy research field site: science infrastructure: version 2. British Geological Survey Available at: http://nora.nerc.ac.uk/id/eprint/525100 (Accessed September 13, 2019).

CrossRef Full Text | Google Scholar

Kneafsey, T. J.,, and Pruess, K. (2010). Laboratory flow experiments for visualizing carbon dioxide-induced, density-driven brine convection. Transp. Porous Media 82, 123–139. doi:10.1007/s11242-009-9482-2

CrossRef Full Text | Google Scholar

Le Quéré, C., Andrew, R. M., Friedlingstein, P., Sitch, S., Pongratz, J., Manning, A. C., et al. (2018). Global carbon budget 2018. Earth Syst. Sci. Data 10, 2141–2194. doi:10.5194/essd-2017-123

Google Scholar

Odenberger, M., Kjärstad, J., and Johnsson, F. (2013). Prospects for CCS in the EU energy roadmap to 2050. Energy Procedia 37, 7573–7581. doi:10.1016/j.egypro.2013.06.701

CrossRef Full Text | Google Scholar

Oelkers, E. H.,, and Schott, J. (1995). Experimental study of anorthite dissolution and the relative mechanism of feldspar hydrolysis. Geochem. Cosmochim. Acta 59, 5039–5053. doi:10.1016/0016-7037(95)00326-6

CrossRef Full Text | Google Scholar

Palandri, J. L.,, and Kharaka, Y. F. (2004). Open File Report.: 2004-1068. A compilation of rate parameters of water-mineral interaction kinetics for application to geochemical modeling. Available at: https://pubs.usgs.gov/of/2004/1068/ (Accessed March 2004).

CrossRef Full Text | Google Scholar

Pec, M., Holtzman, B. K., Zimmerman, M., and Kohlstedt, D. L. (2015). Reaction infiltration instabilities in experiments on partially molten mantle rocks. Geology 43, 575–578. doi:10.1130/G36611.1

CrossRef Full Text | Google Scholar

Riaz, A., Hesse, M., Tchelepi, H. A., and Orr, F. M. (2006). Onset of convection in a gravitationally unstable diffusive boundary layer in porous media. J. Fluid Mech. 548, 87–111. doi:10.1017/S0022112005007494

CrossRef Full Text | Google Scholar

Snæbjörnsdóttir, S., Oelkers, E. H., Mesfin, K., Aradóttir, E. S., Dideriksen, K., Gunnarsson, I., et al. (2017). The chemistry and saturation states of subsurface fluids during the in situ mineralisation of CO₂ and H₂S at the CarbFix site in SW-Iceland. Int. J. Greenh. Gas Control 58, 87–102. doi:10.1016/j.ijggc.2017.01.007

Google Scholar

Soltanian, M. R., Amooie, M. A., Dai, Z., Cole, D., and Moortgat, J. (2016). Critical dynamics of gravito-convective mixing in geological carbon sequestration. Sci. Rep. 6, 35921. doi:10.1038/srep35921

PubMed Abstract | CrossRef Full Text | Google Scholar

Spence, B., Horan, D., and Tucker, O. (2014). The peterhead-goldeneye gas post-combustion CCS project. Energy Procedia 63, 6258–6266. doi:10.1016/j.egypro.2014.11.657

CrossRef Full Text | Google Scholar

Spiegelman, M., Kelemen, P. B., and Aharonov, E. (2001). Causes and consequences of flow organization during melt transport: the reaction infiltration instability in compactible media. J. Geophys. Res. 106, 2061–2077. doi:10.1029/2000jb900240

CrossRef Full Text | Google Scholar

Steefel, C. I.,, and Lasaga, A. C. (1994). A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems. Am. J. Sci. 294, 529–592. doi:10.2475/ajs.294.5.529

CrossRef Full Text | Google Scholar

Sun, Y., Hier-Majumder, S., Xu, Y., and Walter, M. (2020a). Stability and migration of slab-derived carbonate-rich melts above the transition zone. Earth Planet Sci. Lett. 531, 116000. doi:10.1016/j.epsl.2019.116000

CrossRef Full Text | Google Scholar

Sun, Y., Payton, R., Hier-Majumder, S., and Kingdon, A. (2020b). CCS_2D_CSV.tar.gz. doi:10.17637/rh.11770269.v1

Google Scholar

Szymczak, P.,, and Ladd, A. J. C. (2011). Instabilities in the dissolution of a porous matrix. Geophys. Res. Lett. 38, L07403. doi:10.1029/2011GL046720

CrossRef Full Text | Google Scholar

Szymczak, P.,, and Ladd, A. J. C. (2013). Interacting length scales in the reactive-infiltration instability. Geophys. Res. Lett. 40, 3036–3041. doi:10.1002/grl.50564

CrossRef Full Text | Google Scholar

Takei, Y., and Hier-Majumder, S. (2009). A generalized formulation of interfacial tension driven fluid migration with dissolution/precipitation. Earth Planet Sci. Lett. 288, 138–148. doi:10.1016/j.epsl.2009.09.016

CrossRef Full Text | Google Scholar

Thomson, P.-R., Ellis, R., Chiarella, D., and Hier-Majumder, S. (2020). Microstructural analysis from x-ray ct images of the brae formation sandstone, north sea. Front. Earth Sci. 8, 246. 10.3389/feart.2020.00246

CrossRef Full Text | Google Scholar

Thomson, P.-R., Hazel, A., and Hier-Majumder, S. (2019). The influence of microporous cements on the pore network geometry of natural sedimentary rocks. Front. Earth Sci. 7, 48. doi:10.3389/feart.2019.00048

CrossRef Full Text | Google Scholar

Vosper, H., Kirk, K., Rochelle, C., Noy, D., and Chadwick, A. (2014). Does numerical modelling of the onset of dissolution-convection reliably reproduce this key stabilization process in CO₂ Storage? Energy Procedia 63, 5341–5348. doi:10.1016/j.egypro.2014.11.566

CrossRef Full Text | Google Scholar

Wimert, J.,, and Hier-Majumder, S. (2012). A three-dimensional microgeodynamic model of melt geometry in the Earth’s deep interior. J. Geophys. Res. 117, B04203. doi:10.1029/2011JB009012

CrossRef Full Text | Google Scholar

Winkler, K. W. (1983). Frequency dependent ultrasonic properties of high-porosity sandstones. J. Geophys. Res. Solid Earth 88, 9493–9499. doi:10.1029/jb088ib11p09493

CrossRef Full Text | Google Scholar

Zhang, D., and Song, J. (2014). Mechanisms for geological carbon sequestration. Procedia IUTAm 10, 319–327. doi:10.1016/j.piutam.2014.01.027

CrossRef Full Text | Google Scholar