Early Uncertainty Quantification for an Improved Decision Support Modeling Workflow: A Streamflow Reliability and Water Quality Example

1. Introduction

Numerical models are routinely used to inform environmental management decision making by exploring possible system responses to proposed management strategies. Probabilistic assessment of these system responses are a further requirement of model-based decision support (e.g., Freeze et al., 1990; Doherty and Simmons, 2013). This allows the likelihood of any undesired impacts to be assessed alongside relevant management decision thresholds which are defined on the basis of ecological, economic and/or cultural objectives.

It is widely considered that history matching (also known as “model calibration” or “data assimilation”) is a prerequisite for such decision support model deployment (e.g., Barnett et al., 2012). This follows the philosophy “How can a model be robust if it isn’t calibrated?” This philosophy has its basis in the expectation that history matching, which can be considered an implementation of Bayes equation, will result in a reduction of parameter and predictive uncertainty (often expressed in terms of predictive variance; e.g., Moore and Doherty, 2005; Dausman et al., 2010). However, the ability of the history matching process to improve the reliability of parameter estimations, and to appropriately reduce decision-relevant forecast uncertainty, may be limited by a number of important factors.

First, the information content of observation datasets used for history matching may be deficient for inferring values of physically-based model parameters that represent spatially distributed subsurface properties (e.g., Vasco et al., 1997; Vasco et al., 1998; Clemo et al., 2003; Moore and Doherty, 2006), with subsequent implications for reducing forecast uncertainty. This is particularly the case where there is significant hydraulic property heterogeneity, which is typically the major cause of predictive uncertainty in groundwater models. Even where there is significant data available, a lack of forecast relevant data may still inhibit efforts to reduce uncertainty through history matching.

Second, a number of studies have shown that there is potential for history matching to corrupt the quantification of predictive uncertainty, when considering the inevitable presence of model defects (e.g., Doherty and Christensen, 2011; Brynjarsdóttir and O’Hagan, 2014; White et al., 2014; Oliver and Alfonzo, 2018). For example, Knowling et al. (2019) show that there is potential to induce bias and corruption in estimates of predictive variance, as a consequence of inappropriate parameter compensation when history matching “under-parameterized” models. Ultimately, this can compromise the reliability of decisions made on the basis of model forecasts. Additionally, Knowling et al. (2020) showed that there is significant potential to induce predictive bias due to the inability of an imperfect model to appropriately assimilate information-rich data, such as environmental tracer observations. Therefore, when faced with using a model with prediction relevant imperfections, a modeler may wish to critically consider whether history matching is appropriate.

History matching efforts can also place unexpected requirements on labor and computational resources. This is because balancing the expression of prior knowledge with information contained within observation data, during history matching, is not straightforward and is often undertaken in a highly iterative process. This adds significant complexity to the modeling workflow, and risk to project budgets and time-lines. This is particularly the case for large-scale models of real-world systems which are prone to numerical stability issues and long simulation durations.

An additional consideration when examining the usefulness of a history matching effort in a decision support context, is the proximity of forecast probability distributions to predefined management decision thresholds (e.g., Knowling et al., 2019; White et al., 2020b). Evaluation of the relative positions of forecast distributions and decision thresholds can be used to provide a measure of apparent “decision difficulty” (e.g., White et al., 2020b). Where, on the basis of the prior information alone, a forecast probability distribution lies far from the critical threshold (i.e decision difficulty trends to zero), a modeler may elect not to progress with history matching, as it is unlikely to alter the evaluation of management strategy effectiveness.

Finally, uncertainty quantification that underpins decision support relies upon robust definition of the prior parameter probability distributions that express system expert knowledge (i.e., before history matching). Verification of robust prior probability distributions is difficult, especially for complex real-world numerical models, often requiring prohibitively expensive paired model analyses (e.g., Doherty and Christensen, 2011; Gosses and Wöhling, 2019). However, an indication of an inappropriate expression of prior parameter uncertainty, with the potential to undermine model-based decision support, can be provided through comparison of historical system observations with simulated outputs generated on the basis of the prior parameter distributions, in a “prior-data conflict assessment” (e.g., Nott et al., 2016). Formally, prior-data conflict can be identified when there is no overlap between an ensemble of observation data, accounting for potential observation error, and the prior ensemble of simulated outputs. This analysis can be undertaken early in a modeling project, so that indications of an inappropriate prior can be identified and addressed ahead of a full comprehensive history matching process. We note that this criterion alone is not sufficient to demonstrate that the initial prior ensemble is valid, as model error may also be the cause of such prior-data conflict, requiring additional statistical tests (e.g., Brynjarsdóttir and O’Hagan, 2014; Alfonzo and Oliver, 2019).

In this paper we explore the benefits of recasting the typical modeling workflow, which starts with a conceptual system model and ends with a calibrated numerical model (e.g., Barnett et al., 2012), such that uncertainty quantification is undertaken at an early stage in the project, before attempting comprehensive history matching. The recast workflow involves exploration of the prior decision-relevant forecast uncertainty relative to decision thresholds, as well as prior distributions of model outputs relative to system observations. The workflow then involves undertaking an abridged history matching and a preliminary posterior uncertainty assessment, to help identify the extent to which available data informs estimated parameter values and model forecasts, and provide insights into the benefits, or potential hazards, of continuing history matching.

This study is motivated by, and follows, the forecast focused workflow promoted in Doherty (2015) and White (2017). It is also consistent with the recommendations in Doherty and Moore (2019), which suggest undertaking uncertainty quantification early in the decision support modeling process, to identify the extent that available historical observations can inform decision-salient parameter values. Doherty and Moore (2019) outline how this information can then be used to guide the modeling process, from model conceptualization to deployment for decision support. This study adopts this fundamental recommendation, and explores the implications of doing so, for a real-world case study.

The case study contributes to the small body of real-world decision support worked examples that are currently available in the international literature (e.g., Kunstmann et al., 2002; Enzenhoefer et al., 2014; Sepúlveda and Doherty, 2015; Brouwers et al., 2018; Sundell et al., 2019; White et al., 2020a).

2. Methodology

This section describes the proposed workflow for the early assessment of the uncertainty surrounding model predictions that are of particular management interest (“decision-relevant”), which are herein referred to as “forecasts”. Figure 1 provides a flowchart outlining the major steps and decision points in the workflow.

FIGURE 1

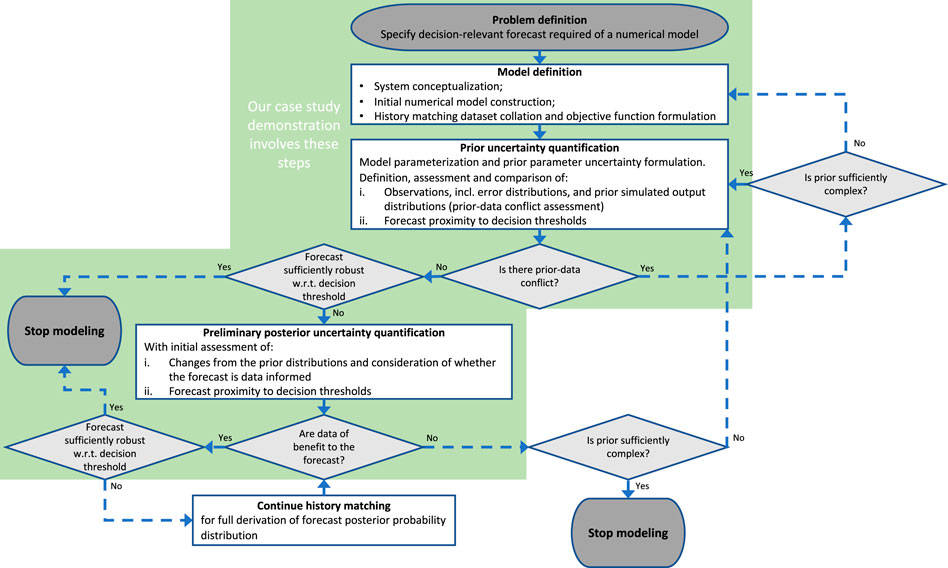
FIGURE 1. Graphical presentation of the proposed decision support modeling workflow, which incorporates uncertainty quantification at an early stage before undertaking more comprehensive history matching. The steps involved in the case study presented herein are highlighted with the green background.

2.1. Problem Definition

“Problem definition” defines the decision context for numerical modeling. It involves the definition of the management problem and the undesirable outcome that the management strategy is designed to prevent, e.g., land-use consent restriction or regulation to prevent ecological degradation of a stream system due to nutrient contamination. This step also includes the specification of forecasts that can be used to evaluate the efficacy of management decisions, and the definition of decision thresholds against which the success (or failure) of a management strategy can be evaluated.

2.2. Model Definition

This step involves defining the pertinent processes and components of the hydrogeological system that the forecasts are likely to be sensitive to. On this basis, an initial numerical model is constructed, ensuring sufficient complexity to represent these aspects of the system (e.g., Hunt et al., 2007). This step also includes formulation of the model objective function, which involves collation and processing of historical system observations and definition of a weighting scheme. The weighting scheme ideally aims to maximize the flow of information during the history matching process, from observation data to model parameters, and subsequently to model forecasts, while accounting for both measurement and model error (Doherty and Welter, 2010; Doherty, 2015).

2.3. Prior Uncertainty Quantification

“Prior uncertainty quantification” is underpinned by the definition of uncertain model parameters and a formulation of prior parameter uncertainty. Simulation of the model with parameter realizations that reflect this prior parameter uncertainty, allows an initial quantification of simulated output and forecast uncertainty. As the relationship between model parameters and simulated outputs can rarely be fully known, a priori, it is advantageous to employ high parameter dimensionality (e.g., Hunt et al., 2007; Fienen et al., 2010; Doherty and Simmons, 2013; Knowling et al., 2019), in concert with a conservative expression of parameter uncertainty, informed by “expert knowledge” of the conceptualized system.

Comparison of simulated output distributions with historically observed system behavior supports an early assessment of the appropriateness of the prior parameter probability distributions. The presence of prior-data conflict may indicate underestimation of measurement error, underestimation of parameter variances and/or insufficient complexity in the numerical model and prior parameterization. If the model and prior parameterization is deemed to be sufficiently complex with respect to the processes that the forecasts are sensitive to, prior-data conflict may be resolved by inflation of parameter variances or observation error, as appropriate. If however, the prior is regarded to represent insufficient forecast relevant complexity, the prior parameterization itself may also need to be revisited. For example, model boundaries may need to be parameterized in a different way, if the forecast is sensitive to these boundary conditions. Or if the connectedness of high hydraulic conductivity facies is relevant to the forecasts being made, a parameter representation of these connected facies may need to be adopted in place of, for example, a multi-variate Gaussian parameter representation.

This part of the workflow also accommodates the situation where there is found to be no forecast relevant data available. In this situation the prior parameterization becomes more important, as it is now the only source of information in the model. In this situation a modeler is freed from all history matching burdens, and may choose to adopt a very complex model parameterization, to ensure a robust probability distribution (Doherty and Moore, 2019).

If prior-data conflict is not present, the assessment of the proximity of the prior forecast probability distributions to the decision threshold may be sufficient for addressing the management decision and the workflow can move to the “Stop modeling” option (left-hand side of Figure 1). However, if reduction in forecast uncertainty is desired to support the management decision, the workflow moves toward a preliminary approximation of the posterior uncertainty, as discussed in Section 2.4 below.

2.4. Preliminary Posterior Uncertainty Quantification

The “Preliminary posterior uncertainty quantification” is undertaken with a view to reducing forecast uncertainty through a preliminary formal assimilation of observation data. This step provides an opportunity to assess the ability of the observation data to inform model parameters and forecasts; a number of modeling workflow decisions may then be made on the basis of this preliminary posterior uncertainty quantification.

If forecast uncertainty reduction through the preliminary conditioning of influential parameters is sufficient for addressing the management decision, the workflow can move to “Stop modeling.” If the assimilation of data is deemed beneficial for reducing forecast uncertainty, but further uncertainty reduction is desired, then this preliminary posterior uncertainty quantification provides justification for continuing to assimilate observation data and deriving more advanced posterior forecast distributions. If, however, the data do not inform forecasts, after verifying that the model, its parameterization, and its prior probability representation, is sufficiently complex to adequately represent the forecast uncertainty, the modeling workflow should move to “Stop modeling.” If the level of forecast uncertainty is not satisfactory for decision support purposes, then the workflow can be re-initiated with options for recasting forecasts, model design, parameterization, and collection or reprocessing of system observations to improve the flow of information to model parameters and forecasts. Alternatively, the decision maker can choose to consider an alternative management scenario, on the basis of this initial iteration through the workflow.

The workflow presented here is essentially agnostic with respect to the methodologies adopted for the uncertainty quantification, with the following proviso: that the uncertainty quantification method must be computationally efficient, as its purpose is to provide guidance on whether or not the investment in a more completed and rigorous data assimilation effort is necessary.

The model simulation and uncertainty quantification methods adopted for this study are described in detail in the following case study section (Section 3). The case study addresses all major steps (boxes with green background) in Figure 1, before shifting the “Stop modeling’ option (left-hand side of Figure 1), based on the results. The alternative options would be relevant for other case studies with differing forecast-data relationships; examples of when these options may be favorable are discussed.

3. Case Study

A numerical modeling case study is used to demonstrate the workflow outlined above. The case study, set within the Ruamāhanga catchment in the Wairarapa Valley, North Island, New Zealand, involves simulation-based forecasting of groundwater abstraction impacts on stream low flows and land-use change impacts on groundwater nutrient concentrations.

3.1. Problem Definition

3.1.1. Decision-Relevant Forecasts

The forecasts considered relate to water availability and water quality issues which are of particular significance within the Wairarapa Valley. Increased groundwater and surface water abstraction in Wairarapa Valley are believed to have impacted stream flows; ensuring stream flows are sufficient to meet environmental and ecological criteria is therefore an important management constraint, when setting groundwater allocation limits. For the security of fish habitats critical criteria are the frequency and persistence of days in which low streamflow (low-flow) conditions exist. The specific streamflow reliability forecasts explored here are the number of low-flow days within a 7-year time period (low-flow frequency) and the maximum number of consecutive low-flow days (low-flow persistence), at three sites (PVW, MS1, and MS2; locations provided in Figure 2). A low-flow day is defined as a day with simulated streamflow that is exceeded for 95% of the simulated period (Q95), under natural conditions (i.e., when no abstraction from either groundwater or surface water occurs).

Land-use practices can present freshwater contamination risks and management strategies often aim to limit this contamination potential. Of particular interest in the Wairarapa Valley is nitrate-nitrogen (hereafter referred to as nitrate) concentrations in groundwater. The specific water quality forecast simulated in this case study is mean nitrate concentration within defined groundwater management zones (GMZs; as presented in Figure 2).

FIGURE 2

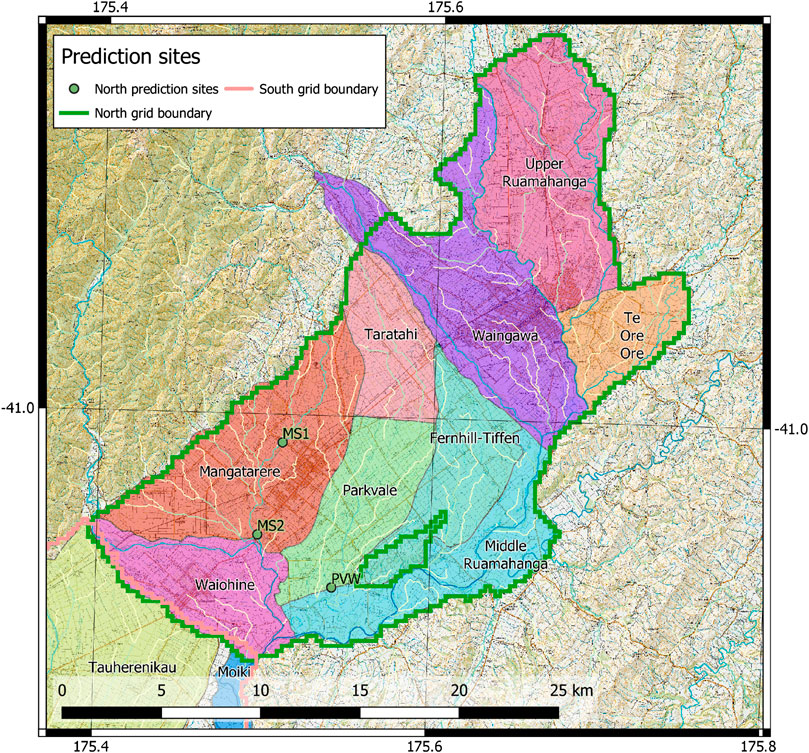
FIGURE 2. Decision-relevant forecast locations. Streamflow reliability forecasts are indicated by green dots. Groundwater management zones (GMZs) for mean zonal nitrate concentration forecasts are delimited by colored polygons.

The case study considers the forecasts described above as absolute quantities and also in a relative sense, as differences, relative to a baseline scenario; e.g., percentage-changes in the simulated output values in response to water-use- and land-use-change management scenarios. The full list of the case study forecasts is presented in Table 1.

TABLE 1

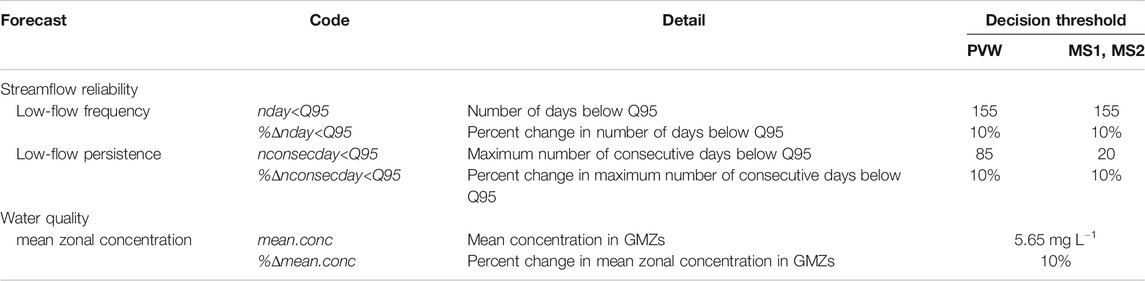
TABLE 1. Decision-relevant forecasts. PVW, MS1 and MS2 relate to the streamflow reliability forecast sites in Figure 1. GMZs refers to groundwater management zones.

3.1.2. Management Scenarios

The scenarios explored constitute simplified examples of water- and land-use management strategies employed in practice, e.g., to satisfy water-supply needs or to reduce water contamination risk. The streamflow reliability scenario reflects the estimated spatial and temporal variation in water-use in the case study area which reflects a mean (in-time) groundwater abstraction rate of 82,000 m³d⁻¹. Changes in the frequency and persistence of low-flow days are compared with a “naturalized” baseline scenario with no abstraction.

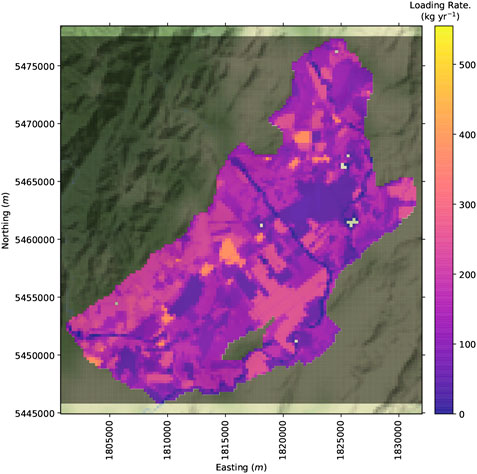
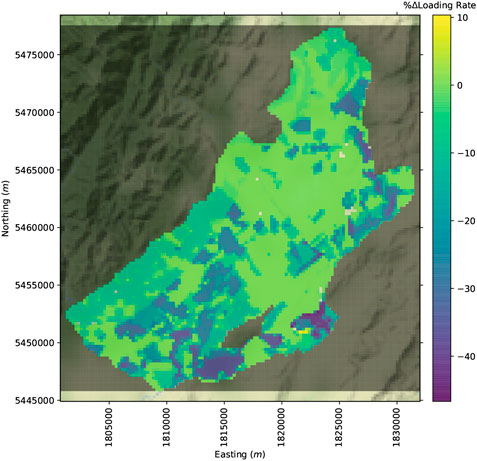
The land-use scenario is combined with the abstraction scenario and is represented with a spatially distributed nitrate loading rate (Figure 3) reflecting a real-world nitrate loading scenario. This nitrate loading rate is a reduction from the current land-use baseline (Figure 4).

FIGURE 3

FIGURE 3. Land-use management scenario nitrate loading rate.

FIGURE 4

FIGURE 4. Percentage change in nitrate loading rate from baseline.

3.1.3. Decision Thresholds

The decision thresholds considered are listed in Table 1. For streamflow reliability forecasts, the simulated groundwater abstraction scenario should not increase the frequency or persistence of low-flow days by greater than 10%. For water quality forecasts, mean zonal nitrate concentrations should not exceed 50% of the maximum acceptable value (MAV) for nitrate-nitrogen in drinking water (5.65 mg L⁻¹; Ministry of Health 2018) and the management goal is that the land-use scenario should result in a 10% decrease in the zonal mean concentration.

3.2. Model Definition

3.2.1. System Conceptualization

The hydrogeological system in the Wairarapa Valley is characterized by successions of unconsolidated, late Quaternary and Holocene, alluvial sediments (Gyopari and McAlister, 2010a; Gyopari and McAlister, 2010b). The general hydraulic gradient results in groundwater flow from the north-east to south-west. Interactions between aquifer units are complicated by variable degrees of compaction, reworking and faulting. Active fault systems that splay from the major Wairarapa Fault, which bounds the western side of the valley, are anticipated to compartmentalize the groundwater system and potentially modify the interaction between groundwater and surface water (Gyopari and McAlister, 2010a; Gyopari and McAlister, 2010b); springs occur along the Masterton and Carterton Fault features. Rainfall recharge within the valleys is supplemented by significant river inflows, especially from the Tararua Range to the west. Nitrate loading is mostly derived from land-use within the plains, with low concentrations anticipated in the inflowing rivers. The Wairarapa Valley is divided into two distinct groundwater domains. Groundwater is discharged to surface water before leaving the northern portion of the valley (425 km²; Figure 2) via the Ruamāhanga River.

3.2.2. Numerical Model Construction

To address the management challenges outlined above, a regional-scale, integrated groundwater/surface-water flow and nitrate transport model was developed. The flow and transport processes were simulated using MODFLOW-NWT (Niswonger et al., 2011) and MT3D-USGS (Bedekar et al., 2016), respectively. The flow and transport simulations were undertaken on a regular finite-difference grid, consisting of five layers, 127 rows and 125 columns at 250 m spacing. Lateral model boundaries were defined as no-flow. Flow and contaminant mass could enter the model via recharge, streamflow and injection wells, and leave the model through streamflow, well abstraction and first-order reactions implemented using the MT3D-USGS reaction package (RCT).

Two simulation periods were considered, a “history matching period” from 1992 to 2007, and a “prediction period” from 2007 to 2014. The history matching period was discretized into 771 weekly stress periods (with a constant time-step of 1.75 days), with varying hydrological stresses (e.g., recharge, well pumping and stream inflows). The prediction period was divided into 2,821 daily stress periods (with daily time-steps), again with varied hydrological stresses.

Both periods consisted of a transient flow model simulation, followed by a 20-years transport simulation with temporally constant (though spatially variable) nitrate mass inputs. The flow solution for the transport simulations were provided by steady-state flow simulations using temporally averaged hydrological stresses for each of the considered time periods. The steady-state flow simulations were also used to provide initial conditions for the respective transient flow simulations.

Additional relevant aspects of the model include:

• surface-water flow and contaminant routing, simulated using the Streamflow-Routing (SFR) (Niswonger and Prudic, 2005) and Stream-Flow Transport (SFT) packages of MODFLOW-NWT and MT3D-USGS, respectively;

• potential fault-bound compartmentalization of the groundwater system, simulated using the Horizontal Flow Barrier package of MODFLOW-NWT (HFB6); and

• use of the total-variation-diminishing (TVD) solver scheme MT3D-USGS to maximize model stability and to reduce numerical dispersion. Note, the use of TVD restricts the transport time step size to honor a Courant number of 1.

3.2.3. History Matching Dataset and Objective Function Formulation

The history matching observations included nitrate concentration measurements from groundwater and surface water, groundwater elevation, in-stream flows and estimates of groundwater to surface water exchanges for the history matching time period. The data included transient time series records, of varied lengths and sampling frequency, and more occasional survey observations. The available observation dataset was composed as follows (observation locations are provided in Supplementary Figure SI 1.1):

• 35 groundwater level sites, including time series (of varied lengths); providing a total of 20,702 observations. The 35 observation sites provided the definition of 35 observation groups. Observations for these sites are provided in Supplementary Section SI 4.1.1.

• 88 surface water gauging sites. Including, continuous, repeat and spot gauging observations; providing a total of 4,385 streamflow observations. Surface water flow observations were partitioned into 12 observation groups, 11 of which relate to sites with 50 or more observations, and the remaining group composed of sites with a low observation count. Observations for these sites are also provided in Supplementary Section SI 4.1.2.

• 23 simultaneous streamflow gaugings, providing a total of 26 surface water to groundwater exchange estimate observations. These observations were assigned to a single observation group.

• 203 groundwater quality monitoring sites, providing a total of 203 mean nitrate concentration observations, assigned to a single observation group.

• 14 surface water quality monitoring sites, providing a total of 14 mean nitrate concentration observations, assigned to a single observation group.

The model objective function was formulated as the sum of weighted, squared residuals between simulated outputs and the historical system observations. Initial observation weights were defined to reflect the uncertainty in system measurements, as the inverse of the estimated measurement standard deviation. For water level observation the standard deviation was defined at 0.5 m; for streamflow observations the standard deviation was 20% of the observed value; for groundwater to surface water exchange estimates, the standard deviation was 10% of the observed value. For concentration observations, where values for each location were averages of different lengths of measurement record, the standard deviations where scaled to account for the number of observation in the record (count). For groundwater concentration the standard deviation used was defined as the standard deviation of the values in the record, multiplied by 100/count. For surface water concentrations the standard deviation used was defined as 100/count multiplied by the mean of the values in the record. The numerator scaling attempts to account for the use of temporally sparse, point concentration measurements, as average system observations. The measurement uncertainties defined on the basis of these standard deviation are illustrated in Supplementary Sections SI 4.1.1, 4.1.2, where red shading denotes three standard deviations from observed values. For the objective function formulation, the initial observations weights were re-balanced such that each group of observations contributed equally to the initial total objective function (e.g., Doherty and Hunt, 2010).

3.3. Prior Uncertainty Quantification

3.3.1. Model Parameterization

A “highly parameterized” parameterization scheme was adopted, as advocated by Hunt et al. (2007); Doherty and Hunt (2010). Model input uncertainty was represented using probability distributions for a total of 2,129 adjustable parameters, all of which are expressed as multipliers on parameter values (e.g., McKenna et al., 2020). The uncertain model parameters considered are as follows:

• horizontal and vertical hydraulic conductivity—520 pilot-point and 82 zonal multipliers

• specific storage—260 pilot-point and 16 zonal multipliers

• specific yield—65 pilot-point and four zonal multipliers

porosity—260 pilot-point and five layer-constant multipliers

• denitrification rate—260 pilot-point and 15 zonal multipliers

groundwater recharge—one global multiplier; 65 pilot-point multipliers; and 12 temporal, monthly multipliers

• nitrate loading rate—1 global multiplier and 65 pilot-point multipliers

• stream-bed conductivity—115 spatial multipliers

• surface-water inflow—117 temporally constant multipliers

• surface-water inflow concentrations—230 spatial multipliers

• groundwater abstraction—one global multiplier; 11 multipliers, by usage type; and 12 temporal, monthly multipliers

• surface-water abstraction—two multipliers, by usage type

Initial model parameter values (to which multipliers were applied) were informed by “expert knowledge” based on hydrogeological assessments incorporating information from, for example, bore logs, aquifer pumping test data and literature studies (e.g., Gyopari and McAlister, 2010a; Gyopari and McAlister, 2010b).

More detail on the spatial and temporal distributions of parameters and the initial native model parameter values is provided in the Supplementary Section SI 3.

3.3.2. Parameter Uncertainty

Prior parameter uncertainty was specified through a block-diagonal prior covariance matrix with prior covariances informed by expert knowledge. Diagonal elements of the prior covariance matrix represent expected individual parameter variances; off-diagonal elements define the correlations between parameters. For the spatially variable parameter types (e.g., hydraulic conductivity, porosity, recharge) the correlation between these parameters were derived from geostatistical analysis of hydrogeolgical field data (e.g., pumping test data; after Moore et al., 2017). Geospatial correlation was defined by exponential variogram with a sill proportional to the expected prior variance (with a proportionality constant of 0.45), and range of 3,500 m. This geospatial correlation estimation also supported the pilot-point parameter interpolation (Doherty, 2003; Doherty et al., 2011). Temporal and non-spatially distributed parameters were defined as uncorrelated.

Two hundred prior realizations were drawn from the prior parameter covariance matrix using a Monte-Carlo multi-variate Gaussian sampling approach (e.g., Tarantola, 2005) to produce the prior parameter ensemble. The statistics for the prior parameter ensemble (in terms of parameters groups) are provided in Supplementary Table SI 3.1 Grouped prior parameter PDFs are illustrated in Supplementary Figure SI 3.8.

3.3.3. Propagation of Prior Uncertainty

Parameter uncertainty was propagated to simulated outputs and forecasts through forward model runs using the 200 prior parameter realizations in the prior parameter ensemble. An assessment of the resultant prior simulated output uncertainty distribution, relative to system observations, was undertaken for the history matching period to identify potential model deficiencies. Predictive period simulations using the same parameter realizations provided forecast distributions which were evaluated against management decision thresholds to provide a prior probabilistic expression of management scenario success or failure.

3.4. Preliminary Posterior Uncertainty Quantification

The preliminary approximation of the posterior forecast uncertainty was derived after assimilation of state observations using an abridged single-iteration history matching and a preliminary approximation of the posterior parameter uncertainty.

3.4.1. Abridged History Matching

History matching was undertaken with a single iteration of the Gauss-Levenberg-Marquardt (GLM) algorithm, using PESTPP-GLM (Welter et al., 2015). The single GLM parameter iteration upgraded the initial parameter vector, effectively constituting and update of the mean of the prior parameter distributions (Supplementary Figure SI 3.8).

The use of a single iteration reduces the computational resource burden compared to undertaking multiple iterations but it is sufficient to provide a Jacobian matrix, which is required to derive the preliminary posterior (see Section 3.4.2), and to support an analysis of the relevance of the available data to the forecasts. The abridged history matching required a total of 2,195 model forward simulations; 2,130 to populate the first-order sensitivity (i.e., Jacobian) matrix, and 65 simulations to test parameter upgrades (aimed at minimizing an objective function). The Jacobian matrix was populated using 1% two-point derivative increments on all parameters, except for surface-water inflow parameters, which were necessarily offset by a value of 100 and used a 0.01% derivative increment (e.g., Doherty, 2016).

3.4.2. Preliminary Posterior Uncertainty Using Linearized Bayes Equation

Using a linear form of Bayes equation, the posterior parameter covariance matrix was approximated via the Schur complement (e.g., Tarantola 2005; Doherty 2015). This approach required: the prior parameter covariance matrix, as introduced above; the Jacobian matrix; and the epistemic noise covariance matrix, which was defined as diagonal with elements specified on the basis of observation “weights.” To account for the effect of model error in an approximate manner, these observations weights were adjusted on the basis of the model-to-measurement residuals after the abridged history matching; weights were defined such that observations within each group contributed equally to the objective function and the total contribution from each group was the same (e.g., Doherty, 2015). Note, this differs from the weighting scheme employed for history matching. More detail on the linearized Bayes equation and the Schur complement method is provided in the Supplementary Section SI 2.

3.4.3. Propagation of Preliminary Posterior Parameter Uncertainty

As with the propagation of prior uncertainty, propagation of the preliminary posterior parameter uncertainty to preliminary posterior forecast uncertainty was achieved through predictive period model forward simulations for each management scenario using 200 parameter realizations, sampled from the preliminary posterior parameter covariance matrix. Sampling was undertaken using the same multi-variate Gaussian Monte-Carlo method (e.g., Tarantola, 2005), outlined above (Section 3.3.2).

The effectiveness of the abridged history matching was evaluated by comparing prior and preliminary posterior parameter and simulated output distributions. The resulting preliminary posterior forecast distributions were evaluated against the defined management decision thresholds. On this basis, the decision points in the workflow were negotiated, leading to a “Stop modeling” outcome.

4. Results

Ongoing or iterative model design, history matching and uncertainty quantification decisions are made on the basis of the “Prior uncertainty quantification” and “Preliminary posterior uncertainty quantification” steps of the workflow depicted in Figure 1. These are decisions that can be informed by an early uncertainty quantification, and therefore, the case study results focus on these parts of the workflow, i.e., after the modeling problem has been defined and a model has been built. To simplify the presentation of the case study results, and to facilitate comparisons, the prior and preliminary posterior uncertainty quantification results figures have been combined.

Note that the case study is used to illustrate the proposed workflow, and the process of negotiating the decision points, within the workflow. It is specifically used to evaluate and demonstrate the insights gained through the steps that constitute early uncertainty quantification (“Prior uncertainty quantification” and “Preliminary posterior uncertainty quantification”). The case study does not iterate through all possible decision pathways of the workflow, but instead demonstrates the workflow in general.

4.1. Prior Uncertainty Quantification

Recall, that purpose of this analysis is twofold. Firstly to check that model outputs, simulated on the basis of the prior parameter probability distributions, encompass the measured observations. Secondly, to assess the proximity of model forecasts to decision thresholds.

4.1.1. Comparison Between Simulated Outputs and Historical Observations

Comparison plots of simulated outputs (both prior and preliminary posterior) and system observations for the history matching period are provided in the Supplementary Sections SI 4.1.1, 4.1.2. The prior simulated output distributions generally encompass their associated observation values—i.e., gray bars in Supplementary Section SI 4.1.1 span the diagonal one-to-one line in the left-hand plot and the zero residual line in right-hand plots; and prior realization outputs in Supplementary Section SI 4.1.2 (gray lines) generally overlap with observations, accounting for observation uncertainty (red shaded areas).

This consistency between the observations and the system conceptualization, as expressed through the numerical model and its prior parameters, was particularly robust for those observations that were of a similar nature and location to the model forecasts. However, this fortunate outcome was not absolute, as some prior-data conflict is evident in the results, e.g., water-level observations for two closely located wells, “s26_0298” and “s26_0308” (highlighted in Supplementary Figure SI 1.1A, see associated plots in Supplementary Sections SI 4.1.1, 4.1.2). Because these observations relate to water levels at relatively distant locations from the streamflow reliability forecast locations, this prior-data conflict is not considered critical to the model forecasts.

Some streamflow observations also demonstrated a degree of prior-data conflict, particularly when simulating short duration, extreme events. For example, the simulated outputs for “fo_s056,” which is close to the streamflow reliability forecast location MS1, fail to reproduce the magnitude of the extreme flow events, generally over predicting high flows (Supplementary Sections SI 4.1.1, 4.1.2). However, the simulated outputs do reproduce the lower flow conditions. This may relate to simplified representation of quick-flow and runoff processes in the numerical model, coupled with the seven-day stress period duration in the history matching period simulation and the relatively sparse temporal parametrization. As the forecasts relate to stream low-flows, this prior-data conflict also not considered critical.

With respect to the workflow schematic in Figure 1, the prior uncertainty analysis indicates that there is no prior-data conflict that is significant for the forecast, and therefore the decision was made to progress to assessing prior forecast uncertainty and (if necessary) approximation of preliminary posterior uncertainty quantification.

4.1.2. Prior Forecast Uncertainty

The prior forecast probability density functions (PDFs) (presented in gray in Figures 5–9) provide the initial indication of the magnitude of the uncertainty surrounding model forecasts and the proximity of these forecast distributions to the decision thresholds.

FIGURE 5

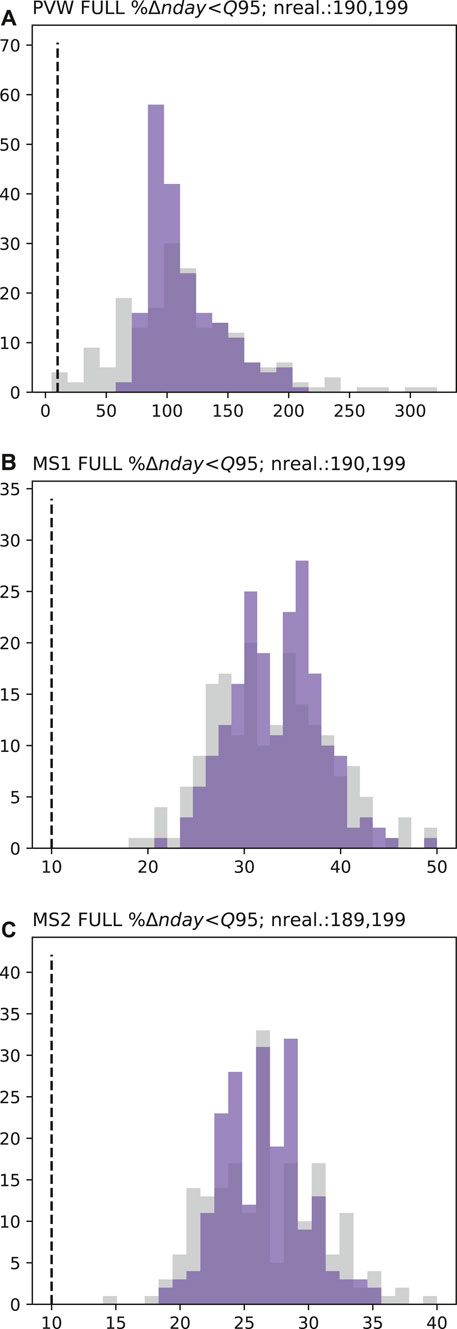
FIGURE 5. Percent change low-flow frequency (%nday<Q95) prior (grey) and posterior (blue) forecast PDFs at PWV (A), MS1 (B) and MS2 (C). Dashed black lines represents the 10% change decision threshold. “nreal.” details the number of successful realizations (therefore the number of data points represented in the PDF) for prior and posterior ensembles, respectively.

FIGURE 6

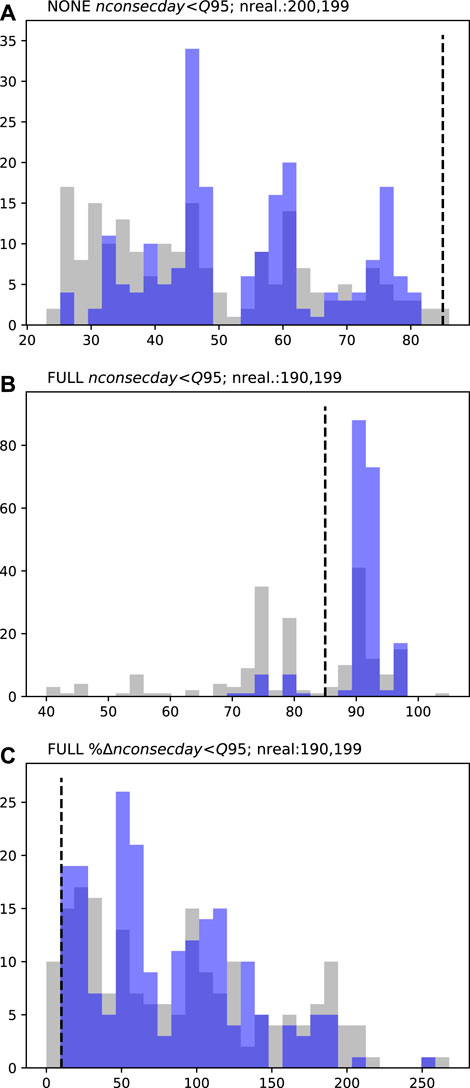
FIGURE 6. PVW low-flow persistence (nconsecday<Q95; A and B) and percent change low-flow persistence (%nconsecday<Q95; C) prior (grey) and posterior (blue) forecast PDFs. Dashed black lines represent the respective decision thresholds (85 days in A and B and 10% change in C). “NONE” represents the “naturalized” baseline and “FULL” the abstraction scenario. “nreal.” details the number of successful realizations (therefore the number of data points represented in the PDF) for prior and posterior ensembles, respectively.

FIGURE 7

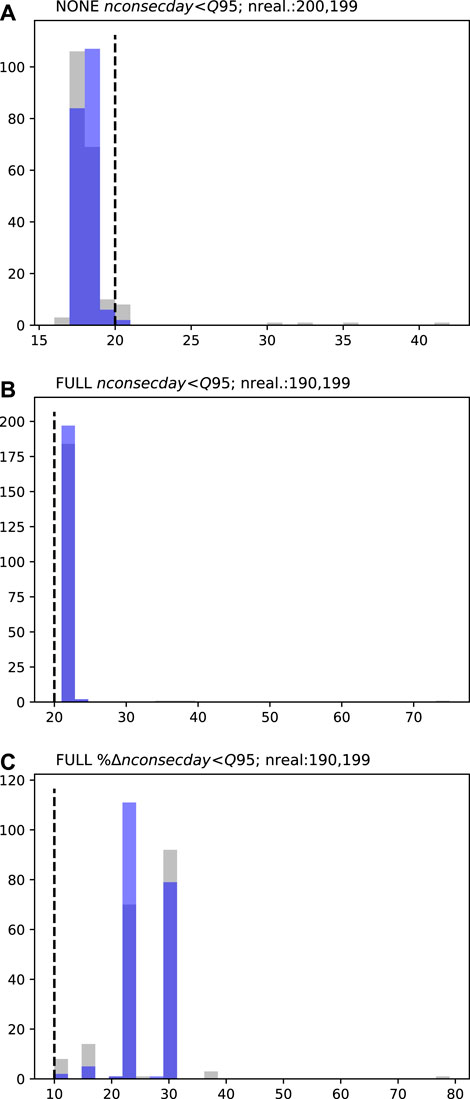
FIGURE 7. MS1 low-flow persistence (nconsecday<Q95; A and B) and percent change low-flow persistence (%nconsecday<Q95; C) prior (grey) and posterior (blue) forecast PDFs. Dashed black lines represent the respective decision thresholds (20 days in A and B and 10% change in C). “NONE” represents the “naturalized” baseline and “FULL” the abstraction scenario. “nreal.” details the number of successful realizations (therefore the number of data points represented in the PDF) for prior and posterior ensembles, respectively.

FIGURE 8

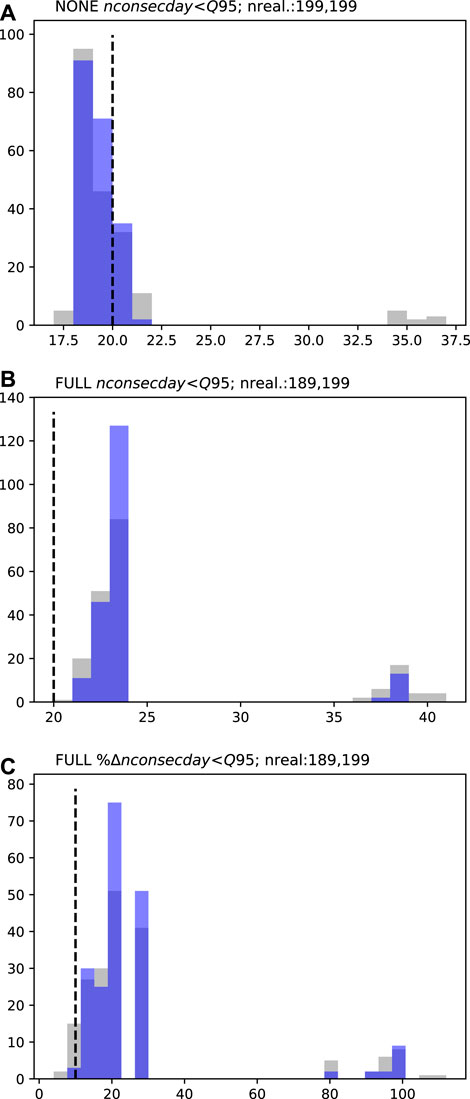
FIGURE 8. MS2 low-flow persistence (nconsecday<Q95;A and B) and percent change low-flow persistence (%nconsecday<Q95;C) prior (grey) and posterior (blue) forecast PDFs. Dashed black lines represent the respective decision thresholds (20 days in A and B and 10% change in C). “NONE” represents the “naturalized” baseline and “FULL” the abstraction scenario. “nreal.” details the number of successful realizations (therefore the number of data points represented in the PDF) for prior and posterior ensembles, respectively.

FIGURE 9

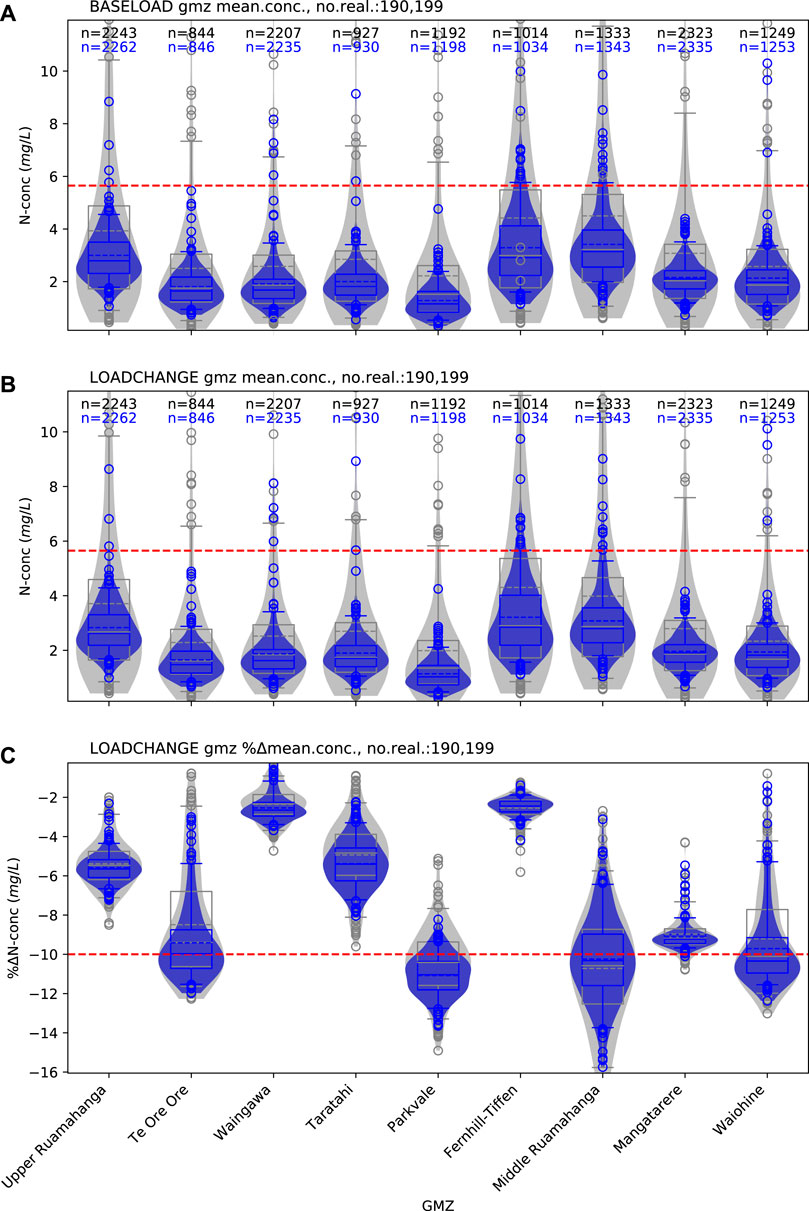
FIGURE 9. Water quality prior (grey) and posterior (blue) forecasts distributions for mean zonal concentration in GMZs (see Figure 2). The width of the distribution indicates the distribution density. Box plots are also displayed to indicate the inter-quartile range (IQR, Q3-Q1, box), median (line in box), and 5th and 95th percentile (whiskers) of the distributions. Red dashed lines represent decision threshold values; for absolute mean zonal concentration forecasts (mean.conc, A and B) this threshold is 5.65mg l–1; for percentage-change forecasts (%mean.conc, C), the threshold is10% reduction in concentration.“no.real.” details the number of realization completed—therefore the number represented in the PDF—for prior and posterior ensembles, respectively. In A and B, “n” represents the mean number of active model cells in each zone, across all prior (black text) and posterior (blue text) realizations. “LOADCHANGE” represents the land-use management scenario explored relative to the baseline (denoted as “BASELOAD”).

4.1.2.1. Streamflow reliability forecasts

The streamflow reliability forecasts relate to the frequency and persistence of low-flow conditions at the three sites of interest (PVW, MS1, and MS2; Figure 2), as well as the percentage changes in these forecasts, associated with abstraction; see Table 1).

4.1.2.1.1. Low-Flow frequency forecasts.

For simplicity, the following presentation of the low-flow frequency forecast results will focus on the percentage change forecast (Figure 5) at each location. The full results for the low-flow frequency forecasts are presented in the Supplementary Section SI 6.

For this forecast the prior PDFs vary between sites. The forecast uncertainty is highest at site PVW (Figure 5A). At this site the prior forecast PDF extends (just) below the decision threshold, indicating that there is potential (albeit with low probability) for the abstraction to comply with the management limit at this site. At MS1 and MS2 sites, the forecast distributions are entirely above their respective decision thresholds (Figures 5B,C), supporting the assumption of certainty that abstraction will cause exceedance of the management limit, i.e., abstraction is predicted to increase the number of low-flow days by more than 10%.

On this basis, the results of the prior uncertainty quantification are sufficient for supporting the management decision relating to low-flow frequency objectives at sites MS1 and MS2. Consequently, when considering these forecasts, the prior uncertainty quantification provides justification for moving to “Stop modeling” in the workflow. However, at site PVW the results indicate that benefit may be gained by reducing forecast uncertainty and the prior uncertainty quantification provides justification for moving to “Preliminary posterior uncertainty quantification.”

4.1.2.1.2. Low-Flow persistence forecasts.

For the low-flow persistence forecasts, the PDFs are multi-modal (Figures 6–8). This is a consequence of their discontinuous nature, where, for example, for any given realization, two consecutive periods low-flow periods may, or may not, be bridged, and when bridging occurs this results in one, significantly longer, low-flow period. This multi-modal nature is most evident for the PVW site (Figure 6) where the under naturalized conditions, the prior forecast PDF spans 23–86 days, beyond the decision threshold, with no single dominant mode apparent (Figure 6A). Under the abstraction scenario, the forecast at this site also indicates high uncertainty and spans the decision threshold (Figure 6B). The prior forecast uncertainty is also high for the percentage change forecast at PVW, extending below the 10% decision threshold, to 0% change, thus indicating the potential for abstraction to have little effect on the persistence of low-flow conditions at this site. These results suggest that the forecast is not sufficiently robust to allow the workflow to progress to “Stop modeling,” indicating the “Preliminary posterior uncertainty quantification” should be undertaken.

For the MS1 and MS2 sites, the prior PDFs for the low-flow persistence forecasts are similar (Figures 7, 8). Both sites display a single dominant mode in the forecast PDFs, with and without abstraction. For the baseline scenario, the prior PDFs at both sites span the decision threshold (Figures 7A, 8A), this indicates that even under “natural” conditions the number of consecutive low flow days may exceed 20 days. With abstraction, the prior PDFs indicate certainty that this decision threshold will be exceeded, i.e., the prior distributions are wholly above the decision threshold (Figures 7B, 8B). On the basis of these absolute forecast results, there would be justification for moving to “Stop modeling” in the workflow. However, for the percentage change forecast, the minimum of the prior PDF at MS1 is at the decision threshold (Figure 7C), while for MS2 it extends below the decision threshold (Figure 8C); this suggests that for these normalized difference forecasts, “Preliminary posterior uncertainty quantification” should be undertaken.

4.1.2.2. Water Quality Forecasts

For the mean zonal concentration forecasts, prior forecast PDFs demonstrate high variance and indicate a potential for mean concentrations to exceed the 5.65 mg L⁻¹ decision threshold in all zones, under both the land-use management scenario and baseline conditions (Figures 9A,B). The prior forecast distributions indicate significant spatial variability in the predicted success of the management strategy, with respect to the decision threshold of a desired 10% reduction in mean zonal concentration (Figure 9C). In some zones (e.g., Te Ore Ore, Parkvale, Middle Ruamāhanga, Waiohine) the percent change forecasts indicate that there is a possibility for management scenario success (forecast PDFs at least span the decision threshold). However, for the other zones these results indicate failure of the land-use management scenario. Generally, for the water quality forecasts, the prior uncertainty quantification indicates that the workflow should move to “Preliminary posterior uncertainty quantification.”

4.2. Preliminary Posterior Uncertainty Quantification

The preliminary posterior uncertainty quantification was undertaken after an abridged history matching and provides approximate posterior parameter distributions which are propagated to approximate posterior forecast distributions.

4.2.1. Parameter Uncertainty

To assist in the interpretation of the uncertainty surrounding the 2,129 model parameters they are grouped by type (Figure 10). Prior parameter distributions (gray PDFs in Figure 10) reflect sampled parameter covariances that are based on expert knowledge alone. Posterior parameter distributions (blue PDFs in Figure 10) reflect the approximated parameter uncertainty after the abridged history matching. Together, the distributions presented in Figure 10 provide an indication of the level of parameter conditioning achieved through the abridged history matching. The prior and posterior distribution statistics for each parameter group are provided in Supplementary Table SI 3.1.

FIGURE 10

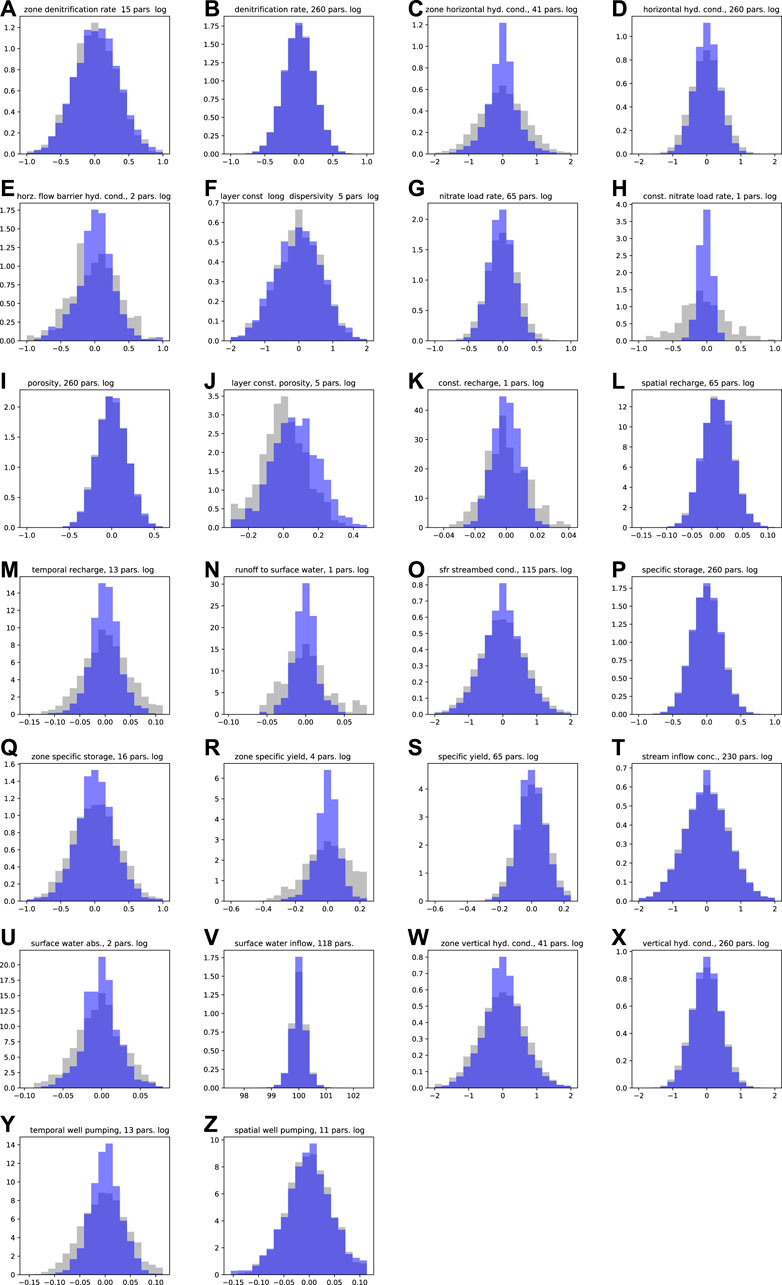
FIGURE 10. Posterior parameter distributions (blue) plotted over prior parameter distribution (grey). The total number of parameters in the grouped distributions are detailed in the individual plot titles. If distributions refer to the log10 transformed parameters values, this is also detailed in the individual plots. Plot of grouped prior parameter distributions alone are presented in Supplementary Figure SI 3.8.

While the grouping of parameters in Figure 10 and Supplementary Table SI 3.1 can obscure visual identification of the extent of the conditioning of individual parameters within a group, it is clear that the abridged history matching has achieved only minor reductions in the uncertainty of most parameters. Generally, reductions in uncertainty are more notable for the lumped, global or layer-wide, parameters, than for the spatially distributed parameters. Illustrations of the spatial distribution of the variance reduction for both zone and pilot point parameters are shown in Supplementary Section SI 5. These plots also highlight that the abridged history matching achieved only minor reduction in parameter uncertainty over large areas of the numerical model spatial domain, coinciding with areas lacking in observation data (Supplementary Figures SI 5.1-5.18). The streamflow reliability forecast locations are coincident with areas where the reduction in parameter variance is minimal (e.g., see Supplementary Figures SI 5.5-5.14).

Collectively these results indicate that the conditioning of model parameters reflects significant parameter non-uniqueness, which is as a combined result of data scarcity and the distributed parameterization required to represent forecast relevant system detail (e.g., Sanford, 2011; Erdal and Cirpka, 2016; Knowling and Werner, 2016).

Despite the fact that variance reductions in the parameter PDFs are very subtle, a number of parameter groups do show uncertainty reduction. The most notable parameter variance reduction occurs for the global nitrate surface-loading rate parameter (Figure 10H). The apparent posterior uncertainty for this parameter is significantly constrained, with the approximated posterior probability distribution reducing from a range of 0.13–10 to a range of 0.45–1.57, with a variance reduction of 91%. This reflects the highly aggregated nature of this parameter; it captures information from all available nitrate concentration observations.

Only a few parameter groups show any evidence of first moment changes after history matching, i.e., the mean of the prior and posterior distributions are generally similar. Differences between mean values of prior and posterior parameter distributions indicate that either the mean in the prior distribution is inadequately defined, or alternatively, that there is a potential for bias due to inadequate model or parameter complexity. The only parameter group that shows a significant first moment response to data assimilation is the layer-constant porosity group (Figure 10J) which displays a first moment shift to higher values; the distribution mean for this porosity multiplier group shifts from 1.01 to 1.17. Higher porosity values effectively reduce simulated flow velocities, which in turn cause increased contaminant reaction (denitrification, in this instance). This inference of higher porosity results from the flow of information in the nitrate concentration observations to groundwater and surface water concentration simulated outputs which are the only simulated outputs that are sensitive to groundwater flow velocities. Over 90% of the 203 groundwater concentration observations are below 10 mg L⁻¹; prior simulated outputs corresponding to many of these observations, however, spanned significantly higher values (up to 80 mg L⁻¹; see Supplementary Section SI 4.1.1). So, while the prior distribution of simulated nitrate concentrations span the observed concentrations (i.e., there is no prior-data conflict), this indicates that the prior distributions for nitrate-loading and layer-based porosity parameters require some refinement.

4.2.2. Comparison of Simulated Outputs With Historical Observations

We note that the prior and posterior simulated output distributions in Supplementary Section SI 4.1.1 indicate that, for these outputs at least, the prior distribution is conservative relative to the posterior distribution, i.e., the prior distributions (gray in Supplementary Sections SI 4.1.1, 4.1.2) fully encapsulate the posterior distributions (blue in Supplementary Sections SI 4.1.1, 4.1.2).

However, after the preliminary posterior uncertainty quantification some simulated output distributions no longer overlap with observations (blue bars and lines in Supplementary Section SI 4.1.1, 4.1.2). An example of this behavior can be seen with the preliminary posterior simulated outputs that relate to observations from well “s26_0656” (see Supplementary Section SI 4.1.2). Discrepancy between posterior simulated output distributions and observed system behavior may be a manifestation of observation error, causing tension in the history matching, or it may be an indication of insufficient complexity in the model parameter conceptualization, which inhibits simulation of system behaviors that are captured by the data. Evaluation of the source and implication of such results is important for assessing the robustness of posterior model forecast distributions.

For the specific example of well “s26_0656” observations, the preliminary posterior simulated outputs for the nearby “s26_0155” well effectively capture the observed water levels. Well “s26_0155” is in model layer 1, while “s26_0656” is in model layer 4, and as such it is anticipated to be more important for informing for the streamflow reliability forecasts. This supports continuing to the assessment of preliminary posterior forecast uncertainty. However, as the presence of such conflict could be an indication of insufficient parameter complexity, this assessment could provide justification for returning to the “Prior uncertainty quantification” step in the workflow and potentially reassessing discretization as well as parameterization, especially before any further history matching is considered.

4.2.3. Preliminary Posterior Forecast Uncertainty

4.2.3.1. Streamflow Reliability Forecasts

4.2.3.1.1. Low-Flow Frequency Forecasts.

The abridged history matching, undertaken as part of the preliminary posterior uncertainty quantification, has reduced the uncertainty of the low-flow frequency percentage change forecasts, as demonstrated by narrower posterior PDFs (blue) compared to prior PDFs (gray) in Figure 5. However, the magnitude of the forecast uncertainty reduction varies between sites. The reduction in uncertainty is greatest at site PVW (Figure 5A) and results in the posterior forecast PDF moving above the decision threshold, indicating a certainty that the abstraction scenario will exceed the decision threshold; such certainty was not achievable based on the prior forecast PDF. At MS1 and MS2, the reduction in forecast uncertainty is relatively low (Figures 5B,C). However, as the prior forecast PDF is already wholly above the decision threshold, this limited reduction in uncertainty is of little consequence in the specific decision support context considered here. On the basis of these results, the workflow could move to “Stop modeling” after this preliminary posterior uncertainty quantification.

4.2.3.1.2. Low-Flow Persistence Forecasts.

For the low-flow persistence forecasts, some apparent uncertainty reduction is achieved by the abridged history matching. At PVW, the reduction in forecast uncertainty moves the baseline scenario forecast away from the decision threshold (Figure 6A). However, for all other forecasts (at all sites), the abridged history matching has had limited impact on the position of forecast distributions, relative to their respective decision thresholds, and therefore provides little additional benefit for decision support. For these forecasts the observation dataset may be considered to be of little benefit for reducing forecast uncertainty. In this case, continued history matching would not be expected to sufficiently reduce forecast uncertainty and the modeling process should move to “Stop modeling.”

4.2.3.2. Water Quality Forecasts

The abridged history matching reduces the uncertainty for the absolute mean zonal concentration forecasts, for all zones (blue PDFs in Figures 9A,B). For the land-use management scenario the variance reduction is such that only forecast outliers (beyond the 95th percentile) extend beyond the decision threshold (Figure 9B). For some zones the variance reduction is such that the posterior PDFs move entirely below the decision threshold (e.g., Te Ore Ore, Parkvale and Mangatarere). While the preliminary posterior forecast PDFs indicate low probability that the nitrate loading management scenario will result in mean zonal concentrations above the decision threshold of 5.65 mg L⁻¹, they are not sufficiently constrained through the abridged history matching to provide apparent certainty. However, the reduction in forecast uncertainty indicates that the observation dataset contains information that is beneficial for this forecast and the preliminary posterior uncertainty quantification provides justification to “Continue history matching.”

For the percentage change forecast, there is relatively little reduction in uncertainty as a result of the abridged history matching (Figure 9C). Consequently, the variability of the predicted outcome of the management strategy, between zones, still persists. This result suggests that although the absolute forecast is informed by the observation data, the conditioning of parameters appears to have little influence on the normalized change forecast. This indicates that if uncertainty reduction for the percentage change in mean zonal concentration forecast is desired, there would be little benefit in continuing history matching with this combination of numerical model and observation data.

5. Discussion

The role of uncertainty quantification in modeling for decision support is widely recognized in the literature (e.g., Freeze et al., 1990; Gupta et al., 2006; Moore and Doherty, 2006; Vrugt, 2016; Ferré, 2017). A requirement for the proposed decision support workflow, is that the forecasts of interest, and the decision thresholds associated with them, are defined at the outset, as outlined by the “Problem definition” step in Figure 1. This follows from a growing recognition that for decision support applications, model design should be based on the pre-definition of decision-relevant forecasts and the hypothesis to be tested (e.g., Guthke, 2017; White, 2017; Doherty and Moore, 2019).

We extend this ‘start from the problem and work backwards’ approach, to one that explicitly considers the environmental threshold that a management decision is seeking to avoid. In this context we demonstrate the important insights provided by a workflow which incorporates a preliminary assessment of forecast uncertainty. This can then support a number of ongoing modeling decisions, e.g.:

• the potential to assess the ability of a model and its associated prior parameter uncertainty to robustly simulate historical system observations, particularly those that are aligned with forecasts (i.e., to evaluate prior-data conflict);

• an opportunity to revisit model design and parameterization to allow simulated outputs to better reproduce system observations that are pertinent to forecasts;

• an opportunity to assess the extent to which forecasts are informed by observation data;

• an opportunity to process system observation data to provide the most appropriate information to inform the parameters that forecasts are sensitive to;

provision of a defensible basis for undertaking (and continuing or stopping) history matching; and

• potentially, an opportunity to forgo history matching altogether, where it is not necessary to further support the decision making process.

As a result of the benefits listed above, the proposed workflow has the potential to reduce the time and effort required for decision support model deployment. For example, the prior uncertainty quantification and preliminary posterior uncertainty quantification (if required) can be achieved at low computational cost, relative to a more complete derivation of posterior uncertainty after a more exhaustive history matching effort. In the case study example, further history matching iterations would require 2,195 model runs per iteration, this equates to a computational cost of around 300 CPU days per iteration.

It should be noted however, that the history matching method used here follows a traditional approach, employing finite-difference gradients. Alternative approaches exist that support efficient data assimilation and uncertainty quantification with relativity few model forward simulations; for example, using ensemble based approximations (e.g., Chen and Oliver, 2013; White, 2018). Nevertheless, such approaches still require additional model forward simulations to approximate and propagate posterior parameter uncertainty. As the general workflow presented in Figure 1 is agnostic of the specific uncertainty quantification methods employed, it still provides the potential for time and effort savings potential as well as protection (and potential for mitigation) against model failure induced by inappropriate history matching.

5.1. Assumption of a Conservative Prior

The proposed workflow is underpinned by the assumption that prior parameter distributions, and therefore prior forecast distributions, are “conservative.” In this context, a conservative prior means that a forecast distribution will tend to inflate the inherent uncertainty in the modeled system behavior. This follows the need to avoid uncertainty variance under-estimation in modeling for decision support (e.g., Doherty and Simmons, 2013). Unfortunately, verification of whether the prior is sufficiently conservative is challenging, requiring, for example, paired model analysis, whereby prior forecast distributions are compared for pairs of models of differing complexity in order to highlight and expose predictive bias or variance corruption induced through model simplification (e.g., Doherty and Christensen, 2011; Gosses and Wöhling, 2019). In real-world decision support applications, undertaking such an analysis is rarely considered due to time and resource limitations, and the uncommon availability of multiple models of varying complexity.

Notwithstanding the challenges associated with formulating and verifying a conservative prior, a number of strategies to circumvent the effects of a non-conservative prior have been postulated in previous studies. These include: adopting high parameter dimensionality (e.g., Hunt et al., 2007; Knowling et al., 2019), with parameterization expressing system uncertainty at different spatial and temporal scales (e.g., White et al., 2020a; McKenna et al., 2020), and processing or transforming simulated outputs to minimize uncertainty, and thereby also the effects of an inadequate prior (e.g., Sepúlveda and Doherty, 2015; Knowling et al., 2019). Deploying such strategies is an important component of “Model definition” and prior formulation in “Prior uncertainty quantification” in the proposed workflow. Accordingly, in the case study presented herein, a highly parameterized scheme was adopted (e.g., Hunt et al., 2007), incorporating a combination of pilot points and zone- and layer-based parameters, with expert knowledge-based parameter variance and correlation; this aligns with an “intermediate” parameterization scheme in Knowling et al. (2019) which was found to be relatively robust for making predictions related to the depletion of low streamflows in response to groundwater pumping. We also considered “differenced” forecasts (e.g., percentage-change forecasts) in an effort to reduce possible ill-effects due the potential presence of large-scale boundary condition errors (e.g., Doherty and Welter, 2010; Sepúlveda and Doherty, 2015).

5.2. Insights and Advantages of Prior Uncertainty Quantification

The “Prior uncertainty quantification” step in the proposed workflow provides insights into the appropriateness of the conservative prior assumption, through comparison of the prior uncertainty surrounding simulated outputs with observations of system behavior (e.g., assessing the presence of prior-data conflict). Through this process the prior uncertainty quantification can also reveal errors in observation data at an early point in the workflow, before effort is wasted trying to match model outputs to errant data. Under the assumption that the observation errors are minimal, and are appropriately represented by the observation weights and the epistemic noise covariance matrix (see Section 3.4.2), the presence of prior-data conflict between simulated outputs and system observations may be an indication of potential inadequacy in the specified prior parameter uncertainty and/or in the way that the forecast relevant aspects of the system are parameterized (e.g., Nott et al., 2016). Where conflicts exist for data that are closely related, in type and/or location, to the decision-relevant forecast, this inadequacy has the potential to propagate to the expression of forecast uncertainty—with the associated risk of incurring “model failure” (Doherty and Simmons, 2013).

In the presented case study example, the “Prior uncertainty quantification” step does indicate instances of prior-data conflict, for example, for some water level and high streamflow observations, as highlighted in Section 4.1. For the specific forecasts in the case study, the conflicts were not considered critical; i.e., the location and/or nature of the conflict between simulated outputs and system observations was not expected to impact on the reliability of the forecasts.

However, where model inadequacy, highlighted through the assessment of prior-data conflict, is deemed to risk the reliability of forecasts, additional work can be undertaken to improve the model parameter representation of forecast relevant aspects of the system and/or formulation of the prior parameter probabilities. The appropriate remedy depends on an assessment of the sufficiency of the model, its parameters, and of the expression of the prior parameter uncertainty, to adequately represent the system processes that are pertinent to the forecasts. If the parameter representation of the modeled system is deemed to be sufficiently complex to support full expression of the processes and process uncertainty that forecasts are sensitive to, the prior-data conflict indicates underestimated prior parameter variances. This can be remedied by revisiting the “Prior uncertainty quantification” step and inflating parameter variances. If however, the prior-data conflict is deemed to be due to an inadequate parameterization of specific processes, essentially creating a type of model structural defect, then the workflow should also return to the “Prior uncertainty quantification” step to revisit the parameterization scheme itself, as well as its probability distribution. In some cases, it will be the model definition itself that needs to be revisited, if the parameterization of a simulated process is not the issue, but rather the complete omission of the process. Iteration through these steps may be required. Importantly, undertaking this prior uncertainty quantification provides the necessary insights for identifying and rectifying model and parameter inadequacies at early stage in the workflow, before significant damage is done to the decision making process.

Once the model and prior parameter distribution is considered to adequately represent forecast relevant system processes, the prior uncertainty quantification also provides an opportunity to forgo a formal history matching effort. In the case study presented here, an example of this justification for forging history matching, is provided by the low-flow frequency forecast at MS1 and MS2 (Figures 5B,C). For this example, the prior forecast PDFs are wholly above the 10% decision threshold indicating that breaching of the management limit is almost certain to occur. In this case, and under the important assumption that the prior forecast uncertainty is conservative, the management decision could be made from a prior stance, with very low apparent risk of an incorrect assessment; efforts to reduce the uncertainty of the prediction through data assimilation would be unnecessary, as this would not change the evaluation of decision threshold exceedance, and the workflow can proceed to “Stop modeling.”

Unfortunately, however, the capability of prior uncertainty quantification to provide a sufficient basis for a particular decision support context, is expected to be highly case specific. It is likely to depend on, for example, the inherent subjective definition of the decision threshold, the system parameterization and how the uncertainty of these parameters is defined (especially in regional-scale numerical models where parameters are abstractions of true natural system properties; Watson et al., 2013), as well as the risk tolerance of the decision-maker. Where the prior quantification of forecast uncertainty fails to provide sufficient certainty to support decision making (and prior-data conflict issues are minimal) the modeler may choose to undertake history matching with the aim of reducing model forecast uncertainty (e.g., the low-flow frequency forecast at PVW and the mean zonal concentration forecasts in the case study). In this instance the results of prior uncertainty quantification provides justification for moving to the “Preliminary posterior uncertainty quantification” step of the workflow.

5.3. Undertaking Approximate Preliminary Posterior Uncertainty Quantification

If history matching is considered necessary, approximation of the preliminary posterior uncertainty surrounding simulated outputs and forecasts at an early stage of the process provides another opportunity to assess the relationship between the model, its parameters, observation data, and ultimately, forecasts. Specifically, this early approximation of the posterior can provide insights into the ability of the observation data to sufficiently and appropriately inform model parameters that forecasts are sensitive to. Additionally, the resulting forecast uncertainty may be such that the preliminary posterior uncertainty quantification is sufficient for decision support model deployment.

For example, from the presented case study, the prior distribution of the low-flow frequency forecast at PVW extends just below the 10% decision threshold (Figure 6A). Consequently, for a decision maker with low risk tolerance (i.e., they desire low probability that the critical condition will not be violated), the prior uncertainty quantification does not provide sufficient support for the specific management decision. However, for this forecast, conditioning of parameters through the abridged history matching in the “Preliminary posterior uncertainty quantification” step was effective at achieving a sufficient reduction in forecast variance to support an assessment of management scenario outcome, with relative certainty; i.e., after the abridged history matching, the posterior forecast distribution was entirely above the decision threshold (Figure 6A). For this example, further history matching is not required, as no further uncertainty reduction is necessary to support management decision making. The modeling workflow could move to “Stop modeling.”

As with the “Prior uncertainty quantification” step of the workflow, the potential to move to “Stop modeling” after “Preliminary posterior uncertainty quantification” is also likely to be highly case specific. For example, for the absolute mean zonal concentration forecasts in this case study (Figure 9), the uncertainty remaining after abridged history matching, is still too high to provide certainty that the tested management scenarios will not result in conditions that exceed the decision threshold. However, in this instance the prior uncertainty quantification and subsequent preliminary approximation of the posterior uncertainty was still beneficial. It provided; i) an early indication of the ability of the model and prior parameterization to reproduce system observations that are pertinent to the forecasts; ii) an indication of the ability for system observations to inform model parameters to promote a sufficient reduction in forecast uncertainty; and, iii) indication of the likely implications of continuing history matching in an attempt to further reduce forecast uncertainty.

For the water quality forecasts in the case study, the data that were most directly relevant for the forecasts were measurements of groundwater nitrate concentration. While these observations are generally encapsulated by the prior simulated output distributions, and although some protection against the ill-effects associated with history matching may have been be gained by employing relatively high parameter dimensionality at multiple-scales, together with the spatially aggregated (mean) nature of the forecasts (e.g., Doherty and Christensen, 2011; White et al., 2014; McKenna et al., 2020), the simulated output distributions associated with the approximated posterior no longer reproduce higher concentration observations (see Supplementary Section 4.1.1). This indicates that the model parameterization and its prior probability distribution may not be sufficiently complex, and potentially may even require a refinement of the model discretization, which for the purposes of the workflow, can be considered part of a parameterization scheme. While further history matching iterations may result in the necessary variance reduction to provide the apparent certainty desired for the water quality forecasts, given the current model parameterization, the efforts to assimilate system data may induce bias in simulated outputs; therefore, further history matching (i.e., moving to the “Continue history matching” step) risks model failure (e.g., Doherty and Simmons, 2013).

6. Concluding Remarks

This study demonstrates the critical role of uncertainty quantification in model-based decision support. The quantification of uncertainty of simulated decision-relevant forecasts underpins the assessment of risks associated with management scenarios. Our case study demonstrates that the suggested workflow, which includes undertaking uncertainty quantification before comprehensive history matching efforts, brings significant advantages.

Quantification of model forecast uncertainty on the basis of prior parameter uncertainty is generally straightforward and relatively computationally efficient. It may be sufficient for informing an evaluation of the efficacy of a management strategy without the need for history matching. Depending on the proximity and considered robustness of the prior forecast probability distribution with respect to the decision threshold, it may be possible to conclude a modeling project this stage.

Prior uncertainty quantification also provides an opportunity to assess the validity of prior parameter distributions, through comparison of historical observations with prior simulated output distributions. Where prior-data conflict exists for forecast relevant observations, a modeler has the opportunity to revisit the model conceptualization and specification, including reformulation of prior parameter uncertainty, before embarking on history matching with a potentially flawed conceptualization.

Using a computationally efficient, albeit approximate, method for quantifying preliminary posterior uncertainty provides a defensible basis for undertaking further history matching. Importantly, this insight can be provided at an early stage of the modeling workflow.

Additionally, undertaking uncertainty quantification early in the modeling workflow can provide important insights into how the information in observation data flows to model parameters and forecasts. These insights can guide further model design and parameterization efforts, objective function formulation and observation processing, if deemed necessary, for example, on the basis of prior-data conflict.

We recommend adjusting the traditional modeling workflow, so that decision support modeling projects can benefit from the insights and potentially significant cost savings afforded by this early uncertainty quantification approach.

In summary, the approach provides:

• an early indication of the capacity of the numerical model and the chosen parameterization to numerically represent the decision-relevant forecasts, and therefore support decision making;

• an indication of the ability of observations to inform model parameters that the decision-relevant forecasts are sensitive to, and the opportunity to rectify incompatibilities between the model (parameters or structural design), observations and forecasts;

• the potential that the forecast uncertainty is sufficiently constrained to support a management decision or assess management strategy effectiveness without requiring history matching; and

• a quantitative and defensible basis for undertaking (and stopping) history matching for the purpose of reducing forecast uncertainty, with respect to management decision thresholds.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The modeling work was led by BH with significant contribution to methods and results interpretation by all authors. All authors contributed to the writing of all components of the manuscript text, after an initial draft by BH.

Funding

This work was funded, in part, through the “Smart Models for Aquifer Management” (SAM) research program Grant Number: C05X1508 funded by the New Zealand Ministry of Business, Innovation and Employment, and was also supported by GNS Science Groundwater Strategic Science Investment Fund (SSIF).

Conflict of Interest

This research was initiated while all authors were employed by the company GNS Science, a Crown Research Institute owned by the New Zealand Government.

Acknowledgments

The case study example development was supported by Greater Wellington Regional Council (GWRC). The authors also thank Jeremy White for assistance throughout and a constructive review of preliminary versions of this manuscript. We also thank the helpful and constructive review of two reviewers whose efforts have helped to improve this manuscript considerably.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2020.565613/full#supplementary-material

References

Alfonzo, M., and Oliver, D. S. (2019). Evaluating prior predictions of production and seismic data. Comput. Geosci. 23, 1331. doi:10.1007/s10596-019-09889-6

CrossRef Full Text | Google Scholar

Barnett, B., Townley, L., Post, V., Evans, R., Hunt, R., Peeters, L., et al. . (2012). Waterlines Report. Australian groundwater modelling guidelines. Canberra: National Water Commission.

Google Scholar

Bedekar, V., Morway, E. D., Langevin, C. D., and Tonkin, M. (2016). Report, U.S. Department of the Interior, U.S. Geological Survey. MT3D-USGS version 1: a U.S. Geological survey release of MT3DMS updated with new and expanded transport capabilities for use with MODFLOW.

CrossRef Full Text | Google Scholar

Brouwers, M., Martin, P. J., Abbey, D. G., and White, J. (2018). Groundwater modeling with nonlinear uncertainty analyses to enhance remediation design confidence. Groundwater 56, 562–570. doi:10.1111/gwat.12669

Pubmed Abstract | CrossRef Full Text | Google Scholar

Brynjarsdóttir, J., and OʼHagan, A. (2014). Learning about physical parameters: the importance of model discrepancy. Inverse Probl. 30, 114007. doi:10.1088/0266-5611/30/11/114007

CrossRef Full Text | Google Scholar

Chen, Y., and Oliver, D. S. (2013). Levenberg-Marquardt forms of the iterative ensemble smoother for efficient history matching and uncertainty quantification. Comput. Geosci. 17, 689–703. doi:10.1007/s10596-013-9351-5

CrossRef Full Text | Google Scholar

Clemo, T., Michaels, P., and Lehman, R. M. (2003). Transmissivity resolution obtained from the inversion of transient and pseudo-steady drawdown measurements. Tech. Rep. Boise, ID: Boise State University.

Google Scholar

Dausman, A. M., Doherty, J., Langevin, C. D., and Sukop, M. C. (2010). Quantifying data worth toward reducing predictive uncertainty. Groundwater 48, 729–740. doi:10.1111/j.1745-6584.2010.00679.x

Pubmed Abstract | CrossRef Full Text | Google Scholar

Doherty, J. (2015). Calibration and uncertainty analysis for complex environmental models, PEST: complete theory and what it means for modelling the real world. Brisbane, Australia: Watermark Numerical Computing.

Google Scholar

Doherty, J., and Christensen, S. (2011). Use of paired simple and complex models to reduce predictive bias and quantify uncertainty. Water Resour. Res. 47. doi:10.1029/2011WR010763

CrossRef Full Text | Google Scholar

Doherty, J. E., Fienen, M. N., and Hunt, R. J. (2011). Report 2010-5168. Approaches to highly parameterized inversion: pilot-point theory, guidelines, and research directions.

Google Scholar

Doherty, J. (2003). Ground water model calibration using pilot points and regularization. Ground Water 41, 170–177. doi:10.1111/j.1745-6584.2003.tb02580.x

Pubmed Abstract | CrossRef Full Text | Google Scholar

Doherty, J., and Hunt, R. (2010). Report 2010-5169. Approaches to highly parameterized inversion―a guide to using PEST for groundwater-model calibration.

Google Scholar

Doherty, J., and Moore, C. (2019). Decision support modeling: data assimilation, uncertainty quantification, and strategic abstraction. Groundwater 58, 327. doi:10.1111/gwat.12969

Pubmed Abstract | CrossRef Full Text | Google Scholar

Doherty, J. (2016). PEST user manual part I and II. 6th Edn. Brisbane, Australia: Watermark Numerical Computing.

Google Scholar

Doherty, J., and Simmons, C. T. (2013). Groundwater modelling in decision support: reflections on a unified conceptual framework. Hydrogeol. J. 21, 1531–1537. doi:10.1007/s10040-013-1027-7

CrossRef Full Text | Google Scholar

Doherty, J., and Welter, D. (2010). A short exploration of structural noise. Water Resour. Res. 46. doi:10.1029/2009WR008377

Pubmed Abstract | CrossRef Full Text | Google Scholar

Enzenhoefer, R., Bunk, T., and Nowak, W. (2014). Nine steps to risk-informed wellhead protection and management: a case study. Groundwater 52, 161–174. doi:10.1111/gwat.12161

Pubmed Abstract | CrossRef Full Text | Google Scholar

Erdal, D., and Cirpka, O. A. (2016). Joint inference of groundwater-recharge and hydraulic-conductivity fields from head data using the ensemble kalman filter. Hydrol. Earth Syst. Sci. 20, 555–569. doi:10.5194/hess-20-555-2016

CrossRef Full Text | Google Scholar

Ferré, T. P. A. (2017). Revisiting the relationship between data, models, and decision-making. Groundwater 55, 604–614. doi:10.1111/gwat.12574

Pubmed Abstract | CrossRef Full Text | Google Scholar

Fienen, M. N., Doherty, J. E., Hunt, R. J., and Reeves, H. W. (2010). Scientific Investigations Report 2010-5159. Using prediction uncertainty analysis to design hydrologic monitoring networks: example applications from the Great Lakes water availability pilot project. U.S. Geological Survey.

Google Scholar

Freeze, R. A., Massmann, J., Smith, L., Sperling, T., and James, B. (1990). Hydrogeological decision analysis: 1. a framework. Groundwater 28, 738–766. doi:10.1111/j.1745-6584.1990.tb01989.x

CrossRef Full Text | Google Scholar

Gosses, M., and Wöhling, T. (2019). Simplification error analysis for groundwater predictions with reduced order models. Adv. Water Resour. 125, 41–56. doi:10.1016/j.advwatres.2019.01.006

CrossRef Full Text | Google Scholar

Gupta, H. V., Beven, K. J., and Wagener, T. (2006). Model calibration and uncertainty estimation. Atlanta, GA: American Cancer Society, Chap. 131. doi:10.1002/0470848944.hsa138

CrossRef Full Text | Google Scholar

Guthke, A. (2017). Defensible model complexity: a call for data-based and goal-oriented model choice. Groundwater 55, 646–650. doi:10.1111/gwat.12554

Pubmed Abstract | CrossRef Full Text | Google Scholar

Gyopari, M., and McAlister, D. (2010a). Wairarapa Valley groundwater resource investigation: Middle Valley catchment hydrogeology and modelling. Technical Publication GW/EMI-T-10/73. Greater Wellington Regional Council.

Google Scholar

Gyopari, M., and McAlister, D. (2010b). Wairarapa Valley groundwater resource investigation: upper Valley catchment hydrogeology and modelling. Technical Publication GW/EMI-T-10/74. Greater Wellington Regional Council.

Google Scholar

Hunt, R. J., Doherty, J., and Tonkin, M. J. (2007). Are models too simple? Arguments for increased parameterization. Ground Water 45, 254–262. doi:10.1111/j.1745-6584.2007.00316.x

Pubmed Abstract | CrossRef Full Text | Google Scholar

Knowling, M. J., and Werner, A. D. (2016). Estimability of recharge through groundwater model calibration: insights from a field-scale steady-state example. J. Hydrol. 540, 973–987. doi:10.1016/j.jhydrol.2016.07.003

Pubmed Abstract | CrossRef Full Text | Google Scholar

Knowling, M. J., White, J. T., Moore, C. R., Rakowski, P., and Hayley, K. (2020). On the assimilation of environmental tracer observations for model-based decision support. Hydrol. Earth Syst. Sci. 24, 1677–1689. doi:10.5194/hess-24-1677-2020

CrossRef Full Text | Google Scholar

Knowling, M. J., White, J. T., and Moore, C. R. (2019). Role of model parameterization in risk-based decision support: an empirical exploration. Adv. Water Resour. 128, 59–73. doi:10.1016/j.advwatres.2019.04.010

CrossRef Full Text | Google Scholar

Kunstmann, H., Kinzelbach, W., and Siegfried, T. (2002). Conditional first-order second-moment method and its application to the quantification of uncertainty in groundwater modeling. Water Resour. Res. 38, 6–1–6–14. doi:10.1029/2000WR000022

CrossRef Full Text | Google Scholar

McKenna, S. A., Akhriev, A., Echeverría Ciaurri, D., and Zhuk, S. (2020). Efficient uncertainty quantification of reservoir properties for parameter estimation and production forecasting. Math. Geosci. 52, 233–251. doi:10.1007/s11004-019-09810-y

CrossRef Full Text | Google Scholar

Ministry of Health (2018). Tech. Rep. Drinking-water standards for New Zealand 2005 (revised 2018). New Zealand Ministry of Health.

Google Scholar

Moore, C., and Doherty, J. (2005). Role of the calibration process in reducing model predictive error. Water Resour. Res. 41. doi:10.1029/2004WR003501

CrossRef Full Text | Google Scholar

Moore, C., and Doherty, J. (2006). The cost of uniqueness in groundwater model calibration. Adv. Water Resour. 29, 605–623. doi:10.1016/j.advwatres.2005.07.003

CrossRef Full Text | Google Scholar

Moore, C., Gyopari, M., Toews, M., and Mzila, D. (2017). Consultancy Report 2016/162. Ruamāhanga catchment groundwater modelling. GNS Science.

Google Scholar

Niswonger, R. G., Panday, S., and Ibaraki, M. (2011). “MODFLOW-NWT, a Newton formulation for MODFLOW-2005,” in Techniques and Methods. (Reston, VA: U.S. Geological Survey), Vol. 6, book section 37.

Google Scholar

Niswonger, R., and Prudic, D. (2005). Report, U.S. Geological Survey Techniques and Methods. Documentation of the Streamflow-Routing (SFR2) Package to include unsaturated flow beneath streams―a modification to SFR1.

CrossRef Full Text | Google Scholar

Nott, D. J., Wang, X., Evans, M., and Englert, B.-G. (2016). Tech. Rep. Checking for prior-data conflict using prior to posterior divergences.

Google Scholar

Oliver, D. S., and Alfonzo, M. (2018). Calibration of imperfect models to biased observations. Comput. Geosci. 22, 145–161. doi:10.1007/s10596-017-9678-4

Pubmed Abstract | CrossRef Full Text | Google Scholar

Sanford, W. (2011). Calibration of models using groundwater age. Hydrogeol. J. 19, 13–16. doi:10.1007/s10040-010-0637-6

CrossRef Full Text | Google Scholar

Sepúlveda, N., and Doherty, J. (2015). Uncertainty analysis of a groundwater flow model in east-central Florida. Groundwater 53, 464–474. doi:10.1111/gwat.12232

Pubmed Abstract | CrossRef Full Text | Google Scholar

Sundell, J., Haaf, E., Tornborg, J., and Rosén, L. (2019). Comprehensive risk assessment of groundwater drawdown induced subsidence. Stoch. Environ. Res. Risk Assess. 33, 427–449. doi:10.1007/s00477-018-01647-x

CrossRef Full Text | Google Scholar

Tarantola, A. (2005). “Inverse problem theory and methods for model parameter estimation.” in Other Titles in Applied Mathematics. (Philadelphia, PA: Society for Industrial and Applied Mathematics). doi:10.1137/1.9780898717921

CrossRef Full Text | Google Scholar

Vasco, D. W., Datta-Gupta, A., and Long, J. C. S. (1997). Resolution and uncertainty in hydrologic characterization. Water Resour. Res. 33, 379–397. doi:10.1029/96WR03301

CrossRef Full Text | Google Scholar

Vasco, D. W., Peterson, J. E., Majer, E. L., and Majer, E. L. (1998). Resolving seismic anisotropy: sparse matrix methods for geophysical inverse problems. Geophysics 63, 970–983. doi:10.1190/1.1444408

CrossRef Full Text | Google Scholar

Vrugt, J. A. (2016). Markov chain Monte Carlo simulation using the dream software package: theory, concepts, and matlab implementation. Environ. Model. Software 75, 273–316. doi:10.1016/j.envsoft.2015.08.013

CrossRef Full Text | Google Scholar

Watson, T. A., Doherty, J. E., and Christensen, S. (2013). Parameter and predictive outcomes of model simplification. Water Resour. Res. 49, 3952–3977. doi:10.1002/wrcr.20145

CrossRef Full Text | Google Scholar

Welter, D. E., White, J. T., Hunt, R. J., and Doherty, J. E. (2015). Report 7-C12. Approaches in highly parameterized inversion-PEST++ version 3, a parameter ESTimation and uncertainty analysis software suite optimized for large environmental models.

CrossRef Full Text | Google Scholar

White, J. T. (2018). A model-independent iterative ensemble smoother for efficient history-matching and uncertainty quantification in very high dimensions. Environ. Model. Software 109, 191–201. doi:10.1016/j.envsoft.2018.06.009

CrossRef Full Text | Google Scholar

White, J. T., Doherty, J. E., and Hughes, J. D. (2014). Quantifying the predictive consequences of model error with linear subspace analysis. Water Resour. Res. 50, 1152–1173. doi:10.1002/2013WR014767

CrossRef Full Text | Google Scholar

White, J. T. (2017). Forecast first: an argument for groundwater modeling in reverse. Groundwater 55, 660–664. doi:10.1111/gwat.12558

Pubmed Abstract | CrossRef Full Text | Google Scholar

White, J. T., Foster, L. K., Fienen, M. N., Knowling, M. J., Hemmings, B., and Winterle, J. R. (2020a). Toward reproducible environmental modeling for decision support: a worked example. Front. Earth Sci. 8, 50. doi:10.3389/feart.2020.00050

CrossRef Full Text | Google Scholar

White, J. T., Knowling, M. J., and Moore, C. R. (2020b). Consequences of groundwater‐model vertical discretization in risk‐based decision‐making. Groundwater 58, 695–709. doi:10.1111/gwat.12957

Pubmed Abstract | CrossRef Full Text | Google Scholar