Quantifying Geodetic Mass Balance of the Northern and Southern Patagonian Icefields Since 1976

Southern Andean glaciers contribute substantially to global sea-level rise. Unfortunately, mass balance estimates prior to 2000 are limited, hindering our understanding of the evolution of glacier mass changes over time. Elevation changes over 1976/1979 to 2000 derived from historical KH-9 Hexagon imagery and NASADEM provide the basis for geodetic mass balance estimates for subsets of the Northern Patagonian Icefield (NPI) and the Southern Patagonian Icefield (SPI), extending current mass balance observations by ∼20 years. Geodetic mass balances were −0.63 ± 0.03 m w.e. yr⁻¹ for 63% of the NPI and −0.33 ± 0.05 m w.e. yr⁻¹ for 52% of the SPI glacierized areas for this historical period. We also extend previous estimates temporally by 25% using NASADEM and ASTER elevation trends for the period 2000 to 2020, and find geodetic mass balances of −0.86 ± 0.03 m w.e. yr⁻¹ for 100% of the NPI and −1.23 ± 0.04 m w.e. yr⁻¹ for 97% of the SPI glacierized areas. 2000–2020 aggregations for the same areas represented in the 1976/1979 to 2000 estimates are −0.78 ± 0.03 m w.e. yr⁻¹ in the NPI and −0.80 ± 0.04 m w.e. yr⁻¹ on the SPI. The significant difference in SPI geodetic mass balance in the modern period for 100% vs. 52% of the glacierized area suggests subsampling leads to significant biases in regional mass balance estimates. When we compare the same areas in each time period, the results highlight an acceleration of ice loss by a factor of 1.2 on the NPI and 2.4 on the SPI in the 21st century as compared to the 1976/1979 to 2000 period. While lake-terminating glaciers show the most significant increase in mass loss rate from 1976/1979–2000 to 2000–2020, mass balance trends are highly variable within glaciers of all terminus environments, which suggests that individual glacier sensitivity to climate change is dependent on a multitude of morphological and climatological factors.

1 Introduction

In this study, we concentrate on the Northern and Southern Patagonian Icefields (NPI and SPI) and surrounding mountain glaciers (Figure 1). The NPI and SPI of South America are the largest ice masses on the continent and in the Southern Hemisphere outside of Antarctica (Schaefer et al., 2015). Glaciers of the Southern Andes, a region dominated by Patagonian Icefields, are the second-largest mountain-glacier contributors to sea-level rise after Alaskan glaciers; however, uncertainties surrounding their mass budgets remain large (Hock et al., 2019). In addition, the NPI and SPI host several intriguing characteristics and phenomena of interest to the scientific community, which previous studies highlight well: many glaciers interact with lakes and fjords at their termini; the San Rafael Glacier in the NPI is the closest marine-terminating glacier to the equator on Earth (Willis et al., 2012a); HPS-12, a small tidewater glacier of the SPI, has alarmingly high thinning rates (−44 m yr⁻¹ in the 21st century (Dussaillant et al., 2019); Pio XI, a large tidewater glacier on the SPI, has anomalously positive mass balance (Rivera et al., 1997; Wilson et al., 2016); glaciers also span from sea level to several thousand meters above sea level (Dussaillant et al., 2019). These myriad factors contribute to the NPI and SPI being ideal targets for assessing spatial and temporal variability in glacier mass changes over time.

FIGURE 1

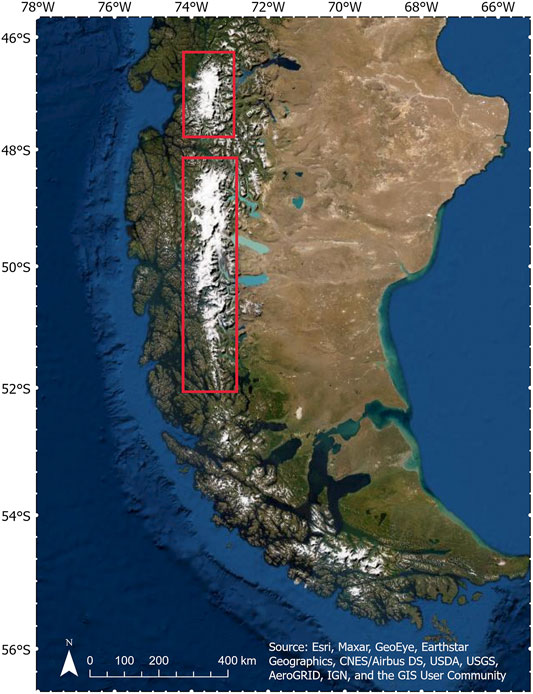
FIGURE 1. Study area. Red boxes indicate the Northern Patagonian Icefield (NPI) and the Southern Patagonian Icefield (SPI).

Observations and model-based studies highlight important changes in the ice fields over the past 40 years. For example, Glasser et al. (2016) found that eastern NPI glaciers experienced a high increase in debris-covered area from 1987–2015. Changes in debris cover often indicate shifts in glacier mass balance and ice flux dynamics. Koppes et al. (2011) used various climatological data in addition to observations of thickness and positional changes over 1950–2005 to quantify fluctuations in the mass balance of San Rafael Glacier. The results show that marine-terminating glaciers are influenced by both morphological and climatological drivers of mass change. Observations over a larger number of marine-terminating glaciers and over longer periods could provide critical information on these complex relationships. Minowa et al. (2021) focus on filling in some of these gaps by estimating frontal ablation from a combination of observations and models for the two icefields. They found that the frontal ablation for lake- and marine-terminating glaciers was −24.1 ± 1.7 Gt yr⁻¹ for the two icefields over 2000–2019, accounting for nearly one half of the total ablation in the SPI, but only 20% of the ablation in the NPI. These results again highlight the importance of mass loss processes of glaciers of differing terminus conditions. Modeling studies also illustrate the spatial heterogeneity in surface mass balance across the ice fields. For example, Schaefer et al. (2013) model surface mass balance for the NPI from 1970–2080. They find increasing accumulation later in the historical period, but an increase in ablation by 2050. Schaefer et al. (2015) model the surface mass balance for the SPI from 1975–2011 and find positive mass balance over the SPI. Bravo et al. (2019) also modeled surface mass balance, as well as equilibrium-line altitudes, and compared results over 1976–2050 for the icefields under different climate scenarios. The model results show significant differences in mass balance between the two ice fields, with the NPI showing a negative mass balance and, similar to the Schaefer et al. (2015) study, a positive mass balance over the SPI in response to climate forcing. Together, these results all point to the significant changes in glaciers occurring across the icefields. Spatially complete data is critical to better identifying the magnitude and variance in these changes.

Geodetic mass balance observations are often used to help fill spatial gaps in mass balance data, and provide opportunities to assess model results and statistical evaluations of spatial patterns in glacier mass changes. Many recent studies (Willis et al., 2012a; Willis et al., 2012b; Dussaillant et al., 2018; Malz et al., 2018; Abdel Jaber et al., 2019; Braun et al., 2019; Dussaillant et al., 2019; Cirací et al., 2020; Hugonnet et al., 2021) have quantified geodetic mass balance for the Patagonia region for the 21st century and explored the spatial heterogeneity across the icefields. The global studies (Cirací et al., 2020; Hugonnet et al., 2021) found the Southern Andes to have the highest rate of mass loss after the Canadian Arctic, Alaska, and High-Mountain Asia. These observations generally show regional mass losses, including for land-terminating glaciers over both the NPI and SPI regions, which contrasts with some modeling studies showing increasing surface mass balance over the SPI (e.g., Schaefer et al., 2015; Bravo et al., 2019). However, since these studies are limited to the past 20 years, it is difficult to attribute the negative geodetic mass balance to changes in climate occurring at longer timescales or assess how persistent these mass loss trends are regionally and for differing glacier types.

Historical imagery and photogrammetric techniques have been utilized by many recent studies to extend the record of glacier geodetic mass balance before 2000 (Pieczonka et al., 2013; Holzer et al., 2015; Pellicciotti et al., 2015; Pieczonka and Bolch, 2015; Maurer et al., 2016; Lamsal et al., 2017; Zhou et al., 2018; Belart et al., 2019; King et al., 2019; Maurer et al., 2019; Dehecq et al., 2020; King et al., 2020; Bhattacharya et al., 2021). One study has generated historical photogrammetric DEMs over three Patagonian glaciers from archived imagery (Falaschi et al., 2019). The authors found negative geodetic mass balance since 1958 for these three glaciers in the Monte San Lorenzo region, near the icefields. This study covers a small spatial extent but provides regional context for the historical geodetic mass balance of the icefields. The authors found that while the mass balance of these glaciers has remained negative, one has become less negative since 1958, one has become consistently more negative, and one has alternated between relative rates of mass loss. Another study quantified 1968/1975–2000 volume change for 63 of the largest glaciers in the icefields using differences in historical cartography and SRTM and found that they contributed 0.042 ± 0.002 mm yr⁻¹ to sea-level rise during this period (Rignot et al., 2003). This study highlights the importance of quantifying ice loss before 2000; however, it lacks geodetic mass balance measurements for individual glaciers and has large uncertainties in elevation estimates (Falaschi et al., 2019).

We focus on reconstructing a longer and spatially distinct record of mass balance observations to further assess spatial and temporal variability in mass balance trends on timescales more relevant to climate trends and glacier dynamics. Herein, we build on previous work by calculating the geodetic mass balance of 275 Patagonian glaciers for 1976/1979–2000 utilizing historical DEMs generated with the Hexagon Imagery Automated Imagery Pipeline (HEXIMAP) (Maurer and Rupper, 2015). This extends the use of HEXIMAP, originally developed for Himalayan mountain glaciers, to large ice-covered areas. We analyze only glaciers with an area of 3 km² or greater, as glaciers smaller than this do not typically have enough data coverage for successful geodetic mass balance calculation (Maurer et al., 2019). In addition, we calculate the geodetic mass balance for 2000–2020 to extend previous estimates to the present and to validate the methodology used for the historical time period.

2 Materials and Methods

2.1 Data Acquisition and Image Processing

Declassified KH-9 Hexagon imagery is utilized for historical DEM generation since global DEMs are not readily available before 2000 (U.S. Geological Survey, 2002). KH-9, or Keyhole Hexagon imagery, was part of a military intelligence satellite mission in operation from 1971–1980 (U.S. Geological Survey, 2008). The United States government declassified these images in 2002 without their corresponding metadata, and therefore the raw images are not georeferenced. Hexagon DEMs are extracted, georeferenced, and co-registered to a reference Copernicus DEM (CopDEM) using HEXIMAP (Maurer and Rupper, 2015).

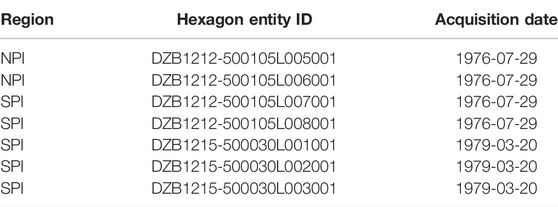
This historical DEM extraction method is described in detail in Maurer and Rupper (2015) and updated in Maurer et al. (2019). Briefly here, HEXIMAP utilizes traditional photogrammetry and structure-from-motion (SfM), removing the need for the manual selection of ground control points. It utilizes the OpenCV library FLANN (Fast Library for Approximate Nearest Neighbors) for stereo rectification and the SGBM (semi-global block-matching) algorithm for disparity map generation. We download raw Hexagon imagery from USGS Earth Explorer at approximately 6–9 m spatial resolution (Figure 2A; Table 1) and the CopDEM from ESA’s Planetary Data Access tool (PANDA) at 30 m resolution (European Space Agency, 2020). The HEXIMAP pipeline resamples the Hexagon DEM to the CopDEM resolution with linear interpolation to allow for elevation change analysis at the pixel scale. The final extracted Hexagon DEMs are in Figures 2B,C.

FIGURE 2

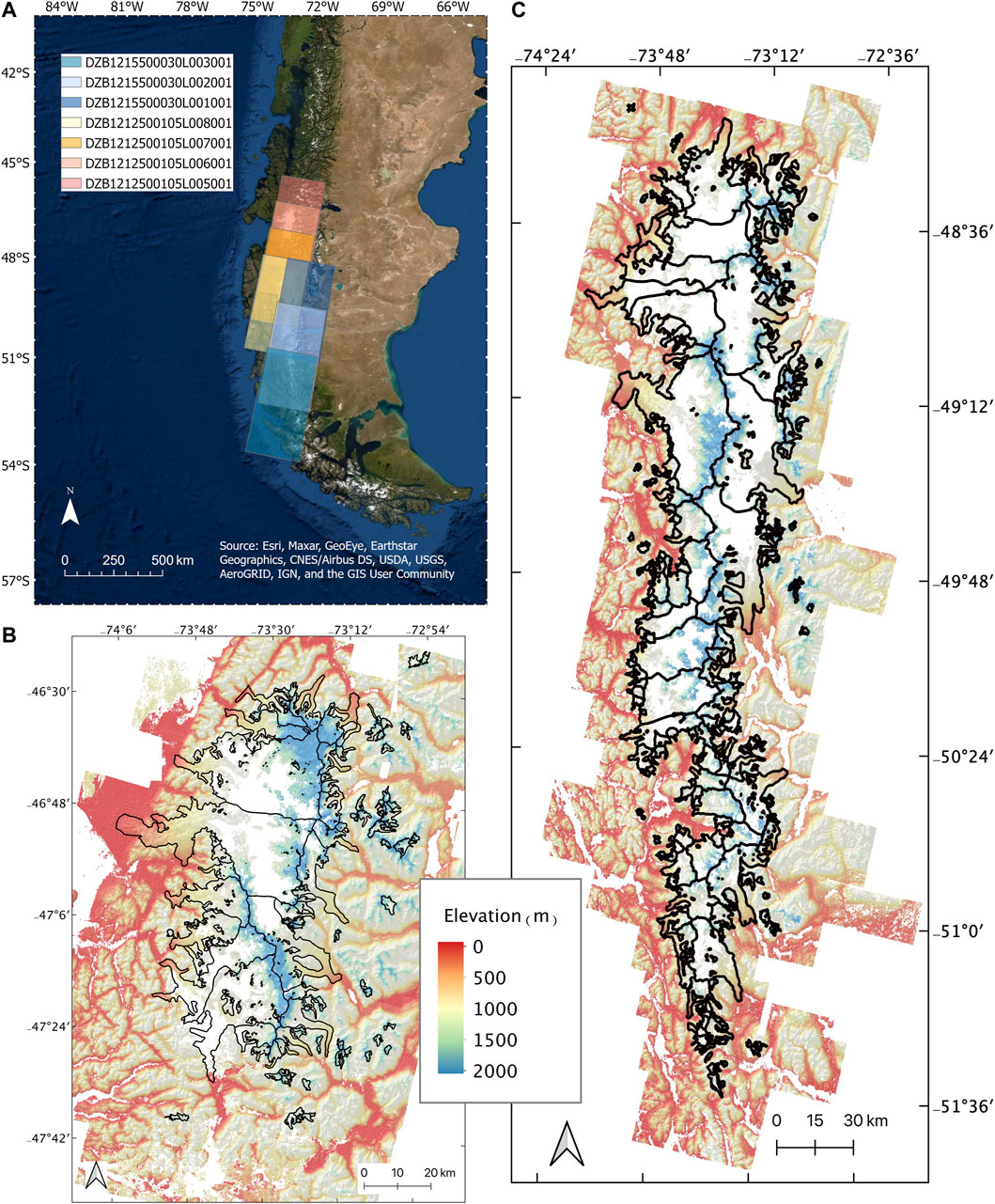
FIGURE 2. (A) Hexagon DEM footprints; (B) Hexagon DEM generated for the NPI (1976); (C) Hexagon DEM generated for the SPI (1976/1979). Polygons represent the historical extents of glaciers, and white areas are no data.

TABLE 1

TABLE 1. Entity IDs of downloaded hexagon imagery.

We utilize Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) DEMs, launched on NASA’s Terra satellite in 1999, for the modern DEMs (NASA JPL, 2004; NASA, METI, AIST, 2019). We download all ASTER DEMs (data1.l3a.demzs product) with acquisition dates 2000–2020 via METI AIST Data Archive System (MADAS) at 30 m spatial resolution. Maurer et al. (2019) provide detailed methods for processing the ASTER DEMs. To summarize here, ASTER DEMs are cleaned and co-registered to the CopDEM which includes the removal of pixels saturated in ASTER’s nadir band 3 (0.76–0.86 µm). The NASADEM is also used in the 2000–2020 elevation trend and is the modern (year 2000) timestamp for differencing with the Hexagon DEM. We download the NASADEM from NASA EarthData at 30 m resolution (NASA JPL, 2020). To co-register the NASADEM to the Copernicus DEM, we utilize an automated software that is based on the algorithm by Nuth and Kääb (2011) and Shean et al. (2016).

During co-registration to the CopDEM, a maximum elevation outlier threshold (E_t) is specified since outliers may still be present in the Hexagon, NASADEM, and ASTER DEMs, in part due to clouds (Eq. 1). We determined the elevation outlier threshold according to the estimated maximum elevation change (ΔE) expected over the glaciers (15 m yr⁻¹ for the NPI and 30 m yr⁻¹ for the SPI) (Dussaillant et al., 2018; Dussaillant et al., 2019) and the time difference between the specific DEM or DEM set and the CopDEM (Δt). As the CopDEM has a temporal range of 2010–2015, the maximum difference in temporal acquisition time is 15 years for the ASTER and NASADEM, and 39 years for the Hexagon DEM. For one glacier in the SPI, HPS-12, thinning rates of 44 m yr⁻¹ have been observed in the 21st century (Dussaillant et al., 2019); therefore, ASTER and NASADEM DEMs were co-registered to the CopDEM again according to this maximum expected elevation change. These DEMs were used in the elevation trend acquisition and geodetic mass balance estimate for 2000–2020 for HPS-12. We conservatively add an additional 5 m to this maximum elevation outlier threshold to account for the maximum expected CopDEM X-band penetration into snow/firn. Maximum penetration depth (δ_p) of X-band (10 GHz) into firn was measured as 4.7 m by Davis and Poznyak (1993) in Antarctica, where drier and colder conditions likely lead to higher penetration than we would see in Patagonia (Gardelle et al., 2012). NASADEM C-band penetration into snow/firn has been found negligible in the Patagonian Icefields (Dussaillant et al., 2018), however, we incorporate a conservative error term in the elevation change uncertainty, which is discussed in the Supplementary Material.

$E_t = \left(\Delta E \ast \Delta t\right) + \delta p(1)$

2.2 Elevation Change Maps

Subtracting the Hexagon DEM from the NASADEM provides an elevation difference over the glaciers in the historical time period. For the 2000–2020 time period, multitemporal ASTER DEM stacks, plus the NASADEM for the year 2000, provide an average elevation trend for the 20 years over each glacier. We use the Random Sample Consensus (RANSAC) trend fitting algorithm to determine the average elevation trend at the pixel-scale (Martinez-Camara et al., 2014; Maurer et al., 2019). RANSAC randomly selects two DEMs within the ASTER stack and fits a trend to the elevation, repeating for 250 iterations. The elevation trend with the least outliers and a standard deviation of less than 50 m was selected for each pixel. In the case where no trend with less than 50 m standard deviation was found for a given pixel, no elevation trend was calculated. We allowed a higher maximum standard deviation between 100 and 200 m for select glaciers due to calving fronts causing nonlinear behavior on their termini (Table 2; Supplementary Figure S2).

TABLE 2

TABLE 2. Geodetic mass balance sensitivity to maximum standard deviation allowed in 2000–2020 elevation trend. For HPS-12, DEMs were co-registered to the CopDEM using higher elevation outlier threshold than other glaciers (see Section 2.1).

In the SPI, many DEMs contained few valid pixels, typically due to persistent cloud cover. A filtering step selects only ASTER DEMs containing at least 10% valid pixels to increase the chances for RANSAC to select DEMs with valid pixels. For data coverage, see Supplementary Figure S3. To fill data gaps, elevation trend/change data is grouped into 50-m elevation bins. Bins with at least 100 pixels within a 2–98% quantile range are used to linearly interpolate gaps within glacier polygons (see the Supplementary Material for information on the error term associated with interpolating data gaps). If the highest and lowest elevation bins did not have at least 100 pixels, zero change was assumed. A 5 × 5-pixel median filter smooths the final elevation trend results and removes unrealistic slopes greater than 45° (Maurer et al., 2019).

2.3 Volume Change and Mass Change

For an individual glacier, multiplying all elevation change pixels by their pixel area converts them to pixel volume change. The sum of these volume change pixels represents the ice volume change for the glacier, which is divided by the average glacier area (the methods used to define the glacier area at each timestamp are provided in Section 2.5). We then multiply the glacier thickness change by 850 km m⁻³, the average ice-firn density (Huss, 2013). The resulting value is geodetic mass balance in meters of water equivalent per year (Maurer et al., 2019). Uncertainty associated with the chosen density value and error propagation for the geodetic mass balance calculation are discussed in Supplementary Section S1.3.

2.4 Regional Aggregations

The volume change rate for an entire region is the summation of individual glacier volume change rates. The volume change rate is converted to Gt yr⁻¹ by multiplying the volume change rate by the density conversion factor of 0.850 Gt/km³. This mass rate (Gt yr⁻¹) is then divided by 362.5 Mm², which is representative of the amount of water needed to raise the eustatic sea level by 1 mm (Cogley, 2012). In each geodetic mass balance aggregation (GMB_region, m w.e. yr⁻¹), the geodetic mass balance of each glacier in the region (GMB_i, m w.e. yr⁻¹) is multiplied by its area (A_i, km²), and all area-weighted mass balance values are summed together and divided by the total area of the aggregation (A_region, km²) (Eq. 2).

$GM{B}_{region}=\frac{{\Sigma }_{i=1}^n\left(GM{B}_i\ast A_i\right)}{A_{region}}(2)$

2.5 Glacier Inventories

Integrating elevation changes over the glacier area requires the average glacier area during each time interval. Thus, we require glacier polygons for the years 1976, 2000, and 2020. Polygons from the Randolph Glacier Inventory 6.0 (RGI 6.0) provide a glacier inventory baseline for each timestamp (Pfeffer et al., 2014; Randolph Glacier Inventory Consortium, 2017). RGI 6.0 can have significant uncertainties associated with them and they are not temporally distinct. Thus, we use the glacier inventories produced by Meier et al. (2018), Google Earth, and the following imagery to aid in the manual delineation of glacier extents. For the 1976 timestamp, we utilize Global Land Survey 1975 (GLS 1975) imagery and a preliminary elevation change map for the historical period. Several glaciers in the southeast SPI are not covered by GLS 1975, and therefore their 2000 outlines were utilized for the 1976 timestamp. We use cloud-free GLS 2000 imagery and summer 2018–2020 Landsat 8 imagery for 2000 and 2020 delineations, respectively.

2.6 Uncertainty

The uncertainty associated with glacier elevation and volume changes, regional geodetic mass balance, and subsequent conversions to Gigatons and millimeters of sea-level rise equivalent are provided in the Supplementary Equations S1–S5. Generally, the errors associated with individual glaciers follow the methodology presented in Maurer et al. (2019). For regional aggregations, the errors are propagated using summation in quadrature.

3 Results

3.1 Elevation Change

Figures 3A, 4A present elevation change over 1976–2000 for the NPI and 1976/1979–2000 for the SPI, respectively. Hatched glaciers have less than 50% valid data coverage. These data gaps tend to occur where elevation data could not be extracted due to low contrast and oversaturation in accumulation zones of the satellite photos (Maurer et al., 2019). Thinning rates increase during 2000–2020 for both the NPI and SPI (Figures 3C, 4C), although spatial patterns in thinning remain similar. For example, higher rates of elevation change generally occur on the glacier termini. For some glaciers, rapid thinning extends to higher elevations in the second time period (e.g., HPN-1, labeled in Figure 3C).

FIGURE 3

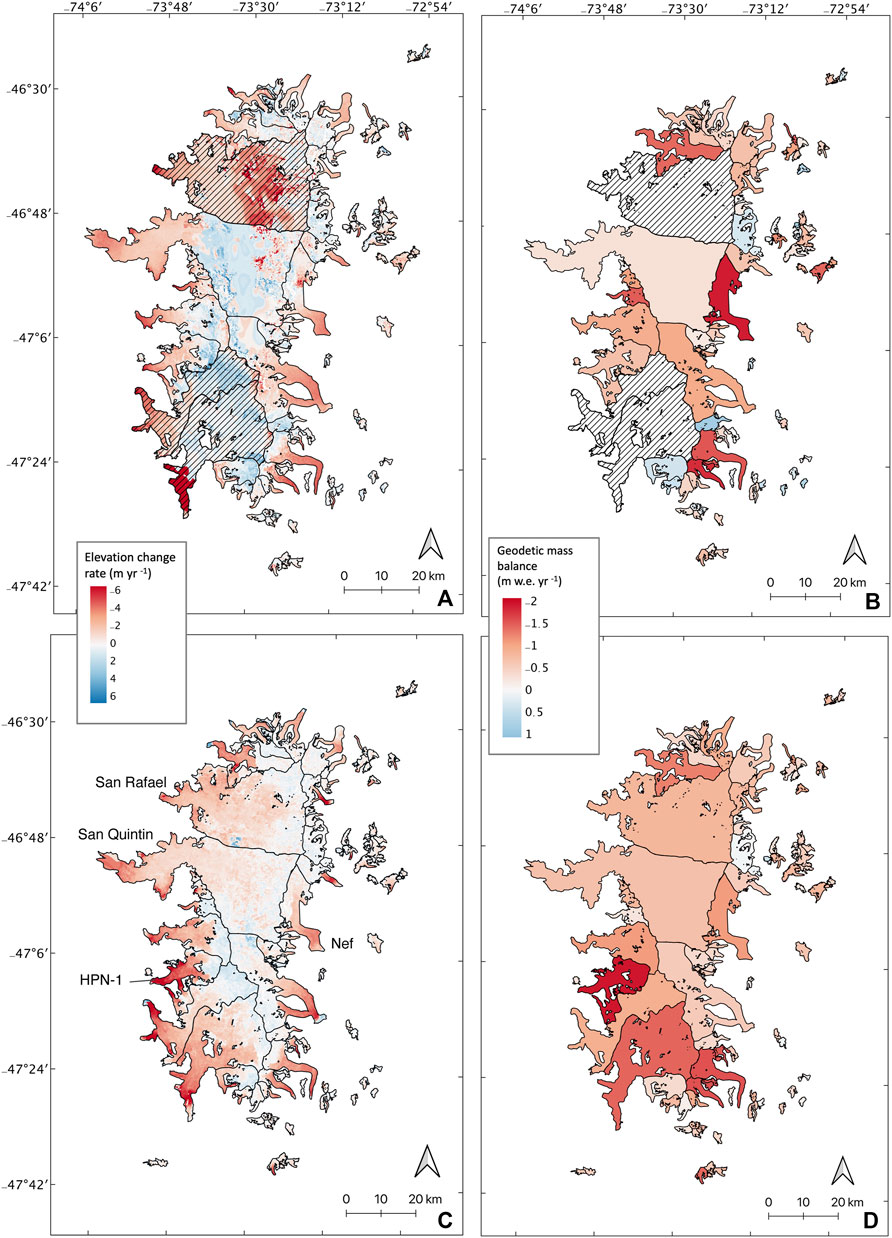
FIGURE 3. Elevation change observed on the NPI in (A) 1976–2000 and (C) 2000–2020. Hatched glaciers are those with less than 50% data coverage. This elevation change integrated over the glacier surfaces results in geodetic mass balance for (B) the historical period and (D) the modern period.

FIGURE 4

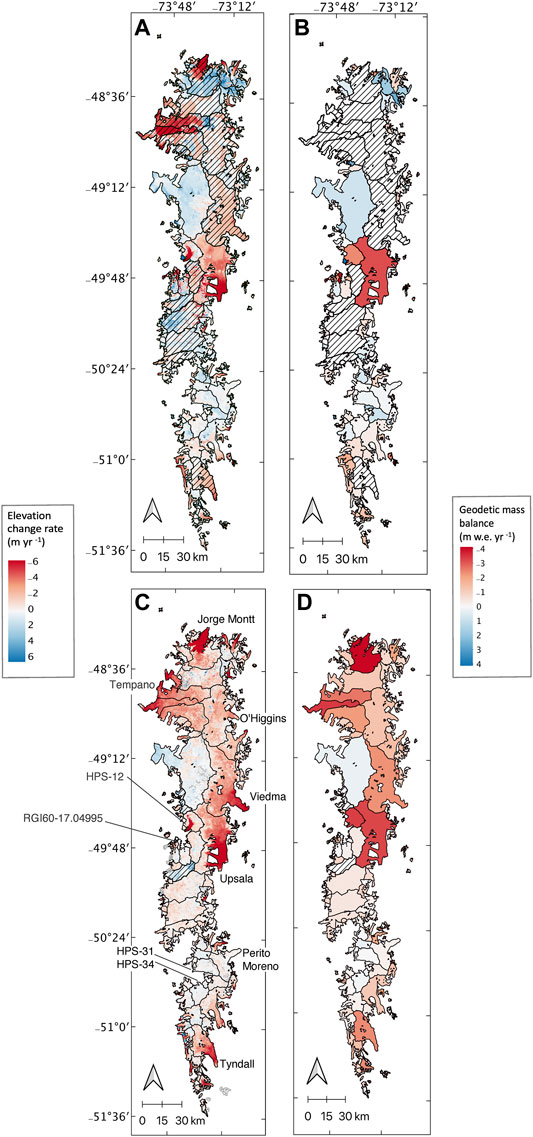
FIGURE 4. Elevation change observed on the SPI in (A) 1976/1979–2000 and (C) 2000–2020. Hatched glaciers are those with less than 50% data coverage. Glacier outlines are representative of their 2000 extent. Glaciers shaded gray in (C) have no geodetic mass balance estimate. This elevation change integrated over the glacier surfaces results in geodetic mass balance for (B) the historical period and (D) the modern period. The geodetic mass balance color range presented does not represent the full range of data. To see all data points for the icefields, see Supplementary Figures S4, S5.

3.2 Geodetic Mass Balance

Choropleth maps (Figures 3B,D, 4B,D) show how elevation change is translated to geodetic mass balance for individual glaciers. The NPI and SPI area-weighted geodetic mass balance averages for the icefields are provided in Table 3. The area-weighted average only includes glaciers with at least 50% data coverage. Both NPI and SPI show negative mass balance trends for the modern period, albeit the SPI is significantly more negative (−1.23 ± 0.04 m w.e. yr⁻¹) as compared to the NPI (−0.86 ± 0.03 m w.e. yr⁻¹). Section 4.6 discusses a comparison to previous studies.

TABLE 3

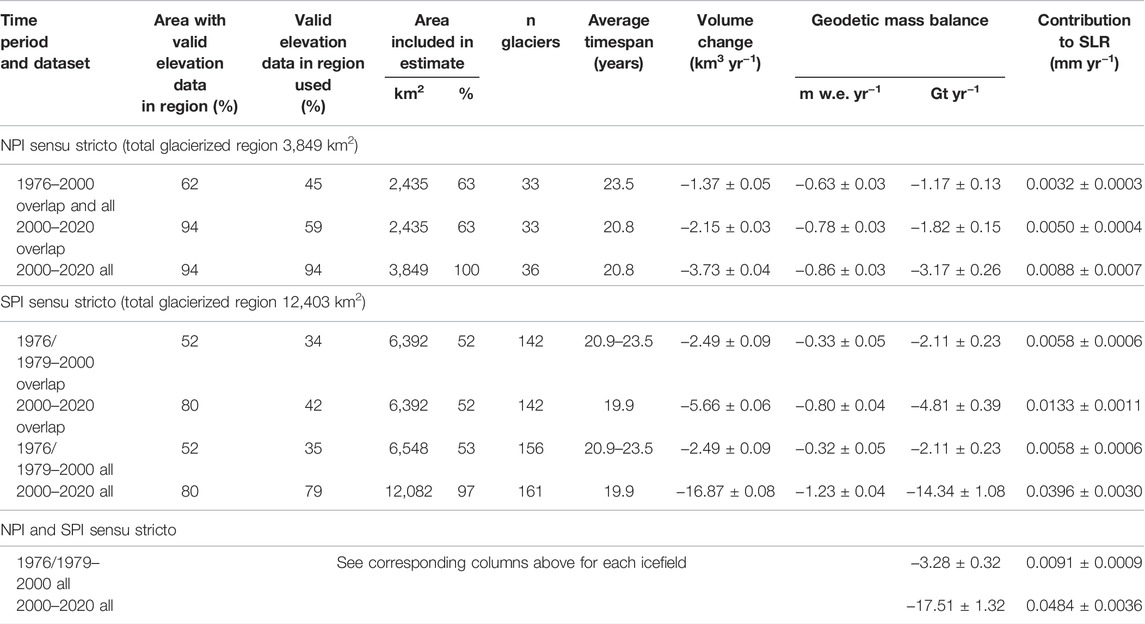
TABLE 3. Area-weighted geodetic mass balance of the icefields. Total glacierized area is calculated from year 2000 glacier outlines. “Area with valid elevation data in region” corresponds to percent of the total glacierized region which has valid elevation data (includes all glaciers, not only those that have more than 50% valid data). “Valid elevation data used” corresponds to the valid data (of the entire region) that is utilized in the aggregation (i.e., the data that was within glaciers with at least 50% data coverage). “Area included in the estimate” is the total area (data plus interpolated area) included in the aggregation for the geodetic mass balance estimate with respect to the total glacierized area, including only glaciers that had at least 50% valid elevation data. For example, 63% in the first column represents the unhatched glaciers on the icefield (which all include some interpolation) in Figure 3A. “Number of glaciers included in the estimate” are those that had at least 50% valid elevation data before interpolation.

There is less coverage for the historical period, but we can compare trends across both time periods for 33 NPI glaciers and 142 SPI glaciers. 33 glaciers on the NPI are equivalent to 63% of the NPI glacierized area and 142 glaciers on the SPI are equivalent to 52% of the SPI glacierized area (Table 3). For the NPI, the 2000–2020 geodetic mass balance of 100% of the area (−0.86 ± 0.03 m w.e. yr⁻¹, 2000–2020 all in Table 3) is similar to that of 63% of the ice field (−0.78 ± 0.03 m w.e. yr⁻¹, 2000–2020 overlap). Conversely, for the SPI, the estimated mass balance for the 2000–2020 period is reduced significantly (−1.23 ± 0.04 m w.e. yr⁻¹ versus -0.80 ± 0.04 m w.e. yr⁻¹) when only utilizing the region of overlapping data (97% vs. 52% areal coverage). This suggests that having data for 63% of the glacierized area is sufficient to capture the regional trend for the NPI, and 52% is not sufficient enough to capture the regional trend for the SPI. Only including glaciers in the icefields with coverage in both periods, geodetic mass balance decreased by 0.15 m w.e. yr⁻¹ from 1976–2000 to 2000–2020 in the NPI, equivalent to a mass loss rate increasing by a factor of 1.2. In the SPI, the geodetic mass balance decreased by 0.47 m w.e. yr⁻¹ and by a factor of 2.4.

3.3 Spatial Variability

While geodetic mass balance on average is negative for the icefields, geodetic mass balances are spatially heterogeneous across the region. In the SPI, Pio XI experiences a positive change while highly negative change is observed on HPS-12, and Perito Moreno experiences little mass change over time. Table 4 presents the average geodetic mass balance for glaciers of each terminus type (including only the icefields). In the overlap aggregations for each terminus type, land-, lake-, and marine-terminating glaciers have similar average geodetic mass balances in the historical time period. In the modern period, lake-terminating glaciers have the most negative geodetic mass balance, while land-terminating glaciers also become more negative. Averages for marine-terminating glaciers are misleading, as they are skewed by a few highly-negative glaciers (Figure 5; Supplementary Figure S4). In Figures 5A,C, geodetic mass balance is plotted against latitude for glaciers that have estimates in each time period. For these 175 glaciers, 64% had a negative geodetic mass balance in the historical period. This percentage increased to 87% in the modern period.

TABLE 4

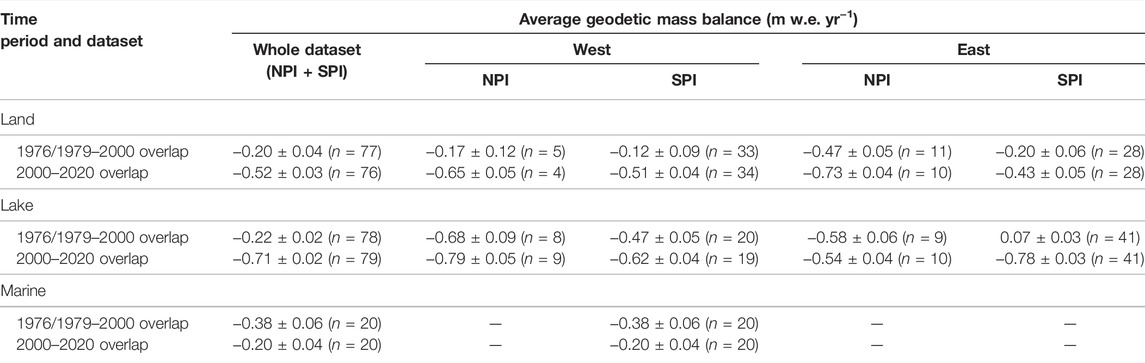
TABLE 4. Geodetic mass balance averages (not area-weighted) for NPI and SPI glacier aggregations described by terminus type and location relative to the ice divide.

FIGURE 5

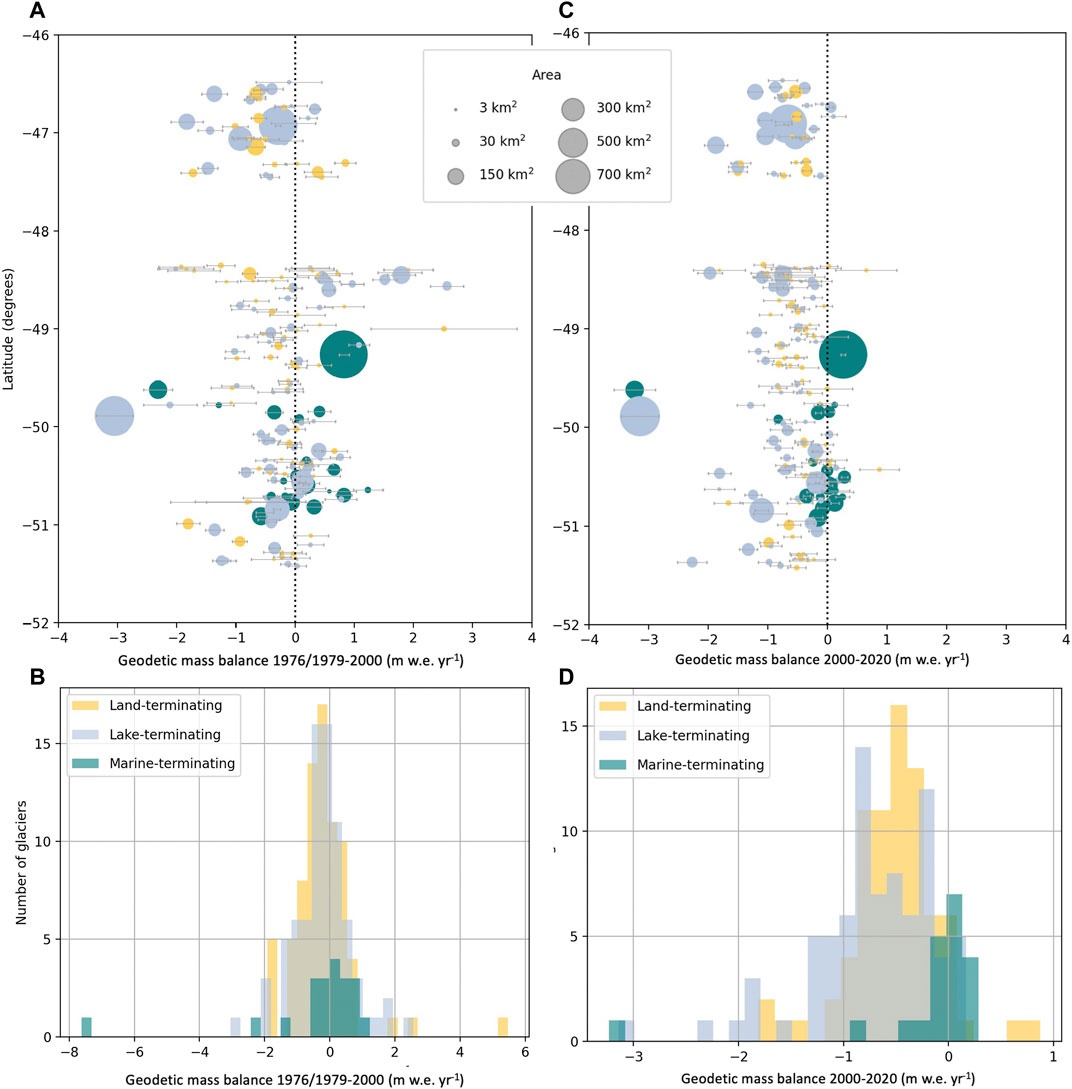
FIGURE 5. Geodetic mass balance plotted with latitude for (A) the historical time period (1976–2000 overlap and 1976/1979–2000 overlap in Table 3), clipped to −4 to +4 m w.e. yr⁻¹ to show the spread around 0 m w.e. yr⁻¹; and (C) the modern time period (2000–2020 overlap in Table 3). Histograms for (B) 1976/1979–2000 and (D) 2000–2020 show the distribution of geodetic mass balance according to glacier terminus type. Panel (B) extends the 1976/1979–2000 results to show all glaciers with data in both time periods.

Histograms (Figures 5B,D) display the mass balance distributions for each terminus type. The histogram for the historical time period (Figure 5B) shows the distribution is centered near 0 m w.e. yr⁻¹ for marine-terminating glaciers, while it is negative for the lake- and land-terminating glaciers. The histogram for the modern time period (Figure 5D) shows marine-terminating glaciers remained centered around 0 m w.e. yr⁻¹ while both land- and lake-terminating glaciers become more negative on average (lake-terminating slightly more so than land-terminating). The distributions are unique for the modern time period (Figure 5D), but are not statistically different for the historical period (Figure 5B), based on a Kruskal–Wallis One-Way ANOVA. A Mann-Whitney U Test on each of the contributions further reveals that all three distributions are statistically different at the 95% confidence interval in the modern time period. We do not repeat statistical tests for “all data” distributions shown in Supplementary Figure S4 (all rows in Table 3), but the overall patterns are the same when all glaciers with data are considered for each time period, rather than only those with data in both periods.

Figure 6A presents the geodetic mass balance of the historical time period subtracted from the modern measurement to visualize how mass change rates have evolved over time. Similar to the results of Falaschi et al. (2019), variation exists for individual glaciers. For the glaciers we can compare between the time periods, all (regardless of terminus type) have shifted more negatively in the 21st century (Figure 6B). A secondary histogram (Figure 6C) shows a handful of glaciers that have changed terminus type between the time periods. Although the sample size is small, those that formed proglacial lakes in the modern time period (blue bars) have become more negative, and those that receded from lakes (orange bars) become less negative.

FIGURE 6

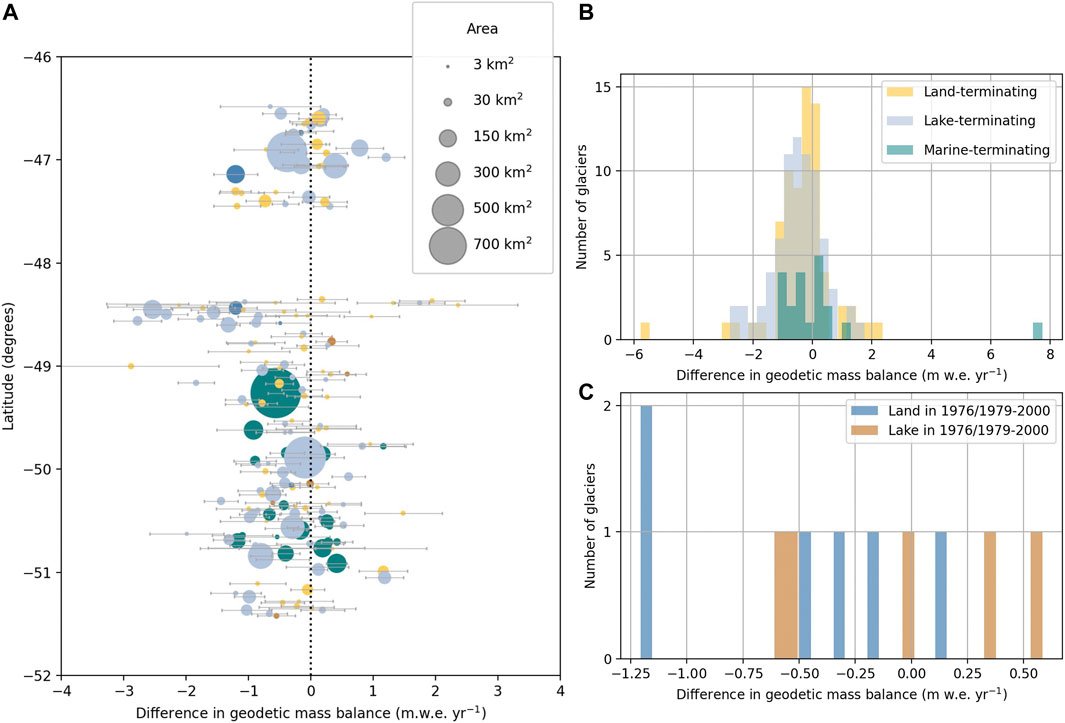
FIGURE 6. (A) Historical geodetic mass balance subtracted from the modern geodetic mass balance plotted with latitude, which is clipped to show the distribution around zero. Dotted line indicates where no change in geodetic mass balance occurs. (B,C) display the full range of geodetic mass balance change for different glacier terminus types.

To explore the potential effects of the orographic barrier on geodetic mass balance, we plotted glacier mass balance against longitude for both time periods (Figures 7A,D). Histograms for the historical period (Figures 7B,C) and modern period (Figures 7E,F) show distributions of western and eastern glaciers for each icefield. In the supplement we provide the same plots for all icefield glaciers that have an estimate in either time period (Supplementary Figure S5). We separate the icefields in the histograms in order to better evaluate the SPI mass balance trends. We focus on the SPI here as the NPI sample size is extremely small and previous work (e.g., Foresta et al., 2018; Abdel Jaber et al., 2019) has stated that spatial heterogeneity in elevation change is particularly apparent in the SPI. Indeed, we observe that SPI eastern, lake-terminating glaciers have undergone the most rapid thinning between 1976/1979–2000 and 2000–2020. In the SPI, east and west distributions appear similar in the historical period, but eastern SPI glaciers appear more negative than western SPI glaciers in the modern time period. We perform a Mann-Whitney U-Test for both time periods and find that the distributions of east versus west for the SPI are statistically different in the modern time period at the 95% confidence interval. Figure 8 displays the difference in geodetic mass balance between the time periods plotted with longitude, and reiterates this observed trend of divergence in the SPI. We do not draw conclusions from the NPI histograms or averages in Table 4 since the sample size is small; however, from the elevation change maps, we can see that western glaciers of the NPI have been retreating very rapidly (i.e., HPN-1 and nearby glaciers in Figure 3C).

FIGURE 7

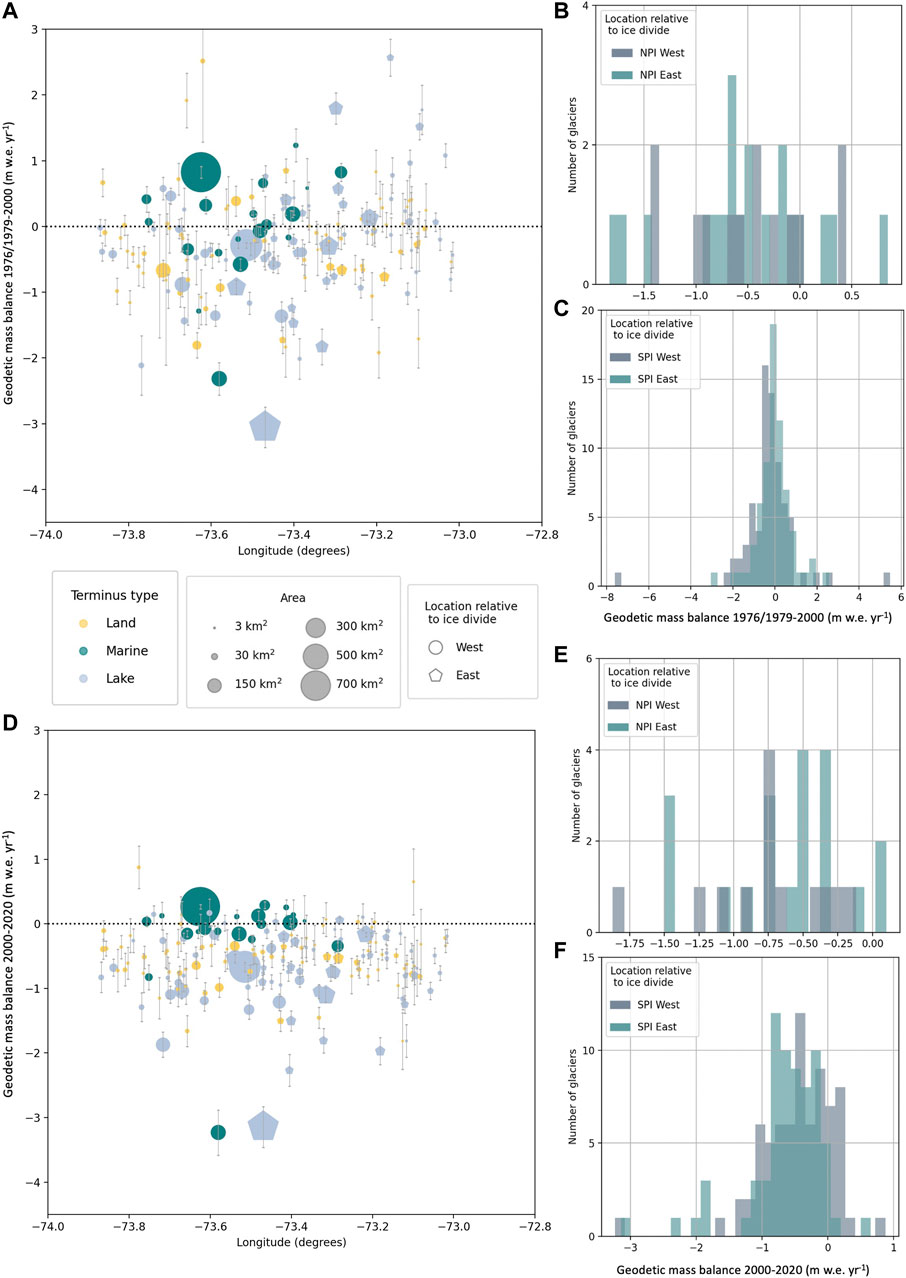
FIGURE 7. Geodetic mass balance plotted with longitude for (A) the historical time period (1976–2000 overlap and 1976/1979–2000 overlap in Table 3), clipped to −4 to +3 m w.e. yr⁻¹ to show the spread around 0 m w.e. yr⁻¹; and (D) the modern time period (2000–2020 overlap in Table 3). Histograms for 1976/1979–2000 (B,C) and 2000–2020 (E,F) show the distribution of geodetic mass balance according to glacier location east or west of the ice divide.

FIGURE 8

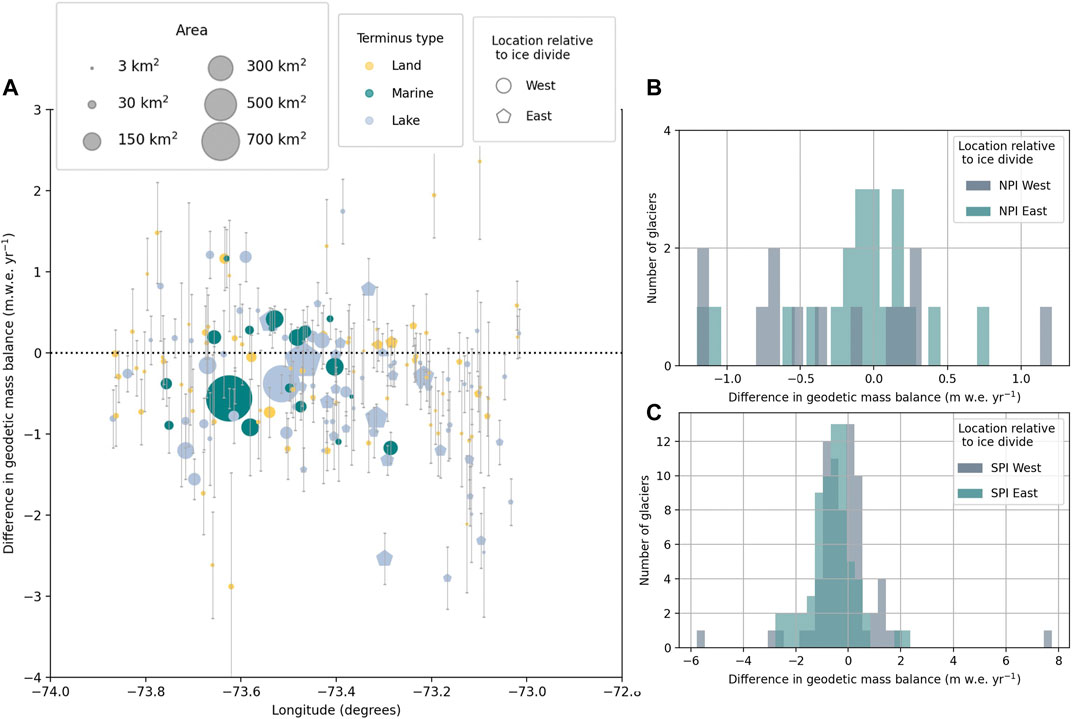
FIGURE 8. (A) Historical geodetic mass balance subtracted from the modern geodetic mass balance plotted with longitude, which is clipped to show the distribution around zero. Dotted line indicates where no change in geodetic mass balance occurs. (B) displays the full range distribution of geodetic mass balance change for NPI glaciers west and east of the ice divide. (C) is the same as (B), but for the SPI glaciers.

3.4 Sea-Level Rise Contributions

While we do not fill in missing glaciers with any regional average, we can estimate the amount of volume the measured glaciers have contributed to eustatic sea-level rise in each time period. Together, 100% of the NPI and 97% of the SPI have a mass change value of -17.51 ± 1.32 Gt yr⁻¹ and contribute 0.0484 ± 0.0036 mm yr⁻¹ to sea-level rise in 2000–2020 (Table 3). Dussaillant et al. (2019) estimate that the entire Andes contributed 0.06 ± 0.02 mm yr⁻¹ from 2000–2018, and cite this value as just over 10% of the glacier contributions across the globe 2002–2016 (Bamber et al., 2018). For 63% of the NPI in 1976–2000 and 53% of the SPI in 1976/1979–2000, the mass change rate was −3.28 ± 0.32 Gt yr⁻¹. These glaciers contributed 0.0091 ± 0.0009 mm yr⁻¹ from 1976/1979–2000. Although we cannot make a direct comparison to their study, Rignot et al. (2003) found the 63 largest glaciers contributed 0.042 ± 0.002 mm yr⁻¹ over 1968/1975–2000. Our estimate includes only those glaciers that are unhatched in Figures 3A, 4A, which are disproportionately smaller glaciers, and we do not extrapolate to the full region due to extreme heterogeneity observed in glaciers across the icefields for 2000–2020. This may contribute to the significant difference in our historical SLR estimates as compared to Rignot et al. (2003).

4 Discussion

4.1 Regional Trends in Geodetic Mass Balance and Climate Drivers

Mass loss rates increased by a factor of 1.2 for 63% of the NPI and 2.4 for 52% of the SPI over 1976/1979–2000 to 2000–2020, which likely indicates an acceleration of warming, a change in precipitation, or a change in glacier sensitivity to climate in the 21st century. Braun et al. (2019) show surface temperatures of South Patagonia have increased significantly over the period 1979–2017, according to climate reanalysis data and suggest warming as a mechanism for increased ablation. In their 2020 Global Climate Report, NOAA (2021) reported that in 2015–2020, South America had experienced the five warmest years on record. Additionally, some studies suggest that snow-covered mountainous regions are experiencing accelerated warming near the zero-degree isotherm due to the snow/ice-albedo feedback (Pepin and Lundquist, 2008; Rangwala and Miller, 2012; Pepin et al., 2015). Factors like this may enhance glacier melt as temperatures increase.

Due to sparse climatological observations, precipitation data is largely modeled for the region and the trend is less clear. Reanalysis data shows that no significant change in precipitation has occurred from 1960–1999 (Rasmussen et al., 2007) or 1979–2017 (Braun et al., 2019), which suggests changes in the amount of precipitation are not likely the dominant driver of mass loss in the region. However, reanalysis data is poorly informed at high elevations due to very sparse observations and coarse spatial resolutions (Lanaerts et al., 2014; Condom et al., 2020). For example, ERA-interim, used in the analysis by Braun et al. (2019), has a horizontal resolution of 80 km (Condom et al., 2020). The width of the NPI and SPI is more narrow than this horizontal resolution in some areas, and the icefields also experience an enormous precipitation gradient from west-east (exceeds 10 m w.e. yr⁻¹ on the west side and is near 1 m w.e. yr⁻¹ to the east) (Lanaerts et al., 2014). Lanaerts et al. (2014) addressed the coarseness of reanalysis products by downscaling ERA-interim to 5.5 km 1979–2012 and observed upward trending, yet insignificant, precipitation with large interannual variability. Downscaling of reanalysis products over the NPI by Schaefer et al. (2013) also found a slight increasing precipitation trend over the NPI from 1975–1990 to 1990–2011. Although the overall precipitation trend is unclear, increased temperatures may cause a change in the state of precipitation that does fall. In the 1960–1999 period, Rasmussen et al. (2007) quantified warming of 0.5°C over the icefields, which translates to 5% of solid precipitation changing to rain. This estimate is also derived from reanalysis data and may vary significantly according to longitude and altitude, but it provides an example of how warming temperatures may affect precipitation in the region.

Although the NPI and SPI are adjacent to each other, they have slightly differing climates. According to a cluster analysis done by Sagredo and Lowell (2012), the NPI receives most precipitation during the winter months, and the SPI receives constant precipitation throughout the year, including more summer precipitation. This difference in climate could result in the SPI having different sensitivity to changes in temperature and precipitation than the NPI. In particular, glaciers that receive significant summer accumulation are much more sensitive to changes in temperature through surface albedo feedbacks (e.g., Johnson and Rupper, 2020). While somewhat speculative, the precipitation seasonality difference between NPI and SPI may point to one mechanism giving rise to SPI losing mass faster than NPI.

While there are large-scale shifts in mass balance across the region that are likely explained by shifts in climate (e.g., differences in average mass balance between SPI and NPI, differences in average mass balance over time), mass balance changes are spatially heterogeneous within these regions. This spatial heterogeneity is likely driven by variable topographic settings, glacier morphology, and terminus conditions that modulate the individual glacier response to regional-scale climate perturbations.

4.2 Spatial Patterns in Geodetic Mass Balance

4.2.1 Terminus Environment

Geodetic mass balance does not distinguish between mass balance processes. For example, we do not distinguish mass loss due to increased surface melt, calving, or subaqueous melt. However, these processes vary significantly between lake, marine, and land-terminating glaciers. We find lake-terminating glaciers to have the most negative geodetic mass balance in the modern time period. This group of glaciers also has the greatest magnitude of change in their average geodetic mass balance between the two time periods (Table 4). Increased retreat for lake-terminating glaciers in the NPI has been attributed to glacial lake development and expansion in other studies (Loriaux and Casassa, 2013; Glasser, 2016). This result also agrees with Falaschi et al. (2019), who found the highest thinning rates among lake-terminating glaciers from 2000–2012 on the eastern flanks of the SPI and in mountain ranges directly east of the icefields. Additionally, our results compare favorably with studies from other regions in the world: Maurer et al. (2019), Sutherland et al. (2020), and Larsen et al. (2007) highlight the phenomenon that lake-terminating glaciers in the Himalayas, New Zealand, and Alaska lose mass faster than land-terminating glaciers due to proglacial lake-enhanced frontal ablation. In our “overlap” aggregations, about half of NPI glaciers are calving. For the SPI, more than half of the glaciers measured are calving, which may be a driver for more negative regional mass balance in the SPI. Modeling studies in the region also support the idea that frontal ablation accounts for a disproportionate amount of mass loss in the icefields. Schaefer et al. (2013) modeled surface mass balance for the NPI and quantified a doubling of calving activity from 1975–2000 to 2000–2009, indicating an acceleration of mass loss from frontal ablation mechanisms over time. Schaefer et al. (2015) used similar methodology for the SPI and found that calving losses also increased for the SPI from 1975–2000 to 2000–2011, and that calving influences more mass loss than melt. Both Bravo et al. (2019) and Schaefer et al. (2015) modeled positive surface mass balance over the SPI (1975–2040 and 1975–2011, respectively), and suggested that mass losses from frontal ablation dominate the observed highly negative geodetic mass balance signal. While these modeling studies do not distinguish between lake- and marine-terminating glaciers, they do illustrate the importance of ablation mechanisms that occur at the ice-water interface.

A notable observation from the geodetic mass balance results is that marine-terminating glaciers have the most variability in mass changes. While several marine-terminating glaciers experience the highest rates of mass loss, many have small magnitudes of mass change or are slightly positive (Figure 5). Subaqueous melt, frontal calving, and sedimentation, as well as surface processes, influence tidewater glaciers. Because of this, they can act anomalously when compared to their land-terminating and freshwater-calving counterparts and appear out of sync with regional climatic forces (Truffer and Motyka, 2016; Brinkerhoff et al., 2017). Long periods of advancement and rapid retreat characterize a tidewater glacier cycle (TGC) (McNabb and Hock, 2014). The period of advancement occurs when the glacier deposits eroded sediments in a proglacial shoal, limiting the glacier’s interaction with the ocean water (Motyka et al., 2006). Where the glacier becomes ungrounded from the shoal, it becomes exposed to deep water and associated calving and thermal undercutting processes, resulting in rapid retreat uninfluenced by climate (although climate perturbations may exacerbate the retreat) (Meier and Post, 1987; Motyka et al., 2006; Brinkerhoff et al., 2017). Taku glacier in Alaska is a well-documented glacier currently undergoing advancements as part of the TGC (Motyka et al., 2006; McNeil et al., 2020). Over 1946–2018, McNeil et al. (2020) found that while Taku was steadily advancing, nearby land-terminating Lemon Creek has been retreating amidst the same regional climate. In our dataset, it is likely Pio XI is in the advancing stage of the TGC (its geodetic mass balance estimates are 0.82 ± 0.09 m w.e. yr⁻¹ in 1976–2000 and 0.26 ± 0.04 m w.e. yr⁻¹ in 2000–2020). Observations of rapid retreat at marine-terminating Columbia glacier in Alaska (Meier and Post, 1987; Pfeffer, 2007) provide insight as to the future of Pio XI. Enderlin et al. (2013) describe how the outlet valley geometry primarily influences the quality of retreat. Recent studies highlight the importance of studying the glacier dynamics and fjord bathymetry of Pio XI (Wilson et al., 2016; Hata and Sugiyama, 2021).

An unnamed tidewater glacier (RGI60-17.04995) displays extremely high mass loss rates in the historical period (−7.62 ± 0.83 m w.e. yr⁻¹) and is close to zero in the modern time period (0.12 ± 0.21 m w.e. yr⁻¹). Upon further inspection, this is a confluence of several glaciers defined as one glacier by RGI 6.0 (Supplementary Figure S6). Our estimate is therefore an average of several individual glaciers here. Nonetheless, this highly negative estimate is likely due to rapid retreat in the historical period when the glacier system became disconnected from the fjord and the associated dynamics. Across the fjord from this glacier, HPS-12 (−2.32 ± 0.25 m w.e. yr⁻¹ in 1976–2000 and −3.23 ± 0.35 m w.e. yr⁻¹ in 2000–2020) is likely affected by the same mechanisms that caused rapid retreat for the RGI60-17.04995 confluence.

An additional factor to consider for marine-terminating glaciers is their connection with the ocean. Although Jorge Montt does not have a geodetic mass balance estimate for the historical time period, we can infer from the elevation change map that it was thinning rapidly (Figure 4A). The 2000–2020 estimate for Jorge Montt is −3.94 ± 0.39 m w.e. yr⁻¹. This glacier is well-connected to the ocean, whereas RGI60-17.04995 and HPS-12 are deeper in the fjords. Tempano glacier is also highly negative but is close to the ocean, like Jorge Montt. Farther south, HPS-31 and HPS-34 are similarly deep into the fjords but undergo small magnitudes of mass change. These results suggest that depth into the fjords and connection with the ocean may not be the most important determinants of geodetic mass balance.

It is important to note that not only tidewater glaciers display contrasting behavior. Perito Moreno, a lake-terminating glacier on the eastern side of the SPI, has a geodetic mass balance notably close to zero in both time periods. This is in contrast to nearby Tyndall glacier, which is highly negative. In the NPI, Nef and HPN-1 are both lake-terminating in 2000–2020, yet HPN-1 is thinning faster (Figures 3B,C). At the northern tip of the SPI (around 48.5°S in Figure 6A), some small, land-terminating glaciers in close proximity to each other exhibit contrasting behavior. Some have become more positive in the 21st century, while others have become more negative. Nearly all larger, lake-terminating glaciers of this area appear to have become more negative in the 21st century.

4.2.2 Position Relative to Ice Divide

Because the distribution of these glacier types is not balanced between the east and west sides of the icefields, this can lead to regionally different mass balances. In particular, there are more lake-terminating glaciers east of the divide, while only the west side of the divide has marine-terminating glaciers. Histograms of eastern versus western glaciers (Figure 7) reveal that eastern, lake-terminating glaciers of the SPI have experienced the most rapid thinning over the observed timespan leading to greater regional mass loss east of the divide. West of the ice divide, lake-terminating glaciers account for one third of the glaciers, as compared to half for east of the divide (Table 4). Eastern SPI glaciers also have larger ablation zones than their western counterparts, which would also lead to greater mass loss as compared to glaciers in the western SPI (Figure 4). These results are broadly consistent with previous work. Willis et al. (2012a) and Willis et al. (2012b) use SRTM and ASTER to calculate elevation and volume changes of the icefields and show that from 2000–2012, 40% of the SPI volume loss is derived from eastern lake-terminating glaciers retreat. Willis et al. (2012a) find that NPI western glaciers are thinning rapidly from 2000–2011 and hypothesize that this is due to their lower elevation. While we do not claim that western NPI glaciers are thinning more rapidly than eastern, we do observe rapid thinning in elevation change maps for this group over 2000–2020 (Figure 3C).

4.3 Spatial Patterns in Elevation Change

While we linearly interpolate elevation bins, assume zero change at the highest and lowest elevation bins, and only use glaciers that had 50% valid data coverage in their areas to calculate geodetic mass balance, many glaciers are lacking most elevation data in their accumulation zones, especially for the historical period. This is a well-documented problem with DEMs in snow-covered areas: the inability to extract elevation data well over low-contrast, featureless accumulation zones (Dussaillant et al., 2019; Maurer et al., 2019). These data voids in accumulation zones introduce additional uncertainty in geodetic mass balance. For glaciers where the Hexagon DEM is successfully extracted at high elevations, notably glaciers in the northern SPI, it is possible that the values are not accurate (blue-colored accumulation zones in Figure 4A). In order for the elevations in the accumulation zones to increase over the time period, while the ablation zones are rapidly thinning, accumulation must be large enough to more than offset any increase in ice flux down-glacier. Since there is no strong evidence of precipitation increasing 1976–2000, this DEM extraction method is likely overestimating thickening in accumulation zones, and we are likely underestimating geodetic mass balance in the historical time period. For the modern time period, the observed thickening in accumulation zones is more plausible. Although there are still issues with extracting elevation data in the accumulation zones using modern imagery, we calculate the elevation trend using multiple DEMs, which decreases uncertainty. Additionally, some evidence does point to an increase in precipitation over the icefields, as discussed above. However, in order for thickening to occur in the accumulation zones, it would have to exceed dynamic thinning in response to mass loss in the lower elevations. Lack of climatological observations is a pervasive issue in this region and makes it particularly difficult to objectively assess the elevation change reconstructions over the accumulation zones. However, we do note that there is a distinct probability that geodetic mass balance estimates in this region may be underestimated due to potential positive elevation-change biases in the accumulation zones in some regions of the icefields.

4.4 Spatial Coverage

While the spatial coverage of the overlapping data (2000–2020 overlap in Table 3) was 63% for the NPI, the geodetic mass balance did not differ much from the 2000–2020 geodetic mass balance representing 100% of the area (2000–2020 all in Table 3). The spatial coverage is 52% of the total area in the SPI for the overlapping data. For this smaller area, the 2000–2020 geodetic mass balance was much less negative than the 2000–2020 geodetic mass balance for 97% of the area. Thus, a subset of glaciers can represent the entire region in some cases (NPI) but not in all (SPI). The historical geodetic mass balance estimate for 63% of the NPI glacierized area likely represents the average geodetic mass balance for the full NPI region. In contrast, with this sample set, the historical estimate for 52% of the SPI is probably biased less negative than the historical mass balance for the full SPI, as the small glaciers do not appear to be representative of the region. Even at a more local scale, our results show that geodetic mass balance can be extremely spatially heterogeneous (e.g., northern tip of SPI). These results strongly suggest it is not always appropriate to use the regional average mass balance to fill in missing glaciers in order to estimate mass balance or sea-level rise contributions for the full glacierized region, as is done by comparable studies (e.g., Dussaillant et al., 2019).

4.5 Regional Versus Glacier-Specific Thresholds

Manipulating processing thresholds, such as maximum allowed standard deviation in an elevation trend, can greatly affect results. While tailoring these parameters for individual glaciers is not feasible at a regional scale, we do additional processing for select glaciers. For several marine- and lake-terminating glaciers, the standard deviation of the elevation trend was allowed to exceed 50 m, to account for non-linear behavior at their termini (Table 2). Although we set the limit to 50 m for the majority of the icefields, several large, calving glaciers are subject to real, irregular behavior on their termini, which would be excluded with a threshold of 50 m. The new thresholds for these glaciers were determined by inspecting the greatest realistic standard deviation values of the elevation trends, before any cleanup of the trend maps (these figures are provided in Supplementary Figure S2). While this does introduce extra noise in the data, we find this has minimal impact on the geodetic mass balance uncertainties. Importantly, the increased threshold captures substantial nonlinear termini behavior, which should be included in the elevation trends. Increasing the maximum allowed standard deviation in the elevation trend from 50 m to 150 m for the Jorge Montt glacier increases the data coverage by 23%, and the resulting geodetic mass balance measurement becomes significantly more negative. Three glaciers of the NPI (Acodado, Steffen, and Fiero), only have their data coverage increase by 0%–1% with the increased standard deviation from 50–100 m, and their resulting geodetic mass balance measurements become less negative. This result could be due to a decrease in interpolation occurring at the termini. In contrast, a medium-sized marine-terminating glacier of the SPI, HPS-12, which is currently losing mass at significantly fast rates, gains only 5% more data coverage by including elevation trends up to a standard deviation of 200 m, but its geodetic mass balance estimate becomes more negative by nearly three-fold. Thresholds have a variable impact on the resulting geodetic mass balance, but for glaciers with known nonlinear terminus mass loss behavior, imposing regional thresholds is likely inappropriate and can significantly impact the geodetic mass balance calculations.

4.6 Comparison With Other Observations

Our geodetic mass balance estimates for the NPI and SPI sensu stricto agree with those provided by Dussaillant et al. (2019) for post-2000 (Figures 9A,B; Supplementary Table S2). Our estimate for the NPI is slightly less negative than Jaber et al. (2016) for the NPI, and our estimate for the SPI is more negative than the value provided by Malz et al. (2018). When mountain glaciers are included (Figures 9C,D; Supplementary Tables S1, S2), our estimates agree with both Braun et al. (2019) and Dussaillant et al. (2019) for the NPI. For the SPI, our estimate is more negative than those studies. Several factors may influence these differences. First, our estimate extends that of other studies by 5–6 years, representing ∼25% increase in temporal coverage. Given the relatively short observation period, these additional years could significantly impact the results. In addition, our methodology and data are different from Jaber et al. (2016) and Malz et al. (2018), who both utilize SRTM and Tan-DEM-X to find an elevation change over the icefields. We utilize the NASADEM (which is based on SRTM) and ASTER stack to fit an elevation trend. This is similar to the approach utilized by Dussaillant et al. (2019), who fit a linear regression to a stack of ASTER DEMs, plus SRTM for glaciers south of 48°S. However, we use RANSAC to fit an elevation trend rather than a linear regression. The total areas used also differ slightly between ours and other studies. Additionally, Dussaillant et al. (2019) and Jaber et al. (2016) do not consider areal changes in their geodetic mass balance calculation, whereas in our method we use the average glacier area over the timespan from the manual delineation of time-specific glacier inventories. Glaciers included in our estimate also required more stringent data coverage thresholds, using only glaciers with greater than 50% valid elevation data in the geodetic mass balance estimate. Dussaillant et al. (2019) include all glaciers except for those with mass balance uncertainty of greater than 1 m w.e. yr⁻¹ and less than 20% data coverage. They also replace those excluded glaciers with the regional mean, which our work demonstrates may not be appropriate in some regions of the Patagonian Icefields, as proximal glaciers may exhibit quite different mass balance trends.

FIGURE 9

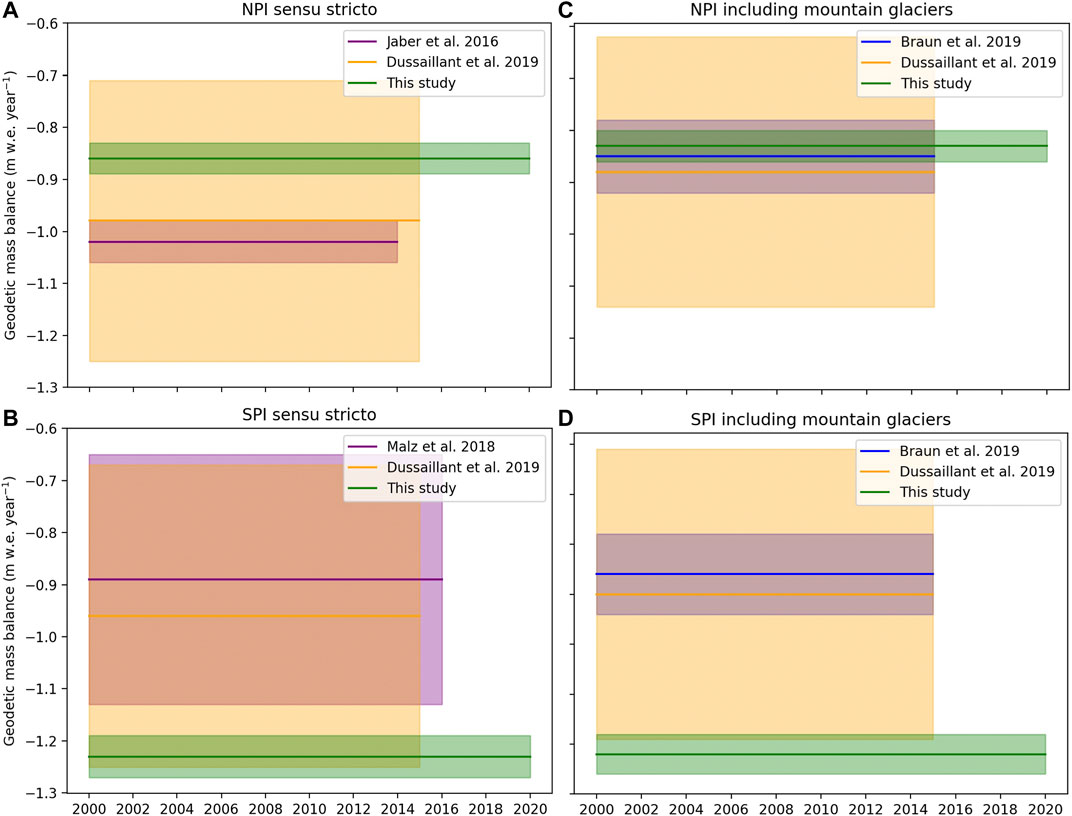
FIGURE 9. Our regional area-weighted geodetic mass balance estimates for the icefields sensu stricto (A,B) and the icefields plus surrounding mountain glaciers (C,D) compared to other recent studies.

The following studies did not publish mass balance estimates in m w.e. yr⁻¹, which precludes including them in the direct comparisons above and in Figure 9. However, we convert our mass balance values to Gt yr⁻¹ in order to provide another set of comparisons. A recent study by Hugonnet et al. (2021) estimated a mass loss rate of −18.7 Gt yr⁻¹ for the southern region of the Southern Andes, containing the icefields. Our work focuses on a subset of that same region and shows the combined icefields mass loss was -17.51 ± 1.32 Gt yr⁻¹ for 2000–2020. Together, these results imply that the icefields make up the bulk of this region’s ice loss. Willis et al. (2012b) provide a combined NPI and SPI mass loss from 2000–2012 of -24.4 ± 1.4 Gt yr⁻¹. This is a significantly larger mass loss estimate than ours. Willis et al. (2012b) use a density assumption of 900 kg m⁻³, which could account for part of the discrepancy between our results and theirs. However, their results are over a much shorter time span, which may be prone to greater influence of interannual variability. Cirací et al. (2020) also estimate a greater mass loss than our results. They estimate 28 ± 6 Gt yr⁻¹ mass loss for both icefields 2002–2019, derived from Gravity Recovery and Climate Experiment (GRACE) measurements. According to Dussaillant et al. (2019), glacial isostatic adjustment in the region likely leads to overestimation of ice loss from GRACE and Velicogna and Wahr (2013) discuss the poor horizontal resolution of GRACE as a limitation of the methodology. Thus, GRACE may be overestimating the magnitude of geodetic mass balance in the region. However, our results may also be underestimating mass loss due to issues extracting accurate elevations in the accumulations zones, as discussed in Section 4.1. The comparisons between the differing studies highlights both the utility of geodetic mass balance estimates as well as remaining issues. Comparisons across different regions and time spans make it difficult to directly assess why differences emerge but also points to the importance of potentially combining different methods in order to circumvent the limitations of any single approach.

5 Conclusion

Geodetic mass balance measurements of −0.86 ± 0.03 m w.e. yr⁻¹ for the NPI and −1.23 ± 0.04 m w.e. yr⁻¹ for the SPI agree with recently published estimates for the 2000–2020 observation period. While the results for the historical period over the NPI are likely representative of the full NPI region, the historical mass balance estimates for the SPI are biased towards the behavior of smaller glaciers for the SPI due to poor data coverage over significant portions of the largest glaciers in the region, which precludes extrapolating the results to the full region. We therefore focus comparisons between the historical and modern periods on glaciers with overlapping data for both periods, which includes 63% of the area of the NPI and 52% of the are for the SPI. For these reduced regions, the negative geodetic mass balance increased by a factor of 1.2 for the NPI and 2.4 for the SPI from 1976/1979–2000 to 2000–2020. Increased warming in the region is likely the dominant driver of increased mass loss over the historical and modern periods. In our dataset, more glaciers are lake-terminating in the SPI than the NPI which likely results in the more negative SPI estimates. Greater intensification of mass loss in the SPI could also be related to a slightly differing mean climate farther south, where glaciers receive year-round precipitation, in contrast to the NPI where winter precipitation dominates. These differences in mean climate can result in different mass balance sensitivity and feedback processes in response to climate change.

There is significant spatial heterogeneity in geodetic mass balance across both NPI and SPI and across both time periods. Capturing that spatial heterogeneity accurately may require glacier-specific processing techniques, especially for calving glaciers. This study looks in detail at the effect of glacier terminus type on geodetic mass balance and finds that lake-terminating glaciers exhibit the highest acceleration of mass loss rate since the 1970s, and on average have the most negative 2000–2020 values. In the modern time period, distributions of geodetic mass balance for glaciers with different terminus environments, and eastern versus western glaciers in the SPI, are statistically unique. Extreme heterogeneity in geodetic mass balance, especially among calving glaciers complicates projections of sea-level rise from this region of the world.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/morgan-mcdonnell/patagonia-gmb.

Author Contributions

MM processed and analyzed the data, produced all figures, and wrote the manuscript. SR conceived of the study. SR and RF provided feedback on data analysis, results and writing. All authors provided feedback and edits on the manuscript.

Funding

This project was funded by NSF Award Number 1853881 awarded to SR and RF.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We thank Simon Brewer for feedback on statistical analyses and Josh Maurer for help accessing and running HEXIMAP. We also acknowledge CHPC at the University of Utah for their installation and maintenance of software required for this research.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2022.813574/full#supplementary-material

References

Abdel Jaber, W., Rott, H., Floricioiu, D., Wuite, J., and Miranda, N. (2019). Heterogeneous Spatial and Temporal Pattern of Surface Elevation Change and Mass Balance of the Patagonian Ice fields between 2000 and 2016. The Cryosphere. 13 (9), 2511–2535. doi:10.5194/tc-13-2511-2019

CrossRef Full Text | Google Scholar

Bamber, J. L., Westaway, R. M., Marzeion, B., and Wouters, B. (2018). The Land Ice Contribution to Sea Level during the Satellite Era. Environ. Res. Lett. 13, 063008. doi:10.1088/1748-9326/aac2f0

CrossRef Full Text | Google Scholar

Belart, J. M. C., Magnússon, E., Berthier, E., Pálsson, F., Aðalgeirsdóttir, G., and Jóhannesson, T. (2019). The Geodetic Mass Balance of Eyjafjallajökull Ice Cap for 1945-2014: Processing Guidelines and Relation to Climate. J. Glaciol. 65, 395–409. doi:10.1017/jog.2019.16

CrossRef Full Text | Google Scholar

Bhattacharya, A., Bolch, T., Mukherjee, K., King, O., Menounos, B., Kapitsa, V., et al. (2021). High Mountain Asian Glacier Response to Climate Revealed by Multi-Temporal Satellite Observations since the 1960s. Nat. Commun. 12 (1), 1–13. doi:10.1038/s41467-021-24180-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Braun, M. H., Malz, P., Sommer, C., Farías-Barahona, D., Sauter, T., Casassa, G., et al. (2019). Constraining Glacier Elevation and Mass Changes in South America. Nat. Clim Change 9 (2), 130–136. doi:10.1038/s41558-018-0375-7

CrossRef Full Text | Google Scholar

Bravo, C., Bozkurt, D., Ross, A. N., and Quincey, D. J. (2019). Projected Increases in Surface Melt and Ice Loss for the Northern and Southern Patagonian Icefields. Scientific Rep. 11 (1), 1–13. doi:10.1038/s41598-021-95725-w2

CrossRef Full Text | Google Scholar

Brinkerhoff, D., Truffer, M., and Aschwanden, A. (2017). Sediment Transport Drives Tidewater Glacier Periodicity. Nat. Commun. 8, 90. doi:10.1038/s41467-017-00095-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Ciracì, E., Velicogna, I., and Swenson, S. (2020). Continuity of the Mass Loss of the World's Glaciers and Ice Caps From the GRACE and GRACE Follow-On Missions. Geophys. Res. Lett. 47 (9), 1–11. doi:10.1029/2019GL086926

CrossRef Full Text | Google Scholar

Cogley, J. G. (2012). Area of the Ocean. Mar. Geodesy 35, 379–388. doi:10.1080/01490419.2012.709476

CrossRef Full Text | Google Scholar

Condom, T., Martínez, R., Pabón, J. D., Costa, F., Pineda, L., Nieto, J. J., et al. (2020). Climatological and Hydrological Observations for the South American Andes: In Situ Stations, Satellite, and Reanalysis Data Sets. Front. Earth Sci. 8, 92. doi:10.3389/feart.2020.00092

CrossRef Full Text | Google Scholar

Davis, C. H., and Poznyak, V. I. (1993). The Depth of Penetration in Antarctic Firn at 10 GHz. IEEE Trans. Geosci. Remote Sensing. 31 (5), 1107–1111. doi:10.1109/36.263784

CrossRef Full Text | Google Scholar

Dehecq, A., Gardner, A. S., Alexandrov, O., McMichael, S., Hugonnet, R., Shean, D., et al. (2020). Automated Processing of Declassified KH-9 Hexagon Satellite Images for Global Elevation Change Analysis since the 1970s. Front. Earth Sci. 8, 566802. doi:10.3389/feart.2020.566802

CrossRef Full Text | Google Scholar

Dussaillant, I., Berthier, E., and Brun, F. (2018). Geodetic Mass Balance of the Northern Patagonian Icefield from 2000 to 2012 Using Two Independent Methods. Front. Earth Sci. 6, 8. doi:10.3389/feart.2018.00008

CrossRef Full Text | Google Scholar

Dussaillant, I., Berthier, E., Brun, F., Masiokas, M., Hugonnet, R., Favier, V., et al. (2019). Two Decades of Glacier Mass Loss along the Andes. Nat. Geosci. 12 (10), 802–808. doi:10.1038/s41561-019-0432-5

CrossRef Full Text | Google Scholar

Enderlin, E. M., Howat, I. M., and Vieli, A. (2013). High Sensitivity of Tidewater Outlet Glacier Dynamics to Shape. The Cryosphere. 7 (3), 1007–1015. doi:10.5194/tc-7-1007-2013

CrossRef Full Text | Google Scholar

European Space Agency (2020). Copernicus DEM (GLO-30) [Data Set]. Available at: https://panda.copernicus.eu/web/cds-catalogue/panda.

Google Scholar

Falaschi, D., Lenzano, M. G., Villalba, R., Bolch, T., Rivera, A., and Lo Vecchio, A. (2019). Six Decades (1958-2018) of Geodetic Glacier Mass Balance in Monte San Lorenzo, Patagonian Andes. Front. Earth Sci. 7, 326. doi:10.3389/feart.2019.00326

CrossRef Full Text | Google Scholar

Foresta, L., Gourmelen, N., Weissgerber, F., Nienow, P., Williams, J. J., Shepherd, A., et al. (2018). Heterogeneous and Rapid Ice Loss over the Patagonian Ice Fields Revealed by CryoSat-2 Swath Radar Altimetry. Remote Sensing Environ. 211, 441–455. doi:10.1016/j.rse.2018.03.041

CrossRef Full Text | Google Scholar

Gardelle, J., Berthier, E., and Arnaud, Y. (2012). Impact of Resolution and Radar Penetration on Glacier Elevation Changes Computed from DEM Differencing. J. Glaciol. 58 (208), 419–422. doi:10.3189/2012JoG11J175

CrossRef Full Text | Google Scholar

Glasser, N. F., Holt, T. O., Evans, Z. D., Davies, B. J., Pelto, M., and Harrison, S. (2016). Recent Spatial and Temporal Variations in Debris Cover on Patagonian Glaciers. Geomorphology 273, 202–216. doi:10.1016/j.geomorph.2016.07.036

CrossRef Full Text | Google Scholar

Hata, S., and Sugiyama, S. (2021). Changes in the Ice-Front Position and Surface Elevation of Glaciar Pío XI, an Advancing Calving Glacier in the Southern Patagonia Icefield, From 2000-2018. Front. Earth Sci. 8, 576044. doi:10.3389/feart.2020.576044

CrossRef Full Text | Google Scholar

Hock, R., Rasul, J., Adler, C., Cáceres, B., Gruber, S., Hirabayashi, Y., et al. (2019). “High Mountain Areas,” in IPCC Special Report on the Ocean and Cryosphere in a Changing Climate. Editor H. O. Pörtner. In press.

Google Scholar

Holzer, N., Vijay, S., Yao, T., Xu, B., Buchroithner, M., and Bolch, T. (2015). Four Decades of Glacier Variations at Muztagh Ata (Eastern Pamir): a Multi-Sensor Study Including Hexagon KH-9 and Pléiades Data. The Cryosphere. 9, 2071. doi:10.5194/tc-9-2071-2015

CrossRef Full Text | Google Scholar

Hugonnet, R., McNabb, R., Berthier, E., Menounos, B., Nuth, C., Girod, L., et al. (2021). Accelerated Global Glacier Mass Loss in the Early Twenty-First century. Nature. 592 (7856), 726–731. doi:10.1038/s41586-021-03436-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Huss, M. (2013). Density Assumptions for Converting Geodetic Glacier Volume Change to Mass Change. The Cryosphere. 7 (3), 877–887. doi:10.5194/tc-7-877-2013

CrossRef Full Text | Google Scholar

Jaber, W. A., Floricioiu, D., and Helmut, R. (2016). “Geodetic Mass Balance of the Patagonian Icefields Derived from SRTM and TanDEM-X Data,” in Paper presented at 2016 IEEE International Geoscience and Remote Sensing Symposium (Beijing, China: IGARSS). doi:10.1109/igarss.2016.7729082

CrossRef Full Text | Google Scholar

Johnson, E., and Rupper, S. (2020). An Examination of Physical Processes that Trigger the Albedo-Feedback on Glacier Surfaces and Implications for Regional Glacier Mass Balance across High Mountain Asia. Front. Earth Sci. 8, 129. doi:10.3389/feart.2020.00129

CrossRef Full Text | Google Scholar

King, O., Bhattacharya, A., Bhambri, R., Bolch, T., Meier, W., Casassa, G., et al. (2019). Glacial Lakes Exacerbate Himalayan Glacier Mass lossElevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data. Sci. Rep.Remote Sensing. 910 (2), 18145188. doi:10.1038/s41598-019-53733-x

PubMed Abstract | CrossRef Full Text | Google Scholar

King, O., Bhattacharya, A., Ghuffar, S., Tait, A., Guilford, S., Elmore, A. C., et al. (2020). Six Decades of Glacier Mass Changes Around Mt. Everest Are Revealed by Historical and Contemporary Images. One Earth. 3 (5), 608–620. doi:10.1016/j.oneear.2020.10.019

CrossRef Full Text | Google Scholar

Koppes, M., Conway, H., Rasmussen, L. A., and Chernos, M. (2011). Deriving Mass Balance and Calving Variations from Reanalysis Data and Sparse Observations, Glaciar San Rafael, Northern Patagonia, 1950-2005. The Cryosphere. 5 (3), 791–808. doi:10.5194/tc-5-791-2011

CrossRef Full Text | Google Scholar

Lamsal, D., Fujita, K., and Sakai, A. (2017). Surface Lowering of the Debris-Covered Area of Kanchenjunga Glacier in the Eastern Nepal Himalaya since 1975, as Revealed by Hexagon KH-9 and ALOS Satellite Observations. The Cryosphere. 11, 2815–2827. doi:10.5194/tc-11-2815-2017

CrossRef Full Text | Google Scholar

Larsen, C. F., Motyka, R. J., Arendt, A. A., Echelmeyer, K. A., and Geissler, P. E. (2007). Glacier Changes in Southeast Alaska and Northwest British Columbia and Contribution to Sea Level Rise. J. Geophys. Res. 112 (F1), F01007. doi:10.1029/2006JF000586

CrossRef Full Text | Google Scholar

Lenaerts, J. T. M., van den Broeke, M. R., van Wessem, J. M., van de Berg, W. J., van Meijgaard, E., van Ulft, L. H., et al. (2014). Extreme Precipitation and Climate Gradients in Patagonia Revealed by High-Resolution Regional Atmospheric Climate Modeling. J. Clim. 27 (12), 4607–4621. doi:10.1175/JCLI-D-13-00579.1

CrossRef Full Text | Google Scholar

Loriaux, T., and Casassa, G. (2013). Evolution of Glacial Lakes from the Northern Patagonia Icefield and Terrestrial Water Storage in a Sea-Level Rise Context. Glob. Planet. Change. 102, 33–40. doi:10.1016/j.gloplacha.2012.12.012

CrossRef Full Text | Google Scholar

Malz, P., Meier, W., Casassa, G., Jaña, R., Skvarca, P., and Braun, M. (2018). Elevation and Mass Changes of the Southern Patagonia Icefield Derived from TanDEM-X and SRTM Data. Remote Sensing. 10 (2), 188–217. doi:10.3390/rs10020188

CrossRef Full Text | Google Scholar

Martinez-Camara, M., Béjar Haro, B., Stohl, A., and Vetterli, M. (2014). A Robust Method for Inverse Transport Modeling of Atmospheric Emissions Using Blind Outlier Detection. Geosci. Model. Dev. 7 (3), 2303–2311. doi:10.5194/gmd-7-2303-2014

CrossRef Full Text | Google Scholar

Maurer, J. M., Rupper, S. B., and Schaefer, J. M. (2016). Quantifying Ice Loss in the Eastern Himalayas since 1974 Using Declassified Spy Satellite Imagery. The Cryosphere. 10 (5), 2203–2215. doi:10.5194/tc-10-2203-2016

CrossRef Full Text | Google Scholar

Maurer, J. M., Schaefer, J. M., Rupper, S., and Corley, A. (2019). Acceleration of Ice Loss across the Himalayas over the Past 40 Years. Sci. Adv. 5 (6), eaav7266. doi:10.1126/sciadv.aav7266

PubMed Abstract | CrossRef Full Text | Google Scholar

Maurer, J., and Rupper, S. (2015). Tapping into the Hexagon Spy Imagery Database: A New Automated Pipeline for Geomorphic Change Detection. ISPRS J. Photogrammetry Remote Sensing. 108, 113–127. doi:10.1016/j.isprsjprs.2015.06.008

CrossRef Full Text | Google Scholar

McNabb, R. W., and Hock, R. (2014). Alaska Tidewater Glacier Terminus Positions, 1948-2012. J. Geophys. Res. Earth Surf. 119 (2), 153–167. doi:10.1002/2013JF002915

CrossRef Full Text | Google Scholar

McNeil, C., O'Neel, S., Loso, M., Pelto, M., Sass, L., Baker, E. H., et al. (2020). Explaining Mass Balance and Retreat Dichotomies at Taku and Lemon Creek Glaciers, Alaska. J. Glaciol. 66 (258), 530–542. doi:10.1017/jog.2020.22

CrossRef Full Text | Google Scholar

Meier, M. F., and Post, A. (1987). Fast Tidewater Glaciers. J. Geophys. Res. 92 (B9), 9051–9058. doi:10.1029/JB092iB09p09051

CrossRef Full Text | Google Scholar

Meier, W. J.-H., Grießinger, J., Hochreuther, P., Braun, M. H., and Braun, M. H. (2018). An Updated Multi-Temporal Glacier Inventory for the Patagonian Andes with Changes between the Little Ice Age and 2016. Front. Earth Sci. 6, 62. doi:10.3389/feart.2018.00062

CrossRef Full Text | Google Scholar

Minowa, M., Schaefer, M., Sugiyama, S., Sakakibara, D., and Skvarca, P. (2021). Frontal Ablation and Mass Loss of the Patagonian Icefields. Earth Planet. Sci. Lett. 561, 116811. doi:10.1016/j.epsl.2021.116811

CrossRef Full Text | Google Scholar

Motyka, R. J., Truffer, M., Kuriger, E. M., and Bucki, A. K. (2006). Rapid Erosion of Soft Sediments by Tidewater Glacier advance: Taku Glacier, Alaska, USA. Geophys. Res. Lett. 33 (24), L24504. doi:10.1029/2006GL028467

CrossRef Full Text | Google Scholar

NASA JPL (2004). ASTER: Advanced Spaceborne thermal Emission and Reflection Radiometer. Available at: https://asterweb.jpl.nasa.gov/.

Google Scholar

NASA JPL (2020). NASADEM Merged DEM Global 1 Arc-Second (001) [Data Set]. Available at: https://search.earthdata.nasa.gov/search.

Google Scholar

NASA, METI, AIST (2019). Japan Spacesystems, and U.S./Japan ASTER Science Team. ASTER GDEM product [Data set]Available at: https://gbank.gsj.jp/madas/map/.

Google Scholar

NOAA (2021). Global Climate Report - Annual 2020. Available at: https://www.ncdc.noaa.gov/sotc/global/202013.

Google Scholar

Nuth, C., and Kääb, A. (2011). Co-registration and Bias Corrections of Satellite Elevation Data Sets for Quantifying Glacier Thickness Change. The Cryosphere. 5, 271–290. doi:10.5194/tc-5-271-2011

CrossRef Full Text | Google Scholar

Pellicciotti, F., Stephan, C., Miles, E., Herreid, S., Immerzeel, W. W., and Bolch, T. (2015). Mass-balance Changes of the Debris-Covered Glaciers in the Langtang Himal, Nepal, from 1974 to 1999. J. Glaciol. 61 (226), 373–386. doi:10.3189/2015jog13j237

CrossRef Full Text | Google Scholar

Pepin, N., Bradley, R. S., Diaz, H. F., Baraer, M., Caceres, E. B., Forsythe, N., et al. (2015). Elevation-dependent Warming in Mountain Regions of the World. Nat. Clim Change. 5 (5), 424–430. doi:10.1038/NCLIMATE2563

CrossRef Full Text | Google Scholar

Pepin, N. C., and Lundquist, J. D. (2008). Temperature Trends at High Elevations: Patterns across the globe. Geophys. Res. Lett. 35 (14), L14701. doi:10.1029/2008GL034026

CrossRef Full Text | Google Scholar

Pfeffer, W. T. (2007). A Simple Mechanism for Irreversible Tidewater Glacier Retreat. J. Geophys. Res. 112, F03S25. doi:10.1029/2006JF000590

CrossRef Full Text | Google Scholar

Pfeffer, W. T., Arendt, A. A., Bliss, A., Bolch, T., Cogley, J. G., Gardner, A. S., et al. (2014). The Randolph Glacier Inventory: a Globally Complete Inventory of Glaciers. J. Glaciol. 60, 537–552. doi:10.3189/2014JoG13J176

CrossRef Full Text | Google Scholar

Pieczonka, T., Bolch, T., Junfeng, W., and Shiyin, L. (2013). Heterogeneous Mass Loss of Glaciers in the Aksu-Tarim Catchment (Central Tien Shan) Revealed by 1976 KH-9 Hexagon and 2009 SPOT-5 Stereo Imagery. Remote Sensing Environ. 130, 233–244. doi:10.1016/j.rse.2012.11.020

CrossRef Full Text | Google Scholar

Pieczonka, T., and Bolch, T. (2015). Region-wide Glacier Mass Budgets and Area Changes for the Central Tien Shan between ∼1975 and 1999 Using Hexagon KH-9 Imagery. Glob. Planet. Change. 128, 1–13. doi:10.1016/j.gloplacha.2014.11.014

CrossRef Full Text | Google Scholar

Randolph Glacier Inventory Consortium (2017). Global Land Ice Measurements from Space Dataset of Global Glacier Outlines: Version 6.0: Technical Report. Colorado, United States: Digital Media. doi:10.7265/N5-RGI-60

CrossRef Full Text | Google Scholar

Rangwala, I., and Miller, J. R. (2012). Climate Change in Mountains: a Review of Elevation-dependent Warming and its Possible Causes. Climatic Change. 114 (3-4), 527–547. doi:10.1007/s10584-012-0419-3

CrossRef Full Text | Google Scholar

Rasmussen, L. A., Conway, H., and Raymond, C. F. (2007). Influence of Upper Air Conditions on the Patagonia Icefields. Glob. Planet. Change. 59 (1-4), 203–216. doi:10.1016/j.gloplacha.2006.11.025

CrossRef Full Text | Google Scholar

Rignot, E., Rivera, A., and Casassa, G. (2003). Contribution of the Patagonia Icefields of South America to Sea Level Rise. Science. 302 (5644), 434–437. doi:10.1126/science.1087393

PubMed Abstract | CrossRef Full Text | Google Scholar

Rivera, A., Lange, H., Carlos Aravena, J., and Casassa, G. (1997). The 20th-century advance of Glaciar Pio XI, Chilean Patagonia. Ann. Glaciol. 24, 66–71. doi:10.1017/s0260305500011952

CrossRef Full Text | Google Scholar

Sagredo, E. A., and Lowell, T. V. (2012). Climatology of Andean Glaciers: A Framework to Understand Glacier Response to Climate Change. Glob. Planet. Change. 86-87, 101–109. doi:10.1016/j.gloplacha.2012.02.010

CrossRef Full Text | Google Scholar

Schaefer, M., Machguth, H., Falvey, M., and Casassa, G. (2013). Modeling Past and Future Surface Mass Balance of the Northern Patagonia Icefield. J. Geophys. Res. Earth Surf. 118 (2), 571–588. doi:10.1002/jgrf.20038

CrossRef Full Text | Google Scholar

Schaefer, M., Machguth, H., Falvey, M., Casassa, G., and Rignot, E. (2015). Quantifying Mass Balance Processes on the Southern Patagonia Icefield. The Cryosphere. 9 (1), 25–35. doi:10.5194/tc-9-25-2015

CrossRef Full Text | Google Scholar

Shean, D. E., Alexandrov, O., Moratto, Z. M., Smith, B. E., Joughin, I. R., Porter, C., et al. (2016). An Automated, Open-Source Pipeline for Mass Production of Digital Elevation Models (DEMs) from Very-High-Resolution Commercial Stereo Satellite Imagery. ISPRS J. Photogrammetry Remote Sensing. 116, 101–117. doi:10.1016/j.isprsjprs.2016.03.012

CrossRef Full Text | Google Scholar

Sutherland, J. L., Carrivick, J. L., Gandy, N., Shulmeister, J., Quincey, D. J., and Cornford, S. L. (2020). Proglacial Lakes Control Glacier Geometry and Behavior during Recession. Geophys. Res. Lett. 47 (19), e2020GL088865. doi:10.1029/2020GL088865

CrossRef Full Text | Google Scholar

Truffer, M., and Motyka, R. J. (2016). Where Glaciers Meet Water: Subaqueous Melt and its Relevance to Glaciers in Various Settings. Rev. Geophys. 54 (1), 220–239. doi:10.1002/2015RG000494

CrossRef Full Text | Google Scholar

U.S. Geological Survey (2002). KH-9 Hexagon Imagery [Data Set]. Available at: https://earthexplorer.usgs.gov/.

Google Scholar

U.S. Geological Survey (2008). Declassified Intelligence Satellite Photographs. Fact Sheet, 2008–3054. doi:10.3133/fs20083054

CrossRef Full Text | Google Scholar

Velicogna, I., and Wahr, J. (2013). Time-variable Gravity Observations of Ice Sheet Mass Balance: Precision and Limitations of the GRACE Satellite Data. Geophys. Res. Lett. 40, 3055–3063. doi:10.1002/grl.50527

CrossRef Full Text | Google Scholar

Willis, M. J., Melkonian, A. K., Pritchard, M. E., and Ramage, J. M. (2012a). Ice Loss Rates at the Northern Patagonian Icefield Derived Using a Decade of Satellite Remote Sensing. Remote Sensing Environ. 117, 184–198. doi:10.1016/j.rse.2011.09.017

CrossRef Full Text | Google Scholar

Willis, M. J., Melkonian, A. K., Pritchard, M. E., and Rivera, A. (2012b). Ice Loss from the Southern Patagonian Ice Field, South America, between 2000 and 2012. Geophys. Res. Lett. 39, a–n. doi:10.1029/2012GL053136

CrossRef Full Text | Google Scholar

Wilson, R., Carrión, D., and Rivera, A. (2016). Detailed Dynamic, Geometric and Supraglacial Moraine Data for Glaciar Pio XI, the Only Surge-type Glacier of the Southern Patagonia Icefield. Ann. Glaciol. 57 (73), 119–130. doi:10.1017/aog.2016.32

CrossRef Full Text | Google Scholar

Zhou, Y., Li, Z., Li, J., Zhao, R., and Ding, X. (2018). Glacier Mass Balance in the Qinghai-Tibet Plateau and its Surroundings from the Mid-1970s to 2000 Based on Hexagon KH-9 and SRTM DEMs. Remote Sensing Environ. 210, 96–112. doi:10.1016/j.rse.2018.03.020

CrossRef Full Text | Google Scholar