- R&D Center of Science and Technology, Sinopec Geophysical Corporation, Nanjing, China
Introduction: Seismic first break (FB) picking helps us with near surface tomography, microseismic detection among other tasks. Using image semantic segmentation (ISS) networks to do so has been a hot topic in recent years, and multi-task learning has also demonstrated excellent data representation capabilities in several areas.
Methods: To improve accuracy, we combine the FB picking task with the seismic data reconstruction task, and propose an enhanced FB picking training method based on multi-task learning network. Specifically, we use two decoding branches of the same size in the network, which are the ISS decoding branch for the FB picking task, and the seismic feature learning decoding branch for the reconstruction task. The introduction of the seismic feature learning decoding branch will further help the network encoder to extract seismic effective features more efficiently, which will improve the accuracy of the ISS decoding branch, and ultimately improve the accuracy of the FB picking. During the training process, we use different loss functions for different decoding branches, and guide the network fitting through joint loss. In addition, we randomly add noise as well as random elimination to the seismic data to simulate the low SNR trace sets and bad traces that may exist in seismic data acquisition, and discuss the impact of different cases on the training results.
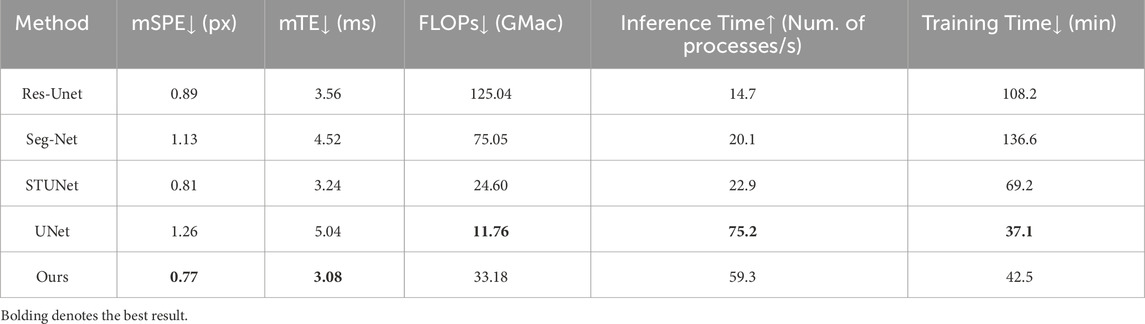
Results and discussion: The experimental results show that this method achieves more accurate FB picking results than the existing single-branch ISS methods, with an average picking error as low as 3.08 ms in the field data, and the percentage of traces with a picking error higher than 15 samples is as low as 0.03%, which is far superior to the network methods such as UNet, STUNet, SegNet, and Res-Unet, and effectively realizes the overall high-quality FB picking.
1 Introduction
Seismic exploration is a geophysical method that utilizes the propagation characteristics of seismic waves to detect underground structures. It is widely applied in mineral resource exploration (Malehmir et al., 2012), oil and natural gas prospecting (ZHAO, 2008), geothermal resource assessment (Maćkowski et al., 2019; Mondol, 2010; Wright et al., 1985), and groundwater investigation (Haeni, 1986). As a crucial step in seismic data processing, the accuracy of seismic first break (FB) picking directly impacts subsequent procedures, such as static correction, near-surface velocity modeling and noise suppression (Mondol, 2010; Coppens, 1985; Socco et al., 2010; Saragiotis et al., 2013). Consequently, the advancement of this technology has garnered sustained attention from both academia and industry.
As exploration scales continue to expand, the number of seismic source shots and geophones recorded in seismic surveys is increasing rapidly. Consequently, the seismic traces requiring processing often reach tens of thousands or even exceed one hundred thousand, posing a significant challenge to achieving efficient and accurate seismic FB picking. Although manual picking methods offer high accuracy, they are inefficient, labor-intensive, and inadequate for handling large-scale exploration data. Over the past few decades, researchers have developed various automated FB picking methods, including the energy ratio method (Coppens, 1985; Lee et al., 2017), cross correlation method (Molyneux and Schmitt, 1999), fractal dimension method (Boschetti et al., 1996; Sabbione and Velis, 2010), and image edge detection method (Luo et al., 2018; Mousa et al., 2011). However, under complex geological conditions, these methods often struggle to maintain picking accuracy when processing low-quality data, thereby limiting their effectiveness in practical applications. In recent years, with the rapid advancement of artificial intelligence technology, intelligent methods have been widely applied in seismic data processing (Jiao and Alavi, 2020; Mousavi and Beroza, 2023; Jia and Ma, 2017). This technology is expected to further enhance the automation of FB picking, improve accuracy and computational efficiency, and meet the demands of increasingly complex geological exploration. Consequently, the development of intelligent FB picking methods with high efficiency and accuracy has become a focal point of research (Yuan et al., 2018; Harsuko and Alkhalifah, 2024).
With the rise of deep learning, this cutting-edge technology—which employs neural network models to fit complex nonlinear mappings—has garnered significant attention, leading numerous researchers to adopt it across various fields (LeCun et al., 2015; Guo et al., 2016; Shinde and Shah, 2018; Wang X. et al., 2024). Since seismic data preprocessing tasks (e.g., seismic FB picking, seismic data denoising, etc.) are often regarded as signal processing or image analysis tasks, and such tasks are the main areas where deep learning techniques are applied, various types of deep learning-based seismic FB picking methods have emerged. In terms of data dimensionality, some researchers proposed 1-D single-channel FB picking methods based on fully convolutional networks (Wu et al., 2019; Zhu and Beroza, 2019; Loginov et al., 2022). These methods achieve high-precision results in high signal-to-noise ratio (SNR) data but fail to capture FB correlation information from neighboring traces and perform poorly on large-scale complex datasets. Compared to 1-D single-trace FB picking, 2-D multi-trace deep learning methods, which frame FB picking as an image semantic segmentation (ISS) task, exhibit superior noise immunity and picking accuracy. By incorporating the spatial information of neighboring traces’ FBs, these methods enhance performance in complex datasets. Consequently, many researchers have explored convolutional network-based architectures such as UNet and its variants (Hu et al., 2019; CHEN et al., 2021; Zwartjes and Yoo, 2022), SegNet (Yuan et al., 2022), as well as Transformer-based models like STUNet (Jiang et al., 2023) and StorSeismic (Harsuko and Alkhalifah, 2022) for multi-trace seismic FB picking. Furthermore, 3-D multi-trace seismic FB picking method based on ISS networks was also proposed (Han et al., 2021; Jiang et al., 2024). In addition to variations in data dimensionality, researchers have explored different types of network models, such as graph neural network-based FB picking method (Wang et al., 2024a) and Bayesian network-based FB picking method (Wang et al., 2024b). Extensive experiments on both simulated and field data have demonstrated that neural network-based seismic FB picking methods outperform traditional automatic approaches. Moreover, since seismic data are often stored in a 2-D format, numerous studies have focused on 2-D multi-trace FB picking methods utilizing ISS networks (Zwartjes and Yoo, 2022; Xu et al., 2021).
Initially, due to hardware limitations and training efficiency constraints, most neural network models were designed for end-to-end mapping within a single encoding-decoding framework, making it challenging to achieve multi-branch, multi-task synchronous training and inference. In addition to variations in data dimensionality, researchers have explored different types of network models. For example, Wu et al. used a multi-task learning network for the realization of airborne transient electromagnetic denoising and inversion (Wu et al., 2022). Ovcharenko et al. achieved low-frequency extrapolation and elastic model building from seismic data through multi-task learning (Ovcharenko et al., 2022). Shan et al. and Deng et al. realized multi-parameter forward modeling of 2-D as well as 3-D magnetotelluric through multi-task learning (Shan et al., 2021; Deng et al., 2025). The above studies demonstrate that multi-task learning can improve a network model’s ability to capture data features, leading to better performance while imposing only a limited increase in network size. Most existing deep learning-based seismic FB picking studies adopt a single-task learning framework, with limited research on applying multi-task learning to this problem. To address this gap, we introduce multi-task learning into the seismic FB picking task and incorporate a seismic feature learning decoding module into the ISS-based FB picking network to enhance the feature extraction capability of the original encoding module. Specifically, the network model consists of two decoding branches of equal size: one for FB picking via image semantic segmentation and the other for data reconstruction in seismic feature learning. We believe that incorporating the seismic feature learning decoding branch will encourage the network encoder to extract effective seismic features more efficiently, thereby enhancing the accuracy of image semantic segmentation decoding and ultimately improving FB picking precision. To simulate low signal-to-noise ratio trace sets and bad traces in seismic pickups, we introduce random noise and randomly remove seismic data, then analyze the impact of different scenarios on the results. During training, we employ distinct loss functions for each decoding branch and optimize the network using a joint loss approach. Experimental results indicate that the proposed method outperforms existing single-branch image semantic segmentation approaches, achieving an average picking error as low as 3.08 m. Notably, the method maintains a high zero-error picking ratio, while the percentage of traces with a picking error exceeding 15 samples is as low as 0.03% —significantly outperforming networks such as STUNet, SegNet, and Res-UNet, effectively achieving high-quality FB picking. Furthermore, the lightweight double-decoding convolutional network exhibits low computational complexity, resulting in shorter training time and higher inference efficiency.
2 Methods
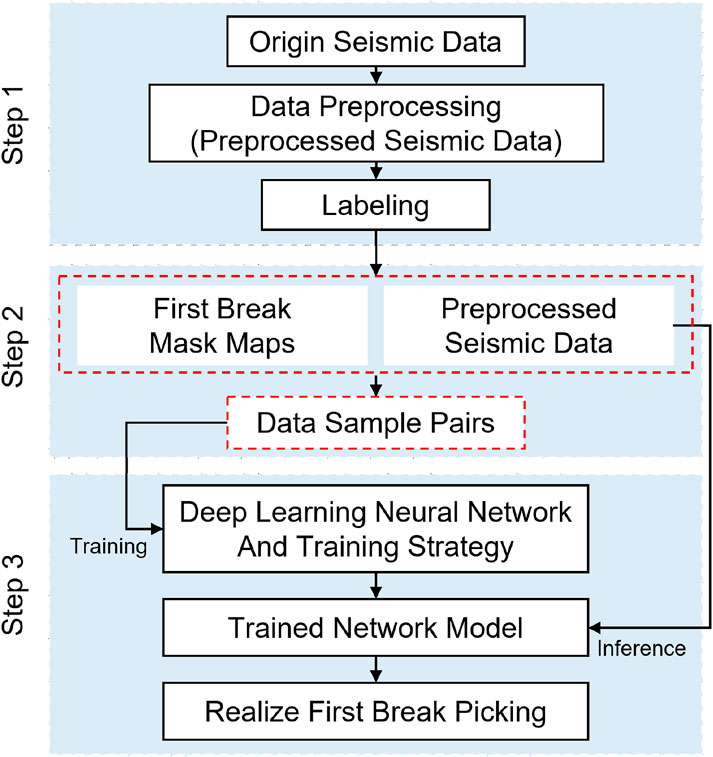
With the widespread adoption of deep learning across various fields, the multi-trace seismic FB picking method based on image semantic segmentation has demonstrated strong noise immunity and significant practical engineering value. As illustrated by the workflow in Figure 1, deep learning-based seismic FB picking consists of three main steps: data preprocessing, labeling and dataset generation, network training and inference. Data preprocessing focuses on formatting and sizing seismic data for network input. Labeling and sample pair generation define the calibration method for FBs and the structure of data sample pairs, playing a crucial role in enabling the network to efficiently recognize FB features. The network training and inference stage involves selecting the network architecture and optimizing training and inference strategies, which directly impact the accuracy of FB picking. In this paper, we propose an efficient and systematic approach for all three steps. High-precision seismic FB picking is achieved through linear correction, pre- and post-mask calibration, and a lightweight double-decoding convolutional network based on multi-task learning. The following section provides a detailed description of the proposed method, covering network principles, data preprocessing, and labeling.
2.1 Network
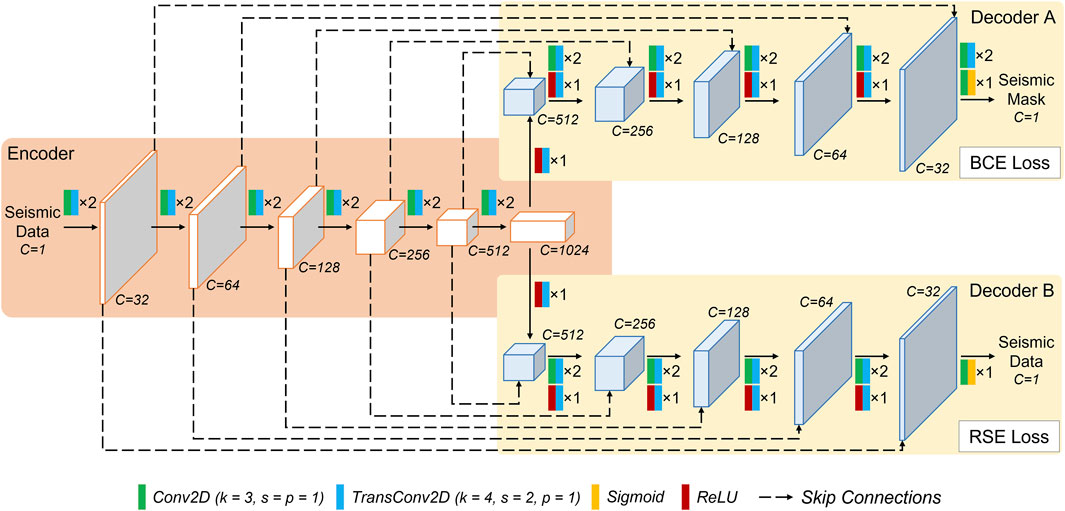
The double-decoding convolutional network for seismic FB picking proposed in this paper is illustrated in Figure 2. The overall design follows the classical UNet architecture (Ronneberger et al., 2015), which is widely recognized for its stability and efficiency in computer vision tasks. The network is primarily composed of an encoding part and a decoding part. In the encoding part, each downsampling stage comprises two convolutional operations with a (3, 3) kernel and (1, 1) strides, followed by two ReLU activation functions and a max-pooling operation. Each downsampling stage reduces the feature map size while increasing the number of feature channels. The reduction in feature map size facilitates long-range feature interactions within the data, whereas the increased number of channels enhances the network’s ability to extract deeper feature representations. A downsampling stage can be mathematically expressed as follows:
where
The network’s decoding stage consists of Decoder A and Decoder B, each corresponding to a distinct task. Decoder A serves as the image semantic segmentation branch, while Decoder B functions as the seismic feature learning branch. Each decoding branch comprises four identical upsampling stages, where each stage includes a transposed convolution operation with a (4, 4) kernel and (2, 2) strides, followed by a ReLU activation function. Each decoding branch employs skip connections via channel concatenation to fuse features from the downsampling path with those from the corresponding upsampling path, facilitating interactions between shallow image textures and deep abstract features. Through these operations, each upsampling stage increases the feature map size while reducing the number of feature channels, gradually restoring the original data dimensions. Mathematically, one upsampling stage in each decoding branch can be expressed as Equation 2:
where
Notably, despite the distinct task characteristics of different branches, their respective downstream tasks lead to diverse output styles. This encourages the encoding part of the network to extract more effective and abstract data features. With the above encoding and decoding network architecture, a nonlinear mapping relationship between seismic data and feature masks can be constructed. The image semantic segmentation branch ultimately applies a Sigmoid function to normalize the data within the range (0, 1), producing a single-trace binary FB mask. This branch employs the Binary Cross-Entropy (BCE) function to compute the loss. As a widely used loss function in binary image semantic segmentation tasks, Binary Cross-Entropy (BCE) is easy to implement and enables efficient training (Ruby and Yendapalli, 2020). It is mathematically defined as follows:
where
The seismic feature learning decoding branch normalizes the data within the range (−1, 1), producing a single-channel reconstructed seismic output. The reconstruction of seismic data in this branch is formulated as a regression task, where the Mean Squared Error (MSE) function is used to compute the loss by measuring the squared differences between predicted values and ground truth labels. The MSE loss is mathematically defined as follows:
where
Combining Equations 3,4, the final joint loss function is as follows:
where
2.2 Data preparation and labeling
Deep learning is a data-driven approach that utilizes large-scale datasets to address various pattern recognition problems. In supervised learning, properly designing training sample pairs enables the network to efficiently establish complex nonlinear data mappings. Existing deep learning-based seismic FB picking methods treat seismic data as images and feed them into neural networks. However, with the continuous advancement of seismic exploration, the size of acquired seismic data has increased significantly. Directly inputting the entire dataset into the network for FB picking imposes high hardware demands, prompting the development of various data cropping techniques (Xu et al., 2021; CHEN et al., 2021; Jiang et al., 2023).
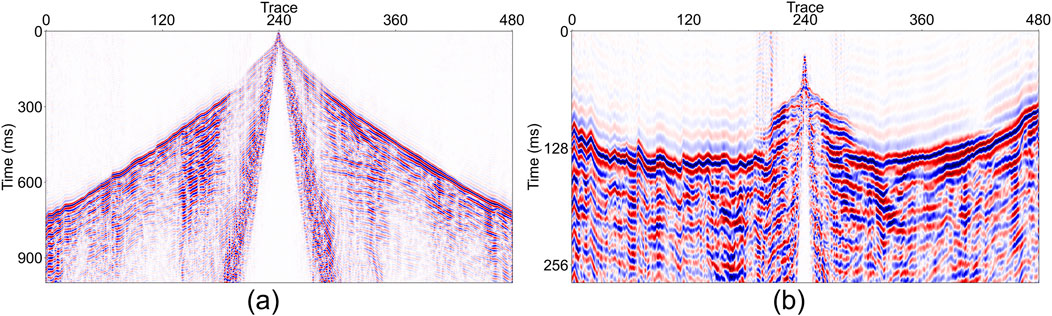
In this study, the linear correction method is applied. The seismic signals recorded by each trace are adjusted by adding a time increment corresponding to its respective shooting distance. This process aligns all FB times to approximately the same range, thereby significantly reducing the temporal sample dimension of the data. As shown in Figure 3, the temporal sample dimension of the original data is reduced by applying linear correction and cropping non-FB regions. Compared to previous cropping methods, the linear correction-based approach enables the entire shot data to be fed into the network while preserving a global perspective. The linear correction is defined by the Equation 6:
where
After the seismic data size is significantly reduced in the time dimension through linear correction, mask labeling is then applied. We employ a commonly used labeling method that classifies seismic wave signals into two categories: pre-FB and post-FB, as shown in Figure 4. This method is used to label the seismic data as positive (1) and negative (0) samples.
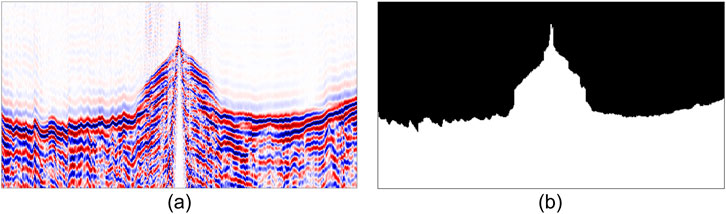
Figure 4. Mask labeling method. (a) Seismic data. (b) labeling method, label the pre-FB and post-FB of the seismic data as positive and negative samples.
3 Experimentation
3.1 Experimental environment and data
The experimental hardware environment consists of an Intel i7-14700 KF processor and a NVIDIA RTX 4090D GPU, with the PyTorch framework used for training. The network hyperparameters are set as follows: the RAdam optimizer is used (Liu et al., 2020), the batch size is 16, the initial learning rate is 0.0002, and the maximum number of training epochs is 130. In this study, 434 shot records of 2-D seismic exploration data acquired in North China are used for field experiments. The data are sampled at 4 m intervals, with each shot record containing 480 traces and 256 time samples after linear correction. All the experiments are randomly divided into training set, validation set and test set according to the ratio of 70%, 20% and 10%, respectively. The training set is used to train the network, the validation set assesses the model’s fitting performance during training, and the test set independently evaluates the FB picking performance of each network.
3.2 Evaluation of indicators
In this study, the accuracy of FB picking for each network is evaluated by comparing the predicted mask plots and analyzing quantitative metrics. In terms of quantitative evaluation, the mean sample point error (mSPE) between the predicted mask and the ground truth label provides a clearer comparison of each network’s FB picking performance. Additionally, analyzing the distribution of errors across different ranges helps to assess the strengths and weaknesses of each network. The mean time error (mTE) between the final prediction and the actual FBs offers a more intuitive understanding of the error range in practical applications. Additionally, the computational complexity and inference time of each network are also critical factors. The computational complexity of the network is measured using the GitHub open-source toolkit pytorch-OpCounter library (Zhu, 2018), and inference time is determined by evaluating the number of data samples processed per second under the same hardware environment. The mSPE and mTE can be mathematically defined as Equations 7, 8:
where
3.3 Results and analysis
To evaluate the performance of the proposed FB picking method on field data, three shot records from the test set are randomly selected for analysis. The results are compared with those of existing single-task methods, including UNet, STUNet (Jiang et al., 2023), SegNet (Yuan et al., 2022), and Res-UNet (Zwartjes and Yoo, 2022). The performance comparison of these FB picking models with the proposed method is illustrated in Figure 5. In each figure, the white masked area represents the time after FB picking, while the gray non-masked area corresponds to the time before FB picking. Red pixels represent the manually labeled actual FBs, identified by professional interpreters. Green pixels indicate the predicted FBs for the given method, while blue pixels highlight instances where the predicted FBs are entirely correct (0 sample point error). The predicted FBs for each method are obtained from the boundaries of the binary mask before and after the FB, with the threshold conventionally set to 0.5.
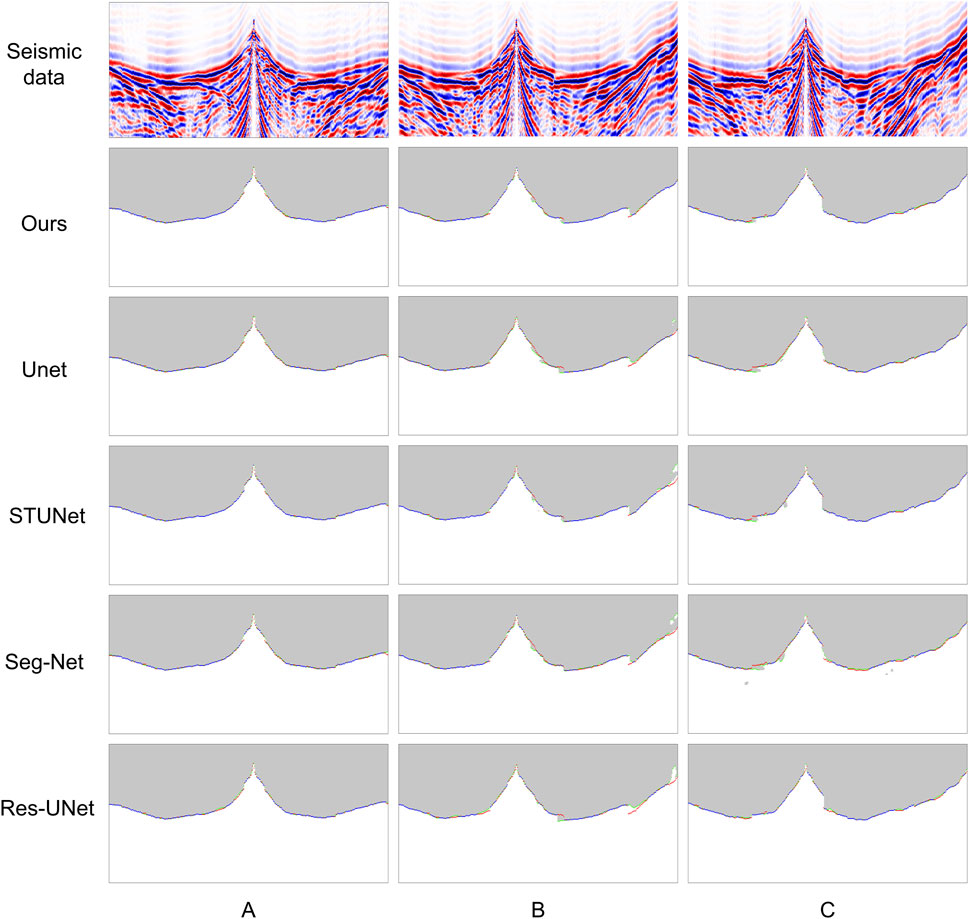
Figure 5. Comparison results of the mask map output by each network method. Red pixels indicate ground truth FBs, green pixels indicate the predicted FBs for the given method, while blue pixels highlight instances where the predicted FBs are entirely correct (0 sample point error).
As observed in Figure 5, the proposed method achieves superior FB picking results in most cases. In shot set A, where FB time variations are more gradual, our method achieves nearly perfect FB picking, exhibiting high continuity and accuracy. In shot sets B and C, which contain traces with insignificant FBs, the single-task UNet, SegNet, and Res-UNet fully convolutional segmentation networks exhibited poor FB picking performance, as indicated by the discontinuities in their predicted masks. In contrast, our method accurately picks FBs in regions with inconspicuous FBs at data boundaries, benefiting from the training of the seismic feature learning decoding branch. Additionally, it demonstrates high precision in identifying FB regions, as shown in Figures 6, 7. As shown in Figures 5–7, the proposed double-decoding multi-task seismic FB picking method effectively mitigates mask discontinuity and boundary ambiguity present in other methods, thereby enhancing the accuracy of FB predictions.
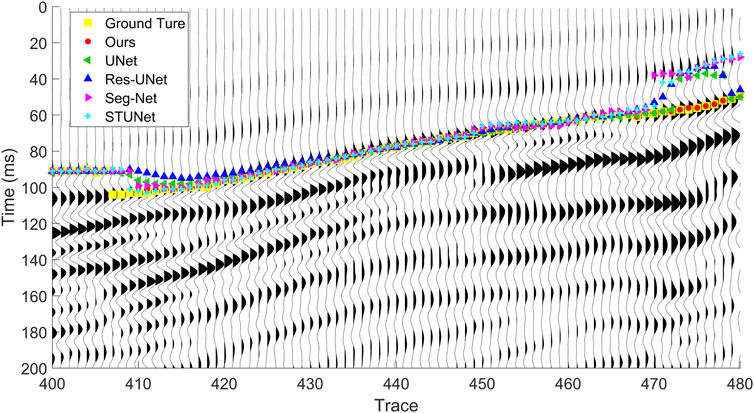
Figure 6. Comparison of FB picking across networks for test set data B. (No.400 traces to No.480 traces localized data).
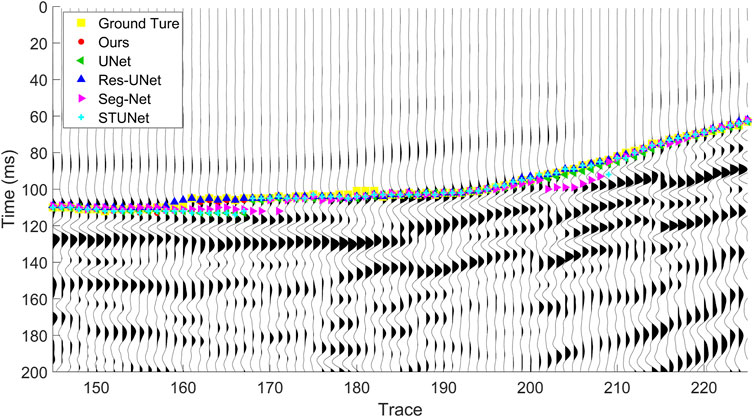
Figure 7. Comparison of FB picking across networks for test set data C. (No.145 traces to No.225 traces localized data).
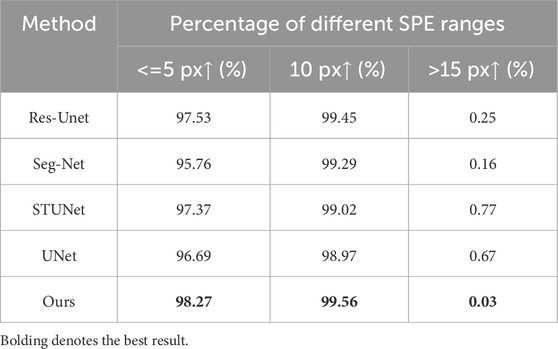
Table 1 presents the error distribution statistics across different sample point error intervals in the test set for each method. As shown in the table, our method achieves the best performance in the ratio of sample point error
Table 2 presents a comparison of the numerical results for each method in the test set. As shown in the table, our method achieves the lowest average sample error and average time error, measuring 0.77 pixels and 3.08 m, respectively. Moreover, the average time error is reduced by 38.9%, 4.9%, 31.8%, and 13.4% compared to single-task UNet, STUNet, SegNet, and Res-UNet, respectively. Since our double-decoding convolutional network is built upon the classical UNet architecture, it exhibits low computational complexity (2.97 GMac) compared to fully convolutional networks (FCNs) such as STUNet, SegNet, and Res-UNet. Additionally, it demonstrates superior training efficiency, requiring only 37.1 min, and achieves a high inference speed of 59.3 inferences per second. It can be easily deployed in real-world engineering applications.
Analyzing the feature maps from the encoder part of the network facilitates a deeper understanding of the characteristics and advantages of multi-task learning. As our proposed network adopts a double-decoding architecture based on the classical UNet, so we compare it with the classical single encoder UNet to evaluate the impact of multi-task learning on feature extraction. A shot from the test set was randomly selected as input, and we extracted the output feature maps at different encoding stages for each network model, as illustrated in Figure 8. To facilitate comparison, we performed channel-wise averaging on the feature maps at each encoding stage and standardized the image size. As observed, for shallow feature maps (down1 to down3), the results produced by the classical UNet and our method are relatively similar. However, in the deeper feature maps (down4 and down5), the features extracted by the single encoder UNet become more abstract and show noticeable deviations from the structure of the original seismic data. In contrast, the feature maps extracted by our multi-task learning network are more complete and concrete, better preserving the structural information of the original seismic data. This is attributed to the structural constraints imposed by the seismic data reconstruction decoding branch, which significantly enhances the model’s ability to perform structural modeling in deeper encoding stages. These results indicate that, with the assistance of the reconstruction decoding branch, the network achieves superior performance in both deeper feature extraction and global representation.
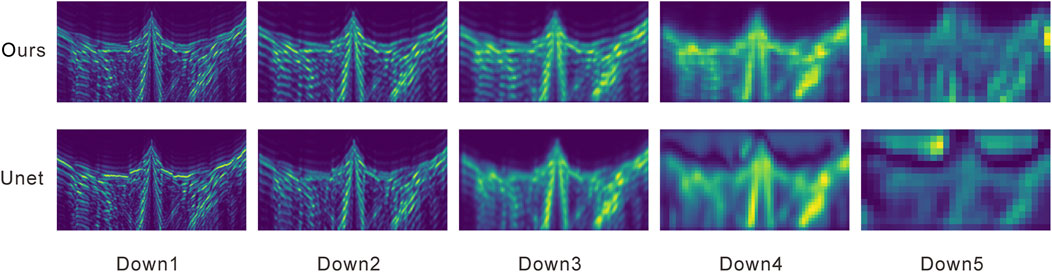
Figure 8. Comparison of feature maps at different encoding stages of the network. Down1 to Down5 represent the encoding stages from shallow to deep.
3.4 Ablation experiments
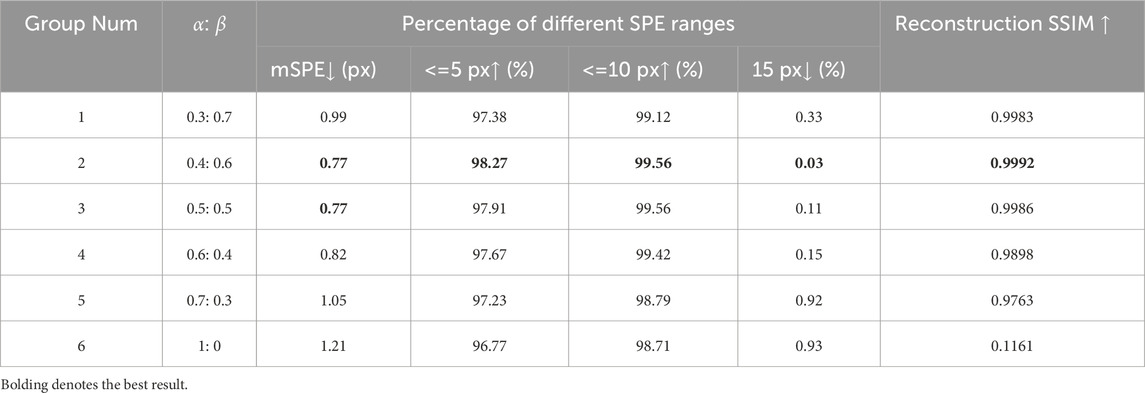
To further evaluate the effectiveness of the seismic feature learning decoding branch introduced by multi-task learning, we conducted ablation experiments on the contribution of each loss term in the joint loss function. The experimental results are presented in Table 3. Referring to Equation (5), we observe that when the loss ratio
To further investigate the impact of loss weight configurations on the data reconstruction task, we computed the Structural Similarity Index Measure (SSIM) under various
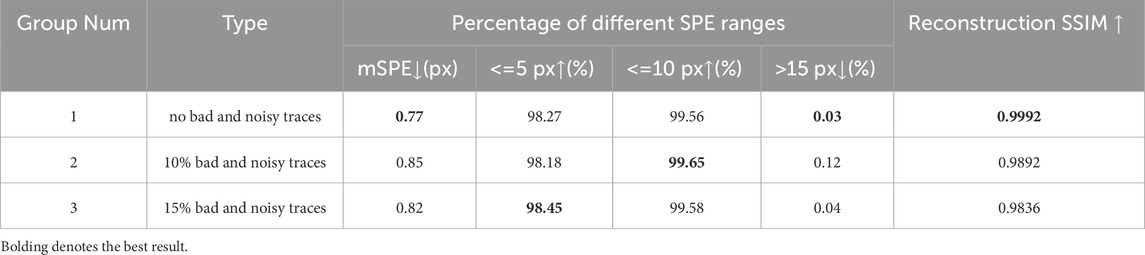
Finally, we conducted an ablation experiment on input seismic data by introducing different levels of noise and bad traces. Noise was simulated by adding 5% Gaussian noise to the original traces, while bad traces were generated by zero-padding the original traces, ensuring that noisy and bad traces did not overlap. This process is commonly considered a form of data enhancement during training, enhancing the network’s ability to extract features from seismic data. Through this ablation experiment, we examine its potential benefits under multi-task learning. The results, presented in Table 4, indicate that different levels of noisy and bad traces lead to optimal performance in different metrics. When no noisy or bad traces are present, the mSPE and the ratio of sample point error
4 Conclusion
In this study, we integrate the seismic FB picking task with the seismic data reconstruction task and propose an enhanced training method based on a multi-task learning network. The network’s feature extraction capability is enhanced by a newly introduced seismic feature learning decoding branch for data reconstruction, which improves deep abstraction modeling and, in turn, enhances the accuracy of the semantic segmentation branch for FB picking. We also analyze the effect of the loss weighting ratio between tasks and identify the optimal balance. Additionally, we introduce random noise and selectively remove seismic traces to simulate low-SNR and poor-quality data, and analyze their impact on the results. Experimental results show that the proposed method outperforms existing single-branch semantic segmentation methods across multiple metrics, yielding more accurate FB picking results. Specifically, it achieves an average picking error of just 3.08 m on field data, with only 0.03% of traces exceeding a picking error of 15 samples—significantly outperforming UNet, STUNet, SegNet, and Res-UNet. These results highlight the method’s effectiveness in achieving high-quality FB picking. Moreover, the lightweight dual-decoding convolutional network proposed in this study demonstrates low computational complexity, fast training, and high inference efficiency, suggesting its potential applicability to higher-dimensional data and real-world engineering applications.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
ZZ: Writing – review and editing, Supervision, Writing – original draft, Funding acquisition. JY: Visualization, Validation, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by China Petroleum & Chemical Corporation Project: Continuous Optimization and Upgrade of Autonomous Node Acquisition System Software and Hardware. Grant Number: P24110.
Conflict of interest
Authors ZZ and JY were employed by Sinopec Geophysical Corporation.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feart.2025.1601134/full#supplementary-material
References
Boschetti, F., Dentith, M. D., and List, R. D. (1996). A fractal-based algorithm for detecting first arrivals on seismic traces. Geophysics 61, 1095–1102. doi:10.1190/1.1444030
Chen, D., Yang, W., Wei, X., Li, D., Lu, J., He, X., et al. (2021). Research on first-break automatic picking based on an improved u-net network. Prog. Geophys. 36, 1493–1503. doi:10.6038/pg2021EE0235
Coppens, F. (1985). First arrival picking on common-offset trace collections for automatic estimation of static corrections. Geophys. Prospect. 33, 1212–1231. doi:10.1111/j.1365-2478.1985.tb01360.x
Deng, F., Shi, H., Jiang, P., and Wang, X. (2025). Three-dimensional magnetotelluric forward modeling using multi-task deep learning with branch point selection. Remote Sens. 17, 713. doi:10.3390/rs17040713
Guo, Y., Liu, Y., Oerlemans, A., Lao, S., Wu, S., and Lew, M. S. (2016). Deep learning for visual understanding: a review. Neurocomputing 187, 27–48. doi:10.1016/j.neucom.2015.09.116
Haeni, F. (1986). Application of seismic refraction methods in groundwater modeling studies in new england. Geophysics 51, 236–249. doi:10.1190/1.1442083
Han, S., Liu, Y., Li, Y., and Luo, Y. (2021). First arrival traveltime picking through 3-d u-net. IEEE Geoscience Remote Sens. Lett. 19, 1–5. doi:10.1109/lgrs.2021.3096572
Harsuko, R., and Alkhalifah, T. (2024). Optimizing a transformer-based network for a deep-learning seismic processing workflow. Geophysics 89, V347–V359. doi:10.1190/geo2023-0403.1
Harsuko, R., and Alkhalifah, T. A. (2022). Storseismic: a new paradigm in deep learning for seismic processing. IEEE Trans. Geoscience Remote Sens. 60, 1–15. doi:10.1109/tgrs.2022.3216660
Hu, L., Zheng, X., Duan, Y., Yan, X., Hu, Y., and Zhang, X. (2019). First-arrival picking with a u-net convolutional network. Geophysics 84, U45–U57. doi:10.1190/geo2018-0688.1
Jia, Y., and Ma, J. (2017). What can machine learning do for seismic data processing? an interpolation application. Geophysics 82, V163–V177. doi:10.1190/geo2016-0300.1
Jiang, P., Deng, F., Wang, X., Lou, W., and Ye, C. (2024). 3-d seismic first break picking based on two channel mask strategy. IEEE Trans. Geoscience Remote Sens. 62, 1–15. doi:10.1109/tgrs.2024.3412673
Jiang, P., Deng, F., Wang, X., Shuai, P., Luo, W., and Tang, Y. (2023). Seismic first break picking through swin transformer feature extraction. IEEE Geoscience Remote Sens. Lett. 20, 1–5. doi:10.1109/lgrs.2023.3248233
Jiao, P., and Alavi, A. H. (2020). Artificial intelligence in seismology: advent, performance and future trends. Geosci. Front. 11, 739–744. doi:10.1016/j.gsf.2019.10.004
LeCun, Y., Bengio, Y., and Hinton, G. (2015). Deep learning. nature 521, 436–444. doi:10.1038/nature14539
Lee, M., Byun, J., Kim, D., Choi, J., and Kim, M. (2017). Improved modified energy ratio method using a multi-window approach for accurate arrival picking. J. Appl. Geophys. 139, 117–130. doi:10.1016/j.jappgeo.2017.02.019
Liu, L., Jiang, H., He, P., Chen, W., Liu, X., Gao, J., et al. (2020). “On the variance of the adaptive learning rate and beyond,” in Proceedings of the eighth international conference on learning representations ICLR 2020.
Loginov, G. N., Duchkov, A. A., Litvichenko, D. A., and Alyamkin, S. A. (2022). Convolution neural network application for first-break picking for land seismic data. Geophys. Prospect. 70, 1093–1115. doi:10.1111/1365-2478.13192
Luo, F., Wang, H., Wu, C., Xu, P., and Zhang, R. (2018). “Automatic first-breaks picking algorithm under the constraint of image segmentation,” in SEG international Exposition and annual meeting SEG, SEG–2018.
Maćkowski, T., Sowiżdżał, A., and Wachowicz-Pyzik, A. (2019). Seismic methods in geothermal water resource exploration: case study from łódź trough, central part of Poland. Geofluids 2019, 1–11. doi:10.1155/2019/3052806
Malehmir, A., Durrheim, R., Bellefleur, G., Urosevic, M., Juhlin, C., White, D. J., et al. (2012). Seismic methods in mineral exploration and mine planning: a general overview of past and present case histories and a look into the future. Geophysics 77, WC173–WC190. doi:10.1190/geo2012-0028.1
Molyneux, J. B., and Schmitt, D. R. (1999). First-break timing; arrival onset times by direct correlation. Geophysics 64, 1492–1501. doi:10.1190/1.1444653
Mondol, N. H. (2010). “Seismic exploration,” in Petroleum geoscience: from sedimentary environments to rock physics, 375–402.
Mousa, W. A., Al-Shuhail, A. A., and Al-Lehyani, A. (2011). A new technique for first-arrival picking of refracted seismic data based on digital image segmentation. Geophysics 76, V79–V89. doi:10.1190/geo2010-0322.1
Mousavi, S. M., and Beroza, G. C. (2023). Machine learning in earthquake seismology. Annu. Rev. Earth Planet. Sci. 51, 105–129. doi:10.1146/annurev-earth-071822-100323
Ovcharenko, O., Kazei, V., Alkhalifah, T. A., and Peter, D. B. (2022). Multi-task learning for low-frequency extrapolation and elastic model building from seismic data. IEEE Trans. Geoscience Remote Sens. 60, 1–17. doi:10.1109/tgrs.2022.3185794
Ronneberger, O., Fischer, P., and Brox, T. (2015). “U-net: convolutional networks for biomedical image segmentation,” in Medical image computing and computer-assisted intervention–MICCAI 2015: 18th international conference, Munich, Germany, October 5-9, 2015, proceedings, part III 18 (Springer), 234–241.
Ruby, U., and Yendapalli, V. (2020). Binary cross entropy with deep learning technique for image classification. Int. J. Adv. Trends Comput. Sci. Eng. 9, 5393–5397. doi:10.30534/ijatcse/2020/175942020
Sabbione, J. I., and Velis, D. (2010). Automatic first-breaks picking: new strategies and algorithms. Geophysics 75, V67–V76. doi:10.1190/1.3463703
Saragiotis, C., Alkhalifah, T., and Fomel, S. (2013). Automatic traveltime picking using instantaneous traveltime. Geophysics 78, T53–T58. doi:10.1190/geo2012-0026.1
Shan, T., Guo, R., Li, M., Yang, F., Xu, S., and Liang, L. (2021). Application of multitask learning for 2-d modeling of magnetotelluric surveys: Te case. IEEE Trans. Geoscience Remote Sens. 60, 1–9. doi:10.1109/tgrs.2021.3101119
Shinde, P. P., and Shah, S. (2018). “A review of machine learning and deep learning applications,” in 2018 Fourth international conference on computing communication control and automation (ICCUBEA) (IEEE), 1–6.
Socco, L. V., Foti, S., and Boiero, D. (2010). Surface-wave analysis for building near-surface velocity models—established approaches and new perspectives. Geophysics 75, 75A83–75A102. doi:10.1190/1.3479491
Wang, H., Long, L., Zhang, J., Wei, X., Zhang, C., and Guo, Z. (2024a). Seismic first break picking in a higher dimension using deep graph learning. arXiv Prepr. arXiv:2404.08408. doi:10.48550/arXiv.2404.08408
Wang, H., Zhang, J., Wei, X., Long, L., Zhang, C., and Guo, Z. (2024b). Upnet: uncertainty-based picking deep learning network for robust first break picking. IEEE Trans. Geoscience Remote Sens. 62, 1–14. doi:10.1109/tgrs.2024.3439685
Wang, X., Jiang, P., Deng, F., Wang, S., Yang, R., and Yuan, C. (2024c). Three dimensional magnetotelluric forward modeling through deep learning. IEEE Trans. Geoscience Remote Sens. 62, 1–13. doi:10.1109/tgrs.2024.3401587
Wright, P. M., Ward, S. H., Ross, H. P., and West, R. C. (1985). State-of-the-art geophysical exploration for geothermal resources. Geophysics 50, 2666–2696. doi:10.1190/1.1441889
Wu, H., Zhang, B., Li, F., and Liu, N. (2019). Semiautomatic first-arrival picking of microseismic events by using the pixel-wise convolutional image segmentation method. Geophysics 84, V143–V155. doi:10.1190/geo2018-0389.1
Wu, X., Xue, G., Zhao, Y., Lv, P., Zhou, Z., and Shi, J. (2022). A deep learning estimation of the earth resistivity model for the airborne transient electromagnetic observation. J. Geophys. Res. Solid Earth 127, e2021JB023185. doi:10.1029/2021jb023185
Xu, Y., Yin, C., Pan, Y., Ni, Y., Zou, X., and Yang, T. (2021). First-break automatic picking technology based on semantic segmentation. Geophys. Prospect. 69, 1181–1207. doi:10.1111/1365-2478.13088
Yuan, S., Liu, J., Wang, S., Wang, T., and Shi, P. (2018). Seismic waveform classification and first-break picking using convolution neural networks. IEEE Geoscience Remote Sens. Lett. 15, 272–276. doi:10.1109/lgrs.2017.2785834
Yuan, S.-Y., Zhao, Y., Xie, T., Qi, J., and Wang, S.-X. (2022). Segnet-based first-break picking via seismic waveform classification directly from shot gathers with sparsely distributed traces. Petroleum Sci. 19, 162–179. doi:10.1016/j.petsci.2021.10.010
Zhao, B.-l. (2008). Application of multi-component seismic exploration in the exploration and production of lithologic gas reservoirs. Petroleum Explor. Dev. 35, 397–412. doi:10.1016/s1876-3804(08)60088-9
Zhu, L. (2018). pytorch-opcounter. Available online at: https://github.com.
Zhu, W., and Beroza, G. C. (2019). Phasenet: a deep-neural-network-based seismic arrival-time picking method. Geophys. J. Int. 216, 261–273. doi:10.1093/gji/ggy423
Keywords: seismic first break (FB), image semantic segmentation, FB picking, multi-task learning, seismic data reconstruction
Citation: Zhang Z and Yang J (2025) Seismic first break picking based on multi-task learning. Front. Earth Sci. 13:1601134. doi: 10.3389/feart.2025.1601134
Received: 27 March 2025; Accepted: 01 July 2025;
Published: 16 July 2025.
Edited by:
Tariq Alkhalifah, King Abdullah University of Science and Technology, Saudi ArabiaReviewed by:
Jinwei Fang, China University of Mining and Technology, ChinaPeifan Jiang, Chengdu University of Technology, China
Nicoletta D'Angelo, University of Palermo, Italy
Copyright © 2025 Zhang and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zhongpo Zhang, amgtemhhbmd6cC5vc2djQHNpbm9wZWMuY29t
 Zhongpo Zhang*
Zhongpo Zhang* Jing Yang
Jing Yang