- 1Faculty of Mathematics and Natural Sciences, Institute of Mathematics Education, University of Cologne, Cologne, Germany
- 2Faculty of Education, University of Hamburg, Hamburg, Germany
In this exploratory case study, the teaching practices of two secondary level mathematics teachers are examined within the framework of a sequential multi-method design. To this end, data on the teachers’ recurrent patterns of action were collected using video-based classroom observations in problem-solving lessons, semi-structured interviews and video-stimulated recalls. The qualitative analyses of the respective data allowed a differentiated description of the self-reported, observable, and articulable elements of their teaching practices. This includes the requirement situations to which the teachers respond with recurrent patterns of actions, their cognitive and affective dispositions on which they rely, and their situation-specific skills that enable them to adaptively orchestrate their problem-solving lessons. An empirical reconstruction of a selected practice, including a description of its constitutive elements, followed from a superordinate integration of the data by triangulation. This study contributes to the discourse on mathematics teacher education by providing an innovative study design for the empirical reconstruction of teaching practices. Moreover, its findings validate the theoretical assumption that teaching practices are an expression of mathematics teachers’ professional competence and expertise.
Introduction
Teachers’ professional practices play a central role in the teaching of mathematics: For example, when teaching problem solving, experienced teachers draw back on routinized actions and recurrently create conditions conducive to the learning for problem solving, provide problems appropriate to the students’ level of knowledge and support them during their problem-solving process, e.g. by fostering their heuristic skills (Cai and Hwang, 2020; Lester, 2013; Schoenfeld, 2015). The focus of this study is therefore on the analysis of these routinized action patterns of teachers that they use to cope with recurrent requirement situations in problem-solving lessons. Although there are already a number of studies on teaching practices in mathematics teacher professional research (for those that focus on problem solving: Bailey and Taylor, 2015; Schoenfeld, 2015; Schoenfeld, 2020), some of these studies originate from different research perspectives (Da Ponte and Chapman, 2006), each of which emphasizes different elements of practices. On the one hand, this is due to the complexity and elusiveness of this research object and, on the other hand, due to the conceptual vagueness of the term “practices” (Brungs et al., 2023; Hirsch and Buchholtz, 2023; Charalambous and Delaney, 2020; Lampert, 2010). On a methodological level these various research approaches can also be located in different research traditions (Brungs et al., 2023; Hirsch and Buchholtz, 2023). Examples include practice-theoretically oriented classroom research (e.g. Häsel-Weide and Nührenbörger, 2022; Lave and Wenger, 1991), whereby Lave and Wenger’s socio-cultural perspective on learning as participation in communities of practice can be seen as conceptually adjacent to practice-theoretical approaches. Other examples include research on teachers’ expertise and professional competence (Baumert and Kunter, 2006; Bromme, 2001; Hiebert et al., 2002; McDonough and Clarke, 2003; Prediger, 2019; Simon and Tzur, 1997). They each imply different assumptions about the empirical accessibility and decomposition of practices into their integral elements, such as their articulability or observability (Brungs et al., 2023; Hirsch and Buchholtz, 2023). This results in various study findings that relate only to certain elements of practices and can hardly be linked to each other, which makes an empirical reconstruction of teaching practices very challenging in general. In qualitative social research, empirical reconstruction means that a particular social or professional process is reconstructed on the basis of the collected empirical data (e.g. observations, interviews, video analyses) in order to understand its structure and dynamics. The focus is not only on description, but also on understanding how certain practices are constituted and which elements constitute them (cf. Bohnsack, 1999). A central goal of empirical reconstruction is to uncover the implicit knowledge and rules of social action that the actors themselves are often not fully aware of.
In this study, we empirically reconstruct selected teaching practices of two secondary level mathematics teachers by triangulating data from video-based classroom observations, semi-structured interviews, and video-stimulated recalls (Muir, 2010; Powell, 2005; Radišić and Baucal, 2016). In doing so, different methodological approaches were combined in a sequential multi-method design (Buchholtz, 2021; Creswell and Plano Clark, 2011; Hunter and Brewer, 2003), which proves to be a coherent and effective strategy (Buchholtz, 2019; Even and Schwarz, 2002). This exploratory and innovative design enables a detailed analysis of teaching practices, allowing for a deeper understanding of their structure and dynamics. In doing so, it addresses a research gap, as previous studies have focused on fewer elements of teaching practices and did not integrate multiple methodical approaches in their investigation. Moreover, the theoretical conceptualization of teaching practices as described below can be empirically validated, which is another aim of the present study. This contributes to the clarification of the concept of practice which remains a contested and ambiguous construct in mathematics teacher professional research (Charalambous and Delaney, 2020).
Theoretical background
In the first subsection, teaching practices are conceptualized from the perspective of teacher professional research. In this respect, one important element of teaching practices is the (recurrent) requirement situation in a specific teaching context. To this requirement situation, a teacher reacts, as it poses a professional demand that requires situational judgment and adaptive action. Therefore, the requirement situations in problem-solving lessons will be addressed in the second subsection. These can serve as a starting point for the empirical reconstruction of selected teaching practices in problem-solving lessons.
Teaching practices and their empirical reconstructability
Teaching practices as part of the professional activities of mathematics teachers have become a central subject of mathematics teacher professional research in recent years (Charalambous and Delaney, 2020; Grossman, 2018). Despite its central importance, however, the concept of practices is often not used consistently and is rarely conceptualized or defined comprehensively (Brungs et al., 2023; Hirsch and Buchholtz, 2023). In the literature on the professional development of teachers, Lampert (2010) identified four conceptualizations of the term “practice” (see also Charalambous and Delaney, 2020). Practice can be understood in contrast to theory, as a synonym for rehearse, as an exercise of a profession and as a habitual action. The latter understanding of practices, which are understood here as recurrent patterns of actions, plays a special role in research on teaching and learning (Bromme, 2001; Grossman, 2018; Häsel-Weide and Nührenbörger, 2022; Kolbe et al., 2008; Moschkovich, 2004; Prediger, 2019; Rabenstein, 2020). Here, practices are ascribed a specific function, which is understood differently depending on the research perspective or tradition. From a practice-theoretical perspective, practices serve social interaction within a specific (socio-cultural) context (Breidenstein, 2023; Häsel-Weide and Nührenbörger, 2022; Kolbe et al., 2008; Lave and Wenger, 1991; Saxe, 1999; Schatzki, 2012). Students and teachers are equally involved in a practice and, conversely, are influenced by it in their actions. The empirical reconstruction of practices therefore seems particularly useful through (video-based) classroom observations or ethnographic approaches (Breidenstein, 2023; Häsel-Weide and Nührenbörger, 2022; Lave and Wenger, 1991).
On the other hand, from the perspective of subject-specific research on teachers’ expertise and professional competence, teachers employ routinized action patterns to address recurrent instructional requirement situations—professional demands that are specified concerning the concrete content and contexts of mathematics lessons (Bromme, 2001; Krauss, 2020; Prediger, 2019). When teachers effectively manage these specific requirement situations, considering the temporal contingency and complexity of the classroom, they provide students with various learning opportunities from which they can benefit. This deliberate and targeted exercise of practice reflects a teacher’s expertise (Stigler and Miller, 2018). To achieve this, teachers utilize pedagogical tools (Llinares, 2002). These are, for example, digital and analog artifacts in the form of worksheets, tasks or digital resources (Prediger, 2019; Ruthven, 2014). Furthermore, it is often assumed that there is an interdependent relationship between the human body and practices, which thus contain a strong performative component (Kolbe et al., 2008; Moschkovich, 2004; Rabenstein, 2020). Pedagogical tools therefore also include verbal impulses (see also Llinares, 2002).
In order to adequately identify and reflect on requirement situations and address them with specific action patterns, teachers draw on certain cognitive dispositions in the form of professional knowledge, which they activate and utilize in situ as they engage with the dynamics of the classroom (Kolbe et al., 2008; Ball and Forzani, 2009; Moschkovich, 2004; Prediger, 2019; Rabenstein, 2020; Simon and Tzur, 1997). In a teaching situation, this happens to a certain extent unconsciously and implicitly (cf. e.g. Polyani, 1966), but through subsequent reflection on a situation, a teacher can become aware of both implicit and explicit knowledge (Schoenfeld, 2011; Cianciolo and Sternberg, 2018) and then transfer this awareness to other, similar situations. Teachers can also become aware of parts of the affective dispositions that come into play in such situations (Kolbe et al., 2008; Moschkovich, 2004; Prediger, 2019) by reflecting on a situation. For the empirical investigation of practices, this means that they can also be methodically determined through self-reports and can be articulated to a certain extent (Prediger, 2019).
The importance of the cognitive and affective dispositions that teachers draw on when carrying out their practices is weighted differently depending on the research perspective. The role of situation-specific skills, commonly known as perception, interpretation and decision-making, is less frequently addressed in this context (Blömeke et al., 2015). Nevertheless, these skills play an important role in coping with requirement situations (Carlson et al., 2020; Schoenfeld, 2015), as they mediate between a teacher’s dispositions and their teaching actions (Blömeke et al., 2015; Blömeke et al., 2022). When repeatedly performing a practice, a teacher must always make minor adjustments to their established practices due to the situation-specific nature of these requirement situations, so that although these are recognizably repeated as recurrent patterns of action, they always appear slightly different in detail and develop and refine further on the basis of experience (Rabenstein, 2020; Alonzo et al., 2020). In this way, the teacher develops their expertise over time, as they can react adequately and adaptively to every structurally similar situation (Alonzo et al., 2020). Methodologically, these often-unconscious cognitive processes shaped by experience can be investigated in teacher professional research using video-stimulated recalls (Muir, 2010; Powell, 2005; Radišić and Baucal, 2016), in which teachers observe their own or others’ lessons and reflect on them using targeted prompts (Kersting et al., 2010).
In the review study by Brungs et al. (2023), these and other theoretical descriptions as well as constitutive elements of teaching practices from different research perspectives were collected and linked in a preliminary conceptualization of this complex research object. Afterwards, it was discussed with respect to important findings of mathematics teacher professional research. The central result of this review study was an integrative theoretical conceptualization of teaching practices which acknowledges their complexity. According to this, teaching practices are “routinized, recurrent patterns of utterances and actions by teachers to cope with certain requirement situations in a specific teaching context. They are constituted by the adaptive planning, enacting and reflecting of pedagogical decisions that serve to cope with the respective requirement situation. The conscious and unconscious affective and cognitive dispositions of teachers and their situation-specific skills play a key role in this. When performing practices, a teacher also draws on their own body and suitable pedagogical tools. Practices are part of a teacher’s expertise and can be learned in the long term through deliberate repetition and adaptation in similar requirement situations, for example when available routines or (action) patterns are gradually internalized” (Brungs et al., 2023, p. 60, translated by the first author).
Figure 2 shows an adapted model developed in Brungs et al. (2023) to visualize corresponding teaching practices.
This model is grounded in teacher expertise research and is suitable for analyzing and reconstructing teaching practices in a differentiated way. It is also based on the well-known model of competence as a continuum by Blömeke et al. (2015) and integrates central elements of the Refined Consensus Model of PCK grounded in science education (Carlson et al., 2020), such as planning, enacting and reflecting, in order to reflect the complexity of teaching actions in a practical way. As this model and the underlying theoretical conceptualization of teachings practices has not yet been empirically validated, the present study aims to do so using the example of problem-solving lessons.
Requirement situations for teaching problem solving
A recurrent requirement situation for teaching problem solving is the adequate selection and preparation of a problem for mathematics lessons (Cai and Jiang, 2017). Mathematical problems are “(usually open) situations that can be roughly divided into an initial and final state, as well as the path between these two states, and which cannot (easily) be solved by the respective processor with a standard procedure (an algorithm), as there is a ‘barrier’ ” (Rott, 2015, p. 31, translated by the first author). Accordingly, problem-based tasks are designed to be open, i.e. there are different possible solutions that cannot be worked out using facts and procedures that are already known, and the solution process provides students with numerous learning opportunities (Clarke and Sullivan, 1992). When teachers select and prepare a mathematical problem for their lessons, they need specific problem-related knowledge (Chapman, 2015).
Based on their selection and preparation of mathematical problems, teachers need to plan their problem-solving lessons accordingly. In doing so, they can use various models that structure the students’ problem-solving process (cf. Fernandez et al., 1994; Jacinto and Carreira, 2017; Mason et al., 2006; Pólya, 1949; Rott et al., 2021; Schoenfeld, 1985; Yimer and Ellerton, 2010), which can provide some orientation. If teachers are guided by these models, the exposition of the mathematical problem at the beginning of the lesson, for example, is one of the structuring features of problem-solving lessons. It is generally agreed that students need to engage with the problem in order to understand it (cf. e.g. Jacinto and Carreira, 2017; Pólya, 1949; Rott et al., 2021; Schoenfeld, 1985). This engagement must be facilitated and, if necessary, encouraged by the teacher. Other phases of the lesson relate to the individual or collaborative development and implementation of a plan for the solution (cf. e.g. Fernandez et al., 1994; Jacinto and Carreira, 2017; Mason et al., 2006, Rott et al., 2021; Yimer and Ellerton, 2010). Finally, the compilation and comparison of solution approaches as well as joint reflection in the context of a review are also central to the planning of problem-solving lessons (Jacinto and Carreira, 2017; Mason et al., 2006; Pólya, 1949; Rott et al., 2021). Especially when reflecting on solution processes, it is important to address strategic (so-called heuristic) aspects that could be used again in other contexts or when transferring to other tasks, and not just to focus on content-related aspects in the solution process (Heinrich et al., 2013).
Although this description of the common ideas in various models on problem-solving processes indicates a specific order of the different phases a problem-solver experiences, the researchers above have “different understandings of how these phases are related and sequenced” (Rott et al., 2021, p. 740). For teachers who have to plan a problem-solving lesson, this means they need to maintain a certain level of flexibility regarding the conduction of their lesson. When conducting the lesson—another recurrent requirement situation—it is of central importance for the teacher to analyze the students’ problem-solving processes in order to diagnose possible ways of thinking and difficulties. For this analysis, teachers might draw on the descriptive model by Rott et al. (2021), which provides “valuable insights into problems solving processes of students” and enables “to compare, contrast, and characterize the idiosyncratic characteristics of the students’ PS [problem-solving] processes” (Rott et al., 2021, p. 751). Based on the outcomes of this analysis, the teachers have to react accordingly through scaffolding and feedback. Thereby, teachers should always encourage their students to engage in self-reflection and metacognitive regulation, to ask questions and to explore their own solutions. This requires specific (content) knowledge of mathematical concepts and procedures, but above all also of specific heurisms of problem solving and (meta-) cognitive strategies (Chapman, 2015; Kilpatrick et al., 2001; Mayer and Wittrock, 2006; Schoenfeld, 1985; Schoenfeld, 2015). In addition, certain beliefs are also involved in teaching problem solving in the classroom (Dougherty, 1990; Mayer and Wittrock, 2006; Rott, 2016), such as beliefs about mathematics, problem solving itself and one’s own problem-solving skills (Chapman, 2015).
Research questions
Our research questions relate to the elements of teaching practices in problem-solving lessons that can be reconstructed using different empirical methodological approaches. This can expand our current understanding of the complex research object of teaching practices, as they to our knowledge have not been studied this way before. Furthermore, the present study might help to gain more insights in currently performed teaching practices and instructional decisions in problem-solving lessons, which serves as an exemplary context for the empirical reconstruction.
RQ1) What elements of teaching practices do teachers report in semi-structured interviews directly following their problem-solving lessons?
RQ2) What elements of teaching practices for problem solving can be captured through video-based classroom observations?
RQ3) Which elements of selected teaching practices do teachers articulate in the context of video-stimulated recalls?
RQ4) How do the three different approaches in RQ1–RQ3 complement each other on a methodological level with regard to the empirical reconstruction of selected teaching practices?
After approaching different elements of teaching practices more broadly with RQ1 and RQ2, the focus of RQ3 and RQ4 lies on selected teaching practices due to a methodological orientation and corresponding decisions.
Methodology
Study design
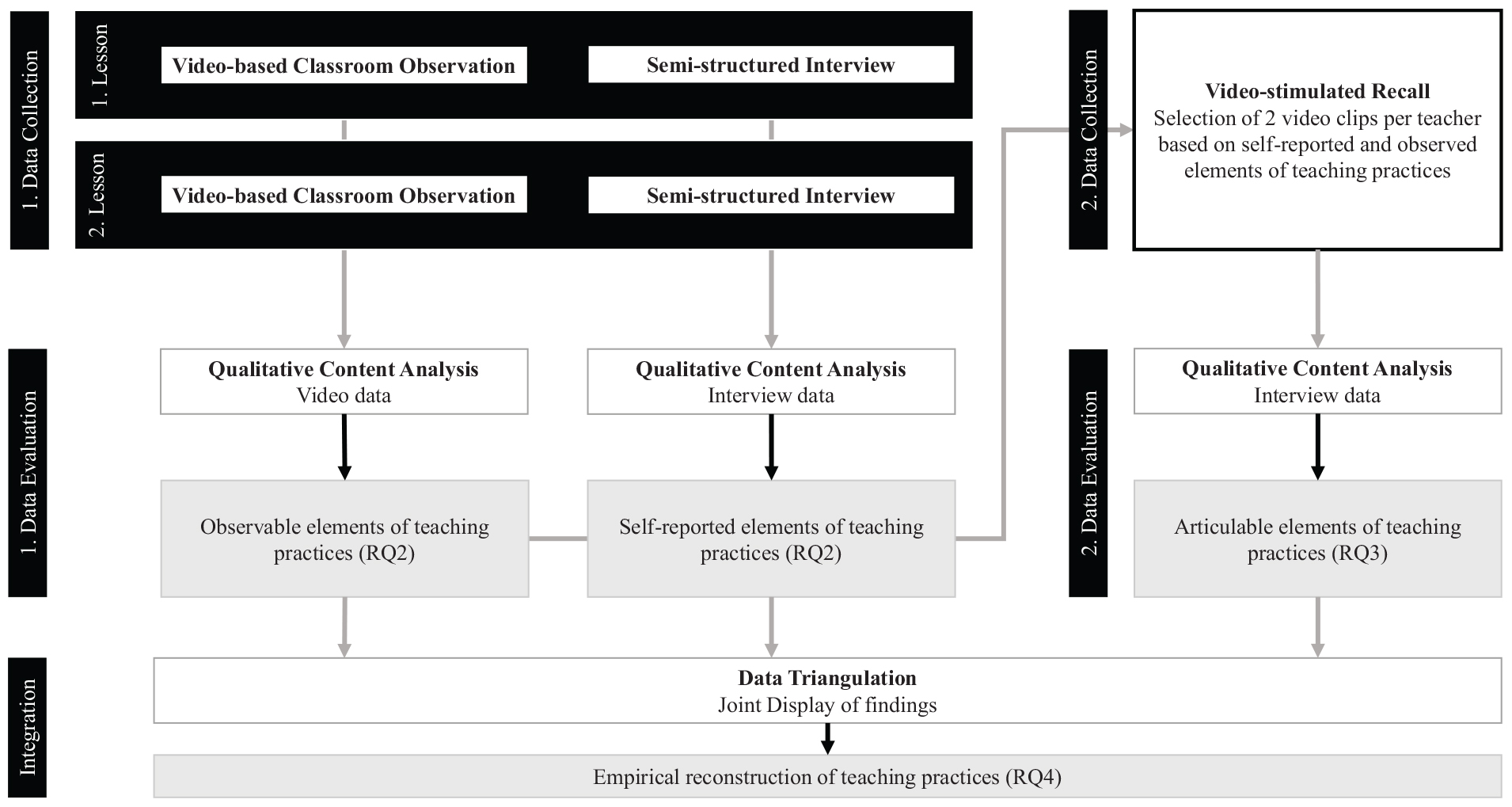
To answer our research questions, a case study with a multi-method design was chosen (Figure 1), in which various qualitative data collection and evaluation approaches were linked and integrated sequentially (Buchholtz, 2019; Creswell and Plano Clark, 2011; Hunter and Brewer, 2003).
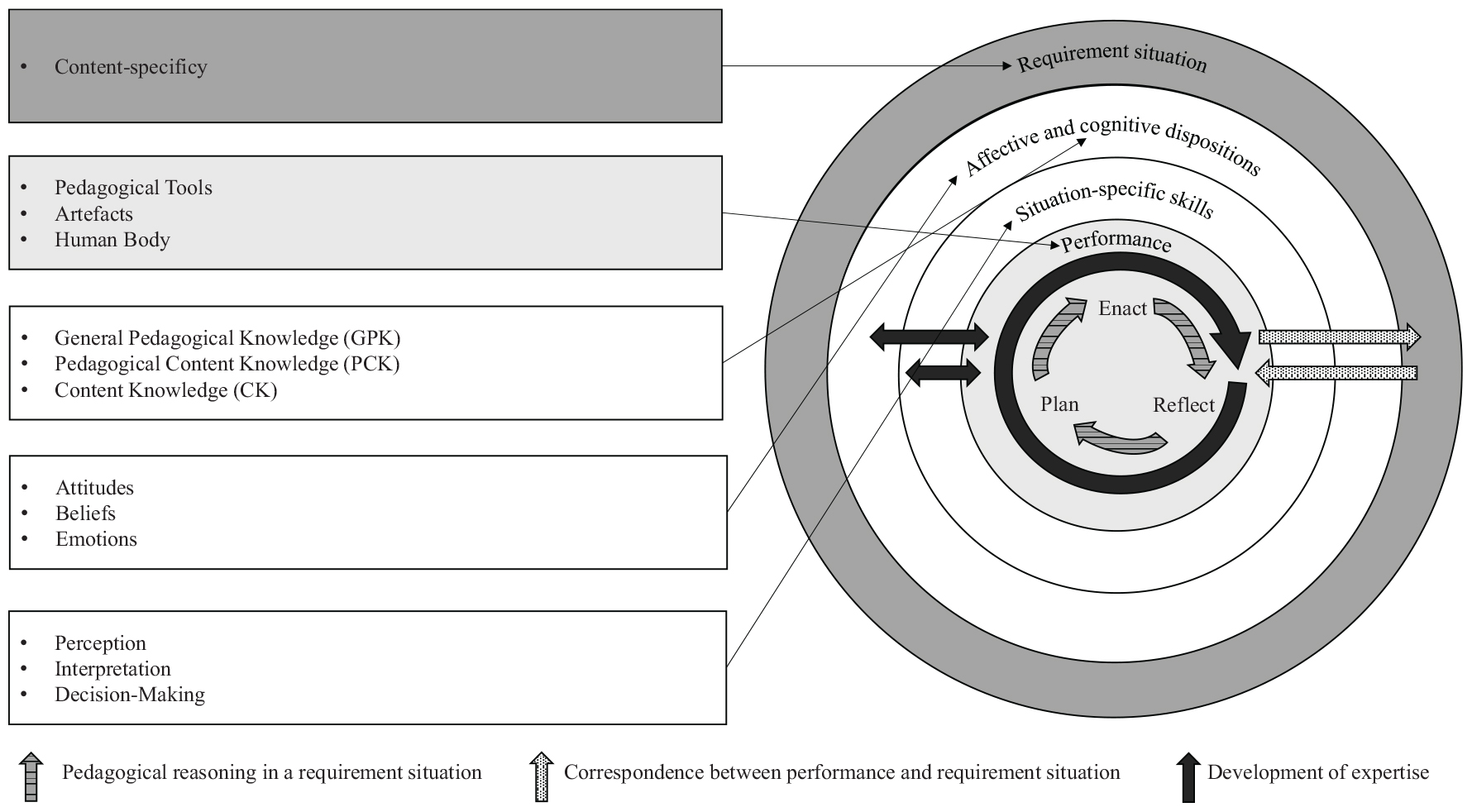
Figure 1. Professional-theoretical understanding of teaching practices (Brungs et al., 2023).
The upper section of Figure 1 describes two time periods for the data collection in this study: First, in December 2023 two problem-solving lessons per teacher were recorded using video-based classroom observations. Each was followed by a semi-structured interview referring to the observed lesson directly after each lesson. Additional data were collected through video-stimulated recalls. This data collection took place in January 2024 because, by that point, the analysis of the first data had to be completed in order to use two video clips per teacher in the video-stimulated recalls. The respective data evaluations are described in the middle section of Figure 1. All collected data were analyzed using qualitative content analysis in order to answer RQ1–RQ3. The results feed the methodical integration of findings during the triangulation of our various data sources into a joint display, which serves to answer RQ4. This is illustrated in the lower section of Figure 1.
Data collection
Two teachers from (North Rhine-Westphalia, Germany), both with many years of professional experience, participated in the study (Table 1). They were selected, among other reasons, because teaching experience is considered a key indicator for the development of teaching practices and professional expertise (Palmer et al., 2005). Furthermore, both teachers showed a particular commitment to problem-solving instruction, suggesting that their practices are potentially well-developed and indicative of long-term expertise. Given the time-consuming and resource-intensive nature of empirically reconstructing teaching practices, the sample size had to be kept small.
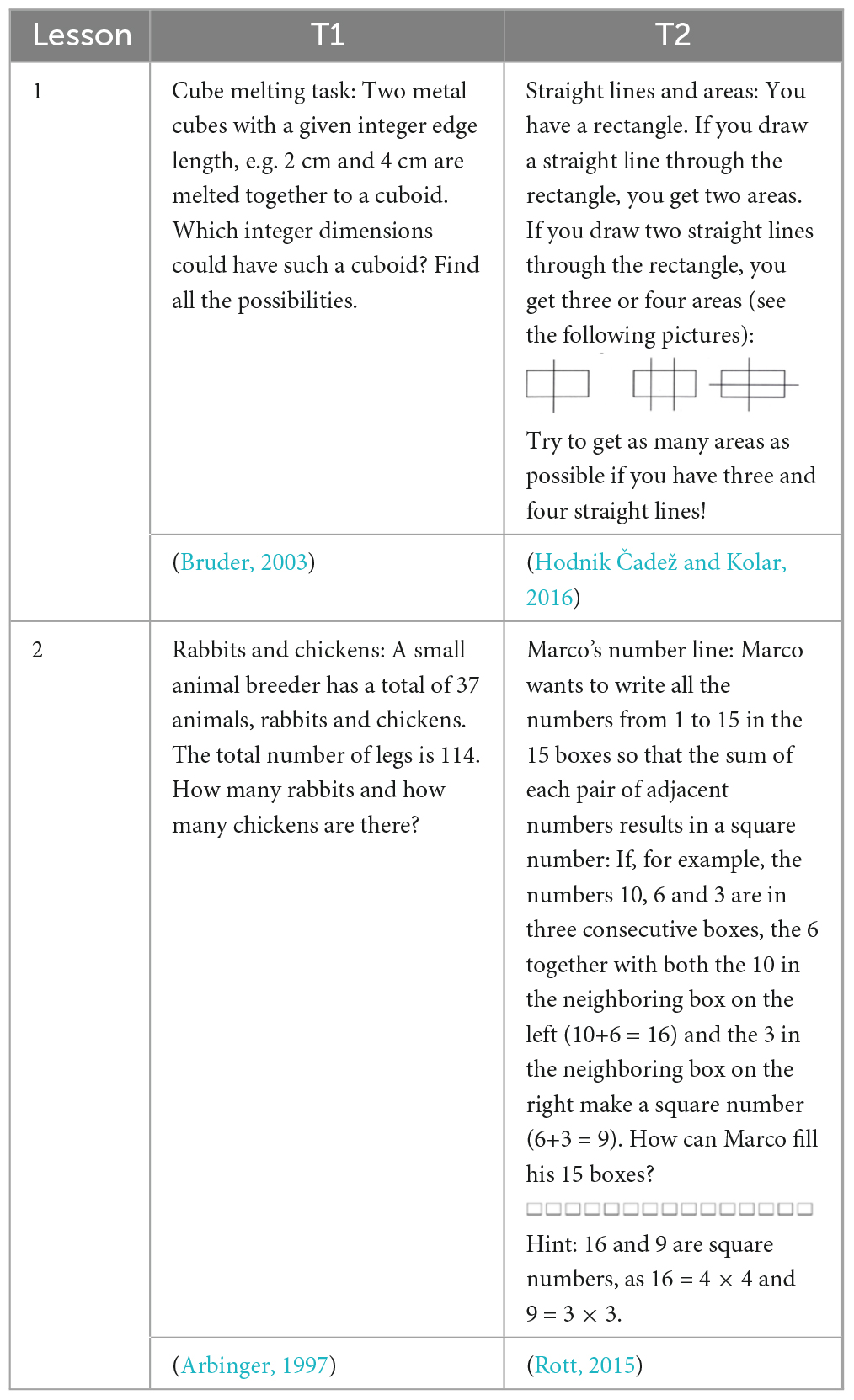
In the first data collection, a video-based classroom observation took place (Klette, 2023). It was carried out for each teacher in two consecutive lessons of 45 min each, in which the teachers focused on problem solving. The planning and methodical design of the lessons were largely up to them; they were only required to use a mathematical problem from a predefined task catalog which was based on problem-solving literature. The tasks were compiled appropriately for the grades the teachers were teaching in (grades 5 and 9 in a secondary school). According to the individual requirements of their students, the teachers selected the following tasks (Table 2).
In order to answer RQ2, one portable camera (GoPro) and two permanently installed cameras were used in every lesson for the video-based classroom observations (Klette, 2023). After each lesson, the teachers participated in a semi-structured interview which aimed to answer RQ1. In each interview a theoretically based interview guide was used (see Supplementary Appendix A), which was designed by using research literature on the development of interview guides (Helfferich, 2011). The first question was a narration-generating one which focused on the problem-solving lesson itself. Follow-up questions focused on deviations from the teachers’ lesson plan. This transitioned to an information question targeting recurrent requirement situations: “Was there a situation today during the problem-solving lesson that you managed routinely or required actions you perform regularly?” This aimed to direct the teachers’ attention to situations they routinely handled. Additional prompts helped the teachers to identify these specific situations. Once identified, teachers were asked how they responded to them and what actions were required.
In the second data collection, which aimed to answer RQ3, two video clips were selected per teacher, each showing a pattern of action for coping with the same requirement situation in the first and second lesson. These patterns had also been described by the teachers in the semi-structured interviews, so that the triangulation of data was possible in further analyses. For T1, video clips about instructing a retrospective review of the students’ problem-solving process was selected, for T2, the video clips focused on guiding the problem-solving process. The corresponding video clips were used as part of video-stimulated recalls (Muir, 2010; Radišić and Baucal, 2016) to examine articulable elements of teaching practices (i.e. reflective thoughts and feelings) (Powell, 2005). Each teacher was first shown a video clip on which they were then asked to comment in a semi-structured interview. The questions from the interview guide (see Supplementary Appendix B) relied on the conceptualization of practices on which this study is based (Brungs et al., 2023). Because of that, they can be assigned to the following main themes: (1) requirement situation and performance, (2) Pedagogical decisions, (3) cognitive and affective dispositions, (4) situation-specific skills, and (5) development of practices and expertise. To ensure the accuracy of the questions in the second interview guide as well, research literature on the development of interview guides was revisited again (Helfferich, 2011). After answering these questions, each teacher was shown a second video clip. Afterwards they were asked to compare both video clips and formulate any similarities and differences they perceived. In this way, they articulated situation-specific adaptive aspects of the presented practices.
Data evaluation
When evaluating the data from the first data collection, the interviews were transcribed and then analyzed using qualitative content analysis according to Mayring (2022). The aim of this analysis was, in the sense of RQ1, the identification of self-reported elements of practices which were further processed into an inductive category system (see Supplementary Appendix C). The development of this category system was inspired by the research on teaching practices (cf. e.g. Brungs et al., 2023) and on recurrent requirement situations in problem-solving lessons (cf. Cai and Jiang, 2017; Rott et al., 2021). One example of an inductive category in this system is guiding the problem-solving process, which is defined as a report of a recurrent requirement situation to which the teacher responds with a pattern of action in which he or she guides the problem-solving process of all students. More details about this category and others will be provided in the results section for RQ1.
Next, the video data was evaluated, again using qualitative content analysis (RQ2). In a first step, the recurrent patterns of actions were coded in the performance, i.e. the observable behavior of the teachers. The findings were processed in another inductive category system, which was again inspired by the research on teaching practices and on recurrent requirement situations in problem-solving lessons (see Supplementary Appendix D for the category system). An example for one inductive category in this system is the activation of students’ prior knowledge, which is defined as observable behavior of a teacher in which they react to a recurrent requirement situation with a pattern of action that activates the students’ prior knowledge. For more details about this and other categories, see the results section for RQ2. The corresponding video sequences for each category were provided with time stamps and then subjected to a second step of analysis. Its aim was to determine the pedagogical tools which the teachers used to shape their practices (Llinares, 2002; Prediger, 2019). The deductive categories used for this second analysis of the video were (1) analog artifacts, defined as the intentional use of objects or materials in physical form to facilitate problem-solving instruction, (2) digital artifacts, defined as the intentional use of objects or materials in digital form to facilitate problem-solving instruction, (3) body language, defined as the intentional use of the teacher’s physical gestures and movements to facilitate problem-solving instruction, and (4) verbal impulses, defined as the intentional use of verbal cues by the teacher to facilitate problem-solving instruction. Afterward, the interview data from the second data collection (video-stimulated recalls) were transcribed and analyzed qualitatively. The deductive category system used to answer RQ3 was as well based on the conceptualization of practices in this study (Brungs et al., 2023). Therefore, it contains main categories that relate to the main themes of the interview guide used for the second data collection. For each main category, multiple subcategories were formulated. These reflect the elements of teaching practices as described in Figure 2. The main category situation-specific skills, for instance, had the subcategories perception, interpretation, and decision making.
Finally, to answer RQ4, selected findings and information regarding RQ1–RQ3 were integrated within a joint display, i.e. a structured representation (Creswell and Plano Clark, 2011). It’s overarching goal is to represent the triangulation of various data and to provide a deeper understanding of the overall findings (Guetterman et al., 2015). By doing so, we demonstrate how the methodological approaches to the empirical reconstruction of teaching practices complement each other.
Results
We first present the results in relation to the self-reported elements of teaching practices (RQ1). As an example, the self-reported elements of a selected teaching practice are presented, which was used in both lessons by T2 to cope with the same requirement situation. This practice is repeatedly taken up in the following sections on RQ2 and RQ3 in order to present the respective findings in a coherent form. Moreover, this enables to integrate all data for one teaching practice in a joint display to answer RQ4.
RQ1: self-reported elements of teaching practices
In the semi-structured interviews, the teachers commented on six recurrent requirement situations to which they reacted in their lessons with routinized patterns of action (see Supplementary Appendix C). These requirement situations align with research on teaching problem solving (see chapter 2.2). For T1, one such situation is the encouragement to deal with a mathematical problem. He reports that he has to motivate his students “again and again frequently” (translated by authors, T1, R1, 4). T2 reports a second requirement situation, describing that he is able to guide the problem-solving process of his students through repeated “intermediate checks for understanding” (translated by authors, T2, R1, 4) in the sense of a focused intervention. In addition, both teachers report the recurrent requirement situation of instructing a retrospective review of the students’ problem-solving process, in which they collect the results of their students. Both teachers also reported routinized support for their students in the problem-solving process. On the one hand, this support refers to individual students (Individual support in the problem-solving process), to whom they “give hints for self-discovery” (translated by authors, T2, R1, 8), for example, in the form of feedback, and on the other hand to groups of students, to whom they provide helping cards as a scaffold (Group-related support in the problem-solving process) (T1, R1, 4). Finally, one teacher reported repeatedly promoting the mathematical language (T2, R2, 8) of his students (Language promotion in the problem-solving process).
Overall, the analysis of the semi-structured interviews revealed that there are some recurrent requirement situations and patterns of actions that both teachers reported after conducting their problem-solving lessons. Some other elements of practices were specific for the self-report of either T1 or T2. The recurrent guidance of the problem-solving process described by T2 in the first interview is one specific example and will be discussed in more detail below in order to illustrate the correspondence between the requirement situation and the teacher’s routinized pattern of action.
T2 selected a variation of the task “Straight lines and areas” (Table 2) in his first lesson. After the teacher has mentioned the “intermediate checks for understanding” (translated by authors, T2, R1, 4) as a routinized pattern of action, he reports in the interview on how exactly he coped with the situation of guiding the problem-solving process:
“I wanted to transfer the two straight lines to the blackboard and […] put the idea into words […] that it could have something to do with intersections of the […] straight lines.” (translated by authors, T2, R1, 4).
The teacher reports that he discusses an idea for the mathematical solution to the task with the students in a focused intervention, concentrating on its structural nature and the change of mathematical representations. Using an inductive approach, he also initially chooses an example that is easy to solve as part of the problem-solving task (investigating the number of areas that are created with initially only two straight lines), which he works out together with the students. By doing so, the teacher draws on heuristic strategies, namely informative figures and working forward step by step, which are crucial for problem-solving lessons (Rott, 2015). Moreover, the teacher wants to provide his students mathematical and verbal support in their problem-solving process, as he assumes that the students may have difficulties finding their own approach. This is suggested by the following quote, in which the teacher retrospectively evaluates his actions as successful:
“Many children discussed this, but were unable to name it, that it was due to the intersections. […] When this then became a topic, the [students] were much more focused on intersections in the second phase with the three [straight lines].” (translated by authors, T2, R1, 4).
After the second lesson, in which a variation of the task “Marco’s number line” (Table 2) was worked on, the teacher reported the same routinized action pattern that he drew on to intervene in guiding the problem-solving process of his students:
“Yes, introducing the type of task [is an action pattern]. Adding up the numbers from 1 to 5 [and asking:] Has a square number now resulted? I think that was the first time some students understood what it was all about. That was the common setting. Um, that wasn’t actually planned, but it was necessary after about 10 min in order to work in a targeted way.” (translated by authors, T2, R2, 4).
The teacher’s comments again illustrate the correspondence between the routinized action pattern and the perceived requirement situation. He noticed some students not yet working in a goal-oriented manner and assumed that this was due to a lack of understanding of the task. He therefore interrupts his students’ problem-solving process with a focused intervention in which the structure of the task is discussed again using a simple minimal example. The teacher discusses with the students what the solution to the task requires of them, with the intention of enabling them to continue working on the task and take the necessary steps to generalize the minimal example by setting clearer goals.
RQ2: observable elements of teaching practices
In a first step, a total of 126 sequences were identified in the video data in which the teachers reacted to requirement situations they perceived by means of recurrent patterns of action. Thereby, 66 sequences were identified for T1 and 60 sequences for T2. While T1 performed most of his patterns of actions in order to provide group-related support in the problem-solving process of his students (47 sequences), T2 focused more on individual support throughout the problem-solving lesson (43 sequences). The inductively determined categories that describe these patterns can be found in Supplementary Appendix D. Thereby, five of the six self-reported elements of practices could be retrieved in the observation. In addition, two further elements of practices were observed: T1 activated his students’ prior knowledge in both lessons by addressing previously known content at the beginning of each of his lessons (Activation of students’ prior knowledge). In both lessons, T1 and T2 also referred to future lessons by means of an announcement and a homework assignment (Giving an outlook).
The identified sequences in the data were then analyzed in a second step with regard to the pedagogical tools that the teachers used to perform their patterns of actions. In sum, T1 and T2 both drew on their body language, verbal impulses as well as on digital and analog artifacts, although not every action contained all of these tools. In the following, we present the correspondingly identified observable elements within the action pattern of “intermediate checks for understanding” (T2, R1, 4), which T2 used in his first lesson to guide the problem-solving process. Table 3 shows the relevant sequence from the video and provides a description of the interaction that could be observed around these scenes.

Table 3. Analysis of the action pattern for guiding the problem-solving process in the first lesson.
In the first scene, the teacher uses his body language to attract the attention of his students. Then, he interrupts his students’ problem-solving processes by announcing a short break and asking for a possible solution to a specific simple case of the problem (minimal example) (verbal impulse). Therefore, the teacher starts to perform his practice using his own body and voice, which emphasized the physical dimension of practices as assumed in the theoretical background of this study (Kolbe et al., 2008; Moschkovich, 2004; Rabenstein, 2020). The projection of the worksheet visible at this point (digital artifact), on which the solution to the problem for a pattern with one straight line has already been drawn, serves as a possible orientation for the students in the subsequent discussion. The worksheet is also available to the students in physical form (analog artifact). In the second scene, the teacher uses a tablet and a pen that are connected to the whiteboard (digital artifacts) so that solutions become visible to all students in the class. So, the teacher combines both, digital and analog artifacts as it is reported in research literature on teaching practices (Prediger, 2019; Ruthven, 2014). Finally, in the third scene, the teacher again uses his body language to direct the students’ attention in the classroom discussion: He makes it clear who he is asking to take a turn by looking at the student and, when she does not respond, by mentioning her name (verbal impulse). After the student has responded, the teacher draws the class’s attention back to the board by asking them (verbal impulse) to enter the number on the tablet, where the corresponding entry becomes visible. In this way, the teacher interlinks the mathematical problem and the iconic representation on the worksheet. At this point, the close interaction between the teacher’s dispositions and skills as well as the pedagogical tools he uses to guide students problem-solving process becomes visible (Brungs et al., 2023). When the teacher asks for a second solution for a different number of people, he implicitly offers the students a scaffold for generalizing the procedure already discussed. The teacher thus uses the systematic collection and reflection of his students’ results in a targeted manner and continues the action pattern (Table 4).

Table 4. Further analysis of the action pattern for guiding the problem-solving process in the first lesson.
In this scene, it can be observed that the teacher uses his body language and verbal impulses again when discussing the differences between the two solutions with two straight lines. He then releases the students back into the problem-solving process.
This teacher’s pattern of action is routinized to the extent that he uses it again in a similar form to cope with the situation when the requirement situation arises again. In the second lesson, the same observable elements could be identified when guiding the problem-solving process (Table 5). Thus, we can see again that the teacher combines different pedagogical tools to perform his practice in this second lesson, as it was assumed by Brungs et al. (2023).

Table 5. Analysis of the action pattern for guiding the problem-solving process in the second lesson.
In the first scene of the sequence, the teacher uses a bell (analog artifact) to draw the attention of his students. The projection of the mathematical problem behind him (digital artifact), serves as an orientation and memory aid for the students. The teacher now explains to his students why he has interrupted their problem-solving process and asks for an explanation of the given task (verbal impulse). In the second scene, the teacher interrupts the student’s answer with a shake of the head and a raised index finger (body language). He gives a hint (verbal impulse) and the student corrects herself. In the third scene, however, no one responds to the new verbal impulse. The teacher therefore provides the students again with a minimal example, which he writes on the board (analog artifacts). When solving the example, the teacher integrates the students’ solutions and then continues the sequence as follows (Table 6).

Table 6. Further analysis of the action pattern for guiding the problem-solving process in the second lesson.
In this fourth scene, the teacher again uses verbal impulses and his body language to focus his students’ attention in the plenary discussion. The teacher pays attention to appropriate formulations in order to avoid misunderstandings in the mathematical language.
Overall, the routinized pattern of action that can be observed in both problem-solving lessons can be described as follows: The teacher interrupts his students’ problem-solving process after a certain time and initiates a teacher-centered plenary discussion in which he works out the generalization of mathematical ideas step by step/inductively together with the students. Depending on the problem-solving task, he draws on a minimal example and works out the structural nature of a mathematical solution approach. His focused intervention is based on the students’ previous results and he uses various stimuli in the form of language, body language and artifacts to focus his students’ attention. He integrates the students’ interim results into the development process in an activating way, placing particular emphasis on the use of mathematical terminology and also intervening to correct this. After he has verbally ensured the students’ understanding, he gives them an impulse for further work, in which the students generalize the solution approach independently and then releases them back into their problem-solving process.
RQ3: articulable elements of teaching practices
The video-stimulated recall lasted 27:40 min for T1, while T2 took 33:09 min. Both teachers were able to reflect in detail on their patterns of actions they were shown as a stimulus. In the following section, the results of T2 are discussed in order to provide a comprehensive insight into the nature of the routinized action pattern described above. After watching the first video sequence [the “intermediate checks for understanding” (translated by authors, T2, R1, 4)], the teacher was asked about the reason for his routinized actions in this situation. He answered this question as follows:
“[…] many students made […] the same portion size in different patterns. So they placed the two parallel straight lines then diagonally parallel, almost parallel or something else, um, and not […] provided with an intersection […]. And that were just too many for me at that point.” (translated by authors, T2, VSR, 14).
The teacher therefore noticed in the sequence that many students did not take any further, goal-oriented solution steps after initially approaching the solution to the problem (perception), and he assessed the number of students with problems as too high (interpretation). In his opinion, it was therefore necessary to guide his students’ problem-solving process (decision making). So, in this turn T2 drew back on his situation-specific skills that were theoretically described by Blömeke et al. (2015).
He coped with this requirement with a focused, planned intervention (correspondence). In the lesson, he pursued the goal “that the [students] get a bit of a grip on the intersections for themselves” (translated by authors, T2, VRS, 14). The teacher goes on to specify this goal as follows:
“So […] that the number of sections could have something to do with the number of intersections, yes, I wanted to share that with them on the journey.” (translated by authors, T2, VRS, 18).
He therefore deliberately wanted the students to discover the connection between the number of sections and the number of intersections that arise when an object is divided by a straight line “until the bell rings” (translated by authors, T2, VRS, 18). T2 adaptively planned the corresponding intervention to achieve his goal based on his ad hoc perception in the lesson (plan). This becomes clear in his answer to the question about the degree of planning of his action, in which he describes the goal-oriented implementation of his action (enact).
“So […] the idea that it’s about the intersection actually only emerged at that point, um, to actually make it clear to the students that these different patterns [exist]. So it was more or less [a] reaction to what they brought.” (translated by authors, T2, VSR, 18).
However, in the video-stimulated recall, T2 initially reacted with laughter when asked whether he had achieved the goal he had pursued at the end of the lesson. He reflected that the students who had already drawn different patterns in the lesson were confirmed in their own approach by his intervention (reflect). The teacher went on to say that all the other students had probably realized that the straight lines could intersect, as they had “clearly corrected and supplemented” their initial work results with two or three intersections (translated by authors, T2, VSR, 24). By doing so, the teacher commented on all aspects of pedagogical reasoning, i.e. planning, enacting and reflecting (Carlson et al., 2020). Nevertheless, T2 limited the success of his practice in retrospect:
“But whether everyone really went out [with the realization of the connection between the number of intersections and the number of pieces] […] I don’t think so.” (translated by authors, T2, VSR, 22).
Thereby, T2 provides an example for the difference between reflection-in-action and reflection-on-action as described by Schön (1983).
Next, the teacher was asked about his cognitive dispositions, i.e. his professional knowledge (cf. Shulman, 1987) that he drew on in the situation presented. Instead of answering the relevant question directly, the teacher commented on various alternative courses of action that would have been available to him in this situation. For example, he described the question he asked his students as “completely improperly posed” and suggested “that it could be done better” (translated by authors, T2, VSR, 28). Accordingly, he has general pedagogical knowledge about the appropriate formulation of discussion impulses. He continues:
“And perhaps a demonstration of a perfect cut would certainly be useful at this point […]. You could also put an original object at the back [of the room], a perfectly cut one, then at least you have ok, how four [cuts] […] can look like.” (translated by authors, T2, VSR, 28).
This quote points to his pedagogical content knowledge present in the sequence, which refers to learning from the model or to the use of illustrative material figures and the change of representations (Bruner, 1967). Furthermore, the teacher showed at various points in the interview that he was able to draw on his mathematical content knowledge in the situation, as he was constantly aware that the solution to the problem had to do with the “intersection points” of the straight lines (cf. e.g. translated by authors, T2, VSR, 14, 28). This knowledge was also reflected in the explanation of the pattern of action that the teacher ultimately used to guide his students’ problem-solving process:
“[…] it’s […] about collecting together and trying to verbalize together what they [the students] actually have in their notebooks. And […] on the children’s side […] the mathematical terms are often missing or if they know them, they […] have not securely understood [them].” (translated by authors, T2, VSR, 28).
This explanation shows that the teacher is aware of the particular importance of mathematical language for learning mathematics in the situation, as emphasized by Haag et al. (2013) and Prediger (2019) (pedagogical content knowledge). According to him, it was important in the situation that as many students as possible took part in the whole-class discussion. This became clear in his answer to the question about his beliefs, which guided him in the presented situation:
“[…] I believe that the students pay more attention or pay better attention when more of their [results] are involved.” (translated by authors, T2, VSR, 30).
At other points in the video-stimulated recall, it became clear that the teacher was also guided by other aspects of his affect (Philipp, 2007), i.e. his emotions and attitudes. For example, he explains the degree of awareness and spontaneity of his actions like this:
“I would like to finish by the bell, at least with one result. And I would have been highly dissatisfied if […] most of the class […] had drawn the same thing six times in different ways. That would not have been an acceptable goal for me.” (translated by authors, T2, VSR, 18).
In addition, the teacher was asked about his development of expertise, i.e. the (structural) changes that he had observed in himself in relation to this pattern of action over time. The teacher replied that after 30 years of professional experience he had noticed a “strong emphasis on […] system-steps or structures” (translated by authors, T2, VSR, 38) in a problem’s solution. He claimed this is “the decisive factor” in teaching (translated by authors, T2, VSR, 40) and explained:
“More children succeed in synthesizing [the individual steps] into a solution than if you only tell them that there is this solution. […] These [system-steps] are […] partly […] calculation tools, but partly just really structural steps [of the solution]. And that’s why I’ve become more of a fan of this.” (translated by authors, T2, VSR, 40).
The teacher reported that, as part of his professional activity, he had learned to concentrate on the structural nature of a task or a (multi-step) solution when guiding the problem-solving process. Proceeding inductively using minimal examples is particularly suitable for this. In this way, his students learn heuristic strategies that they can also transfer to other problems (Rott, 2015). According to the teacher, this was “in contrast” to what he had learned in teacher education (translated by authors, T2, VSR, 40). He therefore pays “rather more” attention to this aspect of the practice today compared to the past (translated by authors, T2, VSR, 40).
After this report, the teacher was shown the video clip from his second lesson on problem solving. When the teacher was then asked about the similarities and differences between the two video clips, he replied:
“They are […] totally different, because in the first lesson many [students] have grasped a large part of the problem, but not in its entirety in order to progress. […] In the [second] lesson [.…] the term ‘square number’ […] is not explained […] [and] many numbers were simply used twice. […] So that wasn’t the basic idea of the task at all.” (translated by authors, T2, VSR, 46).
The teacher therefore notices clear differences between the two lessons: In the first lesson, the students have already successfully completed the first phase of the problem-solving process, i.e. understanding the problem (cf. e.g. Pólya, 1949; Schoenfeld, 1985). The teacher therefore only had to offer them a mathematical stimulus for solving the problem. This was not the case in the second lesson: Here, the teacher first had to give the students access to the understanding of the problem. Nevertheless, at the end of both situations, the students “went in the direction” (translated by authors, T2, VSR, 48) that the teacher had intended.
RQ4: empirical reconstruction of teaching practices
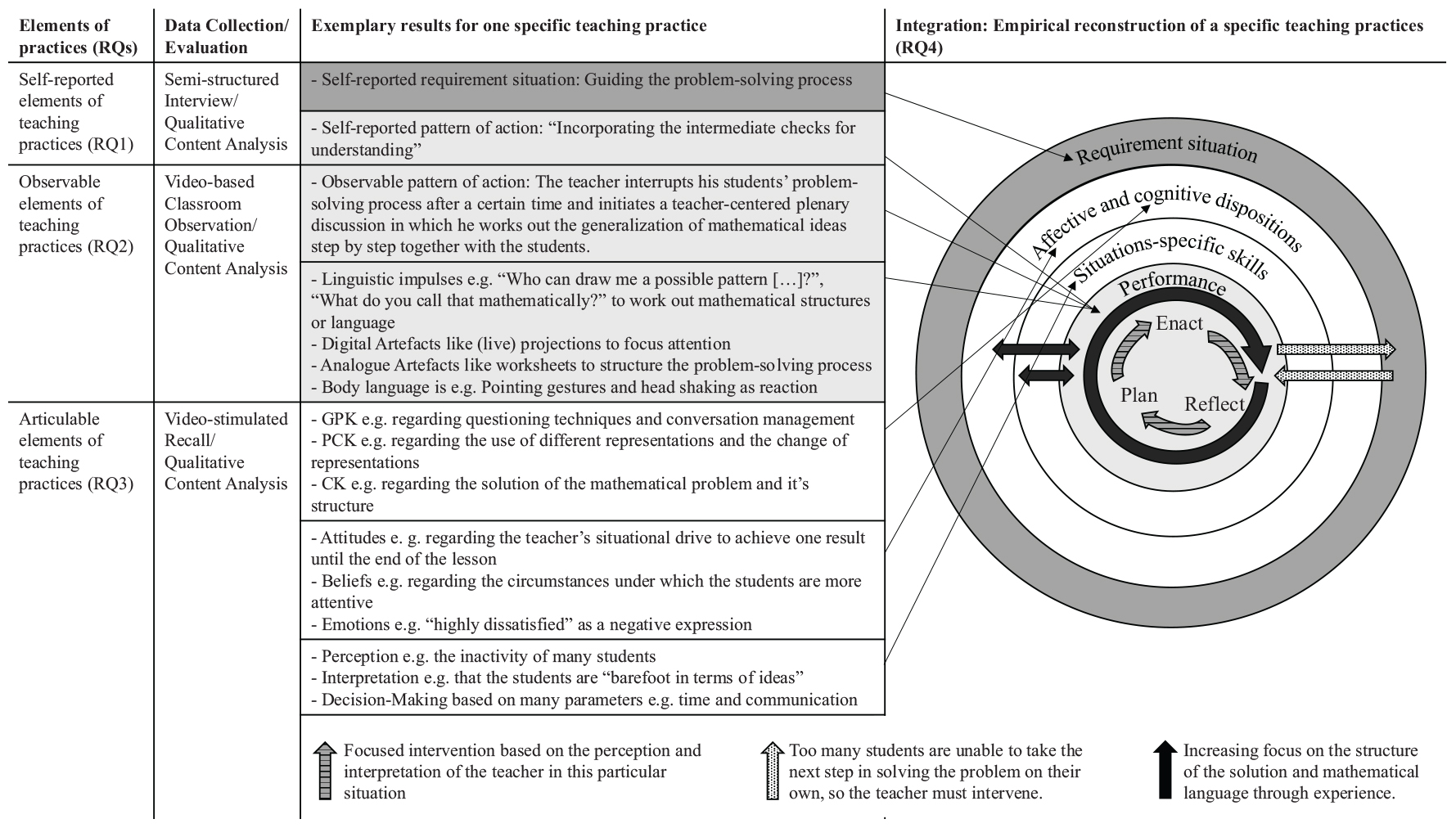
For the empirical reconstruction of a specific teaching practice in the step of data triangulation, the so far gained findings regarding RQ1–RQ3 were integrated into a joint display (Figure 3). Thereby, this informative figure also related to the theoretical model of practices as presented in Figure 2 (cf. Brungs et al., 2023).
On the left-hand side of Figure 3, the specific elements of teaching practices addressed by RQ1–RQ3 are listed. They represent the different perspectives on teaching practices in teacher professional research and also reflect on the different ways to approach (elements of) practices empirically. Therefore, right next to it, the qualitative methods used to collect and evaluate data in order to answer RQ1–RQ3 are presented. In the middle of Figure 3, exemplary results for the specific teaching practice T2 used to guide the problem-solving process of his students are illustrated. These results are described in more detail above, but seeing parts of it in this joint display shows another important thing: The theoretical model for practices (Figure 2) was validated in this study, as for every constitutive element of a teaching practice empirical evidence was found. This means, the different approaches to answer RQ1-RQ3 complement each other on a methodological level.
However, it is also important to look at complementary findings regarding the different approaches: At the methodological level, the reconstruction of the above practice showed that the teachers’ self-reports could complement the analysis of the video-based classroom observations: T2, for instance, described the promotion of mathematical language as a recurrent pattern of action, but this turned out to be an immanent part of other practices, such as guiding the problem-solving process, when analyzing the video data. Comparing the video data with the video-stimulated recall data, more differences could be identified. For example, in the case of T2, a discrepancy between the reflection in the situation and the reflection after the lesson is recognizable: In the situation, the teacher classified his practice of guiding the problem-solving process as successful, as he continued his lesson without further interruptions. In the video-stimulated recall, he explains that in the moment after his intervention he noticed a clear revision of his students’ products, which in his opinion no longer required any further guidance. Now, the teacher expressed doubts as to whether he had actually brought his students closer to solving the problem.
Discussion
In this study, a sequential multi-method design was chosen to empirically reconstruct teachers’ practices using the example of teaching problem solving. The methodical approaches of video-based classroom observations, interviews and video-stimulated recalls were combined in order to illuminate practices from different research perspectives (Escudero and Sánchez, 2002; Even and Schwarz, 2002). In this way, differentiated insights into the self-reported, observable and articulable elements of practices could be gained and integrated into an interconnected whole at a superordinate level (Simon and Tzur, 1997). The similarities and differences between the various data sets were also analyzed, which increased the validity of the results and provided a holistic understanding of teaching practices.
Despite the advantages of a multi-method design, we are confronted with limitations in this study. Practices are an extremely complex research topic, and even with a multi-method approach, it is not certain that the numerous variables involved will result in a coherent picture. Furthermore, the brevity of the observed lesson only ever reflects a moment of the professional expertise of teachers, and it is difficult to draw generalizable conclusions from only two observed lessons. Finally, practices are also linked to years of professional experience, a teacher’s personality and the cultural context, which we were unable to take into account. Additionally, there can also occur some methodological limitations. For example, the integration of different data sources can lead to conflicts of interpretation that require careful and transparent analysis. Thereby, social desirability and retrospective biases should be taken into account as well, as teachers in the moment reflections might be different from the rationalizations and reflections teachers make in an interview situation. In our example of a reconstructed practice we also discovered complementary results that require a differentiated analysis of practices. In addition, the implementation and evaluation of such a multi-method design is time-consuming and resource-intensive, which limits the number of cases examined. In our case study we only analyzed a small sample of two mathematics teachers. This makes it difficult to generalize our findings across diverse educational contexts. However, this was not the primary aim of our study. Instead, we focused on an exploratory study design that enables an empirical reconstruction of teaching practices by using multiple methodical approaches.
Overall, the sequential multi-method design provided a valuable framework for the empirical reconstruction of teaching practices as a complex construct in teacher professional research (Charalambous and Delaney, 2020; Lampert, 2010; Brungs et al., 2023). By combining different methodical approaches, this study empirically validated our conceptual model and enabled a nuanced description of teaching practices as manifestations of teachers’ professional competencies—such as their professional knowledge, beliefs, and decision-making processes (Kunter et al., 2013; Blömeke et al., 2015), —and contributed to a sharper conceptual understanding of practice as a central dimension of teacher expertise (Brungs et al., 2023; Prediger, 2019). More specifically, our findings offer empirical insight into how experienced teachers orchestrate problem-solving instruction and flexibly adapt their practices. This differentiation provides a starting point for characterizing teaching practices not just by their surface structure, but by the underlying pedagogical intentions and responsiveness. It also points to the importance of reflective teaching, as articulated in Schön’s theory of the reflective practitioner (Schön, 1983), and underscores the role of situated expertise in complex teaching environments (Hiebert et al., 2002; Carlson et al., 2020).
These findings have also implications for mathematics teacher education. By using the empirically grounded model of teaching practices developed in this study, it becomes possible to describe and analyze teaching practices—especially those related to problem-solving lessons—in more detail. Based on this model, a catalog of well-understood, research-based practices could be compiled in future research.
Such a catalog could be used in the professional development of (prospective) mathematics teachers, like it is already done e.g. in the U.S. (Grossman and McDonald, 2008). With this, (prospective) mathematics teachers get the chance to approximate teaching practices in less complex settings than real mathematics lessons (Grossman and McDonald, 2008). For example, they can rehearse a specific teaching practice in a role play and get individual feedback on their performance. By doing so, they can develop new practices over a longer period of time or they can improve their practices. This could mean that they learn how to possibly adapt their already developed teaching practices to the specific needs of a certain students or to a specific situation in their problem-solving lesson.
Future research could build on this study and expand it by including a larger sample of teachers and exploring how different levels of teaching experience influence the development and refinement of teaching practices. In doing so, the theoretical model used here could be further validated and differentiated.
Data availability statement
The datasets presented in this article are not readily available because access to the data or parts of the data is strictly limited and only accessible to researchers who are specifically authorized and have undertaken to comply with data protection regulations. The data was collected solely for the purpose of the study and cannot be used for other purposes. This ensures that the data is used exclusively for defined scientific purposes and that the integrity of the data is maintained. Requests to access the datasets should be directed to the corresponding author.
Ethics statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin. Written informed consent was obtained from the participants’ legal guardians/next of kin for the publication of any potentially identifiable images or data included in this article.
Author contributions
CB: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Project administration, Visualization, Writing – original draft, Writing – review & editing. NB: Supervision, Writing – review & editing. HS: Investigation, Methodology, Writing – review & editing. YT: Investigation, Methodology, Writing – review & editing. BR: Data curation, Supervision, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) used DeepL (Pro) for the translation of the manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1555763/full#supplementary-material
References
Alonzo, A. C., Berry, A., and Nilsson, P. (2020). “Unpacking the complexity of science teachers’ PCK in action: Enacted and personal PCK,” in Repositioning Pedagogical Content Knowledge in Teachers’ Knowledge for Teaching Science, eds A. Hume, R. Cooper, and A. Borowski (Singapore: Springer), 273–288.
Bailey, J., and Taylor, M. (2015). Experiencing a mathematical problem-solving teaching approach: Opportunities to identify ambitious teaching practices. Math. Teach. Educ. Dev. 17, 111–124.
Ball, D. L., and Forzani, F. M. (2009). The work of teaching and the challenge for teacher education. J. Teach. Educ. 60, 497–511. doi: 10.1177/0022487109348479
Baumert, J., and Kunter, M. (2006). Stichwort: Professionelle Kompetenz von Lehrkräften. Z. Erziehungswissenschaft 9, 469–520. doi: 10.1007/s11618-006-0165-2
Blömeke, S., Gustafsson, J.-E., and Shavelson, R. J. (2015). Beyond Dichotomies. Competence Viewed as a Continuum. Z. Psychol. 223, 3–13. doi: 10.1027/2151-2604/a000194
Blömeke, S., Jentsch, A., Ross, N., Kaiser, G., and König, K. (2022). Opening up the black box: Teacher competence, instructional quality, and students’ learning progress. Learn. Instruct. 79, 1–11. doi: 10.1016/j.learninstruc.2022.101600
Breidenstein, G. (2023). “Issues in ‘Individualized’ teaching practice in Germany: An ethno-methodological approach,” in Didactics in a Changing World. European Perspectives on Teaching, Learning and the Curriculum, eds F. Ligozat, K. Klette, and J. Almqvist (Cham: Springer), 123–136.
Bromme, R. (2001). “Teacher Expertise,” in International Encyclopedia of the behavioral Sciences, eds S. Semelser and P. Baltes (Elsmford: Pergamon), 15459–15465.
Bruder, R. (2003). Learning Methods and Techniques on How to Solve Problems. Darmstadt: TU Darmstadt.
Brungs, C. L., Buchholtz, N., and Rott, B. (2023). Grundlagen eines professionstheoretischen Verständnisses von Unterrichtspraktiken am Beispiel inklusiver Praktiken von Mathematiklehrkräften. k:On - Kölner Online Journal für Lehrer*Innenbildung 7, 47–70. doi: 10.18716/ojs/kON/2023.3%20
Buchholtz, N. (2019). “Planning and conducting mixed methods studies in mathematics educational research,” in Compendium for Early Career Researchers in Mathematics Education, eds G. Kaiser and N. Presmeg (Cham: Springer), 131–152.
Buchholtz, N. (2021). Voraussetzungen und Qualitätskriterien von Mixed-Methods-Studien in der mathematikdidaktischen Forschung. J. Mathematik-Didaktik 42, 219–242. doi: 10.1007/s13138-020-00173-0
Cai, J., and Hwang, S. (2020). Learning to teach through mathematical problem posing: Theoretical considerations, methodology, and directions for future research. Int. J. Educ. Res. 102, 1–8. doi: 10.1016/j.ijer.2019.01.001
Cai, J., and Jiang, C. (2017). An analysis of problem-posing tasks in Chinese and US elementary mathematics textbooks. Int. J. Sci. Math. Educ. 15, 1521–1540.
Carlson, J., Daehler, K. R., Alonzo, A. C., Barendsen, E., Berry, A., Borowski, A., et al. (2020). “The refined consensus model of pedagogical content knowledge in science education,” in Repositioning Pedagogical Content Knowledge in Teachers’ Knowledge for Teaching Science, eds A. Hume, R. Cooper, and A. Borowski (Singapore: Springer), 77–94.
Charalambous, C. Y., and Delaney, S. (2020). “Mathematics teaching practices and practice-based pedagogies: A critical review of the literature since 2000,” in Knowledge, Beliefs, and Identity in Mathematics Teaching and Teaching Development (Second Edition), eds D. Potari and O. Chapman (Leiden: Brill), 355–390.
Cianciolo, A. T., and Sternberg, R. J. (2018). “Practical intelligence and tacit knowledge: An ecological view of expertise,” in The Cambridge Handbook of Expertise and Expert Performance, eds K. A. Ericsson, R. R. Hoffman, A. Kozbelt, and A. M. Williams (Cambridge: University Press), 770–792.
Clarke, D. J., and Sullivan, P. (1992). “Responses to open-ended tasks in mathematics: Characteristics and implications,” in Proceedings of the 16th International Conference on the Psychology of Mathematics Education (PME), eds W. Geeslin and K. Graham (Durham: Durham University), 137–144.
Creswell, J. W., and Plano Clark, V. L. (2011). Designing and Conducting Mixed Methods Research, 2nd Edn. Thousand Oaks, CA: Sage Publications.
Da Ponte, J. P., and Chapman, O. (2006). “Mathematics Teachers’ Knowledge and Practices,” in Handbook of Research on the Psychology of Mathematics Eductaion: Past, Present and Future, eds A. Gutiérrez and P. Boero (Roterdham: Sense Publishers), 461–494.
Dougherty, B. J. (1990). “Influences of teacher cognitive/conceptual levels on problem-solving instruction,” in Proceedings of the 14th International Conference on the Psychology of Mathematics Education (PME), eds G. Booker, P. Cobb, and T. Mendicuti (Durham: Durham University), 119–126.
Escudero, I., and Sánchez, V. (2002). “Integration of domains of knowledge in mathematics teachers’practice,” in Proceedings of the 26th International Conference on the Psychology of Mathematics Education (PME), eds A. D. Cokburn and E. Nardi (Norwich: University of East Anglia), 177–185.
Even, R., and Schwarz, B. B. (2002). “Implications of competing interpretations of practice to research and theory in mathematics education,” in Proceedings of the 26th International Conference on the Psychology of Mathematics Education (PME), eds A. D. Cokburn and E. Nardi (Norwich: University of East Anglia), 337–344.
Fernandez, M. L., Hadaway, N., and Wilson, J. W. (1994). Problem solving: Managing It All. Math. Teach. 87, 95–199.
Grossman, P., and McDonald, M. (2008). Back to the future: Directions for research in teaching and teacher education. Am. Educ. Res. J. 45, 184–205.
Guetterman, T. C., Creswell, J. W., and Kuckartz, U. (2015). “Using joint displays and MAXQDA software to represent the results of mixed methods research,” in Use of Visual Displays in Research and Testing: Coding, Interpreting, and Reporting Data, eds M. McCrudden and G. Schraw (Charlotte, NC: Information Age Publishing), 145–176.
Haag, N., Heppt, B., Stanat, P., Kuhl, P., and Pant, H. A. (2013). Second language learners’ performance in mathematics: Disentangling the effects of academic language features. Learn. Instruct. 28, 24–34.
Häsel-Weide, U., and Nührenbörger, M. (2022). “Inclusive math practices in primary school,” in Twelfth Congress of the European Society for Research in Mathematics Education, eds G. Bolondi, J. Hodgen, E. Geraniou, and F. Ferretti (Bozen-Bolzano: Free University and ERME), 4453–4460.
Heinrich, F., Pawlitzki, A., and Schuck, L.-D. (2013). “Problemlöseunterricht in der Grundschule,” in Beiträge zum Mathematikunterricht, eds G. Greefrath, F. Käpnick, and M. Stein (Münster: WTM), 448–451.
Helfferich, C. (2011). Die Qualität qualitativer Daten. Manual für die Durchführung qualitativer Interviews. Wiesbaden: VS Verlag für Sozialwissenschaften.
Hiebert, J., Gallimore, R., and Stigler, J. W. (2002). A knowledge base for the teaching profession: What would it look like and how can we get one? Educ. Reserarch. 31, 3–15.
Hirsch, C. L., and Buchholtz, N. (2023). “The concept of practices in mathematics teachers’ competence: A theoretical exploration,” in Thirteenth Congress of the European Society for Research in Mathematics Education (CERME13), eds P. Drijvers, C. Csapodi, H. Palmér, K. Gosztonyi, and E. Kónya (Budapest: Alfréd Rényi Institute of Mathematics), 3775–3782.
Hodnik Čadež, T., and Kolar, V. (2016). “Geometry as a source for investigating numbers,” in Problem Solving in the Mathematics Classroom Perspectives and Practices from Different Countries, eds A. Kuzle, B. Rott, and T. Hodnik Čadež (Münster: WTM), 99–118.
Hunter, A., and Brewer, J. (2003). “Multimethod research in sociology,” in Handbook of mixed methods in social and behavioral research, eds A. Tashakkori and C. Teddlie (Thousand Oaks, CA: Sage), 577–594.
Jacinto, H., and Carreira, S. (2017). Mathematical problem solving with technology: The techno-mathematical fluency of a student-with-GeoGebra. Int. J. Sci. Math. Educ. 15, 1115–1136.
Kersting, N. B., Givvin, K., Sotelo, F., and Stigler, J. W. (2010). Teacher’s analysis of classroom video predicts student learning of mathematics: Further exploration of a novel measure of teacher knowledge. J. Teach. Educ. 61, 172–181.
Kilpatrick, J., Swafford, J., and Findell, B. (eds) (2001). Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press.
Klette, K. (2023). Classroom observation as a means of understanding teaching quality: Towards a shared language of teaching? J. Curric. Stud. 55, 49–62. doi: 10.1080/00220272.2023.2172360
Kolbe, F.-U., Reh, S., Fritze, B., Idel, T.-S., and Rabenstein, K. (2008). Lernkultur: Überlegungen zu einer kulturwissenschaftlichen Grundlegung qualitativer Unterrichtsforschung. Z. Erziehungswissenschaft 11, 125–143. doi: 10.1007/s11618-008-0007-5
Krauss, S. (2020). “Expertise-paradigma in der lehrerinnen- und lehrerbildung,” in Handbuch Lehrerinnen- und Lehrerbildung, eds C. Cramer, J. König, and S. Blömeke (Bad Heilbrunn: Klinkhardt), 154–162.
Kunter, M., Baumert, J., Blum, W., Klusmann, U., Krauss, S., and Neubrand, M. (2013). Cognitive Activation in the Mathematics Classroom and Professional Competence. Results from the COACTIV Project. New York, NY: Waxmann.
Lampert, M. (2010). Learning teaching in, from, and for practice: What do we mean? J. Teach. Educ. 61, 21–34.
Lave, J., and Wenger, E. (1991). Situated Learning: Legitimate Peripheral Participation. Cambridge: Cambridge University Press.
Lester, F. K. Jr. (2013). Thoughts about research on mathematical problem- solving instruction. Math. Enthusiast 10, 245–278. doi: 10.54870/1551-3440.1267
Llinares, S. (2002). La práctica de enseñar y aprender matemáticas. La generación y uso de instrumentos de la práctica. Rev. Enseñanza Univ. 19, 115–124.
Mason, J., Burton, L., and Stacey, K. (2006). Mathematisch denken – Mathematik ist keine Hexerei (4. Überarbeitete Auflage). München: Oldenbourg.
Mayer, R. E., and Wittrock, R. C. (2006). “Problem solving,” in Handbook of Educational Psychology, 2nd Edn, eds P. A. Alexander and P. H. Winne (New York, NY: Routlegde), 287–304.
Mayring, P. (2022). Qualitative Inhaltsanalyse: Grundlagen und Techniken. Weinheim Basel: Beltz Verlag.
McDonough, A., and Clarke, D. (2003). “Describing the practice of effective teachers of mathematics in the early years,” in Proceedings of the 27th International Conference on the Psychology of Mathematics Education (PME), eds N. Pateman, B. J. Dougherty, and J. T. Zilliox (Honolulu: International Group for the Psychology of Mathematics Education), 261–268.
Moschkovich, J. N. (2004). Appropriating mathematical practices: A case study of learning to use and explore functions through interaction with a tutor. Educ. Stud. Math. 55, 49–80.
Muir, T. (2010). “Using video-stimulated recall as a tool for reflecting on the teaching of mathematics,” in Proceedings of the 33rd annual conference of the Mathematics Education Research Group of Australasia: Shaping the Future of Mathematics Education, eds L. Sparrow, B. Kissane, and C. Hurst (Freemantle: MERGA), 438–445.
Palmer, D. J., Stough, L. M., and Burdenski, T. K. (2005). Identifying teacher expertise: An examination of researchers. Decis. Mak. Educ. Psychol. 40, 13–25.
Philipp, R. A. (2007). “Mathematics teachers’ beliefs and affect,” in Second Handbook of Research on Mathematics Teaching and Learning, ed. F. K. Lester (New York, NY: Macmillan), 257–315.
Powell, E. (2005). Conceptualizing and facilitating active learning: Teachers’ video-stimulated reflective dialogues. Reflect. Pract. 6, 407–418.
Prediger, S. (2019). Investigating and prompting teachers’ expertise for language responsive mathematics teaching. Math. Educ. Res. J. 31, 367–392.
Rabenstein, K. (2020). Wiederholung als Veränderung. Zur Normativität pädagogischer Praktiken zwischen Kontinuität und Kontingenz im Unterricht. Z. Schul- und Professionsentwicklung 2, 6–19.
Radišić, J., and Baucal, A. (2016). Using video-stimulated recall to understand teachers’ perceptions of teaching and learning in the classroom setting. Psihološka Istraživanja 19, 165–183.
Rott, B. (2016). “Problem solving in the classroom: The role of beliefs in the organization of lessons with the subject problem solving,” in Proceedings of the 2015 joint conference of ProMath and the GDM Working Group on Problem Solving, eds T. Fritzlar, D. Aßmus, K. Bräuning, A. Kuzle, and B. Rott (Münster: WTM), 201–213.
Rott, B., Specht, B., and Knipping, C. (2021). A descriptive phase model of problem-solving processes. ZDM Math. Educ. 53, 737–752. doi: 10.1007/s11858-021-01244-3
Ruthven, K. (2014). “Frameworks for analysing the expertise that underpins successful integration of digital technologies into everyday teaching practice,” in The Mathematics Teacher in the Digital Era. Mathematics Education in the Digital Era, Vol. 2, eds A. Clark-Wilson, O. Robutti, and N. Sinclair (Dordrecht: Springer), 373–393. doi: 10.1007/978-94-007-4638-1_16
Saxe, G. B. (1999). “Professional development, classroom practices, and students’ mathematics learning:A cultural perspective,” in Proceedings of the 23rd International Conference on the Psychology of Mathematics Education (PME), ed. O. Zaslavsky (Haifa: International Group for the Psychology of Mathematics Education), 25–39.
Schatzki, T. R. (2012). “A primer on practices,” in Practice-Based Education: Perspectives and Strategies, eds J. Higgs, R. Barnett, S. Billett, M. Hutchings, and F. Trede (Boston: Sense Publishers), 13–26.
Schoenfeld, A. H. (2011). How we think: A Theory of Goal-Oriented Decision Making and its Educational Applications. New York, NY: Routledge.
Schoenfeld, A. H. (2015). “How we think: A theory of human decision-making, with a focus on teaching,” in The Proceedings of the 12th International Congress on Mathematical Education, ed. S. Cho (Cham: Springer), 229–243. doi: 10.1007/978-3-319-12688-3_16
Schoenfeld, A. H. (2020). Mathematical practices, in theory and practice. ZDM Math. Educ. 52, 1163–1175. doi: 10.1007/s11858-020-01162-w
Schön, D. A. (1983). The Reflective Practitioner: How Professionals Think in Action. New York, NY: Basic Books.
Shulman, L. S. (1987). Knowledge and teaching: Foundations of the new reform. Harv. Educ. Rev. 57, 1–22.
Simon, M., and Tzur, R. (1997). “Generalizing theoretical accounts of mathematics teachers’ practices,” in Proceedings of the 21st International Conference on the Psychology of Mathematics Education (PME), ed. H. Pekhonen (Jyväskylä: Gummerus), 160–167.
Stigler, J. W., and Miller, K. F. (2018). “Expertise and Expert Performance in Teaching,” in The Cambridge Handbook of Expertise and Expert Performance (Second Edition), eds K. A. Ericsson, R. R. Hoffmann, A. Kozbelt, and A. M. Williams (Cambridge: Cambridge University Press), 431–452.
Keywords: expertise, mathematics teachers, multi-methods, practices, problem solving
Citation: Brungs CL, Buchholtz N, Streit H, Theile Y and Rott B (2025) Empirical reconstruction of mathematics teaching practices in problem-solving lessons: a multi-method case study. Front. Educ. 10:1555763. doi: 10.3389/feduc.2025.1555763
Received: 05 January 2025; Accepted: 08 April 2025;
Published: 01 May 2025.
Edited by:
Hui-Chuan Li, University of Edinburgh, United KingdomReviewed by:
Widodo Winarso, Universitas Islam Negeri Siber Syekh Nurjati Cirebon, IndonesiaPilar Ester, Camilo José Cela University, Spain
Copyright © 2025 Brungs, Buchholtz, Streit, Theile and Rott. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Christine Luise Brungs, Q2hyaXN0aW5lLmJydW5nc0B1bmkta29lbG4uZGU=
 Christine Luise Brungs
Christine Luise Brungs Nils Buchholtz
Nils Buchholtz Hendrik Streit
Hendrik Streit Yasmin Theile
Yasmin Theile Benjamin Rott
Benjamin Rott