Aligning Agent-Based Modeling With Multi-Objective Land-Use Allocation: Identification of Policy Gaps and Feasible Pathways to Biophysically Optimal Landscapes

Introduction

Traditionally, land-use policies put strong emphasis on biomass production (food, feed, fiber). Given increasing landscape degradation in Europe and elsewhere (IPBES, 2018a, b), the concept of multifunctional landscapes has recently gained popularity (O’Farrell and Anderson, 2010), stressing that a landscape can be managed to provide multiple ecosystem services. Still, any landscape’s capacity to provide ecosystem services is limited by its biophysical, geomorphological and climatic characteristics. Different ecosystem services “compete” for scarce underlying resources such as water, space or nutrients. Therefore, management of multifunctional landscapes involves trade-offs between multiple ecosystem services (Cord et al., 2017). An important question is then: how much can a landscape provide in terms of different ecosystem services?

One way of answering this question is multi-objective land-use optimization/allocation (Kaim et al., 2018; Strauch et al., 2019), where metaheuristic search algorithms can be combined with statistical and/or simulation models (e.g., hydrological, biodiversity, or socio-economic models) to efficiently explore a large number of land-use configurations with respect to their potential to minimize trade-offs among multiple, and often competing, objectives. Here, evolutionary optimization algorithms (Coello Coello et al., 2007; Deb, 2014) are of particular value as they allow to identify Pareto-optimal solutions, i.e., solutions for which no objective can be further improved without compromising at least one of the other objectives (non-dominated solutions). However, multi-objective land-use optimization has three major limitations: first, it generates a large number of biophysically Pareto-optimal landscape configurations, and it is non-trivial to identify the societally optimal one among them, i.e., the one that maximizes social welfare¹. Second, even when land-use constraints are included in the optimization procedure (Strauch et al., 2019), the real-world feasibility of a given solution is unclear. Third, the potential pathway from the status quo toward the optimal solution is also unknown, given that the multiple objectives include public goods which will be underprovided by land managers in the absence of appropriate incentives. The first of these limitations has been recognized in the literature (Cavender-Bares et al., 2015; King et al., 2015). The second and third limitations have received little attention so far.

Another increasingly common approach in studies of human-shaped landscapes is agent-based modeling (Schulze et al., 2017). Agent-based models (ABM) are used to analyze the influence of the behavior of individual agents (farmers, households, consumers) on the emergent properties of the system (e.g., landscape) in a dynamic way. This model type can and has been used to generate realistic representations of factors such as preferences, social interactions, policies, property rights and markets (Schlüter et al., 2017; Huber et al., 2018). ABM are usually spatially and temporally explicit, and they can account for path dependencies and (social–technological) lock-ins. When applied to model land-use change, the results of ABM are strongly dependent on assumptions regarding agents’ behavior, their interactions and the social, economic and institutional boundary conditions. Even highly realistic and comprehensive ABM can thus miss the potential of a landscape to provide multiple ecosystem services in a sustainable way. Therefore, both modeling approaches – biophysical land-use optimization and ABM – can benefit from each other. Together, they can provide answers to the questions: how to determine economically, institutionally and socially feasible (i.e., achievable) landscape configurations that are at or close to the biophysical optimum? And, which accompanying policy interventions can be used to trigger pathways toward feasible solutions?

Various approaches dealing with related questions can be found in the literature (a list of selected relevant publications can be found in Supplementary Material S1). For instance, Whittaker et al. (2017) used a bilevel evolutionary optimization approach combining a process-based biophysical model with a data envelopment analysis (DEA) for spatial targeting of agri-environmental policy. Brunner et al. (2016) used an ABM and discrete choice experiments for qualitative backcasting from normative scenarios (see also Mo et al., 2018). Ligmann-Zielinska and Jankowski (2010) loosely coupled multi-objective land-use allocation and ABM to investigate the feasibility of alternative arrangements of residential land from a planning perspective. Haslauer et al. (2016) developed a stylized spatially explicit backcasting model and applied it to future scenarios with ABM. However, few papers combining landscape-scale optimization with ABM or similar modeling approaches explicitly considered the effects of policies within their framework. Exceptions include Brunner et al. (2016), who modeled different pathways of ecosystem services supply based on an elaborated set of agricultural and spatial planning policy interventions within a four-step backcasting procedure, and Whittaker et al. (2017), who focused on the responses of homogeneous agents to a specific spatially targeted policy instrument.

In this paper, we show how multi-objective land-use optimization and agent-based modeling can be fruitfully aligned. Our aim is to develop an approach that uses both modeling frameworks in order to illuminate (i) the social, economic and institutional feasibility of biophysically optimal land-use patterns, (ii) barriers involved, and (iii) paths and mechanisms necessary for their achievement (e.g., in terms of relevant policy instruments). In contrast to other studies, which focus on selected issues related to the challenge at hand, we demonstrate the usefulness and policy relevance of combining biophysical optimization, agent-based modeling and an explicit consideration of governance arrangements (such as policy instruments). We do this by exploring conceptually, and in a virtual case study, how to align static biophysical land-use optimization and dynamic ABM simulation to demonstrate the relevance of various boundary conditions in the social part of the social–ecological system.

Aligning Agent-Based Modeling With Multi-Objective Land-Use Allocation

Multi-objective land-use optimization is one way to understand and navigate the trade-offs between different ecosystem services in multifunctional landscapes. However, conventional optimization approaches focus on the biophysical potential of a landscape and usually ignore or oversimplify other dimensions such as economic, institutional and social feasibility. Therefore, many questions, which multi-objective land-use optimization alone is not well-suited to answer, remain open: is the biophysically optimal landscape configuration also consistent with the economic survival of farm businesses (El Benni et al., 2012)? Can an optimal landscape be achieved given existing property rights regimes (Bartkowski et al., 2018; Binder, 2019)? Are the incentives provided by agricultural and environmental policies conducive to achieving the optimal landscape configuration (Pe’er et al., 2019; Hristov et al., 2020)? What are the societal demands and expectations related to the analyzed landscape (Martín-López et al., 2012; Cavender-Bares et al., 2015)? What about traditions, norms, social pressure and other behavioral and informal institutional factors inhibiting change (Bartkowski and Bartke, 2018; Dessart et al., 2019)? In light of these societally and policy-relevant questions, the valuable information provided by multi-objective land-use optimization needs to be complemented by other types of analysis that allow for including economic, social and institutional factors. Agent-based modeling is a broad class of models particularly well suited to fill these gaps (see Kremmydas et al., 2018; Reidsma et al., 2018).

Agent-based models (ABM) have been used extensively to model social–ecological systems (SES) (Schulze et al., 2017; Schlüter et al., 2019). They represent flexible bottom-up models, which allow for the inclusion of behavioral, economic, social and institutional factors that are usually lacking in multi-objective optimization approaches (e.g., Schulze et al., 2017; Huber et al., 2018). In ABM, SES are analyzed in a dynamic way, i.e., their evolution over time is considered. This allows for explicit analysis of pathways of change and the distinction between incremental and discontinuous changes in the system. Furthermore, ABM usually have a spatial dimension, so they can be used to analyze the evolution and response of the same landscapes as the models used in biophysical optimization. At the same time, the realistic and comprehensive representation of the human part of SES means that the biophysical potential of landscapes may be missed when applying ABM alone, due to the large number of non-biophysical constraints thus introduced.

This provides a strong rationale for combining biophysical land-use optimization with ABM to test the institutional, economic and social feasibility of the former’s results. The main reason is that there might be large differences between landscape configurations generated by an ABM on the one hand, and purely biophysical optimization on the other hand – and these differences can be very instructive and policy-relevant. Even though ABM incorporate many factors related to feasibility, they still must be based on assumptions, holding particular “boundary conditions” (e.g., a given set of policies) constant. Therefore, comparing and aligning (Ligmann-Zielinska and Jankowski, 2010) static biophysical land-use optimization and dynamic ABM can demonstrate the relevance of those boundary conditions and provide hints at which additional institutional, political or economic changes would be needed to fully exploit the potential of multifunctional landscapes. Against this background, the basic conceptual idea of this paper is to use the two modeling approaches alongside each other on the same landscape, and to compare their respective results in a structured way. For the purposes of this paper we call our approach aligning agent-based modeling with multi-objective land-use allocation (ALABAMA).

ALABAMA should be distinguished from related approaches based on backcasting, which have been tentatively discussed in the literature. For instance, Haslauer et al. (2016) presented a generic ABM-based explicit backcasting approach that could potentially be used to backcast from the Pareto frontier generated by means of biophysical optimization. A more qualitative approach was suggested by Brunner et al. (2016), who used ABM simulations to approximate normative scenarios – which could also be generated by multi-objective optimization. However, when using backcasting in combination with multi-objective land-use optimization, the challenge is to choose a subset of Pareto-optimal (non-dominated) landscape configurations to be used in the backcasting procedure; for these solutions, a “feasibility analysis” can be done by means of an ABM. This would require “subsetting” the set of biophysically optimal solutions, e.g., with the help of demand (preference) information, obtained from surveys (Cavender-Bares et al., 2015; Brunner et al., 2016). Those solutions from the subset that are found infeasible (i.e., not attainable via backcasting) can then be analyzed with respect to the boundary conditions as mentioned above. Their analysis can provide useful information about the relevance of the chosen boundary conditions. The downside of this approach, however, is that it requires subsetting and is therefore not applicable to all Pareto optimal configurations (whose number is usually quite large). Thus, “artificial” subsetting of the overall solution space may exclude potentially interesting and policy-relevant cases. Also, it is possible that none of the Pareto-optimal solutions are suitable for backcasting. This would mean that no Pareto-optimal solution is feasible, implying the need to adapt the optimization procedure, e.g., by adding constraints (see Strauch et al., 2019).

The approach we suggest, ALABAMA, follows a different path, namely a structured comparison of the (full set of) biophysically optimal landscapes with an exploration of the parameter space of the ABM (Figure 1). Here, subsetting is neither necessary nor desirable – instead, a large set of solutions (landscape configurations) from the two model approaches is compared in order to (i) check the economic, social, institutional feasibility of the biophysically optimal configurations, and (ii) identify boundary conditions of the ABM responsible for the gap between the biophysically optimal and the feasible solutions. Ideally, the insights from (ii) can then be used to adapt the ABM in a way that helps move the system closer to the biophysical potential.

FIGURE 1

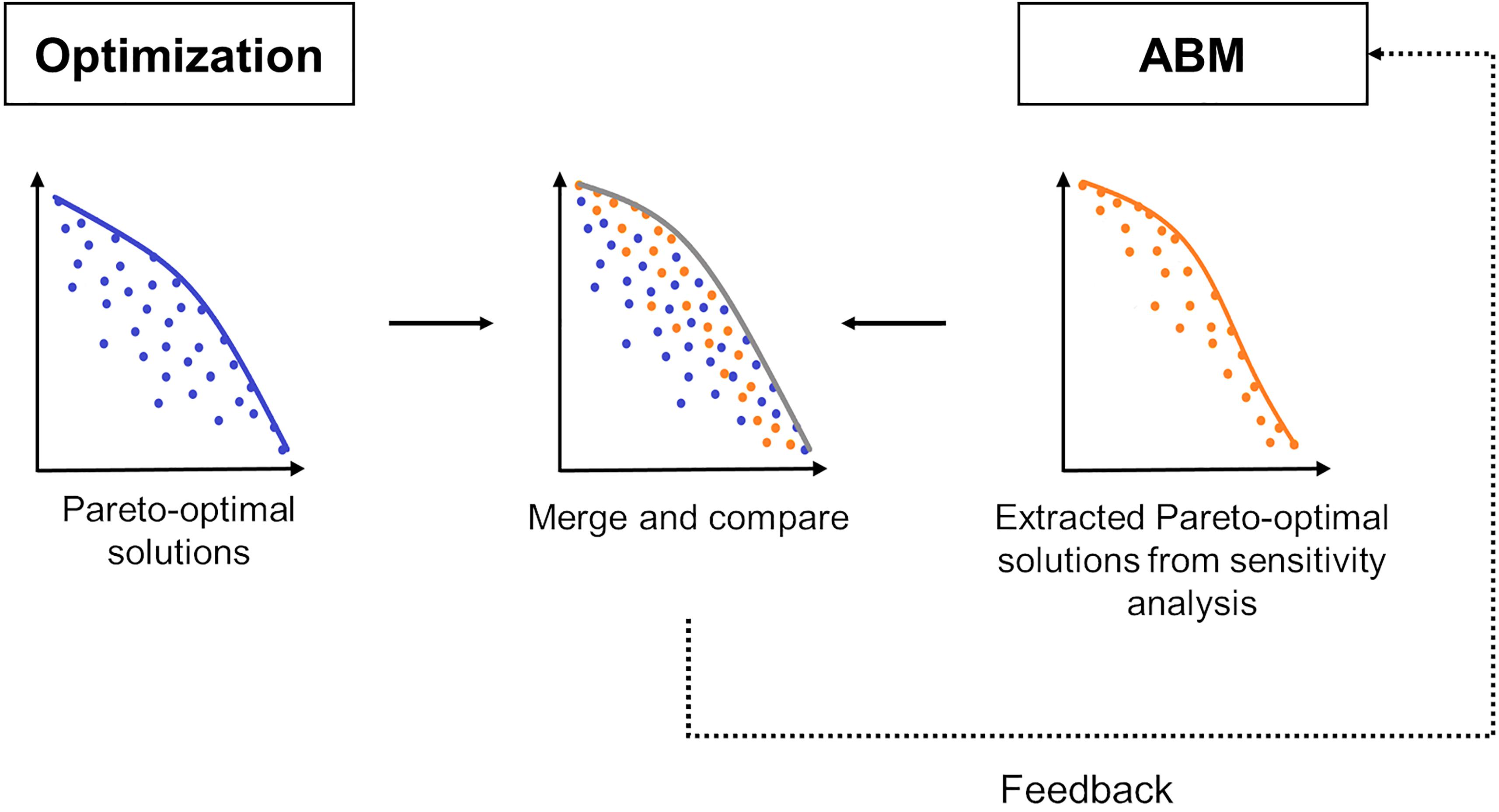
Figure 1. Illustration of the conceptual framework aligning agent-based modeling with multi-objective land-use allocation (ALABAMA).

ALABAMA consists in comparing the Pareto frontier as a whole with the results of an exploration of the parameter space (i.e., sensitivity analysis) within the ABM. In this case, all parameters of the ABM are varied. Subsequently, the set of solutions in terms of ecosystem services can be used to create a Pareto-optimal subset for comparison to the Pareto frontier generated through biophysical optimization. Such a comparison provides an overall picture of the relationship between biophysical optimization results and ABM simulations and can guide further analysis. In that sense, it offers feedback to the ABM and helps identify and understand differences between biophysically attainable and economically, institutionally and socially feasible landscape configurations. An analysis of the effects of different parameters on the position of ABM solutions vis-à-vis the biophysical Pareto frontier can then be used to identify crucial components, assumptions and parameters responsible for the gap between the two solution sets. This may include selecting a subset of (policy-relevant or scientifically interesting) solutions and analysing them in more detail. This kind of exercise can have two consequences: either the assumptions responsible for the gap are deemed realistic and “hard”; then the result is that given some real-world boundary conditions (e.g., property rights or the behavioral characteristics of agents), the biophysical potential cannot be realized. Or the identification of crucial but “soft” assumptions can ignite a search for (realistic, but initially not considered) changes in the institutional setting, such as novel policy instruments or more realistic behavioral assumptions, that would help move the system closer to its biophysical potential. The identified changes can subsequently be implemented in the ABM in order to redo the analysis and check whether they really move the ABM-modeled system closer to the biophysical potential.

To explore the possibilities and limitations of the approach outlined above, in the next section we present and discuss a virtual case study, in which a simple landscape is biophysically optimized and additionally analyzed by means of a simple, conceptual ABM. We compare the results of both analyses and use them to provide general insights into the advantages and disadvantages of this approach.

Virtual Case Study: Optimization and Feasibility in a Virtual Landscape

In our case study, we compared the results of a biophysical land-use optimization using the Constrained Multi-objective Optimization of Land-use Allocation (CoMOLA) tool (Strauch et al., 2019) with an exploration of the parameter space in a simple ABM for a virtual landscape.

Virtual Landscape and Ecosystem Service Models

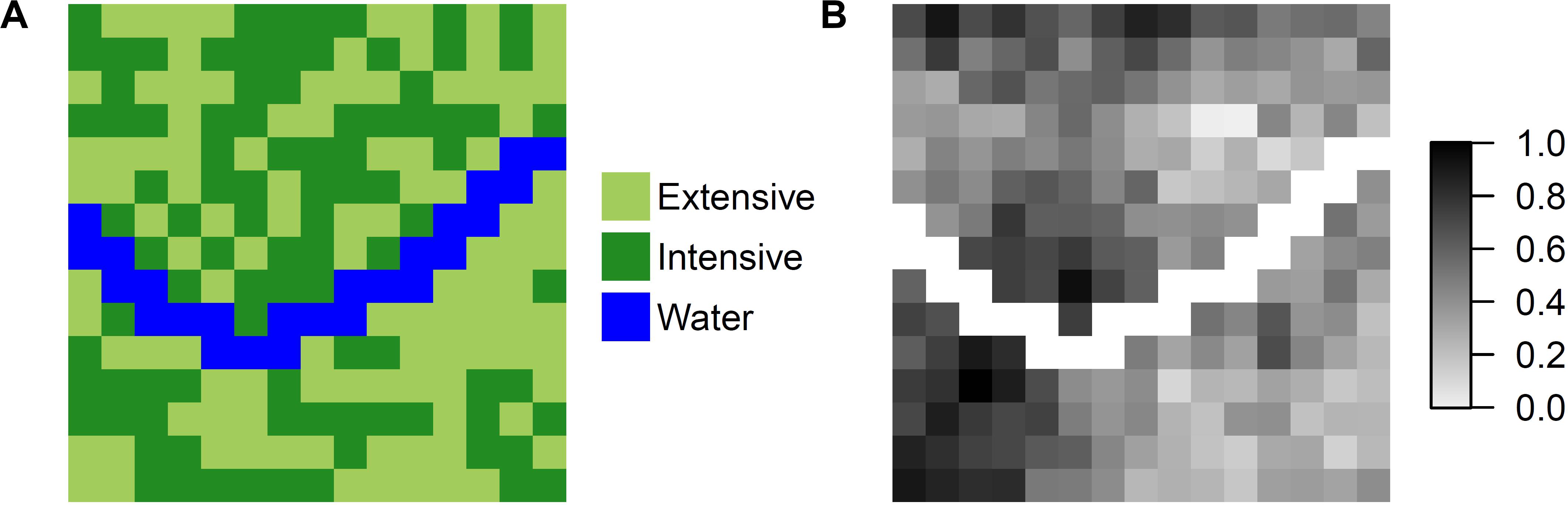
We worked with a virtual landscape based on a regular 15 × 15 grid with a cell size of 1 ha. For simplicity, the landscape consisted of only two land uses: intensive and extensive grassland². Furthermore, we assumed a river flowing through the landscape (Figure 2A; 25 out of 225 grid cells) and a heterogeneous distribution of soil fertility (Figure 2B) ranging from 0.067 (lowest) to 1 (highest).

FIGURE 2

Figure 2. Virtual land use (A) and soil fertility (B) map.

In the virtual case study, new options for the composition of extensive and intensive grassland in the landscape were generated (i.e., each grid cell can be converted to either extensive or intensive grassland). For the sake of simplicity, three conceptual toy models were used to evaluate the landscapes’ provision of ecosystem services (the same models were used in both CoMOLA and ABM); all three models returned normalized indices for each ecosystem service:

• Agricultural yield (AY) was modeled as a function of production intensity level P (with the value of 1.5 for extensive grassland and 2 for intensive grassland) and soil fertility F (Figure 2B), summarized over all 200 grassland grid cells i:

$$AY=\frac{{\sum }_{i=1}^{200}\sqrt{P_i(1+F_i)}-296.8974}{45.9032}(1)$$

AY is normalized to range between 0 (all extensive) and 1 (all intensive).

• Habitat index (HI) was estimated as the total area (i.e., the number of cells) of the two largest patches of extensive grassland (A_2X) divided by the total number of grassland cells:

$$HI=\frac{A_{2X}}{200}(2)$$

assuming that both increasing extent and connectivity of extensive grassland are beneficial for biodiversity. Patches were defined as contiguous extensive grassland cells using the 4-neighbor rule (von Neumann neighborhood). HI can range between 0 (all intensive) and 1 (all extensive).

• Water quality (WQ) was modeled as a function of the Euclidean distance (D) between intensive grassland cells (i) and their respective closest river cells:

$$WQ=1-\frac{{\sum }_{i=1}^I\frac{1}{D_i}}{0.8635082}\mathit{\hspace{1em}}ifI>0orWQ=1ifI=0(3)$$

where I is the total number of intensive grassland cells, with i ∈ {1, …, I}. Decreasing the number of intensive grassland cells and/or increasing their distances to the river would thus increase WQ, which is normalized to range between 0 (all intensive) and 1 (all extensive).

Biophysical Optimization

The virtual landscape was optimized for all three ecosystem service indicators simultaneously (AY, HI, and WQ) using CoMOLA. This tool can be used to couple any kind of spatial statistics or simulation models with NSGA-II, a widely used evolutionary multi-objective optimization algorithm (Deb et al., 2002). It has proven useful for exploring biophysically optimal land-use patterns in agricultural (e.g., Verhagen et al., 2018) and urban landscapes (Schwarz et al., 2020). CoMOLA can consider up to four objectives as well as constraints such as land use change and minimum/maximum values for each of the land use classes (Strauch et al., 2019). As we were interested in the full biophysical optimum of the virtual landscape, constraints were not applied in this study.

CoMOLA starts an evolutionary process by first creating a set of different randomly generated landscapes. As the algorithm is inspired by biological evolution, its terminology and principles are likewise: each landscape is called an individual and is represented by a genome, i.e., a string of integers encoding the land use of each grid cell. All landscapes of one generation form a population which changes over generations due to selection and variation (i.e., crossover and mutation). Using the ecosystem service models described above, each individual is assigned fitness values representing the achieved values for the three objectives. The genetic algorithm then applies a Pareto ranking for each individual based on its fitness values. It archives best individuals and selects individuals for mating to generate a new (offspring) population. In mating, each offspring individual is generated by a random combination (crossover) of two genomes. The likelihood of mating increases for individuals with a higher Pareto rank. Additional random mutations increase the diversity of genomes to consider a wide range of different spatial configurations. The entire procedure, from fitness value calculation to offspring generation, is repeated for a pre-defined number of generations.

Considering the vast number of possible landscapes, no optimization algorithm can guarantee finding the global optimum in a finite number of generations; yet, genetic algorithms are known for their good performance in reasonable run-time (Deb et al., 2002). We ran CoMOLA for 1000 generations with a population size of 500 (which amounts to a total of 500,500 simulations), a crossover rate of 0.9, and a mutation rate of 0.01. These settings performed well in pre-tests and also in previous studies where CoMOLA was used for multi-objective optimization of land use (e.g., Strauch et al., 2019; Schwarz et al., 2020). To evaluate the performance of CoMOLA, we ran the same number of simulations (n = 500,500) based on a Monte Carlo sampling (i.e., each time with a purely random generation of land-use maps).

Agent-Based Model

The virtual landscape was also analyzed by means of a simple ABM developed specifically for the purposes of this paper. For this purpose, the grassland grid cells are interpreted as plots; they are allocated to a variable number of agents. All agents are either myopic income maximizers or satisficers (Simon, 1955) who maximize income until they reach a threshold beyond which they cease making any further changes in management of their plots. The income threshold for the satisficers can be either homogeneous for all agents or individually heterogeneous (i.e., each agent is randomly assigned her own income threshold). The income derived by the agents consists of income from agricultural production and agri-environmental payments. There are no direct interactions between agents.

In the base variant of the model, there are 10 farmers, each owning 20 randomly distributed plots within the landscape. To incentivize environmentally beneficial extensification, three kinds of payments are provided:

• Base payment: farmers receive a fixed payment for each extensive grassland cell;

• Agglomeration bonus³ : farmers receive a bonus based on the number of extensively managed cells in the neighborhood (von Neumann neighborhood) of each of their extensive grassland cells;

• Water quality bonus: farmers receive a bonus for extensively managed cells close to the river (distance of either one or two cells).

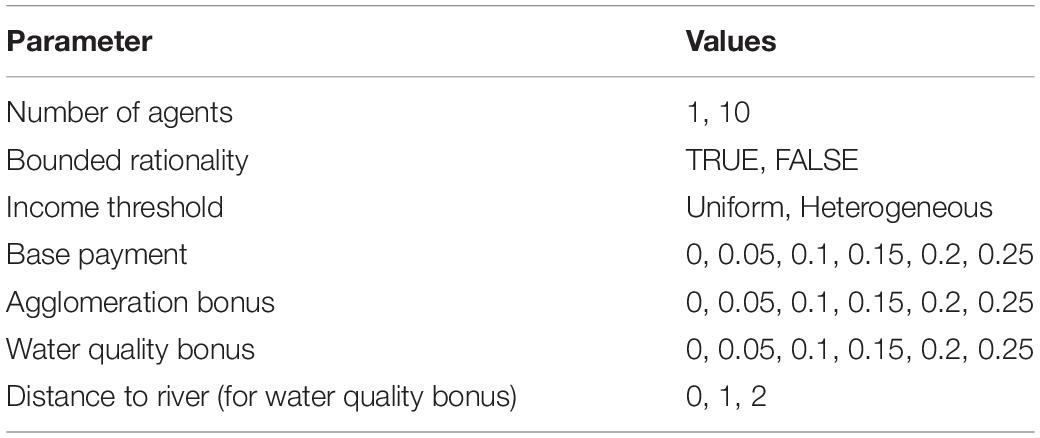
Each payment can be switched on and off and has different values (see Table 1). The income of agent j (Π; the subscript j is suppressed for simplicity) is assumed to be

TABLE 1

Table 1. Parameter values used in the analysis.

$$\mathrm{\Pi }=\sum _{i=1}^{20}p{Y}_i+\sum _{i=1}^{20}{A}_i(4)$$

where p is the price of grass (set to 1 for simplicity), Y_i is the yield from cell i, calculated in line with the ecosystem service model (but without normalization), and A_i is the sum of agri-environmental payments the agent received for cell i. We also assume that the landscape configuration is somewhat persistent: each farmer can change management only for a limited number of plots per period⁴.

A detailed ODD + D description (Müller et al., 2013) of the model can be found in the Supplementary Material S2.

Table 1 summarizes the parameter values used to explore the parameter space in order to then compare the results to CoMOLA (see next section). A full list of parameters can be found in the ODD + D document (S2). For exploring the parameter space, combinations of the parameters listed in Table 1 were run. Because the random assignment of plots to farmers may have effects on the results, each combination was run 10 times. The run time was 100 periods (within which usually an equilibrium was reached), resulting in altogether 77,760 runs. Each run was evaluated after the last period by means of the ecosystem service models; additionally, the total budget spent on the agri-environmental payments and the mean income of the farmers were calculated.

Comparison of Models

To demonstrate the informative power of comparing CoMOLA and the ABM, we analyzed the relationship between the results of the biophysical optimization with multiple subsets of the ABM results (corresponding with different variants of the ABM; Figure 3). For each variant and for the Monte Carlo simulation, we extracted Pareto-optimal solutions (considering the results of the ecosystem service models) to compare them with CoMOLA’s set of Pareto-optimal solutions. As the visual comparison of Pareto frontiers in more than two dimensions can be daunting, we used the hypervolume (HV; Zitzler and Thiele, 1999) to evaluate each of the different solution sets. HV is a widely accepted multi-objective performance metric measuring both convergence and diversity of non-dominated solutions without requiring the knowledge of the true Pareto front for comparison (Jiang et al., 2014). HV represents the volume in the objective space that is dominated by the set of solutions given a certain reference point (such as the origin of the coordinate system). Higher HV values hence indicate that the solutions are closer to the true Pareto front and, at the same time, that they are more evenly scattered in the objective space (Jiang et al., 2014). The analysis was done within the R environment (R Core Team, 2018) using the package “mco” (Mersmann, 2014). Moreover, we computed the Euclidean distance of each Pareto-optimal ABM and Monte Carlo solution to their respective closest solution of CoMOLA.

FIGURE 3

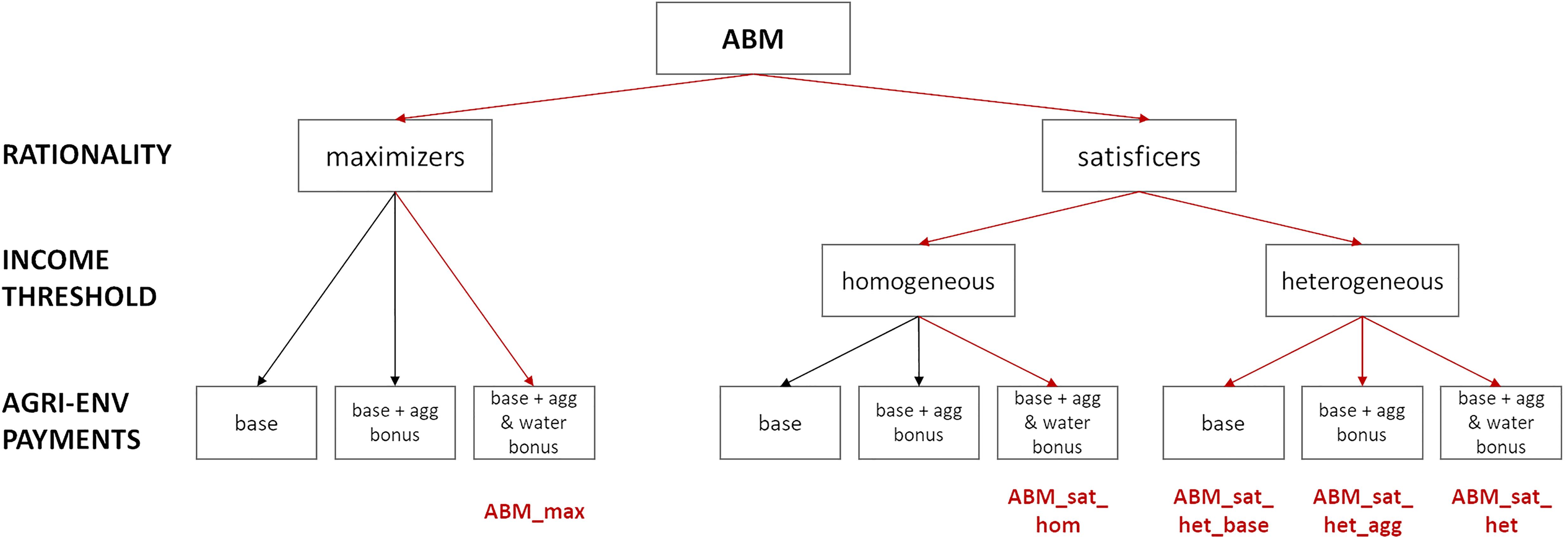
Figure 3. Overview of the different ABM variants. Those that were used in the comparison with CoMOLA are marked with red arrows and include the respective abbreviation.

Figure 3 visualizes the selection of ABM subsets in a systematic manner. Note that not all thinkable subsets were analyzed separately in the comparison with CoMOLA. This could have been done, but to make the paper more illustrative, we selected the potentially most instructive variants of the ABM. The relevant distinctions (see also ABM description in section “Agent-Based Model”) are the rationality assumption (income maximizing farmers vs. satisficing farmers), income threshold for the satisficers variants (either homogeneous for all farmers or heterogeneous) and the presence of the three different agri-environmental payment instruments.

Furthermore, we also created an ABM variant that was supposed to “emulate” CoMOLA (one farmer; water quality bonus function following the WQ model, Eq. 3), in order to test whether both approaches are comparable with respect to the virtual landscape. The results of this check can be found in Supplementary Material, Figure S3.1.

Results

The Pareto-optimal solutions of the biophysical landscape optimization using CoMOLA span the largest hypervolume (HV) among all experimental runs (HV of CoMOLA is twice the HV of a simple Monte Carlo sampling with the same number of tested solutions, see Table 2). Convergence of the HV development (Figure 4) indicates that CoMOLA’s set of non-dominated solutions is close to the true Pareto frontier. However, some variants of the ABM resulted in only slightly lower HV: ABM_max, ABM_sat_hom, and ABM_sat_het (explanation of the abbreviations see Figure 3). These are variants in which all three agri-environmental payments were included (base payment; agglomeration bonus; water quality bonus). Lower HV were achieved by the two ABM variants in which only one (ABM_sat_het_base) or two (ABM_sat_het_agg) payment instruments were included. However, in both cases, the HV was higher than in the case of the Monte Carlo sampled set of landscapes.

TABLE 2

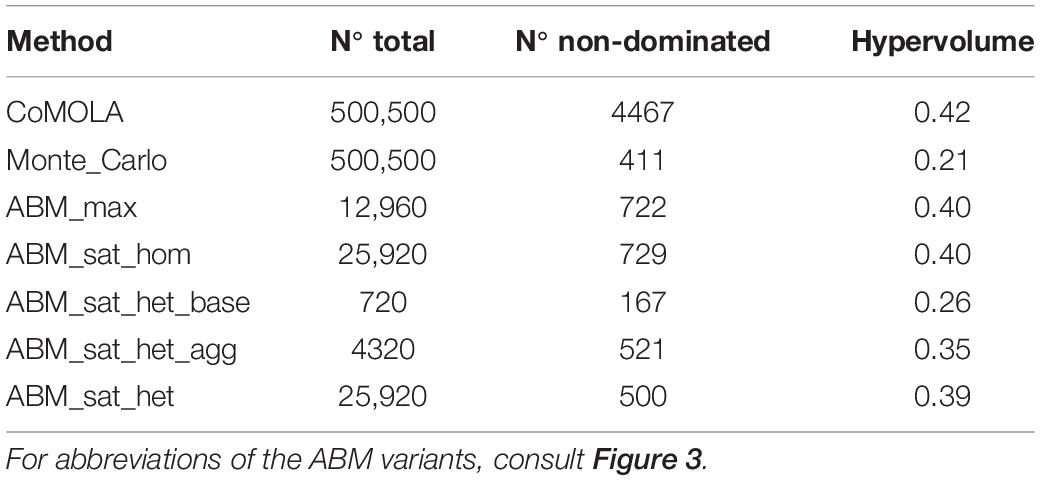
Table 2. Number of tested solutions (N° total) for each simulation experiment, number of non-dominated solutions (N° non-dominated) within each set, and their respective hypervolumes.

FIGURE 4

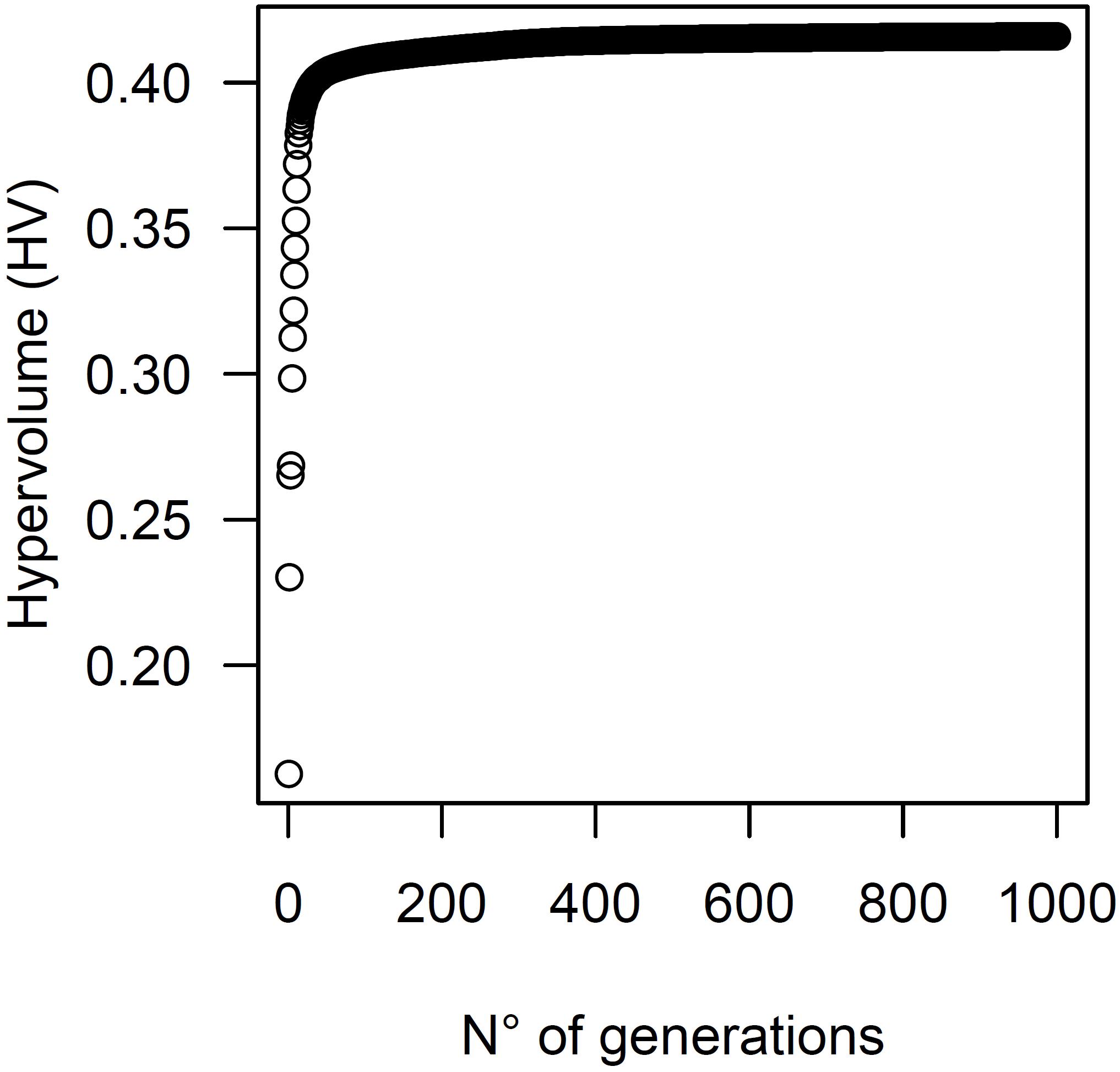
Figure 4. Evolution of the hypervolume over all generations for the land use optimization using CoMOLA.

The full set of Pareto-optimal solutions identified with CoMOLA is shown in Figure 5. From analysing the example maps (also shown in Figure 5), it is fair to assume that the optimization identified at least near-optimal solutions. For example, the numerically “best” compromise solution (i.e., the solution that is closest to the mean of each objective) allocates extensive grassland on one contiguous patch on each riverside while intensively used grassland prevails at a greater river distance and/or on more fertile soils. Maximum agricultural yield is achieved in a purely intensively managed landscape, whereas maximum water quality and habitat quality are achieved in a purely extensively managed one (see also Supplementary Material, Figure S3.2 for measures of correlation between the three objectives).

FIGURE 5

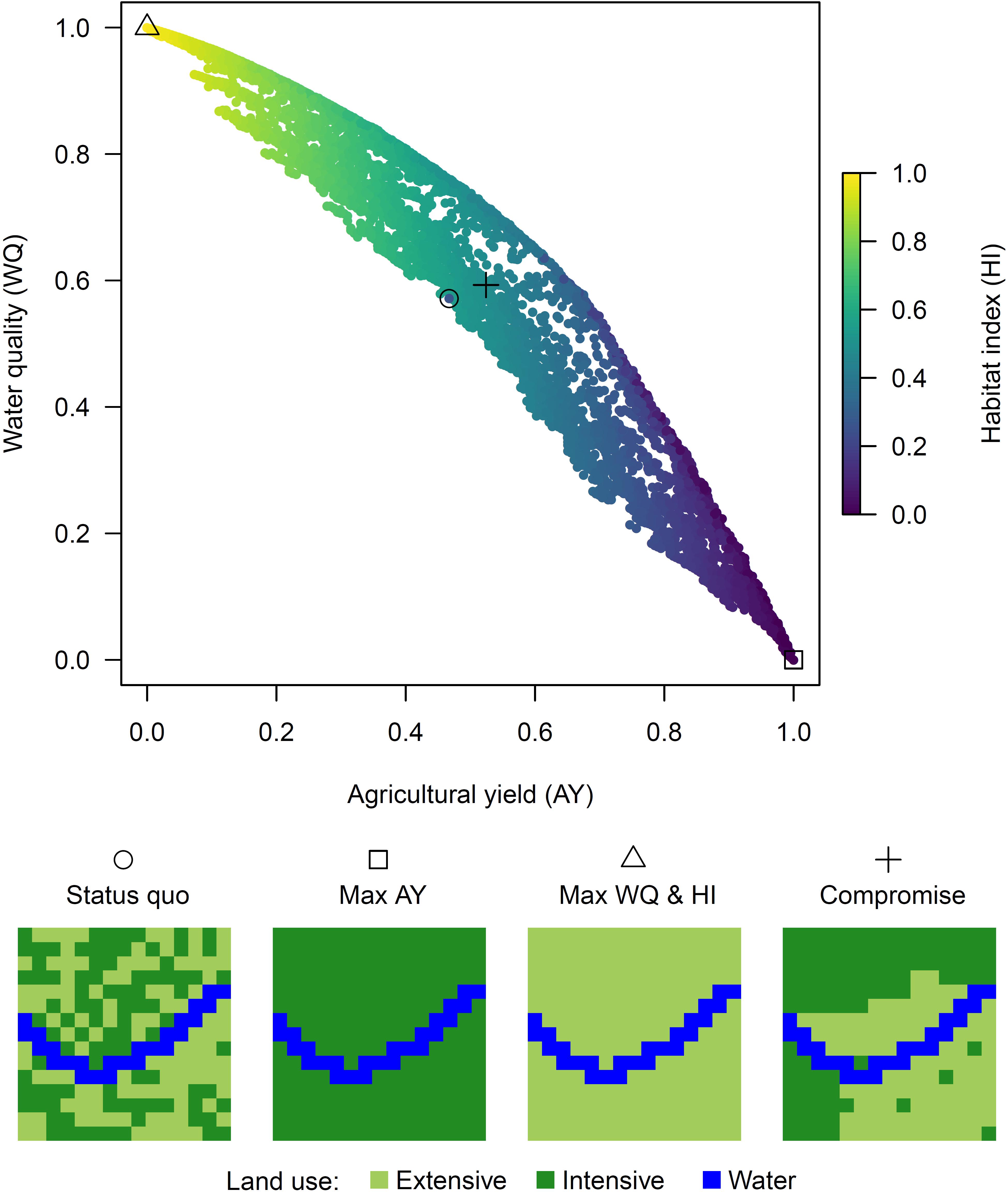
Figure 5. Non-dominated solutions identified by CoMOLA with illustration of the status quo land use as well as maximum solutions and one compromise solution. “Max AY,” “Max WQ,” and “Max HI” are the solutions with maximal agricultural yield, water quality and habitat index, respectively. “Compromise” refers to the solution closest to the mean of each objective.

In Figure 6, the main results of the comparison of the ABM variants with the CoMOLA optimization are presented. To support interpretability of the 3-dimensional solution space, we divided it by presenting three 2-dimensional scatter plots for each comparison. In the first column, the relationship between agricultural yield and water quality are depicted; the second column depicts the relationship between agricultural yield and habitat index; in the third column, we have water quality and habitat index. Each row is the comparison of one ABM variant (and, additionally, the Monte Carlo simulation) with CoMOLA. The CoMOLA solutions are not directly included in the diagrams; rather, for each non-dominated solution derived from an ABM variant, its Euclidean distance to the respective closest non-dominated solution of CoMOLA is represented by means of a color scale.

FIGURE 6

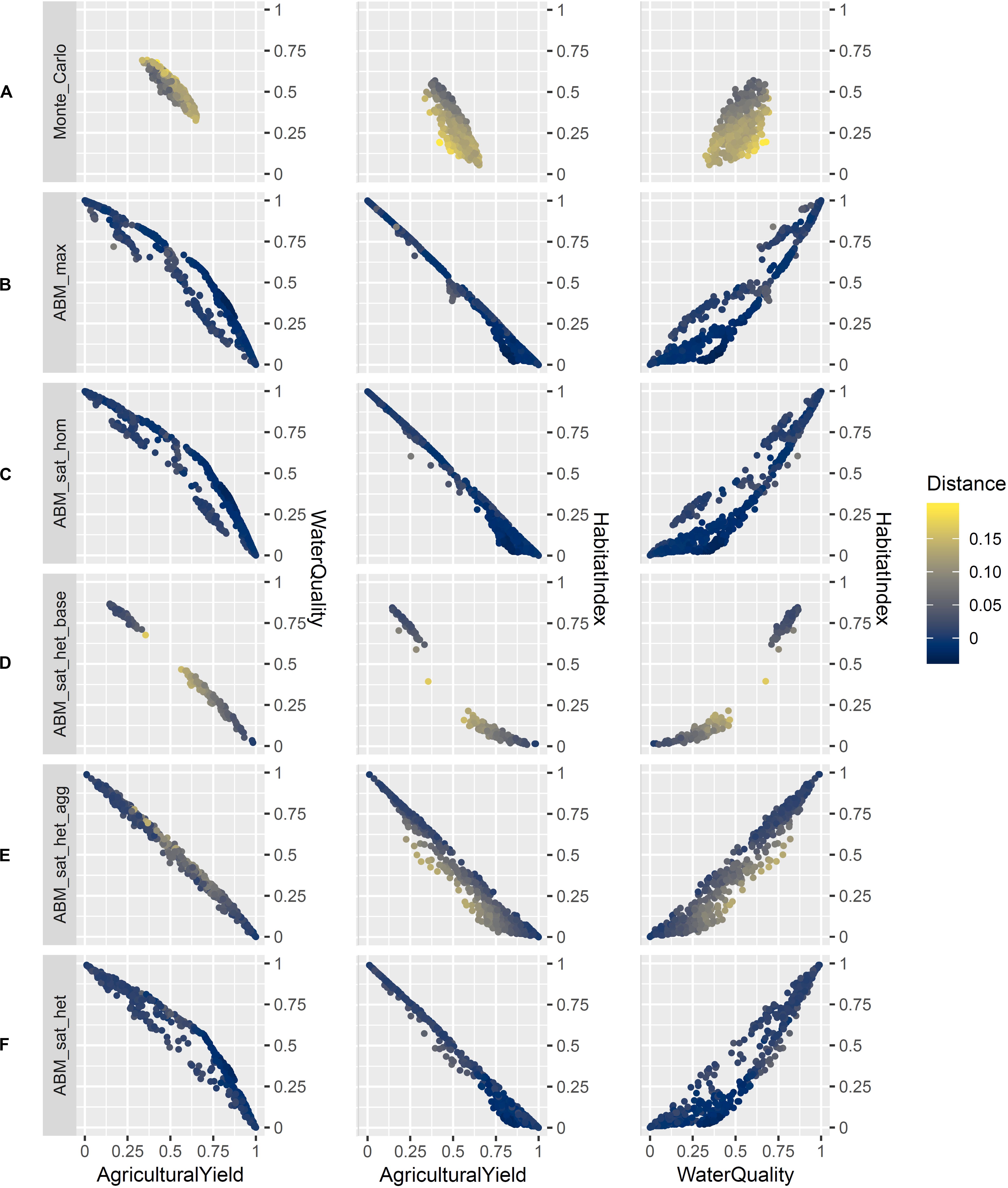
Figure 6. Non-dominated solutions based on Monte Carlo and ABM simulations and their distance to CoMOLA. Note that the 3D solution space is shown in three 2D scatterplots. Distance refers to the Euclidean distance to the respective closest non-dominated solution of CoMOLA. (A) Monte Carlo simulation; (B) ABM, maximizer variant; (C) ABM, satisficer variant, homogeneous income thresholds; (D) ABM, satisficer variant, heterogeneous income thresholds, base payment only; (E) ABM, satisficer variant, heterogeneous income thesholds, base payment and aggregation bonus; (F) ABM, satisficer variant, heterogeneous income thesholds, all payments.

The visual comparisons reflect the effects of single agri-environmental payments and behavioral assumptions and are in line with the HV analysis presented above. Unsurprisingly, according to the ecosystem service models, there is a trade-off between agricultural yield and both environmental objectives, water and habitat quality. Assuming only a base payment for extensive grassland (ABM_sat_het_base; Figure 6D), comparably “poor” solutions were achieved (i.e., CoMOLA clearly dominates this ABM variant), in particular with respect to the environmental targets. The distance to CoMOLA is relatively smaller in boundary regions of the solution space (i.e., near the upper limit of the single-objective domains). ABM solutions improved after adding bonus payments for agglomeration of extensive grassland (ABM_sat_het_agg; Figure 6E). Here, the trade-off curve between agricultural yield and habitat index was less concave than for ABM_stat_het_base, but rather linear, similar to the set of solutions found by CoMOLA. However, ABM_sat_het_agg still fails to achieve a more “opportune” (i.e., convex) trade-off curve between agricultural yield and water quality. Such a convex shape was achieved with all three ABM variants (ABM_max, ABM_sat_hom, ABM_sat_het) in which all environmental targets were addressed by means of agri-environmental payments, adding a water quality bonus to the base payment and the agglomeration bonus. In line with the HV analysis, no clear differences could be found between ABM_max, ABM_sat_hom, and ABM_sat_het, suggesting that for this virtual case study, behavioral assumptions do not seem to play a large role. This is partly related to the random setting of income threshold levels for agents in the bounded rationality (satisficing) variants. A comparison of non-dominated (Pareto-optimal) solutions with the overall population shows that the Pareto-optimal solutions in most cases have pretty high income thresholds and are thus close to the ABM_max variant (see Supplementary Material, Figure S3.3). In a real case study, the income thresholds could possibly be determined empirically; in our virtual case study, their random definition served as a kind of sensitivity analysis.

Figure 7 offers another relevant perspective on the results: it shows the relationship between the Pareto-optimal solutions from the ABM and the total budget for agri-environmental payments in the equilibrium. Not surprisingly, there is a clear gradient from solutions with high agricultural yields (corresponding to low budget for agri-environmental payments) to solutions with high levels of the two non-provisioning ecosystem services (high budget for agri-environmental payments). There are, however, budget variations among solutions close to each other, suggesting that total agri-environmental budget can be a criterion to select a subset of (cost-effective) solutions from a desirable region of the Pareto frontier. The share of agri-environmental payments in total incomes varied across ABM variants; single model runs reached more than 25 per cent (max. 26.7), while average shares ranged between 1.8–6.2 (median) and 4.5–8.3 (mean) (distributions of mean incomes and budget shares across ABM variants can be found in Supplementary Material, Figure S3.4).

FIGURE 7

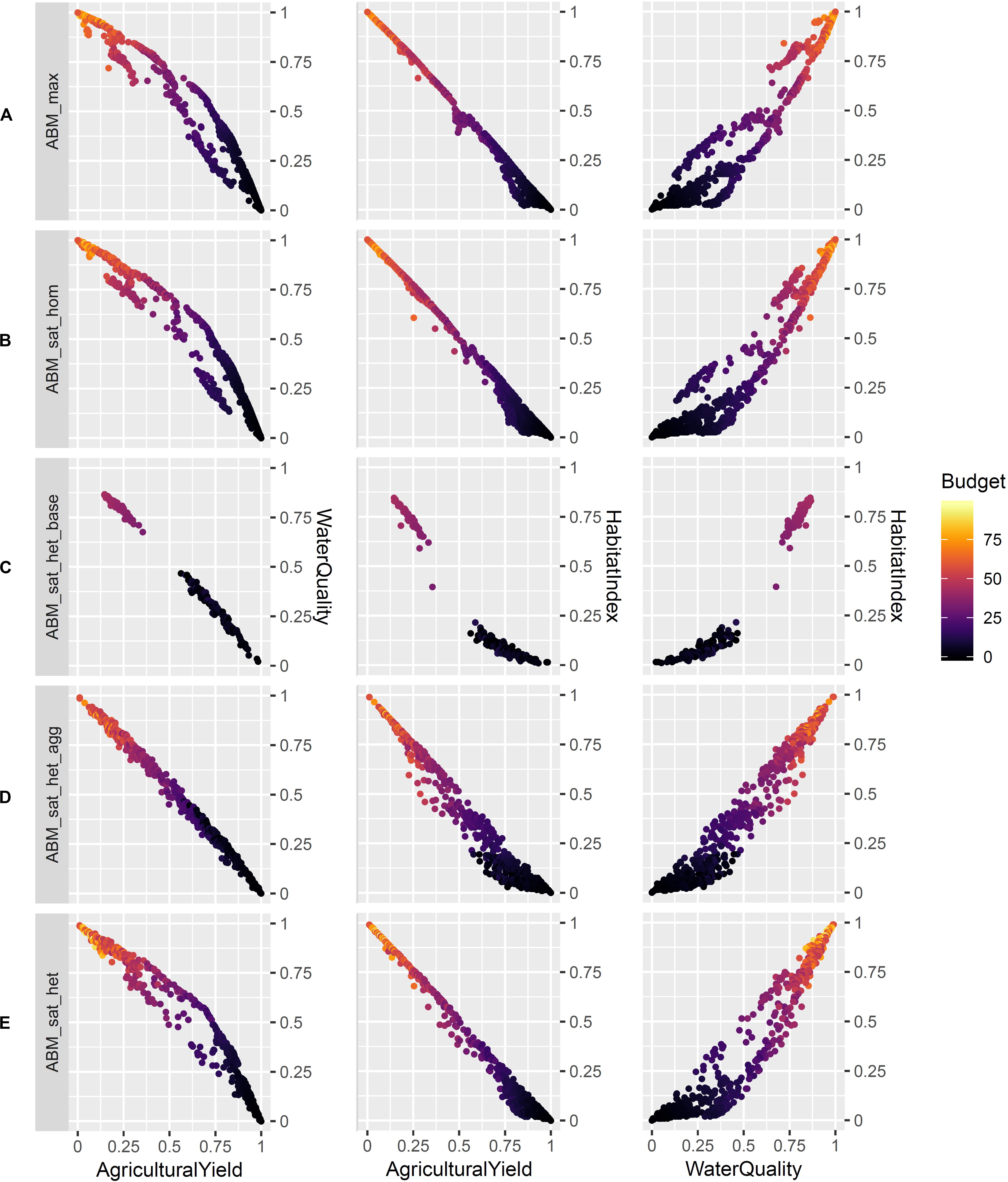
Figure 7. Non-dominated solutions of ABM simulations colored by normalized total budget for agri-environmental payments in equilibrium. Note that the 3D solution space is shown in three 2D scatterplots. (A) ABM, maximizer variant; (B) ABM, satisficer variant, homogeneous income thresholds; (C) ABM, satisficer variant, heterogeneous income thresholds, base payment only; (D) ABM, satisficer variant, heterogeneous income thesholds, base payment and aggregation bonus; (E) ABM, satisficer variant, heterogeneous income thesholds, all payments.

Discussion and Conclusion

The virtual case study above is a first illustration of how the ALABAMA approach can work. In order to appreciate its relevance and contribution, we will first discuss the results of the virtual case study, before then sketching out the potential and challenges of applying ALABAMA to real-world cases.

Virtual Case Study: Insights and Limits

The aim of the virtual case study has been to demonstrate how multi-objective land-use optimization and agent-based modeling can be aligned with each other in order to explore the economic, social and institutional feasibility of biophysically optimal landscapes. Even though the virtual case study and the models involved are very stylized, a number of insights can still be drawn from them. Most importantly, both the visual comparison of Pareto frontiers and the numerical comparison of hypervolumes have shown that using specific policy instruments for each ecosystem service helps to move closer to the biophysical optimum. While this cannot be directly generalized, the result is in line with economic theory of instrument mixes (Braathen, 2007) (for more details, see section “Going Beyond Virtual Landscapes: Potential and Challenges of ALABAMA”). Possibly also due to the relatively simple behavioral assumptions, the presence of all three agri-environmental payments was more decisive for proximity to the biophysical optimum (in terms of hypervolume) than the varying assumptions regarding farmers’ behavior.

Contrasting the trade-off analysis among the three policy objectives (production, water quality, habitat quality) with information on the budget needed to achieve various Pareto-optimal solutions has demonstrated the importance of non-biophysical constraints such as the budget available to public authorities for agri-environmental payments. In the real world, there is only a limited amount of money that can be spent on agri-environmental incentive payments (given opportunity costs, i.e., foregone benefits that would result from spending the funds on alternative public-good purposes). This implies a necessity to design and select cost-effective policy instruments (e.g., Wätzold et al., 2016). In the context of ALABAMA, including a budget constraint would largely reduce the number of “feasible” Pareto-optimal solutions according to the ABM. As can be seen in Figure 7, the reduction would not be symmetrical – rather, the solution space would be reduced much more where the levels of provision of public ecosystem services is high, as compared to the solutions associated with high agricultural yields. This is plausible, since the provision of public ecosystem services requires the use of public funds (in the form of agri-environmental payments). Furthermore, in an empirical case study, it would be sensible to assume a budget constraint depending on society’s maximum aggregate willingness to pay for the promotion of environmental objectives. With a broader spectrum of policy instruments, the use of a specified budget constraint may help distinguish between relatively cost-effective and cost-ineffective instruments or instrument designs, thus complementing the information regarding the feasibility of biophysically optimal landscapes with information about differently efficient ways of achieving them.

The way we implemented bounded rationality (via randomly set individual income thresholds beyond which farmers were assumed to be “satisfied” and cease changing management) had the consequence that there were no significant differences between the Pareto frontiers derived from the maximizers vs. the satisficers variants of the ABM. The alternative would have been an arbitrary specification of the income threshold (in a real case study, income thresholds would be an empirical matter and can be assumed to be pretty stable). Due to this implementation choice, the differences between the behavioral assumptions were partly hidden. However, it turned out that Pareto-optimal ABM solutions tended to be associated with higher mean income thresholds (see Supplementary Material, Figure S3.3). Also, a look at the distributions of values for the ecosystem service indicators water quality and habitat index for maximizers vs. satisficers shows that maximizer specifications tend to extreme solutions with very high or very low levels of ecosystem service provision, while satisficers also create many landscapes with intermediate levels of ecosystem service provision (see Supplementary Material, Figure S3.5). The main reason for this is that after reaching their respective income thresholds, the satisficers stop changing management without having reached an “equilibrium,” which would result from purely maximizing behavior. Conversely, for maximizers, there is only a very narrow range of agri-environmental payment levels that do not “tip” the system in an extreme state (i.e., either purely intensively or purely extensively managed landscape). This adds to the more general fact that the choice of the parameter range of the ABM is decisive for the relative “intensity” with which different areas of the Pareto frontier are explored. In our case, the payment rates ranged from 0 to somewhat above the level beyond which there is a 100% shift to extensive grassland in the equilibrium. Thus, there are relatively many Pareto-optimal solutions with high agricultural production, because for all payment levels below a certain threshold (depending on yield distribution and farmers’ income threshold levels) the end result was a Pareto-optimal 100% intensive grassland landscape, independent of the behavioral assumptions. This apparent sensitivity of system behavior to the level of income thresholds may in practice lead to interactions with policy instruments from other domains that may influence income thresholds, such as e.g., universal basic income⁵.

Going Beyond Virtual Landscapes: Potential and Challenges of ALABAMA

While the virtual case study provides some first impression of the potential of ALABAMA, applying the approach to real-world cases implies additional challenges – but it also bears further potential. When applied to real-world case studies, the aligning of agent-based modeling with multi-objective land-use optimization will provide insights into: (i) the biophysical potential of a landscape to provide multiple ecosystem services; (ii) the gap between the status quo and the biophysical potential; (iii) the economic, institutional and social feasibility of the biophysically optimal landscape configurations; (iv) the relevant policy instruments needed to approach the biophysical optimum; as well as (v) the gap between the biophysical optimum and what can be achieved given economic, institutional and social constraints, including, possibly, the reasons for its existence. These pieces of information could inform policy-making processes aiming at increasing the multifunctionality of landscapes.

The biophysical optimization can be considered as providing a bundle of non-dominated solutions (landscape configurations), which constitute, from society’s point of view, no-regret options with respect to the use of the analyzed landscape – at least assuming that all societally relevant objectives have been included in the optimization procedure. However, the biophysically optimal landscapes generated by multi-objective optimization algorithms such as CoMOLA are not necessarily attainable given institutional, social, behavioral and economic constraints. Furthermore, it is not clear how they can be achieved. In this sense, the role of the ABM is to identify attainable socio-economically feasible solutions – and the policy paths leading there. These policy paths will likely require the careful design of an instrument mix – first, because, in line with the Tinbergen rule (Tinbergen, 1952; Braathen, 2007), multifunctionality as policy objective requires multiple policy instruments (e.g., multiple agri-environmental payments, as in our virtual case study); second, because the presence of various market failures, such as incomplete property rights (Bartkowski et al., 2018), reinforces this requirement (Lipsey and Lancaster, 1956; Schader et al., 2014). In fact, the latter is the very reason why in the most cases, even the most sophisticated instrument mix will not lead to reaching the biophysical optimum. In this context, the ALABAMA approach has an important advantage: it allows a broad comparison of biophysically attainable no-regret and socio-economically feasible model representations of the world, and thus may provide inspiration to the search for new ways to change boundary conditions (e.g., by means of novel instruments, not included in the initial version of the ABM) in order to move closer to the biophysical Pareto frontier. This is especially attractive when the gap between biophysical optimization and ABM is large. The extensive literature on behavioral interventions is relevant here (e.g., Klöckner, 2013; Michie et al., 2014; Dessart et al., 2019). As suggested above in the context of the virtual case study, relevant constraints may be even found outside of the domain of environmental policy.

Explaining the gap can help identify “hard constraints” that cannot be overcome easily (e.g., property rights or financial or technological barriers faced by farmers and/or administrators), and “soft constraints” that can be overcome by changing particular assumptions of the ABM (preferably without loss of realism) or, especially, by adding new policy instruments not thought of initially. Such “soft” constraints will likely be highly context-specific and may include interactions with other policy domains (e.g., residential development in the context of agri-environmental policy), budget constraints or jurisdictional responsibilities (in cases in which the most effective way of closing the biophysical multifunctionality gap would require coordination across national or other administrative borders). This constraint analysis will depend on which parameters and assumptions of the model are mainly responsible for the gap. These insights can then be used as input into discussions with stakeholders in order to make the approach particularly policy relevant (Karner et al., 2019). For instance, participatory approaches such as scenario discovery (Bryant and Lempert, 2010) could be used to identify particularly policy-relevant aspects of the ALABAMA analysis. Stakeholder interactions can be used to elicit preferences for the various solutions – in line with Cavender-Bares et al. (2015), but going beyond their approach by including not only the biophysical (ecosystem service) attributes of the solutions, but also institutional and economic factors. Alternatively, secondary preference information (e.g., from willingness-to-pay surveys) could be used to identify particularly “desirable” regions in the solution space and focus discussions with stakeholders on those. In any case, both the choice and specification of models and the analysis of the political and societal implications of the results would strongly benefit from stakeholder engagement.

By incorporating a dynamic modeling approach in ABM, ALABAMA also allows for analysis of trajectories or pathways toward a desired multifunctional landscape. This may be helpful for conceptualizing and designing indicators (e.g., “milestones”) to check whether the trajectory entered in the real world is in line with the long-term policy objective of a specific multifunctional landscape. This would be particularly relevant for more complex landscape and land-use reconfigurations, which make take time, both in terms of implementation and environmental effects. Also, multi-stage policy processes are thinkable, in which policy instruments are not introduced all at once (e.g., because some instruments may only need minor redesign, while others would require a more time-consuming processes of design and legislation), but sequentially – here, too, the dynamic perspective provided by the ABM may be informative.

But applying ALABAMA to real-world cases, with more complex models and real landscapes, does also come with additional challenges – the virtual case study has only a proof-of-concept character. For instance, due to restrictions in terms of computational power, a full exploration of the parameter space may be impossible or at least overly time- and resource consuming if the ABM is structurally complex. This might require a (multi-objective) optimization already within the ABM, e.g., by means of BehaviorSearch in NetLogo (Stonedahl and Wilensky, 2010; Railsback et al., 2017). Here, the results of a multi-objective optimization within the ABM (i.e., including variation of behavioral, economic and policy parameters) would be compared to the results of biophysical optimization. The optimization within the ABM itself may be highly informative – however, without comparison to the biophysical optimization, it would imply a loss of information regarding the relative “loss” in optimality in provision of ecosystem services due to behavioral, social, economic and institutional constraints. Therefore, optimization within the ABM, aiming at reducing the time required for the exploration of the parameter space, would be a simplification of the process applied in our virtual case study, where we first fully explored the parameter space and only then filtered Pareto-optimal solutions.

More generally, a fully developed application of our approach to a real-world case study would have rather high requirements in terms of data, computational power and expertise. This is a general challenge in the modeling of social–ecological systems (Elsawah et al., 2020). In the case of biophysical optimization of complex real-world case studies, the exploration performance of genetic algorithms or other metaheuristics decreases with increasing number of spatial units and decision variables (Strauch et al., 2019). Accepting some level of simplification (e.g., focusing on local/regional studies and only on selected ecosystem services) remains a necessary compromise. Nevertheless, our approach is very much in line with the recent trend toward model coupling in studying social–ecological systems (Robinson et al., 2018), which allows for a flexible approach toward better understanding the behavior and trajectories of these highly complex systems. While challenging, such approaches have a high potential to provide information relevant to societal preference-building and policy-making processes.

Avenues for Future Research

Going from virtual to real landscapes in the application of the ALABAMA approach requires responses to important questions that were not central in our virtual case study. For instance, what are the relevant ecosystem services and how well can they be represented in models? Spatially explicit assessments of ecosystem service supply still need considerable progress, especially for quantifying individual species effects, species diversity, functional traits, and their interaction with ecosystem functions while considering effects of scale and embracing good practice in model uncertainty quantification and validation – see Lavorel et al. (2017), who comprehensively reviewed the biophysical realism gap in ecosystem service mapping approaches, and Elsawah et al. (2020) for a more general perspective on these issues in the context of social–ecological modeling. Given that some selection of ecosystem services is required to make multi-objective optimization computationally tractable, there is a need for research into methods and criteria to make such selection structured, transparent and policy-relevant.

Turning to ABM, further questions arise. For example, what (types of) instruments are to be included and how can they be parameterized? So far, the focus in social–ecological models has mostly been on financial incentives such as area-based direct payments and agri-environmental payments (e.g., Brady et al., 2012; Brunner et al., 2016), while other types of instruments and broader instrument mixes remain understudied. Relatedly, an important but understudied issue with high relevance for the economic feasibility of instrument mixes aiming at biophysically optimal provision of multiple ecosystem services are difficult-to-represent, but potentially highly important factors such as transaction costs (DeBoe and Stephenson, 2016), which may render otherwise highly attractive policy mixes cost-ineffective, or the conflict between legal and “economic” property rights (Bartkowski et al., 2018). The explicit inclusion of such issues in studies following the ALABAMA approach would strongly increase their policy relevance. Another question regards which behavioral models to choose and how to implement them – there is a broad spectrum of potentially useful behavioral models and theories (Groeneveld et al., 2017; Huber et al., 2018), and no obvious way to select a “right” one. Rather, each policy context and particular set of research questions may require a different choice. Nonetheless, guidance and criteria are needed for transparent choices of appropriate behavioral assumptions and their implementation in the model (Smajgl et al., 2011).

An open question for real-world case studies, which could not be addressed comprehensively in our virtual case study, regards how exactly the feedback from the structured comparison to the agent-based model is supposed to work. As discussed above, if it is found that “hard” boundary conditions are responsible for the gap between ABM and the biophysical potential of the landscape, little can be done to improve the results. However, if “soft” boundary conditions are responsible, this should trigger a structured (and previously planned, as far as possible) process of improving the parameterization of the ABM and possibly also adding components (for instance, different types of policy instruments that cannot be implemented by simply adjusting existing parameters). This feedback analysis will likely be highly context-specific and will require a strong participatory element.

All the questions formulated above require intensive analysis of the specific social–ecological system prior to modeling, by means of surveys, interviews, focus groups and secondary data analysis. Also, they require careful and transparent planning of the application of ALABAMA. Therefore, the next step in order to provide responses needs to be a real-world application of the approach.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: https://github.com/BartoszBartk/magenta.

Author Contributions

BB and MS developed the models, conducted the modeling analysis, and wrote the first draft of the manuscript. All authors contributed to the conception and design of the study, and to revisions of the manuscript.

Funding

This research was supported by funding from the Integrated Project “IP12 Land-Use Conflicts” of the UFZ.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank Anna Cord, Gunnar Dreßler, Nicolai Heinz, Kathleen Hermans, Christoph Schröter-Schlaack, and Jule Thober for valuable discussions and brainstorming in the early stages of this project.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2020.00103/full#supplementary-material

Footnotes

1. ^ Note that it is non-trivial to formulate a social welfare function, and there are various objectives that may enter such a function (including individual preference satisfaction, distributional concerns etc.). See also Klauer et al. (2017).
2. ^ Intensity in grassland management may be measured e.g., in terms of fertilization or mowing/grazing intensity. For a discussion of the difficulties to provide measures of intensive and extensive land use, see Beckmann et al. (2019).
3. ^ The agglomeration bonus has been widely discussed in the economic literature; see Parkhurst et al. (2002) and Krämer and Wätzold (2018).
4. ^ This does not affect the equilibrium landscape configuration, only the speed at which it is reached.
5. ^ We are thankful to a reviewer for pointing this out.

References

Bartkowski, B., and Bartke, S. (2018). Leverage points for governing agricultural soils: a review of empirical studies of European farmers’ decision-making. Sustainability 10:3179. doi: 10.3390/su10093179

CrossRef Full Text | Google Scholar

Bartkowski, B., Hansjürgens, B., Möckel, S., and Bartke, S. (2018). Institutional economics of agricultural soil ecosystem services. Sustainability 10:2447. doi: 10.3390/su10072447

CrossRef Full Text | Google Scholar

Beckmann, M., Gerstner, K., Akin-Fajiye, M., Ceauşu, S., Kambach, S., Kinlock, N. L., et al. (2019). Conventional land-use intensification reduces species richness and increases production: a global meta-analysis. Glob. Change Biol. 25, 1941–1956. doi: 10.1111/gcb.14606

PubMed Abstract | CrossRef Full Text | Google Scholar

Binder, S. (2019). Flurbereinigungsplanung und Ökosystemschutz als Rechts- und Governance-Problem. Marburg: Beiträge zur sozialwissenschaftlichen Nachhaltigkeitsforschung. Metropolis-Verlag.

Google Scholar

Braathen, N. A. (2007). Instrument mixes for environmental policy: how many stones should be used to kill a bird? Int. Rev. Environ. Resour. Econ. 1, 185–235. doi: 10.1561/101.00000005

CrossRef Full Text | Google Scholar

Brady, M., Sahrbacher, C., Kellermann, K., and Happe, K. (2012). An agent-based approach to modeling impacts of agricultural policy on land use, biodiversity and ecosystem services. Landsc. Ecol. 27, 1363–1381. doi: 10.1007/s10980-012-9787-3

CrossRef Full Text | Google Scholar

Brunner, S. H., Huber, R., and Grêt-Regamey, A. (2016). A backcasting approach for matching regional ecosystem services supply and demand. Environ. Model. Softw. 75, 439–458. doi: 10.1016/j.envsoft.2015.10.018

CrossRef Full Text | Google Scholar

Bryant, B. P., and Lempert, R. J. (2010). Thinking inside the box: a participatory, computer-assisted approach to scenario discovery. Technol. Forecast. Soc. Change 77, 34–49. doi: 10.1016/j.techfore.2009.08.002

CrossRef Full Text | Google Scholar

Cavender-Bares, J., Polasky, S., King, E., and Balvanera, P. (2015). A sustainability framework for assessing trade-offs in ecosystem services. Ecol. Soc. 20:17. doi: 10.5751/ES-06917-200117

PubMed Abstract | CrossRef Full Text | Google Scholar

Coello Coello, C. A., Lamont, G. B., and Van Veldhuizen, D. A. (2007). Evolutionary Algorithms for Solving Multi-Objective Problems, Genetic and Evolutionary Computation Series, 2nd Edn. New York, NY: Springer.

Google Scholar

Cord, A. F., Bartkowski, B., Beckmann, M., Dittrich, A., Hermans-Neumann, K., Kaim, A., et al. (2017). Towards systematic analyses of ecosystem service trade-offs and synergies: main concepts, methods and the road ahead. Ecosyst. Serv. 28(Pt C), 264–272. doi: 10.1016/j.ecoser.2017.07.012

CrossRef Full Text | Google Scholar

Deb, K. (2014). “Multi-objective optimization,” in Search Methodologies, eds E. K. Burke and G. Kendall (Boston, MA: Springer), 403–449.

Google Scholar

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 6, 182–197. doi: 10.1109/4235.996017

CrossRef Full Text | Google Scholar

DeBoe, G., and Stephenson, K. (2016). Transactions costs of expanding nutrient trading to agricultural working lands: a Virginia case study. Ecol. Econ. 130, 176–185. doi: 10.1016/j.ecolecon.2016.06.027

CrossRef Full Text | Google Scholar

Dessart, F. J., Barreiro-Hurlé, J., and van Bavel, R. (2019). Behavioural factors affecting the adoption of sustainable farming practices: a policy-oriented review. Eur. Rev. Agric. Econ. 46, 417–471. doi: 10.1093/erae/jbz019

CrossRef Full Text | Google Scholar

El Benni, N., Finger, R., and Mann, S. (2012). Effects of agricultural policy reforms and farm characteristics on income risk in Swiss agriculture. Agric. Finance Rev. 72, 301–324. doi: 10.1108/00021461211277204

CrossRef Full Text | Google Scholar

Elsawah, S., Filatova, T., Jakeman, A. J., Kettner, A. J., Zellner, M. L., Athanasiadis, I. N., et al. (2020). Eight grand challenges in socio-environmental systems modeling. Soc. Environ. Syst. Model. 2, 16226–16226. doi: 10.18174/sesmo.2020a16226

CrossRef Full Text | Google Scholar

Groeneveld, J., Müller, B., Buchmann, C. M., Dressler, G., Guo, C., Hase, N., et al. (2017). Theoretical foundations of human decision-making in agent-based land use models – A review. Environ. Model. Softw. 87, 39–48. doi: 10.1016/j.envsoft.2016.10.008

CrossRef Full Text | Google Scholar

Haslauer, E., Biberacher, M., and Blaschke, T. (2016). A spatially explicit backcasting approach for sustainable land-use planning. J. Environ. Plan. Manag. 59, 866–890. doi: 10.1080/09640568.2015.1044652

CrossRef Full Text | Google Scholar

Hristov, J., Clough, Y., Sahlin, U., Smith, H. G., Stjernman, M., Olsson, O., et al. (2020). Impacts of the EU’s common agricultural policy “Greening” reform on agricultural development, biodiversity, and ecosystem services. Appl. Econ. Perspect. Policy (in press). doi: 10.1002/aepp.13037

CrossRef Full Text | Google Scholar

Huber, R., Bakker, M., Balmann, A., Berger, T., Bithell, M., Brown, C., et al. (2018). Representation of decision-making in European agricultural agent-based models. Agric. Syst. 167, 143–160. doi: 10.1016/j.agsy.2018.09.007

CrossRef Full Text | Google Scholar

IPBES (2018a). The Assessment Report on Land Degradation and Restoration. Bonn: IPBES Secretariat.

Google Scholar

IPBES (2018b). The Regional Assessment Report on Biodiversity and Ecosystem Services for Europe and Central Asia. Bonn: IPBES Secretariat.

Google Scholar

Jiang, S., Ong, Y.-S., Zhang, J., and Feng, L. (2014). Consistencies and contradictions of performance metrics in multiobjective optimization. IEEE Trans. Cybern. 44, 2391–2404. doi: 10.1109/TCYB.2014.2307319

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaim, A., Cord, A. F., and Volk, M. (2018). A review of multi-criteria optimization techniques for agricultural land use allocation. Environ. Model. Softw. 105, 79–93. doi: 10.1016/j.envsoft.2018.03.031

CrossRef Full Text | Google Scholar

Karner, K., Cord, A. F., Hagemann, N., Hernandez-Mora, N., Holzkämper, A., Jeangros, B., et al. (2019). Developing stakeholder-driven scenarios on land sharing and land sparing – Insights from five European case studies. J. Environ. Manage. 241, 488–500. doi: 10.1016/j.jenvman.2019.03.050

PubMed Abstract | CrossRef Full Text | Google Scholar

King, E., Cavender-Bares, J., Balvanera, P., Mwampamba, T., and Polasky, S. (2015). Trade-offs in ecosystem services and varying stakeholder preferences: evaluating conflicts, obstacles, and opportunities. Ecol. Soc. 20:25. doi: 10.5751/ES-07822-200325

PubMed Abstract | CrossRef Full Text | Google Scholar

Klauer, B., Bartkowski, B., Manstetten, R., and Petersen, T. (2017). Sustainability as a fair bequest: an evaluation challenge. Ecol. Econ. 141, 136–143. doi: 10.1016/j.ecolecon.2017.06.001

CrossRef Full Text | Google Scholar

Klöckner, C. A. (2013). A comprehensive model of the psychology of environmental behaviour—A meta-analysis. Glob. Environ. Change 23, 1028–1038. doi: 10.1016/j.gloenvcha.2013.05.014

CrossRef Full Text | Google Scholar

Krämer, J. E., and Wätzold, F. (2018). The agglomeration bonus in practice—An exploratory assessment of the Swiss network bonus. J. Nat. Conserv. 43, 126–135. doi: 10.1016/j.jnc.2018.03.002

CrossRef Full Text | Google Scholar

Kremmydas, D., Athanasiadis, I. N., and Rozakis, S. (2018). A review of agent based modeling for agricultural policy evaluation. Agric. Syst. 164, 95–106. doi: 10.1016/j.agsy.2018.03.010

CrossRef Full Text | Google Scholar

Lavorel, S., Bayer, A., Bondeau, A., Lautenbach, S., Ruiz-Frau, A., Schulp, N., et al. (2017). Pathways to bridge the biophysical realism gap in ecosystem services mapping approaches. Ecol. Indic. 74, 241–260. doi: 10.1016/j.ecolind.2016.11.015

CrossRef Full Text | Google Scholar

Ligmann-Zielinska, A., and Jankowski, P. (2010). Exploring normative scenarios of land use development decisions with an agent-based simulation laboratory. Comput. Environ. Urban Syst. 34, 409–423. doi: 10.1016/j.compenvurbsys.2010.05.005

CrossRef Full Text | Google Scholar

Lipsey, R. G., and Lancaster, K. (1956). The general theory of second best. Rev. Econ. Stud. 24:11. doi: 10.2307/2296233

CrossRef Full Text | Google Scholar

Martín-López, B., Iniesta-Arandia, I., García-Llorente, M., Palomo, I., Casado-Arzuaga, I., Amo, D. G. D., et al. (2012). Uncovering ecosystem service bundles through social preferences. PLoS One 7:e38970. doi: 10.1371/journal.pone.0038970

PubMed Abstract | CrossRef Full Text | Google Scholar

Mersmann, O. (2014). Multiple Criteria Optimization Algorithms and Related Functions.

Google Scholar

Michie, S., Atkins, L., and West, R. (2014). The Behaviour Change Wheel: A Guide to Designing Interventions. Sutton: Silverbeck Publishing.

Google Scholar

Mo, W., Lu, Z., Dilkina, B., Gardner, K., Huang, J.-C., and Foreman, M. (2018). Sustainable and resilient design of interdependent water and energy systems: a conceptual modeling framework for tackling complexities at the infrastructure-human-resource nexus. Sustainability 10:1845. doi: 10.3390/su10061845

CrossRef Full Text | Google Scholar

Müller, B., Bohn, F., Dreßler, G., Groeneveld, J., Klassert, C., Martin, R., et al. (2013). Describing human decisions in agent-based models – ODD + D, an extension of the ODD protocol. Environ. Model. Softw. 48, 37–48. doi: 10.1016/j.envsoft.2013.06.003

CrossRef Full Text | Google Scholar

O’Farrell, P. J., and Anderson, P. M. (2010). Sustainable multifunctional landscapes: a review to implementation. Curr. Opin. Environ. Sustain. 2, 59–65. doi: 10.1016/j.cosust.2010.02.005

CrossRef Full Text | Google Scholar

Parkhurst, G. M., Shogren, J. F., Bastian, C., Kivi, P., Donner, J., and Smith, R. B. W. (2002). Agglomeration bonus: an incentive mechanism to reunite fragmented habitat for biodiversity conservation. Ecol. Econ. 41, 305–328. doi: 10.1016/S0921-8009(02)00036-8

CrossRef Full Text | Google Scholar

Pe’er, G., Zinngrebe, Y., Moreira, F., Sirami, C., Schindler, S., Müller, R., et al. (2019). A greener path for the EU Common Agricultural Policy. Science 365, 449–451. doi: 10.1126/science.aax3146

PubMed Abstract | CrossRef Full Text | Google Scholar

R Core Team (2018). R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Railsback, S., Ayllón, D., Berger, U., Grimm, V., Lytinen, S., Sheppard, C., et al. (2017). Improving execution speed of models implemented in netlogo. J. Artif. Soc. Soc. Simul 20:3. doi: 10.18564/jasss.3282

CrossRef Full Text | Google Scholar

Reidsma, P., Janssen, S., Jansen, J., and van Ittersum, M. K. (2018). On the development and use of farm models for policy impact assessment in the European Union – A review. Agric. Syst. 159, 111–125. doi: 10.1016/j.agsy.2017.10.012

CrossRef Full Text | Google Scholar

Robinson, D. T., Di Vittorio, A., Alexander, P., Arneth, A., Barton, C. M., Brown, D. G., et al. (2018). Modelling feedbacks between human and natural processes in the land system. Earth Syst. Dyn. 9, 895–914. doi: 10.5194/esd-9-895-2018

CrossRef Full Text | Google Scholar

Schader, C., Lampkin, N., Muller, A., and Stolze, M. (2014). The role of multi-target policy instruments in agri-environmental policy mixes. J. Environ. Manage. 145, 180–190. doi: 10.1016/j.jenvman.2014.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Schlüter, M., Baeza, A., Dressler, G., Frank, K., Groeneveld, J., Jager, W., et al. (2017). A framework for mapping and comparing behavioural theories in models of social-ecological systems. Ecol. Econ. 131, 21–35. doi: 10.1016/j.ecolecon.2016.08.008

CrossRef Full Text | Google Scholar

Schlüter, M., Müller, B., and Frank, K. (2019). The potential of models and modeling for social-ecological systems research: the reference frame ModSES. Ecol. Soc. 24:31. doi: 10.5751/ES-10716-240131

PubMed Abstract | CrossRef Full Text | Google Scholar

Schulze, J., Müller, B., Groeneveld, J., and Grimm, V. (2017). Agent-based modelling of social-ecological systems: achievements, challenges, and a way forward. J. Artif. Soc. Soc. Simul. 20:8.

Google Scholar

Schwarz, N., Hoffmann, F., Knapp, S., and Strauch, M. (2020). Synergies or trade-offs? Optimizing a virtual urban region to foster plant species richness, climate regulation, and compactness under varying landscape composition. Front. Environ. Sci. 8:16. doi: 10.3389/fenvs.2020.00016

CrossRef Full Text | Google Scholar

Simon, H. A. (1955). A behavioral model of rational choice. Q. J. Econ. 69, 99–118. doi: 10.2307/1884852

CrossRef Full Text | Google Scholar

Smajgl, A., Brown, D. G., Valbuena, D., and Huigen, M. G. A. (2011). Empirical characterisation of agent behaviours in socio-ecological systems. Environ. Model. Softw. 26, 837–844. doi: 10.1016/j.envsoft.2011.02.011

CrossRef Full Text | Google Scholar

Stonedahl, F., and Wilensky, U. (2010). BehaviorSearch. Center for Connected Learning and Computer Based Modeling. Evanston, IL: Northwestern University.

Google Scholar

Strauch, M., Cord, A. F., Pätzold, C., Lautenbach, S., Kaim, A., Schweitzer, C., et al. (2019). Constraints in multi-objective optimization of land use allocation – Repair or penalize? Environ. Model. Softw. 118, 241–251. doi: 10.1016/j.envsoft.2019.05.003

CrossRef Full Text | Google Scholar

Tinbergen, J. (1952). On the Theory of Economic Policy. Amsterdam: North-Holland.

Google Scholar

Verhagen, W., van der Zanden, E. H., Strauch, M., van Teeffelen, A. J. A., and Verburg, P. H. (2018). Optimizing the allocation of agri-environment measures to navigate the trade-offs between ecosystem services, biodiversity and agricultural production. Environ. Sci. Policy 84, 186–196. doi: 10.1016/j.envsci.2018.03.013

CrossRef Full Text | Google Scholar

Wätzold, F., Drechsler, M., Johst, K., Mewes, M., and Sturm, A. (2016). A Novel, spatiotemporally explicit ecological-economic modeling procedure for the design of cost-effective agri-environment schemes to conserve biodiversity. Am. J. Agric. Econ. 98, 489–512. doi: 10.1093/ajae/aav058

CrossRef Full Text | Google Scholar

Whittaker, G., Färe, R., Grosskopf, S., Barnhart, B., Bostian, M., Mueller-Warrant, G., et al. (2017). Spatial targeting of agri-environmental policy using bilevel evolutionary optimization. Omega 66, 15–27. doi: 10.1016/j.omega.2016.01.007

CrossRef Full Text | Google Scholar

Zitzler, E., and Thiele, L. (1999). Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans. Evol. Comput. 3, 257–271. doi: 10.1109/4235.797969

CrossRef Full Text | Google Scholar