- 1Department of Soil System Science, Helmholtz Centre for Environmental Research – UFZ, Halle (Saale), Germany
- 2Thünen Institute of Climate-Smart Agriculture, Braunschweig, Germany
Societal demands on soil functionality in agricultural soil-landscapes are confronted with yield losses and environmental impact. Soil functional information at national scale is required to address these challenges. On behalf of the well-known theory that soils and their site-specific characteristics are the product of the interaction of the soil-forming factors, pedometricians seek to model the soil-landscape relationship using machine learning. Following the rationale that similarity in soils is reflected by similarity in landscape characteristics, we defined soil functional types (SFTs) which were projected into space by machine learning. Each SFT is described by a multivariate soil parameter distribution along its depth profile. SFTs were derived by employing multivariate similarity analysis on the dataset of the Agricultural Soil Inventory. Soil profiles were compared on behalf of differing sets of soil properties considering the top 100 and 200 cm, respectively. Various depth weighting coefficients were tested to attribute topsoil properties higher importance. Support vector machine (SVM) models were then trained employing optimization with a distributed multiple-population hybrid Genetic algorithm for parameter tuning. Model training, tuning, and evaluation were implemented in a nested k-fold cross-validation approach to avoid overfitting. With regards to the SFTs, organic soils were differentiated from mineral soils of various particle size distributions being partly influenced by waterlogging and groundwater. Further SFTs reflect soils with a depth limitation within the top 100 cm and high stone content. Altogether, with SVM predictive model accuracies between 0.7 and 0.9, the agricultural soil-landscape of Germany was represented with eight SFTs. Soil functionality with regards to the soil’s capacity to store plant-available water and soil organic carbon is well characterized. Four additional soil functions are described to a certain extent. An extension of the approach to fully cover soil functions such as nutrient cycling, agricultural biomass production, filtering of contaminants, and soil as a habitat for soil biota is possible with the inclusion of additional soil properties. Altogether, the developed data product represents the 3D multivariate soil parameter space. Its agglomerated simplicity into a limited number of spatially allocated process units provides the basis to run agricultural process models at national scale (Germany).
1 Introduction
Soils are at the center of the agricultural ecosystem. On the one hand, their capacity to cycle and store nutrients and to provide plant-available water determines agricultural production with the ultimate goal to feed mankind. On the other hand, the interplay between their storage and filter capacity determines how much of the applied fertilizer percolates to the groundwater and potentially contaminates our drinking water. In today’s agricultural landscapes in Central Europe and other parts of the world, we face multiple challenges for soil functionality impacting ecosystem services. In the last decades, drought events that empty the soils’ water stores causing yield losses are becoming more frequent in Europe (van Hateren et al., 2020; Markonis et al., 2021). Inadequate agricultural management may lead to losses in soil organic carbon to the atmosphere, whereas the opposite can enhance carbon sequestration and, thereby, help to mitigate climate change (Liu et al., 2006; Wiesmeier et al., 2019). Excessive groundwater nitrate pollution with values of 50–380 mg L−1 is found in areas with intensive agriculture in Germany (Sundermann et al., 2020). More than 25% of the respective measurement sites report average values above the threshold of 50 mg L−1 (Jakobs et al., 2020). Overall, economic and environmental risk is site-specific and depends on soil characteristics (Bönecke et al., 2020; Webber et al., 2020). Hence, the estimation of environmental impact and vulnerability of the farmer’s income as well as the development of adequate agricultural management strategies, policies, and farmers’ subsidies require site-specific soil information at national scale.
In pedometrics, continuous, site-specific soil information is generated by pedometric modeling approaches. Pedometrics is an interdisciplinary science integrating soil science, applied mathematics, statistics, and geoinformatics. The object of investigation is the spatial-temporal soil variability at multiple scales. Empirical modeling approaches are used along with multiple aspects of soil sensing and geodata analysis. Please compare Minasny et al. (2013), Rossiter (2018), and Scull et al. (2003) for a review. Any modeling approach relies on a conceptual model on how traits and objects presuppose one another. Pedometric modeling to understand spatial soil distribution at the landscape scale follows the conceptual model of pedogenesis (Jenny, 1941), with soils and their site-specific characteristics being the product of the interaction of the soil-forming factors through long periods of time. The functional approach was extended by McBratney et al. (2003) to include geographic location and proxies to soil itself. The so-called SCORPAN factors include S (proxies to soil), C (climate), O (organisms including land use, agricultural management etc.), R (relief), P (parent material), A (age), and N (geographic location).
Empirical modeling approaches heavily rely on the available data and how well these data capture or approximate the object of interest, its causes and drivers, or any functional relation between them. Limitations in data availability in pedometric modeling concern 1) the pedosphere and its characteristics, and 2) the soil-forming factors. In Germany and many other countries, access to soil profile data is still limited or cumbersome. There is some light at the horizon with the soil profile database of the Agricultural Soil Inventory, which was recently published open access (Poeplau et al., 2020). The same applies to the LUCAS European topsoil database (Tóth et al., 2013). Still, access to the large amount of soil profile data that was collected by the regional and national soil survey institutions requires tedious negotiation with multiple parties. On the contrary, nationwide spatially continuous geodata to approximate the soil-forming factors, are freely available from multiple sources. These include data products derived from remote sensing, products obtained by interpolating local point measurements, and map products. There are of course restrictions. The landscape’s geomorphology, climate, vegetation and land use have changed during the long period of pedogenesis. Whereas the available data to approximate the soil-forming factors only cover the last decades.
Machine learning algorithms are good at deriving knowledge from highly complex data. They are, therefore, often applied in pedometric modeling to extract the functional soil-landscape relation and to project soil information into space. The complexity of the task ranges from single variable values at geographic point locations that are projected into the continuous two-dimensional univariate soil parameter space up to multivariate auto-correlated transect data (soil profiles) that need to be projected into the continuous three-dimensional multivariate space. Recent applications addressing individual topsoil properties are presented by e.g. Møller et al. (2020), or Zeraatpisheh et al. (2020). Approaches to model the three-dimensional soil parameter space can be summarized as follows: The ‘2.5D approach’ builds individual models for single soil properties at selected soil depths and combines the spatial predictions (e.g. Taghizadeh-Mehrjardi et al., 2020; Ma et al., 2021). The ‘depth function approach’ fits a continuous mathematical function through the available horizon data and then projects the function’s parameters into space (e.g. Bishop et al., 1999; Veronesi et al., 2012). “3D regression kriging” models the spatial trend and spatial autocorrelation (e.g. Poggio and Gimona, 2014; Poggio and Gimona, 2017). Furthermore, convolutional neural networks are becoming increasingly popular for multi-target machine learning advancing the 2.5D approach and the depth function approach (e.g. Behrens et al., 2018a; Padarian et al., 2019). A somewhat different path to model the multivariate 3D soil parameter space is the spatial prediction of soil systematic units (SUs) and their associated soil characteristics. It has the benefit that soil profile information is not disassembled. Horizontation and property characteristics in the predictions resemble true pedons. Recent studies following this approach are by Esfandiarpour-Boroujeni et al. (2020) and Sharififar et al. (2019). However, in many soil classification systems, important soil properties guiding soil functionality are only distinguished at a low systematic level and rather similar soils concerning their properties and functionality are assigned to different upper-level SUs. The problem concerns the differentiation between mineral and organic soils, soil particle size distribution, the occurrence of stagnic properties, groundwater influence and many more. Accordingly, this approach would largely benefit from the definition of soil functional types (SFTs).
To bring about their full potential, machine learning algorithms usually require tuning, i.e. searching for the best combination of the algorithm’s parameters. “Best” means that the model algorithm is adapted to provide the prediction with the lowest error on independent data. The approach generally followed in pedometric modeling, is testing a set of predefined parameter combinations (e.g. Emadi et al., 2020; Zhang et al., 2020). While this works fine for algorithms with discrete parameters (e.g. Random Forest) allowing for an exhaustive search, it most likely will not find the optimal solution in case of continuous parameters with an infinite number of possible values (e.g. boosted regression trees or support vector machines). Consequently, the flexibility of most machine learning algorithms can only be exploited if they are combined with optimization algorithms for parameter tuning. A promising group of optimization algorithms are the so-called genetic or evolutionary algorithms, developed by Holland (1975). They simulate biological processes to optimize highly complex objective functions. The algorithms optimize parameters with extremely complex cost surfaces, provide a list of optimal solutions, and are well suited for parallel computing (Haupt and Haupt, 1998). Pedometric applications using optimization for parameter tuning are scarce (e.g. Gebauer et al., 2019; Wadoux et al., 2019; Gebauer et al., 2020). Further applications related to soil science include e.g. Ardakani and Kordnaeij (2017), Mazaheri and Jafarian (2019), and Nguyen et al. (2020).
The currently available spatially continuous soil information for Germany consists of a conventional digital polygon map product (BÜK) at map scales 1:1,000,000 and 1:250,000 (BGR, 2013; BGR, 2018). Unfortunately, these valuable map products with high information content have limitations when it comes to their usage for soil parametrization in spatially explicit agricultural process models. This is not surprising as they were neither intended for this purpose nor to provide site-specific information. Their spatial map units (SMUs) each define a paragenesis of SUs with highly differing properties. The spatial allocation of these SUs within the SMUs is unknown. Further BÜK derived map products of topsoil, and pedon agglomerated values of soil properties and functions are commonly generated by assigning the properties of the SMU’s dominating soil type to the whole SMU. Further SUs with sometimes high areal coverages that amount to more than 50% of the SMU are often neglected. Site-specific data products covering entire Germany were developed by pedometric modeling approaches at European and global scale. Nonetheless, the European products only cover the top 20 soil centimetres (de Brogniez et al., 2015; Ballabio et al., 2016). The global map products (SoilGrids, Hengl et al., 2017) are unreliable for German subsoils due to the previously discussed problem in soil profile data access (Tifafi et al., 2018).
Soils are complex systems characterised by their horizontation with the respective physical and chemical properties. It is these soil characteristics that determine major soil functions (SFs): The specification of the properties shape the soil as a habitat for adapted communities of soil organisms (SF1), who subsequently control nutrient cycling (SF2). SF2 and the soil’s capacity to store plant-available water (SF3) enable agricultural biomass production (SF4). Furthermore, in the context of environmental protection, soils act as a filter for contaminants (SF5) and contribute to the mitigation of climate change due to their carbon storage capacity (SF6). The nationwide site-specific evaluation of the state and potential of our soils with regards to these functions (e.g. Terribile et al., 2011; Greiner et al., 2018; Vogel et al., 2019) requires site-specific information targeting soil functionality. The same applies to the modeling of soil functional dynamics due to agricultural management (Vogel et al., 2018), the evaluation and modeling of climate change on agricultural yields (e.g. White et al., 2011; Webber et al., 2020), and the environmental impact of agricultural production on ecosystem services such as clean drinking water (e.g. Knoll et al., 2020; Sundermann et al., 2020). We ultimately seek to generate the required nationwide representation of the respective 3D soil parameter space of the agricultural soil-landscape (Germany). The approach we follow comprises two parts: First, we distinguish SFTs, each being represented by the corresponding multivariate distribution of soil properties along its depth profile. Then we derive the SFTs’ functional relation with the soil-forming factors by machine learning, to understand their embedding in the particular landscape context. Finally, the trained machine learning models are used to project the SFTs to the continuous space.
2 Material and Methods
2.1 Landscape Setting
Germany covers an area of 357.6 km2 of which 51% are currently under agricultural land use (Statistisches Bundesamt, 2020). Figure 1A provides an overview of the spatial pattern on behalf of the CORINE Land Cover Inventory (Büttner et al., 2017). Germany comprises four morphologic regions from north to south: The North German Lowland, the Central German Uplands, the Alpine Foreland, and the Alps. Figure 1B shows the altitudinal specification, Figure 1E provides details of topographical landforms. Most of the North German Lowland has an altitude below 100 m above sea level (a.s.l.). While there are wetlands, peatlands and marshy terrain along the North Sea Coast, the North-Eastern part of Germany shows glacial influence with many lakes, and moraines. The mountains of the central upland region are moderate in height, rarely above 1,000 m a.s.l. They were influenced by various phases of upheaval and subsidence, developed basin structures with sedimentary deposits, and comprise alluvial glacial loess deposits in between them. Besides, many of the mountain ranges display signs of ancient volcanism altogether leading to a complex geological pattern. Ranging between c 400 and 750 m a.s.l., the Alpine Foothills region was shaped under glacial influence and displays a high variety of geomorphological landforms, being a molasses basin with sedimentary deposits from Alpine erosion, morainic hills and aprons. The German part of the Alps belongs to the Northern Calcareous Alps. U-shaped valleys remind of ice age influences. Figure 1F shows the soil parent material at map scale 1:5,000,000. Please compare (Asch et al., 2003; Küster and Stöckhert, 2003; Liedtke and Mäusbacher, 2003) for further details.
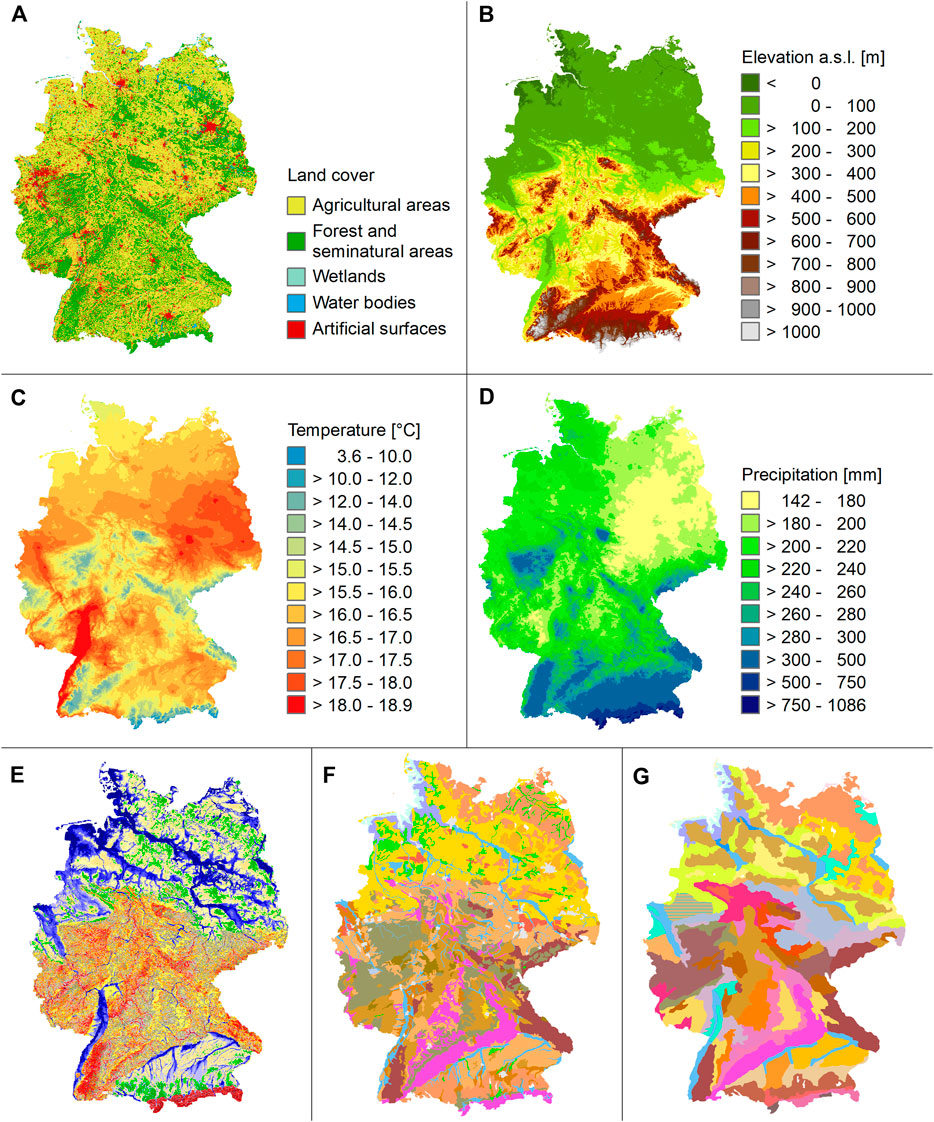
FIGURE 1. Landscape setting, maps of selected parameters. (A) CORINE Land Cover Inventory 2018 (Büttner et al., 2017), (B) EU Digital Elevation Model (© European Union, Copernicus Land Monitoring Service 2017, European Environment Agency (EEA)), (C) Average air temperature of the summer months (DWD, 2018a), (D) Sum of precipitation of the summer months (DWD, 2018b), (E) Geomorphographic units (BGR, 2007) [Legend], (F) Parent material (BGR, 2008b) [Legend], and (G) Soil scapes of Germany (BGR, 2008a) [Legend].
German climate is guided by a decrease in a maritime and an increase in a continental climatic character from west to east expressed by an eastward higher yearly temperature range. Likewise, in the north German lowlands, there is a clear decrease in the amount of precipitation to the east (Figures 1C,D). This continental effect is less pronounced in central and southern Germany since the precipitation-differentiating effect of the central mountain ranges superimposes the west-east decrease and ensures a more varied, local precipitation regime. The mountain climate of the low mountain ranges and the German Alps stands out due to the mean vertical decrease in air temperature of about 0.6–0.7 K (spring and summer) and 0.4–0.5 K (autumn and winter) per 100 m increase in altitude. Mean annual precipitation varies spatially between c. 400 and 3,200 mm (period 1961–1990). Seasonally, precipitation is lower in the hydrological winter half-year than in the summer half-year. Concerning air temperature, there is a predominant temperature gradient from south to north and from east to west. The nationwide regional mean value of the air temperature is 8.2°C (1961–1990). The recorded extremes are a maximum of 42.6°C and a minimum of −37.8°C. Please refer to Alexander (2003), Endlicher and Hendl (2003), Klein and Menz (2003) for further details.
Soil distribution in Germany is primarily determined by parent material and topography. Figure 1G displays the soil scapes of Germany (BGR, 2008a). The map distinguishes soils of the coast region and peatlands, soils of river valleys, soils of slightly hilly landscapes, soils of the loess region, soils of the Central German Uplands, and soils of the alpine region. For further details please refer to Adler et al. (2003) and BGR (2018).
2.2 Data
2.2.1 Soil Profile Database
Soil profile data was collected on an 8 × 8 km raster at 3,104 sites in the context of the first national Agricultural Soil Inventory (Jacobs et al., 2018). The dataset available for this study comprises the soil profile location (coordinates), horizontation and soil profile description according to the German soil survey system (Boden, 2005) to a maximum depth of 200 cm, as well as lab measurements concerning the particle size distribution, bulk density, stone content, total organic carbon content (TOC), total inorganic carbon content (TIC), electrical conductivity (EC) and the pH value in depth increments of 0–10, 10–30, 30–50, 50–70, 70–100, 100–150, and 150–200 cm. Samples were taken per depth increment while taking into account the horizontation, i.e. including multiple samples per depth increment for each corresponding soil horizon present with ≥5 cm.
Sampling comprised disturbed samples and undisturbed samples (steel cores). Depending on the present stone content and the size of the fragments, steel cores of varying sizes (250, 100, or 5 cm³) were taken to determine the bulk density of the fine earth fraction. The bag samples were dried to constant weight at 40°C, with samples high in TOC (≥ 87 g kg-1) being dried at a higher temperature of 60°C. Steel core samples were dried at 105°C to then determine bulk density. Further sample preparation included sieving to 2 cm to separate the fine earth fraction from the coarser material. Soil texture determination with seven particle size separates — sand [2.0–0.63, 0.63–0.2, 0.2–0.063 mm], silt [0.063–0.02, 0.02–0.0063, 0.0063–0.002 mm], and clay [<0.002 mm] was conducted according to DIN ISO 11277. The total carbon content was determined using dry combustion. TOC and TIC were differentiated with the removal of TOC via thermo gradient dry combustion. pH and EC were determined in H2O. Details of the agricultural soil inventory soil survey, lab methodology, data overview and summary statistics can be obtained from Jacobs et al. (2018), and Poeplau et al. (2020).
2.2.2 Gridded Geo-Information
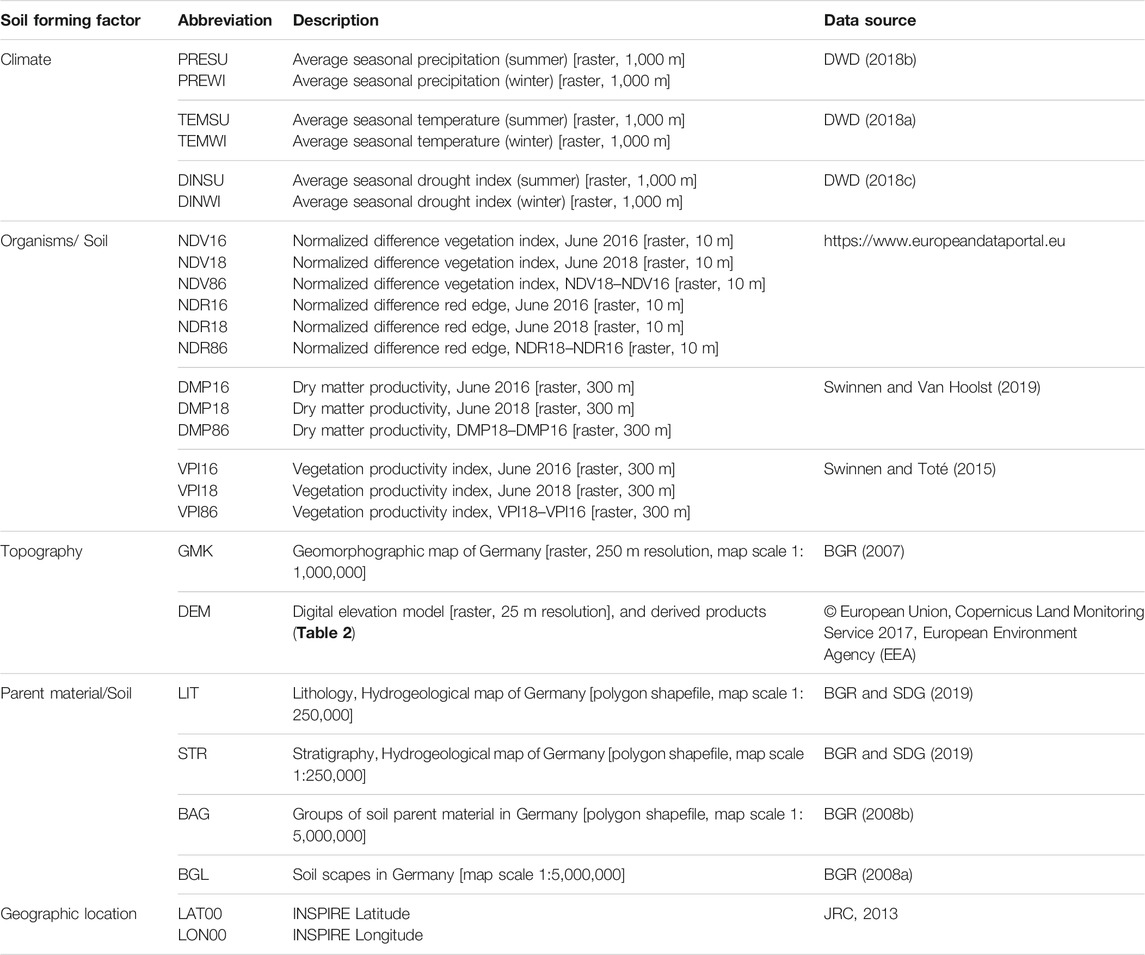
Proxies of the SCORPAN factors were derived from multiple sources. Table 1 provides an overview. Concerning SCORPAN C, 30 years’ seasonal averages (1961–1990) of air temperature and the sum of precipitation of the winter (DJF) and the summer (JJA) months were derived from the German Weather Service (DWD, 2018a; DWD, 2018b). Seasonal averages of the summer and winter drought index (DWD, 2018c) were calculated as
To approximate SCORPAN O, four data products were included. The 2016 and 2018 yearly average composites of two vegetation indices were derived from the European Data Portal. The indices were calculated from Sentinel-2 Level 2A data. The Normalized Difference Vegetation Index (NDVI) combines the vegetation specific reflection characteristics of the wavelength ranges 600–700 nm (RED) and 700–1,300 nm (NIR) and, thereby, provides insight into plant vitality. The Normalized Difference Red Edge (NDRE) is similar to the NDVI but uses the NIR range and the red edge inflexion point (Barnes et al., 2000). Data on dry matter productivity (DMP) and the Vegetation Productivity Index (VPI) of the time slot June 11th-20th of the years 2016 and 2018 were derived from the Copernicus Global Land Service. DMP reflects the overall growth rate of the vegetation with units adapted for agro-statistical purposes (Swinnen and Van Hoolst, 2019). The VPI assesses the condition of the vegetation. It is a percentile ranking of the current NDVI against its historical range of variability. A value of 100% indicates the best, a value of 50% the median vegetation state (Swinnen and Toté, 2015). Differences between the dry year 2018 and the rather wet year 2016 of all four indices were additionally included to relate crop phenology affected by drought to soil properties such as the root-zone plant available water capacity. They, therefore, also refer to SCORPAN S.
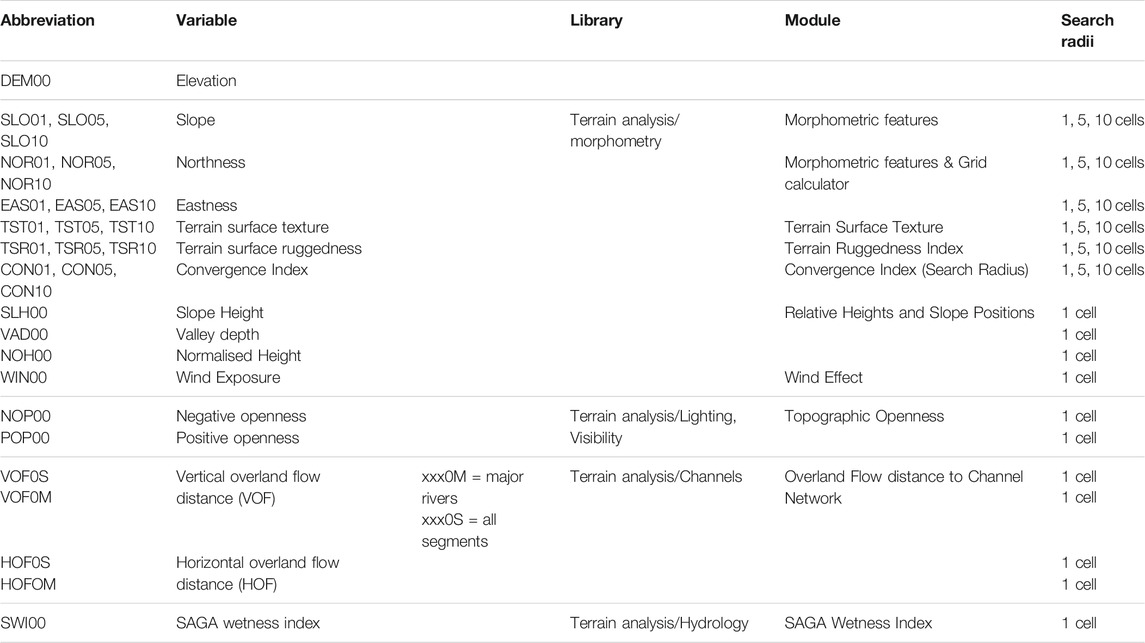
SCORPAN R is represented by a map product of terrain classification. The geomorphographic map of Germany in map scale 1:1,000,000 (Figure 1E) comprises 25 discrete units differentiating between the four major German landscape types. In addition, terrain parameters relating to surface topography were calculated by the SAGA — System for Automated Geoscientific Analyses (Conrad et al., 2015) on behalf of the EU–DEM v1.0 digital elevation model. An overview of the terrain parameters and the respective modules to calculate them is given in Table 2. The circular variable “aspect” was decomposed into northness and eastness. Hydrological terrain parameters were calculated on behalf of the pre-processed DEM: Sinks were filled and the stream network was burned into the DEM. Major streams and further river segments were derived from the CCM River and Catchment Database (Vogt and Foisneau, 2007). The German coastline was added to the river network previous to calculating the overland flow distance, to take the inclination towards the sea into account.
The map of the “Groups of soil parent material” in Germany (BAG, Figure 1F) was included to approximate SCORPAN P. Lithology and stratigraphy according to the hydrogeological map of Germany (HÜK, map scale 1:250.000, BGR and SDG, 2019) were additionally incorporated. While the geological information on lithology, stratigraphy, and genesis of the geological map of Germany provided the basic data, the information was replaced and completed by other regional geological and hydrogeological maps and data where necessary.
Proxies to soil itself (SCORPAN S) can generally be included in the form of conventional soil polygon maps, and remote sensing data products relating to soil properties (e.g. Castaldi et al., 2019; Safanelli et al., 2020; Vaudour et al., 2021). We included the map of the German soil scapes (Figure 1G). It subdivides Germany into 12 soil regions comprising clearly defined soil scapes that follow topography and geology. As previously mentioned, differences in vegetation indices between the dry year 2018 and the rather wet year 2016 relate to crop phenology affected by drought. Accordingly, they may relate to soil properties such as root-zone plant available water capacity.
All obtained covariates were resampled to the INSPIRE — Infrastructure for Spatial Information in Europe — grid topology at 100 m resolution (JRC, 2013). The nearest-neighbor method was used for categorical predictors, B-spline interpolation was applied for numeric predictors. INSPIRE latitude and longitude were additionally included to represent geographic location (SCORPAN N), and particularly to represent spatial patterns not captured in the other data sources. The national border and coastline of Germany were derived on behalf of the digital land model at map scale 1:250,000 (version 2.0) provided by the Federal Agency for Cartography and Geodesy (© GeoBasis-DE / BKG, 2020).
2.3 Procedure to Derive Soil Functional Types
The aforementioned major soil functions are determined by the soil’s physical and chemical properties. The soil’s habitat function (SF1) is characterised by most if not all of the properties. Particle size distribution, bulk density, organic matter content and composition, redox conditions, pH, and salinity shape the composition of the biological community. Nutrient cycling (SF2) depends on the biological community and the aforementioned characteristics. The storage of plant available water (SF3) depends on the corresponding soil volume’s particle size distribution, the organic matter content, bulk density, and the depth to a root-impenetrable layer or bedrock. Agricultural biomass production (SF4) depends on SF1, SF2, and SF3. Furthermore, prolonged times of water logging negatively impact plant roots. The particle size distribution and the amount of coarse fragments shape the soil’s pore space and hence determine water percolation to the groundwater. Together with the soil’s buffering capacity through soil mineralogy and organic compounds these properties determine the soil’s filter capacity for contaminants (SF5). Last but not least, the soil’s storage capacity for TOC (SF6) in mineral soils is determined by the particle size distribution. In organic soils, it largely depends on the thickness of the peat layer. Decomposition processes of the organic matter change during prolonged periods of water logging. However, long-term stabilization of SOC depends on multiple aspects which shall not be elaborated in the context of this study.
The variables available from the soil profile database were used to approximate these soil characteristics. The variables particle size distribution, bulk density, stone content, TOC, and pH were included. Furthermore, horizon symbols according to the German soil survey system were considered to a certain extent. The occurrence, depth and thickness of horizons with symbol H (peat horizon) was included to differentiate organic from mineral soil horizons. The occurrence, depth and thickness of symbol S (stagnic horizon) were included to acknowledge zones of frequent water logging. Likewise, symbol G (gleyic horizon) was included to defer to the zone of groundwater influence. The occurrence, depth and thickness of the C horizon were included to attribute to layers little affected by pedogenetic processes and, hence, the absence of pedogenic oxides, organic matter, and soil structure. Likewise, symbol mC (a subcategory of C) was included to acknowledge depth to bedrock (Boden, 2005). Though, it has to be mentioned that it sometimes occurred in only part of the horizon. Additionally, EC was included to refer to soil salinity. TIC was considered to differentiate soils originating from calcareous parent material.
SFTs were then derived by grouping soil profiles similar in their properties. This was done in the form of a pair-wise comparison by 1 cm depth slices using R-package “AQP” (Beaudette et al., 2013). Slice-wise depth weighting was implemented by an exponential decay function:
The weight of each slice i is determined according to depth weighting coefficient k. Gower’s generalized dissimilarity metric (Gower, 1971) was used since it accounts for any combination of binary, categorical, or continuous variables. For the horizon symbol information, each depth slice was assigned a 1 for the occurrence and a 0 for the non-occurrence. As each additionally considered soil property reduces the impact of the other soil properties on the dissimilarity metric, dissimilarity matrices with a varying number of soil properties were calculated. All of the 50 variables sets included the particle size distribution. They differed 1) in the number of particle size separates (2, 3, or 7), 2) in the inclusion of horizon information (none| H, S, G and C | H, S, G, C, and mC), and 3) the additionally considered physical properties (stone content, bulk density), and 4) the considered chemical properties (TOC, TIC, pH, and EC). All variable sets were tested alongside with two soil depths (0–100 or 0–200 cm) and three depth weighting coefficients (k = 0.00, 0.01, and 0.1). Increasing values of the latter indicate that topsoil information was assigned a higher weight compared to subsoil information. A value of 0 indicates that no depth weighting was applied, a value of 0.1 indicates that between-profile differences were dominated by topsoil properties. To account for variable soil depth in the dissimilarity calculations, undefined dissimilarities were replaced by the maximum between-slice dissimilarity. Undefined dissimilarities were only preserved, when both depth slices represented non-soil material, i.e. bedrock. For each of the computed 300 dissimilarity matrices (50 variable sets × 2 soil depths × 3 coefficients), a cluster analysis with algorithm Ward (Ward, 1963) was conducted to test cluster solutions with 2–50 clusters. R package “NbClust” (Charrad et al., 2014) was used for this purpose. The overall best cluster solution per dissimilarity matrix was then selected according to the Silhouette Index (Kaufman and Rousseeuw, 1990). Of the, thereby, resulting 300 cluster solutions only those with a reasonable high number of clusters (≥8) were kept, assuming that solutions with very few clusters would be way too simple to represent the variability of German soils under agricultural use. Furthermore, cluster solutions with <50 soil profiles in any of their clusters were excluded.
The remaining cluster solutions were then compared according to their specification with respect to the soil properties. Among the soil properties, a good definition with regards to particle size distribution, symbol H, symbol S, and symbol G was given priority over the other soil properties due to their importance for all six soil functions. The final aim was to select one overall best cluster solution. Each cluster of this best cluster solution would then define an SFT with a multivariate distribution of soil properties along its depth profile.
2.4 Modeling
2.4.1 Model Algorithm
Machine learning algorithms are often applied for supervised classification problems. In this case, landscape positions were classified according to the presence or absence of a particular SFT. Each landscape position was described by an n-dimensional vector of predictor values extracted from nationwide gridded geodata, i.e. proxies of the soil-forming factors. The machine learning algorithm was then used to build a model that learns on behalf of a training dataset — landscape positions of known presence or absence — to then spatially apply the model throughout the respective landscape.
There is a high variety of machine learning algorithms applied in pedometric modeling. And while random forest is becoming increasingly popular (Padarian et al., 2020), due to its simplicity in structure and parameter tuning, the high potential of algorithms such as support vector machines (SVMs) is not yet well exploited. Nonetheless, SVMs are a “hot topic” in the broader machine learning community due to their high flexibility and potential to perform complex learning tasks (e.g. Bennett and Campbell, 2000; Meyer, 2019). SVMs were developed by Cortes and Vapnik (1995). In binary classification tasks, they search for the hyperplane that maximizes the margin between the two classes’ closest points. The properties of this decision surface ensure the SVM’s high generalization ability (Cortes and Vapnik, 1995). Points along the boundary are called support vectors. The data are projected to the higher dimensional space via kernel techniques to allow for separation in case of nonlinearity. The radial basis function (RBF) kernel is commonly applied for this purpose. It helps to build complex decision boundaries and includes two parameters: C and γ. Their choice is crucial for obtaining good results. The γ parameter can be interpreted as the inverse of the radius of influence of the support vectors. C is often referred to as the cost or penalty parameter. With a small C, the penalty for misclassified points is low; high values increase the risk of overfitting. Finally, it balances the misclassification of training samples against the simplicity of the hyperplane. R package “e1071” provides the R interface to the LIBSVM library for Support Vector Machines (Chang and Lin, 2011; Meyer, 2019).
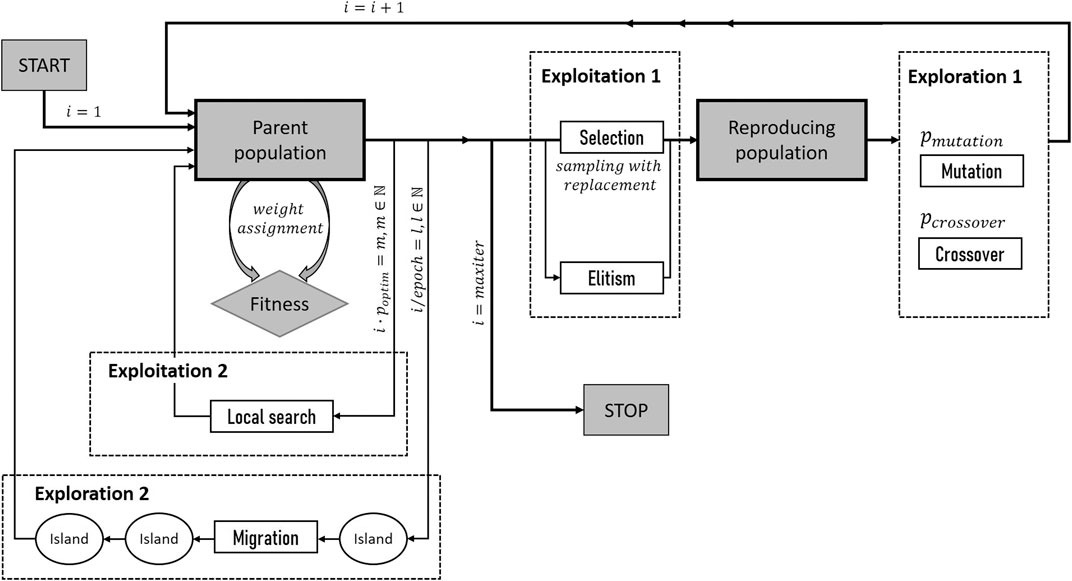
2.4.2 Optimization Approach
The search for optimal SVM parameters was conducted by optimization employing a genetic algorithm (GA). Figure 2 provides an overview of the procedure that was implemented with R package “GA” (Scrucca, 2013; Scrucca, 2017). The GAs’ operational structure is inspired by the general principles of biological evolution involving mutation, crossover, selection, and elitism. The parameter space to be searched for the optimal combination of tuning parameter values has to be predefined by providing a minimum and maximum value for each parameter. Then, a random population of
GAs can balance between the exploration of new areas of the given parameter space and the exploitation of good solutions. Exploitation (Exploitation 1, Figure 2) is usually controlled by the two operators, selection and elitism, whereas exploration (Exploration 1, Figure 2) is conducted by mutation and crossover. The trade-off between exploitation and exploration is controlled by aspects such as the population size, and the probability for mutation (
A couple of test runs were conducted to choose the GA settings starting from recommendations given by Scrucca (2017). Finally, GA search was conducted in the two-dimensional space considering the SVM parameters γ and C to range between 0.01 and 10. The population size was set to 125, and the number of islands for parallel search to 5. The interval for the migration between islands was set to 20, the migration rate to 0.1. Single-point crossover between parameter vectors was conducted with a probability of 0.8, uniform random mutation with a probability of 0.1. Linear rank selection was applied allowing for the best five individuals to survive at each generation (elitism). The probability of applying local search was set to 0.1, and the selection pressure to 0.7. The overall maximum number of iterations was set to 500, the number of consecutive generations without any improvement in the best fitness value before the GA was stopped was set to 20. Please refer to Scrucca (2017) and Scrucca (2013) for the details and available options.
2.4.3 Model Training and Evaluation
For SVM, the n-dimensional vectors of predictor data can only include real numbers. Accordingly, all categorical predictors were recoded into dummy variables. All numerical data were scaled to the range 0, 1 to avoid misbalance and numerical problems. The predictor-response dataset was then compiled by extracting the predictor values at the soil profile sites and assigning each soil profile to the respective SFT. SVM models were trained separately for each SFT. Accordingly, the response data was coded into presence-absence data. The misbalance between SFT occurrence and absence was taking into account through the assignment of weights during model building.
A nested approach of 5-fold stratified cross-validation (CV) was applied for model training, tuning and evaluation to obtain robust models (Figure 3). For model evaluation, the outer CV cycle was repeated five times. Overall, in both CV cycles, the available predictor-response dataset (X-Y) was subdivided into five folds of equal size using the response variable for stratification. Of these five folds, then always one fold was kept out as a test set while the other four were combined to form the model training set, leading to five separate test set evaluations (one per data instance). Each of the outer CV’s training sets was again subdivided to provide the datasets for parameter tuning in the inner CV cycle. Accordingly, the inner CV cycle reflects the fitness function for the GA optimization procedure. To combat computation time, the optimization was conducted for only 1 out of 25 training sets. Predictions from the five test sets were combined to compute model performance on behalf of the confusion matrix as accuracy accounting for sensitivity and specificity, i.e. true positives and true negatives. The value ranges between 0 and 1 with a value of 0.8 indicating that 80% of the data instances were classified correctly.
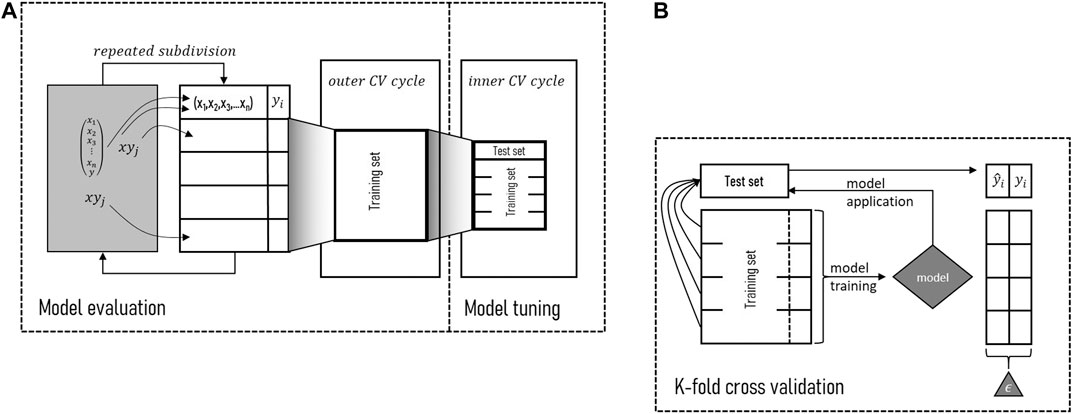
FIGURE 3. Resampling approach for model tuning and evaluation. (A) Nested 5-fold cross-validation with repeating the outer cycle. (B) Zoom in on 5-fold cross-validation.
The coding into dummy variables led to a dominance of the categorical information (258 predictors) over the numerical (50) predictors. The original data sources differ in their degree of reproducibility and the amount of included expert knowledge. This will affect the obtained modeling result and, therefore, requires careful consideration. The numerical predictors were mostly derived from measured data, i.e. the topographical predictors derived from digital terrain analysis (SCORPAN R: 30 predictors), vegetation proxies derived from remote sensing (SCORPAN O: 12), and latitude, longitude (SCORPAN N: 2). The climate proxies are slightly different, for they were interpolated from point data on behalf of the DEM (SCORPAN C: 6). The categorical predictors were derived from spatial vector information (polygons), i.e. SCORPAN P: 195, R: 25, and S: 38. All of these data include expert knowledge. However, while GMK provides a classification on behalf of numerical data (DEM), the others have used geological and soil data at point locations to derive map products with spatial map units separated by strict boundaries drawn according to expert judgment. The corresponding map products HÜK, BAG, and BGL are of high value, particularly due to their high information content with regards to SCORPAN P. Nonetheless, while using these data to train spatial prediction models, these map units’ boundaries are taken for granted since their uncertainty is unknown. As the modeling approach is empirical, it heavily relies on the quality of the used data. Still, excluding data sources of unknown uncertainty is no option either as we would neglect valuable information. However, we may consider balancing between numerical and categorical data. And there is yet another aspect to consider in model training concerning the usage of categorical predictor data. Categories that are not well represented in the data used for model training, tuning and evaluation, will hamper model performance. So finally, the number of dummy variables was reduced for two reasons: 1) to address the misbalance between categorical and numerical predictors, and 2) to build robust models, i.e. guarantee adequate predictor representation in training, tuning, and test datasets. Data subdivision according to the nested CV made it a reasonable choice to delete all categories with less than 100 occurrences. In this way, each data subset for testing in the inner CV cycle would still include 16 instances on average. After data subdivision, it was verified whether each data subset included at least 10 instances. Finally, 89 predictors were included: 50 numerical and 39 categorical predictors. The following indicates the original number of categories per predictor (x/_/_), the number of categories after extraction at point locations (_/x/_), and the remaining number after excluding all categories with non-sufficient instances (_/_/x): GMK 25/24/12, BAG 18/17/8, LIT 80/47/5, STR 97/73/7, and BGL 38/36/7.
2.4.4 Model Interpretation
It is a common perception that machine learning models are black-box models which hampers their interpretation. While there are restrictions concerning the visualization of the complex model structure — particularly in the case of a high number of interacting predictors — there are, nonetheless, useful tools to understand the importance of individual predictors and their functional relation with the target variable. Variable importance (VI) plots display the importance of individual predictors. A general approach to compute them independent of the particular machine learning algorithm relies on predictor permutation. Individual predictors are permuted in the test set before model application to eliminate any predictor-response relationship present with regards to that predictor. The resulting relative loss in model performance can then be attributed as VI value to the respective predictor. According to the five times repeated 5-fold CV approach (outer CV cycle), our VI plots display boxplots of 25 VI values for each predictor. Values of 5 permutations were averaged.
Partial dependence plots (PDPs) are helpful to visualize the relationship between the predictors and the response. They are low-dimensional graphical renderings of the prediction function accounting for the average effect of the other predictors in the model (Friedman, 2001; Greenwell, 2017). But they may be misleading in the case of strong predictor interaction. An approach to address this issue are individual conditional expectation (ICE) plots (Goldstein et al., 2015). They display the estimated relationship between a selected predictor and the response for each observation. The PDP can then be obtained by averaging the corresponding ICE curves across all observations. PDPs according to the latter approach were computed with R package “pdp” (Greenwell, 2018). The five times repeated 5-fold CV approach resulted in 25 PDP realisations per SFT model. The median of these 25 realisations was used to analyze the functional relationships.
3 Results and Discussion
3.1 Comparison Between Cluster Solutions
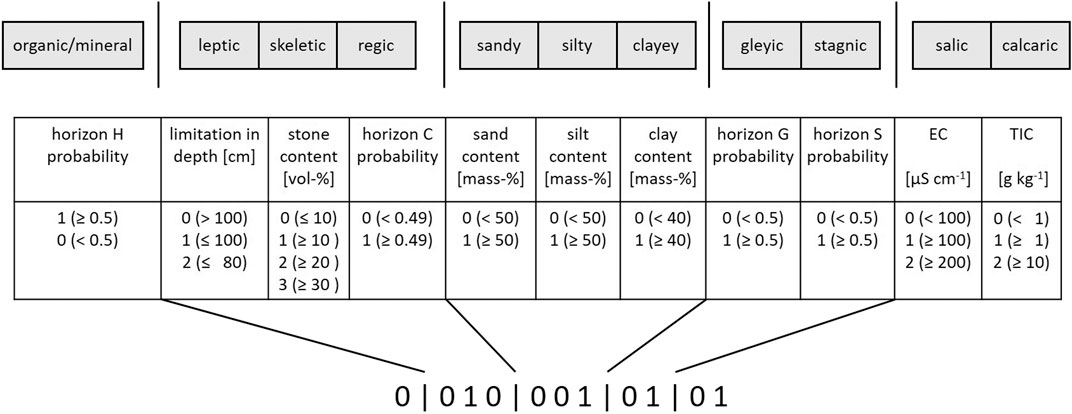
The original 300 best cluster solutions (best solution per dissimilarity matrix) were reduced to 22 solutions due to the criteria 1) number of clusters ≥8 and 2) minimum number of profiles ≥50 in any of their clusters. The remaining cluster solutions (Supplementary Table S1), were sorted according to a decreasing number of clusters (12–8) and a decreasing number of considered input variables (14–7), and, hence, from higher to lower complexity. From these 22 solutions, only three correspond to a soil depth of 0–200 cm, the others to a soil depth of 0–100 cm. Most of the solutions (16 out of 22) were derived while no depth-weighting was applied. None of the solutions was obtained with a depth weighting coefficient of 0.1, which would indicate a dominance of topsoil information for the calculation of the between-profile dissimilarity. This gives a first hint on the importance of subsoil dissimilarity when it comes to agricultural soils, whose topsoils are strongly managed to serve agricultural production, and are, hence, less diverse. Concerning the considered input variables, the picture is more diverse. Each of the considered soil properties was included in a couple of cluster solutions. Though, it has to be mentioned that particle size distribution with a number of 2, 3, or 7 particle size classes had been included in all 300 dissimilarity matrices due to its high importance for soil functionality.
In General, each cluster solution defines its clusters differently by grouping soil profiles according to their similarity on behalf of a different set of variables. Accordingly, cluster IDs do not match. To still allow for their comparison with regards to the definition of their multivariate distributions along the depth profile, attributes were assigned to each of the clusters, reflecting soil traits. These attributes were assigned on behalf of each cluster’s mean of the median depth profile for the respective soil property. An 11-digits barcode was then assigned to each cluster according to the scheme depicted in Figure 4. The 22 cluster solutions were first grouped according to their number of clusters. Then, from each group, the cluster solution was kept that would best differentiate its clusters according to the multivariate distributions along the depth profile. Exceptionally, the two cluster solutions with 12 clusters were both kept as there was no clear prevalence of one over the other. Finally, 5 solutions remained, labeled S1–S5 as indicated in Supplementary Table S1. These remaining five solutions consider a rather differing number of clusters 8–12 and a similar number of variables 10–11. Still, the variables themselves also differ. They all comprise the same basic set of the following variables: particle size distribution (three classes), stone content, and the information on the occurrence, depth, and thickness of the horizons H, S, G, and C. Information concerning the mC horizon was included in all but S3. S4 was the only solution that additionally includes bulk density and no further properties. S1, S2, S3, and S5 differ in the additional chemical properties they consider.
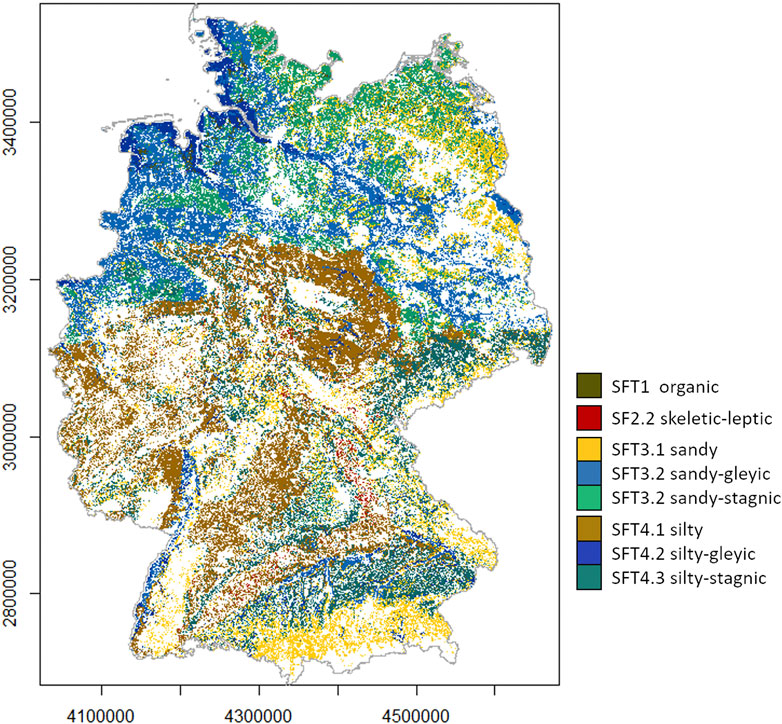
Figure 5 provides a summary indicating the number of profiles per solution and barcode. Similar colors reflect similar soils. Clusters with organic soils are displayed in dark brown colors, clusters of soils with a high stone content with red colors, clusters with gleyic soils by blue colors, clusters with stagnic soils by turquoise colors, clusters with sandy soils in yellow, and clusters with silty soils in light brown. Please be aware that the two to three shades for the clusters with gleyic and stagnic soils also reflect a difference in their particle size distribution. While there is a high percentage of soils defined by a sandy or silty texture and soils being influenced by ground water or displaying stagnic properties, there are much fewer profiles attributed to the clusters which are predominantly organic, with a high stone content, or with a depth limitation in the top 100 cm.
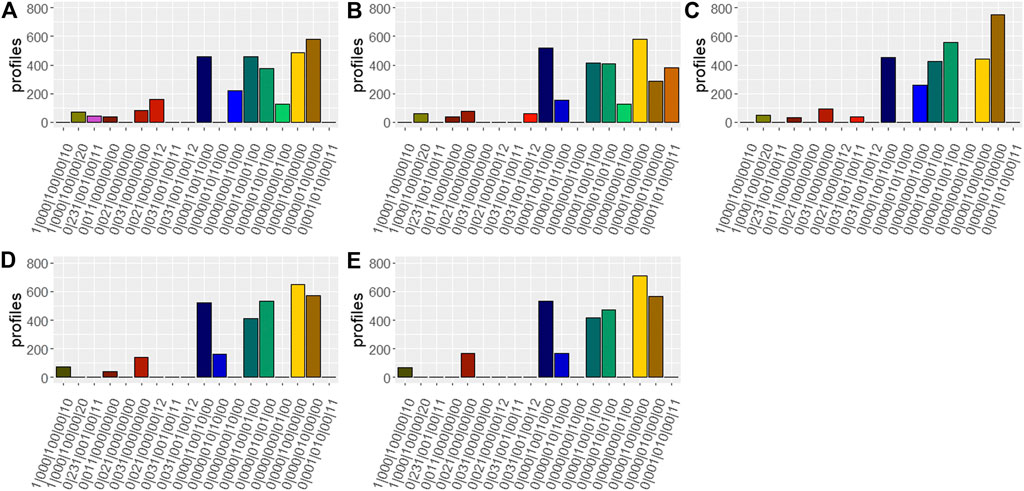
FIGURE 5. Number of soil profiles per cluster solution and barcode. (A) S1, (B) S2, (C) S3, (D) S4, (E) S5.
Finally, due to the different definition of clusters, i.e. SFTs, it was expected that the SFTs of certain cluster solutions could be better related to the soil-forming factors than those of others, and would, therefore, result in a better performance of the models for their spatial prediction. Accordingly, the best overall model performance would then determine the final definition of SFTs. SVM models were trained for all five cluster solutions. Comparison with regards to model performance between the solutions was based on those eight clusters similar among them. As all of the solutions only include one cluster with the first barcode digit corresponding to organic, these clusters’ spatial models were compared. The same applies for one cluster with a high stone content (bar code digit “skeletic” = 3 if available, otherwise = 2), three clusters with sandy properties (barcode digit “sandy” = 1), and three clusters with a comparatively high silt content (barcode digit “silty” = 1). Of the three sandy and silty clusters, there was one cluster with additional gleyic properties and one with additional stagnic properties, respectively. For S1 and S3, from the two clusters with gleyic properties, one fulfilled the criterion of sandy, the other had a somewhat too little silt content to classify as silty. Both were still included in this comparison.
Figure 6 displays the predictive model performance of the eight clusters similar in all five cluster solutions. The boxplots reflect 5 values (repeated outer CV cycle). S4 achieved the best predictive model performance. It had the best median accuracy for four out of eight, and the highest average accuracy among the eight considered clusters. S3 was superior in model performance concerning the three clusters corresponding to organic, sandy, and sandy-gleyic soils (Figures 6A, C, D). The slightly different assignment of soil profiles to these clusters led to a better spatial prediction. Overall, there is very little difference in model performance for certain clusters, namely those with organic, sandy-gleyic, and sandy-stagnic soils (Figures 6A, D, E), likely due to a large overlap in soil profile assignment.
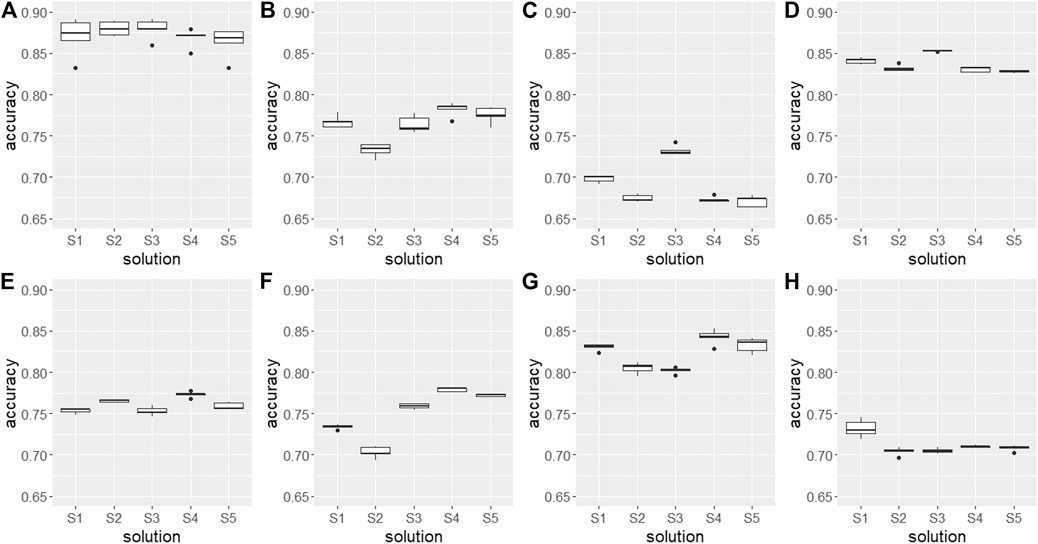
FIGURE 6. Boxplots of predictive model performance corresponding to the eight clusters similar among the five solutions S1–S5. (A) organic, (B) skeletic, (C) sandy, (D) sandy-gleyic, (E) sandy-stagnic, (F) silty, (G) silty-gleyic, and (H) silty-stagnic.
3.2 Soil Functional Types With Multivariate Soil Parameter Distributions Along the Depth Profile
S4 is the cluster solution that considered the particle size distribution (three classes), the stone content, the bulk density, and the occurrence, depth and thickness of the horizons H, S, G, C, and mC to compute soil profile similarity to differentiate the SFTs (Supplementary Table S1). Figures 7, 8 display the corresponding multivariate distribution along the depth profile (0–100 cm) of the nine SFTs corresponding to S4. Soil profile data were aggregated per 1 cm depth slice and displayed as horizon occurrence probability (Figure 7), and median values with the interquartile range in the case of continuous data (Figure 8). Figure 5D indicates the barcodes corresponding to the respective SFTs. For simplicity, these barcodes were now renamed to refer to the SFTs more easily. The following naming convention was applied. SFTs with similar properties were assigned to the same main identifier: this applies for two SFTs with stone contents ≥10% and ≥30% (SFT2.1 and 2.2), three SFTs with sandy properties (SFT3.1, SFT3.2, and SFT3.3), and three SFTs with silty properties (SFT4.1, SFT4.2, and SFT4.3). Of the sandy and silty soils, there is one SFT with additional gleyic and one with additional stagnic properties each. Altogether, this results in the following naming convention: SFT1 (organic), SFT2.1 (skeletic), SFT2.2 (skeletic with depth limitation), SFT3.1 (sandy), SFT3.2 (sandy-gleyic), SFT3.3 (sandy-stagnic), SFT4.1 (silty), SFT4.2 (silty-gleyic), and SFT4.3 (silty-stagnic).
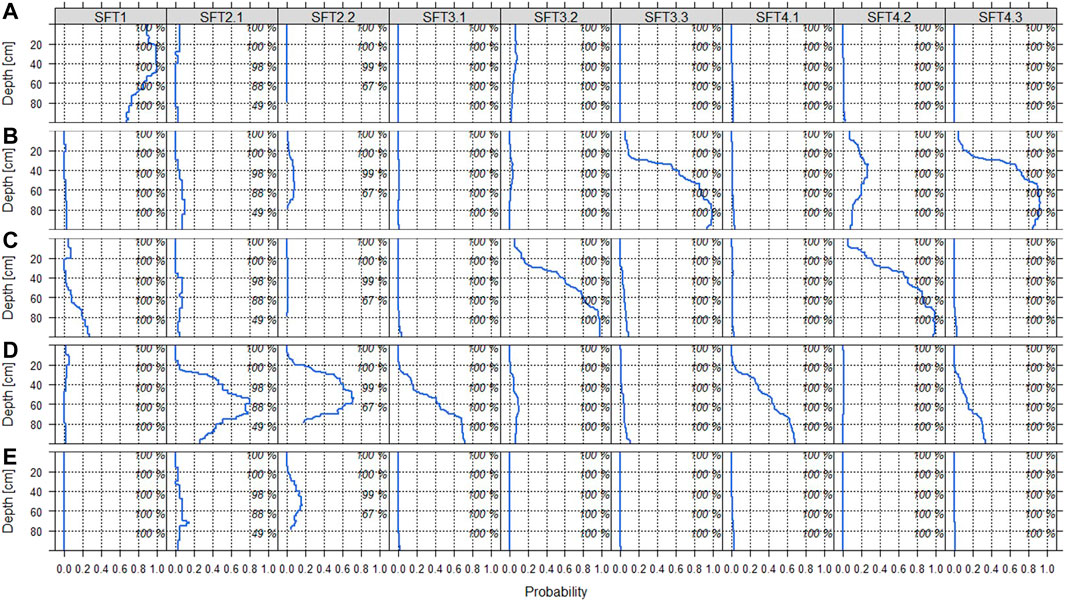
FIGURE 7. Multivariate soil parameter distribution along the depth profiles of the SFTs, part 1: horizon occurrence probability. (A) organic horizon (symbol H), (B) horizon with stagnic properties (symbol S), (C) groundwater influence (symbol G), (D) C horizon, and (E) depth limitation by bedrock (symbol mC). Percentages along the right figure margin indicate the contributing fraction of soil profiles per 20 cm depth increment.
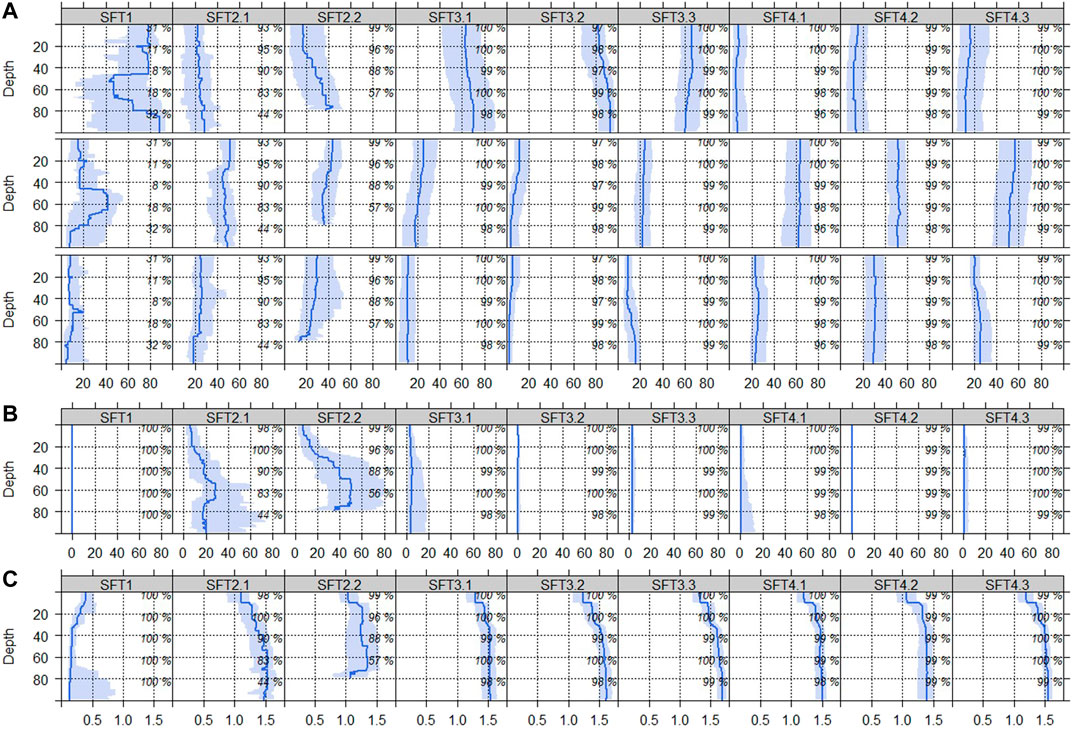
FIGURE 8. Multivariate soil parameter distribution along the depth profile of the SFTs, part 2: median of soil properties with interquartile range. (A) particle size distribution, displayed as sand, silt, and clay content [mass-%], (B) stone content [vol-%], and (C) bulk density [g cm−3]. Percentages along the depth profiles indicate the contributing fraction of soil profiles per 20 cm depth increment.
Figure 7 reflects the occurrence probability of the horizons H, S, G, C, and mC from top to bottom. Figure 7A indicates that soils that include an organic horizon in some part throughout their profile (SFT1) were well separated from soils that do not include an organic horizon. However, SFT1 still includes a high variety of soils: Soils that are organic throughout the top 100 cm were combined with soils that include mineral soil horizons in their top 20 cm (10%) and/or below c. 50 cm (10–30%). Furthermore, 10–28% of the soils have groundwater influence in some part of their profile (Figure 7C). For the mineral soils, most soils with groundwater influence (SFT3.2 and SFT4.2) were well separated from soils with no groundwater influence. The same applies to soils with stagnic properties in the top 100 cm (SFT3.3 and SFT4.3, Figure 7B). SFT2.1 and SFT2.2 include many soils with a C horizon starting at low soil depths indicating rather initial stages of soil development (Figure 7D). 20% of these soils have a C horizon starting at 20 cm (SFT2.2) or 25 cm (SFT2.1) soil depth. Further down the pedon, this percentage augments to 80 and 75%, respectively. The decrease in C horizon probability below these depths is because many soil profiles in these SFTs have a soil depth <100 cm as indicated by the decreasing contributing fraction: Only 49% of the profiles of SFT2.1 are deeper than 80 cm, SFT2.2 soil depth does not reach below 80 cm at all. SFT2.1 and SFT2.2 are also the two SFTs with profiles including bedrock (Figure 7E). From the SFTs corresponding to sandy soils (SFT3.1, SFT3.2, and SFT3.3), it is the exclusively sandy SFT3.1 which includes a rather high percentage of profiles with C horizon occurrence within the top 100 cm: 40% at 52 cm depth augmenting to 70% at 72 cm depth. The same applies to the silty SFT (SFT4.1). Although, the silty-stagnic soils (SFT4.3) also partly include a C horizon within their top 100 cm (Figure 7D).
Figure 8 displays the second part of the multivariate soil parameter distribution along the depth profile of the SFTs, corresponding to measured soil properties. This includes particle size distribution (Figure 8A), stone content (Figure 8B), and bulk density (Figure 8C). The multivariate distributions along the depth profile of each SFT are represented by the following quantiles: Q5, Q25, Q50, Q75, and Q95 (Ließ, 2021). SFT1 is described by sandy soil material in the top 20 cm and below 80 cm depth. In between, most soils have organic horizons as observed from H horizon probability (Figure 7A) and the contributing fraction (Figure 8A). As expected from the barcodes and reflected in the naming convention, SFT3.1, SFT3.2, and SFT3.3 have a particle size distribution dominated by the sand content, whereas SFT4.1, SFT4.2, and SFT4.3 have a particle size distribution dominated by the silt content. Among the former, SFT3.2 displays the highest median sand content throughout the top 100 cm. Among the latter, SFT4.1 has the lowest sand and highest silt content. The difference in texture between SFT2.1 and 2.2 is not so pronounced. Still, SFT2.2 differs from SFT2.1 by its increasing sand and decreasing clay content with depth. The stone content of SFT2.1 and 2.2, the two skeletic SFTs, is much higher as compared to the other SFTs (Figure 8B). In both SFTs the stone content is increasing with depth, reaching its maximum somewhere around 60 cm. Figure 8C displays the SFT’s distribution of the depth profile with regards to bulk density. As expected, the organic SFT1 has much lower values compared to the others. The rather high interquartile range below 70 cm corresponds to the high amount of soils with mineral horizons starting at this depth. The other SFTs’ distributions along the depth profile display a clear step around 10 cm depth reflecting the loosely settled soil after tillage operations by cultivators (croplands) and/or the crump structure caused by an active soil fauna on grassland or non-tilled soils. SFT2.2 differs from the other mineral SFTs due to a slightly lower bulk density with a higher interquartile range throughout its depth and a step of decreasing bulk density around 70 cm depth. Further soil properties were not included in the multivariate distributions along the depth profiles of the SFTs as they were not part of the variable set to compute the dissimilarity matrix of S4.
Altogether, organic soils were differentiated from mineral soils of various particle size distributions partly influenced by waterlogging and groundwater within their top 100 cm. Further SFTs reflect soils with a depth limitation and a high stone content. In the evaluation of the various cluster solutions, higher importance was given to particle size distribution and characteristics distinguishing organic horizons, horizons of water logging and horizons of groundwater influence due to their uttermost importance for all previously listed soil functions. As a consequence, the SFTs of the selected solution S4 do not differentiate well concerning the soil properties TOC and EC. Accordingly, we decided to reduce the parameter space of the SFTs to those soil properties included in the computation of the dissimilarity matrix of S4. Organic soils differ from mineral soils in their pedogenesis, composition and structure. Soil particle size distribution largely determines the available water capacity in the root zone and, hence, the soil’s capability to cope with drought and prevent yield losses. Furthermore, it determines the soil’s storage potential for SOC. Accordingly, it largely determines soil fertility and the soils’ production function. Periodic water logging in the root zone affects the soil microbial community, decomposition processes, and nutrient turnover. The closeness of the soil horizon with changing groundwater level determines — after fertilizer application and percolation through the profile — how much nitrate increases groundwater contamination. And while the properties that are currently included in the definition of the SFTs’ multivariate distributions along the depth profile are reflecting the most important properties, we are well aware that processes such as nutrient cycling and filtering of contaminants require the inclusion of further soil properties particularly stabilizing and buffering agents related to soil mineralogy and cation exchange capacity. Currently, only C horizon occurrence, thickness and depth and the assumed absence of pedogenic oxides, structure and TOC give some hint to approximate this aspect. And while other soil properties such as pH and TOC are manipulated through fertilization and liming, the soils have different states of origin with regards to these properties which should also show as they provide important information for agricultural management planning and intitial values for agricultural process modeling. Still, the current definition of soil functional types provides a decent basis to represent soil functionality with regards to the storage of plant available water (SF3), and the soil’s storage capacity for TOC (SF6). The other four soil functions are represented to a certain extent. Vogel et al. (2019) argue that it is the inherent soil properties (properties that do not change within decades) that allow for the evaluation of the soil’s potential to fulfill the soil functions. Whereas it is those properties changed under agricultural management that allow for the evaluation of the current state and fulfilment of the soil functions with regards to these potentials.
Pedon similarity with regards to the multivariate soil profile information has previously been considered in the context of numerical soil classification as opposed to conceptual soil classification (e.g. Rayner, 1966; Moore et al., 1972). However, to our knowledge, it has not been used to derive soil functional types for agricultural landscapes. The data-driven approach we follow may further benefit by considering property-specific depth weighting to differentiate between soil properties affected by agricultural management and those that don’t. The consideration of soil properties such as TOC, pH, EC and bulk density to define SFTs in agricultural landscapes is tricky as they are heavily manipulated by fertilizer application, liming, and tillage operations. Nonetheless, past agricultural management may also have impacted the occurrence, depth and thickness of mineral and organic soil horizons. Particularly in northwest Germany, nutrient-poor, sandy topsoil was often improved by mixing it with grass or heather plagues and, thereby, altering their particle size distribution and SOC content. This praxis was still common at the beginning of the 20th century but stopped with upcoming mineral fertilisers. In the same area, the deep ploughing of peatlands and Podsols for amelioration until a depth of 1.50 m took place. The result was a mixture of organic with mineral — mostly sandy — underlying soil material, or alternating inclined layers of mineral and organic soil material.
3.3 Spatial Prediction, Model Interpretation, and Evaluation
Figure 9 shows the median occurrence probability of the SFTs throughout Germany. Median predictive model performance is indicated by the respective accuracy in the bottom right corner of each map. Please be aware that Figure 8B has a different map legend due to the predicted low probabilities. Median predictive model performance decreases in the following order: SFT1 – SFT4.2 – SFT3.2 – SFT2.2 – SFT4.1 – SFT3.3 – SFT4.3 – SFT3.1 – SFT2.1 from 0.87 to 0.67 and the exceptional low predictive performance of 0.54 for SFT2.1. Model performance was particularly good for SFT1 (organic) and the two SFTs representing gleyic soils (SFT3.2, SFT4.2). Sandy-gleyic (SFT3.2) and sandy-stagnic (SFT3.3) soils could be better predicted than sandy soils without gleyic or stagnic properties (SFT3.1). The same applies to silty-gleyic (SFT4.2) as compared to silty soils (SFT4.1), but not for silty-stagnic soils (SFT4.3).
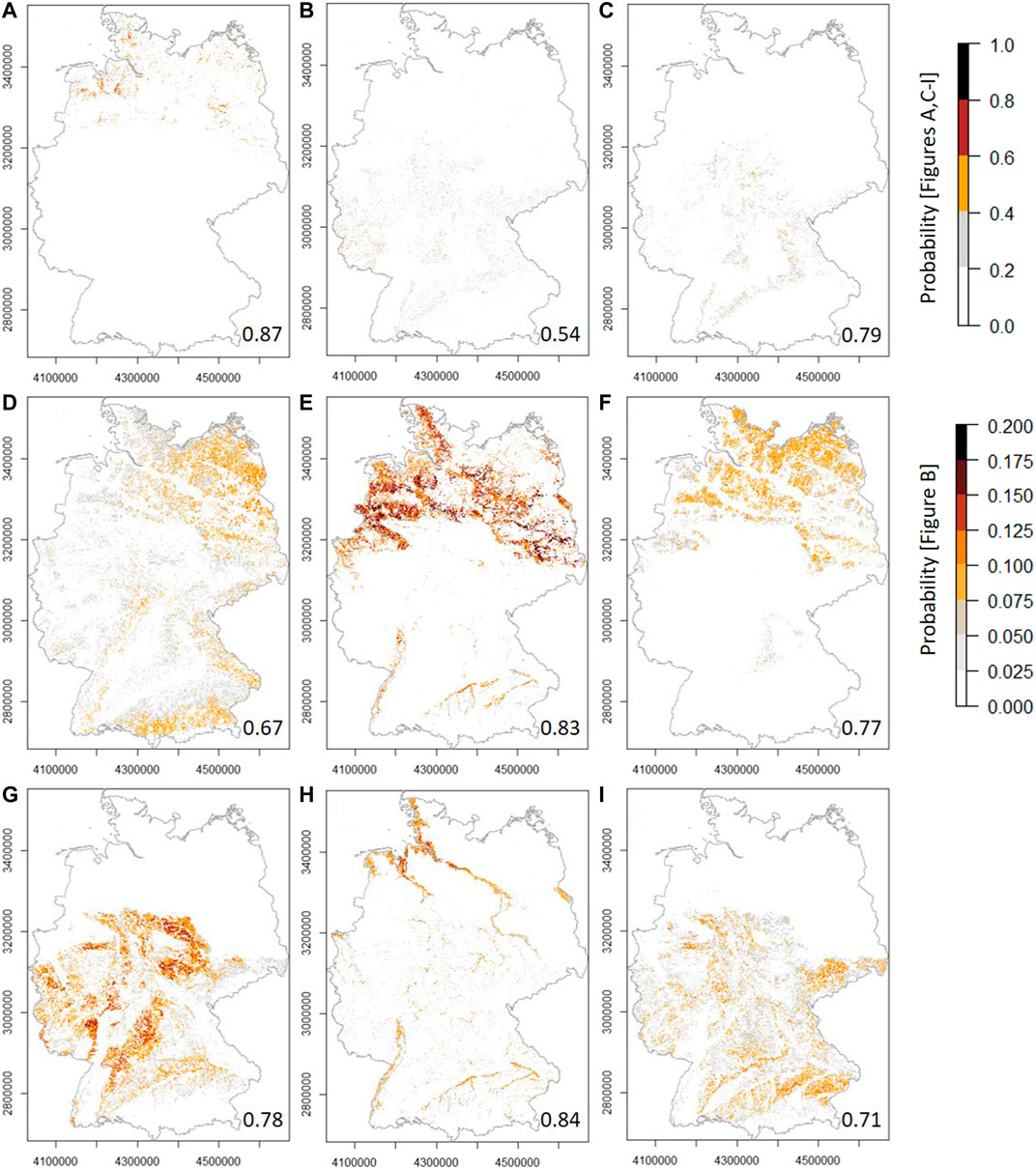
FIGURE 9. Predicted median occurrence probability of the SFTs at national scale. (A) SFT1, (B) SFT2.1, (C) SFT2.2, (D) SFT3.1, (E) SFT3.2, (F) SFT3.3, (G) SFT4.1, (H) SFT4.2, (I) SFT4.3. Non-agricultural areas were masked out on behalf of the CORINE Land Cover Inventory 2018 (Figure 1A). The corresponding predictive model accuracy is indicated in the bottom right corner.
Figure 10 shows the variable importance (VI) for the nine models corresponding to S4. High relative VI values that amount to a multiple of 100% display a high degree of predictor interaction within the models. Most dummy predictors have values above 30 or even 40%. Some predictors have very low VI values close to zero. Still, the exclusion of predictors below VI values of 2 led to a reduced model performance (results not shown). In the first predictor group (SORPAN C), the drought index of the winter and summer months was of low importance for all SFTs, probably due to its calculation from temperature and precipitation, which were also included as predictors. Still, the exclusion of highly correlated predictors led to a decreased model performance (results not shown). Temperature (TEMSU, TEMWI) and precipitation (PREWI, PRESU) of the summer and winter months have VI values above 10% for all SFTs. For most SFTs they are around 20%. For SFT1 (Figure 10A) and SFT2.1 (Figure 10B), they are above 30 or even 40%. Among the SCORPAN O proxies, there is an increase in VI values in the order DMP – NDR – NDV – VPI, with VPI being of comparatively much higher importance for all SFTs. The selected time slot in June displays the percentile ranking of the current NDVI against its historical range of variability and is, therefore, a good indicator of comparatively dry (2018) or wet (2016) conditions. Vegetation on sandy soils will likely have been more impacted by drought than vegetation on silty soils, although the opposite may apply in case the soils are covered by a narrow sandy topsoil horizon. The NDVI and NDRE values of yearly composites of single years will not show this effect as strongly, even though the spatial resolution of the data is higher. Again the vegetation indices (particularly VPI) are of comparatively higher importance for SFT1 and SFT2.1. This might be due to a prevailing usage as grasslands of the soils assigned to these SFTs. A similar effect is observable in the next predictor group concerning these two SFTs (R1). For all SFTs, elevation (DEM00) and easting (EAS) have rather low importance. The low importance of elevation is not that surprising as it is often included in pedometric models to reflect the climatic gradient, which is in this case already captured by predictor group C. The remaining predictors of the group have particularly high importance for SFT1 and SFT2.1, but even for the other SFTs, they reach VI values above 10 or 20%. Among the hydrological terrain parameters (R2), VOF0S and VOF0M display the highest importance followed by SWI00. The high information content contained in the geomorphographic map units (R3) displayed by particularly high VI values of 30–50%, likely reduces the importance of the numerical predictors (R1, R2). The particularly high importance of the dummy predictors is also observable for predictor groups P and S. Latitude and longitude display VI values around 10% for SFT2.1 indicating that there are likely some spatial patterns not captured by the other predictors. Consequently, a less restrictive approach in the consideration of the categorical predictors could even improve model performance. Though the benefit of including additional predictors may differ among the SFTs. The transmission of polygon map boundaries to the pedometric modeling result is a well-known problem particularly observed while applying recursive partitioning algorithms (e.g. Behrens et al., 2018b; Nussbaum et al., 2018).
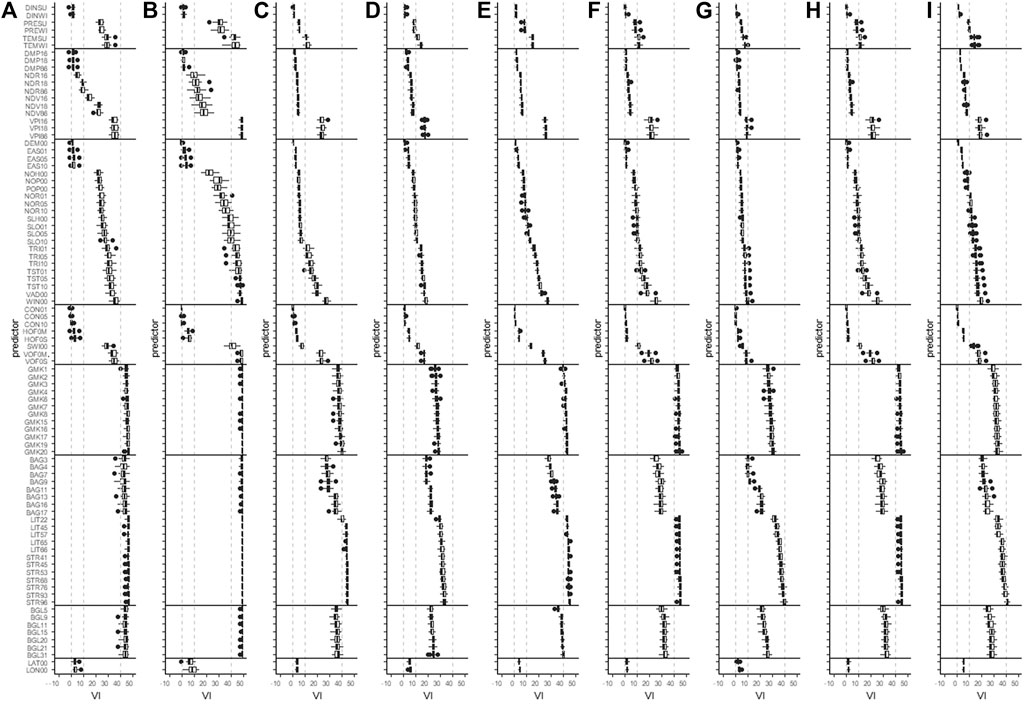
FIGURE 10. VI plots. The Subfigures display the VI values for the individual models to predict the occurrence probability of the SFTs. The boxplots reflect the variance in VI due to the CV approach. (A) SFT1, (B) SFT2.1, (C) SFT2.2, (D) SFT3.1, (E) SFT3.2, (F) SFT3.3, (G) SFT4.1, (H) SFT4.2, and (I) SFT4.3.
The spatial patterns of the sandy SFT3.1, the sandy-gleyic SFT3.2, and the sandy-stagnic SFT3.3 (Figures 9D–F), display their development from sandy parent material (yellow color in Figure 1F). Soils of the sandy SFT3.1 additionally developed from sandstones, acid magmatites and metamorphites in the mountains of the Central German Upland region and loose material in the Alpine Foreland. Likewise, the spatial patterns of the silty SFT4.1 (Figure 9G) and the silty-stagnic SFT4.3 (Figure 9I) display their development from loess (light orange color, Figure 1F). On the other hand, soils that developed from clay stones (mud color, Figure 1F) and are, therefore, likely to have a clayey texture, are seldom used for agriculture (Figure 1A), which explains the lack of a corresponding SFT. The spatial prediction of the silty-gleyic SFT4.2 (Figure 9H) is clearly showing the strong influence of certain dummy predictors derived from the BAG (Figure 1F). The soil of the silty-gleyic SFT4.2 developed from floodplain sediments and sediments in the tidal range. Their distinction is also visible from terrain morphology (Figure 1E). The spatial patterns of SFT2.1 (Figure 9B) and SFT2.2 (Figure 9C) are similar. They mainly occur in the mountains of the Central German Uplands (Figure 1B), which explains their high stone contents.
The direct influence of selected numerical predictors on the respective SFTs is displayed in the PDPs in Figure 11. The shown probability values for the individual SFTs are rather low due to the averaging over all ICE plots. The plots are probably good to see general trends but not in reflecting a comparison concerning these average probabilities between SFTs. Still, it is interesting to see that the two skeletic SFTs SFT2.1 and SFT2.2 show very similar trends with SFT2.2 always displaying higher probabilities. Both SFTs are likely assigned to the same raster cells and can probably not be well separated in space. The two gleyic SFTs (SFT3.2 and SFT4.2) and the two stagnic SFTs (SFT3.3 and SFT4.3) show a remarkable similarity in sudden changes in the slope for a couple of SCORPAN R proxies such as NOP00, SLH00, SLO10, TRI10, VOF0M, and VOF0S. Having developed from different parent material, these soils likely occur in similar topographical landscape positions. Though, not all trends can be well explained. Overall, the predictors are proxies describing today’s landscape while the changing interaction of the soil-forming factors throughout time is not captured by the available data.
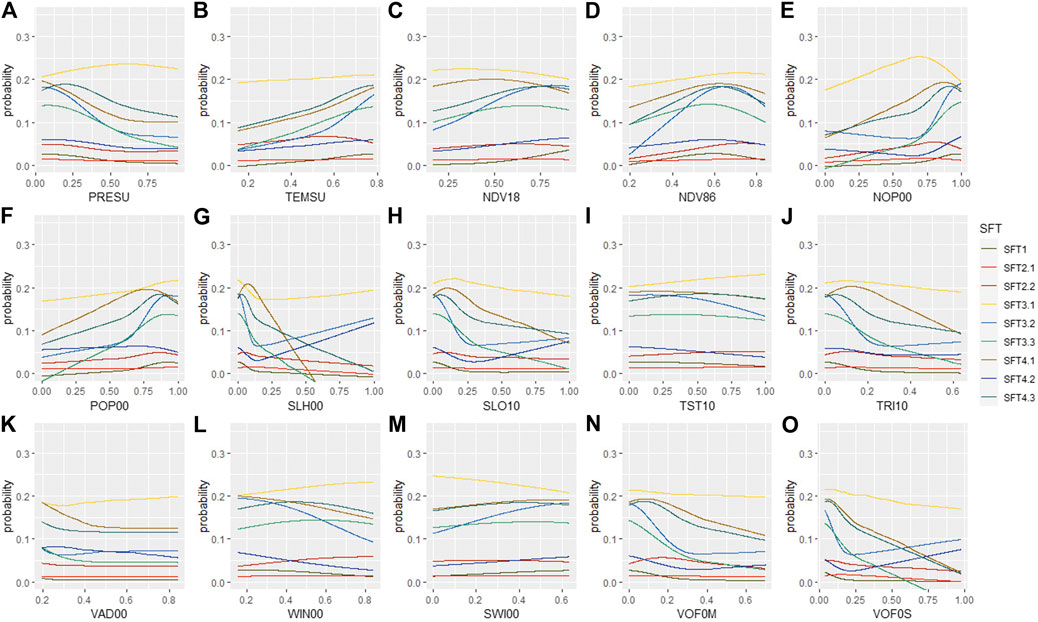
FIGURE 11. Median PDPs of selected continuous predictors. (A) PRESU, (B) TEMSU, (C) NDV18, (D) NDV86, (E) NOP00, (F) POP00, (G) SLH00, (H) SLO10, (I) TST10, (J) TRI10, (K) VAD00, (L) WIN00, (M) SWI00, (N) VOF0M, and (O) VOF0S. Please refer to Tables 1,2 for the predictor abbreviations. The predictor values along the X-axis correspond to the values extracted from the normalized nationwide gridded geodata.
Model results concerning the predicted SFT probability were combined to generate the final spatial allocation of the SFTs (Figure 12) in the following way: For each SFT, the median probability of the 25 predicted values (CV approach) was calculated per raster cell (Figure 8). Then for each raster cell, the SFT with the highest median occurrence probability was assigned (Figure 11). Due to its low probabilities (Figure 8B), SFT2.1 was not assigned to any raster cell, as we also assumed on behalf of the PDPs. As can be seen from the corresponding model accuracy of 0.54, this was also the SFT whose spatial distribution could not be well predicted.
Together the SFT spatial allocation (Figure 12) and the SFT-specific multivariate soil parameter distributions along the depth profiles provide a representation of the multivariate 3D soil parameter space of the agricultural soil-landscape (Germany) which can be used to evaluate certain soil functions, and as input data to agricultural process models. While being operated at national scale, the latter require a representation of the pedosphere with regards to its spatially varying properties. The pedosphere constitutes a spatial continuum. Its properties vary in the magnitude of micrometres, centimetres or meters. But, at this high spatial resolution, the provision of soil information at national scale would result in inconceivable amounts of multivariate data in three dimensions. However, this is hardly necessary to answer current agricultural challenges. The modeling of the impact of drought on agricultural yield, the storage of soil organic carbon, or excess fertilizer percolation to the groundwater, would merely require a spatial resolution to represent individual agricultural fields. And while we maintain this spatial resolution, we may, still, agglomerate soils according to their similarity in their properties with the ultimate fin to provide a limited set of spatially assigned process units of specified characteristics to run agricultural process models, and, thereby, reduce the required computing power. For example, the agricultural soil-landscape of Germany at a spatial resolution of 100 m augments to 19.5 million raster cells. And this amount is multiplied while we acknowledge the pedon behind each raster cell by its multivariate parameter distribution along the depth profile, and the corresponding site-, property-, and depth-specific uncertainty resulting from pedometric modeling. Process models considering this high amount of data would likely run into problems concerning the required computing power.
To spatially represent the soil continuum in maps, soil scientists have since long started to agglomerate soils into SUs. It is these SUs that may then depict SMUs in soil maps of a large map scale. At small map scales, the SUs are often combined with other SUs to form larger SMUs still visible at that scale. However, the SUs defined in soil classification systems have the main purpose to facilitate communication about the complex system of soil. They are nowadays often reflecting pedogenesis, and are, therefore, not necessarily well suited to represent soil functionality (Mueller et al., 2010). In many soil classification systems, important soil properties guiding soil functionality are only distinguished at a low systematic level and rather similar soils concerning their properties and functionality are assigned to different upper-level SUs. This partly also hampers their spatial differentiation in pedometric modeling. Promising to derive spatial units to represent soil functionality are also approaches that spatially predict characteristic soil horizons relating to stagnic properties, or organic carbon accumulation and soil depth instead of SUs (e.g. Gessler et al., 1995; Gastaldi et al., 2012; Ließ et al., 2012). Overall, the domain of application-oriented pedometric mapping follows the same rationale: Ließ et al. (2011) and Ließ and Huwe (2012) estimate natural landslide risk in a tropical mountain environment. Jeong et al. (2017) assess land potentials in forest soils under monsoon climate. Greiner et al. (2018) thematise uncertainty indication in soil function maps.
To adequately simulate and evaluate the impact of climate change on crop production, it is important to assess the impact of local to regional soil variability with regards to soil water conditions at critical crop development states (e.g. Challinor et al., 2009; White et al., 2011; Kasampalis et al., 2018). Accordingly, approaches that estimate the impact of drought on agricultural yields throughout Germany could largely benefit from the developed data product. Currently, they rely on the initially described soil maps with spatially-unresolved SMUs and can, therefore, not provide site-specific predictions (e.g. Zink et al., 2016; Webber et al., 2020). Besides knowledge on nitrogen surplus on soils under agricultural use and lateral transport in aquifers, studies to investigate nitrate pathways to the groundwater would also clearly benefit from continuous, site-specific soil information (e.g. Knoll et al., 2020).
The soil-property-wise evaluation of the final product for selected depths (5, 20, 40, 60, and 80 cm) shows a good predictive performance (Figure 13). The increase of the RMSE with depth corresponding to the original SFT assignment while considering the interquantile ranges (Q5–Q95 and Q25–Q75) of the respective distribution along the depth profile, indicates that the properties of the subsoil need to be weighted more heavily in the similarity analysis to identify the SFTs. For the RMSE values of the model predictions (boxplots), this increase with depth is even stronger. This is because the SFTs differ more in their subsoil compared to their topsoil. Correspondingly, misclassifications show a stronger effect. Overall, the good model performance indicates successful model training and tuning due to the implemented SVM with optimization. The corresponding RMSE values of predictive model performance for topsoil texture from the European (Ballabio et al., 2016) and global (Hengl et al., 2017) predictions, evaluated on behalf of the same test data sets, are 17.3 and 18.8% for sand, 13.6 and 15.3% for silt, and 9.1 and 9.5% for clay.
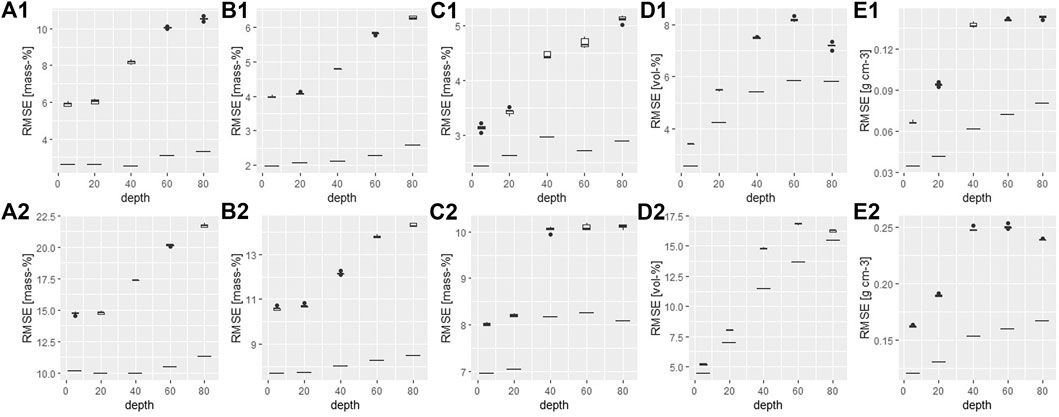
FIGURE 13. Soil property-wise model performance for selected soil depths. Boxplots of 5 RMSE values per soil property and depth. (A) sand content, (B) silt content, (C) clay content, (D) stone content, and (E) bulk density. The horizontal line below each boxplot refers to the RMSE of the original SFT assignment of the soil profiles. Concerning the first line of figures, residuals for the RMSE calculation refer to the difference to the SFTs’ 5–95% interquantile range for the respective property of the multivariate distribution of the depth profile. Concerning the second line of figures, the interquartile range was considered for computing the RMSE.
4 Conclusion
The presented approach to derive a realisation of the multivariate 3D soil parameter space of the agricultural soil-landscape (Germany) consists of 1) the differentiation of SFTs with multivariate distributions along their depth profiles, and 2) the projection of these SFTs to continuous space by machine learning. It simplifies the agricultural soil-landscape by agglomerating similar soils according to their properties. This has two benefits: On the one hand, it well addresses the general concept behind pedometric modeling at the landscape scale, which seeks to explain similarity in soils by similarity in landscape characteristics related to the soil-forming factors. In this sense, it provides a valuable approach to model multiple soil properties with their respective 3D distribution simultaneously. On the other hand, the obtained data product reduces the multivariate complexity of the spatial soil continuum to a limited number of spatial process units to run agricultural process models at national scale. The required computing power is reduced to a large extent.
Overall, the current product published alongside this manuscript (Ließ, 2021) has to be understood as a first version in the iterative process of pedometric modeling. The current definition of SFTs provides a decent basis to represent soil functionality with regards to the storage of plant available water (SF3), and the soil’s storage capacity for TOC (SF6). The other four soil functions are represented to a certain extent. Perspectively, it shall be further enhanced by extending the multivariate distributions along the depth profiles by further soil properties and adapting the definition of the SFTs through the implementation of property-specific depth weighting. This will likely increase the number of SFTs and reduce the respective ranges of their multivariate distribution along the depth profiles. Moreover, any pedometric model can be further improved by including an ever-increasing amount, and information content of input data, and by enhancing the modeling approach to derive an ever-increasing predictive accuracy. We are positive that the implemented machine learning approach resulted in robust models that extracted the highest possible information content concerning the landscape allocation of SFTs due to the implemented resampling and SVM with optimization. A further improvement would, therefore, mainly rely on additional soil profile data, and the inclusion of further gridded geodata to approximate the soil-forming factors. And the latter will never be sufficient as we strive to model the result of 10,000 years of pedogenesis by data covering the last few decades.
Data Availability Statement
The dataset of the multivariate 3D soil parameter space is available from DOI 10.17605/OSF.IO/GQBMD (Ließ, 2021).
Author Contributions
Conceptual approach, programming, modeling, scientific embedding, and preparation of figures (ML), predictor preparation (ML and AG), manuscript writing (ML, AD, and AG).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is part of the SoilSpace3D-DE project and contributes to the BonaRes Centre — Soil as a Sustainable Resource for the Bioeconomy — modeling framework.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenvs.2021.692959/full#supplementary-material
References
Adler, G., Behrens, J., Eckelmann, W., Hartwich, R., and Richter, A. (2003). “Böden im Überblick,” in ifL: Nationalatlas Bundesrepublik Deutschland, Band 2 – Natur und Umwelt I: Relief, Boden und Wasser (Leipzig: Leibniz-Institut für Länderkunde), 100–103.
Affenzeller, M., Winkler, S., Wagner, S., and Beham, A. (2009). Genetic Algorithms and Genetic Programming. Boca Raton, FL: Taylor and Francis Group.
Alexander, J. (2003). “Die heißesten und kältesten Gebiete,” in ifL: Nationalatlas Bundesrepublik Deutschland, Band 3 - Natur und Umwelt II: Klima, Pflanzen- und Tierwelt (Leipzig: Leibniz-Institut für Länderkunde), 36–37.
Ardakani, A., and Kordnaeij, A. (2017). Soil Compaction Parameters Prediction Using GMDH-Type Neural Network and Genetic Algorithm. Eur. J. Environ. Civ. Eng. 23, 449–462. doi:10.1080/19648189.2017.1304269
Asch, K., Lahner, L., and Zitzmann, A. (2003). “Die Geologie von Deutschland – ein Flickenteppich,” in ifL: Nationalatlas Bundesrepublik Deutschland - Relief, Boden und Wasser (Leipzig: Leibniz-Institut für Länderkunde), 32–35.
Ballabio, C., Panagos, P., and Monatanarella, L. (2016). Mapping Topsoil Physical Properties at European Scale Using the LUCAS Database. Geoderma 261, 110–123. doi:10.1016/j.geoderma.2015.07.006
Barnes, E. M., Clarke, T. R., and Richards, S. E. (2000). “Coincident Detection of Crop Water Stress, Nitrogen Status and Canopy Density Using Ground-Based Multispectral Data,” in Proceedings of the Fifth International Conference on Precision Agriculture. Bloomington, MN, United States
Beaudette, D. E., Roudier, P., and O'Geen, A. T. (2013). Algorithms for Quantitative Pedology: A Toolkit for Soil Scientists. Comput. Geosci. 52, 258–268. doi:10.1016/j.cageo.2012.10.020
Behrens, T., Schmidt, K., MacMillan, R. A., and Viscarra Rossel, R. A. (2018a). Multi-Scale Digital Soil Mapping With Deep Learning. Sci. Rep. 8, 2–10. doi:10.1038/s41598-018-33516-6
Behrens, T., Schmidt, K., Viscarra Rossel, R. A., Gries, P., Scholten, T., and MacMillan, R. A. (2018b). Spatial Modelling with Euclidean Distance Fields and Machine Learning. Eur. J. Soil Sci. 69, 757–770. doi:10.1111/ejss.12687
Bennett, K., and Campbell, C. (2000). Support Vector Machines: Hype or Hallelujah. SIGKDD Explor. 2, 1–13. doi:10.1145/380995.380999
BGR (2008a). Soil Scapes in Germany 1:5,000,000. BGL5000. Hanover: Federal Institute for Geosciences and Natural Resources.
BGR (2008b). Groups of soil parent material in Germany 1:5,000,000. BAG5000, Version 3.0. Hanover: Federal Institute for Geosciences and Natural Resources.
BGR (2007). Geomorphographic Map of Germany, GMK1000. Hanover: Federal Institute for Geosciences and Natural Resources.
BGR (2013). Soil Map of Germany 1:1,000,000. BÜK1000. Hanover: Federal Institute for Geosciences and Natural Resources.
BGR (2018). Soil Map of Germany 1:250,000. Hanover: Federal Institute for Geosciences and Natural Resources.
BGR and SDG (2019). Hydrogeological Map of Germany 1:250,000 (HÜK250). Hanover: Federal Institute for Geosciences and Natural Resources (BGR) and German State Geological Surveys (SGD).
Bishop, T. F. A., McBratney, A. B., and Laslett, G. M. (1999). Modelling Soil Attribute Depth Functions With Equal-Area Quadratic Smoothing Splines. Geoderma 91, 27–45. doi:10.1016/S0016-7061(99)00003-8
BKG (2020). Digital Land Model at Map Scale 1:250,000 (version 2.0). Federal Agency for Cartography and Geodesy
Boden, Ad-hoc-A. G. (2005). Bodenkundliche Kartieranleitung. 5th Edn. Hannover, Germany: E.Schweizerbart’sche Verlagsbuchhandlung.
Bönecke, E., Breitsameter, L., Brüggemann, N., Chen, T. W., Feike, T., Kage, H., et al. (2020). Decoupling of Impact Factors Reveals the Response of German Winter Wheat Yields to Climatic Changes. Glob. Change Biol. 26, 3601–3626. doi:10.1111/gcb.15073
Büttner, G., Kostztra, B., Soukup, T., Sousa, A., and Langanke, T. (2017). CLC2018 Technical Guidelines. Vienna: European Environment Agency. Available at:https://land.copernicus.eu/user-corner/technical-library/clc2018technicalguidelines_final.pdf (Accessed June 1, 2020)
Castaldi, F., Chabrillat, S., Don, A., and van Wesemael, B. (2019). Soil Organic Carbon Mapping Using LUCAS Topsoil Database and Sentinel-2 Data: An Approach to Reduce Soil Moisture and Crop Residue Effects. Remote Sens. 11, 2121. doi:10.3390/rs11182121
Challinor, A. J., Ewert, F., Arnold, S., Simelton, E., and Fraser, E. (2009). Crops and Climate Change: Progress, Trends, and Challenges in Simulating Impacts and Informing Adaptation. J. Exp. Bot. 60, 2775–2789. doi:10.1093/jxb/erp062
Chang, C.-C., and Lin, C.-J. (2011). Libsvm. ACM Trans. Intell. Syst. Technol. 2, 1–39. doi:10.1145/1961189.1961199
Charrad, M., Ghazzali, N., Boiteau, V., and Niknafs, A. (2014). NbClust: AnRPackage for Determining the Relevant Number of Clusters in a Data Set. J. Stat. Soft. 61, 1–36. doi:10.18637/jss.v061.i06
Conrad, O., Bechtel, B., Bock, M., Dietrich, H., Fischer, E., Gerlitz, L., et al. (2015). System for Automated Geoscientific Analyses (SAGA) v. 2.1.4. Geosci. Model Dev. 8, 1991–2007. doi:10.5194/gmd-8-1991-2015
Cortes, C., and Vapnik, V. (1995). Support-Vector Networks. Mach. Learn. 20, 273–297. doi:10.1007/BF00994018
de Brogniez, D., Ballabio, C., Stevens, A., Jones, R. J. A., Montanarella, L., and van Wesemael, B. (2015). A Map of the Topsoil Organic Carbon Content of Europe Generated by a Generalized Additive Model. Eur. J. Soil Sci. 66, 121–134. doi:10.1111/ejss.12193
DWD (2018a). Seasonal Grids of Monthly Averaged Daily Air Temperature (2m) Over Germany. version v1.0. Offenbach, Deutscher Wetterdienst.
DWD (2018b). Seasonal Grids of Sum of Precipitation over Germany. version v1.0. Offenbach, Deutscher Wetterdienst.
DWD (2018c). Seasonal Grids of Sum of Drought Index (de Martonne) Over Germany. version v1.0. Offenbach: Deutscher Wetterdienst.
Emadi, M., Taghizadeh-Mehrjardi, R., Cherati, A., Danesh, M., Mosavi, A., and Scholten, T. (2020). Predicting and Mapping of Soil Organic Carbon Using Machine Learning Algorithms in Northern Iran. Remote Sens. 12 (14), 2234. doi:10.3390/rs12142234
Endlicher, W., and Hendl, M. (2003). “Klimaspektrum zwischen Zugspitze und Rügen,” in ifL: Nationalatlas Bundesrepublik Deutschland, Band 3 - Natur und Umwelt II: Klima, Pflanzen- und Tierwelt (Leipzig: Leibniz-Institut für Länderkunde), 32–33.
Esfandiarpour-Boroujeni, I., Shahini-Shamsabadi, M., Shirani, H., Mosleh, Z., Bagheri-Bodaghabadi, M., and Salehi, M. H. (2020). Assessment of Different Digital Soil Mapping Methods for Prediction of Soil Classes in the Shahrekord Plain, Central Iran. Catena 193, 104648. doi:10.1016/j.catena.2020.104648
Friedman, J. H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. Ann. Statist. 29, 1189–1232. doi:10.1214/aos/1013203451
Gastaldi, G., Minasny, B., and Mcbratney, A. B. (2012). “Mapping the Occurrence and Thickness of Soil Horizons within Soil Profiles,” in Digital Soil Assessments and beyond. Editors B. Minasny, B. P. Malone, and A. McBratney (London, United Kingdom: Taylor & Francis Group), 145–148.
Gebauer, A., Brito Gómez, V. M., and Ließ, M. (2019). Optimisation in Machine Learning: An Application to Topsoil Organic Stocks Prediction in a Dry forest Ecosystem. Geoderma 354, 113846. doi:10.1016/j.geoderma.2019.07.004
Gebauer, A., Ellinger, M., Brito Gómez, V. M., and Ließ, M. (2020). Development of Pedotransfer Functions for Water Retention in Tropical Mountain Soil Landscapes: Spotlight on Parameter Tuning in Machine Learning. Soil 6, 215–229. doi:10.5194/soil-6-215-2020
Gessler, P. E., Moore, I. D., McKenzie, N. J., and Ryan, P. J. (1995). Soil-Landscape Modelling and Spatial Prediction of Soil Attributes. Int. J. Geogr. Inf. Syst. 9, 421–432. doi:10.1080/02693799508902047
Goldstein, A., Kapelner, A., Bleich, J., and Pitkin, E. (2015). Peeking inside the Black Box: Visualizing Statistical Learning with Plots of Individual Conditional Expectation. J. Comput. Graph. Stat. 24, 44–65. doi:10.1080/10618600.2014.907095
Gower, J. C. (1971). A General Coefficient of Similarity and Some of its Properties. Biometrics 27, 857–874. doi:10.1109/ultsym.1987.199076
Greenwell, B. M. (2017). pdp: An R Package for Constructing Partial Dependence Plots. R. J. 9, 421–436. doi:10.32614/rj-2017-016
Greiner, L., Nussbaum, M., Papritz, A., Zimmermann, S., Gubler, A., Grêt-Regamey, A., et al. (2018). Uncertainty Indication in Soil Function Maps - Transparent and Easy-to-Use Information to Support Sustainable Use of Soil Resources. Soil 4, 123–139. doi:10.5194/soil-4-123-2018
Haupt, R. L., and Haupt, S. E. (1998). Practical Genetic Algorithms. New York, NY: John Wiley & Sons, Inc.
Hengl, T., Mendes De Jesus, J., Heuvelink, G. B. M., Ruiperez Gonzalez, M., Kilibarda, M., Blagotić, A., et al. (2017). SoilGrids250m: Global Gridded Soil Information Based on Machine Learning. PLoS One 12, e0169748. doi:10.1371/journal.pone.0169748
Holland, J. H. (1975). Adaptation in Natural and Artificial Systems. Ann Arbor, MI: The University of Michigan Press.
Jacobs, A., Flessa, H., Don, A., Heidkamp, A., Prietz, R., Gensior, A., et al. (2018). Landwirtschaftlich genutzte Böden in Deutschland - Ergebnisse der Bodenzustandserhebung, Thünen Report 64. Braunschweig, Germany: Johann Heinrich von Thünen-Institut.
Jakobs, I., Grimm, F., Keppner, L., and Hilliges, F. (2020). Nitratbericht 2020. Hannover: Bundesministerium für Ernährung und Landwirtschaft (BMEL) und Bundesministerium für Umwelt, Naturschutz und nukleare Sicherheit (BMU).
Jenny, H. (1941). Factors of Soil Formation: A System of Quantitative Pedology. New York, NY: Dover Publications, Inc.
Jeong, G., Oeverdieck, H., Park, S. J., Huwe, B., and Ließ, M. (2017). Spatial Soil Nutrients Prediction Using Three Supervised Learning Methods for Assessment of Land Potentials in Complex Terrain. Catena 154, 73–84. doi:10.1016/j.catena.2017.02.006
JRC (2013). INSPIRE Metadata Implementing Rules: Technical Guidelines based on EN ISO 19115 and EN ISO 19119 - V.1.3. 99. Available at: http://inspire.ec.europa.eu/ (Accessed June 1, 2020).
Kasampalis, D. A., Alexandridis, T. K., Deva, C., Challinor, A., Moshou, D., and Zalidis, G. (2018). Contribution of Remote Sensing on Crop Models: A Review. J. Imaging 4. doi:10.3390/jimaging4040052
Kaufman, L., and Rousseeuw, P. J. (1990). Finding Groups in Data: An Introduction to Cluster Analysis. New York, NY: John Wiley & Sons.
Klein, D., and Menz, G. (2003). “Der Niederschlag im Jahresverlauf,” in ifL: Nationalatlas Bundesrepublik Deutschland, Band 3 – Natur und Umwelt II Klima, Pflanzen- und Tierwelt (Leipzig: Leibniz-Institut für Länderkunde), 44–47.
Knoll, L., Breuer, L., and Bach, M. (2020). Nation-wide Estimation of Groundwater Redox Conditions and Nitrate Concentrations through Machine Learning. Environ. Res. Lett. 15, 064004. doi:10.1088/1748-9326/ab7d5c
Küster, M., and Stöckhert, B. (2003). “Der tektonische Bau Deutschlands,” in ifL: Nationalatlas Bundesrepublik Deutschland, Band 2 – Natur und Umwelt I: Relief, Boden und Wasser (Leipzig: Leibniz-Institut für Länderkunde), 36–37.
Liedtke, H., and Mäusbacher, R. (2003). “Grundzüge der Reliefgliederung,” in ifL: Nationalatlas Bundesrepublik Deutschland, Band 2 – Natur und Umwelt I: Relief, Boden und Wasser (Leipzig: Leibniz-Institut für Länderkunde), 58–59.
Ließ, M. (2021). Multivariate 3D Soil Parameter Space — Germany [Agricultural Soil-Landscape, Version 1.0]. doi:10.17605/OSF.IO/GQBMD
Ließ, M., Glaser, B., and Huwe, B. (2011). Functional Soil-Landscape Modelling to Estimate Slope Stability in a Steep Andean Mountain Forest Region. Geomorphology 132, 287–299. doi:10.1016/j.geomorph.2011.05.015
Ließ, M., Glaser, B., and Huwe, B. (2012). Making Use of the World Reference Base Diagnostic Horizons for the Systematic Description of the Soil Continuum - Application to the Tropical Mountain Soil-Landscape of Southern Ecuador. Catena 97, 20–30. doi:10.1016/j.catena.2012.05.002
Ließ, M., and Huwe, B. (2012). “Uncertainty in Soil Regionalisation and its Influence on Slope Stability Estimation,” in Large Slow Active Slope Movements with a Section on Landslide Hydrology – Hillslope Hydrological Modelling for a Landslides Prediction. Editors U. G. L. Picarelli, and R. Greco (Napels: Book of Proceedings: Italian Workshop on Landslides 2011), 171–177.
Liu, X., Herbert, S. J., Hashemi, A. M., Zhang, X., and Ding, G. (2011). Effects of Agricultural Management on Soil Organic Matter and Carbon Transformation – a Review. Plant Soil Environ. 52, 531–543. doi:10.17221/3544-pse
Ma, Y., Minasny, B., McBratney, A., Poggio, L., and Fajardo, M. (2021). Predicting Soil Properties in 3D: Should Depth be a Covariate? Geoderma 383, 114794. doi:10.1016/j.geoderma.2020.114794
Markonis, Y., Kumar, R., Hanel, M., Rakovec, O., Máca, P., and AghaKouchak, A. (2021). The Rise of Compound Warm-Season Droughts in Europe. Sci. Adv. 7, eabb9668. doi:10.1126/sciadv.abb9668
Mazaheri, A. R., and Jafarian, F. (2019). Artificial Neural Network and Optimization Algorithm to Improve Soil Resistance by Means of Aggregation Size Variation. 3, 179–186. doi:10.22060/ajce.2018.14988.5512
McBratney, A. B., Mendonca Santos, M. L., and Minasny, B. (2003). On Digital Soil Mapping. Geoderma 117, 3–52. doi:10.1016/S0016-7061(03)00223-4
Minasny, B., Whelan, B. M., Triantafilis, J., and McBratney, A. B. (2013). Pedometrics Research in the Vadose Zone-Review and Perspectives. Vadose Zone J. 12, 1–20. doi:10.2136/vzj2012.0141
Møller, A. B., Beucher, A. M., Pouladi, N., and Greve, M. H. (2020). Oblique Geographic Coordinates as Covariates for Digital Soil Mapping. SOIL 6, 269–289. doi:10.5194/soil-6-269-2020
Moore, A. W., Russell, J. S., and Ward, W. T. (1972). Numerical Analysis of Soils: A Comparison of Three Soil Profile Models With Field Classification. J. Soil Sci. 23, 193–209. doi:10.1111/j.1365-2389.1972.tb01653.x
Mueller, L., Schindler, U., Mirschel, W., Shepherd, T. G., Ball, B. C., Helming, K., et al. (2010). Assessing the Productivity Function of Soils. A Review. Agron. Sustain. Dev. 30, 601–614. doi:10.1051/agro/2009057
Nguyen, H., Choi, Y., Bui, X.-N., and Nguyen-Thoi, T. (2020). Predicting Blast-Induced Ground Vibration in Open-Pit Mines Using Vibration Sensors and Support Vector Regression-Based Optimization Algorithms. Sensors 20, 132. doi:10.3390/s20010132
Nussbaum, M., Spiess, K., Baltensweiler, A., Grob, U., Keller, A., Greiner, L., et al. (2018). Evaluation of Digital Soil Mapping Approaches With Large Sets of Environmental Covariates. Soil 4, 1–22. doi:10.5194/soil-4-1-2018
Padarian, J., Minasny, B., and McBratney, A. B. (2020). Machine Learning and Soil Sciences: A Review Aided by Machine Learning Tools. Soil 6, 35–52. doi:10.5194/soil-6-35-2020
Padarian, J., Minasny, B., and McBratney, A. B. (2019). Using Deep Learning for Digital Soil Mapping. Soil 5, 79–89. doi:10.5194/soil-5-79-2019
Poeplau, C., Don, A., Flessa, H., Heidkamp, A., Jacobs, A., and Prietz, R. (2020). First German Agricultural Soil Inventory – Core Dataset Göttingen: Open Agrar Repositorium. doi:10.3220/DATA20200203151139
Poggio, L., and Gimona, A. (2017). 3D Mapping of Soil Texture in Scotland. Geoderma Reg. 9, 5–16. doi:10.1016/j.geodrs.2016.11.003
Poggio, L., and Gimona, A. (2014). National Scale 3D Modelling of Soil Organic Carbon Stocks with Uncertainty Propagation - An Example From Scotland. Geoderma 232–234, 284–299. doi:10.1016/j.geoderma.2014.05.004
Rayner, J. H. (1966). Classification of Soils by Numerical Methods. J. Soil Sci. 17, 79–92. doi:10.1111/j.1365-2389.1966.tb01454.x
Rossiter, D. G. (2018). Past, Present & Future of Information Technology in Pedometrics. Geoderma 324, 131–137. doi:10.1016/j.geoderma.2018.03.009
Safanelli, J. L., Chabrillat, S., Ben-Dor, E., and Demattê, J. A. M. (2020). Multispectral Models From Bare Soil Composites for Mapping Topsoil Properties Over Europe. Remote Sens. 12, 1369. doi:10.3390/RS12091369
Scrucca, L. (2013). GA: A Package for Genetic Algorithms inR. J. Stat. Soft. 53, 1–37. doi:10.18637/jss.v053.i04
Scrucca, L. (2017). On Some Extensions to GA Package: Hybrid Optimisation, Parallelisation and Islands Evolution on Some Extensions to GA Package: Hybrid Optimisation, Parallelisation and Islands Evolution. R. J. 9, 187–206. doi:10.32614/RJ-2017-008
Scull, P., Franklin, J., Chadwick, O. A., and McArthur, D. (2003). Predictive Soil Mapping: A Review. Prog. Phys. Geogr. Earth Environ. 27, 171–197. doi:10.1191/0309133303pp366ra
Sharififar, A., Sarmadian, F., Malone, B. P., and Minasny, B. (2019). Addressing the Issue of Digital Mapping of Soil Classes With Imbalanced Class Observations. Geoderma 350, 84–92. doi:10.1016/j.geoderma.2019.05.016
Statistisches Bundesamt (2020). Land Use - Agriculture and Forestry, Fisheries. Available at: https://www.destatis.de/EN/Themes/Economic-Sectors-Enterprises/Agriculture-Forestry-Fisheries/Land-Use/_node.html;jsessionid=D40446229B48722918EED994173D1868.internet8732 (Accessed August 14, 2020).
Sundermann, G., Wägner, N., Cullmann, A., von Hirschhausen, C. R., and Kemfert, C. (2020). Nitrate Pollution of Groundwater Long Exceeding Trigger Value: Fertilization Practices Require More Transparency and Oversight. DIW Weekly. Berlin, Germany: Deutsches Institut für Wirtschaftsforschung (DIW).
Swinnen, E., and Toté, C. (2015). Gio Global Land Component - Lot I ”Operation of the Global Land Component Framework Service Contract N° 388533, JRC, Normalized Difference Vegetation Index (NDVI) V2, Vegetation Condition Index, Vegetation Productivity Index. Algorithm Theor. Basis Doc. (I2.11). Available at: https://land.copernicus.eu/global/sites/cgls.vito.be/files/products/GIOGL1_ATBD_NDVI-VCI-VPI_I2.11.pdf (Accessed June 1, 2020)
Swinnen, E., and Van Hoolst, R. (2019). Copernicus Global Land Operations “Vegetation and Energy”. Version 1. Available at: https://land.copernicus.eu/global/sites/cgls.vito.be/files/products/CGLOPS1_ATBD_DMP300m-V1_I1.12.pdf (Accessed June 1, 2020).
Taghizadeh-Mehrjardi, R., Schmidt, K., Amirian-Chakan, A., Rentschler, T., Zeraatpisheh, M., Sarmadian, F., et al. (2020). Improving the Spatial Prediction of Soil Organic Carbon Content in Two Contrasting Climatic Regions by Stacking Machine Learning Models and Rescanning Covariate Space. Remote Sens. 12, 1095. doi:10.3390/rs12071095
Terribile, F., Coppola, A., Langella, G., Martina, M., and Basile, A. (2011). Potential and Limitations of Using Soil Mapping Information to Understand Landscape Hydrology. Hydrol. Earth Syst. Sci. 15, 3895–3933. doi:10.5194/hess-15-3895-2011
Tifafi, M., Guenet, B., and Hatté, C. (2018). Large Differences in Global and Regional Total Soil Carbon Stock Estimates Based on SoilGrids, HWSD, and NCSCD: Intercomparison and Evaluation Based on Field Data From USA, England, Wales, and France. Glob. Biogeochem. Cycles 32, 42–56. doi:10.1002/2017GB005678
Tóth, G., Jones, A., and Montanarella, L. (2013). The LUCAS Topsoil Database and Derived Information on the Regional Variability of Cropland Topsoil Properties in the European Union. Environ. Monit. Assess. 185, 7409–7425. doi:10.1007/s10661-013-3109-3
van Hateren, T. C., Chini, M., Matgen, P., and Teuling, A. J. (2020). Ambiguous Agricultural Drought: Characterising Soil Moisture and Vegetation Droughts in Europe From Earth Observation. Hydrol. Earth Syst. Sci. Discuss. [Epub ahead of print]. doi:10.5194/hess-2020-583
Vaudour, E., Gomez, C., Lagacherie, P., Loiseau, T., Baghdadi, N., Urbina-Salazar, D., et al. (2021). Temporal Mosaicking Approaches of Sentinel-2 Images for Extending Topsoil Organic Carbon Content Mapping in Croplands. Int. J. Appl. Earth Obs. Geoinf. 96, 102277. doi:10.1016/j.jag.2020.102277
Veronesi, F., Corstanje, R., and Mayr, T. (2012). Mapping Soil Compaction in 3D With Depth Functions. Soil Tillage Res. 124, 111–118. doi:10.1016/j.still.2012.05.009
Vogel, H.-J., Bartke, S., Daedlow, K., Helming, K., Kögel-Knabner, I., Lang, B., et al. (2018). A Systemic Approach for Modeling Soil Functions. Soil 4, 83–92. doi:10.5194/soil-4-83-2018
Vogel, H.-J., Eberhardt, E., Franko, U., Lang, B., Ließ, M., Weller, U., et al. (2019). Quantitative Evaluation of Soil Functions: Potential and State. Front. Environ. Sci. 7. 164. doi:10.3389/fenvs.2019.00164
Vogt, J., and Foisneau, S. (2007). CCM River and Catchment Database — Version 2.0 Analysis Tools. EUR 22649 EN JRC36122.
Wadoux, A. M. J.-C., Padarian, J., and Minasny, B. (2019). Multi-Source Data Integration for Soil Mapping Using Deep Learning. SOIL 5, 107–119. doi:10.5194/soil-5-107-2019
Ward, J. H. (1963). Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 58, 236–244. doi:10.1080/01621459.1963.10500845
Webber, H., Lischeid, G., Sommer, M., Finger, R., Nendel, C., Gaiser, T., et al. (2020). No Perfect Storm for Crop Yield Failure in Germany. Environ. Res. Lett. 15, 104012. doi:10.1088/1748-9326/aba2a4
White, J. W., Hoogenboom, G., Kimball, B. A., and Wall, G. W. (2011). Methodologies for Simulating Impacts of Climate Change on Crop Production. Field Crops Res. 124, 357–368. doi:10.1016/j.fcr.2011.07.001
Wiesmeier, M., Urbanski, L., Hobley, E., Lang, B., von Lützow, M., Marin-Spiotta, E., et al. (2019). Soil Organic Carbon Storage as a Key Function of Soils - A Review of Drivers and Indicators at Various Scales. Geoderma 333, 149–162. doi:10.1016/j.geoderma.2018.07.026
Zeraatpisheh, M., Bakhshandeh, E., Hosseini, M., and Alavi, S. M. (2020). Assessing the Effects of Deforestation and Intensive Agriculture on the Soil Quality Through Digital Soil Mapping. Geoderma 363, 114139. doi:10.1016/j.geoderma.2019.114139
Zhang, M., Shi, W., and Xu, Z. (2020). Systematic Comparison of Five Machine-Learning Models in Classification and Interpolation of Soil Particle Size Fractions Using Different Transformed Data. Hydrol. Earth Syst. Sci. 24, 2505–2526. doi:10.5194/hess-24-2505-2020
Keywords: pedometrics, soil functional types, soil parameter space, machine learning, optimization
Citation: Ließ M, Gebauer A and Don A (2021) Machine Learning With GA Optimization to Model the Agricultural Soil-Landscape of Germany: An Approach Involving Soil Functional Types With Their Multivariate Parameter Distributions Along the Depth Profile. Front. Environ. Sci. 9:692959. doi: 10.3389/fenvs.2021.692959
Received: 09 April 2021; Accepted: 31 May 2021;
Published: 25 June 2021.
Edited by:
Asim Biswas, University of Guelph, CanadaReviewed by:
Chongchong Qi, Central South University, ChinaSongchao Chen, Institut National de recherche pour l’agriculture, l’alimentation et l’environnement (INRAE), France
Copyright © 2021 Ließ, Gebauer and Don. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mareike Ließ, bWFyZWlrZS5saWVzc0B1ZnouZGU=
 Mareike Ließ
Mareike Ließ Anika Gebauer1
Anika Gebauer1 Axel Don
Axel Don