- Department of Theoretical Physics and Cosmology, Institut d'Estudis Espacials de Catalunya, Instituto de Ciencias del Espacio, CSIC, Barcelona, Spain
The work of Bernhard Riemann is discussed under the perspective of present day mathematics and physics, and with a prospective view toward the future, too. Against the (unfortunately rather widespread) trend—which predominantly dominated national scientific societies in Europe during the last century—of strictly classifying the work of scientists with the aim to constrain them to separated domains of knowledge, without any possible interaction among those and often even fighting against each other (and which, no doubt, was in part responsible for the decline of European in favor of American science), it will be here argued, using Riemann as a model, archetypical example, that good research transcends any classification. Its uses and applications arguably permeate all domains, subjects and disciplines one can possibly define, to the point that it can be considered to be universally useful. After providing a very concise review of the main publications of Bernhard Riemann on physical problems, some connections between Riemann's papers and contemporary physics will be considered: (1) the uses of Riemann's work on the zeta function for devising applications to the regularization of quantum field theories in curved space-time, in particular, of quantum vacuum fluctuations; (2) the uses of the Riemann tensor in general relativity and in recent generalizations of this theory, which aim at understanding the presently observed acceleration of the universe expansion (the dark energy issue). Finally, it will be argued that mathematical physics, which was yet not long ago a model paradigm for interdisciplinary activity—and had a very important pioneering role in this sense—is now quickly being surpassed by the extraordinarily fruitful interconnections which seem to pop up from nothing every day and simultaneously involve several disciplines, in the classical sense, including genetics, combinatorics, nanoelectronics, biochemistry, medicine, and even psychology, with such intriguing issues that include, e.g., artificial life and the modelization of the process of consciousness.
1. Introduction
A proper discussion of Riemann's work would no doubt need much more space and time than the few pages at disposal here. Thus, I am somehow afraid I will have to present very deep concepts in a rather light, almost casual way. Moreover, as the abstract indicates, the purpose of this article extends far beyond a discussion, even if detailed, of Bernhard Riemann's contributions to mathematics and physics, to view them under the light of what we will consider as a new conceptual definition or specification of the role and overextended purposes of the mathematical physics of the twenty-first century.
Let us start with some short biographic notes (1–4). Bernhard Riemann (1826–1866) was born in 1826 in the, at the time, kingdom of Hannover, now Germany. His mathematical talent was already noticed at the gymnasium, at Lüneburg, which he entered at the age of 14. It is documented that, while being there, he mastered in 6 days a ca. 900 page textbook on number theory by Legendre. In 1846 Riemann matriculated at Göttingen University but, very probably, Gauss who was on the Göttingen faculty then, had not much contact with him at that point. After 1 year there he moved to Berlin University, where Dirichlet's teaching influenced him specially; they later became collaborators. In 1850 Riemann returned to Göttingen, where he was to spend the rest of his career. There, he studied mathematics under Gauss and physics with Wilhelm Weber. To qualify as a Privatdozent (lecturer) Riemann had to submit a Habilitationsschrift (essay) and give a Habilitationsvortrag (lecture). He chose for the first the subject of Fourier series, presenting an essay in 1853, in which he gave a criterion for a function to be (Riemann) integrable, and then obtained a necessary condition for an integrable function to be representable by a Fourier series. For his Vortrag Riemann had to propose three topics and, against his preferences, Gauss chose the one on geometry. Riemann delivered his lecture in 1854, On the hypotheses that lie at the foundation of geometry, where he introduced the revolutionary concept of an n-dimensional manifold and its curvature tensor, and discussed the relation of his mathematical “space” (it is said that Gauss summoned him not to call it space, but rather Mannigfaltigkeit, that is, variety or manifold) to actual space. Indeed, the only person in the audience who could appreciate the enormous depth of Riemann's work was Gauss. A report of Riemann's seminal lecture was only published in 1868, after his death. Dirichlet, who had succeeded Gauss, died in 1859. Riemann was then appointed to the chair of mathematics at Göttingen and was immediately elected to the Berlin Academy of Sciences. He had, therefore, to report once more on his research, and Riemann sent again a magnificent report On the number of primes less than a given magnitude, where he stated that the (Riemann) zeta function (more on it later) had infinitely many non-trivial roots and that it seemed probable that they all should have common real part 1/2. This is the Riemann hypothesis which remains today one of the most important unsolved problems of mathematics. Riemann died of tuberculosis in 1866, while trying to recover from it in Selasca (Italy), surrounded by his wife and 3-year-old daughter. He was only 39.
From his work, it is very clear that Riemann was interested in physics. This may sound a weird statement nowadays, when he is generally considered as a very influential pure mathematician, who gave name to so many concepts in different fields of mathematics, as the Riemann integral, the Riemann surface, the Cauchy–Riemann equations, the Riemann–Roch theorem, the Riemannian manifolds, the Riemann curvature tensor and, most notably the Riemann zeta function, with its associated conjecture—the only one of Hilbert's problems that after the turn of the twentieth century has been included in the new list of Million Dollar Problems of the twenty-first (awarded by the Clay Foundation). To contradict this view, historians of science tell us that during his life and until as late as 60–80 years after his death, Riemann was counted among the list of important physicists, whose ideas on the unification of all known forms of energy preceded the ground-breaking work of Hilbert and Einstein (now the standard starting point of any book on general relativity). Even more surprising was to this author to learn (5–7) that Riemann was not a theoretical physicist, but rather an experimentalist, and that he made use of elaborated experimental verifications with charged surfaces and different materials in order to perform supplementary checks of the validity of some of his mathematical theorems (as boundary problems involving partial differential equations). Mathematics was not, at that time, the kind of axiomatic construct of our days and the ways of proof differed very substantially from those of the Bourbaki school we are now used to. I am happy to have the possibility to convey this valuable ideas with the present paper.
Let us further recall that, as a student at Göttingen university, Riemann worked with Weber on electromagnetism, which happened starting around 1849. Like Riemann, Weber was also a student of Gauss, but at that time Weber had already a faculty position. He had proposed a theory of electromagnetism and did work which gained him a name in history, as every physicist knows, although not through his theory in fact, that was eventually superseded by Maxwell's one, the real landmark in classical electromagnetism. Gauss himself is also famous for his important work on this subject.
Riemann publications include some 15 papers, four of which where released after his death. This does not actually include a number of important notes, letters, books and other writings that also form part of his written scientific production. In section 1, a brief summary will be provided of the six papers (among the mentioned 15) which are devoted to physical problems. In section 2, a panoramic view will be presented of the enormous influence that Riemann's work on pure mathematics has had into past and present day physics. Section 3 concentrates in more detail on a couple of issues of the author's speciality, namely, for one, in the use of zeta functions as a very elegant regularization tool in quantum field theory, including a description of its uses for the calculation of quantum vacuum fluctuations, the Casimir effect, and the seemingly related cosmological constant problem. The other subject to be addressed is the very well known applications of the Riemann curvature tensor and all his geometrical formalism in general relativity and the, much less known but a very hot topic nowadays, proposed modifications (substantiated by quantum corrections) of the Einstein–Hilbert Lagrangian with additional terms—generally a function of the curvature scalar, the so-called f(R) theories. Only ca. 100 years after the first formulation of general relativity, and in response to the preceptorial demand of the observed acceleration of the universe expansion (the crucial dark energy issue), have some attempts at a modification of Einstein's equations started to be considered. But again, notably, in terms of its basic Riemannian building blocks, in higher powers of the scalar curvature, as we shall see. As a way of conclusion, in section 5 we will try to extract an important lesson for the future, by arguing that, in the very wide way of the concept of what a modern definition of a mathematical physicist could be, we could undoubtedly count B. Riemann among the most successful of them in history. And this even if he lyes far from the ordinary stereotype of what the model mathematical physicist has been considered to be for decades. This is again an extraordinary lesson for the future of this discipline as we travel deeper into the twenty-first century.
2. On Riemann's Work on Physical Problems
The Mathematical Papers of Georg Friedrich Bernhard Riemann (1826–1866), is a collection which contains scientific papers of Bernhard Riemann as transcribed and edited by David R. Wilkins (5). These texts are based on the second edition of the Gesammelte Mathematische Werke and, in the case of some of the papers, the original printed text in the Journal für die reine und angewandte Mathematik, Annalen der Physik und Chemie and Annali di Matematica. Included in Ref. (5) are all papers published in Riemann's lifetime, papers and correspondence published after Riemann's death by Dirichlet and others prior to the publication of the first edition of the Gesammelte Mathematische Werke (with the exception of the fragment Mechanik des Ohres, which is non-mathematical in character), and one of the papers from his Nachlass, first published in the Gesammelte Mathematische Werke. There is also a translation by W. K. Clifford of Riemann's inaugural lecture on the foundations of geometry, and a biographical sketch by Richard Dedekind which was included in the Gesammelte Mathematische Werke.
I will not go here through all these works, but restrict my attention to a subset which, although not complete as viewed by a historian of science, I deem it sufficient in order to establish my point that Riemann's production on physics was actually a fairly good part of his complete scientific work. I will reduced the whole sample in Ref. (5) to that of the published papers—during Riemann's lifetime and posthumously—and restrict my discussion to the papers, among them, on physical issues. The list of these published articles reads as follows.
2.1. Papers Published in Riemann's Lifetime
1. Grundlagen für eine allgemeine Theorie der Functionen einer veränderlichen complexen Grösse, Inauguraldissertation, Göttingen (1851).
2. Ueber die Gesetze der Vertheilung von Spannungselectricität in ponderabeln Körpern, wenn diese nicht als vollkommene Leiter oder Nichtleiter, sondern als dem Enthalten von Spannungselectricität mit endlicher Kraft widerstrebend betrachtet werden, Amtlicher Bericht über die 31. Versammlung deutscher Natur-forscher und Aerzte zu Göttingen (im September 1854).
3. Zur Theorie der Nobili'schen Farbenringe, Annalen der Physik und Chemie, 95 (1855) 130–139.
4. Beiträge zur Theorie der durch die Gauss'sche Reihe F(α, β, γ, x) darstellbaren Functionen, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 7 (1857) 3–32.
5. Selbstanzeige: Beiträge zur Theorie der durch die Gauss'sche Reihe darstellbaren Functionen, Göttinger Nachrichten (1857) 6–8.
6. Theorie der Abel'schen Functionen, Journal für die reine und angewandte Mathematik, 54 (1857) 101–155.
7. Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse, Monatsberichte der Berliner Akademie (November, 1859) 671–680.
8. Ueber die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 8 (1860) 43–65.
9. Selbstanzeige: Ueber die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite, Göttinger Nachrichten (1859) 192–197.
10. Ein Beitrag zu den Untersuchungen über die Bewegung eines flüssigen gleichartigen Ellipsoides, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 9 (1860) 3–36.
11. Ueber das Verschwinden der Theta-Functionen, Journal für die reine und angewandte Mathematik, 65 (1866) 161–172.
2.2. Riemann's Papers Published After his Death
12. Ueber die Darstellbarkeit einer Function durch eine trigonometrische Reihe, Habilitationsschrift, 1854, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 13 (1868).
13. Ueber die Hypothesen, welche der Geometrie zu Grunde liegen, Habilitationsschrift (1854), Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 13 (1868).
14. Ein Beitrag zur Elektrodynamik (1858), Annalen der Physik und Chemie, 131 (1867) 237–243.
15. Ueber die Fläche vom kleinsten Inhalt bei gegebener Begrenzung, Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen, 13 (1868).
Six among these fifteen papers (namely, those with numbers 2, 3, 8, 9, 10, 14) are the ones that I have selected because they directly address issues of theoretical and experimental physics. I now provide a free translation of their titles, together with a short summary of each of them.
2.3. Riemann's Papers “On Physics”
2. About the distribution laws of electric tension in ponderable bodies, when these cannot be considered as absolutely conductors or non-conductors, but as opposing with a finite force to the electric tension they contain, Official Report at the 31st Meeting of German Scientists and Physicians at Göttingen (September, 1854).
Riemann considers in this paper Leyden jars, where an electric charge is kept, and studies in particular how, once the bottle has been emptied, a certain amount of charge still remains, which gradually disappears with time. He studies in detail the corresponding law describing this phenomenon. Riemann deals, in particular, as the title clearly indicates, with bodies that are neither perfect conductors nor perfect isolators. He elaborates on previous work by Ohm, Weber, Kirchhoff and Kohlrausch. An important point in the whole development is the contact with the corresponding experimental results. The mathematical basis of the paper are partial differential equations, as is also the case in the ones which follow.
3. On the theory of noble color rings, Annals of Physics and Chemistry, 95 (1855) 130–139.
Here an experimental study of the propagation and of the distribution of an electrical current in a conductor is presented. The rings mentioned in the title are generated when one covers a plate of a noble metal, as platinum, gold plated silver, or similar, with a solution of lead oxide. Then, an electric current, produced by a battery, is connected to the plate. In this way, so-called Newton color rings are produced. Riemann elaborates here on previous results by Becquerel, Du-Bois-Reymond and Beetz, improving their calculation and discussing about the hypothesis previously considered by these authors.
8. About the propagation of plane airwaves of finite oscillation amplitude, Sessions of the Royal Science Society at Göttingen, 8 (1860) 43–65.
Riemann integrates in this paper the differential equations corresponding to the movement of gases, under different conditions of pressure and temperature. He remarks that he can bring his calculations further away in the order of approximation, with respect to those previously carried out by Helmholtz, for instance, who only got to the second order in the perturbative expansion. He refers to previous results by Helmholtz, Regnault, Joule and Thomson, improving their calculations, discussing the set up and improving the hypothesis appearing in the works by these authors. With 22 pages, this is quite a long paper as compared with other papers by Riemann.
9. Self-announcement: About the propagation of plane airwaves of finite oscillation amplitude, Göttingen Notices (1859) 192–197.
This is a very short compendium of the main mathematical formalism that is used in the former paper, of the same title, in order to obtain the results. In spite of its title, this one could be considered as a mathematical article. Indeed, it deals with the theory of propagation of a gas, but the only physical input in the whole paper is the mathematical equation giving the behavior of gas pressure as a function of the density (that is, its equation of state), in the absence of any heat exchange. He develops the mathematical formalism in detail and compares with previous results by other mathematical physicists as Challis, Airy, Stokes, Petzval, Doppler and von Ettinghausen (several of them have given names to quite famous equations).
10. A contribution to the investigation of the movement of a uniform fluid ellipsoid, Sessions of the Royal Science Society at Göttingen, 9 (1860) 3–36.
Again as clearly indicated in the title, Riemann deals here with the movement of a uniform fluid ellipsoid, which is considered to be constituted by isolated points that attract themselves under the influence of gravity. This is generally considered to be one of the finest papers by Riemann within the class of those considered here, i.e., the ones dealing with actual physical problems. In the paper, the equilibrium configurations of the ellipsoid are identified, what has many and important applications, e.g., to the study of the possible forms of celestial bodies as galaxies or clusters. Riemann studies in particular the evolution of the principal axis of the ellipsoid and the relative movement of its components. As the one before, this is also a rather mathematical paper, since the only physics it contains is practically reduced to the initial conditions and Newton's law. Previous results of Dirichlet and Dedekind on this problem are extended.
14. A contribution to Electrodynamics, Annals of Physics and Chemistry, 131 (1867) 237–243.
This paper is generally considered to incorporate the main results of Riemann's physical (and philosophical) ideas on the “unification” of gravity, electricity, magnetism, and heat. It contains indeed his observation on how a theory of electricity and magnetism is closely related with those for the propagation of light and heat radiation. He presents in the paper a complete mathematical theory, with “an action that does not differentiate” the already mentioned four cases of “gravity, electricity, magnetism, and temperature”. The finite velocity of propagation of the interaction (as opposed to the predominant concept, at the epoch, of action at a distance) is clearly presented, identifying such velocity with that of light, which has been considered by many to be a really remarkable achievement of Riemann's genius. The paper, which with only six pages is in fact quite short, relies on experimental results by Weber and Kohlrausch, Busch, and by Bradley and Fizeau.
2.4. Additional Considerations
1. Once again, those above are not all the works on physical issues Riemann actually wrote, but just the ones extracted from a uniform sample, namely his published articles.
2. A good example of a work not in the list is the well-known book by H. Weber and B. Riemann, Die partiellen Differential-Gleichungen der mathematischen Physik nach Riemanns Vorlesungen, 6. unveranderte Aufl., 2 vols (Vieweg, Braunschweig, 1919), that was used for many years as a textbook in different universities, together with several other papers by Riemann.
3. An interesting biography of Riemann is the book by Monastyrsky (6). A lot of emphasis is made there on the importance of the contribution to physics of paper 14 of the list above. In particular, it is underlined how Riemann was searching for “… a completely self-contained mathematical theory …, which would lead from the elementary laws up to the actions in an actually given filled space, without making a difference between gravity, electricity, magnetism or the equilibrium of temperature.”
4. In the celebrated biography of David Hilbert by Constance Reid (8) we can read that Hilbert sustained the opinion (referring to what is nowadays known as the Einstein–Hilbert action) that “… the invariance of the action integral unifies electromagnetism with gravity …”, yielding in this way a solution to a problem that, as he recognizes, “… was already posed by Riemann: the connection between gravitation and light.” Hilbert goes on to observe that, since then, many investigators had tried to arrive at a deeper understanding of this connection by merging the gravitational and electromagnetic potentials into a unity. The one example Hilbert mentions explicitly is Weyl's unification of the two fields in a “unified world metric,” as he calls it, by means of Weyl's notion of gauge invariance.
5. Remarkably enough, in what is probably one the most exhaustive biographies of Riemann ever written, Laugwitz (9) forgets almost completely about Riemann's work on physical issues. This is, in my view, to push to an extreme the opinion that I defended in the introduction, which was a lot more moderate and faceted.
3. Importance for Physics of Riemann's Mathematical Papers
It is the opinion of this author, also shared by others (see, e.g., Ref. (9)), that the influence in Physics of Riemann's purely mathematical papers exceeds by far, in its manifest importance, that of the above mentioned contributions on actual physical problems; even if the interest of the last attains already, as we have seen, a fairly high level.
I would need more space and time than I have at disposal in order to describe all such intertwining influences. In the following, and to start, a rather short list of items will provide some basic ideas about those influences. Then we will elaborate on some of them in more detail, not only because of their importance, but also because of the fact that they have to do with the author's own scientific expertise and published works.
3.1. On the Concept of Space
One reason why the discovery of non-Euclidean geometry took so long to happen may be due to the fact that there was universal belief that Euclidean geometry was special, the only possibility because it described the space we live in. In way it was mathematics completely attached to our physical world. Thus, stemming from this uncritical acceptance of the view that the geometry of space is Euclidean was the conviction that there was no other possible geometry. Philosophers like Emmanuel Kant argued that the Euclidean nature of space was indeed “a fact of nature”, and the weight of their authority was very powerful. From our present perspective, we know of course that the question of the geometry of space is in fact entirely different from the question of the possible existence of geometries which are non-Euclidean. Gauss was the first who clearly understood the difference between these two issues. In Gauss' Nachlass one can find his computations of the sums of the angles of each of the triangles that occurred in his triangulation of the Hanover region. His conclusion was that the sum was always two right angles, within the limits of observational errors. Recently this same experiment has been carried out at much larger, cosmic scales, trying to ascertain what the topology of space and the universe is like (10, 11).
In spite of the negative result of the Hanover triangulations, quite early in his scientific career Gauss was convinced of the possibility of constructing non-Euclidean geometries, and in fact came up with a “theory of parallels,” but because of the fact that the general belief in Euclidean geometry was so deeply ingrained, Gauss decided not to publish his researches on the “theory of parallels” and the construction of non-Euclidean geometries, for fear that there would arise criticisms of such investigations by people who did not understand those things (“the outcry of the Boeotians”, as he put it).
Riemann, who studied under Gauss, took this entire circle of ideas to a much higher and completely different level. In his famous inaugural lecture of 1854, written under the advice (or, better, as a compulsory choice) of Gauss himself, he touched, in an extraordinarily brilliant way, upon all of the aspects that his thesis advisor had considered. He pointed out, to start, the very crucial idea that a space does not have, to start with, any structure except that it is a continuum in which points are specified by the values of n coordinates, n being the dimension of the space. On such a space one can then impose many geometrical structures. His great insight was that a geometry should be built from these infinitesimal parts. He treated in depth geometries where the distance between pairs of infinitely near points is pythagorean, formulated also central questions about such geometries, and discovered the set of functions—the sectional curvatures—whose vanishing characterized the geometries which are Euclidean, namely those whose distance function is pythagorean not only for infinitely near points, but even for points which are a finite but small distance apart.
If the space is the one we live in, he formulated the principle that its geometrical structure could only be determined empirically. In fact he stated explicitly that the question of the geometry of physical space does not make sense independently of physical phenomena, i.e., that space has no geometrical structure until we take into account the physical properties of matter in it, and that this structure can be determined by measurement only. Indeed, he went so far as to say that “the physical matter determines the geometrical structure of space”. This ground-breaking idea took definite form some half a century later with Einstein's equations.
Indeed, it is also important to remark that Riemann's ideas constituted a profound departure from the perceptions that had prevailed until his time. Isaac Newton had asserted that space by itself is an “absolute entity endowed with Euclidean geometric structure”, and had built his entire theory of motion and celestial gravitation on that premise. Riemann went completely away from this point of view. Thus, for Riemann, space derived its properties from the matter that occupied it, and he asserted that the only question that could be studied was whether the physics of the world made its geometry Euclidean. It followed from this idea that only a mixture of geometry and physics could be tested against experience. For instance, measurements of the distance between remote points clearly depended on the assumption that a light ray would travel along shortest paths. This merging of geometry and physics, which is a central and dominating theme of modern physics, since Einstein's work, may be thus traced back to Riemann's inaugural lecture (12–14).
3.2. Linear Algebra, the Concept of n−Dimensional Space (A Linear, or Trivial “Variety”)
It has been often reported that linear algebra was a “trivial matter” for Riemann. However, in Laugwitz's book (9) (p. 242) we can read that the early developments of Riemannian geometry were “prolix and opaque” because “the development of linear algebra failed for a long time to keep pace with the progress of analysis.” This may be true, in fact: although nowadays n-dimensional linear spaces and their algebraic properties are considered to be one of the simplest theories in Mathematics, and its uses in classical and quantum physics are so basic and widespread (including infinite dimensional spaces, topological spaces, Banach and Hilbert spaces, etc.), that even the most basic issues of modern physics would not be possible to formulate without such concepts. One cannot simply translate this view to Riemann's epoch. But it was already clear that these abstract linear spaces had nothing to do with the space we live in, and were not even called “spaces” by Riemann or Gauss, but rather “varieties” or “manifolds”. Anyway, this concept was such a breakthrough for mathematics and mathematical physics that one may say it changed the world more radically than the Copernican perception, its importance being only paralleled by that of the development of infinitesimal calculus by Newton and Leibniz. All descriptions of the universe and of physical reality at any scale—be at the fundamental, effective, or phenomenological level—all thinkable developments of mathematical physics make use of the concept of n-dimensional space or manifold, as they do of differential equations. These concepts are nowadays so deeply engraved in our minds, as something that it is naturally just there, that we only barely appreciate their extreme, invaluable, paramount importance1.
3.3. Riemann's Integral
Riemann may have arrived at his notion of an “integral” in answer to the question of whether the Fourier coefficients, cn , of a given function tend to 0 (as n goes to infinity). Yet Laugwitz (9) characterizes Riemann's introduction of his integral as ad hoc and remarks that “History would have been different if he had asked himself this other mathematical question: what kind of integral implies the equality
where fn is a monotonically increasing sequence of integrable functions that converge pointwise to the limit f?”
It is of course true that Lebesgue's integral is the ultimate, natural extension of Riemann's one and a most fundamental tool in measure theory. But it is not less certain that, concerning the subject at discussion here, Riemann's integral is a lot more intuitive for a physicist, in the sense that even Egyptians or Babylonians could have arrived to such concept (although lacking, of course the rigorization of the concept of limit, that would have had to wait to the formulation of infinitesimal calculus). This I know first hand since I have been teaching both kind of integrals to physicists during many years, and also a non-rigorous concept of limit even to school children. The Riemann integral is indeed a physically fashionable object, in particular the incremental version before the limit is taken, before an “increment” is transformed into a “differential”, which is a far more elusive concept indeed! (again, I know this quite well from my own students).
3.4. Complex Variables, Cauchy–Riemann Equations
Riemann's Thesis discusses the theory of complex variables and, in particular, what we now call Riemann surfaces. It therefore introduced topological methods into complex function theory. The work elaborates on Cauchy's foundations of the theory of complex variables built up over many years and also on Puiseux's ideas of branch points. However, Riemann's Thesis is a strikingly original piece of work which examined geometric properties of analytic functions, conformal mappings and the connectivity of surfaces. Riemann's work was always based on intuitive reasoning which would fall at instances a little below the rigor required to make the conclusions watertight. However, the brilliant ideas which his works contain are so much clearer because his papers are not overly filled with lengthy computations (1), and this is why they were so frequently used in lecture courses (in special in Italy) afterwards. Again, one recognizes the physicist's approach in many of his discussions, but more important than this is the enormous use that both classical and quantum physics have made of the complex calculus that Riemann (among others) contributed to expand and popularize in a very efficient way.
3.5. Riemann Surface, Sphere, Manifold
In principle, those are very abstract concepts, but which have been applied, e.g., by engineers to the study of aerodynamics and hydrodynamics. At a different level, theoretical physicists have more recently drawn upon them very heavily in their formulations of string theory.
String theory is the modern version of a would be Theory of Everything (TOE). It suggests replacing pointlike particles with infinitesimal vibrating strings as the basic units of the physical world. Some years ago, when string theory was overwhelmingly dominating the landscape in theoretical physics2, there have been jokes about the typical theoretical physicist always carrying Farkas and Kra's book (Riemann Surfaces) everywhere (15). Edward Witten, from the Institute for Advanced Study at Princeton, has been, and continues to be, one of the main architects of string theory. He has given frequent talks on Riemann's work, when discussing some of the relations between physics and mathematics in the 20th and twenty-first centuries, to which the reader is addressed for material that complements a lot, from a different, much more ambitious perspective, what I discuss here.
3.6. Analytic Continuation, Complex Power Series
Most of Riemann's predecessors concentrated on the power series expansion rather than on the function that it represents. By shifting emphasis to the latter, Riemann could eliminate superfluous information, determining a complex function from its singularities. Riemann's work used simple concepts in place of the lengthy and sometimes obscure computations typical of his predecessors and contemporaries. The steady decrease in the amount of attention Riemann seems to have paid to power series between 1856 and 1861 indicates how his thought matured, shifting further away from computation. Even when using his good computational abilities, Riemann still focused upon concepts rather than the computation itself. Since relations obtained from series expansions of functions retain their validity outside their regions of convergence, he asked himself what actually continues functions from region to region? For example, Riemann constructed a function that has simple zeros at z = 0, 1, 2,… and is finite for all finite z (see Laugwitz (9)). The road to his function g(z) was heuristic, but this was of no consequence to Riemann. All he wanted was to find some function with the prescribed zeros. By contrast, Weierstrass always aimed to obtain formula representations of given functions. The Riemann approach to this issue is one of the main starting points in a large part of my own work, as will be commented later in more detail.
3.7. Curvature Tensor: Differential Geometry
In his general theory of relativity, Einstein used Riemann's concept of curved space as the basis for his elegant explanation of gravitation. Massive objects put a dimple in space in their vicinity. So when other physical objects, including photons, which do not have any mass, wander into the object's vicinity, they encounter this curved space. Such curvature determines the path the objects follow, in a way that was formerly attributed to the force of attraction that we call gravity.
In much the same way that Riemann conceived the curving and twisting space in innovative ways, he also described a set of abstract surfaces that were created by cutting and pasting together normal surfaces in ways that cannot be employed with real surfaces, but can be thought of abstractly. You can do a lot of mathematics on those abstract surfaces. And this has actually been an amazingly important idea for many parts of mathematics, and also for physics. In particular, general relativity, quantum field theory in curved spaces, string theories, gravitation, and modern cosmology, would had been impossible without those basic concepts introduced by Riemann.
3.8. The Riemann Zeta Function
This is known to be of extreme importance in analytic number theory. But also, through its analytical continuation (the so called functional equation, or reflection formula, of the zeta function), and extrapolating the concept of the zeta function to the class of pseudodifferential operators (the spectral values of the operator replace the natural numbers in the zeta function definition), as a regularization tool in quantum field theory (notably in curved space-time), for dynamical systems (classical and quantum), the concept of chaos (also present nowadays in the issue of the distribution of non-trivial zeros, or Riemann conjecture), etc. The interconnections between pure mathematics and physical uses is becoming here more on more profound, as years advance into the new century.
4. Selected Hot Subjects: On the Concept of Space, Zeta Regularization, and Modified Gravity Theories
4.1. The Concept of Space
4.1.1. Historical evolution of the concept of space
A very short summary of the evolution of the concept of space, from the very remote times of its inception, could be as follows.
1. The introduction of the concept of space goes back at least to the pre-Socratic philosophers, who already had coined this notion, together with some other very important ones, as those of substance, number, power, infinity, movement, being, atom, and of course time, among others.
2. The Pythagorean school should be mentioned as another important step, in its attempt at bringing all these concepts, in particular the one of space to the domain of numbers (“all things are numbers”). Just recall the importance of Pythagoras theorem, that has so much to do with space and with Gauss' search to check if the space we live in was or not Euclidean.
3. Euclid's “Elements”, this goes without saying as one of he most important pieces of work in the History of Mankind. It was so influential, for generations, that departing from the concept of Euclidean space was absolutely impossible for many centuries to come.
4. Indeed, still for Isaac Newton “space is, by itself, an absolute entity embedded with a Euclidean geometrical structure”. For him space and time provide a fixed, immutable and eternal background, a “stage”, with respect to which all things move. Like actors on that stage, particles move, exert forces onto each other and generally act out the drama of dynamics, while the stage itself does never change.
5. On the side of the philosophers, for Immanuel Kant “that space is Euclidean is a property of nature itself”.
6. The works of Nikolai Lobachevsky and János Bolyai ended a millennium-year struggle with Euclid's axiom of the parallels and provided inspiration to Gauss, who was arguably the first who clearly understood the difference between the question of the geometry of space and that of the possible existence of geometries which are non-Euclidean.
7. Now Bernhard Riemann came to clearly say, as we already remarked before, that: “many spaces are possible; it is the physical matter that determines the geometrical structure of space”.
8. And Albert Einstein gave a precise mathematical formulation of this concept, with the important help of Marcel Grossmann and making use of Riemann's manifolds and tensors: space-time is curved by matter, as prescribed by Einstein's equations (in terms of the Riemann curvature tensor).
9. To finish, an embracing reflection by Eugene Wigner, a much celebrated mathematical physicist which can, in particular, be extended to the whole development of the concept of space above, is that of “the unreasonable effectiveness of Mathematics in the Natural Sciences”, when in fact we understand now that they are absolutely independent endeavors.
4.1.2. On the topology and curvature of our universe
Let us now connect, briefly, these philosophical ideas about space with recent precise determinations of the topology and geometrical curvature of the universe we live in—what can be considered as the modern version of the pioneering attempts by Gauss, already mentioned. The Friedmann-Robertson-Walker (FRW) model, which constitutes the only family of solutions to the Einstein's equations compatible with the assumptions of homogeneity and isotropy of space, is the generally accepted model of our cosmos, nowadays. But, as the reader surely knows, the FRW is a family with a free parameter, k, the curvature, that could be positive, negative or zero (the flat or Euclidean case). This curvature, equivalently the curvature radius, R, is not fixed by the theory and must be determined by cosmological observations. Moreover, the FRW model, and Einstein's equations themselves, are differential, they can only provide local properties, not global ones, so they cannot tell about the overall topology of our world: is it closed or open? is it finite or infinite? Those questions are very appealing to the human being. All this discussion will only concern three dimensional space curvature and topology, time not being for the moment involved.
To repeat, serious attempts to measure the possible curvature of the space we live in go back to Gauss, who measured the sum of the three angles of a big triangle with vertices on the picks of three far away mountains—Brocken, Inselberg, and Hohenhagen. He was actually looking for evidence that the geometry of space could be non-Euclidean. The idea was brilliant, but condemned to failure: one needs a much bigger triangle to try to find the possible non-zero curvature of space. Now cosmologist have recently measured the curvature radius, R, by using the largest triangle available, namely one with us at one vertex and with the other two on the hot opaque surface of the ionized hydrogen that delimits our visible universe and emits the cosmic microwave background radiation (CMB, some 3.8 × 105 years after the Big Bang) (16). The CMB maps exhibit hot and cold spots. It can be shown that the characteristic spot angular size corresponds to the first peak of the temperature power spectrum, which is reached for an angular size of 0.5° (approximately the one subtended by the Moon) if space is flat. If it has a positive curvature, spots should be larger (with a corresponding displacement of the position of the peak), and correspondingly smaller for negative curvature.
The joint analysis of the considerable amount of data obtained during the last years by balloon experiments (BOOMERanG, MAXIMA) (17), combined also with galaxy clustering data, have produced a lower bound for |R| > 20 h−1 Gpc, that is, twice as large as the radius of the observable universe, of about RU ≃ 9 h−1 Gpc.
Again, general relativity does not prescribe the topology of the universe, or its being finite or not. The universe could perfectly be flat and finite. The simplest non-trivial model from the theoretical viewpoint is the toroidal topology (that of a tyre or a donut, but in one dimension more). Traces for the toroidal topology (and more elaborated ones, as negatively curved but compact spaces) have been carefully investigated, and some circles in the sky with near identical temperature patterns were identified (11). And yet more papers appear, from time to time, proposing a new topology (18). For the most recent results constraining the possible topologies of the universe at large scale, see (10, 11). However, to summarize all these efforts and the observational situation, and once the numerical data are interpreted without bias (what sometimes was not the case, and led to erroneous conclusions), it seems at present that available data still point toward a very large (we may call it infinite) flat space. The high precision data that are accumulating from the PLANCK mission (21) seem to show a richer structure for the CMB spots and could bring surprises in the next couple of years when the data analysis will be completed.
4.2. On Zeta-Function Regularization and its Uses in Quantum Field Theory
What would be the sum of the following series?
The obvious answer is s = ∞, since everybody recognizes in this last expression the definition itself of the concept of infinity. Now, this is ok in principle but it is, at the same time, of little or no use in modern Physics: since the appearance of quantum field theory (QFT) calculations are plagued with divergent series, and it is stupid to just say that all of them are divergent. One gets non-false but also no useful information in this way. And it is the fact that we actually do not observe these many infinities (or divergences) in laboratory observations. This was discovered in the 30's and 40's: something very important was missing from the formulation of quantum field theory processes. Either all these theoretical approaches to physics were nuts (as Dirac and Einstein proclaimed at some point) or one should be able to give direct sense to the resulting divergent series (what actually was the case, in the end).
Within the mathematical community, there was the longstanding suspicion that one could indeed give sense to divergent series. And this has now been shown, in a way, to be true in Physics, and with enormous success, as will be explained later. But it were the mathematicians—many years before—who first realized such possibility. To wit, Leonard Euler (1707–1783) was convinced that “To every series one could assign a number” (19, 20) (that is, in a reasonable, consistent, and possibly useful way, of course). Euler was unable to prove this statement in full, but he devised a technique (Euler's summation criterion) in order to “sum” a large family of divergent series. His statement was, however, controverted by some other great mathematicians, as Abel, who said that “The divergent series are the invention of the devil, and it is a shame to base on them any demonstration whatsoever” (22). There is a classical treatise due to G.H. Hardy and entitled simply Divergent Series (23) that can be highly recommended to the reader.
Actually, regularization and renormalization procedures are essential in present-day Physics. Among the different techniques at hand in order to implement these processes, zeta function regularization is one of the most beautiful, particularly for a mathematical physicist. Use of this method yields, for instance, the vacuum energy corresponding to a quantum physical system, which could, e.g., contribute to the cosmic force leading to the present acceleration of the expansion of our universe. The zeta function method is unchallenged at the one-loop level, where it is rigorously defined and where many calculations of QFT basically reduce to the computation of determinants of elliptic pseudodifferential operators (ΨDOs) (24). It is thus no surprise that the preferred definition of determinant for such operators is obtained through the corresponding zeta function (see, e.g., (25–31)).
4.2.1. The zeta function as a summation method
The method of zeta regularization evolved from the consideration of the Riemann zeta function as a “series summation method”. The zeta function, on its turn, was actually introduced by Euler, from considerations of the harmonic series
which is logarithmically divergent, and of the fact that, putting a real exponent s over each term,
then for s > 1 the series is convergent, while for s ≤ 1 it is divergent. Euler called this expression, as a function of s, the ζ-function, ζ(s), and found the following important relation
which is crucial for the applications of this function in number theory. By allowing the variable s to be complex, Riemann saw the relevance of this function (that now bears his name) for the proof of the prime number theorem3, and formulated thereby the Riemann hypothesis, which is one of the most important problems (if not the most important one) in the history of Mathematics. More of that in the excellent reviews (32, 33).
For the Riemann ζ(s), the corresponding complex series converges absolutely on the open half of the complex plane to the right of the abscissa of convergence Re s = 1, while it diverges on the other side, but it turns out that it can be analytically continued to that part of the plane, being then everywhere analytic and finite except for the only, simple pole at s = 14.
Let us sketch Riemann's second proof of the analytic continuation and derivation of the functional equation of the ζ function. He started from the (Euler) representation of the Gamma function (for Re s > 0)
which, by making the change of variables t → n2πt, yields
and summing now over n from 1 to ∞ and interchanging sum and integral (what is allowed by the uniform convergence of the series), we get
where θ is Jacobi's theta function. Now, using the functional equation for the θ function, which is obtained, by use of the Fourier transform, as a very fundamental formula on the same level as the Poison summation formula (see a very detailed description of the connection between all these expressions in (44)), after some simple manipulations Riemann obtained that
which shows that the expression on the left is analytic except for the simple poles at s = 0 and s = 1/2 (the pole at 0 comes from the Gamma function). Moreover, this formula is clearly symmetric under the change of variables s → 1/2 − s, so that, changing from 2s to s one sees that the function
satisfies the very beautiful functional equation
(also called by physicists, for obvious reasons, reflection formula). In terms of the Riemann zeta function, the functional equation that we have is, for Re s < 1,
These expressions, obtained by Riemann, provide the explicit analytic continuation of the zeta function to the rest of the complex plane beyond the abscissa of convergence of the initial series expression. They will be employed, in the examples below, to explain the use of the zeta function as an infinite series summation procedure. This does not mean, however, that the functional equation is the best suited expression to perform the analytic continuation, nor is the initial series well suited to obtain values of the zeta function in the original convergence domain, because of its very slow convergence speed. Indeed, in practice these formulas above are of very little use for accurate calculations, since they are given in terms of power series expansions (as the Riemann zeta itself), which are very slowly convergent near the corresponding abscissa of convergence. Fortunately, much better expressions exist which converge exponentially fast, are everywhere valid on the complex plane, and explicitly display the poles with the corresponding residua of the zeta function, as the celebrated Chowla–Selberg (53, 54) formula and many other (55, 56). Finding these valuable formulas, a speciality of the present author, yields enormous power (and elegance) to the method of zeta function regularization.
In more general cases, namely corresponding to the Hamiltonians which are relevant in physical applications (34–45), the situation is in essence quite similar, albeit in practice it can be rather more cumbersome. A mathematical theorem exists, which assures that, under very general conditions, the zeta function corresponding to a Hamiltonian operator will be also meromorphic, with just a discrete number of possible poles, which are usually simple (at most double) and extend to the negative side of the real axis5.
The above picture hints toward the use of the zeta function as a summation method to help solve the problem we had at the beginning of this section. Let us consider two very simple examples.
1. We interpret our starting series
as a particular case of the Riemann zeta function, e.g., for the value s = 0. This value is on the left hand side of the abscissa of convergence, where the series as such diverges but where the analytic continuation of the zeta function provides a perfectly finite value:
So this is the value to be attributed to the series 1 + 1 + 1 + 1 + ….
2. The series
corresponds to the exponent s = −1, so that
A comment is here in order. The fact that positive series, as the ones above, can yield a negative result may seem nonsense. However, it turns out that the most precise experiments ever carried out in Physics do support such results: models of regularization in QED built upon these techniques lead to final numbers which are in agreement with the experimental values up to the 9th figure. Actually, the latest experimental results for the electron g-factor is, to my knowledge, the Harvard 2008 result (46). This measures ge to a relative accuracy of about 10−12 (a little better if one only consider 1−σ errors). The latest theoretical calculation is the recently completed 10th order calculation by the Kinoshita group (47). A comparison of their results with the experimental value does not by itself provide a check between theory and experiment, since it only serves to determine a value of the fine structure constant, α. For a true verification one needs an independent determination of α, which is provided through the Rubidium measurement (ħ/mRh ) (48), which yields α with an accuracy of 6.6 × 10−10, which sets the limit of how well QED can currently be tested, namely, (ge(exp) − ge(theory))/ge(exp) ≈ 0.8 × 10−12, to 1 − σ accuracy. However, since the 2 in the g-factor comes essentially for free, both theoretically and experimentally, it is probably more prudent to consider the relative accuracy of the anomalies, namely, (ae(exp) − ae(theory))/ae(exp) ≈ 10−9. This is actually the number often used by the authority in the field, Kinoshita6. In recent experimental proofs of the Casimir effect (49) the agreement is also quite remarkable (given the difficulties of the experimental setup) (50–52).
4.2.2. Zeta regularization in physics
As advanced already, the regularization and renormalization procedures are essential issues of contemporary physics—without which it would simply not exist, at least in the form we now know it (57, 58). Among the different methods, zeta function regularization—which is obtained by analytic continuation in the complex plane of the zeta function of the relevant physical operator in each case—is no doubt the most beautiful of all. Use of this method yields, for instance, the vacuum energy corresponding to a quantum physical system (with constraints of any kind, in principle). Assume the corresponding Hamiltonian operator, H, has a spectral decomposition of the form (think, as simplest case, in a quantum harmonic oscillator): {λi, φi}i ∈ I, where I is a set of indices (which can be discrete, continuous, mixed, multiple, …). Then, the quantum vacuum energy is obtained as follows (34–45):
where ζA is the zeta function corresponding to the operator A, and the equalities are in the sense of analytic continuation (since, generically, the Hamiltonian operator will not be of the trace class). It must be pointed out that this ζ-trace is actually no trace in the usual sense. To start with, while a trace is a linear functional this one is highly non-linear, as is clear to see from the central step in the calculation, namely
as often explained by the author (59). Some colleagues are unaware of this obvious fact, which has lead to important mistakes and erroneous conclusions in the literature. Note that the formal sum over the eigenvalues is usually ill defined, and that the last step in (16) involves analytic continuation, inherent with the definition of the zeta function itself. Also, the unavoidable regularization parameter with dimensions of mass, μ, appears in the process, in order to render the eigenvalues of the resulting operator dimensionless, so that the corresponding zeta function can indeed be defined. We shall not discuss these very important details here, which are just at the starting point of the whole renormalization procedure. The mathematically simple-looking relations above involve very deep physical concepts (no wonder that understanding them took several decades in the recent history of quantum field theory).
4.2.3. The casimir energy
In fact things do not turn out to be so simple. To start with, one cannot assign a meaning to the absolute value of the zero-point energy, and any physical effect is an energy difference between two situations, such as a quantum field in curved space as compared with the same field in flat space, or one satisfying BCs on some surface as compared with the same in its absence, etc. This difference is the so-called Casimir energy:
But here a problem appears. Imposing mathematical boundary conditions (BCs) on physical quantum fields turns out to be a highly non-trivial act. This was discussed in much detail in a paper by Deutsch and Candelas some years ago (60). These authors quantized electromagnetic and scalar fields in the region near an arbitrary smooth boundary, and calculated the renormalized vacuum expectation value of the stress-energy tensor, to find out that the energy density diverges as the boundary is approached. Therefore, regularization and renormalization did not seem to cure the problem with infinities in this case and an infinite physical energy was obtained if the mathematical BCs were to be fulfilled. However, the authors argued that surfaces have non-zero depth, and its value could be taken as a handy (dimensional) cutoff in order to regularize the infinities. Just 2 years after Deutsch and Candelas' work, Kurt Symanzik carried out a rigorous analysis of QFT in the presence of boundaries (61). Prescribing the value of the quantum field on a boundary means using the Schrödinger representation, and Symanzik was able to show rigorously that such representation exists to all orders in the perturbative expansion. He showed also that the field operator being diagonalized in a smooth hypersurface differs from the usual renormalized one by a factor that diverges logarithmically when the distance to the hypersurface goes to zero. This requires a precise limiting procedure and point splitting to be applied. In any case, the issue was proven to be perfectly meaningful within the domains of renormalized QFT. In this case the BCs and the hypersurfaces themselves were treated at a pure mathematical level (zero depth) by using (Dirac) delta functions.
Ten years ago a new approach to the problem was postulated (62–65). BCs on a field, ϕ, are enforced on a surface, S, by introducing a scalar potential, σ, of Gaussian shape living on and near the surface. When the Gaussian becomes a delta function, the BCs (Dirichlet here) are enforced: the delta-shaped potential kills all the modes of ϕ at the surface. For the rest, the quantum system undergoes a full-fledged QFT renormalization, as in the case of Symanzik's approach. The results obtained confirm those of (60) in the several models studied albeit they do not seem to agree with those of (61). They are also in clear contradiction with the ones quoted in the usual textbooks and review articles dealing with the Casimir effect (66–69), where no infinite energy density when approaching the Casimir plates has been reported. This issue is also of importance at the cosmological level, in braneworld models.
4.3. Present Day Cosmology from Modified Einsteinian Gravity
4.3.1. Uses of the Riemann tensor in cosmology
As was mentioned before, Riemann's revolutionary ideas about the concept of physical space where given a definite form by Albert Einstein when he formulated the Theory of General Relativity, with the help of his, more mathematically minded, classmate and friend Marcel Grossmann7. The community of relativists celebrates Grossmann's contributions to physics by organizing the very important Marcel Grossman meetings, every 3 years (MG13 took place in Rio, in 2012). Let us summarize the main points of the so called “curved-space-time physics” (excellent references are the books by Robert Wald (70, 71)):
1. Space-time, the set of all events, is a four-dimensional manifold endowed with a metric (M, g).
2. The metric is physically measurable by rods and clocks.
3. The metric of space-time can be put in the Lorentz form momentarily at any particular event by an appropriate choice of coordinates.
4. Freely-falling particles, unaffected by other forces, move on time-like geodesics of the space-time.
5. Any physical law that can be expressed in tensor notation in special relativity has exactly the same form in a locally-inertial frame of a curved space-time.
We cannot go into much detail in the standard theory of General Relativity, since we here aim at putting our emphasis on the very recent developments concerning its application to modern cosmology. Let us just recall Einstein's equations
where on the lhs we have the curvature, the geometry of space-time, under the form of contractions of the Riemann curvature tensor:
the Γ's being, as usual, Christoffel symbols of the Riemannian connection, and
Einstein observed that the solution of these equations, subject to the constraints of the cosmological principle, led to a universe that was not static. He was disappointed because at that time (1915–1920) the expansion of the Universe had not yet been discovered (Hubble, 1925–1930, see (72)) and the universe was considered to be in a stationary state. This led Einstein to introduce (against his actual will) a constant term in his equations (known now as the cosmological constant, Λ), that was perfectly compatible with all of the principles of his gravity theory (but otherwise unnecessary):
When a few years later Hubble discovered that the universe was in fact expanding, Einstein said the introduction of the cosmological constant had been the greatest blunder of his life. He was right to be upset since, had he possessed sufficient confidence in his original equations, he could have predicted (in order for his theory to describe the Universe) that the Universe had to be expanding, and this well before there was any experimental evidence of this expansion!8.
An important historical issue (also for what will follow) was the derivation of Einstein's equations from a variational principle, starting from what is now called the Einstein–Hilbert action9:
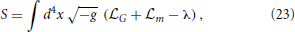
where λ = Λ/8πG. Here the first two terms within the brackets are the Lagrangians corresponding to gravity and matter, and the last one is the cosmological constant term. By variation in the Euler–Lagrange sense, one obtains
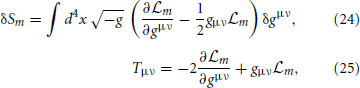
wherefrom Einstein's equations follow.
4.3.2. Cosmological constant and the quantum vacuum energy
However, this was not the end of the story. Any attempt at a unification of all fundamental interactions—already envisaged by Riemann, as reported, and to which Einstein devoted an important part of his life—that is, a physical theory describing the gravitational interactions of matter and energy as described by quantum theory, has failed. In most theories aiming at this, gravity itself is quantized and since it describes gravitation as the curvature of space-time by matter and energy, a quantization of gravity implies some sort of quantization of space-time itself. But all existing physical theories rely on a classical space-time background and this presents profound methodological and ontological challenges.
Not to forget is the fact that new theories must always contain the successful previous ones, that have proven already to be perfectly valid in their corresponding domains of applicability. Thus, special relativity reduces to classical Newtonian mechanics when the velocities v involved are v « c, and corrections to the classical formulas start with terms of the form v/c and higher powers (post-Newtonian, post-post-Newtonian approaches, and so on). In this sense, some successful semi-classical approaches to quantum gravity have been constructed. Summing up, even if we do not have a quantum theory of gravity, it is by now clear that quantum corrections to the Einstein equations corresponding to the fluctuations of the quantum vacuum will show out as an additional term in the energy-momentum tensor Tμν, side by side with Einstein's cosmological constant contribution, namely
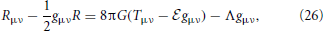
where 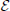 denotes this vacuum energy density. More precisely, the combination of this two terms (including all fundamental physical constants) reads
denotes this vacuum energy density. More precisely, the combination of this two terms (including all fundamental physical constants) reads
ωi being the energy modes (spectrum) of the Hamiltonian operator of the quantum theory. This fact will remain true in any quantum theory of gravitation, as far as vacuum fluctuations behave as an ordinary form of energy (e.g., they satisfy the equivalence principle), what seems indeed to be the case, although it has not been proven in a rigorous, gauge invariant way (73). Also to be noted is that those quantum corrections appear in the form of additional terms in higher powers of the curvature.
The dramatic consequence of this issue (already pointed out by Zel'dovich in the 1960's) is that we cannot get rid any more of the cosmological constant as Einstein finally did. It will pop up, under this new form, as fluctuations of the quantum vacuum, that are allowed by the fundamental Heisenberg's uncertainty principle (unless, of course, all quantum vacuum fluctuations add up to zero, which is very difficult to realize; this is known as the cosmological constant problem).
4.3.3. The acceleration of the cosmic expansion
Astrophysical observations clearly indicate that huge amounts of “dark matter” and “dark energy” are needed to explain the observed large scale structures (rotation curves of galaxies and clusters) and cosmic accelerating expansion of our entire universe. Up to now, no experimental evidence has been found, at the fundamental level, to convincingly explain such weird components. In particular, concerning the problem of the accelerating expansion, the only possibility to solve it within the domains of Einsteinian gravity is, again, through the cosmological constant term, that with the convenient sign provides the negative pressure contribution needed to produce the observed acceleration. However, this is not easy to do (74–76). First, when computed with care, the contribution of the vacuum energy density is many orders of magnitude larger than the value needed to explain the small acceleration rate of the universe expansion10. This is called the “new” problem of the cosmological constant, and is even worse than the older one. Second, it is not even clear (very specific models must be involved) whether the sign of the contribution of the vacuum fluctuations is the correct one in order to obtain expansion (and not contraction!). In a few words, there are models where these two problems could be understood, but always with the help of some tailored hypothesis, and the general consensus is that the problem is far from having been solved yet.
This has led to consider completely different approaches (see, for instance, (77, 78)). One of the most successful is the so-called f(R) gravity, which is a deviation from Einstein's GR in the way we are going to see (note that the R stands here for the Riemann tensor contraction or Ricci curvature). This is an alternative theory of gravity in which dark energy and dark matter could be effects—illusions, in a sense—created by the curvature of space-time (the same bending of space and time as in General Relativity, caused by extremely massive objects, like galaxies, but now a bit modified). This theory does not require the existence of dark energy and dark matter. The problem then could be completely reversed considering dark matter and dark energy as “shortcomings” of General Relativity and claiming for a more “correct” theory of gravity as derived phenomenologically by matching the largest number of observational data available. As a result, accelerating behavior of cosmic fluid and rotation curves of spiral galaxies have been reported to be well fitted by means of “curvature effects” (79).
To make the story short, realistic modified gravity models are being constructed which ultimately lead to the unification of the inflationary epoch with the late-time accelerating epoch of the universe history, under rather simple and natural conditions (80–82). But this is only a first step. Now those models should be studied in further quantitative detail (83–93), to match very precisely all the different stages in the evolution of the universe, by comparing their predictions with the highly precise cosmological data that no doubt will be delivered by ongoing and future sky observations. It is expected that this can be done rather soon, having in mind the possibility to slightly modify the early universe features of the theories here discussed (83–93), while still preserving all of their nice universal properties. Anyway some formidable tasks remain, in that context, as the study of the formation and evolution of cosmological perturbations, in particular the massive ones.
4.3.4. Non-local models for the universe
We are now trying to address some of the severe problems faced up by the modifications to Einsteinian gravity discussed above, and which can be summarized as follows (94): (1) a lack of simple guidelines, gedanken experiments, reasons of elegance and simplicity, as those of Einstein in constructing GR using the Riemannian formalism (a masterpiece impossible to imitate here); (2) the presence of a mass scale to be set much smaller than any mass found in nature, <10−33 eV, and which moreover should be protected from interactions with the rest of physics; (3) a well-known fine tuning problem in time, since the modifications to gravity happen to be important only now, not at any time in the past; (4) the non-trivial to satisfy constraint that modified gravity models should comply with the successes of GR in the Solar System domain.
One class of modified gravity models that overcomes most of these problems contains non-local interactions (95). The idea is to consider terms that are functionals of □−1R, with □ the d'Alembertian and R the Ricci scalar. At cosmological scales, □−1R grows very slowly: as (t/teq)1/2 in the radiation dominated era and logarithmically in the matter dominated era. Also, in a natural way, these terms are irrelevant at early times and begin to affect the dynamics of the Universe only after the matter-radiation transition, what solves some of the worst fine tuning problems. Moreover, since □−1R is dimensionless, the functional which multiplies R has no new mass parameter. And furthermore, because □−1R is extremely small in the Solar System, these models easily pass local tests of gravity.
There is, on the other hand, sufficient theoretical motivation for these models since, in string theory, R □−1R is precisely the term generated by quantum corrections (away from the critical dimension) as first pointed out by Polyakov. And a very nice feature we discovered (96–99) is that it may be possible to rewrite these models in terms of local ones with one or more auxiliary scalar field. Also, non-local interactions could as well describe the early epoch of inflation, and they have been used by Park and Dodelson (94) to discuss structure formation in a non-locally modified gravity. Very recently we have investigated (100) if we could find similar power-law solutions in modified gravity theories (in particular, the above non-local theories), as those of type H = n/t corresponding to models for GR with a perfect fluid, and see how much they will deviate from the ones for GR. Recasting original non-local action into its local form, we obtained power-law solutions, with and without a cosmological constant, both in the Jordan and in the Einstein frames, and showed that the power-law solutions obtained in the Jordan frame do satisfy the original non-local equations, and the complete set of solutions were found in this frame. In Einstein's one, we obtained the power-law solutions either by solving the equations of motion, or by performing a conformal transformation of the solutions obtained in Jordan's. For this purpose, we extended the correspondence to include the matter sector.
Those are clear advances of these theories, all of them based on the very rich and useful Riemannian formalism and which, no doubt, will continue to be basic for the theories to appear during the rest of this century. As next steps to be undertaken we can mention respective analysis of the stability of the solutions encountered and, moreover, of the cosmological perturbations corresponding to these models, so that they can be physically differentiated, at last, from the by now standard ΛCDM model.
5. Final Conclusions
Let us finish this short overview of Riemann's work and its important uses in modern Physics—a clear example of the extraordinarily fruitful interrelation between the worlds of Physics and Mathematics—with a touching sentence that appears in a letter written by Albert Einstein and addressed to Arnold Sommerfeld, of the year 1912—this means, some 60 years after the celebrated Habilitationschrifft of Bernhard Riemann—where Einstein comments on the efforts he is doing in trying to understand Riemannian Geometry:
“Aber eines ist sicher, dass ich mich im Leben noch nicht annähend so geplagt habe und dass ich große Hochachtung vor der Mathematik eingeflößt bekommen habe, die ich bis jetzt in ihren subtileren Teilen in meiner Einfalt für puren Luxus gehalten habe!”
What means, in a free English translation: “But one thing is sure, namely that never before in my life had I invested such an effort, and that I never had such a high opinion of Mathematics, which I considered till very recently, in my boldness, and for what respects its most subtle parts, as a mere luxury!”
In order to seek inspiration for the challenging future of mathematical physics, for what we can expect from it and for how things will probably evolve from now on, I have thrown here a view toward the past, not in a comprehensive, rigorously historical fashion, but just using the work of a single, albeit very remarkable scientist, Bernhard Riemann. Of course I could have chosen other icons, that are by general agreement much more archetypical examples for a mathematical physicist. But the point I wanted to make here is precisely that Riemann may define a much better paradigm for the future of mathematical physics than the more standard, well established type. I am fully against the still rather widespread trend, that predominantly dominated national scientific societies in Europe during the last century, of classifying the work of scientists with the aim to strictly constraint them to separated domains of knowledge, without any feasible interaction among them and often even fighting against each other, and which, I am pretty sure, was in part responsible for the decline of European in favor of American science, which still continues. I wanted to convey the idea of Riemann being a perfect, archetypical example of the mathematical physicist of the future, to stress thereby that good research transcends any classification. To start with, Riemann just published a dozen works during his life, but the usefulness and applications of such masterpieces permeate all domains, subjects and disciplines one can possibly define, to the point that they can be considered to be universally useful. I have just highlighted in the previous section two important applications of his work to fundamental problems in quantum field theory and present day cosmology, but the number of those is unbelievably large. It is in this sense that I consider Riemann to be a more modern mathematical-physicist than others, his research transcending the stereotyped classification and adapting more to the new paradigm, as I will now explain in a bit more detail.
For, actually, the second step in my reasoning is even more dramatic. After recognizing the very important role that mathematical physics has been playing in the last century as a model paradigm for interdisciplinary activity, in demolishing the strict, impenetrable borders existing in “the establishment” between these two domains of knowledge (and for which many of us, mathematical-physicists, had to pay a—sometimes very high—personal price); after rendering tribute, I repeat, to its very important pioneering role in this sense, with respect to other interdisciplinary activities which appeared latter, it is now time to recognize that mathematical physics is quickly being surpassed by other extraordinarily fruitful and competitive interconnections which seem to pop up from nothing every day and which simultaneously involve several disciplines (in the classical sense), including, aside from the mentioned two, genetics, combinatorics, nanoelectronics, biochemistry, medicine, and even psychology, to name only a few, with such intriguing issues that include, e.g., artificial life and the modelization of the process of consciousness. We should be very attentive to all these new developments which represent crucial new challenges for mathematical physics and were it could play a very fundamental role for the nearby future of scientific development.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This investigation has been supported in part by MINECO (Spain), grant PR2011-0128 and project FIS2010-15640, by the CPAN Consolider Ingenio Project, and by AGAUR (Generalitat de Catalunya), contract 2009SGR-994. Research was partly carried out while the author was visiting the Department of Physics and Astronomy, Dartmouth College, NH, USA.
Footnotes
- ^Often, after having attended some conference by a string theorist or brane cosmologist I have approached the speaker with a request to mention Riemann and his key contributions.
- ^There is in fact a fashionable string theory landscape which contains an enormous amount (maybe 10500 or 101000) of possible vacuum solutions of the corresponding theory. Choosing one among them seems quite hopeless, for the moment, and it is one of the main problems of M theories (M stands for “Mother”, or “Mysterious”).
- ^Which states that the number Π(x) of primes which are less than or equal to a given natural number x behaves as x/logx, as x → ∞. It was finally proven, using Riemann's work, by Hadamard and de la Vallé-Poussin.
- ^Where it yields the harmonic series: there is no way out for this divergence.
- ^Although there are some exceptions to this general behavior, they correspond to rather twisted situations, and are outside the scope of this brief presentation.
- ^Thanks are given to a reviewer for valuable information on this point.
- ^Who later became a Professor of Mathematics at the Federal Polytechnic Institute in Zurich, today the ETH Zurich, specializing in descriptive geometry.
- ^What would have been an enormous accomplishment. This explains why Einstein was so angry.
- ^In fact Hilbert preceded Einstein by 1 day in the submission of his results for publication, in 1915.
- ^It is of the order of 10123, one of the largest discrepancies between theory and observation in the history of Physics.
References
1. Riemann biography. MacTutor History of Mathematics, University of St Andrews, Scotland. http://www-history.mcs.st-andrews.ac.uk/Biographies/Riemann.html
2. Bernhard Riemann, Mike Hoffman. Department of Mathematics, United States Naval Academy, Annapolis, MD. http://www.usna.edu/Users/math/meh/riemann.html
3. Bernhard Riemann, Wikipedia, The Free Encyclopedia. http://en.wikipedia.org/wiki/Bernhard_Riemann
4. Bernhard Riemann, Science World, Wolfram Research. http://scienceworld.wolfram.com/biography/Riemann.html
5. Wilkins DR. The Mathematical Papers of Georg Friedrich Bernhard Riemann. Trinity College, Dublin. http://www.maths.tcd.ie/pub/HistMath/People/Riemann/Papers.html
7. Elizalde E. Riemann and Physics. Lecture given at the Riemannn Journee, UPC, Barcelona (Feb. 20, 2008).
9. Laugwitz D. Bernhard Riemann, 1826–1866: Turning Points in the Conception of Mathematics. Boston: Birkhäuser (1999).
10. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F, et al., Planck Collaboration. Planck 2013 Results. XXVI. Background Geometry and Topology of the Universe. (2013). arXiv:1303.5086 [astro-ph].
11. Cornish NJ, Spergel DN, Starkman GD, Komatsu E. Constraining the topology of the universe. Phys Rev Lett. (2004) 92:201302.
12. Majer U, Sauer T. Hilbert's ‘world equations’ and his vision of a unified science. Einstein Studies. (2005) 11:259. arXiv:physics/0405110
13. Varadarajan VS. The Concept of a Supermanifold. Department of Mathematics, UCLA. http://www.math.ucla.edu/~vsv/papers/ch2.pdf
14. Riemann B. On the hypotheses which lie at the bases of geometry, (Translated by Clifford WK). Nature. (1873) VIII:14–7 36, 37. http://www.emis.ams.org/classics/Riemann/WKCGeom.pdf
15. Farkas H, Kra I. Riemann Surfaces. Berlin; Heidelberg; New York: Springer (1980) (2nd ed. 1992).
16. Tegmark M. Measuring spacetime: from Big Bang to Black Holes. Science. (2002) 296:1427. doi: 10.1126/science.1072184
17. Bond JR, Ade P, Balbi A, Bock J, Borrill J, Boscaleri A, et al., The MaxiBoom collaboration. CMB analysis of Boomerang and Maxima and the cosmic parameters. In: Proceedings of the IAU Symposium 201 (PASP), CITA-2000-65. arXiv:astro-ph/0011378
18. Luminet J-P, Weeks J, Riazuelo A, Lehoucq R, Uzan J-P. Dodecahedral space topology as an explanation for weak wide-angle temperature correlations in the cosmic microwave background. Nature. (2003) 425:593. doi: 10.1038/nature01944
21. PLANCK Science Team home page. http://www.rssd.esa.int/index.php?project=planck
22. Maor E. To Infinity and Beyond: A Cultural History of the Infinite. Princeton: Princeton University Press (1991).
26. Elizalde E, Romeo A. Rigorous extension of the proof of zeta-function regularization. Phys Rev. (1989) D40:436.
27. Elizalde E. On the zeta-function regularization of a two-dimensional series of Epstein-Hurwitz type. J Math Phys. (1990) 31:170.
28. Elizalde E. Derivative of the generalised Riemann zeta-function ζ(z, q) at z = −1. J Phys. (1985) A18:1637.
29. Elizalde E. An asymptotic expansion for the first derivative of the generalized Riemann zeta function. Math Comput. (1986) 47:347.
30. Elizalde E, Romeo A. An integral involving the generalized zeta function. Int J Math Math Sci. (1990) 13:453. doi: 10.1155/S0161171290000679
31. Fried D. Analytic torsion and closed geodesics on hyperbolic manifolds. Invent Math. (1984) 84:523. doi: 10.1007/BF01388745
33. Iwaniec H. Prime numbers and L-functions. In: Proceedings of the International Congress of Mathematicians. Madrid, (2006). p. 279–306.
34. Elizalde E, Odintsov SD, Romeo A, Bytsenko AA, Zerbini S. Zeta Regularization Techniques with Applications. Singapore: World Scientific (1994). doi: 10.1142/9789812779342
35. Kirsten K. Spectral Functions in Mathematics and Physics. London: Chapman and Hall (2001). doi: 10.1201/9781420035469
36. Bordag M, Elizalde E, Kirsten K. Heat-kernel coefficients of the Laplace operator on the D-dimensional ball. J Math Phys. (1996) 37:895. doi: 10.1063/1.531418
37. Elizalde E, Bordag M, Kirsten K. Casimir energy for a massive fermionic quantum field with a spherical boundary. J Phys. (1998) A31:1743. doi: 10.1088/0305-4470/31/7/009
38. Bordag M, Elizalde E, Kirsten K, Leseduarte S. Casimir energies for massive scalar fields in a spherical geometry. Phys Rev. (1997) D56:4896. doi: 10.1103/PhysRevD.56.4896
39. Elizalde E, Vanzo L, Zerbini S. Zeta function regularization, the multiplicative anomaly and the Wodzicki residue. Commun Math Phys. (1998) 194:613. doi: 10.1007/s002200050371
40. Elizalde E. Zeta functions: formulas and applications. J Comput Appl Math. (2000) 118:125. doi: 10.1016/S0377-0427(00)00284-3
41. Elizalde E. Explicit zeta functions for bosonic and fermionic fields on a non-commutative toroidal spacetime. J Phys. (2001) A34:3025. doi: 10.1088/0305-4470/34/14/309
42. Elizalde E, Kirsten K. Topological symmetry breaking in self-interacting theories on toroidal spacetime. J Math Phys. (1994) 35:1260. doi: 10.1063/1.530588
43. Elizalde E, Romeo A. Expresssions for the zeta-function regularized Casimir energy. J Math Phys. (1989) 30:1133. doi: 10.1063/1.528332
44. Elizalde E. Ten Physical Applications of Spectral Zeta Functions. 2nd ed., Lecture Notes in Physics 855. Berlin: Springer-Verlag (2012).
45. Bytsenko AA, Cognola G, Elizalde E, Moretti V, Zerbini S. Analytic Aspects of Quantum Fields. Singapore: World Scientific (2004).
46. Hanneke D, Fogwell S, Gabrielse G. New measurement of the electron magnetic moment and the fine structure constant. Phys Rev Lett. (2008) 100:120801. doi: 10.1103/PhysRevLett.100.120801
47. Aoyama T, Hayakawa M, Kinoshita T, Nio M. Complete tenth-order QED contribution to the Muon g-2. Phys Rev Lett. (2012) 109:111808. doi: 10.1103/PhysRevLett.109.111808
48. Bouchendira R, Cladé P, Guellati-Khélifa S, Nez F, Biraben F. New determination of the fine structure constant and test of the quantum electrodynamics. Phys Rev Lett. (2011) 106:080801. doi: 10.1103/PhysRevLett.106.080801
49. Casimir HBG. On the attraction between two perfectly conducting plates. Proc K Ned Akad Wet. (1948) 51:793.
50. Lamoreaux SK. Demonstration of the Casimir force in the 0.6 to 6μm range. Phys Rev Lett. (1997) 78:5. doi: 10.1103/PhysRevLett.78.5
51. Mohideen U, Roy A. Precision measurement of the Casimir force from 0.1 to 0.9μm. Phys Rev Lett. (1998) 81:4549. doi: 10.1103/PhysRevLett.81.4549
52. Harris BW, Chen F, Mohideen U. Precision measurement of the Casimir force using gold surfaces. Phys Rev. (2000) A62:052109. doi: 10.1103/PhysRevA.62.052109
53. Chowla S, Selberg A. On Epstein's zeta function. Proc Natl Acad Sci USA. (1949) 35:317. doi: 10.1073/pnas.35.7.371
54. Selberg A, Chowla S. On Epstein's zeta-function. J Reine Angew Math (Crelle's J.) (1967) 227:86.
55. Elizalde E. An extension of the Chowla-Selberg formula useful in quantizing with the Wheeler-De Witt equation. J Phys. (1994) A27:3775. doi: 10.1088/0305-4470/27/11/027
56. Elizalde E. Multidimensional extension of the generalized Chowla-Selberg formula. Commun Math Phys. (1998) 198:83. doi: 10.1007/s002200050472
57. Collins J. Renormalization: An Introduction to Renormalization, the Renormalization Group and the Operator-Product Expansion. Cambridge: Cambridge University Press (1984). doi: 10.1017/CBO9780511622656
58. McComb WD. Renormalization Methods: A Guide for Beginners. Oxford: Oxford University Press (2004).
59. Elizalde E. On the concept of determinant for the differential operators of quantum physics. J High Energy Phys. (1999) 9907:015. doi: 10.1088/1126-6708/1999/07/015
60. Deutsch D, Candelas P. Boundary effects in quantum field theory. Phys Rev. (1979) D20:3063. doi: 10.1103/PhysRevD.20.3063
61. Symanzik K. Schrödinger representation and Casimir effect in renormalizable quantum field theory. Nucl Phys. (1981) B190:1. doi: 10.1016/0550-3213(81)90482-X
62. Jaffe RL. Unnatural acts: unphysical consequences of imposing boundary conditions on quantum fields. AIP Conf Proc. (2003) 687:3 [hep-th/0307014]. doi: 10.1063/1.1632169
63. Graham N, Jaffe RL, Khemani V, Quandt M, Scandurra M, Weigel H. Casimir energies in light of quantum field theory. Phys Lett. (2003) B572:196.
64. Graham N, Jaffe RL, Khemani V, Quandt M, Scandurra M, Weigel H. Calculating vacuum energies in renormalizable quantum field theories: a new approach to the Casimir problem. Nucl Phys. (2002) B645:49. doi: 10.1016/S0550-3213(02)00823-4
65. Graham N, Jaffe RL, Weigel H. Casimir effects in renormalizable quantum field theories. Int J Mod Phys. (2002) A17:846. doi: 10.1142/S0217751X02010224
66. Mostepanenko VM, Trunov NN. The Casimir effect and its application. Oxford: Clarendon Press (1997).
67. Milton KA. The Casimir Effect: Physical Manifestations of Zero-Point Energy. Singapore: World Scientific (2001). doi: 10.1142/9789812810526
68. Bordag M, Mohideen U, Mostepanenko VM. New developments in the Casimir effect. Phys Rep. (2001) 353:1. doi: 10.1016/S0370-1573(01)00015-1
69. Bordag M, Klimchitskaya GL, Mohideen U, Mostepanenko VM. Advances in the Casimir Effect. International Series of Monographs on Physics 145. Oxford: Oxford University Press (2009). doi: 10.1093/acprof:oso/9780199238743.001.0001
71. Wald RM. Quantum Fields in Curved Spacetime and Black Hole Thermodynamics. Chicago: University of Chicago Press (1994).
72. Elizalde E. Galaxies: an international multidisciplinary open access journal. Galaxies (2013) 1:1. doi: 10.3390/galaxies1010001
73. Fulling SA, Milton KA, Parashar P, Romeo A, Shajesh KV, Wagner J. How does Casimir energy fall? Phys Rev. (2007) D76:025004. arXiv:hep-th/070209
74. Elizalde E, Odintsov SD, Saharian AA. Repulsive Casimir effect from extra dimensions and Robin boundary conditions: from branes to pistons. Phys Rev. (2009) D79:065023. arXiv:0902.0717 [hep-th].
75. Elizalde E, Nojiri S, Odintsov SD, Sebastiani L, Zerbini S. Nonsingular exponential gravity: a simple theory for early- and late-time accelerated expansion. Phys Rev. (2011) D83:086006. arXiv:1012.2280 [hep-th].
76. Brevik I, Elizalde E, Nojiri S, Odintsov SD. Viscous little rip cosmology. Phys Rev. (2011) D84:103508 arXiv:1107.4642 [hep-th].
77. Elizalde E, Nojiri S, Odintsov SD. Late-time cosmology in (phantom) scalar-tensor theory: dark energy and the cosmic speed-up. Phys Rev. (2004) D70:043539. doi: 10.1103/PhysRevD.70.043539
78. Elizalde E, Nojiri S, Odintsov SD, Wang P. Dark energy: vacuum fluctuations, the effective phantom phase, and holography. Phys Rev. (2005) D71:103504. doi: 10.1103/PhysRevD.71.103504
79. Capozziello S, Cardone VF, Troisi A. Dark energy and dark matter as curvature effects. J Cosmol Astropart Phys. (2006) 0608:001. doi: 10.1088/1475-7516/2006/08/001
80. Hu W, Sawicki I. Models of f(R) cosmic acceleration that evade solar system tests. Phys Rev. (2007) D76:064004. doi: 10.1103/PhysRevD.76.064004
81. Appleby SA, Battye RA. Do consistent F(R) models mimic general relativity plus Λ? Phys Lett. (2007) B654:7. doi: 10.1016/j.physletb.2007.08.037
82. Starobinskii A. Disappearing cosmological constant in f(R) gravity. JETP Lett. (2007) 86:157. doi: 10.1134/S0021364007150027
83. Dunsby PKS, Elizalde E, Goswami R, Odintsov S, Sáez-Gómez D. On the LCDM universe in f(R) gravity. Phys Rev. (2010) D82:023519. arXiv:1005.2205 [gr-qc].
84. Cognola G, Elizalde E, Nojiri S, Odintsov SD, Sebastiani L, Zerbini S. A class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys Rev. (2008) D77:046009. arXiv:0712.4141[hep-th].
85. Cognola G, Elizalde E, Nojiri S, Odintsov SD, Zerbini S. One-loop f(R) gravity in de Sitter universe. JCAP (2005) 0502:010. arXiv:hep-th/0501096
86. Cognola G, Elizalde E, Nojiri S, Odintsov SD, Zerbini S. Dark energy in modified Gauss-Bonnet gravity: late-time acceleration and the hierarchy problem. Phys Rev. (2006) D73:084007. arXiv:hep-th/0601008
87. Elizalde E, Nojiri S, Odintsov SD, Ogushi S. Casimir effect in de Sitter and anti-de Sitter braneworlds. Phys Rev. (2003) D67:063515. arXiv:hep-th/0209242
88. Elizalde E, Quiroga Hurtado J. Phantom and quantum matter in an Anti-deSitter universe. Mod Phys Lett. (2004) A19:29 (GR-QC 0310128).
89. Elizalde E, Naftulin S, Odintsov SD. Covariant effective action and one-loop renormalization of two-dimensional dilaton gravity with fermionic matter. Phys Rev. (1994) D49:2852. doi: 10.1103/PhysRevD.49.2852
90. Cognola G, Elizalde E, Odintsov SD, Tretyakov P, Zerbini S. Initial and final de Sitter universes from modified f(R) gravity. Phys Rev. (2009) D79:044001. arXiv:0810.4989 [hep-th].
91. Elizalde E, Silva PJ. F(R) gravity equation of state. Phys Rev. (2008) D78:061501. arXiv:0804.3721 [hep-th].
92. Carloni S, Elizalde E, Silva PJ. An analysis of the phase space of Horava-Lifshitz cosmologies. Class Quant Grav. (2010) 27:045004. arXiv:0909.2219 [hep-th].
93. Elizalde E, Myrzakulov R, Obukhov VV, Sáez-Gómez D. ΛCDM epoch reconstruction from F(R,G) and modified Gauss-Bonnet gravities. Class Quant Grav. (2010) 27:095007. arXiv:1001.3636 [gr-qc].
94. Park S, Dodelson S. Structure formation in a nonlocally modified gravity model. Phys Rev. (2013) D87:024003. arXiv:1209.0836
96. Capozziello S, Elizalde E, Nojiri S, Odintsov SD. Accelerating cosmologies from non-local higher-derivative gravity. Phys Lett. (2009) B671:193. arXiv:0809.1535 [hep-th].
97. Cognola G, Elizalde E, Nojiri S, Odintsov SD, Zerbini S. One-loop effective action for non-local modified Gauss-Bonnet gravity in de Sitter space. Eur Phys J. (2009) C64:483. arXiv:0905.0543
98. Elizalde E, Pozdeeva EO, Vernov SYu. De Sitter universe in non-local gravity. Phys Rev. (2012) D85:044002. arXiv:1110.5806
Keywords: Bernhard Riemann, physics vs. mathematics, mathematical physics, general relativity, gravity, zeta function, quantum vacuum regularization, interdisciplinary
Citation: Elizalde E (2013) Bernhard Riemann, a(rche)typical mathematical-physicist? Front. Physics 1:11. doi: 10.3389/fphy.2013.00011
Received: 24 July 2013; Paper pending published: 08 August 2013;
Accepted: 23 August 2013; Published online: 24 September 2013.
Edited by:
Iver H. Brevik, Norwegian University of Science and Technology, NorwayReviewed by:
Iver H. Brevik, Norwegian University of Science and Technology, NorwayKåre Olaussen, NTNU, Norway
Copyright © 2013 Elizalde. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Emilio Elizalde, Institut d'Estudis Espacials de Catalunya, Instituto de Ciencias del Espacio, CSIC, Campus UAB, Torre C5-Par-2a pl, 08193, Barcelona, Spain e-mail:ZWxpemFsZGVAaWVlYy51YWIuZXM=
