How can we determine if a spacetime is flat?

1. Introduction

The presence of tidal forces, i.e., geodesic deviation for causal geodesics, can be adopted to give a notion of gravitation valid in the general relativistic context, as the geodesic deviation is not affected by the equivalence principle and thus it cannot be canceled out by an appropriate choice of the reference frame. By direct inspection (see 2), one sees that the absence of geodesic deviation referred to all type of geodesics is equivalent the fact that the Riemann tensor vanishes everywhere in a spacetime (M, g). The latter fact, in turn, is equivalent to the locally flatness of the spacetime, i.e., There is a open covering of M, 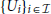, such that every subspacetime 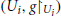is a portion of Minkowski spacetime. However, from a physical viewpoint, the geodesic deviation can easily be measured for causal geodesic, observing the stories of (infinitesimal) falling bodies, but it can hardly be measured for spacelike geodesics. Therefore the popular slogan “gravitation = curvature,” that is “absence of gravitation ⇔ (local) flatness,” seems to encounter an obstruction on the physical ground to be rigorously proved. This is not the case because we establish by Theorem 2.1 that, in a generic spacetime, the absence of geodesic deviation for timelike geodesics – or, equivalently, for null geodesics – is equivalent to the local flatness.

1.1. Basic Definitions and Known Results

If ∇ is a C¹ affine connection (1; 3) on a C² manifold M, the curvature tensor (field) is the tensor field defined, point by point, as the unique multi-linear operator R_p : T_p M ⊗ T_p M ⊗ T_p M → T_p M with:

$\begin{array}{cc}{R}_p\left(X_p,Y_p\right)Z_p={\left({\nabla }_X{\nabla }_{Y}Z\right)}_p-{\left({\nabla }_Y{\nabla }_{X}Z\right)}_p-{\left({\nabla }_{[X,Y]}Z\right)}_p,& (1)\end{array}$

for every p ∈ M and for every triple of C² vector fields X, Y, Z. It fulfills the following algebraic properties (5), valid for every p ∈ M and all X_p, Y_p, Z_p ∈ T_pM which will play a role in the rest of the paper.

$\begin{array}{cc}{R}_p\left(X_p,Y_p\right)Z_p+R_p\left(Y_p,X_p\right)Z_p=0,& (2)\end{array}$

$\begin{array}{cc}\begin{array}{l}{R}_p\left(X_p,Y_p\right)Z_p+R_p\left(Y_p,Z_p\right)X_p+R_p\left(Z_p,X_p\right)Y_p=0,\\ \text{ provided }\nabla \text{ is torsionfree}.\end{array}& (3)\end{array}$

A result, often mentioned but rarely proved in relativity txtbooks¹, establishes that:

Theorem 1.1. Let M be a C² n-dimensional manifold equipped with a C¹ torsionfree affine connection ∇. The curvature tensor vanishes everywhere on M, if and only if M admits an atlas 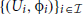such that, the connection coefficients of ∇ vanish in every local chart (U_i, ϕ_i),

(See the Appendix for a proof). In the following, for a C² manifold M equipped with a C² metric g, the symbol ∇ denotes the Levi-Civita connection, i.e., the unique torsionfree, g-metrical (i.e., ∇g = 0), affine connection. The curvature tensor, in this case, is called Riemann (curvature) tensor of g.

2. Local Flatness and Geodesic Deviation

A spacetime (M, g) is a smooth (i.e., C^∞) four-dimensional manifold M, equipped with a smooth metric g with Lorentzian signature (−, +, +, +). We state our definition of locally flat spacetime.

Definition 2.1. A spacetime (M, g) is locally flat if it admits a covering 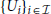made of open subsets, such that every spacetime 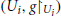is isometric to a spacetime 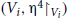, V_i being an open set in Minkowski spacetime 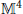and η⁴ being the standard Minkowski metric of .

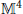The issue about global flatness of a locally flat spacetime (M, g) – i.e., if (M, g) is globally isometric to Minkowski spacetime (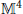, η⁴) – is of topological nature and will not be addressed here. Locally flat spacetims which are not globally flat can be constructed easily, taking some discrete-isometry-invariant identifications in 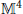. From a pure mathematical point of view, Theorem 2.1 immediately implies that:

Lemma 2.1. A spacetime (M, g) is locally flat if and only if the Riemann tensor R vanishes everywhere.

Proof. Locally flatness yields R = 0 everywhere. If R = 0 everywhere, consider the atlas 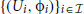of Theorem 1. The components of g are constant in each (U_i, ϕ_i) since the connection coefficients vanish and ∇g = 0. Using constant linear transformations, one diagonalizes the matrix-valued function representing g in every U_i, obtaining the Minkowskian standard form of the metric in each U_i.

  □

As a second step, let us review the notion of geodesic deviation (2; 5) starting with a definition.

Definition 2.2. Consider, in the spacetime (M, g), a pair ({γ_s}_{s ∈ I}, J), such that I, J ⊂ ℝ are open nonempty intervals, for every fixed s ∈ I, $J:t\mapsto {\gamma }_s(t)$ is a geodesic, t being a (common) affine parameter, and the map $I\times J\ni (s,t)\mapsto {\gamma }_s(t)$ is smooth. Defining $T:=\frac{\partial }{\partial t}$ and $S:=\frac{\partial }{\partial s}$, assume that

$\begin{array}{cc}\begin{array}{l}{T}_{{\gamma }_s(t)},S_{{\gamma }_s(t)}arelinearlyindependentand{\left[T,S\right]}_{{\gamma }_s(t)}=0,\\ forevery(s,t)\in I\times J.\end{array}& (4)\end{array}$

Such a pair ({γ_s}_{s ∈ I}, J) will be called a smooth congruence of geodesics.

The constraint (4) assures that, as is physically expected, one can adapt a coordinate system to the smooth class of geodesics, at least locally, such that two coordinates just coincide with t and s. For nonnull geodesics, t can be chosen as the proper length parameter for spacelike geodesics, or the proper time for timelike geodesics. At least when S is spacelike, ∇_TS defines the relative speed, referred to the parameter t, between infinitesimally close geodesics (say γ_s and γ_{s + δs}). Similarly, ∇_T(∇_TS) defines the relative acceleration, referred to the parameter t, between infinitesimally close geodesics. Starting form ∇_T(∇_TS), employing the definition (1), applying (4), and taking the geodesic equation ∇_T T = 0 into account, one finds the geodesic deviation equation:

$\begin{array}{cc}{\nabla }_T({\nabla }_{T}S)=-R(S,T)T.& (5)\end{array}$

Let us restrict, from now on, to smooth congruences of causal geodesics with spacelike vectors S, since they have a dynamical interpretation, describing the stories of of free falling bodies, ∇_T(∇_TS) being the relative acceleration. The presence of tidal forces on free falling bodies, represented by the left-hand side of (5), cannot be canceled by means of a suitable choice of the reference frame, but it is a property of the geometry of the spacetime. Thus, the presence of geodesic deviation for a smooth congruences of causal geodesics with spacelike S can be used to give a sensible, relativistic, definition of gravitation, which is not affected by the equivalence principle. In locally flat spacetimes, where R = 0, there is no geodesic deviation – so that gravitation disappears. It is interesting to study if the absence of geodesic deviation for causal geodesics – i.e., the absence of gravitation – implies the local flatness of the spacetime. It is important to remark that the full information about the curvature may be obtained from the equation of geodesic deviation (5), if considering also smooth congruences of spacelike geodesics (2). However, from the experimentalist's viewpoint, ∇_T(∇_TS) can hardly be measured along spacelike geodesics, excluding particular cases of spacetimes as static ones, and referring to a very special choice of the field S. For this reason we stick to smooth congruences of causal geodesics with spacelike S only. The following theorem shows that, actually, geodesic deviation of timelike geodesics, or equivalently, geodesic deviation of null geodesics, encodes all information on the curvature.

Theorem 2.1. Consider a spacetime (M, g). The following facts are equivalent.

(a) (M, g) is locally flat;

(b) for every smooth congruence of geodesics ({γ_s}_{s ∈ I}, J) such that, γ_s is a timelike geodesic and S_γs(t) is spacelike ∀(s, t) ∈ I × J, there is no geodesic deviation, i.e., (∇_T(∇_T S))_γs(t) = 0, for all (s, t) ∈ I × J;

(c) for every smooth congruence of geodesics ({γ_s}_{s ∈ I}, J) such that, γ_s is a null geodesic and S_γs(t) is spacelike ∀(s, t) ∈ I × J, there is no geodesic deviation, i.e., (∇_T(∇_TS))_γs(t) = 0, for all (s, t) ∈ I × J.

Proof. In view of Lemma 2.1 and of Equation (5), (a) implies both (b) and (c). Let us demonstrate that (b) implies (a). The idea is to prove, making use of (b), (2) and (3), that for each point p ∈ M, it holds R_p(X_p, Y_p)Z_p = 0 for every choice of vectors X_p, Y_p, Z_p ∈ T_pM. This is equivalent to say that the Riemann tensor vanishes everywhere on M. At this point, Lemma 2.1 implies (a). Let us proceed step-by-step along this way. Fix p ∈ M and assume that (b) is valid. The following lemma holds, whose proof stays in the Appendix.

Lemma 2.2. If (M, g) is a spacetime, p ∈ M, let T_p ∈ T_p M\{0} and S_p ∈ T_p M\{0} be, respectively timelike and spacelike, vectors with g(T_p, S_p) = 0. There is a smooth congruence of geodesics ({γ_s}_{s ∈ I}, J) as in (b) of Theorem 2.1, fulfilling T_γs0(t0) = T_p, and S_γs0(t0) = S_p, for some (s₀, t₀) ∈ I × J.

In view of Lemma 2.2 and Equation (5), one has that, for every p ∈ M, R_p(S_p, T_p)T_p = 0 for all T_p, S_p ∈ T_pM, respectively timelike and spacelike, with g(T_p, S_p) = 0. To extend this result to all possible arguments of R, we start noticing that R_p(S_p, T_p)T_p = 0 is still valid if dropping the requirements S_p spacelike and g(T_p, S_p) = 0. Indeed, if S_p ∈ T_pM is generic, we can decompose it as S_p = S'_p + cT_p, where c ∈ ℝ and S'_p is spacelike with g(T_p, S'_p) = 0, for some timelike vector T_p. Then R_p(S_p, T_p)T_p = R_p(S'_p, T_p)T_p + cR_p(T_p, T_p)T_p = 0 + cR_p(T_p, T_p)T_p = 0, where we have used Equation (3). Summarizing, (b) implies that R_p(S_p, T_p)T_p = 0 for all T_p, S_p ∈ T_pM with T_p timelike. Let us show that this last constraint can be dropped, too. To this goal, fix S_p ∈ T_pM arbitrarily and consider the bi-linear map $T_{p}M\ni T_p\mapsto F_{S_p}(T_p):=R_p(S_p,T_p)T_p$. If we restrict F_Sp to one of the two open halves V_p⁽⁺⁾ of the light-cone at p, e.g. that containing the future-directed timelike vectors, we find 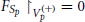in view of the discussion above. Since F_Sp is analytic (it being a polynomial) and defined on the connected open domain T_pM, it must vanish everywhere on T_pM. Summarizing, we have obtained that R_p(S_p, T_p)T_p = 0 for every vectors T_p, S_p ∈ T_pM. To conclude, let us prove that the identity above holds true if replacing the latter T_p with a generic vector Z_p. Starting from R_p(S_p, T_p)T_p = 0, assuming T_p = U_p + V_p and T_p = U_p − V_p, subtracting side-by-side the obtained results, taking bi-linearity into account, one finds:

$\begin{array}{cc}{R}_p\left(S_p,U_p\right)V_p+R_p\left(S_p,V_p\right)U_p=0,& (6)\end{array}$

which is valid for every S_p, U_p, V_p ∈ T_pM. Identity (3) can be specialized here as:

$\begin{array}{cc}{R}_p\left(S_p,U_p\right)V_p+R_p\left(U_p,V_p\right)S_p+R_p\left(V_p,S_p\right)U_p=0.& (7)\end{array}$

Summing side-by-side (6) and (7), taking Equation (2) into account, it arises 2R_p(S_p, U_p)V_p + R_p(U_p, V_p)S_p = 0, which can be recast as 2R_p(S_p, U_p)V_p − R_p(U_p, S_p)V_p = 0, where we employed Equation (6) (with different names of the vectors). Using Equation (2) again, we can restate the obtained result as: 2R_p(S_p, U_p)V_p + R_p(S_p, U_p)V_p = 0. In other words R_p(S_p, U_p)V_p = 0 for all vectors S_p, U_p, V_p ∈ T_pM, so that R_p = 0 as wanted. This concludes the proof that (b) implies (a), in view of Lemma 2.1.

Let us finally demonstrate that (c) implies (a) by reducing to the proof of the implication (b) ⇒ (a). Fix p ∈ M and assume that (c) is valid. The following lemma holds, whose proof stays in the Appendix.

Lemma 2.3. If (M, g) is a spacetime, p ∈ M, let T_p ∈ T_p M\{0} and S_p ∈ T_p M\{0} be, respectively timelike and spacelike and with g(T_{p, Tp) = − g(Sp, Sp). Defining the null vectors N^± := Tp ± Sp, there are smooth congruences of geodesics ({γ^±s}s ∈ I^±}, J^±) as in (c) of Theorem 2.1, fulfilling T_γ^±s0(t0) = N^±_p, and S_γ^±s0(t0) = S_p, for some (s^±₀, t^±₀) ∈ I^± × J^±.

In view of the lemma and of Equation (5), one has that, for every p ∈ M, R_p(S_p, N^±_p)N^±_p = 0 for all N^±_p, S_p ∈ T_pM as in the hypotheses of the lemma. Consequently, if T_p and S_p, respectively timelike and spacelike, satisfies g(T_p, T_p) = − g(S_p, S_p), it holds:

$\begin{array}{l}R(S,T)T=R\left(S_p,N_p^{+}-S_p\right)\left(N_p^{+}-S_p\right)=-R_p\left(S_p,S_p\right)N_p^{+}\\ -R_p\left(S_p,N_p^{+}\right)S_p=-R_p\left(S_p,N_p^{+}\right)S_p,\end{array}$

where we have used Equation (2), and also

$\begin{array}{l}R(S,T)T=R\left(S_p,N_p^{-}+S_p\right)\left(N_p^{-}+S_p\right)=R_p\left(S_p,S_p\right)N_p^{-}\\ +R_p\left(S_p,N_p^{-}\right)S_p=R_p(S_p,N_p^{-})S_p.\end{array}$

Summing the two expressions found for R(S, T)T we have that, using Equation (2) again:

$\begin{array}{l}2R(S,T)T=R_p\left(S_p,N_p^{-}\right)S_p-R_p\left(S_p,N_p^{+}\right)S_p\\ =-2R_p\left(S_p,S_p\right)S_p=0.\end{array}$

We have found that R_p(S_p,T_p)T_p = 0 for all T_p, S_p ∈ T_pM, respectively timelike and spacelike, with g(T_p, S_p) = 0 (the requirement g(T_p, T_p) = − g_p(S_p, S_p) may be dropped in view of multi-linearity of R_p). Henceforth the proof goes on as in the proof of (b) ⇒ (a) given above.

        □

3. Summary

We have rigorously analyzed the popular statement “absence of gravitation ⇔ local flatness of the spacetime,” using a notion of gravitation based on the presence of geodesic deviation, measured along congruences of causal geodesics representing the stories of free falling bodies. Spacelike geodesics have not been considered since on a hand they have not dynamical meaning, on the other hand, they are not suitable for direct experimentation in general spacetimes. We have found that, in view of Theorem 2.1 the popular statement holds true. That theorem is interesting also disregarding the definition of relativistic gravitation we have adopted. Indeed it relates, through an if and only if clause, the curvature of a spacetime with purely dynamical properties of free falling bodies which, ideally, may be measured experimentally.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Footnotes

¹ ^A sketch of proof can be found in 2 for Levi-Civita connections.

References

1. Kobayashi S, Nomizu K. Foundations of Differential Geometry Vol. 1. New York: Interscience Publishers (1963).

2. Minsner CW, Thorne KS, Wheeler JA. Gravitation New York: Freeman (2003).

3. O'Neill B. Semi-Riemannian Geometry with Applications to Relativity New York: Academic Press (1983)

4. Silov GE. MatematiČeskij Analiz Vol.2, Moskow: Nauka (1979).

5. Wald RM. General Relativity Chicago: Chicago University Press (1984).

Appendix

Proof of Some Statements

Proof of Theorem2.1. If the connection coefficients vanish in the local chart (U_i,ψ_i), the curvature tensor vanishes therein as well. As 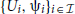is an atlas of M, the curvature tensor vanishes everywhere on M. The converse property is much less trivial to establish. We will exploit the well-known (4):

Frobenius Theorem for first order PDE. Consider the Cauchy problem for the field X: Ω → ℝⁿ,

$\begin{array}{cc}\text{Grad }X(x)=F(x,X(x)),X(p)=X_0& (8)\end{array}$

where F: Ω × ℝ^m → ℝ^m, Ω ⊂ ℝⁿ being an open subset, F is a C^s function with s fixed in {1, 2,…} ∪ {∞}, p ∈ Ω, and X₀ ∈ ℝ^m. A unique solution exists in a sufficiently small neighborhood of p, and it is of class C^{s + 1} (or C^∞ when s = ∞), provided the following conditions are fulfilled in Ω × ℝⁿ

$\begin{array}{cc}\begin{array}{l}\frac{\partial F_i^j}{\partial x^k}+{\displaystyle \sum _{r=1}^m\frac{\partial F_i^j}{\partial X^r}}{F}_k^r\left(x,X(x)\right)=\frac{\partial F_k^j}{\partial x^i}+{\displaystyle \sum _{r=1}^m\frac{\partial F_k^j}{\partial X^r}}{F}_i^r\left(x,X(x)\right),\\ i,k=1,2\dots ,n,j=1,2,\dots ,m.\end{array}& (9)\end{array}$

[The conditions (9) are obtained using Schwartz commuting second-order partial derivatives theorem for X and taking (8) into account.] Now consider a C² manifold M equipped with a C¹ torsionfree connection ∇. Fix a point p ∈ M and coordinate patch (Ω, ψ) about p, denoting by x ≡ (x¹, …, xⁿ) ∈ ℝ the values attained by ψ: Ω → ℝⁿ. From now on, with some obvious misuse of notation, we identify Ω with the corresponding open set in ℝⁿ in order to exploit Frobenius' theorem. We consider the Cauchy problem in Ω × ℝⁿ² for the composite vector field X ≡ (X₍₁₎,…, X_(n)), given by

$\nabla X_{(a)}=0,X_{(a)}(p)=V_{(a)},a=1,\dots ,n,$

where {V_a}_{a = 1,…, n} is a base of T_pM ≡ T_p ℝⁿ ≡ ℝⁿ. Making explicit the covariant derivatives ∇ in the left-hand side in terms of standard coordinate derivatives and connection coefficients (they are C¹ functions in our hypotheses), the system of equations takes the form (8) for the composite vector field X. Then, using the expression of the curvature tensor in coordinates, and reminding that the connection is torsionfree, one straightforwardly finds that the condition (9) is valid if the curvature tensor vanishes on Ω. Therefore the vector fields X_(a) exist in a neighborhood U' of p. These fields are obtained by parellely transporting the basis of fields V_(a) along any curve connecting p and q. Therefore they individuate a basis of T_qM at each q ∈ U'. Finally, we notice that, in a neighborhood U⊂ U' of p, there is a coordinate system ϕ with coordinates y¹, …, yⁿ such that $\frac{\partial }{\partial y^a}=X_{(a)}$ for a = 1, 2,…, n. This is because the distribution of the C² fields X₍₁₎, … X_(n) is integrable: as the connection is torsion free, [X_(a), X_(b)] = ∇_X(b) X_(a) − ∇_X(a) X_(b), and ∇X_(c) = 0 by hypotheses. The condition $0={\nabla }_{X_{(b)}}{X}_{(a)}={\nabla }_{\frac{\partial }{\partial y^b}}\frac{\partial }{\partial y^a}$ says that in the coordinate patch (U, ϕ) the connection coefficients of ∇ vanish. Varying p ∈ M, the associated charts (U, ϕ) define the wanted atlas.

        □

Proof of Lemma 2.2. Take two spacelike orthogonal vectors U_p, V_p ∈ T_pM such that they are also orthogonal with T_p and S_p and consider a normal coordinate system (3) $D\ni (x^0,x^1,x^2,x^3)\mapsto \exp \left(x^0{T}_p+x^1{S}_p+x^2{U}_p+x^3{V}_p\right)$. D ⊂ ℝ⁴ is a sufficiently small neighborhood of the origin of ℝⁿ. Since $\frac{\partial }{\partial x^0}{|}_p=T_p$ is timelike, the vectors $\frac{\partial }{\partial x^0}$ have to be timelike by continuity, restricting the domain D sufficiently about the origin. With this restriction, the embedded submanifold Σ through p, individuated by (x⁰, x¹, x², x³) ∈ D and x⁰ = 0, turns out to be timelike, x¹, x², x³ are coordinates on Σ and $\frac{\partial }{\partial x^0}{|}_{(0,x^1,x^2,x^3)}$ is the (timelike) normal vector at each point of Σ. Finally consider the system of normal coordinates t, s, s², s³ about Σ (3), individuated by $G\ni (t,s,s^2,s^3)\mapsto {\exp }_{q(s,s^2,s^3)}\left(t\frac{\partial }{\partial x^0}{|}_{q(s,s^2,s^3)}\right)$, where q(s, s², s³) in the right-hand side indicates the point on Σ with coordinates x¹ = s, x² = s², x³ = s³ and the exponential map is that in M. The open set G is a sufficiently small neighborhood of the origin of ℝ⁴ which, obviously, can always be taken of the form J × I × I × I, where I, J ⊂ ℝ are open intervals containing the origin of ℝ. The wanted smooth congruence of geodesics is ${\gamma }_s(t):={\exp }_{q(s,0,0)}\left(t\frac{\partial }{\partial x^0}{|}_{q(s,0,0)}\right)$. The vectors $S_{{\gamma }_s(t)}=\frac{\partial }{\partial s}$ and $T_{{\gamma }_s(t)}=\frac{\partial }{\partial t}$ are linearly independent and their commutator vanishes because they are tangent to a coordinate system. T_γs(t) is timelike, since it is the tangent vector to geodesics with timelike initial tangent vector $\frac{\partial }{\partial x^0}{|}_{(0,s,0,0)}$. As requested, it also trivially arises that T_γ0(0) = T_p and S_γ0(0) = S_p. As S_p is spacelike, $S_{{\gamma }_s(t)}=\frac{\partial }{\partial s}$ has to be spacelike everywhere by continuity (shrinking I and J if necessary).

        □

Proof of Lemma 2.3. Starting from T_p and S_p, construct the coordinates x⁰, x¹, x², x³ about the spacelike hypersufrace Σ, individuated by x⁰ = 0, exactly as in the proof of Lemma 2.2. Next, at each point q ∈ Σ, define the null vectors $N_{q(x^1,x^2,x^3)}^{\pm }:=\sqrt{\frac{g({\partial }_{x^1},{\partial }_{x^1})}{-g({\partial }_{x^0},{\partial }_{x^0})}}\frac{\partial }{\partial x^0}{|}_{q(x^1,x^2,x^3)}\pm \frac{\partial }{\partial x^1}$. Notice that those fields are well-defined and coincides to N^±_p if q = p. From now on we focus on the N⁺ case only, the other case being closely similar. Since N⁺ is nowhere tangent to Σ by construction, one may define a system of null-Riemannian coordinates t, s, s², s³ about Σ (3), individuated by the expression $G\ni (t,s,s^2,s^3)\mapsto {\exp }_{q(s,s^2,s^3)}\left(t{N}_{q(s,s^2,s^3)}^{+}\right)$, where q(s, s², s³) in the right-hand side indicates the point on Σ with coordinates x¹ = s, x² = s², x³ = s³ and the exponential map is that in M. The open set G is a sufficiently small neighborhood of the origin of ℝ⁴ which, obviously, can always be taken of the form J⁺ × I⁺ × I⁺ × I⁺, where I⁺, J⁺ ⊂ ℝ are open intervals containing the origin of ℝ. The wanted smooth congruence of geodesics is γ⁺_s(t) := exp_{q(s, 0, 0)} (t N⁺_{q(s, 0, 0)}). The vectors $S_{{\gamma }_s^{+}(t)}=\frac{\partial }{\partial s}$ and $T_{{\gamma }_s^{+}(t)}=\frac{\partial }{\partial t}$ are linearly independent and their commutator vanishes because they are tangent to a coordinate system. T_γ⁺s(t) is null, since it is the tangent vector to geodesics with null initial tangent vector N⁺_{(0, s, 0, 0)}. As requested, it also trivially arises that T_γ⁺0(0) = N⁺_p and S_γ⁺0(0) = S_p. As S_p is spacelike, by continuity (shrinking I⁺ and J⁺ if necessary), $S_{{\gamma }_s(t)}=\frac{\partial }{\partial s}$ has to be spacelike everywhere it is defined.

        □