- 1Key Laboratory for the Physics and Chemistry of Nanodevices, Department of Electronics, Peking University, Beijing, China
- 2Department of Engineering Mechanics, Institute of High Performance Computing, A*Star, Singapore, Singapore
Graphene and Graphene nanoribbons (GNRs) are found to have superior high thermal conductivity favorable for high-performance heat dissipation. In this letter, by using molecular dynamics simulations, we show that constructing specific structure can further enhance high thermal conduction of GNRs. By introducing a small gap at the center, the average heat flux (thermal conductivity) can be enhanced by up to 23% the corresponding increase in total heat current is 16%. This unusual thermal conduction enhancement is achieved by an intriguing physical mechanism of suppress phonon-phonon scattering. Our findings uncover new mechanism to increase thermal conduction of GNRs.
Graphene (1, 2) is a single-atom-thick two-dimensional material, which has attracted immense interests in recent years because of its extensive fascinating properties. The ultra-high thermal conductivity of graphene (3–5) has raised the exciting prospect of using them for phononics devices (6–9). Moreover, rapidly increasing power density in electronic devices made efficient heat removal a crucial issue for progress in information technology. In addition to electronic and photonic devices, thermal management is also required for energy devices, such as solar cells. The increasing interest to the thermal conductivity of graphene was driven by the application for heat dissipation. It is a strong motivation to study thermal property of graphene and graphene nanoribbons (GNRs) from the viewpoints of fundamental physics and practical application.
Room temperature thermal conductivity of suspended single-layer graphene (SLG) exfoliated from highly oriented pyrolytic graphite was measured to reach a high value of 4800–5300 W/m-K [10]. This high thermal conductivity was confirmed in both exfoliated and chemical vapor deposition grown graphenes (11–13). However, thermal conductivity in fully supported graphene is much lower. The room temperature thermal conductivity of SLG supported on silicon dioxide substrate revealed a value about 600 W/m-K, which may be due to backside scatterings and the flexural phonons leakage into the substrate (14). Wang et al. measured thermal conductance of both suspended and supported few-layer graphene (FLG) by using typical thermal-bridge configuration, and the impacts of sample size and substrate have been reported (15).
There are rich physical phenomena about thermal property of GNRs. The presence of a substrate (16–18) and layer-layer interaction (19, 20) can lower the thermal conductivity, which was attributed to the graphene-substrate and interlayer coupling. Moreover, the effects of edge, roughness, strain, random defect and hydrogen termination have been investigated by different simulation methods (21–28). For instance, with only 10% isotopic doping, the thermal conductivity of GNR is reduced up to 50% (24). With 20% hydrogen coverage, thermal conductivity is only about 30% of that of pristine GNR (25). Moreover, compare to the random doped GNR, much stronger dependence of the thermal conductivity on the isotope concentration for the superlattice structures was observed, with 30% reduction in the thermal conductivity at 50% of the isotope concentration (26). Obviously, almost all of these impacts reduce the thermal conductivity of graphene. As the high thermal conductivity is one of the main advantages of graphene for thermal management device, all the above factors are “negative” impacts. A natural question immediately arises: can we enhance the extremely high thermal conductivity of GNR further? Obviously, exploring approach to enhance thermal conduction of GNR is of both fundamental significance and technological interest.
Moreover, in existing theoretical studies, thermal conductivity of GNR is calculated from the Fourier's law: J = −κ∇T, where J is defined as the heat energy transported along the GNR in unit time through unit cross sectional area, and ∇T is the temperature gradient. Although thermal conductivity of GNRs has been studied theoretically, only average heat flux is used in the calculation. So far it is not clear does heat flux distribute uniformly in the cross section plane of GNR? And on the cross section, which section is with higher capability for heat transfer? Here heat current is the rate of heat energy transfer through a given surface, the SI unit is watt [W]. Heat flux is the heat current per unit area, the SI unit is [W/m2]. In this letter, we will investigate numerically the position dependent local heat flux distribution in cross section plane of perfect GNRs. Then we propose to enhance the ultra-high thermal conduction of GNR by introducing a small gap at the center, i.e., construct a “comb” GNR structure. Our numerical results demonstrate that 0.48 nm gap in cross sectional area can induce 23% increase of average heat flux at room temperature. The surprising thermal conduction enhancement we discovered can be understood from the analysis of phonon scattering mechanism. Our study extends the understanding of heat transport characteristic in GNRs, and may inspire experimentalists to develop new approach to enhance thermal conduction of graphene ribbons.
In our simulations, classical molecular dynamics (MD) method is adopted, by using the LAMMPS simulation package. (29) The advantage of the MD method is that it does not rely on any thermodynamic-limit assumptions and is thus applicable for the study of realistic nanoscale systems. The carbon-carbon interactions are described by using adaptive intermolecular reactive empirical bond order (AIREBO) potential (30), which depends not only on the distance between atoms, but also on the bounding environment around atoms, so they implicitly contain many-body information. The accuracy of this potential has been demonstrated in MD simulations in many carbon-based systems, such as carbon nanotubes and graphene for studying thermal as well as mechanical properties. (25) Figure 1 shows the structure of the armchair graphene nanoribbon used in this work. The length is 9.9 nm and width various from 0.97 to 7.3 nm. Following the conventional notation (21), N-GNR denotes a GNR with N carbon-dimer lines across the ribbon width. Before non-equilibrium MD simulation, the canonical ensemble MD simulation with Nosé–Hoover heat bath (31, 32) first runs for 107 steps to equilibrate the whole system at room temperature. After structure relaxation, fixed boundary condition is used at the two ends of the length (x) direction (Figure 1). Next to the fixed boundary, Nosé–Hoover heat baths with different temperature are applied to the two ends of x direction to establish a temperature gradient along the longitudinal direction. At each end, 4-layers of Nosé–Hoover heat bath are used to avoid any artificial effect induced by the localized edge modes. (33) Free boundary condition is used in the width (y) direction and out-of-plane (z) direction. The equations of motion for the atom i in heat baths are:
Here the subscript i runs over all the atoms in the thermostat, mi and are the mass and momentum of the i-th atom, is the total force acting on the i-th atom, Nis the total number of degrees of freedom of the atoms in the thermostat, kB is the Boltzmann constant, γ and τ are the dynamic parameter and relaxation time of the thermostat. Tis the desired temperature of the thermostats. Ti(t) is the instant temperature of atom i calculated from the kinetic energy , where αdenotes Cartesian coordinate and vα (t) is the time-dependent velocity. Due to the high Debye temperature in graphene, quantum correction is applied to MD calculated temperature (19). The velocity Verlet algorithm is used to integrate the differential equations of motion. The non-equilibrium MD simulations are performed long enough (108 time steps, time step is 0.5 fs) to allow the system to reach the non-equilibrium steady state where the temperature gradient is well established and the heat current passing through the system is time independent.
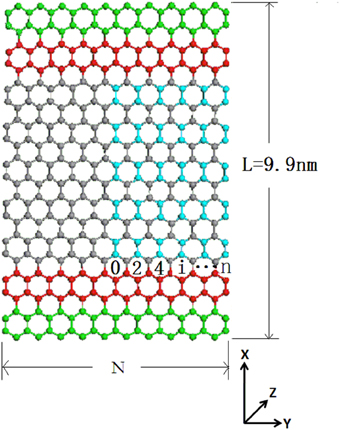
Figure 1. Schematic picture of the graphene nanoribbon. The last layers of atoms at the two ends (in green) are fixed, and the atoms (in red) next to the fixed layers are placed in thermostats. Here “0” line corresponds to the central dimer of GNR, and “n” line is the edge dimer, with N = 2 × n + 1.
To explore the spacial distribution of local heat flux, we refer to the different atom lines in the GNR width direction as I = 0, 1 … n lines, with N = 2 × n + 1. Here “0” line corresponds to the central dimer of GNR, and “n” line is the edge dimer. Figure 2 shows the local heat flux distribution along the cross section of 21-GNR. Using the local heat flux along the center of GNR (line 0) as reference, we show the normalized local heat flux here. It is interesting the local heat flux along the center of GNR is obviously larger than those close to the GNR boundary. For local heat flux at the boundary, it is only about 35% of that at the center. This demonstrates heat flux distribution across GNR cross section is not uniform. In non-equilibrium steady state, the temperature in the same layer (atoms in the same layer means they have the same x coordinate) is the same, so different dimer line is with the same temperature gradient. Thus in GNR, the thermal transport capability of the boundary atoms is much lower than those at the centers. This can be understood from the energy distribution of phonon localized modes. It has been shown that in GNR (34), the intensity of localized modes is almost zero in the center, while with finite value at the boundary. Compared with two-dimensional sheet, there are edge scattering-induced localized phonon modes in the low frequency region in nanoribbons. The edge-localized phonons are responsible for the simulation results that the local heat flux along the center of GNR is larger than those close to the boundary.
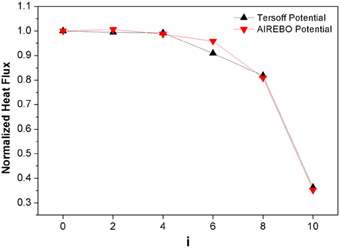
Figure 2. Local heat flux distribution in the cross section of 21-GNR. The local heat flux along the center of GNR is used as reference.
This position dependent local heat flux also provides idea in manipulating thermal conduction by other factors, such as random doping. Thermal conduction is obviously less sensitive to edge doping than doping at the center, simply because the local heat flux at the edge is much lower than that at the center. To control thermal conduction, phononic engineering at the center of GNR is more efficient.
To avoid artifact caused by different empirical potential used, we also calculated the heat flux distribution with Tersoff potential (35). As shown in Figure 2, the results by Tersoff potential coincide with those by AIREBO potential indicating that our results are independent of the empirical potential used. In the next, all the results are calculated by using AIREBO potential.
Next we increase the width of the GNR, change N from 9 to 61. As shown in Figure 3A, for all the width range, the local heat flux in the GNR is confined to the central region. Thus the observed spacial dependent local heat flux is a general characteristic in GNRs. Figure 3B shows the ratio of the edge heat flux to the average heat flux decreases with the GNR width. With width increases, the phonon boundary scattering is suppressed, leads to increases in average heat flux across the GNR. Thus compare to the average heat flux, the contribution from edge to total heat flux decreases.
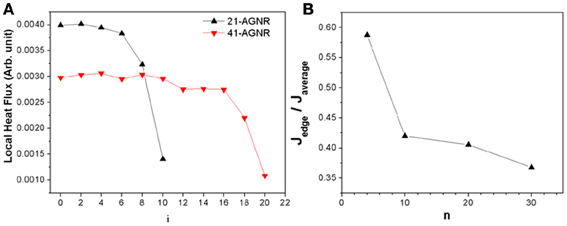
Figure 3. (A) Local heat flux distribution in 21-GNR and 41-GNR, respectively. (B) The ratio of the edge heat flux to the average heat flux for different GNR width.
Furthermore, it is interesting to observe the central heat flux decreases with GNR width. With the increase of width, more and more phonons are excited, which results in the increase of thermal conductivity. Moreover, when the width increases, thermal conductivity increases as a consequence of suppressed phonon scattering at edge. On the other hand, the increase of phonon modes will also increase phonon-phonon scattering that in turn will increase the thermal resistance, thus suppress the energy transport. The thermal conduction is determined by these effects that compete with each other. In narrow GNR, the central atoms are distanced from the edge, and the less phonon-phonon scattering leads to the higher central local heat flux than that in wide GNRs.
Due to the high local heat flux at center, it is interesting to find the total heat current in 21-GNR is 0.07 (in arb. unit), which is higher than half of total heat current (0.11) in 41-GNR. It is obvious that the total heat current in two 21-GNRs is larger than that of one 41-GNR, although they have the similar entire width. The total heat current in two 21-GNRs is about 27% higher than that in one 41-GNR. The enhancement of total heat current by a factor of 27% can promote performance as heat dissipation devices. As in steady state, different dimer line is with the same temperature gradient, the enhancement in total heat current corresponds to increase in thermal conductivity. This provides an idea to enhance the thermal conduction of GNRs. For a GNR consists two narrow branches, its total heat current is hoped to be higher than that in a whole GNR with the same entire width. This idea is verified in 21-GNR and 41-GNR. Inspired by this characteristic, next we explore how to increase total heat current (thermal conduction) of GNR by constructing some spectral structures.
To directly confirm the above mechanism to increase heat current, we “cut” a whole GNR by introducing a small gap at the center, i.e., construct a “comb” GNR structure. A typical comb GNR and the corresponding perfect GNR are shown in Figure 4. A 0.48 nm gap is used to eliminate the interaction between these two branches. The length of the whole GNR is 20 nm, and its width changes from 4.3 to 9.2 nm. The width of each branch in the comb GNR is W', with W = 2 × W' + Δ. Then the heat current in comb GNR is compared with that in whole GNR. Here we introduce the thermal enhancement ratio R to describe quantitatively the heat flux enhancement efficiency, , where J0 is the average heat flux in the original GNR, and J is the average heat flux in the comb GNR.
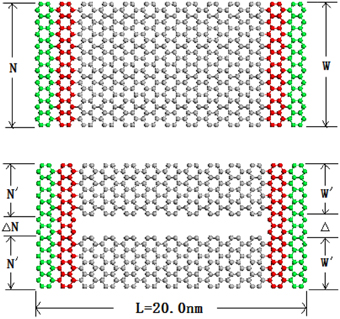
Figure 4. Schematic picture of the whole GNR and “comb” GNR. The last layers of atoms at the two ends (in green) are fixed, and the atoms (in red) next to the fixed layers are placed in thermostats. The width of each branch in the comb GNR is W', with W = 2 × W' + Δ.
As shown in Figure 5, there is obvious enhancement in average heat flux by introducing a small gap at the center of GNR. For comb GNR, the enhancement in average heat flux is due to less phonon-phonon scattering. On the other hand, the small gap will also increase phonon-boundary scattering that in turn will increase the thermal resistance, thus suppress the energy transport. The thermal conduction is determined by these effects that compete with each other. In narrow GNR branch, boundary scattering is the dominant process to limit thermal conduction. At wide range phonon-phonon scattering is the limiting mechanism. As a result, we conclude that the average heat flux enhancement arise primarily due to the phonon-phonon scattering in the narrow GNR is less than the effect in the wide ones. Moreover, this enhancement ratio depends on GNR width remarkably. We change the width of GNR and find the enhancement ratio reaches maximum when width W = 6.3 nm. For the comb GNR, with width increases, more phonons are excited in each branch, and the strong phonon-phonon scattering leads to weaken the enhancement ratio. On the other side, with width decreases, the impact of edge scattering increases, and also decreases the enhancement ratio. Thus there is an optimal width to maximize this enhancement effect. For a GNR with width of 6.3 nm, a 0.48 nm wide gap can enhance its average heat flux of 23%. As the temperature difference of the comb GNR is the same as that in the original GNR, it is reasonable to predict corresponding 23% enhancement in the thermal conductivity. One should note here that comb GNR has a smaller cross sectional area than the original GNR does, therefore the increase in total heat current (heat flux times cross sectional area) is about 16%. Recently, several experiments (36, 37) report the possibilities of cutting GNRs with controlled edge structures. Thus the comb GNR structure proposed in our work can be realized experimentally.
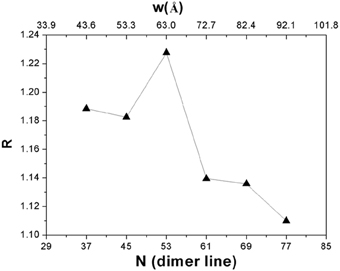
Figure 5. The average heat flux enhancement ratio vs. GNR width. There is an optimal width to maximize this enhancement effect.
In summary, for the first time, we have demonstrated that Graphene nanoribbons with small gap at the center are promising high thermal conductivity materials. The proposed “comb” structure can increase average heat flux of GNR and the optimal GNR structure parameters are discussed. For GNR with width of 6.3 nm, a 0.48 nm-wide gap in the center can enhance the average heat flux (thermal conductivity) up to 23% at room temperature, and the corresponding increase in total heat current is 16%. The reported impacts can be well understood from the analysis of phonon edge scattering. Furthermore, we have also studied the spacial distribution of local heat flux in the cross section of GNR. Due to the edge scattering, the local heat flux at the edge is only 35% of that at the center of GNR. The ultra-high thermal conductivity of suspended graphene has raised the exciting prospect that the high efficiency heat dissipation device can be realized with graphene. Combined with the availability of experimental fabrication technology, our results shed light on heat conduction enhancement in graphene nanoribbons and may favor graphene applications in thermal management.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is supported by National Natural Science Foundation of China (Grant No. 11274011), the Ministry of Education of China (Grant No. 20110001120133), the Ministry of Science and Technology of China (Grant No. 2011CB933001).
References
1. Novoselov KS, Geim AK, Morozov SV, Jiang D, Zhang Y, Dubonos SV, et al. Electric field effect in atomically thin carbon films. Science (2004) 306:666–669. doi: 10.1126/science.1102896
2. Zhang Y, Tan YW, Stormer HL, Kim P. Experimental observation of the quantum Hall effect and Berry's phase in graphene. Nature (2005) 438:201–204. doi: 10.1038/nature04235
3. Balandin AA. Thermal properties of graphene and nanostructured carbon materials. Nat Mater. (2011) 10:569–581. doi: 10.1038/nmat3064
4. Shahil KMF, Balandin AA. Thermal properties of graphene and multilayer graphene: applications in thermal interface materials. Solid State Commun. (2012) 152:1331–1340. doi: 10.1016/j.ssc.2012.04.034
5. Zhang G, Li B. Impacts of doping on thermal and thermoelectric properties of nano materials. Nanoscale (2010) 2:1058–1068. doi: 10.1039/c0nr00095g
6. Li N, Ren J, Wang L, Zhang G, Hänggi P, Li B. Colloquium: phononics: manipulating heat flow with electronic analogs and beyond. Rev Mod Phys. (2012) 84:1045–1066. doi: 10.1103/RevModPhys.84.1045
7. Yang N, Zhang G, Li B. Thermal rectification in asymmetric graphene ribbons. Appl Phys Lett. (2009) 95:033107. doi: 10.1063/1.3183587
8. Hu J, Ruan X, Chen YP. Thermal conductivity and thermal rectification in graphene nanoribbons: a molecular dynamics study. Nano Lett. (2009) 9:2730–2735. doi: 10.1021/nl901231s
9. Tian H, Xie D, Yang Y, Ren TL, Zhang G, Wang YF, et al. A novel solid-state thermal rectifier based on reduced graphene oxide. Sci Rep. (2012) 2:523. doi: 10.1038/srep00523
10. Balandin AA, Ghosh S, Bao W, Calizo I, Teweldebrhan D, Miao F, et al. Superior thermal conductivity of single-layer graphene. Nano Lett. (2008) 8:902–907. doi: 10.1021/nl0731872
11. Cai W, Moore AL, Zhu Y, Li X, Chen S, Shi L, et al. Thermal transport in suspended and supported monolayer graphene grown by chemical vapor deposition. Nano Lett. (2010) 10:1645–1651. doi: 10.1021/nl9041966
12. Lee JU, Yoon D, Kim H, Lee SW, Cheong H. Thermal conductivity of suspended pristine graphene measured by Raman spectroscopy. Phys Rev B (2011) 83:081419. doi: 10.1103/PhysRevB.83.081419
13. Ghosh S, Bao W, Nika DL, Subrina S, Pokatilov EP, Lau CN, et al. Dimensional crossover of thermal transport in few-layer graphene. Nat Mater. (2010) 9:555–558. doi: 10.1038/nmat2753
14. Seol JH, Jo I, Moore AL, Lindsay L, Aitken ZH, Pettes MT, et al. Two-dimensional phonon transport in supported graphene. Science (2010) 328:213–216. doi: 10.1126/science.1184014
15. Wang Z, Xie R, Bui C, Liu D, Ni X, Li B, et al. Thermal transport in suspended and supported few-layer graphene. Nano Lett. (2011) 11:113–118. doi: 10.1021/nl102923q
16. Guo ZX, Zhang D, Gong XG. Manipulating thermal conductivity through substrate coupling. Phys Rev B (2011) 84:075470. doi: 10.1103/PhysRevB.84.075470
17. Ong Z, Pop, E. Effect of substrate modes on thermal transport in supported graphene. Phys Rev B (2011) 84:075471. doi: 10.1103/PhysRevB.84.075471
18. Cao HY, Guo ZX, Xiang H, Gong XG. Layer and size dependence of thermal conductivity in multilayer graphene nanoribbons. Phys. Lett. A (2012) 376:525–528. doi: 10.1016/j.physleta.2011.11.016
19. Zhang G, Zhang H. Thermal conduction and rectification in few-layer graphene y junctions. Nanoscale (2011) 3:4604–4607. doi: 10.1039/c1nr10945f
20. Yang N, Ni X, Jiang JW, Li B. How does folding modulate thermal conductivity of graphene? Appl Phys Lett. (2012) 100:093107. doi: 10.1063/1.3690871
21. Xu Y, Chen X, Gu BL, Duan W. Intrinsic anisotropy of thermal conductance in graphene nanoribbons. Appl. Phys Lett. (2009) 95:233116. doi: 10.1063/1.3272678
22. Evans WJ, Hu L, Keblinski, P. Thermal conductivity of graphene ribbons from equilibrium molecular dynamics: effect of ribbon width, edge roughness, and hydrogen termination. Appl Phys Lett. (2010) 96:203112. doi: 10.1063/1.3435465
23. Wang Y, Chen S, Ruan X. Tunable thermal rectification in graphene nanoribbons through defect engineering: a molecular dynamics study. Appl Phys Lett. (2012) 100:163101. doi: 10.1063/1.3703756
24. Jiang JW, Lan J, Wang JS, Li, B. Isotopic effects on the thermal conductivity of graphene nanoribbons: localization mechanism. J Appl Phys. (2010) 107:054314. doi: 10.1063/1.3329541
25. Pei QX, Sha ZD, Zhang YW. A theoretical analysis of the thermal conductivity of hydrogenated graphene. Carbon (2011) 49:4752–4759. doi: 10.1016/j.carbon.2011.06.083
26. Hu J, Schiffli S, Vallabhaneni A, Ruan X, Chen YP. Tuning the thermal conductivity of graphene nanoribbons by edge passivation and isotope engineering: a molecular dynamics study. Appl Phys Lett. (2010) 97:133107. doi: 10.1063/1.3491267
27. Wei N, Xu LQ, Wang HQ, Zheng JC. Strain engineering of thermal conductivity in graphene sheets and nanoribbons: a demonstration of magic flexibility. Nanotechnology (2011) 22:105705. doi: 10.1088/0957-4484/22/10/105705
28. Xie ZX, Tang LM, Pan CN, Li KM, Chen KQ, Duan W. Enhancement of thermoelectric properties in graphene nanoribbons modulated with stub structures. Appl Phys Lett. (2012) 100:073105. doi: 10.1063/1.3685694
29. Plimpton SJ. Fast parallel algorithms for short-range molecular dynamics. J Comp Phys. (1995) 117:1–19. doi: 10.1006/jcph.1995.1039
30. Stuart SJ, Tutein AB, Harrison JA. A reactive potential for hydrocarbons with intermolecular interactions. J Chem Phys. (2000) 112:6472. doi: 10.1063/1.481208
31. Nosé SJ. A unified formulation of the constant temperature molecular dynamics methods. Chem J Phys. (1984) 81:511. doi: 10.1063/1.447334
32. Hoover WG. Canonical dynamics: equilibrium phase-space distributions. Phys Rev A (1985) 31:1695. doi: 10.1103/PhysRevA.31.1695
33. Chen J, Zhang G, Li B. Molecular dynamics simulations of heat conduction in nanostructures: effect of heat bath. J Phys Soc Jpn. (2010) 79:074604. doi: 10.1143/JPSJ.79.074604
34. Ni X, Zhang G, Li B. Rectifying heat flux through unzipped carbon nanotubes. J Phys Condens Matter (2011) 23:215301. doi: 10.1088/0953-8984/23/21/215301
35. Tersoff J. Modeling solid-state chemistry: interatomic potentials for multicomponent systems. Phys Rev B (1989) 39:5566. doi: 10.1103/PhysRevB.39.5566
36. Jiao L, Zhang L, Wang X, Diankov G, Dai H. Narrow graphene nanoribbons from carbon nanotubes. Nature (2009) 458:877–880. doi: 10.1038/nature07919
Keywords: thermal conductivity, graphene, molecular dynamics simulation, heat flux, nanoribbon
Citation: Li X and Zhang G (2013) Enhancing the extremely high thermal conduction of graphene nanoribbons. Front. Physics 1:19. doi: 10.3389/fphy.2013.00019
Received: 19 August 2013; Paper pending published: 10 September 2013;
Accepted: 24 September 2013; Published online: 31 October 2013.
Edited by:
Nicholas X. Fang, Massachusetts Institute of Technology, USAReviewed by:
Rui-Qin Zhang, City University of Hong Kong, ChinaRenkun Chen, University of California, San Diego, USA
Copyright © 2013 Li and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gang Zhang, Department of Engineering Mechanics, Institute of High Performance Computing, 1 Fusionopolis Way, #16-16 Connexis North, Singapore 138632, Singapore e-mail:emhhbmdnQGlocGMuYS1zdGFyLmVkdS5zZw==
 Xiuqaing Li1
Xiuqaing Li1 Gang Zhang
Gang Zhang