- Center for Biomedical Computing, Simula Research Laboratory and Center for Cardiological Innovation, Oslo University Hospital, Oslo, Norway
Over the past half century, there has been intense and fruitful interaction between experimental and computational investigations of cardiac function. This has led, for example, to more profound understanding of cardiac excitation-contraction coupling; how it works, as well as how it fails. However, many lines of inquiry remain unresolved, among them the initiation of each heartbeat. The sinoatrial node, a cluster of specialized pacemaking cells in the right atrium of the heart, spontaneously generates an electro-chemical wave that spreads through the atria and the cardiac conduction system to the ventricles, initiating the contraction of cardiac muscle essential for pumping blood to the body. Despite the fundamental importance of this primary pacemaker, this process is still not fully understood, and ionic mechanisms underlying cardiac pacemaking function are currently under heated debate. Several mathematical models of sinoatrial node cell membrane electrophysiology have been constructed as based on different experimental data sets and hypotheses. As could be expected, these differing models offer diverse predictions about cardiac pacemaking activities. This paper aims to present the current state of debate over the origins of the pacemaking function of the sinoatrial node. Here, we will specifically review the state-of-the-art of cardiac pacemaker modeling, with a special emphasis on current discrepancies, limitations, and future challenges.
1. Introduction
Complex biological systems rely on numerous yet well-coordinated interactions at various scales to achieve proper physiological function (1). In the heart, for example, complex signaling pathways regulate chemical processes within the cytosol, cardiac ion channels mediate membrane fluxes, and nexus junctions between cardiac myocytes allow the tissue to function as a syncytium. Although governing principles describing e.g., kinetics for each component may be considered relatively simple, the dynamics of the ensemble is anything but. The processes involved are highly non-linear and may be almost impossible to dissect without the aid of mathematical modeling and computer simulations (2). Current cardiac models range from subcellular structures to the entire organ and from aforementioned ion channels to signaling pathways (a variety of spatial scales), from Purkinje cells to ventricular myocytes (a variety of subtypes of cardiac cells), and from rat to human (a variety of species) (3). The interactions between these diverse models and associated experimental measurements have greatly advanced our basic understanding of cardiac physiology and pathophysiology.
Yet after decades of modeling and experimental studies, one of the most important questions in cardiac physiology remains unanswered: what keeps the heart ticking (4)? The sinoatrial node, a cluster of specialised pacemaking cells in the right atrium of the heart, spontaneously generates an electro-chemical wave known as the action potential (AP). The AP spreads throughout the atria and the cardiac conduction system to the ventricles, initiating the contraction of cardiac muscle essential for pumping blood to the body. The underlying mechanism of this cardiac spontaneous pacemaking activity (known as automaticity) has been under heated debate, with seemingly exclusive hypotheses proposed by different groups (5). Following this debate, a number of mathematical models of cardiac pacemaker cells have been developed (3, 6). These models are based on different experimental data, different hypotheses, and, not surprisingly, they result in diverse predictions about cardiac pacemaker activity (7). A single model or hypothesis has, thus far, been unable to provide convincing explanations which address all experimental findings.
Here, we will review the state-of-the-art of mathematical models of cardiac pacemaking function, with a special emphasis on current discrepancies, limitations and future challenges. It is hoped that this review will allow readers a quick grasp of the core of the debate, and potentially attract a greater number of researchers with interdisciplinary backgrounds to tackle present challenges.
2. Models of Cardiac Pacemaking Cells
In the healthy human heart, the sinoatrial node (SAN) is the primary pacemaker which spontaneously generates APs to initiate each heartbeat. The location and size of SAN vary among different species; in human, the SAN is typically located both laterally and inferior to the terminal crest (crista terminalis), and has been found to take the form of a cigar, with an estimated length of 20 mm and width of 5 mm (8, 9). Morphologies of isolated SAN cells can be either elongated and spindle-shaped (about 150 μm long) or spider-shaped (about 50 μm long) (10). These cells are electrically coupled via gap junctions; the spatial distribution of gap junctions in the SAN is sparse as compared to other cardiac tissues. This leads to relatively weak intercellular coupling and slow, non-uniform conduction through the SAN (11). Cardiac pacemaking is robust, however: in the case of SAN failure, secondary [atrioventricular node (AVN)] and tertiary (Purkinje fiber network) pacemakers will ensure repetitive ventricular contractions (see Figure 1) (12). All pacemaker tissues share certain cellular characteristics which distinguish them from non-pacemaking cardiac myocytes; e.g., pacemaking cells lack a T-tubular system (13) and share similar tissue-specific expression levels of various ion channels (14, 15). It is likely that they share also share similar underlying pacemaking mechanisms.
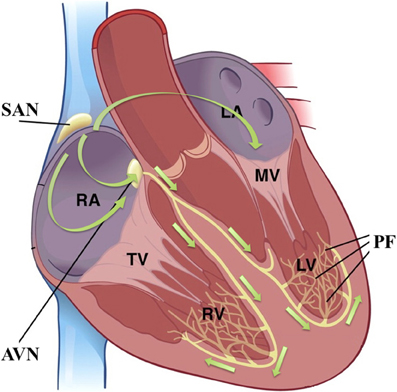
Figure 1. The cardiac conduction system and the cascade of cardiac pacemaking tissues; figure modified from (17). Green arrows indicate the cardiac activation sequence during sinus rhythm. SAN, sinoatrial node; AVN, atrioventricular node; PF, Purkinje fibre; RA, right atrium; LA, left atrium; RV, right ventricle; LV, left ventricle; TV, tricuspid valve; MV, mitral valve.
Many models of cardiac pacemaking cells have been developed since the 1960s. A recent publication noted twenty-one such mathematical models of pacemaking cells, including nine Purkinje cell models, eleven SAN cell models and an AVN cell model (3). All mathematical models of cardiac cellular electrophysiology are based, at least in part, on the seminal electrophysiological work of Hodgkin and Huxley in the giant squid axon (16), which quantified the ionic mechanisms underlying the neuronal AP. Based on their work, the cellular AP can be conceptualized as a momentary, active change in the transmembrane electrical potential (the difference between intracellular and extracellular electrical potentials) of an excitable membrane that occurs when it is stimulated. In short, an AP relies on a “depolarization” phase, classically mediated by inward sodium current, wherein the membrane is positively polarized with respect to its resting state, followed by “repolarization,” wherein outward potassium current(s) return the membrane to rest. A cardiac pacemaking cell additionally experiences a “diastolic depolarization” (DD) phase, wherein the transmembrane potential becomes progressively depolarized through time in the absence of stimulus, eventually triggering an AP; see Figure 2B. For an automatic, pacemaking cell (and indeed any cardiac cell), these processes can be modeled via an electrical circuit, where the membrane is represented as a capacitance, and the voltage-gated channels permitting the passage of ions through this membrane are represented as electrical conductances.
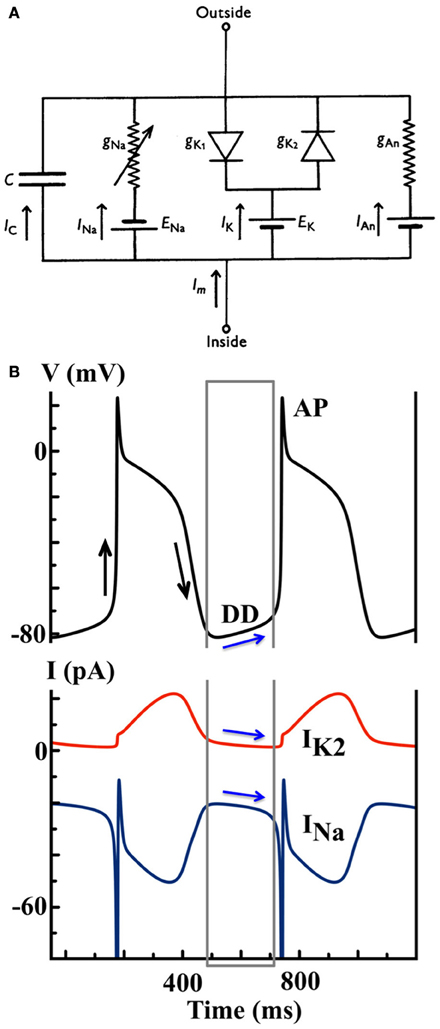
Figure 2. (A) Model schematic of the Noble 1962 model, where the Purkinje cell membrane is represented as an electrical circuit [Figure modified from (18)]. (B) Simulated AP and ion currents using the Noble 1962 Purkinje cell model to illustrate the IK2 “decay” hypothesis. Black arrows indicate the depolarization and repolarization phases during an AP. Blue arrows indicate the shift between inward and outward current balance during the DD that finally triggers a spontaneous AP.
Instead of providing complete review of the many extant pacemaker cell models, we will instead categorize these based on their implied pacemaking hypotheses. For each mechanistic hypothesis, we will present and comment on the most representative mathematical models.
2.1. The Ik2-Based Models
The first cardiac cell model to describe a Purkinje cell AP and its automaticity was developed by Noble in 1962 (18). Following Hodgkin-Huxley formalism, the cell is represented as an electrical circuit, where the membrane is represented as a capacitance, and voltage-gated ion channels are represented as electrical conductances (Figure 2A):
Here Cm is the membrane capacitance, Vm is the transmembrane potential, and three types of ionic currents are considered: a Na+ current (INa), a K+ current (IK) and a non-specific leak (IL) current. More specifically,
where m and h are the activation and inactivation gates respectively, and
Furthermore,
where n is the activation gate, and
Functionally, INa is a fast inward current mediated by Na+ ions responsible for membrane depolarization, IK1 is the inward rectifier K+ current that repolarizes the transmembrane potential to its resting state, and IK2 is the K+-mediated pacemaker current. The so-called “decay” hypothesis of pacemaking, as mediated by IK2, surmises that, during DD, the outward IK2 gradually decays and “unmasks” inward sodium current, INa, to trigger a spontaneous AP (as shown in Figure 2B). The membrane will repolarize following the elicited AP via the outward IK2 current, and so on. This cyclical activity is an oscillator known as the “membrane oscillator,” as it describes cycles in the transmembrane potential, or simply as the membrane “clock” (M-clock).
In 1975, McAllister, Noble and Tsien constructed an updated model of a cardiac Purkinje cell (the MNT model) based on newly available experimental data (19), and reformulated the pacemaker current IK2 as:
Here, is the maximum IK2 current, and s is the activation gate of IK2. This reformulation was based on a number of experimental studies that further characterized IK2. For instance, the newer data revealed that the role of IK2 during the AP plateau had been overestimated, so an additional current Ix was introduced to represent the additional small contribution to the AP plateau from ions other than K+. The kinetics of IK2 were also found to have certain resemblance to those of IK1, i.e., inward rectification following instantaneous changes in potential. In addition, for any particular potential, it was suggested that IK2 was directly proportional to a first-order variable (see Equation 5), instead of a fourth-order variable as in the Noble 1962 model (see Equation (4)) (20).
For over a decade, until the late 1970s, the IK2 “decay” hypothesis was the basis for modeling cardiac pacemaking activities. It was supported by an array of experimental and theoretical papers; e.g., evidence suggesting that the catecholaminergic regulation of IK2 could lead to the acceleration of the pacing rate induced by sympathetic stimulation (21).
2.2. If-Based Hypothesis and Models
In 1979, Brown et al. reported a novel current and its involvement in the generation and catecholamine-induced acceleration of SAN pacemaking activities (22). Know as the “funny” current, If, it is considered so in a number of ways: (1) it has a mixed Na+-K+ current; (2) it activates on hyperpolarization, or negative deflection from the resting membrane potential (most voltage-gated channels activate upon depolarization); (3) it has a very slow kinetics. All these properties are well-suited for If to function as a pacemaker current; however, they share no similarities with the properties of IK2. While IK2 is an outward current activated on depolarization, If is an inward current activated on hyperpolarization. The community considered the simultaneous evolution of two distinct yet mechanistically opposed pacemaking functions in the heart quite unlikely. Thus, the discovery of If in SAN cells led to a series of experimental and modeling studies aimed at radical reinterpretation of IK2 (23). It was confirmed that, although IK2 has a reversal potential near the expected K+ equilibrium potential, it is, in fact, not a pure K+ current. With the application of Ba2+, a K+ current blocker, IK2 was converted into an inward, hyperpolarization-activated current with a mixed Na+ and K+ permeability, similar to that of If (24).
In 1985, DiFrancesco and Noble published an updated Purkinje cell model (the DN model) based on these new findings about If and the new interpretation of IK2 as the primary mechanism underlying the M-clock (25). An activation gate, y, for If was introduced, corresponding to the fully deactivated state of IK2 in the MNT model, so that
and If is formulated as
where Kc is the cleft K+ concentration, Km is half activation concentration, and EK and ENa are the reversal potentials for K+ and Na+, respectively. Instead of the decay of an outward current (see Figure 2B), the gradual activation of the inward If gives rise to DD until reaching the voltage threshold for INa activation, as predicted by the DN model (see Figure 3).
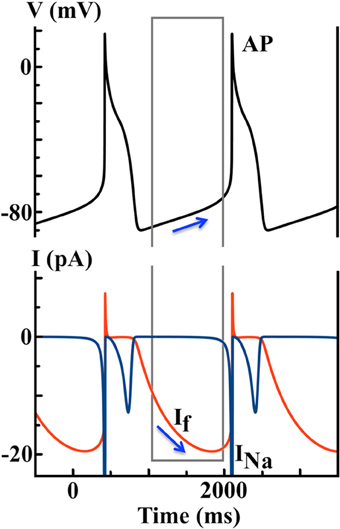
Figure 3. Simulated AP and ionic currents using the DiFrancesco Noble (DN) 1985 Purkinje cell model to illustrate the If hypothesis. Blue arrows indicate that the hyperpolarization-activated If during the diastolic depolarization (DD) finally triggers a spontaneous AP.
In 2001, Altomare et al. combined both experimental and theoretical approaches to illustrate the limitation of Hodgkin-Huxley formalism in describing If, the current originating from the now generally-called hyperpolarization-activated cyclic nucleotide-gated (HCN) channels (26). They found that some features of HCN channel gating do not comply with classic Hodgkin-Huxley kinetics, such as sigmoidal channel activation and deactivation. Thus, they proposed an allosteric Markovian scheme of voltage gating of HCN channels. In this scheme, HCN channels are considered to be composed of four subunits each. Each subunit is gated independently by voltage, and possesses one voltage sensor that can be either in the “willing” state or the “reluctant” state. These assumptions result in a 10-state model, with 5 open and 5 closed states. Using different sets of rate constants, the model is capable of quantitative representation of the voltage gating of different HCN isoforms, and thus permits an interpretation of various kinetic properties of these isoforms. However, this sophisticated HCN gating scheme has not yet been incorporated into whole SAN cell models to investigate the cellular mechanisms underlying pacemaking activities.
In 2012, Severi et al. developed an updated model (the SD model) of a rabbit SAN cell based on the most recent experimental data, with a updated representation of intracellular Ca2+ dynamics (27). If remains the major pacemaker current in the Severi model, and it is formulated using a similar Hodgkin-Huxley scheme as in the DN Purkinje cell model. As predicted by the SD model (see Figure 4), If and the Na+ − Ca2+ exchange current INCX are of similar size during DD. Yet If gradually increases to promote depolarization, while the inward INCX decays slightly over time. In addition, the model predicts that complete blockade of If will lead to cessation of cell automaticity.
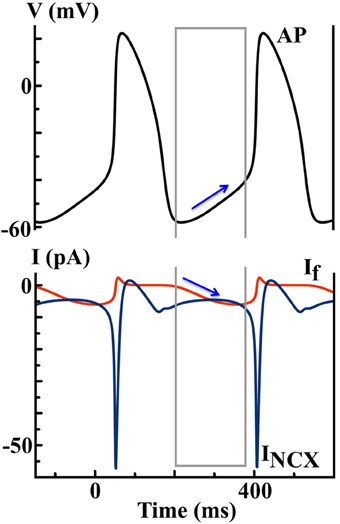
Figure 4. Simulated AP and ionic currents using the SD SAN model to illustrate the If hypothesis. Blue arrows indicate the changes of If during the DD finally triggers a spontaneous AP, while the contribution of INCX is less important.
2.3. ICa-Based Hypothesis and Models
Shortly after the discovery of If in the SAN by (22), Yanagihara, Noma and Irisawa published the very first SAN cell model (the YNI model) (22, 28). One major difference between SAN and Purkinje cells is the expression level of Na+ channels. While a strong INa is critical for Purkinje cells to maintain a rapid AP upstroke velocity and secure the robustness of electric conduction (15), INa is very small in SAN cells, especially those localized at the SAN center (29). In contrast to the If hypothesis (see Figure 3), the YNI model suggests that changes in K+ current during DD are quite moderate, and the major pacemaking current is ICa instead of If. They propose that ICa plays a major role in generating both the AP and the pacemaker potential.
The formulation of ICa in the YNI model is modified from Beeler and Reuter's model of ventricular myocytes (30):
where d and f represent the activation and inactivation of ICa, respectively. As shown in Figure 5, ICa is the largest inward current and dominates both DD and AP upstroke, while the predicted contributions from If and INa are relatively small.
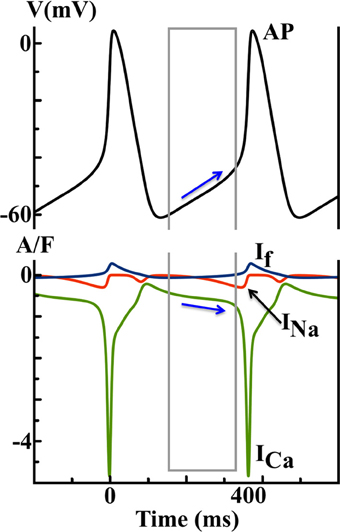
Figure 5. Simulated AP and ionic currents using the YNI SAN model to illustrate the ICa hypothesis. Blue arrows indicate that the changes in ICa during diastolic depolarization finally trigger a spontaneous AP.
Two decades later, Endresen et al. presented an alternative approach wherein membrane potential (Vm) of cells could be derived as a function of intracellular and extracellular ionic concentrations, instead of a function of channel gating per Hodgkin-Huxley formalism (31). Along with this novel approach, they presented a simple model of an SAN cell, where, as in the YNI model, ICa is the pacemaker current driving cellular automaticity.
2.4. Ca2+-Clock-Based Hypothesis and Models
Motivated by the formidable success of the Hodgkin-Huxley model, mathematical modeling of cardiac cells was first strongly focused on the cell membrane. Later, experiments revealed that internal Ca2+ machinery is of great importance for the action potential of cardiac cells and is essential for understanding excitation-contraction coupling. In addition to the aforementioned membrane oscillator (M-clock), an internal oscillator associated with Ca2+ cycling across the sarcoplasmic reticulum (SR) membrane (or Ca2+ “clock”) exists in all cardiac cells. In fact, this internal clock can work independently of the sarcolemma (32). Although various experimental studies had reported a possible involvement of the Ca2+-clock in cardiac pacemaking activities (33–37), it was only recently that mathematical models of the SAN with integrated SR membranes and thus Ca2+-clocks become available. In contrast to earlier membrane-delimited models of the SAN cell, in 2009, Maltsev and Lakatta (the ML model) first developed a model of a coupled membrane- and Ca2+-clock to address the ionic mechanism of cardiac pacemaking (see Figure 6) (32). Importantly, they quantitatively described the contribution of spontaneous Ca2+ release during late DD to SAN pacemaking, by triggering an inward Na+ − Ca2+ exchange current (INCX). They concluded that only a coupled system of membrane- and Ca2+-clocks offers both the robustness and flexibility that are required to maintain normal pacemaking function. The ML model predicts that the most important pacemaker current during late DD is the inward INCX, instead of If. Updated versions of the ML model have recently become available to accomodate additional experimental results (38, 39).
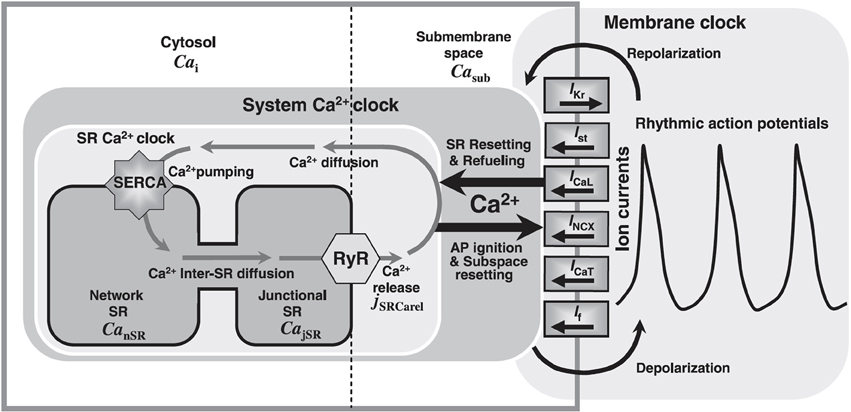
Figure 6. Model schematic of the ML SAN cell model, figure modified from (32). Cai: Ca2+ in bulk cytosol; Casub: Ca2+ in the subspace; SERCA: SR Ca2+ pump; CanSR: Ca2+ in the network SR (nSR); CajSR: Ca2+ in the junctional SR (jSR); jSRCarel: SR Ca2+ release rate global variable; RyR: cardiac ryanodine receptor; AP: action potential; IKr: rapid delayed rectifier current; Ist: sustained current; INCX: NCX current; ICaT: T-type Ca2+ current; If: hyperpolarization-activated or funny current.
As shown in Figure 7, INCX is the leading current during the DD, and is secondary to dynamic changes in [Ca]i and the Ca2+-clock. Without the Ca2+-clock, the M-clock alone is not capable of maintaining normal pacemaking function, as predicted by the ML model (27).
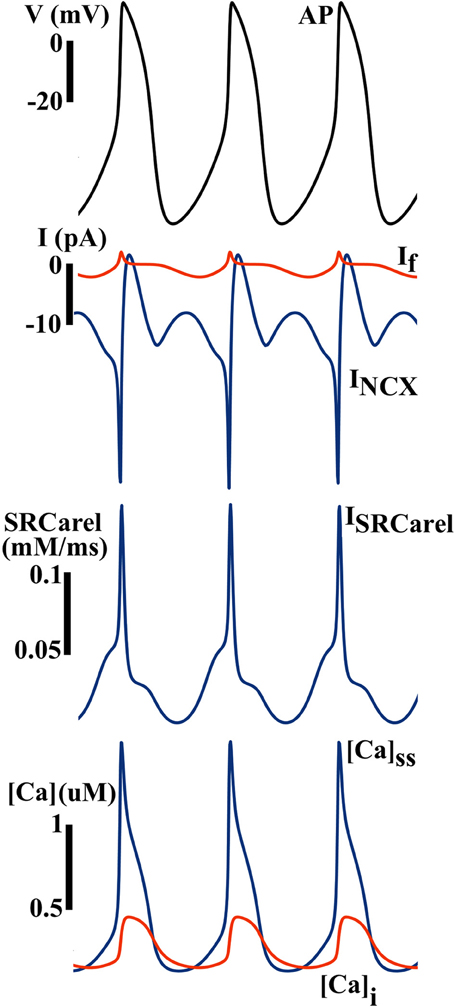
Figure 7. Simulated AP and ionic currents using the ML SAN model to illustrate the Ca clock hypothesis. Blue arrows indicate that the changes in INCX during the diastolic depolarization finally trigger a spontaneous AP, while the contribution of If is much less. Inward INCX during the DD is secondary to spontaneous Ca release from the SR (ISRCarel), which gives rise to subspace and myoplasmic Ca concentrations ([Ca]ss and [Ca]i) elevation during the DD.
3. The “Ca2+-Clock vs. If” Debate
Although many ionic currents in pacemaker cells have been proposed as potentials pacemaker currents, the present debate is primarily split between two popular candidates: the Ca2+-clock and If (4). These two candidate hypotheses can be well represented by the ML and the SD models, respectively, and there exists experimental evidence in support of or in opposition to each hypothesis.
The expression level of HCN channels is much higher in pacemaking tissue as compared to elsewhere in heart (40); it is thus reasonable to associate the tissue specificity of If with its role in pacemaking function (23). During beta-adrenergic stimulation, If can easily adjusted its working range to promote a faster heart rate by local cAMP-dependent regulation (41). Furthermore, If does not consume energy (at least directly), whereas the Ca2+-clock hypothesis relies on the SR Ca2+ pump to re-cycle Ca2+ against the concentration gradient across the SR membrane (42). These data would suggest If to be the primary pacemaker current in the SAN. However, there are experimental data to suggest that pharmacological or genetic blockade of If only moderately alters the pacing rate, and neither blockade terminates the pacemaking activity completely (43).
Spontaneous Ca2+ release has been experimentally observed during DD of SAN cells; the involvement of a Ca2+-clock in pacemaking activities seems hard to dispute. One ultrastructural property that all cardiac pacemaking tissues lack is a t-tubular system, which is known to have major impact on subcellular Ca2+ cycling. Could such lack of a defined t-tubular system be considered characteristic of cardiac pacemaker tissues, as is the expression of HCN channels? During beta-adrenergic stimulation, both the SR Ca2+ pump and RyR are phosphorylated to accommodate the faster pacing rate, as is the case for If (44). The major evidence against the Ca2+-clock hypothesis is that either RyR blockade/knockout or the application of BAPTA to suppress intracellular Ca2+ cycling does not have major effects on pacemaking activities. Indeed, in some cases, the heart rate accelerates (45, 46). ATP consumption is likely to be substantial if basal pacemaking activities were mostly Ca2+-clock driven (42).
In addition, it should be noted that similar questions concerning the respective roles of membrane and Ca2+ dynamics have been raised for models of cardiac myocytes as well (47, 48). At fast pacing rates, cardiac myocytes can develop alternans, charaterized by beat-to-beat alternations in both AP duration (APD) and Ca transient. However, it remains unclear if APD alternans is driven by Ca2+ alternans or vice versa, since membrane and Ca2+ subsystems are bidrectionally coupled, and it is experimentally challenging to identify which subsystem is the follower. To resolve this “chicken or the egg” debate, some computational protocols have been implemented, e.g., combined voltage and Ca clamping, and these novel numerical approaches could be helpful to address the “Ca2+-clock vs. If” discussion in the realm of cardiac pacemaking function.
3.1. Comparison of Model Formulations
The ML and SD models offer diverse predictions about cardiac pacemaking activities (e.g., the effect of If blockade), yet their model formulations have much in common. For example, ion channels in both models are described using Hodgkin-Huxley formalism, with similar channel gating schemes. The Ca2+ cycling subsystem is essentially identical between these two models. A major difference between ML and SD, however, is the experimental data used to fit ion channel properties (27). In Figure 8, significant differences in If are shown between the two models. The If channel availability (y2ss) is much higher at a given pacemaking voltage range, e.g., at −60 mV, SD y2ss is about 2.5 times the size of ML y2ss, while the difference in rate constants is much smaller. The difference in channel kinetics is consistent with the difference in the functional role of If during APs. In Figure 9, phase plots of INCX and If against membrane voltage (V) are shown. It is straightforward to observe that, at pacemaking voltage ranges; i.e., −60 to −40 mV, that SD If can be up to two times larger than in ML. On the contrary, SD INCX is about half the size of that in ML in the pacemaking voltage range, yet larger as compared to the ML INCX during AP upstroke. In other words, Ca2+-mediated INCX is important to promote DD in the ML model, and to enhance AP upstroke in the SD model.
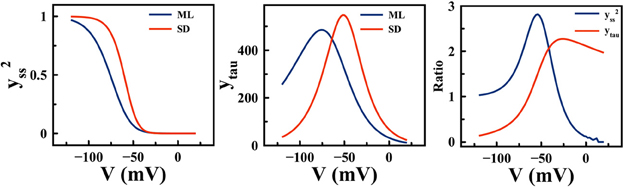
Figure 8. Differences in If steady state activation (y2ss) (left) and activation rate constant (ytau) (middle) between the ML and SD model. (right) the ratios between SD and ML y2ss, and between SD and ML ytau.
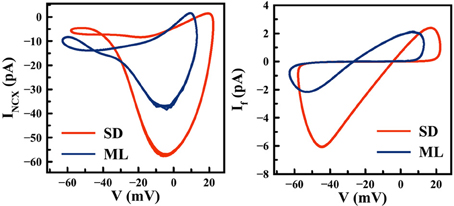
Figure 9. Differences in INCX (left) and If (right) between the ML and SD model. Computer simulations are performed over a number of pacemaking cycles using default parameter settings.
When there is little difference in model formulation, the experimental data that was used for validation, especially the properties of key ion channels or receptors, will largely determine the ultimate behavior of a model. If such discrepancies between mathematical models are primarily the result of different experimental data used to constrain these models in the first place, it is logical to conclude that mechanistic insights gleaned using these models may be limited, especially in consideration of the current debate between If and the Ca2+-clock. On the other hand, inconsistencies among experimental measurements are inevitable, assuming natural variations in experimental conditions, tissue preparations, and existing limitations of experimental protocols. So how can mathematical models be more helpful when there are existing uncertainties in the experiments, e.g., the steady-state activation of If (Figure 8)(left)? One option is to include model constraints that can be quantitatively characterized by additional experiments at tissue level, for example, the responses of SAN and atrial tissue excitation patterns to If or Ca2+ blockade. These tissue-level constraints are likely to help in evaluation of existing single SAN cell models. Another option could be to keep uncertain parameter values (e.g., the half-activation voltage of If) open within experimentally reported ranges, then identify the optimal value(s) that can produce the best pacemaking performance in terms of robustness, stability and flexibility.
As mentioned earlier, both the If and Ca2+-clock hypotheses are facing supporting and opposing experimental evidence. It thus seems reasonable to hypothesize that these two mechanisms are not necessarily exclusive. Their “redundant” coexistence may be important to maintain the robustness of cardiac pacemaking function against possible disturbances through one's lifetime. This idea is supported by the fact that neither If or Ca2+ blockade eliminates pacemaking activities entirely. But it is also possible that these independent pacemaking oscillators in the heart are assigned with different, complementary roles. It has recently been suggested that, while If is essential for maintenance of the basal heart rate, the Ca2+-clock is more important for regulation of the heart rate during beta-adrenergic stimulation (49). It may be worthwhile to take a step back from the debate, and consider the question as a design problem: if one could implement any theoretical pacemaker cell for the heart, which would be ideal, a If-based M-clock, or a Ca2+-clock, or both? In other words, is it possible to define numerical protocols to evaluate and compare the pacemaking performance of theoretical pacemaker cells? And, if so, what are the ultimate properties we are looking for in a pacemaker cell?
In 2013, Maltsev and Lakatta employed a different approach to probe some of these questions (39). Based on the original ML 2009 model, they identified the minimal set of model components (i.e., membrane ion currents and SR Ca2+-dynamics - termed simply the Ca2+-clock) required to generate robust, flexible and energy-efficient cardiac pacemaking function. Extensive parameter sensitivity analyses were performed to evaluate the pacemaking performance of 13 different model types, each with either 4 or 5 model components. They found that a minimal model with 4 components (ICaL + IKr + INCX + Ca2+-clock) is capable of producing the full range of autonomic modulation. Inclusion of If or ICaT increased model robustness, yet reduced model flexibility. In addition, they quantified and compared the energy efficiency of the derived minimal model against earlier models, and suggested that by keeping a small Na+ influx, cell energy required to maintain Na+ homeostasis can be largely reduced to accommodate the energy associated with SR Ca2+ pumping. These numerical findings provided a number of valuable insights into basal cardiac pacemaking function. More importantly, however, these numerical approaches (parameter sensitivity analysis and quantitative pacemaking performance evaluation) should prove useful toward reaching a generalized theory of cardiac pacemaking.
4. Modeling β-Adrenergic Regulation of the SAN
Under the conditions of exercise or stress, heart rate increases to accommodate the needs of the body, achieved via β-adrenergic regulation (βAR) of the SAN. During βAR, there are a variety of functional modifications of ion channels and transporters, and the properties of both membrane and Ca2+-clocks are altered. It is thus quite difficult to evaluate the contribution of each ion current to heart rate regulation experimentally during βAR.
It has long been known that If can be activated by direct binding of cyclic AMP (cAMP), a second messenger important in βAR. This voltage-independent regulation of If is achieved by shifting the steady state activation curve according to the local concentration of cAMP. In 1999, DiFrancesco proposed an allosteric reaction model to describe the dual activation of If by voltage hyperpolarization and cAMP (41). Specifically, the steady state open probability of If (Po) is described as:
where V1/2 is the half-activation voltage, v is the inverse slope factor, and Vs is a cAMP-dependent term that represents the effects of cAMP on channel properties. Furthermore, Vs is described as:
where Ko and Kc are the cAMP dissociation constants when the channel is open and closed, respectively. As local [cAMP] increases, the channel open probability curve will shift to more positive voltages, e.g., about 14 mV shift with 10 μM [cAMP] (41), thus increasing the current availability during DD, and accelerating the pacing rate.
Later, a more complete βAR regulation system was modeled in ventricular myocytes, then incorporated into existing SAN cell models (see Figure 10) (50–52). These models describe both the βAR signaling cascade and changes to electrophysiological substrates after phosphorylation, and have been very useful tools to quantify the ionic mechanisms underlying the rate adaptation of SAN, e.g., using the lead potential (VL) analysis proposed by Sarai et al. (53). More recently, βAR system models that describe the complexity of localized signaling domains have become available (54). This level of detail has not been included in most recent SAN cell models, e.g., the ML and SD models, yet very well might be a critical piece leading to resolution of the Ca2+-clock vs If debate.
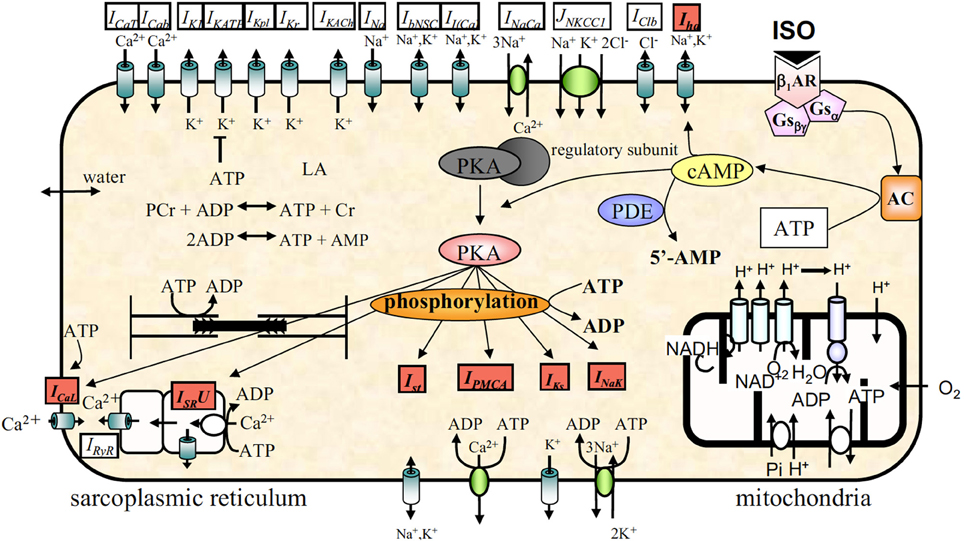
Figure 10. Model schematic of a SAN cell model with integrated βAR system, figure modified from (52).
5. Tissue Level Complications of SAN Pacemaking Function
The SAN achieves its physiological function via electrical coupling with atrial tissue (29, 55). To illustrate the effects of SAN-atrial coupling on pacemaking patterns, a simplified 2D SAN model is implemented on a 1 by 1 cm grid, with the elliptically shaped SAN in the center (half-axes 3 and 1 mm, see Figure 11A). Here, we use the SD model (27), and the model developed by Malecker et al. (56), to describe the electrophysiological properties of SAN and atrial cells, respectively. Electric diffusion in the whole 2D tissue is anisotropic, with atrial tissue fibre orientation pointing 30° off from the SAN long axis. The conductivity is 1.2 m/cm along the fibre direction, and 0.25 ms/cm trasversely (57, 58). The cell-area-to-volume ratio is 3000 cm−1. When the coupling is weak (about 40% of the control value), atrial tissue fails to respond to every SAN beat; when the coupling is strong (the control value), SAN and atrial excitations are in synchrony with a slower pacing rate (Figure 11B); when the coupling is too strong (more than 250% of the control value), the whole 2D tissue became quiescent. Figure 12 further illustrates the relationship between tissue pacing frequency and SAN-atrial coupling, and the effects of If or Ca2+ blockade. Specifically, when the SAN-atrial coupling is below a certain threshold, the SAN beats much faster than surrounding atrial tissue and the stimulus-to-response ratio is increased; when the coupling is increased, the SAN and atrial tissue activate in concert, yet at slower rates. When the coupling is above a certain threshold, the SAN remains quiescent due to enhanced electrotonic (electrical sink) effects. With either If or Ca2+ blockade (by adding strong Ca2+ buffers), beats-per-minute (BPM) of both the SAN and atrial tissue are largely reduced. Proper coupling to non-pacemaking tissue is clearly a delicate balance and is essential to achieve robust and rhythmic whole-heart excitation.
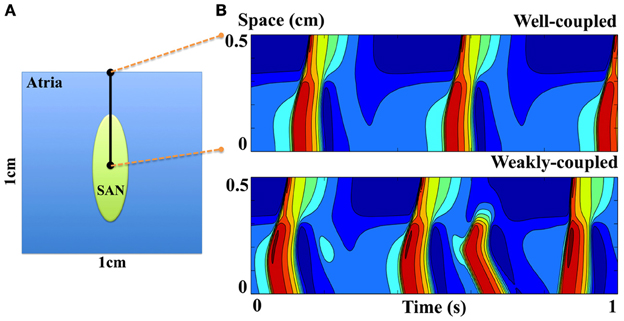
Figure 11. (A) Model schematic of a simplified 2D SAN model. (B) Space-time plots of SAN and atrial excitation patterns when the SAN is either weakly or well coupled to atrial tissue. The proximal (at 0 cm) and distal (at 0.5 cm) sites correspond to the central SAN cell and peripheral atrial cell respectively, indicated as black dots in (A).
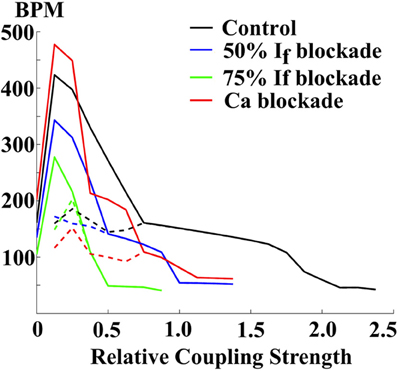
Figure 12. The relationship between pacing rates (in beats-per-minute (BPM)) and the SAN-atrial electric coupling, and the effects of If or Ca blockade. Solid lines: the central SAN cell. Dashed lines: the peripheral atrial cell.
To further illustrate the importance and complexities of SAN-atrial interaction, we implemented a 3D atrial model to quantify the effects of weak SAN-atrial coupling on cardiac excitation patterns. The 3D mesh of right atria and SAN is a courtesy of Dr Edward J. Vigmond, Université de Bordeaux. The mesh comprised 315986 nodes, and 1065333 tetrahedral elements with an average edge length of 100 μm [please see (59) for more details]. Same cell models are used as in the 2D model (27, 56). The conductivity is zero in the block zone adjacent to the SAN, and 1 ms/cm elsewhere. Within 500 ms of simulation time, there are seven spontaneous SAN excitations, while only three of these successfully trigger atrial excitation (#1, #4, and #7). In addition, chaotic dynamics at the SAN pacemaking site and dyssynchronous SAN excitations are observed (#2, #3, #5, #6); see Figure 13. The complex tissue dynamics seen in this example highlight the difficulty of employing only single-cell studies to discern SAN pacemaking function. 3D tissue effects are important to consider in any study of the cardiac pacemaking mechanism, and may serve as additional constraints to evaluate SAN single cell models. For example, when coupled to atrial tissue, SAN cell models should be capable of producing robust and rhythmic atrial excitations at the complete range of physiological pacing rates. However, none of the current SAN cell models have been systematically evaluated with respect to these tissue-level constraints.
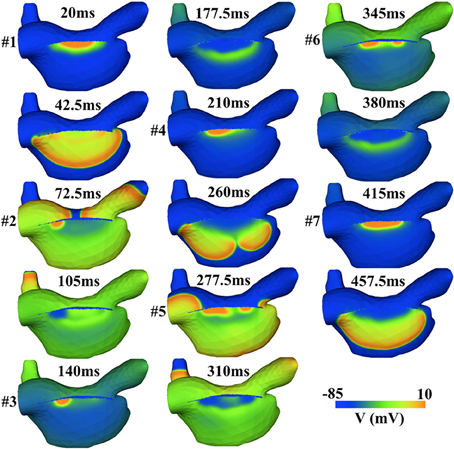
Figure 13. Simulated irregular SAN and atrial excitation patterns induced by the weak SAN-atrial coupling in a 3D atrial model. Only 3 (#1, #4, and #7) out of 7 SAN excitations successfully activate the atrial tissue.
Current multi-scale models of the SAN integrate anatomical details of SAN heterogeneity and fiber direction. This permits quantitative description of the functional heterogeneity and synchronization within the SAN, investigation of the role of SAN dysfunction in atrial arrhythmias, and characterization of the complex interactions among SAN, atrial tissue and, more, recently AVN tissue (9, 59–65). Yet most of these models are constructed by scaling-up existing compartmental single cell models to tissue and organ levels based on either simplified or realistic geometries of the SAN. However, the subcellular heterogeneity of SAN cells is much more pronounced as compared to ventricular or even atrial myocytes, due to the lack of a well-defined t-tubular system (13). Without the t-tubular system, the coupling between membrane and Ca2+ subsystmes is relatively weak, since most local Ca2+-release machineries are not located in conjunction with the cell membrane, and do not directly respond to changes in membrane polarization. Thus consideration of the ultrastructural details of SAN cells is critical to a quantitative understanding of SAN pacemaking function. The importance of the spatial hierarchy of subcellular Ca2+ patterns in determining the behaviors of Ca2+-clock, i.e., from localized Ca2+ sparks to global Ca2+ waves, is now clear. Despite this fact, the subcellular heterogeneity of SAN cells has not yet been carefully considered in model construction and spatially distributed models are not yet available (66, 67).
6. Summary
The underlying mechanism of cardiac pacemaking activity has historically been under debate, often with seemingly exclusive hypotheses proposed by different groups. In this review, we have presented these hypotheses and discussed the developments in mathematical models of cardiac pacemaking function in detail. A first group of models supports a driving M-clock (membrane oscillator). For over a decade until the late 1970s, the IK2 “decay” hypothesis was the basis for cardiac pacemaker modeling (Noble 1962 SAN model and its iterations). In 1979, the discovery of If (HCN channels) in SAN cells led to a series of experimental and modeling studies aimed at radical reinterpretation of the IK2-based hypothesis, leading to the debut of the If-based hypothesis. The DN Purkinje cell model (1985) relies on If as the current underlying the M-clock. Further experimental data regarding sarcolemmal currents and Ca2+ cycling are both incorporated into the recent (2012) SD model; If and thus the M-clock remains the major pacemaking mechanism. The YNI model published in 1980, in contrast, suggests that changes in K+ current during DD are quite moderate, and that the major pacemaking current is ICa instead of If. Although focused on the sarcolemmal current, this first suggestion of the importance of Ca2+ to cardiac cell automaticity may be seen as prescient; in addition to the M-clock, the SR-membrane-dependent Ca2+-clock is also involved for cardiac pacemaking. In 2009, Maltsev and Lakatta debuted the first coupled M- and Ca2+-clock mathematical model (ML) and suggested that a coupled system offered both the flexibility and robustness required to maintain normal pacemaking function. ML predicts that the most important pacemaker current during late DD is the inward INCX, rather than If, as for SD. It is reasonable to conjecture that these two mechanisms may not be mutually exclusive. Indeed, a recent study shows that these could be complementary, and together generate robust, flexible, and energy-efficient cardiac pacemaking (39).
ML and SD may offer diverse predictions about cardiac pacemaking activities, yet their model formulations have much in common. Their distinct emergent behaviors result from the diverse data sets upon which they were built. It is actually elementary, from a methodological perspective, to incorporate new data into these models. When new experimental knowledge becomes available, it is thus tempting to augment extant models by default. However, it is essential to first consider how model expansion leading to a more comprehensive model will help us to further understand SAN function. Alternatively, is it possible to use employ novel experimental data as additional model constraints to simplify existing models? Indeed, as compared to model expansion, model reduction can be more challenging (68).
A number of natural further directions extends the trajectory of pacemaker cell model development. Critically, a proposed Markovian scheme for HCN channels was put forward by Altomare in 2001, but has yet to be incorporated into whole cell models. Furthermore, subcellular heterogeneity of SAN cells is much more pronounced as compared to other cardiac cell types; consideration of ultrastructural details of SAN cells may be essential to a quantitative understanding of SAN pacemaking function. In addition, under conditions of exercise or stress, our heart rate increases to accommodate the needs of the body, achieved via βAR regulation of the SAN. This level of detail has not been included in the most recent SAN cell models, yet very well may also be a critical piece leading to resolution of the M- vs Ca2+-clock analysis. Finally, it is important to consider that the SAN is not an isolated cell; rather it achieves its physiological function via electrical coupling with atrial tissue. Our simulations showed that, when coupling between SAN and atrial cells is weak, atrial tissue fails to respond to every SAN beat. However, when coupling is strong, SAN and atrial excitations are in synchrony with a slower pacing rate. When coupling is above a certain threshold, the SAN remains quiescent due to enhanced electrotonic effects. Clearly, an appreciation of both the SAN's electrophysiology as well as its delicate relationship to surrounding tissue is essential to understanding the mechanisms of robust and rhythmic whole-heart excitation.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is supported by the Research Council of Norway, through which Simula is supported via its partnership in the Center for Cardiological Innovation.
References
1. Noble D. Systems biology and the heart. Biosystems (2006) 83:75–80. doi: 10.1016/j.biosystems.2005.05.013
3. Noble D, Garny A, Noble PJ. How the Hodgkin–Huxley equations inspired the cardiac Physiome Project. J Physiol. (2012) 590:2613–28. doi: 10.1113/jphysiol.2011.224238
4. Billman GE. Does the ‘coupled clock’ make the heart tick? Cardiovasc. Res. (2012) 96:343–4. doi: 10.1093/cvr/cvs300
5. Lakatta EG, DiFrancesco D. What keeps us ticking: a funny current, a calcium clock, or both? J Mol Cell Cardiol. (2009) 47:157–70. doi: 10.1016/j.yjmcc.2009.03.022
6. Wilders R. Computer modelling of the sinoatrial node. Med Biol Eng Comput. (2007) 45:189–207. doi: 10.1007/s11517-006-0127-0
7. Noble D, Noble PJ, Fink M. Competing oscillators in cardiac pacemaking historical background. Circ Res. (2010) 106:1791–7. doi: 10.1161/CIRCRESAHA.110.218875
8. Dobrzynski H, Boyett MR, Anderson RH. New insights into pacemaker activity promoting understanding of sick sinus syndrome. Circulation (2007) 115:1921–32. doi: 10.1161/CIRCULATIONAHA.106.616011
9. Seemann G, Höper C, Sachse FB, Dössel O, Holden AV, Zhang H. Heterogeneous three-dimensional anatomical and electrophysiological model of human atria. Philos Trans R Soc A Math Phys Eng Sci. (2006) 364:1465–81. doi: 10.1098/rsta.2006.1781
10. Dobrzynski H, Li J, Tellez J, Greener I, Nikolski V, Wright S, et al. Computer three-dimensional reconstruction of the sinoatrial node. Circulation (2005) 111:846–54. doi: 10.1161/01.CIR.0000152100.04087.DB
11. Kwong KF, Schuessler RB, Green KG, Laing JG, Beyer EC, Boineau JP, et al. Differential expression of gap junction proteins in the canine sinus node. Circ Res. (1998) 82:604–12. doi: 10.1161/01.RES.82.5.604
12. Irisawa H. Comparative physiology of the cardiac pacemaker mechanism. Physiol Rev. (1978) 58:461–98.
13. Brette F, Orchard C. T-tubule function in mammalian cardiac myocytes. Circ Res. (2003) 92:1182–92. doi: 10.1161/01.RES.0000074908.17214.FD
14. Musa H, Lei M, Honjo H, Jones SA, Dobrzynski H, Lancaster MK, et al. Heterogeneous expression of Ca2+ handling proteins in rabbit sinoatrial node. J Histochem Cytochem. (2002) 50:311–24. doi: 10.1177/002215540205000303
15. Boyden PA, Hirose M, Dun W. Cardiac Purkinje cells. Heart Rhythm (2010) 7:127–35. doi: 10.1016/j.hrthm.2009.09.017
16. Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiology. (1952) 117:500.
17. Munshi NV. Gene regulatory networks in cardiac conduction system development. Circ Res. (2012) 110:1525–37. doi: 10.1161/CIRCRESAHA.111.260026
18. Noble D. A modification of the Hodgkin–Huxley equations applicable to Purkinje fibre action and pacemaker potentials. J Physiol. (1962) 160:317–52.
19. McAllister RE, Noble D, Tsien R. Reconstruction of the electrical activity of cardiac Purkinje fibres. J Physiol. (1975) 251:1–59.
20. Noble D, Tsien R. The kinetics and rectifier properties of the slow potassium current in cardiac Purkinje fibres. J Physiol. (1968) 195:185–214.
21. Hauswirth O, Noble D, Tsien R. Adrenaline: mechanism of action on the pacemaker potential in cardiac Purkinje fibers. Science (1968) 162:916–7. doi: 10.1126/science.162.3856.916
22. Brown H, DiFrancesco D, Noble S. How does adrenaline accelerate the heart? Nature (1979) 280:235–36. doi: 10.1038/280235a0
23. DiFrancesco D. The role of the funny current in pacemaker activity. Circ Res. (2010) 106:434–46. doi: 10.1161/CIRCRESAHA.109.208041
24. DiFrancesco D. A new interpretation of the pace-maker current in calf Purkinje fibres. J Physiol. (1981) 314:359–76.
25. DiFrancesco D, Noble D. A model of cardiac electrical activity incorporating ionic pumps and concentration changes. Philos Trans R Soc Lond B Biol Sci. (1985) 307:353–98. doi: 10.1098/rstb.1985.0001
26. Altomare C, Bucchi A, Camatini E, Baruscotti M, Viscomi C, Moroni A, et al. Integrated allosteric model of voltage gating of HCN channels. J Gen Physiol. (2001) 117:519–32. doi: 10.1085/jgp.117.6.519
27. Severi S, Fantini M, Charawi LA, DiFrancesco D. An updated computational model of rabbit sinoatrial action potential to investigate the mechanisms of heart rate modulation. J Physiol. (2012) 590:4483–99. doi: 10.1113/jphysiol.2012.229435
28. Yanagihara K, Noma A, Irisawa H. Reconstruction of sino-atrial node pacemaker potential based on the voltage clamp experiments. Jpn J Physiol. (1980) 30:841. doi: 10.2170/jjphysiol.30.841
29. Zhang H, Holden A, Kodama I, Honjo H, Lei M, Varghese T, et al. Mathematical models of action potentials in the periphery and center of the rabbit sinoatrial node. Am J Physiol Heart Circ Physiol. (2000) 279:H397–H421. Available online at: http://ajpheart.physiology.org/content/279/1/H397
30. Beeler GW, Reuter H. Reconstruction of the action potential of ventricular myocardial fibres. J Physiol. (1977) 268:177–210.
31. Endresen L, Hall K, Høye J, Myrheim J. A theory for the membrane potential of living cells. Eur Biophys J. (2000) 29:90–103. doi: 10.1007/s002490050254
32. Maltsev VA, Lakatta EG. Synergism of coupled subsarcolemmal Ca2+ clocks and sarcolemmal voltage clocks confers robust and flexible pacemaker function in a novel pacemaker cell model. Am J Physiol Heart Circ Physiol. (2009) 296:H594–H615. doi: 10.1152/ajpheart.01118.2008
33. Vinogradova TM, Zhou YY, Maltsev V, Lyashkov A, Stern M, Lakatta EG. Rhythmic ryanodine receptor Ca2+ releases during diastolic depolarization of sinoatrial pacemaker cells do not require membrane depolarization. Circ Res. (2004) 94:802–9. doi: 10.1161/01.RES.0000122045.55331.0F
34. Vinogradova TM, Maltsev VA, Bobdanov KY, Lyashkov AE, Lakatta EG. Rhythmic Ca2+ oscillations drive sinoatrial nodal cell pacemaker function to make the heart tick. Ann NY Acad Sci. (2005) 1047:138–56. doi: 10.1196/annals.1341.013
35. Méry A, Aimond F, Ménard C, Mikoshiba K, Michalak M, Pucéat M. Initiation of embryonic cardiac pacemaker activity by inositol 1, 4, 5-trisphosphate–dependent calcium signaling. Mol Biol Cell. (2005) 16:2414–23. doi: 10.1091/mbc.E04-10-0883
36. Lakatta EG, Vinogradova T, Lyashkov A, Sirenko S, Zhu W, Ruknudin A, et al. The integration of spontaneous intracellular Ca2+ cycling and surface membrane ion channel activation entrains normal automaticity in cells of the heart's pacemaker. Ann NY Acad Sci. (2006) 1080:178–206. doi: 10.1196/annals.1380.016
37. Vinogradova TM, Lyashkov AE, Zhu W, Ruknudin AM, Sirenko S, Yang D, et al. High basal protein kinase A–dependent phosphorylation drives rhythmic internal Ca2+ store oscillations and spontaneous beating of cardiac pacemaker cells. Circ Res. (2006) 98:505–14. doi: 10.1161/01.RES.0000204575.94040.d1
38. Yaniv Y, Stern MD, Lakatta EG, Maltsev VA. Mechanisms of beat-to-beat regulation of cardiac pacemaker cell function by Ca cycling dynamics. Biophys J. (2013) 105:1551–61. doi: 10.1016/j.bpj.2013.08.024
39. Maltsev VA, Lakatta EG. Numerical models based on a minimal set of sarcolemmal electrogenic proteins and an intracellular Ca clock generate robust, flexible, and energy-efficient cardiac pacemaking. J Mol Cell Cardiol. (2013). 59:181–95. doi: 10.1016/j.yjmcc.2013.03.004
40. Shi W, Wymore R, Yu H, Wu J, Wymore RT, Pan Z, et al. Distribution and prevalence of hyperpolarization-activated cation channel (HCN) mRNA expression in cardiac tissues. Circ Res. (1999) 85:e1–e6. doi: 10.1161/01.RES.85.1.e1
41. DiFrancesco D. Dual allosteric modulation of pacemaker (f) channels by cAMP and voltage in rabbit SA node. J Physiol. (1999) 515:367–76. doi: 10.1111/j.1469-7793.1999.367ac.x
42. Matsuoka S, Sarai N, Jo H, Noma A. Simulation of ATP metabolism in cardiac excitation–contraction coupling. Prog Biophys Mol Biol. (2004) 85:279–99. doi: 10.1016/j.pbiomolbio.2004.01.006
43. Bucchi A, Barbuti A, DiFrancesco D, Baruscotti M. Funny current and cardiac rhythm: insights from HCN knockout and transgenic mouse models. Front Physiol. (2012) 3:240. doi: 10.3389/fphys.2012.00240
44. Vinogradova TM, Bogdanov KY, Lakatta EG. β-Adrenergic stimulation modulates ryanodine receptor Ca2+ release during diastolic depolarization to accelerate pacemaker activity in rabbit sinoatrial nodal cells. Circ Res. (2002) 90:73–9. doi: 10.1161/hh0102.102271
45. Lappi MD, Billman GE. Effect of ryanodine on ventricular fibrillation induced by myocardial ischaemia. Cardiovasc Res. (1993) 27:2152–9. doi: 10.1093/cvr/27.12.2152
46. Himeno Y, Toyoda F, Satoh H, Amano A, Cha CY, Matsuura H, et al. Minor contribution of cytosolic Ca2+ transients to the pacemaker rhythm in guinea pig sinoatrial node cells. Am J Physiol Heart Circ Physiol. (2011) 300:H251–H261. doi: 10.1152/ajpheart.00764.2010
47. Tolkacheva EG, Zhao X. Nonlinear dynamics of periodically paced cardiac tissue. Nonlin Dyn. (2012) 68:347–63. doi: 10.1007/s11071-011-0241-x
48. Krogh-Madsen T, Christini DJ. Nonlinear dynamics in cardiology. Ann Rev Biomed Eng. (2012) 14:179–203. doi: 10.1146/annurev-bioeng-071811-150106
49. Gao Z, Chen B, Joiner MlA, Wu Y, Guan X, Koval OM, et al. If and SR Ca release both contribute to pacemaker activity in canine sinoatrial node cells. J Mol Cell Cardiol. (2010) 49:33–40. doi: 10.1016/j.yjmcc.2010.03.019
50. Saucerman JJ, Brunton LL, Michailova AP, McCulloch AD. Modeling β-adrenergic control of cardiac myocyte contractility in silico. J Biol Chem. (2003) 278:47997–8003. doi: 10.1074/jbc.M308362200
51. Kuzumoto M, Takeuchi A, Nakai H, Oka C, Noma A, Matsuoka S. Simulation analysis of intracellular Na+ and Cl- homeostasis during β1-adrenergic stimulation of cardiac myocyte. Prog Biophys Mol Biol. (2008) 96:171–86. doi: 10.1016/j.pbiomolbio.2007.07.005
52. Himeno Y, Sarai N, Matsuoka S, Noma A. Ionic Mechanisms underlying the positive chronotropy induced by β1-adrenergic stimulation in guinea-pig sinoatrial node cells: a simulation study. J Physiol Sci. (2008) (0):0801180027. doi: 10.2170/physiolsci.RP015207
53. Sarai N, Matsuoka S, Kuratomi S, Ono K, Noma A. Role of individual ionic current systems in the SA node hypothesized by a model study. Jpn J Physiol. (2003) 53:125–34. doi: 10.2170/jjphysiol.53.125
54. Heijman J, Volders PG, Westra RL, Rudy Y. Local control of β-adrenergic stimulation: effects on ventricular myocyte electrophysiology and Ca transient. J Mol Cell Cardiol. (2011) 50:863–71. doi: 10.1016/j.yjmcc.2011.02.007
55. Garny A, Kohl P, Hunter PJ, Boyett MR, Noble D. One-Dimensional rabbit sinoatrial node models. J Cardiovasc Electrophysiol. (2003) 14:S121–S132. doi: 10.1046/j.1540.8167.90301.x
56. Maleckar MM, Greenstein JL, Giles WR, Trayanova NA. K+ current changes account for the rate dependence of the action potential in the human atrial myocyte. Am J Physiol Heart Circul Physiol. (2009) 297:H1398–H1410. doi: 10.1152/ajpheart.00411.2009
57. Klepfer RN, Johnson CR, Macleod RS. The effects of inhomogeneities and anisotropies on electrocardiographic fields: a 3-D finite-element study. Biomed Eng IEEE Trans. (1997) 44:706–19. doi: 10.1109/10.605427
58. Henriquez CS, Muzikant AL, Smoak CK. Anisotropy, fiber curvature, and bath loading effects on activation in thin and thick cardiac tissue preparations. J Cardiovasc Electrophysiol. (1996) 7:424–44. doi: 10.1111/j.1540-8167.1996.tb00548.x
59. Muñoz MA, Kaur J, Vigmond EJ. Onset of atrial arrhythmias elicited by autonomic modulation of rabbit sinoatrial node activity: a modeling study. Am J Physiol Heart Circ Physiol. (2011) 301:H1974–H1983. doi: 10.1152/ajpheart.00059.2011
60. Michaels DC, Matyas EP, Jalife J. Mechanisms of sinoatrial pacemaker synchronization: a new hypothesis. Circ Res. (1987) 61:704–14. doi: 10.1161/01.RES.61.5.704
61. Garny A, Noble D, Kohl P. Dimensionality in cardiac modelling. Progress Biophys Mol Biol. (2005) 87:47–66. doi: 10.1016/j.pbiomolbio.2004.06.006
62. Chandler NJ, Greener ID, Tellez JO, Inada S, Musa H, Molenaar P, et al. Molecular architecture of the human sinus node insights into the function of the cardiac pacemaker. Circulation (2009) 119:1562–75. doi: 10.1161/CIRCULATIONAHA.108.804369
63. Oren RV, Clancy CE. Determinants of heterogeneity, excitation and conduction in the sinoatrial node: a model study. PLoS Comput Biol. (2010) 6:e1001041. doi: 10.1371/journal.pcbi.1001041
64. Chandler N, Aslanidi O, Buckley D, Inada S, Birchall S, Atkinson A, et al. Computer three-dimensional anatomical reconstruction of the human sinus node and a novel paranodal area. Anat Record (2011) 294:970–9. doi: 10.1002/ar.21379
65. Podziemski P, Zebrowski JJ. A simple model of the right atrium of the human heart with the sinoatrial and atrioventricular nodes included. J Clin Monitor Comput. (2013) 27:481–98. doi: 10.1007/s10877-013-9429-6
66. Gaur N, Rudy Y. Multiscale modeling of calcium cycling in cardiac ventricular myocyte: macroscopic consequences of microscopic dyadic function. Biophys J. (2011) 100:2904–12. doi: 10.1016/j.bpj.2011.05.031
67. Nivala M, de Lange E, Rovetti R, Qu Z. Computational modeling and numerical methods for spatiotemporal calcium cycling in ventricular myocytes. Front Physiol. (2012) 3:114. doi: 10.3389/fphys.2012.00114
Keywords: mathematical modeling, cardiac automaticity, pacemaker, ion channels, electrophysiology
Citation: Li P, Lines GT, Maleckar MM and Tveito A (2013) Mathematical models of cardiac pacemaking function. Front. Physics 1:20. doi: 10.3389/fphy.2013.00020
Received: 29 August 2013; Accepted: 08 October 2013;
Published online: 30 October 2013.
Edited by:
Leonid L. Rubchinsky, Indiana University - Purdue University, USAReviewed by:
Elena Tolkacheva, University of Minnesota, USAXiaopeng Zhao, University of Tennessee, USA
Copyright © 2013 Li, Lines, Maleckar and Tveito. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aslak Tveito, Simula Research Laboratory, Martin Linges vei 17, Fornebu, P.O. Box 134, 1325, Oslo, Norway e-mail:YXNsYWtAc2ltdWxhLm5v
 Pan Li
Pan Li Glenn T. Lines
Glenn T. Lines Mary M. Maleckar
Mary M. Maleckar Aslak Tveito
Aslak Tveito