Entropic transport in confined media: a challenge for computational studies in biological and soft-matter systems

1. Introduction

The study of transport has been traditionally performed by means of Langevin or Fokker-Planck equations (1) where the nature of the boundaries that may absorb or reflect particles, imposes conditions on the probability distribution function. To obtain the solution of these equations for the case of an irregular boundary is in general difficult and may sometimes constitute a formidable task. For example, different numerical methods such as Lattice Boltzmann (2, 3), or Molecular Dynamics (4) as been employed to study the transport properties of heterogeneous media. A variety of experimental techniques such as Nuclear Magnetic Resonance (5, 6) or neutron scattering (7) have been used to capture tracer dynamics in porous media. Theoretically, different perturbation approaches have been developed in order to capture the overall dynamics have been proposed (8–11).

In many cases of interest, such as those encountered in ion translocation through protein channels, in nanopores or in microfluidic devices, the geometry of the system is such that transport takes place along a preferred direction of motion. Changes in the position and momentum of the particles thus occur mainly along this direction whereas local equilibration is rapidly reached in the transverse directions. Under this circumstance, transport becomes practically one-dimensional and one can consider the effect of the tortuosity of the boundaries through the presence of an entropic barrier.

To analyze diffusion in confined systems such as those shown in Figure 1, an entropy driven diffusion theory has been developed in References (12–14). Subsequent works have shown that this theoretical framework, and in particular the expression for the diffusion coefficient proposed in reference (14) can be derived by a systematic expansion in a parameter related to the tortuosity of the channel where the first order term represents the contribution of the planar channel (15–17). Therefore, as opposed to other phenomenological schemes, Fick-Jacobs constitutes a theoretically well established homogeneization scheme.

FIGURE 1

Figure 1. Suspended particles in a confined environment. Left: the presence of vesicles, organelles and filaments affect molecules and proteins dynamics by reducing the accessible space. Right: suspended particles in a rough channel are affected by the varying-effective-section of the channel.

This theory has allowed to clarify the many peculiarities of transport through entropic barriers, or entropic transport (18), that differ essentially from those of the case of energetic barriers. Its range of applicability has been established in (19). It has been shown that entropic transport characterizes the diffusion (20, 21) or currents (22) of tracers through neutral or charged pores (23–25). Using the same framework, it has been possible to characterize particle-particle interaction through a pore (26), or through a soft-wall channel (27), and to analyze hard-disks dynamics as well, (28). The presence of the entropic barriers gives rise to the appearance of new resonant phenomena such as entropic stochastic resonance (29–33), in which the presence of entropic barriers may amplify an external signal. Moreover, the diffusion of neutral tracers through a wedge have been shown to be significantly affected by the geometrical confinement due to the local rectification induced by the local symmetry breaking (34). Theoretical works have also shown phenomena out of the reach of the present scheme (35) and rectification currents have been explored. Alternatively, the limit of very steep modulations in channel width has been explored. In this regime the abrupt change in channel width, named entropic traps, significantly affects the overall particle dynamics (36) leading to a non-monotonous dependence of the diffusion coefficient on particle size (37).

Our purpose in this article is to review recent development in the study of diffusion in confined systems and its applications to biological and soft condensed matter problems. We will illustrate the effect of the confinement in the transport properties by analyzing two situations: the diffusion of charged particles in a pore and the functionality of a Brownian motor proceeding in a confined medium system. In both cases, we observe the appearance of emergent properties, such as current inversion, cooperative rectification (38) not observed when the systems evolves in an unlimited space. The paper is organized as follows. In Section 2, we will present the entropic transport model. In Sections 3 and 4, we will discuss the examples mentioned. Finally, in Section 5 we will summarize our main conclusions.

2. Charged Particle in a Confined Environment

When charged particles suspended in a electrolyte are embedded in a porous medium their dynamics is governed by the interplay of several, distinct physical mechanism such as electrostatic, steric and hydrodynamic interactions. Several numerical techniques (39) have been developed to address such a problem. If the particle-particle interaction can be disregarded, i.e., in the dilute regime, the motion of a suspension of particles is characterized by a convection-diffusion equation, that in the overdamped regime, reads:

$\begin{array}{cc}{\partial }_{t}P\left(x,y,t\right)=\nabla ·D\beta \left(P(x,y,t)\nabla U(x,y)\right)+D{\nabla }^{2}P\left(x,y,t\right)& (1)\end{array}$

where D is the diffusion coefficient and U(x, y) is the total energy coming from a conservative potential acting on the particles, β = k_BT⁻¹ with k_B the Boltzmann constant and T the temperature. When particles move in a confined region such as a narrow channel, the boundary condition for the probability distribution will vary according to the channel amplitude. If the channel y-section varies solely along the x-direction and it is constant along z, the free space accessible to the center of mass of a point-like particle is 2h(x)L_z, being h(x) the half-width of the channel along the y-direction and L_z the width along the z-direction. For such a situation, we encode the presence of the channel and of all conservative potentials, in the overall potential energy U(x, y, z) defined as:

$\begin{array}{l}U\left(x,y,z\right)=U\left(x+L,y,z\right)\\ U\left(x,y,z\right)=V\left(x,y\right),\left|y\right|\le h(x)\left|z\right|\le L_z/2\\ U\left(x,y,z\right)=\infty ,\left|y\right|>h(x)or\left|z\right|>L_z/2\end{array}$

that is periodic along the longitudinal direction, x, and confines the particles inside the channel.

We will assume that the particle distribution equilibrates much faster in the cross section of the channel than along the main transport direction. This condition is fulfilled for smoothly varying-section channels, ∂_xh « 1, in which particle distribution reaches local equilibrium in the cross section almost immediately. Under this condition, we can approximate the radial profile of the probability distribution function, P(x, y, t), can be approximated as:

$\begin{array}{cc}P\left(x,y,z,t\right)=p\left(x,t\right)\frac{e^{-\beta V\left(x,y\right)}}{e^{-\beta A(x)}}& (2)\end{array}$

where

$\begin{array}{cc}{e}^{-\beta A(x)}={\displaystyle {\int }_{-L_z/2}^{L_z/2}{\displaystyle {\int }_{-h(x)}^{h(x)}{e}^{-\beta V(x,y)}}}dydz.& (3)\end{array}$

being A(x) the potential of the mean force that can be identified with the free energy in the coarse-grained description. By integration of Equation1 over dy, dz one then obtains:

$\begin{array}{cc}\dot{p}(x,t)={\partial }_{x}D\left[\beta p(x,t){\partial }_{x}A(x)+{\partial }_{x}p(x,t)\right].& (4)\end{array}$

Equation 4 encodes both the confining and the conservative potentials given by Equation 2 in the free energy A(x).

Since all the quantities of interest are independent of z, without loss of generality we express quantities in units of L_z. It is possible to identify the contribution to the free energy coming from conservative potentials as:

$\begin{array}{cc}\langle V(x)\rangle =e^{\beta A(x)}{\displaystyle {\int }_{-h(x)}^{h(x)}V}(x,y)e^{-\beta V(x,y)}dy& (5)\end{array}$

Therefore we can identify the entropic contribution in Equation 3 by TS(x) = 〈V(x)〉 − A(x) hence resulting:

$\begin{array}{cc}S(x)=\ln \left({\displaystyle {\int }_{-h(x)}^{h(x)}{e}^{-\beta V(x,y)}}dy\right)+\beta \langle V(x)\rangle .& (6)\end{array}$

In the linear regime, reached when βV(x, y) « 1, Equation 6 yields:

$S(x)\simeq \ln (2h(x))$

The entropy, S(x), has a clear geometric interpretation, being the logarithm of the space, 2h(x), accessible to the center of mass of the tracer. Accordingly, we introduce the entropy barrier, ΔS, defined as:

$\begin{array}{cc}\Delta S=\ln \left(\frac{h_{\text{max}}}{h_{\text{min}}}\right)& (7)\end{array}$

where h_max and h_min are the maximum and the minimum of the channel width respectively. We will consider a channel whose x-dependent width has the same periodicity as V(x, y) and is given by

$\begin{array}{cc}h(x)=h_0-R+h_1\sin \left[\frac{2\pi }{L}(x+{\varphi }_0)\right]& (8)\end{array}$

where h₀ is the average channel section, h₁ determines its modulation and R is the particle radius. h_max and h_min depend both on h₁, R and the dephasing, ϕ₀. The latter will be useful to control the relative displacement between geometrical and potential modulations, as discussed in the next Sections.

3. Diffusion Through a Pore

The motion of charged tracers in an electrolyte has become a matter of interest due to its relevance in both biological situations (40) as well in the development of micro- nano-fluidic devices (41). In many cases, tracers move in an electrolyte that is embedded in a channel or in a porous medium. Due to the interaction with the electrolyte, the walls of the channel or the porous medium accumulate net charge (42). Hence a net, screened, electric field develops inside the channel. This feature is at the basis of phenomena such as electro-osmosis and it has been exploited for micro- nano-pumping (41). The currents in these devices generally rely on the control of some external force such as hydrostatic or electric fields. Tuning the external forcing leads to the control of particle currents as it happens, for example, in sodium-potassium pumping in neurons (40). The treatment of the motion of the electrolyte and the fluid inside channels of varying shape (43) or the diffusion of charged tracers in porous media (44) is challenging computationally.

Recently, different groups (45), (46) have characterized the flow in varying-section channels when the electrostatic field generated by the charge channel walls is characterized by a Debye screening length, k⁻¹, that is vanishing small compared to the channel half-amplitude, h(x) (42), and homogenization techniques have been proposed for the regime where the k⁻¹ is larger than the channel width for channels of generic shape (47). The regime where k⁻¹ is comparable to the channel bottleneck has not been characterized before. In this regime, the comparable length scales of the Debye double layer and the channel amplitude lead to a competition between electrostatic forcing and geometric confinement and can induce new dynamic scenarios where channel modulation plays a relevant role in charged tracer transport (Malgaretti, in preparation). This regime has already shown interesting features, such as current inversion and negative mobility for forced electrolytes (Malgaretti, in preparation).

In order to study the motion of tracers embedded in a varying-section channel, as sketched in Figure 2 characterized by charged walls, the electrostatic potential, ψ(x, y), inside the channel must be known. In order to do so, one should solve the, 2D, Poisson equation:

$\begin{array}{cc}{\partial }_x^2\psi (x,y)+{\partial }_y^2\psi (x,y)=-\frac{{\rho }_q(x,y)}{ϵ}& (9)\end{array}$

with the boundary condition given by Equation 2, being ρ_q = ρ₀ exp(−βzeψ(x, y)) the, equilibrium, charge density inside the channel. Assuming smoothly-varying channel walls, ∂_xh « 1, one can take advantage of the lubrication approximation, ∂²_xψ(x, y) « ∂²_yψ(x, y). It is possible to reduce Equation 9 to an effective 1D equation for the potential ψ(x, y). Such an approximation introduces an error in the electrostatic field that can be estimated. In fact we know that, prior to the lubrication approximation, the electrostatic field is perpendicular to the channel wall. Hence, for varying-section channel, one should count for the projection of the electrostatic field along the radial direction when solving the Poisson equation. For smoothly-varying channel amplitude case under study the projected electrostatic field reads:

$\begin{array}{cc}E=E_0\cos (\alpha )& (10)\end{array}$

being α = arctan (∂_xh(x)). Due to the assumption on the smoothness of the variation of channel amplitude, ∂_xh(x) « 1 leading to a second order correction in ∂_xh(x) for the electrostatic field

$\begin{array}{cc}E=E_0\left(1-\frac{1}{2}{({\partial }_{x}h(x))}^2\right).& (11)\end{array}$

FIGURE 2

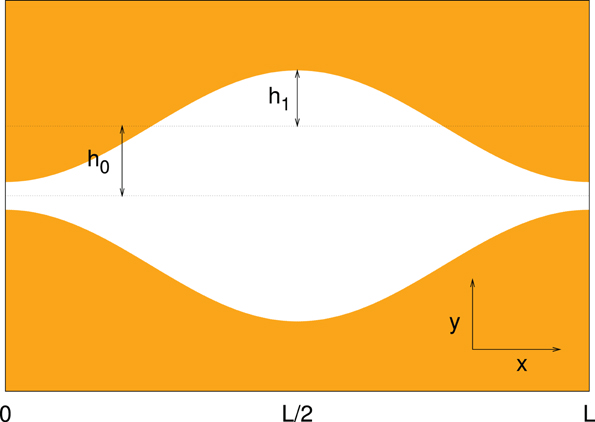
Figure 2. Schematic view of a channel characterized by an average width h₀, modulation h₁ and period L. The channel width is assumed constant along the z direction assumed to point out of the page.

In the following we will neglect such a correction assuming, E = E₀ along the channel. Assuming low salt concentration in the electrolyte and small ζ potential on channel walls Equation 9 can be further simplified by linearizing the charge density ρ_q(x, y) ≃ ρ₀ (1 − βzeψ(x, y)), hence getting:

$\begin{array}{cc}\psi (x,y)=\zeta \frac{\cosh (ky)}{\cosh (kh(x))}& (12)\end{array}$

for a channel made by conducting walls or

$\begin{array}{cc}\psi (x,y)=\frac{\sigma }{2ϵ}\frac{\cosh (ky)}{\sinh (kh(x))}& (13)\end{array}$

for an insulating-wall channel characterized by a constant surface-density of electric charge σ, being ϵ the dielectric constant of the electrolyte. Such an assumption, known as Debye-Huckel approximation, allows to identify the screening length, k⁻¹, of the electrostatic potential as k² = βzeρ₀/ϵ.

3.1. Mean First Passage-Time

In order to characterize the geometrically induced contribution to the diffusion of charged tracers at equilibrium, we will analyze the first passage time distribution. In particular we focus on the the mean first passage time (MFPT) that tracers take to pass through the channel. Such a quantity has a twofold interest. On one hand, the MFPT captures, even at equilibrium where all currents vanish, the role played by the geometrically-induced potential. On the other hand, it is an interesting quantity for situations like ion trapping or chemical segregation as happens in nuclear waste containers. In the following, we assume that one of the ends of the channel, namely the one at x = 0, is in contact with a reservoir of tracers and we are interested in the MFPT that positive, negative or neutral tracers, t_{±, 0}(x), take to diffuse from x to the other end of channel located at x = L. Such a situation leads to a reflecting boundary condition on the end of the channel in contact with the reservoir, i.e., at x = 0, and to an absorbing condition on the other end, at x = L. Taking advantage of the 1D projection, Equation 4, we can calculate the x-dependent MFPT, t(x), by solving (48):

$\begin{array}{cc}\beta D{\partial }_{x}A(x){\partial }_x{t}_{\pm ,0}(x)+D{\partial }_x^2{t}_{\pm ,0}(x)=-1& (14)\end{array}$

where A(x), according to Equation 3, is given by

$\begin{array}{cc}A(x)=-\frac{1}{\beta }\ln {\displaystyle {\int }_{-h(x)}^{h(x)}{e}^{-\beta ze\psi (x,y)}}dy& (15)\end{array}$

By numerically solving Equation 14, the MFPT of tracers crossing the channel is given by T_±,0 = t_±,0(0). Figure 3A shows the MFPTs for positive (blue squares) as well negative tracers (red dots) across a varying-section channel normalized by the MFPT of neutral tracers, T₀, whose MFPT does not depend on k⁻¹. When the Debye length, k⁻¹, is comparable with the channel minimum amplitude, h_min, negative tracers, attracted towards the positive charged walls, benefit from the modulation induced by the corrugation of the channel and their MFPT is smaller than the one corresponding to neutral tracers. Positive tracers, depleted from the channel walls, experience an enhanced electrostatic barrier at the channel bottleneck that increases their MFPT. Interestingly, such a modulation in the MFPT for charged tracers vanishes for kh_min « 1 as well as for kh_min» 1, underlying the relevance of the regime, kh_min ~ 1, under study.

FIGURE 3

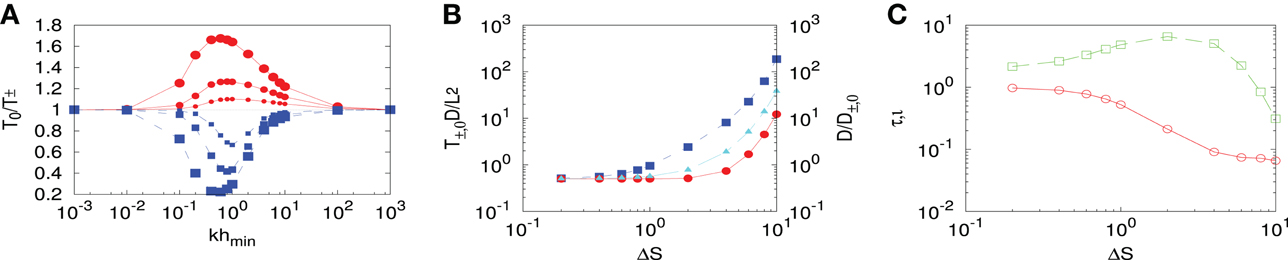
Figure 3. Influence of the entropic barrier on the MFPT. (A): inverse of the MFPT, 1/T_±, normalized by the MFPT of neutral tracers T₀, as a function of the inverse Debye length, k⁻¹, normalized by the minimum channel amplitude h_min for positive, βqζ = 3, (blue squares) or negative, βqζ = −3, (red dots) tracers in a conducting channel characterized by ΔS = 2.2. (B) MFPT, T, normalized by L²/D, as a function of the entropic barrier ΔS for positive (blue squares), βqζ = 3, neutral (cyan triangles), or negative (red dots), βqζ = −3, tracers in a conducting channel being kh_min = 1 for all points in the figure. (C) ratio of the MFPTs (red circles), τ = T₋/T₊, and “current” (green squares), $i=\frac{2L^3}{\sigma D}\frac{\left|{\rho }_{+}{T}_{-}-{\rho }_{-}{T}_{+}\right|}{T_{-}{T}_{+}}$ being T_± the MFPT of positive (negative) tracers and σ the charge density on the channel walls as a function of the entropic barrier ΔS for the same parameters as in (B).

The dependence of the MFPTs on the entropy barrier is shown in Figure 3B. While for vanishing values of ΔS all tracers show the same MFPT, a monotonous increase in the MFPT for all tracers is observed upon increasing ΔS. The increase in the MFPT even for neutral tracers is of solely entropic origin. Hence Figure 3B confirms the enhanced sensitivity of positive tracers with respect to negative ones upon variation of the geometry of the channel. The relative behavior of positive with respect to negative tracers can be useful for application as chemical segregation or particle separation. The ratio of the MFPTs of positive and negative tracers, $\tau =\frac{T_{+}}{T_{-}}$ is shown in Figure 3C. For vanishing values of ΔS, positive and negative tracers experience the same MFPT while for increasing ΔS negative tracers can be as faster as an order of magnitude leading to a ratio of the order of τ ~ 10⁻¹. The asymmetry in the MFPT for positive and negative tracers suggest the onset of net currents as a response to fluctuations in tracers density. According to linear response theory one can define the dimensionless current $i=\frac{2L^3}{\sigma D}\frac{\left|{\rho }_{+}{T}_{-}-{\rho }_{-}{T}_{+}\right|}{T_{-}{T}_{+}}$. In equilibrium the distribution probability of the fluctuations is such that these relaxation currents, on average, cancel out. However, it is interesting to notice the non monotonous behavior of such currents with respect to the entropic barrier and the presence of a maximum in the region ΔS ~ 1 reminding what the out-of-equilibrium system behavior (Malgaretti, in preparation).

4. Confined Brownian Ratchets

Since Feynman in 1962 proved that the coupling of a periodic substrate with thermal fluctuation in an out-of-equilibrium environment, i.e., a Brownian ratchet, might bring to rectification of the thermal fluctuations, Brownian ratchets have spread in many fields ranging from biophysics, where they are used to model molecular motors (49), to synthetic systems (50), and artificial steppers (51–53). Due to their reduced dimensions, these micro-nano-metric systems are often embedded in a confined region whose boundary condition might affect significantly the behavior of the system. The rational is that the confinement, by modulating the free space particles can explore, affects the overall particle dynamics. Such a scenario has been observed in several experimental situations ranging from micrometric systems, like microfluidic devices (54, 55) or colloids moving in optical tweezer arrays (56), to nanometric conditions, as realized with molecular motors (49, 57), down to the atomic scale where optical trapping allows to manipulate cold atoms (58).

To analyze the impact of confinement in the rectification of a Brownian particle, we will consider two different types of complementary, well-established ratchet models that have the same periodicity as the geometric confinement (38, 59). In the former case we deal with a rocking ratchet where the position dependence of the amplitude of the noise (multiplicative noise) breaks detailed balance leading to net currents for asymmetric ratchet potentials. Alternatively, we consider a bio-inspired model developed to study molecular motors dynamics. For both models the potential is given by:

$\begin{array}{cc}V(x)=V_0\left[\sin \frac{2\pi }{L}x+\lambda \sin \frac{4\pi }{L}x\right]& (16)\end{array}$

where the parameter λ measures the degree of asymmetry of the potential

4.1. Flashing Ratchet

A possible route to generate particle fluxes out of the rectification of thermal fluctuation is provided by flashing ratchets. In such devices a colloidal particle is subjected to a periodic external potential

and it is exposed to a position-dependent random force that breaks detailed balance (56). This can be simply achieved for a Gaussian white noise with a second moment amplitude $g(x)=\sqrt{D(x)+Q{\left({\partial }_x{V}_0(x)\right)}^2}$ (60), where Q controls Brownian rectification and D(x) accounts for the corrugation-induced modulations in the effective diffusion coefficient (14). In the Fick-Jacobs limit, the equation for such a flashing ratchet in a varying-section channel reads

$\begin{array}{cc}\frac{\partial }{\partial t}p(x)=\frac{\partial }{\partial x}\left\{g(x)\frac{\partial \left[p(x)g(x)\right]}{\partial x}+D(x)p(x)\frac{\partial \beta A(x)}{\partial x}\right\}& (18)\end{array}$

According to the last expression, equilibrium is achieved for Q = 0. For Q > 0 detailed balance is broken and net fluxes arise when the effective free energy difference over the channel period, ΔF = ∫^L₀∂_xA(x)dx, is not vanishing, i.e., for:

$\begin{array}{cc}\beta \Delta F={\displaystyle {\int }_0^L\left[\frac{D(x){\partial }_{x}A(x)}{g{(x)}^2}+\frac{\partial }{{\partial }_x}\ln g(x)\right]}dx\ne 0.& (19)\end{array}$

The second term, ${\displaystyle {\int }_0^L{\partial }_x}\ln g(x)dx$, is vanishingly small for a periodic channel. As a result particle currents emerge from the interplay between both the entropic and enthalpic forces, encoded in A(x) and the position-dependent noise, g(x). Three dimensionless parameters govern the Brownian ratchet performance: β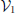 and ΔS quantify the relevance of the enthalpic and entropic contributions, respectively, while Q/(L²D₀(R)) determines rectification.

The relative performance of a ratchet in a uniform channel, defined as the ratio between the Brownian ratchet average speed, v and the average speed of a particle with mobility ũ ≡ βD₀ under the action of a uniform effective force, f₀ ≡ ΔF₀/L can be quantified in terms of the dimensionless parameter:

$\begin{array}{cc}{\mu }_0=\frac{L\overline{v}}{\tilde{\mu }\Delta F_0}& (20)\end{array}$

where $\overline{v}=\frac{1}{L}{\displaystyle {\int }_0^{L}J}(x)dx$ with J(x) = D[βp(x, t)∂_xA(x) + ∂_xp(x, t)] derived from Equation 4. When the ratchet does not lead to rectification, ΔF₀ = 0, μ₀ remains 1. Alternatively, when the ratchet leads to an intrinsic rectification, in order to capture the overall performance we need to replace the free energy drop ΔF₀, typical of a flat channel, with the overall free energy drop, ΔF, as given by Equation 19. Accordingly we define the dimensionless parameter

$\begin{array}{cc}\mu =\frac{L\overline{v}}{\tilde{\mu }\Delta F}& (21)\end{array}$

Uniform channels, for which there is no coupling between he ratchet potential and the confinement, lead to μ/μ₀ = 1. Therefore, deviations of μ/μ₀ from 1 can be regarded as a convenient means to address the interplay between the geometrical confinement and the intrinsic dynamics of the Brownian ratchet. In particular, when μ/μ₀ > 1 the geometrical constraints cooperate with the force associated to the Brownian ratchet to induce an efficient cooperative rectification, larger than the one obtained in an unstructured environment. On the contrary, when μ/μ₀ < 1 the confinement and the ratchet counter balance each other reducing the value of μ/μ₀. A part of the comparison with μ₀ the absolute value of μ provides insight into the dynamics. On one hand, when μ > 1 the performance of the cooperative rectification beats the one obtained under a constant, effective, force f ≡ ΔF/L, while the opposite holds for μ < 1 On the other hand μ easily identifies the non-linear rectifying regime, when ∂_fμ ≠ 0.

4.2. Two State Molecular Motor

Molecular motors are characterized by an heterogeneous dynamics for which motors perform very quick steps along the filament they move on interspersed with larger pauses. Different models have been proposed to account for such a dynamics, ranging from discrete (61), to continuous (62) [for a quite comprehensive review on molecular motors model see ref. (60)]. Here we use the so called “two-state ratchet model” that is a standard, simple framework to describe molecular motor motion along filaments. According to this model, a molecular motor is regarded as a Brownian particle characterized by two internal states, i = 1, 2, (strongly and weakly bound) that determine under which potential, V_{i = 1, 2}, the particle displaces (63). It is possible to break detailed balance by a proper choice of the hopping rates ω_12,21 between the two states. In this situation, the energy injected into the system by the hopping dynamics couples to the potential of the bound sate, V₁(x), and, for asymmetric potentials V₁, it leads to a net molecular motor velocity v₀≠0. The processive nature of the motors significantly affects motors overall dynamics. Infinitely-processive molecular motors remain always attached to the filament along which they displace and are affected by the geometrical restrictions only while displacing along the filament; accordingly, we choose channel-independent binding rates ω_{21, p}(x) = k₂₁. On the contrary, highly non-processive molecular motors detach frequently from the biofilament and diffuse away; an effect we account for considering a channel-driven binding rate, ω_21,np(x) = k₂₁/h(x). Motors jump to the weakly bound state only in a region of width δ around the minima of V₁(x), with rate ω₁₂ = k₁₂. Accordingly, the motor densities in the strong(weak) states, p₁₍₂₎ along the channel follow (63)

$\begin{array}{cc}\begin{array}{l}{\partial }_t{p}_1(x)+{\partial }_x{J}_1=-{\omega }_{12}(x)p_1(x)+{\omega }_{21}(x)p_2(x)\\ {\partial }_t{p}_2(x)+{\partial }_x{J}_2={\omega }_{12}(x)p_1(x)-{\omega }_{21}(x)p_2(x)\end{array}& (22)\end{array}$

where J_{1, 2}(x) = −D(x)[∂_xp_{1, 2}(x) + p_{1, 2}(x)∂_xβA_{1, 2}(x)] stands for the current densities in each of the two states in which motor displaces and D(x) accounts for the corrugation-induced modulations in the effective diffusion coefficient (14). Depending on the motor internal state, two free energies, A_{1, 2}(x) = V_{1, 2}(x) − k_BTS(x), account for the interplay between the biofilament interaction and the channel constraints.

4.3. Cooperative Rectification

The case of a symmetric potential and a symmetric channel, h₂ = λ = 0, is challenging because rectification is not possible when considering both potential separately and therefore no net particle current is observed. Currents may, however, arise due to the interplay between bot potentials.

4.3.1. Flashing ratchet

The steady state (ṗ(x) = 0), numerical solution of Equation 18, with h₂ = λ = 0, is shown Figure 4. As shown in Figure 4A, when the channel and the ratchet potential are not in registry a net particle current develops. Therefore the interplay between confinement and the ratchet potential leads, when out-of-phase, to net particle currents as captured by Equation 19. When the channel and the ratchet are not in phase, ϕ₀ ≠ 0, the overall free energy drop, Equation 19, is finite and a net current develops. The Fick-Jacobs equation identifies ϕ₀ and ΔS (defined in Equation 7) as the relevant parameters that control rectification. For any finite channel modulation, the spatial symmetry breaking is controlled by ϕ₀. On the contrary, a straight channel, ΔS = 0, will not induce rectification because the underlying potential is symmetric. Figure 4B shows that ΔS, as given by Equation 7, captures the changes in the system geometrical properties. In fact variations in both the particle radius, R, and the channel corrugation, h₁, are properly captured by ΔS. In particular, particle current dependence upon both, R and h₁, collapse on a main curve when represented as a function of ΔS.

FIGURE 4

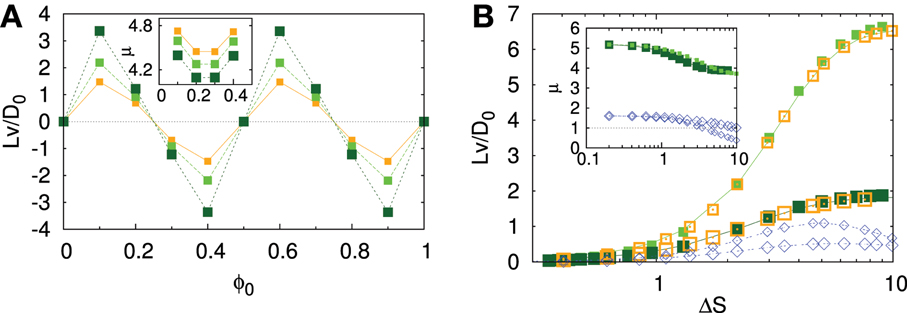
Figure 4. Cooperative-rectification induced velocity of a Brownian motor under the action of a symmetric flashing ratchet and confined in a symmetric channel. (A) Normalized particle velocity, in units of D₀/L with D₀ = D₀(R = 1), upon variation of the phase shift ϕ₀ for different values of the parameter ΔS = 1.73, 2.19, 2.94 (the larger the symbol size, the larger ΔS), with 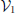= 0.2 and Q = 2. Inset: μ as a function of ϕ₀ for the same parameters. (B) Normalized particle velocity upon variation of ΔS for different particle radii R (solid lines, with h₀ = 1.25, h₁ = 0.2), h₀ (solid points, with R = 1, h₁ = 0.2) or h₁ (open points, with R = 1, h₀ = 1.25) with ϕ₀ = 0.1, 0.2 and 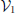= 0.2, Q = 2 (the larger the symbol the larger ϕ₀). As a comparison the case with 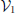= 0.2, Q = 0.02 and ϕ₀ = 0.1, 0.2, (the larger the symbol the larger ϕ₀)., is shown (blue diamonds). Inset: μ as a function of ΔS for the same parameters. Reprinted with permission from (59). Copyright (2013) by the American Physical Society.

The dependence of particle rectification on Q is quite smooth. For example the value of ΔS providing the maximum current is only weakly affected by a drop of Q of two orders of magnitude, as shown in Figure 4B. Since both the channel corrugation and the ratchet potential are symmetric, Figure 4A is symmetric under inversion of the velocity and dephasing angle. Therefore, a uniform distribution of ϕ₀ will not induce any net current, but any asymmetric distribution will.

The insets of Figure 4 display the changes of the dimensionless velocity, μ, as given by Equation 21, as a function of the relevant dimensionless parameters. They show that both regimes, μ > 1 and μ < 1 can be achieved. In particular for μ > 1 the confinement and the ratchet potential cooperate to induce an efficient particle rectification, while for μ < 1 they compete with each other, partially hindering rectification. Both regimes depend weakly on confinement, as shown in Figure 4, while μ is significantly affected by the magnitude of the noise amplitude, Q.

4.3.2. Two state molecular motor

The steady state (ṗ(x) = 0), numerical solution of Equation 22, with h₂ = λ = 0, is shown Figure 5. Net particle currents set when the ratchet potential and the channel corrugation are out of registry as shown in Figure 5A. The symmetry of the channel and rectifying potentials imply that the velocity profile is invariant if both axis of the figure are inverted; hence a uniform distribution of ϕ₀ will not induce a net current, but any asymmetric distribution will. The internal reorganization of the molecular motor as it moves along the channel allows for qualitatively new scenarios with respect to the rectification features observed for the flashing ratchet. Interestingly, we observe particle flux reversal, see Figure 5B, upon increase in ΔS. This flux reversal can be exploited to induce particle separation according to its size (due to the implicit dependence of ΔS on particle radius, R), or the differential particle response to .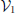

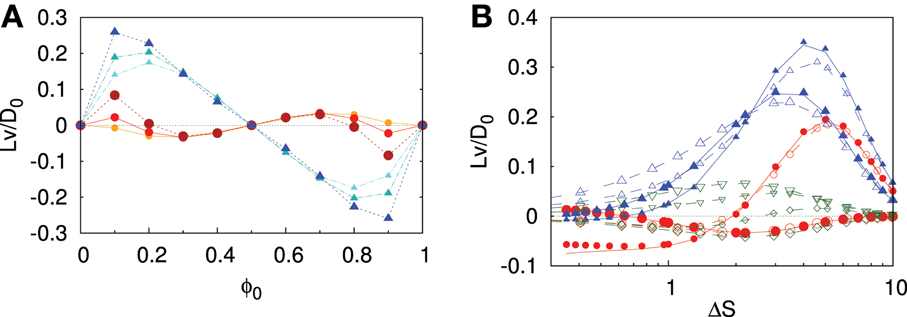
FIGURE 5

Figure 5. Cooperative-rectification induced velocity of processive (circles) and non-processive (triangles) molecular motors embedded in a symmetric channel. (A) Normalized particle velocity, in units of D₀/L with D₀ = D₀(R = 1), upon variation of the phase shift ϕ₀ for different values of the parameter ΔS = 1.73, 2.19, 2.94 (the larger the symbol size, the larger ΔS), for 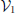= 0.2 and ω_{2, 1}/ω_{1, 2} = 0.01. (B) Normalized velocity, in units of D₀/L, against entropic barrier for processive (circles), non-processive (triangles) molecular motor as a function of ΔS upon variation of particle radius R (solid lines, for h₀ = 1.25, h₁ = 0.2), h₀ (solid points, for R = 1, h₁ = 0.2) or h₁ (open points, for R = 1, h₀ = 1.25) for ϕ₀ = 0.1, 0.2(larger symbols correspond to larger ϕ₀). As a comparison, the case for ϕ₀ = 0.1, 0.2 and 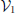= 0.2 is shown (green diamonds) (the larger the symbol the larger ϕ₀) with ω_{2, 1}/ω_{1, 2} = 0.01. (The curves for 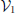= 1 have been magnified by a factor of 5 for the sake of clarity). Reprinted with permission from (59). Copyright (2013) by the American Physical Society.

As for the flashing ratchet, ΔS captures the essential features of net molecular motor motion upon variations of the overall geometry of the system. However, Figure 5B shows a weaker separate sensitivity of motors currents on the geometrical channel parameters, h₀, h₁, as well as motor size R. As ΔS increases, the sensitivity to the separate variation of h₀, h₁ and R for the case of non-processive motors intensifies. These deviation from the geometrical dependence only through ΔS arise because the binding rate, ω_{2, 1}, depends on the probability that the motor is close to the filament, which depends indirectly on the channel section. Hence, different channel amplitudes h₀, h₁, R, even if leading to the same ΔS, give rise to different binding rates that modulate the molecular motor velocity.

Molecular motors show a maximum current for an optimal ΔS that depends weakly on 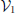, as displayed in Figure 5B.

4.4. Effect of the Confinement on Rectification

The case of an asymmetric ratchet, λ ≠ 0, and a symmetric channel, h₂ = 0, allows us to address the impact that an inhomogeneous environment has on an intrinsically rectifying Brownian ratchet. In this regime, the net current provided by the ratchet will be affected by the corrugation. Interestingly, we find that such modulations are quite relevant and can lead to significant velocity speed and even to velocity reversal.

4.4.1. Flashing ratchet

The steady state (ṗ(x) = 0), numerical solution of Equation 18, with h₂ = 0, λ ≠ 0, is shown Figure 6. The interplay between the ratchet and the corrugation strongly affects the intrinsic Brownian ratchet net velocity, v₀, as shown in Figure 6A. In this case we observe two regimes. On one hand the average velocities exceed v₀, showing strong velocity enhancements, while on the other the velocities change sign, indicating confinement-induced flow reversal. In the latter case, particles moving against the direction imposed by the ratchet can display speeds larger than v₀. As for the previous cases, the entropy barrier ΔS captures the dependence of particle current upon variation of the geometric parameters and the interplay between the ratchet and the entropic potential is magnified when rising the entropy barrier ΔS, as shown in Figure 6B. In the presence of flux reversal, geometrical confinement leads to a mechanism for particle separation based on their size because ΔS depends both on the channel geometry and the particle size. As shown in Figure 6B, modulating the size of the particles one can control and switch their velocities, offering new venues to manipulate particles and even to trap them. The average particle current obtained in a disordered channel, i.e., with a uniform distribution of ϕ₀, is not much affected by the geometrical constraint.

FIGURE 6

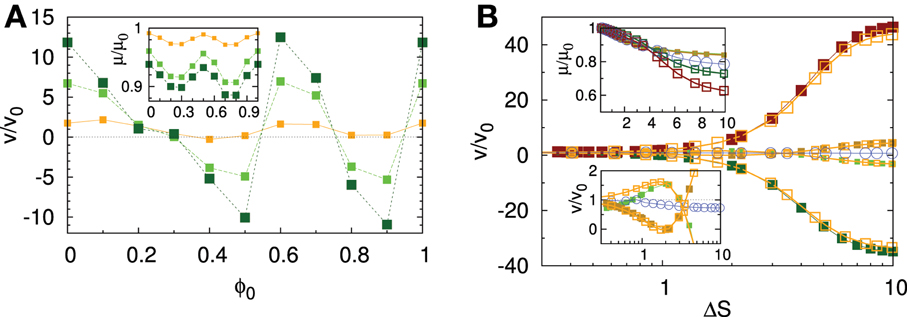
Figure 6. Confinement modulated velocity for a Brownian motor moving due to an asymmetric flashing ratchet in a symmetric channel. (A) Normalized particle velocity, in units of v₀ = v(ΔS = 0), upon variation of the phase shift ϕ₀ for different values of the parameter ΔS = 0.84, 2.19, 2.94 (the larger the symbol size, the larger ΔS), for 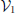= 0.2 and Q = 2. Inset: μ, in units of the dimensionless mobility, μ₀, as a function of ϕ₀ for the same parameters. (B) Normalized particle velocity upon variation of ΔS as obtained by varying particle radius R (solid lines, with h₁ = 1.25, h₂ = 0.2), h₁ (solid points, with R = 1, h₂ = 0.2) or h₂ (open points, with R = 1, h₁ = 1.25) for ϕ₀ = 0.2, 0.3, 0.5, 0.6 and 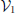= 0.2, Q = 2 (the larger the symbol size, the larger ϕ₀). Cyan open circles represent the average velocity obtained by a uniform distribution of ϕ₀ as a function of ΔS. Inset: μ/μ₀ as a function of ϕ₀ for the same parameters. Reprinted with permission from (59). Copyright (2013) by the American Physical Society.

Since the Brownian ratchet is characterized by an intrinsic rectifying velocity, v₀, it is useful to study the ratio μ/μ₀ in order to quantify the relative variation in the mobility of the system due to geometrical constraints. In Figures 6A,B μ₀ = 6.1, hence the system takes advantage of the x-dependent effective free energy drop, ΔF, induced by the intrinsic ratchet mechanism.

4.4.2. Two state model

The, steady state (ṗ(x) = 0), numerical solution of Equation 22, with h₂ = 0 λ ≠ 0, is shown Figure 7. The net velocity as a function of the dephasing between the geometric confinement and the underlying ratchet potential is shown in Figure 7A. Cooperative rectification now shows a strong dependence on the phase shift, ϕ₀, leading to large velocity amplification and also to flux reversal, a feature that was not possible for symmetric channels. In fact, both processive and non-processive motors show velocity enhancement and reversal when varying the channel corrugation, ΔS, as shown in Figure 7B. Hence, even symmetric channels offer the possibility to control molecular motor motion according to their size, allowing for segregation and particle trapping. As compared to the case of a symmetric ratchet, for asymmetric ratchets the entropic barrier ΔS captures even better the dynamics and only at smaller ΔS the different behavior upon variation of h₀, h₁ and R becomes appreciable.

FIGURE 7

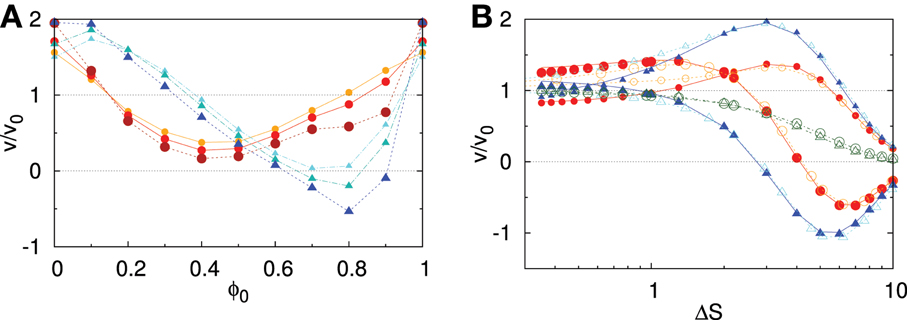
Figure 7. Confinement modulated velocity for a processive (circles), non-processive (triangles) molecular motor moving in symmetric channel. (A) Normalized particle velocity, in units of v₀ = v(ΔS = 0) as a function of the phase shift ϕ₀ for different values of the parameter ΔS = 1.73, 2.19, 2.94 (the larger the symbol size, the larger ΔS), for ΔV₁ = 0.2 and ω_{2, 1}/ω_{1, 2} = 0.01. (B) Normalized processive (circles), non-processive (triangles) molecular motor velocity, in units of v₀, as a function of ΔS and particle radius R (solid lines, with h₀ = 1.25, h₁ = 0.2), h₀ (solid points, with R = 1, h₁ = 0.2) or h₁ (open points, with R = 1, h₀ = 1.25) for ϕ₀ = 0.1, 0.9 (the larger the symbol size, the larger ϕ₀) for 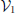= 1 and ω_{2, 1}/ω_{1, 2} = 0.01. Green open circles (triangles) represent the average velocity of processive (non-processive) motors obtained by a uniform distribution of ϕ₀ as a function of ΔS. Reprinted with permission from (59). Copyright (2013) by the American Physical Society.

5. Conclusions

In this article, we have shown the relevance of confinement in the transport properties of small-scale systems. We have used a diffusion theory which models the presence of spatial constrictions by entropic barriers and proposes the Fick-Jacobs equation to derive the main transport properties.

We have analyzed two different cases, namely the motion of Brownian motors in a varying section channel and the case of charged tracers diffusion trough a pore. In the former case, the energy injected in the system by the ratchet mechanism couples to the entropic potential induced by the confinement leading to new dynamic behavior not observed in the unbounded cases. In particular, net particle fluxes are predicted in situations in which neither of the two possible rectification mechanisms, i.e., the ratchet and the entropic rectification, are active. Moreover, even when Brownian motors develop net fluxes for unbound systems, the coupling with the confinement strongly affects the overall dynamics allowing both for velocity enhancement and velocity reversal. The latter shows a remarkable dependence on particle size opening the possibility of a new route for particle segregation. In the case of diffusion in a pore we have observed a size and corrugation dependence in the MFPT for neutral tracers underlying the relevant role played by the confinement for diffusive processes. For charged tracers, we observe an interplay between the inhomogeneous transverse tracer distribution and the confinement leading to more involved, charge dependent, MFPTs. In particular, varying the Debye screening length it is possible to almost prevent pore crossing for ions depleted from the walls whereas the diffusion of ions attracted to the walls is promoted.

Entropic transport is now being used to study transport of atoms in nanoporous materials, of particles in microfuidic devices and of ions in protein channels. The theoretical framework described enables one to consider in a simple way the influence of the shape of those quasi-1D structures on the main transport properties, an issue not addressed up to now due to the difficulties in solving the 2D and 3D transport equations. All in all, entropic transport offers new mechanisms for particle manipulation at small scales.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We acknowledge the Dirección General de Investigación (Spain) and DURSI project for financial support under projects FIS 2011-22603 and 2009SGR-634, respectively. J.M. Rubi acknowledges financial support from Generalitat de Catalunya under program Icrea Academia

References

1. van Kampen NG. Explicit calculation of a model for diffusion in nonconstant temperature. J Math Phys. (1988) 29:1220–4. doi: 10.1063/1.527963

CrossRef Full Text

2. Narváez A, Zauner T, Raischel F, Hilfer R, Harting J. Quantitative analysis of numerical estimates for the permeability of porous media from lattice-Boltzmann simulations. J Stat Mech. (2010), P11026. doi: 10.1088/1742-5468/2010/11/P11026

CrossRef Full Text

3. Narváez A and Yazdchi K. From creeping to inertial flow in porous media: a lattice Boltzmann-finite element study. J Stat Mech. (2013), P02038. doi: 10.1088/1742-5468/2013/02/P02038

CrossRef Full Text

4. Calero C, Faraudo J, Aguilella-Arzo M. First-passage-time analysis of atomic-resolution simulations of the ionic transport in a bacterial porin. Phys Rev E. (2011) 83:021908. doi: 10.1103/PhysRevE.83.021908

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

5. Song Yq, Ryu S, Sen PN. Determining multiple length scales in rocks. Nature (2000) 406:178–81. doi: 10.1038/35018057

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

6. Novikov DS, Kiselev VG. Effective medium theory of a diffusion-weighted signal. NMR Biomed. (2010) 23:682–97. doi: 10.1002/nbm.1584

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

7. Roosen-runge F, Hennig M, Zhang F, Jacobs RMJ, Sztucki M, Schober H, et al. Protein self-diffusion in crowded solutions. Proc Natl Acad Sci USA. (2011) 108:11815–20. doi: 10.1073/pnas.1107287108

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

8. Calvo-mu EM, Selvan ME, Xiong R, Ojha M, Keffer DJ, Nicholson DM, et al. Applications of a general random-walk theory for confined diffusion. Phys Rev E (2011) 83:011120–31. doi: 10.1103/PhysRevE.83.011120

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

9. Laachi N, Kenward M, Yariv E, Dorfman KD. Force-driven transport through periodic entropy barriers. EPL (2007) 80:50009. doi: 10.1209/0295-5075/80/50009

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

10. Su T, Purohit PK. Entropically driven motion of polymers in nonuniform nanochannels. Phys Rev E (2011) 83:061906–17. doi: 10.1103/PhysRevE.83.061906

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

11. Holcman D, Hoze N, Schuss Z. Narrow escape through a funnel and effective diffusion on a crowded membrane. Phys Rev E (2011) 84:021906–17. doi: 10.1103/PhysRevE.84.021906

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

12. Jacobs H M. Diffusion Processes. New York, NY: Springer-Verlag, (1967).

13. Zwanzig R. Dynamical disorder: Passage through a fluctuating bottleneck. J Chem Phys. (1992) 96:3926.

14. Reguera D, Rubi JM. Kinetic equations for diffusion in the presence of entropic barriers. Phys Rev E (2001) 64:061106. doi: 10.1103/PhysRevE.64.061106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

15. Kalinay P, Percus JK. Corrections to the Fick-Jacobs equation. Phys Rev E (2006) 74:041203. doi: 10.1103/PhysRevE.74.041203

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

16. Kalinay P, Percus JK. Approximations of the generalized Fick-Jacobs equation. Phys Rev E (2008) 78:021103. doi: 10.1103/PhysRevE.78.021103

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

17. Martens S, Schmidt G, Schimansky-Geier L, Hänggi P. Entropic particle transport: higher-order corrections to the Fick-Jacobs diffusion equation. Phys Rev E (2011) 83:051135. doi: 10.1103/PhysRevE.83.051135

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

18. Reguera D, Schmid G, Burada PS, Rubi JM, Reimann P, Hänggi P. Entropic Transport: Kinetics, Scaling, and Control Mechanisms. Phys Rev Lett. (2006) 96:130603. doi: 10.1103/PhysRevLett.96.130603

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

19. Burada PS, Schmid G, Reguera D, Rubi JM, Hänggi P. Biased diffusion in confined media: test of the Fick-Jacobs approximation and validity criteria. Phys Rev E (2007) 75:051111. doi: 10.1103/PhysRevE.75.051111

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

20. Berezhkovskii AM, Pustovoit, MA Bezrukov SM. Diffusion in a tube of varying cross section: Numerical study of reduction to effective one-dimensional description. J Chem Phys. (2007) 126:134706. doi: 10.1063/1.2719193

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

21. Vazquez MV, Berezhkovskii AM, Dagdug L. Diffusion in linear porous media with periodic entropy barriers: A tube formed by contacting spheres. J Chem Phys. (2008) 129:046101. doi: 10.1063/1.2955447

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

22. Ai BQ, Liu LG. Current in a three-dimensional periodic tube with unbiased forces. Phys Rev E (2006) 74:051114. doi: 10.1103/PhysRevE.74.051114

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

23. Siwy Z, Kosinska ID, Fulinski A, Martin CR. Rectification properties of conically shaped nanopores: consequences of miniaturization. Phys Rev Lett. (2005) 94:048102. doi: 10.1103/PhysRevLett.94.048102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

24. Kosinska ID, Fulinski A. Asymmetric nanodiffusion. Phys Rev E (2005) 72:011201. doi: 10.1103/PhysRevE.72.011201

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

25. Cheng KL, Sheng YJ, Tsao HK. Electrophoretic size separation of particles in a periodically constricted microchanne. J Chem Phys. (2008) 128:101101. doi: 10.1063/1.2890960

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

26. Berezhkovskii AM, Pustovoit MA, Bezrukov SM. Entropic effects in channel-facilitated transport: Interparticle interactions break the flux symmetry. Phys Rev E (2009), 80:020904. doi: 10.1103/PhysRevE.80.020904

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

27. Kalinay P, Percus JK. Mapping of diffusion in a channel with soft walls. Phys Rev E (2011) 83:031109. doi: 10.1103/PhysRevE.83.031109

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. Bowles RK, Mon KK, Percus JK. Normal and anomalous diffusion in highly confined hard disk fluid mixtures. J Chem Phys. (2004) 121:10668. doi: 10.1063/1.1811075

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

29. Burada PS, Schmid G, Reguera D, Vainstein MH, Rubi JM, Hnggi P. Entropic Stochastic Resonance. Phys Rev Lett. (2008) 101:130602. doi: 10.1103/PhysRevLett.101.130602

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

30. Burada PS, Schmid G, Reguera D, Rubi JM, Hnggi P. Double entropic stochastic resonance. Europhys Lett. (2009) 87:50003–9. doi: 10.1209/0295-5075/87/50003

CrossRef Full Text

31. Burada PS, Schmid G, Reguera D, Rubi JM, Hnggi P. Entropic stochastic resonance: the constructive role of the unevenness. Eur Phys J B (2009) 69:11. doi: 10.1140/epjb/e2009-00051-5

CrossRef Full Text

32. Ghosh PK, Marchesoni F, Savel'ev SE, Nori F. Geometric Stochastic Resonance. Phys Rev Lett. (2010) 104:020601. doi: 10.1103/PhysRevLett.104.020601

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

33. Borromeo M, Marchesoni F. The role of bistability in stochastic resonance. Eur Phys J B. (2009) 69:23–7. doi: 10.1140/epjb/e2009-00068-8

CrossRef Full Text

34. Rubi JM, Reguera D. Thermodynamics and stochastic dynamics of transport in confined media. Chem Phys. (2010) 375:518–23. doi: 10.1016/j.chemphys.2010.04.029

CrossRef Full Text

35. Marchesoni F, Savelev S. Rectification currents in two-dimensional artificial channels. Phys Rev E (2009) 80:011120. doi: 10.1103/PhysRevE.80.011120

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

36. Berezhkovskii AM, Makhnovskii YA, Zitserman VY. Transient diffusion in a tube with dead ends. J Chem Phys. (2007) 127:224712. doi: 10.1063/1.2805068

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

37. Dagdug L, Berezhkovskii AM, Makhnovskii YA, Zitserman VY. Particle size effect on diffusion in tubes with dead ends: nonmonotonic size dependence of effective diffusion constant. J Chem Phys. (2008) 129:184706. doi: 10.1063/1.3010709

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

38. Malgaretti P, Pagonabarraga I, Rubi JM. Cooperative rectification in confined Brownian ratchets. Phys Rev E (2012) 85:010105(R). doi: 10.1103/PhysRevE.85.010105

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

39. Pagonabarraga I, Rotenberg B, Frenkel D. Recent advances in the modelling and simulation of electrokinetic effects: bridging the gap between atomistic and macroscopic descriptions. Phys Chem Chem Phys. (2010) 12:9566–80. doi: 10.1039/c004012f

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

40. Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. Oxford: Garland Science, (2007).

41. Boquet L, Charlaix E. From microfluidic application to nanofluidic phenomena. Chem Soc Rev. (2010) 39:1073–95. doi: 10.1039/b909366b

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

42. Russell DB, Saville DA, Schowalter WR. Colloidal Dispersions. Cambridge: Cambridge University Press, (1989). doi: 10.1017/CBO9780511608810

CrossRef Full Text

43. Marini Bettolo Marconi U, Melchionna S. Charge transport in nanochannels: a molecular theory. Langmuir (2012) 28:13727–40. doi: 10.1021/la302815z

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

44. Rotenberg B, Pagonabarraga I, Frenkel D. Dispersion of charged tracers in charged porous media. EPL (2008) 83:34004. doi: 10.1209/0295-5075/83/34004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

45. Kosinska ID, Goychuk I, Kostur M, Schmidt G, Hänggi P. Rectification in synthetic conical nanopores: a one-dimensional Poisson-Nernst-Planck model. Phys Rev E (2008) 77:031131. doi: 10.1103/PhysRevE.77.031131

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

46. Ghosal S. Lubrication theory for electro-osmotic flow in a microfluidic channel of slowly varying cross-section and wall charge. J Fluid Mech. (2002), 459:103–128. doi: 10.1017/S0022112002007899

CrossRef Full Text

47. Marini Bettolo Marconi U, Melchionna S, Pagonabarraga I. Effective electrodiffusion equation for non-uniform nanochannels. J Chem Pys. (2013) 138:244107. doi: 10.1063/1.4811516

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

48. Risken H. The Fokker-Planck Equation. Berlin: Springer-Verlag, (1988).

49. Thomas G, Prost J, Martin P, Joanny JF. Coordination and collective properties of molecular motors: theory. Curr Opin Cell Biol. (2010) 22:14–20. doi: 10.1016/j.ceb.2009.12.012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

50. Hänggi P, Marchesoni F. Artificial Brownian motors: Controlling transport on the nanoscale. Rev Mod Phys. (2009) 81:387–442. doi: 10.1103/RevModPhys.81.387

CrossRef Full Text

51. Allison A, Abbott D. A MEMS Brownian ratchet. Microelectron J. (2002) 33:235–43. doi: 10.1016/S0026-2692(01)00096-9

CrossRef Full Text

52. Zhu BY, Marchesoni F, Nori F. Controllable stepmotors and rectifiers of magnetic flux quanta. Phys Rev Lett. (2004) 92:180602–12. doi: 10.1103/PhysRevLett.92.180602

CrossRef Full Text

53. Linke H, Xu H, Lo A, Sheng W, Svensson A, Omling P, et al. Voltage and temperature limits for the operation of a quantum dot ratchet. Physica B (1999) 272:61–3. doi: 10.1016/S0921-4526(99)00370-1

CrossRef Full Text

54. Dagdug L, Berezhkovskii AM, Makhnovskii YA, Zitsereman VY, Bezrukov S. Communication: Turnover behavior of effective mobility in a tube with periodic entropy potential. J Chem Phys. (2011) 134:101102. doi: 10.1063/1.3561680

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

55. Altintas E, Sarajlic E, Bohringerb FK, Fujita H. Numerical and experimental characterization of 3-phase rectification of nanobead dielectrophoretic transport exploiting Brownian motion. Sens Actuat A (2009) 154:123–31. doi: 10.1016/j.sna.2009.05.022

CrossRef Full Text

56. Lee SH, Ladavac K, Polin M, Grier DG. Observation of flux reversal in a symmetric optical thermal ratchet. Phys Rev Lett. (2005) 94:110601. doi: 10.1103/PhysRevLett.94.110601

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

57. Astumian RD. Thermodynamics and kinetics of molecular motors. Biophys J. (2010) 98:2401–9. doi: 10.1016/j.bpj.2010.02.040

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

58. Zelan M, Hagman H, Labaigt G, Jonsell S, Dion CM. Experimental measurement of efficiency and transport coherence of a cold-atom Brownian motor in optical lattices. Phys Rev E (2011) 83:020102. doi: 10.1103/PhysRevE.83.020102

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

59. Malgaretti P, Pagonabarraga I, Rubi JM. Confined Brownian ratchets. J Chem Phys. (2013) 138:194906. doi: 10.1063/1.4804632

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

60. Reimann P. Brownian motors:noisy transport far from equilibrium. Phys Rep. (2002) 361:57–265. doi: 10.1016/S0370-1573(01)00081-3

CrossRef Full Text

61. Chou T, Mallick K, Zia RKP. Non-equilibrium statistical mechanics: from a paradigmatic model to biological transport. Rep Prog Phys. (2011) 74:116601–42. doi: 10.1088/0034-4885/74/11/116601

CrossRef Full Text

62. Huxley AF. Muscle structure and theories of contraction. Prog Biophys. (1957) 7:255–318.

Pubmed Abstract | Pubmed Full Text

63. Jülicher F, Ajdari A, Prost J. Modeling molecular motors. RMP Colloquia. (1997) 69:1269. doi: 10.1103/RevModPhys.69.1269

CrossRef Full Text