Invisible decays of ultra-high energy neutrinos

The source of ultra high energy cosmic rays remains a mystery. In gamma-ray burst (GRB) models such as the fireball model cosmic-ray acceleration should be accompanied by neutrinos produced in the decay of charged pions created in interactions between the high-energy protons and γ-rays [39]. Recently the Ice-Cube collaboration reported an upper limit on the flux of energetic neutrinos associated with GRBs almost four times below this prediction [3].

Various possible explanations have been considered to explain the non-observation of this ultra high energy neutrino flux. For example, a complete detailed numerical analysis of the fireball neutrino model predicts a neutrino flux that is one order of magnitude lower than the analytical computations [24]. On the other hand, another recent computation [22] of the neutrino flux in the fireball model gives a mild reduction in the neutrino flux if a relation between the bulk Lorentz factor, Γ, and the burst energy is assumed. Finally, based on the specific case of GRB 130427A, it has been argued that the low neutrino flux can be explained with relatively large values for the bulk Lorentz factor (Γ ≥ 500) and for the dissipation radius (R_d ≥ 10¹⁴ cm); it was shown in the same reference that both the internal shock and the baryon photosphere models satisfied these conditions.

Here we focus on a different approach to explain the neutrino flux deficit. Instead of studying the astrophysical mechanism of the source objects, we look for a high energy physics explanation. Some mechanisms involving new physics in order to explain a possible deficit in the observed neutrino flux have already been suggested. For instance, the possibility of an oscillation involving a quasi Dirac neutrino [38] has been considered in Reference [13]; a specific model for this case has been studied in [25] and the possibility of a resonance effect has also been discussed [29]. Another mechanism recently discussed has been the case of a spin precession into a sterile neutrino as a result of a non-zero neutrino magnetic moment [35] and the strong magnetic fields expected to be present in a GRB [8].

Here we speculate on the plausibility of the neutrino decay hypothesis as a possible explanation for the mismatch between observation and expectation. The most attractive possibility involves invisible decays, which have been considered theoretically since the eighties [17, 18, 21, 34, 37], and recently revisited for the case of GRB neutrino fluxes [31]. These decays arise in models with spontaneous violation of ungauged lepton number [12], though typically suppressed [34]. A natural scenario to test neutrino stability are astrophysical objects [7, 9, 10, 27]. In particular, limits on Majoron couplings from solar and supernova neutrinos have been obtained in Reference [26]. For non-astrophysical constraints, for example from 0νββ searches, see [5, 16, 28, 36]. Moreover, as already mentioned, recent results from the Pierre Auger Observatory (PAO) [4], ANTARES [11] and IceCube [2] have placed strong constraints on the neutrino flux coming from distant ultra high energy (UHE) neutrino sources.

Here we explore the phenomenological plausibility and theoretical consistency of the decay hypothesis within a class of low-scale SU(3)_c ⊗ SU(2)_L ⊗ U(1)_Y seesaw schemes with spontaneous family-dependent lepton number violation. We show that the required neutrino decay lifetime range hinted by the non-observation of UHE muon neutrinos is theoretically achievable for the majoron-emitting neutrino decays and, moreover, consistent with all existing phenomenological constraints.

The decay rate ν_i → ν_j + J in the rest frame of ν_i is

$\begin{array}{cc}\Gamma ({\nu }_i\to {\nu }_j+J)=\frac{g_{ij}^2}{16\pi }\frac{{(m_i+m_j)}^2}{m_i^3}(m_i^2-m_j^2),& (1)\end{array}$

where ν_i and ν_j are active neutrinos and J is a massless or very light majoron associated to the spontaneous violation of ungauged lepton number. Taking m_j = 0, we can estimate the decay length (in meters) for a relativistic neutrino as given by

$\begin{array}{cc}L=c\tau =\frac{c{E}_i}{m_i\Gamma }\simeq 1\times {10}^9\left(g_{ij}^{-2}\right)\left(\frac{E_i}{100\text{TeV}}\right){\left(\frac{1\text{eV}}{m_i}\right)}^2\text{m}.& (2)\end{array}$

For typical AGN distances we obtain the required values of g_ij for a given neutrino mass m_i which would cause decay before reaching the detector. In Figure 1 we took AGN distances from 3.6 Mpc (the distance to Centaurus A) up to 100 Mpc. In the bottom panel of the same Figure 1 we have plotted the corresponding result for GRBs, at typical distances of 10–10³ Mpc. The vertical lines correspond to the relevant region for m₂ and m₃ for the case m₁ = 0. We have explicitly verified that, for the GRB case, this approximation is in agreement with more detailed estimates of neutrino lifetime ranges [6].

FIGURE 1

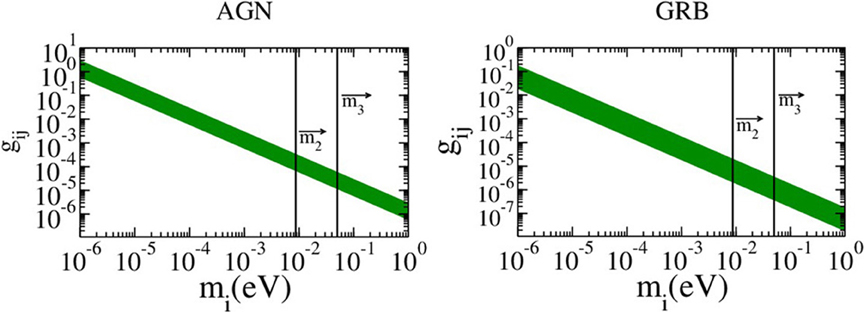
Figure 1. Neutrino mass m_i vs. the required coupling constant g_ij for the case of AGN's (left panel) and GRBs (right panel).

As we will discuss below, putting into a theory context, such couplings are fairly large to achieve theoretically. In order to have an estimate of the neutrino flux reduction resulting from neutrino decay we note that, since coherence is lost, the final flux of a given neutrino flavor will be

$\begin{array}{cc}{\varphi }_{{\nu }_{\alpha }}(E)={\displaystyle \sum _{i\beta }{\varphi }_{{\nu }_{\beta }}^{\text{source}}}(E)|U_{\beta i}{|}^2|U_{\alpha i}{|}^2{e}^{-L/{\tau }_i(E)},& (3)\end{array}$

where ϕ's are neutrino fluxes at production and detection, L the travel distance, τ_i the neutrino lifetime in the laboratory frame and U_αi the elements of the lepton mixing matrix [33]. Typical neutrino energies lie in the range of 10⁵ TeV and 10³ TeV for AGNs and GRBs, respectively. Note that, in the limit that L » τ_i where only the stable state survives Equation (3) becomes

$\begin{array}{cc}{\varphi }_{{\nu }_{\alpha }}(E)={\displaystyle \sum _{i(\text{stable})\beta }{\varphi }_{{\nu }_{\beta }}^{\text{source}}}(E)|U_{\beta i}{|}^2|U_{\alpha i}{|}^2.& (4)\end{array}$

Here we take a normal hierarchy neutrino mass spectrum, the disappearance of all states except the lightest (in this case ν₁) is allowed. The final flux of ν_e, ν_μ and ν_τ can be computed from Equation (4) and will depend on the three mixing angles and the Dirac CP phase δ. In particular, we can calculate the suppression of the muon neutrino flux, ϕ_νμ, using the ratio

$\begin{array}{cc}{R}_{{\nu }_e:{\nu }_{\mu }}\equiv \frac{{\varphi }_{{\nu }_e}}{{\varphi }_{{\nu }_{\mu }}}={\left(\frac{\cos {\theta }_{12}\cos {\theta }_{13}}{|-\sin {\theta }_{12}\cos {\theta }_{23}-\sin {\theta }_{13}\sin {\theta }_{23}\cos {\theta }_{12}{e}^{ı\delta }|}\right)}^2,& (5)\end{array}$

where θ₁₂, θ₂₃ and θ₁₃ are the neutrino mixing angles determined in neutrino oscillation experiments. The left panel of Figure 2 shows the expected values for this ratio when the neutrino mixing angles lie within the 1σ bands from their current global best fit values [14, 15, 20] One can also see, in the right panel of the same Figure 2 that by allowing these parameters to vary up to their three sigma ranges, R_νe:νμ can be as large as 25 or as low as 2. Very similar results are found for global fit of Reference [20], as shown in Table 1.

FIGURE 2

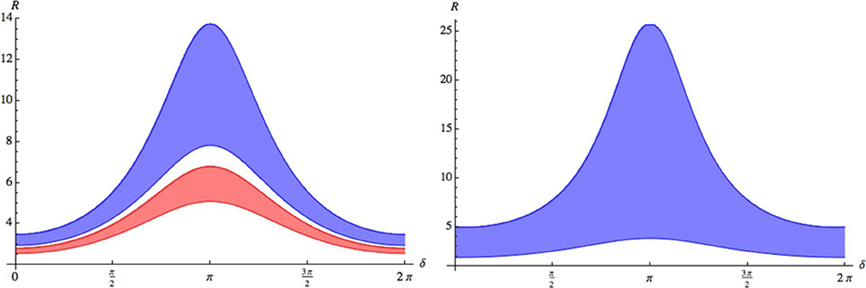
Figure 2. R_νe:νμ vs. the CP phase δ for neutrino mixing angles [15] at 1σ (left panel) and at 3σ (right panel). For the 1σ case we show two regions: one for θ₂₃ in the 1st octant (orange lower band) and another one for θ₂₃ in the 2nd octant (blue higher band). One can see that values of θ₂₃ in the 2nd octant give a stronger effect.

TABLE 1

Table 1. Allowed values of R_νe:νμ according to different neutrino oscillation fits.

It is important to notice that, in this picture, the neutrino decay will lead to a decrease in the muon neutrino flux while the electron neutrino flux will increase. Alternatively in the presence of light sterile states one can envisage a scenario where the muon neutrino decays to the sterile state. Here we do not consider this case. Recent data from Icecube reports the observation of two neutrinos with energies around 10¹⁵ eV, probably electron neutrinos [1]. Moreover, there have been recent announcements of more neutrino events detected in IceCube [40].

We now turn to the issue of theoretical consistency of the decay hypothesis. In most SU(3)_c ⊗ SU(2)_L ⊗ U(1)_Y seesaw models with spontaneous lepton number violation when one diagonalizes the neutrino mass matrix one also diagonalizes, to first approximation, the coupling of the resulting Nambu-Goldstone boson to the mass eigenstate neutrinos [34]. The exact form of the light-neutrino majoron couplings can be determined explicitly by perturbative diagonalization of the seesaw mass matrix, or by using a more general approach using only the symmetry properties. The result is [34]

$\begin{array}{cc}{g}_{ij}=-\frac{m_i}{v_1}{\delta }_{ij}+{\left[\frac{m_i}{v_1}{\left(V_1^{†}{D}^{\ast }{M}^{\ast -1}{M}^{-1}{D}^T{V}_1\right)}_{ij}\right]}_{\text{S}}+\dots & (6)\end{array}$

where the subscript S denotes symmetrization, D and M are the Dirac and Majorana mass terms in, say, the type-I seesaw scheme and V₁ is the light neutrino diagonalization matrix. One sees that the majoron couples proportionally to the light neutrino mass, hence the coupling matrix is diagonal to first approximation. The off-diagonal part of the g_ij is inversely proportional to three powers of lepton number violation scale v₁ ≡ 〈σ〉, since M ∝ v₁. This is tiny, the only hope being to use a seesaw scheme that allows for a very low lepton number violation scale, such as the inverse seesaw [30]. The particle content is the same as that of the Standard Model (SM) except for the addition of a pair of two component gauge singlet leptons, ν^c_i and S_i, within each of the three generations, labeled by i. The isodoublet neutrinos ν_i and the fermion singlets S_i have the same lepton number, opposite with respect to that of the three singlets ν^c_i associated to the “right-handed” neutrinos. In the ν, ν^c, S basis the 9 × 9 neutral lepton mass matrix M_ν has the form:

$\begin{array}{cc}{M}_{\nu }=\left[\begin{array}{ccc}0& m_D^T& 0\\ m_D& 0& M^T\\ 0& M& \mu \end{array}\right],& (7)\end{array}$

where m_D ∝ 〈Φ〉 is the standard Dirac term coming from the SM Higgs vev and M is a bare mass term. The term μ ∝ 〈σ〉, the vacuum expectation value of σ responsible for spontaneous low-scale lepton number violation as proposed in [21]. This gives rise to a majoron J,

$\begin{array}{cc}J=\sqrt{2}\text{Im}\sigma .& (8)\end{array}$

As a result of diagonalization one obtains an effective light neutrino mass matrix. Note that lepton number symmetry is recovered as μ → 0, making the three light neutrinos strictly massless. The majoron couplings of the light mass eigenstate neutrinos are determined again as a sum of two pieces as in Equation (6). Detailed calculation shows that its off-diagonal part behaves as P′ ~ μ²D²M⁻⁴. Even if the M can be significantly lower than that of the standard high-scale type-I seesaw it is clear that this is way too small in order to produce neutrino decay within the relevant astrophysical scales.

The only way out is to induce a mismatch between the neutrino mass basis and the coupling basis. This can be achieved by making lepton number a family-dependent symmetry [17, 18]. The model is by no means unique, here we give an example based on SU(3)_c ⊗ SU(2)_L ⊗ U(1)_Y ⊗ U(1)_H assigned as shown in Table 2.

TABLE 2

Table 2. Model field representation content and transformation properties.

The SU(3)_c ⊗ SU(2)_L ⊗ U(1)_Y ⊗ U(1)_H invariant Lagrangian would be

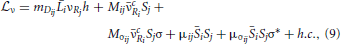
where the relevant sub-matrices are

$\begin{array}{cc}{m}_D=\left[\begin{array}{ccc}{m}_a& m_b& 0\\ m_c& m_d& 0\\ 0& 0& m_e\end{array}\right],M=\left[\begin{array}{ccc}0& 0& M_1\\ 0& 0& M_2\\ 0& 0& 0\end{array}\right],& (10)\end{array}$

$\begin{array}{cc}{M}_{\sigma }=\left[\begin{array}{ccc}{M}_3& M_4& 0\\ M_5& M_6& 0\\ 0& 0& M_7\end{array}\right]& (11)\end{array}$

$\begin{array}{cc}\mu =\left[\begin{array}{ccc}{M}_8& M_9& 0\\ M_{10}& M_{11}& 0\\ 0& 0& 0\end{array}\right],{\mu }_{\sigma }=\left[\begin{array}{ccc}0& 0& M_{12}\\ 0& 0& M_{13}\\ M_{14}& M_{15}& 0\end{array}\right]& (12)\end{array}$

One can check explicitly that the first term in Equation (6) is already non-diagonal and, for sufficiently low values of the U(1)_H breaking scale can induce a decay sufficiently fast as to suppress the flux of ϕ_νμ to account for its non-observation of ν_μ by IceCube.

As an additional interesting feature of this scheme, we propose an indirect test of our neutrino decay hypothesis through the single majoron-emitting J0νββ decay mode [19]

$\begin{array}{cc}(A,Z)\to (A,Z+2)+2e^{-}+J.& (13)\end{array}$

The decay rate for single Majoron emission is given by [32]

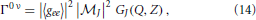
where |〈g_ee〉| is an averaged coupling constant, G_J(Q,Z) accounts for the phase space factor and the nuclear matrix element (NME) 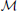_J depends on the mechanism and the relevant nucleus. For single Majoron emission one can use the same NMEs from the standard 0νββ decay [23].

We can see from Equation (14) that the decay width for single Majoron emission in neutrinoless double beta decay depends on the coupling constant g_ee and it is therefore an indirect relation with the expression in Equation (1) through the coupling g₁₂.

Indeed if the majoron exists and its coupling to the electron neutrino is not expected to significantly differ from the one required to explain the muon neutrino deficit in IceCube through the neutrino decay hypothesis, there will be a correlation between R_νe:νμ and 〈g_ee〉. This correlation is depicted in Figure 3. We plot in the left panel the correspondence between g_ee and g₁₂ when we fix the neutrino mixing angles at their best fit values and we consider a Dirac mass entry at m_D ~ 10 GeV, M ~ 1 TeV M_σ ~ 1 TeV and μ ~ 1 keV where the ~ sign takes into account order one differences among the various flavor components of each block. In the right panel of the same figure, we take one the of the points shown in the left panel and vary its CP phase from 0 to 2π in order to obtain an estimate for the ratio R_νe:νμ relevant at IceCube. The dotted (blue) curve corresponds to the case when we consider the second octant of the atmospheric mixing angle, particularly its central value sin²θ₂₃ = 0.61 (we have also chosen the central values of the other mixing angles, sin²θ₁₂ = 0.320 and sin²θ₁₃ = 0.0246); from this case it is possible to see that, for example, for a coupling constant 〈g_ee〉 = 4.33 × 10⁻⁶ a reduction by a factor five in the muon flux can be obtained for an appropriate value of the CP phase, δ = 2.5, while the suppression could be as high as a factor 10. The solid (red) line corresponds to a point in the first octant (sin²θ₂₃ = 0.427). Although in this particular case the values of the ratio, R_νe:νμ are lower than for the second octant, one can still achieve an important suppression; in particular, we can see that a reduction by a factor five is again possible (for the values 〈g_ee〉 = 7.34 × 10⁻⁶ and δ = 1.6) This is an interesting observation, considering that currently the “preferred” octant is not yet uniquely determined by the neutrino oscillation fits [14, 15, 20]. Moreover, we can see that even with the central values of the neutrino mixing angles one can obtain a suppression factor of five or higher that could be sufficient to explain the limits reported by the IceCube collaboration [3].

FIGURE 3

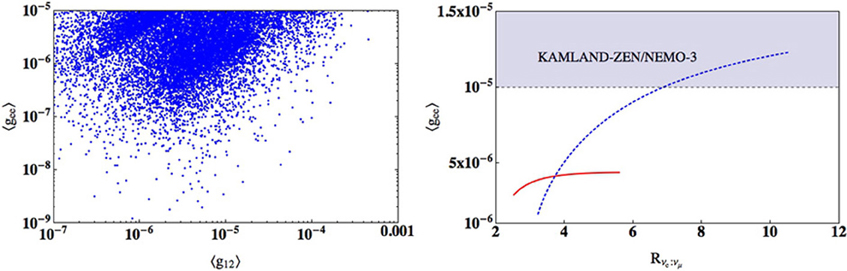
Figure 3. Left panel: single majoron-emitting J0νββ coupling 〈g_ee〉 vs. 〈g₁₂〉, when varying the values of the neutrino mass terms, for the best fit values of the neutrino mixing angles and δ = 0. Right panel: correlation between R_νe:νμ and the parameter 〈g_ee〉 for two particular points of the left panel, varying in this case the value of δ.

In conclusion one sees that the decay hypothesis invoked to account for the IceCube results may be tested in the upcoming searches for the J0νββ decay.

Work supported by MINECO grants FPA2011-22975 and MULTIDARK Consolider CSD2009-00064, by Prometeo/2009/091 (Gen. Valenciana), and by EPLANET. L. D. is supported by JAE Predoctoral fellowship. O. G. M. was supported by CONACyT grant 132197.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Aartsen MG, Abbasi R, Abdou Y, Ackermann M, Adams J, Aguilar JA, et al. [IceCube Collaboration], First observation of PeV-energy neutrinos with IceCube. Phys Rev Lett. (2013) 111:021103 [arXiv:1304.5356 [astro-ph.HE]]. doi: 10.1103/PhysRevLett.111.021103

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

2. Abbasi R, Abu-Zayyad T, Allen M, Amann J, Archbold G, Belov K, et al. An upper limit on the electron-neutrino flux from the HiRes detector. (2008). [arXiv:0803.0554]. doi: 10.1086/590335

CrossRef Full Text

3. Abbasi, R., Abdou, Y., Abu-Zayyad, T., Ackermann, M., Adams, J., Aguilar, J. A., et al. An absence of neutrinos associated with cosmic-ray acceleration in γ-ray bursts. Nature (2012) 484:351–3. doi: 10.1038/nature11068

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

4. Abreu P, Aglietta M, Ahn EJ, Albuquerque IFM, Allard D, Allekotte I, et al. The pierre auger observatory III: other astrophysical observations. (2011). [arXiv:1107.4805].

5. Argyriades J, Arnold R, Augier C, Baker J, Barabash AS, Basharina-Freshville A, et al. Measurement of the two neutrino double beta decay half-life of Zr-96 with the NEMO-3 detector. Nucl Phys. (2010) A847:168–79. doi: 10.1016/j.nuclphysa.2010.07.009

CrossRef Full Text

6. Baerwald P, Bustamante M, Winter W. Neutrino decays over cosmological distances and the implications for neutrino telescopes. JCAP (2012) 1210:020. doi: 10.1088/1475-7516/2012/10/020

CrossRef Full Text

7. Bahcall JN, Petcov S, Toshev S, Valle J. Tests of neutrino stability. Phys Lett. (1986) B181:369–74. doi: 10.1016/0370-2693(86)90065-1

CrossRef Full Text

8. Barranco J, Miranda O, Moura C, Parada A. A reduction in the UHE neutrino flux due to neutrino spin precession. Phys Lett. (2012) B718:26–9. doi: 10.1016/j.physletb.2012.10.024

CrossRef Full Text

9. Beacom, JF, Bell NF. Do solar neutrinos decay? Phys Rev. (2002) D65:113009. doi: 10.1103/PhysRevD.65.113009

CrossRef Full Text

10. Beacom JF, Bell NF, Hooper D, Pakvasa S, Weiler TJ. Decay of high-energy astrophysical neutrinos. Phys Rev Lett. (2003) 90:181301. doi: 10.1103/PhysRevLett.90.181301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

11. Biagi S. Upper limit on the diffuse flux of cosmic ν_μ with the antare neutrino telescope. Nucl Phys Proc Suppl. (2011) 212–213:109–114. doi: 10.1016/j.nuclphysbps.2011.03.015

CrossRef Full Text

12. Chikashige Y, Mohapatra RN, Peccei R. Are there real goldstone bosons associated with broken lepton number? Phys Lett. (1981) B98:265. doi: 10.1016/0370-2693(81)90011-3

CrossRef Full Text

13. Esmaili A, Farzan Y. Implications of the pseudo-dirac scenario for ultra high energy neutrinos from GRBs. JCAP (2012) 1212:014. doi: 10.1088/1475-7516/2012/12/014

CrossRef Full Text

14. Fogli G, Lisi E, Marrone A, Montanino D, Palazzo AM, Rotunno AM. Global analysis of neutrino masses, mixings and phases: entering the era of leptonic CP violation searches. Phys Rev. (2012) D86:013012. doi: 10.1103/PhysRevD.86.013012

CrossRef Full Text

15. Forero D, Tortola M, Valle, J. Global status of neutrino oscillation parameters after Neutrino-2012. Phys Rev. (2012) D86:073012. doi: 10.1103/PhysRevD.86.073012

CrossRef Full Text

16. Gando A, Gando Y, Hanakago H, Ikeda H, Inoue K, Kato R, et al. Limits on majoron-emitting double-beta decays of Xe-136 in the KamLAND-Zen experiment. Phys Rev. (2012) C86:021601. doi: 10.1103/PhysRevC.86.021601

CrossRef Full Text

17. Gelmini G, Schramm DN, Valle J. Majorons: a simultaneous solution to the large and small scale dark matter problems. Phys Lett. (1984) B146:311. doi: 10.1016/0370-2693(84)91703-9

CrossRef Full Text

18. Gelmini G, Valle J. Fast invisible neutrino decays Phys Lett. (1984) B142:181. doi: 10.1016/0370-2693(84)91258-9

CrossRef Full Text

19. Georgi HM, Glashow SL, Nussinov S. Unconventional model of neutrino masses. Nucl Phys. (1981) B193:297. doi: 10.1016/0550-3213(81)90336-9

CrossRef Full Text

20. Gonzalez-Garcia M, Maltoni M, Salvado J, Schwetz T. Global fit to three neutrino mixing: critical look at present precision. JHEP (2012) 1212:123. doi: 10.1007/JHEP12(2012)123

CrossRef Full Text

21. Gonzalez-Garcia M, Valle J. Fast decaying neutrinos and observable flavor violation in a new class of majoron models. Phys Lett. (1989) B216:360. doi: 10.1016/0370-2693(89)91131-3

CrossRef Full Text

22. He H-N, Liu R-Y, Wang X-Y, Nagataki S, Murase K, Dai Z-G. Icecube non-detection of GRBs: constraints on the fireball properties. Astrophys J. (2012) 752:29. doi: 10.1088/0004-637X/752/1/29

CrossRef Full Text

23. Hirsch M, Klapdor-Kleingrothaus H, Kovalenko S, Pas H. On the observability of majoron emitting double beta decays. Phys Lett. (1996) B372:8–14. doi: 10.1016/0370-2693(96)00038-X

CrossRef Full Text

24. Hummer S, Baerwald P, Winter W. Neutrino emission from gamma-ray burst fireballs, revised. Phys Rev Lett. (2012) 108:231101. doi: 10.1103/PhysRevLett.108.231101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

25. Joshipura AS, Mohanty S, Pakvasa S. Pseudo-dirac neutrinos via mirror-world and depletion of UHE neutrinos. (2013). [arXiv:1307.5712].

26. Kachelriess M, Tomas R, Valle J. Supernova bounds on Majoron emitting decays of light neutrinos. Phys Rev. (2000) D62:023004. doi: 10.1103/PhysRevD.62.023004

CrossRef Full Text

27. Keranen P, Maalampi J, Peltoniemi J. Testing neutrino instability with active galactic nuclei. Phys Lett. (1999) B461:230–4. doi: 10.1016/S0370-2693(99)00862-X

CrossRef Full Text

28. Lessa A, Peres O. Revising limits on neutrino-majoron couplings. Phys Rev. (2007) D75:094001. doi: 10.1103/PhysRevD.75.094001

CrossRef Full Text

29. Miranda O, Moura C, Parada A. Sterile neutrinos, dark matter, and resonant effects in ultra high energy regimes. (2013). [arXiv:1308.1408].

30. Mohapatra R, Valle J. Neutrino mass and baryon number nonconservation in superstring models. Phys Rev. (1986) D34:1642. doi: 10.1103/PhysRevD.34.1642

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

31. Pakvasa S, Joshipura A, Mohanty S. Explanation for the low flux of high energy astrophysical muon-neutrinos. Phys. Rev. Lett. (2013) 110:171802. doi: 10.1103/PhysRevLett.110.171802

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

32. Rodejohann W. Neutrino-less double beta decay and particle physics. Int J Mod Phys. (2011) E20:1833–1930. doi: 10.1142/S0218301311020186

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

33. Schechter J, Valle J. Neutrino masses in SU(2) x U(1) theories. Phys Rev. (1980) D22:2227. doi: 10.1103/PhysRevD.22.2227

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

34. Schechter J, Valle, J. Neutrino decay and spontaneous violation of lepton number. Phys Rev. (1982) D25:774. doi: 10.1103/PhysRevD.25.774

CrossRef Full Text

35. Schechter J, Valle JWF. Majorana neutrinos and magnetic fields. Phys Rev. (1981) D24:1883.

36. Tomas R, Pas H, Valle J. Generalized bounds on Majoron-neutrino couplings. Phys Rev. (2001) D64:095005. doi: 10.1103/PhysRevD.64.095005

CrossRef Full Text

37. Valle J. Fast neutrino decay in horizontal majoron models. Phys Lett. (1983) B131:87. doi: 10.1016/0370-2693(83)91097-3

CrossRef Full Text

38. Valle J. Neutrinoless double beta decay with quasi dirac neutrinos. Phys Rev. (1983) D27:1672–4. doi: 10.1103/PhysRevD.27.1672

CrossRef Full Text

39. Waxman E, Bahcall JN. High-energy neutrinos from cosmological gamma-ray burst fireballs. Phys Rev Lett. (1997) 78:2292–5. doi: 10.1103/PhysRevLett.78.2292

CrossRef Full Text

40. Whitehorn N, Kopper C, Neilson NK. Talk Given at the IceCube Particle Astrophysics Symposium (IPA). Madison, WI. (2013).