Theories relating baryon asymmetry and dark matter

The nature of dark matter and the origin of the baryon asymmetry are two of the deepest mysteries of modern particle physics. In the absence of hints regarding a possible solution to these mysteries, many approaches have been developed to tackle them simultaneously leading to very diverse and rich models. We give a short review where we describe the general features of some of these models and an overview on the general problem. We also propose a diagrammatic notation to label the different models.

1. Introduction

The latest results on the cosmological parameters [1] reveal that only 4.9% of the content of the Universe is in the form of baryonic matter whereas 26.8% is constituted by dark matter. The rest is accounted for by the mysterious dark energy. If we focus on the matter front then two disturbing questions are readily asked: What is the nature of dark matter? and why is its density so close to the baryonic matter density, i.e., Ω_DM ~ 5Ω_B?

Moreover, the above-mentioned visible matter density does not include anti-baryons i.e., the visible universe is asymmetric with an initial excess of baryons over anti-baryons parametrized by η(b) = (n_b − n_b)/s ~ 10⁻¹⁰, where n denotes the number density and s the entropy density. Therefore, another fundamental question is what is the origin of the observed baryon asymmetry of the universe (BAU)?

This puts finding the nature of DM and the mechanism behind baryogenesis at the top of the agenda of modern physics¹. While the solutions to these two problems might well be unrelated to each other, it is nevertheless tempting to assume the new physics to be minimal and unifying enough so that it solves both of them with the same ingredients. Moreover, if we discard simple numerical coincidence as an explanation to the intriguing closeness of matter densities, we are left with the task to construct theories relating them or unifying their genesis.

Indeed, numerous models have been proposed in the recent years to achieve this end. Broadly speaking, there are three approaches that are followed to relate dark matter to baryons. The first idea is that there is a sector connecting DM and baryons in the early universe. The connecting sector acts either as a parent sector, generating DM and baryons through decay for instance, or as a mediator mechanism transferring the asymmetry from the dark to the baryonic sector or vice versa. Asymmetric DM models (see below) used this approach extensively. The second approach uses the DM sector as an auxiliary to a successful baryogenesis scenario. The strength of the phase transition in electroweak baryogenesis may for instance be enhanced by the presence of DM. The third approach uses the thermal WIMP paradigm as a framework to relate the abundances.

The purpose of this mini-review is to provide a succinct yet global picture on these models focusing on the key concepts and ingredients that are used in each reviewed model and on the predictions that are made. While there are some similarities between these models, it is difficult to classify them in a consistent and easy way. Instead we opt for a diagrammatic approach Figure 1 and we review models that follow the main roads of the schematic. It is not our goal to be exhaustive with the references and we will refer to more systematic reviews when possible.

FIGURE 1

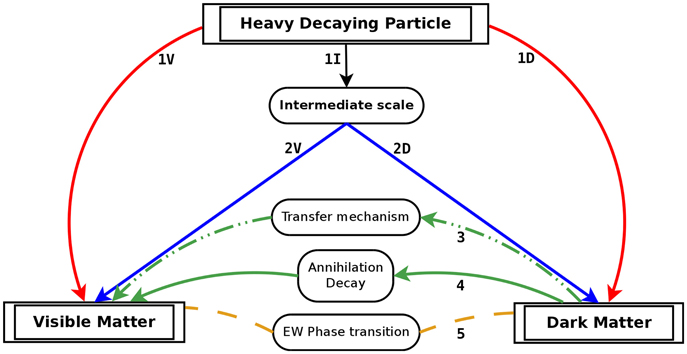
Figure 1. A schematic of the different mechanisms relating DM to baryon asymmetry. The lines are the different stages of the considered mechanism. The labels on the lines are used to describe the model.

From the baryogenesis side we know that any mechanism that satisfies the three Sakharov condition[6]: B violation, C and CP violation and departure from thermal equilibrium can lead to a successful BAU. Whereas from the cold dark matter side we can generally speak of three classes of candidates: weakly interacting massive particles (WIMPs), asymmetric dark matter (ADM) and non-thermal dark matter (NTDM)².

In principle, we can organize the paper in terms of either one of these categories, we chose however to focus on the DM nature.

The paper is organized as follows. In section 2 we review models relating DM to the baryon asymmetry while preserving the WIMP miracle. Section 3 is devoted to ADM models, where we will review different mechanisms and highlight the key concepts that are needed to construct them. In section 4 we quickly mention the possibility of non-thermal DM. Finally we summarize the different models and the roads taken in Table 1. To simplify the understanding of the different models, we will specify in the text (in bold face) whenever it is helpful and in the table the path that is followed in the schematic. We will use the following convention: A * denotes the stage in the diagram where a new asymmetry appears while a bar on the top means that the direction of the arrow is flipped. We will also use the letter T to refer to a thermalization stage.

TABLE 1

Table 1. Summary of the models presented in this review and others.

2. WIMP Dark Matter Models

It has been noted that relic particles from a thermal bath provide in a miraculous way the correct relic density of DM. Indeed, the number density of dark particles in the primordial thermal bath is frozen-out when the expansion rate drops below the rate of the dark matter interactions. The abundance of the relic particle scales then as:

$\begin{array}{cc}{\Omega }_{\text{CDM}}{h}^2\simeq \frac{0.3\times {10}^{-26} {\text{cm}}^3{\text{s}}^{-1}}{{\langle \sigma v\rangle }_{\text{f}.\text{o}.}},& (1)\end{array}$

where 〈σv〉_f.o. is the thermal average of the annihilation cross-section of DM times the relative velocity at the time of freeze-out. Which gives the observed abundance for weak interactions cross-sections. This coincidence between DM and the weak scale has been dubbed the WIMP miracle. In addition to easily providing the observed relic abundance of DM, the WIMP paradigm is falsifiable. It offers a very rich array of phenomenological tests from underground direct detection experiments to astrophysical signals passing by colliders. Without any doubt, maintaining the success of the WIMP paradigm and extending it to related DM to the baryon asymmetry is an attractive possibility. In this section we review the main theories attaining this goal.

2.1. Electroweak Baryogenesis

Electroweak baryogenesis is an appealing minimal scenario of baryogenesis based on the realization of the third Sakharov condition at the electroweak phase transition, see [5] for a review on the mechanism. In the SM a strong first order phase transition, which is necessary in this scenario, requires a very light higgs boson (<42 GeV), moreover the amount of CP violation in the SM is not enough to accommodate the observed BAU. These two considerations imply the need for new physics in order to have a successful baryogenesis and this is where DM comes in. The idea is to use the DM itself (or the dark sector particles) to make this scenario compatible with the SM higgs. A minimal extension of the SM with an extra (complex) scalar [7–11] or two charged singlets [12] achieves this goal, although recent data from LHC and WIMP direct detection experiments render this possibility less attractive because such a DM would have to be sub-dominant (i.e., cannot account for the total density of DM). The same applies for inert higgs extensions of the SM [13] (higher SU(2) representations were considered in [14, 15]). However, models with vector-like fermions are able to produce the total DM density and BAU for a wide range of masses [16].

An even more extended higgs sector, say a 2-higgs-doublet model improves further the prospects of this scenario by providing the needed CP phases [17, 18]. There is no direct correlation between DM and baryonic abundances in such theories, however the presence of the dark sector is necessary to have a successful baryogenesis which at the same time constrains the DM mass and couplings. Lastly, LHC and WIMP direct detection experiments may be used to constrain or rule out such a possibility. We note in passing that there are also models based on leptogenesis that follow the same philosophy outlined here, as in [19–21].

2.2. WIMPy Baryogenesis

Another possibility linking WIMP DM to the baryon asymmetry is the WIMPy baryogenesis model [22]. Here the baryon asymmetry arises from WIMP annihilation instead of the decay of some heavy state like for instance in the usual leptogenesis mechanism. It has been remarked that the annihilation of DM in the early universe can satisfy the Sakharov conditions and leads to a net baryon asymmetry and the observed WIMP relic density.

The baryon asymmetry generated with the WIMP annihilation can be washout from two kind of processes: inverse annihilation of baryons into DM and baryon to antibaryon processes. Therefore, the main requirement for any available WIMPy baryogenesis scenario is that washout processes must freeze-out before that WIMP freeze-out. Inverse annihilations are Boltzmann suppressed for T < m_DM but baryon to antibaryon washout can be relevant also for T « m_DM. One way to suppress such a processes is by introducing an exotic heavy antibaryon ψ to which WIMP annihilate through the process DMDM → Bψ where B is a SM baryon. If the exotic antibaryon ψ has mass m_ψ > m_DM, for T < m_DM its abundance is Boltzmann suppressed and therefore the baryon to antibaryon washout processes are suppressed. So the condition is

$\begin{array}{cc}{m}_{\text{DM}}\lesssim m_{\psi }\lesssim 2m_{\text{DM}}& (2)\end{array}$

where the last condition comes from kinematic. B (L) violation is achieved by annihilating the DM to two sectors: baryons (leptons) and exotic antibaryons (antileptons) that are individually asymmetric but together symmetric. It is important that the decay of the exotic particles do not erase the baryon asymmetry generated in the SM sector. For this extra symmetry is required to decouple the exotic fields from the SM.

Solving the model-independent Boltzmann equations for the WIMPy baryogenesis framework, it is possible to show that the baryon asymmetry is proportional to the DM density at the time of freeze-out of the washout processes, i.e.,³

$\begin{array}{cc}{Y}_{\text{B}}\approx \frac{ϵ}{2}\left[Y_{D{M}_{\text{wo}}}-Y_{DM}\right]& (3)\end{array}$

where Y_DMwo is the DM density at the washout while Y_B,DM are the observed baryon and DM densities and ϵ is the baryon-antibaryon asymmetry. From Equation (3) and the relation

$\begin{array}{cc}{Y}_{DM}=\frac{(5GeV)}{m_{\text{DM}}}{Y}_{\text{B}}& (4)\end{array}$

it follows that Y_DMwo » Y_DM, namely it is crucial to freeze-out the wash out processes before the WIMP freeze-out temperature otherwise any generated asymmetry would be quickly erased.

As a concrete example we consider a realization of the WIMPy idea in which the WIMP annihilate to leptons generating a lepton asymmetry then converted into a baryon asymmetry through sphaleron like in leptogenesis. The DM candidate consists of a pair of gauge singlet Dirac fermions Y and Y. In addition to DM two new weak-scale states ψ (fermion SU_L(2) doublet) and S₁ and S₂ (pseudo-scalar gauge singlets) are added. The fields {Y, Y, ψ, ψ, S_i} transform under an extra Z₄ symmetry respectively as {+i, −i, −1, −1, −1}. The Lagrangian contains the extra terms

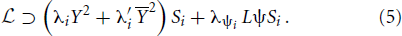
Since there is more than one scalar S_i, it remains a relative complex phase between the λ couplings. Then as in the common leptogenesis case the interference between tree level and loop diagrams give rise to CP violation resulting in an asymmetries in L (4*)⁴ and subsequently converted to B asymmetry by means of the sphalerons. Here differently from leptogenesis, the dark matter Y annihilates into SM leptons L and ψ through the pseudo-scalars (T)⁵ then a lepton asymmetry also accumulate in ψ. The processes linking ψ to the SM do not erase the lepton asymmetry thanks to the extra Z₄ symmetry that decouples ψ from the SM.

At the end an asymmetry is generated from a 2 → 2 process instead of a 1 → 2. An important requirement is that m_ψ > m_Y because it implies that the dominant washout process Lψ → L^† ψ^† is Boltzmann-suppressed when DM is annihilating. We summarize diagrammatically the signature of the model as (T–4*), as it appears in the Table 1.

The detection prospects are rich in this scenario and include direct (for models with annihilation to quarks), indirect detection (anti-deuteron) and collider signals. See [23, 24] for a general phenomenological study of this class of models. Other models preserving the WIMP miracle and attempting to relate the DM to BAU can be found in [25, 26].

2.3. Meta-Stable WIMP

As in the case of WIMPy baryogenesis, this model [27] attempts to explain the DM/baryon relic density coincidence using the WIMP miracle. The idea is to use a decaying WIMP instead of a stable one. A thermal WIMP Y freeze out at a temperature T_f that is typically T_f ~ m_Y/20. At freeze out the WIMP density is Y_Y(T_f) which is equal to the DM density today Y_Y(T_f) ≃ Y_Y(T₀) if the WIMP is stable. The authors consider two kinds of WIMPs: one stable Y₁ that is the DM candidate and one Y₂ that decay after freeze out, with the densities of the two WIMPS at the freeze out being almost the same Y_Y1(T_f) ≈ Y_Y2(T_f). The density of the decay WIMP at the freeze out temperature is the initial condition for the baryogenesis.

The meta-stable WIMP Y₂ decays after thermal freeze-out into baryons in such a way that the baryon number B and CP are violated. In a minimal realization of the idea, the SM is extended to include a di-quark scalar ϕ and ψ which are Majorana fermions and a singlet scalar S. The relevant couplings are

$\begin{array}{cc}\varphi dd,Y_2\overline{u}\varphi ,\psi \overline{u}\varphi ,Y_2^{2}S,|H{|}^{2}S& (6)\end{array}$

Where u and d are the SM quarks. The scalar S mediates the thermal annihilation of Y₂Y₂ into SM. The meta-stable WIMP decay as Y₂ → uϕ* followed by the decay of ϕ → dd. A CP asymmetry ϵ_CP in Y₂ → uϕ* and Y₂ → uϕ arises from the interference between the tree-level diagram with the one loop diagram mediated by ψ (that shares with Y₂ the same quantum numbers). In order to generate a baryon asymmetry the WIMP must decay before the BBN and after WIMP freeze out, i.e., T_BBN < T_Y2 < T_f. Solving the Boltzmann equations it is possible to find the baryon density today

$\begin{array}{cc}{Y}_B(T_0)\approx {ϵ}_{CP}{\displaystyle {\int }_{T_0}^{T_D}\frac{d{Y}_{Y_2}}{dT}}dT\simeq {ϵ}_{CP}{Y}_{Y_2}(T_f)& (7)\end{array}$

Using the relations Y_Y(T_f) ≈ Y_Y2(T_f) and that Y_Y(T_f) ≃ Y_Y(T₀) we arrive at the result

$\begin{array}{cc}{\Omega }_B={ϵ}_{CP}\frac{m_p}{m_{DM}}{\Omega }_{DM}& (8)\end{array}$

where Ω_DM is the relic abundance of the DM. The model lies at the electroweak scale and therefore it can be probed in colliders.

3. Asymmetric Dark Matter Models

ADM [28–35] is a class of DM models often seen as an alternative to the WIMP paradigm. The rationale of ADM is based on the hypothesis that DM abundance is, similarly to baryons, only the surviving asymmetric part of the initial density and is of the same order as the baryon asymmetry, i.e.,

$\begin{array}{cc}{n}_Y-n_{\overline{Y}}~n_b-n_{\overline{b}}& (9)\end{array}$

where Y denotes the DM particle. The motivation comes from the fact that the observed DM and visible matter abundances are remarkably close to each other. These models usually lead to a relation between DM mass and proton mass: M_DM ~ 5M_P in contrast with WIMP DM models where the scale of reference is the weak scale. The relation between the DM mass and the proton mass is however not explained except in some models based on hidden sectors such as in mirror worlds [36–38], models with a dark QCD [39] or composite models (see below).

ADM can be implemented in many ways leading to a very rich theoretical and phenomenological landscape. While it is difficult to classify these models in a straightforward way, it is nevertheless enriching to highlight the key principles they usually rely on. Basically two main approaches are followed: (1) Dark and visible matter asymmetries are generated at the same time. This is usually achieved with the decay of a heavy particle. (2) The asymmetry is generated in the dark sector then is transferred (via sphaleron processes, higher dimension operators or renormalizable interactions) to the visible sector or vice versa. It is also necessary to pass at some point by a thermalization phase to get rid or to avoid the production of the symmetric part of DM (a less extreme cancelation of the asymmetric part leads to mixed scenarios between WIMP and ADM [40]).

We will present here ADM models explicitly showing the key assumptions and principles used as well as their phenomenological impact. They make use of the main ADM concepts and pass by the main diagrammatic roads. For a recent review and an exhaustive list of reference we refer the reader to [41–43] and for a more succinct overview [44].

3.1. Composite ADM

The idea of the ADM has been proposed in the seminal work of Nussinov [28] who suggested that in analogy with the visible sector's baryon asymmetry, a technibaryon asymmetry is a natural possibility. This idea has been recently revamped in the context of walking dynamics [45–48]. If the model is arranged such that the lightest technibaryon (LTB) is neutral and stable, the density of the LTB scales as:

$\begin{array}{cc}\frac{{\Omega }_{TB}}{{\Omega }_B}=\frac{TB}{B}\frac{m_{TB}}{m_p}& (10)\end{array}$

Where m_p is the proton mass, m_TB is the mass of the LTB. TB and B are the technibaryon and baryon number densities, respectively. This is the typical scaling of ADM models.

The model discussed in [45] is a technicolor theory based on the SU(4) global symmetry spontaneously broken down to SO(4). Such a breaking gives rise to 9 Goldston bosons, three of them corresponding to the SM gauge bosons. The remmant six Goldstone bosons carry technibaryon charge and the lightest of them (LTB) is the DM candidate⁶. In [49, 50] the properties of composite (asymmetric or symmetric) dark matter candidates have been computed in detail via first-principle lattice simulations.

3.2. Kitano-Low

The model implemented in [34] considers a mechanism originally proposed in [31] to unify in an elegant way the abundances of DM and baryons. It is a prototype of the ADM models based on decay of a field connecting the dark and visible sectors.

The authors postulate a new symmetry, namely a Z₂ parity, under which the SM particles are neutral and new particles are charged, forming a dark or hidden sector. The lightest of the hidden particle is stable and is a DM candidate. A generalized B-L number is unbroken and is shared between the SM and the dark sector, thus any excess of B-L that is generated in one of the two sectors is compensated by the same excess in the other sector. After baryogenesis the interactions between the visible and the dark sectors become negligible and the B-L excesses are separately conserved in the two sectors giving a relation between the visible and dark relic densities.

A simple model realizing the idea consists of a heavy particle P, a messenger particle X which carries a color charge and the DM candidate Y, all odd under the Z₂ while the SM is even. The mechanism passes through 3 stages. In the first stage P has CP-violating out of equilibrium decays into SM and to a lighter messenger X generating an excess in both sectors but preserving the generalized B-L globally. Then is assumed that below the baryogenesis temperature the two sector are decoupled and the two asymmetries are conserved such that we have:

$\begin{array}{cc}{n}_{\text{B}-\text{L}}^{\text{SM}}=-n_{\text{B}-\text{L}}^X~n_X-n_{\overline{X}}& (11)\end{array}$

In the second stage the dark X messenger annihilate away its symmetric part with X through gauge interactions and we are left with its asymmetric part only. In the third and final stage the decay of X to DM particle Y and therefore

$\begin{array}{cc}{n}_{\text{DM}}\propto n_{\text{B}-\text{L}}^X& (12)\end{array}$

giving a tight relation between the visible (baryonic) and DM number densities. To ensure that such a relation exists it is important that X is long lived enough such that it decays after its symmetric part cancels out.

We summarize the mechanism: Decay of P that produces the asymmetries in X (1*_I) and SM (1*_V, since an asymmetry in the visible sector is generated by the decay) followed by symmetric annihilation of X (T) and finally the decay of X to the lightest dark particle Y (2_D). We denote the full mechanism in a compact way as (1*_V–1*_I–T–2_D).

An interesting possibility is to consider X itself as the DM particle. This possibility is not possible here here because of charge assignment of X (colored particle). However, we will see now that Hylogenesis realizes this possibility. Note that the original asymmetry can be generated through the Affleck-Dine [51, 52] mechanism in a SUSY framework [53–56] or through leptogenesis as in [57].

3.3. Hylogenesis

This model [58] is based on a hidden sector composed of 3 Dirac fermions X₁, X₂, Y and a complex scalar ϕ. It is assumed that M_ϕ ~ M_Y ~ GeV and TeV < M_X1 < M_X2. X_i are made to couple to the visible sector through the neutron portal (X_i d^c u^c d^c), the relevant terms in the Lagrangian are:

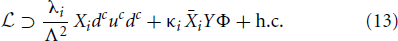
The particle content and the symmetries of the model permit the definition of a generalized baryon number (B), conserved by both sectors, under which B_X = −(B_Y + B_Φ) = 1 as well as non-reducible CP phases.

In the early universe an equal number of X₁ and its antiparticle X₁ are generated non-thermally (e.g. during reheating) and the total baryon number is zero at this stage. Then both states X₁ and X₁ decay into the visible and hidden states as X₁ → udd (1*_V) and X₁ → Y Φ* (1*_D) and their conjugates at tree level and through loops (including the lighter dark particles ϕ and Y), generating an asymmetry in the visible sector ϵ_V and an asymmetry in the hidden sector ϵ_D á la leptogenesis

$\begin{array}{cc}{ϵ}_V=\frac{\Gamma \left(X_1\to udd\right)-\Gamma \left({\overline{X}}_1\to \overline{u}\overline{d}\overline{d}\right)}{{\Gamma }_{X_1}}\simeq \frac{m_{X_1}^{5}Im\left({\lambda }_1^{\ast }{\lambda }_2{\kappa }_1{\kappa }_2^{\ast }\right)}{256{\pi }^3|{\kappa }_1{|}^2{\Lambda }^4{m}_{X_2}}.& (14)\end{array}$

where Γ_X1 is the total rate and ϵ_D can be obtained in a similar way. We have

$\begin{array}{cc}\begin{array}{l}\Gamma (X_1\to udd)={\Gamma }_V+{ϵ}_V{\Gamma }_{X_1},\hfill \\ \Gamma \left({\overline{X}}_1\to \overline{u}\overline{d}\overline{d}\right)={\Gamma }_V-{ϵ}_V{\Gamma }_{X_1},\hfill \\ \Gamma \left(X_1\to \overline{Y}{\Phi }^{\ast }\right)={\Gamma }_D-{ϵ}_D{\Gamma }_{X_1},\hfill \\ \Gamma \left({\overline{X}}_1\to Y\Phi \right)={\Gamma }_D+{ϵ}_D{\Gamma }_{X_1}.\hfill \end{array}& (15)\hfill \end{array}$

Because X₁ is a Dirac particle, the asymmetry generated in the visible sector is then translated as an asymmetry in the hidden sector. Indeed, CPT invariance forces the particle and its anti-particle to have equal total decay rates Γ[X₁ → n + YΦ*] = Γ[X₁ → n + YΦ], which translates as a relation between asymmetries, that is ϵ_D = −ϵ_V where we have used the Equation (15). Therefore, in the decay of X₁ and X₁ a baryon number is generated in the visible sector and an equal and opposite baryon number is generated in the hidden sector so that the total baryon number is zero. The two asymmetries are frozen-in thanks to the weakness of the interactions between the two sectors.

The final step is to cancel out the symmetric part of the dark matter particles and this is achieved for instance with an extra U(1)_D gauge symmetry in the hidden sector under which Y and Φ have opposite charges and X_1,2 are neutral. The symmetric part is depleted (T) by the annihilation processes YY → Z′Z′ and ΦΦ* → Z′Z′ with m_Z′ < m_{Y, Φ} ~ GeV (this is consistent with present observations for 10⁻⁶ < κ < 10⁻²) with Z′ decaying to SM through photon. These cross section are much larger to the one need to obtain the correct DM relic density by thermal freeze-out. Then the DM density is given by the residual asymmetric component and we are then left with the relation:

$\begin{array}{cc}{n}_Y=n_{\Phi }=n_B& (16)\end{array}$

that gives a strong relation between the visible and dark matter abundances:

$\begin{array}{cc}\frac{{\Omega }_{DM}}{{\Omega }_B}=\frac{(M_Y+M_{\Phi })}{M_P}~5.& (17)\end{array}$

We denote in a compact way this mechanism with the signature (1*_V–1*_D–T). Because of the neutron portal, hylogenesis provides an interesting signature of the DM: the induced proton decay (IND). Indeed DM can scatter with protons producing mesons ϕ*p → YK⁺.

3.4. ADM from Leptogenesis

If we take Majorana instead of Dirac decaying fields in the previous model, we get different consequences on the DM mass. The model considered in [59] is based on the decay of a heavy right handed neutrino field N.

The model is an extension of the SM and consists of two right-handed neutrinos and a scalar ϕ and fermion Y gauge singlets, charged under an extra Z₂ parity, that made the hidden sector

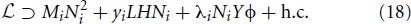
N couples to the SM with Dirac Yukawa coupling and to the hidden sector, Y is the DM candidate. Therefore, N can decay (out of equilibrium) simultaneously as N → LH (1*_V) and N → Yϕ (1*_D) generating two different and unrelated CP-asymmetries ϵ_L and ϵ_DM respectively. Here N is a Majorana particle and CPT does not imply that |ϵ_L| = |ϵ_DM| like in Hylogenesis (see previous section). The DM must be a Dirac particle in order to preserve a lepton number. Because both Y and ϕ are charged under the extra Z₂, the DM is stable and the hidden sector can interact with the SM only by means of the heavy right-handed neutrino. In order to cancel out the symmetric component of the DM, an additional gauged U(1) interaction is imposed to annihilate the Y, Y pair. We are left with the asymmetric parts of Y (T). The DM and baryon density Ω_DM/Ω_B is then proportional to the ratio of the CP-asymmetries ϵ_DM/ϵ_L,

$\begin{array}{cc}\frac{{\Omega }_{\text{DM}}}{{\Omega }_B}~\frac{m_{\text{DM}}}{m_p}\frac{{ϵ}_{DM}}{{ϵ}_L}\frac{{\eta }_{DM}}{{\eta }_L}& (19)\end{array}$

where η_DM,L are the washout factor. Therefore, the DM mass can be very different from the value of 5M_p given in most ADM models. A similar model based on type-II leptogenesis instead of type-I has been proposed in [60]. See also [57] for an earlier ADM model based on leptogenesis and where the DM mass is in the typical few GeV scale.

3.5. Darkogenesis

In this model [61] an asymmetry is generated in the dark sector and is then transferred to the visible sector. The DM asymmetry arises from a first order dark phase transition in the hidden sector to which the SM does not participate. The dark baryogenesis proceed through the symmetry breaking phase transition of a dark non-Abelian gauge group G_D. The fields in the dark sector have a global dark symmetry U_D(1) which is anomalous under G_D. During the symmetry breaking first order phase transition an dark asymmetry is generated by means of CP violating interactions.

The asymmetry can be transferred to the visible sectors in two ways: by fields that carry both hidden and visible charges (perturbatively)or via electroweak sphalerons (non-perturbatively). In the last case, in order to transmit the asymmetry from the dark sector to the SM one, it is required a mediator charged under both the SU_L(2) and the dark symmetry U_D(1). Then the dark number is anomalous under SU_L(2) and the SM electroweak sphaleron can convert the asymmetry of the dark sector into an asymmetry in the SM.

In the first case the connectors can consists of higher order effective operators of the type

$\begin{array}{cc}{O}_{d}LH,O_{d}udd,O_{d}LLe,O_{d}LQd,O_{d}LHLH,& (20)\end{array}$

where O_d is a dark sector operator like for instance O_d = X, X². The hidden sector phase transition occurs at a temperature above the temperature at which the effective transfer operator freeze-out The dark matter mass lies around 5 to 15 times the mass of the proton.

Direct detection cannot falsify the darkogenesis mechanism, however the gravitational wave signal from dark first order transition could in principle probe this mechanism. The asymmetry in the dark sector can also be generated via a different baryogenesis mechanism, see [62] for an example where a heavy particle decays to the dark sector, creating an asymmetry there that is then transferred to the visible sector. For the opposite case, see [63] or aidnogenesis[64], for instance where the asymmetry is transferred through sphalerons from the SM to the dark sector. Diagrammatically we denote this model as : *−3−*, which means that an original asymmetry in the dark sector (following the direction the arrow) is transferred to the visible sector. See also [65] for a recent model where sphalerons are responsible for cogenerating the dark matter.

3.6. Xogenesis

Like in the darkogenesis model, here [66] a DM asymmetry is created and then transferred to the baryon by means of transfer operators. The problem of the creation of a DM asymmetry is not addressed here and the authors focuses on the transfer mechanisms. The main difference between this mechanism and the classic ADM ones going in the same direction is that the DM mass can be around the weak scale instead of the proton mass (for a different idea how to obtain heavy ADM see [67]) without fine-tuning the parameters. The main idea can be summarized as follows: If DM is not relativistic at the temperature where the transfer operator decouples T_D then the DM number density undergoes a thermal suppression allowing the DM to be heavy.

The transfer can be due from the SU_L(2) sphalerons (or the exotic sphalerons of a new gauge group) or lepton/baryon number violation from higher order operators. In any transfer scenario chemical equilibrium between DM and baryon is maintained until the transfer operator decouples. When the transfer is active, we have:

$\begin{array}{cc}{\mu }_{DM}~{\mu }_B.& (21)\end{array}$

Given a specie i in general its asymmetry n_Δi = n_i − n_i is proportional to its chemical potential

$\begin{array}{cc}{n}_i=c_i{\mu }_i& (22)\end{array}$

The coefficients c_i are function of the mass and temperature c_i = c_i (m_i, T) [29]:

$\begin{array}{cc}{c}_i=g_{i}f(m_i/T)T^2{R}^3,f(x)=\frac{1}{4{\pi }^2}\text{}{\displaystyle {\int }_0^{\infty }\text{}}\frac{y^{2}dy}{{\cosh }^2\left(\sqrt{x^2+y^2}/2\right)}& (23)\end{array}$

where g_i is the statistical weight and R is the Robertson-Walker scale factor at temperature T. For small value of m_i/T then f(m_i/T) tend to a constant, while for large m_i/T then f(m_i/T) is very small

$\begin{array}{cc}f(m_i/T)~\left[\begin{array}{l}{m}_i/T\ll 1,1/6\hfill \\ m_i/T\gg 1,2{(m/2\pi T)}^{3/2}{e}^{-m/T}\hfill \end{array}\right]& (24)\end{array}$

Typically only the first possibility where m_DM/T_D « 1 is taken (T_D is the decoupling temperature of the transfer operator). In this case from Equations (21) and (22) it follows that n_ΔDM ~ n_ΔB leading to the ‘prediction’ m_DM ~ 5m_p. However, a second solution is possible. If the ratio m_DM/T_D is large, then the coefficients c_DM is suppressed, see Equations (22) and (24). This results in a lower n_DM with respect to the case where the ratio m_i/T_D is small and thus a larger DM is allowed. For a given value of T_D the non-relativistic solution give about m_DM ~ 10 T_D instead of 5GeV (relativistic solution), giving a mass for the DM of the order of the TeV.

A simple example is given by a DM particle Y that transform as a fermion doublet of SU_L(2) with hypercharge +1/2. Since the DM is charged under SU_L(2), it interacts with the SM sphaleron. Thanks to the sphaleron Y and quarks are in thermal equilibrium, therefore the DM and quarks chemical potential are releted, i.e., μ_Y = −3 μ_uL. In this example the decoupling temperature T_D of the transfer operator is the temperature where the spahleron is no more active, that is around 200 GeV. Solving equations (21) and (22) one gets for the DM a value of about 2000 GeV.

The idea has been illustrated with different classes of transfer operators: SM sphalerons, exotic sphalerons of a new gauge group and lepton or baryon number violation higher order operators. Since the DM is heavy it will be difficult to search for it but new particles at the weak or TeV scale are can be probed in collider experiments.

4. Non-Thermal Dark Matter Models

4.1. Cladogenesis

Cladogenesis [68] is based on the observation that the dilution factor due to entropy release by moduli decay is very close to the observed baryon asymmetry. Indeed for a modulus τ with a reheating temperature in the range MeV – GeV (corresponding to M_τ of order 20–1000 TeV) the dilution factor is given by

$\begin{array}{cc}{Y}_{\tau }=\frac{3T_{RH}}{4M_{\tau }^4}~{10}^{-9}-{10}^{-7}& (25)\end{array}$

a value that is close to η_B and also to Y_DM as long as M_DM is within a factor or two from the proton mass. At the same time any previous DM abundance will be suppressed by the same factor. These considerations lead the authors of Cladogenesis to consider a non-thermal origin of DM from modulus decay. The scenario goes as follow: τ decays to some species N (1_I) and to DM (directly or via dark sector particles following 1_D). The decay to DM must be suppressed down to 10⁻³ to achieve the observed relic abundance. N then decays to SM by violating baryon (or lepton) number and CP to produce the correct baryon asymmetry (2*_V). Note that the DM is not asymmetric in this model because baryogenesis is done in the visible sector only.

Another example of non-thermal mechanism is given in [69] where the DM arises from the out-off equilibrium decay of the inflaton instead of the moduli.

5. Summary

In this short review we have given an overview of the models linking the generation of the baryon asymmetry of the universe and dark matter. These models are varied and diverse and tackle the problematic from different points of view. Models attempting to preserve the WIMP miracle lead to a very rich phenomenology and their couplings can be probed at LHC soon. These models do not address the coincidence between the baryon and DM asymmetries and the link between the two abundances is not strong. ADM models, one the other hand, give a natural explanation to this ratio at the price of WIMP phenomenology. Lastly non-thermal production models are yet another possibility relating the genesis of the dark and visible sector. LHC and dark matter search experiments will probe large chunks from the theoretical landscape of DM, hopefully shedding light on its nature and on the mechanism at work for baryogenesis.

We summarize the models discussed here in Table 1 where we give information about the nature of their DM, the BAU mechanism at work, the existence of a hidden sector, range of the DM mass allowed in the model as well as the expected signal. The last column shows the diagrammatic signature of the model based on Figure 1 and the convention outlined in the introduction.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Stefano Morisi thanks to DFG grant WI 2639/4-1 for financial support. Sofiane. M. Boucenna was supported by the Spanish MINECO under grants FPA2011-22975 and MULTIDARK CSD2009-00064 (Consolider-Ingenio 2010 Programme), by Prometeo/2009/091 (Generalitat Valenciana), by the EU ITNUNILHC PITN-GA-2009-237920.

Footnotes

1. ^For reviews on DM we refer the reader to [2, 3] and for baryogenesis to[4, 5].

2. ^Where we include any non-thermally produced DM that does not fall in the ADM case.

3. ^>Here Y_X is the ratio of the number density n_X of the specie X with the entropy s.

4. ^The depiction of this step in the schematic: the DM annihilates into the visible sector (line 4), with the * is there to show that an asymmetry is produced in this step.

5. ^We use here the letter T to emphasize that the DM is thermally produced.

6. ^The Goldstone bosons are supposed to pick up a mass from a higher scale.

References

1. Ade PAR, Aghanim N, Armitage-Caplan C, Arnaud M, Ashdown M, Atrio-Barandela F. et al. Planck 2013 Results. XV I. Cosmological Parameters. (2013) arXiv: 1303.5076

2. Bertone G, Hooper D, Silk J. Particle dark matter: evidence, candidates and constraints. Phys Rept. (2005) 405:279–390. doi: 10.1016/j.physrep.2004.08.031

CrossRef Full Text

3. Bergstrom L. Nonbaryonic dark matter: observational evidence and detection methods. Rept Prog Phys. (2000) 63:793. doi: 10.1088/0034-4885/63/5/2r3

CrossRef Full Text

4. Dine M, Kusenko A. The origin of the matter - antimatter asymmetry. Rev Mod Phys. (2003) 76:1. doi: 10.1103/RevModPhys.76.1

CrossRef Full Text

5. Riotto A, Trodden M. Recent progress in baryogenesis. Ann Rev Nucl Part Sci. (1999) 49:35–75. doi: 10.1146/annurev.nucl.49.1.35

CrossRef Full Text

6. Sakharov AD. Violation of CP invariance, c asymmetry, and baryon asymmetry of the universe. Pisma ZhEksp Teor Fiz. (1967) 5:32–5.

7. Profumo S, Ramsey-Musolf MJ, Shaughnessy G. Singlet higgs phenomenology and the electroweak phase transition. JHEP (2007) 0708:010. doi: 10.1088/1126-6708/2007/08/010

CrossRef Full Text

8. Espinosa JR, Konstandin T, Riva F. Strong electroweak phase transitions in the standard model with a singlet. Nucl Phys. (2012) B854:592–630. doi: 10.1016/j.nuclphysb.2011.09.010

CrossRef Full Text

9. Barger V, Langacker P, McCaskey M, Ramsey-Musolf M, Shaughnessy G. Complex singlet extension of the standard model. Phys Rev. (2009) D79:015018. doi: 10.1103/PhysRevD.79.015018

CrossRef Full Text

10. Cline JM, Kainulainen K. Electroweak baryogenesis and dark matter from a singlet higgs. JCAP (2013) 1301:012. doi: 10.1088/1475-7516/2013/01/012

CrossRef Full Text

11. Ahriche A, Nasri S. Light dark matter, light higgs and the electroweak phase transition. Phys Rev. (2012) D85:093007. doi: 10.1103/PhysRevD.85.093007

CrossRef Full Text

12. Ahriche A, Nasri S. Dark matter and strong electroweak phase transition in a radiative neutrino mass model. JCAP (2013) 1307:035. doi: 10.1088/1475-7516/2013/07/035

CrossRef Full Text

13. Cline JM, Kainulainen K. Improved electroweak phase transition with subdominant inert doublet dark matter. Phys Rev. (2013) D87:071701. doi: 10.1103/PhysRevD.87.071701

CrossRef Full Text

14. Chowdhury TA, Nemevsek M, Senjanovic G, Zhang Y. Dark matter as the trigger of strong electroweak phase transition. JCAP (2012) 1202:029. doi: 10.1088/1475-7516/2012/02/029

CrossRef Full Text

15. AbdusSalam SS, Chowdhury TA. Scalar representations in the light of electroweak phase transition and cold dark matter phenomenology. (2013) arXiv: 1310.8152.

16. Fairbairn M, Grothaus P. Baryogenesis and dark matter with vector-like fermions. JHEP (2013) 1310:176. doi: 10.1007/JHEP10(2013)176

CrossRef Full Text

17. McLerran LD, Shaposhnikov ME, Turok N, Voloshin MB. Why the baryon asymmetry of the universe is approximately 10**-10. Phys Lett. (1991) B256:451–6.

18. Cline JM, Kainulainen K, Trott M. Electroweak baryogenesis in two higgs doublet models and B meson anomalies. JHEP (2011) 1111:089. doi: 10.1007/JHEP11(2011)089

CrossRef Full Text

19. Basso L, Fischer O, van der Bij JJ. A natural Z′ model with inverse seesaw and leptonic dark matter. Phys Rev. (2013) D87:035015. doi: 10.1103/PhysRevD.87.035015

CrossRef Full Text

20. Canetti L, Drewes M, Shaposhnikov M. Sterile neutrinos as the origin of dark and baryonic matter. Phys Rev Lett. (2013) 110:061801. doi: 10.1103/PhysRevLett.110.061801

CrossRef Full Text

21. Canetti L, Drewes M, Frossard T, Shaposhnikov M. Dark matter, baryogenesis and neutrino oscillations from right handed neutrinos. Phys Rev. (2013) D87:093006. doi: 10.1103/PhysRevD.87.093006

CrossRef Full Text

22. Cui Y, Randall L, Shuve B. A WIMPy baryogenesis miracle. JHEP (2012) 1204:075. doi: 10.1007/JHEP04(2012)075

CrossRef Full Text

23. Bernal N, Josse-Michaux FX, Ubaldi L. Phenomenology of WIMPy baryogenesis models. JCAP (2013) 1301:034. doi: 10.1088/1475-7516/2013/01/034

CrossRef Full Text

24. Bernal N, Colucci S, Josse-Michaux FX, Racker J, Ubaldi L. On baryogenesis from dark matter annihilation. (2013). JCAP (2013) 1310:035. doi: 10.1088/1475-7516/2013/10/035

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

25. Davidson S, Elmer M. Similar dark matter and baryon abundances with TeV-scale leptogenesis. JHEP (2012) 1210:148. doi: 10.1007/JHEP10(2012)148

CrossRef Full Text

26. McDonald J. Baryomorphosis: relating the baryon asymmetry to the “WIMP miracle.” Phys Rev. (2011) D83:083509. doi: 10.1103/PhysRevD.83.083509

CrossRef Full Text

27. Cui Y, Sundrum R. Baryogenesis for weakly interacting massive particles. Phys Rev. (2013) D87:116013. doi: 10.1103/PhysRevD.87.116013

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

28. Nussinov S. Technocosmology: could a technibaryon excess provide a “natural” missing mass candidate? Phys Lett. (1985) B165:55.

29. Barr SM, Chivukula RS, Farhi E. Electroweak fermion number violation and the production of stable particles in the early universe. Phys Lett. (1990) B241:387–91.

30. Barr SM. Baryogenesis, sphalerons and the cogeneration of dark matter. Phys Rev. (1991) D44:3062–6.

Pubmed Abstract | Pubmed Full Text

31. Kuzmin VA. A Simultaneous solution to baryogenesis and dark matter problems. Phys Part Nucl. (1998) 29:257–65. doi: 10.1134/1.953070

CrossRef Full Text

32. Hooper D, March-Russell J, West SM. Asymmetric sneutrino dark matter and the Omega(b) / Omega(DM) puzzle. Phys Lett. (2005) B605:228–36. doi: 10.1016/j.physletb.2004.11.047

CrossRef Full Text

33. Farrar GR, Zaharijas G. Dark matter and the baryon asymmetry of the universe. (2004) Phys Rev. Lett. (2006) 96:041302. doi: 10.1103/PhysRevLett.96.041302

CrossRef Full Text

34. Kitano R, Low I. Dark matter from baryon asymmetry. Phys Rev. (2005) D71:023510. doi: 10.1103/PhysRevD.71.023510

CrossRef Full Text

35. Kaplan DE, Luty MA, Zurek KM. Asymmetric dark matter. Phys Rev. (2009) D79:115016. doi: 10.1103/PhysRevD.79.115016

CrossRef Full Text

36. Foot R, Volkas RR. Explaining omega(Baryon) approximately 0.2 omega(Dark) through the synthesis of ordinary matter from mirror matter: a more general analysis. Phys Rev. (2004) D69:123510. doi: 10.1103/PhysRevD.69.123510

CrossRef Full Text

37. Hodges HM. Mirror baryons as the dark matter. Phys Rev. (1993) D47:456–9.

Pubmed Abstract | Pubmed Full Text

38. Mohapatra RN, Teplitz VL. Mirror dark matter. Phys Rev. (2000) D62:063506.

39. Bai Y, Schwaller P. The Scale of Dark QCD. (2013) arXiv: 1306.4676.

40. Graesser ML, Shoemaker IM, Vecchi L. Asymmetric WIMP dark matter. JHEP (2011) 1110:110. doi: 10.1007/JHEP10(2011)110

CrossRef Full Text

41. Sannino F. Conformal dynamics for TeV physics and cosmology. Acta Phys Polon. (2009) B40:3533–743.

42. Petraki K, Volkas RR. Review of asymmetric dark matter. Int J Mod Phys. (2013) A28:1330028. doi: 10.1142/S0217751X13300287

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

43. Zurek KM. Asymmetric dark matter: theories, signatures, and constraints. (2013) arXiv: 1308.0338

44. Davoudiasl H, Mohapatra RN. On relating the genesis of cosmic baryons and dark matter. New J Phys. (2012) 14:095011. doi: 10.1088/1367-2630/14/9/095011

CrossRef Full Text

45. Gudnason SB, Kouvaris C, Sannino F. Towards working technicolor: effective theories and dark matter. Phys Rev. (2006) D73:115003. doi: 10.1103/PhysRevD.73.115003

CrossRef Full Text

46. Gudnason SB, Kouvaris C, Sannino F. Dark matter from new technicolor theories. Phys Rev. (2006) D74:095008. doi: 10.1103/PhysRevD.74.095008

CrossRef Full Text

47. Nardi E, Sannino F, Strumia A. Decaying dark matter can explain the e+- excesses. JCAP (2009) 0901:043. doi: 10.1088/1475-7516/2009/01/043

CrossRef Full Text

48. Del Nobile E, Kouvaris C, Sannino F. Interfering composite asymmetric dark matter for DAMA and CoGeNT. Phys Rev. (2011) D84:027301. doi: 10.1103/PhysRevD.84.027301

CrossRef Full Text

49. Lewis R, Pica C, Sannino F. Light asymmetric dark matter on the lattice: SU(2) technicolor with two fundamental flavors. Phys Rev. (2012) D85:014504. doi: 10.1103/PhysRevD.85.014504

CrossRef Full Text

50. Hietanen A, Lewis R, Pica C, Sannino F. Composite goldstone dark matter: experimental predictions from the lattice. (2013) arXiv: 1308.4130.

51. Affleck I, Dine M. A new mechanism for baryogenesis. Nucl Phys. (1985) B249:361.

52. Allahverdi R, Mazumdar A. A mini review on affleck-dine baryogenesis. New J Phys. (2012) 14:125013. doi: 10.1088/1367-2630/14/12/125013

CrossRef Full Text

53. Bell NF, Petraki K, Shoemaker IM, Volkas RR. Pangenesis in a baryon-symmetric universe: dark and visible matter via the affleck-dine mechanism. Phys Rev. (2011) D84:123505. doi: 10.1103/PhysRevD.84.123505

CrossRef Full Text

54. Cheung C, Zurek KM. Affleck-dine cogenesis. Phys Rev. (2011) D84:035007. doi: 10.1103/PhysRevD.84.035007

CrossRef Full Text

55. von Harling B, Petraki K, Volkas RR. Affleck-dine dynamics and the dark sector of pangenesis. JCAP (2012) 1205:021. doi: 10.1088/1475-7516/2012/05/021

CrossRef Full Text

56. Roszkowski L, Seto O. Axino dark matter from Q-balls in affleck-dine baryogenesis and the omega(b) - omega(DM) coincidence problem. Phys Rev Lett. (2007) 98:161304. doi: 10.1103/PhysRevLett.98.161304

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

57. Cosme N, Lopez Honorez L, Tytgat MHG. Leptogenesis and dark matter related? Phys Rev. (2005) D72:043505. doi: 10.1103/PhysRevD.72.043505

CrossRef Full Text

58. Davoudiasl H, Morrissey DE, Sigurdson K, Tulin S. Hylogenesis: a Unified Origin for Baryonic Visible Matter and Antibaryonic Dark Matter. Phys Rev Lett. (2010) 105:211304. doi: 10.1103/PhysRevLett.105.211304

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

59. Falkowski A, Ruderman JT, Volansky T. Asymmetric dark matter from leptogenesis. JHEP (2011) 1105:106. doi: 10.1007/JHEP05(2011)106

CrossRef Full Text

60. Arina C, Sahu N. Asymmetric inelastic inert doublet dark matter from triplet scalar leptogenesis. Nucl Phys. (2012) B854:666–99. doi: 10.1016/j.nuclphysb.2011.09.014

CrossRef Full Text

61. Shelton J, Zurek KM. Darkogenesis: a baryon asymmetry from the dark matter sector. Phys Rev. (2010) D82:123512. doi: 10.1103/PhysRevD.82.123512

CrossRef Full Text

62. Feng WZ, Mazumdar A, Nath P. Baryogenesis from dark matter in an inflationary universe. Phys Rev. (2013) D88:036014. doi: 10.1103/PhysRevD.88.036014

CrossRef Full Text

63. Feng WZ, Nath P, Peim G. Cosmic coincidence and asymmetric dark matter in a stueckelberg extension. Phys Rev. (2012) D85:115016. doi: 10.1103/PhysRevD.85.115016

CrossRef Full Text

64. Blennow M, Dasgupta B, Fernandez-Martinez E, Rius N. Aidnogenesis via leptogenesis and dark sphalerons. JHEP (2011) 1103:014. doi: 10.1007/JHEP03(2011)014

CrossRef Full Text

65. Barr SM, Chen HY. Cogeneration of dark matter and baryons by non-standard-model sphalerons in unified models. JHEP (2013) 1310:129. doi: 10.1007/JHEP10(2013)129

CrossRef Full Text

66. Buckley MR, Randall L. Xogenesis. JHEP (2011) 1109:009. doi: 10.1007/JHEP09(2011)009

CrossRef Full Text

67. Gu PH, Lindner M, Sarkar U, Zhang X. WIMP dark matter and baryogenesis. Phys Rev. (2011) D83:055008. 10.1103/PhysRevD.83.055008

68. Allahverdi R, Dutta B, Sinha K. Cladogenesis: baryon-dark matter coincidence from branchings in moduli decay. Phys Rev. (2011) D83:083502. doi: 10.1103/PhysRevD.83.083502

CrossRef Full Text

69. Kohri K, Mazumdar A, Sahu N, Stephens P. Probing unified origin of dark matter and baryon asymmetry at PAMELA/Fermi. Phys Rev. (2009) D80:061302. doi: 10.1103/PhysRevD.80.061302

CrossRef Full Text

70. Cheung C, Zhang Y. Electroweak cogenesis. JHEP (2013) 1309:002. doi: 10.1007/JHEP09(2013)002

CrossRef Full Text