Planck-scale effects on WIMP dark matter

1. Introduction

The historic discovery of neutrino oscillations and their profound implications for neutrino properties [1] as well as the growing evidence for the existence of some sort of non-baryonic dark matter [2] indicate the need to ammend the Standard Model picture of matter. Here we focus on the issue of dark matter and its stability, which is usually assumed to result from the implementation of some ad-hoc global discrete symmetry, like R-parity in supersymmetric models.

It has been argued that non-perturbative gravitational effects break all global (continuous and discrete alike) symmetries [3]. The original motivation was based on black hole physics arguments but since then perturbative string theory has confirmed this conjecture in various cases [4]. Such gravitational effects have already been considered in a number of scenarios and models invoked to solve a number of theoretical problems [5–13]. Here, we turn our attention to the implications of such a claim on dark matter phenomenology, in the particular the case of weakly interacting dark matter candidates.

Weakly Interacting Massive Particles (WIMPs) present in various extensions of the Standard Model (SM) are among the best studied candidates for cold DM, as they quite naturally account for the observed relic abundance. Indeed, their abundance at the freeze–out epoch scales as:

$\begin{array}{cc}{\Omega }_{\text{CDM}}{h}^2\simeq 0.1\frac{3\times {10}^{-26} {\text{cm}}^{\text{3}}{\text{s}}^{-\text{1}}}{{\langle \sigma v\rangle }_{\text{f}.\text{o}.}},& (1)\end{array}$

where 〈σv〉_f.o. is the thermal average of the annihilation cross–section of DM times the relative velocity at freeze–out. For weak strength interacions and DM masses in the range from GeV to few TeV, the observed abundance is naturally obtained and the DM candidate passes all constraints arising from Big–Bang Nucleosynthesis (BBN), Cosmic Microwave Background (CMB) and structure formation. This non-trivial interplay between the weak–scale physics and the cosmological dark matter has been dubbed as the “WIMP miracle.”

Besides theoretical motivation and consistency, the WIMP paradigm provides interesting direct and indirect detection prospects, through recoil off–nuclei and annihilation to photons, neutrinos and charged particles. As the level of sensitivity reached by direct and indirect detection experiments [14–19] improves, there is growing hope that WIMP DM may be discovered soon. Complementary searches at the LHC [20] and specific indirect searches [for example: 21–23] may help unravel the mystery.

In the absence of a protecting symmetry ensuring their stability WIMPs are generally expected to decay. The latter is avoided in most models by imposing in an ad-hoc way a global symmetry (usually a Z₂) that forbids the decay of the DM candidate. In this case unless the symmetry responsible for the DM stability is local, it is expected to be broken at short distances by gravitational effects leading to a decaying WIMP DM. Dark matter will then be stable at the level of renormalizable operators, with the Planck-mass suppressed dimension five and higher operators responsible for its late decay. From the phenomenological point of view, absolute stability is not a necessary condition for being a viable DM candidate. Instead, what is required is a lifetime larger than the current age of the Universe H⁻¹ ≈ 10¹⁷ s, where H is the Hubble constant. Cosmic and gamma rays analysis constrain the lifetime of a WIMP DM candidate even further to be τ_DM ≳ 10²⁶s [24–27]. An important question to be addressed then is what are the requirements on the Planck physics induced operators in order to preserve the validity of a WIMP DM candidate?

In this article we will show that a sufficient requirement to ensure an adequately long WIMP lifetime is to suppress the dimension-five operators. These suppressed operators will at the same time provide us with a new source of indirect detection signals which arise from the dark matter decay, particularly interesting in regions where annihilation alone delivers a very faint signal. Finally, we will see that a number of phenomenologically interesting decaying dark matter candidates with electroweak scale masses and weak–strength couplings fit within a WIMP paradigm, characterized by a well-controlled cosmological history (thermal production) and viable direct detection prospects.

We note that similar decay effects from higher scales have been analyzed before in the context of supersymmetric unified theories [28] or technicolor theories [29], where the dimension-6 GUT-suppressed operators lead to astrophysical signals that are similar to ours. However the dimension-5 operators in that case lead to too short a lifetime for DM. In contrast, the Planck scale provides a stronger suppression allowing for signals emerging from the first non-renormalizable operators.

2. Prototype Scenario

In order to illustrate the discussion, let us consider a very simple prototype scheme, exhibiting generic WIMP dark matter features over a broad phenomenological parameter range. For definiteness we assume the Standard Model (SM) to be extended by S_i (i = 1 …N) real scalar gauge-singlets [30, 31]. In addition, we impose a parity symmetry to which the SM particles are blind. Thus, the S_i sector can only interact with the SM via scalar states present in the scalar potential. The choice of the Z₂ symmetry is motivated by simplicity alone, in principle any global (discrete or continuous) symmetry that forbids the decay of the lightest S_i is a possible valid choice.

This scenario provides well-known production and thermalization mechanism via Higgs boson exchange, the so-called Higgs portal [32, 33]. The simplest model, i.e., N = 1, is highly constrained by current direct detection experiments for DM mass lower than 130 GeV¹. The presence of extra gauge singlets helps overcoming these constraints thanks to coannilihations between the LSP (lightest singlet particle) S₁ and the remaining S_{i > 1}. In this case one can reduce the value of the cross sections involved in indirect and direct searches to an adequate level. In order to be efficient this process requires small enough mass splittings [34].

In a conventional WIMP dark matter scenario our LSP would be stable and the extra terms in the scalar potential would read as (summation over indexes is understood):

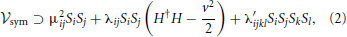
where μ²_ij, λ_ij and λ′_ijkl are the parameters of the potential. Here H is the SM Higgs doublet.

For the sake of simplicity we consider the case N = 2 and suppose μ²_ij to be diagonal with positive entries. Equation 2 contains the relevant interaction terms. The annihilation processes involved in the determination of the relic abundance calculation are presented in Figure 1.

FIGURE 1

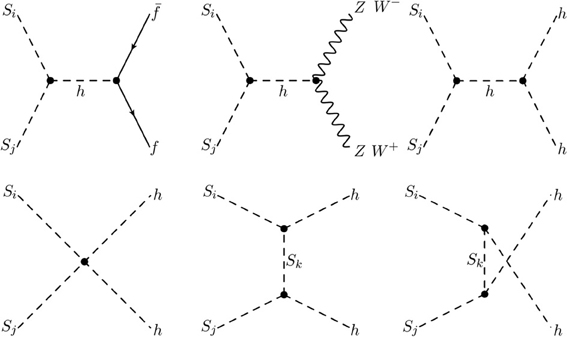
Figure 1. Model's Feynman diagrams present in the calculation of the relic abundance. This model provides the relic abundance, annihiliation and direct detection cross sections via the Higgs portal.

3. Parametrizing the Planck-Induced Effects

As mentioned above, the global symmetry stabilizing dark matter is likely to be broken due to the presence of gravitational effects. In order to implement the violation of the global symmetry responsible for the stability of dark matter we add to 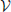_sym (Equation 2) an effective potential

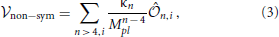
that breaks explicitly the stabilizing symmetry through non-renormalizable terms suppressed by powers of the Planck mass M_pl ≈ 10¹⁹ GeV. Here 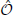_n,i are operators of dimension n > 4 and κ_n are free parameters. In the presence of these operators induced by Planck scale effects one has that the symmetry stabilizing DM is explicitly broken, but none of the Standard Model symmetries. This leads to the decay of S_i, the most important of which will be the decay of the LSP.

In order to illustrate the interplay between decay and annihilation we consider the following dimension five operators:

where F_L is an doublet SM fermion, f_R the corresponding right-handed SU(2) singlet partner and Y_f its Yukawa coupling. This type of operators can be generated via the spontaneous breaking of the stabilizing symmetry. Notice that we model the gravitational effects by parameterizing them as a scaling factor κ₅ times the corresponding Yukawa coupling. These operators lead to a decay lifetime τ_DM = ℏ/Γ^ff where

$\begin{array}{cc}{\Gamma }^{ff}(M_{\text{DM}})={\displaystyle \sum _f\frac{N_c}{8{\pi }^2}}{\left(\frac{{\kappa }_5{Y}_{f}v}{M_{pl}}\right)}^2{M}_{\text{DM}}{\left(1-\frac{4m_f^2}{M_{\text{DM}}^2}\right)}^{\frac{3}{2}},& (5)\end{array}$

is the dark matter decay width to fermions of mass m_f and N_c is the color number (3 for quarks and 1 for leptons). Under these assumptions, one has that in our prototype scenario the dark matter phenomenology is essentially determined by 6 parameters:

$\begin{array}{cc}{M}_{S_1},M_{S_2},{\lambda }_{11},{\lambda }_{12},{\lambda }_{22}\text{and}{\kappa }_5.& (6)\end{array}$

4. WIMP Dark Matter Annihilation and Decay

We will now show how the mere fact of considering the global symmetry leading to dark matter stability as an approximate one leads to extra observational signals, in addition to the standard DM annihilation signals. This is particularly interesting in regions of parameter space where the latter is very faint.

The first five parameters in Equation (6) come from the scalar potential (Equation 2). Among these, the coupling with the Higgs field λ₁₁ is mainly responsible for DM abundance and direct detection signal. On the other hand κ₅ contributes to the indirect detection signal. The mass splitting ΔM = M_S2 − M_S1 characterizes the strength of coannihilations and their relevance for the relic abundance calculation. When it is small enough, co-annihilations are active and the parameter λ₁₂ controls their strength. The coupling λ₂₂ is the coupling of S₂ (the next-to-LSP) to the Higgs scalar. It has direct impact on the dark matter relic abundance in regions of the parameter space where both annihilations and co-annihilations are inefficient to reproduce a good relic abundance. In this case the latter could arise partly from the early decays of S₂ → S₁.

We present in Figure 2 the attainable values of the thermal average of the annihilation cross–section times velocity at present time, 〈σ_Av〉, compatible with DM relic abundance (Equation 1). The couplings are varied randomly within the limits of perturbativity, and the Higgs mass is fixed to 126 GeV [35, 36]. The results were obtained using the Micromegas code [37, 38]. In the presence of pure annihilations, 〈σ_Av〉 reproduces the expected thermal value 〈σv〉_f.o. ≃ 3 × 10⁻²⁶ cm³/s.

FIGURE 2

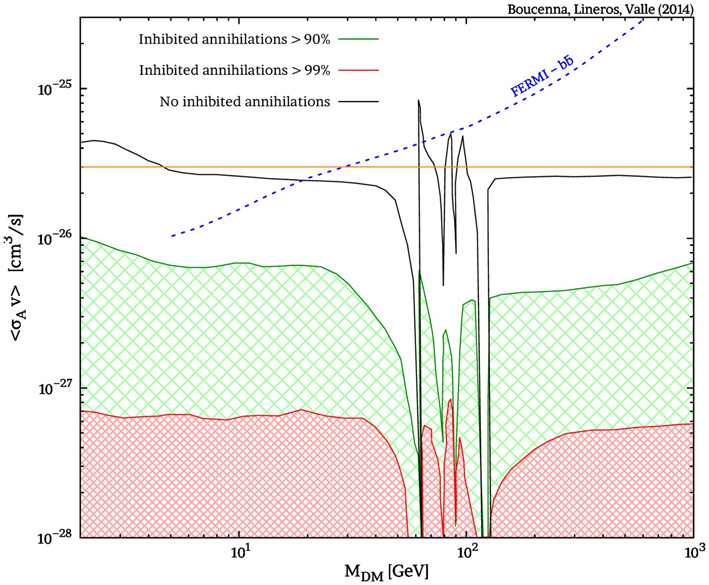
Figure 2. Annihilation cross section 〈σ_Av〉 compatible with DM relic abundance vs. DM mass. The line shown in black corresponds to the simplest case of unsuppressed annihilation. The case of where annihilations at freeze–out are inhibited (see text) above 90 and 99% is illustrated by the green and red shaded regions, respectively. The thermal cross section 〈σv〉_f.o. = 3× 10⁻²⁶cm²/s and FERMI's constraints for annihilation into bb are also shown.

Deviations from the thermal value exist in parameter regions where the cross-section is velocity-dependent, as in the case of the Breit–Wigner enhancement at the threshold of the Higgs pole [39].

In regions where 〈σv〉_f.o. is dominated by co-annihilation (S₁S₂ → SM + SM and/or S₂S₂ → SM + SM) processes, the annihilation cross–section is suppressed well below the expected thermal value. Such “inhibited annihilation” regions can arise in various ways. Co-annihilation is one possible mechanism, common to many dark matter models such as the minimal supersymmetric standard model two-Higgs-doublet dark matter models [40], whose generic features are mimicked by our illustrative prototype scheme. Inhibition mechanisms have been invoked in order to obtain (or to extend) an allowed region in the parameters space [41, 42]. However, the general drawback is that the stable WIMP's indirect detection signal becomes much fainter.

Now we turn to the effects of dark matter Planck–induced decays. In Figure 3, we display the expected gamma–ray fluxes arising from dark matter annihilation and decay, assuming that the signal comes only from the production of bb through the operator ^bbh₅. For illustrative purpose, we compare with the constraints for 〈σ_Av〉 from FERMI on annihilation into bb from dwarf satellite galaxies [43]. In order to compare the decay and annihilation signals we define the η–flux:

$\begin{array}{cc}\eta (M_{\text{DM}})=\{\begin{array}{ll}\frac{1}{4\pi }\frac{\langle {\sigma }_{A}v\rangle J_{\Delta \Omega }^{\text{ann}}}{2M_{\text{DM}}^2}\hfill & \text{for}\text{annihilations}\hfill \\ \frac{1}{4\pi }\frac{J_{\Delta \Omega }^{\text{dec}}}{2{\tau }_{\text{DM}}{M}_{\text{DM}}}\hfill & \text{for}\text{decays},\hfill \end{array}& (7)\end{array}$

where J_ΔΩ is the angular averaged line of sight integral of the DM density (squared) for decaying (annihilating) WIMP dark matter. In order to estimate the η–fluxes we use the J_ΔΩ for galaxy clusters reported in [26]. The latter provide weaker constraints than the analysis based on dwarf galaxies. The observable gamma–rays flux is directly related to the η–flux as:

$\begin{array}{cc}{\Phi }_{\gamma }(E,M_{\text{DM}})=\eta (M_{\text{DM}})\times \frac{d{n}_{\gamma }}{dE}(E),& (8)\end{array}$

where dn_γ/dE is the photon spectrum per single annihilation (or decay) event. This quantity allows us to compare on the same footing both annihilation and decay signals with FERMI constraints for an equivalent photon spectrum. In our particular case, we compare the signal associated to the production of bb pairs.

FIGURE 3

Figure 3. The η–flux associated with dark matter decay vs. DM mass (see text for details). We give estimates for the annihilation flux for the cases of 90%, 99%, and no suppression (solid green, red, and black lines respectively). Purple lines correspond to decay signal induced by the operator 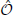^bbh₅ for fixed κ₅ values. A combined signal annihilation and decay is in red doted–dashed line assuming κ₅ = 3 × 10⁻⁸ and 99% inhibited annihilation. The bound from FERMI on annihilation into bb [43] is also shown.

We notice that η–fluxes coming only from decays quickly rise with the DM mass. For instance, for a 50 GeV DM mass, we would require κ₅ to be smaller than ~ 10⁻⁷ in order to fulfill the observational constraints. In Table 1, we present upper bounds on κ₅ for different DM mass values that produce DM lifetime larger than 10²⁷ sec, which is the current lower limit for the DM lifetime. In contrast, inhibited annihilations (same regions as in Figure 2) lead to signals that are faint and well below observational sensitivities of indirect dark matter searches.

TABLE 1

Table 1. DM mass and upper bound of κ₅ for DM life time larger than 10²⁷ sec.

Before turning to the direct detection signal, a comment on non-thermal dark matter is in order here.

Decaying DM candidates are commonly assumed to have a non-thermal origin, hence not to be WIMPs. This is indeed the case of particles with masses below or much above the weak scale. Dark matter candidates in this class include keV–majorons [8, 44–47], sterile neutrinos [48], super-heavy dark matter [49] and dark matter particles with extremely weak couplings with Standard Model particles, such as decaying gravitinos [50, 51].

However, we see that a WIMP can be seen as purely decaying dark matter in some regions. This implies that a number of phenomenologically interesting decaying dark matter candidates with electroweak scale masses and weak–strength couplings fit within a WIMP paradigm, characterized by a well-controlled cosmological history (thermal production) and viable direct detection prospects.

In order to ascertain the feasibility of indirect dark matter detection one must also take into account the restrictions arising from searches in nuclear recoil experiments.

5. Direct Detection of WIMPs

We now turn to the direct dark matter detection signal. This can be calculated in terms of the DM mass and parametrized by σ_SI, as shown in Figure 4. Note that regions with inhibited annihilations are associated with reduced values of σ_SI. This model–dependent feature is common to many constructions where M_DM < M_W and annihilations are dominated by quark final states [see for a particular case: 57]. The correlation between σ_SI and 〈σ_Av〉 is strong and the suppression of annihilations is translated as a weakening or absence of direct detection signal.

FIGURE 4

Figure 4. Spin–independent cross section vs. dark matter mass. Exclusions from XENON100 [52, 53], CDMS [54, 55], EDELWEISS [56] and LUX [19] are shown. As in Figure 2, we present cases where inhibited annihilations produce compatible SI cross section. WIMPs with masses larger than 8 GeV would produce extremely faint gamma–ray fluxes in order to fulfill direct detection constraints.

This correlation is certainly important to enlarge the space of parameters allowed within the limits established by XENON100 [52, 53], CDMS [54, 55], EDELWEISS [56] and LUX [19] experiments and opens an interesting interplay between phenomenologically favored light WIMP DM annihilation, decay and direct detection.

Apart from the narrow Higgs pole region, dark matter in the mass range from 8 to 100 GeV, requires substantial suppression of the annihilation cross section, as seen in Figure 4. From Figure 3 this would preclude the indirect detection through the conventional annihilation signal. However, after including the signal originating from the decay modes, for “reasonable” choices of the κ_n parameters characterizing the strength of the non-renormalizable Planck–scale operators, one can obtain a sizeable signal over all the mass range. For the case of heavy dark matter candidates (> (100)GeV), FERMI is not sensitive enough to probe the thermal annihilation cross–section and decay modes naturally dominate the signal. Higher order operators are highly suppressed by the Planck scale and one would require unreasonably large couplings (~10¹⁰) in order to be able to see a signal from the decay. As a result, the only operators leading to a sizable decay signals are of dimension five. In other words, the stable WIMP hypothesis requires a mechanism of protection from Planck–effects that forbids only the dimension five operators. This is in contrast to the dramatic impact upon the axion solution by such operators [5, 6]. Alternative mechanisms to destabilize the DM in the context of Grand Unified Theories [58], horizontal symmetries [59], instanton mediation [60] and kinetic mixing with hidden abelian gauge groups [61] also lead to similar conclusions, namely, long-lived WIMPs require a high level of suppression of the DM decay rate.

In summary, WIMP dark matter schemes with inhibited annihilation cross section have a very faint indirect detection signal. However, taking into account Planck-induced decay channels may re-open the indirect detection potential while still compatible with direct detection constraints.

6. Conclusions

In this paper, we have considered the effect of explicit gravitational breaking of the global symmetry responsible for WIMP dark matter stability. We find that Planck-suppressed operators of dimension six and higher do not lead to sizable decays and can be safely neglected, while, under reasonable assumptions, dark matter decay induced by dimension five operators yields can be under control.

Assuming that these breaking effects are small enough to yield sufficiently long DM decay lifetimes, there appears a genuine new signal in regions of parameter space that were previously dark. This illustrates the importance of taking into account the rich interplay between direct and indirect detection of decaying WIMP dark matter. Indeed, in models where annihilations are suppressed, the expected signal of indirect detection is very faint which also leads to a small direct detection signal in most cases. However, including the WIMP decays induced by the Planck–scale effects, one has an extra source of signal which makes the WIMP dark matter detectable.

On the other hand, a large class of decaying dark matter candidates, with masses in the WIMP range and weak–strength couplings, naturally accommodates a WIMP thermal production scenario.

Finally, an unambiguous detection of a mixed decay and annihilation signal may offer a very interesting window into Planck–scale physics, opening an unexpected phenomenological implication of the WIMP paradigm.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank N. Fornengo and M. Taoso for their comments and suggestions upon reading the manuscript. This work was supported by the Spanish MINECO under grants FPA2011-22975 and MULTIDARK CSD2009-00064 (Consolider-Ingenio 2010 Programme), by Prometeo/2009/091 (Generalitat Valenciana), by the EU ITN UNILHC PITN-GA-2009-237920.

Footnotes

1. ^There are also collider constraints for low masses (particularly from the invisible decay of the Higgs at LHC) however we do not include them here as our goal is illustrative.

References

1. Maltoni M, Schwetz T, Tortola MA, Valle JWF. Status of global fits to neutrino oscillations. New J Phys. (2004) 6:122. doi: 10.1088/1475-7516/2009/08/017

CrossRef Full Text

2. Bertone G, Hooper D, Silk J. Particle dark matter: evidence, candidates and constraints. Phys Rep. (2005) 405:279–390. doi: 10.1016/j.physrep.2004.08.031

CrossRef Full Text

3. Giddings SB, Strominger A. Loss of incoherence and determination of coupling constants in quantum gravity. Nuclear Phys B (1988) 307:854–66. doi: 10.1016/0550-3213(88)90109-5

CrossRef Full Text

4. Banks T, Seiberg N. Symmetries and strings in field theory and gravity. Phys Rev D (2011) 83:084019. doi: 10.1103/PhysRevD.83.084019

CrossRef Full Text

5. Kamionkowski M, March-Russell J. Planck scale physics and the Peccei-Quinn mechanism. Phys Lett. (1992) B282:137–41. doi: 10.1016/0370-2693(92)90492-M

CrossRef Full Text

6. Holman R, Hsu SDH, Kephart T, Kolb E, Watkins R, Widrow L. Solutions to the strong CP problem in a world with gravity. Phys Lett. (1992) B282:132–6. doi: 10.1016/0370-2693(92)90491-L

CrossRef Full Text

7. Akhmedov EKh, Berezhiani ZG, Mohapatra RN, Senjanovic G. Planck scale effects on the majoron. Phys Lett B (1993) 299:90–3. doi: 10.1016/0370-2693(93)90887-N

CrossRef Full Text

8. Berezinsky V, Valle JWF. The KeV majoron as a dark matter particle. Phys Lett. (1993) B318:360–6. doi: 10.1016/0370-2693(93)90140-D

CrossRef Full Text

9. Rothstein IZ, Babu KS, Seckel D. Planck scale symmetry breaking and majoron physics. Nuclear Phys B (1993) 403:725–48. doi: 10.1016/0550-3213(93)90368-Y

CrossRef Full Text

10. Berezinsky V, Joshipura AS, Valle JWF. Gravitational violation of R-parity and its cosmological signatures. Phys Rev. (1998) D57:147–51.

11. de Gouvêa A, Valle JWF. Minimalistic neutrino mass model. Phys Lett B (2001) 501:115–27. doi: 10.1016/S0370-2693(01)00103-4

CrossRef Full Text

12. Masso E, Rota F, Zsembinszki G. Planck-scale effects on global symmetries: cosmology of pseudo-Goldstone bosons. Phys Rev D (2004) 70:115009. doi: 10.1103/PhysRevD.70.115009

CrossRef Full Text

13. Frigerio M, Hambye T, Masso E. Sub-GeV dark matter as pseudo-nambu-goldstone bosons from the seesaw scale. Phys Rev X (2011) 1:021026. doi: 10.1103/PhysRevX.1.021026

CrossRef Full Text

14. Bernabei R, Belli P, Cappella F, Cerulli R, Dai CJ, d'Angelo A, et al. First results from DAMA/LIBRA and the combined results with DAMA/NaI. Eur Phys J C (2008) 56:333. doi: 10.1140/epjc/s10052-008-0662-y

CrossRef Full Text

15. Aalseth CE, Barbeau PS, Bowden NS, Cabrera-Palmer B, Colaresi J, Collar JI, et al. Results from a search for light-mass dark matter with a p-type point contact germanium detector. Phys Rev Lett. (2011) 106:131301. doi: 10.1103/PhysRevLett.106.131301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

16. Angloher G, Bauer M, Bavykina I, Bento A, Bucci C, Ciemniak C, et al. Results from 730 kg days of the CRESST-II Dark Matter search. Eur Phys J C (2012) 72:1971. doi: 10.1140/epjc/s10052-012-1971-8

CrossRef Full Text

17. Agnese R, Ahmed Z, Anderson AJ, Arrenberg S, Balakishiyeva D, Thakur RB, et al. Silicon detector dark matter results from the final exposure of CDMS II. Phys Rev Lett. (2013) 111:251301. doi: 10.1103/PhysRevLett.111.251301

CrossRef Full Text

18. Aprile E, Alfonsi M, Arisaka K, Arneodo F, Balan C, Baudis L, et al. Dark matter results from 225 live days of XENON100 data. Phys Rev Lett. (2012) 109:181301. doi: 10.1103/PhysRevLett.109.181301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

19. Akerib DS, Araujo HM, Bai X, Bailey AJ, Balajthy J, Bedikian S, et al. First results from the LUX dark matter experiment at the Sanford Underground Research Facility. (2013) arXiv:1310.8214

20. Bertone G, Cerdeno DG, Fornasa M, Pieri L, de Austri RR, Trotta R. Complementarity of indirect and accelerator dark matter searches. Phys Rev D (2012) 85:055014. doi: 10.1103/PhysRevD.85.055014

CrossRef Full Text

21. Hooper D, Goodenough L. Dark matter annihilation in the Galactic Center as seen by the Fermi Gamma Ray Space Telescope. Phys Lett B (2011) 697:412–28. doi: 10.1016/j.physletb.2011.02.029

CrossRef Full Text

22. Weniger C. A tentative gamma-ray line from Dark Matter annihilation at the Fermi Large Area Telescope. J Cosmol Astropart Phys. (2012) 8:7. doi: 10.1088/1475-7516/2012/08/007

CrossRef Full Text

23. Fornengo N, Lineros R, Regis M, Taoso M. Possibility of a dark matter interpretation for the excess in isotropic radio emission reported by ARCADE. Phys Rev Lett. (2011) 107:271302. doi: 10.1103/PhysRevLett.107.271302

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

24. Ibarra A, Tran D. Decaying dark matter and the PAMELA anomaly. J Cosmol Astropart Phys. (2009) 2:21. doi: 10.1088/1475-7516/2009/02/021

CrossRef Full Text

25. Ibarra A, Tran D, Weniger C. Decaying dark matter in light of the PAMELA and Fermi LAT data. J Cosmol Astropart Phys. (2010) 1:9. doi: 10.1088/1475-7516/2010/01/009

CrossRef Full Text

26. Huang X, Vertongen G, Weniger C. Probing dark matter decay and annihilation with Fermi LAT observations of nearby galaxy clusters. J Cosmol Astropart Phys. (2012) 1:42. doi: 10.1088/1475-7516/2012/01/042

CrossRef Full Text

27. Esmaili A, Ibarra A, Peres OLG. Probing the stability of superheavy dark matter particles with high-energy neutrinos. J Cosmol Astropart Phys. (2012) 11:34. doi: 10.1088/1475-7516/2012/11/034

CrossRef Full Text

28. Arvanitaki A, Dimopoulos S, Dubovsky S, Graham PW, Harnik R, Rajendran S. Astrophysical probes of unification. Phys Rev. (2009) D79:105022. doi: 10.1103/PhysRevD.79.105022

CrossRef Full Text

29. Nardi E, Sannino F, Strumia A. Decaying dark matter can explain the e+-excesses. J Cosmol Astropart Phys. (2009) 1:43. doi: 10.1088/1475-7516/2009/01/043

CrossRef Full Text

30. McDonald J. Gauge singlet scalars as cold dark matter. Phys Rev D (1994) 50:3637–49. doi: 10.1103/PhysRevD.50.3637

CrossRef Full Text

31. Burgess CP, Pospelov M, ter Veldhuis T. The minimal model of nonbaryonic dark matter: a singlet scalar. Nucl Phys. (2001) B619:709–28. doi: 10.1016/S0550-3213(01)00513-2

CrossRef Full Text

32. Davoudiasl H, Kitano R, Li T, Murayama H. The new minimal standard model. Phys Lett B (2005) 609:117–23. doi: 10.1016/j.physletb.2005.01.026

CrossRef Full Text

33. Goudelis A, Mambrini Y, Yaguna C. Antimatter signals of singlet scalar dark matter. J Cosmol Astropart Phys. (2009) 12:8. doi: 10.1088/1475-7516/2009/12/008

CrossRef Full Text

34. Griest K, Seckel D. Three exceptions in the calculation of relic abundances. Phys Rev. (1991) D43:3191–203.

Pubmed Abstract | Pubmed Full Text

35. Adam W, Aguilo E, Bergauer T, Dragicevic M, Erö J, Fabjan C, et al. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. Phys Lett B (2012) 716:30–61. doi: 10.1016/j.physletb.2012.08.021

CrossRef Full Text

36. Aad G, Abajyan T, Abbott B, Abdallah J, Abdel Khalek S, Abdelalim AA, et al. Observation of a new particle in the search for the Standard Model Higgs boson with the ATLAS detector at the LHC. Phys Lett B (2012) 716:1–29. doi: 10.1016/j.physletb.2012.08.020

CrossRef Full Text

37. Belanger G, Boudjema F, Pukhov A, Semenov A. MicrOMEGAs 2.0: a program to calculate the relic density of dark matter in a generic model. Comput Phys Commun. (2007) 176:367–82. doi: 10.1016/j.cpc.2006.11.008

CrossRef Full Text

38. Belanger G, Boudjema F, Pukhov A, Semenov A. Dark matter direct detection rate in a generic model with micrOMEGAs 2.2. Comput Phys Commun. (2009) 180:747–67. doi: 10.1016/j.cpc.2008.11.019

CrossRef Full Text

39. Ibe M, Murayama H, Yanagida TT. Breit-wigner enhancement of dark matter annihilation. Phys Rev. (2009) D79:095009. doi: 10.1103/PhysRevD.79.095009

CrossRef Full Text

40. Lopez Honorez L, Nezri E, Oliver JF, Tytgat MHG. The inert doublet model: an archetype for dark matter. J Cosmol Astropart Phys. (2007) 2:28. doi: 10.1088/1475-7516/2007/02/028

CrossRef Full Text

41. Cohen T, Kearney J, Pierce A, Tucker-Smith D. Singlet-doublet dark matter. Phys Rev D (2012) 85:075003. doi: 10.1103/PhysRevD.85.075003

CrossRef Full Text

42. Edsjo J, Gondolo P. Neutralino relic density including coannihilations. Phys Rev. (1997) D56:1879–94.

43. Ackermann M, Ajello M, Albert A, Atwood WB, Baldini L, Ballet J, et al. Constraining dark matter models from a combined analysis of milky way satellites with the fermi large area telescope. Phys. Rev. Lett. (2011) 107:241302. doi: 10.1103/PhysRevLett.107.241302

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

44. Lattanzi M, Valle JWF. Decaying warm dark matter and neutrino masses. Phys Rev Lett. (2007) 99:121301. doi: 10.1103/PhysRevLett.99.121301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

45. Bazzocchi F, Lattanzi M, Riemer-Sorensen S, Valle JWF. X-ray photons from late-decaying majoron dark matter. J Cosmol Astropart Phys. (2008) 8:13. doi: 10.1088/1475-7516/2008/08/013

CrossRef Full Text

46. Esteves JN, Joaquim FR, Joshipura AS, Romão JC, Tórtola MA, Valle JWF. A₄-based neutrino masses with Majoron decaying dark matter. Phys Rev. (2010) D82:073008. doi: 10.1103/PhysRevD.82.073008

CrossRef Full Text

47. Lattanzi M, Riemer-Sorensen S, Tortola M, Valle JWF. Updated CMB, X- and gamma-ray constraints on majoron dark matter. Phys Rev D (2013) 88:063528. doi: 10.1103/PhysRevD.88.063528

CrossRef Full Text

48. Dodelson S, Widrow LM. Sterile-neutrinos as dark matter. Phys Rev Lett. (1994) 72:17–20. doi: 10.1103/PhysRevLett.72.17

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

49. Chung DJH, Kolb EW, Riotto A. Nonthermal supermassive dark matter. Phys Rev Lett. (1998) 81:4048–51. doi: 10.1103/PhysRevLett.81.4048

CrossRef Full Text

50. Takayama F, Yamaguchi M. Gravitino dark matter without R-parity. Phys Lett B (2000) 485:388–92. doi: 10.1016/S0370-2693(00)00726-7

CrossRef Full Text

51. Restrepo D, Taoso M, Valle JWF, Zapata O. Gravitino dark matter and neutrino masses with bilinear R-parity violation. Phys Rev D (2012) 85:023523. doi: 10.1103/PhysRevD.85.023523

CrossRef Full Text

52. Aprile E, Arisaka K, Arneodo F, Askin A, Baudis L, Behrens A, et al. Dark matter results from 100 live days of XENON100 data. Phys Rev Lett. (2011) 107:131302. doi: 10.1103/PhysRevLett.107.131302

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

53. Aprile E, Alfonsi M, Arisaka K, Arneodo F, Balan C, Baudis L, et al. Dark matter results from 225 live days of XENON100 data. Phys Rev Lett. (2012) 109:181301. doi: 10.1103/PhysRevLett.109.181301

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

54. Ahmed Z, Akerib DS, Arrenberg S, Bailey CN, Balakishiyeva D, Baudis L, et al. Dark matter search results from the CDMS II experiment. Science (2010) 327:1619–21. doi: 10.1126/science.1186112

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

55. Ahmed Z, Akerib DS, Arrenberg S, Bailey CN, Balakishiyeva D, Baudis L, et al. Results from a low-energy analysis of the CDMS II germanium data. Phys Rev Lett. (2011) 106:131302. doi: 10.1103/PhysRevLett.106.131302

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

56. Armengaud E, Augier C, Benoît A, Bergé L, Blümer J, Broniatowski A, et al. Final results of the EDELWEISS-II WIMP search using a 4-kg array of cryogenic germanium detectors with interleaved electrodes. Phys Lett B (2011) 702:329–35. doi: 10.1016/j.physletb.2011.07.034

CrossRef Full Text

57. Boucenna MS, Profumo S. Direct and indirect singlet scalar dark matter detection in the lepton-specific two-Higgs-doublet model. Phys Rev D (2011) 84:055011. doi: 10.1103/PhysRevD.84.055011

CrossRef Full Text

58. Arvanitaki A, Dimopoulos S, Dubovsky S, Graham PW, Harnik R, Rajendran S. Astrophysical probes of unification. Phys Rev D (2009) 79:105022. doi: 10.1103/PhysRevD.79.105022

CrossRef Full Text

59. Sierra DA, Restrepo D, Zapata O. Decaying neutralino dark matter in anomalous U(1)_H models. Phys Rev D (2009) 80:055010. doi: 10.1103/PhysRevD.80.055010

CrossRef Full Text

60. Carone CD, Erlich J, Primulando R. Decaying dark matter from dark instantons. Phys Rev D (2010) 82:055028. doi: 10.1103/PhysRevD.82.055028

CrossRef Full Text

61. Ibarra A, Ringwald A, Tran D, Weniger C. Cosmic rays from leptophilic dark matter decay via kinetic mixing. J Cosmol Astropart Phys. (2009) 8:17. doi: 10.1088/1367-2630/6/1/122

CrossRef Full Text