Programmable ferroelectric tunnel memristor

Introduction

In analogy to the resistor, inductor, and capacitor the memristor (memory resistor) is the passive circuit element, which was until recently considered to be “the missing circuit element” [1, 2]. Memristance, the memristor's main characteristic, which has the dimension of a resistance, should be tunable and history-dependent. Almost 40 years after the theoretical description, memristive behavior was firstly demonstrated in nanoscale systems possessing ionic transport properties [3]. Very recently genuine electronic effects, such as the direct tunnel effect in ultrathin ferroelectric films, so-called ferroelectric tunnel junctions (FTJ), [4] have been proposed as memristors [5, 6]. It has been shown that the resistance of a ferroelectric tunnel junction is indeed tunable and history-dependent. Nevertheless, programming the resistance of such a device in a designed way remains a major goal to be achieved.

In this letter, we investigate memristor characteristics and switching kinetics of a memristor based on a ferroelectric tunnel junction that has been shown to obey proper quantum tunneling [7, 8] and not thermionic injection, as it has been shown on ferroelectric semiconductors [9]. We demonstrate that the memristive states are univocally related to the polarization switching and that every memristor state can be achieved by design. Based on the analytical description given by the Kolmogorov-Avrami-Ishibashi [KAI] model [10, 11] we are able to explain the memristive behavior as being a result of coexisting, parallel-connected ferroelectric domains of opposite polarity inside 3600 μm² capacitor devices. This said, in principle every ferroelectric tunnel junction with a bigger capacitor area than the nuclei size of its ferroelectric domains is intrinsically a memristor, irrespective of the injection mechanism.

Materials and Methods

According to the definition given by Chua [2] the time-dependent characteristics of a charge-controlled memristor can be described by:

$\begin{array}{cc}\text{v}\left(t\right)=M\left(q(t)\right)i(t)& \left(1\right)\end{array}$

where v(t) is the output voltage characteristics, M the memristance (with the dimension of a resistance) and the time-dependency given through the charge q(t) and the current i(t). In the very specific situation where M = constant, the equation describes the behavior of a simple resistor.

In the present case of a ferroelectric tunnel junction, the electronic tunneling probability through the ferroelectric layer and thus the resistance is controlled by the ferroelectric polarization, which is equivalent to a surface charge at the electrodes [12]. Therefore, we can state that a FTJ is a charge-controlled memristor and Equation (1) applies. The charge q(t) can now simply be replaced by the time-dependent polarization P(t):

$\begin{array}{cc}\text{v}\left(t\right)=M\left(P(t)\right)i(t)& \left(2\right)\end{array}$

The memristive state of a FTJ is therefore dependent on the ferroelectric polarization and its time-dependent evolution is univocally related to the time dependence of the polarization and it can in principle be predicted. This is based on the working principle of FTJ, i.e., the electric current through a metal-ferroelectric-metal heterostructure is polarization dependent through the band alignment at the metal-ferroelectric interface [13, 14]. On the other hand, the time-dependent function P(t) is the result of the ferroelectric switching process. The polarization switching kinetics are usually described in terms of nucleation and growth of ferroelectric domains. The most common theoretical description of ferroelectric switching kinetics is based on the growth of nuclei that are randomly distributed across the ferroelectric capacitor [15] by ferroelectric domain wall propagation [16, 17]. After an initial nucleation process that takes place in the sub-picosecond range, ferroelectric domains grow laterally until they coalesce and the entire polarization will be in the opposite direction [18]. The time dependence of the switching polarization P is given by the KAI equation: [10]

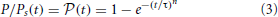
with 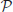(t) = P(t)/P_s being the normalized switched polarization, where P_s is the saturated value of polarization, τ is the characteristic switching time and n the domain switching dimensionality, which describes the domain wall movement. The exponent n can have ideally only integer values of 1, 2, and 3 representing one-, bi-, and three-dimensional domain growth during the switching process. From Equations (2) and (3) the memristance characteristics should be given by the following function:

$\begin{array}{cc}M/P_s(t)\approx 1-e^{-{\left(\text{t}/\tau \right)}^n}& \left(4\right)\end{array}$

In other words the memristance would be directly proportional to the amount of polarization switched by an applied external pulse of time interval t.

We have applied the above concept to ferroelectric tunnel junctions based on epitaxial oxide layers. The active layer of the structure is an ultrathin lead zirconate titanate Pb(Zr_0.2Ti_0.8)O₃ (PZT) film epitaxially grown on a La_0.7Sr_0.3MnO₃ (LSMO)/ SrTiO₃ (STO) (100) substrate. A high-resolution TEM image of part of the structure is shown in Figure 1. Rather large-area capacitor-like active devices (60 × 60 μm²) were defined by thermal evaporation of cobalt through a shadow mask.

FIGURE 1

Figure 1. High-resolution transmission electron micrograph of the Co/PZT/LSMO tunnel junction used in the present study. The thickness of PZT is 8 unit cells (about 3.2 nm).

Results

A typical current-voltage characteristic of a FTJ device is shown in Figure 2. This figure shows for the first time a hysteretic behavior similar to the i–v data of a TiO₂-based memristor discussed by Strukov et al. [3] The switching voltages, viz. the voltages at which the resistance switches from the OFF to the ON state and vice-versa, correspond to the coercive fields of the ferroelectric thin film, [19] while the above dynamic current-voltage characteristic (see Figure 2) is not necessarily identical to the memristor characteristics. The latter should reveal the memristance dependence on time as for example given by Equation (4). Assuming that the memristor states in the FTJ are univocally defined by the polarization switching we may presume that switching kinetics of a FTJ is identical with the switching kinetics of polarization in ultrathin ferroelectric films.

FIGURE 2

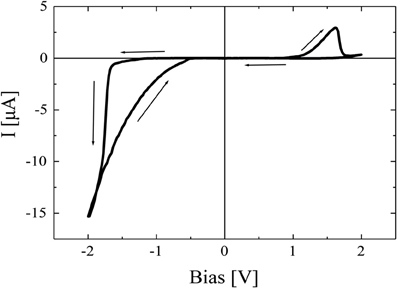
Figure 2. Current-voltage characteristic of the Co/PZT/LSMO structure shown in Figure 1. The switching from R_ON to R_OFF states and vice-versa is correlated to ferroelectric switching [11].

In order to experimentally study this phenomenon we have determined the memristor characteristics of a FTJ by measuring the resistive states induced by voltage pulses with variable width and amplitude. As the memristance is a history-dependent quantity, it is desirable to set the memristor device into a defined state before setting any other intermediate state. In the present case we used a negative voltage pulse with constant amplitude and width as a reset pulse, which sets the FTJ into the ON state defined by the lowest achievable tunnel resistance R_ON. From this reference state the FTJ can be driven into any intermediate state between R_ON and R_OFF using a writing pulse, i.e., a positive voltage pulse with variable amplitude and width. This can be done repeatedly until the polarization is fully switching into the opposite direction driving the junction into the OFF state defined by the highest achievable R_OFF resistance. Figure 3A shows the memristor characteristics determined using pulses of constant amplitude and variable width, following the scheme in Figure 3B. Between the R_ON and R_OFF states there is in principle an infinite number of memristance states. The time scale of the writing pulses to access these intermediate states is in the sub-μ s range, which is comparable with the switching time of ferroelectric polarization that has been shown in previous studies [20]. While the absolute values of the saturated (R_ON and R_OFF) tunnel resistances might slightly vary, mostly due to additional conducting paths represented by defects, [21] the R_ON/R_OFF ratio remains constant irrespective of the write amplitude and/or width.

FIGURE 3

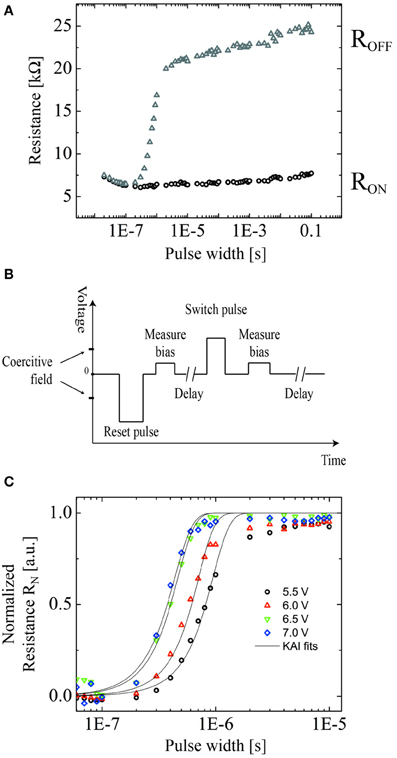
Figure 3. Memristor characteristics of a Co/PZT/LSMO tunnel junction with PZT thickness of 8 u.c. (A) Tunneling resistance as function of the writing pulse width. The black data points were measured after each reset pulse, the gray data points after each writing pulse. (B) The applied voltage train of the measuring setup: in this case the amplitude and width of the reset pulse were −6 V and 200 ms, respectively, the writing pulse had the same amplitude as the reset pulse. The measurement of the tunnel current is performed with an applied voltage of 0.1 V. (C) Normalized ON/OFF ratios for different amplitudes of the write pulse. The lines are fits with Equation (9).

To normalize the measured data, we define R_N as:

$\begin{array}{cc}{R}_N=\frac{R\text{−}{R}_{\text{ON}}}{R_{\text{OFF}}\text{−}{R}_{\text{ON}}}& \left(5\right)\end{array}$

where R_N takes values between 0 and 1. If the R_OFF/R_ON ratio or the tunneling electro resistance value is very large, i.e., larger than 100, Equation (5) can be simplified to R_N = $\frac{1}{R_{\text{OFF}}}$ (R − R_ON).

In Figure 3C, R_N is plotted vs. the applied pulse time for different amplitude values of the applied pulses. For higher pulse voltages the system switches faster into the saturated R_OFF state, which we contribute to the field-dependent domain wall velocity [22], leading to a faster unipolar formation of the domains in the ferroelectric tunnel barrier.

We now postulate that a memristive state can be described by a resistance resulting from a parallel connection of individual resistances given by coexisting ferroelectric domains of opposite polarity inside one capacitor similar to the case of a multilevel ferroelectric memory [20] (Figure 4). In other words, the effective resistance R of the tunnel junction after applying a certain pulse is given by the equivalent resistance of a circuit of resistors connected in parallel, which are defined by the area of domains with polarization up and down, R_↑ and R_↓ respectively. The areas which define R_↑ and R_↓ are complementary and the growth of one is on the expense of the other and happens according to the KAI dependence Equation (3). We can now write the reciprocal value of the resistance as a function of the normalized polarization P(t)/P_s = 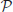(t), which represents the time evolution of the switched domains by an applied pulse:

FIGURE 4

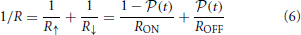
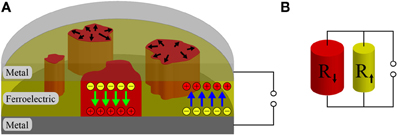
Figure 4. (A) A schematic cross section of the ferroelectric layer with visible domains. The red areas inside the sketch visualize the domains with pointing down polarization, marked by green arrows. The bright yellow area is the “unswitched” area and defined by polarization pointing up (blue arrows). The black arrows indicate the growth direction of the ferroelectric domains with opposite polarity. (B) Simplifying (A) to a model of parallel connected resistances, where R_↑ is the summarized resistance of areas with polarization up and R_↓ with polarization down accordingly.

From Equations (5) and (6) the time dependence of the normalized resistance can be written as (see also supplementary online material):

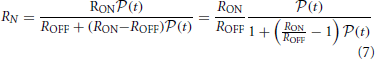
In the case of very large TER, Equation (7) simplifies to:

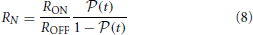
Equations (7) or (8) together with Equation (3) represent the characteristic transfer function of the ferroelectric memristor:

$\begin{array}{cc}{R}_N=\frac{R_{\text{ON}}}{R_{\text{OFF}}}\frac{\left(\text{1−}{e}^{\text{−}{\left(t/\tau \right)}^n}\right)}{\text{1+}\left(\frac{R_{\text{ON}}}{R_{\text{OFF}}}\text{−1}\right)\left(\text{1−}{e}^{\text{−}{\left(\text{t}/\tau \right)}^n}\right)}\approx \frac{R_{\text{ON}}}{R_{\text{OFF}}}\left(e^{{\left(t/\tau \right)}^n}\text{+1}\right)& \left(9\right)\end{array}$

The experimental data can be fitted with Equation (9) in order to obtain the chatacteristic value of the switching time τ. As we know that in ultrathin epitaxial ferroelectric films the polarization switching is mostly bi-dimensional, the value of the parameter n in the above relation can be assumed to be 2, and thus one can constrain the fitting only to one parameter τ. As it can be easily seen in Figure 3C, the fit of the experimental data is very good which we interpret as the univocal result of ferroelectric domain wall kinetics. The value of the characteristic switching time is in the range of sub-μ s wich is, as expected, similar to the characteristic switching time in thin ferroelectric epitaxial PZT films of the same composition [23].

The analytical expression (9) can be used to predict or—better to say—to program any desired memristor state, independent from the memristor history. To show this experimentally, we analyzed the response of a ferroelectric memristor by successively applying programming pulses of constant amplitude, starting from a well-defined reference state ON, using different pulse width t_A = 800 ns and t_B = 1600 ns. In Figure 5, we present the time evolution of the resistance of a junction, where it can be easily seen that memristor states marked by horizontal lines can be achieved either with a long pulse t_B or with a larger number of shorter pulses t_A demonstrating the ability of programming any intermediate state between R_OFF and R_ON.

FIGURE 5

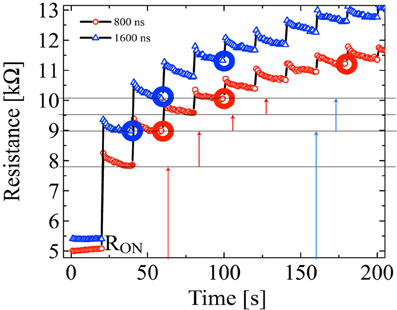
Figure 5. Memristor programming. The data points represent the resistance after switching from a pre-defined ON-state with a pulse width of t_A = 8 · 10⁻⁷ s (red) and t_B = 16 · 10⁻⁷ s (blue). The vertical lines between the data points are the indicators for pulses that were applied. The horizontal lines are the programmed memristor states. The long time relaxation after applying the switching pulse is related to back-switching and relaxation of polarization [24].

According to the model, applying one programming pulse with the total width t_t should always drive the FTJ to the same resistance as a sequence of pulses with width t_f < t_t of which the total time is t_t = ∑_n t_f where n = t_t/t_f.

Conclusion

In summary, we have shown that a ferroelectric tunnel junction memristor based on epitaxial ferroelectric oxide ultra-thin films can be programmed in a designed way. The characteristic transfer function of this device is directly related to the polarization switching mechanism, viz. to the Kolmogorov-Avrami-Ishibashi model with two-dimensional domain growth. The characteristic transfer function of the FTJ memristor is dependent only on the characteristic switching time of the ferroelectric polarization which is in the present case of the order of 10⁻⁷ s. The physical model of MTJ-based memristors proposed above satisfies the mathematical equations describing the general features of memristors.

In comparison to other memristor devices, [3] the present device is based on a genuine electronic effect, respectively on quantum electronic transport and does not rely on ionic transport or phase change. The writing process, i.e., the partial switching of ferroelectric polarization, is achieved with rather large voltage approaching the coercive voltage of the ferroelectric layer, but still sufficiently low to comply to the nowadays microelectronic requirements. The current-based nondestructive readout, although performed at low voltages (<0.2 V) provides sufficient current density to allow downscaling and high integration density. However, further investigations have to be performed in order to identify and understand issues related to reliably, polarization back-switching, fatigue phenomena, etc.

Author Contributions

Andy Quindeau, PhD student at the Max Planck Institute of Microstructure Physics. Dietrich Hesse, Professor at the Max Planck Institute of Microstructure Physics. Marin Alexe, Professor at Warwick University.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This research was financed by the German Research Foundation (DFG) via SFB762. The authors acknowledge D. Pantel and S. Götze for the TER sample.

References

1. Di Ventra M, Pershin Y. The parallel approach. Nat Phys. (2013) 9:200–2. doi: 10.1038/nphys2566

CrossRef Full Text

2. Chua LO. Memristor—the missing circuit element. IEEE Trans Circuit Theory (1971) 18:507–19. doi: 10.1109/TCT.1971.1083337

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

3. Strukov D, Snider GS, Stewart DR, Williams RS. The missing memristor found. Nature (2008) 453:80–3. doi: 10.1038/nature06932

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

4. Tsymbal EY, Kohlstedt H. Tunneling across a ferroelectric. Science (2006) 313:181–3. doi: 10.1126/science.1126230

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

5. Chanthbouala A, Garcia V, Cherifi RO, Bouzehouane K, Fusil S, Moya X, et al. A ferroelectric memristor. Nat Maerials. (2012) 11:860–4. doi: 10.1038/nmat3415

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

6. Kim DJ, Lu H, Ryu S, Bark C-W, Eom C-B, Tsymbal EY, et al. Ferroelectric tunnel memristor. Nano Lett. (2012) 12:5697–702. doi: 10.1021/nl302912t

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

7. Pantel D, Goetze S, Hesse D, Alexe M. Reversible electrical switching of spin polarization in multiferroic tunnel junctions. Nat Mater. (2012) 11:289–93. doi: 10.1038/nmat3254

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

8. Pantel D, Lu H, Goetze S, Werner P, Kim DJ, Gruverman A, et al. Tunnel electroresistance in junctions with ultrathin ferroelectric Pb(Zr0.2Ti0.8)O3 barriers. Appl Phys Lett. (2012) 100:23. doi: 10.1063/1.4726120

CrossRef Full Text

9. Jiang A, Chen Z, Hui W, Wu D, Scott JF. Subpicosecond domain switching in discrete regions of Pb(Zr0.35Ti0.65)O3 thick films. Adv Funct Materials (2012) 22:2148–53. doi: 10.1002/adfm.201102829

CrossRef Full Text

10. Ishibashi Y, Takagi Y. On distribution of relaxation times in some ferroelectrics. J Phys Soc Japan (1971) 31:54–5. doi: 10.1143/JPSJ.31.54

CrossRef Full Text

11. Dimmler K, Parris M, Butler D, Eaton S, Pouligny B, Scott JF, et al. Switching kinetics in KNO3 ferroelectric thin-film memories. J Appl Phys. (1987) 61:12. doi: 10.1063/1.338237

CrossRef Full Text

12. Lines ME, Glass AM. Principles and Applications of Ferroelectrics and Related Materials. Oxford: Clarendon Press (1977).

13. Pantel D, Alexe M. Electroresistance effects in ferroelectric tunnel barriers. Phys Rev B (2012) 82:134105. doi: 10.1103/PhysRevB.82.134105

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

14. Zhuravlev MY, Sabirianov RF, Jaswal SS, Tsymbal EY. Giant electroresistance in ferroelectric tunnel junctions. Phys Rev Lett. (2005) 94:246802. doi: 10.1103/PhysRevLett.94.246802

CrossRef Full Text

15. Gruverman A, Wu D, Scott JF. Piezoresponse force microscopy studies of switching behavior of ferroelectric capacitors on a 100-ns time scale. Phys Rev Lett. (2008) 100:097601. doi: 10.1103/PhysRevLett.100.097601

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

16. McQuaid RGP, McMillen M, Chang L-W, Gruverman A, Gregg JM. Domain wall propagation in meso- and nanoscale ferroelectrics. J Phys Condens Matter. (2012) 24:024204. doi: 10.1088/0953-8984/24/2/024204

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

17. Yang SM, Jo JY, Kim DJ, Sung H, Noh TW, Lee HN, et al. Domain wall motion in epitaxial Pb (Zr, Ti) O 3 capacitors investigated by modified piezoresponse force microscopy. APL (2008) 92:252901. doi: 10.1063/1.2949078

CrossRef Full Text

18. Gruverman A. Nanoscale insight into the statics and dynamics of polarization behavior in thin film ferroelectric capacitors. J Mater Sci. (2009) 44:5182–8. doi: 10.1007/s10853-009-3623-4

CrossRef Full Text

19. Pantel D, Goetze S, Hesse D, Alexe M. Room-temperature ferroelectric resistive switching in Ultrathin Pb(Zr0.2Ti0.8)O3 films. ACS Nano (2011) 5:6032–8. doi: 10.1021/nn2018528

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

20. Lee D, Yang SM, Kim TH, Jeon BC, Kim YS, Yoon J-G, et al. Multilevel data storage memory using deterministic polarization control. Adv Materials (2012) 24:402–6. doi: 10.1002/adma.201103679

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

21. Ventura J, Teixeira JM, Araujo JP, Sousa JB. Pinholes and temperature-dependent transport properties of MgO magnetic tunnel junctions. Phys Rev B (2008) 78:024403 doi: 10.1103/PhysRevB.78.024403

CrossRef Full Text

22. Shur V, Rumyantsev E, Makarov S. Kinetics of phase transformations in real finite systems: application to switching in ferroelectrics. J Appl Phys. (1998) 84:445–51. doi: 10.1063/1.368047

CrossRef Full Text

23. Li W, Alexe M. Investigation on switching kinetics in epitaxial Pb(Zr0.2Ti0.8)O3 ferroelectric thin films: role of the 90° domain walls. Appl Phys Lett. (2007) 91:26093. doi: 10.1063/1.2825414

CrossRef Full Text

24. Kim DJ, Jo JY, Kim YS, Chang YJ, Lee JS, Yoon J-G, et al. Polarization relaxation induced by a depolarization field in ultrathin ferroelectric capacitors. Phys Rev Lett. (2005) 95:237602. doi: 10.1103/PhysRevLett.95.237602

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text