- Group of Modeling of Physicochemical Processes, Department of Physics, Institute of Mathematics and Physics, University of Technology and Life Sciences, Bydgoszcz, Poland
Introduction: Meso- vs. Nanoscale Passage Associated with Atomic/Molecular Detail
As pointed out by Hamacher [1] computational physics methodologies have become the third leg of natural sciences, specifically, of biological physics and chemistry, because they are striving for effective merging of theory and experiment, sometimes also extending crucially their influence ranges.
As addressed by Klingenberg [2] discretized mathematics and computer science have in last decades extensively developed their tools that virtually serve the (bio)physicists to be adopted within their dedicated areas of interests. Yet, a simple random-generator based Monte Carlo method (say, in Java) after being naturally applied to certain long-existing probelms, such as DLA/diffusion limited aggregation or percolation (also, Ising magnet) require a good basic knowledge for successful realization [3]. Thus, a physicist ought to be able to select and comprehend the method as being most efficiently applicable to her/his own problem.
In this Opinion, we are going to address but three types of problems coming from our own experience. As the first, let us invoke biomatter (dis)orderly aggregation and soft crystal formation mostly of protein/lysozyme type [4–6]. As the second, let us focus on storage vs. loss viscoelastic (non)linear characteristics of amphiphilic assemblages [7]. As the third, let us introduce a problem of nanoscale friction-lubrication effects on facilitated functioning of articulating systems [8, 9]. The so-offered selection is believed to be of formidable interest to biomedical engineering and biotechnology, to name but two disciplines, influencing greatly the quality of our live.
As to achieve a clear presentation, we wish to rest upon the following scheme. First, state the problem (P). Second, invoke its up-to-date solutions (S), then show its limitations (L): weaknesses and strenghts. Next, introduce a modus-vivendi actual solution (M-VS). Last, draw a brief scenario (SC) for future tasks, and possibly reveal a perspective (PE). Finally, boldface the importance of nanoscale effects/NE (range of 1–100 nm) in all instances discussed. Notice that there should be an entropy-assisted passage to this scale from its corresponding upper counterpart, termed the mesoscale [10].
Example One: Biomatter (Dis)orderly Aggregation and Soft Crystal Formation
P: While based on discrete-units depiction of the biomatter aggregation, the modeling principles [11] can be proposed as follows: (a) define a biomolecular (sub)mesoscopic unit (sMU), Figure 1; (b) select a minimalistic set of units' aggregation rules, AR-s, that allow to produce (dis)orderly aggregates and/or crystals; (c) apply the AR-s to a desired number of sMU-s, discerning between nucleation (N)- and growth (G) events, underlying the corresponding N-G phase transition, and subsequent thermodynamic-kinetic (T-K) evolution of the resulting (non)equilibrium phases. To look at how the AR-s yield clustering outputs upon geometrical confinements, see Hermann [11]. To refer to specific biomaterial examples, see Siodmiak [5], Kruszewska and Gadomski [7]. A continuum N-G version of the model is presented in Gadomski [4]. In close-to-equilibrium conditions, it serves to reveal the problem as a T-K entropy-production (σentr) engaging task [10]. It then leads to establish by σentr ∝ dR/dt, the growing rule (GR), in which dR/dt = σV is the aggregate's growth rate, based on changes of its radius R≡ R(t) upon time t, given by a product of σ, a thermodynamic supersaturation factor, and V- a suitably designed stochastic-kinetic macroion-velocity addressing co-factor [4, 6].
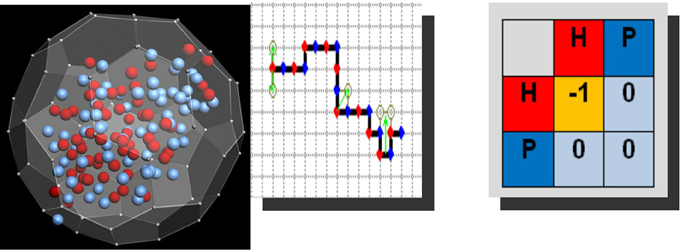
Figure 1. Left: Fullerene type mesoscopic, computation-prone unit (courtesy of J. Siodmiak), equipped with a number of hydrophobic (red) and polar (blue) residues. N-G phase change, resting on these units occurs most efficiently when red residues, by their binary interactions, yield the hydrophobic attraction-prone effects. Middle and right: Spaghetti type mesoscopic unit immersed in square lattice, along which polar and hydrophobic residues are distributed by choice in an alternative way; green arrows indicate elementary local moves of the chain: crankshaft-like, end-flips and corner-flips. Shown is at r.h.s. a generic energetic map, wherein the only nonzero value points to the elementary free energy gain of importance in Metropolis MC realization. The energetic scheme itself is called a Larsson-Dill scheme—the generic force field is of hydrophobic character.
S: The model, as confined to the limit of σentr → min. dicloses the T-K procedure of producing soft-material crystals. Especially, in the long-time conditions it satisfies a diffusion-zone diluted regime T-K characteristics at the interface upon σ → min [6]. Otherwise, at some suitably prescribed factor σ → min, σentr → min. is not fulfilled and (dis)orderly aggregation occurs. The factor σ → min suits very well the crystalline output if the protein velocity field is stationary Gaussian with a zero mean and with algebraic (power-law) correlations in time [12]. Otherwise, it is much more suitable for emergence of disorderly aggregation, which does not obey the condition of σentr → min [10].
L: The model, as applied to colloid-type crystal growth, has been realized experimentally [13] and by means of Monte Carlo (MC) computer simulation with Metropolis rules, assuming Boltzmann type probability-acceptance conditions. In the latter, the sMU has primarily been taken as cube-shaped, with projection of hydrophobic and polar residues onto cube's walls from which the resulting amphiphilic property of each wall can be inferred. The model worked efficiently in a spiral-like Burton-Cabrera mode of non-Kossel crystal formation [5], satisfying the T-K main properties coming from experiment [13]. The AR-s have been assumed as simple as possible: energetically favorable hydrophobic attachment to the terrace's corners, as contrasted with surface (on-terrace and sMU involving orientational) diffusion and/or diffusion-controlled detachment from the crystal terrace [6]. The generic force field, Figure 1, is hydrophobic [14].
M-VS: It is foreseen that the sMU such as the cube is judged to be far too crude to obey at length the N-G phase change peculiarities. In particular, the formation of a thermodynamically stable nucleus, also satisfying the molecular close-packing conditions, needs a more refined sMU, Figure 1. In order to simulate controllably the nucleation stage [15], one ought to switch, except of MC, to another computer simulation method, i.e., to Molecular Dynamics (MD) and/or, because of prevalence of stochastic-kinetic factor in oscillatory environmental weak-plasma conditions [16], just to resort to Brownian Dynamics (BD), [6].
SC: It is proposed that at the computer-simulation level the nucleation stage of the N-G should first be performed for a few test proteins, as it has been completed before for three types of lysozyme (and, their crystals), having assigned the following PDB codes: 193L (basic); 1LYY (amyloidogenic); 2AUB (tetramer-forming), [5]. After fixing the temperature (T) sensitive nucleation part of the N-G, preferentially by MD coupled to a carefully chosen thermostat (aided by BD), one should be able to exploit thereafter, in sufficient detail, the growing and cessation-to-growth stages, resorting then again to less memory-consuming MC technique equipped, however, with better tested than before force (or, energy-funnel) field, in contrast to that based on simple hydrophobic-polar (HP) model by Dill [14], and also by Larsson, or their Myiazawa-Jernigan advanced extension [5]. The refinement looks worth to address because of different protein folding vs. aggregation T-K energy-entropy GR-pathways, very challengeable in terms of medical and biotechnological applications [17].
PE: The simulations can first be run safely on standard computers with preferred compilers, the computers being equipped with GPU units, possibly assimilated with CUDA environment. More atomisitic detail [1, 2], unavoidable when embarking on biomolecule's folding events, can be tested by means of, e.g., Yasara software, or if really needed, in all-atom framework. Or, predictions toward molecule's conformational changes can be made with popular CASP tests, preceding other attempts for probing some mutations in molecule's configuration subspace [14].
NE: Proper introduction of basic nanoscale effects by computer simulation should first contain a molecular-detail possessing compromise between sMU-s from Figure 1, left and middle sMU-s, the latter being much more suitable for semiflexible chain deformation acts [18]. Moreover, in contrast with Dill et al. [14], designing so-dedicated (hybrid) computer simulation should not skip easily over the explicit solvent viz water account for the process - the issue itself being often divided to random and hydrodynamic (directed) parts [19]. This way, one may also introduce the H-bonding effect with an assistance of the corresponding breakages of the bonds, as well as some T−affected electrostatics with Poisson-Debye-Hückel scenario, possibly modifying the main force field of the simulation, and addressing so-called structured-water biomolecular envelopes [15], serving for passages of ions—another entropic issue to disclose [10].
Example Two: Storage vs. Loss Microrheological Viscoelastic Characteristics of Amphiphiles
P: Given a viscoelastic, d−dimensional, and well networked matrix. By probing with a suitable testing particle (TP) its interior, comprising first of hydrophobic (H) and polar (P) biochemical units of the chains constituting the net, linked by stronger (H − H), intermediate (H − P) and weak (P − P) bonds, with typical neglect of the latter, Figure 1, determine the random-walk characteristics (r-wChs) of the TP upon its interaction with the matrix.
S: Both MC (by Kramers' type energetic-barrier crossing) and MD (by adequate force-field prescription) methods are capable of recovering the r-wChs. The detailed address of the problem relies upon realizing about (i) which type of TP we are engaging for the testing? (ii) how do we define the interaction matrix vs. TP fields? (iii) which is the proportion of matrix elasticity (H − H bonds) as compared to its viscoelasticity (H − P bonds), and finally, to its viscosity (P − P bonds)? The r-wChs, to be anticipated as the problem's solution, render its final output as a power law, with the mean-square displacement (MSD) to be scalable with time t as MSD∝ tμ, cf. [20].μ uncovers typically three distinguished behaviors: subdiffusive (0 < μ <1), purely diffusive (μ = 1) and superdiffusive (μ > 1), in which latter case elasticity strongly prevails; otherwise, an (ab)normally viscous nature of the H − P matrix manifests. Note that by a Laplace transform of the MSD the three behaviors can be presented in terms of loss and elastic moduli, fully disclosing this way the viscoelasticity of the H − P dissipative assemblage, which could be also a micelle [8].
L: The method is primarily limited to linear viscoelasticity, and the Boltzmann superposition principle, enabling to unravel the compliance of examined H − P model biomaterials [7, 14]. It covers typical situations of interest, and stands by virtue of the method as an approximation. An experimental realization of the method is called diffusion wave spectroscopy [20].
M-VS: One may have a look at non-linear viscoelasticity by performing it first analytically in terms of fractional differential equations both in space and time; the system's behavior can be mimicked by non-linear Maxwell-Kelvin or Voigt, also Thompson, rheological mechanical-circuit elements, somehow by adopting a style of electrical circuits. As in the latter, wherein the electric current is transmitted through them, and a dissipation of its energy, with a necessary heat by-effect occurs, in mechanical circuits too, one expects an entropy-driven co-effect, to be estimated from the model [20].
SC: Engineering rationale would be designing the circuits by finite element method of simulation. Another more ambitious way could be to resort to cellular automata (CA), cf. [3]. On the other hand, as has already been mentioned, MC and MD, despite of their known limitations, such as lack of reliable time scale (MC), and huge memory and processor capacities' demands (MD), respecitvely, can be used as to derive the r-wChs of interest, especially, if complemented by the BD.
PE: As before, the simulations can be run in a preliminary way on available computers with preferred compilers (Fortran, C++), the computers being equipped with GPU units, associated with CUDA environment for achieving better memory capacities.
NE: The non-linearities invoked, if unravelled by an approropriate combination of the simulation techniques, may, to a great extent, uncover the nanoscale picture [17] of the viscoelastic matrix under testing microrheological conditions [20].
Example Three: Nanoscale Biotribological Effects in Articulating Systems
P: If two rubing, rough articulating surfaces, acted oppositely on one another upon friction conditions, relaxed by presence of a complex-fluid and multi-component interlayer, at least two questions were legitimate to pose: (i) how does the viscoelastic interlayer structurally (re)arrange upon the friction conditions? (ii) what are, if any, relevant levels of such a structuration in terms of the natural scale metrics' conditions, such as characteristic object sizes, magnitudes of the forces and values of the energies involved?
S: Supposed that the key mesoscopic unit in the friction-lubrication process in articulating joints is a multilayered amphiphilic aggregate, one might build an overall picture of its decisive role played by the micelle as a roller bearing, and, concerning the nanoscale, a channeling superstructure, capable of transmitting ions through its intra- and interspaces [9]. A reversed micelle, Refs. 4 and 8 in Gadomski et al. [8], is supposed to be a structural device responsible for the transmission. It is comprised of amphiphilic molecules each of which consists of one hydrophilic/polar head and two hydrophobic legs. The heads are always exposed toward water basins, whereas the micellar core also represents a channel for small ions, such as hydrogen ions, expressing their flickering motions, a structural cooperative effect of relevance in facilitated lubrication of the cartilage.
L: The limits imposed on the above picture concern first comprehensive experimental evidences confirming it in full—the picture should be taken fairly hypothetical as yet [8]. However, at the micelles' formation mesoscopic level, the Avrami-Kolmogorov/A-K (though dispersive) phase-change kinetic scenario can first be drawn: the near-surface amphiphiles, assembled there as multilayer phases are to be converted to reversed miceles. The dispersive kinetics assumes that a tribomicellization kernel K(t) would be, in the most simplistic terms, dependent inverse-powerly upon time [9], K(t)∝ t−ν (ν, a tribomicellization characteristic exponent), which provides other r-wChs coming from an association between the viscosity-expressing K(t) term, and its corresponding diffusional counterpart, such as <r2H+ (t) > (average <…> taken over nano-channel space), which is the MSD of the most energetic small ions in the articulating system, i.e., the hydrogen (H+) ones [8]. This way the nanoscale effects due to H−bonds breakages, and creations of cascades of H+ ions, able to penetrate the inter-micellar and intra-micellar subspaces, enter inevitably. But another question arises: what about other ions that are as usual at system's disposal [9]? Could one count on changing the complex-fluid viscosity picture based on either ions? If yes, to which extent?
M-VS: A partial solution could be to examine, in terms of an MD type simulation, the interacting behavior in such complex hydrodynamic, explicit-water containing, milieus, in a way comparative to multiparticle-collision dynamics (M-CD) in low Re-number environments [21]. A realization with star polymers [19], being to some extent reminiscent of micelles' interactions, can be helpful.
SC: After performing M-CD experiment, one may also look more deeply into bulk vs. structured water behavior, associated with the changes within the assumed interaction map, trying then to relate them with appearences of the H+ cascades [8], undergoing, for instance, the Grotthuss type H+ conduction mechanism [9], to be transformed to suitable r-wChs of the friction system in nanoscale confinements [10].
PE: So-envisioned hybrid type, thus M-CD technique, working in liaison with some BD (generalized Langevin), and assisted, due to the A-K schematics, by a kinetic, t−scale including MC technique, is proposed to shed more light here.
NE: A highlight of such computer experiment at the nanoscale would be to link sensitively the Grotthuss type H+ conduction mechanism [9] with subtle structural changes within the micellar assemblages. The latter are directly transferable to poor or good ability to sustain even harsh friction conditions, also the ones under shear [19]. Both of them are associated with some conversion of the electromagnetic complex-fluid energy [17] when the system is subjected to a type of electrostrictive factor, capable of virually imposing quite drastic changes on it.
Summary and Perspective
The unquestionable complexity of the three soft-matter systems addressed purposely here can be successfully tackled with adequate hybrid models [3]; [19], consisting of clear analytical and numerical attempts first, followed then by comprehensive simulation methods, merging suitably MC, MD, BD, etc. Such statement is true if the methods are applied to thoroughly performed experiments [13, 15, 17, 20].
The most reliable perspective on further biomatter-aggregation, microrheological and biotribological, and similar [16] soft-matter studies, can be established on high-level professional dialog of representatives of the three types of investigators: theoreticians, computer simulators and experimenters, working in parallel interrelation toward some dedicated (sub)problems of utmost importance. The underlying Opinion aims at uniting them in their common effort.
Conflict of Interest Statement
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Support by BS39/14 is acknowledged by Adam Gadomski. Discussions with Roland G. Winkler (FZ Jülich) are appreciated.
References
1. Hamacher K. Grand challenges in computational physics. Front. Physics (2013) 1:4. doi: 10.3389/fphy.2013.00004
2. Klingenberg CF. Grand challenges in computational physics. Front. Physics (2013) 1:2. doi: 10.3389/fphy.2013.00002
3. Sedgewick R, Wayne K. Introduction to Programming in Java: An Interdisciplinary Approach. Boston, MA: Pearson. Addison Wesley (2008).
4. Gadomski A. Kinetic-thermodynamic effects accompanying model protein-like aggregation: the wave-like limit and beyond it. Phys A (2007) 373:43–57. doi: 10.1016/j.physa.2006.04.119
5. Siodmiak J. Protein crystal's shape and polymorphism prediction within the limits resulting from the exploration of the Miyazawa-Jernigan matrix. Biosystems (2008) 94:233–41. doi: 10.1016/j.biosystems.2008.05.032
6. Gadomski A, Siodmiak J, Santamarìa-Holek I. On the origin of the phase–space diffusion limit in (dis)ordered protein aggregation. Phys A (2013a) 392:3155–67. doi: 10.1016/j.physa.2013.03.031
7. Kruszewska N, Gadomski A. Revealing sol-gel type main effects by exploring a molecular cluster behavior in model in-plane amphiphilic aggregations. Phys A (2010) 389:3053–68. doi: 10.1016/j.physa.2010.04.012
8. Gadomski A, Pawlak Z, Oloyede A. Directed ion transport as virtual cause of some facilitated friction-lubrication mechanism prevailing in articular cartilage. Tribol Lett. (2008) 30:83–90. doi: 10.1007/s11249-008-9311-8
9. Gadomski A, Beldowski P, Rubì JM, Urbaniak W, Augé II WK, Santamarìa-Holek I, et al. Some conceptual thoughts toward nanoscale oriented friction in a model of articular cartilage. Math Biosci. (2013b) 244:188–200. doi: 10.1016/j.mbs.2013.05.004
10. Malgaretti P, Pagonabarraga I, Rubì JM. Entropic transport in confined media: a challenge for computational studies in biological and soft-matter systems. Front. Physics (2013) 1:21. doi: 10.3389/fphy.2013.00021
11. Hermann HJ. Geometrical cluster growth models and kinetic gelation. Phys Rep. (1986) 136:153–227. doi: 10.1016/0370-1573(86)90047-5
12. Luczka J, Niemiec M, Rudnicki R. Kinetics of growth process controlled by convective fluctuations. Phys Rev E (2002) 65:051401. doi: 10.1103/PhysRevE.65.051401
13. Chernov A. Crystals built of biological macromolecules. Phys Rep. (1997) 288:61–75. doi: 10.1016/S0370-1573(97)00021-5
14. Dill KA, Banu Ozkan S, Scott Shell M, Weikl TR. The protein folding problem. Annu Rev Biophys. (2008) 37:289–316. doi: 10.1146/annurev.biophys.37.092707.153558
15. Galkin O, Vekilov P. Control of protein crystal nucleation around the metastable liquid–liquid phase boundary. Proc Natl Acad Sci USA (2000) 97:6277–81. doi: 10.1073/pnas.110000497
16. Gitterman M, Kessler DA. Mass dependence of instabilities of an oscillator with multiplicative and additive noise. Phys Rev E (2013) 87:022137. doi: 10.1103/PhysRevE.87.022137
18. Winkler RG. Deformation of semiflexible chains. J Chem Phys. (2003) 118:2919. doi: 10.1063/1.1537247
19. Ripoll M, Winkler RG, Gompper G. Star polymers in shear flow. Phys Rev Lett. (2006) 96:188302. doi: 10.1103/PhysRevLett.96.188302
20. Sarmiento-Gomez E, Santamarìa-Holek I, Castillo R. Mean-square displacement of particles in slightly interconnected polymer networks. J Phys Chem B (2014) 118:1146–58. doi: 10.1021/jp4105344
Keywords: soft-matter, computation, aggregation, microrheology, biotribology, amphiphile, viscoelasticity
Citation: Gadomski A (2014) Three types of computational soft-matter problems revisited, an own-selection-based opinion. Front. Physics 2:36. doi: 10.3389/fphy.2014.00036
Received: 04 April 2014; Accepted: 21 May 2014;
Published online: 10 June 2014.
Edited by:
Miguel Rubi, Uniersitat de Barcelona, SpainReviewed by:
Ivan Santamaria Holek, Universidad Nacional Autónoma de México, MexicoAgustin Perez Madrid, Univeritat de Barcelona, Spain
Copyright © 2014 Gadomski. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence:YWdhZEB1dHAuZWR1LnBs
 Adam Gadomski
Adam Gadomski